Abstract
This paper examines temporal symmetry breaking and structural duality in a class of time-changed McKean–Vlasov neutral stochastic differential equations. The system features super-linear drift coefficients satisfying a one-sided local Lipschitz condition and incorporates a fundamental duality: one drift component evolves under a random time change , while the other progresses in regular time t. Within the symmetric framework of mean-field interacting particle systems, where particles exhibit permutation invariance, we establish strong convergence of the tamed Euler–Maruyama method over finite time intervals. By replacing the one-sided local condition with a globally symmetric Lipschitz assumption, we derive an explicit convergence rate for the numerical scheme. Two numerical examples validate the theoretical results.
1. Introduction
This work concerns the following time-changed MV-NSDE of Itô form:
Here, the coefficients G, f, h and g satisfy specific regularity conditions (detailed in Assumption 1), while denotes the distribution of X at time t. The process is a standard Brownian motion, and is defined as the inverse of a subordinator. The composition , termed a time-changed Brownian motion, models subdiffusive behavior (see [1,2]). Formal mathematical definitions are provided in Section 2.
Recently, time-changed semimartingales and their extensions have become prominent tools in modeling anomalous diffusion phenomena across disciplines such as cell biology, finance, hydrology, and physics (cf. Umarov et al.’s recent monograph [2]). Seminal contributions by Kobayashi [3] introduced stochastic integration theory for these processes, deriving a time-changed Itô formula applicable to the first hitting time of a -stable subordinator (). This breakthrough catalyzed investigations into SDEs driven by Lévy noise or time-changed Brownian motion, for example, ref. [4,5] for harnack inequalities; ref. [6,7] for the numerical approximation scheme; and ref. [8,9] for averaging principles.
Given the general absence of explicit solutions for such SDEs, numerical methods become crucial when modeling real-world phenomena with uncertainty. To our knowledge, ref. [10] presents the first study on finite-time strong convergence of direct discretization schemes for time-changed SDEs. Therein, the authors employed the duality principle from [3] to develop the Euler–Maruyama (EM) method. Subsequent work by Deng [11] and Liu [12] extended this approach to semi-implicit and truncated EM methods respectively, addressing equations with superlinearly growing coefficients while establishing strong convergence and convergence rates. These four contributions fundamentally rely on the duality principle introduced by Kobayashi [3], which links the time-changed SDE (2)
with the classical SDE (3)
in the following manner: if solves (3), then solves (2), while if solves (2), then solves (3), where D is the original subordinator.
Crucially, the duality principle fails when both drifts f and h are present simultaneously. This occurs because the corresponding non-time-changed SDE (2) would contain a D-driven term, rendering Y dependent on E and invalidating the duality principle for (3). Alternatively, ref. [13] examines the EM approximate for time-changed SDE (4):
and ref. [14] proposed an EM scheme for time-changed MV-SDEs (5):
Compared to [13] and [14], this work establishes, to the best of our knowledge, the first strong convergence results and convergence rates for the tamed EM method applied to the time-changed MV-NSDE (1), under significantly weaker assumptions on the drift coefficient. Specifically, we require only a one-sided local Lipschitz condition and allow for super-linear growth, thereby lifting the constraints on the coefficients prevalent in existing literature. This extension significantly broadens the applicability of the tamed EM scheme to model complex systems involving mean-field interactions and stochastic time change, such as the migration dynamics of cell populations or animal groups, where individual interactions (mean-field effects) and environmentally driven random time-scale transformations (e.g., induced by seasonal shifts or abrupt environmental changes) can be naturally captured by the time-changed MV-NSDE (1).
This paper makes two primary contributions:
- We establish strong convergence of the tamed EM method over finite time horizons, obtaining a -order convergence rate with respect to step size. Integration with propagation of chaos yields an overall convergence rate for the scheme.
- For the drift coefficient h, we employ a one-sided local Lipschitz condition (versus the one-sided Lipschitz condition in [14]) and super-linear growth condition (replacing the linear growth condition in [14]).
The rest of the paper is organized as follows. In Section 2, we introduce some necessary preliminaries for the Wasserstein metric and the time-changed MV-NSDEs. In Section 3, chaos propagation and strong convergence have been proven under one-sided local Lipschitz conditions. In Section 4, by replacing the one-sided local Lipschitz condition with a global condition, we further derive an explicit convergence rate for the numerical scheme. In Section 5, two numerical examples validate the theoretical results.
2. Preliminaries
We fix notation used throughout this work. For , denote the Euclidean norm by and inner product by . The transpose of any vector or matrix A is , while for matrices, the trace norm is . Define , and . For , set and .
In the paper, C denotes a generic positive constant, whose value may change for different usage. Similarly, denotes the generic positive constant depending on parameter p. If it is necessary, the dependence of constants on parameters will be indicated.
2.1. Empirical Measure and Wasserstein Metric
Let denote all probability measures on , where is the Borel -algebra over . For any , a measure belongs to if it possesses a finite p-th moment, i.e.,
For , the Wasserstein distance between and v is defined by
where is the denotes the collection of all couplings between and . For a random variable X, denote the law of X. In particular, if and , then
where represents the joint distribution of random variable . As is a metric, for , we always have (see [15])
Given a random process , assuming N independent and identically distributed (i.i.d.) samples , , …, are observed at time s, and the corresponding empirical measure is defined as
where is the Dirac measure concentrated at sample point . Empirical measurement approximates the true probability distribution of the random variable by weighted average of sample points (see [16]). Hence, the Wasserstein distance between empirical measures and satisfies
Unlike standard SDEs, time-changed MV-NSDEs require approximating at each time step. When in (1) is known a priori, these equations reduce to classical time-changed SDEs with time-dependent coefficients. Since this is typically not feasible, we approximate (1) via an N-dimensional stochastic interacting particle system.
Let and consider N particles satisfying
with the independent identical initial value , where are independent Brownian motion and means the empirical distribution corresponding to , , …, , that is
where is the Dirac measure at point .
Propagation of chaos governs the convergence behavior as . We further investigate the stochastic non-interacting particle systems
with initial value , where . Since are independent for all , we have for all i.
Since are identically distributed, from (9), we obtain
From this fact (see [17], Theorem 5.8), there exists a constant such that
2.2. Time-Changed Brownian Motion
Consider a complete probability space endowed with a filtration satisfying the standard hypotheses: right continuity and inclusion of all -null sets in . Separately, let be a subordinator (a non-decreasing Lévy process with right-continuous paths and left limits) initialized at zero. This process resides on another complete probability space equipped with filtration that also fulfills the standard hypotheses. Define and as the expectation operators corresponding to probability measures and , respectively.
A subordinator process is termed a β-stable subordinator when strictly increasing, denoted , with Laplace transform characterization:
Given an adapted -stable subordinator , its generalized inverse process
represents the first hitting time. This time change is continuous and non-decreasing, yet non-Markovian (see [1,18]).
Consider a standard Brownian motion independent of . The filtration is constructed as
where indicates the -algebra generated by . Consequently, the time-changed process forms a square integrable martingale relative to with .
The product probability space is defined by
Denoting by the expectation under , we have the identity
Direct simulation of (10) is generally infeasible, necessitating numerical schemes like the tamed Euler–Maruyama method. Fixing a uniform step size , we approximate over (for arbitrary ) following [19,20] (see Figure 1). This entails simulating a subordinator path with independent stationary increments: Initialize and compute iteratively
where are i.i.d. with . The sequence is generated via [21] (Chapter 6), terminating when for some integer M.
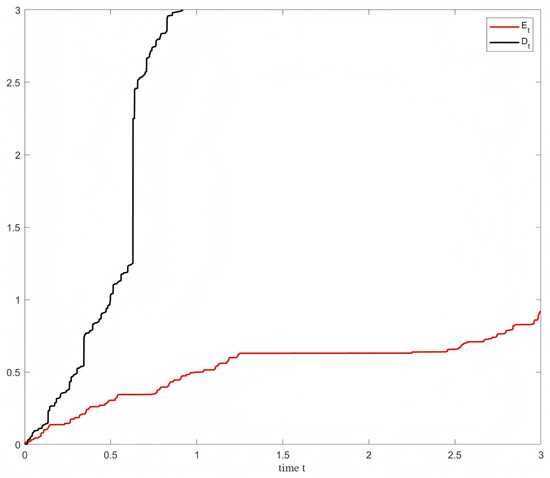
Figure 1.
Sample paths for and associated inverse subordinator .
Next, the approximate to is generated by
It is clear that for , when
The next Lemma 1 will be used as the approximation error of to , whose proof can be found in [10,20].
Lemma 1.
Almost surely,
holds for all .
Now, for , let
and let
Then it is easy to see that for any
Define . It can be easily observed that for any
We adapt the approach in [13,22] for discrete and continuous-time approximations. Exploiting the independence of B and E, we discretize B at grid points . Define a discrete-time process by setting and
where
It can be easily observed that
and define the continuous-time process via continuous interpolation: when ,
Using (20), we reformulate the latter expression as
where .
2.3. Assumption
Assumption 1.
In order to derive the main results, we require that the coefficients G, f, h and g satisfy the following assumptions. Regarding convergence, we propose the following hypotheses.
Hypothesis 1.
Let be Borel-measurable functions and . There exists positive constant and such that for all , and
Regarding well-posedness, we propose the following hypothesis
Hypothesis 2.
Let be Borel-measurable functions and . For any , there exists a constant such that
Hypothesis 3.
Let be Borel-measurable and continuous functions. For any , a positive constant a and all , there exists a positive constant such that for any , and
Hypothesis 4.
Let be Borel-measurable and continuous functions. There exists positive constant such that for any , and
Hypothesis 5.
There exists constant such that for any , and
Hypothesis 6.
There exists constant and such that for any , and
Hypothesis 7.
There exists constant such that for any , and
Hypothesis 8.
If is a right continuous with left limit and -adapted process, then
where denotes the class of left continuous with right limit.
Under Assumption 1, we establish the well-posedness of (1).
Lemma 2.
Let Assumption 1 hold. Then, the time-changed neutral stochastic differential Equation (1) has a unique strong solution which is a continuous -semimartingale.
Proof.
The proof of existence and uniqueness is almost similar to [3,11,23,24], so it is omitted here. □
3. Strong Convergence
In this section, we will study the numerical solution of (1) based on the previous section. Firstly, we have constructed the N-dimensional interacting particle system (10), and we prove that the N-dimensional interacting particle system (10) converges to the non-interacting particle system (11). Then, we use the tamed EM method (21) to approximate the N-dimensional interacting particle system (10). Strong convergence has been proven. When the local one-sided Lipschitz condition is replaced by the global one-sided Lipschitz condition, the convergence order is obtained.
3.1. A New Time-Changed Gronwall’s Inequality
This section aims to develop the mean square convergence rate of (21) in any finite time . To this end, the following lemma connects different types of time-changed integrals.
Lemma 3.
([3]) Let be a β-stable subordinator with inverse . If is -measurable and are -measurable integrable functions, then for any ,
Now, we establish a novel Gronwall inequality essential for our analysis.
Proposition 1.
Let be a subordinator with infinite Lévy measure and its inverse is . Consider -adapted functions that are integrable with respect to s and . If is monotonic and non-decreasing, then the following inequality
implies
Proof.
Let
Since f, b and are positive and k is non-decreasing, the function defined in (32) is non-decreasing. Moreover, from (30) and (31),
which implies that
Applying the connections among different kinds of time-changed integrals (see the Lemma 3) yields
For , is defined as
yielding the fundamental properties:
From the retarded Gronwall-like inequality (see Proposition 1 in [25]), we get
For any , we easily know that there is such that provided E is strictly increasing in a certain neighborhood of s. Since is non-decreasing, applying (33) and the connections among different kinds of time-changed integrals (see Lemma 3), we can get
If E is a constant in a certain neighborhood of s, then . Since is non-decreasing, by (32), we can get
Then, for any , we have by the connections among different kinds of time-changed integrals (see the Lemma 5.1)
The proof is complete. □
3.2. Interacting Particle Systems
Denote
By Chebyshev’s inequality,
Lemma 4.
(The weighted Young inequality) For any , there exists a constant such that
Proposition 2.
Proof.
For , by using the time-changed Itô’s formula to yields
For every integer , define the stopping time . We will estimate , , , , and one by one. For , by using (23) and Lemma 4 with , we obtain that for any
For , applying (23) and (22) and the Fubini theorem, we have
For , applying (23) and (27), the Young inequality and Fubini theorem, we can get
For , applying (23) and (29), the Young inequality and Fubini theorem, we can get
For , applying (23) and (29), the Young inequality and Fubini theorem, we get
For , applying (23) and (29), the Young inequality, Fubini theorem and Burkhold-Davis-Gundy’s inequality, we have
From (23) and Lemma 4, we get
From , we have
Taking on both sides, by Proposition 1, we get
According to the Borel–Cantelli lemma, we see that for almost all , there exists an integer such that if , . By the arbitrariness of t, we obtain , a.s. By choosing and letting on both sides (36), applying Fatou’s lemma, we obtain that
For , by using the Lyapunov inequality, we can obtain that for any ,
In summary, for any , there exist a positive constant which is independent of n, such that
The proof establishing uniform boundedness of follows analogously to that for , and is therefore omitted. This completes the proof. □
The next Theorem shows the propagation of chaos.
Theorem 1.
Suppose that Assumption 1 holds. Let be the solution to (10) and be the solution to (11) with , for any p. Then, for any ,
If we further assume that h satisfies one-side global Lipschitz condition, then there exists a positive constant C such that
with C may be dependent on , but independent of N and R.
Proof.
For every fixed , define . By using the time-changed Itô’s formula to , we obtain that for any ,
Note, for any ,
For , we obtain that for any ,
By using (14) and (26), the elementary inequality and the Fubini theorem, we have
By using (24) and the Fubini theorem, we get
By using (28), the elementary inequality, the Cauchy-Schwarz inequality and the Fubini theorem, we have
For , By using (14), (25), (26) and the Fubini theorem, we get
For , By using (46), the Burkholder–Davis–Gundy inequality and the Fubini theorem, we have
Hence, by using (45), (46) and (47), we obtain
From (23) and the weighted Young inequality, we have
Taking on both sides, by Proposition 1 and (34), we get
Note that . Choosing . Let and , we have
Moreover, if is independent of R, in other words, h satisfies one-side global Lipschitz condition. From (49), we have
where may be dependent on , but independent of N and R. The proof is complete. □
3.3. Tamed Euler–Maruyama Method
Proposition 3.
Suppose that Assumption 1 holds and is the solution to (21) with . Then, for some positive constant C independent of N and δ,
Proof.
For every fixed i, applying Itô formula again yields that
We will estimate , , , and one by one. For , from (23), we have
In the present work, we employ the technical approach outlined in Theorem 4.1 of reference [22]:
For , from (29) and the Fubini theorem, we have
Hence, we have
From Lemma 4, we get
From Proposition 1, take on both side of (53), we get
where may be dependent on , but independent of N and .
Hence, we obtain that for any ,
The proof is complete. □
Proposition 4.
Suppose that Assumption 1 holds and is the solution to (21) with . Then, for any , there exists a constant , which is not depend on N and δ, such that for any ,
and
Proof.
For any , applying the Burkhold–Davis–Gundy inequality and the Hölder inequality, we can get
When , it follows from Proposition 3 that
From the weighted Young inequality, we get
Hence, for , there exists a constant , which is independent of N and , such that
Furthermore, we employ the technical approach outlined in Theorem 4.1 of reference [22]:
For , applying Lyapunov’s inequality, (55) and (56) follow. When and (58) holds, it follows from (59) that
The proof is complete. □
Proposition 5.
Suppose that Assumption 1 holds and is the solution to (21) with . Then, there exists a constant such that for any ,
where constant C is independent of N and δ.
Proof.
As we have proved before, (62) holds for and (55), (57) holds for ; if we set , by (51) and Hölder’s inequality, we obtain
For , from (29) and the Fubini theorem, we have
For , from (23), (29), Burkhold-Davis-Gundy’s inequality, Hölder’s inequality and the Fubini theorem, we get
Hence, we have
From the weighted Young inequality, we get
From Proposition 1, take on both sides of (53), and we have
where may be dependent on , but independent of N and .
Hence, we obtain that for any
4. Mean Square Convergence Rate
Assumption 2.
Hypothesis 3′
Let be Borel-measurable and continuous functions. For any , a positive constant a and all , there exists a positive constant such that for all , and ,
Hypothesis 3″
Let be Borel-measurable and continuous functions. There exists positive constant K and such that for all , and ,
and
As we have proved before, for any , there exists a constant such that
Denote
By Chebyshev’s inequality,
Proposition 6.
Proof.
For every fixed , define . By using Itô’s formula to , we have
Note, for any ,
For , by using (22) and (74), the elementary inequality and the Fubini theorem, we have
For , we get
Similarly, we here use the technique of Theorem 4.1 in [22]:
By using (22) and the Fubini theorem, we get
Hence, we obtain
For , by using (46), the Burkholder–Davis–Gundy inequality and the Fubini theorem, we have
Hence, by using (75), (79), (81) and (82), we obtain
From Lemma 4, we get
Taking on both sides, by Proposition 1 and (70), we have
Note that . Choosing . Let and , we get
Similarly, we have
Thus, it follows that
where may be dependent on , but independent of , N and R. The proof is complete. □
5. Example
In this section, we construct three numerical experiments to validate the convergence rate established in preceding theoretical analyses. First, by fixing the particle count at N = 1000 and N = 20,000, we ensure the avoidance of ‘‘particle corruption’’ phenomena (as discussed in [24]). Subsequently, we rigorously demonstrate the strong convergence of the tamed EM method for time-changed MV-NSDEs. Finally, a systematic comparison is conducted between the tamed EM scheme and the classical EM method (see [14]) in the context of time-changed MV-SDEs, highlighting the tamed EM scheme performance characteristics. Throughout this section, we focus on the case that is an inverse -stable subordinator.
Example 1.
Our analysis begins with scalar time-changed MV-NSDEs:
It is straightforward to verify compliance of and h with Assumption 1 holding for (88) with . For numerical implementation methodologies regarding the inverse subordinator E and time-changed Brownian motion , we direct readers to [10,22,26]. As demonstrated in Figure 2, under the condition that B is a standard Brownian motion independent of the inverse subordinator E, the jump discontinuities of exhibit a one-to-one correspondence with those of . Furthermore, whenever remains constant over a subinterval, simultaneously maintains a constant trajectory.
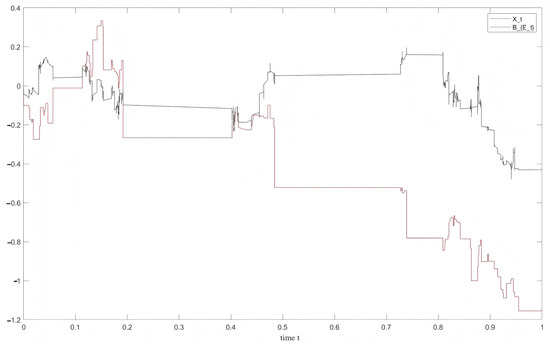
Figure 2.
Sample paths of and .
Then, for numerical validation, we perform simulations with particle counts N = 10,000 and N = 20,000, employing a time step . Figure 3 and Figure 4 confirm the absence of ‘‘particle corruption’’ phenomena (as discussed in [24]) throughout the entire path simulation, indicating that all particle trajectories exhibit stable and well-regularized behavior.
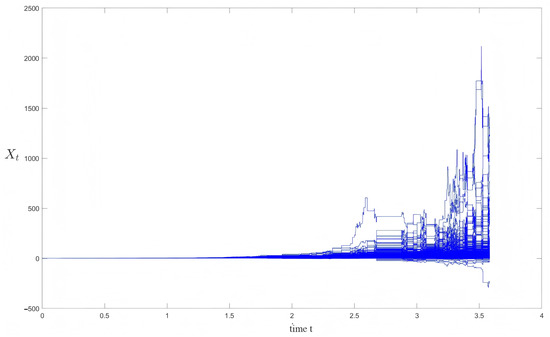
Figure 3.
Realizations of 10,000 particle paths.
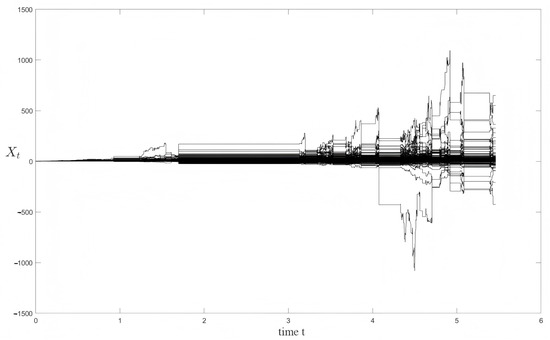
Figure 4.
Realizations of 20,000 particle paths.
In order to detect the mean square convergence rate of the tamed EM method, the unavailable exact solution is identified with a numerical approximation generated by (21) with a fine step size . The other numerical approximations are calculated by (21) and applied to (88) with five different step sizes . For the given step size , time horizon , number of particles , the strong error is calculated by
In Figure 5, the red line is the reference line with the slope of . We can see that the slopes of the two curves appear to match well. A simple regression shows that the slope of the line for the tamed EM method is 0.4963, identifying Theorem 2 numerically.
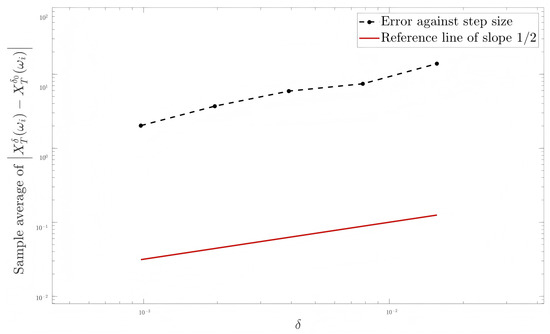
Figure 5.
Convergence order simulations for (88) with .
Example 2.
We focus on the following time-changed MV-NSDEs:
It is easy to verify that the Assumptions 1 hold for (88). Select , other settings are the same as in Example 1.
In Figure 6, Figure 7 and Figure 8, we can see that the slopes of the two curves appear to match well. A simple regression shows that the slope of the line for the tamed EM method are 0.2871, 0.3106, and 0.3967 (see Table 1), respectively, which numerically confirms Theorem 2.
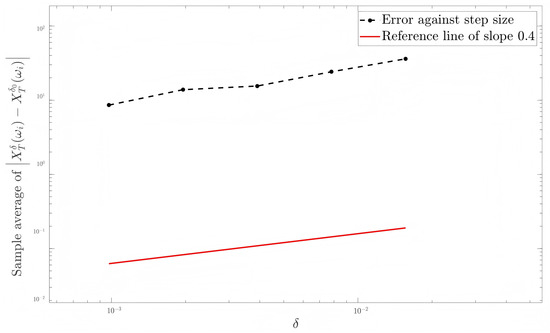
Figure 6.
Convergence order simulations for (90) with and .
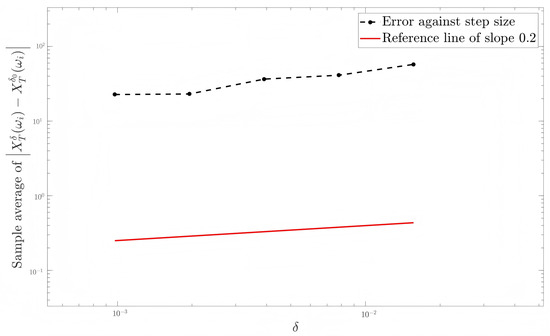
Figure 7.
Convergence order simulations for (90) with and .
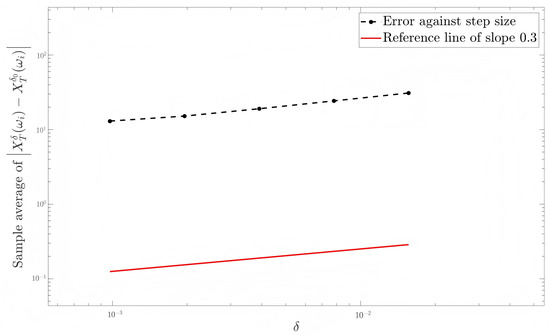
Figure 8.
Convergence order simulations for (90) with and .

Table 1.
Convergence results under different parameter combinations.
Example 3.
Consider the following time-changed MV-NSDEs.
In a very recent work [14], the authors studied the EM method for a class of time-changed MV-SDEs with linear drift and diffusion coefficients.
Step size and five different step sizes are used to generate the unavailable exact solution and the other numerical approximations via (21) and (92), respectively. Figure 9 shows that when , the tamed EM method is also applicable to the time-changed MV-SDEs in [14], and the convergence rate and accuracy are better.
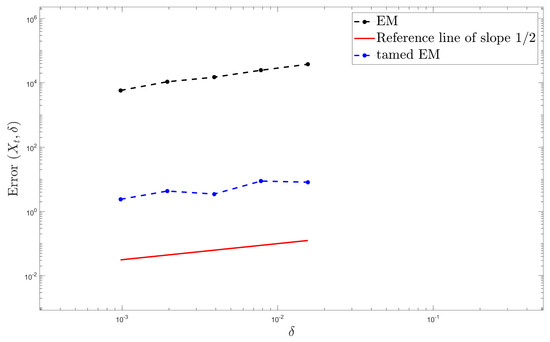
Figure 9.
Convergence order simulations for (91).
6. Conclusions
This paper establishes convergence results for time-changed MV-NSDEs driven by two drift terms and one diffusion term, analyzed through interacting particle systems. Our main results show that the investigated method converges strongly in the mean square sense with order . These theoretical results are finally validated by two numerical experiments. Concerning that strong convergence rates for numerical approximations are particularly important to design efficient multilevel Monte Carlo approximation methods [27], there are two interesting ideas for our future work. One of them is to add the time variable t to the coefficient in (1), and the other is to develop numerical methods with higher-order convergence rates [28].
Author Contributions
Methodology, J.Z.; Validation, L.X.; Formal analysis, Z.L.; Writing—original draft, J.Z.; Writing—review and editing, L.X.; Supervision, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the National Natural Science Foundation of China (No.11901058) Natural Science Foundation of Hubei Province (No. 2021CFB543).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meerschaert, M.; Scheffler, H. Limit theorems for continuous-time random walks with infinite mean waiting times. J. Appl. Probab. 2004, 41, 623–638. [Google Scholar] [CrossRef]
- Umarov, S.; Hahn, M.; Kobayashi, K. Beyond the Triangle: Brownian Motion, Itô Calculus, and Fokker-Planck Equation—Fractional Generalizations; World Scientific: Singapore, 2018. [Google Scholar]
- Kobayashi, K. Stochastic calculus for a time-changed semimartingale and the associated stochastic differential equations. J. Theor. Probab. 2011, 24, 789–820. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Y.; Yan, L. Harnack inequalities for functional SDEs driven by subordinate fractional Brownian motion. J. Math. Inequal. 2022, 16, 1429–1453. [Google Scholar] [CrossRef]
- Li, Z.; Yan, L.; Xu, L. Harnack inequalities for functional SDEs driven by subordinate multifractional Brownian motion. Math. Inequal. Appl. 2021, 24, 1149–1166. [Google Scholar] [CrossRef]
- Guo, Q.; Mao, X.; Yue, R. The truncated Euler-Maruyama method for stochastic differential delay equations. Numer. Algorithms 2018, 78, 599–624. [Google Scholar] [CrossRef]
- Ji, Y.; Yuan, C. Tamed EM scheme of neutral stochastic differential delay equations. J. Comput. Appl. Math. 2017, 326, 337–357. [Google Scholar] [CrossRef]
- Khas, M.; Rafail, Z. The averaging principle for stochastic differential equations. Probl. Peredachi Inf. 1968, 4, 86–87. [Google Scholar]
- Shen, G.; Xu, W.; Wu, J. An averaging principle for stochastic differential delay equations driven by time-changed Lévy noise. Acta Math. Sci. 2022, 42, 540–550. [Google Scholar] [CrossRef]
- Jum, E.; Kobayashi, K. A strong and weak approximation scheme for stochastic differential equations driven by a time-changed Brownian motion. Probab. Math. Stat. 2016, 36, 201–220. [Google Scholar]
- Deng, C.; Liu, W. Semi-implicit Euler-Maruyama method for non-linear time-changed stochastic differential equations. BIT Numer. Math. 2020, 60, 1133–1151. [Google Scholar] [CrossRef]
- Liu, W.; Mao, X.; Tang, J.; Wu, Y. Truncated Euler-Maruyama method for classical and time-changed non-autonomous stochastic differential equations. Appl. Numer. Math. 2020, 153, 66–81. [Google Scholar] [CrossRef]
- Jin, S.; Kobayashi, K. Strong approximation of stochastic differential equations driven by a time-changed Brownian motion with time-space-dependent coefficients. J. Math. Anal. Appl. 2019, 476, 619–636. [Google Scholar] [CrossRef]
- Wen, X.; Li, Z.; Xu, L. Strong approximation of non-autonomous time-changed McKean-Vlasov stochastic differential equations. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107122. [Google Scholar] [CrossRef]
- Graham, C.; Kurtz, T.; Mélxexard, S.; Protter, P.; Pulvirenti, M.; Talay, D. Asymptotic behaviour of some interacting particle systems; McKean-Vlasov and Boltzmann models. In Probabilistic Models for Nonlinear Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 1996; pp. 42–95. [Google Scholar]
- Carmona, R. Lectures on BSDEs, Stochastic Control, and Stochastic Differential Games with Financial Applications; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Carmona, R.; Delarue, F. Probabilistic Theory of Mean Field Games: Vol. I, Mean Field FBSDEs, Control, and Games; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Meerschaert, M.; Scheffler, H. Triangular array limits for continuous time random walks. Stoch. Process. Their Appl. 2008, 118, 1606–1633. [Google Scholar] [CrossRef]
- Magdziarz, M. Langevin picture of subdiffusion with infinitely divisible waiting times. J. Stat. Phys. 2009, 135, 763–772. [Google Scholar] [CrossRef]
- Magdziarz, M. Stochastic representation of subdiffusion processes with time-dependent drift. Stoch. Process. Their Appl. 2009, 119, 3238–3252. [Google Scholar] [CrossRef]
- Tankov, P. Financial Modelling with Jump Processes; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Jin, S.; Kobayashi, K. Strong approximation of time-changed stochastic differential equations involving drifts with random and non-random integrators. BIT Numer. Math. 2021, 61, 829–857. [Google Scholar] [CrossRef]
- Li, Z.; Xu, L.; Yan, L. McKean-Vlasov stochastic differential equations driven by the time-changed Brownian motion. J. Math. Anal. Appl. 2023, 527, 107122. [Google Scholar] [CrossRef]
- Reis, G.; Engelhardt, S.; Smith, G. Simulation of McKean-Vlasov SDEs with super-linear growth. IMA J. Numer. Anal. 2022, 42, 874–922. [Google Scholar] [CrossRef]
- Lipovan, O. A retarded Gronwall-like inequality and its applications. J. Math. Anal. Appl. 2000, 252, 389–401. [Google Scholar] [CrossRef]
- Higham, D. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Giles, M. Improved Multilevel Monte Carlo Convergence Using the Milstein Scheme; Springer: Berlin/Heidelberg, Germany, 2006; pp. 343–358. [Google Scholar]
- Yang, X.; Shen, Y. Runge-Kutta method for solving uncertain differential equations. J. Uncertain. Anal. Appl. 2015, 3, 1–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).