Abstract
In this work, the symmetries of a H2+ molecule confined within potential energy wells of various shapes are highlighted. This system has been long regarded as a model for small molecules trapped in crystalline cavities and molecular cages; in this context, the role of symmetry assumes significant importance. Symmetries are determined by the well shape, molecular position, and orientation. They allow the classification of H2+ states, the identification of fixed nodal surfaces for the identification of excited states in Monte Carlo simulations, and the estimation of potential energy surfaces.
1. Introduction
Symmetry plays a fundamental role in the determination of quantum eigenstates of a chemical system, particularly when such systems are in a chemical environment that itself exhibit significant symmetry [1,2]. A paradigmatic case in chemical theory is provided by crystal field theory, which is employed to derive the atomic orbitals of perturbed transition metal ions. In the presence of an octahedral symmetry, this leads to the well-established Tanabe–Sugano diagrams [3]. Another significant application of symmetry is observed in the formulation of correlation diagrams for molecular orbitals [4].
The present work aims to highlight the application of symmetry principles in a comparatively less explored field of theoretical chemistry that has, nonetheless, attracted sustained interest. Specifically, it addresses the quantum states of one-electron systems confined within potential wells defined primarily by geometric considerations. These models serve as simplified analogues of more complex scenarios encountered in chemistry and materials science (see [5] and references therein).
Over the years, various one-electron systems have been the focus of theoretical investigations, most notably the hydrogen atom and the molecular ion H2+. The heteronuclear ion HeH2+, despite its marginal stability, has also been studied as a minimal model for heteronuclear diatomic systems [6,7]. In contrast, systems that are effectively one-electron in nature—such as alkali metal atoms—have received comparatively little attention, despite their potential chemical relevance, particularly when confined.
The concept of a confined quantum system was formulated 90 years ago; initially, the primary motivation for investigating such systems was the understanding of the high-pressure effect, in fields such as astrophysics and geophysics [8,9]. Given this context, it was natural to adopt the simplest geometries dictated by the coordinate systems of the particles involved—spherical wells for atoms and ellipsoidal wells for diatomic molecules [10,11,12,13]. Even in this case symmetry plays a critical role, particularly in the determination of excited states [14].
Over the past fifteen years, a growing body of literature has emerged concerning the confinement of quantum systems within cavities of various geometries, including polyhedral and cylindrical shapes (see next section). This development reflects a change in the possible applications of confinement models—from their original role in high-pressure physics to their use in interpreting the modified physical and chemical behaviour of species embedded in crystalline lattices or within molecular cages [15].
These systems hold high potential for technological applications. Notably, they may contribute to the understanding of hydrogen storage mechanisms in solid matrices or clathrate compounds [16,17]. In this respect, the quantum states of H2 confined within various water cages in clathrate hydrate structures, as well as within several fullerene cages, have been computed [18,19,20]. The confinement and symmetry of H2 molecules in clathrate hydrate cages strongly influence their quantum dynamics and spectroscopic behaviour. Computational studies [21,22] showed that cage occupancy and symmetry affect the Raman spectra through shifts and splittings related to intermolecular interactions and spatial constraints. Ranieri et al. [23] confirmed that in sII clathrates, H2 in large cages retains significant rotational freedom, with quantum delocalization shaped by the cage geometry. In quantum computing and optoelectronics, confined H2+ is a model system for a molecular qubit in solid [24], provides an analogous for a F2+ centre in crystals [25], and quantum dots by replacing the electron mass with the effective electron mass in the involved material like GaAs, while the unmoving nuclei take the role of donor impurities [26,27]. In the field of chemistry, confined H2+ is a reaction intermediate of electrochemical reactions involving molecular hydrogen on Pt electrodes [28,29].
The focus on one-electron systems in much of this literature is largely attributable to the desire to reduce computational complexity. However, the study of such systems holds intrinsic theoretical value. The analysis of a single-electron wavefunction—essentially a single orbital—from the point of view of symmetry provides insights that are readily accessible to chemical intuition. Moreover, geometric confinement, while often introduced as an idealized construct, serves a valuable conceptual function in understanding analogous real-world phenomena.
2. H-Confinement in Polyhedral and Cylindrical Wells
Ab-initio results that correlate the shape of a three-dimensional potential well with the energy eigenstates of a confined atom or molecule are quite rare, whether for hydrogen species like H or H2+.
One of the earliest studies on the cubic, octahedral and icosahedral confinement of the hydrogen species was conducted by two of the present authors [30,31,32].
In his works, Pupyshev [33,34] examines the consequence of symmetry breaking—specifically, the lifting of degeneracy in the energy levels of one-electron atoms, as they transition from a free system to confinement within a polyhedral (cubic and octahedral) and tetrahedral cavity.
In [35], the common features of hydrogen atoms confined within boxes of arbitrary geometry are investigated and a theoretical framework that predicts the ground-state energy of a compressed hydrogen atom as a function of the system’s geometric parameters is developed, providing a unified picture of how the structure of a confining box influences the hydrogen ground state.
A cylindrical potential well serves as a natural analogue for the confinement environment created by nanotubes. However, it can also be employed as a model for cylindrical quantum dots, wherein confined hydrogenic species can represent quantum dots containing one or more donor impurities. This geometry is generally representative of nanoscopic systems relevant to fields such as optoelectronics, hydrogen storage, and quantum computing. It is therefore unsurprising that the confinement of simple atomic or molecular species within cylindrical potential wells has been the subject of prior quantum mechanical investigations. Yurenev [36] underlines how the relatively low symmetry in the problem of electronic states of the hydrogen atom confined within an impenetrable cylindrical cavity precludes a comprehensive analytical treatment of the energy spectrum and its variation with changes in the cylinder’s geometry. In earlier work by two of the present authors, this geometry was explored due to its conceptual similarity to plasma generation systems—ionized gases which typically exhibit cylindrical symmetry [37].
3. Numerical Method
A highly versatile computational technique for addressing problems of this nature has been detailed in previous studies [38,39]. This approach, the diffusion Monte Carlo (DMC), is based on the formal analogy between the Schrödinger equation and a classical reaction-diffusion problem. The latter is effectively solved using a Monte Carlo method that simulates a large ensemble of interacting Brownian trajectories in a three-dimensional space.
The evolution of the stochastic process is governed by an imaginary time parameter. This variable is purely numerical in nature, as the underlying equation is time-independent. The method represents a variant of the DMC technique. The specific implementation employed by the authors incorporates time averaging and uses a modified form of the short-time diffusion–reaction Green’s function. These adaptations enhance computational efficiency and facilitate flexible modification of the Schrödinger equation’s boundary conditions, thus allowing for the treatment of arbitrary geometries within Cartesian coordinates. The short time propagator is given by the following:
Here, N is the number of quantum particles in the system, and is a numerical step. The diffusion term (first exponential in Equation (1)) is implemented by simulating the corresponding stochastic process through an ensamble of mathematical points (walkers) in a set Ri in the 3N-configuration space. These walkers move randomly by small time steps based on the short-time diffusion propagator. In addition, according to the second exponential term of equation 1, the walkers can disappear in regions of high potential energy, while they can replicate in regions of low potential energy. The estimated energy ET, the so-called energy offset, regulates the total population of the walkers. This parameter is dynamically adjusted through a relaxation method until the walker population reaches a stationary distribution.
where is a small positive parameter, and , , , and are the energy values and number of walkers at time step i and i − 1. In particular, is computed by a mobile time average over multiple time steps preceding i, in order to enhance the stability and accuracy of the calculation of ET.
For each configuration, the method provides the solution corresponding to the ground energy state under the specified boundary conditions, with a very limited number of numerical parameters to be optimized (typically: energy offset , time step , number of walkers ). To further reduce the number of numerical parameters, we set
In this work, the DMC method is implemented in its unbiased form, without the use of geometry-dependent trial functions (importance sampling). This way one gets straightforward adaptation to different confinement geometries. Furthermore, in this approach, the propagator in Equation (1) is replaced by a step-function distribution with an equivalent variance, which remains equivalent in the diffusion regime while enhancing computational efficiency [40].
Although DMC is primarily a ground-state method, it can be extended to access excited states with specific symmetries through the fixed-node approximation. This technique introduces a nodal surface—typically a plane—on which the wave function is constrained to be exactly zero. The presence of this nodal boundary restricts the walkers' diffusion to a single nodal region where the wave function maintains positive, effectively forcing convergence to an excited state solution. In order to constrain the wavefunctions to vanish at the nodal surface, the walkers that come into contact with it are removed from the simulation.
In some cases, appropriate nodal surfaces can be systematically determined based on molecular symmetry. This ensures compatibility between the nodal structure, the symmetry of the molecule in a given configuration, and the boundary conditions—thereby aligning with the site symmetry of the system. Thus, symmetry plays a critical role in performing the calculations.
The calculations presented in this work are performed within the Born–Oppenheimer approximation, where the nuclei of the molecules are treated as classical point-like sources of Coulomb potentials. The H2+ Hamiltonian, in atomic units, can be expressed as follows:
In this expression, ra and rb are the position vectors of the two nuclei, and d is the internuclear distance.
A complete description of the methodology, briefly summarized here, can be found in [40], while the practical application of the method will be discussed in the subsequent sections.
All calculations are performed with the open source fortran code DMC_basic, developed by some of the present authors and available online (see Data Availability).
4. Symmetry of H2+ in Different Positions of a Cubic Cavity
In this section, we examine the site symmetries of specific states of the H2+ ion confined within a cubic cavity. The methodological framework and the criteria for selecting nodal surfaces are equivalent to the case of an octahedral cavity, owing to the geometric duality between these two polyhedra.
The group Oh is relatively large, comprising 48 symmetry operations. Among these are nine symmetry planes: three horizontal (σh) and six dihedral (σd). These planes can be employed to select nodal planes in DMC calculations, thereby enabling the selection of excited states. The number of selectable excited states is not strictly bounded by the number of symmetry planes, as multiple planes can simultaneously serve as nodal surfaces: for example, a plane containing the molecular axis permits the detection of a pair of degenerate Πu states, while a plane perpendicular to the molecular axis can isolate a Σu state. These planes can also be used in combination, as in the detection of a Πg.
The number of available symmetry planes for computational use depend on the actual symmetry of the combined system—i.e., the cavity and the confined molecule. These symmetries are formally described by subgroups of the full Oh group, each of which has an order that divides 48. However, not all these subgroups are physically realizable through symmetry breaking induced by a diatomic molecule. For instance, it is impossible to preserve the full cubic symmetry upon introducing a diatomic species, even when it is placed at the geometric centre of the cavity—a condition that would maintain the full symmetry in the case of a single hydrogen atom.
Moreover, some of the subgroups can be realized through specific placements of the nuclei that break the original symmetry of the cavity. In certain configurations, this symmetry breaking allows for a continuum of symmetry-reduced systems. In Figure 1, a representative subset of such configurations is illustrated, using colour coding to denote the corresponding symmetry groups.
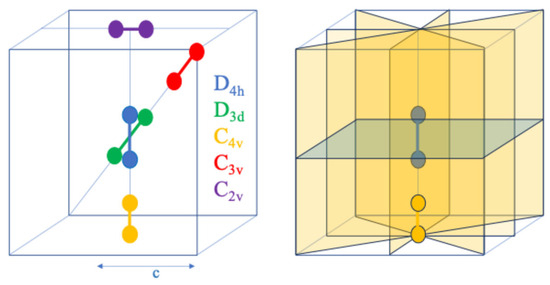
Figure 1.
Left: Representative subset of confined molecular configurations, with colour coding indicating the associated symmetry groups. The depicted point groups include D4h, D3d, C4v, C3v, and C2v. Right: Selected symmetry planes accessible to a molecule confined within a cubic potential well. c is the half-edge length of the cube and defines the confinement dimension, that is the geometric parameter characteristic of the specific shape considered, which is varied to increase or decrease the volume of the confinement box.
In each of the configurations presented, the molecule occupies a specific site within the structure, and the symmetry of that site—which, in this context, defines the overall system symmetry—must be compatible with both the intrinsic symmetry of the molecule and that of the surrounding cavity. Figure 2 illustrates the symmetry planes that remain as nodal planes when a H2+ molecule is positioned at one of three equivalent D4h sites, as well as at one of the infinitely many possible D3d sites. It is also feasible to reduce the system symmetry to chiral groups such as C1, and to the less trivial C2 and Ci groups, which, although not suitable for DMC calculations, nonetheless possess intrinsic theoretical interest.
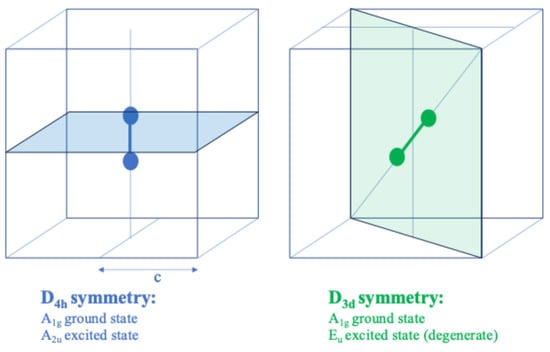
Figure 2.
Symmetry planes acting as nodal planes for a H2+ molecule confined at representative sites. Shown are the planes preserved when the molecule is placed at one of the three equivalent D4h sites (left), and at one of the infinitely many D3 sites (right). c is the half-edge length of the cube and defines the confinement dimension.
As an illustration, in this study we examine a selection of molecular sites that effectively demonstrate the impact of symmetry reduction induced by the presence of a molecule and its role in the computational procedures. A clarification is necessary: our objective is to explore these systems as examples of symmetry realization, where an initially high-symmetry configuration is broken by the introduction of a diatomic molecule. The nuclear positions of the molecule are not assumed to correspond to points of stable mechanical equilibrium. Attempting to impose such a condition would severely limit the variety of high-symmetry systems available for investigation. The cubic cavity, in this context, serves as an abstract model representing confinement under a specific symmetry and should not be interpreted literally.
To be explicit, when we present potential energy surfaces (PESs) in geometries of reduced dimensionality, we do not imply mechanical stability in directions orthogonal to the one considered. The purpose of our calculations is to highlight the influence of symmetry through simplification and analogy, rather than to capture the full physical detail of any specific system. It should be emphasized that the systems studied do not necessarily correspond to diatomic molecules in crystalline cavities; they may also represent quantum dots with embedded donor impurities. In the latter case, the potential energy function reflects the system’s total energy landscape, but it is not to be interpreted as a true force-generating potential, since the donor atoms are fixed within the lattice and do not participate in free mechanical motion.
Although each of these curves originates from exact quantum mechanical calculations, many of their features can be semi-quantitatively interpreted through the concept of a nodal plane. This plane, derived from the symmetry properties of the electronic state, may either be employed in the computation itself or used within the geometric framework of the potential well construction. In the latter case, the interpretation is less rigorous, as the confining surface of the potential well has finite spatial extension.
Referring to Figure 3, we observe the relationship between the ground state (A1g symmetry) and the excited state (A2u symmetry). c is the half-edge length of the cube and defines the confinement dimension, that is the geometric parameter characteristic of the shape under consideration and is within the same range as those considered in other studies. The ground state exhibits a potential energy minimum even at extended well dimensions, whereas the excited state does not, as it is purely repulsive. Nonetheless, both states display a steep rise in potential energy with increasing interatomic distance d, which arises from the confining effects of the potential well.
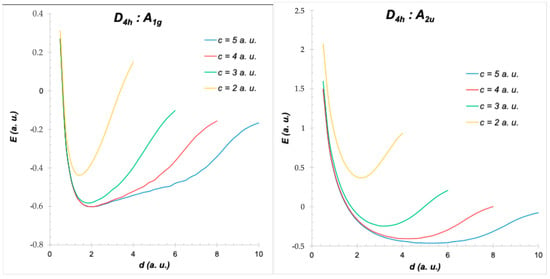
Figure 3.
PESs of H2+ in D4h symmetry: ground state (left) and excited state (right). d is the internuclear distance, and c is the confinement dimension (half-hedge length of the cube).
Based on the symmetry characteristics of these states, the transition from A1g to A2u is optically allowed. Unlike the unconfined scenario—where such a transition might lead to ion dissociation—this confined system exhibits a bound-to-bound transition, preserving the integrity of the ion.
Similar considerations apply to the case of reduced symmetry D3d in Figure 4.
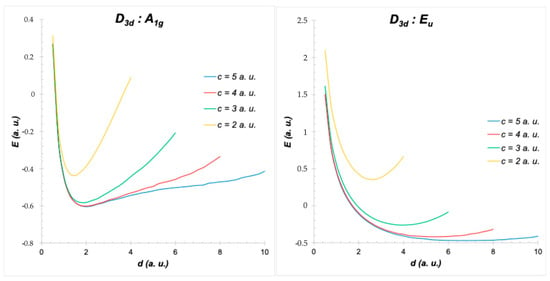
Figure 4.
PESs of H2+ in D3d symmetry: ground state (left) and excited state (right). d is the internuclear distance, and c is the confinement dimension (half-edge length of the cube).
For instance, examining Figure 3 left, and the curve corresponding to the largest confinement dimension (), it is evident that following the repulsive region and the potential minimum, two distinct energy-increasing trends emerge. The first is molecular in nature, while the second begins around 7 atomic units and results from the proximity of the nuclei to the boundaries of the confining well—boundaries which effectively act as additional nodal planes. Owing to the large confinement, it becomes apparent that the first trend asymptotically approaches the energy of the atomic 2S state. The second trend, however, increases sharply toward the continuum. Although it does not fully reach the energy corresponding to the 2P state—due to Coulomb interactions—it approaches it closely.
In the case of the A2u state, the corresponding asymptotic atomic limit is also the 2P state. However, the nodal plane introduced in the calculation remains distant from the relevant well surface. For a 2Π state, the asymptotic limit is the 2D state (as illustrated in Figure 5). In contrast, for the A1g state exhibiting D3d symmetry, the associated atomic limit is the 2F state, attributable to the presence of three planar faces converging at a single cube vertex. Table 1 shows some low-lying molecular states are related asymptotic atomic states, which results for several well shapes and system symmetries, including much more cases than those illustrated in this paper.
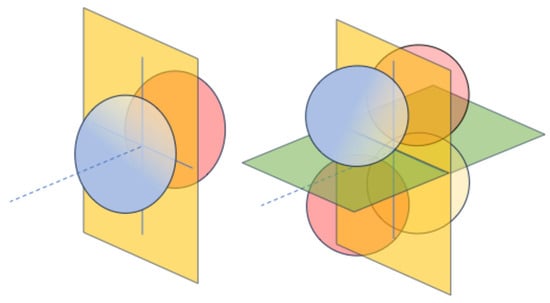
Figure 5.
Limit atomic orbitals correlated with molecular states for nuclei positioned at polyhedral surfaces. Left: P state correlating with a Σ state. Right: D state correlating with a Π state. The orange plane indicates the polyhedral face; the green plane represents an additional face, forming a dihedral angle, or a nodal plane added to select the molecular state.

Table 1.
Selected symmetries and asymptotic atomic states (for large wells) of centre-symmetric configurations. Only S, P, D, and F atomic states are reported. The symbol “~“ means that the state has components with higher orbital momentum.
The one presented here is not only a theoretical concept that can provide important information on the best choice of orbitals for ab initio calculations: it is accessible, in principle, to experiments in solids: bound e-donor states with the prescribed symmetry should appear in quantum dots when the donor is placed at its boundary. However, this requires a level of control over the donor impurity’s placement that is currently not accessible.
A further general observation is that all computed potential energy curves exhibit a minimum, indicating the presence of infrared and Raman-active vibrational modes. These vibrational modes are also subject to symmetry-based classification. Additionally, confinement can induce vibrational activities which are not present in the case of the free ion, as they correspond to motions with translational or rotational character that become active under confinement.
5. Cylindrical Confined H2+
The symmetry group of the cylindrical potential well is D∞h, a continuous group characterized by an infinite number of vertical mirror planes containing the principal axis of rotation. When a diatomic molecule is confined along this principal axis, the system retains this continuous symmetry, which enables the classification of an infinite series of excited states with increasing orbital angular momentum, such as Π, Δ, and so on. Conversely, when the molecule is displaced from the axis, the system symmetry is reduced to one of the finite subgroups of D∞h, typically belonging to the C or D point groups. These lower-symmetry configurations allow for the identification of a finite set of excited states, following principles analogous to those previously discussed for confinement in cubic geometries. Several of these configurations are illustrated in Figure 6, which also indicates the symmetry planes that can be used in the computational analysis. We consider a “standard” cylinder of radius c (that represent the confinement dimension) and height .
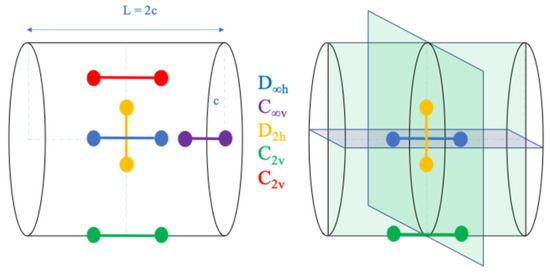
Figure 6.
Left: Representative subset of confined molecular configurations, with colour coding indicating the associated symmetry groups. The depicted point groups include D∞h, C∞v, D2h, and C2v. Right: Selected symmetry planes accessible to a molecule confined within a cylindrical potential well. c is the cylinder radius and represents the confinement dimension, that is the geometric parameter characteristic of the specific shape considered, which is varied to increase or decrease the volume of the confinement box.
In Figure 7, the molecular configurations (D∞h, D2h, and C2v) and the nodal planes selected for the confined H2+ within the cylinder are depicted.
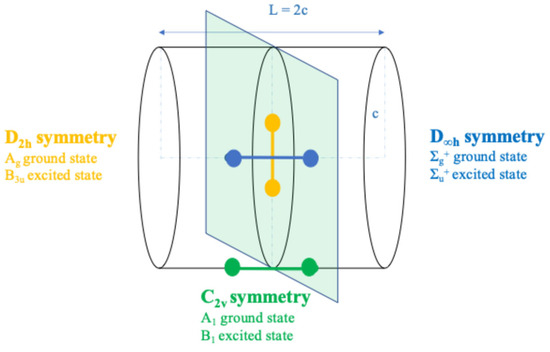
Figure 7.
Symmetry plane acting as nodal plane for a H2+ molecule in three different configurations (D∞h, D2h, and C2v) and confined in a finite cylinder. c is the cylinder radius and represents the confinement dimension.
A distinctive feature of this type of potential well is that it shares the same symmetry as the H2+ molecule, thereby permitting the molecule to adopt a position and orientation such that the overall system preserves molecular symmetry. In this configuration, it becomes possible to select excited states of Σ, Π, Δ type. The potential curves corresponding to the ground and the excited states are reported in Figure 8, Figure 9 and Figure 10 for D∞h, D2h, and C2v configurations, respectively. It is worth noting that although the symmetry is conserved, the confined molecule exhibits different physical behaviour compared to the free molecule—often with more complex and intriguing characteristics. For instance, vibrational modes may appear under confinement that are absent in the free case, as they would otherwise be classified as mere translational or rotational motions. Moreover, confinement within a narrow cylindrical potential well enables the investigation of anisotropic pressure effects.
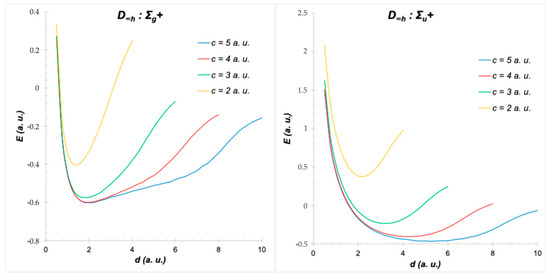
Figure 8.
PESs of H2+ in D∞h symmetry: ground state (left) and excited state (right). d is the internuclear distance, and c is the confinement dimension (cylinder radius).
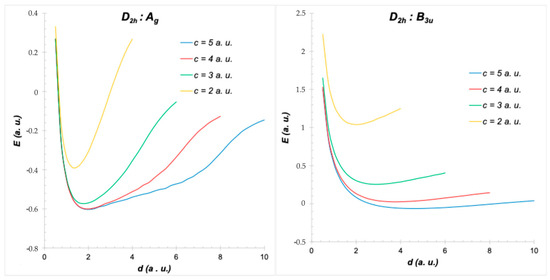
Figure 9.
PESs of H2+ in D2h symmetry: ground state (left) and excited state (right). d is the internuclear distance, and c is the confinement dimension (cylinder radius).
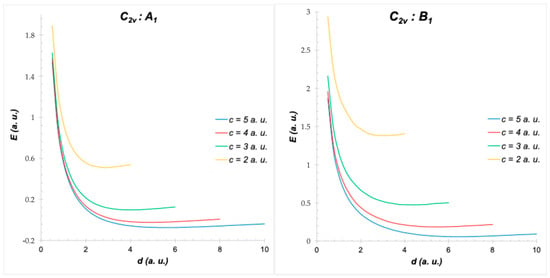
Figure 10.
PESs of H2+ in C2v symmetry: ground state (left) and excited state (right). d is the internuclear distance, and c is the confinement dimension (cylinder radius).
6. Conclusions
The confinement of hydrogen-containing species within cavities of various geometries has been a topic of interest in theoretical chemistry for several decades. While such confinement models cannot be interpreted literally—since potential wells cannot have perfectly smooth walls, even spherical ones, at the atomic scale—their study has proven to yield significant insights into realistic chemical systems that share comparable geometric characteristics with the model systems.
In the present work, the authors aim to demonstrate that such systems also offer a unique framework for the exploration of molecular symmetry groups, including advanced concepts such as group–subgroup relationships and site symmetry. Beyond their foundational role in identifying the geometries and symmetries of molecular orbitals—regardless of the computational methodology employed—symmetry considerations are shown to be critical for the a priori identification of nodal planes. These planes are essential in implementing the fixed-node quantum Monte Carlo method.
Through the study of these theoretical confinement systems, group theory plays a new role into contemporary chemical research, particularly within a geometric context like that of crystallography, where it remains both relevant and naturally suited to the analysis of fundamental chemical systems.
Author Contributions
Conceptualization, G.M.L., G.B. and S.L.; Software, G.M.L. and S.L.; Formal analysis, G.M.L., G.B. and S.L.; Investigation, G.M.L., G.B. and S.L.; Resources, S.L.; Data curation, G.M.L. and S.L.; Writing—original draft, G.M.L., G.B. and S.L.; Writing—review & editing, G.M.L., G.B. and S.L.; Visualization, G.M.L., G.B. and S.L.; Supervision, S.L.; Funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PNRR MUR project PE0000023-NQSTI (National Quantum Science and Technology Institute) and PRIN2022 MUR project P20224C3NJ Brave New Worlds.
Data Availability Statement
All simulations are performed with a standard fortran DMC code. The program employed by the authors, DMC_basic, is open source: it is available by contacting the authors, or on GitHub: https://github.com/SavinoLongoPhD/DMC_basic/ (accessed on 7 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dmitriev, I.S. Symmetry in the World of Molecules; Mir Publishers: Moscow, Russia, 1979. [Google Scholar]
- King, R.B. Atomic orbitals, symmetry, and coordination polyhedra. Coord. Chem. Rev. 2000, 197, 141–168. [Google Scholar] [CrossRef]
- Sugano, S.; Tanabe, Y.; Kamimura, H. Multiplets of Transition Metal Ions in Crystals; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Harris, D.C.; Bertolucci, M.D. Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy; Courier Corporation: North Chelmsford, MA, USA, 1989. [Google Scholar]
- Sen, K.D.; Sen, K.D. (Eds.) Electronic Structure of Quantum Confined Atoms and Molecules; Springer: Cham, Switzerland, 2014; Volume 10, pp. 978–983. [Google Scholar]
- Ley-Koo, E.; Cruz, S.A. The hydrogen atom and the H2+ and HeH++ molecular ions inside prolate spheroidal boxes. J. Chem. Phys. 1981, 74, 4603–4610. [Google Scholar] [CrossRef]
- Olivares-Pilón, H.; Cruz, S.A. The H, H2+, and HeH2+ systems confined by an impenetrable spheroidal cavity: Revisited study via the Lagrange-mesh approach. Int. J. Quantum Chem. 2017, 117, e25399. [Google Scholar] [CrossRef]
- Michels, A.; De Boer, J.; Bijl, A. Remarks concerning molecural interaction and their influence on the polarisability. Physica 1937, 4, 981–994. [Google Scholar] [CrossRef]
- De Groot, S.R.; Ten Seldam, C.A. On the energy levels of a model of the compressed hydrogen atom. Physica 1946, 12, 669–682. [Google Scholar] [CrossRef]
- Laughlin, C.; Burrows, B.L.; Cohen, M. A hydrogen-like atomconfined within an impenetrable spherical box. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 701. [Google Scholar] [CrossRef]
- Mateos-Cortés, S.; Ley-Koo, E.; Cruz, S.A. Hydrogen molecular ion inside penetrable prolate spheroidal boxes: Electronic and vibrational properties. Int. J. Quantum Chem. 2002, 86, 376–389. [Google Scholar] [CrossRef]
- Aquino, N.; Campoy, G.; Montgomery, H.E., Jr. Highly accurate solutions for the confined hydrogen atom. Int. J. Quantum Chem. 2007, 107, 1548–1558. [Google Scholar] [CrossRef]
- Colín-Rodríguez, R.; Díaz-García, C.; Cruz, S.A. The hydrogen molecule and the H2+ molecular ion inside padded prolate spheroidal cavities with arbitrary nuclear positions. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 241001. [Google Scholar] [CrossRef]
- Micca Longo, G.; Longo, S.; Giordano, D. Quantum states of confined hydrogen plasma species: Monte Carlo calculations. Plasma Sources Sci. Technol. 2015, 24, 065019. [Google Scholar] [CrossRef]
- Sveshnikov, K.A.; Tolokonnikov, A.V. H2+ in a lattice of cavities: Ammonia-like splitting of the lowest level. Mosc. Univ. Phys. Bull. 2015, 70, 181–189. [Google Scholar] [CrossRef]
- Strobel, T.A.; Kim, Y.; Andrews, G.S.; Ferrell Iii, J.R.; Koh, C.A.; Herring, A.M.; Sloan, E.D. Chemical–clathrate hybrid hydrogen storage: Storage in both guest and host. J. Am. Chem. Soc. 2008, 130, 14975–14977. [Google Scholar] [CrossRef] [PubMed]
- Chattaraj, P.K.; Bandaru, S.; Mondal, S. Hydrogen storage in clathrate hydrates. J. Phys. Chem. A 2011, 115, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Bačić, Z. Perspective: Accurate treatment of the quantum dynamics of light molecules inside fullerene cages: Translation-rotation states, spectroscopy, and symmetry breaking. J. Chem. Phys. 2018, 149, 100901. [Google Scholar] [CrossRef]
- Powers, A.; Scribano, Y.; Lauvergnat, D.; Mebe, E.; Benoit, D.M.; Bačić, Z. The effect of the condensed-phase environment on the vibrational frequency shift of a hydrogen molecule inside clathrate hydrates. J. Chem. Phys. 2018, 148, 144304. [Google Scholar] [CrossRef]
- Lauvergnat, D.; Felker, P.; Scribano, Y.; Benoit, D.M.; Bačić, Z. H2, HD, and D2 in the small cage of structure II clathrate hydrate: Vibrational frequency shifts from fully coupled quantum six-dimensional calculations of the vibration-translation-rotation eigenstates. J. Chem. Phys. 2019, 150, 154303. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Ripmeester, J.A. Raman spectroscopy and cage occupancy of hydrogen clathrate hydrate from first-principle calculations. J. Am. Chem. Soc. 2009, 131, 14132–14133. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Ripmeester, J.A.; Becker, U. Molecular-dynamics and first-principles calculations of raman spectra and molecular and electronic structure of hydrogen clusters in hydrogen clathrate hydrate. J. Phys. Chem. C 2010, 114, 21042–21050. [Google Scholar] [CrossRef]
- Ranieri, U.; Del Rosso, L.; Bove, L.E.; Celli, M.; Colognesi, D.; Gaal, R.; Hansen, T.C.; Koza, M.M.; Ulivi, L. Large-cage occupation and quantum dynamics of hydrogen molecules in sII clathrate hydrates. J. Chem. Phys. 2024, 160, 164706. [Google Scholar] [CrossRef]
- Kang, S.; Liu, Y.M.; Shi, T.Y. The characteristics for H2+-like impurities confined by spherical quantum dots. Eur. Phys. J. B 2008, 63, 37–42. [Google Scholar] [CrossRef]
- Henderson, B.; Imbusch, G.F. Optical Spectroscopy of Inorganic Solids; Oxford University Press: Oxford, UK, 2006; Volume 44. [Google Scholar]
- Al, E.B.; Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sökmen, I. Photoionization cross section of a complex in quantum dots: The role of donor atoms configuration. Eur. Phys. J. Plus 2022, 137, 919. [Google Scholar] [CrossRef]
- Wang, D.H.; Tang, T.T.; An, Z.K.; Chu, B.H.; Zhao, G. Quantum Rényi entropy of hydrogenic impurity states in the GaAsxP1-x semiconductor quantum dot. Micro Nanostruct. 2025, 204, 208167. [Google Scholar] [CrossRef]
- Juodkazis, K.; Juodkazytė, J.; Grigucevičienė, A.; Juodkazis, S. Hydrogen species within the metals: Role of molecular hydrogen ion H2+. Appl. Surf. Sci. 2011, 258, 743–747. [Google Scholar] [CrossRef]
- Juodkazytė, J.; Šebeka, B.; Juodkazis, S. Reversible hydrogen evolution and oxidation on Pt electrode mediated by molecular ion. Appl. Surf. Sci. 2014, 290, 13–17. [Google Scholar] [CrossRef]
- Micca Longo, G.; Longo, S.; Giordano, D. Confined H(1s) and H(2p) under different geometries. Phys. Scr. 2015, 90, 085402. [Google Scholar] [CrossRef]
- Longo, S.; Micca Longo, G.; Giordano, D. Monte Carlo calculation of the potential energy surface for octahedral confined H2+. Rend. Lincei. Sci. Fis. E Nat. 2018, 29, 173–177. [Google Scholar] [CrossRef]
- Longo, S.; Lonigro, D.; Lerario, G.; Stripoli, C.; Micca Longo, G. Quantum states of H2+ and H2 in an icosahedral potential well. Eur. Phys. J. D 2023, 77, 29. [Google Scholar] [CrossRef]
- Pupyshev, V.I. Electronic states of hydrogen atom in tetrahedral and similar polyhedral cavities. Int. J. Quantum Chem. 2011, 111, 2510–2518. [Google Scholar] [CrossRef]
- Pupyshev, V.I.; Scherbinin, A.V. Symmetry reduction and energy levels splitting of the one-electron atom in an impenetrable cavity. In Electronic Structure of Quantum Confined Atoms and Molecules; Springer: Cham, Switzerland, 2014; pp. 31–58. [Google Scholar]
- Van Gorder, R.A. Compressed hydrogen atoms confined within generic boxes. Proc. R. Soc. A 2022, 478, 20220467. [Google Scholar] [CrossRef]
- Yurenev, P.V.; Scherbinin, A.V.; Pupyshev, V.I. Energy levels of the hydrogen atom in a cylindrical cavity. Int. J. Quantum Chem. 2006, 106, 2201–2207. [Google Scholar] [CrossRef]
- Micca Longo, G.; Longo, S. Quantum states and static field ionization of a cylindrical confined hydrogen atom: A diffusion Monte Carlo study. Int. J. Quantum Chem. 2024, 124, e27392. [Google Scholar] [CrossRef]
- Foulkes, W.M.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33. [Google Scholar] [CrossRef]
- Annarelli, A.; Alfè, D.; Zen, A. A brief introduction to the diffusion Monte Carlo method and the fixed-node approximation. J. Chem. Phys. 2024, 161, 241501. [Google Scholar] [CrossRef] [PubMed]
- Micca Longo, G.; Coppola, C.M.; Giordano, D.; Longo, S. The unbiased diffusion Monte Carlo: A versatile tool for two-electron systems confined in different geometries. Eur. Phys. J. D 2021, 75, 83. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).