A Novel Bondage Parameter for Network Analysis

Abstract

In this study, we explore the paired disjunctive domination number—a recently introduced parameter by Henning et al.—within the broader framework of graph and network sensitivity and vulnerability analysis. Building on this concept, we introduce and investigate the paired disjunctive bondage number (PDBN), which measures the minimum number of edge deletions required to increase the paired disjunctive domination number of a graph or its corresponding network model. We begin by computing this new bondage number for several well-known network classes. The focus then shifts to specific families of trees, where we first determine their paired disjunctive domination numbers in detail. Using these values, we calculate the corresponding bondage numbers for various structurally symmetric, hierarchical, and compound tree structures, including double star, comet, double comet, $E_p^t$, and binomial trees, all of which model different types of infrastructural networks. Finally, we present an algorithm for computing PDBN, accompanied by a complexity analysis, and illustrate the practical relevance of the parameter through a case study applying it to a real-life network problem. Our results offer foundational insights into the behavior of this new domination parameter and its bondage variant, contributing to the growing literature on graph vulnerability and suggesting potential applications in the design of resilient and failure-aware networks.

1. Introduction

Graph theory is one of the fundamental branches of mathematics frequently utilized for problem-solving and modeling in fields such as computer science, network analysis, biology, social sciences, and many other fields. It offers a wide range of opportunities for both theoretical exploration and practical applications, making it well-suited for multidisciplinary studies. Graph theory provides a powerful framework for modeling and analyzing relationships and structures, especially in infrastructural networks [1,2,3].

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple, finite, and undirected graph, where $V\left(G\right)$ represents the set of vertices (often referred to simply as V), and $E\left(G\right)$ denotes the set of edges (or E for short). An edge e is written as $\{u,v\}\in E\left(G\right)$, where u and v are the vertices it connects. The open neighborhood of a vertex v is defined as $N\left(v\right)=\{u\in V$:$\{u,v\}\in E\}$, while its closed neighborhood is given by $N\left[v\right]=$ $\left\{v\right\}$∪$N\left(v\right)$. The degree of a vertex is the number of neighbors of vertex $v,$ $deg\left(v\right)=\left|N\left(v\right)\right|$. A vertex with a degree of zero is called an isolated vertex, as it has no edges incident to it. A vertex with a degree of one is referred to as a pendant vertex (or leaf vertex), as it is connected to exactly one other vertex. A support vertex is a vertex that is adjacent to at least one pendant vertex, providing its sole connection in the graph. Furthermore, a strong support vertex is a vertex that is adjacent to two or more pendant vertices.

When analyzing network structures such as infrastructural networks, these graph-theoretic concepts become essential for understanding connectivity, robustness, and vulnerability. Graph theoretic techniques provide a convenient and effective framework for investigating such networks. It is well-known that an interconnection network can be represented by a graph where vertices correspond to the nodes or sites of the network, and edges represent the communication or connection links between these sites. Consequently, a wide range of network-related problems can be approached and solved using graph theoretical methods. While solving problems in graph theory, the graph is analyzed using certain graph-theoretic parameters and solution techniques by utilizing the relationships between vertices and edges.

One significant area of study in this field is domination parameters, which play a crucial role in understanding the structural and functional properties of graphs. The theory of domination has emerged as a cornerstone of graph vulnerability studies, offering a robust framework for analyzing and optimizing the structure and functionality of complex networks. Its conceptual richness and adaptability have enabled its application across a wide spectrum of disciplines, including computer science, communication and transportation networks, biological and social systems, operations research, chemistry, economics, engineering, and applied mathematics. In recent years, domination-based research has gained increasing prominence within graph theory, driven by the formulation of novel parameters and variants derived from the classical notion of domination. These advancements have not only deepened theoretical understanding but have also opened new avenues for practical implementations in network design and analysis. Domination parameters focus on identifying specific subsets of vertices, such as dominating sets, which ensure that every vertex in the graph is either part of this subset or adjacent to at least one vertex in it. The domination number of a graph is the minimum size of a dominating set and denoted by $\gamma \left(G\right).$ Domination parameters can vary depending on the problems they address, and there is a wide variety of such parameters in graph theory.

In this paper, we focus on a newly introduced domination parameter, the paired disjunctive domination number, defined by Henning et al. Additionally, Henning and Goddard previously introduced the concept of disjunctive domination in [4]. In a graph G, a set $S\subseteq V$ is called a b-disjunctive dominating set if every vertex not in S is either adjacent to a vertex in S or has at least b vertices at a distance of two from it. Specifically, for $b=2$, the set S is referred to as a disjunctive dominating set (or $2DD$-$set$). Furthermore, the concept of the paired dominating set was introduced by Haynes and Slater [5], and it refers to a dominating set in which the induced subgraph contains a perfect matching. To gain more detailed information about domination parameters, the reader is referred to the comprehensive works in the literature, such as [6,7,8,9,10].

Expanding on these ideas, in a graph G without isolated vertices, a set $S\subseteq V$ is defined as a paired disjunctive dominating set ($PDD$-$set$) if S is a disjunctive dominating set and the subgraph induced by S, $G\left[S\right]$, contains a perfect matching. The minimum size of such a set is known as the paired disjunctive domination number, denoted by ${\gamma }_{pr}^d\left(G\right).$ Additionally, we will adapt the bondage number concept, introduced by Fink [11], to the paired disjunctive parameter. The bondage number of a graph G, denoted by $b\left(G\right)$, is defined as the minimum cardinality of a subset $B\subseteq E\left(G\right)$ such that $\gamma (G-B)>\gamma \left(G\right)$. If such a subset cannot be found, the bondage number is represented using the infinity notation, ∞.

The paired disjunctive domination number, recently introduced by Henning et al., offers a novel blend of disjunctive and paired domination concepts in graph theory. Noticing the absence of studies addressing the vulnerability of this new parameter under structural perturbations, we were motivated to explore its stability characteristics. This led us to define the bondage number associated with the paired disjunctive domination parameter, which quantifies the minimum number of edges whose removal increases the parameter. Our motivation stemmed from a desire to understand the structural robustness of this newly defined domination concept and to contribute to the broader study of domination-based resilience measures. Accordingly, we determine the corresponding bondage numbers for several classes of networks. By this motivation, we introduce the paired disjunctive bondage number (PDBN) which is denoted by $b_{pr}^d\left(G\right)$ and represents the minimum cardinality among all subsets $B^{\prime }\subseteq$ $E\left(G\right)$ that satisfy ${\gamma }_{pr}^d(G-B^{\prime })>{\gamma }_{pr}^d\left(G\right)$. For detailed information about the bondage number and its related invariants, the reader is referred to [12,13,14,15,16,17,18,19,20,21].

We consider PDBN as a metric for network vulnerability. In this model, we find the critical vertices with an important position in the graph. Edges or vertices associated with a low paired disjunctive bondage number are elements that significantly influence the paired disjunctive domination structure of a graph. In particular, if the removal of certain edges or their adjacent vertices results in an increase in the paired disjunctive domination number, these components can be considered critical in terms of network control, monitoring, or security. Therefore, calculating PDBN involves analyzing the structural impact of specific edges and their connected vertices, which in turn provides valuable insight into identifying key or influential nodes in the graph. Although the paired disjunctive bondage parameter does not directly define the notion of a “critical vertex”, it offers an indirect assessment by highlighting edges—and consequently vertices—that substantially affect the paired disjunctive domination properties of the network. Since PDBN is considered to be a reasonable measure for the vulnerability of graphs, it is of particular interest to evaluate PDBN of different classes of graphs. If a complex network can be decomposed into smaller networks, then under certain conditions, the solutions of optimization problems on smaller networks can be combined to solve the corresponding problem on the larger network. Thus, calculation of PDBN for simple graph types is important.

Motivated by this, PDBN has been determined not only for special graph classes but also for certain tree structures, double star, comet, double comet, $E_p^t$, and binomial trees, which exhibit hierarchical and partially symmetric configurations. The notion of symmetry in these structural forms provides valuable insight into their vulnerability characteristics. Hence, our analysis contributes to understanding how such structural symmetry impacts vulnerability measures in graph-based models.

A double star, $D(n,m)$, is a type of graph that consists of two star graphs with n and m pendant vertices joined by an edge between their central vertices. A comet graph, $C_{n,m},$ is a graph consisting of a star graph $S_{1,m}$ (a central vertex connected to m leaves) and a path graph $P_n$ where one end vertex of $P_n$ is connected to the center of the star [22]. A double comet graph $D_{m,n_1,n_2}$ is formed by a path $P_{m-n_1-n_2}$ on $m-n_1-n_2$ vertices, where two pendant sets of vertices are attached at the ends of the path: one pendant set consisting of $n_1$ vertices attached to one end vertex, and another pendant set consisting of $n_2$ vertices attached to the other end vertex. Here, $n_1,n_2>1$ and $m\ge n_1+n_2+2$ [23]. The $E_p^t$ tree has p vertices path graph in t legs and the graph has $pt+2$ vertices and $pt+1$ edges. A binomial tree $B_k$ is a recursively defined tree structure used in computer science and graph theory. It has the following properties: $B_0$ consists of a single vertex and $B_k$ is formed by linking two $B_{k-1}$ trees, making one the child of the other [24]. For better clarity, the structures of all the graphs considered in this study are illustrated in the following figures (Figure 1).

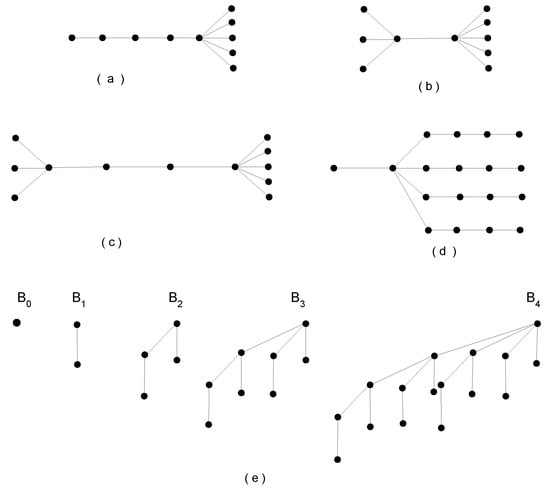
Figure 1. (a) Comet graph $C_{5,5}$, (b) double star graph, $D(3,5)$ (c) double comet graph, $D_{12,3,5}$ (d) $E_4^4$ graph, and (e) binomial trees $B_0,B_1,B_2,B_3,B_4$.

In Section 2, we reviewed some significant results in the literature related to the paired disjunctive domination number. In Section 3, we derived paired disjunctive bondage results for certain specific graph structures. In Section 4, we obtained the paired disjunctive domination and paired disjunctive bondage values for some tree structures. Section 5 is devoted to an algorithmic analysis of PDBN, including its computational complexity. Finally, in Section 6, we present a case study focusing on infrastructural networks by examining a specific segment of a metro transportation network. We apply PDBN to this transport network subsection to observe and analyze the behavior of the parameter in a practical, real-world setting.

2. Known Results

In this section, we will share some results from the existing literature that are necessary for the article.

Theorem 1

([25]). Paired disjunctive domination number of cycle, $C_n$, and path $P_n$ graphs are as follows:

• For the cycle graph with $n\ge 3,$ ${\gamma }_{pr}^d\left(C_n\right)=2⌈{\displaystyle \frac{n}{5}}⌉.$
• For the path graph with $n\ge 2,$ ${\gamma }_{pr}^d\left(P_n\right)=2⌈{\displaystyle \frac{n+1}{5}}⌉.$

Theorem 2

([25]). If T is a tree of order $n\ge 3$ with s support vertices, then

$${\gamma }_{pr}^d\left(T\right)\le {\displaystyle \frac{1}{2}}(n+2s-1)$$

and the bound is sharp.

Corollary 1

([25]). If $G\simeq$ $K_{n,m},$ $K_p,$ $p\ge 2$, where they are complete bipartite and complete graphs, respectively, then ${\gamma }_{pr}^d\left(G\right)=2$.

Remark 1.

It is obvious that the paired domination number for star and wheel graphs ${\gamma }_{pr}^d\left(S_{1,n}\right)={\gamma }_{pr}^d\left(W_{1,n}\right)=2.$

Observation 1

([26]). Let G be the connected graph. The paired disjunctive domination number of G, ${\gamma }_{pr}^d\left(G\right)$, is even.

Theorem 3

([27]). Let G and $G-e$ be connected graphs for an edge e. Then,

$${\gamma }_{pr}^d(G-e)\le {\gamma }_{pr}^d\left(G\right)+2.$$

3. Results About Some Special Networks

In this section, we obtain the paired disjunctive bondage values for special networks. Observing the values of this parameter on fundamental structures is crucial for analyzing graphs in terms of the considered parameter.

Theorem 4.

Let $P_n$ be a path graph with $n\ge 6$. Then,

$$b_{pr}^d\left(P_n\right)=\left\{\begin{array}{cc}2,& n=6\\ 1,& otherwise\end{array}\right.$$

and $b_{pr}^d\left(P_i\right)=\infty$ where $i=2,3,4,5.$

Proof. 

Let the vertex set of $P_n$ be $\{v_1,v_2,\dots ,v_n\}.$ It is obvious that $b_{pr}^d\left(P_2\right)=$ $b_{pr}^d\left(P_3\right)=b_{pr}^d\left(P_4\right)=b_{pr}^d\left(P_5\right)=\infty .$ Therefore, $n\ge 6$. Let us analyze using two cases.

Case 1: First, let us consider the $n=6$.

In this case, let $H=P_6-e$, where $e\in \{\{v_2,v_3\},\{v_3,v_4\},\{v_4,v_5\}\}$. From Theorem 1, we have ${\gamma }_{pr}^d\left(H\right)=4$ $=2{\gamma }_{pr}^d\left(P_2\right)$. Thus, $b_{pr}^d\left(P_6\right)$ $\ge 2$. If $H^{\prime }=P_6$ $- \{\{v_2,v_3\},\{v_4,v_5\}\}$, then ${\gamma }_{pr}^d\left(H^{\prime }\right)=3{\gamma }_{pr}^d\left(P_2\right)$ = 6 $=2$ + ${\gamma }_{pr}^d\left(P_6\right)$. Therefore, $b_{pr}^d\left(P_6\right)$ $\le 2$. From the lower and upper bounds, we conclude that $b_{pr}^d\left(P_6\right)=2$ for $n=6$.

Case 2: Now, let us analyze the case where $n\ne 6$. Let $H=P_n-\left\{\{v_5,v_6\}\right\}$. In this case, H contains two sub-path graphs, $P_5$ and $P_{n-5}$. Let $n\equiv i(mod5),$ $n^{\prime }=n-5=5k+i$. Thus,

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d\left(H\right)& =& {\gamma }_{pr}^d\left(P_5\right)+{\gamma }_{pr}^d\left(P_{n^{\prime }}\right)\hfill \\ & =& 4+2⌈{\displaystyle \frac{n^{\prime }+1}{5}}⌉\hfill \\ & =& 2+2⌈{\displaystyle \frac{n+1}{5}}⌉\hfill \end{array}$$

from [25], we have ${\gamma }_{pr}^d\left(H\right)=2+{\gamma }_{pr}^d\left(P_n\right).$ Therefore, we have $b_{pr}^d\left(P_n\right)=1forn\ne 6.$ The desired result is proven.    □

Theorem 5.

Let $C_n$ be a cycle graph with $n\ge 4$. Then,

$$b_{pr}^d\left(C_n\right)=\left\{\begin{array}{cc}3,\hfill & n=6\hfill \\ 1,\hfill & n\equiv 0\left(mod5\right)\hfill \\ 2,\hfill & otherwise\hfill \end{array}\right.$$

and $b_{pr}^d\left(C_i\right)=\infty$ provided that $i=3.$

Proof. 

Let $C_n$ be the cycle graph with the vertex set $\{v_1,v_2,\dots ,v_n\}.$ It is easy to check that $b_{pr}^d\left(C_n\right)=\infty .$ Therefore, $n\ge 4$ must hold. An analysis will be conducted in three cases.

Case 1: If $n=6$, then $H=C_6-e=P_6.$ It is known from Theorem 1, ${\gamma }_{pr}^d\left(H\right)={\gamma }_{pr}^d\left(P_6\right)={\gamma }_{pr}^d\left(C_6\right).$ This implies that $b_{pr}^d\left(C_6\right)\ge 2.$ Assume that $b_{pr}^d\left(C_6\right)=2.$ If two non-adjacent edges are removed from the $C_6$ graph, then $H^{\prime }=C_6-\{\{v_i,v_{i+1}\},\{v_j,v_{j+1}\}\}$ provided that $\left|i-j\right|>1.$ In this case ${\gamma }_{pr}^d\left(H^{\prime }\right)={\gamma }_{pr}^d\left(C_6\right)=4$. Since the removal of two edges does not cause any change in PDBN, the situation implies that $b_{pr}^d\left(C_6\right)\ge 3$. Assume that three non-adjacent edges are removed from the $C_6$ graph, then we have $H^{″}=C_6-\{\{v_1,v_2\},\{v_3,v_4\},\{v_5,v_6\}\}.$ Hence, we get three $P_2$ structures. Thus, ${\gamma }_{pr}^d\left(H^{″}\right)=3{\gamma }_{pr}^d\left(P_2\right)=6>{\gamma }_{pr}^d\left(C_6\right).$ From this, it can be understood that $b_{pr}^d\left(C_6\right)\le 3.$ The result $b_{pr}^d\left(C_6\right)=3$ is obtained from the lower and upper bounds.

Case $2:$ Let $n\equiv 0(mod5)$. In this situation, if one edge is removed from the $C_n$ then $H=C_n-\left\{\{v_1,v_2\}\right\}=P_n$ path structure is formed.

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d\left(H\right)& =& {\gamma }_{pr}^d\left(P_n\right)=2⌈{\displaystyle \frac{n+1}{5}}⌉\hfill \\ & =& 2⌈{\displaystyle \frac{n}{5}}⌉+2,forn\equiv 0(mod5)\hfill \\ & =& {\gamma }_{pr}^d\left(C_n\right)+2\hfill \end{array}$$

$b_{pr}^d\left(C_n\right)=1,$ for $n\equiv 0(mod5).$

Case $3:$ If $n\equiv i(mod5),$ $i\in \{2,3,4\}$. In this situation, if one edge is removed from the $C_n$, then we have $H=C_n-\left\{\{v_1,v_2\}\right\}=P_n$ and the path structure is formed. However, it can be calculated using the result of Theorem 1, ${\gamma }_{pr}^d\left(H\right)={\gamma }_{pr}^d(C_n-\left\{\{v_1,v_2\}\right\})={\gamma }_{pr}^d\left(P_n\right)={\gamma }_{pr}^d\left(C_n\right)$ for $n\equiv 2,3,4(mod5)$. Therefore, we have $b_{pr}^d\left(C_n\right)\ge 2$ for $n\equiv 2,3,4(mod5)$. Let two edges be removed from the $C_n$; then it is obtained that $H=C_n-\{\{v_1,v_2\},\{v_6,v_7\}\}.$ Here, H, $P_5$, and $P_{n-5}$ are divided into two sub-path graphs. Let $n^{\prime }=n-5$. In this case, $n^{\prime }=n-5=5k+i-5$, where $k\ge 1$.

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d\left(H\right)& =& {\gamma }_{pr}^d\left(P_5\right)+{\gamma }_{pr}^d\left(P_{n^{\prime }}\right)\hfill \\ & =& 4+2⌈{\displaystyle \frac{5k+i-4}{5}}⌉\hfill \\ & =& 2+2⌈{\displaystyle \frac{n+1}{5}}⌉\hfill \\ & =& 2+2⌈{\displaystyle \frac{n}{5}}⌉,\mathrm{for}n\equiv i(mod5),i\in \{2,3,4\}\hfill \\ & =& 2+{\gamma }_{pr}^d\left(C_n\right).\hfill \end{array}$$

Hence, $b_{pr}^d\left(C_n\right)=2$ for $n\equiv i(mod5),i\in \{2,3,4\}.$ The proof is complete.    □

Theorem 6.

Let $W_{1,n}$ be a wheel graph with $n\ge 10$. Then,

$$b_{pr}^d\left(W_{1,n}\right)=2.$$

Proof. 

Let $\{c,v_1,\dots ,v_n\}$ be a vertex set of $W_{1,n}$ where c is the center vertex. Assume that one edge, $e,$ is removed from the $W_{1,n}$ as $H=W_{1,n}-e.$ It is obvious that ${\gamma }_{pr}^d\left(H\right)=2={\gamma }_{pr}^d\left(W_{1,n}\right).$ Therefore, this implies that $b_{pr}^d\left(W_{1,n}\right)\ge 2.$

Now, assume that two edges are removed from the $W_{1,n}.$ The edges removed from the graph are in the form of $E^{\prime }=\{\{v_i,c\},\{v_j,c\}:$ $i\ne j$, $i,j\in \{1,2,\dots ,n\},$ $d_{C_n}(v_i,v_j)=5\}$ and let $H=W_{1,n}-\{e_1,e_2\}$ where $e_1$ and $e_2$ are the elements of $E^{\prime }$. As a result, ${\gamma }_{pr}^d$$\left(H\right)=4>$ ${\gamma }_{pr}^d$$\left(W_{1,n}\right)=2$ is obtained. Thus, $b_{pr}^d\left(W_{1,n}\right)\le 2$ holds. From the lower and upper bounds, $b_{pr}^d\left(W_{1,n}\right)=2$ is yielded.    □

Theorem 7.

Let $K_{m,n}$ be a complete bipartite graph with $m,n\ne 1$. Then,

$$b_{pr}^d\left(K_{m,n}\right)=min\{m,n\}.$$

Proof. 

Let us split the vertex set of $K_{m,n}$ into two disjoint independent sets $V_1$ and $V_2$ and label the sets as $V_1=\{v_1,\dots ,v_m\}$ and $V_2=\{v_{m+1},\dots ,v_{m+n}\}$. Here, each vertex in $V_1$ is adjacent to every vertex in $V_2$, and there are no edges within each set. It is known from Corollary 1 that ${\gamma }_{pr}^d\left(K_{m,n}\right)=2$ and each ${\gamma }_{pr}^d-set$ contains two vertices, one from $V_1$ and the other from $V_2$.

Without loss of generality, choose $min\{m,n\}=n$ and let $H=K_{m,n}-E^{\prime }$ where $E^{\prime }\subset E\left(K_{m,n}\right).$ If $\left|E^{\prime }\right|<n$, then it is possible to find a $PDD-set$ with two vertices. Therefore, PDBN must be $b_{pr}^d\left(K_{m,n}\right)\ge n$. Let the set $E^{\prime }=\{\{v_i,v_{m+i}\}:i\in \{1,\dots ,n\}\}$ form with cardinality $n.$ When we examine $H=K_{m,n}-E^{\prime }$, it is obtained that ${\gamma }_{pr}^d\left(H\right)=4>{\gamma }_{pr}^d\left(K_{m,n}\right)=2.$ Therefore, it is implied that $b_{pr}^d\left(K_{m,n}\right)\le n.$ From lower and upper bounds of $b_{pr}^d\left(K_{m,n}\right),$ we conclude that $b_{pr}^d\left(K_{m,n}\right)=n$ (same manner is valid for $min\{m,n\}=m,$ choosing set $E^{\prime }=\{\{v_j,v_{m+j}\}:j\in \{1,\dots ,m\}\}$). Hence, $b_{pr}^d\left(K_{m,n}\right)=min\{m,n\}.$    □

Corollary 2.

Let $S_{1,n}$ be a star graph. Then,

$$b_{pr}^d\left(S_{1,n}\right)=\infty .$$

Proof. 

It is obvious from the structure of the star graph.    □

Theorem 8.

Let $K_n$ be a complete graph with $n\ge 4$ vertices. Then,

$$b_{pr}^d\left(K_n\right)=2n-4.$$

Proof. 

Let $\{v_1,\dots v_n\}$ be a vertex set of $K_n$ and m be a number of edges. It is known from Corollary 1 that ${\gamma }_{pr}^d\left(K_n\right)=2$. Assume that all edges incident to $v_1$ and $v_2$, except the edge connecting $v_1$ to $v_2$ are removed from the graph. Thus, the graph transforms into the structure $K_2+K_{n-1}$, and ${\gamma }_{pr}^d(K_2+K_{n-1})=4>{\gamma }_{pr}^d\left(K_n\right).$ Therefore, it is obtained that $b_{pr}^d\left(K_n\right)\le 2(n-2)=2n-4$.

Assume that $b_{pr}^d\left(K_n\right)\le 2n-5.$ Let S be the set of edges that is removed from the graph. To maximally damage a vertex by removing edges, let us remove $(n-2)$ edges from the graph that are incident to this vertex, leaving it as a pendant vertex. Label this pendant vertex as $v_1$ and its support vertex as $v_2$. For ${\gamma }_{pr}^d(K_n-S)>$ 2, there must exist a vertex $v_j\in K_n$ such that $v_j\notin N\left[v_2\right]$. Under this condition, the number of edges between the vertices, except $v_1$ and $v_j,$ is at most ${\displaystyle \frac{(n-2)(n-3)}{2}}$. Adding the edge $\{v_1,v_2\}$ to this count, the total number of edges becomes ${\displaystyle \frac{n^2-5n+8}{2}}$. However, this value is less than $m-2n+5={\displaystyle \frac{n^2-5n+10}{2}}$, and it is a contradiction. Hence, $v_j\in N\left[v_2\right]$, which leads ${\gamma }_{pr}^d(K_n-S)=2$. Thus, it follows that $b_{pr}^d\left(K_n\right)\ge 2n-4$. Considering both the lower and upper bounds, it must hold that $b_{pr}^d\left(K_n\right)=2n-4.$    □

4. Results About Some Trees

In this section, we determined the paired disjunctive domination numbers and the bondage numbers of this parameter for the double star, comet, double comet, $E_p^t$, and binomial trees structures, which are commonly used to model hierarchical and infrastructural network structures.

Theorem 9.

Let $D(n,m)$ be a double star graph with $n+m+2$ vertices. Then, the paired disjunctive domination number of $D(n,m)$ is

$${\gamma }_{pr}^d\left(D(n,m)\right)=2.$$

Proof. 

For ease of expression, let the vertex labeling be represented as $c_1$ with n vertices connected to it, and $c_2$ with m vertices connected to it, such that the vertex set is denoted as $\{c_1,1,2,\dots ,$n, $c_2$, $n+1,\dots ,n+m\}$. Let S be $PDD$-$set$ of $D(n,m).$ Therefore, $S=\{c_1,c_2\}$ is a $PDD$-$set$ and $\left|S\right|\le 2.$ It is also known from [25] that $\left|S\right|\ge 2.$ Then, we have ${\gamma }_{pr}^d\left(D(n,m)\right)=2.$    □

Theorem 10.

Let $D(n,m)$ be a double star graph with $n+m+2$ vertices. Then, the PDBN of the double star graph is

$$b_{pr}^d\left(D(n,m)\right)=1.$$

Proof. 

For ease of expression, let the vertex labeling be represented as $c_1$ with n vertices connected to it, and $c_2$ with m vertices connected to it, such that the vertex set is denoted as $\{c_1,1,2,\dots ,$n, $c_2$, $n+1,\dots ,n+m\}$. Let $\{c_1,c_2\}$ be a ${\gamma }_{pr}^d-set$, where it is known from previous theorem that ${\gamma }_{pr}^d\left(D(n,m)\right)=2$. Due to the structure of the double graph, leaf edges cannot be removed from the graph. In this case, let $e=\{c_1,c_2\}$, and consider $H=D(n,m)-e$. For this structure, the paired disjunctive domination number satisfies ${\gamma }_{pr}^d\left(H\right)=4>2$. Thus, $b_{pr}^d\left(D(n,m)\right)=1.$    □

Theorem 11.

Let $C_{n,m}$ be a comet graph with $(n+m)$ and $n\ge 5$. Then, the paired disjunctive domination number of the comet graph is

$${\gamma }_{pr}^d\left(C_{n,m}\right)=2+2⌈{\displaystyle \frac{n-2}{5}}⌉.$$

Proof. 

Let the vertex labeling of the comet graph be $\{v_1,\dots ,v_n,u_1,\dots ,u_m\}$, where $deg\left(u_i\right)=1$ for $i\in \{2,\dots ,m\}$, making these vertices pendants, and $deg\left(u_1\right)=m+1$ and $v_n$ is adjacent to $u_1$. Thus, the comet graph contains both a path subgraph and a star subgraph. Let S be a $PDD$-$set$ of the graph $C_{n,m}$. To dominate the pendant vertices $u_i$, $i\in$ $\{2,\dots ,m\}$; the strong support vertex $u_1$ must belong to the set S.

Case 1: To ensure the paired property, vertex $v_n$ can also be added to S. In this case, all vertices forming the star subgraph of G are paired disjunctively dominated. Furthermore, since the vertex subset $\{u_1,v_n\}$ satisfies $\{u_1,v_n\}\subseteq S,$ $v_n$ paired disjunctively dominates $v_{n-1}$, which is a vertex of the path subgraph. Since $d(v_{n-2},v_n)$ $=2$, $v_{n-2}$ is partially paired disjunctively dominated, requiring the addition of $v_{n-4}$ to S to complete its domination. It is known from [25] that ${\gamma }_{pr}^d\left(P_n\right)=2⌈{\displaystyle \frac{n+1}{5}}⌉$, and from the proof of ${\gamma }_{pr}^d\left(P_n\right)$, the support vertex vertex $v_2$ belongs to the ${\gamma }_{pr}^d-set$. For $v_{n-2}$, only $v_{n-4}$ needs to be added to S. With the vertex subset $\{u_1,v_n\}$ satisfies $\{u_1,v_n\}\subseteq S$; the remaining graph H is isomorphic to $P_{n-3}$ and $n\ge 5$. Therefore, we have $\left|S\right|=2+{\gamma }_{pr}^d\left(P_{n-3}\right).$

Case 2: To ensure the paired property, a pendant vertex $u_i,$ $i\in \{2,\dots ,m\}$ can also be added to $S.$ Without loss of generality, let the vertex $u_2$ add to $S.$ Since $\{u_1,u_2\}\subseteq S$, the vertex $v_n$ is dominated as paired disjunctively, and the set also contributes to the domination of vertex $v_{n-1}$. As in Case 1, the remaining structure becomes isomorphic to $P_{n-2}$. Therefore, we get $\left|S\right|=2+{\gamma }_{pr}^d\left(P_{n-2}\right).$ When the S values obtained from Case 1 and Case 2 are compared, ${\gamma }_{pr}^d\left(C_{n,m}\right)=2+{\gamma }_{pr}^d\left(P_{n-3}\right)$ is obtained. Thus, using Theorem 1, the result is obtained as ${\gamma }_{pr}^d\left(C_{n,m}\right)=2+2⌈{\displaystyle \frac{n-2}{5}}⌉.$    □

Corollary 3.

Let $C_{n,m},$ $S_{1,m-1},$ and $P_n$ be comet, star, and path structures, respectively. Then,

$${\gamma }_{pr}^d\left(C_{n,m}\right)\le {\gamma }_{pr}^d\left(S_{1,m-1}\right)+{\gamma }_{pr}^d\left(P_n\right)$$

and the equality holds $n\equiv 3,4(mod5).$

Theorem 12.

Let $C_{n,m}$ be a comet graph with $n+m$ vertices. Then, the PDBN comet graph is

$$b_{pr}^d\left(C_{n,m}\right)=\left\{\begin{array}{cc}1,\hfill & ifn\equiv 0,1,2(mod5)\hfill \\ 2,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let the vertex labeling of the comet graph be $\{v_1,\dots ,v_n,u_1,\dots ,u_m\}$, where $deg\left(u_i\right)=1$ for $i\in \{2,\dots ,m\}$, making these vertices pendants, and $deg\left(u_1\right)=m+1$ and $v_n$ is adjacent to $u_1$. According to the form of comet graph, it is known that $C_{n,m}\simeq P_n\cup S_{1,m-1}.$

Let us assume that by removing the edge $e=\{v_n,u_1\}$ from the graph, the comet graph is split into $P_n$ and $S_{1,m-1}$. From the Corollary 3, when $n\equiv 3,4(mod5)$, ${\gamma }_{pr}^d(C_{n,m}-e)={\gamma }_{pr}^d\left(C_{n,m}\right)$. Therefore, $b_{pr}^d\left(C_{n,m}\right)\ge 2$ for $n\equiv 3,4(mod5)$. Now, let us consider the upper bound. Assume that $B=\{\{v_n,u_1\},\{v_{n-2},v_{n-1}\}\}$ are the edges removed from the graph $C_{n,m}$. In this case, the subgraphs $P_{n-3},K_2$, and $S_{1,m-1}$ are obtained. Therefore, we have

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d(C_{n,m}-B)& =& {\gamma }_{pr}^d\left(P_{n-3}\right)+{\gamma }_{pr}^d\left(K_2\right)+{\gamma }_{pr}^d\left(S_{1,m-1}\right)\hfill \\ & =& 4+{\gamma }_{pr}^d\left(P_{n-3}\right)\hfill \\ & =& 2+{\gamma }_{pr}^d\left(C_{n,m}\right).\hfill \end{array}$$

Thus, we have ${\gamma }_{pr}^d(C_{n,m}-B)>{\gamma }_{pr}^d\left(C_{n,m}\right).$ In consequence, $b_{pr}^d\left(C_{n,m}\right)=2$ for $n\equiv 3,4(mod5).$

When $n\equiv 0,1,2(mod5)$ then it is known from Corollary 3

$${\gamma }_{pr}^d\left(C_{n,m}\right)<{\gamma }_{pr}^d\left(S_{1,m-1}\right)+{\gamma }_{pr}^d\left(P_n\right).$$

It follows that $e=\{v_n,u_1\}$, and the following result holds:

$${\gamma }_{pr}^d(C_{n,m}-e)>{\gamma }_{pr}^d\left(C_{n,m}\right).$$

Therefore, $b_{pr}^d\left(C_{n,m}\right)=1$ for $n\equiv 0,1,2(mod5).$ As a result, it is obtained that

$$b_{pr}^d\left(C_{n,m}\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}n\equiv 0,1,2(mod5)\hfill \\ 2,\hfill & otherwise.\hfill \end{array}\right.$$

This completes the proof.   □

Theorem 13.

Let $D(m,n_1,n_2)$ be a double comet graph with $m=(n_1+n_2+n)$ vertices and $n\ge 7$. Then, the paired disjunctive domination number of double comet graph is

$${\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)=4+2⌈{\displaystyle \frac{n-7}{5}}⌉.$$

Proof. 

Let the double comet structure be labeled with the vertex set $\{u_1,\dots ,u_{n_1},v_1,\dots ,v_n,w_1,\dots ,w_{n_2}\}.$ Here, $deg\left(u_i\right)$ = $deg\left(w_j\right)=1$, where $1<i<n_1$, $1<j<n_2$, and $v_1$ and $v_n$ are strong support vertices. Let S be the $PDD$-set of $D(m,n_1,n_2)$. To dominate the pendant vertices, it is necessary for the strong support vertices $\{v_1,v_n\}$ and their paired vertices to be included in the set S. To obtain the minimum $PDD$-set, the subset $\{v_1,v_2,v_{n-1},v_n\}$ must be part of S. Considering the remaining structure that is not dominated in a paired disjunctive sense, the following result is obtained for $D(m,n_1,n_2)$:

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)& =& 4+{\gamma }_{pr}^d\left(P_{n-8}\right)\hfill \\ & =& 4+2⌈{\displaystyle \frac{n-7}{5}}⌉\hfill \end{array}$$

where $n=m-n_1-n_2.$    □

Corollary 4.

Let $S_{1,n_1}$ and $C_{(n-1),(n_2+1)}$ be star and comet graphs, respectively, and let $D(m,n_1,n_2)$ be a double comet graph with $m=n+n_1+n_2$. Then,

$${\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)\le {\gamma }_{pr}^d\left(S_{1,n_1}\right)+{\gamma }_{pr}^d\left(C_{(n-1),(n_2+1)}\right)$$

the equality holds $n\equiv 3,4(mod5).$

Theorem 14.

Let $D(m,n_1,n_2)$ be a double comet graph with $m=(n_1+n_2+n)$ vertices. Then, the PDBN of the double comet graph is

$$b_{pr}^d\left(D(m,n_1,n_2)\right)=\left\{\begin{array}{cc}2,\hfill & ifn\equiv 3,4(mod5)\hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let the double comet structure $D(m,n_1,n_2)$ be labeled with the vertex set $\{u_1,\dots ,u_{n_1},v_1,\dots ,v_n,w_1,\dots ,w_{n_2}\}.$ Here, $deg\left(u_i\right)$ = $deg\left(w_j\right)=1$, where $1<i<n_1$ and $1<j<n_2$, and $v_1$ and $v_n$ are strong support vertices. Let $e=\{v_1,v_2\}$, and consider the graph $D(m,n_1,n_2)-e$. When $D(m,n_1,n_2)-e$ is formed, it becomes a graph consisting of a star graph $S_{1,n_1}$ with $n_1+1$ vertices and a comet graph $C_{n-1,n_2+1}$ with $n+n_2$ vertices. Thus, by Corollary 4, ${\gamma }_{pr}^d(D(m,n_1,n_2)-e)={\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)$ for n $\equiv 3,4(mod5)$. Consequently, for n $\equiv 3,4(mod5)$, $b_{pr}^d\left(D(m,n_1,n_2)\right)\ge 2$ holds.

Now, let us consider the upper bound for the PDBN. Assume that the edges in the set $B=\{\{v_1,v_2\},\{v_{n-1},v_n\}\}$ are removed from the graph $D(m,n_1,n_2)$. In this case, the graph transforms into a form consisting of the subgraphs $S_{1,n_1}$, $S_{1,n_2}$, and $P_{n-2}$. Therefore, we have

$$\begin{array}{ccc}\hfill {\gamma }_{pr}^d(D(m,n_1,n_2)-B)& =& {\gamma }_{pr}^d\left(S_{1,n_1}\right)+{\gamma }_{pr}^d\left(S_{1,n_2}\right)+{\gamma }_{pr}^d\left(P_{n-2}\right)\hfill \\ & =& 4+{\gamma }_{pr}^d\left(P_{n-2}\right)>4+{\gamma }_{pr}^d\left(P_{n-8}\right).\hfill \end{array}$$

Thus, it is obtained that ${\gamma }_{pr}^d(D(m,n_1,n_2)-B)>{\gamma }_{pr}^d\left(D(m,n_1,n_2)\right).$ Consequently, $b_{pr}^d\left(D(m,n_1,n_2)\right)\le 2$ and it can be said from upper and lower bounds that $b_{pr}^d\left(D(m,n_1,n_2)\right)$ = 2 for $n\equiv 3,4(mod5).$ For $n\equiv 0,1,2(mod5)$, ${\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)<{\gamma }_{pr}^d\left(S_{1,n_1}\right)+{\gamma }_{pr}^d\left(C_{n-1,n_2+1}\right)$ from Corollary 4. If $e=\{v_1,v_2\}$ is removed from graph then ${\gamma }_{pr}^d(D(m,n_1,n_2)$−$e)>{\gamma }_{pr}^d\left(D(m,n_1,n_2)\right)$ for the case n $\equiv 0,1,2$ $(mod5)$. Hence, $b_{pr}^d\left(D(m,n_1,n_2)\right)=1$ is yielded for n $\equiv 0,1,2$$(mod5).$    □

Theorem 15.

Let $E_p^t$ be a tree containing t times $P_p$ path graphs. Then, the paired disjunctive domination number of $E_p^t$ graph is

$${\gamma }_{pr}^d\left(E_p^t\right)=\left\{\begin{array}{cc}2t⌈{\displaystyle \frac{p-1}{5}}⌉,\hfill & p\equiv 2(mod5)\hfill \\ \\ 2t⌈{\displaystyle \frac{p-1}{5}}⌉+2,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let us label the $E_p^t$ graph as follows $:\{v_1,v_2,v_i^j:1\le i\le p,1\le j\le t\}$ where $deg\left(v_1\right)=1$, and $v_2$ is the support vertex of $v_1$. To construct a $PDD$-set, there are two cases to consider.

Case 1: Let S be a $PDD$-set. In this case, $v_2\in S$ because it is a support vertex. If we consider one of the $P_p$ structures, the $P_{p+2}$ structure consisting of the vertices $\{v_1,v_2,V\left(P_p\right)\}$ can be paired disjunctively dominated by number of ${\gamma }_{pr}^d\left(P_{p+2}\right)$ vertices. Since $v_2$ is in S, it dominates the $v_1^j$ vertices in the remaining $(t-1)P_p$ legs and is at a distance of two from the $v_2^j$ vertices, where $1<j<t.$ The remaining $(p-2)$ vertices in each of the $(t-1)$ legs can be disjunctively dominated by $(t-1){\gamma }_{pr}^d\left(P_{p-2}\right)$ vertices. Therefore, we have

$${\gamma }_{pr}^d\left(E_p^t\right)=(t-1){\gamma }_{pr}^d\left(P_{p-2}\right)+{\gamma }_{pr}^d\left(P_{p+2}\right).$$

Case 2: In this case, it must also hold that $v_2 \in$ S. To ensure the paired property of $v_2$, let us include $v_1$ in the set S. However, this selection creates a disadvantage for dominating the $P_p$ structures in the t legs when $n\equiv 2(mod5)$. For the case that $n\equiv 2(mod5)$, the result $t{\gamma }_{pr}^d\left(P_{p-2}\right)+2$ is obtained, which is greater than the result in Case 1. In conclusion, ${\gamma }_{pr}^d\left(E_p^t\right)=(t-1){\gamma }_{pr}^d\left(P_{p-2}\right)+{\gamma }_{pr}^d\left(P_{p+2}\right)$ is obtained. Using Theorem 1 the result follows as

$${\gamma }_{pr}^d\left(E_p^t\right)=\left\{\begin{array}{cc}2t⌈{\displaystyle \frac{p-1}{5}}⌉\hfill & ,p\equiv 2(mod5)\hfill \\ \\ 2t⌈{\displaystyle \frac{p-1}{5}}⌉+2\hfill & ,otherwise.\hfill \end{array}\right.$$

Hence, the desired result is obtained.   □

Theorem 16.

Let $E_p^t$ be a tree containing t times $P_p$ path graphs with $p\ge 9$. Then, the PDBN of $E_p^t$ is

$$b_{pr}^d\left(E_p^t\right)=1.$$

Proof. 

As in the previous theorem, the vertex set of the $E_p^t$ graph is $\{v_1,v_2,v_i^j:1\le i\le p,1\le j\le t\}.$ Consider the proof in two cases.

Case 1: For $n\not\equiv 2(mod5),$ the $PDD$-sets S defined in proof of Theorem 15 provided the same ${\gamma }_{pr}^d\left(E_p^t\right)$ value. Therefore, if the edge $e=\{v_3^j,v_4^j\}$ is removed from the graph for any $j\in \{1,...,t\}$ then the ${\gamma }_{pr}^d\left(E_p^t\right)$ value will be increased. In each situation, the vertices $\{v_2^j,v_3^j\}$ will be added to $S.$ Thus, we have

$${\gamma }_{pr}^d(E_p^t-e)=2+{\gamma }_{pr}^d\left(E_p^t\right).$$

Hence, ${\gamma }_{pr}^d(E_p^t-e)>{\gamma }_{pr}^d\left(E_p^t\right)$ is yielded.

Case 2: For $n\equiv 2(mod5),$ as in proof of Theorem 15, ${\gamma }_{pr}^d-set$ selection will be possible with $\{v_2,v_1^j\}\subseteq S,$ $j\in \{1,\dots ,t\}.$ In this case, removing the edge $\{v_3^j,v_4^j\}$ for any j value does not change the value of ${\gamma }_{pr}^d\left(E_p^t\right)$. However, when we remove the edge $e=\{v_7^j,v_8^j\}$, $j\in \{1,\dots ,t\}$ from the graph, we need to add two vertices to S according to each choice j. If the removal edge belongs to the $j^{\mathrm{th}}$ foot of $E_p^t$ graph that includes $v_1^j\in S$, then it is necessary to add vertices $\{v_8^j,v_9^j\}$ to the set S. Otherwise, it is necessary to add vertices $\{v_6^j,v_7^j\}$. In each situation, we have

$${\gamma }_{pr}^d(E_p^t-e)=2+{\gamma }_{pr}^d\left(E_p^t\right).$$

Therefore, ${\gamma }_{pr}^d(E_p^t-e)>{\gamma }_{pr}^d\left(E_p^t\right)$ is obtained. From Case 1 and Case $2,$ the result $b_{pr}^d\left(E_p^t\right)=1$ for $p\ge 9$ is achieved.    □

Lemma 1.

Let G be a connected graph and S be a ${\gamma }_{pr}^d$-$set$ of G. Suppose v is any support vertex of G, and v has no non-leaf neighbors other than w. In this case, S must include the vertex $v.$

Proof. 

Assume that $v\in S$. Since v has only one non-leaf neighbor, w, there is only a single vertex in G at a $2-$ distance from the leaf vertices. Hence, if $v\notin S$, at least two leaf vertices of v must be added to S to disjunctively dominate the leaf vertices. However, in this case, the paired property cannot be ensured for the vertices in S. If v, as a support vertex, is adjacent to only one leaf, then $v\notin S$ is not possible. Therefore, $v\in S$.    □

Theorem 17.

Let $B_n$ be a binomial tree containing $2^n$ vertices, $n\ge 3$. Then, the paired disjunctive domination number of the $B_n$ graph is

$${\gamma }_{pr}^d\left(B_n\right)=2^{n-1}.$$

Proof. 

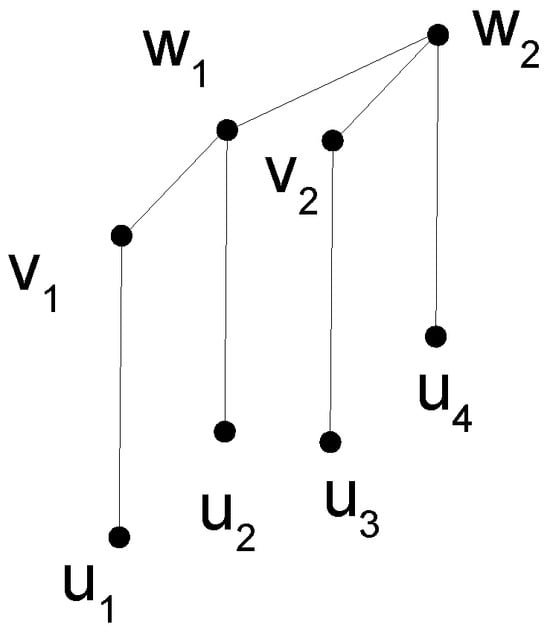
Let S be a ${\gamma }_{pr}^d-set$ of $B_n$. From Lemma 1, exactly two vertices in the $B_3$ structure must belong to the set S. As seen in Figure 2, label these two vertices as $\{v_1,v_2\}$.

Figure 2. A labeling of the vertices of the binomial tree $B_3$.

Since $v_2\notin N_{B_n}\left(v_1\right)$, the paired property does not hold for $\{v_1,v_2\}\subset S$. It is obvious that $\{v_1,v_2,w_1,w_2\}$ is the only ${\gamma }_{pr}^d-set$ for $B_3.$ Then, we have ${\gamma }_{pr}^d\left(B_3\right)=4.$ Due to the recursive structure of the binomial tree graph, $B_n$ contains $2^{n-3}$ subgraphs that are each isomorphic to $B_3$. Thus, the result is obtained as

$$\begin{array}{ccc}\hfill \left|S\right|& =& {\gamma }_{pr}^d\left(B_n\right)=2^{n-3}{\gamma }_{pr}^d\left(B_3\right)\hfill \\ & =& 2^{n-1}. \square \hfill \end{array}$$

Theorem 18.

Let $B_n$ be a binomial graph containing $2^n$ vertices, $n\ge 3.$ Then, the PDBN of the $B_n$ graph is

$$b_{pr}^d\left(B_n\right)=1.$$

Proof. 

Let $v_i$ be a support vertex satisfying Lemma 1, and let $w_i$ be the non-leaf neighbor of $v_i$. For any $i\in \{1,...,2^{n-2}\}$, if the edge $e=\{v_i,w_i\}$ is removed from the graph,

$${\gamma }_{pr}^d(B_n-e)={\gamma }_{pr}^d\left(B_n\right)+2$$

is obtained. Thus, $b_{pr}^d\left(B_n\right)=1$ is yielded.    □

5. Algorithmic Analysis of PDBN

In this section, we transition from the theoretical foundations to a practical perspective by presenting an algorithm for computing the PDBN. We also provide a detailed complexity analysis to assess the computational feasibility and efficiency of the proposed method. The detailed steps of the algorithm are described in Algorithm 1.    

Algorithm 1: Paired Disjunctive Bondage Number (PDBN) of G

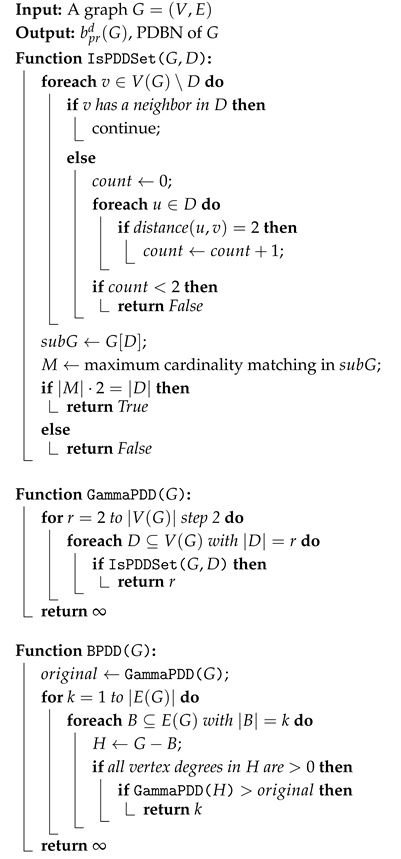The PDBN problem seeks to determine the minimum number of edges whose removal from a graph G increases the size of a minimum paired disjunctive dominating set. In other words, it identifies the minimal set of critical edges that, when deleted, cause the graph to require a larger dominating set that is also paired and disjunctively dominating.

The algorithm operates in two major stages:

• First, it computes the parameter ${\gamma }_{pr}^d\left(G\right)$, which represents the size of the smallest paired disjunctive dominating (PDD) set in the original graph. This involves checking all even-sized subsets of vertices to find the minimum set satisfying both the disjunctive domination and perfect matching properties.
• Second, it exhaustively searches through subsets of edges, starting from size 1 up to $\left|E\right(G\left)\right|$, and removes each such subset B to form a new graph $G^{\prime }=G-B$. For each $G^{\prime }$, the algorithm checks whether ${\gamma }_{pr}^d\left(G^{\prime }\right)>{\gamma }_{pr}^d\left(G\right)$. The smallest such $\left|B\right|$ is returned as the PDBN of G.

The computational complexity of the algorithm is driven by two key factors:

1.

Computing ${\gamma }_{pr}^d\left(G\right)$. For each even-sized vertex subset $D\subseteq V\left(G\right)$, the algorithm checks the following:

• Whether every vertex not in D is either adjacent to a vertex in D, or has at least two vertices in D at distance two (disjunctive domination check).
• Whether $G\left[D\right]$ contains a perfect matching (using Edmonds’ algorithm in $O\left(n^3\right)$ time).

This step has an overall complexity of $O(2^n·n^3)$ due to the enumeration of vertex subsets.

2.

Computing PDBN. For each $k=1$ to $\left|E\right(G\left)\right|$, all subsets of k edges are considered (i.e., $\left({\displaystyle \genfrac{}{}{0pt}{}{m}{k}}\right)$ possibilities). For each such subset B, the value ${\gamma }_{pr}^d(G-B)$ is recomputed using the above method.

The total time complexity becomes

$$O\left(2^m·2^n·n^3\right),$$

which is exponential in both the number of vertices n and edges m.

The PDBN problem is proven to be NP-hard and even $W\left[2\right]$-hard in the parameterized complexity framework. This indicates that it is highly unlikely that an efficient (polynomial-time) or fixed-parameter tractable algorithm exists for general graphs. As a result, exact algorithms are only practical for very small graphs.

Due to its combinatorial explosion in both vertex and edge subsets, the PDBN problem is intractable for large-scale graphs. Therefore, heuristic and approximation algorithms, such as greedy strategies, genetic algorithms, or metaheuristics, are essential for practical applications. The Python 3.11.4 implementation computes the PDBN of a graph G.

6. Case Study

The PDBN serves as a powerful indicator for assessing the robustness of networks that require both structural redundancy and distributed control. In infrastructural networks—such as communication systems, transport grids, and health service delivery networks—ensuring reliable connectivity under potential failures is a critical design objective. The PDBN quantifies the minimum number of edge deletions required to increase the PDBN, and hence measures the network’s sensitivity to edge-level disruptions under joint paired and disjunctive coverage constraints. To illustrate the practical significance, consider a stylized metro network of a capital city where vertices represent stations and edges denote direct rail lines. By computing the PDBN for the network, and analyzing its change under edge deletions (e.g., due to maintenance), one can identify critical vulnerabilities. For example, if the removal of a single track increases the PDBN, then that edge is critical for maintaining paired and alternative access routes. This insight can inform both physical infrastructure investment and scheduling of non-overlapping maintenance operations. To demonstrate the structural significance of the PDBN, consider the portion of stylized map M, represented in a metro-style layout in Figure 3. Vertices represent stations, and edges represent direct rail connections.

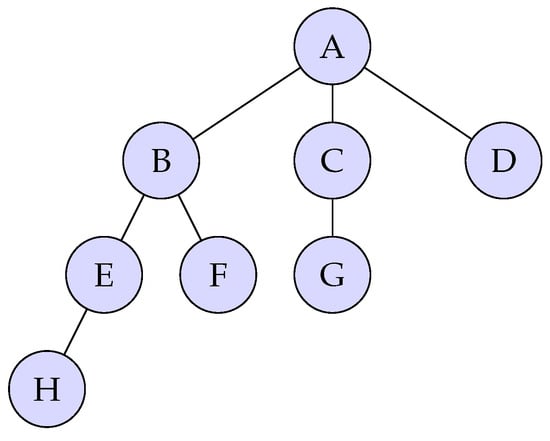
Figure 3. Metro-style map of M, where vertices labeled A, B, C, …, H represent stations.

The paired disjunctive domination number of M is computed as follows:

$${\gamma }_{pr}^d\left(M\right)=4$$

This means that a minimum of four vertices are needed to dominate the graph in a paired disjunctive sense.

Now we analyze the effect of an edge deletions on this parameter. We find the following:

• Removing the edge {A,C} increases ${\gamma }_{pr}^d$ from 4 to 6.
• Removing the edge {B,E} also increases ${\gamma }_{pr}^d$ from 4 to 6.
• Other single edge deletions do not affect the PDD value.

This implies that M contains at least one edge whose removal increases the PDD number. Hence, the PDBN of M is

$$b_{pr}^d\left(M\right)=1$$

As shown in Table 1 summarizes how the deletion of edges affects the paired disjunctive domination number of the graph M. The edge set {A,C}, {B,E} contains critical links in the structure. Their removal causes the paired disjunctive domination number to increase significantly. Thus, the graph’s vulnerability to link failures is measurable via its PDBN value.

Table 1. Effect of edge deletions on ${\gamma }_{pr}^d\left(M\right)$.

Edge Removed	${\mathit{\gamma }}_{\mathbf{pr}}^{\mathit{d}}$ Before	${\mathit{\gamma }}_{\mathbf{pr}}^{\mathit{d}}$ After	Interpretation
None	4	4	Base case: PDD set exists with 4 nodes
{A,C}	4	6	Critical connection—removal increases PDD
{B,E}	4	6	Critical connection—removal increases PDD
Others	4	4	Structurally mandatory edge, redundant or non-impactful edges

7. Discussion

This study introduced and analyzed the concept of the PDBN, a new graph parameter derived from the paired disjunctive domination number, recently proposed by Henning et al. [25], and further developed through contributions by Tuncel Golpek and Aytac [26,27]. While the paired disjunctive domination number encapsulates both structural reachability and pairwise matching conditions in graphs, its bondage variant quantifies the vulnerability of network structures to edge deletions, thereby measuring their structural robustness.

Our findings for various standard graph classes, including path, cycle, complete, and bipartite graphs, confirm that the PDBN behaves consistently with known characteristics of classical bondage numbers. We also observed that complete graphs possess relatively high PDBNs, which indicates their significant resilience to edge deletions.

In the case of tree structures—such as double stars, comets, double comets, $E_p^t$, and binomial trees—our results illustrate how hierarchical or recursive structures impact the stability of paired disjunctive domination. The exact values derived for these trees demonstrate that even small structural perturbations (e.g., removal of one or two key edges) can significantly affect the domination properties.

These findings contribute meaningfully to the growing body of knowledge on domination-based resilience in network analysis. The PDBN not only extends classical graph vulnerability measures but also introduces new combinatorial challenges. The alignment of our results with previously established bounds (e.g., for ${\gamma }_{pr}^d\left(G\right)$ and $b_{pr}^d\left(G\right)$) reinforces the mathematical soundness and applicability of this parameter in network vulnerability studies.

Furthermore, some bondage parameters can be compared in terms of their magnitude or relative values for a given graph, which offers insight into their discriminatory power and how restrictive or robust the domination conditions are.

For instance, consider two graphs $G_1$ and $G_2$, each having six vertices and six edges, illustrated in Figure 4. Their paired bondage and disjunctive bondage numbers are equal, but their PDBNs differ, as shown in Table 2.

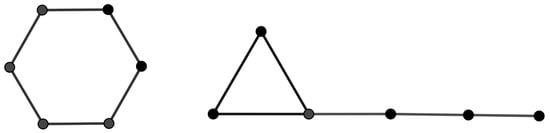
Figure 4. Two graphs with the same number of vertices and edges but different structures.

Table 2. Comparison of paired bondage, disjuctive bondage, and paired disjunctive bondage numbers for two graphs $G_1=C_6$ and $G_2=\mathrm{cycle}+\mathrm{path}$ illustraited in Figure 4.

Parameter	${\mathit{G}}_1={\mathit{C}}_6$	${\mathit{G}}_2$ = Cycle + Path	Comment
Vertices $\left|V\right|$	6	6	Same
Edges $\left|E\right|$	6	6	Same
Paired Bondage $b_{pr}\left(G\right)$	1	1	Equal
Disjunctive Bondage $b^d\left(G\right)$	1	1	Equal
Paired Disjunctive Bondage $b_{pr}^d\left(G\right)$	1	2	Different

This example highlights that while the classical bondage parameters may coincide for different graphs with the same order and size, the PDBN can distinguish between them, reflecting its greater discriminatory capability. The comparison results are presented in Table 2. Thus, rather than sensitivity, we emphasize the distinctiveness and comparative scale of these parameters in capturing subtle structural differences.

In conclusion, bondage parameters should be viewed as complementary measures, each offering unique insights into the graph’s domination robustness under different conditions.

Future research could extend this analysis to several types of graph structures and improve our algorithmic approaches for computing $b_{pr}^d\left(G\right)$ efficiently. Furthermore, many problems previously examined in the context of the bondage number and its variants in the literature can be revisited and analyzed through the lens of the paired disjunctive bondage parameter. Moreover, given the computational hardness of the PDBN problem for large-scale graphs, the development of heuristic and approximation algorithms emerges as a significant future research direction. Greedy algorithms, genetic algorithms, and metaheuristic methods such as simulated annealing or tabu search could be explored to obtain near-optimal solutions in reasonable computation time. These approaches may provide practical alternatives for network analysts dealing with real-life large-scale infrastructure networks, where exact computation is infeasible due to exponential complexity.