Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm
Abstract
1. Introduction
1.1. Backgrounds
1.2. Related Works
1.3. Contributions
- The interval possibility model in interval theory is applied to the modeling of three-dimensional submarine currents and hazardous environments, capturing the uncertainty of these factors. A multi-objective optimization mathematical model for the path planning of underwater vehicles considering uncertain currents and dangerous sources is established.
- An interval multi-objective optimization framework is designed, which integrates interval non-dominated sorting, an individual update mechanism of secretary bird optimization algorithm, and an individual variation mechanism, aiming to improve the optimization performance and find a balance between the safety, speed, energy efficiency, and feasibility of the path.
2. Environmental Modeling
- The AUV obtained topographic and current information about the mission area.
- The AUV was operated at a constant speed.
- The AUV was modeled as a prime model [24], focusing only on the position information in a three-dimensional space during path planning.
2.1. Three-Dimensional Marine Environment Model
2.2. Representation of Three-Dimensional Ocean Current
2.3. Kinematic Modeling of the AUV
2.4. Path-Smoothing Processing
3. AUV Path-Planning Objective Function
- Seafloor terrain limitations: When navigating through current environments, underwater vehicles should maintain a height above the seafloor terrain to prevent collisions and avoid hazards.
- The voyage minimizes time and energy consumption, and safe arrival at the destination is ensured.
3.1. Navigation Time Cost Interval
3.2. Uncertain Obstacle Constraint Cost Interval
3.3. Path Smoothness
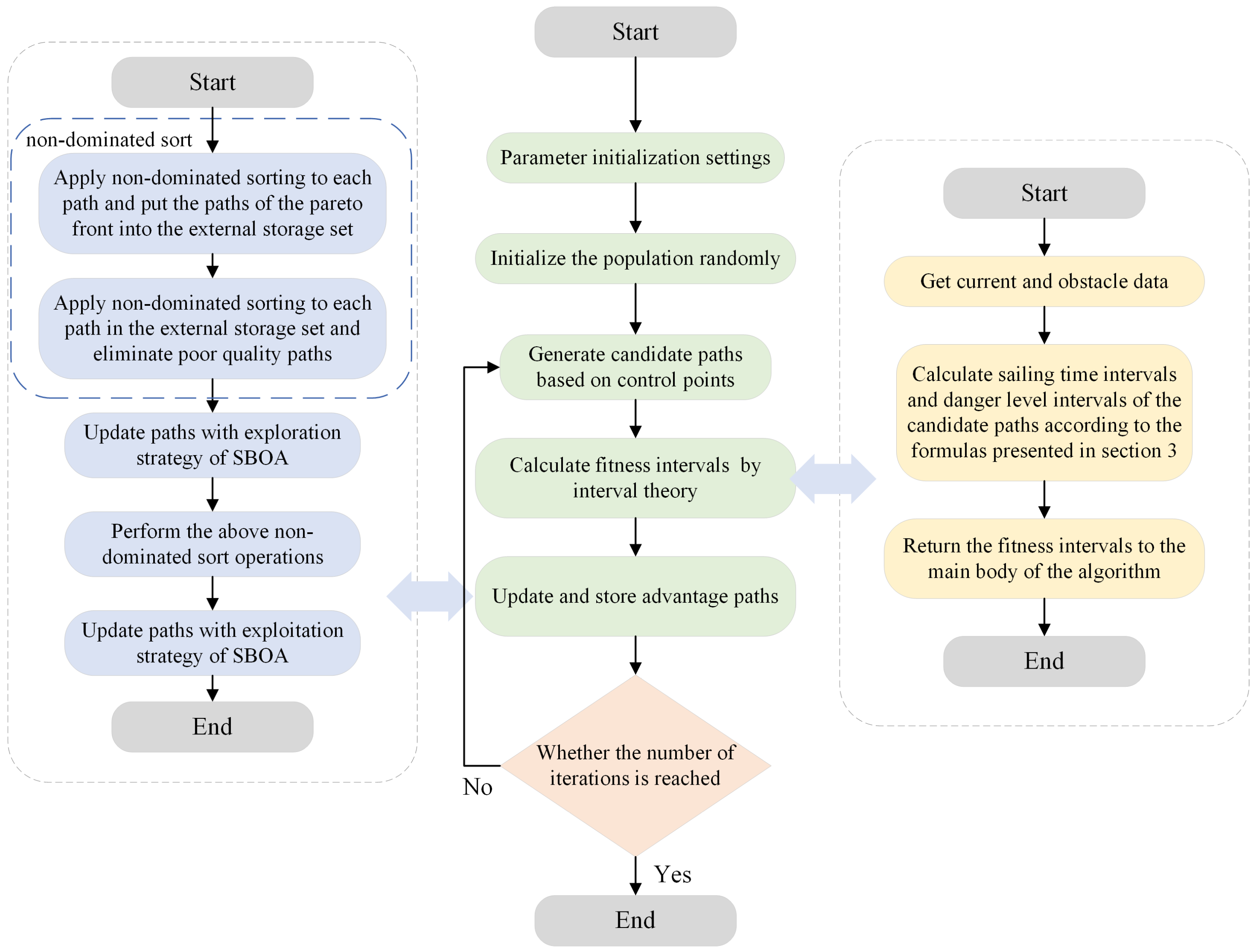
4. AUV Path-Planning Based on IMOSBOA
4.1. Dominance Relationship Based on the Interval Possibility Degree Model
4.2. Secretary Bird Optimization Algorithm
4.2.1. Secretary Bird Exploration Strategies
4.2.2. Secretary Bird Exploitation Strategies
4.2.3. Improvement Approach
4.3. Interval Multi-Objective Path-Planning Algorithm
| Algorithm 1: IMOSBOA |
| 1: Create 3D environmental model, including obstacles and currents. |
| 2: Initialize problem setting, including the number of control points and individuals, maximum iteration (T), current iteration (t), and number of paths. |
| 3: Initialize the population randomly and calculate the fitness intervals of each object. |
| 4: For t = 1:T do Update each secretary bird’s best position. For each particle do Use exploration strategy to update secretary bird position according to Equation (16). Update each secretary bird’s best position. Do undominated sort for all individuals and put which ranks 1 into external storage set. Use exploitation strategy to update secretary bird position according to Equation (17). Update each secretary bird’s best position. Do undominated sort for all individuals and put which ranks 1 into external storage set. end Do undominated sort for all individuals in the external storage set. If the number of individuals in the external storage set exceeds the set value then Compare the Pareto levels and crowding distances of individuals and delete a certain number of individuals. end Use mutation operations to update disadvantaged individuals according to Equation (18). end 5: Calculate the smoothness of individuals in the external storage set and select the individual with the highest smoothness the optimal solution. 6: Output the optimal value (the optimal path). |
5. Simulation Analysis
5.1. Comparison of Planning Results
5.2. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Zhu, D.; Pang, W.; Zhang, Y. A survey of underwater search for multi-target using Multi-AUV: Task allocation, path planning, and formation control. Ocean Eng. 2023, 278, 114393. [Google Scholar] [CrossRef]
- Yan, Z.; Li, Y. Data collection optimization of ocean observation network based on AUV path planning and communication. Ocean Eng. 2023, 282, 114912. [Google Scholar] [CrossRef]
- Wu, Y. Coordinated path planning for an unmanned aerial-aquatic vehicle (UAAV) and an autonomous underwater vehicle (AUV) in an underwater target strike mission. Ocean Eng. 2019, 182, 162–173. [Google Scholar] [CrossRef]
- Zeng, Z.; Lian, L.; Sammut, K.; He, F.; Tang, Y.; Lammas, A. A survey on path planning for persistent autonomy of autonomous underwater vehicles. Ocean Eng. 2015, 110, 303–313. [Google Scholar] [CrossRef]
- Auh, E.; Kim, J.; Joo, Y.; Park, J.; Lee, G.; Oh, I.; Pico, N.; Moon, H. Unloading sequence planning for autonomous robotic container-unloading system using A-star search algorithm. Eng. Sci. Technol. Int. J. 2024, 50, 101610. [Google Scholar] [CrossRef]
- Sedeño-Noda, A.; Colebrook, M. A biobjective Dijkstra algorithm. Eur. J. Oper. Res. 2019, 276, 106–118. [Google Scholar] [CrossRef]
- Kulkarni, C.S. Three-Dimensional Time-Optimal Path Planning in Dynamic and Realistic Environments. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2017. Available online: http://hdl.handle.net/1721.1/111730 (accessed on 15 January 2024).
- Hadi, B.; Khosravi, A.; Sarhadi, P. Deep reinforcement learning for adaptive path planning and control of an autonomous underwater vehicle. Appl. Ocean Res. 2022, 129, 103326. [Google Scholar] [CrossRef]
- Tang, Z.; Cao, X.; Zhou, Z.; Zhang, Z.; Xu, C.; Dou, J. Path planning of autonomous underwater vehicle in unknown environment based on improved deep reinforcement learning. Ocean Eng. 2024, 301, 117547. [Google Scholar] [CrossRef]
- Yao, X.; Wang, F.; Wang, J.; Wang, X. Optimal time path planning for underwater robots in uncertain current environments. Control Theory Appl. 2020, 37, 1302–1310. Available online: https://jcta.ijournals.cn/cta_cn/ch/reader/create_pdf.aspx?file_no=CCTA190273&flag=1&journal_id=cta_cn&year_id=2020 (accessed on 15 January 2024).
- Zhao, J.; Deng, C.; Yu, H.; Fei, H.; Li, D. Path planning of unmanned vehicles based on adaptive particle swarm optimization algorithm. Comput. Commun. 2024, 216, 112–129. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, W.; Rahmani, A. Multi-robot path planning using learning-based artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2024, 129, 107579. [Google Scholar] [CrossRef]
- Li, G.; Liu, C.; Wu, L.; Xiao, W. A mixing algorithm of ACO and ABC for solving path planning of mobile robot. Appl. Soft Comput. 2023, 148, 110868. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Wu, W. A hybrid path planning algorithm considering AUV dynamic constraints based on improved A* algorithm and APF algorithm. Ocean Eng. 2023, 285, 115333. [Google Scholar] [CrossRef]
- Huang, H.; Wen, X.; Niu, M.; Miah, M.S.; Wang, H.; Gao, T. Multi-Objective Path Planning of Autonomous Underwater Vehicles Driven by Manta Ray Foraging. J. Mar. Sci. Eng. 2024, 12, 88. [Google Scholar] [CrossRef]
- Zhan, B.; An, S.; He, Y.; Wang, L. Three-Dimensional Path Planning for AUVs Based on Standard Particle Swarm Optimization Algorithm. J. Mar. Sci. Eng. 2022, 10, 1253. [Google Scholar] [CrossRef]
- Li, X.; Yu, S. Three-dimensional path planning for AUVs in ocean currents environment based on an improved compression factor particle swarm optimization algorithm. Ocean Eng. 2023, 280, 114610. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Khlie, K.; Bektemyssova, G.; Dehghani, M.; Gherabi, Y. Bobcat Optimization Algorithm: An Effective Bio-Inspired Metaheuristic Algorithm for Solving Supply Chain Optimization Problems. Sci. Rep. 2024, 14, 20099. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 1–102. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Elsayed, S. Efficient algorithms for optimal path planning of unmanned aerial vehicles in complex three-dimensional environments. Knowledge-Based Syst. 2025, 316, 113344. [Google Scholar] [CrossRef]
- Yan, Z.; Zhao, Y.; Chen, T.; Chi, D. UUV path planning under imprecise navigation information. J. Harbin Eng. Univ. 2016, 34, 715–720. Available online: https://kns.cnki.net/kcms2/article/abstract?v=C4JADW50D8s1hinXkUZ97bX3anrmFYfaH23Ol6exB1K9ryYMxrbYSuPB_wb_QdPyy9XTipAK9myKiPDdftpYPEIJBQgXSz6cienHrEqvfGvBNaBfVE--nwldTCckIS_Fj4qtZBkWkEu6BVDTjzgJozIXxPQOgUT7i7Go7-oUEkz3aY3KA49CBg==&uniplatform=NZKPT&language=CHS (accessed on 15 January 2024).
- Li, B.; Chiong, R.; Lin, M. A two-layer optimization framework for UAV path planning with interval uncertainties. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Production and Logistics Systems (CIPLS), Orlando, FL, USA, 9–12 December 2014; IEEE: New York, NY, USA, 2014; pp. 120–127. [Google Scholar]
- Yao, X.; Wang, F.; Yuan, C.; Wang, J.; Wang, X. Path planning for autonomous underwater vehicles based on interval optimization in uncertain flow fields. Ocean Eng. 2021, 234, 108675. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Integrated path planning and tracking control of an AUV: A unified receding horizon optimization approach. IEEE/ASME Trans. Mechatron. 2016, 22, 1163–1173. [Google Scholar] [CrossRef]
- Garrido, S.; Moreno, L.; Lima, P.U. Robot formation motion planning using fast marching. Robot. Auton. Syst. 2011, 59, 675–683. [Google Scholar] [CrossRef]
- National Earth System Science Data Sharing Platform. Scientific Data Center for the South China Sea and Adjacent Sea Areas. 2024. Available online: https://mds.nmdis.org.cn/pages/home.html (accessed on 15 June 2024).
- Li, D.; Luo, K.; Dang, J.; Wang, Y.; Zhang, Y. Kinematics and dynamics modeling of super-vacuum underwater vehicles. Syst. Eng. Theory Pract. 2013, 22, 2437–2442. Available online: https://sysengi.cjoe.ac.cn/CN/10.12011/1000-6788(2013)9-2437 (accessed on 15 January 2024).
- Zeng, Z.; Sammut, K.; He, F.; Lammas, A. Efficient path evaluation for AUVs using adaptive B-spline approximation. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; IEEE: New York, NY, USA, 2012; pp. 1–8. [Google Scholar]
- Zhang, Y. Particle Swarm Optimization Theory and Application to Interval Multi-Objective Optimization Problems. Ph.D. Thesis, China University of Mining and Technology, Jiangsu, China, 2009. Available online: https://kns.cnki.net/kcms2/article/abstract?v=WYPw_9jmhsJ08KKY_p1h5c8hH_dt7sQMK2Qgp8TnkzsXD5wSnfOF7zq1-fxix8vpINggLDot1JN6kDysz7_4J-hhj8NigUMGkHwdRaq7Lwdeo3cm0XXfFC6QB5PawIY49erFT9_M2juP8HTj2hwvJmCFQuknIxxh&uniplatform=NZKPT&language=CHS (accessed on 15 January 2024).
- Guo, X.; Ji, M.; Zhang, W.; Zhang, J.; Lingrui, K. Improved QPSO algorithm for dynamic path planning of autonomous underwater vehicles in variable ocean current environment. Syst. Eng. Theory Pract. 2021, 41, 2112–2124. [Google Scholar] [CrossRef]
- Jiang, C.; Han, X.; Xie, H. Theory and Methods of Optimal Design with Interval Uncertainty; Science Press of China: Beijing, China, 2017. [Google Scholar]
- Kim, S.; Noh, Y. Optimizing and Visualizing Drone Station Sites for Cultural Heritage Protection and Research Using Genetic Algorithms. Systems 2025, 13, 435. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
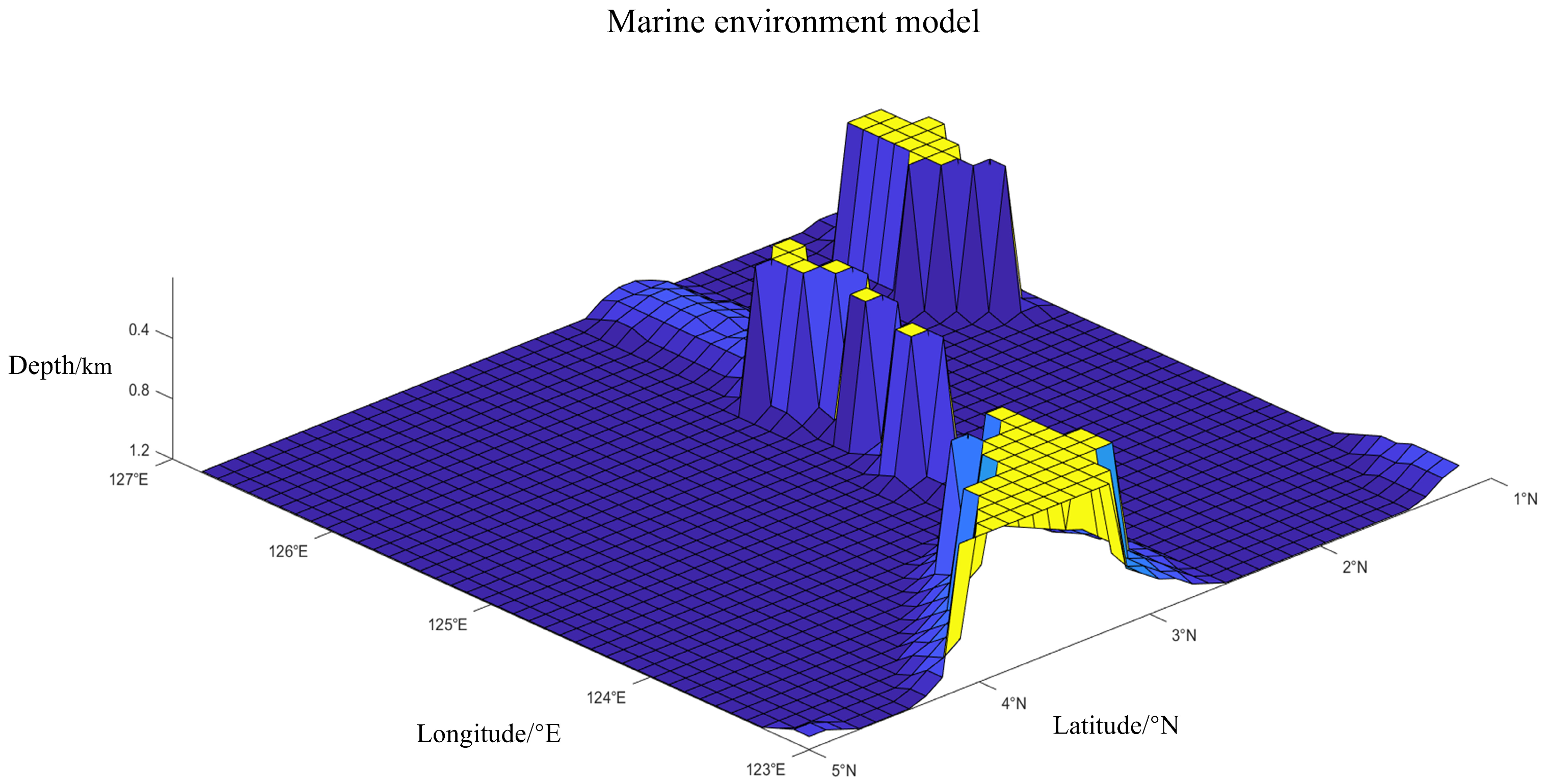
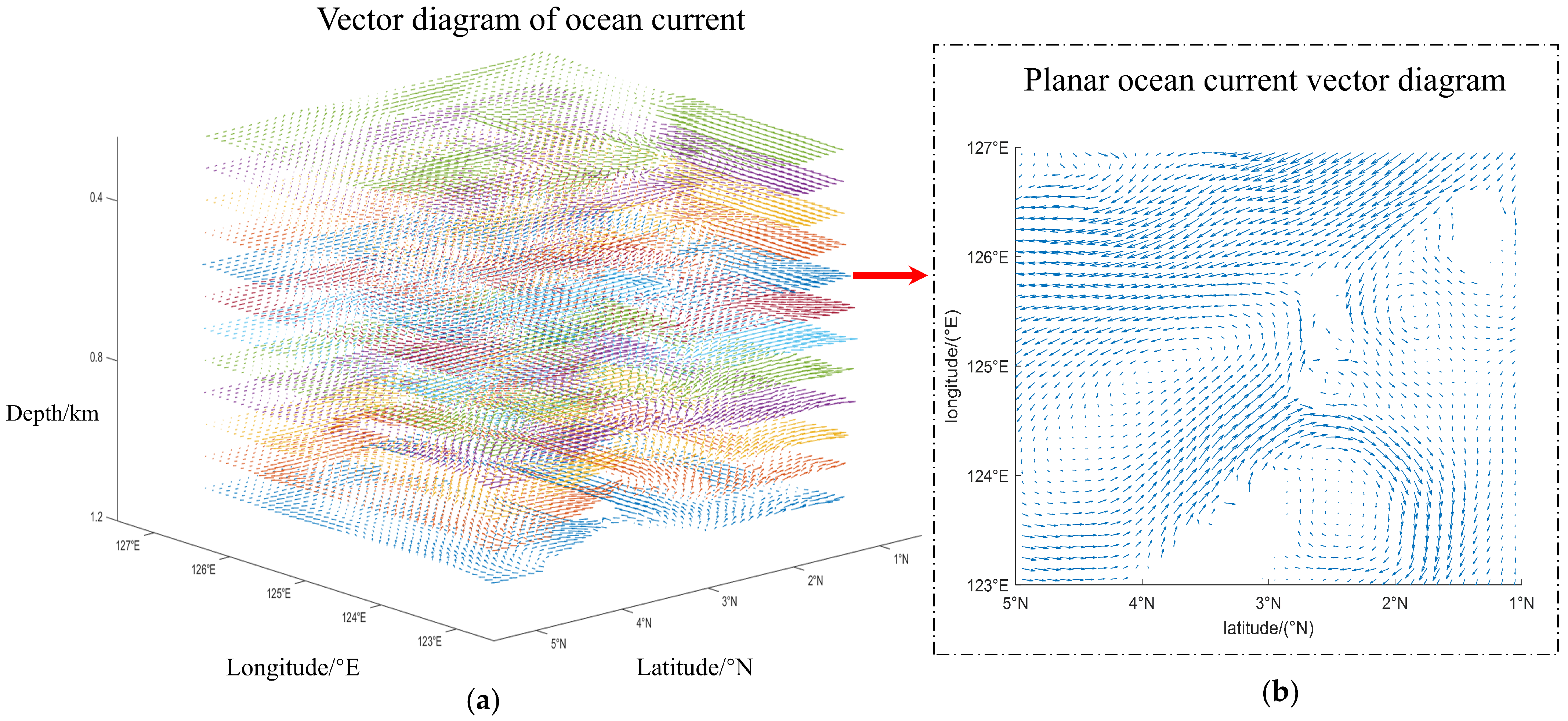

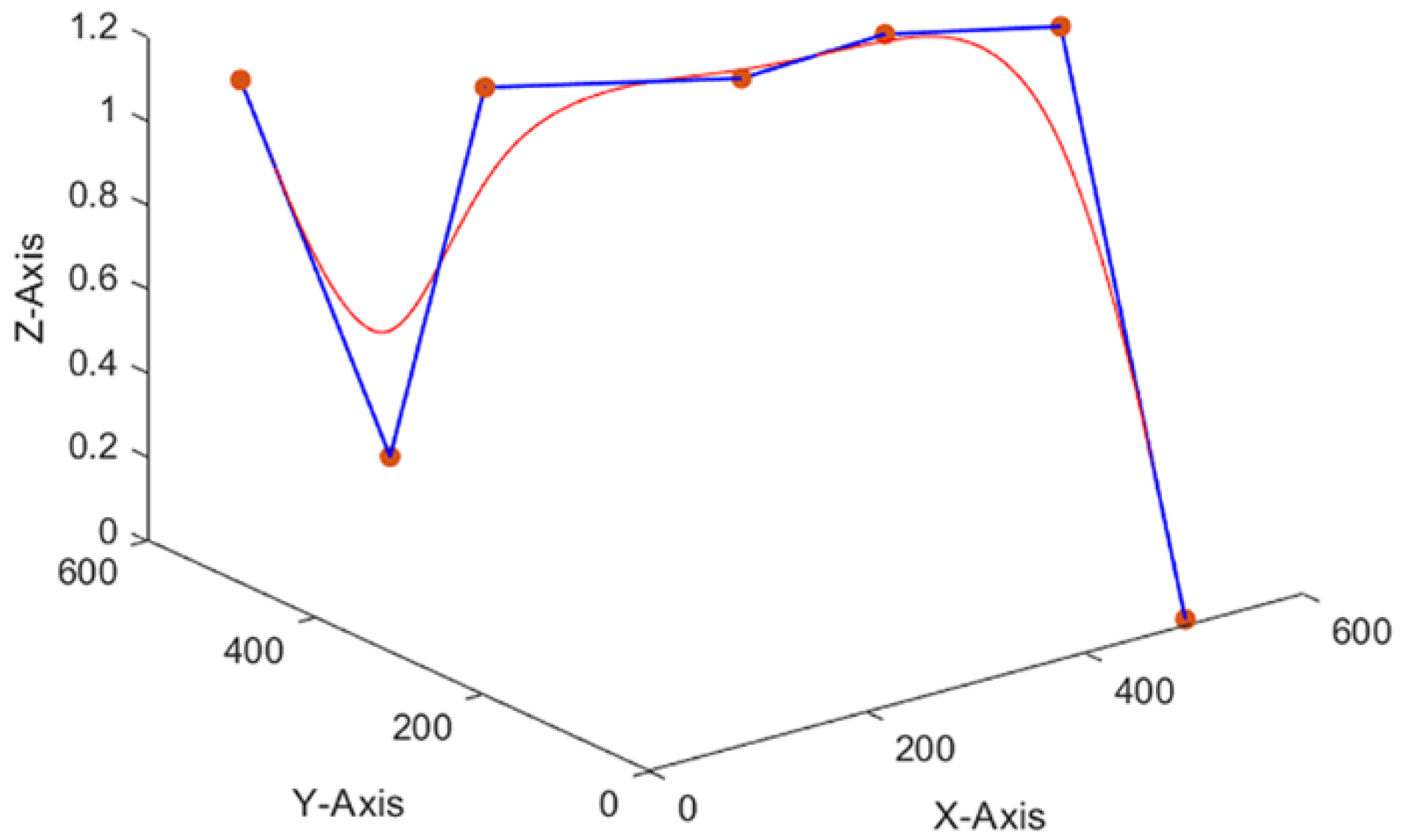
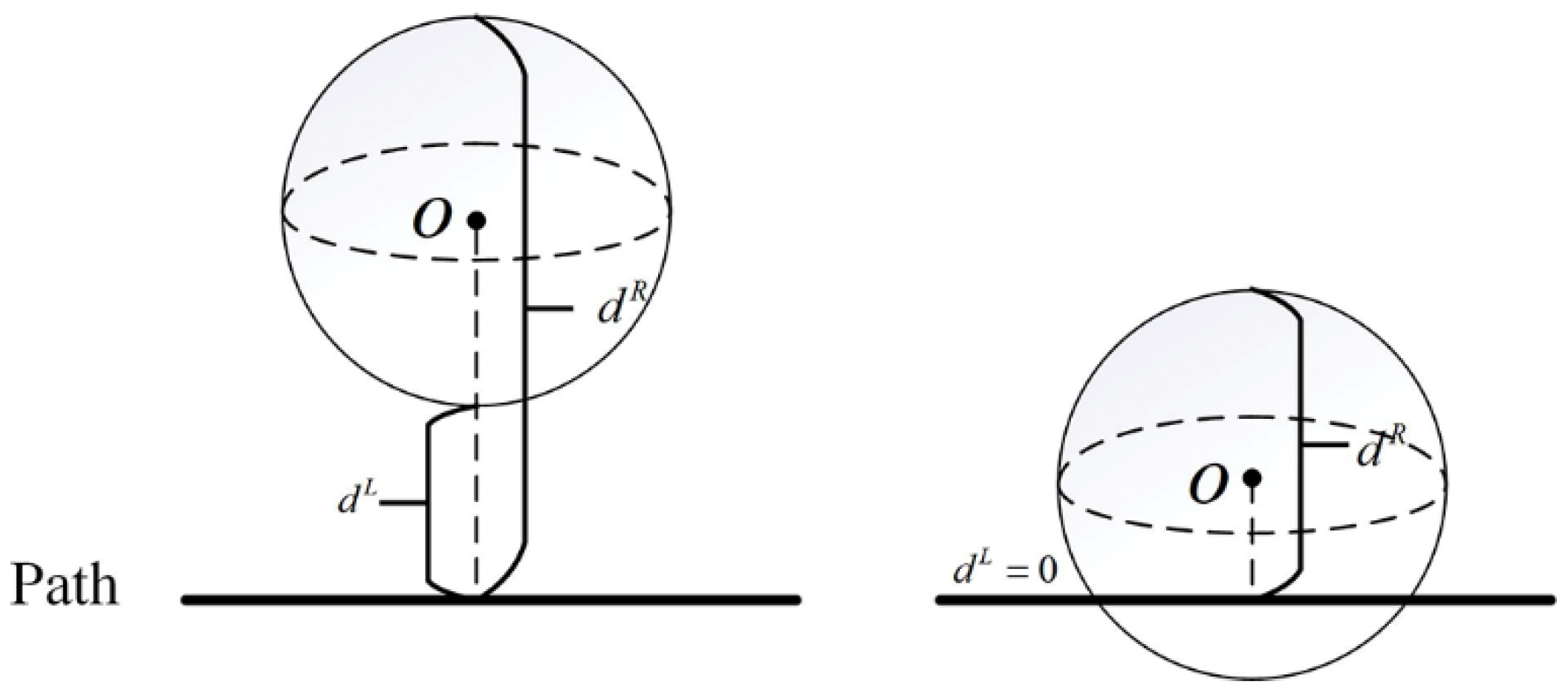
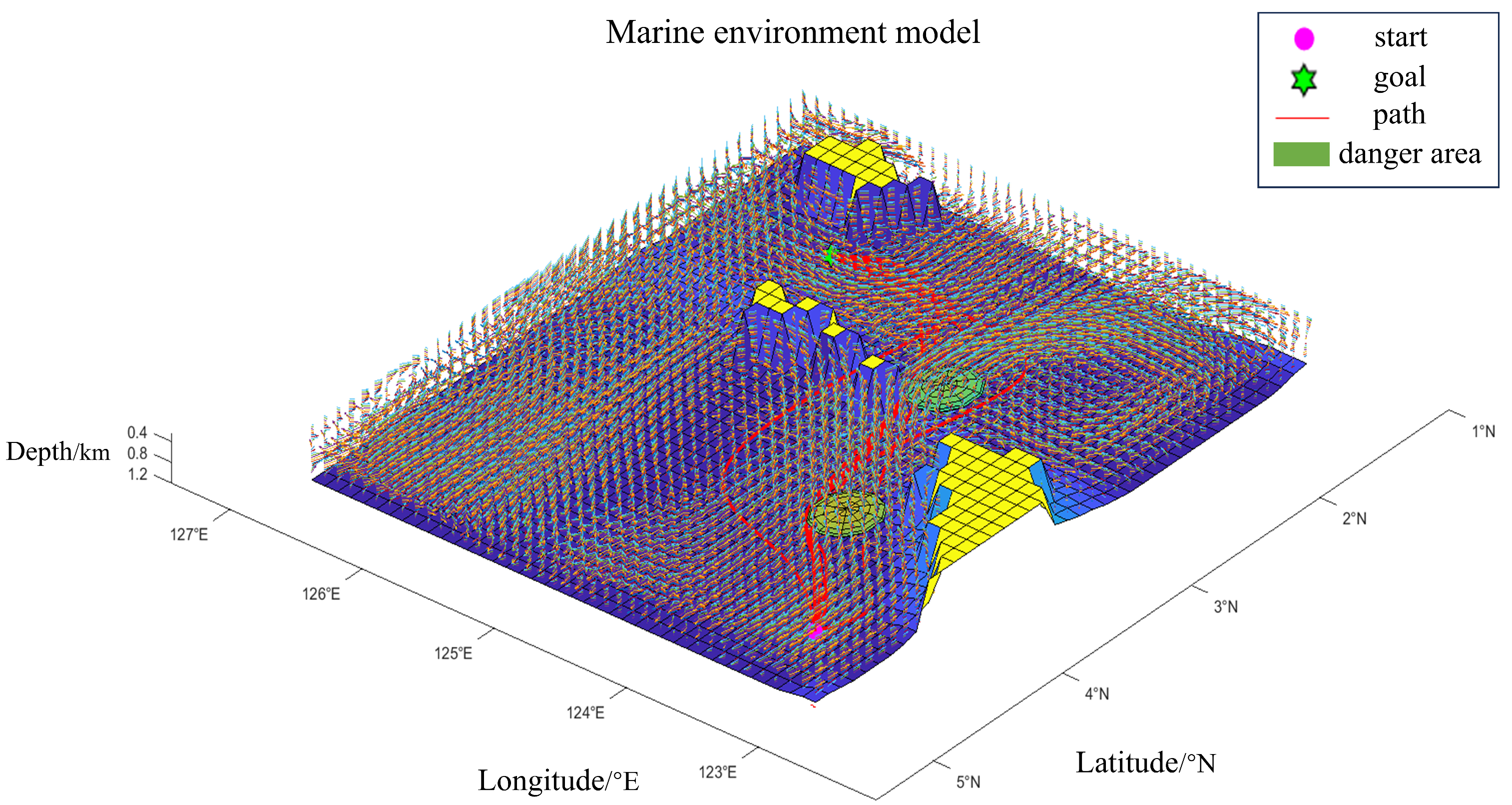
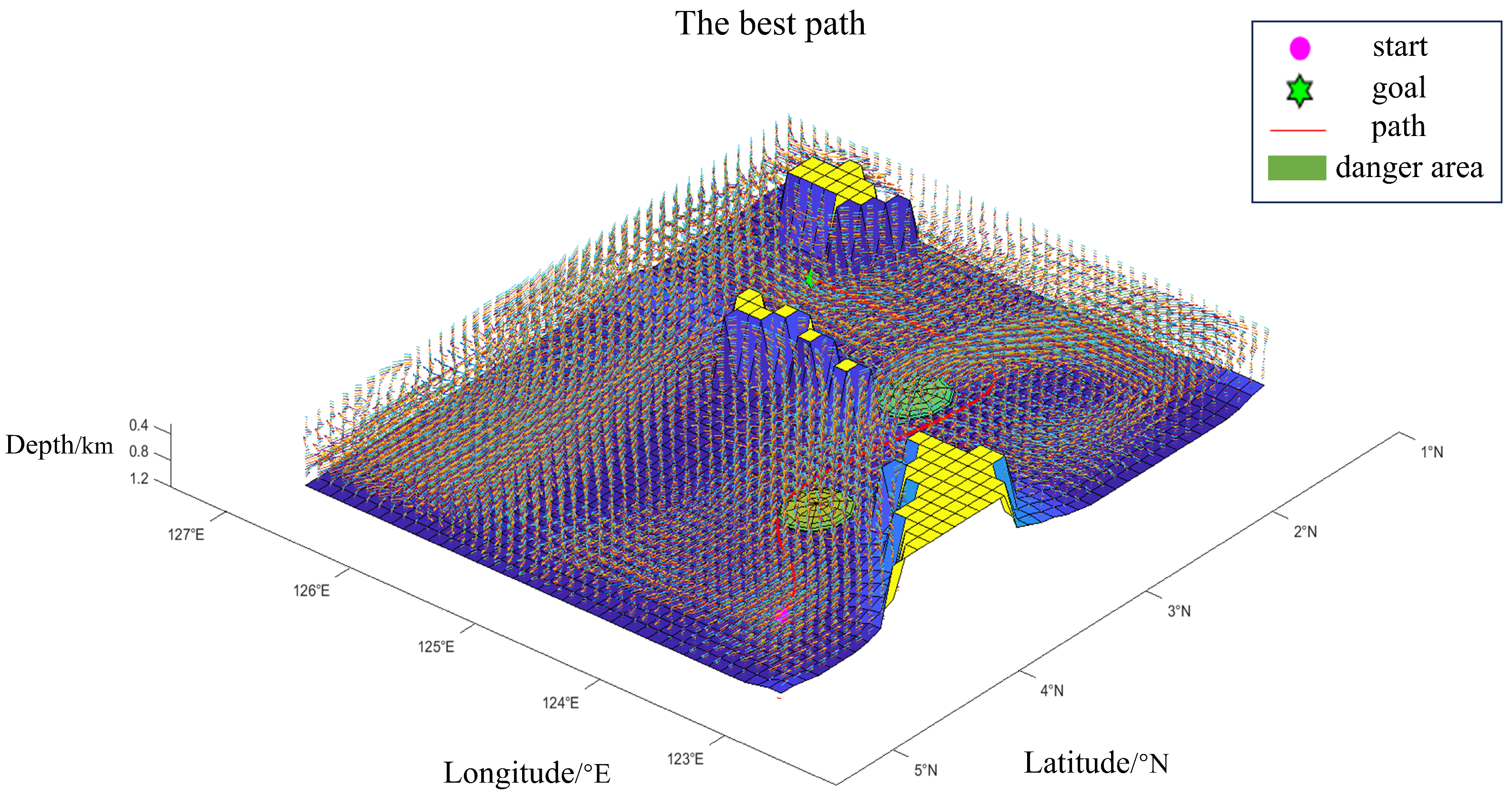
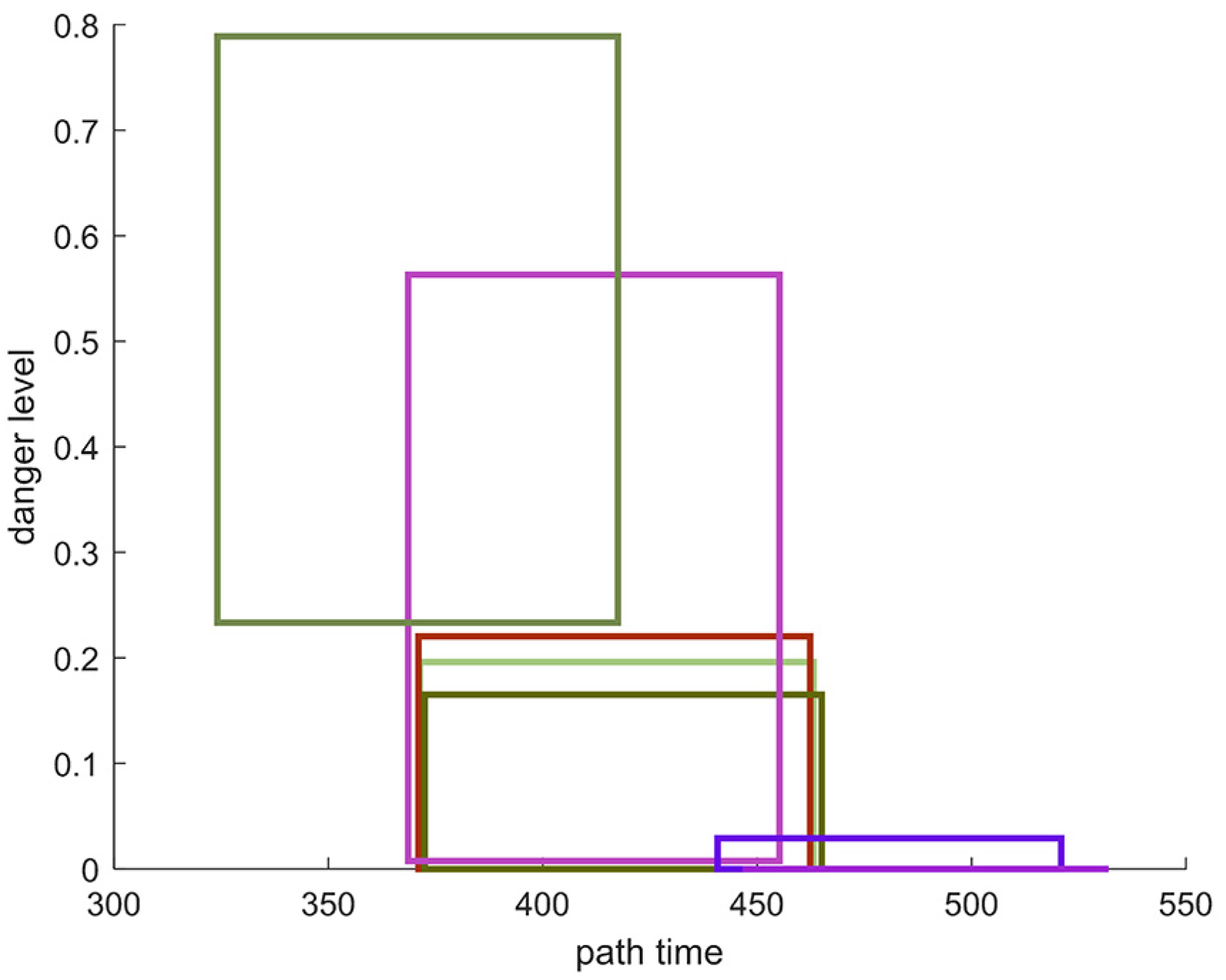
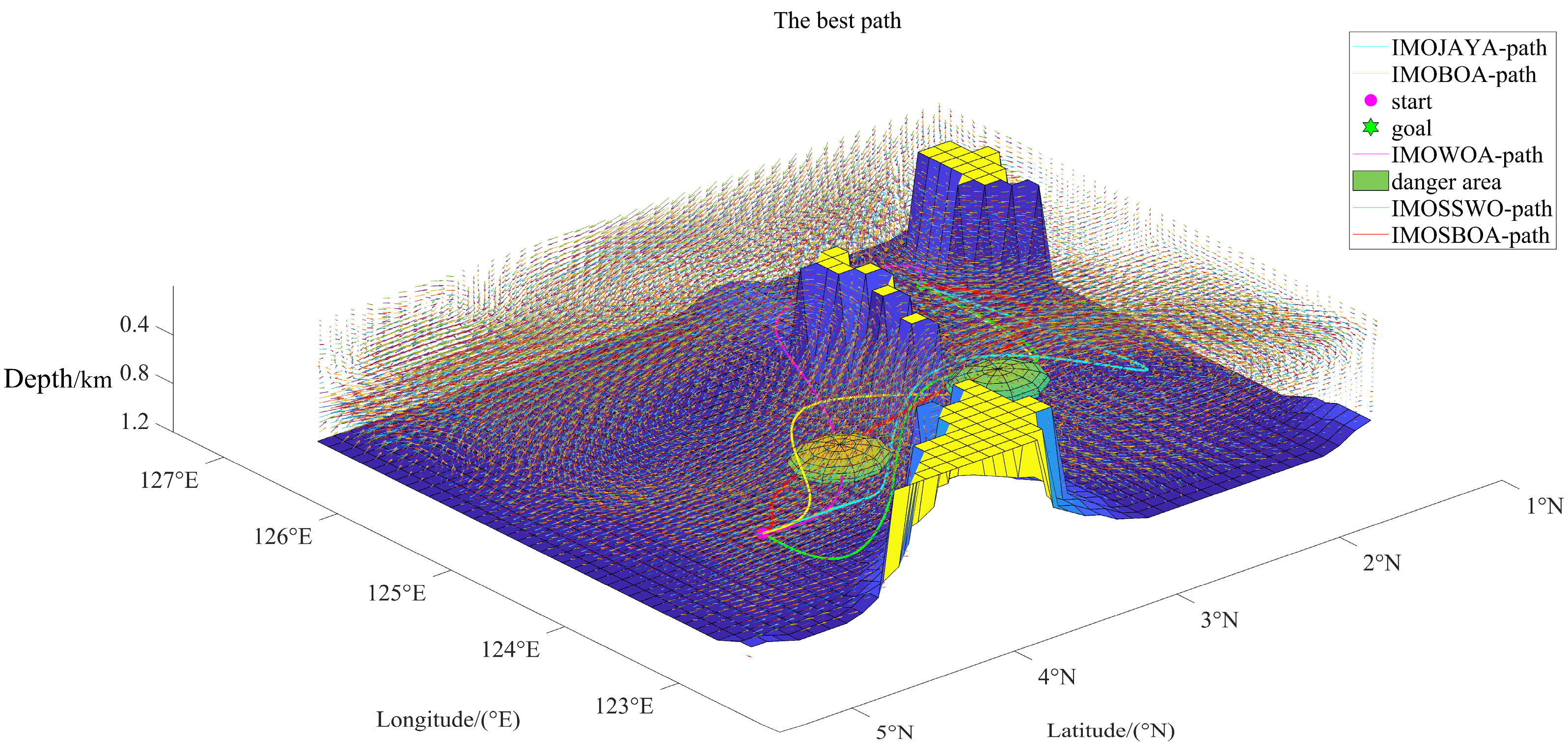
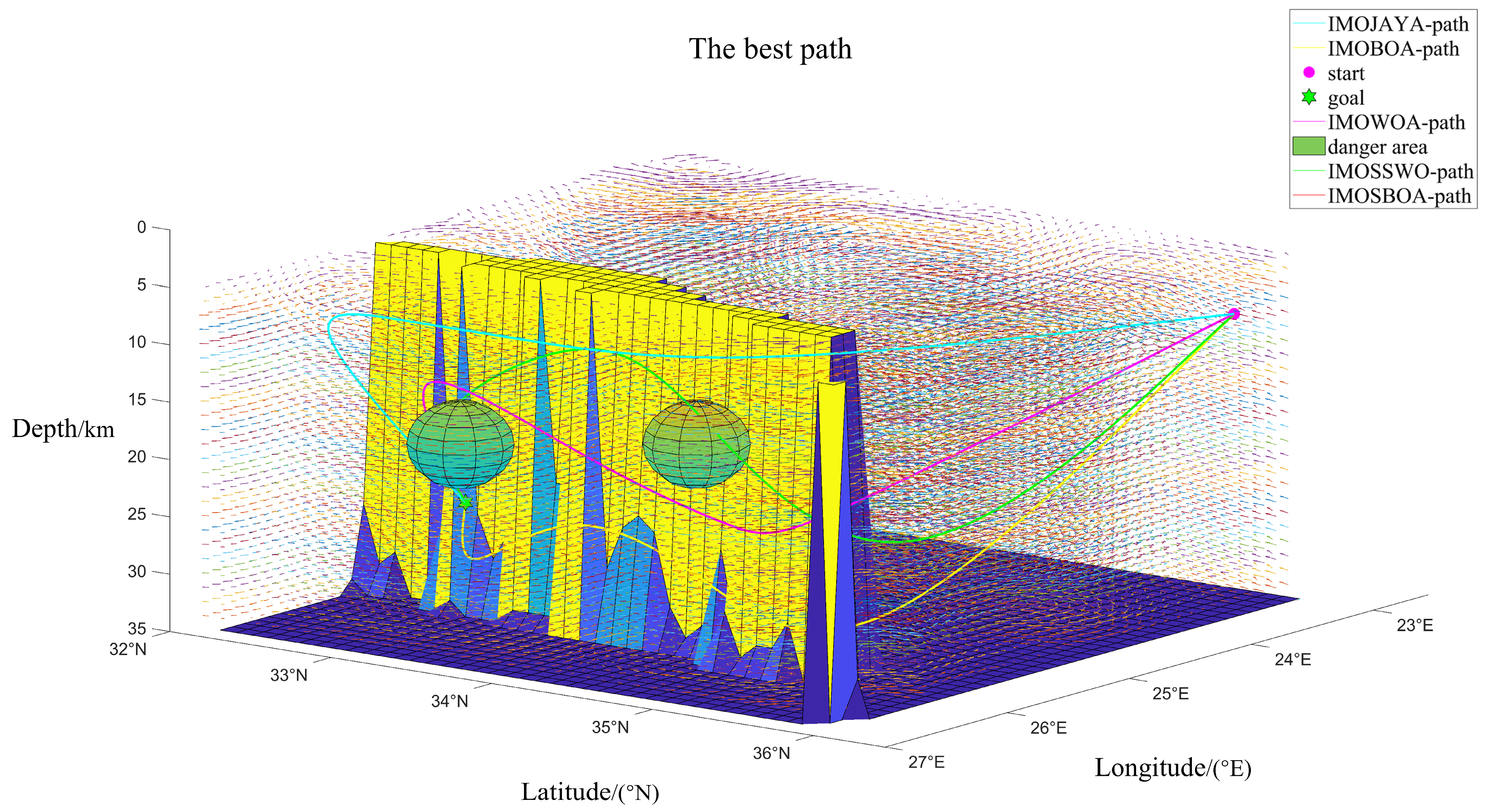
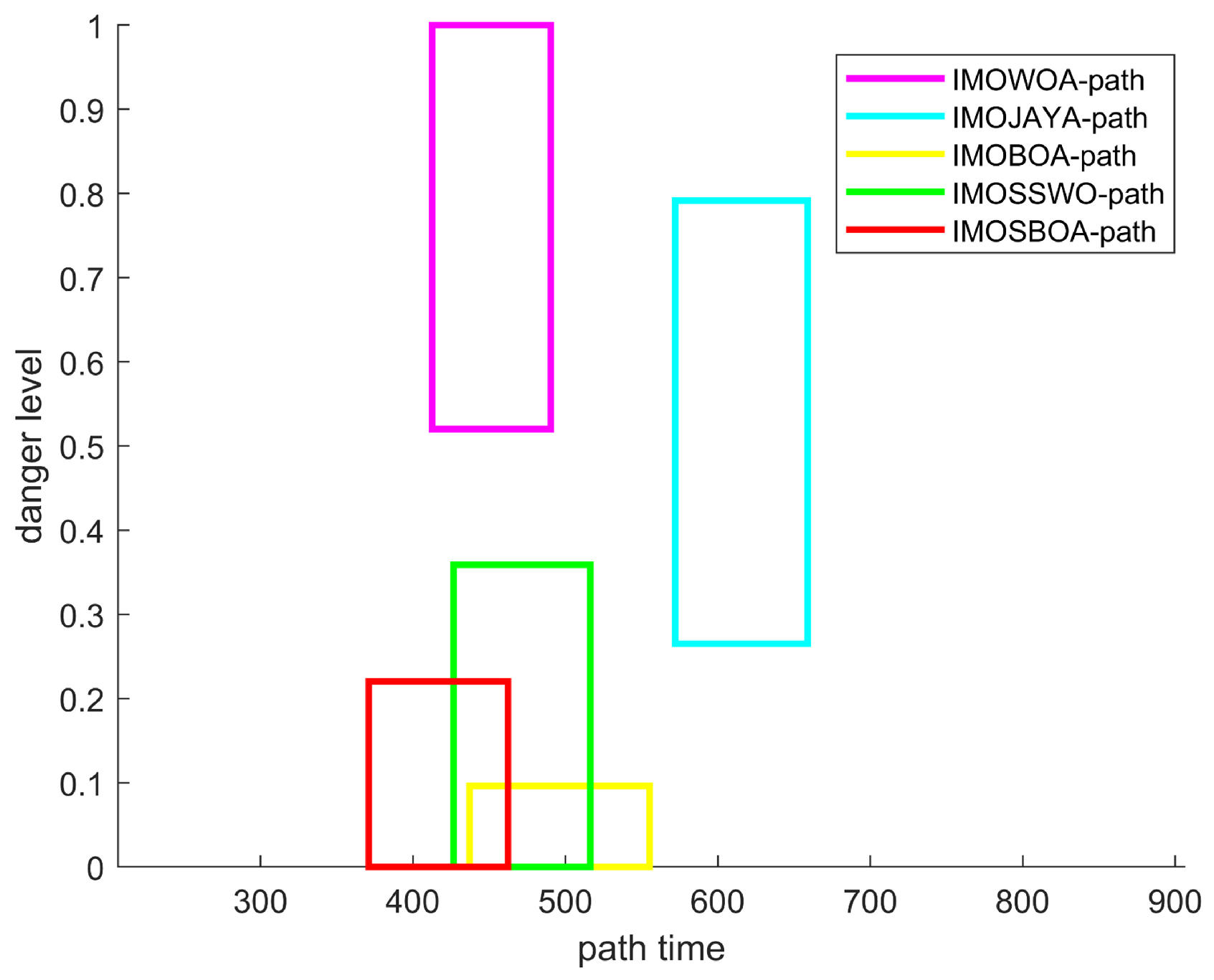




| Path | Path Length/km | Navigation Time Interval/103s | Danger Level Interval | Smoothness |
|---|---|---|---|---|
| 1 | 500.9485 | [446.6056, 531.9796] | [0, 0] | 10.9812 |
| 2 | 492.8639 | [440.7722, 520.9105] | [0, 0.0291] | 11.5765 |
| 3 | 477.1668 | [324.0923, 417.5034] | [0.2333, 0.7889] | 2.4798 |
| 4 | 464.5595 | [368.5957, 455.2428] | [0.0075, 0.5631] | 10.2770 |
| 5 | 467.4834 | [372.4773, 465.0564] | [0, 0.1651] | 10.4107 |
| 6 | 468.0104 | [371.0080, 462.3871] | [0, 0.2204] | 11.0351 |
| 7 | 468.3167 | [371.2707, 463.1554] | [0, 0.1961] | 10.4973 |
| Algorithm | Navigation Time Interval/103 s | Danger Level Interval | Path Length/km | Computing Time/s |
|---|---|---|---|---|
| IMOWOA | [412.5829, 490.4883] | [0.5201, 1] | 498.3725 | 61.23 |
| IMOJAYA | [572.0301, 658.7970] | [0.2651, 0.7914] | 598.5563 | 39.41 |
| IMOBOA | [437.1723, 555.1822] | [0, 0.0962] | 547.7081 | 56.15 |
| IMOSSWO | [426.7163, 516.3460] | [0, 0.3589] | 479.7072 | 57.54 |
| IMOSBOA | [371.0080, 462.3871] | [0, 0.2204] | 468.0104 | 53.31 |
| Algorithm | Navigation Time Interval/103 s | Danger Level Interval | Path Length/km | Computing Time/s |
|---|---|---|---|---|
| IMOWOA | [623.9901, 681.0871] | [0, 0.6395] | 642.1754 | 66.12 |
| IMOJAYA | [803.1691, 873.0247] | [0, 0] | 762.6046 | 42.43 |
| IMOBOA | [592.7619, 646.0583] | [0.4824, 1] | 604.2674 | 59.21 |
| IMOSSWO | [619.6304, 672.3713] | [0, 1] | 629.9831 | 64.12 |
| IMOSBOA | [587.0511, 622.3068] | [0.1724, 0.6904] | 614.4075 | 57.41 |
| Path | Path Length/km | Navigation Time/103 s | Danger Level | Smoothness |
|---|---|---|---|---|
| 1 | 458.0690 | 355.0283 | 0.0151 | 10.5530 |
| 2 | 483.1942 | 345.9630 | 0.2304 | 10.5788 |
| 3 | 471.0274 | 366.1326 | 0.0139 | 10.3139 |
| 4 | 490.9841 | 367.1387 | 0 | 6.8358 |
| 5 | 457.0748 | 349.1657 | 0.0339 | 10.5089 |
| 6 | 457.0778 | 349.1484 | 0.0334 | 10.5088 |
| 7 | 456.0678 | 348.1328 | 0.0339 | 10.4975 |
| Path | Navigation Time/103 s | Danger Level | Infeasible Frequency | ||||
|---|---|---|---|---|---|---|---|
| Min | Max. | Variance | Min | Max. | Variance | ||
| 1 | 454.4884 | 461.7078 | 0.9808 | 0 | 0 | 0 | 0 |
| 2 | 394.8548 | 400.4809 | 0.7680 | 0 | 0.1624 | 0.0027 | 0 |
| 3 | 385.0747 | 389.5581 | 0.6118 | 0 | 0.1669 | 0.0030 | 0 |
| 4 | 380.2231 | 384.7294 | 0.5359 | 0 | 0.3515 | 0.0095 | 0 |
| 5 | 369.2018 | 374.4385 | 0.6850 | 0 | 0.3759 | 0.0078 | 0 |
| 6 | 362.6054 | 366.5972 | 0.4089 | 0.0631 | 0.5399 | 0.0068 | 0 |
| 7 | 365.2121 | 369.3468 | 0.4218 | 0.0639 | 0.5044 | 0.0101 | 0 |
| Path | Navigation Time/103 s | Danger Level | Infeasible Frequency | ||||
|---|---|---|---|---|---|---|---|
| Min | Max. | Variance | Min | Max. | Variance | ||
| 1 | 353.1453 | ∞ | - | 0 | 0.1996 | 0.0041 | 9 |
| 2 | 339.7723 | ∞ | - | 0.0248 | 0.4321 | 0.0062 | 5 |
| 3 | 337.6752 | 341.7815 | 0.4310 | 0 | 0.2911 | 0.0046 | 0 |
| 4 | 359.9571 | ∞ | - | 0 | 1 | 0.0080 | 23 |
| 5 | 324.5049 | 328.3586 | 0.3118 | 0.1178 | 0.6212 | 0.0107 | 0 |
| 6 | 325.7989 | 330.0194 | 0.3675 | 0.0280 | 0.4172 | 0.0051 | 0 |
| 7 | 325.8614 | 329.2105 | 0.3165 | 0.1313 | 0.5334 | 0.0053 | 0 |
| Uncertainty | Infeasible Frequency | ||
|---|---|---|---|
| sdirect (◦) | smangi (m/s) | IMOSBOA | MOSBOA |
| 5 | 0.05 | 0 | 0 |
| 5 | 0.1 | 0 | 0 |
| 5 | 0.15 | 0 | 0 |
| 10 | 0.05 | 0 | 0 |
| 10 | 0.1 | 0 | 21 |
| 10 | 0.15 | 3 | 54 |
| 20 | 0.05 | 5 | 87 |
| 20 | 0.1 | 9 | 132 |
| 20 | 0.15 | 20 | 275 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Qi, L.; Ye, S.; Li, C.; Ni, T.; Guo, J.; Liu, H.; Li, Y.; Zuo, D.; Shi, J.; et al. Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm. Symmetry 2025, 17, 993. https://doi.org/10.3390/sym17070993
Tang R, Qi L, Ye S, Li C, Ni T, Guo J, Liu H, Li Y, Zuo D, Shi J, et al. Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm. Symmetry. 2025; 17(7):993. https://doi.org/10.3390/sym17070993
Chicago/Turabian StyleTang, Runkang, Liang Qi, Shuxia Ye, Changjiang Li, Tian Ni, Jia Guo, Huan Liu, Yushan Li, Danfeng Zuo, Jiayu Shi, and et al. 2025. "Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm" Symmetry 17, no. 7: 993. https://doi.org/10.3390/sym17070993
APA StyleTang, R., Qi, L., Ye, S., Li, C., Ni, T., Guo, J., Liu, H., Li, Y., Zuo, D., Shi, J., & Gong, J. (2025). Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm. Symmetry, 17(7), 993. https://doi.org/10.3390/sym17070993






