In this study, we extend the classical single-particle approximation by incorporating the implications of a hidden SL(2,R) symmetry in the governing equations of motion. Using Riccati-type differential structures and projective geometry, we investigated emergent behaviors associated with inertial instability in a rotating, stratified atmosphere. These include synchronization phenomena such as phase coupling, quasi-periodic transitions, and bifurcations, which arise from local imbalances in geostrophic shear and vorticity. Unlike traditional models that linearize around balanced flows, our approach captures nonlinear coherence across dynamically distinct atmospheric regions through geometric invariants. By projecting the inertial dynamics onto the SL(2,R) group manifold, we constructed a framework in which symmetry-preserving transformations generate structured transitions between dynamical regimes.
Such an analysis is not isolated. Recent applications of SL(2,R) symmetry in complex fluid systems support the use of this formalism in the context of inertial instability [
16]. Moreover, studies such as [
17,
18] emphasized the foundational role of projective geometry in physics, showing that homographic transformations preserve the structural form of fundamental equations—validating their use in modeling the projective synchronization of dynamically distinct regions within the atmosphere. Rebelo and Winternitz [
19] demonstrated that differential equations possessing SL(2,R) symmetry exhibit robust qualitative features under symmetry-preserving transformations, reinforcing our interpretation of structural coherence as an emergent property governed by the Schwarzian derivative. In addition, the work of Arkani-Hamed, Bai, and Lam [
20] illustrated how complex dynamical systems can be embedded within projective geometries and positive structures, offering a contemporary theoretical basis for our application of projective parameters to describe emergent synchronization patterns in inertially unstable flows.
Inertial-gravity waves and Rossby waves (associated with baroclinic instability) can interact within nonlinear systems. In weakly stratified regimes or in the presence of strong vertical shear, hybrid instabilities may emerge. Certain models such as those based on the primitive equations or extended quasi-geostrophic formulations can be employed to analyze the transition between weak baroclinic instability and inertially unstable regimes. All computations were performed using GNU Octave 8.4.0 (Free Software Foundation, Boston, MA, USA), a MATLAB-compatible open-source software.
2.1. Synchronizations/Desynchronizations and Atmospheric Dynamics
By generalizing the inertial motion of a particle moving horizontally in a flow corresponding to a zonal geostrophic basic state with velocity
, and assuming that the particle’s displacement does not perturb the pressure field, one obtains the equation of motion (1), as detailed in
Appendix A [
8]:
which represents the motion of a particle moving horizontally and meridionally in the atmosphere. In our model, we assumed that the atmosphere can be assimilated, both structurally and functionally, into a complex system in which its structural units are in continuous interaction. This relation describes inertial oscillations in a sheared geostrophic flow, where stability depends on the sign of the quantity
. It is important to note that this formulation addresses inertial instability rather than baroclinic instability, as the latter requires vertical shear
.
Equation (1) models the meridional oscillations of an air parcel under the influence of planetary rotation and shear, which serve as a local representation of such instabilities. Each atmospheric cell can thus be interpreted as an oscillatory unit whose dynamics are governed by this fundamental differential equation.
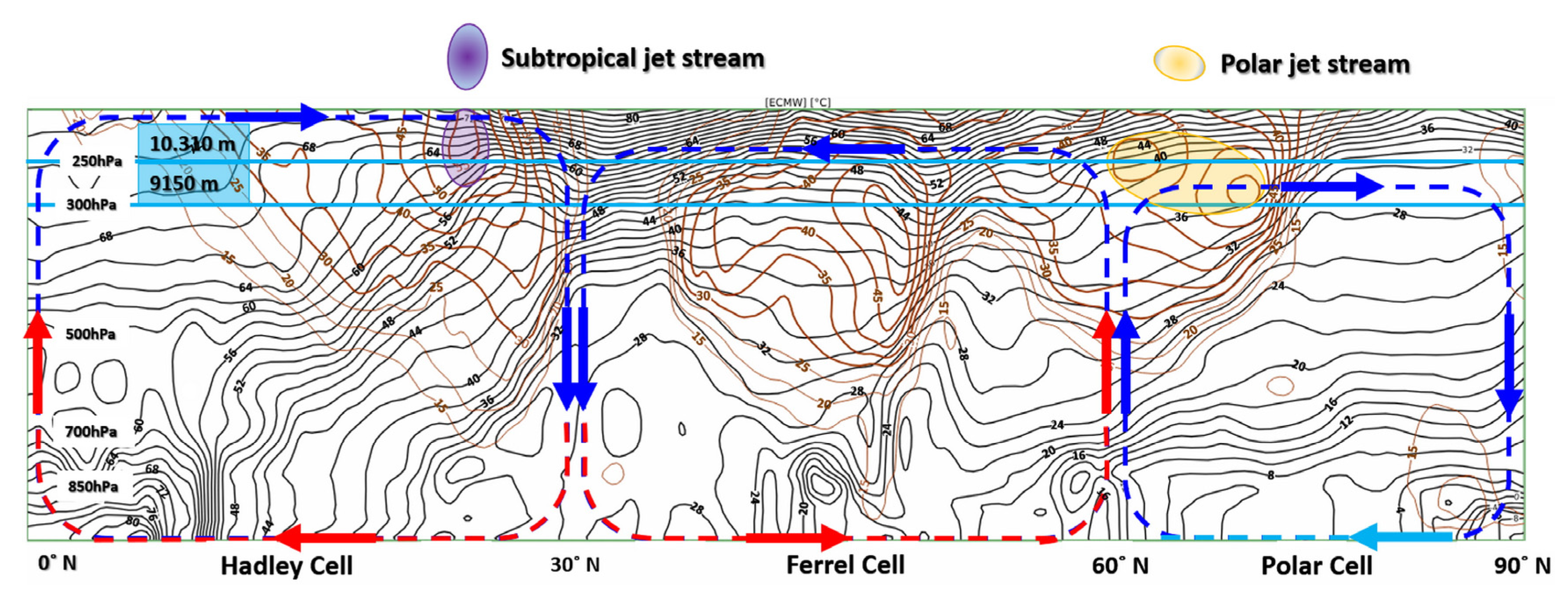
The Coriolis force influences the winds in the Ferrel cell by causing their deflection, which results in the prevailing westerlies between 30° and 60° latitude. In addition, the polar jet stream influences mid-latitude weather patterns by steering storm systems and affecting temperature contrasts. In summer, its northward shift generally leads to weaker storm activity, while in winter, its southward displacement contributes to more frequent and intense storms, cold spells, and precipitation events [
2,
3,
4].
Rossby waves, whose propagation is enabled by the variation of the Coriolis parameter with latitude (the so-called β-effect), play an essential role in large-scale atmospheric dynamics. While the β-effect does not generate Rossby waves directly, it allows their existence and provides the restoring force that governs their behavior. In a barotropic environment, where density depends only on pressure, Rossby waves conserve absolute vorticity. In contrast, in a baroclinic environment, where density depends on both pressure and temperature, air parcels conserve potential vorticity under adiabatic and frictionless conditions. These waves are fundamental in the development of mid-latitude weather patterns and in the large-scale transport of energy and momentum in the atmosphere. These waves facilitate the transport of energy and matter between atmospheric regions. Barotropic instability is associated with horizontal variations in flow and contributes to the transfer of kinetic energy, while baroclinic instability is linked to vertical variations and promotes the conversion of potential energy into kinetic energy. These mechanisms are crucial for the formation of cyclones and atmospheric fronts.
Now, we must mention that Equation (1) originates from a classical inertial instability derivation under the quasi-geostrophic framework [
8]. These result from linearizing the motion of a parcel displaced meridionally in a zonal geostrophic shear, using the assumption that vertical motion is negligible compared to horizontal dynamics. While this simplification focuses on horizontal accelerations in a rotating frame, it serves here as a proxy for instability onset, allowing for analytical tractability and symmetry analysis (for details, see
Appendix A).
Although Equation (1) is a linear equation, certain nonlinear behaviors may result not from the differential form itself but from symmetries induced by both the structure of the equation and its solutions (we call this a hidden symmetry). Lie symmetries are usually used to obtain analytical solutions of differential equations; their composition under projective mappings (e.g., Riccati flows and Schwarzian derivatives) may induce emergent behavior such bifurcations, period doubling, or intermittent dynamics. This happens in extended dynamical settings, particularly in cases when non-autonomous or connected systems undergo transformations, preserving their symmetry [
21,
22].
Using the notations
the differential Equation (1) becomes
The most general solution of Equation (3) can be written as
where
is the complex conjugate of
. The quantities
and
give the initial conditions, which are not the same for every point in space. More precisely, the various atmospheric structural units corresponding to different points in space are in different states and have different phases. A problem arises: is it possible to give a priori connection between the parameters
,
and
of the various atmospheric structural units at a given time? Since Equation (4) is a solution of Equation (3), it allows us to give an affirmative answer to this problem. Indeed Equation (3) possesses a hidden “symmetry” that can be expressed by the homographic group: the ratio of two solutions of Equation (3) is a solution of Schwartz’s equation [
16,
23,
24,
25]:
where the symbol
defines the derivative with respect to time.
The homographic transformation connects the analytical solutions of the linear equation with the nonlinear behaviors of the atmosphere.
In the context of this study, it transforms a simple local model into a framework capable of explaining the emergent organization of the global atmospheric circulation, providing a bridge between advanced mathematics (SL(2,R)) and dynamical meteorology.
Equation (5) arises from the ratio of two linearly independent solutions of Equation (3) (which is derived from Equation (1)). This ratio satisfies a Schwarzian differential equation that is invariant under the homographic transformations. Physically, this captures how phase synchronization between atmospheric structural units occurs in a system with inertial instability, which is governed by a shared underlying pulsation.
This construction implies that structural units (e.g., segments of an atmospheric cell) within the atmosphere as a complex system can interact and synchronize not only through explicit external forces, but also via a shared geometric symmetry. The ratio of the solutions thus becomes an “internal message” of the system, encoding how the relative phases of these structural units evolve over time. If two atmospheric structural units evolve such that the ratio of their solutions remains invariant with respect to a homographic transformation, they are said to be projectively synchronized—their individual evolutions differ, yet remain geometrically coherent.
This approach provides a unified framework for understanding collective oscillation modes, including intermittency, bifurcations, and nonlinear synchronization—phenomena that are experimentally observable in atmospheric, electrical, and optical systems [
26,
27,
28]. From a practical standpoint, one can envision a network of “atmospheric oscillators” that, although locally governed by linear equations, collectively give rise to complex emergent behaviors—precisely what is observed in jet streams, planetary waves, and stable climate cells.
This equation is invariant under the homographic transformation of : any homographic function of is itself a solution of Equation (5). As homography characterizes projectivity on a straight line, it can be stated that the ratio of two solutions of Equation (3) is a projective parameter for the set of atmospheric structural units of the same pulsation from a given spatial region.
We can easily construct a convenient projective parameter, which would be in one-to-one correspondence with the atmospheric structural unit. First, we observe a “universal” projective parameter—the ratio of the fundamental solutions of Equation (3):
Any homographic function of this ratio will again be a projective parameter. Among all the functions, the function
has, first of all, the advantage of being specific to each atmospheric structural unit. But not only that, another function
Is specific to another atmospheric structural unit.
The fact that Equations (7) and (8) are solutions of Equation (5) shows us that there is a homographic relationship between them:
Which, after it is clearly expressed, leads to the group equations [
16]
In such a framework, Equation (10) is identified with the synchronization group of atmospheric structural units. Through this group, the temporal adjustment of the dynamics of the atmospheric structural units (i.e., the local dynamics) is achieved with the global atmospheric dynamics. In practice, the atmospheric structural units adjust their behaviors so that they oscillate or vibrate synchronously. The structure of the group is typical of SL(2R), i.e., of the form
where
, k = 1, 2, 3 are the infinitesimal operators of the group with the expressions
This group admits the differential 1- forms (absolutely invariant through the group) [
14,
15,
16]
and differential 2-forms (metric):
The existence of a parallel transport of angles in the Levi-Civita sense [
16], which corresponds to the constraint
which transforms Equation (14) as follows:
Constraint (15) corresponds to in-phase synchronization of atmospheric structural unities. Thus, we can explain such a situation.
Let us consider an atmospheric field described by the variables
for which the metric
was discovered in an ambient metric space
In such a context, the field equations derive from the variational principle:
where
is the elementary volume, relative to the Lagrange function.
In our case, metric (17) is given by Equation (16), and the field variables are
and
. Then, the Lagrangian results are
which, according to the variational principle (19), leads to the atmospheric field equations
The solution of the first differentiable equation is written in the form
with
and real and arbitrary
. Obviously, the variational principle (19) and the atmospheric field Equations (22) respectively describe a harmonic mapping between the Euclidean space of metric
and the upper half of the plane complex space—the Poincaré representation of the hyperbolic plane with the metric given by Equation (16), known as the invariant metric of the group
.
2.2. Coherences/Decoherences in Atmospheric Dynamics
Let us reconsider Equation (9) which represents the homographic action of the matrix:
The problem we want to solve is the following: find the relationship between the set of matrices and a set of values of for which remains constant (in this context, a constant (derivative of the projective parameter) identifies a specific class of solutions where two atmospheric units evolve in such a way that their projective relationship remains geometrically fixed. This condition corresponds to projective synchronization and is used to define coherent dynamical relationships between regions). Geometrically, this means finding the set of points that uniquely corresponds to the parameter values .
Using Equation (9), our problem is solved by a Riccati differential equation that is obtained as a consequence of the constancy of
[
16], i.e.,
where we use the notations
It is easy to verify that the metric
is directly related to the discriminant of the quadratic polynomial from Equation (26):
The three differential 1-forms from Equation (27) construct a co-frame at any point in the absolute space [
16]. This co-frame allows us to translate the geometric properties of the absolute space into algebraic properties in correlation with differential Equation (26).
Most of these properties concern the motion on geodesics of the metric. In this case, differential 1-forms
are exact differentials in the same parameter—the length of the arc of the geodesic, for example,
s. Along these geodesics, Equation (26) transforms into an ordinary differential equation of the Riccati type (gauge of Riccati type):
Here, parameters
are constants that characterize a certain geodesic of the family. The most general solution of Equation (30) is obtained using the procedure from [
16,
17,
29]. For this purpose, let us consider the roots of the quadratic polynomial be incorporated in the right-hand side of differential Equation (30), i.e.,
Making the transformation
it follows that
is a solution of the differential equation:
Now, if we conveniently express the initial condition y (0), we can give the general solution of Equation (30) by simply inverting transformation (32), with the result
where
r and
s0 are two real constants that characterize the solution. Using Equation (31), we can write these solutions in real terms, that is
which explains a modulation of
by a Stoler transformation [
30], which leads us to the complex form of this parameter. Given the standard meaning of the Stoler transformation in the current context, it refers to the coherence/decoherence of atmospheric structural units in a given atmosphere (spatio-temporal correlation of local dynamics of atmospheric structural units within the global dynamics of a given atmosphere). Moreover, if we adopt the notation
Equation (35) becomes
where
has the expression
The meaning of the complex parameter was given in the previous section (see Equation (23)). For the moment, let us note that the coherence/decoherence process in the dynamics of atmospheric structural units is assimilated here to a process of modulation of
. More precisely, this process is a calibration of the difference between kinetic and potential energy—the classical definition of the Lagrangian—which leads this quantity to a perfect square. The physical significance of the perfect square Lagrangian is that it describes a fundamental physical unit (in our case, an atmospheric structural unit) within a complex system (in our case, the atmosphere), just as kinetic energy describes a free particle in space. Under these conditions, identifying Equation (23) with Equation (38) results in two-time scales, one corresponding to the time for the atmospheric structural unit and another corresponding to the time for the atmosphere. In general, by using Equation (35), various behaviors of the atmospheric structural units in the dynamics of atmosphere can be highlighted: period doubling, damped oscillations, quasi-periodicity, intermittency, chaos, etc., in accordance with [
16].
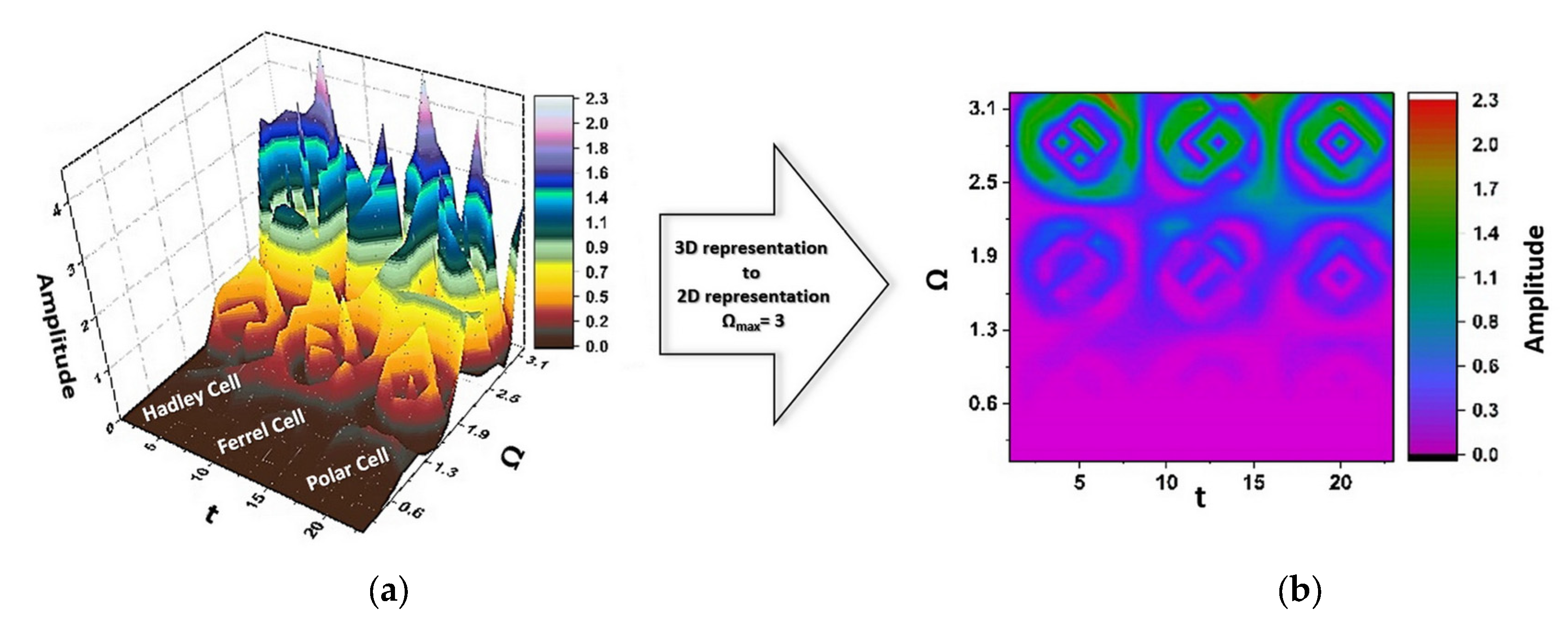
In such a context, we present in
Figure 2a,b the 3D and 2D dependences of Re (
) by
for
and r = 0.5, which mimic quasi-periodic-type behaviors. In our opinion, the tricellular model of general circulation of the atmosphere can be correlated with the quasi-periodicity modes of atmospheric dynamics.
In such a framework, the holographic behavior (the part reflects the whole and the whole reflects the part) appears as a universal property of the dynamics of structures in nature.
Then, Equation (1) with the substitution becomes
which takes the form
and admits the general solution
with
constants.
For
, Equation (42) describes inertial motion in Galilei’s description:
For
, Equation (42) has a limit that we find based on the following mathematical procedure: we first derive the relation (42) with respect to time and eliminate
between the initial and the derived relation. This results in
This limit has the expression
Such a solution, for an ensemble of coherent atmospheric structural units, in our opinion, corresponds to atmospheric jets.
In
Figure 3, we present the bifurcation diagram in the context of an inertially unstable atmosphere (where
is the integration degree between atmospheric structural unity for a given atmosphere). In our paper, υ represents a structural index parameter that quantifies the relative spatial or dynamical position of an atmospheric unit within the system. It can encode variables such as latitude, vertical level, or local frequency class depending on the context of the synchronization analysis. Specifically, in the bifurcation diagrams,
serves as a labeling axis for units or regions whose individual solutions are characterized by distinct projective parameters
, allowing us to track the emergence of coherent regimes and identify zones of enhanced structural stability. Higher ν values correlate to polar cells if index ν is believed to be proportional to latitude, for instance, intermediate values map to the Ferrel cell. This lets ν encode spatial phase information in the synchronizing analysis.
We also mention that this bifurcation diagram illustrates how coherent oscillatory regimes emerge as functions of the local frequency and a structural or spatial parameter . Each stability “island” in the diagram corresponds to a preferred natural frequency, associated with distinct atmospheric regimes such as the Hadley cell or the polar jet stream.