Complex-Valued Electromagnetic Fields in Matter: Their Relevance to Electromagnetic Field Theories of Conscious Experience
Abstract
1. Introduction
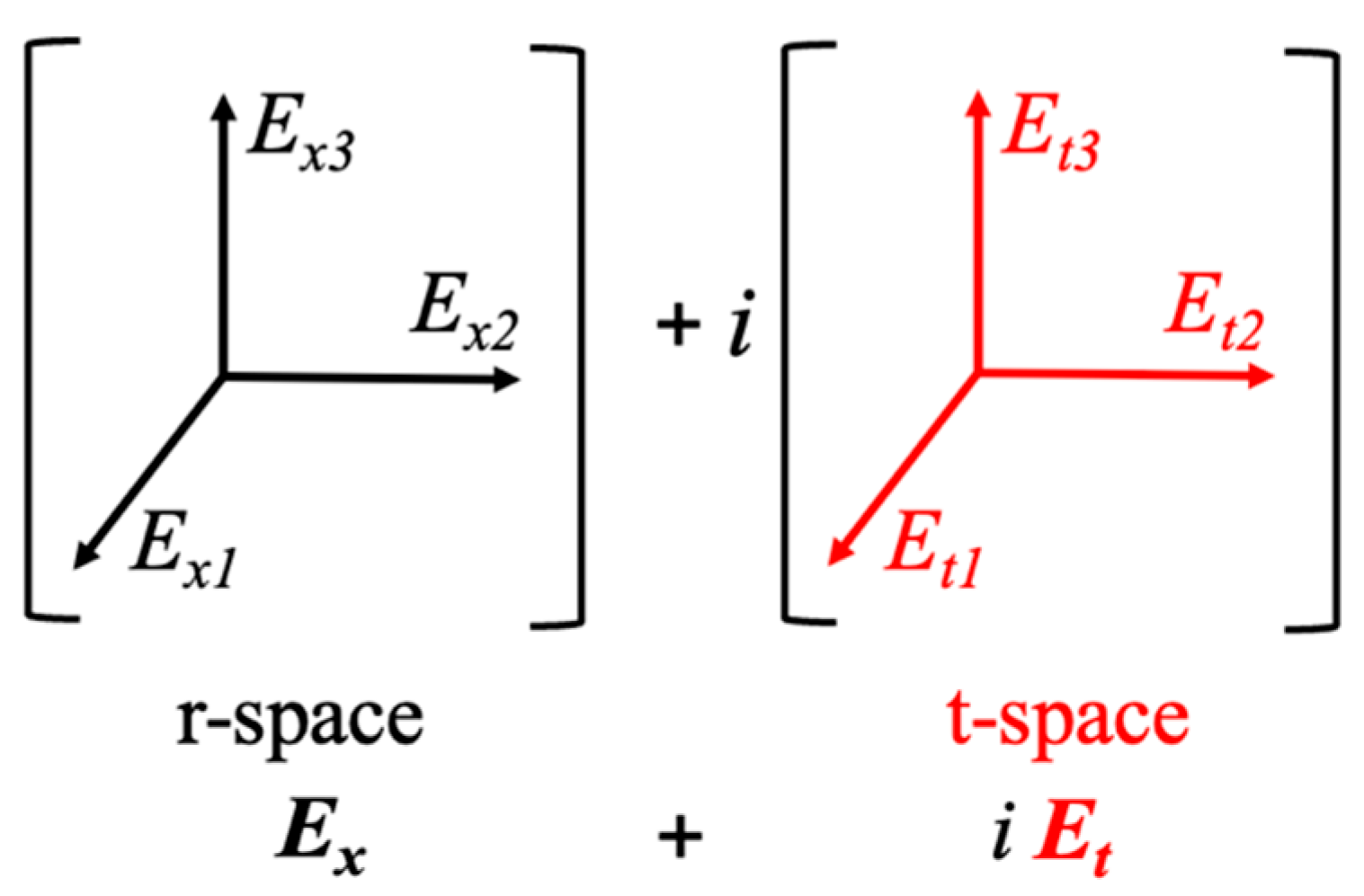
2. Methods: Accommodating Complex-Valued Electromagnetic Fields
3. Complex-Valued Maxwell’s Equations in Matter
3.1. Complex Maxwell’s Equations in Linear Homogeneous Matter
3.2. Complex Maxwell Equations in Conducting Matter
4. Complex-Valued Wave Equation Inside of Conducting Matter
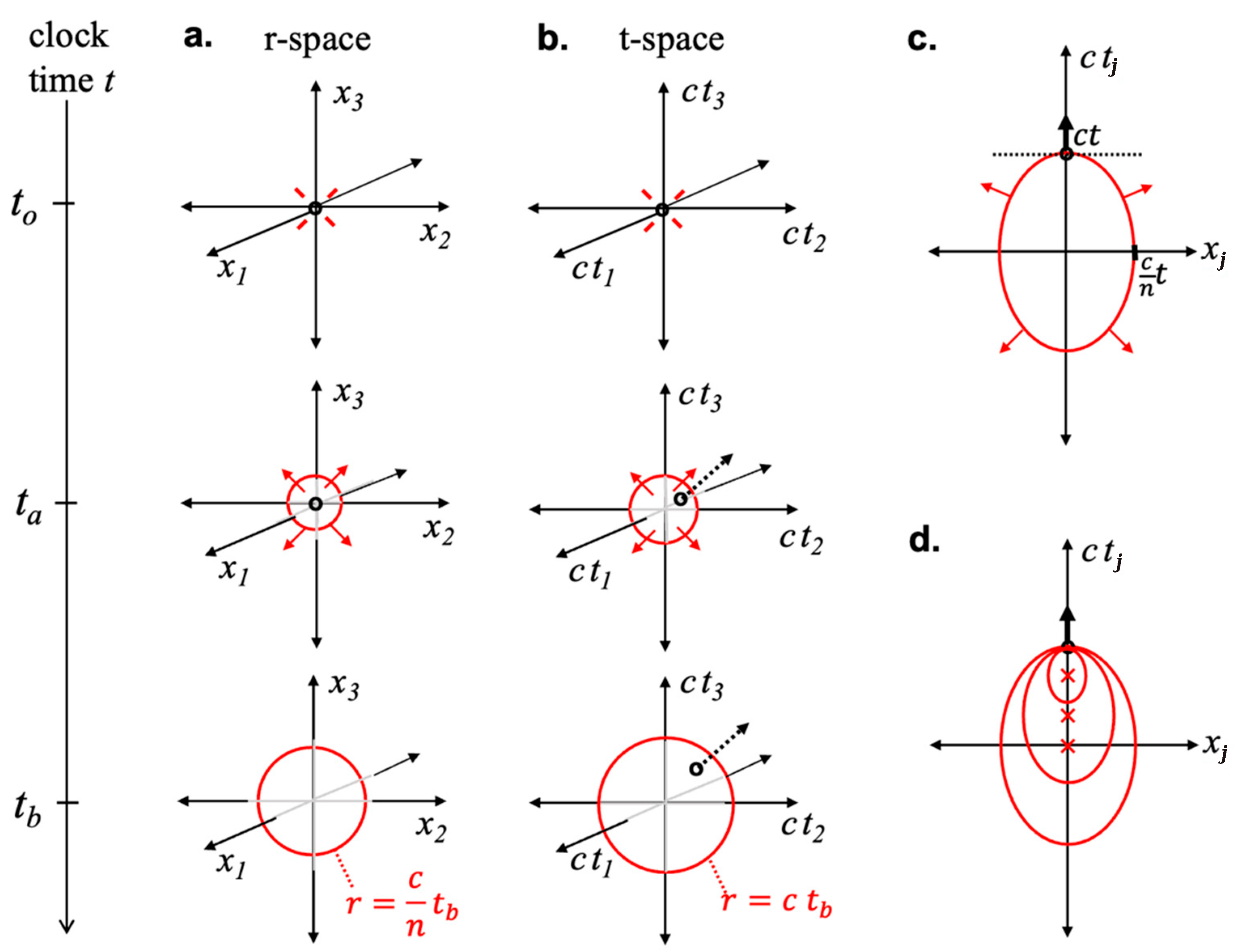
4.1. The Underlying Spacetime
4.2. The Complex Wave Equation in Conductors
4.3. Plane Wave Solution to the Wave Equation and Its Implications
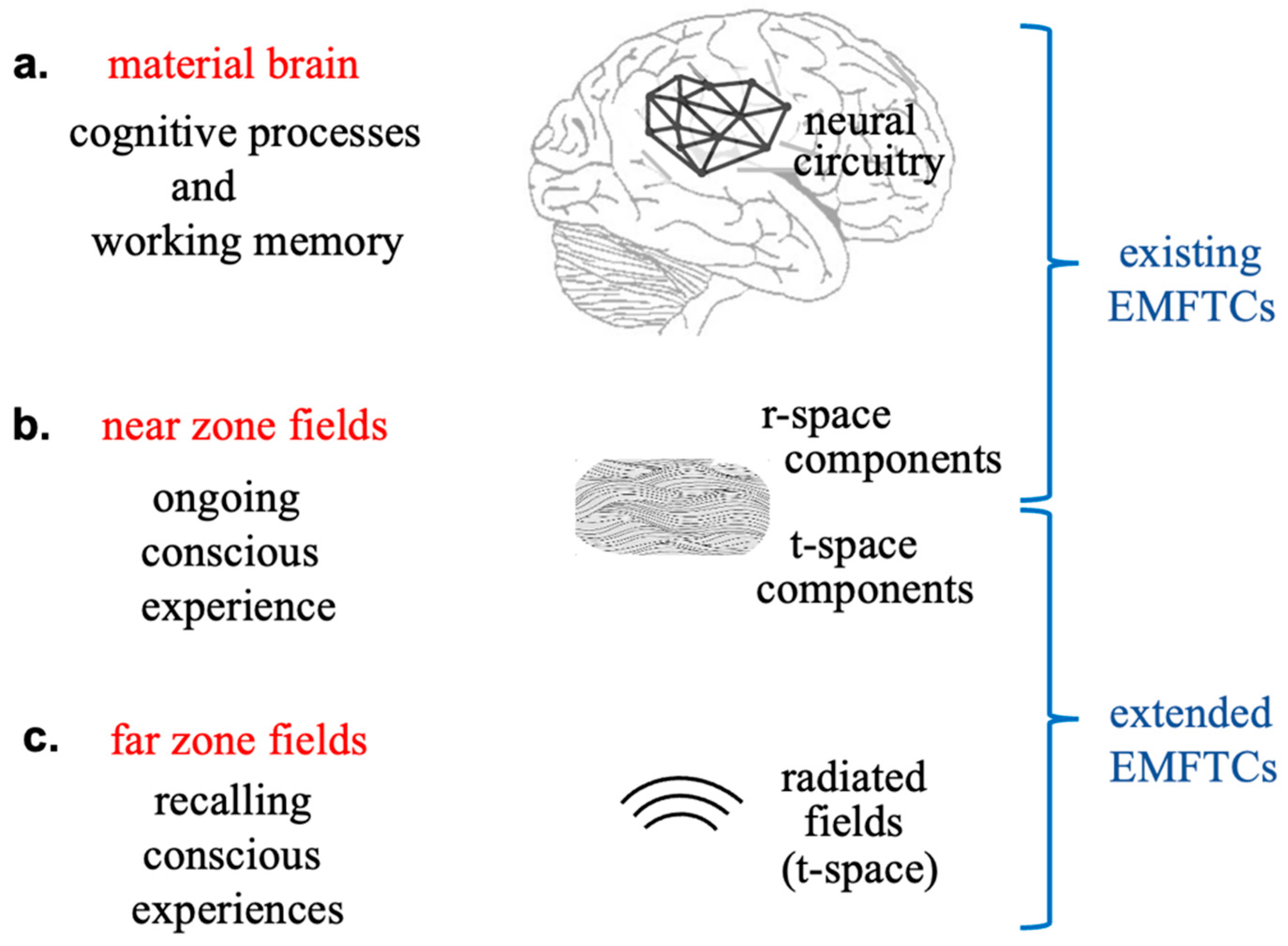
5. Implications for Electromagnetic Field Theories of Consciousness
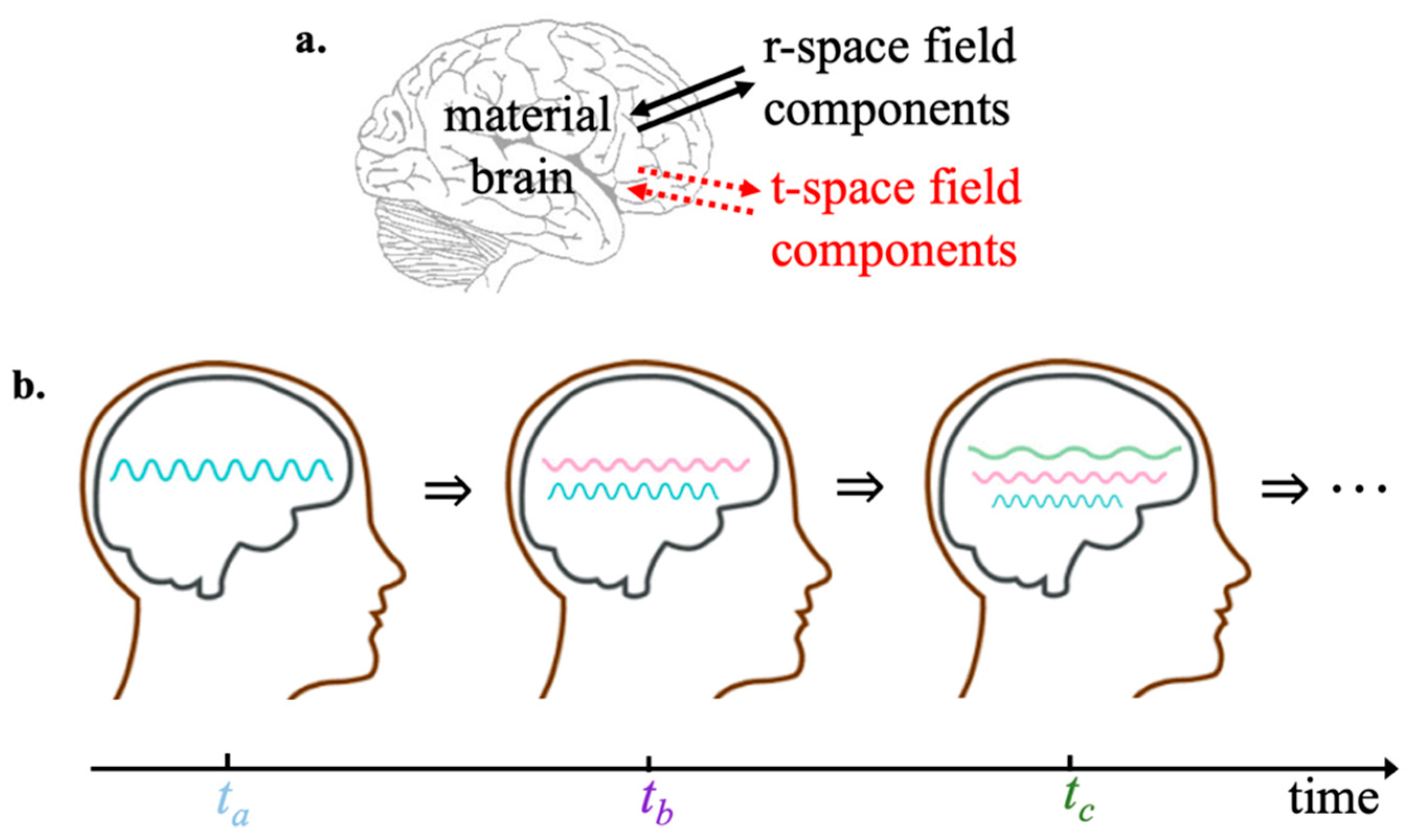
5.1. Extending Past Electromagnetic Field Theories of Consciousness
5.2. Properties of the Subjective Experience of Time
5.3. Properties of Recalling Previous Conscious Experiences
6. Discussion
7. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MEs | Maxwell’s Equations |
| EMFTC | Electromagnetic Field Theory of Consciousness |
References
- Griffiths, D. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Zangwill, A. Modern Electrodynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Fialova, S.; Pochyly, F. A New Formulation of Maxwell’s Equations. Symmetry 2021, 13, 868. [Google Scholar] [CrossRef]
- Reggia, J. Generalizing Maxwell’s Equations to Complex-Valued Electromagnetic Fields. Phys. Scr. 2024, 99, 15513. [Google Scholar] [CrossRef]
- Reggia, J. Maximizing the Symmetry of Maxwell’s Equations. Front. Phys. 2024, 12, 1388397. [Google Scholar] [CrossRef]
- Amoroso, R.; Rauscher, E. The Complexification of Maxwell’s Equations. In Orbiting the Moons of Pluto; World Scientific: Singapore, 2011; pp. 74–108. [Google Scholar]
- Arbab, A. Complex Maxwell’s Equations. Chin. Phys. B 2013, 22, 030301. [Google Scholar] [CrossRef]
- Aste, A. Complex Representation Theory of the Electromagnetic Field. J. Geom. Symm. Phys. 2012, 28, 47–58. [Google Scholar]
- Livadiotis, G. Complex Symmetric Formulation of Maxwell’s Equations for Fields and Potentials. Mathematics 2018, 6, 114. [Google Scholar] [CrossRef]
- Mohr, P. Solutions of the Maxwell Equations and Photon Wave Functions. Ann. Phys. 2010, 325, 607–663. [Google Scholar] [CrossRef]
- Salih, M. Complex Maxwell Equations. J. Mod. Phys. 2023, 14, 1662–1671. [Google Scholar] [CrossRef]
- Haug, E. Three Dimensional Space-Time Gravitational Metric, 3 Space + 3 Time Dimensions. J. High Energy Phys. Gravit. Cosmol. 2021, 7, 1230–1254. [Google Scholar] [CrossRef]
- Bars, I. Gauge Symmetries in Phase Space. Int. J. Mod. Phys. A 2010, 25, 5235–5252. [Google Scholar] [CrossRef]
- Medina, M.; Nieto, J. Nieto-Marin, P. Cosmological Duality in Four Time and Four Space Dimensions. J. Mod. Phys. 2021, 12, 1027–1039. [Google Scholar] [CrossRef]
- Nieto, J.; Espinoza, M. Dirac Equation in Four Time and Four Space Dimensions. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750014. [Google Scholar] [CrossRef]
- Martínez-Olivas, B.; Nieto, J.; Sandoval-Rodríguez, A. (4 + 4)-Dimensional Space-Time as a Dual Scenario for Quantum Gravity and Dark Matter. J. Appl. Math. Phys. 2022, 10, 688–702. [Google Scholar] [CrossRef]
- Mermin, N. It’s About Time; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Penrose, R. Consciousness Must be Beyond Computable Physics. New Sci. 2022, 256, 30–33. [Google Scholar]
- Hales, C.; Ericson, M. Electromagnetism’s Bridge Across the Explanatory Gap. Front. Human Neurosci. 2022, 16, 836046. [Google Scholar] [CrossRef] [PubMed]
- Reggia, J. Time, Memory, and the Physical Basis of Consciousness. J. Conscious. Stud. 2025, 32, 34–62. [Google Scholar] [CrossRef]
- Kent, L.; Wittmann, M. Time Consciousness: The Missing Link in Theories of Consciousness. Neurosci. Conscious. 2021, 7, niab011. [Google Scholar] [CrossRef] [PubMed]
- Power, S. Introduction: Time and Consciousness. J. Conscious. Stud. 2017, 24, 7–13. [Google Scholar]
- Hales, C. The origins of the brain’s endogenous electromagnetic field and its relationship to provision of consciousness. J. Integr. Neurosci. 2014, 13, 313–361. [Google Scholar] [CrossRef]
- Nunez, P.; Srinivasan, R. Electric Fields of the Brain; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Piastra, M.; Oostenveld, R.; Homolle, S.; Han, B.; Chen, Q.; Oostendorp, T. How to Assess the Accuracy of Volume Conduction Models. Front. Hum. Neurosci. 2024, 18, 1279183. [Google Scholar] [CrossRef]
- Frohlich, F.; McCormick, D. Endogenous Electric Fields May Guide Neocortical Network Activity. Neuron 2010, 67, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.; Hunt, T. Electromagnetic-field Theories of Qualia: Can They Improve Upon Standard Neuroscience? Front. Psychol. 2023, 14, 1015967. [Google Scholar] [CrossRef] [PubMed]
- MacIver, M. Consciousness and Inward Electromagnetic Field Interactions. Front. Human Neurosci. 2022, 16, 1032339. [Google Scholar] [CrossRef]
- McFadden, J. Consciousness: Matter or EMF? Front. Human Neurosci. 2023, 16, 1024934. [Google Scholar] [CrossRef] [PubMed]
- McFadden, J. The CEMI Field Theory. J. Conscious. Stud. 2013, 20, 153–168. [Google Scholar]
- Fingelkurts, A.; Fingelkurts, A. Brain-Mind Architectonics Imaging. Open Neuroimaging J. 2008, 2, 73–93. [Google Scholar] [CrossRef]
- Hunt, T.; Schooler, J. The “Easy Part” of the Hard Problem: A Resonance Theory of Consciousness. Authorea 2019, 13, 378. [Google Scholar] [CrossRef]
- Jones, M. A Simple Testable Mind-Body Solution. J. Consciousness Studies 2024, 31, 51–75. [Google Scholar] [CrossRef]
- LaBerge, D.; Kasevich, R. The Apical Dendrite Theory of Consciousness. Neural Netw. 2007, 20, 1004–1020. [Google Scholar] [CrossRef]
- Pockett, S. The Electromagnetic Field Theory of Consciousness. J. Conscious. Stud. 2012, 19, 191–223. [Google Scholar]
- Ward, L.; Guevara, R. Qualia and Phenomenal Consciousness Arise from the Information Structure of an Electromagnetic Field in the Brain. Front. Hum. Neurosci. 2022, 16, 874241. [Google Scholar] [CrossRef]
- Buzsaki, G. Rhythms of the Brain; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Buzsaki, G. Scaling Brain Size, Keeping Timing. Neuron 2013, 80, 751–764. [Google Scholar] [CrossRef]
- Madl, T.; Baars, B.J.; Franklin, S. The Timing of the Cognitive Cycle. PLoS ONE 2011, 6, e14803. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P. Brain, Mind, and the Structure of Reality; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Miller, P.; Cannon, N. Combined Rates of Neural Firing Rate Homeostasis. Biol. Cybern. 2019, 113, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Arstila, V.; Lloyd, D. Subjective Time; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Wearden, J. Internal Clocks and the Representation of Time. In Time and Memory; Hoerl, C., McCormack, T., Eds.; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Grondin, S. The Perception of Time; Routledge: New York, NY, USA, 2020. [Google Scholar]
- Wittmann, M. Felt Time; MIT Press: New York, NY, USA, 2017. [Google Scholar]
- Petkov, V. On the Reality of Minkowski Space. Found. Phys. 2007, 37, 1499–1502. [Google Scholar] [CrossRef]
- Proctor, A. On Time, Causality, and the Block Universe; Clink Street Publishing: London, UK, 2022. [Google Scholar]
- Weinert, F. The March of Time; Springer-Verlag: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wittmann, M. Modulations of the Experience of Self and Time. Conscious. Cogn. 2015, 38, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Tulving, E. Episodic Memory. Annu. Rev. Psychol. 2002, 53, 1–25. [Google Scholar] [CrossRef]
- Kim, H. Neural Activity that Predicts Subsequent Memory and Forgetting: A Meta-Analysis. NeuroImage 2011, 54, 2446–2461. [Google Scholar] [CrossRef]
- Moscovitch, M.; Cabeza, R.; Winocur, G.; Nadel, L. Episodic Memory and Beyond. Annu. Rev. Psychol. 2016, 67, 105–124. [Google Scholar] [CrossRef]
- Benna, M.; Fusi, S. Place Cells May Simply be Memory Cells. Proc. Nat. Acad. Sci. USA 2021, 118, e2018422118. [Google Scholar] [CrossRef]
- Eichenbaum, H. Time Cells in the Hippocampus. Nat. Rev. Neurosci. 2014, 15, 732–744. [Google Scholar] [CrossRef]
- Moser, M.; Rowland, D.; Moser, E. Place Cells, Grid Cells, and Memory. Cold Spring Harb. Perspect. Biol. 2015, 7, a021808. [Google Scholar] [CrossRef] [PubMed]
- Shimbo, A.; Izawa, E.; Fujisawa, S. Scalable Representation of Time in the Hippocampus. Sci. Adv. 2021, 7, eabd7013. [Google Scholar] [CrossRef] [PubMed]
- Favila, S.; Kuhl, B.; Winawer, J. Perception and Memory Have Distinct Spatial Tuning Properties in Human Visual Cortex. Nat. Commun. 2022, 13, 5864. [Google Scholar] [CrossRef]
- Michaelian, K. Mental Time Travel; MIT Press: Cambridge, USA, 2016. [Google Scholar]
- Baddeley, A.; Eysenck, M.; Anderson, M. Memory; Routledge: New York, NY, USA, 2020. [Google Scholar]
- Slotnick, S. Cognitive Neuroscience of Memory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Brown, G.; Chater, N. The Chronological Organization of Memory. In Time and Memory; Hoerl, C., McCormack, T., Eds.; Oxford University Press: Oxford, UK, 2001; pp. 77–110. [Google Scholar]
- Fernández, R.S.; Picco, S.; Beron, J.C.; Bavassi, L.; Campos, J.; Allegri, R.F.; Pedreira, M.E. Improvement of Episodic Memory Retention by a Memory Reactivation Intervention Across the Lifespan. Trans. Psych. 2022, 12, 144. [Google Scholar] [CrossRef] [PubMed]
- MacLeod, S.; Reynolds, M.; Lehmann, H. The Mitigating Effect of Repeated Memory Reactivations on Forgetting. Sci. Learn. 2018, 3, 9. [Google Scholar] [CrossRef]
- Brady, T.; Konkle, T.; Alvarez, G.; Oliva, A. Visual Long-term Memory has a Massive Storage Capacity for Object Details. Proc. Nat. Acad. Sci. USA 2008, 105, 14325–14329. [Google Scholar] [CrossRef]
- Standing, L. Learning 10,000 Pictures. Quart. J. Exper. Psych. 1973, 25, 207–222. [Google Scholar] [CrossRef]
- Courtney, S.; Petit, L.; Haxby, J.; Ungerleider, L. The Role of Prefrontal Cortex in Working Memory. Proc. Trans. Royal Soc. Lond. B 1998, 353, 1819–1828. [Google Scholar] [CrossRef]
- Lara, A.; Wallis, J. The Role of Prefrontal Cortex in Working Memory. Front. Sys. Neurosci. 2015, 9, 173. [Google Scholar] [CrossRef]
- Baars, B.; Franklin, S. How Conscious Experience and Working Memory Interact. Trends Cog. Sci. 2003, 7, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Baddeley, A. Short-term and Working Memory. In The Oxford Handbook of Memory; Tulving, E., Craik, F., Eds.; Oxford University Press: Oxford, UK, 2000; pp. 77–92. [Google Scholar]
- Cowan, N. The Magical Number 4 in Short Term Memory. Behav. Brain Sci. 2001, 24, 87–185. [Google Scholar] [CrossRef] [PubMed]
- Persuh, M.; LaRock, E.W.; Berger, J. Working Memory and Consciousness. Front. Hum. Neurosci. 2018, 12, 78. [Google Scholar] [CrossRef] [PubMed]
- Zaidel, E.; Iacoboni, M.; Zaidel, D.; Bogen, J. The Callosal Syndromes. In Clinical Neuropsychology; Heilman, K., Valenstein, E., Eds.; Oxford University Press: Oxford, UK, 2003; pp. 347–403. [Google Scholar]
- Reggia, J.; Katz, G.; Davis, G. Artificial Conscious Intelligence. J. Artif. Intell. Conscious. 2020, 7, 1–13. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reggia, J.A. Complex-Valued Electromagnetic Fields in Matter: Their Relevance to Electromagnetic Field Theories of Conscious Experience. Symmetry 2025, 17, 992. https://doi.org/10.3390/sym17070992
Reggia JA. Complex-Valued Electromagnetic Fields in Matter: Their Relevance to Electromagnetic Field Theories of Conscious Experience. Symmetry. 2025; 17(7):992. https://doi.org/10.3390/sym17070992
Chicago/Turabian StyleReggia, James A. 2025. "Complex-Valued Electromagnetic Fields in Matter: Their Relevance to Electromagnetic Field Theories of Conscious Experience" Symmetry 17, no. 7: 992. https://doi.org/10.3390/sym17070992
APA StyleReggia, J. A. (2025). Complex-Valued Electromagnetic Fields in Matter: Their Relevance to Electromagnetic Field Theories of Conscious Experience. Symmetry, 17(7), 992. https://doi.org/10.3390/sym17070992





