1. Introduction
Financial management decisions remain at the base of organizational success in determining organic growth, competitive positioning, and profitability. To compete effectively in a constantly fluctuating marketplace, organizations face a number of interconnected issues and concerns in the efficient and effective use of resources in resource scarcity, risk management, and business growth opportunities in financial environment. Organizations must navigate multifaceted challenges to optimize resource allocation, manage risks, and seize growth opportunities [
1]. It shows financial activities that can be referred to as the practice of finance consisting of investment appraisal, capital budgeting, risk management as well as financial forecasting. All these decisions influence the nature and future of any organization in terms of profitability, resource management, and market positioning [
2]. The ever-evolving conditions of global markets provoked by technology development, changes in legislation and economic instability require sound and flexible decision-making tools. The mostly qualitative methods based on the experienced operators, as well as historical statistics, are not very effective to cope with multilayer modern financial processes’ interfaces. As a result, there is an acute demand for better ways to combine multiple types of data, capture intricate structures, and deliver insights for guiding higher-level endeavors [
3].
Machine learning (ML) has gained significant attention over the years and has become the driving power in the financial business, with various advanced techniques in data analysis and prediction as well as automation. ML techniques are used in finance across several fields such as algorithm trading, credit risk assessment, fraud detection, portfolio optimization, and forecasting [
4]. Since ML models can learn from large datasets, recognize non-linear patterns, and develop into recognizing new emerging patterns, statistical methods are enhanced with them significantly [
5]. Another more crucial benefit of machine learning in finance is that it provides a much better prediction rate. Machine learning techniques of a higher level, like ensemble learning methods and deep learning, have shown better results for estimating business performance, outlier detection, and optimizing investment strategies [
6]. These models are able to take inputs of features which may be in high dimensions and incorporate unstructured texts such as news articles, social media post, and market reports into the decision-making processes, enhancing the decision-making processes with comprehensive information in real time. In addition, ML helps automate specific tasks that are commonly assessed to support financial reports, making it easier to do and with less chance of errors. Some applications of AI include but are not limited to automated trading system using ML to trade at the right time, informed by analysis, boosting profitability, and effectiveness [
7]. Likewise, investor protection through concepts like fair value enhances risk management and machine learning-driven credit scoring improves the lender’s ability to rate the borrower effectively, hence promoting minority access to credit [
8].
However, a problem occurs when applying ML for strategic financial decision-making. Indeed, one of the key problems is the explainability of the results obtained in ML models. While complex algorithms like deep neural networks and ensemble methods offer high predictive performance, they often operate as “black boxes”, providing limited transparency into their decision-making processes [
9]. In finance, where regulatory compliance, accountability, and trust are paramount, the inability to explain model predictions poses significant barriers to adoption [
10]. The other vital bane is the quality and accessibility of the information. Financial data are always noisy, high-dimensional, and contain various forms of biases. Data preprocessing steps involving the protection of data integrity together with methods for treating missing values and managing outliers create fundamental performance changes in models [
11]. The players involved in financial markets exhibit continuous movement while market trends along with variable relationships undergo constant changes. A statistical model built on previous market data becomes unfit for purpose when it cannot adapt to industry trends along with market structure changes. Financial applications of ML require ethical examination due to crucial questions that need assessment. Data privacy together with algorithmic bias and systemic risks demand comprehensive governance structures for proper management according to [
12]. Organizations should deploy ML models by putting innovation beside responsibility to protect security and fair treatment while maintaining system transparency [
13].
The solution to address these challenges depends on joint capabilities from ML methods together with conventional approaches which we have already considered. Research has indicated that combined systems that combine human experts with machine analysis (Human-in-the-loop, HITL) represent a strong approach for boosting financial decision processes [
14]. Organizations can achieve better analysis and correct reasoning from experts by uniting the numeric analysis of ML with human specialists who understand context. Several techniques are used to incorporate human knowledge in the frameworks used in ML. Expert-driven feature selection, for instance, ensures that models incorporate domain-relevant variables that could not be automatically identified by algorithms [
15]. This collaboration enhances the model’s ability to capture critical financial indicators and improves its overall predictive performance. Additionally, expert feedback can be used to refine model outputs, implement rule-based adjustments, and validate predictions, thereby bridging the gap between data-driven analytics and practical financial insights [
16]. Hence, there is an intensive utilization of human judgments in model interpretability and responsibility. Experts can interpret complex model results, provide explanations for predictions, and ensure that the models align with regulatory and ethical standards [
17]. This collaborative approach not only enhances trust in ML-driven decisions but also facilitates regulatory compliance and ethical responsibility [
18].
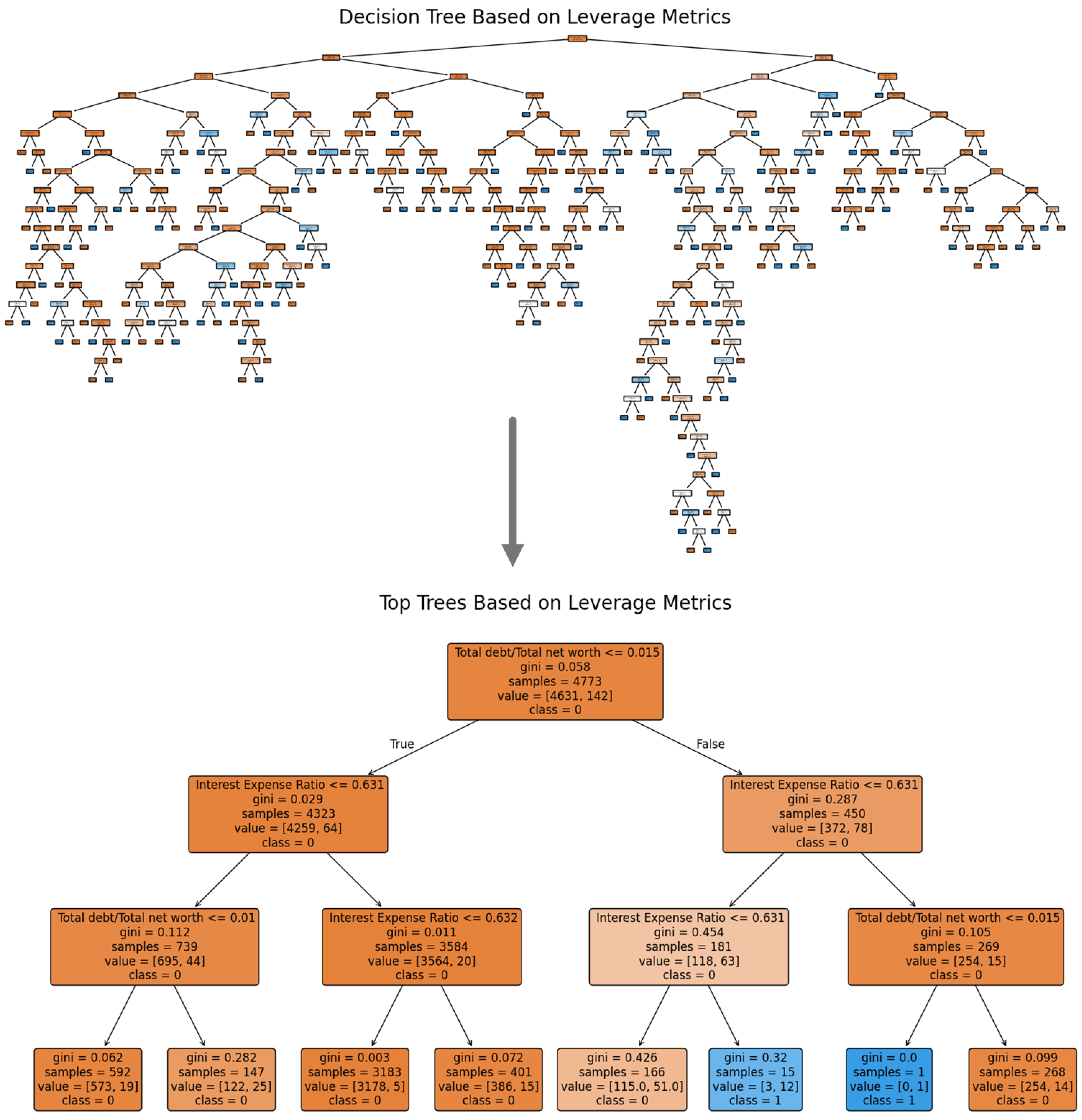
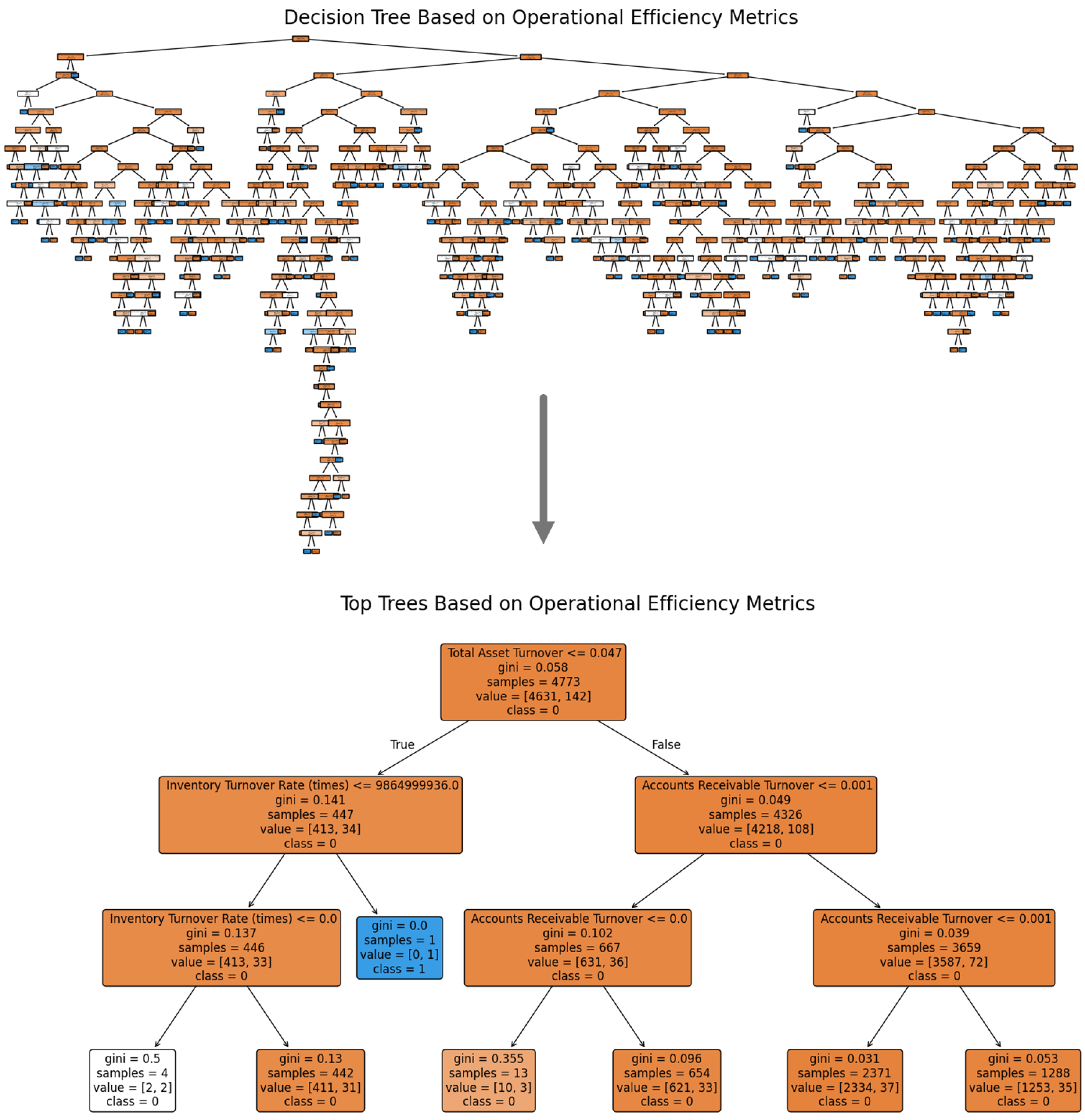
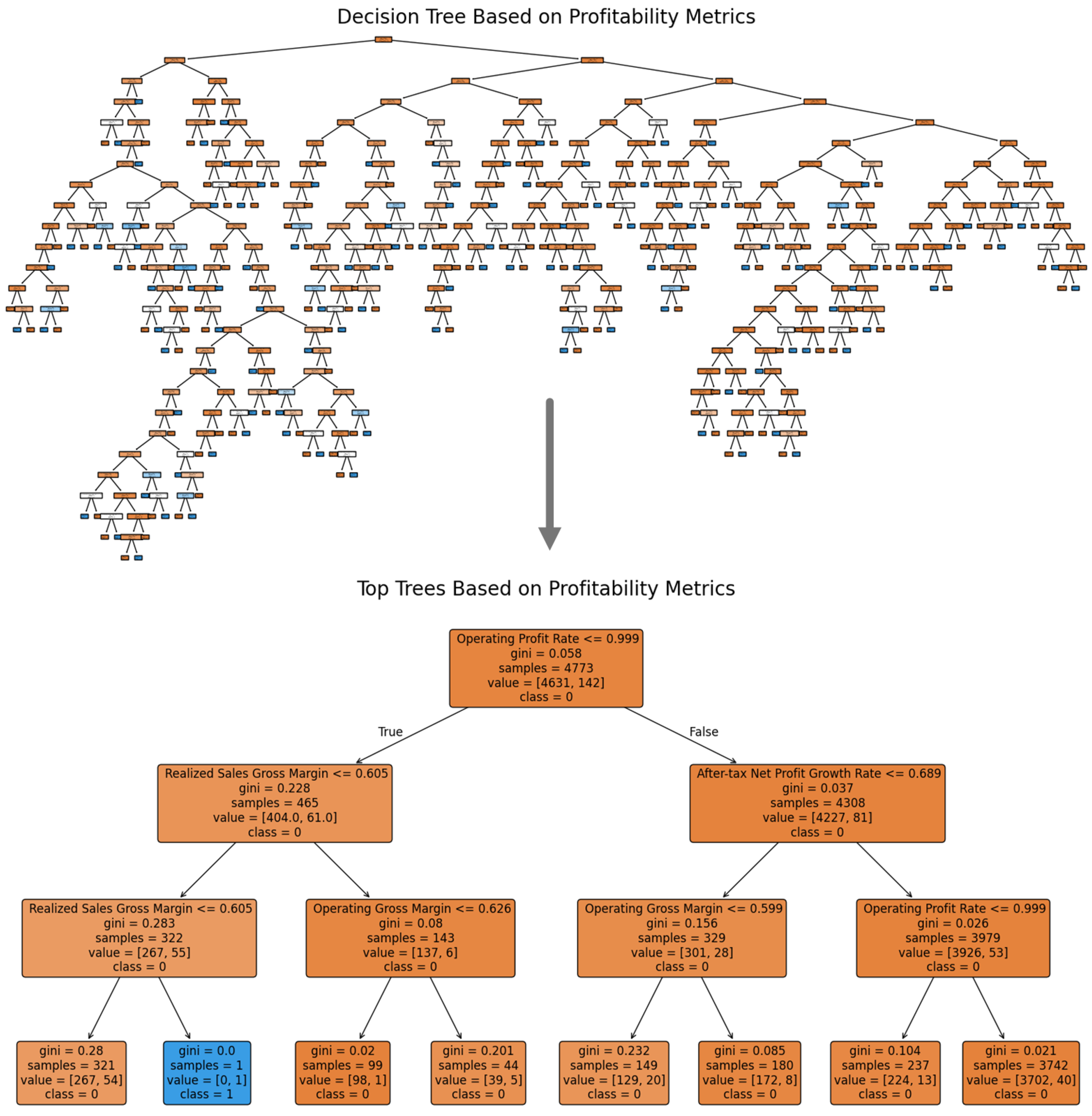
Decision trees (DTs) are one of the basic ML approaches, very popular among the financial sector because of their explainability and ease. DTs partition data into subsets based on feature values, making them highly intuitive and easy to visualize [
19]. They provide clear decision rules that can be directly applied to financial decision-making processes, such as credit risk assessment and investment evaluation [
20]. However, single decision trees are prone to overfitting and may exhibit limited predictive performance on complex datasets [
21]. In order to overcome these limitations, the newer methods like Random Forest (RF) and Gradient Boosting Machine (GBM) techniques, namely extra gradient boosting (XGboost), light GBM, etc., have evolved. These techniques generate multiple decision trees and then use the invents to make them more robust, less variable, and more generalized.
Random Forests combine multiple decision tree (DT) predictions which rely on various subsets of data and features in order to reduce overfitting and maximize prediction accuracy [
22]. Gradient Boosting Machines construct multiple trees through serial ensemble operations that focus on fixing errors made by previous models to achieve very precise predictive models [
23]. Various financial applications use high-performing ensemble methods like these for stock price prediction, portfolio optimization, and fraud detection systems according to [
24]. Our team has discovered that ensemble methods generate their own set of interpretability issues despite their effective performance. The aggregation method is used by multiple trees for better accuracy results in decision-making processes that become harder to understand as the certification process becomes more complicated [
25]. The competing demands between performance and interpretation require integrated systems that effectively strike this trade-off according to [
26].
This study aims to bridge the identified gaps by developing and validating an integrated ML framework that combines decision trees, advanced ensemble techniques, and human expertise to enhance strategic financial decision-making. The specific objectives of this research are the following: (i) to create a hybrid framework that leverages the interpretability of decision trees and the predictive power of advanced ensemble ML models, augmented by human expertise for feature selection and model refinement; (ii) to demonstrate that the integrated framework achieves superior predictive performance compared to individual models while maintaining high levels of interpretability through expert-driven adjustments; (iii) to apply the framework to comprehensive financial datasets, evaluating its effectiveness in real-world financial decision-making scenarios such as bankruptcy prediction, risk assessment, and investment strategy optimization; (iv) to incorporate ethical considerations into the framework development, ensuring data privacy, mitigating algorithmic bias, and enhancing model accountability through transparency and expert validation.
In this study, the main contributions are as follows:
Introduces a unique methodology that synergizes decision trees, advanced ensemble ML models, and human expertise, providing a balanced solution that enhances both accuracy and interpretability.
Offers robust empirical evidence demonstrating the framework’s effectiveness in improving financial decision-making processes, thereby advancing the application of ML in finance.
Establishes a comprehensive approach that integrates ethical considerations into ML framework development, promoting responsible AI practices in financial analytics.
Provides actionable insights and tools for financial analysts and strategic managers, enabling more informed and effective decision-making through the combined use of ML and human expertise.
This study is structured into eight major sections:
Section 1 is about introducing how energy efficiency analysis techniques of houses need to undergo a radical change.
Section 2 reviews existing studies on ML applications in finance, decision trees and ensemble methods, and the integration of human expertise in ML frameworks, highlighting the gaps that this research addresses.
Section 3 discusses the methodology used in the study, detailing data sources, feature descriptions, and preprocessing steps, and outlines the methodology underpinning the integrated ML framework.
Section 4 details the development of the automated feature selection and expert feedback-integrated ML framework.
Section 5 presents the model development, integration of human expertise, training, and optimization.
Section 6 presents empirical findings, comparing the performance of the integrated framework against baseline and advanced ML models, and analyzing feature importance and model interpretability.
Section 7 concludes the key findings, contributions, and practical implications of the study, and offers recommendations for future research.
2. Literature Review
The adoption of machine learning in the financial decision-making process has imparted a new form of versatility and populism to the financial analysis. These algorithms are capable of dealing with big and intricate data, identifying interconnections and dependencies unknown to basic statistics [
27]. These computational tools have been applied to numerous financial applications, such as credit scoring, fraud detection, algorithmic trading, risk management, portfolio optimization, etc. [
28]. For instance, the supply chain credit risk evaluation based on the ML has provided more reliable predictions about borrowers’ default compared to the traditional models, which enhances credit risk management and lending decisions and mitigates default risks [
29]. Aside from enhancing forecasting precision, developing ML models provides real-time processing to detect and manage emerging risk factors that have not been accounted for in earlier models [
30]. Their ability to generalize allows them to hold high predictive accuracy over time while the financial environment continues to change [
31]. However, there is a lot of hurdles in implementing ML in finance, yet it does not pose a serious threat to displacement of human managerial decisions; rather, it has the goals of augmenting managerial instinct and, hence, problems such as data quality and interpretability and ethical issues [
32] are core aspects that should be conquered in order to deploy perfect tools of ML in finance.
Decision trees (DTs) have emerged as a key ML methodology in financial contexts due to their inherent simplicity and interpretability [
33]. DTs rely on a hierarchical structure of decision rules, providing a transparent model that resonates with the way human experts conceptualize strategic financial choices [
34]. This characteristic is especially valuable where explainability is critical, as in regulatory environments and high-stakes decision-making settings [
35]. In practice, DTs have been utilized for segmenting borrowers into risk categories, guiding loan approval processes, and identifying relevant indicators that inform investment strategies [
36]. However, DTs are prone to overfitting, potentially diminishing their predictive robustness and limiting their applicability to highly volatile financial domains [
37]. The development of ensemble methods Random Forests (RFs) and Gradient Boosting Machines (GBMs) enabled the use of multiple decision trees for improving model accuracy and generalized performance as well as stability [
38]. The outcomes of numerous decorrelated trees are averaged in Random Forests to minimize both variance and prevent overfitting problems according to [
39]. Two widely used Gradient Boosting Machine versions, known as XGBoost and LightGBM, function by updating predictions in a serial manner through iterative error correction processes [
40]. These superior ensemble techniques operate successfully throughout multiple financial settings by predicting stock movements and identifying fraudulent transactions while managing portfolio investments [
41]. The implementation of complex models results in lower interpretability, which means stakeholders struggle to grasp the information in unpredictable ways.
The strategic financial decision-making process faces a significant drawback because it requires a balance between model performance and transparency. Managers who make strategic decisions need to integrate ensemble modeling results with their professional knowledge and business expertise because sophisticated ensemble systems deliver the best predictive performance. HITL frameworks are increasingly important to research because they use expert knowledge to improve ML capabilities, as shown in [
3]. Strategic financial direction and ethical boundaries can be reinforced by practitioner expertise, which guides the model development through feature selection and model validation as well as decision rule interpretation [
42]. The incorporation of expert input with management intuition into AI systems leads to improved capabilities in financial prediction technology and clarification of their output logic. The ability of experts to find relevant characteristics among leverage metrics in specific industries will enhance both domain suitability and predictive strength of the model [
43]. This progression enables successive review stages to permit experts to revise models based on their advice and regulatory standards. The combination of expert-based collaboration enables organizations to both follow established business rules and compliance standards while using ML-generated recommendations that maintain alignment with organizational norms and policies [
44].
That being said, there is still a myriad of issues to be addressed. Model interpretability stands out as a critical issue, particularly in complex ensemble methods and deep learning architectures that function as “black boxes” [
45]. Financial decision-making often necessitates transparent, justifiable reasoning to satisfy internal governance, regulatory mandates, and stakeholder scrutiny [
46]. Ensuring data quality is another persistent challenge, as financial datasets are frequently noisy, incomplete, or biased, requiring comprehensive preprocessing and fairness-aware modeling approaches [
47]. Moreover, markets are inherently dynamic, compelling models to adapt continuously and prevent performance degradation over time [
48]. The role of ethical concerns in ML for financial models has grown as of today. Data privacy, discrimination prevention, algorithmic bias, and systemic risk represent ongoing concerns that must be integrated into the model development lifecycle [
49]. Tackling such ethical considerations before an incident occurs can increase stakeholder trust and diminish foul play or negative side effects in a system constructed on a combination of machine learning and finance.
Table 1 presents a summary of key studies in this domain. These works underline the transformative potential of ML in finance, the strengths and limitations of decision trees, the effectiveness of ensemble methods, and the need for expert integration. They also emphasize the centrality of ethical and interpretability challenges that remain unresolved. As indicated in
Table 1, while ML technologies offer transformative potential for financial decision-making, challenges remain. Decision trees provide interpretability but require complementary methods such as ensemble modeling and expert integration to avoid overfitting and to achieve sufficient robustness [
50]. Ethical dimensions are increasingly prominent, with researchers advocating fairness-aware algorithms and explainable AI (XAI) techniques to enhance trust, transparency, and regulatory compliance [
51]. In [
52,
53], the most common financial tasks that XAI was used for were fraud detection, stock price prediction, and credit management. The explainability of the three most widely used AI black-box techniques in finance Random Forest, Extreme Gradient Boosting (XGBoost), and Artificial Neural Networks (ANNs) was assessed. Shapley additive explanations (SHAP), feature importance, and rule-based approaches are used in the majority of the reviewed publications [
54,
55].
A critical gap in the current literature lies in the comprehensive integration of DT-based methods with advanced ensemble techniques and management intuition within a unified strategic decision-making framework. Existing studies largely focus on either maximizing predictive performance through advanced ML models or maintaining interpretability using simpler models, while seldom combining the strengths of both approaches with domain-specific human insight [
50]. This oversight restricts the development of holistic solutions that not only deliver superior predictive accuracy but also preserve transparency, adhere to ethical standards, and align with organizational strategic objectives. Similarly, while ethics and interpretability are emphasized as priorities, they are often tackled piecemeal rather than as integral parts of the model development and deployment process [
12]. Moreover, empirical evidence demonstrating how human expertise can effectively refine model outputs to better support strategic managerial decisions remains limited [
56].
In light of these identified gaps, this study proposes an integrated ML framework tailored to the strategic choice of augmenting management intuition with machine learning. By leveraging decision trees as an interpretable foundation and enhancing their robustness through advanced ensemble methods and iterative expert involvement, the framework aims to deliver both high predictive accuracy and clear, context-driven explanations. Furthermore, embedding ethical considerations and governance mechanisms from the outset ensures that the resulting models are not only effective in real-world financial contexts but also aligned with broader social responsibilities and regulatory mandates.
This approach offers an avenue to move beyond the dichotomy of accuracy versus interpretability, forging a path toward practical, trustworthy, and strategically informed financial decision-making. In doing so, it aligns the analytical capabilities of ML with the nuanced judgments that financial managers and executives must bring to critical strategic choices.
Table 1.
Summary of key literature.
Table 1.
Summary of key literature.
| Author(s) | Year | Purpose | Methodology | Findings |
|---|
| Mashrur et al. [4] | 2020 | Explore ML applications in financial decision-making | Review | ML enhances predictive accuracy in finance. |
| Deep [6] | 2024 | Compare ensemble ML techniques in financial contexts | Empirical study | GBMs outperform single DTs in predictive tasks. |
| Mestiri et al. [8] | 2024 | Develop ML-based credit scoring models | ML modeling | ML models improve prediction of borrower defaults. |
| Nguyen & Tran [12] | 2024 | Address ethical concerns in ML for finance | Theoretical analysis | Data privacy and bias are key ethical challenges. |
| Breiman et al. [33] | 2021 | Introduce and analyze decision trees (DT) | Theoretical framework | DTs are interpretable but prone to overfitting. |
| Charbuty & Abdulazeez [34] | 2021 | Examine limitations of decision trees | Analytical study | Single DTs have low generalizability in dynamic environments. |
| Chen et al. [57] | 2022 | Develop XGBoost algorithm for financial forecasting | Algorithm development | XGBoost achieves high accuracy and efficiency. |
| Singh & Gupta [7] | 2014 | Implement ML-based automated trading systems | Case study | ML improves profitability in trading strategies. |
| Jha et al. [5] | 2025 | Integrate expert knowledge into ML models | Hybrid modeling | Expert integration enhances model reliability and trust. |
| Lappas & Yannacopoulos [56] | 2021 | Incorporate expert feedback into ML models | Experimental study | Expert feedback refines model performance in financial settings. |
| Puchakaya et al. [10] | 2023 | Ensure model transparency in financial applications | Policy analysis | Recommends explainable AI (XAI) techniques. |
| Piramuthu et al. [11] | 2006 | Improve data preprocessing for ML models | Data analysis | Enhanced preprocessing boosts model accuracy. |
3. Methodology
Financial decisions are critical to the performance of any business since they determine a firm’s profitability, growth rate, and sustainability. The ratios of profitability, liquidity, solvency, and efficiency are used as the financial performance measures of a firm. These metrics tend to provide useful information on the firm’s profitability status, debt position, operational efficiency, and financial sustainability. This paper examines how integration of prior knowledge with the use of machine learning can improve the accuracy of strategic financial decisions that may otherwise be informed by such financial measures. This section presents a detailed description of the rigorous method used to construct and verify the strategic financial decision-making integrated ML framework. The method comprises data acquisition, data preprocessing, feature extraction, integration of expert knowledge, model creation and tuning, model assessment, model implementation, and model refinement. They are all well thought out so that each one is rugged, precise, and grounded in sound financial realities.
The dataset utilized in this study collected from [
58] includes a wide range of financial features, organized into five distinct categories and can be seen in
Table 2: Profitability, Liquidity, Leverage, Growth, and Operational Efficiency. The dataset used in this study consists of 6820 observations, each representing a financial record of a company with various input features and a binary output feature. The output feature is “Bankrupt”, indicating whether the company went bankrupt (1) or not (0). The input features include a comprehensive set of financial ratios, performance metrics, and growth indicators, such as ROA before interest and depreciation, Operating Gross Margin, Operating Profit Rate, Net Value Per Share, Cash Flow Rate, Debt Ratios, and several others related to profitability, liquidity, asset management, and financial leverage. These features are crucial for assessing the financial health and predictive power of the model, particularly in forecasting bankruptcy and other financial outcomes. The dataset provides a rich set of financial indicators, which can be used for model training and testing in the context of strategic financial decision-making.
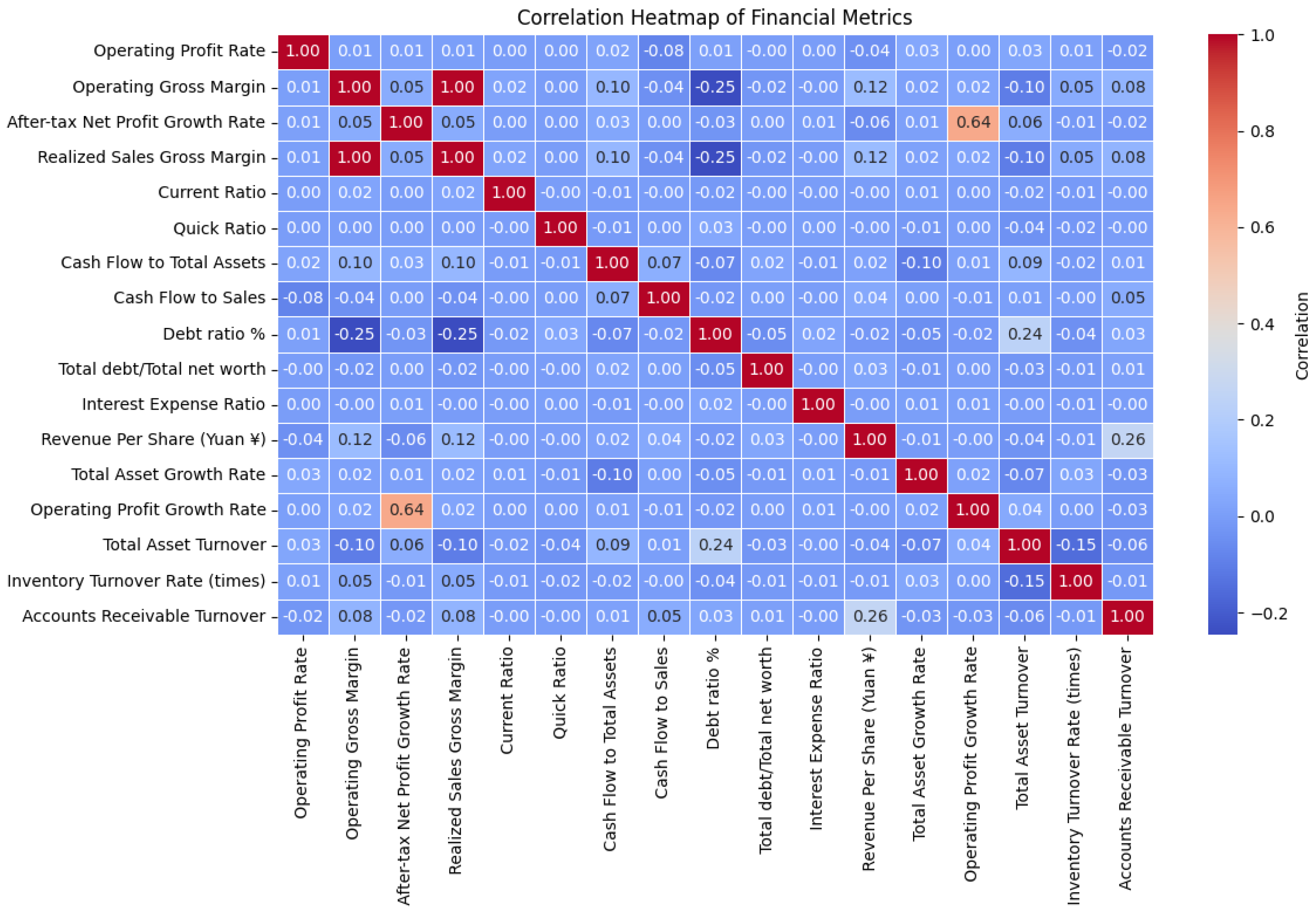
In the Exploratory Data Analysis at the beginning, some nice relations between the financial characteristics were revealed. From the Pearson’s correlation heatmap in
Figure 1, it can be observed that there are linear relationships between the metrics that could be anticipated and some others as well that could not be predicted. For example, Operating Gross Margin and After-tax Net Profit Growth Rate have a relationship of positive correlation, which means that the higher the profitability level of the company, the higher post-tax profit growth rate will be. Likewise, the Debt Ratio % and the Total Debt to Total Net Worth are highly synchronized, which demonstrates the relationship between the debt ratios. Such relationships indicate that there exists a tendency of co-movement of some dimensions of financial characteristics such as profitability and leverage, while there may be a weak relationship between other characteristics such as operational efficiency and growth. However, the heatmap also indicates that there are relatively low levels of connection between some efficiency factors, including Inventory Turnover Rate and Accounts Receivable Turnover, which implies that these indicators may function as measures of a distinct financial characteristic. This further intensifies the nature of financial data, and that a simple model might not be enough to capture some of the characteristics. These correlations suggest the need for a model that can simultaneously consider multiple financial ratios and their interactions. Thus arises a need for a higher form of modeling, as a basic model may fail to capture all these aspects.
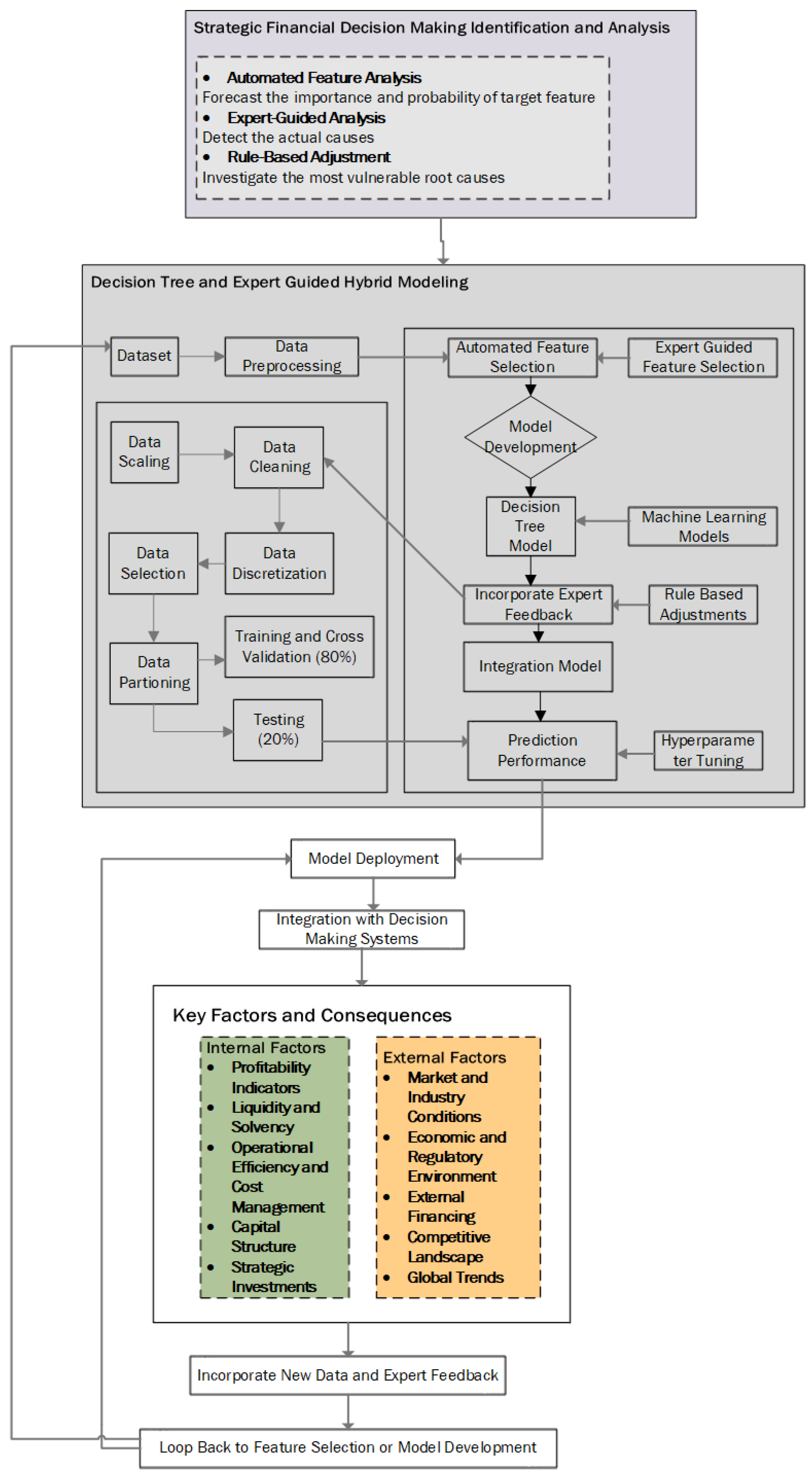
Given these findings, we propose a hybrid model in
Figure 2: decision trees are merged with feedback from experts into a novel approach called Neural Information Framework to address the challenges that are present in financial decision-making. This model will be capable of recognizing relationships between different variables which are typical for the scope of the company’s financial performance, as well as taking into account such factors which are considered only in the given domain and are based on the experience of the financial specialists. In the following section, we will talk about the proposed framework, which is based on the combination of machine learning algorithms and financial analysts’ expertise to improve the efficiency of financial forecasts.
3.1. Research Design
The proposed hybrid framework can be seen in
Figure 2, which depicts a comprehensive, iterative framework for strategic financial decision-making that synthesizes automated analytics, expert insight, and rule-based refinement. At the highest level, the Strategic Financial Decision-Making Identification and Analysis module encompasses three parallel streams: (1) automated feature analysis, in which statistical and tree-based methods forecast feature importance and target probabilities; (2) Expert-Guided Analysis, whereby domain specialists interrogate model outputs to uncover root causes; and (3) rule-based adjustment, which applies predefined financial thresholds (e.g., debt-to-equity limits) to diagnose vulnerable corporate conditions. The central “Hybrid Modeling” panel is divided into a data preprocessing subsystem (left) and a model development pipeline (right). In preprocessing, raw observations undergo scaling, cleaning, discretization into categorical bins, and feature selection before being partitioned into a training set (with cross-validation) and a hold-out test set. The model development pipeline first performs automated feature selection via decision-tree criteria, then integrates Expert-Guided Feature Selection to incorporate practitioner knowledge. Next, a suite of learners (decision tree, Random Forest, XGBoost) is trained; expert feedback and rule-based adjustments are then embedded into an Integration Model, which is subsequently refined through hyperparameter tuning and evaluated for Prediction Performance on the test data. Upon validation, the integrated model is deployed and embedded within organizational decision-support systems to generate real-time risk assessments. A dedicated Key Factors and Consequences module distinguishes between Internal Factors (e.g., profitability, liquidity, capital structure) and External Factors (e.g., market conditions, regulatory environment, competitive landscape), reinforcing the dual focus of the framework. Finally, new data and ongoing expert feedback are continuously looped back into feature selection or model retraining, ensuring that the system remains adaptive, transparent, and aligned with evolving financial realities.
3.2. Data Preprocessing for Financial Datasets
The data preprocessing stage involves transforming the raw financial data into a suitable format for modeling. The key steps include data scaling, data cleaning, and data discretization.
3.2.1. Data Scaling
Given that machine learning algorithms are sensitive to the range of feature values, data scaling is necessary. This is achieved using Z-score normalization:
where
is the feature value,
is the mean of the feature, and
is its standard deviation. This transforms the features into a standard normal distribution with a mean of 0 and a standard deviation of 1, ensuring that all features contribute equally during training.
3.2.2. Data Cleaning
Financial datasets often contain missing values and outliers. Missing values are handled using K-Nearest Neighbors (KNN) imputation, where the missing value is predicted based on the mean of the nearest neighbors. Outliers are detected using the Z-score method, where any feature value with a Z-score greater than 3 is considered an outlier:
Any value with is treated as an outlier and is either removed or capped based on the context of the financial model.
3.2.3. Data Discretization
For certain features, particularly continuous data such as Revenue Growth and Profitability Metrics, discretization is applied to convert continuous values into categorical bins. The discretization function Discretize(x) is used to transform continuous financial metrics into predefined intervals. This includes features like Operating Profit Rate, Operating Gross Margin, Operating Profit Growth Rate, After-tax Net Profit Growth Rate, Regular Net Profit Growth Rate, Continuous Net Profit Growth Rate, Total Asset Growth Rate, and Net Value Growth Rate. By converting these continuous variables into distinct categories, discretization enhances the model’s interpretability, especially in decision trees. This process helps in better identifying patterns within the data, allowing the model to make decisions based on grouped financial thresholds, which is particularly useful for understanding financial health and growth trends of companies.
4. Automated Feature Selection and Expert Feedback Integration
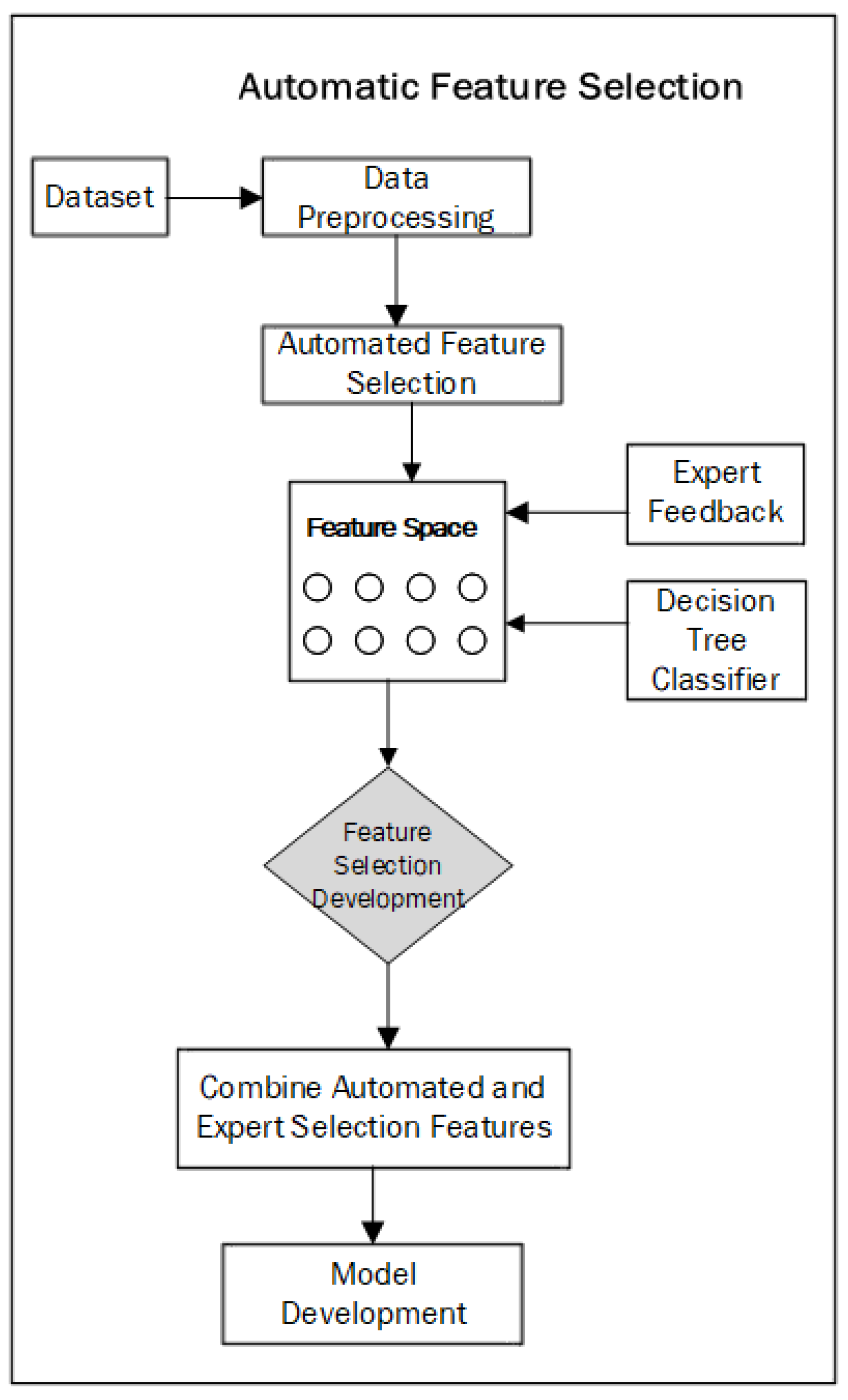
In the proposed framework, automated feature selection and expert feedback integration form a key part of the modeling process. The goal of this phase is to identify the most influential features from a financial dataset and refine the selection through expert domain knowledge, thus ensuring that the final model is both statistically sound and relevant from a financial perspective. As depicted in
Figure 3, the automated feature selection process begins by preprocessing the dataset to clean the data and handle any issues such as missing values and outliers. After that, the model automatically evaluates the importance of each feature using decision trees, a fundamental machine learning technique that enables both automatic feature selection and interaction with domain-specific knowledge.
4.1. Automated Feature Selection
Automated feature selection is crucial for identifying which variables (or features) in the financial dataset are most predictive of the target variable. A decision tree model is employed in this stage due to its ability to assess the importance of each feature through recursive binary splits. Decision trees are built by evaluating how each feature splits the dataset into subsets that reduce a certain measure of impurity. The impurity of a node in a decision tree is commonly measured using the Gini index or entropy.
4.1.1. Gini Index
The Gini Index is used to measure the degree of impurity or impurity reduction in a node. For a binary classification, the Gini Index is calculated as follows:
where
For each potential feature split, the decision tree algorithm computes the Gini index at each child node. The feature that leads to the largest decrease in Gini index is chosen as the best feature to split on at each step.
4.1.2. Entropy
Another impurity measure used in decision trees is entropy, which quantifies the amount of information or uncertainty in the dataset. The entropy for a given node
t is calculated as follows:
where
represents the probability of class
i in the node
t. The decision tree aims to reduce the entropy by splitting on features that maximize information gain.
4.1.3. Information Gain
Information gain is the reduction in entropy achieved by splitting a node based on a particular feature. The information gain
for a feature
f is defined as follows:
where
is the entropy of the parent node;
m is the number of child nodes (i.e. the number of subsets ) produced by splitting on feature f;
is the k-th subset of the data resulting from that split; and
is the proportion of samples in subset k relative to the entire dataset.
The higher the information gain, the more important the feature is for predicting the target.
4.2. Expert Feedback Integration
While automated feature selection provides a solid statistical basis for identifying relevant features, it is equally important to incorporate expert feedback to ensure that the feature space reflects domain-specific knowledge, especially when working with financial data. Financial experts can identify important factors that could not be evident through automated techniques alone, such as the following:
Macroeconomic Indicators: Features like interest rates, inflation, or gross domestic product (GDP) growth can have significant effects on financial performance.
Industry-Specific Metrics: Certain ratios or indicators are more important for specific industries, such as the operating profit margin for manufacturing companies or solvency ratios for financial institutions.
Expert feedback helps refine the selected features by introducing additional features that are believed to have predictive value based on the expert’s domain knowledge. These expert-driven features may include macroeconomic indicators or adjustments based on industry knowledge, which could not have been identified in the automated feature selection process.
4.3. Knowledge-Driven Rules
Experts can also propose rule-based adjustments. For example, if the debt-to-equity ratio exceeds a threshold (e.g., 3.0), it may indicate a company is at risk of bankruptcy, regardless of what the automated selection suggests. Rules can be based on financial norms and industry practices, such as the following:
If debt-to-equity > 3.0, label the company as “high-risk”.
If profitability margin < 5%, adjust the feature weighting to reflect a potential risk.
These rules are particularly useful for addressing situations where machine learning models might miss contextual insights, as they provide a domain-specific layer of decision-making.
4.4. Combining Automated Selection with Expert Feedback
Once the automated feature selection process identifies the most statistically significant features and expert feedback provides additional insights, the next step is to combine these feature sets for model development and can be seen in the Algorithm 1.
| Algorithm 1: Integrating expert feedback with feature set. |
![Symmetry 17 00976 i001]() |
The proposed algorithm implements a rule-based mechanism for embedding domain expertise directly into the feature engineering pipeline. Starting from an initial set of financial variables, it systematically examines each expert-specified metric—debt-to-equity ratio, profitability margin, quick ratio, operating profit margin, and a macroeconomic indicator—and applies threshold-based rules to generate new binary risk flags (e.g., high risk, profitability risk, low liquidity, operating profit risk, economic downturn). Whenever a given metric is present in the feature set, the algorithm creates the corresponding risk flag by testing whether the metric exceeds or falls below a critical value (for instance, marking debt-to-equity above 3.0 as high-risk, or quick ratio below 1.0 as low liquidity), and then appends this flag to the updated feature list. The output is an enriched feature set that combines raw financial measures with expert-driven indicators, thereby improving the model’s ability to incorporate practitioner insights and increasing overall interpretability.
4.4.1. Feature Space Consolidation
The features selected by the decision tree are combined with those provided by expert feedback. This creates an enriched feature space that incorporates both data-driven insights and domain knowledge:
where
represents the final feature space;
are the features selected by automated methods; and
are the features identified by the expert.
4.4.2. Feature Development and Transformation
New features are created by combining existing features or transforming them based on expert feedback. For example, a Profitability-to-Liquidity ratio might be created by dividing profitability metrics by liquidity metrics, reflecting the company’s ability to convert profits into cash flow:
4.4.3. Final Feature Set
After feature selection and transformation, the final feature set is ready for use in model development. This feature set combines both the automated selections made by the decision tree algorithm and the domain-specific insights from the experts.
7. Conclusions
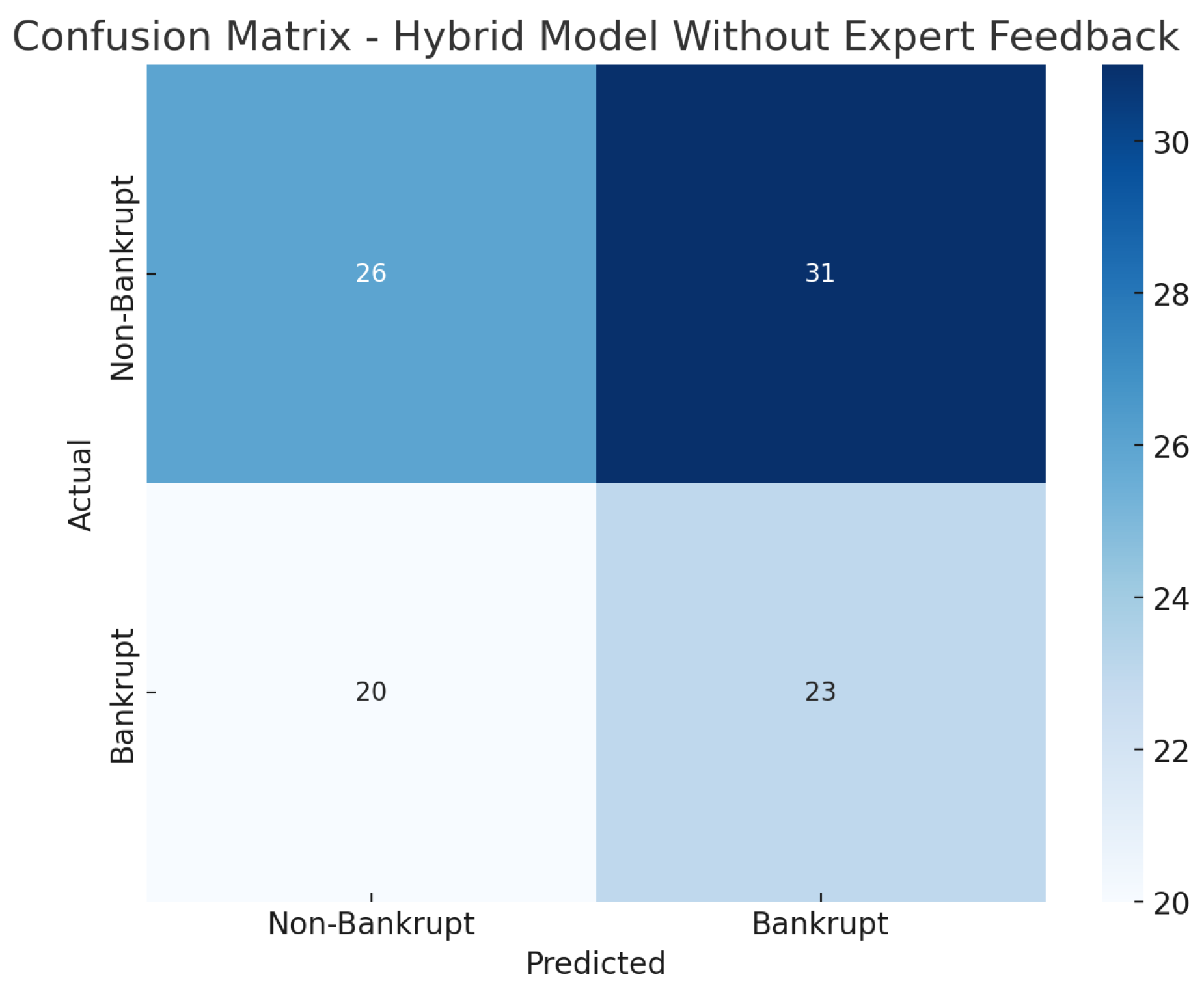
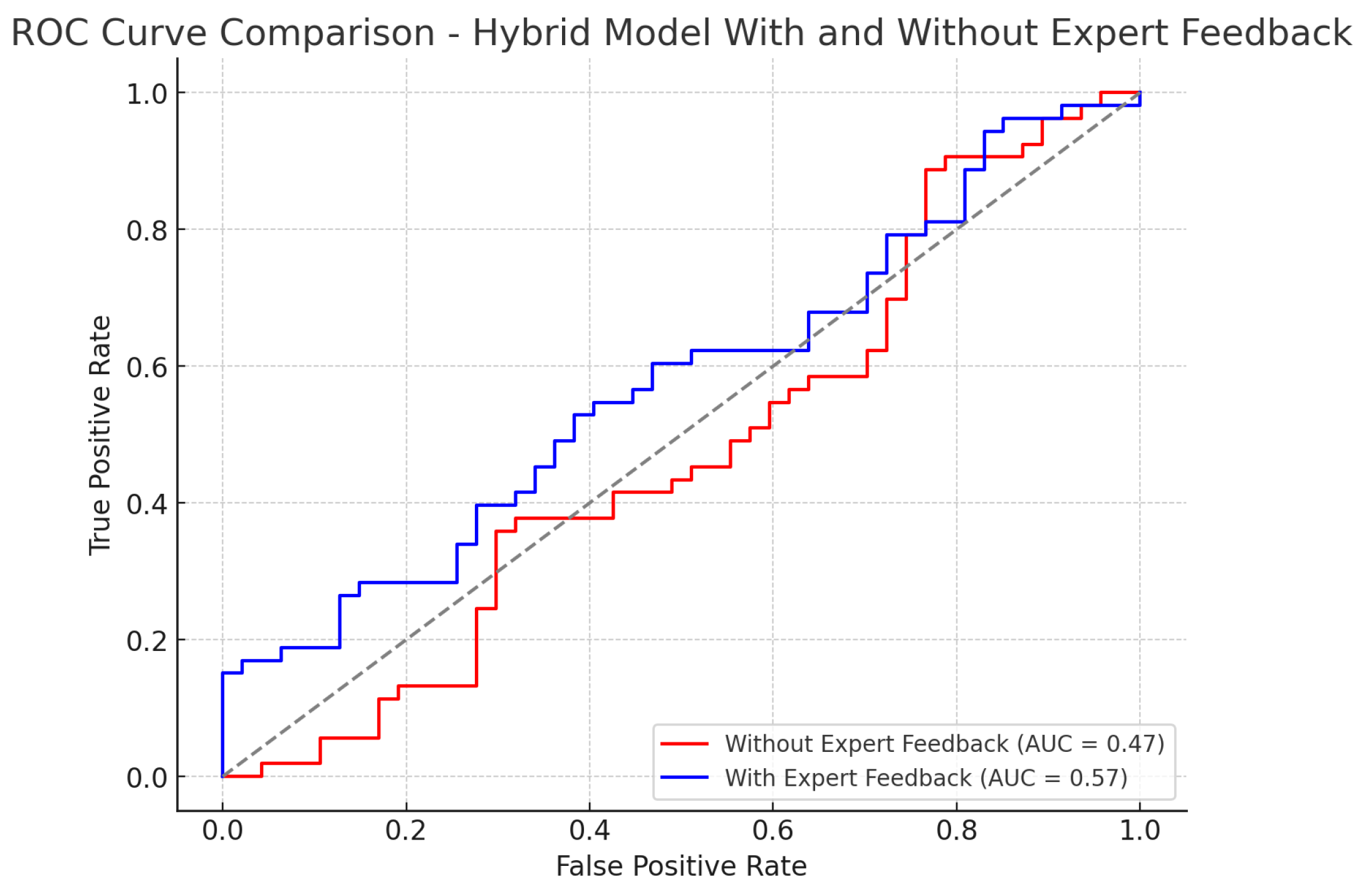
In this study, we proposed a hybrid framework that combines decision trees with advanced ensemble methods to predict corporate bankruptcy, and we examined the impact of expert feedback on model performance. The hybrid model without expert feedback achieved an accuracy of 0.82, precision of 0.84, recall of 0.78, F1-score of 0.81, and an AUC-ROC of 0.88. These results outperformed the baseline decision tree (accuracy 0.78, precision 0.76, recall 0.74, F1 0.75, AUC-ROC 0.83), Random Forest (0.80, 0.79, 0.76, 0.77, 0.86), and XGBoost (0.81, 0.82, 0.79, 0.80, 0.87). When expert feedback was incorporated, the hybrid framework exhibited further gains across all metrics—most notably, accuracy and AUC-ROC—underscoring that domain-specific rules and thresholds can refine model decisions beyond what automated feature selection alone provides. Overall, these findings demonstrate that (1) ensemble methods significantly enhance predictive accuracy compared to a single decision tree, and (2) the addition of expert-driven adjustments yields a more robust, transparent, and context-aware decision-support tool for strategic financial management.
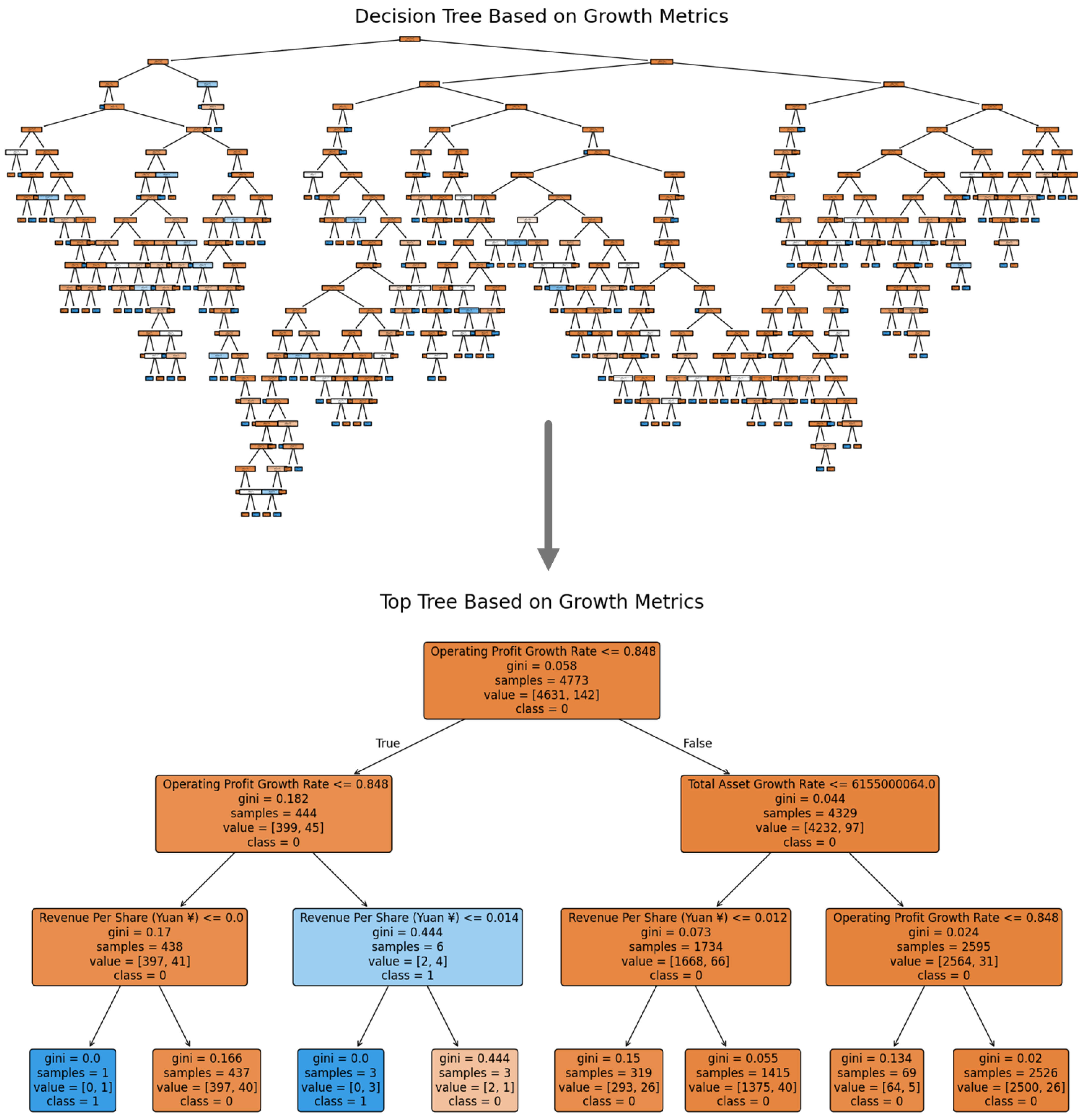
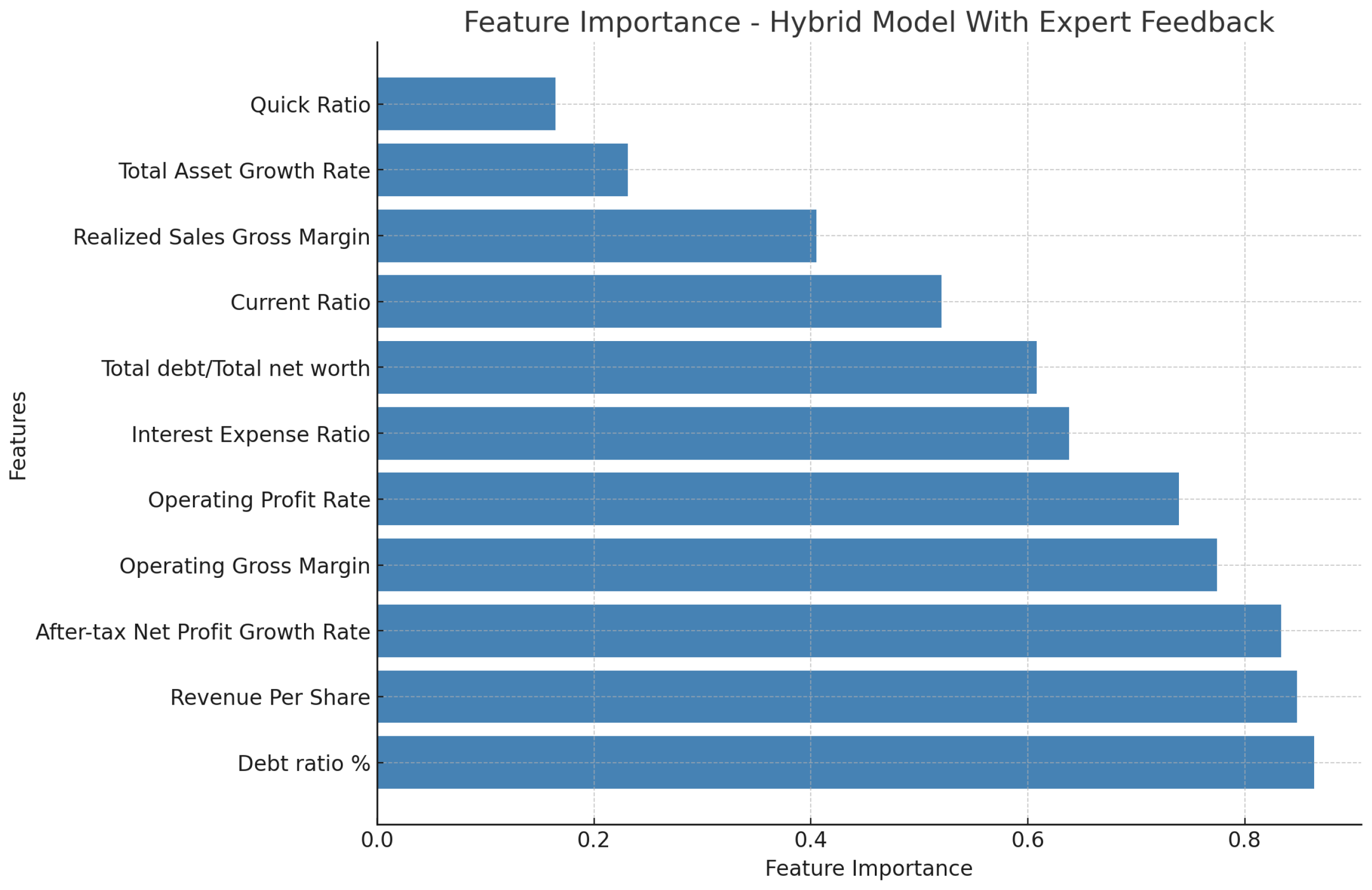
The integration of expert feedback in the hybrid model further refined the decision tree by incorporating domain-specific rules and insights. Expert-driven rules, such as thresholds for debt-to-equity ratios and profitability margins, allowed the model to account for real-world conditions that automated models might overlook. This inclusion of human intuition provided an additional layer of validation, ensuring that the decision tree adhered to financial norms and practices. Our experimental results demonstrated the effectiveness of the hybrid decision tree model. The AUC-ROC scores, precision, recall, and F1-scores were all improved when expert feedback was incorporated, highlighting the added value of combining automated machine learning techniques with domain knowledge. The visualizations of decision trees provided clear interpretability, allowing stakeholders to understand how various financial metrics contributed to the decision-making process. In conclusion, the proposed hybrid model significantly enhances the prediction accuracy for bankruptcy risk by combining automated feature selection and expert-driven adjustments. It not only improves the precision of predictions but also provides a more transparent and interpretable decision-making process.
Future Research
This framework can be applied in various financial industries to better inform strategic decisions, offering a reliable tool for early identification of potential bankruptcies. Future research could explore the incorporation of additional expert feedback and the integration of more advanced machine learning techniques, such as ensemble methods, to further improve predictive performance and model generalization across different industries.