Statistical Analysis Under a Random Censoring Scheme with Applications

Abstract

The Gumbel Type-II distribution is a widely recognized and frequently utilized lifetime distribution, playing a crucial role in reliability engineering. This paper focuses on the statistical inference of the Gumbel Type-II distribution under a random censoring scheme. From a frequentist perspective, point estimates for the unknown parameters are derived using the maximum likelihood estimation method, and confidence intervals are constructed based on the Fisher information matrix. From a Bayesian perspective, Bayes estimates of the parameters are obtained using the Markov Chain Monte Carlo method, and the average lengths of credible intervals are calculated. The Bayesian inference is performed under both the squared error loss function and the general entropy loss function. Additionally, a numerical simulation is conducted to evaluate the performance of the proposed methods. To demonstrate their practical applicability, a real world example is provided, illustrating the application and development of these inference techniques. In conclusion, the Bayesian method appears to outperform other approaches, although each method offers unique advantages.

1. Introduction

The Gumbel Type-II (G-II) distribution was initially put forth by German mathematician Emil Gumbel in [1]. For simulating “extreme values”, like earthquakes, floods, and natural calamities, it is an effective tool. The distribution is frequently used in disciplines including hydrology, life expectancy research, and rainfall analysis. According to Gumbel, it excels at simulating the anticipated lifespan of goods, especially in comparative lifetime testing. The G-II distribution has also been helpful in predicting the probability of specific meteorological phenomena and natural disasters.

Statistical inference techniques for the G-II distribution have been extensively studied by numerous researchers. For example, Mousa et al. [2] utilized simulations with predetermined parameter values to evaluate Bayesian estimates, while [3] explored Bayesian estimation under the k-th lower value scenario. Nadarajah and Kotz [4] investigated maximum likelihood methods for the beta Gumbel distribution. Additionally, Miladinovic and Tsokos [5] examined the sensitivity of Bayesian reliability estimates for a modified Gumbel failure model using the SE loss function.

Feroze and Aslam [6] explored Bayesian estimation for the G-II distribution under doubly censored samples and various loss functions. This work was further developed by Abbas et al. [7], who investigated Bayesian inference for the G-II distribution, including applications for two competing units, as initially proposed in [8]. Abbas et al. [9] derived Bayesian estimation for type-II censored data under various loss functions and non-informative priors, employing Lindley’s approximation. More recently, Qiu and Gui [10] applied joint type-II censoring to achieve Bayesian estimation for two G-II distributions.

These investigations demonstrate the distribution’s adaptability and significance in advanced statistical modeling and estimation methods. The cumulative distribution function (CDF) is given as follows:

$$F\left(x\right)=e^{-\rho x^{-\psi }},x>0,\rho >0,\psi >0,$$

(1)

Furthermore, the corresponding probability density function (PDF) is expressed as follows:

$$f\left(x\right)=\rho \psi x^{-(\psi +1)}{e}^{-\rho x^{-\psi }},x>0,\rho >0,\psi >0.$$

(2)

In this case, $\psi$ represents the shape parameter, while $\rho$ is the scale parameter of the distribution. Figure 1 illustrate the PDF and CDF of the G-II distribution for various values of the parameters $\psi$ and $\rho$.

Censoring data plays a critical role in statistical estimation, particularly in fields like survival analysis, reliability engineering, and medical research. It arises when complete information about a data point is not observed due to limitations in study design, time constraints, or other practical barriers. For instance, in reliability studies, the lifetime of a product might only be partially observed if the study ends before all items fail. Censoring allows researchers to make efficient use of incomplete data, ensuring that valuable information is not discarded. By employing appropriate statistical methods, such as likelihood-based approaches or Bayesian frameworks, censored data can provide robust parameter estimates and deeper insights into underlying distributions. The ability to model censored data effectively enhances the precision and applicability of statistical analyses in real-world scenarios, where complete data collection is often infeasible.

Due to time and economic limitations, which often hinder the data acquisition process, obtaining a complete data set can be challenging. Such incomplete information is referred to as “observed data”. To analyze this kind of data, different observational methods are described in the literature. The two most widely utilized observation categories are Type-I and Type-II. Events in Type-I observation are only recorded if they occur before to a certain time. Under Type-II observation, information is gathered up until a certain quantity of noteworthy occurrences has been noted.

One method that has been extensively discussed in the literature is randomly censoring (RC). This happens when a research subject disappears or is removed from an experiment prior to the event of interest. RC is commonly used in medical time-to-event research, including clinical trials, due to the potential for treatment discontinuation or early study termination. Consequently, the data from these participants is considered to be RC. In his dissertation, Gilbert initially proposed the idea of RC [11]. Numerous studies have addressed this topic, including Breslow and Crowley [12], Koziol and Green [13], Ghitany and Al-Awadhi [14], Saleem and Aslam [15], Danish and Aslam [16], Krishna et al. [17], Garg et al. [18], Krishna and Goel [19], Krishna and Goel [20], Garg et al. [21], Ajmal et al. [22], Goel and Krishna [23], Hasaballah et al. [24], Alshenawy et al. [25], Hassan et al. [26], Almetwally et al. [27], Hassan and Ahmed [28], and El-Saeed and Abdellatif [29].

The manuscript emphasizes the statistical inference of the Gumbel Type-II (G-II) distribution, a model extensively utilized in reliability engineering with broad practical applications across various domains. It introduces both frequentist and Bayesian approaches to parameter estimation. The frequentist method employs maximum likelihood estimation (MLE) and derives asymptotic confidence intervals (ACIs), while the Bayesian approach utilizes Markov Chain Monte Carlo (MCMC) techniques to compute Bayes estimators and credible intervals (CRIs). The manuscript compares the performance of these methods through numerical simulations, demonstrating that Bayesian methods typically outperform traditional techniques, particularly concerning average relative bias (ARB) values. Furthermore, it examines the influence of different loss functions, such as squared error (SE) and general entropy (GE), on estimation performance, providing valuable insights into their efficacy under diverse conditions. A real-world example is also presented to highlight the practical relevance of the proposed inference methods. The primary aim is to enhance the understanding and application of the G-II distribution under RC, while delivering robust estimation techniques and comprehensive comparative analyses.

This article explores inferential techniques for the G-II distribution under a RC model using both classical and Bayesian frameworks. The structure of the paper is as follows: Section 2 provides the mathematical foundation for RC, including the distributions of censoring times and failures. The MLE approach and the creation of ACIs for the parameters are the main topics of Section 3. The Bayesian inferential approach is detailed in Section 4, which incorporates two loss functions SE and GE along with gamma informative priors. The MCMC method is employed to derive CRIs for the parameters. Section 5 demonstrates the practical application of the proposed methods through a real-world dataset. Section 6 examines the characteristics of the various estimators based on simulation analysis. Concluding remarks are presented in Section 7.

2. Randomly Censoring Scheme

For a study with (b) participants, let $X_1,\dots ,X_b$ represent the event times for each participant. The CDF $Q_X\left(x\right)$ and the PDF $q_X\left(x\right)$ are used to model these event timings as independent and identically distributed (iid) random variables. With the accompanying CDF $Q_T\left(t\right)$ and PDF $q_T\left(t\right)$, the sequence $T_1,\dots ,T_b$ represents the RC times, which are also iid. Since $H_i=\min (X_i,T_i)$ for $i=1,\dots ,n$, the observed data consists of iid random pairings $(H_1,G_1),\dots ,(H_b,G_b)$, indicating the mutual independence of $X_i$ and $T_i$. The definition of the variable $G_i$ is as follows:

$$G_i=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}{X}_i\le T_i,\hfill \\ \hfill 0\hfill & \hfill \mathrm{if}{X}_i>T_i.\hfill \end{array}\right.$$

Under this setup, the joint PDF of $H_i$ and $G_i$ is given by

$$q_{H,G}(h,g)={\left[q_X\left(h\right)(1-q_T\left(h\right)\right]}^g{\left[q_T\left(h\right)(1-Q_X\left(h\right))\right]}^{1-g},h\ge 0,g=0,1.$$

Assuming a proportionality constant $\eta >0$, the random variables X and T follow the proportional hazards model if

$$1-Q_T\left(t\right)={\left[1-Q_X\left(t\right)\right]}^{\eta }.$$

When $\eta =0$, this model corresponds to the case of no censoring. By combining the expressions for the joint PDF $q_{H,G}(h,g)$ and the proportional hazards model, the joint PDF of $H_i$ and $G_i$ is derived as

$$q_{H,G}(h,g)=q_X\left(h\right){\left[1-Q_X\left(h\right)\right]}^{\eta }{\eta }^{1-g},h\ge 0,g=0,1.$$

(3)

By combining Equations (1)–(3), the joint PDF can be further expressed in terms of the specific parameters $\psi$, $\rho$, and $\eta$ as

$$\begin{array}{c}\hfill q_{H,G}(h,g;\psi ,\rho ,\eta )=\psi \rho h^{-(\psi +1)}{e}^{-\rho h^{-\psi }}{\left[1-e^{-\rho h^{-\psi }}\right]}^{\eta }{\eta }^{1-g},h\ge 0,g=0,1.\end{array}$$

(4)

3. Classical Inference

Classical inference is a cornerstone of statistical analysis, widely used in various scientific disciplines for parameter estimation and hypothesis testing. It relies on the concept of long-run frequencies, interpreting probabilities as the relative frequency of an event occurring over repeated experiments. This approach offers objective results that are independent of prior beliefs, making it particularly valuable in situations where prior information is unavailable or unreliable. Frequentist methods, such as MLE and Confidence Intervals, provide robust tools for analyzing data, ensuring reproducibility and consistency of results. Its importance extends to applications in experimental design, quality control, clinical trials, and more, where reliable, data-driven conclusions are critical for informed decision-making.

3.1. Maximum Likelihood Estimation

MLE is a fundamental method in statistical inference, widely used for estimating the parameters of a probability distribution. MLE operates by identifying the parameter values that maximize the likelihood function, which represents the probability of observing the given data under specific parameter assumptions. Its importance lies in its versatility and efficiency, as it provides consistent and asymptotically unbiased estimators under regular conditions. MLE is particularly valuable in a broad range of applications, including machine learning, econometrics, and experimental sciences, where accurate parameter estimation is essential for model interpretation and prediction. Additionally, MLE facilitates hypothesis testing and model comparison, making it a critical tool for data-driven decision-making in both theoretical and applied research.

In this article, we use a RC framework to obtain the MLEs for the unknown parameters of the G-II distribution. Using the formula $(h,g)=(h_1,g_1),(h_2,g_2),\dots ,(h_b,g_b)$, we consider a sample of size b that has been RC according to Equation (4). For this censored sample $(h,g)$, the likelihood function can be written as follows:

$$\begin{array}{c}\hfill L(H,G;\psi ,\rho ,\eta )={\psi }^b{\rho }^b{e}^{-(\psi +1){\sum }_{i=1}^b{h}_i}{e}^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}{e}^{\eta {\sum }_{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right]}{\eta }^{b-{\sum }_{i=1}^b{g}_i}.\end{array}$$

Taking the natural logarithm of both sides yields

$$\begin{array}{cc}\hfill \ell (\psi ,\rho ,\eta )=& bln\psi +bln\rho -(\psi +1)\sum _{i=1}^{b}ln{h}_i-\rho \sum _{i=1}^b{h}_i^{-\psi }+\eta \sum _{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right]\hfill \\ & +(b-\sum _{i=1}^b{g}_i)ln\eta .\hfill \end{array}$$

(5)

The following system of normal equations is obtained by differentiating the likelihood function (5) with regard to the parameters $\rho$, $\psi$, and $\eta$:

$${\displaystyle \frac{b}{\widehat{\psi }}}-\sum _{i=1}^{b}ln{h}_i+\widehat{\rho }\sum _{i=1}^b{h}_i^{-\widehat{\psi }}ln{h}_i-\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }\widehat{\rho }{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}{h}_i^{-\widehat{\psi }}ln{h}_i}{1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}}}=0,$$

(6)

$${\displaystyle \frac{b}{\widehat{\rho }}}-\sum _{i=1}^b{h}_i^{-\widehat{\psi }}+\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}{h}_i^{-\widehat{\psi }}}{1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}}}=0,$$

(7)

$$\sum _{i=1}^{b}ln\left[1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right]+{\displaystyle \frac{(b-{\sum }_{i=1}^b{g}_i)}{\widehat{\eta }}}=0.$$

(8)

From Equation (8), we obtain the MLE for $\widehat{\eta }$ as

$$\widehat{\eta }={\displaystyle \frac{b-{\sum }_{i=1}^b{g}_i}{{\sum }_{i=1}^{b}ln\left[1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right]}}.$$

(9)

The equations for $\widehat{\rho }$ and $\widehat{\psi }$ presented above do not have closed-form solutions. As a result, we use numerical iteration methods to compute the estimates.

3.2. Confidence Interval

Confidence intervals (CIs) are crucial tools in statistical inference that provide a range of values within which an unknown parameter is likely to lie, with a certain level of confidence. Typically expressed as a lower and upper bound, CIs offer more information than a simple point estimate by reflecting the uncertainty and variability in the data. The width of the confidence interval is influenced by factors such as sample size, variability in the data, and the chosen confidence level, often set at 95%. A narrower interval indicates more precise estimation, while a wider interval suggests greater uncertainty. CIs are particularly valuable in decision-making processes, as they help quantify the reliability of parameter estimates, allowing researchers to assess the strength of their conclusions. Furthermore, they are essential in hypothesis testing, as they provide a framework for evaluating whether a parameter falls within a hypothesized range, supporting more robust and informed statistical interpretations.

This subsection begins with the derivation of Fisher’s Information Matrix (FIM) to construct the ACI. Next, the observed FIM is utilized to calculate the estimated variances of $\widehat{\rho }$, $\widehat{\psi }$, and $\widehat{\eta }$, as presented below.

$$\begin{array}{cc}\hfill I^{-1}(\widehat{\rho },\widehat{\psi },\widehat{\eta })={\left(\begin{array}{ccc}-{\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\rho }}^2}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\rho }}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\eta }}}\\ -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\rho }}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\rho }}^2}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\eta }}}\\ -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\eta }\partial \widehat{\rho }}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\eta }\partial \widehat{\rho }}}& -{\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\eta }}^2}}\end{array}\right)}^{-1}& \hfill =\left(\begin{array}{ccc}\widehat{var}\left(\widehat{\rho }\right)& cov(\widehat{\rho },\widehat{\psi })& cov(\widehat{\rho },\widehat{\eta })\\ cov(\widehat{\psi },\widehat{\rho })& \widehat{var}\left(\widehat{\psi }\right)& cov(\widehat{\psi },\widehat{\eta })\\ cov(\widehat{\eta },\widehat{\rho })& cov(\widehat{\eta },\widehat{\psi })& \widehat{var}\left(\widehat{\eta }\right)\end{array}\right),\hfill \end{array}$$

(10)

where

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\psi }}^2}}=& {\displaystyle \frac{b}{{\widehat{\psi }}^2}}-\sum _{i=1}^{b}ln{h}_i+\widehat{\rho }\sum _{i=1}^b{h}_i^{-\widehat{\psi }}ln{h}_i+\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }\widehat{\rho }\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\left[{(h_i^{-\widehat{\psi }}ln{h}_i)}^2-h_i^{-\widehat{\psi }}{(ln{h}_i)}^2\right]}{{\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)}^2}}\hfill \\ & +\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }{\left[\widehat{\rho }{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}{h}_i^{-\widehat{\psi }}ln{h}_i\right]}^2}{{\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)}^2}}=0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\rho }}^2}}=& \hfill {\displaystyle \frac{n}{{\widehat{\rho }}^2}}-\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}{h}_i^{-2\widehat{\psi }}+\eta {\left[e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}{h}_i^{-\widehat{\psi }}\right]}^2}{{\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)}^2}}=0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial {\widehat{\eta }}^2}}=& \hfill {\displaystyle \frac{{(b-{\sum }_{i=1}^b{g}_i)}^2}{{\widehat{\eta }}^2}},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\eta }\partial \widehat{\rho }}}={\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\eta }}}=& \hfill \sum _{i=1}^b{\displaystyle \frac{h_i^{-\widehat{\psi }}{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}}{1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}}},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\psi }\partial \widehat{\rho }}}=& {\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\rho }\partial \widehat{\psi }}}=\sum _{i=1}^b{h}_i^{-\widehat{\psi }}ln{h}_i+\sum _{i=1}^b{\displaystyle \frac{\widehat{\eta }\widehat{\rho }\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}ln{h}_i\left[h_i^{-\widehat{\psi }}-1\right]}{{\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)}^2}}\hfill \\ & +\sum _{i=1}^b{\displaystyle \frac{\widehat{\rho }{h}_i^{-\widehat{\psi }}{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}ln{h}_i}{{\left(1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}\right)}^2}}=0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\psi }\partial \widehat{\eta }}}={\displaystyle \frac{{\partial }^2\ell }{\partial \widehat{\eta }\partial \widehat{\psi }}}=& \hfill -\sum _{i=1}^b{\displaystyle \frac{\widehat{\rho }{h}_i^{\widehat{\psi }}{e}^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}ln{h}_i}{1-e^{-\widehat{\rho }{h}_i^{-\widehat{\psi }}}}}.\hfill \end{array}$$

(16)

The asymptotic normality of the MLEs enables the computation of $(1-\phi )100\%$ ACIs for the parameters $\widehat{\rho }$, $\widehat{\psi }$, and $\widehat{\eta }$, which are expressed as follows:

$$\begin{array}{cccc}\hfill & \hfill \left(\widehat{\rho }\pm Z_{\phi /2}\sqrt{\widehat{var}\left(\widehat{\rho }\right)}\right),\hfill & \hfill \left(\widehat{\psi }\pm Z_{\phi /2}\sqrt{\widehat{var}\left(\widehat{\psi }\right)}\right), \mathrm{and}& \hfill \left(\widehat{\eta }\pm Z_{\phi /2}\sqrt{\widehat{var}\left(\widehat{\eta }\right)}\right).\hfill \end{array}$$

(17)

Here, $Z_{\phi /2}$ is the $\phi /2$ quantile of the standard Gaussian distribution.

4. Bayesian Estimation

Bayesian inference is a powerful statistical approach that integrates prior knowledge with observed data to estimate unknown parameters and make predictions. Unlike frequentist methods, Bayesian inference explicitly incorporates uncertainty in parameter estimates through the use of probability distributions. This is achieved by applying Bayes’ theorem, which updates prior beliefs based on new evidence to produce posterior distributions. The approach is particularly useful in complex models, small sample sizes, or when prior information is available, as it provides a coherent framework for decision-making under uncertainty. Bayesian inference has widespread applications across fields, including medicine, engineering, and machine learning, where understanding uncertainty and making probabilistic predictions are crucial. Its flexibility and ability to handle hierarchical models and incorporate expert knowledge make it an essential tool in modern statistical analysis. For more information, see Geman and Geman [30] and Gamerman [31].

4.1. Prior Information and Posterior Distribution

Prior information and posterior distribution are foundational concepts in Bayesian inference. Prior information represents the knowledge or beliefs about an unknown parameter before observing any data, expressed as a probability distribution called the prior. This allows the incorporation of expert opinions, historical data, or subjective judgment into the analysis. When new data are observed, Bayes’ theorem combines the prior distribution with the likelihood of the observed data to produce the posterior distribution, which represents the updated beliefs about the parameter. The posterior distribution provides a comprehensive view of parameter uncertainty, enabling probabilistic interpretations and predictions. The importance of priors and posteriors lies in their ability to formalize and quantify uncertainty, integrate past and current information, and offer a flexible framework for modeling complex systems. These features make Bayesian methods invaluable in applications requiring adaptive learning, decision-making, or robust estimation under uncertainty.

The Bayes estimates for the RC G-II distribution’s unknown parameters are obtained in this section. The parameters $\rho$, $\psi$, and $\eta$ are assumed to be independent, each following a gamma prior distribution. Each prior is characterized by its corresponding PDF and specific hyperparameters: $(a_1,d_1)$, $(a_2,d_2)$, and $(a_3,d_3)$.

$${\pi }_1\left(\rho \right)\propto {\rho }^{a_1-1}{e}^{-d_1\rho },\rho >0,a_1,d_1>0,$$

$${\pi }_2\left(\psi \right)\propto {\psi }^{a_2-1}{e}^{-d_2\psi },\psi >0,a_2,d_2>0,$$

$${\pi }_3\left(\eta \right)\propto {\eta }^{a_3-1}{e}^{-d_3\eta },\eta >0,a_3,d_3>0.$$

Assuming that $\rho$, $\psi$, and $\eta$ have independent prior distributions, we construct a combined prior distribution. The joint posterior distribution is then derived by combining this prior with the likelihood function, as outlined below:

$$\begin{array}{cc}\hfill {\pi }^{\ast }(\rho ,\psi ,\eta )\propto & \hfill {\rho }^{b+a_1-1}{\psi }^{b+a_2-1}{e}^{-(\psi +1){\sum }_{i=1}^b{h}_i}{e}^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}{e}^{\eta {\sum }_{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right]}\hfill \\ & \hfill {\eta }^{b+a_3-{\sum }_{i=1}^b{g}_i}{e}^{-d_1\rho -d_2\psi -d_3\eta }.\hfill \end{array}$$

(18)

As a result, the Bayes estimator for the function $U(\rho ,\psi ,\eta )$ under the SE loss function is expressed as follows:

$$\begin{array}{cccc}\hfill {\widehat{U}}_{BSE}(\rho ,\psi ,\eta )=& \hfill E\left[U(\rho ,\psi ,\eta )|\mathbf{h},\mathbf{g}\right]\hfill & \hfill ={\int }_{\rho }{\int }_{\psi }{\int }_{\eta }U(\rho ,\psi ,\eta )& \hfill \times {\pi }^{\ast }(\rho ,\psi ,\eta |\mathbf{h},\mathbf{g})d\rho d\psi d\eta .\hfill \end{array}$$

(19)

The GE loss function is a versatile and widely used tool in statistical estimation and decision-making. It is designed to penalize estimation errors asymmetrically, allowing for greater flexibility in applications where overestimation and underestimation have different consequences. The GE loss function is particularly important in scenarios such as reliability analysis, risk assessment, and economics, where the cost of errors varies depending on the direction of deviation from the true value. By incorporating a parameter that controls the relative weights of overestimation and underestimation, the GE loss function provides a tailored approach to minimizing the expected loss. This adaptability makes it a critical component in Bayesian analysis, where it is often used to derive posterior-based estimates that align with specific practical objectives. Its importance lies in enabling more accurate and context-sensitive decision-making across diverse fields.

The Bayes estimator for the function $U(\rho ,\psi ,\eta )$ can be expressed using the GE loss function in the following form:

$$\begin{array}{cc}\hfill {\widehat{U}}_{BGE}(\rho ,\psi ,\eta )={\left[E{\left[U(\rho ,\psi ,\eta )\right]}^{-\tau }|\mathbf{h},\mathbf{g}]\right]}^{-{\displaystyle \frac{1}{\tau }}}& \hfill = [{\int }_{\rho }{\int }_{\psi }{\int }_{\eta }{\left[U(\rho ,\psi ,\eta )\right]}^{-\tau }\hfill \\ & \hfill \times {\pi }^{\ast }(\rho ,\psi ,\eta |\mathbf{h},\mathbf{g})d\rho d\psi d\eta {]}^{-{\displaystyle \frac{1}{\tau }}}.\hfill \end{array}$$

(20)

Because it is difficult to derive complete expressions for the marginal posterior distributions associated with every parameter, Equations (19) and (20) are not able to solved mathematically. In order to estimate these equations while accounting for the loss functions, the MCMC method is recommended as a suitable approach.

4.2. MCMC Techniques

MCMC techniques are powerful computational methods used to approximate complex probability distributions, particularly when direct analytical solutions are infeasible. By building a Markov chain that gradually converges to the intended distribution, MCMC produces samples from the target distribution. This method is particularly useful in Bayesian inference, as posterior distributions sometimes require difficult-to-solve high-dimensional integrals. Algorithms such as Metropolis-Hastings or Gibbs sampling allow MCMC to estimate parameters, credible intervals, and predictive distributions. Its flexibility and efficiency make it indispensable in fields such as statistics, machine learning, genetics, and physics, where exact solutions would otherwise be computationally prohibitive. CRIs, a key component of Bayesian estimation, provide a range of values for a parameter based on the posterior distribution. Unlike CIs in frequentist statistics, which rely on repeated sampling, CRIs represent the range within which the parameter lies with a specified probability, given the observed data and prior information. For example, a 95% CRI means that there is a 95% probability the true parameter value falls within this range, conditioned on the data and prior. This probabilistic interpretation enhances the flexibility of Bayesian analysis by integrating prior knowledge, enabling more context-specific conclusions. The width of the CRIs reflects both the data’s influence and the strength of the prior, with a narrower interval indicating greater precision. CRIs are vital in decision-making and risk assessment, offering a more intuitive understanding of uncertainty and enabling more informed, context-aware decisions based on the range of plausible parameter values. For more details about the MCMC methods, see, for example, Chen and Shao [32].

Samples are generated using the MCMC approach based on Equation (18). The process is described in this section. After identifying the parameters $\rho$, $\psi$, and $\eta$, the Bayes estimates are calculated, and the CRI estimates are produced. Equation (18) facilitates maintaining proportionality while deriving the conditional posterior density distributions for $\rho$, $\psi$, and $\eta$. To simplify representation and avoid complex conditional expressions, these distributions are denoted as ${\pi }_1^{\ast }\left(\rho \right)$, ${\pi }_2^{\ast }\left(\psi \right)$, and ${\pi }_3^{\ast }\left(\eta \right)$. Refer to the following for the formulation of these distributions:

$$\begin{array}{cc}\hfill {\pi }_1^{\ast }\left(\rho \right)& \hfill \propto {\rho }^{b+a_1-1}{e}^{-\rho \left[d_1+{\sum }_{i=1}^b{h}_i^{-\psi }\right]},\hfill \end{array}$$

(21)

$$\begin{array}{c}\hfill {\pi }_2^{\ast }\left(\psi \right)\propto {\psi }^{b+a_2-1}{e}^{-\psi \left(d_2+{\sum }_{i=1}^b{h}_i\right)},\end{array}$$

(22)

$$\begin{array}{c}\hfill {\pi }_3^{\ast }\left(\eta \right)\propto {\eta }^{b+a_3-{\sum }_{i=1}^b{g}_i-1}{e}^{-\eta \left(d_3-{\sum }_{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right]\right)}.\end{array}$$

(23)

Notably, the density function in Equation (21) is equivalent to a gamma distribution with a shape parameter $(a_1+b)$ and a scale parameter $\left[d_1+{\sum }_{i=1}^b{h}_i^{-\psi }\right]$. Likewise, the density function in Equation (22) illustrates a gamma distribution with a shape parameter $(a_2+n)$ and a scale parameter $\left(d_2{\sum }_{i=1}^b{h}_i\right)$. Furthermore, the density function in Equation (23) characterizes a gamma distribution with a shape parameter $(a_3+b)$ and a scale parameter $(d_3-{\sum }_{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right)$. It is possible to create samples for $\rho$, $\psi$, and $\eta$ using gamma-generating techniques.

According to Equations (21)–(23), the complete conditional posterior densities of $\rho$, $\psi$, and $\eta$ are mutually independent in this situation. As a result, the Metropolis–Hastings (M-H) algorithm can be used to independently extract Bayesian samples from each density. Consult Metropolis et al. [33] and Hastings [34] for more information. The following procedures outline how to use the M-H method to create samples from these conditional densities:

• Begin by initializing the parameters $\rho$, $\psi$, and $\eta$ with their initial values, denoted as ${\rho }^{\left(0\right)}$, ${\psi }^{\left(0\right)}$, and ${\eta }^{\left(0\right)}$, respectively. Set $j=1$. Choose an appropriate value for k, which implies the burn-in period.
• Utilizing a gamma distribution with parameters $\left[b+a_1,d_1+{\sum }_{i=1}^b{h}_i^{-\psi }\right]$, compute the value of ${\rho }^{\left(i\right)}$.
• Finding ${\psi }^{\left(i\right)}$ with a gamma distribution and parameters $\left(b+a_2,d_2{\sum }_{i=1}^b{h}_i\right)$ is possible.
• With a gamma distribution’s parameters $\left(n+a_3,d_3-{\sum }_{i=1}^{b}ln\left[1-e^{-\rho {\sum }_{i=1}^b{h}_i^{-\psi }}\right]\right)$, calculate ${\eta }^{\left(i\right)}$.
• Set $j=1$
• To obtain the parameter values $({\rho }^{\left(j\right)},{\psi }^{\left(j\right)},{\eta }^{\left(j\right)})$, iterate Steps 2 through 5 a total of A times, where $j=K+1,\dots ,A$.
• Using $j=K+1,\dots ,A$, arranged the parameter values ${\rho }^{\left(j\right)}$, ${\psi }^{\left(j\right)}$, and ${\eta }^{\left(j\right)}$ in ascending order to determine the CRIs for $\rho$, $\psi$, and $\eta$. Since $\mu =(\rho ,\psi ,\eta )$, $\left({\phi }_{{\left(A-K\right)}_{\phi /2}},{\phi }_{{\left(A-K\right)}_{(1-\phi /2)}}\right)$ represents the $100(1-\phi )\%$ CRIs.
• The Bayes estimate for the parameter $\mu$ under the SE loss function can be determined using the following formula:

  $${\widehat{\mu }}_{BSE}={\displaystyle \frac{1}{A-K}}\sum _{i=K+1}^b{\mu }^{\left(i\right)}.$$

  (24)
  The GE loss function is utilized to obtain the estimations as follows:

  $${\widehat{\mu }}_{BGE}={\left[{\displaystyle \frac{1}{A-K}}\sum _{i=K+1}^b{\left[{\mu }^{\left(i\right)}\right]}^{-\tau }\right]}^{{\displaystyle \frac{-1}{\tau }}}.$$

  (25)

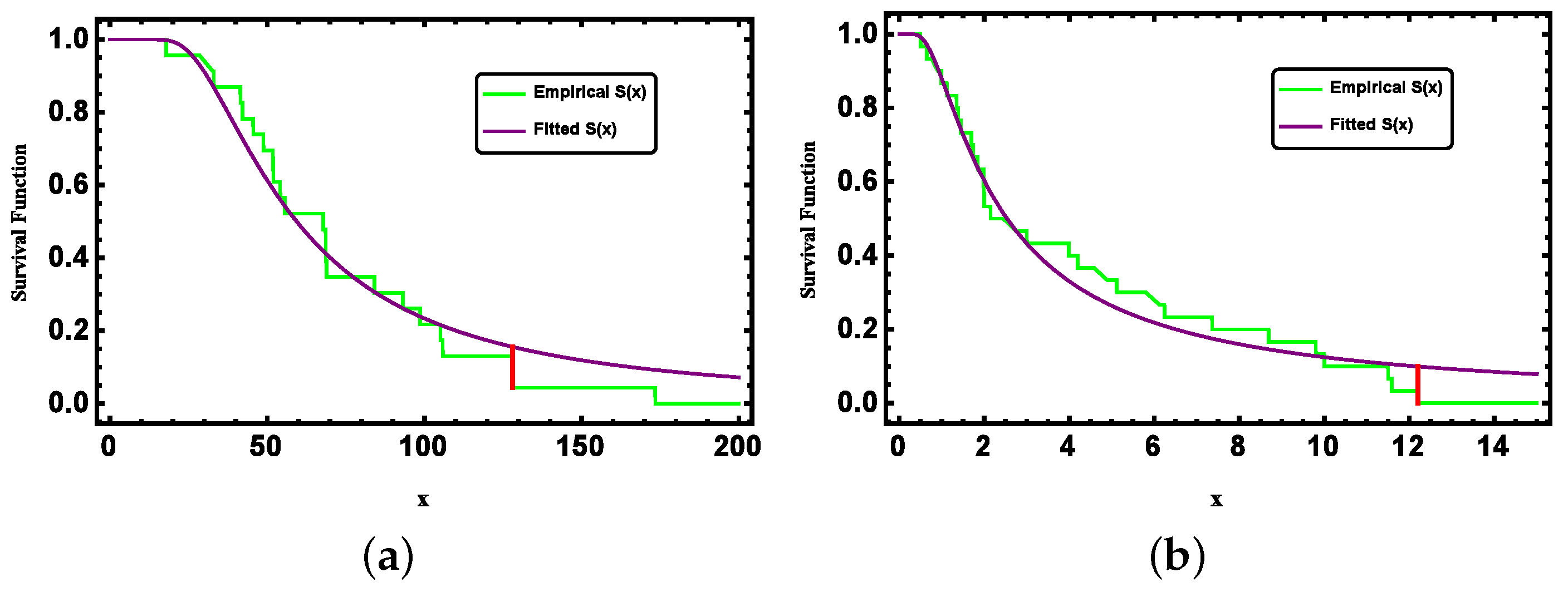
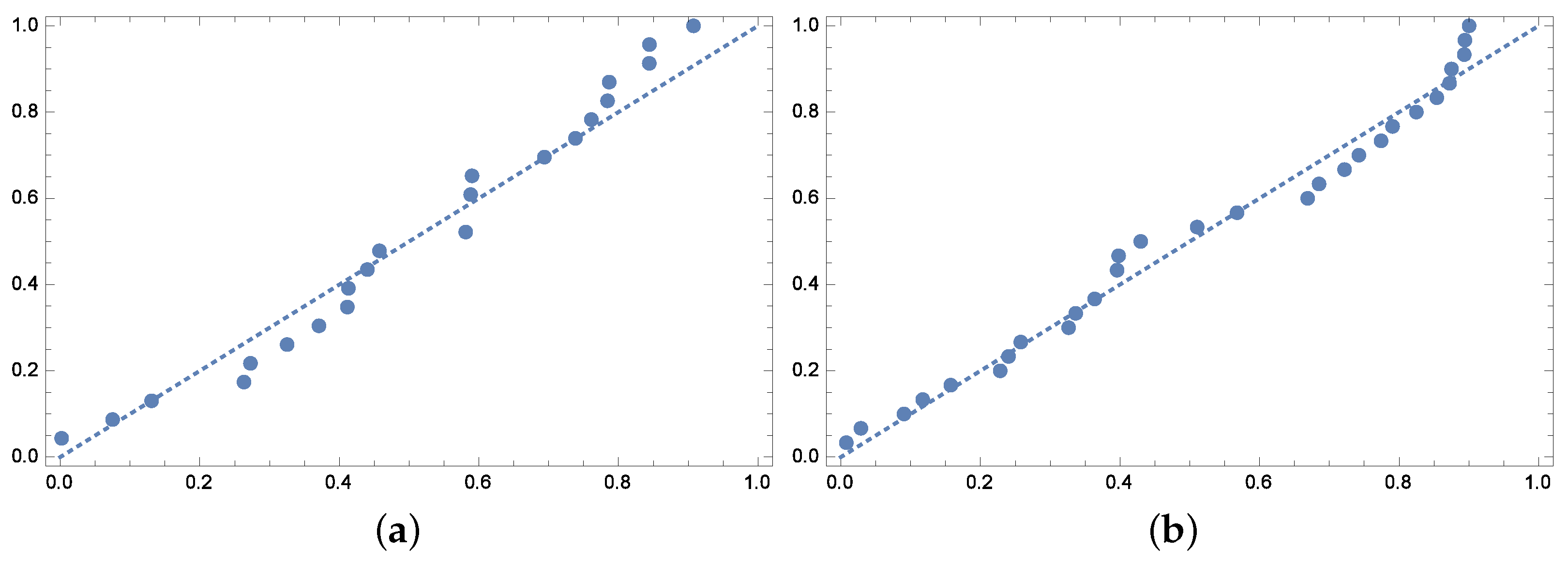
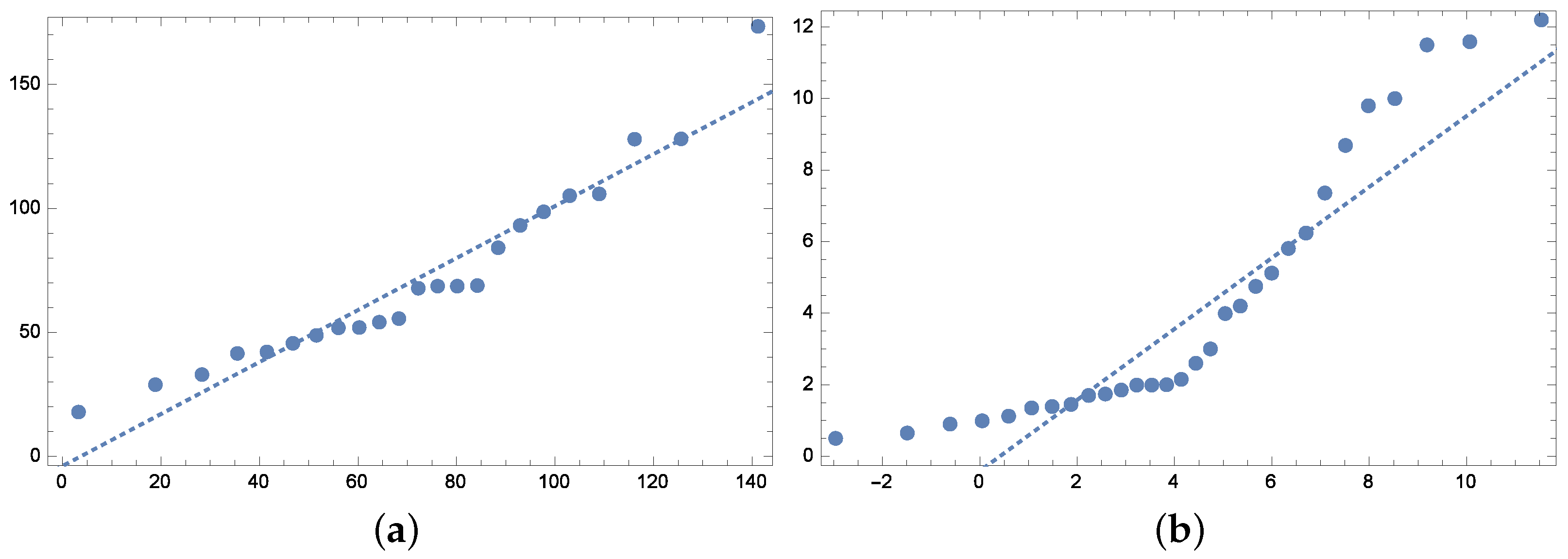
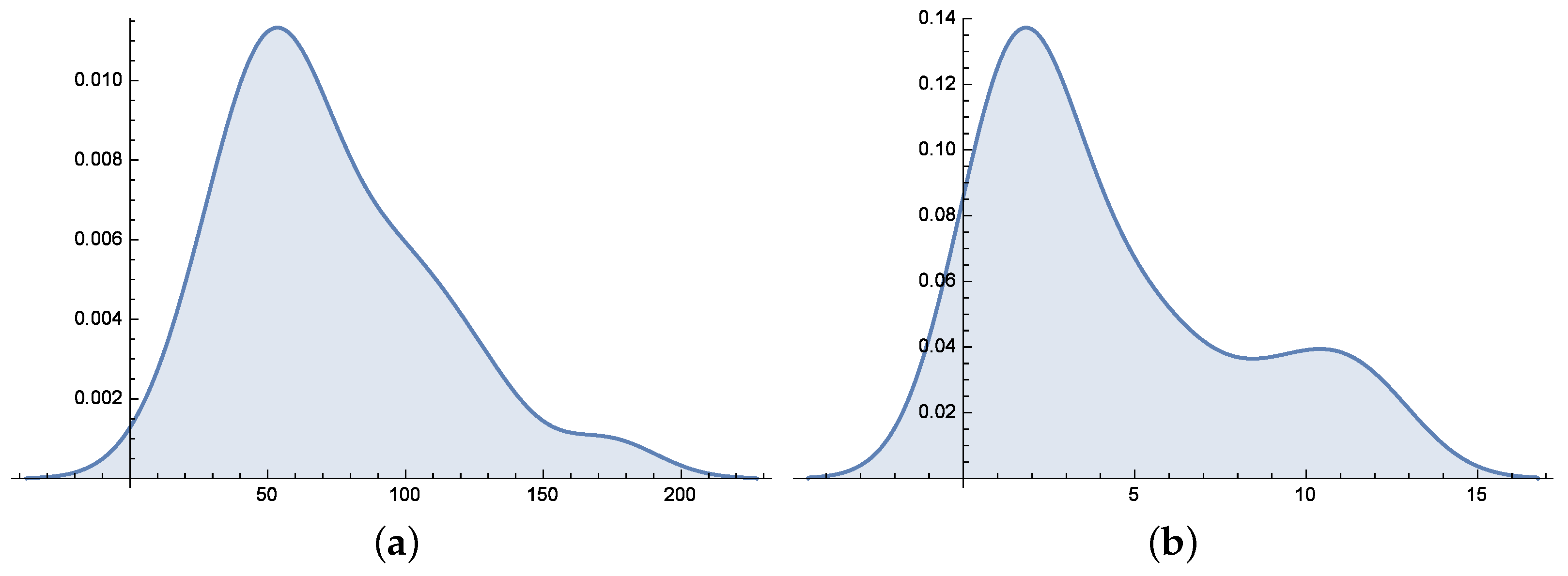
5. Application to Real Data

To demonstrate the application of the G-II distribution to censored data, we analyze two real-world datasets in this section. Below is a description of the datasets and their corresponding fits.

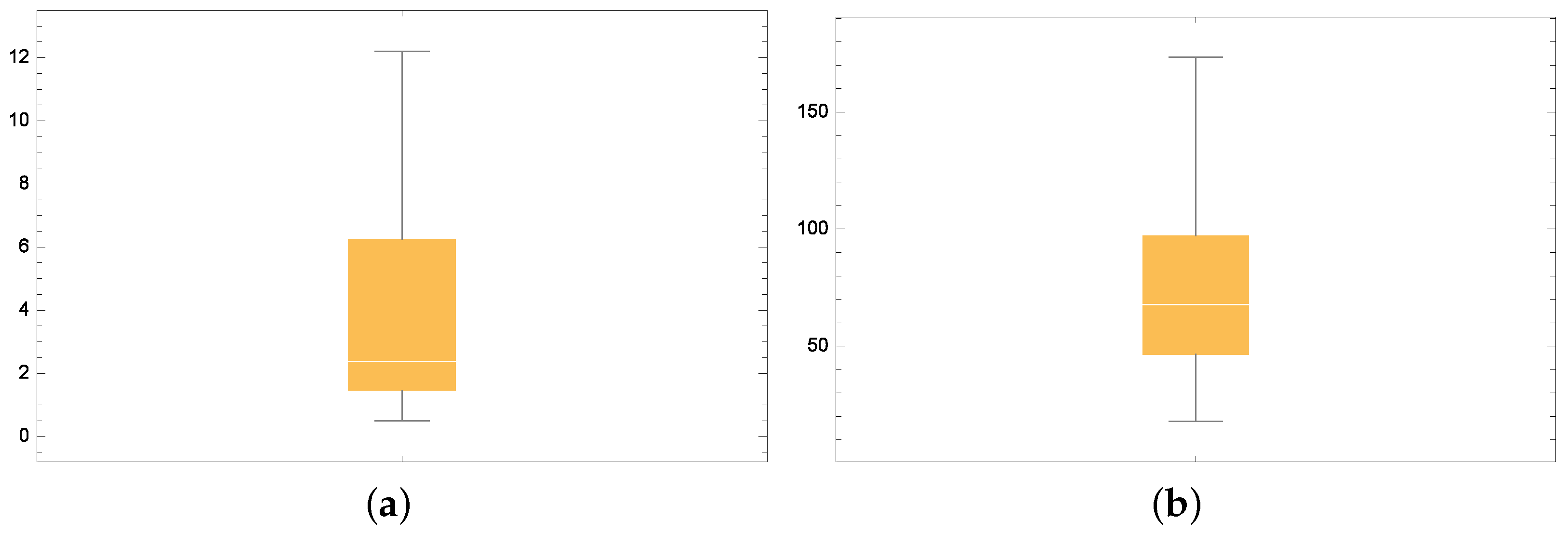
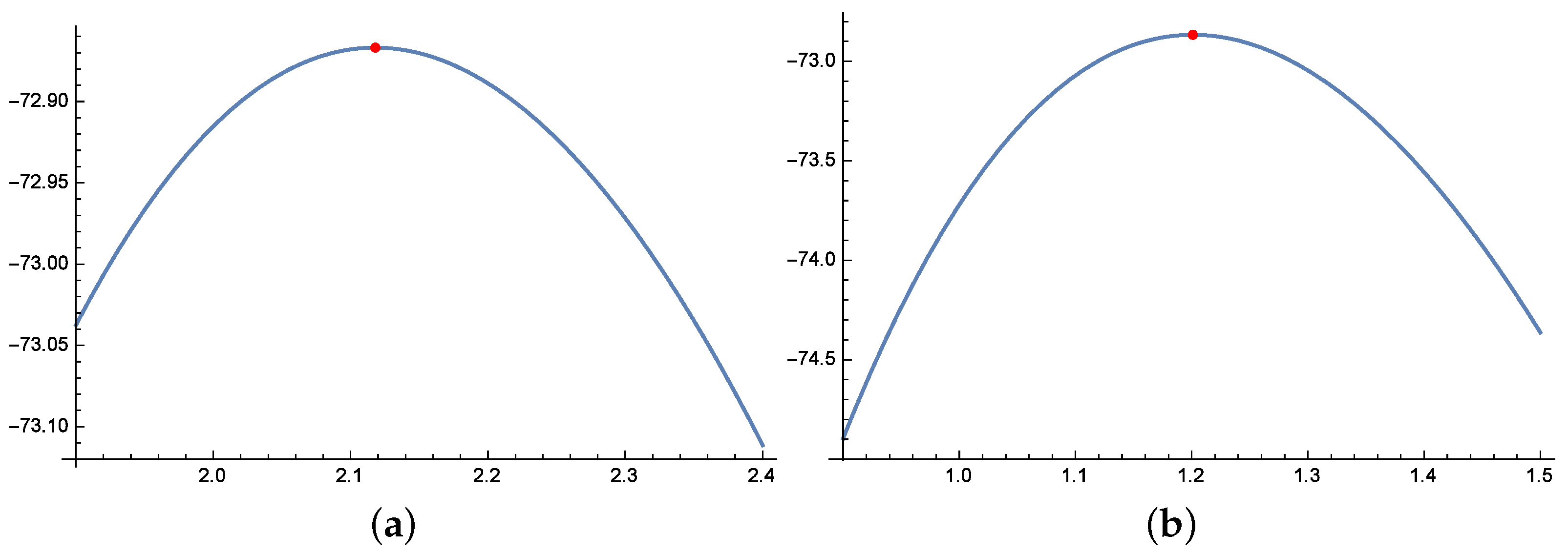
5.1. Wooden Toy Cost Dataset

The first dataset, sourced from The Open University (1993), represents the costs of 31 different children’s wooden toys sold in a Suffolk craft store in April 1991. This dataset has been previously analyzed by Shafiei and colleagues [35]. The dataset is presented as follows:

$$\begin{array}{cccccccc}4.2^{\ast }\hfill & 1.{12}^{\ast }\hfill & 1.39\hfill & 2.0\hfill & 3.99\hfill & 2.15\hfill & 1.74\hfill & 5.{81}^{\ast }\hfill \\ 1.7\hfill & 0.5\hfill & 0.{99}^{\ast }\hfill & 11.5\hfill & 5.12\hfill & 0.9\hfill & 1.{99}^{\ast }\hfill & 6.24\hfill \\ 2.6\hfill & 3.0\hfill & 12.2^{\ast }\hfill & 7.36\hfill & 4.{75}^{\ast }\hfill & 11.59\hfill & 8.69\hfill & 9.8\hfill \\ 1.{85}^{\ast }\hfill & 1.99\hfill & 1.35\hfill & 10.0\hfill & 0.{65}^{\ast }\hfill & 1.45\hfill & \end{array}$$

5.2. Ball Bearing Data

To evaluate the various estimation techniques discussed in this study, real-world data are introduced in this section. Meintanis [36] provides data from a life test, detailing the number of revolutions until failure for each of 23 ball bearings. The dataset includes the following values:

$$\begin{array}{cccccccc}17.{88}^{\ast }& 28.92& 33.{00}^{\ast }& 41.52& 42.12& 45.60& 48.80& 51.84\\ 51.96& 54.12& 55.{56}^{\ast }& 67.80& 68.{64}^{\ast }& 68.64& 68.{88}^{\ast }& 84.12\\ 93.{12}^{\ast }& 98.64& 105.{12}^{\ast }& 105.84& 127.92& 128.04& 173.40& \end{array}$$

Asterisks indicate which observations have been censored. To analyze the model’s efficacy, we applied several goodness-of-fit tests, including

• the Anderson–Darling test;
• the Kolmogorov–Smirnov (KS) test;
• Pearson’s ${\chi }^2$ test.
• the Cramér–von Mises test.

To assess the model’s fit to the data, we examine both the distance statistics and p-values. If the p-value is less than 0.05, we reject $H_0$ (and accept $H_1$) at a significance level of $\gamma =0.05$. The test statistics are shown in

Table 1. Statistical measures for goodness-of-fit analysis of observed data.

Modes	Anderson-Darling		Cramer-von Mises		Pearson ${\mathit{\chi }}^2$		K-S
	Statistic	p-Value	Statistic	p-Value	Statistic	p-Value	Statistic	p-Value
Dataset I	0.4163	0.8311	0.0548	0.8463	1.4666	0.9834	0.1023	0.8804
Dataset II	0.5781	0.6665	0.0784	0.7008	5.8695	0.5550	0.1328	0.7635

. As indicated by the table, we cannot reject the null hypothesis that the data follows the G-II distribution because the p-values are relatively high for all tests, confirming the proposed model’s fit to the actual data. For visual confirmation, Figure 2 displays both the fitted and empirical survival functions of the G-II distribution for the two datasets. The figures show a close alignment between the empirical and fitted distributions. Furthermore, Figure 3 and Figure 4 present the quantile plots and the observed versus expected probability plots for the two datasets, respectively. Therefore, this distribution can be used to analyze the dataset efficiently. The box-and-whisker chart and smooth histogram for Data I and II are shown in Figure 5 and Figure 6, respectively. The profile log-likelihood function exhibits unimodal behavior, as shown in Figure 7 and Figure 8. It reaches a single maximum, as indicated by the contour plot and 3D plot of the log-likelihood function for the parameters $\rho$ and $\psi$ in Figure 9.

We computed estimates using MLEs for $\psi =1.2$, $\rho =2.1$, and $\eta =0.5$ based on Dataset I. Along with the 95% ACI values, these findings are presented in

Table 2. Estimates for censored Dataset I using classical and Bayesian methods.

Parameters	MLE		MCMC
	Mean	Length	SE	GE		Length
				$\mathit{\tau }=-\mathbf{4}$	$\mathit{\tau }=\mathbf{4}$
$\psi$	0.6746	0.4631	0.92887	0.9760	0.8497	0.3707
$\rho$	3.3605	1.9848	1.9362	2.0455	1.7501	1.4811
$\eta$	2.4216	3.7625	0.9489	1.1339	0.7207	1.2759

. For the Bayesian estimate, we employed the MCMC approach with a total of 11,000 samples. During the “burn-in” phase, the first 2000 samples were discarded to ensure the stability of the estimation process. Bayesian estimates were obtained for $\psi$, $\rho$, and $\eta$ under both the SE and GE loss functions, using non-informative priors with hyperparameters set to $a_i=0$ and $d_i=0$ for $i=1,2,3$. Table 2 provides a comprehensive display of the Bayesian estimation results, including the 95% CRIs for $\psi$, $\rho$, and $\eta$.

MLEs were used to calculate estimates for $\psi =2.0$, $\rho =1.6$, and $\eta =1.5$ using Dataset II. These results are shown in

Table 3. Estimates for censored Dataset II using classical and Bayesian methods.

Parameters	MLE		MCMC
	Mean	Length	SE	GE		Length
				$\mathit{\tau }=-\mathbf{4}$	$\mathit{\tau }=\mathbf{4}$
$\psi$	1.1006	0.8115	0.2410	0.2562	0.2146	0.1940
$\rho$	162.66	469.962	2.7646	3.169	2.2328	3.2405
$\eta$	2.6153	4.6647	1.7678	5.9376	0.9432	4.3552

, which also provides the corresponding 95% ACIs. Using the MCMC approach, we generated 12,000 samples for Bayesian estimation. The burn-in phase discarded the first 2000 samples to ensure the stability of the estimation process. With non-informative priors, Bayesian estimates for $\psi$, $\rho$, and $\eta$ under both the SE and GE loss functions were obtained, with hyperparameters set to $a_i=0$ and $d_i=0$ for $i=1$ to 3. The results of the Bayesian estimation are presented in detail in Table 3, which also provides information on the 95% CRIs for $\psi$, $\rho$, and $\eta$.

6. Simulation Study

To evaluate the effectiveness and performance of various estimating techniques, a Monte Carlo simulation study is presented in this section. Using a predetermined procedure, a RC sample is generated from the G-II distribution. The parameters for the simulation are $\rho =2.5$, $\psi =1.5$, and $\eta =1.5$. The MLEs for $\rho$, $\psi$, and $\eta$ are calculated, along with the ARB for various sample sizes. In the Bayesian analysis, a gamma prior is applied to all parameters, with the prior hyperparameters set as $a_1=a_2=a_3=1.5$ and $d_1=d_2=d_3=2.5$. Bayesian parameter estimates are obtained under the SE and GE loss functions using the MCMC method. A chain of 11,000 iterations is generated using the M-H algorithm, with the first 2000 iterations discarded to minimize the influence of initial values.

The ARB is determined using the following formula:

$$\mathrm{ARB}\left(\widehat{\mu }\right)={\displaystyle \frac{\left|\frac{{\sum }_{i=1}^{1000}{\widehat{\mu }}_i}{1000}-\mu \right|}{\mu }},\mathrm{where}i=1,2,3,\mathrm{and}({\mu }_1,{\mu }_2,{\mu }_3)=(\rho ,\psi ,\eta ).$$

The classical and Bayesian estimates for the parameters $\rho$, $\psi$, and $\eta$, along with their respective ARB values, are presented in

Table 4. MLE and MCMC estimates for the parameter $\rho$ with corresponding ARB values in bold.

b	MLE		MCMC
	Mean	Length	SE	GE		Length
				$\mathit{\zeta }=-\mathbf{4}$	$\mathit{\zeta }=\mathbf{4}$
20	2.9346	2.1735	1.5229	1.6319	1.3380	1.3060
	0.5738		0.3908	0.3473	0.4648
30	2.5733	1.5961	1.5249	1.5982	1.4003	1.0787
	0.4593		0.3900	0.3307	0.4399
40	3.3643	1.9056	1.8653	1.9485	1.7290	1.2581
	0.4457		0.2539	0.2206	0.3084
50	2.5349	1.2073	1.5810	1.6282	1.5018	0.8701
	0.4140		0.2476	0.2187	0.3013
60	2.9744	1.3019	1.7239	1.7697	1.6470	0.9024
	0.4097		0.2105	0.2121	0.2912
70	2.5467	1.0239	1.5809	1.6144	1.5246	0.7377
	0.3987		0.2076	0.2042	0.2902
80	2.9456	1.1217	1.7825	1.8197	1.7204	0.8294
	0.3782		0.2070	0.2021	0.2818
90	2.6377	16.2483	1.8427	1.8766	1.7858	0.8017
	0.3551		0.1929	0.1793	0.2757
100	2.6869	0.9027	1.7477	1.7750	1.7017	0.7015
	0.2448		0.1809	0.1600	0.2193

,

Table 5. MLE and MCMC estimates for the parameter $\psi$ with corresponding ARB values in bold.

b	MLE		MCMC
	Mean	Length	SE	GE		Length
				$\mathit{\zeta }=-\mathbf{4}$	$\mathit{\zeta }=\mathbf{4}$
20	1.3716	1.0946	1.6522	1.7645	1.4606	1.0866
	0.4856		0.2014	0.1963	0.4648
30	2.0664	1.3210	2.4353	2.5505	2.2397	1.7023
	0.4770		0.1936	0.1903	0.4231
40	1.9421	1.1234	1.6681	1.7280	1.5667	1.0192
	0.4647		0.1921	0.1820	0.4145
50	1.3639	0.6845	1.7855	1.8379	1.6968	0.9850
	0.4607		0.1903	0.1752	0.4012
60	1.3816	0.9112	1.6975	1.738	1.6287	0.8464
	0.4589		0.1817	0.1687	0.3858
70	1.3785	0.5861	1.9144	1.9542	1.8475	0.8859
	0.2510		0.1763	0.1528	0.2316
80	1.5702	0.6234	1.8020	1.8349	1.7469	0.7824
	0.2468		0.1613	0.1502	0.2146
90	1.5457	17.3011	1.6925	1.7201	1.6463	0.6927
	0.2305		0.1484	0.1468	0.1976
100	1.4231	0.5175	1.7495	1.7754	1.7059	0.6842
	0.2113		0.1263	0.1206	0.1373

and

Table 6. MLE and MCMC estimates for the parameter $\eta$ with corresponding ARB values in bold.

b	MLE		MCMC
	Mean	Length	SE	GE		Length
				$\mathit{\zeta }=-\mathbf{4}$	$\mathit{\zeta }=\mathbf{4}$
20	1.9024	3.5259	0.7470	0.8930	0.5432	1.0342
	0.6683		0.5020	0.4047	0.6379
30	1.2744	1.8249	0.6677	0.7643	0.5262	0.7987
	0.6504		0.5019	0.4004	0.6192
40	1.0430	1.2680	0.7309	0.8314	0.5874	0.8499
	0.6447		0.4127	0.3957	0.6084
50	1.2638	1.3819	0.6350	0.6934	0.5474	0.6116
	0.6074		0.4067	0.3377	0.5351
60	1.5063	1.5373	0.7227	0.7814	0.6336	0.6481
	0.6042		0.3582	0.2791	0.5176
70	1.3843	1.2938	0.6437	0.6850	0.5787	0.5181
	0.5771		0.4708	0.2433	0.5142
80	1.3324	1.1611	0.7151	0.7611	0.6437	0.5756
	0.5117		0.4233	0.1926	0.4709
90	1.3086	45.4285	0.6929	0.7340	0.6291	0.5343
	0.4076		0.3381	0.1106	0.3806
100	1.2364	0.9588	0.6736	0.7066	0.6217	0.4731
	0.3058		0.2509	0.1089	0.2855

.

From the findings of the simulation study, we conclude the following:

• From Table 4, Table 5 and Table 6, it is observed that as the sample size increases, the ARB decreases.
• Bayesian methods demonstrate superior performance compared to traditional methods, as the ARB values obtained using MCMC are lower than those obtained with MLE.
• When using the GE loss function, the performance under underestimation is better than overestimation. Specifically, ARB values at $\mu =-4$ are better than those at $\mu =4$.
• The performance of MCMC at $\mu =-4$ is also observed to be better than the SE loss function in terms of achieving smaller ARB values.
• The interval length in Bayesian methods is shorter compared to that observed in conventional methods.

7. Conclusions

The study presents key findings and contributions on the statistical inference of the G-II distribution under a RC scheme. The MLE method provides reliable point estimates, with decreasing ARB as sample sizes increase, indicating greater accuracy in parameter estimation. The Bayesian approach, utilizing MCMC techniques, outperforms frequentist methods, offering higher precision through shorter CRI lengths. The practical significance of these methods is demonstrated through successful applications in real-world scenarios like reliability engineering, underscoring the importance of selecting statistical tools suited to specific data characteristics. The research also identifies opportunities for future work, such as examining other distributions under similar censoring conditions, enhancing computational approaches, and incorporating prior information in Bayesian methods to improve estimates in cases of limited data. These findings offer valuable insights into the G-II distribution and highlight the need for robust methodologies in reliability analysis, paving the way for further advancements in the field.

8. Directions for Future Research

• Extend to other lifetime distributions
  Apply the same inference framework to other two-parameter or three-parameter distributions like Weibull, Log-logistic, or Burr Type XII under random censoring.
• Handle more complex censoring mechanisms
  Investigate models under progressive, interval, or informative censoring schemes. These reflect more realistic experimental settings in survival and reliability studies.