Abstract
Leaf shape is a crucial visual cue for plant recognition. However, distinguishing among plants with high inter-class shape similarity remains a significant challenge, especially among cultivars within the same species where shape differences can be extremely subtle. To address this issue, we propose a novel shape representation and an advanced heterogeneous fusion framework for accurate leaf image retrieval. Specifically, based on the local polar coordinate system, multiscale analysis, and statistical histograms, we first propose local polar coordinate feature representation (LPCFR), which captures spatial distribution from two orthogonal directions while encoding local curvature characteristics. Next, we present heterogeneous feature fusion with exponential weighting and Ranking (HFER), which enhances the compatibility and robustness of fused features by applying exponential weighted normalization and ranking-based encoding within neighborhood distance measures. Extensive experiments on both species-level and cultivar-level leaf datasets demonstrate that the proposed representation effectively captures shape features, and the fusion framework successfully integrates heterogeneous features, outperforming state-of-the-art (SOTA) methods.
1. Introduction
Shape is a crucial visual cue for object recognition, often serving as the primary basis for human perception [1,2]. Therefore, shape analysis has become an active research direction in image processing and pattern recognition, with widespread applications across various domains, including object shape classification [3], medical image segmentation [4], CAD model reconstruction [5], and more. Among these applications, analyzing leaf shape for plant recognition has become a research topic, leading to the development of numerous shape methods that demonstrate strong recognition performance [6,7,8,9,10,11,12,13,14,15,16,17,18].
However, extracting discriminative shape features and accurately recognizing plants with highly similar inter-class shapes remains a significant challenge. With the growing demands of modern agriculture, researchers increasingly focus on fine-grained cultivar-level leaf recognition [10,19]. Unlike the relatively coarse differences in leaves among species, shape variations among cultivars are often subtle and visually imperceptible, even to domain experts [10]. As shown in Figure 1, leaves from different woody species (top row) and soybean cultivars (bottom row) exhibit highly similar shape patterns, highlighting the complexity of leaf recognition tasks.

Figure 1.
Leaves from different woody species (top row) and soybean cultivars (bottom row) exhibit highly similar shape patterns.
In such cases, relying solely on shape features is often insufficient, as homogeneous shape methods may fail to comprehensively capture the distinctive characteristics of leaves. Surface texture features [20,21,22] can provide additional discriminative cues, particularly when leaves exhibit similar shapes. Moreover, deep representations derived from convolutional neural networks effectively capture high-level semantic features and have demonstrated significant improvements in plant leaf recognition performance [23,24,25,26]. However, these features often lose important visual shape information, limiting their effectiveness.
To address these issues, we propose a novel shape representation and an advanced heterogeneous fusion framework for both species-level and cultivar-level leaf image retrieval. For the shape representation, we first establish a local polar coordinate (LPC) system based on a curve segment to extract the LPC features (LPCF). By varying the length of the curve segment, the LPCF is naturally extended into a multiscale description that remains invariant to translation, rotation, and scaling transformations. Finally, by aggregating the LPCF into statistical histograms, we construct the robust and efficient representation, termed the local polar coordinate feature representation. In the heterogeneous fusion framework, we first individually perform exponential weighted normalization on the K-nearest neighbor distance measures of heterogeneous features. Subsequently, we incorporate the relative ranking information from the distance measures. Lastly, we aggregate the normalized and ranked distances to present a new fusion framework, referred to as heterogeneous feature fusion with exponential weighting and ranking.
The main contributions of this paper are summarized as follows:
- We propose a novel shape representation, LPCFR, which captures the spatial distribution from two locally orthogonal perspectives while simultaneously extracting local curvature characteristics, thus improving the discriminative power of shape representation.
- We develop a new heterogeneous fusion framework, HFER, which enhances the compatibility and robustness of heterogeneous features by encoding both local contextual information and structural relations.
- Extensive experiments on both species-level and cultivar-level leaf datasets validate the effectiveness and generality of the proposed representation and fusion framework, consistently outperforming state-of-the-art methods.
The remainder of this paper is structured as follows: Section 2 briefly reviews the related work on leaf image recognition. Section 3 presents the details of proposed shape representation and heterogeneous fusion framework. Section 4 reports the experimental results against the benchmark datasets. At last, Section 5 concludes this paper.
2. Related Work
Shape, texture, and deep convolutional features all provide valuable visual cues for leaf image recognition. Among them, leaf shape is one distinctive trait and numerous shape methods have been proposed, which can be broadly divided into two categories: contour curvature-based methods and relative spatial distribution-based methods. Curvature-based methods capture rich geometric information and are often extracted by differential invariants for shape recognition [27]. However, differential computation would introduce sensitiveness to noise and geometric perturbations. To address this, relative stable measurements, such as turning angles [28] and derived vectors [29], have been employed to describe the curvature characteristic of leaf shapes more robustly. Relative spatial distribution serves as another significant shape characteristic and is generally measured by calculating the line distances between pairs of contour points [8,13,30]. However, the approaches face two primary challenges. (1) The expensive computational cost of establishing point-to-point correspondence often requires optimization algorithms like dynamic programming or the Hungarian algorithm [10], which limits its wide utilization. (2) Simple line segments connecting boundary-point pairs fail to accurately represent the spatial distribution characteristics in a two-dimensional shape.
To improve leaf recognition performance, recent studies have proposed novel shape approaches with enhanced discriminative power. For instance, Yang et al. [31] developed a novel multiscale Fourier descriptor (MFD) based on triangular features to effectively capture the local and global characteristics of a shape for leaf image recognition. Chen et al. [10] proposed the Gaussian convolution vector (GCV) by convolving the contour vector functions with Gaussian kernels of different widths to encode both the curvature features and proportional relationship of leaf shape contour for plant species and soybean cultivar retrieval. Yang [11] proposed the multiscale triangle descriptor (MTD) to capture the curvature characteristics across multiple scales. Building upon this, Wu et al. [12] integrated MTD with the speeded-up robust features (SURF) [32] approach and proposed an improved multiscale triangle descriptor (IMTD), which jointly considers both the shape boundary and interior information of leaf images. Nevertheless, these methods primarily focus on spatial distribution or curvature characteristics independently and fail to fully describe shape information, limiting their recognition accuracy.
In addition to shape, texture is another crucial visual attribute for leaf recognition. Classical texture descriptors such as local binary pattern (LBP), gray level co-occurrence matrix (GLCM), and their variants have been widely applied in leaf image recognition. For example, Qi et al. [33] proposed the pairwise rotation invariant co-occurrence local binary pattern (PRICoLBP) to capture the spatial context co-occurrence information effectively, and applied it for leaf image classification. Tang et al. [34] presented a texture extraction method combing a non-overlap window LBP and GLCM for green tea leaf classification. Lv et al. [21] employed a partition block strategy to propose a multi-feature fusion approach based on LBP, named the multiscale block local binary pattern (MB-LBP), and combined it with the original LBP for leaf image recognition. Recently, Wang et al. [22] proposed a novel local R-symmetry co-occurrence method for characterizing discriminative local symmetry texture patterns for distinguishing subtle differences among cultivars. Chen et al. [20] investigated a novel symmetric geometric configuration, named the symmetric binary tree (SBT) to mine the multiple scale co-occurrence texture patterns for the challenging task of cultivar leaf recognition.
With the advancement of deep learning, deep representations learned by convolutional neural networks have demonstrated strong performance across a wide range of visual tasks. Some studies retrain CNN models to better adapt to specific characteristics of leaf images. For example, Dyrmann et al. [35] built a convolutional neural network from scratch for recognizing plant species in color images. Beikmohammadi et al. [24] designed a system named SWP-LeafNet, which consists of three separate and distributable CNN-based models aimed at maximizing the behavioral resemblance of a botanist for plant species recognition. However, retraining CNN models to enhance the representational capacity is time-consuming and requires significant computational resources [36]. Consequently, some studies have explored off-the-shelf convolutional feature aggregation for image retrieval. Liu et al. [37] proposed a novel method called deep-seated features histogram (DSFH), which combines low-level features with fully connected layer features from a pretrained VGG16 model [38] for general image retrieval. More recently, Wu et al. [39] presented a deep convolutional feature aggregation approach for fine-grained cultivar identification by combining complementary regional convolution covariance features (RCCF) with multiresolution regional maximum activation of convolution (RMAC) features, both extracted from a pretrained VGG16 model [38].
Although shape, texture, and deep convolutional features each contribute meaningfully to leaf image recognition, relying solely on homogeneous features limits their capacity to capture the rich and diverse leaf image information. Therefore, it is critical to explore novel representation that can more comprehensively describe leaf shapes and to consider heterogeneous feature fusion for more accurate leaf image retrieval. To address these challenges, this paper proposes a novel shape descriptor that simultaneously captures both spatial distribution and curvature characteristics. Furthermore, a fusion framework is presented, which incorporates exponentially weighted normalization and ranking-based encoding to effectively integrate heterogeneous features, further enhancing retrieval performance.
3. The Methodology
This section starts by presenting the proposed LPCFR method, including its definition and characters. Then, the proposed fusion framework is elaborated in detail.
3.1. Local Polar Coordinate Feature Representation
Mathematically, the shape contour of a leaf can be represented as an ordered set of uniformly sampled complex-valued points along the counterclockwise direction , where is the imaginary unit, and N denotes the number of sampled points along the contour. Since the contour is closed, the function satisfies for the periodic condition .
3.1.1. Definition
To improve the discriminative capacity of shape representation, a local polar coordinate system is established using a contour point and its two neighboring points at a curve segment (local reference points). Based on the LPC system, the relative spatial distribution and local curvature of are quantified to extract discriminative local polar coordinate features. To enhance retrieval performance, LPCF is extended into a multiscale description through multiscale analysis. Furthermore, to improve robustness to noise and reduce computational complexity, LPCF is aggregated into a compact descriptor using statistical histograms, resulting in the final local polar coordinate feature representation.
Local Polar Coordinate System: Let be the scale level. For a point on the contour set , its corresponding local reference points are and . The midpoint of the line segment connecting these two reference points, denoted as , is designated as the pole O, while the ray serves as the local polar axis x. Then, a local polar coordinate system is established, where one pixel represents a unit length, and the counterclockwise direction is considered positive.
Local Polar Coordinate Features: Within this LPC system, we extract the following geometric features: (1) the radial distance from the point to the pole O, (2) the polar angle of relative to the local polar axis x, and (3) the turning angle between the adjacent chords and with respect to the x. The three quantities are utilized to construct the discriminative LPC features. Then, the LPCF at point with the curve segment , denoted as , can be elegantly and efficiently computed as follows:
where and respectively indicate the modulus and argument of complex number. The polar angle and turning angle are constrained in the range . Figure 2 shows an illustration of LPCF on the LPC system, including the radial distance (red line), the polar angle (red arc), and the turning angle (green arc) of the contour point .
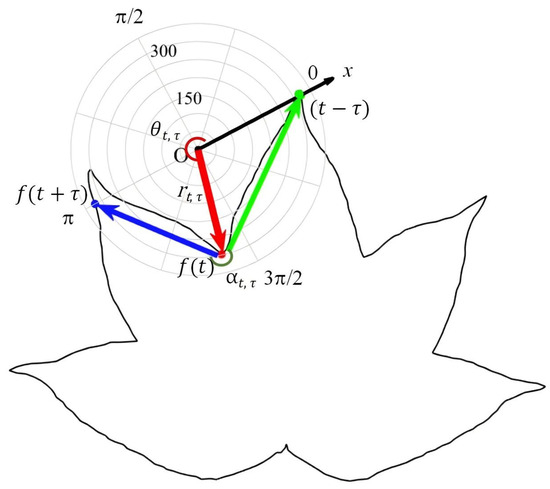
Figure 2.
An illustration of LPCF on the LPC system, including the (red line), (red arc), (green arc), adjacent chords (blue line) and (green line) of the contour point .
The proposed LPCF offers a rich and discriminative shape description, mainly stemming from two aspects. (1) The two components and jointly capture the spatial distribution characteristics along two locally orthogonal radial and angular dimensions. Compared to shape descriptors based on a single spatial dimension, LPCF more accurately characterizes the spatial distribution on a two-dimensional plane. (2) By incorporating the turning angle , the LPCF simultaneously captures both spatial distribution and curvature information, providing a more comprehensive geometric description.
Multiscale LPCF: The LPCF can be easily extended to a multiscale description. First, by fixing the scale level and varying the contour point over the index set , the would be computed along the contour, thus capturing the geometric characteristics of the entire leaf shape. Figure 3 shows the LPCF computed at different contour points. Then, by varying the scale level within the set of integer powers of two, (where ), a coarse-to-fine shape description is enabled. The multiscale LPCF is, thus, represented as follows:
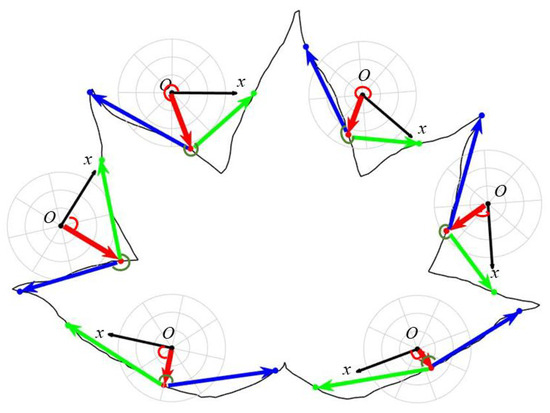
Figure 3.
The LPCF computed at different contour points. The red line, red arc, green arc, and the blue and green lines represent the radial distance, polar angle, turning angle, and adjacent chords, respectively.
Figure 4 shows the LPCF of different scale levels.
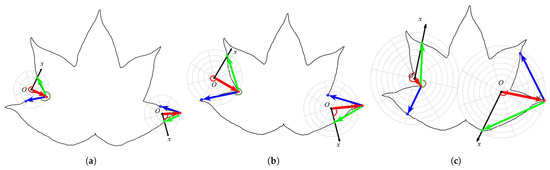
Figure 4.
The LPCF of different scale levels. The red line, red arc, green arc, and the blue and green lines represent the radial distance, polar angle, turning angle, and adjacent chords, respectively. Figure 4a–c display the LPCF at three different scale levels: (a) The fine level ( = 2). (b) The intermediate scale level ( = 4). (c) The coarse scale level ( = 8).
Local Polar Coordinate Features Representation: Instead of directly applying the proposed LPCF to point-to-point correspondence matching, statistical histograms are introduced at each scale level to achieve a more robust and efficient shape representation. Specifically, for each scale level , the radial distance (max normalization would be employed to ensure scale invariance, see Section 3.1.2), the polar angle , and the turning angle are uniformly divided into U, V, and W intervals, respectively denoted as to , to , and to . Based on this, a spatial distribution histogram of size UxV and a curvature histogram of size W are constructed. For the of the scale level , each bin of the histograms and can be computed as follows:
where denotes the cardinality of a set. The histograms from each scale are first reshaped to row vectors and , and then concatenated to construct the final shape representation, referred to as LPCFR:
where ∥ denotes vector concatenation, and concatenate denotes concatenation over the scale . Figure 5 shows the visualization of the spatial distribution histogram at different scales for one sample leaf shape, where .
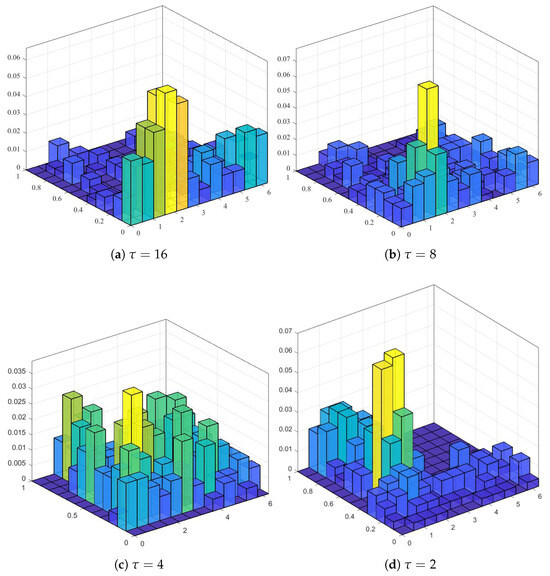
Figure 5.
The visualization of the spatial distribution histogram at different scales from one sample leaf shape, where .
3.1.2. Characters of LPCFR
Invariance Analysis: Invariance to translation, rotation, and scaling transformations is desirable for robust shape representation and matching. The proposed LPCF has inherent invariance, which can be proved as follows:
Theorem 1.
Leveraging Euler’s formula , the linear transformed version (translation, rotation, and scaling) of contour point could be represented as , where is the scaling factor, is the rotation angle, and is the complex translation factor. Let be the LPCF of the contour at the scale level τ. Then, .
Proof of Theorem 1.
By the definition of LPCF, for the radial distance and polar angle , we have
Similarity to (11), for the turning angle , we could obtain
Clearly, the components and have invariance to translation, rotation, and scaling transformations, whereas is invariant only to translation and rotation. To achieve scale invariance, max normalization is applied to at scale level , constraining its values to the range . This ensures that the LPCF is invariant to translation, rotation, and scaling changes. As the histogram statistics preserve the invariance characters of the LPCF, so the resulting LPCFR maintains invariance to translation, rotation, and scaling. □
Computational Complexity: In an image retrieval task, the computational complexity mainly involves the construction of shape representations and the matching stage. During shape representation construction, to reduce the number of loops and improve computational efficiency, one one-dimensional vector is predefined to store the scale levels for all contour points. For each contour point, this vector is used to locate its local reference points, and the corresponding LPCFs across all scale levels are computed simultaneously, so the time complexity for calculating the LPCF of all the scales is N. At the same, to obtain robust and efficient shape representation, we employ statistical histograms. At each scale level, each point contributes to the histogram in constant time by identifying the appropriate bin and updating its count; thus, the time complexity for constructing both the spatial distribution and curvature histograms is . As a result, the time complexity for building the LPCFR is . For the shape matching stage, we adopt the simple norm to measure the similarity of two shapes, resulting in a computational cost of , which could be ignored. Overall, the proposed shape representation framework is computationally efficient, with a total complexity of .
3.2. Heterogeneous Feature Fusion with Exponential Weighting and Ranking
Single shape representations are insufficient to comprehensively capture the leaf image information, especially for cultivar leaves with extremely subtle shape differences. To address this limitation, fusing shape features with heterogeneous features enables a more complete description of leaf images, thereby enhancing the performance of plant leaf retrieval [11,40]. This paper proposes a novel heterogeneous fusion framework, named heterogeneous feature fusion with exponential weighting and ranking, which leverages exponential weighted normalization and ranking-based encoding within the neighborhood distance measure to incorporate both local contextual information and structural relations, enhancing the compatibility and robustness of heterogeneous features.
Let , and , , respectively, represent an image from the query set and database . The and are the shape and heterogeneous feature representation of , while the and are those of . The similarity between and could be calculated by the shape and heterogeneous distance measure, denoted as and . The fusion distance between the leaf images and is defined as follows:
where avg denotes the averaging function, ∘ indicates the Hadamard (element-wise) product, sv represents the vector obtained by sorting the set in ascending order, and top−K refers to the indices corresponding of the K smallest distances. In the current HFER framework, we adopt an equal-weight strategy when fusing shape with heterogeneous representations, aiming for simplicity and fairness across different representations. However, future work will explore adaptive weighting mechanisms to better capture feature complementarity.
By introducing an exponential weighting function, the HFER emphasizes the contributions of closer and more similar samples during normalization, thereby enhancing the compatibility of feature fusion. Additionally, HFER transforms the relative positional and distributional relationships among neighborhood samples into ranking and positional encodings. Combined with a penalty mechanism, this mitigates the impact of distance scale variations, noise interference, and feature instability, thereby improving the robustness of the fused features.
4. Experiments
In this section, we first present the experimental details, including the experimental setting, evaluation metrics, baseline methods, and datasets. Then, we present the experimental results, covering baseline shape methods, fusion results based on the proposed framework HFER combining shape methods with baseline heterogeneous representations, and comparison with the KNN-HDFF framework, which has demonstrated strong performance in recent studies [20,40].
4.1. Experimental Details
4.1.1. Experimental Setting
To ensure the effectiveness and stability of the proposed LPCFR, we conducted parameter sensitivity analysis on both the species-level ICL220 leaf subset and cultivar-level lower part of SoyCultivar200 datasets (see Section 4.1.4 for details). Figure 6 illustrates the retrieval performance curves of the LPCFR under different parameter settings on the ICL220 leaf subset and lower part of SoyCultivar200 datasets. The results show that increasing the number of sampling points and the number of curvature histogram intervals initially improves performance, but beyond a certain threshold, the performance saturates or slightly declines. Similarly, increasing the number of spatial distribution histogram intervals improves performance up to 10, after which further gains become negligible. Based on these observations, we set the parameters as follows: , , and , achieving a good trade-off between accuracy and computational efficiency. It is worth noting that, under the assumption that radial distance and polar angle contribute equally to shape retrieval, we assigned the same values to U and V in all experiments. For the fusion framework, the parameter K is empirically set 50. Before feature extraction, all RGB images were first converted to grayscale using a weighted average method, and then binarized using Otsu’s thresholding to obtain clear contour lines. All algorithms are implemented in MATLAB 2023b and executed on a workstation equipped with an Intel(R) Core(TM) i7-7800X CPU and 64 GB of RAM.
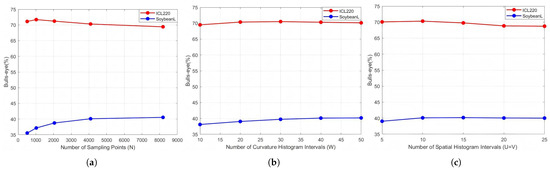
Figure 6.
Retrieval performance curves of the LPCFR under different parameter settings on the ICL220 leaf subset and lower part of SoyCultivar200 datasets. Figure 6a–c display the LPCFR retrieval performance of each parameter under keeping the other parameters fixed: (a) and . (b) and . (c) and .
4.1.2. Evaluation Metrics
To evaluate retrieval performance, the standard Bulls-eye protocol widely adopted in numerous studies [1,41,42] is employed. In this protocol, each image in the database is, in turn, served as a query to retrieve matches from the entire database. Suppose there are q relevant images in the dataset; the top matches are retrieved and the number of images correctly matching the query image is counted as p. Then, the retrieval rate of the query is calculated as . The Bulls-eye score denotes as the average of retrieval accuracies for all the queries.
4.1.3. Baseline Methods
Several shape methods including MDM [8], MFD [31], HoGCV [10], and IMTD [12] were chosen as baseline methods to test the superiority of raised LPCFR shape representation on the leaf image retrieval task.
In addition, within the HFER framework, we selected five heterogeneous representations for fusion with shape features: RsCoM [22] and SBT [20], which are texture descriptors with excellent performance; ResNet50 [43], a deep model widely used in leaf recognition; and DSFH [37] and sublimated deep feature histogram (SDFH) [36], deep representations known for their outstanding performance and publicly available source codes, facilitating reproducibility. Resnet50 [43] generated from the output of the last layer (before classification) of the Resnet50 model pretrained on the ImageNet dataset. In all experiments, the retrieval results of DSFH [37] and SDFH [36] were obtained by directly running the source codes, while the results of other methods are either reproduced using the same experimental setup or obtained from the results reported in the public papers.
4.1.4. Datasets
We conducted extensive experiments on the publicly available ICL220 [8] and MEW2012 [44] species-level leaf datasets, as well as on a newly constructed SoyCultivar200 [20] cultivar-level leaf dataset.
- ICL220. The ICL220 leaf dataset [8] is a classic database, primarily designed for assessing the performance of plant recognition methods. It is collected from 220 plant species, each of which involves at least 26 leave images. All the images have a resolution of approximately 250 × 500 pixels and exhibit low intra-class variation alongside medium inter-class similarity. Here, the same equal set is adopted as in this paper [45], namely, taking the first 26 leaf images from each species and discarding the remainder for obtaining the ICL220 leaf subset with a total of 26 × 220 = 5720 images. Sample leaves from each species in the benchmark leaf datasets are displayed in Figure 7. Obviously, some leaves belonging to different species are very similar in shape.
 Figure 7. Sample leaves from each species on the ICL220 leaf dataset.
Figure 7. Sample leaves from each species on the ICL220 leaf dataset. - MEW2012. The second dataset used to test the recognition performance of our approach is the MEW2012 leaf dataset [44]. This dataset contains 9745 leaf images categorized into 153 species and each category has at least 50 leaf images. The images have a resolution of approximately 1000 × 2000 pixels and demonstrate moderate intra-class variation as well as moderate inter-class similarity. Sample leaves from each species in the MEW2012 leaf dataset are displayed in Figure 8. It is evident that the shapes of some images are highly similar, which makes the plant leaf recognition very challenging.
 Figure 8. Sample leaves from each species on the MEW2012 leaf dataset.
Figure 8. Sample leaves from each species on the MEW2012 leaf dataset. - SoyCultivar200. To further access the effectiveness and generality of the proposed methods, we perform retrieval experiments on the SoyCultivar200 [20] leaf dataset, which consists of three subsets. Each subset contains leaves collected from 200 soybean cultivars, with 10 leaf samples obtained from the upper, middle, and lower parts of each cultivar, respectively. The images possess a resolution of roughly 2000 × 3000 pixels and exhibit low variability within the same class, while showing a high degree of similarity between different classes. Figure 9, Figure 10, and Figure 11, respectively, show the sample leaves from the upper, middle, and lower parts of selected cultivars on the SoyCultivar200 dataset. It can be observed that the SoyCultivar200 dataset poses great challenges due to the high morphological similarity among different cultivars, which increases the difficulty of image retrieval. We conduct single leaf image pattern retrieval experiments on the three subsets. In addition, the 6000 leaf images are grouped into 2000 groups for joint pattern matching. These two retrieval tasks effectively reflect the performance of the proposed methods.
 Figure 9. Sample leaves from the upper part of selected cultivars on the SoyCultivar200 dataset.
Figure 9. Sample leaves from the upper part of selected cultivars on the SoyCultivar200 dataset. Figure 10. Sample leaves from the middle part of selected cultivars on the SoyCultivar200 dataset.
Figure 10. Sample leaves from the middle part of selected cultivars on the SoyCultivar200 dataset. Figure 11. Sample leaves from the lower part of selected cultivars on the SoyCultivar200 dataset.
Figure 11. Sample leaves from the lower part of selected cultivars on the SoyCultivar200 dataset.
Table 1 shows the comparative summary of the datasets.

Table 1.
Comparative summary of the datasets.
4.2. Experimental Results
4.2.1. Species-Level ICL220 Leaf Dataset
Table 2 presents the Bulls-eye scores (%) of various shape methods on the ICL220 leaf subset. From the table, we can see that our LPCFR achieved the highest Bulls-eye rates. Specifically, the retrieval accuracy of LPCFR reached 70.13%, which is 19.8%, 6.25%, 7.22%, and 3.15% higher than that of MDM, MFD, HoGCV, and IMTD. To further demonstrate the efficiency and effectiveness of the proposed LPCFR, Table 2 also presents the feature dimension and average retrieval time of various methods. All times were obtained under identical experimental conditions, specifically, by calculating the full similarity matrix on the ICL220 leaf subset, which contains 220 categories and 26 images in total. As shown in the Table 2, although the LPCFR has a slightly higher feature dimension compared to other shape methods [8,12], it remains within a reasonable range and does not impose a significant computational burden. In terms of time efficiency, our method outperforms the HoGCV [10], which relies on chi-square distance, and the IMTD [12], which utilizes SURF [32] to extract interior image information. Even when compared with other classic and efficient methods such as MDM [8] and MFD [31], our approach achieves at least a six-percentage-point improvement in performance while increasing retrieval time by only about twofold, demonstrating a favorable balance between efficiency and accuracy.

Table 2.
The Bulls-eye scores (%), feature dimension, and average retrieval time (ms) of various shape methods on the ICL220 leaf subset [8].
Table 3 shows the Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations on the ICL220 leaf subset (the numbers shown in parentheses indicate the original scores of the corresponding representations). It can be observed that most fusions of shape methods with texture or deep representations obtained notable improvements in retrieval performance. For instance, the fusion of HoGCV and ResNet50 obtained an impressive improvement of over 18.34% in retrieval accuracy. In addition, among all fusions, those incorporating LPCFR achieved higher or comparable Bulls-eye scores and the fusion of LPCFR and SDFH won the highest retrieval rate of 86.16%. These results demonstrate the effectiveness of the proposed fusion framework, as well as the strong complementarity of the proposed LPCFR on the species-level leaf dataset.

Table 3.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations on the ICL220 leaf subset [8] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
Table 4 reports the Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations on the ICL220 leaf subset [8] (the numbers shown in parentheses indicate the original scores of the corresponding representations). The experimental results demonstrated that the HFER framework consistently outperformed the baseline KNN-HDFF across all fusions. Specifically, the HFER framework achieved higher retrieval accuracy in all 25 fusions, with performance gains ranging from a marginal 0.11% to a significant 4.03%, particularly when combined with deep representations such as DSFH and SDFH. Moreover, when integrating the proposed LPCFR, retrieval performance was further enhanced. For instance, the fusion of LPCFR and SDFH achieved the highest retrieval rate of 86.16%. In summary, comparing to the KNN-HDFF [20] fusion framework, the proposed HFER demonstrates superior performance in the species-level leaf retrieval task.

Table 4.
The Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations on ICL220 leaf subset [8] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
To further illustrate the practical behavior of LPCFR and HFER, Figure 12 shows the retrieval results on the ICL220 leaf subset using different baseline shape methods, as well as the results after integrating these shape methods with deep representation within the HFER fusion framework. In each sub-figure, the first column shows the query image, while the remaining columns present the retrieved images sorted in ascending order of distance. Leaf images outlined in red rectangles indicate retrieval errors, i.e., samples whose classes do not match that of the query image. From the results, it can be observed that both our LPCFR alone and its fusion with the DSFH [37] representation outperform or are at least comparable to HoGCV [10] and IMTD [12] as well as their respective fusion counterparts. Notably, for the second query image with an unclear contour, although LPCFR and IMTD exhibit similar retrieval performance prior to fusion, the retrieval accuracy improves significantly after HFER-based fusion. This demonstrates the proposed LPCFR’s strong discriminative ability, robustness, and complementary power for heterogeneous representations.
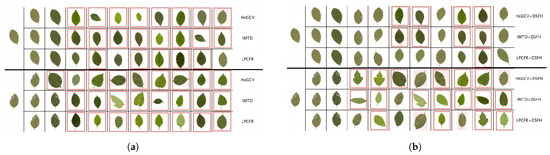
Figure 12.
Some leaf image retrieval examples of three methods on the ICL220 leaf subset. The red rectangle indicates the retrieval error. Figure 12a,b display the retrieval results without and with fusion: (a) Before fusion. (b) After fusion.
4.2.2. Species-Level MEW2012 Leaf Dataset
Table 5 shows the Bulls-eye scores (%) of various shape methods on the MEW2012 leaf dataset [44]. As shown in the table, our LPCFR achieved the best retrieval accuracy of 78.91%, which is 28.28%, 13.68%, 10.89%, and 4.56% higher than that of MDM, MFD, HoGCV, and IMTD, verifying the effectiveness of LPCFR.

Table 5.
The Bulls-eye scores (%) of various shape methods on the MEW2012 [44] leaf dataset.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations on the MEW2012 leaf dataset [44] (the numbers shown in parentheses indicate the original scores of the corresponding representations) are presented in Table 6. We could find that most fusions of shape methods with texture or deep representations obtained significant improvements in retrieval performance. For instance, the fusion of IMTD with SDFH resulted in the exciting increase of over 12.41%. Moreover, among all fusions, the LPCFR-based integrations consistently demonstrated the highest or comparable retrieval accuracy, with the best performance reaching a retrieval rate of 89.59%. All these results further indicate the effectiveness of the HFER framework and the strong complementary power of LPCFR on the species-level leaf datasets.

Table 6.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations on the MEW2012 leaf dataset [44] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
Table 7 presents the Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations on the MEW2012 leaf dataset [44] (the numbers shown in parentheses indicate the original scores of the corresponding representations). The results show that HFER consistently surpasses KNN-HDFF [20] across all 25 fusions. The performance gains range from as little as 0.01% to as much as 2.10%, with particularly notable improvements observed when fused with deep representations such as DSFH and SDFH. In addition, the fusions incorporating the LPCFR resulted in higher performance. For example, the combination of LPCFR and SDFH achieved the highest retrieval accuracy of 89.59%. Overall, comparedto the KNN-HDFF [20] fusion framework, the proposed HFER demonstrates higher retrieval scores in species-level leaf datasets.

Table 7.
The Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations on the MEW2012 leaf dataset [44] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
4.2.3. Cultivar-Level SoyCultivar200 Leaf Dataset
Table 8 shows the Bulls-eye scores of various shape methods on the SoyCultivar200 [20] leaf dataset under the single leaf image pattern matching and joint leaf image matching. It was noted that the proposed LPCFR method achieved the best retrieval accuracy of 35.62%, 37.56%, 40.10%, and 70.99% for single pattern matching on the upper, middle, and lower parts, and joint pattern matching, respectively. These results outperformed those of the baseline shape methods by at least 6.58%, 6.08%, 6.62%, and 11.18%. All the experimental results indicate the superiority of the proposed LPCFR on the cultivar-level leaf dataset.

Table 8.
The Bulls-eye scores (%) of various shape methods on the SoyCultivar200 leaf dataset [20] under the single leaf image pattern matching and joint leaf image matching.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations under the single matching pattern on the upper, middle, and lower part subsets and joint matching pattern on the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations) are summarized in Table 9, Table 10, Table 11, and Table 12, respectively. It can be observed that most fusions achieved significant performance improvements. For example, the fusion of IMTD with RsCoM resulted in notable increases in retrieval accuracy by more than 3.13%, 4.63%, 5.95%, and 10.34% on the upper, middle, lower, and joint test cases, respectively. Among all fusions, those incorporating the LPCFR consistently achieved superior retrieval scores. In addition, the LPCFR-based fusions invariably achieved the highest retrieval accuracy: 62.15% for the upper part, 59.35% for the middle part, 56.64% for the lower part, and 90.16% for the joint leaf image sets. The retrieval scores confirm the effectiveness of the proposed HFER and the powerful complement of proposed shape representation on the cultivar-level leaf dataset.

Table 9.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations under the single matching pattern on the upper part subset of the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations ).

Table 10.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations under the single matching pattern on the middle part subset of the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations).

Table 11.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations under the single matching pattern on the lower part subset of the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations).

Table 12.
The Bulls-eye scores (%) for various fusions based on the HFER framework combining shape methods with baseline texture or deep representations under the joint matching pattern on the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
The Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations under the single matching pattern on the lower part subset of the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations) are shown in Table 13. The experimental results indicate that the HFER framework outperformed the KNN-HDFF [20] across the majority of fusions. Notably, even on the more challenging cultivar-level leaf dataset, the HFER achieved superior performance in 23 out of 25 fusions. In addition, among all fusion results, those incorporating LPCFR achieved higher or comparable Bulls-eye scores, with the fusion of LPCFR with SDFH achieving the highest retrieval accuracy 56.64%. Compared to the KNN-HDFF [20] fusion framework, HFER demonstrates enhanced retrieval performance on the cultivar-level leaf dataset.

Table 13.
The Bulls-eye score (%) comparison (KNN-HDFF/HFER) for various fusions combining shape methods with baseline texture or deep representations under the single matching pattern on the lower part subset of the SoyCultivar200 leaf dataset [20] (the numbers shown in parentheses indicate the original scores of the corresponding representations).
To further analyze the differences in experimental results, we summarize the feature extraction mechanisms of various methods. Specifically, MDM [8] primarily captures one-dimensional spatial distribution, offering high computational efficiency but exhibiting certain limitations in robustness; MFD [31] integrates multiscale curvature information, enhancing shape representation capability at a moderate computational cost; HoGCV [10] encodes the curvature features and proportional relationship of leaf shape contour, achieving a trade-off between performance and efficiency; while IMTD [12] combines curvature with interior image information, demonstrating stronger robustness despite its higher computational complexity. However, these methods inherently focus on either single spatial distribution or curvature characteristics, which limits their ability to comprehensively describe the geometric features of leaf shape. In contrast, our proposed LPCFR captures spatial distributions along two local orthogonal directions while simultaneously integrating curvature characteristics. By employing histograms, LPCFR achieves a better balance between discriminative power and computational efficiency, significantly improving robustness and recognition capability against inter-class shape variations. For the fusion framework, compared to the KNN-HDFF [20] that relies solely on neighborhood distance mean normalization, the proposed HFER framework introduces exponential weighted normalization and ranking-based encoding. These enhancements enable the fusions to better focus on truly similar samples while mitigating the effects of distance scale variation, noise interference, and feature instability, exhibiting improved compatibility and robustness. In summary, all the experimental results indicate that the proposed LPCFR and HFER achieve significant improvements on both species-level and cultivar-level leaf retrieval tasks.
5. Conclusions
This paper proposes a novel shape representation, LPCFR, and an advanced heterogeneous fusion framework, HFER, for accurate leaf image retrieval. The LPCFR is derived from the local polar coordinate system, multiscale analysis, and statistical histograms, capturing spatial distribution along two locally orthogonal dimensions (radial distance and polar angle) and simultaneously encoding local curvature characteristics of leaf shapes to improve the discriminative power. The HFER framework leverages exponential weighted normalization and ranking-based encoding within the neighborhood distance measure, incorporating both local contextual information and structural relations to enhance the compatibility and robustness of heterogeneous features. Extensive experiments conducted on both species-level and cultivar-level leaf datasets demonstrate the effectiveness and generality of the proposed methods, which achieve superior retrieval performance compared to state-of-the-art techniques.
While the proposed method achieves competitive performance on clean and well-controlled datasets, we recognize its potential limitations in more complex real-world environments. In particular, the presence of occlusion, extreme leaf rotations, or cluttered backgrounds may degrade the quality of contour extraction and adversely affect shape retrieval accuracy. Although the integration of heterogeneous features (e.g., texture and deep representations) partially alleviates these issues, it remains an open challenge to develop representations that are robust under such conditions. To address these limitations, in future work, we will explore more diverse and realistic datasets and investigate advanced deep learning-based solutions to further enhance the generalization and robustness of leaf image retrieval systems.
Author Contributions
Conceptualization, M.Y.; methodology, M.Y.; software, M.Y. and D.Y.; validation, M.Y. and Y.Y.; formal analysis, M.Y., Y.C., and G.J.; investigation, M.Y.; resources, M.Y. and D.Y.; data curation, Y.Y.; writing—original draft preparation, M.Y.; writing—review and editing, Y.C.; visualization, M.Y.; supervision, D.Y. and G.J.; project administration, Y.Y.; funding acquisition, G.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was part supported by the Natural Science Foundation of Jiangsu Higher Education Institutions of China (Grant No. 24KJB520005).
Data Availability Statement
Data and code for this study are available from the corresponding author on reasonable request.
Acknowledgments
We sincerely thank the anonymous reviewers for their insightful suggestions and support, which greatly improved the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Adamek, T.; O’Connor, N. A multiscale representation method for nonrigid shapes with a single closed contour. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 742–753. [Google Scholar] [CrossRef]
- Wang, X.; Feng, B.; Bai, X.; Liu, W.; Latecki, L.J. Bag of contour fragments for robust shape classification. Pattern Recognit. 2014, 47, 2116–2125. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, B.; Li, C.; Yan, Y. A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition. Symmetry 2019, 11, 693. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, Y.; Duan, X.; Hou, Q.; Li, Z. Dual-axis generalized cross attention and shape-aware network for 2D medical image segmentation. Biomed. Signal Process. Control 2025, 107, 107791. [Google Scholar] [CrossRef]
- Feng, Y.F.; Shen, L.Y.; Yuan, C.M.; Li, X. Deep shape representation with sharp feature preservation. Comput.-Aided Des. 2023, 157, 103468. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Wang, X. Plant species recognition based on global–local maximum margin discriminant projection. Knowl.-Based Syst. 2020, 200, 105998. [Google Scholar] [CrossRef]
- Saleem, G.; Akhtar, M.; Ahmed, N.; Qureshi, W. Automated analysis of visual leaf shape features for plant classification. Comput. Electron. Agric. 2019, 157, 270–280. [Google Scholar] [CrossRef]
- Hu, R.X.; Jia, W.; Ling, H.; Huang, D. Multiscale distance matrix for fast plant leaf recognition. IEEE Trans. Image Process. Publ. IEEE Signal Process. Soc. 2012, 21, 4667–4672. [Google Scholar]
- Sokic, E.; Konjicija, S. Phase preserving Fourier descriptor for shape-based image retrieval. Signal Process. Image Commun. 2016, 40, 82–96. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B. Invariant leaf image recognition with histogram of Gaussian convolution vectors. Comput. Electron. Agric. 2020, 178, 105714. [Google Scholar] [CrossRef]
- Yang, C. Plant leaf recognition by integrating shape and texture features. Pattern Recognit. 2021, 112, 107809. [Google Scholar] [CrossRef]
- Wu, H.; Fang, L.; Yu, Q.; Jingrong, Y.; Yang, C. Plant leaf identification based on shape and convolutional features. Expert Syst. Appl. 2023, 219, 119626. [Google Scholar] [CrossRef]
- Zhao, C.; Chan, S.F.; Cham, W.K.; Chu, L. Plant Identification using leaf shapes—A pattern counting approach. Pattern Recognit. 2015, 48, 3203–3215. [Google Scholar] [CrossRef]
- de Souza, M.M.; Medeiros, F.N.; Ramalho, G.L.; de Paula, I.C., Jr.; Oliveira, I.N. Evolutionary optimization of a multiscale descriptor for leaf shape analysis. Expert Syst. Appl. 2016, 63, 375–385. [Google Scholar] [CrossRef]
- Ben Haj Rhouma, M.; Žunić, J.; Younis, M.C. Moment invariants for multi-component shapes with applications to leaf classification. Comput. Electron. Agric. 2017, 142, 326–337. [Google Scholar] [CrossRef]
- Mahajan, S.; Raina, A.; Gao, X.Z.; Kant Pandit, A.; Yin, P.Y. Plant Recognition Using Morphological Feature Extraction and Transfer Learning over SVM and AdaBoost. Symmetry 2021, 13, 356. [Google Scholar] [CrossRef]
- Wu, H.; Fang, L.; Yu, Q.; Yang, C. Composite descriptor based on contour and appearance for plant species identification. Eng. Appl. Artif. Intell. 2024, 133, 108291. [Google Scholar] [CrossRef]
- Wang, B.; Gao, Y. Hierarchical String Cuts: A Translation, Rotation, Scale, and Mirror Invariant Descriptor for Fast Shape Retrieval. IEEE Trans. Image Process. 2014, 23, 4101–4111. [Google Scholar] [CrossRef]
- Yang, C.; Lyu, W.; Yu, Q.; Jiang, Y.; Zheng, Z. Learning a discriminative region descriptor for fine-grained cultivar identification. Comput. Electron. Agric. 2025, 229, 109700. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B.; Gao, Y. Symmetric binary tree based co-occurrence texture pattern mining for fine-grained plant leaf image retrieval. Pattern Recognit. 2022, 129, 108769. [Google Scholar] [CrossRef]
- Lv, Z.; Zhang, Z. Research on plant leaf recognition method based on multi-feature fusion in different partition blocks. Digit. Signal Process. 2023, 134, 103907. [Google Scholar] [CrossRef]
- Wang, B.; Gao, Y.; Yuan, X.; Xiong, S. Local R-symmetry co-occurrence: Characterising leaf image patterns for identifying cultivars. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 19, 1018–1031. [Google Scholar] [CrossRef]
- Hamrouni, L.; Kherfi, M.L.; Aiadi, O.; Benbelghit, A. Plant Leaves Recognition Based on a Hierarchical One-Class Learning Scheme with Convolutional Auto-Encoder and Siamese Neural Network. Symmetry 2021, 13, 1705. [Google Scholar] [CrossRef]
- Beikmohammadi, A.; Faez, K.; Motallebi, A. SWP-LeafNET: A novel multistage approach for plant leaf identification based on deep CNN. Expert Syst. Appl. 2022, 202, 117470. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, X.; Zhang, J.; Han, Y.; Ai, H.; Dong, C.; Liu, H. Weed identification in soybean seedling stage based on UAV images and Faster R-CNN. Comput. Electron. Agric. 2024, 227, 109533. [Google Scholar] [CrossRef]
- Sharma, S.; Vardhan, M. AELGNet: Attention-based Enhanced Local and Global Features Network for medicinal leaf and plant classification. Comput. Biol. Med. 2025, 184, 109447. [Google Scholar] [CrossRef]
- Abbasi, S.; Mokhtarian, F.; Kittler, J. Curvature scale space image in shape similarity retrieval. Multimed. Syst. 1999, 7, 467–476. [Google Scholar] [CrossRef]
- Cao, J.; Wang, B.; Brown, D.B. Similarity based leaf image retrieval using multiscale R-angle description. Inf. Sci. 2016, 374, 51–64. [Google Scholar] [CrossRef]
- Ni, F.; Wang, B. Integral contour angle: An invariant shape descriptor for classification and retrieval of leaf images. In Proceedings of the IEEE International Conference on Image Processing, Athens, Greece, 7–10 October 2018; pp. 1223–1227. [Google Scholar]
- Barré, P.; Stöver, B.C.; Müller, K.F.; Steinhage, V. Leafsanp: A computer vision system for automatic plant species identification. Ecol. Inform. 2017, 40, 50–56. [Google Scholar] [CrossRef]
- Yang, C.; Yu, Q. Multiscale Fourier descriptor based on triangular features for shape retrieval. Signal Process. Image Commun. 2019, 71, 110–119. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-Up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Qi, X.; Xiao, R.; Li, C.G.; Qiao, Y.; Guo, J.; Tang, X. Pairwise rotation invariant co-occurrence local binary pattern. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2199–2213. [Google Scholar] [CrossRef]
- Tang, Z.; Su, Y.; Er, M.J.; Qi, F.; Zhang, L.; Zhou, J. A local binary pattern based texture descriptors for classification of tea leaves. Neurocomputing 2015, 168, 1011–1023. [Google Scholar] [CrossRef]
- Dyrmann, M.; Karstoft, H.; Midtiby, H.S. Plant species classification using deep convolutional neural network. Biosyst. Eng. 2016, 151, 72–80. [Google Scholar] [CrossRef]
- Liu, G.H.; Li, Z.Y.; Yang, J.Y.; Zhang, D. Exploiting sublimated deep features for image retrieval. Pattern Recognit. 2024, 147, 110076. [Google Scholar] [CrossRef]
- Liu, G.H.; Yang, J.Y. Deep-seated features histogram: A novel image retrieval method. Pattern Recognit. 2021, 116, 107926. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1097–1105. [Google Scholar]
- Wu, H.; Fang, L.; Yu, Q.; Yang, C. Deep convolutional feature aggregation for fine-grained cultivar recognition. Knowl.-Based Syst. 2023, 275, 110688. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B. Symmetry-constrained linear sliding co-occurrence LBP for fine-grained leaf image retrieval. Comput. Electron. Agric. 2024, 218, 108741. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Ling, H.; Jacobs, D. Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 286–299. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Novotný, P.; Suk, T. Leaf recognition of woody species in Central Europe. Biosyst. Eng. 2013, 115, 444–452. [Google Scholar] [CrossRef]
- Wang, B.; Brown, D.; Gao, Y.; Salle, J.L. MARCH: Multiscale-arch-height description for mobile retrieval of leaf images. Inf. Sci. 2014, 302, 132–148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).