Sliding Mode Control for Stochastic SIR Models with Telegraph and Lévy Noise: Theory and Applications

Abstract

This paper establishes a new stochastic SIR epidemic model that incorporates telegraph noise and Lévy noise to simulate the complex environmental disturbances affecting disease transmission. Given the susceptibility of epidemic spread to environmental noise and its intricate dynamics, an adaptive sliding mode controller based on an integral sliding surface and an adaptive control law is proposed. This controller is capable of stabilizing the constructed model and effectively suppressing the spread of the disease. The main contributions of this paper include the following: establishing a comprehensive and realistic stochastic SIR model that accounts for the complex impacts of telegraph noise (symbolizing periodic environmental changes) and Lévy noise (representing sudden environmental shocks) on the dynamics of disease transmission; employing T-S fuzzy modeling, which considers the design of fuzzy rules and the symmetry of membership functions, to ensure linearization of the model; constructing an integral sliding surface and designing an adaptive sliding mode controller for the fuzzy-processed model. Finally, the effectiveness of the proposed control method is validated through numerical simulations.

1. Introduction

Infectious diseases have always been an important factor in endangering human health, and pandemics of infectious diseases have brought great disasters to human society on many occasions in history. With the deepening of globalization and the expansion of the scope of human activities, the spread of infectious diseases has continued to increase in speed and scope. Emerging infectious diseases, renewed outbreaks of infectious diseases, and the increase in drug-resistant microorganisms are current challenges [1,2]. Infectious disease modeling is an important tool to study the rate and magnitude of transmission of infectious diseases, through which the effects of different interventions, such as isolation of patients, social distancing, and mass vaccination, can be assessed [3,4]. Significant progress has been made in the research of infectious disease modeling, with a variety of models being proposed and refined, from deterministic models to later stochastic models, and now complex network models [5,6,7]. These models can simulate the transmission process of infectious diseases, reveal their epidemiological patterns, and provide a scientific basis for the development of prevention and control strategies.

Traditionally, infectious disease modeling has focused on biotic factors, such as biological characteristics, intra-population interactions, and inter-population relationships, and portrayed the disease transmission mechanism through parameters such as exposure rate, infection rate, birth rate, and death rate [8,9]. However, with the deepening of research, the influence of abiotic factors, especially environmental noise, has gradually been emphasized. Key environmental factors such as temperature and air humidity, which actually have a significant impact on the survival and spread of pathogens, are often neglected in the initial modeling of infectious diseases. To address this gap, scholars have begun to incorporate stochastic elements, particularly white noise, into deterministic infectious disease models, to simulate subtle disturbances in the environment [10,11]. This innovation not only enhances the realism of the models, but also allows us to capture the dynamics of disease transmission more accurately.

However, when facing sudden and discontinuous environmental noise, such as extreme weather events, the limitations of white noise gradually appear. Therefore, scholars have introduced Lévy noise to characterize the impact of such extreme environmental events on disease transmission, and its characteristic jumping feature can better simulate the impact of these events on disease transmission [12,13]. In addition, due to the long duration of some infectious diseases and the disturbance of periodic environmental factors such as seasonal changes, the system may frequently switch between different environmental states. To capture this key feature, scholars use continuous-time finite-state Markov chains to simulate the transition process of environmental states, and introduce telegraph noise into infectious disease models [14,15]. Compared with the traditional model, the infectious disease model we constructed with both Lévy noise and telegraph noise can more comprehensively and accurately reflect the real propagation dynamics of the disease in different environmental states.

As an advanced control strategy, sliding mode control, with its unique robustness and excellent control performance, demonstrates significant advantages in dealing with uncertainties and external disturbances in complex systems. The control method achieves the predefined control objectives by designing a specific sliding mode surface along which the system state can slide after reaching the surface, thus maintaining the stability and performance of the system even when facing challenges such as parameter variations, model inaccuracies, or external disturbances. For example, in the field of vehicle engineering, reference [16] considered an event-triggered transmission mechanism and established a suitable sliding mode controller to ensure the asymptotic stability of the vehicle active suspension system, which effectively coped with the challenges posed by external perturbations and system parameter variations, This study demonstrates the advantages of sliding mode control in dealing with uncertainty and external disturbances in complex systems, and provides theoretical support and practical examples for the application of sliding mode control to stochastic SIR models in this paper. In the aerospace field, reference [17] proposed a new flight control system with an adaptive fuzzy terminal sliding mode controller and two proportional differential controllers, which successfully solved the stabilization and trajectory tracking problems of a quadrotor UAV under external perturbations and model uncertainties. By drawing on the adaptive fuzzy technique in reference [17], this paper designs more flexible and effective sliding mode controllers to adapt to the complex and variable noise environments in stochastic SIR models.

The literature [18] designed a vaccination strategy using sliding mode control and demonstrated its effectiveness under uncertainty of disease parameters; and the literature [19] analyzed an epidemic control strategy through optimal control theory and verified its potential in the prevention and control of COVID-19. In the field of infectious disease modeling, although there have been research attempts to apply control methods to disease prevention and control, the application of control methods for infectious disease models with significant uncertainty and stochasticity, especially those containing complex environmental perturbations such as telegraph noise and Lévy noise, is still relatively rare. The presence of these complex noises makes the prediction and control of infectious disease models more difficult.

Therefore, this paper focuses on constructing a stochastic SIR infectious disease model incorporating complex noise and designing a sliding mode control strategy adapted to it. The core objective of this study is to deeply intervene in the field of infectious disease modeling by implementing human control measures, especially in the complex situation where infectious diseases show long-term transmission and are simultaneously interfered with by dual environmental noise, to design scientifically sound sliding mode controllers to simulate effective human intervention strategies, and thus to effectively control the transmission of infectious diseases. The main contributions of this paper are as follows: (1) A more general stochastic SIR infectious disease model is proposed, considering that the spread of infectious disease may take a longer time and the dual environmental noise can better simulate the real situation. (2) Corresponding integral sliding surfaces and sliding-mode control criterion are established for the proposed stochastic SIR infectious disease model, and it is verified that the designed control method can inhibit the development of infectious disease.

This paper is organized as follows. In Section 2, a SIR model is constructed in a complex noise environment, which innovatively incorporates telegraph noise and Lévy noise to develop a more realistic infectious disease model. In Section 3, the SIR model is T-S fuzzified to enhance the model’s ability to handle uncertainty. In Section 4, the integral sliding mode surface and corresponding control criterion are designed for this fuzzy stochastic SIR model using the sliding mode control technique. Through theoretical analysis, the stability of the model and the accessibility of the sliding mode surface under the control strategy are demonstrated to ensure the effective suppression of infectious disease transmission. Finally, numerical simulations are carried out to support the ideas presented in this paper.

2. Model

2.1. Model Establishment

On the traditional SIR model with birth rate and mortality rate, considering small-scale population mobility within the scope, such as population migration, the SIR infectious disease model considered is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}\hfill \dot{S}\left(t\right)& =A-\beta S\left(t\right)I\left(t\right)-\mu S\left(t\right)+a_{1}S\left(t\right)\hfill \\ \hfill \dot{I}\left(t\right)& =\beta S\left(t\right)I\left(t\right)-(\epsilon +\mu +d)I\left(t\right)+a_{2}I\left(t\right)\hfill \\ \hfill \dot{R}\left(t\right)& =\epsilon I\left(t\right)-\mu R\left(t\right)+a_{3}R\left(t\right)\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(1)

In the model, $S\left(t\right)$, $I\left(t\right)$, and $R\left(t\right)$ represent the population of susceptible, infected, and recovered at time t, respectively. Normal numbers $\beta$ represent the infection rate, $\epsilon$ represent the recovery rate, A represent the newborn population, $\mu$ represent the mortality rate, and d represent the mortality rate due to illness. Unknown parameter $a_i$, $i=1,2,3$ represents the rate of migration in and out of the population.

In addition, considering that infectious diseases are inevitably affected by environmental noise, telegraph noise and Lévy noise are added to the deterministic model to simulate the effects of climate change and adverse environmental disasters in real life. Therefore, the following stochastic SIR infectious disease model is obtained:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}\hfill dS& =(A-\beta \left(r\left(t\right)\right)SI-\mu \left(r\left(t\right)\right)S+a_1\left(r\left(t\right)\right)S)dt+{\theta }_1\left(r\left(t\right)\right)Sd{B}_1\left(t\right)\hfill \\ \hfill & +{\int }_U{P}_1\left(z\right)S\left(t^{-}\right)N(dt,dz)\hfill \\ \hfill dI& =\left(\beta \right(r\left(t\right))SI-(\epsilon \left(r\right(t\left)\right)+\mu \left(r\right(t\left)\right)+d\left(r\right(t\left)\right))I\hfill \\ & +a_2\left(r\left(t\right)\right)I)dt+{\theta }_2\left(r\left(t\right)\right)Id{B}_2\left(t\right)+{\int }_U{P}_2\left(z\right)I\left(t^{-}\right)N(dt,dz)\hfill \\ \hfill dR& =(\epsilon \left(r\left(t\right)\right)I-\mu \left(r\left(t\right)\right)R+a_3\left(r\left(t\right)\right)R)dt+{\theta }_3\left(r\left(t\right)\right)Rd{B}_3\left(t\right)\hfill \\ & +{\int }_U{P}_3\left(z\right)R\left(t^{-}\right)N(dt,dz)\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(2)

where $B_i\left(t\right)(i=1,2,3)$ represents the standard Brownian motion on the complete probability space $(\mathsf{\Omega },F,P)$ with filter ${\left\{F_t\right\}}_{t\ge 0}$, the normal number ${\theta }_i(i=1,2,3)$ represents the intensity of white noise, $X\left(t^{-}\right)$ represents the left limit of $X\left(t\right)$, $P_i\left(z\right)(i=1,2,3)$ represents the intensity of Lévy noise, $N(dt,dz)$ is a real valued Poisson count measure, and feature measure $\lambda$ is defined on the measurable subset U of $[0,+\infty )$ to satisfy

$$\lambda \left(U\right)<\infty ,\tilde{N}(dt,dz)=N(dt,dz)-\lambda \left(dz\right)dt,\lambda \left(dz\right)dt=\tau \varphi \left(dz\right)dt$$

, where $\tau$ is the intensity of Poisson distribution and $\varphi$ is the probability distribution of the random variable z. $B\left(t\right)$ and $N(t,z)$ are independent of each other, and $(B,N)$ is called Lévy noise.

${\left\{r\left(t\right)\right\}}_{t\ge 0}$ is a finite Markov jump process that takes a value on a given state set $\mathbb{S}=\{1,2,\dots ,N\},\mathsf{\Gamma }={\left({\pi }_{ij}\right)}_{N\times N}$ is the transition probability matrix, and the transition probability of the model is represented as:

$$[\mathbb{P}\{r(t+\mathsf{\Delta })=j|r\left(t\right)=i\}=\left\{\begin{array}{c}{\pi }_{ij}\mathsf{\Delta }+o\left(\mathsf{\Delta }\right),i\ne j\\ 1+{\pi }_{ii}\mathsf{\Delta }+o\left(\mathsf{\Delta }\right),i=j\end{array}\right.$$

where ${\pi }_{ij}\ge 0$ represents the transition rate from i to j when $i\ne j$, satisfying ${\pi }_{ii}=-\sum _{j\ne i}{\pi }_{ij}$.

When infectious diseases persist, it can seriously affect people’s lives. Therefore, we can take necessary protective measures for susceptible populations, such as vaccines and isolation, and add human control strategies to the model to simulate the corresponding measures. In order to facilitate subsequent research and simplify the model representation, let $x_1=S,x_2=I,x_3=R,r\left(t\right)=i$, which can be expressed as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}\hfill d{x}_1& =(A-{\beta }_i{x}_1{x}_2-{\mu }_i{x}_1+u\left(t\right)+a_{i1}{x}_1)dt+{\theta }_{i1}{x}_{1}d{B}_1\left(t\right)\hfill \\ & +{\int }_U{P}_1\left(z\right)x_1\left(t^{-}\right)N(dt,dz)\hfill \\ \hfill d{x}_2& =({\beta }_i{x}_1{x}_2-({\epsilon }_i+{\mu }_i+d_i)x_2+a_{i2}{x}_2)dt+{\theta }_{i2}{x}_{2}d{B}_2\left(t\right)\hfill \\ & +{\int }_U{P}_2\left(z\right)x_2\left(t^{-}\right)N(dt,dz)\hfill \\ \hfill d{x}_3& =({\epsilon }_i{x}_2-{\mu }_i{x}_3+a_{i3}{x}_3)dt+{\theta }_{i3}{x}_{3}d{B}_3\left(t\right)\hfill \\ & +{\int }_U{P}_3\left(z\right)x_3\left(t^{-}\right)N(dt,dz)\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(3)

2.2. T-S Fuzzy Linearization

We employ the T-S fuzzy approach [20] to linearize System (3). When designing fuzzy rules and membership functions, we take symmetry into account to ensure the balance and effectiveness of control inputs under different system states. This subsequently transforms the system into a form that is more conducive to handling uncertainties, represented as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill dx& =[(E_i+C_i)x\left(t\right)+D_i(u\left(t\right)+A)]dt+G_i\theta (x\left(t\right),i)dB\left(t\right)\hfill \\ \hfill & +H_i{\int }_{U}P\left(x\right(t),i,z)N(dt,dz)\hfill \end{array}\end{array}$$

(4)

where

$$E_i=\left(\begin{array}{ccc}{a}_{i1}& 0& 0\\ 0& a_{i2}& 0\\ 0& 0& a_{i3}\end{array}\right)$$

it satisfies norm boundedness, in which $E_i=TZ\left(t\right)J$, T, and J are known constant matrices, $Z\left(t\right)$ is an unknown matrix and satisfies $Z^T\left(t\right)Z\left(t\right)\le L$. Other system parameters are given as follows.

$$C_i=\left(\begin{array}{ccc}-{\mu }_i& -{\beta }_i{x}_1\left(t\right)& 0\\ 0& {\beta }_i{x}_1\left(t\right)-({\epsilon }_i+{\mu }_i+d_i)& 0\\ 0& {\epsilon }_i& {\mu }_i\end{array}\right)$$

and

$$D_i=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),G_i=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),{\mathsf{\Gamma }}_i=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right).$$

Setting $z\left(t\right)={\beta }_i{x}_1\left(t\right)$, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill maxz\left(t\right)={\beta }_i{x_1}^{max}\left(t\right),minz\left(t\right)={\beta }_i{x_1}^{min}\left(t\right).\end{array}\end{array}$$

By applying the principle of maximum and minimum values, we express $z\left(t\right)$  as:

$$z\left(t\right)=M_{11}\left(z\left(t\right)\right)maxz\left(t\right)+M_{12}\left(z\left(t\right)\right)minz\left(t\right)$$

where $M_{11}+M_{12}=1$, $M_{ij}$ represent membership function.

Using the standard fuzzy mixing method, System (4) is written as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}dx={\displaystyle \sum _{i=1}^2}{h}_i\left(z\left(t\right)\right)[(E_i+C_i)x\left(t\right)+D_i(u\left(t\right)+A)]dt\hfill \\ +G_i\theta (x\left(t\right),i)dB\left(t\right)+{\mathsf{\Gamma }}_i{\int }_{U}P\left(x\right(t),i,z)N(dt,dz)]\hfill \end{array}\end{array}\end{array}$$

(5)

where

$$\begin{array}{c}\hfill \begin{array}{c}\hfill h_i\left(z\left(t\right)\right)={\displaystyle \frac{{\displaystyle \prod _{j=1}^r}{\omega }_{ij}\left(z_j\left(t\right)\right)}{{\displaystyle \sum _{i=1}^g}{\displaystyle \prod _{j=1}^r}{\omega }_{ij}\left(z_j\left(t\right)\right)}},h_i\left(z\left(t\right)\right)\ge 1,{\displaystyle \sum _{i=1}^2}{h}_i\left(z\left(t\right)\right)=1\end{array}\end{array}$$

$h_i\left(z\left(t\right)\right)$ is the defined weight, and ${\omega }_{ij}\left(z_j\left(t\right)\right)$ is the membership degree of $z_j\left(t\right)$ in fuzzy set ${\omega }_{ij}$ . To simplify, write  ${\displaystyle \sum _{i=1}^2}{h}_i\left(z\left(t\right)\right)C_i$ and ${\displaystyle \sum _{i=1}^2}{h}_i\left(z\left(t\right)\right)D_i$ as ${\overline{C}}_i$ and ${\overline{D}}_i$ respectively. The T-S fuzzy stochastic SIR infectious disease model is as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill dx& =[(E_i+{\overline{C}}_i)x\left(t\right)+{\overline{D}}_i(u\left(t\right)+A)]dt+G_i\theta (x\left(t\right),i)dB\left(t\right)\hfill \\ \hfill & +{\mathsf{\Gamma }}_i{\int }_{U}P\left(x\right(t),i,z)N(dt,dz)\hfill \end{array}\end{array}$$

(6)

2.3. Construction of Sliding Surfaces

In this section, for the stochastic SIR model (6) that has undergone T-S fuzzy processing, an integral sliding mode surface is designed. The equivalent control criterion ensuring that the system state reaches this sliding mode surface within a finite time, as well as the stability conditions, are derived. Moreover, the construction of the sliding mode surface and the control criterion exhibits symmetry. To verify the reachability condition of the sliding mode surface, an adaptive sliding mode control criterion is established. This criterion can automatically adjust the control parameters based on real-time changes in the system state, maintaining symmetry in the control response and ensuring that the system state remains on the sliding mode surface at all times.

The selection of integral sliding mode surface is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill s\left(t\right)=F_{i}x\left(t\right)-{\int }_0^t{F}_i({\overline{C}}_i+{\overline{D}}_i{K}_i)x\left(v\right)dv\end{array}\end{array}$$

(7)

where $F_i\in {\Re }^{m\times n}$, $F_i{\overline{D}}_i$ is a non-singular matrix, and $F_i{\aleph }_i=0$, where ${\aleph }_i=\left[\begin{array}{cc}{G}_i& {\mathsf{\Gamma }}_i\end{array}\right]$, $K_i\in {\Re }^{m\times n}$ is a constant matrix and ${\overline{C}}_i+{\overline{D}}_i{K}_i$ satisfies Hurwitz [21].

From system (4), it can be obtained that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\dot{s}\left(t\right)=F_i[(E_i+{\overline{C}}_i)x\left(t\right)+{\overline{D}}_i(u\left(t\right)+A)]-F_i({\overline{C}}_i+{\overline{D}}_i{K}_i)x\left(t\right)\\ =F_i[E_{i}x\left(t\right)+{\overline{D}}_i(u\left(t\right)+A)]-F_i{\overline{D}}_i{K}_{i}x\left(t\right)\end{array}\end{array}\end{array}$$

(8)

According to the sliding mode control theory, when $\dot{s}\left(t\right)=0$, we can obtain the equivalent control criterion:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u_{eq}\left(t\right)=-{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_i{E}_{i}x\left(t\right)-A+K_{i}x\left(t\right)\end{array}\end{array}$$

(9)

Introducing Equation (9), the system (6) can be written as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill dx& =\left[(E_i+{\overline{C}}_i+{\overline{D}}_i{K}_i-{\overline{D}}_i{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_i{E}_i)x\left(t\right)\right]dt+G_i\theta (x\left(t\right),i)dB\left(t\right)\hfill \\ \hfill & +{\mathsf{\Gamma }}_i{\int }_{U}P\left(x\right(t),i,z)N(dt,dz)\hfill \end{array}\end{array}$$

(10)

Then, System (10) is the sliding mode dynamic system of the original system on the sliding mode surface.

Compared with the traditional sliding mode control (SMC) [22], the sliding mode control method proposed in this study is able to better deal with the uncertainties and nonlinearities in the model by introducing the T-S fuzzy method, which significantly improves the robustness of the system, and the method also specifically considers the effects of telegraphic and Lévy noises, and designs the corresponding integral sliding mode surfaces and control criterion, so that it can more effectively suppress the the adverse effects of complex noise on system stability and performance.

3. Main Results

3.1. Stability Analysis

Lemma 1.

For System (10), if it satisfies

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{T\to \infty }{lim}\mathbb{E}{\displaystyle \underset{0}{\overset{T}{\int }}}{\Vert x\left(t\right)\Vert }^{2}dt<\infty \end{array}\end{array}$$

(11)

the state of System (10) is exponentially stable on the mean square.

Assumption 1

([23]). There exists a semi-positive definite matrix $W_{i1}$, such that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill trace\left\{{\theta }^T(x\left(t\right),i)\theta (x\left(t\right),i)\right\}\le x^T\left(t\right)W_{i1}x\left(t\right)\end{array}\end{array}$$

(12)

Assumption 2

([23]). There exists a semi-positive definite matrix $M_{i1}$, such that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\int }_U{P}^T(x\left(t\right),i,z)P(x\left(t\right),i,z)v\left(dz\right)\le x^T\left(t\right)M_{i1}x\left(t\right)\end{array}\end{array}$$

(13)

Theorem 1.

If there exist $R_i={R_i}^T>0$, $Q>0$, N and positive scalars $\eta ,\rho ,{\epsilon }_1,{\epsilon }_2,{\epsilon }_3$ satisfy

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{ccccc}\mathit{\Psi }& R{\overline{D}}_i& RT& \sqrt{\lambda }{\mathsf{\Gamma }}^{T}R\mathsf{\Gamma }& 0\\ \ast & -{{\overline{D}}_i}^{T}R{\overline{D}}_i& 0& 0& 0\\ \ast & \ast & -{\epsilon }_{1}L& 0& RT\\ \ast & \ast & \ast & -{\epsilon }_{2}L& 0\\ \ast & \ast & \ast & \ast & -{\epsilon }_{3}L\end{array}\right]<0\end{array}\end{array}$$

(14)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{cc}-R& RT\\ T^T{R}^T& -{\epsilon }_{3}L\end{array}\right]<0\end{array}\end{array}$$

(15)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {G_i}^T{R}_i{G}_i<{\eta }_{i}L,{{\mathsf{\Gamma }}_i}^T{R}_i{\mathsf{\Gamma }}_i<{\rho }_{i}L\end{array}\end{array}$$

(16)

then System (10) is said to be exponentially stable on the mean square, where

$$N={{\overline{D}}_i}^{T}R,\Psi =2R_i({\overline{C}}_i+{\overline{D}}_i{K}_i)+({\epsilon }_1+{\epsilon }_3)J{J}^T+{\eta }_i{W}_{i1}+({\rho }_i+{\epsilon }_2)M_{i1}+{\displaystyle \sum _{j=1}^N}{\pi }_{ij}{P}_j+Q$$

Proof. 

Consider the following Lyapunov function:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V=V_1+V_2\end{array}\end{array}$$

(17)

where

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V_1=x^T\left(t\right)R_{i}x\left(t\right)V_2={\int }_0^t{x}^T\left(t\right)Qx\left(t\right)dt\end{array}\end{array}$$

(18)

Based on Ito’s Formula [23], we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\mathcal{L}{V}_1=2x^T\left(t\right)R_i\left[(E_i+{\overline{C}}_i+{\overline{D}}_i{K}_i-{\overline{D}}_i{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_i{E}_i)x\left(t\right)\right]\hfill \\ +\underset{U}{\int }[{(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))}^T{R}_i(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))-x^T\left(t\right)R_{i}x\left(t\right)]v\left(dz\right)\hfill \\ +trace\left[{\sigma }_i^T{G}_i^T{R}_i{G}_i{\sigma }_i\right]+{\displaystyle \sum _{j=1}^N}{\pi }_{ij}{P}_j\hfill \end{array}\end{array}\end{array}$$

(19)

Combining Lemma 3 in [24], we can obtain:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}-2x^T\left(t\right)R_i{\overline{D}}_i{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_i{E}_{i}x\left(t\right)=-2x^T\left(t\right)R_i{\overline{D}}_i{\left({{\overline{D}}_i}^T{R}_i{\overline{D}}_i\right)}^{-1}{{\overline{D}}_i}^T{R}_i{E}_{i}x\left(t\right)\hfill \\ \le x^T\left(t\right)R_i{\overline{D}}_i{\left({{\overline{D}}_i}^{-1}{R}_i{\overline{D}}_i\right)}^{-1}{{\overline{D}}_i}^{-1}{R}_{i}x\left(t\right)+x^T{E_i}^T{R}_i{E}_{i}x\left(t\right)\hfill \end{array}\end{array}\end{array}$$

(20)

According to Lemma 1 in [25], we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}2x^T\left(t\right)R_i{E}_{i}x\left(t\right)=2x^T\left(t\right)R_{i}TZJx\left(t\right)\hfill \\ \le {\epsilon }_1{x}^T\left(t\right)J{J}^{T}x\left(t\right)+{{\epsilon }_1}^{-1}{R}_{i}T{T}^T{R}_{i}x\left(t\right)\hfill \end{array}\end{array}\end{array}$$

(21)

By Assumption 1, we can obtain:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill trace\left[{\sigma }_i^T{G}_i^T{R}_i{G}_i{\sigma }_i\right]\le x^T\left(t\right){\eta }_i{W}_{i1}x\left(t\right)\end{array}\end{array}$$

(22)

Based on the theorem conditions and Lemma 1 in [25], there is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\underset{U}{\int }[{(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))}^T{R}_i(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))-x^T\left(t\right)R_{i}x\left(t\right)]v\left(dz\right)\hfill \\ \le \rho \underset{U}{\int }\left(P^T(x\left(t\right),i,z)P(x\left(t\right),i,z)\right)v\left(dz\right)+{\epsilon }_2\underset{U}{\int }\left(P^T(x\left(t\right),i,z)P(x\left(t\right),i,z)\right)v\left(dz\right)\hfill \\ +{{\epsilon }_2}^{-1}\underset{U}{\int }\left(x^T\left(t\right){R_i}^{2}x\left(t\right)\right)v\left(dz\right)\hfill \end{array}\end{array}\end{array}$$

(23)

Using Assumption 2, it can be obtained that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\underset{U}{\int }[{(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))}^T{R}_i(x\left(t\right)+{\mathsf{\Gamma }}_{i}P(x\left(t\right),i,z))-x^T\left(t\right)R_{i}x\left(t\right)]v\left(dz\right)\hfill \\ \le (\rho +{\epsilon }_2)x^T\left(t\right)M_{i1}x\left(t\right)+\lambda {{\epsilon }_2}^{-1}{x}^T\left(t\right){R_i}^{2}x\left(t\right)\hfill \end{array}\end{array}\end{array}$$

(24)

We can further have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\mathcal{L}{V}_1\le 2x^T\left(t\right)R_i({\overline{C}}_i+{\overline{D}}_i{K}_i)x\left(t\right)+x^T\left(t\right)R_i{\overline{D}}_i{\left({{\overline{D}}_i}^T{R}_i{\overline{D}}_i\right)}^{-1}{{\overline{D}}_i}^T{R}_{i}x\left(t\right)\hfill \\ +x^T{E_i}^T{R}_i{E}_{i}x\left(t\right)+{\epsilon }_1{x}^T\left(t\right)J{J}^{T}x\left(t\right)+{{\epsilon }_1}^{-1}{R}_{i}T{T}^T{R}_{i}x\left(t\right)\hfill \\ +(\rho +{\epsilon }_2)x^T\left(t\right)M_{i1}x\left(t\right)+\lambda {{\epsilon }_2}^{-1}{x}^T\left(t\right){R_i}^{2}x\left(t\right)\hfill \\ +{\displaystyle \sum _{j=1}^N}{x}^T\left(t\right){\pi }_{ij}{P}_{j}x\left(t\right)+x^T\left(t\right){\eta }_i{W}_{i1}x\left(t\right)\hfill \end{array}\end{array}\end{array}$$

(25)

Combining $V_2={\int }_0^t{x}^T\left(t\right)Qx\left(t\right)dt,\mathcal{L}{V}_2=x^T\left(t\right)Qx\left(t\right)$, we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{L}V=\mathcal{L}{V}_1+\mathcal{L}{V}_2\le x^T\left(t\right)\mathsf{\Omega }x\left(t\right)\end{array}\end{array}$$

(26)

where

$$\begin{array}{c}\mathsf{\Omega }=2R_i({\overline{C}}_i+{\overline{D}}_i{K}_i)+R_i{\overline{D}}_i{\left({{\overline{D}}_i}^T{R}_i{\overline{D}}_i\right)}^{-1}{{\overline{D}}_i}^T{R}_i+{E_i}^T{R}_i{E}_i+{\epsilon }_{1}J{J}^T\\ +{{\epsilon }_1}^{-1}{R}_{i}T{T}^T{R}_i+\lambda {{\epsilon }_2}^{-1}{R_i}^2+{\eta }_i{W}_{i1}+({\rho }_i+{\epsilon }_2)M_{i1}+{\displaystyle \sum _{j=1}^N}{\pi }_{ij}{P}_j+Q\end{array}$$

From $\mathsf{\Omega }<0$, according to Schur’s complement, we can conclude that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{ccccc}\mathsf{\Phi }& 0& R{\overline{D}}_i& RT& \sqrt{\lambda }R\\ \ast & -R& 0& 0& 0\\ \ast & \ast & -{{\overline{D}}_i}^T{R}_i{\overline{D}}_i& 0& 0\\ \ast & \ast & \ast & -{\epsilon }_{1}L& 0\\ \ast & \ast & \ast & \ast & -{\epsilon }_{2}L\end{array}\right]+\overline{J}{Z}^T\overline{T}+{\overline{T}}^{T}Z{\overline{J}}^T<0\end{array}\end{array}$$

(27)

where

$$\mathsf{\Phi }=2R_i({\overline{C}}_i+{\overline{D}}_i{K}_i)+{\epsilon }_{1}J{J}^T+{\eta }_i{W}_{i1}+({\rho }_i+{\epsilon }_2)M_{i1}+{\displaystyle \sum _{j=1}^N}{\pi }_{ij}{P}_j+Q$$

$$\overline{J}={\left[\begin{array}{ccccc}J& 0& 0& 0& 0\end{array}\right]}^T,\overline{T}=\left[\begin{array}{ccccc}0& T^{T}R& 0& 0& 0\end{array}\right]$$

Using the Schur’s complement and Lemma 1 in [25], there exists ${\epsilon }_3>0$, such that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{ccccc}\mathsf{\Phi }& 0& R{\overline{D}}_i& RT& \sqrt{\lambda }R\\ \ast & -R& 0& 0& 0\\ \ast & \ast & -{{\overline{D}}_i}^T{R}_i{\overline{D}}_i& 0& 0\\ \ast & \ast & \ast & -{\epsilon }_{1}L& 0\\ \ast & \ast & \ast & \ast & -{\epsilon }_{2}L\end{array}\right]+{\epsilon }_3{\overline{T}}^T\overline{T}+{{\epsilon }_3}^{-1}\overline{J}{\overline{J}}^T<0\end{array}\end{array}$$

(28)

Thus it can be obtained that:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{L}V\le -{\kappa }_i \Vert x\left(t\right){\Vert }^2\le -\widehat{\kappa } \Vert x\left(t\right){\Vert }^2\end{array}\end{array}$$

(29)

where

$$-{\kappa }_i={\lambda }_{max}\left(\mathsf{\Omega }\right)({\kappa }_i>0,i\in S),-\widehat{\kappa }=\underset{i\in S}{max}\{-{\kappa }_i\}$$

According to Dynkin’s formula [25], there is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill -E{\displaystyle \underset{0}{\overset{T}{\int }}}\mathcal{L}Vdt=E{V}_0-E{V}_T\le E{V}_0\end{array}\end{array}$$

(30)

which means:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill E{\displaystyle \underset{0}{\overset{T}{\int }}}{ \Vert x\left(t\right)\Vert }^{2}dt\le {\displaystyle \frac{1}{\widehat{\kappa }}}E{V}_0<\infty \end{array}\end{array}$$

(31)

It can be obtained that System (10) is exponentially stable on the mean square. □

3.2. Accessibility Analysis

Theorem 2.

For system (10), the sliding mode control criterion is designed as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u\left(t\right)=K_{i}x\left(t\right)-\left[∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥+\mu ∥x\left(t\right)∥+\delta \right]\mathrm{sgn}\left(s\left(t\right)\right)\end{array}\end{array}$$

(32)

So the state of the System (10) is driven to the sliding surface within a finite time, where $\mathrm{sgn}\left(s\left(t\right)\right)={\displaystyle \frac{s\left(t\right)}{∥s\left(t\right)∥}}$, $\mu$ and $\delta$ are positive scalars.

Proof. 

Consider the Lyapunov function as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V\left(t\right)={\displaystyle \frac{1}{2}}{s}^T\left(t\right){\left(F_i{\overline{D}}_i\right)}^{-1}s\left(t\right)\end{array}\end{array}$$

(33)

From the above conditions, we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\dot{s}\left(t\right)=F_i{E}_{i}x\left(t\right)+F_i{\overline{D}}_i(K_{i}x\left(t\right)-\left[∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥+\mu ∥x\left(t\right)∥+\delta \right]\mathrm{sgn}\left(s\left(t\right)\right))\hfill \\ +F_i{\overline{D}}_{i}A-F_i{\overline{D}}_i{K}_{i}x\left(t\right)\hfill \\ =F_i{E}_{i}x\left(t\right)+F_i{\overline{D}}_{i}A-F_i{\overline{D}}_i\left[∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥+\mu ∥x\left(t\right)∥+\delta \right]\mathrm{sgn}\left(s\left(t\right)\right))\hfill \end{array}\end{array}\end{array}$$

(34)

Taking the derivative of (33), it follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\dot{V}\left(t\right)=s^T\left(t\right){\left(F_i{\overline{D}}_i\right)}^{-1}\dot{s}\left(t\right)\hfill \\ \le ∥A∥∥s\left(t\right)∥+∥s\left(t\right)∥∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥\hfill \\ -∥s\left(t\right)∥\left[∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥+\mu ∥x\left(t\right)∥+\delta \right]\hfill \end{array}\end{array}\end{array}$$

(35)

For any $\Vert s\left(t\right)\Vert \ne 0$, we can obtain:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \dot{V}\left(t\right)\le -\delta \Vert s\left(t\right)\Vert <0\end{array}\end{array}$$

(36)

So it is true that the control input drives the system’s state trajectory onto the sliding surface, which means that the reachability condition of the sliding surface is satisfied. □

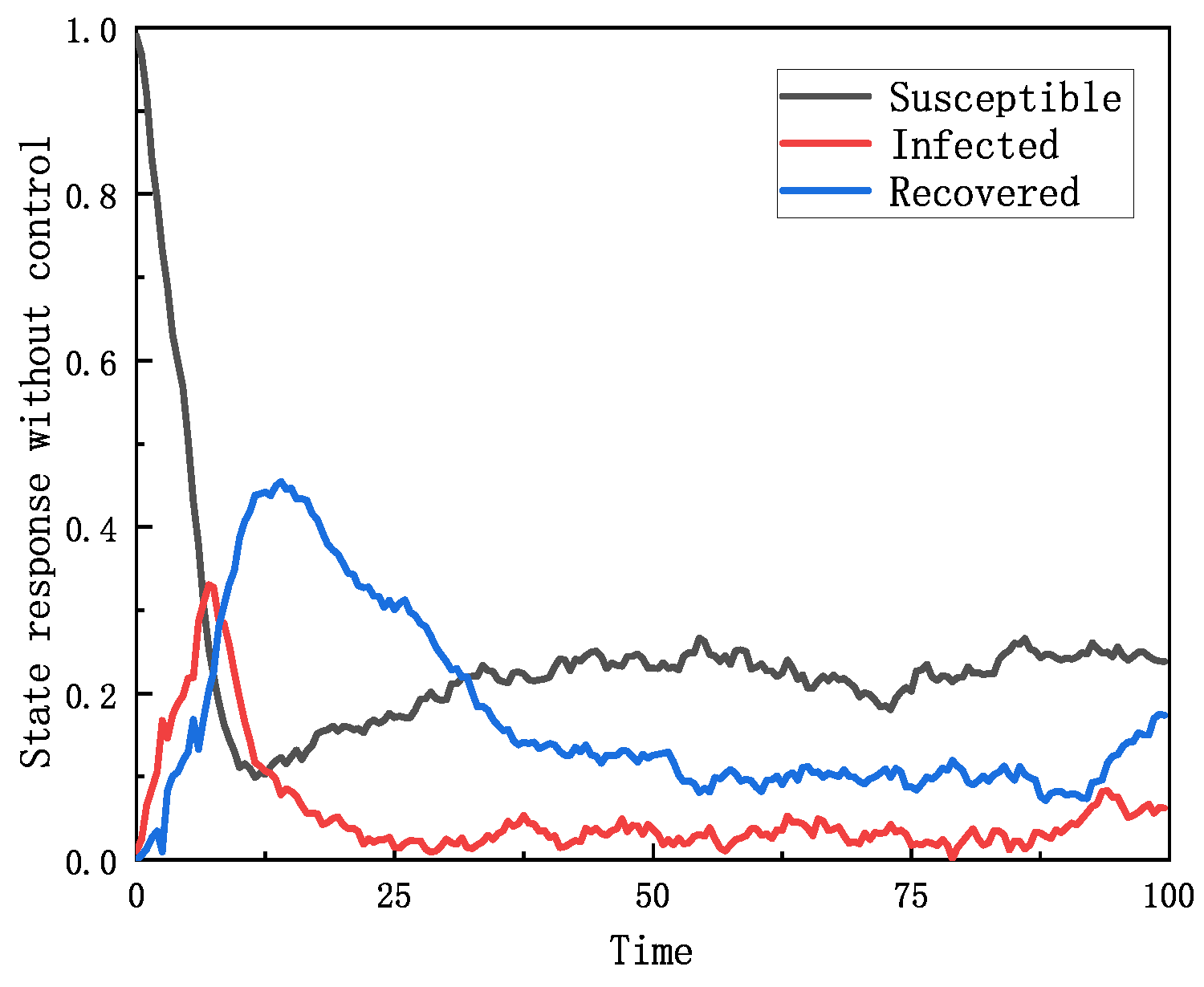
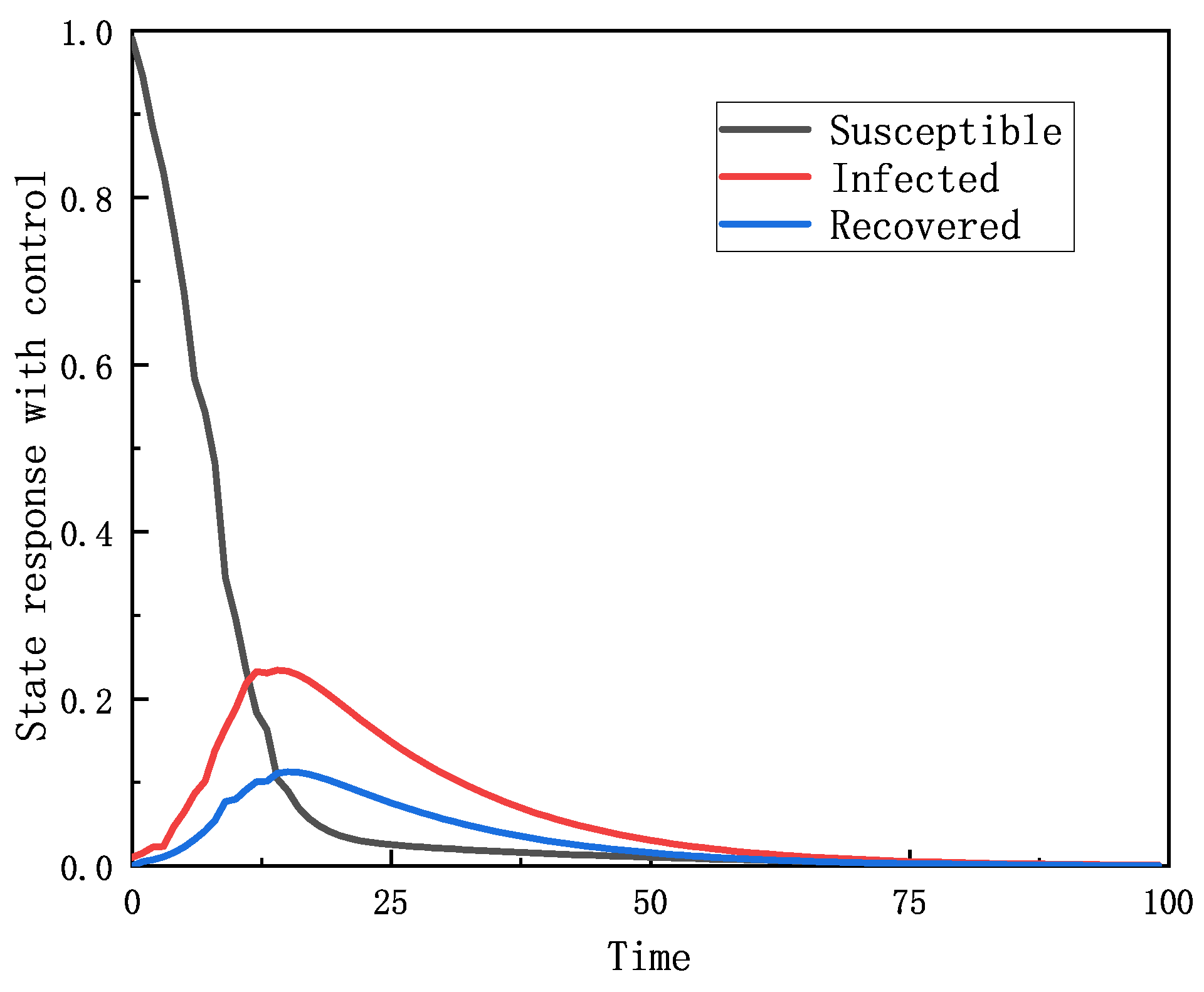
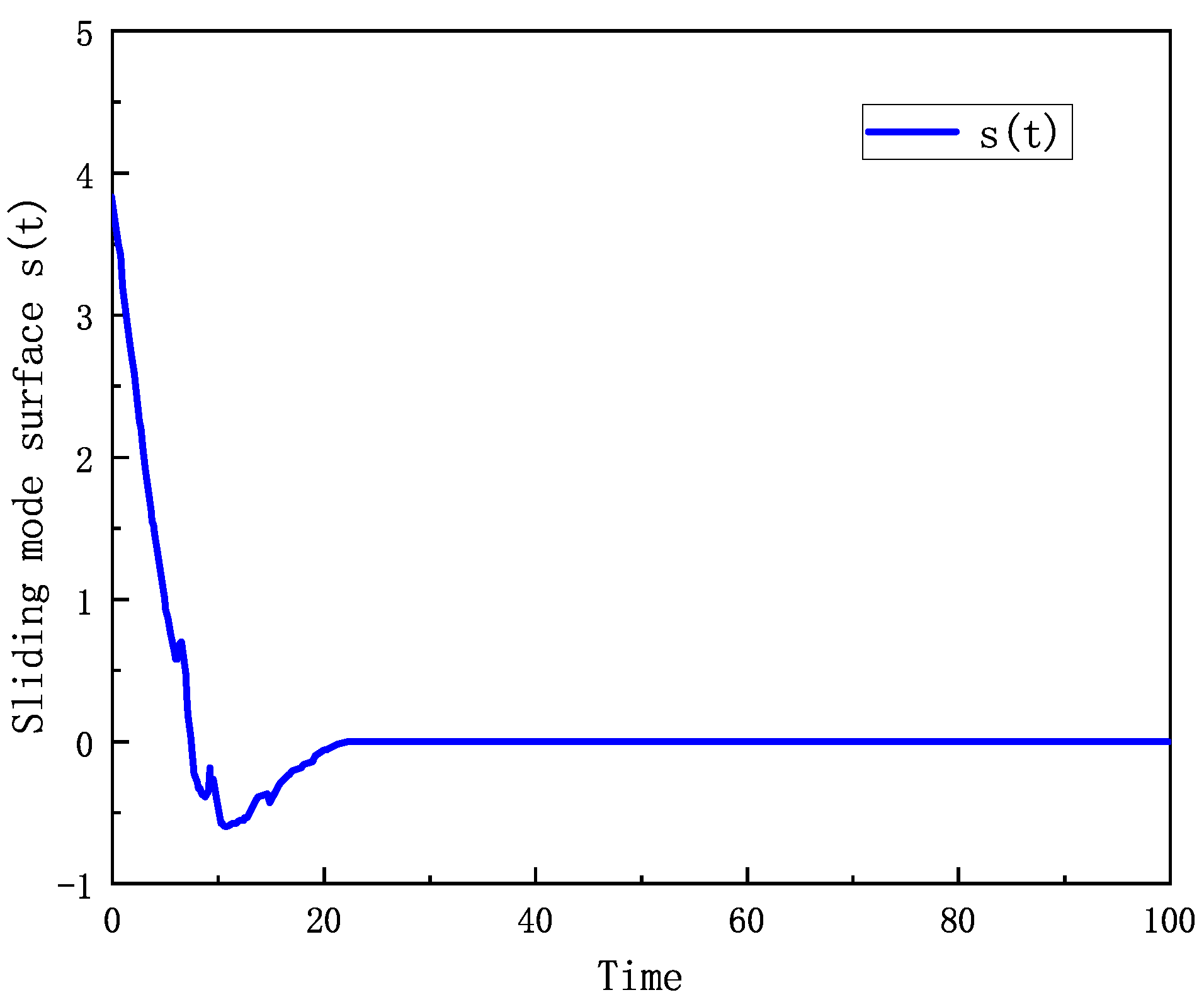
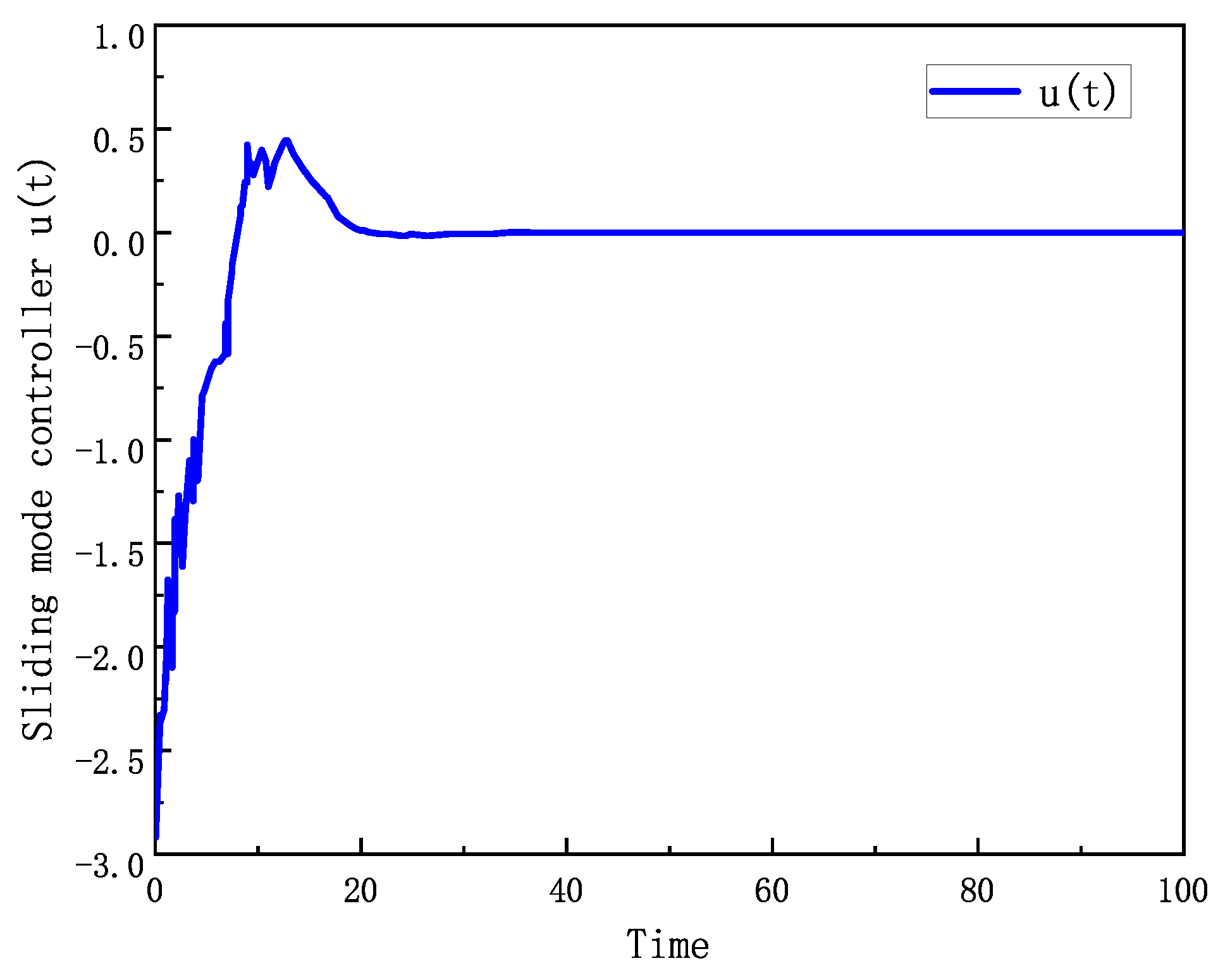
4. Results

In recent years, research on infectious diseases has received a lot of attention due to the frequency of outbreaks, while the frequency of natural disasters has also added challenges to prevention and control efforts. Fluctuations in the natural environment, such as extreme weather and climate change, significantly affect the dynamics of infectious diseases, with severe conditions such as typhoons and heavy rains and temperature fluctuations accelerating or altering their transmission patterns. In view of this, flexible and context-based human interventions and adjustments in government strategies are key to effectively managing the spread of infectious diseases. In this paper, we focus on the stochastic SIR infectious disease model and set specific parameter values to explore its dynamic characteristics and the effectiveness of prevention and control strategies:

$S\left(0\right)=0.99,I\left(0\right)=0.01,R\left(0\right)=0$ where $S\left(t\right),I\left(t\right),R\left(t\right)\in [0,1]$,$A=0.00639$

$\beta =0.6,\mu =0.02,\epsilon =0.1,d=0.0002$, ${\theta }_i=0.2,P_i\left(z\right)=0.3,i=1,2,3$,  ${\alpha }_i\in [-1,1]$. we consider ${\alpha }_2>-0.0715$, at this point, the basic reproduction number of the deterministic infectious disease model is $R_0>1$, which means that infectious diseases will persist. The state space is $\mathbb{S}=\{1,2\}$, and the transfer probability matrix is $\mathsf{\Gamma }=\left[\begin{array}{cc}-4& 4\\ 3& -3\end{array}\right]$.

The model parameters were chosen to be close to the actual situation, with the infection rate ($\beta$) set at 0.6, which integrates the virulence of the pathogen, the frequency of exposure, and preventive measures; the recovery rate ($\epsilon$) set at 0.1, which reflects the characteristics of the pathogen, the medical conditions, and the immune response; and the birth rate (A) and the death rate ($\mu$) are maintained to maintain the stability of the population, and the death rate caused by the disease (d) is set to be 0.0002. At the same time, intensity parameters such as telegraphic noise and Lévy noise are introduced to simulate the environmental disturbances. In addition, intensity parameters such as telegraph noise and Lévy noise to model environmental disturbances.

Numerical calculations were performed using the Euler–Maruyama method with a time step of 0.01 to ensure stability and accuracy. White noise and Lévy noise are simulated by a random number generator, and Poisson count measures are generated based on intensity parameters.

The parameters in the T-S fuzzy are as follows:

$$\begin{array}{c}maxz\left(t\right)=0.5,minz\left(t\right)=0\end{array}$$

According to the fuzzy rules provided in the paper, the fuzzy model is:

$$\begin{array}{c}dx={\displaystyle \sum _{i=1}^2}{h}_i\left(z\left(t\right)\right)[(E_i+C_i)x\left(t\right)+D_i(u\left(t\right)+A)]dt+G_i\theta (x\left(t\right),i)dB\left(t\right)\\ +{\mathsf{\Gamma }}_i{\int }_{U}P\left(x\right(t),i,z)N(dt,dz)]\end{array}$$

where

$$C_{i1}=\left(\begin{array}{ccc}-0.02& -0.6& 0\\ 0& 0.4798& 0\\ 0& 0.1& 0.02\end{array}\right),C_{i2}=\left(\begin{array}{ccc}-0.02& 0& 0\\ 0& -0.1202& 0\\ 0& 0.1& 0.02\end{array}\right)$$

$$M_{11}={\displaystyle \frac{z\left(t\right)}{0.5}},M_{12}={\displaystyle \frac{-z\left(t\right)+0.5}{0.5}}$$

The sliding surface function is given as follows:

$$s\left(t\right)=\left\{\begin{array}{c}\left[\begin{array}{ccc}0.5& 0.8& 1\end{array}\right]x\left(t\right)-{\int }_0^t\left[\begin{array}{ccc}-0.618& -1.347& -2.117\end{array}\right]x\left(v\right)dv\\ \left[\begin{array}{ccc}0.3& -1& 0.7\end{array}\right]x\left(t\right)-{\int }_0^t\left[\begin{array}{ccc}-0.394& 1.665& -1.127\end{array}\right]x\left(v\right)dv\end{array}\right.$$

The sliding surface gain determines the dynamic behavior of the system state after it reaches the sliding surface, as well as the robustness of the system to external disturbances and uncertainties. Larger gains can speed up the arrival of the system state to the sliding surface, but may introduce too large control inputs, leading to increased system jitter and affecting control accuracy and stability.

In order to reduce chattering, ${\displaystyle \frac{s\left(t\right)}{\left|\right|of}}$ $\mathrm{sgn}\left(s\right(t\left)\right)$, the sliding mode control criterion designed here is:

$$u\left(t\right)=\left\{\begin{array}{c}\left[\begin{array}{ccc}0.046& -0.124& -0.411\end{array}\right]x\left(t\right)-X_i{\displaystyle \frac{s\left(t\right)}{∥s\left(t\right)∥+0.01}}\\ \left[\begin{array}{ccc}-0.323& -0.172& -0.413\end{array}\right]x\left(t\right)-X_i{\displaystyle \frac{s\left(t\right)}{∥s\left(t\right)∥+0.01}}\end{array}\right.$$

where $X_i=\left[∥{\left(F_i{\overline{D}}_i\right)}^{-1}{F}_{i}T∥∥Jx\left(t\right)∥+0.1∥x\left(t\right)∥+2\right].$

Figure 1 depicts the switching state distribution of $r\left(t\right)$, where $r\left(0\right)=1$, which visualizes the stochastic switching process of the environmental state in continuous time, reflecting the effect of telegraph noise on the system dynamics. Figure 2 depicts the state response of the stochastic SIR contagion model when the fundamental regeneration number $R_0>1$ in the absence of control measures. It is obvious from the figure that the infectious disease model exhibits great instability due to environmental noise. The number of susceptible, infected and recovered populations fluctuates sharply with time, which indicates that it is difficult to predict and control the spread of infectious diseases under the effect of complex environmental noise.

Figure 3 illustrates the state response of the stochastic SIR infectious disease model after applying the sliding mode control strategy. In sharp contrast to Figure 2, the spread of the infectious disease model in Figure 3 is effectively suppressed. The downward trend of the number of susceptible people is effectively slowed down, and the growth rate of infected people is significantly reduced. This result fully proves the effectiveness of the sliding mode control strategy in suppressing the spread of infectious diseases.

Figure 4 and Figure 5 show the trajectories of the sliding mode surface and the control signal, respectively. The sliding mode surface trajectory in Figure 4 shows that the system state can quickly reach and stabilize on the sliding mode surface under the control strategy, which reflects the fast response and stability of the control strategy. The trajectory of the control signal in Figure 5 shows how the controller adjusts the control inputs in real time according to the system state to ensure that the system state is always maintained on the sliding mode surface.

5. Conclusions and Outlook

In this paper, a stochastic SIR infectious disease model incorporating the dual perturbations of telegraph noise and Lévy noise is proposed and controlled by a sliding mode variable structure control method. First, an infectious disease model that simultaneously considers these two noise effects is constructed to more closely match the complexity of infectious disease transmission in the real world. Human prevention and control measures were introduced into the model as control inputs for susceptible populations, and the model was fuzzified using the T-S fuzzy method. Subsequently, an integral sliding mode surface was established for the fuzzified model and an adaptive sliding mode controller was designed to verify the stability of the infectious disease model through Liapunov stability theory. In addition, the adaptive sliding mode control law was formulated to prove the reachability of the sliding mode surface. Finally, the significant effect of the proposed control strategy in suppressing the spread of infectious diseases is verified by numerical simulation. The research results in this paper can not only be used for the formulation and evaluation of infectious disease prevention and control strategies, but also be generalized to other complex system control problems affected by environmental noise, providing a powerful reference for related fields. It should be noted that this paper does not consider the time lag problem in infectious disease research, and a future direction is to apply adaptive sliding mode control to stochastic infectious disease models with time lag.