Abstract
From collective intelligence to evolutionary computation and machine learning, symmetry can be leveraged to enhance algorithm performance, streamline computational procedures, and elevate solution quality. Grasping and leveraging symmetry can give rise to more resilient, scalable, and understandable algorithms. In view of the flaws of the original Sailfish Optimization Algorithm (SFO), such as low convergence precision and a propensity to get stuck in local optima, this paper puts forward an Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm (OCSFO). The enhancements are mainly carried out in three aspects: (1) Using the Logistic map to initialize the sailfish and sardine populations. (2) In the first stage of the local development phase of sailfish individual position update, adopting the global exploration strategy of the Osprey Optimization Algorithm to boost the algorithm’s global search capability. (3) Introducing Cauchy mutation to activate the sailfish and sardine populations during the prey capture stage. Through the comparative analysis of OCSFO and seven other swarm intelligence optimization algorithms in the optimization of 23 classic benchmark test functions, as well as the Wilcoxon rank-sum test, it is evident that the optimization speed and convergence precision of OCSFO have been notably improved. To confirm the practicality and viability of the OCSFO algorithm, it is applied to solve the optimization problems of piston rods, three-bar trusses, cantilever beams, and topology. Through experimental analysis, it can be concluded that the OCSFO algorithm has certain advantages in solving practical optimization problems.
1. Introduction
With the ongoing progress and evolution of society, the attributes of engineering optimization problems have undergone significant transformations. These issues have developed from small-scale and simple structures to large-scale and highly intricate systems, from single-peak solution landscapes to multi-peak setups, and from linear to strongly non-linear features [1,2]. Such changes present considerable challenges to traditional optimization algorithms, which usually depend on accurate mathematical models and gradient-based techniques. When dealing with large-scale, multi-peak, and non-linear problems, these conventional algorithms struggle to efficiently explore the solution space [3]. As a result, they often fail to find the global optimal solution or get stuck in local optima, making them insufficient for dealing with the increasing complexity of modern engineering optimization tasks [4,5]. In the complex realm of computational algorithms, symmetry appears as a powerful yet underappreciated concept with broad implications. For instance, in swarm intelligence, the behavioral patterns of social insects like ants and bees inherently show symmetrical properties. Ant colonies display symmetrical foraging patterns around their nests when searching for food. By imitating this symmetry in artificial swarm intelligence algorithms, such as Ant Colony Optimization (ACO), more effective search strategies can be created. ACO algorithms make use of the symmetrical distribution of pheromone trails left by ants to guide the search process, ensuring a balanced exploration of all potential paths. This symmetry-driven method not only speeds up the convergence towards optimal solutions but also lowers the chance of being trapped in local optima.
Evolutionary computation, inspired by biological evolution, also gains a lot from symmetry. Genetic algorithms, a typical case, work based on genetic operators such as crossover and mutation. By incorporating symmetry into the encoding of genetic information, more efficient and effective search spaces can be built. For example, symmetrical chromosome representations can ensure that similar genetic configurations are grouped together, facilitating a more systematic exploration of the solution space. This allows for faster evolution of superior solutions, as the algorithm can more easily recognize and spread beneficial genetic traits. Swarm intelligence optimization algorithms have become a promising alternative. Based on the study of group behavior in nature, these algorithms take inspiration from the collective activities of biological groups like ants, birds, and fish [6]. They imitate behaviors such as ant foraging, bird flocking, or fish schooling. By emulating these natural behaviors, swarm intelligence algorithms use information exchange and cooperation mechanisms among group members [7,8], enabling a more comprehensive exploration of the solution space and a gradual convergence towards the optimal solution for a specific problem. Their unique ability to handle complex and uncertain situations has led to their wide application in solving various complex optimization problems [9]. For example, in path planning for autonomous vehicles or drones, these algorithms can efficiently find the shortest and safest routes while avoiding obstacles. In workshop scheduling, they can optimize resource allocation (such as machines and labor) to minimize production time and costs [10]. These applications show the effectiveness and versatility of swarm intelligence optimization algorithms in addressing real-world complex optimization challenges.
The Sailfish Optimization Algorithm (SFO), put forward by scholar Shadravan in 2019, is a notable addition to the family of swarm intelligence optimization algorithms [11]. This algorithm is cleverly designed based on the hunting dynamics between sailfish (predators) and sardines (prey) in marine ecosystems. In the SFO framework, sailfish are regarded as candidate solutions for the optimization problem, with their positions in the solution space corresponding to potential solutions that are updated iteratively to approach the optimal solution. Sardines, on the other hand, play a crucial role in enhancing the algorithm’s randomness by introducing unpredictability, which helps the algorithm avoid local optima and promotes a more thorough exploration of the solution space [12]. During the optimization process, the SFO algorithm simulates three different behavioral strategies that occur when sailfish groups hunt sardine schools. The first is the population elite strategy, in which the best-performing sailfish (elite solutions) guide the movement of other members of the population. By sharing their information and positions, elite sailfish help the entire group converge more quickly towards promising areas of the solution space. The second is the alternating attack strategy [13], which imitates the way sailfish take turns attacking sardine schools from different directions. Through alternating attack patterns, the algorithm can explore various parts of the solution space, increasing the probability of finding the global optimal solution. The third is the prey capture strategy, which focuses on the actual process of sailfish catching sardines. In an algorithmic context, this represents the exploitation phase, where the algorithm refines identified solutions and seeks a more precise convergence towards the optimal solution. Through these three strategies, the SFO algorithm systematically searches for feasible solutions within the solution space, gradually getting closer to the optimal solution.
The SFO algorithm has been widely applied and studied in many fields. In engineering design, it has been used to optimize the parameters of mechanical systems, electrical circuits, and structural designs, enabling performance improvements while reducing costs. In data mining and machine learning, it has been used for tasks such as feature selection, classifier parameter tuning, and clustering, improving the efficiency and accuracy of these algorithms. These applications have, to a certain extent, verified the flexibility and reliability of the SFO algorithm, showing its potential to become a powerful tool in the optimization field.
The following are this paper’s primary contributions:
- Propose an OCSFO hybrid algorithm that enhances global exploration capability through OOA and avoids local optima by combining Cauchy mutation;
- Design a multi-stage adaptive parameter strategy to dynamically balance search accuracy and speed;
- Validate algorithm performance in 23 benchmark functions and 4 types of engineering problems, outperforming 7 compared algorithms.
2. Related Work
Analogous to other swarm intelligence optimization algorithms, the SFO algorithm also faces drawbacks, including a tendency to converge to local optima and a sluggish convergence rate. To boost SFO’s optimization capacity and expedite its convergence, many scholars have put forward various enhancements. Reference [14] presented a new DESFO algorithm that combines the Differential Evolution (DE) algorithm with SFO. When utilized for feature selection tasks, this algorithm can effectively pinpoint the most discriminative features and showcases remarkable advantages in both convergence speed and accuracy. Reference [15] proposed an improved ISFO algorithm by integrating an adaptive non-linear iteration factor, Lévy flight strategy, and differential mutation strategy. Experimental results indicate that the ISFO algorithm displays superior robustness and precision on standard test functions. Reference [16] enhanced the SFO algorithm through strategies such as inertia weight adjustment, modification of the global search formula, and adoption of the Lévy flight strategy. This improved variant was successfully applied to select optimal controller nodes from a group of sensor nodes, yielding favorable results. Reference [17] developed an advanced SFO algorithm with enhanced performance by introducing two search strategies: population switching and random mutation. When tested on the CEC2017 benchmark suite and classical engineering problems, this improved algorithm demonstrated notably higher convergence accuracy.
While the above-mentioned improved algorithms have enhanced the optimization performance of the standard SFO to varying degrees, they still encounter challenges such as premature convergence and vulnerability to local optima when tackling complex multi-peak problems. To further enhance SFO’s performance, this paper proposes an Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm (OCSFO). The improvements are carried out in three key aspects:
(1) Initializing the sailfish and sardine populations using the Logistic map to enhance population diversity;
(2) Employing the global exploration strategy of the Osprey Optimization Algorithm during the first stage of the local development phase in sailfish individual position updates, thereby strengthening the algorithm’s global search capability;
(3) Introducing Cauchy mutation to stimulate the activity of sailfish and sardine populations during the prey capture stage, enhancing local exploitation and escaping from local optima.
Subsequently, OCSFO is tested on 23 classical benchmark test functions, and four engineering design optimization problems to verify its effectiveness in solving complex optimization tasks.
3. Standard Sailfish Optimization Algorithm
The conventional Sailfish Optimization Algorithm (SFOA) comprises two populations. One is the sailfish population, which conducts searches around the current optimal solution’s location to enhance the local search capability [18,19]. The other is the sardine population. As the prey of sailfish, the sardine population explores positions within the search space to improve the global search comprehensiveness. Sailfish are capable of searching in multi-dimensional spaces [20]. Thus, sailfish are regarded as candidate solutions, and the number of variables in the problem to be solved corresponds to the dimension of the search space, which is represented as the sailfish’s position in the algorithm. The standard Sailfish Optimization Algorithm includes four steps [21]:
(1) Population Initialization
As a population-based meta-heuristic algorithm, in the Sailfish Optimization Algorithm, it is assumed that sailfish stand for candidate solutions, and the problem variables are equivalent to the sailfish’s positions in the search space. Correspondingly, the population in the solution space is generated randomly. Sailfish can perform searches in one-dimensional, two-dimensional, three-dimensional, or even higher-dimensional spaces, and their position vectors are changeable [22]. In a d-dimensional search space, the current position of of the i-th member in the k-th search is
where, the parameter m represents the number of sailfish, d represents the number of variables, and SFij represents the value of the i-th sailfish in the j-th dimension. In addition, the fitness of each sailfish is calculated through the fitness function as follows:
To evaluate each sailfish, the following matrix shows the fitness values of all solutions:
where, the parameter m is the number of sailfish, SFij is the value of the i-th sailfish in the j-th dimension, the parameter f is the fitness function used for calculation, and SFFitness is used to store the fitness values returned for each sailfish’s fitness or objective function value [23]. The first row of the matrix SFposition is fed into the fitness function, and its output represents the fitness value of the corresponding sailfish in the SFFitness matrix.
The sardine population is another important component of the Sailfish Optimization Algorithm. The algorithm assumes that the sardine school also swims in the search space. Therefore, the positions of the sardines and their fitness values are utilized as follows:
The parameter n is the number of sardines, Sij is the value of the i-th sardine in the j-th dimension, and the Sposition matrix represents the positions of all sardines [24].
The parameter n is the number of sardines, Sij represents the value of the i-th sardine in the j-th dimension, f is the objective function, and it is used to store the fitness value of each sardine. It is worth noting that the sailfish and sardines are corresponding factors in finding solutions. In this algorithm, the sailfish are the main factor, scattered in the search space, while the sardines can cooperate to find the best position in the area. In fact, when searching the space, the sardines may be preyed upon by the sailfish. If a sailfish discovers a better solution obtained so far, it will update its position [25].
(2) Population Elite Strategy
To enable the algorithm to retain the optimal solution of each iteration, the population elite strategy is introduced. The individual with the highest fitness value in the sailfish population is selected as the elite sailfish for each attack iteration . The individual with the highest fitness value in the sardine population is selected as the injured sardine that is most likely to be captured after being attacked by the sailfish in each iteration [26].
(3) Alternating Attack Strategy
During the process of preying on sardines, sailfish adopt an alternating attack method, which can minimize the energy consumption of sailfish and make it easier to capture sardines. The SFO algorithm simulates this process, and the position update formula of the sailfish is as follows:
Wherein, is the position of the elite sailfish formed up to the current time, determines the best position of the injured sardine formed currently, is the current position of the sailfish, rand (0,1) is a random number between 0 and 1, and i is a coefficient generated in the i-th iteration. The generation method is as follows [27]:
where PD is a factor set considering the change in prey density caused by the predation of sailfish during the hunting period. The generation formula is as follows:
NSF and NS are the number of sailfish and sardines in the loop, respectively.
(4) Prey Capture Strategy
In the SFO algorithm, the random update of the sardine population’s position helps to find the optimal solution in the search space, thereby simulating the process of sailfish capturing sardines. The sardines update their positions in each iteration based on the current attack power of the sailfish and the current best position. The position update formula is as follows [28]:
The position of the sardine before update is , the position after update is , the parameter r is a random number between 0 and 1, The parameter AP is the attack power of the sailfish in each iteration, and its value gradually decreases as the number of iterations increases. The generation formula is as follows:
The parameters A and are coefficients that make the attack power AP decrease from A to 0. The AP parameter helps to balance the exploration and exploitation of the search space. When the attack power of the sailfish is high (i.e., AP ≥ 0.5, all sardine positions are updated. When the attack power of the sailfish is low (i.e., AP < 0.5), only the positions of α sardines with a shift amount of β are updated. The calculation formulas for α and β are as follows:
The parameter di is the dimension of the sardine, and Ns is the number of sardines.
When the fitness value of the updated sardine is better than that of the sailfish, the process of the sailfish capturing the sardine is simulated. The position of the sailfish at the current position is replaced with the position of the current sardine, and the position of the replaced sardine is randomized. The formula is as follows:
The parameter is the position of the sailfish in the i-th iteration. The parameter is the position of sardine in the i-th iteration.
Summarizing the above operating mechanism of the Sailfish Optimization Algorithm, the steps of the SFO algorithm can be simplified as follows:
Step 1: Parameter Setting. Set the sailfish population size M, the sardine population size N, the search space dimension D, the maximum number of iterations Maxiter, and the non-linear factor parameters A = 4 and ε = 0.01 in the algorithm.
Step 2: Population Initialization. Initialize the positions of the sailfish and sardine populations in the search space.
Step 3: Elite Selection. Calculate the fitness values of each sailfish and sardine, record and find the positions and fitness values of the optimal individuals among them. Select the sailfish with the best fitness value as the elite sailfish, and select the sardine with the best fitness value as the injured sardine.
Step 4: Start Iteration. Update the positions of the sailfish according to Formula (6) and the positions of the sardines according to Formula (9). Consider the attack power factor. If the attack power AP < 0.5, calculate α and β according to Formulas (11) and (12), and update the positions of some sardines. Otherwise, update the positions of all sardines.
Step 5: Fitness Value. Evaluation of Sailfish and Sardines Determine whether to perform position replacement.
Step 6: Calculate the Fitness Values of Sailfish and Sardines Record and update the global optimal value and position.
Step 7: Check Iteration Termination Condition. If the current iteration meets the termination condition, stop the iteration and output the global optimal solution. Otherwise, jump to Step 3 to continue the iterative operation.
4. Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm
4.1. Chaotic Map Initialization
The population initialization method has a certain impact on the optimization effect and robustness of swarm intelligence algorithms [29]. Compared with completely random population initialization, introducing an appropriate chaotic sequence for initialization can generate a more uniformly distributed initial population in the search space, making the selected elite sailfish and injured sardines more representative and accurate [30]. This paper optimizes the population initialization using the Logistic map. Its iteration formula is as follows:
where , r is the control parameter, and r = 0.3 in this paper.
4.2. Osprey Optimization Algorithm
The Osprey Optimization Algorithm (OOA), proposed by Dehghani et al. in 2023 [31], is a swarm intelligence optimization algorithm inspired by the strategy of ospreys catching fish on water [31,32]. That is, after detecting the position of prey, ospreys hunt and kill it and then take the prey to a suitable place to eat. The OOA has the advantages of few parameters and high optimization efficiency. During the local development phase of sailfish individual position update, the global exploration strategy of the OOA in the first stage is adopted to enhance the global search ability of the algorithm [33].
The global exploration strategy formula of the OOA in the first stage is used to replace the position update formula of the explorers in the original Sailfish Optimization Algorithm [34]. The OOA can compensate for the position update method of the SFO algorithm that overly relies on the positions of the previous-generation sailfish. It randomly detects the position of one of the fish and attacks it. The position update method of the explorers in the SFO algorithm is updated based on the movement simulation method of ospreys towards fish [35]. The global exploration strategy formula of the OOA in the first stage is as follows:
where represents the position of the i-th osprey in the j-th dimension, represents the fish selected by the i-th osprey, is a random number between [0, 1], and is a random number in the set {1,2} [36,37].
4.3. Cauchy Mutation
To address the problem that the Sailfish Optimization Algorithm is prone to getting trapped in local optima, Cauchy mutation is introduced to improve the globally optimal individual, avoiding the algorithm from falling into local optima and enhancing its global optimization ability [38].
Cauchy mutation has the advantage of a relatively small peak at the origin and a long distribution at both ends, which can generate large perturbations during the mutation operation [39]. The Cauchy mutation formula is as follows:
where Cauchy(0,1) is the standard Cauchy distribution function. and are the positions of the sailfish and sardine before mutation, respectively. and are the positions of the sailfish and sardine after mutation, respectively, and rand is a random number between [0, 1].
4.4. Pseudo-Code of the Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm
In summary, the Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm (OCSFO) proposed in this paper can increase the swarm diversity to a certain extent, balance the local and global search abilities of the algorithm, and improve its optimization ability. The pseudo-code of the Algorithm 1 is as follows:
| Algorithm 1. Pseudo-code of the OCSFO Algorithm |
Start
|
The flowchart of the Osprey and Cauchy Mutation integrated sailfish optimization algorithm is shown in Figure 1. In view of the flaws of the original Sailfish Optimization Algorithm (SFO), such as low convergence precision and a propensity to get stuck in local optima, this paper puts forward an Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm (OCSFO). The enhancements are mainly carried out in three aspects: (1) Using the Logistic map to initialize the sailfish and sardine populations. (2) In the first stage of the local development phase of sailfish individual position update, adopting the global exploration strategy of the Osprey Optimization Algorithm to boost the algorithm’s global search capability. (3) Introducing Cauchy mutation to activate the sailfish and sardine populations during the prey capture stage.
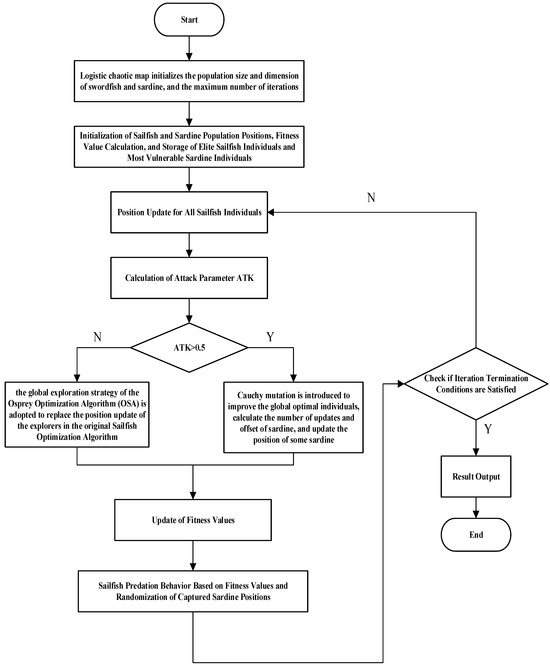
Figure 1.
The flowchart of the Osprey and Cauchy Mutation integrated sailfish optimization algorithm.
5. Simulation Experiments and Analysis
5.1. Experimental Environment Setup
In the experiments to verify the performance of the OCSFO algorithm, the experimental environment is set up as follows: The operating system is Windows 10 (64-bit), the processor is Intel(R) Core(TM) i7-10875H with a main frequency of 2.3 GHz, the computer memory is 16 GB, and the simulation software is MATLAB R2020b. To verify the effectiveness and advantages of the OCSFO algorithm, the OCSFO algorithm is compared with the standard SFO algorithm and six other well-known intelligent algorithms: PSO [40], GWO [41], HHO [42], DBO [43], POA [44], and PO [45]. To ensure the fairness of the algorithm comparison, the population size of all algorithms is set to 50, the number of iterations is set to 1000, and the dimension is set to 30. The fitness values obtained from 30 independent runs of each algorithm, including the optimal value (Min), standard deviation (Std), average value (Avg), median value (Median), and worst value (Worse), are used as evaluation indicators. The optimal data in the statistical results are shown in bold.
5.2. Test Functions
This section describes the 23 classic benchmark test functions and the benchmark functions test set used in this paper. Table 1 presents the information of the 23 classic benchmark test functions, including the function expressions, dimensions, search ranges, and optimal values. Among them, F1–F7 are unimodal functions, F8–F13 are multimodal functions, and F14–F23 are fixed-dimension multimodal functions.

Table 1.
Classic benchmark test functions.
5.3. Test Results and Analysis of Classic Benchmark Functions
(1) Test Results and Analysis
Under the above-mentioned experimental environment and parameter settings, each algorithm is used to independently run 30 times on the 23 classic benchmark test functions, and the test results shown in Table 2 are obtained. The optimal values of each index in the table are marked in bold.

Table 2.
Test Results of Classic Benchmark Test Functions.
The data in the table reveals that OCSFO has delivered robust optimization outcomes across the majority of the 23 classical benchmark test functions. Specifically, in nine test functions—F5, F9, F10, F11, F12, F13, F15, F16, and F21—OCSFO consistently outperformed other algorithms in all evaluated metrics. For most functions, OCSFO successfully identified the theoretical optimal values. Even when other algorithms matched this achievement, OCSFO exhibited notably smaller standard deviations, underscoring its superior convergence accuracy and stability. These results highlight OCSFO’s enhanced capability to balance exploration and exploitation, positioning it as an effective solution for complex optimization tasks.
(2) Wilcoxon Rank-Sum Test
To test the significance of the optimization effect of OCSFO, based on the optimal values obtained from 30 independent runs of each algorithm, the OCSFO is compared with the other seven algorithms through the Wilcoxon rank-sum test. The Wilcoxon rank-sum test is a non-parametric statistical test method mainly used to compare whether there is a significant difference in the medians of two independent samples. The hypothesis is set that there is no significant difference between the two algorithms. When the result of the Wilcoxon rank-sum test is less than 0.05, it means that the hypothesis is not valid, that is, there is a significant difference between the two algorithms. When the result of the Wilcoxon rank-sum test is greater than 0.05, it means that the hypothesis is valid, that is, there is no significant difference between the two algorithms. When the result of the Wilcoxon rank-sum test is NaN, it means that the effects of the two algorithms are equivalent and cannot be compared. The results of the Wilcoxon rank-sum test are shown in Table 3.

Table 3.
Results of Wilcoxon Rank-Sum Test for Classic Benchmark Test Functions.
It can be seen from Table 3 that most of the results of the Wilcoxon rank-sum test is less than 0.05, indicating that the optimization effect of OCSFO has a significant improvement compared with other algorithms. The OCSFO algorithm performs much better than the other seven algorithms.
(3) Convergence Performance Analysis
To verify the convergence performance of the OCSFO algorithm, this experiment lists the comparison charts of the iterative convergence curves of the OCSFO algorithm and other intelligent optimization algorithms on 23 classic benchmark test functions. The name of the benchmark function is shown at the top of each comparison chart. The convergence curves of 8 comparison algorithms on the classic benchmark test functions are shown in Figure 2.
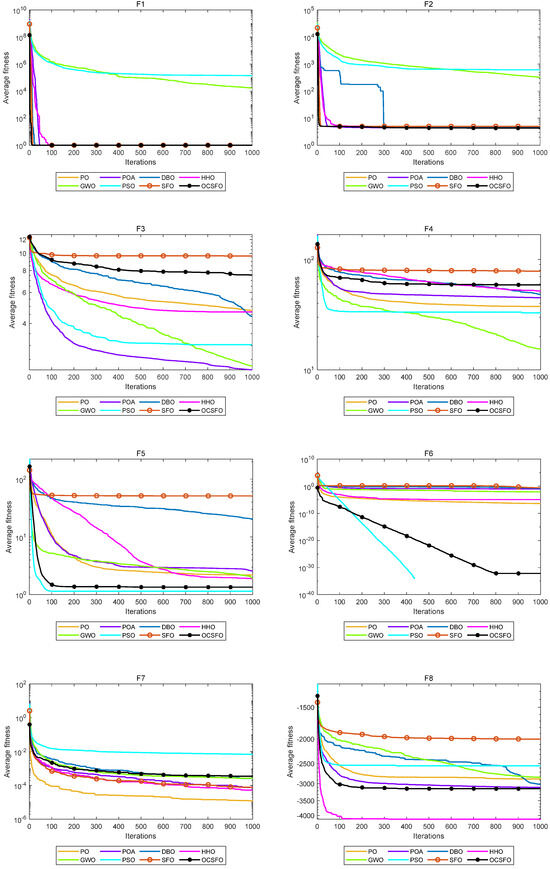
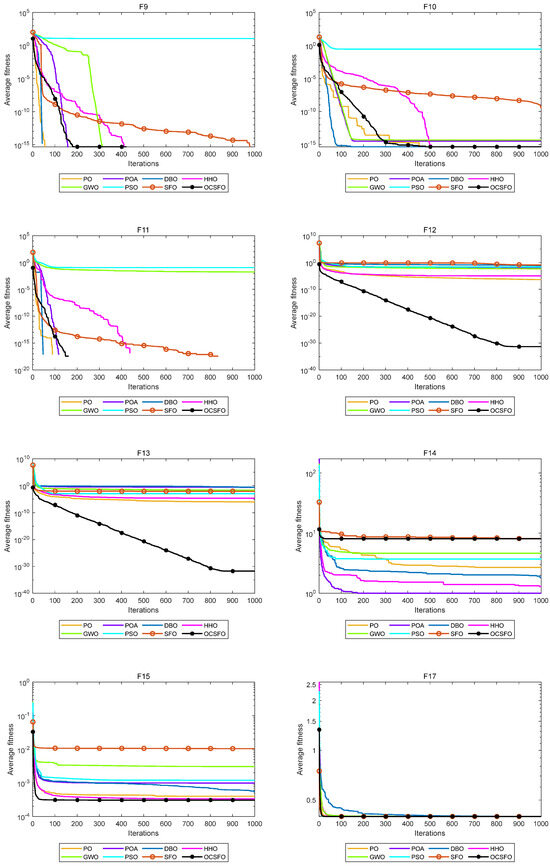
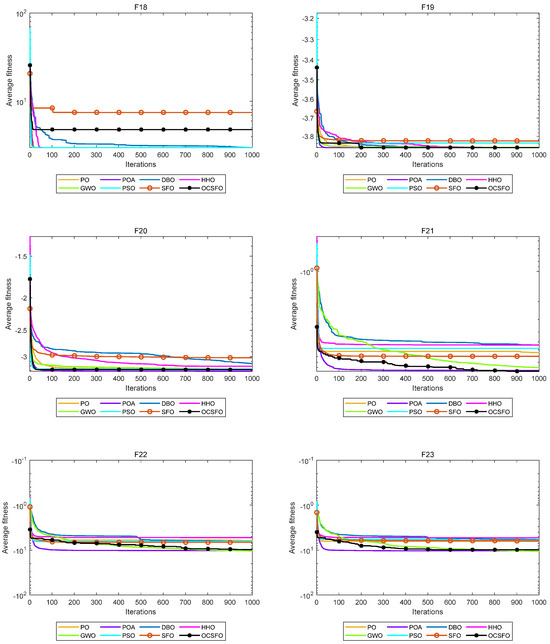
Figure 2.
Convergence curves of 8 comparison algorithms on classic benchmark test functions.
Comparison of 23 classical function radar charts for 8 algorithms is shown in Figure 3.
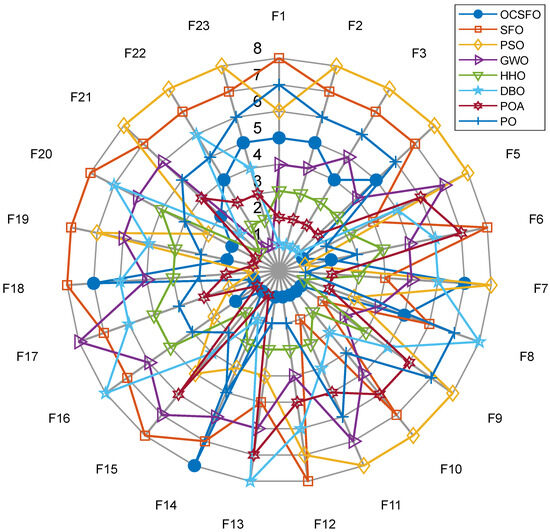
Figure 3.
Comparison of 23 classical function radar charts for 8 algorithms.
As illustrated in Figure 2 and Figure 3, OCSFO demonstrates superior convergence behavior by attaining better solutions in F1, F2, and F5, while closely approaching the theoretical optimal value in F6. For the unimodal functions F3 and F4, although OCSFO does not fully converge to the theoretical optimum, it still achieves substantial improvements in solution accuracy and convergence velocity when juxtaposed with the classical SFO algorithm. This highlights the effectiveness of its hybrid exploration-exploitation mechanism in gradient-based optimization landscapes.
Notably, OCSFO excels in multimodal function optimization. In F9, F10, F11, F12, and F13—characterized by complex, multi-peak structures—it not only converges to the theoretical optimal values but also does so with significantly faster convergence kinetics compared to other algorithms. This proficiency underscores its enhanced ability to navigate rugged fitness landscapes and avoid premature stagnation in local optima. Further validation is observed in fixed-dimension multimodal functions (F15, F17, F19, F20, F21, F22, F23), where OCSFO consistently exhibits stronger global search capabilities. Function F16 encountered an error and did not display the image, it is not be displayed. Its performance across these diverse problem classes demonstrates remarkable adaptability to highly non-linear, multi-peak search spaces, a critical advantage for real-world engineering applications.
Collectively, these results establish that OCSFO surpasses the classical SFO algorithm in both convergence speed and accuracy. When benchmarked against other state-of-the-art comparison algorithms, it demonstrates distinct dominance in handling multimodal and fixed-dimension multimodal challenges, showcasing robust escape mechanisms from local optima, superior convergence precision, and overall optimal performance. The findings solidify OCSFO’s utility as a versatile and efficient optimization framework for complex, high-dimensional problems in engineering and machine learning. In response to the problems of search ability, convergence speed, and local optima in the SFO benchmark algorithm, this paper proposes a swordfish optimization algorithm (OCSFO) that integrates the Osprey and Cauchy mutation. The first stage exploration strategy of the Osprey algorithm is used to improve the discoverer position update formula, increasing the exploration ability of SFO in identifying optimal regions and escaping local optima. The variable spiral update strategy and Cauchy mutation strategy are used to improve the follower update formula and dynamically update the target position. Through comparative analysis of experiments, the algorithm has shown significant improvements in convergence speed, convergence accuracy, probability of escaping local optima, and global search capability.
5.4. Engineering Problem Optimization Experiments
Solving practical engineering problems is one of the main applications of swarm intelligence algorithms. However, the results in test functions cannot fully reflect the application effect of the algorithm in practical problems. Engineering constraint optimization problems are widely used in various fields. Such problems usually revolve around aspects such as time, quality, and resource consumption. They optimize one or more objectives under a given engineering background while satisfying engineering constraint conditions, maximizing efficiency, minimizing costs, and balancing various indicators. This paper evaluates the practicality of OCSFO by solving four engineering problems: piston rod, three-bar truss, cantilever beam, and topology optimization.
(1) Piston Rod Optimization
The main goal of the piston rod problem is to locate the piston components H(=x1), B(=x2), D(=x3), X(=x4) by minimizing the oil volume, as shown in Figure 4 [46].
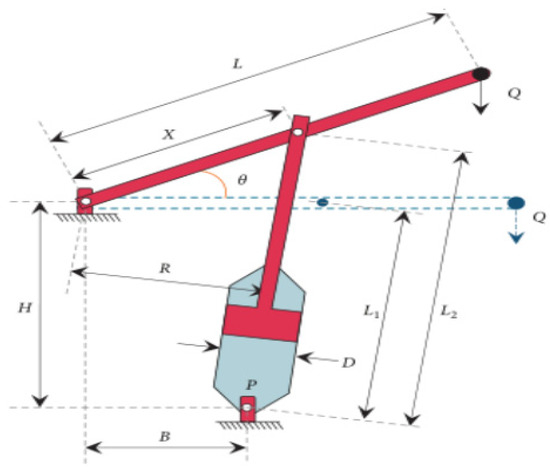
Figure 4.
Piston rod design problem.
The mathematical model of the piston rod design problem is expressed as follows:
(1) Objective Function:
(2) Constraint Conditions:
(3) Variable Range:
(4) Parameter Setting:
The optimized results are shown in Table 4.

Table 4.
Comparison of Results of Piston Rod Design Problem.
It can be seen from Table 4, Figure 5 and Figure 6 that compared with the other seven algorithms, OCSFO can find the minimum optimization result of the piston rod problem. The optimal value obtained by OCSFO for the piston rod problem is 1.0574, and the optimal solution is x = [0.05, 1.0081, 2.0162, 500].
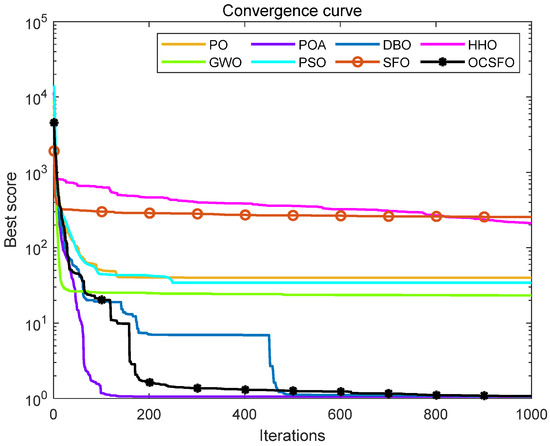
Figure 5.
Average convergence curve of piston rod design problem.
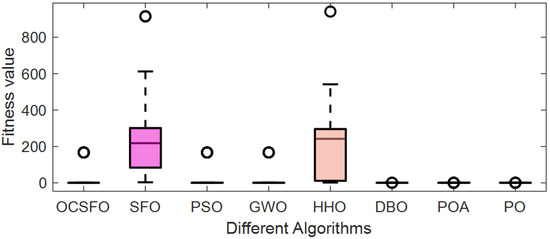
Figure 6.
Box plot of piston rod design problem.
(2) Three-Bar Truss Optimization
As shown in Figure 7, the three-bar truss design problem (TBTD) is a problem involving optimization and constraint satisfaction. In the process of solving this problem, it is necessary to adjust two key parameters S1 and S2 to achieve the minimum weight of the truss while satisfying 3 specific constraint conditions [47].
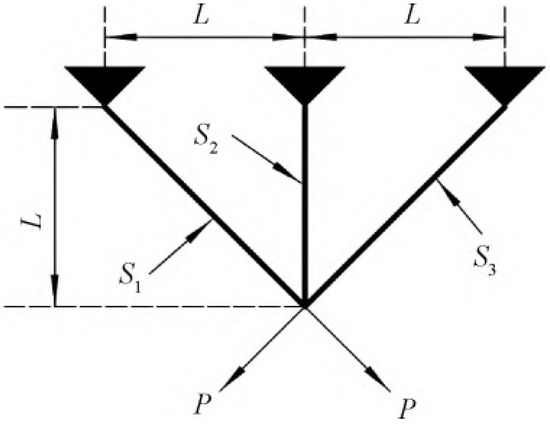
Figure 7.
Three-bar truss design problem.
The mathematical model of the three-bar truss design problem is expressed as follows:
(1) Objective Function:
(2) Constraint Conditions:
(3) Variable Range:
(4) Parameter Setting:
The optimized results are shown in Table 5.

Table 5.
Comparison of Results of Three-Bar Truss Design Problem.
It can be seen from Table 5, Figure 8 and Figure 9 that compared with the other seven algorithms, OCSFO can find a result close to the minimum optimization of the three-bar truss design problem. The optimal value obtained by OCSFO for the piston rod problem is 263.8958, and the optimal solution is s = [0.7887, 0.4082].
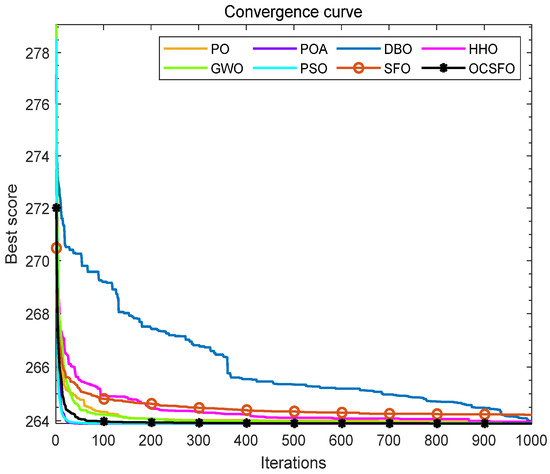
Figure 8.
Average convergence curve of three-bar truss design problem.
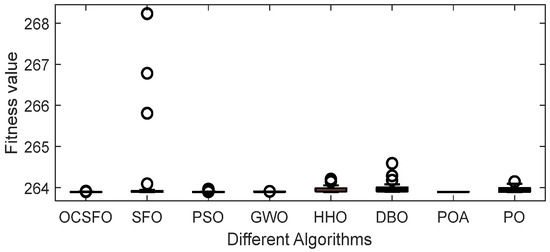
Figure 9.
Box plot of three-bar truss design problem.
(3) Cantilever Beam Optimization
The cantilever beam problem is a structural engineering design example involving the weight optimization of a rectangular-cross-section cantilever beam. One end of the beam is rigidly supported, and the free node of the cantilever is subjected to a vertical force, as shown in Figure 10. The beam consists of 5 hollow squares with a constant thickness. The height (or width) of the square is the decision variable, and the thickness remains fixed [48].
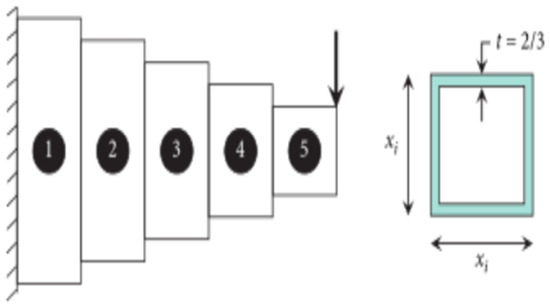
Figure 10.
Cantilever Beam Design Problem.
The mathematical model of the cantilever beam design problem is expressed as follows:
(1) Objective Function:
(2) Constraint Conditions:
(3) Variable Range:
The optimized results are shown in Table 6.

Table 6.
Comparison of Results of Cantilever Beam Design Problem.
It can be seen from Table 6, Figure 11 and Figure 12 that compared with the other seven algorithms, OCSFO can find a result close to the minimum optimization of the cantilever beam design problem. The optimal value obtained by OCSFO for the cantilever beam design problem is 1.33996, and the optimal solution is x = [6.0082, 5.3148, 4.49383, 3.5022, 2.1548].
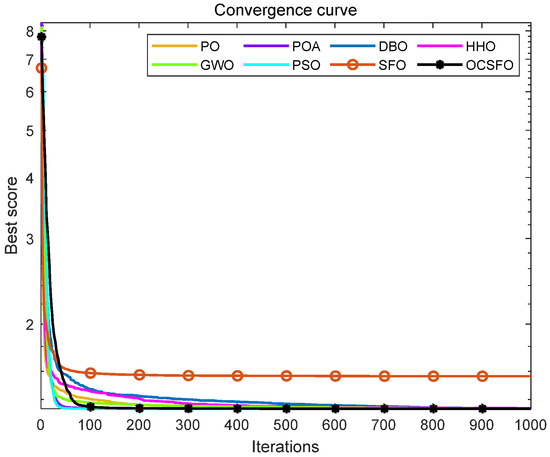
Figure 11.
Average Convergence Curve of Cantilever Beam Design Problem.
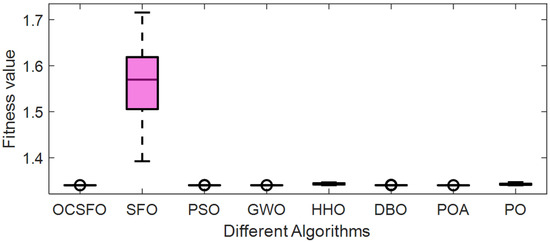
Figure 12.
Box Plot of Cantilever Beam Optimization.
(4) Topology Optimization
The main purpose of the topology optimization problem is to optimize the material layout of a set of provided loads within a given design search space and under constraint conditions related to system performance. This problem is based on the power-law method, and its mathematical model is expressed as follows [49]:
(1) Objective Function:
(2) Constraint Conditions:
(3) Variable Range:
The optimized results are shown in Table 7.

Table 7.
Comparison of Results of Topology Optimization Problem.
The average convergence curve of topology optimization problem is shown in Figure 13. The box plot of topology optimization problem is shown in Figure 14.
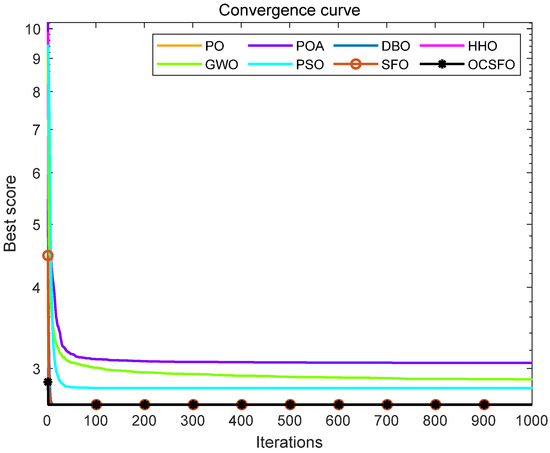
Figure 13.
Average convergence curve of topology optimization problem.
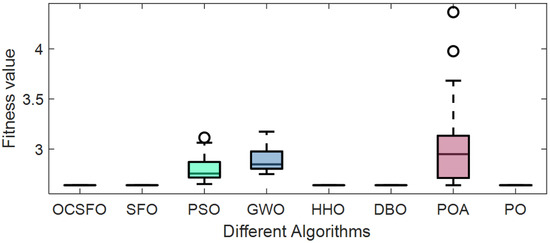
Figure 14.
Box plot of topology optimization problem.
It can be seen from Table 7, Figure 13 and Figure 14 that compared with the other seven algorithms, OCSFO can find a result close to the minimum optimization of the topology optimization problem. The optimal value obtained by OCSFO for the topology optimization problem is 2.6393.
From the comparison of four engineering application algorithms, the optimal value of the OCSFO algorithm ranks first compared to the seven comparison algorithms, indicating that OCSFO has good optimization ability in solving design problems of piston rods, three bar trusses, cantilever beams, and topology optimization. Compared with the SFO algorithm, it can be seen that the proposed OCSFO has an enhanced ability to jump out of local optima. Under the fusion of the Fishhawk and Cauchy mutation, its optimization accuracy is high, the optimization speed is fast, and the stability is strong.
6. Conclusions
The Osprey and Cauchy Mutation Integrated Sailfish Optimization Algorithm (OCSFO) proposed in this paper effectively improves and enhances the optimization performance of the Sailfish Optimization Algorithm (SFO). (1) The sailfish and sardine populations are initialized using the Logistic map. (2) The global exploration strategy of the Osprey Optimization Algorithm in the first stage is adopted during the local development phase of sailfish individual position update to enhance the global search ability of the algorithm. (3) Cauchy mutation is introduced to stimulate the activity of the sailfish and sardine populations during the prey capture stage. Through experimental verification, in the process of solving 23 classic benchmark test functions, the convergence speed, optimization accuracy, and robustness of OCSFO have been significantly improved. At the same time, the results of OCSFO in solving 4 complex engineering design optimization problems show that it has good applicability and superior solution effects in dealing with different types of practical complex optimization problems. In future research, further studies can be carried out on applying the OCSFO algorithm to multi-objective optimization problems.
Author Contributions
Conceptualization, L.C.; validation, L.C.; data curation, C.C.; writing—original draft preparation, Y.Y. writing—review and editing, Y.Y.; methodology, B.C.; software, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the Natural Science Foundation of Zhejiang Province under Grant LY23F010002, the School-level Scientific Research Project of Wenzhou university of Technology under Grant ky202403.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request. There are no restrictions on data availability.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Tian, A.Q.; Liu, F.F.; Lv, H.X. Snow Geese Algorithm: A novel migration-inspired meta-heuristic algorithm for constrained engineering optimization problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Wang, G.; Tao, J. New Trends in Symmetry in Optimization Theory, Algorithms and Applications. Symmetry 2024, 16, 284. [Google Scholar] [CrossRef]
- Zhong, R.; Yu, J.; Zhang, C.; Munetomo, M. SRIME: A strengthened RIME with Latin hypercube sampling and embedded distance-based selection for engineering optimization problems. Neural Comput. Appl. 2024, 36, 6721–6740. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, Y.; Li, J. Multi-strategy-based adaptive sine cosine algorithm for engineering optimization problems. Expert Syst. Appl. 2024, 248, 123444. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Wang, S.; Yue, Y.; Cai, S.; Li, X.; Chen, C.; Zhao, H.; Li, T. A comprehensive survey of the application of swarm intelligent optimization algorithm in photovoltaic energy storage systems. Sci. Rep. 2024, 14, 17958. [Google Scholar] [CrossRef]
- Hu, G.; Huang, F.; Chen, K.; Wei, G. MNEARO: A meta swarm intelligence optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2024, 419, 116664. [Google Scholar] [CrossRef]
- Chen, B.; Cao, L.; Chen, C.; Chen, Y.; Yue, Y. A comprehensive survey on the chicken swarm optimization algorithm and its applications: State-of-the-art and research challenges. Artif. Intell. Rev. 2024, 57, 170. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Chen, H.; Chen, Y.; Su, Z. Towards an Optimal KELM Using the PSO-BOA Optimization Strategy with Applications in Data Classification. Biomimetics 2023, 8, 306. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, T.; Yang, S.; Yan, F.; Zhao, J. Intelligent rockburst level prediction model based on swarm intelligence optimization and multi-strategy learner soft voting hybrid ensemble. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 12. [Google Scholar] [CrossRef]
- Shadravan, S.; Naji, H.R.; Bardsiri, V.K. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Rajamoorthy, R.; Arunachalam, G.; Kasinathan, P.; Devendiran, R.; Ahmadi, P.; Pandiyan, S.; Muthusamy, S.; Panchal, H.; Kazem, H.A.; Sharma, P. A novel intelligent transport system charging scheduling for electric vehicles using Grey Wolf Optimizer and Sail Fish Optimization algorithms. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 3555–3575. [Google Scholar] [CrossRef]
- Chen, C.; Cao, L.; Chen, Y.; Yue, Y. A comprehensive survey of convergence analysis of beetle antennae search algorithm and its applications. Artif. Intell. Rev. 2024, 57, 141. [Google Scholar] [CrossRef]
- Azzam, S.M.; Emam, O.E.; Abolaban, A.S. An improved Differential evolution with Sailfish optimizer (DESFO) for handling feature selection problem. Sci. Rep. 2024, 14, 13517. [Google Scholar] [CrossRef]
- Li, L.; Liu, J.; Tseng, M.L.; Lim, M.K. Accuracy of IGBT junction temperature prediction: An improved sailfish algorithm to optimize support vector machine. IEEE Trans. Power Electron. 2024, 39, 6864–6876. [Google Scholar] [CrossRef]
- Rajoriya, M.K.; Gupta, C.P. ISFO-CS: An Improved Sailfish Optimization Algorithm for Controller Selection in SDWSN. Wirel. Pers. Commun. 2025, 140, 299–331. [Google Scholar] [CrossRef]
- Peng, F.; Zhong, R.; Fan, Q.; Zhang, C.; Yu, J. Improving Sailfish Optimizer with Population Switching Strategy and Random Mutation Strategy. In Proceedings of the 2023 7th Asian Conference on Artificial Intelligence Technology (ACAIT), Piscataway, NJ, USA, 10–12 November 2023. [Google Scholar]
- Kumar, B.S.; Santhi, S.G.; Narayana, S. Sailfish optimizer algorithm (SFO) for optimized clustering in wireless sensor network (WSN). J. Eng. Des. Technol. 2022, 20, 1449–1467. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Dehrashid, A.A.; Zhang, B.; Chen, Z.; Le, B.N.; Moayedi, H. A novel swarm intelligence: Cuckoo optimization algorithm (COA) and SailFish optimizer (SFO) in landslide susceptibility assessment. Stoch. Environ. Res. Risk Assess. 2023, 37, 1717–1743. [Google Scholar] [CrossRef]
- Mohammadi, R.; Akleylek, S.; Ghaffari, A. SDN-IoT: SDN-based efficient clustering scheme for IoT using improved Sailfish optimization algorithm. PeerJ Comput. Sci. 2023, 9, e1424. [Google Scholar] [CrossRef]
- Nassef, M.G.A.; Hussein, T.M.; Mokhiamar, O. An adaptive variational mode decomposition based on sailfish optimization algorithm and Gini index for fault identification in rolling bearings. Measurement 2021, 173, 108514. [Google Scholar] [CrossRef]
- Geetha, P.; Nanda, S.J.; Yadav, R.P. A parallel chaotic sailfish optimization algorithm for estimation of DOA in wireless sensor array. Phys. Commun. 2022, 51, 101536. [Google Scholar]
- Amin, S.A.; Alqudah, M.K.S.; Almutairi, S.A.; Almajed, R.; Al Nasar, M.R.; Alkhazaleh, H.A. Optimal extreme learning machine for diagnosing brain tumor based on modified sailfish optimizer. Heliyon 2024, 10, e34050. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, K.K.; Ahmed, S.; Singh, P.K.; Geem, Z.W.; Sarkar, R. Improved binary sailfish optimizer based on adaptive β-hill climbing for feature selection. IEEE Access 2020, 8, 83548–83560. [Google Scholar] [CrossRef]
- Naji, H.R.; Shadravan, S.; Jafarabadi, H.M.; Momeni, H. Accelerating sailfish optimization applied to unconstrained optimization problems on graphical processing unit. Eng. Sci. Technol. Int. J. 2022, 32, 101077. [Google Scholar]
- Kumar, M.; Suman, S. Scheduling in iaas cloud computing environment using sailfish optimization algorithm. Trends Sci. 2022, 19, 4204. [Google Scholar] [CrossRef]
- Gutte, V.S.; Parasar, D. Sailfish invasive weed optimization algorithm for multiple image sharing in cloud computing. Int. J. Intell. Syst. 2022, 37, 4190–4213. [Google Scholar] [CrossRef]
- Al Duhayyim, M.; Malibari, A.; Dhahbi, S.; Nour, M.K.; Al-Turaiki, I.; Obayya, M.I.; Mohamed, A. Sailfish Optimization with Deep Learning Based Oral Cancer Classification Model. Comput. Syst. Sci. Eng. 2023, 45, 753–767. [Google Scholar] [CrossRef]
- Huang, H.; Yao, Z.; Wei, X.; Zhou, Y. Twin support vector machines based on chaotic mapping dung beetle optimization algorithm. J. Comput. Des. Eng. 2024, 11, 101–110. [Google Scholar] [CrossRef]
- Jawed, M.S.; Sajid, M. COBLAH: A chaotic OBL initialized hybrid algebraic-heuristic algorithm for optimal S-box construction. Comput. Stand. Interfaces 2025, 91, 103890. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Ismaeel, A.A.K.; Houssein, E.H.; Khafaga, D.S.; Abdullah Aldakheel, E.; AbdElrazek, A.S.; Said, M. Performance of osprey optimization algorithm for solving economic load dispatch problem. Mathematics 2023, 11, 4107. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P. Research on reactive power optimization based on hybrid osprey optimization algorithm. Energies 2023, 16, 7101. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, Q.; Ren, J.; Mu, X.; Wang, Z.; Shen, Q.; Zhao, W. Attack-defense strategy assisted osprey optimization algorithm for PEMFC parameters identification. Renew. Energy 2024, 225, 120211. [Google Scholar] [CrossRef]
- Alqahtani, A.H.; Fahmy, H.M.; Hasanien, H.M.; Tostado-Véliz, M.; Alkuhayli, A.; Jurado, F. Parameters estimation and sensitivity analysis of lithium-ion battery model uncertainty based on osprey optimization algorithm. Energy 2024, 304, 132204. [Google Scholar] [CrossRef]
- Somula, R.; Cho, Y.; Mohanta, B.K. SWARAM: Osprey optimization algorithm-based energy-efficient cluster head selection for wireless sensor network-based internet of things. Sensors 2024, 24, 521. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, X.; Tian, R.; Wang, W.; Jin, G. A modified osprey optimization algorithm for solving global optimization and engineering optimization design problems. Symmetry 2024, 16, 1173. [Google Scholar] [CrossRef]
- Chen, T.; Sun, Y.; Chen, H.; Deng, W. Enhanced wild horse optimizer with cauchy mutation and dynamic random search for hyperspectral image band selection. Electronics 2024, 13, 1930. [Google Scholar] [CrossRef]
- Wu, L.; Wu, J.; Wang, T. The improved grasshopper optimization algorithm with Cauchy mutation strategy and random weight operator for solving optimization problems. Evol. Intell. 2024, 17, 1751–1781. [Google Scholar] [CrossRef]
- Zaini, F.A.; Sulaima, M.F.; Razak, I.A.W.A.; Zulkafli, N.I.; Mokhlis, H. A review on the applications of PSO-based algorithm in demand side management: Challenges and opportunities. IEEE Access 2023, 11, 53373–53400. [Google Scholar] [CrossRef]
- Hatta, N.M.; Zain, A.M.; Sallehuddin, R.; Shayfull, Z.; Yusoff, Y. Recent studies on optimisation method of Grey Wolf Optimiser (GWO): A review (2014–2017). Artif. Intell. Rev. 2019, 52, 2651–2683. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Wang, X.; Wei, Y.; Guo, Z.; Wang, J.; Yu, H.; Hu, B. A sinh–cosh-enhanced DBO Algorithm applied to global optimization problems. Biomimetics 2024, 9, 271. [Google Scholar] [CrossRef] [PubMed]
- Rubavathy, A.H.; Sundar, S. Optimizing relay node selection in cooperative wireless body area networks with modified POA. Results Eng. 2024, 24, 103215. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-kenawy, E.S.M.; Abualigah, L.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Clust. Comput. 2024, 27, 5235–5283. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, H.; Wang, X.; Wang, F.; Gao, G. Multi-objective prediction and optimization of working condition parameters for piston rod cap seal in Stirling engine. J. Mech. Sci. Technol. 2024, 38, 6817–6839. [Google Scholar] [CrossRef]
- Cai, Q.; Ma, J.; Xie, Y.M.; San, B.; Zhou, Y. Topology optimization and diverse truss designs considering nodal stability and bar buckling. J. Constr. Steel Res. 2025, 224, 109128. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, A.; Li, Y.; Jin, Y. Design and optimization of piezoelectric cantilever beam vibration energy harvester. Micromachines 2022, 13, 675. [Google Scholar] [CrossRef]
- Prathyusha, A.L.R.; Babu, G.R. A review on additive manufacturing and topology optimization process for weight reduction studies in various industrial applications. Mater. Today Proc. 2022, 62, 109–117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).