Abstract
The aim of sequential recommendation (SR) is to predict a user’s next interaction by analyzing their historical behavioral sequences. The proposed framework leverages the inherent symmetry in user behavior patterns, where temporal and spectral representations exhibit complementary structures that can be harmonized for robust recommendation. Conventional SR methods predominantly utilize implicit feedback (e.g., clicks and views) as model inputs, whereby observed interactions are treated as positive instances, while unobserved ones are considered negative samples. However, the inherent randomness and diversity in user behaviors inevitably introduce noise into such implicit feedback, potentially compromising the accuracy of recommendations. Recent studies have explored noise mitigation through two primary approaches: temporal-domain methods that reweight interactions to distill clean samples for comprehensive user preference modeling, and frequency-domain techniques that purify item embeddings to reduce the propagation of noise. While temporal approaches excel in sample refinement, frequency-based methods demonstrate superior capability in learning noise-resistant representations through spectral analysis. Motivated by the desire to synergize these complementary advantages, we propose SR-DFN, a novel framework that systematically addresses noise interference through coordinated time–frequency processing. Self-guided sample purification is implemented in the temporal domain of our architecture via adaptive interaction weighting, effectively distilling behaviorally significant patterns. The refined sequence is then transformed into the frequency domain, where learnable spectral filters operate to further attenuate residual noise components while preserving essential preference signals. Drawing on the convolution theorem’s revelation regarding frequency-domain operations capturing behavioral periodicity, we critically examine conventional position encoding schemes and propose an efficient parameterization strategy that eliminates redundant positional embeddings without compromising temporal awareness. Comprehensive experiments conducted on four real-world benchmark datasets demonstrate SR-DFN’s superior performance over state-of-the-art baselines, with ablation studies validating the effectiveness of our dual-domain denoising mechanism. Our findings suggest that coordinated time–frequency processing offers a principled solution for noise-resilient sequential recommendation while challenging conventional assumptions about positional encoding requirements in spectral-based approaches. The symmetry principles underlying our dual-domain approach demonstrate how the balanced processing of temporal and frequency domains can achieve superior noise resilience.
1. Introduction
Recommender systems are a pivotal solution to information overload that have been extensively implemented across diverse platforms to predict potential user preferences from massive item catalogs. Representative applications include course recommendations in online learning ecosystems [1,2], context-aware point-of-interest recommendations for location-based services [3], and personalized product recommendations in e-commerce platforms [4]. In practical scenarios, user behaviors exhibit temporal dynamics that continuously evolve over time [5], necessitating the effective modeling of behavioral dependencies to generate appropriate suggestions, which is the core objective of sequential recommendation (SR) [6]. This capability to decipher user preference trajectories from historical interaction patterns has driven growing research interest in SR [7], positioning SR as a fundamental paradigm for temporal preference understanding.
Numerous deep neural network-based sequential recommendation models have been developed [8] to explore the temporal dynamics of user preferences. These approaches leverage two primary data types to represent interaction histories: explicit feedback (e.g., ratings or dislikes) and implicit feedback (e.g., views and clicks). Existing research mainly focuses on implicit feedback due to its abundant availability and scalability in real-world applications [9,10]. In such paradigms, observed user–item interactions are treated as positive samples, while unobserved pairs are presumed to be negative instances. However, this binary assumption introduces significant noise as a user’s non-interaction with an item may stem from exposure limitations rather than inherent disinterest, which is a critical challenge arising from the stochastic nature and behavioral diversity in implicit feedback systems. Consequently, naively optimizing recommendation models without addressing these inherent noise issues leads to suboptimal preference extraction, diminished recommendation accuracy, and degraded user satisfaction [11], highlighting the necessity of noise-aware modeling frameworks.
Some research has recognized the ubiquity of implicit feedback and its profound influence on recommendation quality and acknowledged the criticality of noise mitigation in implicit interaction data. Current denoising methodologies predominantly operate within the temporal domain and are broadly categorized into two streams: sample selection techniques [12] and sample re-weighting strategies [11,13]. The former involve the design of specialized samplers to filter out noisy interactions, while the latter dynamically assign reduced weights to high-loss instances during training, guided by the memorization effect [14]. These approaches are aligned with the frequency principle [15], through which neural networks prioritize learning low-frequency (simpler, cleaner) patterns before assimilating high-frequency (complex, potentially noisy) features. Despite their empirical success, these temporal-domain approaches overlook a critical dimension of noise propagation, i.e., the contamination introduced through high-dimensional item embedding spaces. This limitation stems from their exclusive focus on instance-level noise in interaction sequences, failing to account for latent noise amplification during the embedding learning process.
Recent advancements in frequency-domain denoising have led to the introduction of FMLP-Rec [7] and DWTRec [16], which enhance item embeddings through spectral processing to address noise in sequential recommendation. Drawing inspiration from digital signal processing principles [17], this approach leverages the Fast Fourier Transform (FFT) [18] to project input embeddings into the frequency domain, where learnable filters attenuate noise before reconstructing purified embeddings via the inverse FFT. Empirical evaluations have demonstrated FMLP-Rec’s superiority over Transformer-based baselines, underscoring its efficacy in spectral feature refinement. Although this method is effective, its exclusive focus on frequency-domain operations neglects temporal noise inherent in raw interaction sequences, potentially propagating biased signals into the embedding space. The reliance on fixed-phase reconstructions with learnable weights restricts adaptive phase alignment, limiting the model’s capacity to preserve temporal coherence during spectral denoising. The equivalence between frequency-domain filtering and circular convolution in the time domain [18] raises fundamental questions about the necessity of explicit positional encoding mechanisms in spectral architectures. These shortcomings highlight unresolved challenges in harmonizing temporal and spectral features for robust preference modeling.
Drawing on these insights, we present symmetry-aware sequential recommendation with dual-domain filtering networks, a novel hybrid framework that synergistically integrates temporal and spectral denoising mechanisms to address noise propagation in sequential recommendation systems. Our architecture first introduces a self-guided item denoising distiller that dynamically filters noisy interactions in the temporal domain, adhering to the frequency principle [15] by prioritizing low-frequency (clean) preference signals before transitioning to high-frequency noise patterns during training. The purified interaction sequence is subsequently processed through an embedding denoising encoder, which implements adaptive spectral filtering via learnable basis functions and phase-aware weights in the frequency domain to further suppress residual noise in latent representations. Additionally, we conducted a systematic investigation of the role of positional encoding within spectral architectures, challenging conventional assumptions through theoretical analysis grounded in the convolution theorem. The concept of symmetry plays a fundamental role in our approach, manifesting in two key aspects, i.e., the symmetric relationship between temporal- and frequency-domain representations of user behavior and the balanced coordination between these dual domains. This symmetry-aware design enhances the robustness of recommendations by harmonizing sequential and spectral features. Comprehensive evaluations across four benchmark datasets demonstrate SR-FDN’s significant performance gains over representative baselines, including RNN-, CNN-, and attention-based architectures as well as specialized denoising models. These results validate the necessity of coordinated time–frequency processing for robust preference modeling. The code of SR-DFN is available at https://github.com/MuziLee-x/SR-FDN, (accessed on 13 April 2025).
The main contributions of this paper are summarized as follows:
- We propose SR-DFN, a novel dual-domain denoising framework for sequential recommendation that synergistically integrates a temporal-domain item denoising distiller with a frequency-domain embedding denoising encoder. The former employs self-adaptive filtering to identify behaviorally significant interactions, while the latter operates through spectral transformations to distill noise-resistant item representations, establishing a new paradigm for implicit feedback purification.
- We integrate a multi-layered spectral processing module within the embedding denoising encoder, where each filtering layer implements parameterized spectral transformations through trainable basis functions and adaptive weights. This design enables the hierarchical refinement of item embeddings between the Fast Fourier Transform (FFT) and inverse FFT operations, effectively separating preference signals from spectral noise components.
- Through theoretical analysis grounded in the convolution theorem, we challenge the necessity of conventional positional encoding in frequency-domain recommendation architectures. Systematic ablation studies empirically substantiate that positional embeddings introduce parameter redundancy without performance benefits, providing critical insights for efficient spectral modeling.
- Extensive empirical evaluations across four benchmark datasets demonstrate SR-DFN’s consistent superiority over representative baselines spanning RNN-, CNN-, and attention-based paradigms and specialized denoising models. The quantitative results and ablation analyses jointly validate the framework’s effectiveness in cross-domain noise mitigation and preference modeling.
The organizational structure of this paper is as follows: Section 2 critically reviews the pertinent literature in sequential recommendation and noise mitigation methodologies. Section 3 formally introduces the proposed SR-DFN framework, elucidating its architectural components and theoretical underpinnings. Section 4 presents comprehensive experimental evaluations, including comparative analyses with representative baselines and ablation studies. Finally, Section 5 synthesizes key findings and outlines prospective research trajectories for dual-domain denoising in recommendation systems.
2. Related Works
This section systematically examines two critical research domains pertinent to our investigation, i.e., sequential recommendation systems that model temporal user behavior patterns and denoising recommendation methodologies addressing noise contamination in implicit feedback data. Our analysis positions these interconnected paradigms within the broader landscape of robust preference learning architectures.
2.1. Sequential Recommendation
Recommender systems (RSs) serve as critical infrastructure across diverse digital ecosystems, spanning personalized course suggestions in e-learning platforms [19] to context-aware music recommendations in e-commerce environments [3]. Within this landscape, sequential recommendation systems (SRSs) emerge as a pivotal research frontier specifically designed to capture temporal dependencies among items in behavioral sequences for the accurate prediction of subsequent user interactions [6,20]. This paradigm shift from static to dynamic preference modeling fundamentally enhances the capability to decode evolving user interests through sequential pattern analysis.
Contemporary research has led to the development of diverse methodological frameworks for sequential recommendation systems (SRSs) organized through the following interconnected paradigms, such as RNN-based architectures exemplified by GRU4Rec [21], which employs gated recurrent units to model temporal session dynamics, and CNN-based approaches such as that of Caser [22], pioneering the use of convolutional neural networks to extract localized sequential patterns. In addition, GNN-based models, including SR-GNN [23] and multimodal extensions [24], leverage graph structures to encode complex item transition dependencies. Attention-driven mechanisms span self-attention architectures [25], transformer-based designs [26], and hierarchical attention frameworks [27]. Furthermore, RL-based strategies reformulate recommendation as reinforcement learning tasks, as demonstrated in [28]. Finally, foundational methodologies such as factorized Markov chains [29] probabilistically model dynamic preference evolution. This progression reflects the field’s evolution from basic sequential pattern modeling to sophisticated behavioral dynamics captured through neural architectures.
In summary, foundational sequential recommendation approaches employ the uniform processing of sequential items, particularly RNN- and CNN-based methods, inadvertently introducing extraneous noise signals that degrade recommendation efficacy. Subsequent paradigm shifts resulted in the introduction of attention-enhanced architectures [26], which dynamically modulate interaction significance through the differential weighting of historical items. Despite demonstrating empirical improvements, these attention-based models lack explicit mechanisms for discriminating authentic preference signals from noise contamination in implicit feedback, resulting in suboptimal generalization capabilities.
2.2. Denoising Recommendation
The application of deep neural networks to model dynamic user preference evolution has gained significant traction in recommendation systems research. However, the inherent presence of noise in implicit feedback data collected from online platforms remains a persistent challenge. Deep recommendation models exhibit heightened vulnerability to overfitting on contaminated training patterns [30], and such overfitting directly compromises recommendation accuracy and generalization capabilities, as substantiated by empirical investigations [11,13]. These phenomena persist despite the theoretical advantages of deep architectures in capturing nonlinear preference dynamics, underscoring the imperative for noise-resilient modeling frameworks.
Contemporary research in recommendation system denoising is primarily characterized by three strategic paradigms: temporal-domain sample manipulation, auxiliary information integration, and spectral embedding refinement. Within the temporal domain, approaches are categorized into two subclasses: sample selection methods such as WBPR [12], which prioritizes high-confidence negative samples by probabilistically selecting missing interactions of popular items, and sample re-weighting techniques exemplified by DeCA [13], which identifies noisy interactions by minimizing knowledge graph divergence through model ensemble strategies. Parallel to these efforts, auxiliary guidance frameworks [31] enhance noise discrimination through the integration of supplementary modalities, including knowledge graphs and multimodal signals. Complementing these approaches, spectral methods such as FMLP-Rec [7] perform frequency-domain denoising via adaptive filtering of item embeddings transformed through Fourier analysis. DWTRec [16] employs the Discrete Wavelet Transform (DWT) to construct an adaptive time–frequency filter. DFT-SR [32] integrates temporal and frequency information through a timestamp embedding, effectively capturing the temporal aspects of user interactions. However, these approaches remain confined to unilateral denoising strategies; i.e., temporal methods optimize interaction sequences while neglecting spectral noise propagation, whereas spectral techniques purify embeddings without addressing raw interaction contamination. This dichotomy underscores the need for unified frameworks that address noise across both temporal and spectral dimensions.
In summary, our work establishes methodological orthogonality by synergistically integrating temporal-domain clean interaction selection with frequency-domain pure embedding learning. This dual-domain denoising paradigm represents the first framework to simultaneously address noise contamination in both raw interaction sequences and latent representation spaces, thereby introducing a previously unexplored dimension to implicit feedback purification. By bridging temporal signal refinement with spectral embedding optimization, our approach establishes a novel research trajectory for robust sequential recommendation systems.
3. Methodology
This section provides a systematic exposition of the SR-FDN architecture through three methodological pillars. First, we establish the architectural framework and formal problem formulation. Second, we elaborate on the two core architectural constituents, namely, a temporal-domain item denoising distiller for interaction purification and a frequency-domain embedding denoising encoder for spectral representation refinement. Third, we delineate the operational mechanics of the prediction layer, accompanied by computational complexity analysis.
3.1. Problem Formulation
Sequential recommendation addresses the problem of predicting the subsequent item interaction within anonymized user behavior sequences, with a specific focus on preference modeling through implicit feedback signals [9]. Formally, let denote the user set and represent the item set, where behavioral engagements (e.g., clicks) are encoded through binary indicators: if user interacted with item ; otherwise, it is 0. Each user u’s interaction history is represented as a temporal sequence , where corresponds to the t-th interaction within sequence length . Conventional sequential recommendation approaches [26,33] assume that the interaction could represent the users’ true preferences and directly fit the implicit feedback to model f with parameters in the time domain without explicit noise mitigation mechanisms.
The inherent presence of noise contamination in implicit feedback undermines conventional sequential recommendation models’ capacity to discern authentic user preferences, thereby compromising predictive accuracy. Consequently, our work addresses this challenge by developing a filter-enhanced denoising architecture to predict the -th item of potential interest to user u from noise-corrupted interaction sequences . This formulation explicitly recognizes the discrepancy between observed interactions and true preferences, necessitating dual-domain noise mitigation to recover preference signals from contaminated temporal sequences prior to spectral embedding refinement.
3.2. Model Overview
Figure 1 presents the architectural blueprint of SR-DFN, which systematically addresses noise contamination through coordinated temporal and spectral processing. The framework initiates with an item denoising distiller (IDD) that operates on raw implicit feedback sequences , performing self-guided temporal purification by identifying optimal memorization thresholds in accordance with the frequency principle [15]. This module outputs distilled interaction sequences , where spurious interactions are suppressed through adaptive dropout. The refined sequences are then processed by the embedding denoising encoder (EDE), which executes spectral refinement through three key operations, i.e., the frequency transformation of item embeddings, learnable spectral filtering with parameterized basis functions, and inverse FFT reconstruction of noise-attenuated embeddings. This dual-domain architecture enables hierarchical noise mitigation, i.e., the temporal pruning of interaction sequences followed by spectral purification of latent representations. The final prediction layer computes preference scores through the attention-weighted aggregation of denoised embeddings. The IDD and EDE modules pursue the common goal of noise suppression while functioning in complementary domains, thereby establishing structural symmetry. Subsequent sections elaborate on the technical implementation.
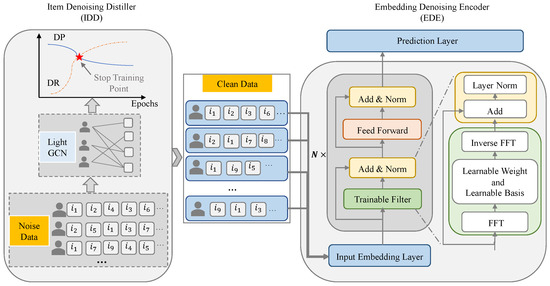
Figure 1.
The overview of SR-DFN. The proposed SR-DFN integrates dual-domain denoising mechanisms for robust sequential recommendation. The item denoising distiller (IDD) operates in the temporal domain, processing noisy implicit feedback sequences to distill purified interaction signals. The refined output of the IDD is subsequently fed into the embedding denoising encoder (EDE), which transforms the temporal sequences into the frequency domain via spectral analysis.
3.3. Item Denoising Distiller
The item denoising distiller (IDD) strategically terminates training at the critical juncture where model optimization transitions from low-frequency preference signals to high-frequency noise memorization. It is guided by the frequency principle [15], which posits that deep neural networks initially assimilate low-frequency patterns before progressively learning high-frequency components (including noise artifacts). This operational paradigm aligns with self-supervised denoising strategies discussed in [34], enabling the IDD to preserve interaction patterns corresponding to authentic user preferences while discarding high-frequency noise contaminants. The distilled outputs, representing noise-filtered temporal interactions, subsequently serve as optimized inputs for the embedding denoising encoder (EDE). Next, we introduce how our method filters the noise items in the implicit feedback and memorizes the clean interactions.
3.3.1. Recommendation Model
The principal objective of the item denoising distiller (IDD) involves training a recommendation model to dynamically identify clean interaction samples through the continuous monitoring of training dynamics. Established architectures such as NeuMF [35] and LightGCN [33] serve as viable candidates for this recommendation model, as demonstrated in prior work [34]. LightGCN [33] is highly effective at capturing high-order collaborative signals within user–item bipartite graphs. By eliminating nonlinear feature transformations, LightGCN simplifies the graph convolution network. Its inherent simplicity and strong performance make it an excellent choice for this application. Therefore, we adopted LightGCN within the IDD module to enable a focused effort on filtering noisy interactions.
LightGCN [33] employs linear propagation mechanisms over user–item interaction graphs to iteratively refine embeddings, where final representations are derived through layer-wise weighted aggregation. Formally, let and denote the trainable user and item embeddings at the initialization layer. The layer representations are computed via graph convolution:
where and represent neighbor sets, and the normalization term can avoid the scale of representations increasing with graph convolution operations. The final embedding is obtained through learnable layer combination:
with as aggregation weights. Following LightGCN [33], we set uniformly to . This design eliminates nonlinear transformations while preserving collaborative signals.
3.3.2. Model Training
Following the architectural paradigm established in LightGCN [33], we adopted the Bayesian Personalized Ranking (BPR) pairwise loss [9] to optimize model parameters, formulated as follows:
where denotes the triplet training set, represents the sigmoid function, and controls -regularization intensity. This objective function enforces positive items i to be ranked higher than negative samples j for each user u, preserving the relative preference ordering.
3.3.3. Distilling Interactions
Building upon the memorization-driven denoising framework established in [34], we define interaction as a clean sample eligible for memorization at epoch tt if it resides within the user-specific ranking list . To enhance distillation reliability, each user’s ranking list is populated with their top-k predicted items based on current model outputs. To mitigate instability inherent in single-epoch distillation, we implemented an h-epoch moving window mechanism that aggregates recent distillation outcomes. The final distilled interaction set is formally defined as follows:
where selects the most recent h epoch histories of interaction . We define an interaction memorized by the LightGCN if the majority of the recent histories coincide with the memorization state; that is, is larger than 0.5.
3.3.4. Early Stop Mechanism
Guided by the frequency principle [15], neural networks progressively assimilate low-frequency components (authentic interactions) during initial training phases before transitioning to high-frequency noise memorization. Consequently, the critical challenge for the IDD module lies in dynamically monitoring training dynamics to terminate optimization at the critical juncture when high-frequency noise assimilation commences (i.e., the inflection point where model behavior shifts from preference learning to overfitting). This operational threshold is identified through spectral analysis of loss curvature and gradient coherence metrics.
Formally, let denote the distilled interaction set at epoch t, with representing the latent true label of interaction , which is a variable obscured by implicit feedback. Following [34], we introduce two distillation metrics to monitor training dynamics:
where denotes correctly distilled interactions, and represents the ground-truth clean interaction set. As theoretical foundations suggest [15], exhibits a monotonically decreasing trend (i.e., initially capturing low-frequency clean interactions before progressively memorizing high-frequency noise). Conversely, demonstrates a monotonically increasing trajectory as the model eventually assimilates all clean patterns. The optimal equilibrium point occurs when , signifying the critical juncture where maximal clean interaction retention aligns with minimal noise contamination. This inflection point serves as the training termination threshold for the IDD module.
We formally demonstrate the monotonic evolution of and across training epochs t. Let denote the subset of memorized interactions with erroneous predictions at epoch t. By definition, the relationship among , and satisfies
Guided by the frequency principle [15], the inequality holds post model stabilization, as noise assimilation outpaces clean interaction learning. This relationship yields (7), which establishing the monotonically decreasing property of .
Conversely, the frequency principle [15] posits that clean interactions dominate early-stage learning, implying . This leads to the following:
Thus, exhibits a monotonically increasing trajectory. Collectively, these proofs confirm that decreases and increases monotonically throughout training.
The learning algorithm of the IDD is summarized in Algorithm 1.
| Algorithm 1: Learning algorithm of IDD. |
 |
3.4. Embedding Denoising Encoder
While the majority of denoising research in recommendation systems operates within the temporal domain, recent work by FMLP-Rec [7] pioneers frequency-domain denoising through spectral filtering. However, we identify two critical limitations in FMLP-Rec: (I) The convolution theorem [18] establishes that frequency-domain filtering corresponds to circular convolution in the temporal domain. This equivalence introduces parameter redundancy through circular padding artifacts, impairing model efficiency and recommendation accuracy. (II) FMLP-Rec restricts spectral adaptation to learnable amplitude weights, neglecting phase alignment optimization. This constraint inhibits the adaptive reconstruction of denoised embeddings, as phase coherence governs temporal signal preservation during inverse Fourier transforms. To address these limitations, we propose the embedding denoising encoder (EDE), depicted in Figure 1. The EDE comprises three components: an embedding layer that projects distilled interactions into latent representations; a filtering layer implementing adaptive spectral transformations with phase-aware modulation; and a prediction layer for final preference scoring. The subsequent sections detail each component’s architectural implementation.
3.4.1. Embedding Layer
The embedding layer transforms sparse, one-hot item encodings into dense, low-dimensional representations through an embedding lookup procedure. Formally, given an item sequence of length n, we construct the input embedding matrix via linear projection from the item embedding matrix . To mitigate the instability caused by stochastic initialization, we adopted the stabilization strategy from FMLP-Rec [7], applying dropout and layer normalization sequentially:
This preprocessing yields stabilized sequence representations , where dd denotes the latent dimension. The layer normalization operation ensures zero-mean and unit-variance distributions across embedding dimensions, while dropout regularizes against overfitting to spurious correlations in the initial training phase.
3.4.2. Filtering Layer
In addition to the embedding layer, we implemented hierarchical noise reduction through N cascaded filtering layers, where the output of layer k serves as input to layer . Each filtering layer comprises two core components: a filtering block that executes parameterized spectral transformations and a feed-forward network that introduces nonlinear feature interactions. This modular architecture enables the progressive refinement of item embeddings across successive layers while maintaining gradient flow through residual connections.
To attenuate noise in item embeddings, we implemented spectral filtering operations through frequency-domain transformations coupled with skip connections and layer normalization for training stabilization. Given sequence embedding , we first apply a one-dimensional Fast Fourier Transform (FFT) along the temporal axis to project embeddings into the frequency domain:
where denotes the FFT operator and represents the complex-valued spectral tensor encoding both amplitude and phase information. This transformation preserves the structural integrity of temporal patterns while enabling frequency-selective noise suppression through spectral manipulation.
To enhance the denoising efficacy of the filtering block, we modulate both the Fourier spectrum and phase components through two adaptive mechanisms: a learnable frequency filter and a learnable spectral basis . This dual modulation is formalized as follows:
where ⊙ denotes the Hadamard product. The learnable filter enables the frequency-selective attenuation of noise components, while the learnable basis facilitates adaptive phase alignment to preserve temporal coherence during signal reconstruction. This dual modulation aligns with signal processing principles, wherein phase distortions degrade temporal fidelity. Unlike conventional approaches that solely optimize amplitude spectra, this joint spectral-phase optimization empowers the model to learn arbitrary frequency-domain transformations, thereby capturing both magnitude and temporal-shift characteristics for denoising.
The modulated spectrum is transformed back to the temporal domain via an inverse Fast Fourier Transform (IFFT), reconstructing denoised sequence representations:
where denotes the IFFT operator converting complex spectral tensors into real-valued temporal embeddings. This spectral-to-temporal transformation, governed by the convolution theorem [18], effectively suppresses high-frequency noise artifacts while preserving low-frequency preference signals. The synergistic application of the FFT and IFFT operations enables hierarchical noise attenuation; that is, spectral filtering removes high-dimensional noise components, while phase-aware reconstruction maintains temporal coherence in the purified embeddings .
To conclude the filtering block operations, we adopted the stabilization techniques from SASRec [25] by integrating residual connections with dropout and layer normalization. This design mitigates gradient vanishing and enhances training stability through the following transformation:
where denotes the original input embeddings to the filtering block. The residual connection preserves raw signal integrity, while dropout regularizes high-frequency noise reintroduction during spectral reconstruction. Layer normalization ensures stable activation distributions across the transformed embeddings.
The feed-forward network (FFN) enhances model expressiveness by capturing nonlinear feature interactions through hierarchical transformations. Formally, the FFN processes filters embeddings via a two-layer perceptron:
where and denote weight matrices, and and are bias terms. To stabilize gradient flow and mitigate optimization instability, we integrate residual connections and layer normalization. This architecture enables adaptive feature recalibration while preserving information integrity through skip connections.
3.4.3. Prediction Layer
The prediction layer couples with the final output of the EDE to compute user preference scores for candidate items based on interaction history. Formally, the likelihood of item being the -th interaction is calculated as follows:
where denotes the final embedding of item , and represents the temporal position-specific output from the N-th filtering layer at timestep . Here, N corresponds to the total number of stacked filtering layers in the EDE architecture. This dot-product formulation preserves the inner-product space compatibility between user preference vectors and item embeddings while ensuring computational efficiency.
The training objective for the EDE module employs a pairwise ranking loss to optimize model parameters. For a given user u with interaction sequence , the user-specific loss is formulated as follows:
where T denotes the sequence length, represents the observed positive item at timestep , and corresponds to randomly sampled negative instances. The sigmoid function ensures the probabilistic normalization of preference score differentials. The global optimization objective aggregates losses across all users in the training set, i.e., , enforcing discriminative ranking between positive and negative interactions throughout the user population. This objective function aligns with Bayesian Personalized Ranking principles [9], prioritizing relative preference ordering over absolute score calibration.
The pseudocode for EDE is summarized in Algorithm 2.
| Algorithm 2: Learning algorithm of EDE. |
 |
3.5. Complexity Analysis
3.5.1. Model Size
The parameter composition of SR-DFN originates from two principal modules: the item denoising distiller (IDD) and the embedding denoising encoder (EDE). LightGCN [33] was adopted as the backbone recommendation model of the IDD module, and the trainable parameters are exclusively derived from item ID embeddings. This design yields a parameter-efficient architecture with total parameters quantified as , where denotes the item cardinality, and represents the embedding dimension in the IDD module. The EDE module employs a multi-layer perceptron (MLP) framework, with parameters accumulated across the embedding layer and stacked filtering layers. The total parameter count is expressed as , where denotes the embedding dimension in the EDE module; N is the number of filtering layers; and are the parameters from spectral filtering operations; and are the parameters in the feed-forward networks.
3.5.2. Time Complexity
The computational complexity analysis of SR-DFN involves the following: Assuming LightGCN [33] exhibits a baseline time complexity of , the additional computational overhead introduced by SR-DFN primarily stems from the embedding denoising encoder (EDE). The EDE’s complexity arises from two key operations, i.e., the Fast Fourier Transform (FFT) and inverse FFT with asymptotic time complexity and feed-forward networks with linear complexity , where nn denotes the sequence length. Consequently, the incremental time complexity of SR-DFN relative to LightGCN is dominated by , demonstrating favorable scalability with respect to data volume. Overall, for stacked layers N and embedding size d, the complexity of EDE becomes . Crucially, the convolution theorem [18] underpins this design by establishing mathematical equivalence between frequency-domain filtering and circular convolution in the temporal domain. This theoretical foundation enables SR-DFN to achieve global sequence modeling capabilities through spectral transformations, circumventing the locality constraints of traditional convolutional operations while maintaining computational tractability.
3.6. Relation to Previous Work
The proposed SR-DFN framework intersects with and advances two key research directions: frequency-domain denoising (FMLP-Rec [7]) and temporal-domain sample selection (SDGL [34]). We delineate their conceptual and technical distinctions as follows:
3.6.1. Differentiation from FMLP-Rec
- Dual-Domain Denoising Scope: FMLP-Rec exclusively focuses on the spectral purification of item embeddings, neglecting temporal noise in interaction sequences. In contrast, SR-DFN implements coordinated denoising through temporal interaction filtering (IDD module) and spectral embedding refinement (EDE module).
- Spectral Modulation Mechanism: While FMLP-Rec employs learnable amplitude weights, SR-DFN introduces joint amplitude–phase optimization via Equation (11), the adaptive phase alignment of which is absent in FMLP-Rec. Further analysis of the ablation experiment is given in Section 4.3.2.
- Position Encoding Efficiency: FMLP-Rec incorporates learnable positional embeddings, whereas SR-DFN eliminates this component (see Equation (9)) based on the empirical evidence of parameter redundancy (see Section 4.3.3).
3.6.2. Differentiation from SDGL
SDGL operates solely in the temporal domain through two-phase sample selection, disregarding spectral noise propagation. SR-DFN includes SDGL’s temporal distillation strategy, but this is augmented with theoretical grounding via the frequency principle [15] and complementary spectral denoising in the EDE module.
3.6.3. Integrative Innovations
SR-DFN introduces critical enhancements:
- Phase-Aware Spectral Filtering: The learnable basis in Equation (11) enables dynamic phase modulation, addressing FMLP-Rec’s phase rigidity.
- Parameter Efficiency: Ablation studies (Section 4.3.3) validate SR-DFN’s elimination of redundant positional embeddings, reducing parameters by (where denotes positional dimensions).
- Synergistic Superiority: As demonstrated in Section 4.3, SR-DFN’s performance gains stem not from isolated components but from the symbiotic integration of temporal distillation, spectral-phase optimization, and parameter-efficient design.
This holistic architecture establishes SR-DFN as a novel paradigm rather than a naive hybrid of prior works, advancing both theoretical and practical frontiers in denoising recommendation systems.
4. Experiments and Analysis
Our empirical evaluation systematically addresses four critical research questions to validate the effectiveness and innovation of SR-DFN:
- RQ1 How does SR-DFN perform compared to the representative recommendation baselines across diverse datasets?
- RQ2 What are the individual contributions of SR-DFN’s core components (the IDD and EDE) to the overall performance?
- RQ3 How does SR-DFN perform with varying noise levels and flitering numbers?
- RQ4 What are SR-DFN’s convergence properties?
To rigorously address these questions, we first delineate the experimental setup, including benchmark datasets, evaluation protocols, and baseline implementations. The subsequent sections present quantitative analyses, ablation studies, and sensitivity tests to comprehensively validate SR-DFN’s capabilities.
4.1. Experimental Settings
4.1.1. Dataset
To validate the proposed methodology, comprehensive empirical evaluations were performed across four real-world public datasets sourced from diverse application domains. We confirm full compliance with data usage policies stipulated by each dataset provider throughout our experimentation. Table 1 provides a statistical synopsis of the benchmark datasets.
- MovieLens (https://grouplens.org/datasets/movielens, accessed on January 2009.): A benchmark dataset for recommendation systems comprising user-provided movie ratings on a 1–5 scale. In our implementation, interactions with ratings below 3 were identified as noisy instances.
- MOOCCube (http://moocdata.cn/data/MOOCCube, accessed on July 2020.): An open educational dataset derived from XuetangX [36]. This repository captures fine-grained user engagement through video-watching durations spanning seconds to hours. In our implementation, interactions with viewing durations below 5 min were annotated as noisy instances.
- PEEK (https://github.com/sahanbull/PEEK-Dataset, accessed on October 2021.): An open-access dataset designed for personalized educational engagement analysis [37]. This resource annotates learner–video interactions as positive when viewing progress exceeds 75% of the video duration, with shorter engagements labeled as 0. Following established noise filtering strategies in the recommendation literature, instances labeled as 0 were treated as noise interaction.
- Yelp (https://www.yelp.com/dataset, accessed on January 2019.): A publicly available benchmark dataset for business recommendation systems, curated from establishment reviews and transaction records. Following temporal filtering protocols, we utilized interaction data with ordinal ratings below 3 annotated as noisy interactions.
We implemented data partitioning and preprocessing protocols to ensure rigorous experimental evaluation across all datasets. For each user’s interaction sequence, the first 80% of temporally ordered interactions were allocated for training, the subsequent middle 10% for validation, and the final 10% for testing. Prior to partitioning, we grouped interactions by user identifiers, sorted them chronologically in ascending order, and filtered users with fewer than five historical interactions.

Table 1.
Statistics of the datasets utilized in this work.
Table 1.
Statistics of the datasets utilized in this work.
| Dataset | #Users | #Items | Avg. Length | Sparsity |
|---|---|---|---|---|
| MovieLens | 0.9 K | 1.7 K | 96.8 | 94.1% |
| MOOCCube | 17.6 K | 32.7 K | 59.1 | 99.7% |
| PEEK | 7.2 K | 7.0 K | 7.8 | 99.8% |
| Yelp | 3.6 K | 73.1 K | 16.7 | 99.9% |
4.1.2. Evaluation Metrics
We adopted a leave-one-out evaluation protocol aligned with established practices in sequential recommendation research [34] to evaluate the recommendation efficacy of SR-DFN under implicit feedback conditions. Recommendation quality was quantified through three widely adopted metrics for top-K ranking assessment, namely, the Hit Ratio (HR@k), Normalized Discounted Cumulative Gain (NDCG@k), and Mean Reciprocal Rank (MRR), which have been widely adopted in related works [34]. Given the equivalence , we report HR@{1, 5, 10}, NDCG@{5, 10}, and MRR for comprehensive analysis. Following the negative sampling strategy in [7], each ground-truth positive item was paired with randomly sampled negative instances that the user had not interacted with, ensuring balanced evaluation under practical computational constraints.
4.1.3. Baselines
To evaluate the comparative performance of our proposed SR-DFN framework, we conducted extensive benchmarking against state-of-the-art baselines spanning five architectural paradigms, namely, RNN-based, CNN-based, attention-based, GNN-based, and denoising-based recommendation methods.
- NeuMF [35]: A state-of-the-art method that generalizes factorization machines with a multi-layer perceptron to model non-linearities.
- GRU4Rec [21]: An RNN-based model that applies GRU with ranking loss to model user behavior interactions.
- Caser [22]: A CNN-based model that uses convolutions to model the sequence information for recommendation.
- SASRec [25]: An attention-based method that utilizes a unidirectional self-attention mechanism to model the whole sequence for the sequential recommendation.
- BER4Rec [26]: A model including a deep bidirectional self-attention network to model user preference.
- SR-GNN [23]: A GNN-based method that models a session as the combination of the global preference and the current interest of that session.
- SDGL [34]: An approach that identifies informative data based on an adaptive denoising scheduler to enhance robustness.
- FMLP-Rec [7]: A new denoising method that performs item embedding denoising via an all-MLP architecture in the frequency domain.
- FEARec [38]: A novel denoising method that augments time-domain self-attention with a frequency-domain approach.
4.1.4. Implementation Details
The implementation and experimental configuration of SR-DFN were as follows: The framework was developed using PyTorch 1.4, optimized via the Adam optimizer with default momentum parameters. In the case of the IDD module, we inherited architectural components and hyperparameters (e.g., layer configurations and batch size) from LightGCN [33] to ensure fair benchmarking. The SR-FDN model underwent rigorous evaluation through iterative training cycles, with key parameters, i.e., specifically dropout rate, learning rate, batch size, and filtering layer, systematically adjusted to identify optimal configurations for each experimental scenario. Specifically, the learning rate and batch size in the EDE module were set to 0.001 and 128, respectively. We set the dropout rate of turning off neurons to 0.5 on the five datasets. We stacked three filtering layers on the MovieLens and Yelp datasets to enable the model to learn robust sequence representation. As for the MOOCCube and PEEK datasets, we stacked two filtering layers. Moreover, we set the dimensions of the item embeddings to 64 for the MovieLens, PEEK, and Yelp datasets and 128 for the MOOCCube dataset. Experiments were repeated five times with identical configurations and performance metrics averaged to mitigate stochastic variance. This ensures statistically robust comparisons against baselines.
As for the baseline methods NeuMF (https://github.com/hexiangnan/neural_collaborative_filtering, accessed on April 2017), GRU4Rec (https://github.com/hidasib/GRU4Rec, accessed on May 2016), Caser (https://github.com/graytowne/caser, accessed on February 2018), SASRec (https://github.com/kang205/SASRec, accessed on November 2018), BER4Rec (https://github.com/FeiSun/BERT4Rec, accessed on November 2019), SR-GNN (https://github.com/CRIPAC-DIG/SR-GNN, accessed on January 2019), SDGL (https://github.com/ZJU-DAILY/SGDL, accessed on July 2022), FMLP-Rec (https://github.com/RUCAIBox/FMLP-Rec, accessed on April 2022), and FEARec (https://github.com/sudaada/FEARec, accessed on July 2023), we utilized the source code released by the corresponding authors. We employed the same model structure present in the original work, including the hyperparameters, and focused on tuning the learning rate.
4.2. Overall Performance (RQ1)
The comparative performance analysis between SR-DFN and baselines across evaluation metrics is summarized in Table 2, with key observations articulated as follows:
- In general, SR-DFN demonstrates statistically significant performance advantages over all baselines across most datasets. In the case of the MovieLens dataset, SR-DFN demonstrates improvements of about 12.27% HR@10, 9.40% NDCG@10, and 7.19% MRR against the strongest baseline. With the MOOCCube dataset, SR-DFN exceeds the optimal baseline by about 1.36% for NDCG@10 and 1.31% for MRR. Using the PEEK dataset, SR-DFN demonstrates improved results by about 4.52% for HR@10, 6.45% for NDCG@10, and 6.73% for MRR compared with the best baseline, while for the Yelp dataset, SR-DFN exhibits a reduction in performance by about 4.73% in terms of NDCG@10, attributed to shorter sequence lengths.
- FEARec leads the attention-based methods, followed by FMLP-Rec, SR-GNN, and BERT4Rec. SR-DFN surpasses all three on MovieLens, MOOCCube, and PEEK, validating its dual-domain denoising efficacy. Attention mechanisms inherently perform soft denoising via relevance weighting but fail to eliminate noise propagation entirely. However, even with a small weight, the noise items may mislead model training and pass negative information to the prediction layer, thus reducing recommendation performance. More importantly, as discussed in Section 3, the denoising operation in the frequency domain enables the SR-DFN and FMLP-Rec methods to possess a global attention-like mechanism.
- In the non-attention methods, context-aware models (Caser, GRU4Rec) outperform NeuMF by capturing local sequential dependencies. However, FMLP-Rec’s spectral denoising exceeds these methods across datasets, underscoring the importance of frequency-domain purification. SR-DFN further outperforms FMLP-Rec on three datasets, confirming the necessity of coordinated time–frequency denoising. This indicates that learning robust item embeddings in the frequency domain is beneficial for improving recommendation accuracy.
- The recommendation accuracy of SR-DFN is better than that of the baseline methods in the case of datasets with long average lengths (e.g., MovieLens and MOOCCube). These results were not observed for the datasets with short average sequence lengths (e.g., Yelp). In scenarios characterized by sparse interactions and ambiguous preferences, both temporal and spectral denoising face inherent challenges: sparse interactions limit IDD’s sample purification, while short sequences hinder EDE’s ability to capture periodic patterns. On the one hand, the longer the average length of the user behavior, the more information can be utilized to capture user preferences. Based on this, it is easier for SR-DFN to distinguish between clean data and noisy data in long average length datasets, thereby improving recommendation accuracy. On the other hand, the datasets with shorter average sequences contain less user preference information, and coupled with the randomness and diversity of user behavior, it is not trivial to select the clean samples in the implicit feedback. However, the recommendation accuracy of SR-DFN on the PEEK dataset is better than that on the Yelp dataset. The reason is that in PEEK, the user’s short-term learning objective (preference) is explicit, which reduces the behavior’s randomness.

Table 2.
Performance comparison of SR-DFN versus baselines across datasets. Bold values indicate the highest scores.
Table 2.
Performance comparison of SR-DFN versus baselines across datasets. Bold values indicate the highest scores.
| MovieLens | HR@1 | HR@5 | HR@10 | NDCG@5 | NDCG@10 | MRR |
| NeuMF | 0.1256 | 0.3875 | 0.5230 | 0.2503 | 0.3081 | 0.2510 |
| GRU4Rec | 0.1382 | 0.3914 | 0.5335 | 0.2673 | 0.3136 | 0.2643 |
| Caser | 0.1305 | 0.3903 | 0.5300 | 0.2537 | 0.3098 | 0.2586 |
| SASRec | 0.1774 | 0.4401 | 0.5989 | 0.3033 | 0.3569 | 0.2998 |
| BERT4Rec | 0.2020 | 0.5127 | 0.6226 | 0.3681 | 0.3681 | 0.3441 |
| SR-GNN | 0.1502 | 0.3804 | 0.5021 | 0.2716 | 0.3205 | 0.2733 |
| SDGL | 0.2104 | 0.5261 | 0.6413 | 0.3844 | 0.4092 | 0.3447 |
| FMLP-Rec | 0.2233 | 0.5352 | 0.6559 | 0.3871 | 0.4267 | 0.3699 |
| FEARec | 0.2304 | 0.5590 | 0.7058 | 0.4056 | 0.4548 | 0.3892 |
| SR-DFN | 0.2394 | 0.5775 | 0.7364 | 0.4153 | 0.4668 | 0.3965 |
| MOOCCube | HR@1 | HR@5 | HR@10 | NDCG@5 | NDCG@10 | MRR |
| NeuMF | 0.3510 | 0.5411 | 0.6814 | 0.4095 | 0.4572 | 0.3910 |
| GRU4Rec | 0.6519 | 0.7504 | 0.7671 | 0.7006 | 0.7332 | 0.6888 |
| Caser | 0.6496 | 0.7529 | 0.7711 | 0.7001 | 0.7287 | 0.6902 |
| SASRec | 0.7757 | 0.8364 | 0.8610 | 0.8223 | 0.8381 | 0.8210 |
| BERT4Rec | 0.8006 | 0.9174 | 0.9333 | 0.8597 | 0.8746 | 0.8341 |
| SR-GNN | 0.6701 | 0.7718 | 0.7900 | 0.7345 | 0.7519 | 0.6948 |
| SDGL | 0.8090 | 0.9027 | 0.9218 | 0.8714 | 0.8893 | 0.8775 |
| FMLP-Rec | 0.8445 | 0.9289 | 0.9454 | 0.8924 | 0.8977 | 0.8841 |
| FEARec | 0.8503 | 0.9333 | 0.9495 | 0.9006 | 0.9091 | 0.8900 |
| SR-DFN | 0.8549 | 0.9430 | 0.9579 | 0.9051 | 0.9099 | 0.8957 |
| PEEK | HR@1 | HR@5 | HR@10 | NDCG@5 | NDCG@10 | MRR |
| NeuMF | 0.0822 | 0.2007 | 0.2864 | 0.1839 | 0.2248 | 0.2131 |
| GRU4Rec | 0.1031 | 0.2546 | 0.3323 | 0.2169 | 0.2471 | 0.2138 |
| Caser | 0.3719 | 0.5550 | 0.5879 | 0.4549 | 0.4856 | 0.4513 |
| SASRec | 0.3892 | 0.5596 | 0.5930 | 0.4684 | 0.4921 | 0.4660 |
| BERT4Rec | 0.3217 | 0.5301 | 0.5634 | 0.4417 | 0.4792 | 0.4368 |
| SR-GNN | 0.3171 | 0.5106 | 0.5401 | 0.4508 | 0.4816 | 0.4463 |
| SDGL | 0.3622 | 0.5204 | 0.5731 | 0.4665 | 0.4891 | 0.4602 |
| FMLP-Rec | 0.3953 | 0.5436 | 0.5978 | 0.4754 | 0.4929 | 0.4710 |
| FEARec | 0.4117 | 0.5648 | 0.6006 | 0.4814 | 0.5198 | 0.4989 |
| SR-DFN | 0.4281 | 0.5788 | 0.6248 | 0.5099 | 0.5247 | 0.5027 |
| Yelp | HR@1 | HR@5 | HR@10 | NDCG@5 | NDCG@10 | MRR |
| NeuMF | 0.1846 | 0.5302 | 0.6863 | 0.3527 | 0.4190 | 0.3458 |
| GRU4Rec | 0.2053 | 0.5437 | 0.7265 | 0.3784 | 0.4375 | 0.3630 |
| Caser | 0.2188 | 0.5111 | 0.6661 | 0.3696 | 0.4198 | 0.3595 |
| SASRec | 0.2375 | 0.5745 | 0.7373 | 0.4113 | 0.4642 | 0.3927 |
| BERT4Rec | 0.2405 | 0.5976 | 0.7597 | 0.4252 | 0.4778 | 0.4026 |
| SR-GNN | 0.2176 | 0.5442 | 0.7096 | 0.3860 | 0.4395 | 0.3711 |
| SDGL | 0.2569 | 0.5870 | 0.7005 | 0.4552 | 0.4760 | 0.4002 |
| FMLP-Rec | 0.3312 | 0.6363 | 0.7268 | 0.6363 | 0.5227 | 0.4664 |
| FEARec | 0.3321 | 0.6377 | 0.7278 | 0.6227 | 0.5117 | 0.4454 |
| SR-DFN | 0.2884 | 0.6180 | 0.7283 | 0.4621 | 0.4980 | 0.4340 |
4.3. Influence of Components (RQ2)
To systematically evaluate the contributions of SR-DFN’s core components, we conducted ablation studies through three architectural variants:
- SR-DFN_1: A truncated architecture retaining only frequency-domain operations by implementing Fourier basis modulation (Equation (11)) and omitting positional encoding. This variant disregards temporal-domain item denoising, isolating the impact of spectral processing.
- SR-DFN_2: A temporal-domain specialization that preserves IDD-based item denoising but removes spectral filtering (learnable basis in Equation (11)). This configuration evaluates temporal purification efficacy.
- SR-DFN_3: A hybrid model integrating temporal denoising, spectral filtering, and learnable positional encoding to assess encoding redundancy claims.
Figure 2, Figure 3, Figure 4 and Figure 5 present the comparative performance of these variants across datasets.
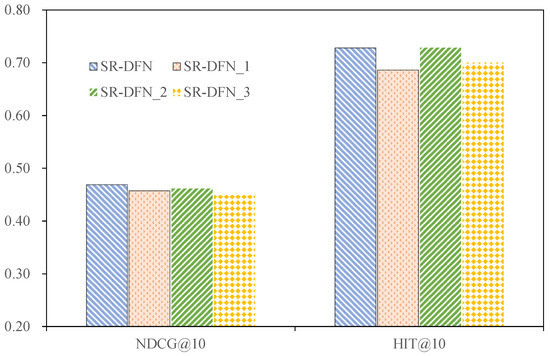
Figure 2.
The performance of SR-DFN and its different variants on the MovieLens dataset.
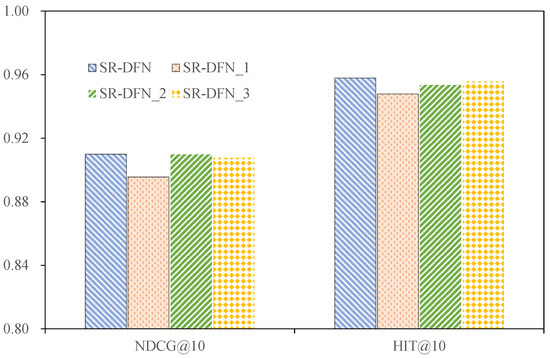
Figure 3.
The performance of SR-DFN and its different variants on the MOOCCube dataset.
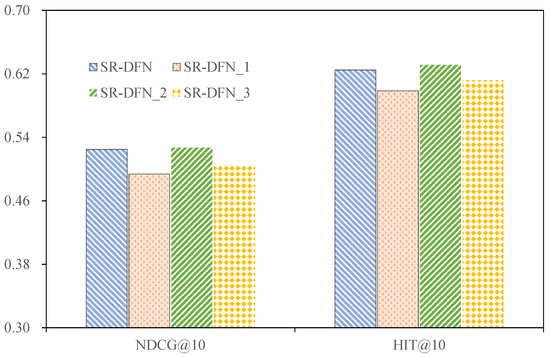
Figure 4.
The performance of SR-DFN and different variants of SR-DFN on the PEEK dataset.
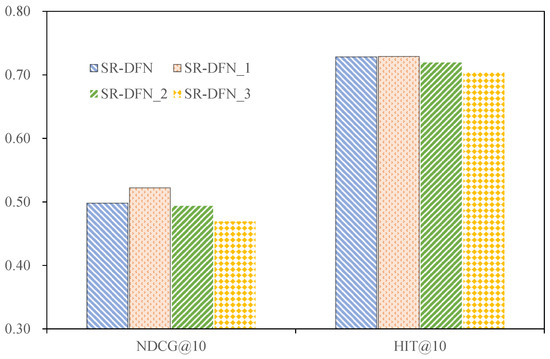
Figure 5.
The performance of SR-DFN and different variants of SR-DFN on the Yelp dataset.
4.3.1. Utility of IDD
The ablation study reveals critical insights into the IDD module’s contribution across datasets. Removing the IDD induces performance degradation on MovieLens (NDCG@10 ↓2.56%), MOOCCube (NDCG@10 ↓1.60%), and PEEK (NDCG@10 ↓6.30%), underscoring its efficacy in temporal-domain noise suppression. However, on Yelp—a dataset characterized by ambiguous preferences across a large item pool—the IDD reduces NDCG@10 by 4.60%. This divergence stems from two factors:
- Behavioral Ambiguity: Yelp’s sparse interactions (avg. sequence length = 16.7) amplify randomness, diminishing the IDD’s ability to discern clean patterns.
- Explicit Learning Context: PEEK’s explicit, short-term learning objectives mitigate behavioral noise despite comparable sequence lengths (avg. = 7.8), enabling effective IDD operation.
While the IDD generally enhances recommendation fidelity, its efficacy is contingent on dataset-specific interaction characteristics. This observation motivates future investigations into adaptive temporal denoising thresholds based on sequence sparsity.
4.3.2. Utility of Fourier Basis
The ablation analysis of the learnable Fourier basis reveals critical performance impacts across datasets. Disabling this component in SR-DFN_2 induces measurable degradation: NDCG@10 decreases by 1.6% on MovieLens and 0.91% on Yelp compared to the full SR-DFN model while maintaining parity on MOOCCube and PEEK. This divergence stems from the Fourier basis’s role in enabling adaptive phase alignment, which enhances spectral denoising flexibility by jointly optimizing amplitude and phase components. Such optimization stabilizes preference signal reconstruction during inverse FFT operations, which is crucial for datasets with complex temporal dynamics (e.g., MovieLens’s long sequences and Yelp’s sparse interactions).
These empirical results validate the theoretical motivation outlined in Section 1, that is, the concept that phase-aware spectral filtering is essential for disentangling noise from authentic preferences in frequency-domain representations. The retained performance on MOOCCube and PEEK suggests domain-specific robustness where behavioral patterns exhibit stronger periodicity or lower noise variance, reducing phase sensitivity. These results empirically substantiate that the joint amplitude–phase optimization in Equation (11) outperforms amplitude-only filtering.
4.3.3. Utility of Position Encoding
The empirical evidence demonstrates that integrating learnable positional encoding into SR-DFN adversely impacts recommendation accuracy across all benchmark datasets. Quantitatively, the inclusion of positional encoding reduces NDCG@10 by 4.41% (MovieLens), 0.24% (MOOCCube), 3.98% (PEEK), and 6.16% (Yelp). This degradation stems from two interrelated factors:
- Parameter Redundancy: Positional embeddings introduce unnecessary parameters in frequency-domain architectures, contradicting the convolution theorem [18], which inherently encodes temporal relationships through spectral transformations.
- The added parameters amplify model complexity, increasing susceptibility to overfitting on noise-contaminated implicit feedback.
This demonstrates that the implicit periodicity of circular convolution suffices for temporal modeling, while explicit embeddings disrupt frequency-domain coherence.
4.4. Hyperparameter Study (RQ3)
A systematic analysis of two critical hyperparameters influencing SR-DFN’s performance (i.e., the depth of filtering layers in the spectral processing module and the dimensionality of item embeddings) was conducted. Experimental outcomes are presented in Table 3 (filtering layer analysis) and Table 4 (embedding dimension analysis). To quantify model robustness under parameter variation conditions, we computed the standard deviation of each evaluation metric across hyperparameter configurations, where lower values indicate greater stability.

Table 3.
The performance of SR-DFN concerning the different number of the learnable filtering layers on the four datasets. Notably, the results of Yelp datasets are based on the variant of SR-DFN ignoring the item-level denoising.

Table 4.
The performance of SR-DFN concerning different settings of the embedding size on the four datasets. Notably, the results of Yelp datasets are based on the variant of SR-DFN ignoring the item-level denoising in the time domain.
4.4.1. The Filtering Number
The hyperparameter sensitivity analysis in Table 3 reveals critical insights into the impact of filtering layer depth on SR-DFN’s performance. When configured with a single filtering layer (), SR-DFN exhibits suboptimal performance across all datasets, attributable to insufficient hierarchical refinement for disentangling noise from spectral embeddings. Incrementing NN enhances recommendation accuracy, with optimal results achieved at for MovieLens (NDCG@10: 0.742) and for MOOCCube (NDCG@10: 0.681), demonstrating the necessity of dataset-specific architectural configurations. Beyond these optima (), performance plateaus or marginally degrades (MovieLens NDCG@10: −0.8% at ), suggesting over-smoothing or overfitting risks from excessive spectral transformations.
This behavior aligns with the spectral bias of deep networks—shallow architectures underfit high-frequency noise patterns, while overly deep models overfit to training artifacts. The dataset-dependent optimal NN underscores the interplay between sequence complexity (e.g., MovieLens’s long-term dependencies) and spectral processing depth. These findings emphasize the importance of balancing denoising granularity with model parsimony, motivating future research into adaptive layer selection mechanisms for diverse recommendation scenarios.
4.4.2. The Embedding Size
The analysis of embedding dimensionality impacts in Table 4 reveals dataset-specific optimization requirements. SR-DFN achieves peak performance with an embedding dimension of 64 across most datasets, while MOOCCube necessitates a larger dimensionality of 128 to accommodate its higher interaction complexity. This divergence stems from a critical trade-off: insufficient dimensionality (e.g., ) constrains the model’s capacity to capture nuanced preference patterns, whereas excessive dimensions (e.g., ) introduce parameter redundancy, amplifying overfitting risks on noise-contaminated interactions.
Robustness metrics further demonstrate SR-DFN’s stability across configurations, with standard deviations for all evaluation metrics across embedding sizes. This low variance underscores the framework’s resilience to dimensional scaling, maintaining consistent performance despite parametric variations. The observed stability arises from SR-DFN’s dual-domain architecture, which inherently regularizes embeddings through coordinated temporal purification and spectral refinement, mitigating overfitting while preserving generalization capability.
4.5. Convergence Analysis (RQ4)
To examine the convergence properties of SR-DFN, we analyzed its training dynamics with optimized hyperparameter configurations. The modular architecture operates through two coordinated phases: the item denoising distiller (IDD) distills clean interactions from implicit feedback, while the embedding denoising encoder (EDE) learns purified item embeddings from the refined sequences. We tracked the EDE module’s training loss alongside testing metrics (HR@5, NDCG@5, MRR) across four datasets, as illustrated in Figure 6, Figure 7, Figure 8 and Figure 9. From these figures, we can see that the training process of SR-DFN can converge in about 40, 50, 70, and 100 rounds for MovieLens, MOOCCUbe, PEEK, and Yelp datasets, respectively.
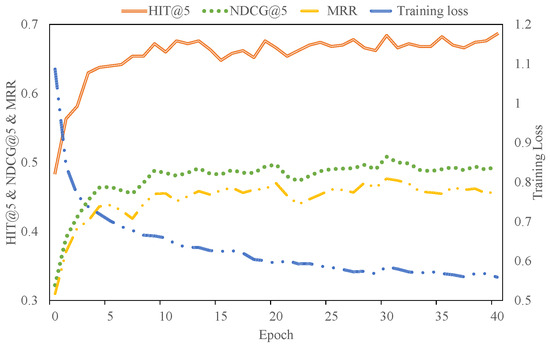
Figure 6.
Testing metrics (HIT@5, NDCG@5, and MRR) and the training loss of our approach for the MovieLens dataset with the increase in epochs.
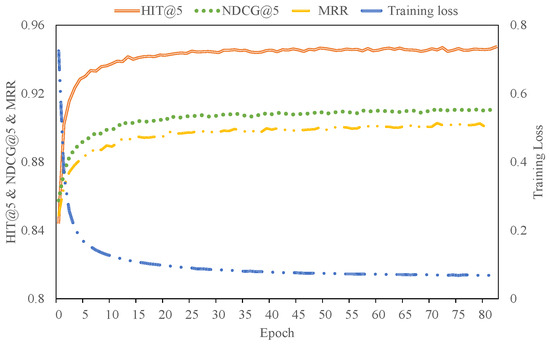
Figure 7.
Testing metrics (HIT@5, NDCG@5, and MRR) and the training loss of our approach for the MOOCCube dataset with the increase in epochs.
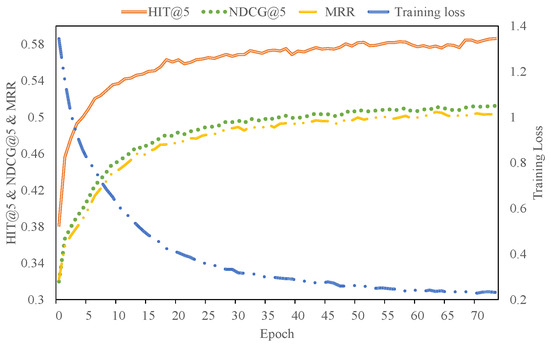
Figure 8.
Testing metrics (HIT@5, NDCG@5, and MRR) and the training loss of our approach for the PEEK dataset with the increase in epochs.
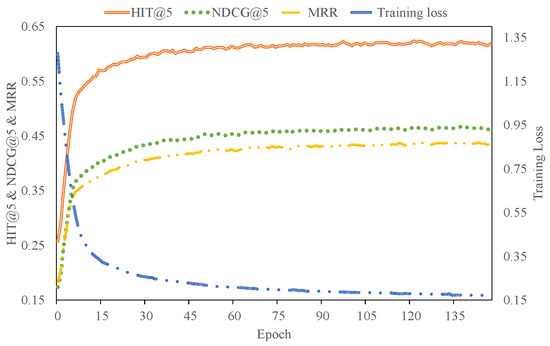
Figure 9.
Testing metrics (HIT@5, NDCG@5, and MRR) and the training loss of our approach for the Yelp dataset with the increase in epochs.
These results demonstrate SR-DFN’s capacity to efficiently assimilate training signals while suppressing noise propagation through hierarchical spectral filtering. The progressive attenuation of training loss correlates with metric improvements, validating the framework’s dual-phase denoising efficacy. The extended convergence duration for Yelp aligns with its shorter average sequence length and higher noise prevalence, necessitating extended optimization cycles to disentangle sparse preference signals. This empirical validation confirms that SR-DFN’s stacked filtering layers effectively balance model capacity with noise resilience.
4.6. Limitations
Frequency-domain processing inherently discards explicit positional information; however, our research outcomes challenge the conventional belief regarding the necessity of positional encoding in spectral methods. Through the theoretical analysis presented in Section 4.3.3, we have verified that circular convolution operations during frequency-domain filtering can implicitly maintain sequence order, thereby rendering explicit positional embeddings seemingly unnecessary.
This discovery opens up a new research avenue: devising frequency-compatible positional encoding mechanisms that harmonize with spectral transformations while preventing excessive parameter growth. Possible strategies include phase modulation or the introduction of frequency-bin-specific positional biases, which may strike a balance between preserving temporal order and ensuring spectral efficiency. Since this exploration extends beyond the current study’s focus on dual-domain denoising, we plan to pursue it in future research.
Additionally, we recognize the potential significance of absolute and relative positions in non-periodic sequences. In upcoming investigations, we aim to conduct in-depth analyses, potentially integrating concepts from information theory and signal processing to precisely define the role of positional embeddings in frequency-domain-based recommendation models. Moreover, we intend to combine adaptive spectral thresholds with auxiliary signals, such as temporal intervals, to address noise separation in non-periodic situations for sparse datasets.
5. Conclusions
In this work, we presented SR-DFN, which simultaneously denoises implicit feedback through coordinated denoising in both the time and frequency domains. To perform item-level denoising, a model-agnostic item denoising distiller selects the clean interactions in the time domain in a self-guided manner. Then, an embedding denoising encoder incorporating learnable filters and a trainable basis in the frequency domain attenuates noise information to extract purer user preferences. The experimental results confirm our insights that the item position encoding in the embedding denoising encoder is parameter-redundant and degrades the recommendation performance. One merit of SR-DFN is that the item denoising distiller and the embedding denoising encoder are decoupled, which opens up the research space of denoising implicit feedback for sequential recommendations. Experiments on four real-world datasets showed that our SR-DFN achieves competitive recommendation accuracy compared with several representative recommended methods. The symmetry principles underlying our dual-domain approach demonstrated their effectiveness in balancing temporal sequence processing with spectral analysis, leading to more robust recommendation performance.
In future work, we intend to advance SR-DFN in the following directions: Following the frequency principle [15], a valuable contribution would be to explore a better stop training mechanism with additional information. The learnable item position encoding leads to parameter redundancy, resulting in the degradation of recommendation performance. However, the item position information is lost when sequential recommendations are performed in the frequency domain. Accordingly, we will consider introducing position information for the sequential recommendation in the frequency domain, such as modeling coarse-grained position information in the form of a sliding window. In addition, future work should explore additional applications of symmetry principles in recommendation systems, particularly in the context of graph-based methods where structural symmetries in user–item interactions could be exploited for more efficient and accurate recommendations.
Author Contributions
Conceptualization, L.L., Y.D. and Y.W.; methodology, L.L. and Y.W.; software, L.L.; validation, Y.D. and Y.W.; formal analysis, L.L.; investigation, Y.D.; resources, L.L.; data curation, Y.W.; writing—original draft preparation, L.L.; writing—review and editing, Y.D.; visualization, Y.W.; supervision, L.L.; project administration, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shenzhen Polytechnic University Research Fund (grant number 6025310014K).
Data Availability Statement
The repository for MovieLens is publicly available at https://grouplens.org/datasets/movielens, accessed on January 2009, while MOOCCube can be accessed through http://moocdata.cn/data/MOOCCube, accessed on July 2020. The Dataset PEEK has been archived at https://github.com/sahanbull/PEEK-Dataset, accessed on October 2021, and Yelp is maintained in the repository located at https://www.yelp.com/dataset, accessed on January 2019.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| RSs | Recommender Systems |
| SR | Sequential Recommendation |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fast Fourier Transform |
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| GNN | Graph Neural Network |
| FFN | Feed-forward Network |
| IDD | Item Denoising Distiller |
| EDE | Embedding Denoising Encoder |
| HR | Hit Ratio |
| NDCG | Normalized Discounted Cumulative Gain |
| MRR | Mean Reciprocal Rank |
References
- Alhwayzee, A.; Araban, S.; Zabihzadeh, D. A Robust Recommender System Against Adversarial and Shilling Attacks Using Diffusion Networks and Self-Adaptive Learning. Symmetry 2025, 17, 233. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Huang, Z. A Path-Planning Method Recommended for Multi-UAV Police Patrols Based on the Wolf Pack Optimization Algorithm Using CDRS and DRSS. Symmetry 2025, 17, 208. [Google Scholar] [CrossRef]
- Han, P.; Li, Z.; Liu, Y.; Zhao, P.; Li, J.; Wang, H.; Shang, S. Contextualized Point-of-Interest Recommendation. In Proceedings of the the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020. [Google Scholar] [CrossRef]
- Wu, C.; Yuan, H.; Zhao, P.; Qu, J.; Sheng, V.S.; Liu, G. Dual-Supervised Contrastive Learning for Bundle Recommendation. IEEE Trans. Comput. Soc. Syst. 2023, 11, 3955–3965. [Google Scholar] [CrossRef]
- Liangming, P.; Chengjiang, L.; Juanzi, L.; Jie, T. Prerequisite relation learning for concepts in moocs. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Vancouver, BC, Canada, 30 July–4 August 2017; pp. 1447–1456. [Google Scholar] [CrossRef]
- Wang, S.; Cao, L.; Wang, Y.; Sheng, Q.Z.; Orgun, M.A.; Lian, D. A survey on session-based recommender systems. ACM Comput. Surv. CSUR 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Zhou, K.; Yu, H.; Zhao, W.X.; Wen, J.R. Filter-enhanced MLP is all you need for sequential recommendation. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 2388–2399. [Google Scholar] [CrossRef]
- Qiu, R.; Huang, Z.; Yin, H.; Wang, Z. Contrastive learning for representation degeneration problem in sequential recommendation. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Tempe, AZ, USA, 21–25 February 2022; pp. 813–823. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the UAI ’09 Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- Du, Y.; Zhu, X.; Chen, L.; Zheng, B.; Gao, Y. HAKG: Hierarchy-Aware Knowledge Gated Network for Recommendation; ACM: New York, NY, USA, 2022; pp. 1390–1400. [Google Scholar] [CrossRef]
- Wang, W.; Feng, F.; He, X.; Nie, L.; Chua, T.S. Denoising implicit feedback for recommendation. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual, 8–12 March 2021; pp. 373–381. [Google Scholar] [CrossRef]
- Gantner, Z.; Drumond, L.; Freudenthaler, C.; Schmidt-Thieme, L. Personalized ranking for non-uniformly sampled items. In Proceedings of the KDD Cup 2011, PMLR, San Diego, CA, USA, 21 August 2011; pp. 231–247. [Google Scholar]
- Wang, Y.; Xin, X.; Meng, Z.; Jose, J.M.; Feng, F.; He, X. Learning Robust Recommenders through Cross-Model Agreement. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 2015–2025. [Google Scholar] [CrossRef]
- Arpit, D.; Jastrzebski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A closer look at memorization in deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 233–242. [Google Scholar]
- Xu, Z.Q.J.; Zhang, Y.; Luo, T. Overview frequency principle/spectral bias in deep learning. Commun. Appl. Math. Comput. 2024, 7, 827–864. [Google Scholar] [CrossRef]
- Lu, S.; Ge, M.; Zhang, J.; Zhu, W.; Li, G.; Gu, F. Filtering with Time-frequency Analysis: An Adaptive and Lightweight Model for Sequential Recommender Systems Based on Discrete Wavelet Transform. arXiv 2025, arXiv:2503.23436. [Google Scholar]
- D’Antona, G.; Ferrero, A. Digital Signal Processing for Measurement Systems: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Soliman, S.S.; Srinath, M.D. Continuous and discrete signals and systems. In Englewood Cliffs; Pearson: London, UK, 1990. [Google Scholar]
- Wang, S.; Gong, J.; Wang, J.; Feng, W.; Peng, H.; Tang, J.; Yu, P.S. Attentional Graph Convolutional Networks for Knowledge Concept Recommendation in MOOCs in a Heterogeneous View. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 79–88. [Google Scholar] [CrossRef]
- Ma, C.; Ma, L.; Zhang, Y.; Sun, J.; Liu, X.; Coates, M. Memory augmented graph neural networks for sequential recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5045–5052. [Google Scholar] [CrossRef]
- Jannach, D.; Ludewig, M. When Recurrent Neural Networks meet the Neighborhood for Session-Based Recommendation. In Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, 27–31 August 2017; pp. 306–310. [Google Scholar] [CrossRef]
- Tang, J.; Wang, K. Personalized Top-N Sequential Recommendation via Convolutional Sequence Embedding. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Los Angeles, CA, USA, 5–9 February 2018; pp. 565–573. [Google Scholar] [CrossRef]
- Wu, S.; Tang, Y.; Zhu, Y.; Wang, L.; Xie, X.; Tan, T. Session-based Recommendation with Graph Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 346–353. [Google Scholar] [CrossRef]
- Liu, K.; Xue, F.; Li, S.; Sang, S.; Hong, R. Multimodal hierarchical graph collaborative filtering for multimedia-based recommendation. IEEE Trans. Comput. Soc. Syst. 2022, 11, 216–227. [Google Scholar] [CrossRef]
- Kang, W.C.; McAuley, J. Self-Attentive Sequential Recommendation. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 197–206. [Google Scholar] [CrossRef]
- Sun, F.; Liu, J.; Wu, J.; Pei, C.; Lin, X.; Ou, W.; Jiang, P. BERT4Rec: Sequential Recommendation with Bidirectional Encoder Representations from Transformer. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1441–1450. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Wu, M.; Xu, Y.; Zhao, H.; Huang, P.; Kang, G.; Chen, Q.; Li, W.; Lee, D.L. Multi-interest network with dynamic routing for recommendation at Tmall. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 2615–2623. [Google Scholar] [CrossRef]
- Xin, X.; Karatzoglou, A.; Arapakis, I.; Jose, J.M. Self-supervised reinforcement learning for recommender systems. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 931–940. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Schmidt-Thieme, L. Factorizing Personalized Markov Chains for Next-Basket Recommendation. In Proceedings of the 19th International Conference on World Wide Webe, Raleigh, NC, USA, 26–30 April 2010; pp. 811–820. [Google Scholar] [CrossRef]
- Caruana, R.; Lawrence, S.; Giles, C. Overfitting in neural nets: Backpropagation, conjugate gradient, and early stopping. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; Volume 13. [Google Scholar]
- Bian, Z.; Zhou, S.; Fu, H.; Yang, Q.; Sun, Z.; Tang, J.; Liu, G.; Liu, K.; Li, X. Denoising user-aware memory network for recommendation. In Proceedings of the Fifteenth ACM Conference on Recommender Systems, Amsterdam, The Netherlands, 27 September–1 October 2021; pp. 400–410. [Google Scholar] [CrossRef]
- Luo, S.; Chen, J.; Yu, T.; Dong, S.; Jiang, G.; Ding, N. Dual Frequency-based Temporal Sequential Recommendation. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar] [CrossRef]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 639–648. [Google Scholar] [CrossRef]
- Gao, Y.; Du, Y.; Hu, Y.; Chen, L.; Zhu, X.; Fang, Z.; Zheng, B. Self-Guided Learning to Denoise for Robust Recommendation; ACM: New York, NY, USA, 2022; pp. 1412–1422. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar] [CrossRef]
- Yu, J.; Luo, G.; Xiao, T.; Zhong, Q.; Wang, Y.; Feng, W.; Luo, J.; Wang, C.; Hou, L.; Li, J.; et al. MOOCCube: A large-scale data repository for NLP applications in MOOCs. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Virtual, 5–10 July 2020; pp. 3135–3142. [Google Scholar] [CrossRef]
- Bulathwela, S.; Perez-Ortiz, M.; Novak, E.; Yilmaz, E.; Shawe-Taylor, J. PEEK: A Large Dataset of Learner Engagement with Educational Videos. arXiv 2021, arXiv:2109.03154. [Google Scholar]
- Du, X.; Yuan, H.; Zhao, P.; Qu, J.; Zhuang, F.; Liu, G.; Liu, Y.; Sheng, V.S. Frequency enhanced hybrid attention network for sequential recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 23–27 July 2023; pp. 78–88. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).