Robust Load Frequency Control in Hybrid Microgrids Using Type-3 Fuzzy Logic Under Stochastic Variations
Abstract
1. Introduction
- Firstly, although type-1 and type-2 fuzzy logic controllers have been extensively studied in the literature, a type-3 fuzzy logic controlled load frequency control (LFC) mechanism has not been thoroughly investigated in microgrid systems. Our study presents a novel method that utilizes type-3 fuzzy logic to more effectively model uncertainties and enhance system stability.
- Furthermore, in contrast to the microgrid analyses in the literature, which are usually performed under deterministic (fixed) conditions, this study allows for stochastic modeling and analysis of wind speed, solar radiation, and load variations, thus contributing to a more comprehensive understanding of the impact of real-world uncertainties on microgrid systems and to the evaluation of the dynamic performance of the system.
- This study involves the testing of various combinations of energy sources and storage systems utilized within the microgrid. This is achieved by analyzing the contributions of BESS, DG, FC, and FW to system stability across five distinct scenarios. Additionally, a comprehensive evaluation of disparate energy management strategies is conducted. This comprehensive approach has the potential to serve as a guide for the selection of system components in future microgrid designs.
- This study also examines the limitations of traditional fuzzy logic methods, which typically have fixed membership functions and are unable to adapt to changing system conditions. Type-3 fuzzy logic addresses this shortcoming by offering a more adaptable approach.
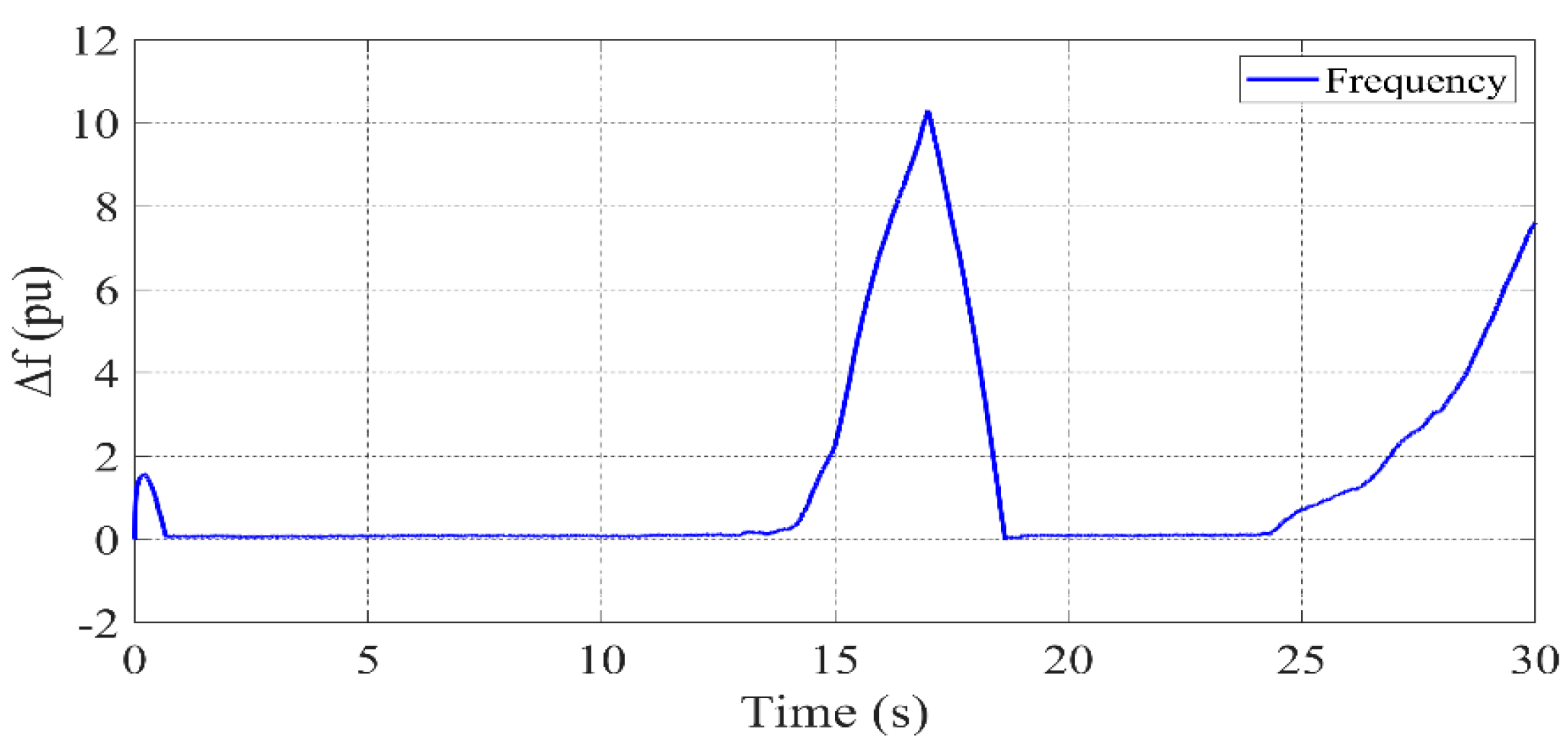
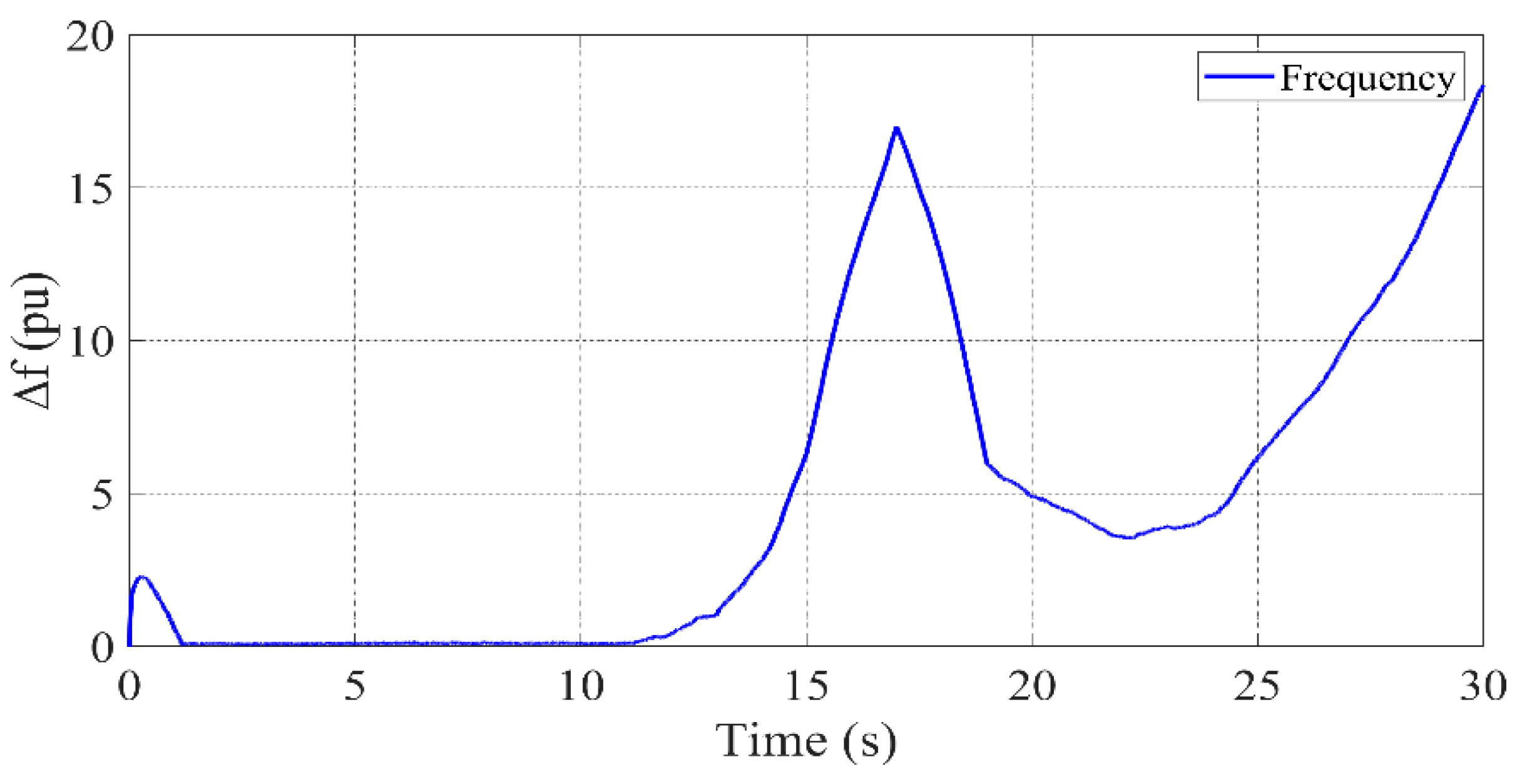
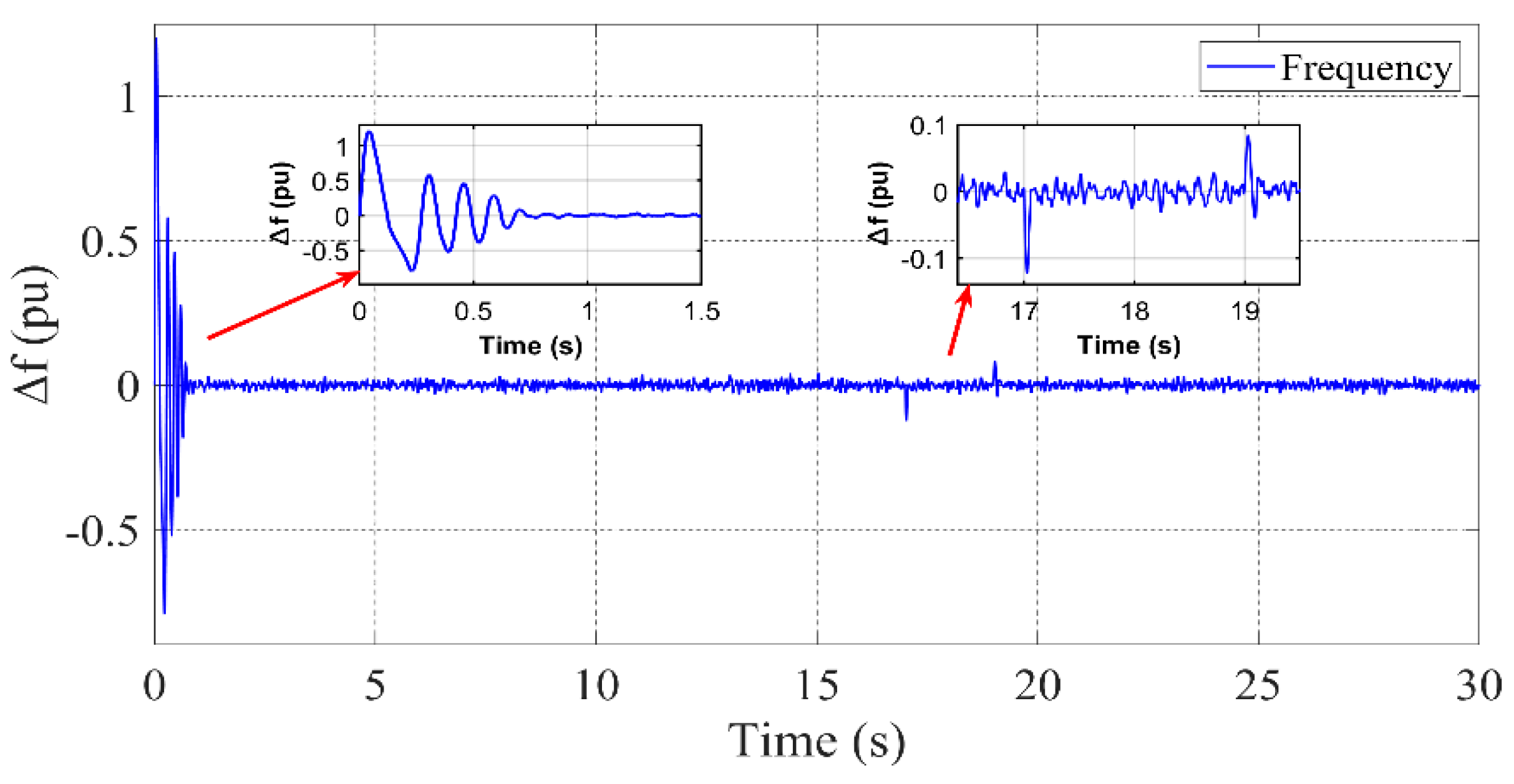
- It is evident that PID-based methods are incapable of sufficiently dampening frequency fluctuations. The proposed controller, however, exhibits a superior capacity to suppress such deviations due to its adaptive nature.
2. Materials and Methods
2.1. Microgrid Model
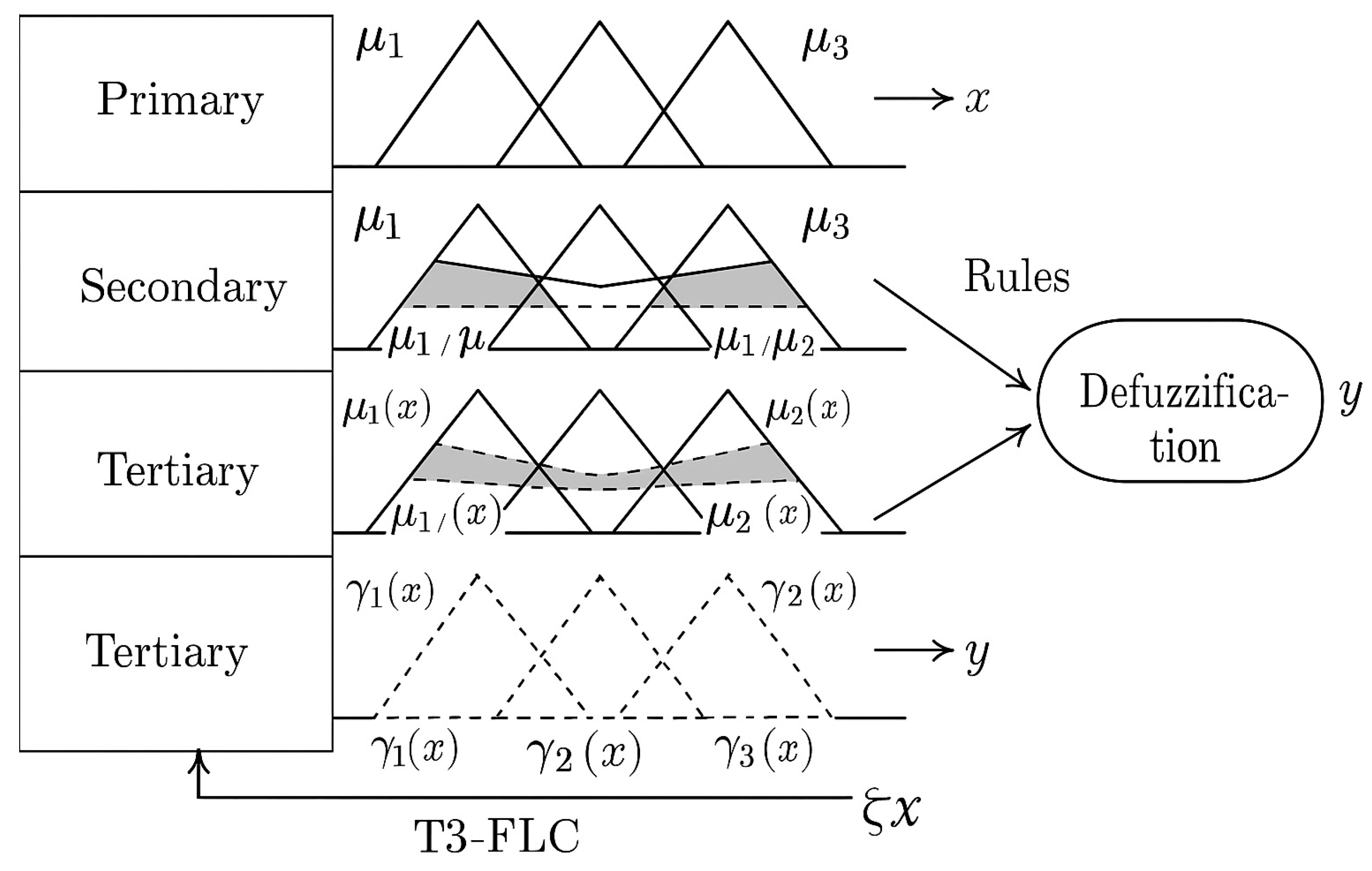
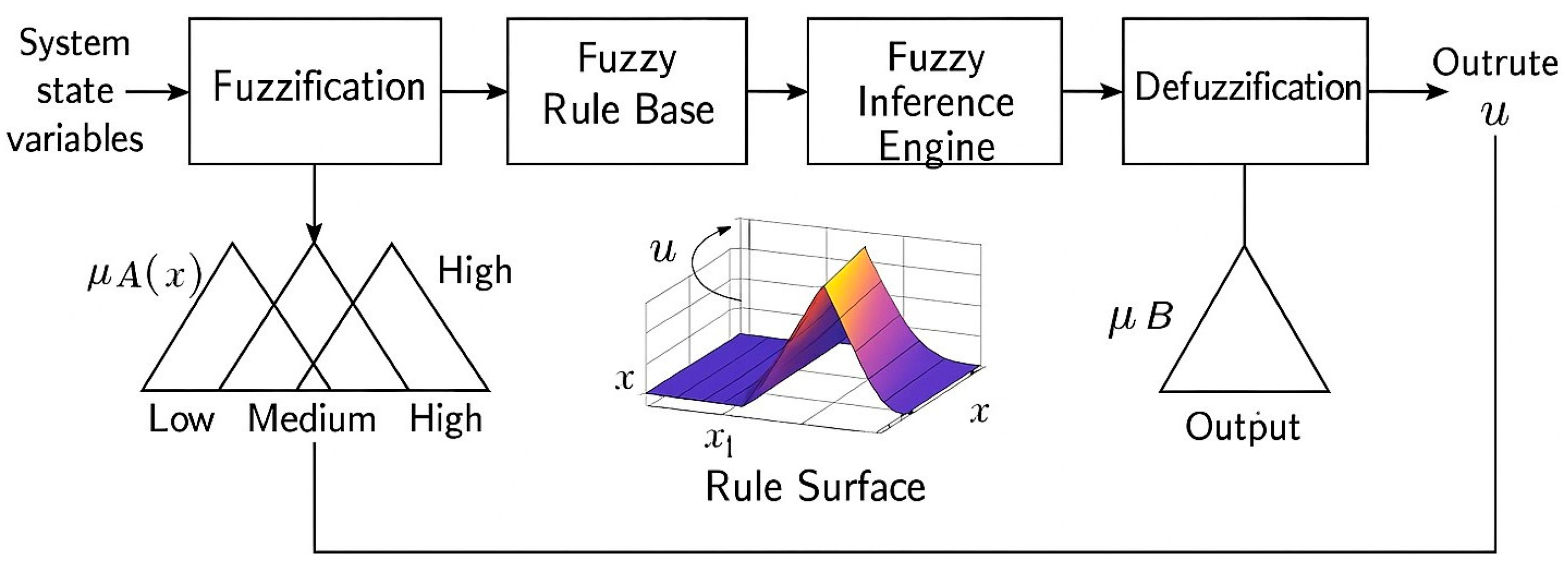
2.2. Type3 Fuzzy Logic Controller
- NB: Negative Big;
- NM: Negative Medium;
- Z: Zero;
- PM: Positive Medium;
- PB: Positive Big.
- The primary layer maps crisp inputs and into triangular membership functions .
- The secondary layer transforms into interval type-2 fuzzy sets using upper and lower bounds, denoted as , .
- The tertiary layer models uncertainty over uncertainty by applying a tertiary membership grade using an exponential uncertainty kernel, such as:
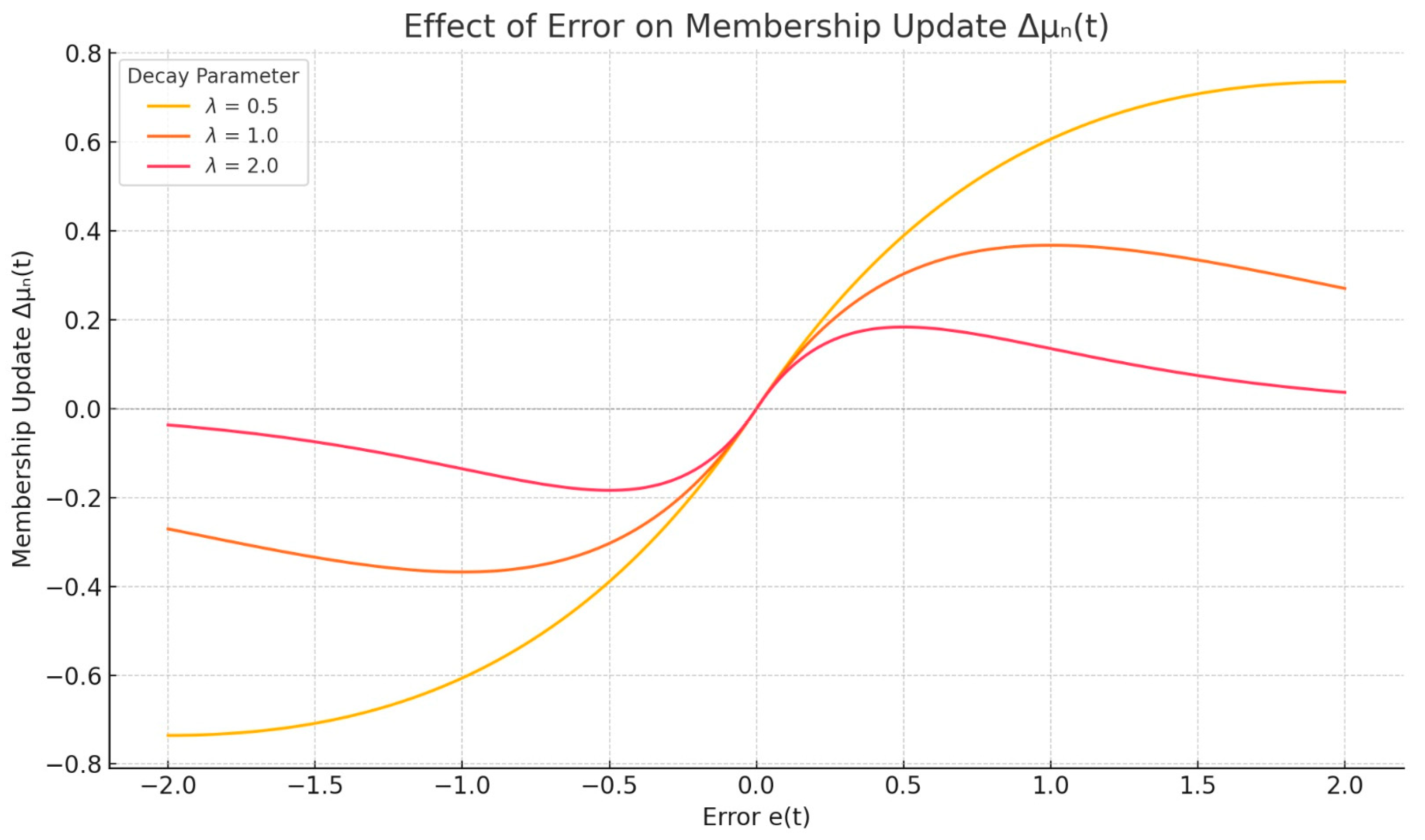
Online Adaptation Mechanism in T3-FLC
- Error between the reference frequency and actual system frequency.
- Rate of change of error.
- Control output of the T3-FLC.
- Type-3 fuzzy membership function for input h in the i-th fuzzy rule.
- Rule activation weight for the i-th fuzzy rule.
- : Fuzzy sets for and , respectively.
- Tunable consequent parameters.
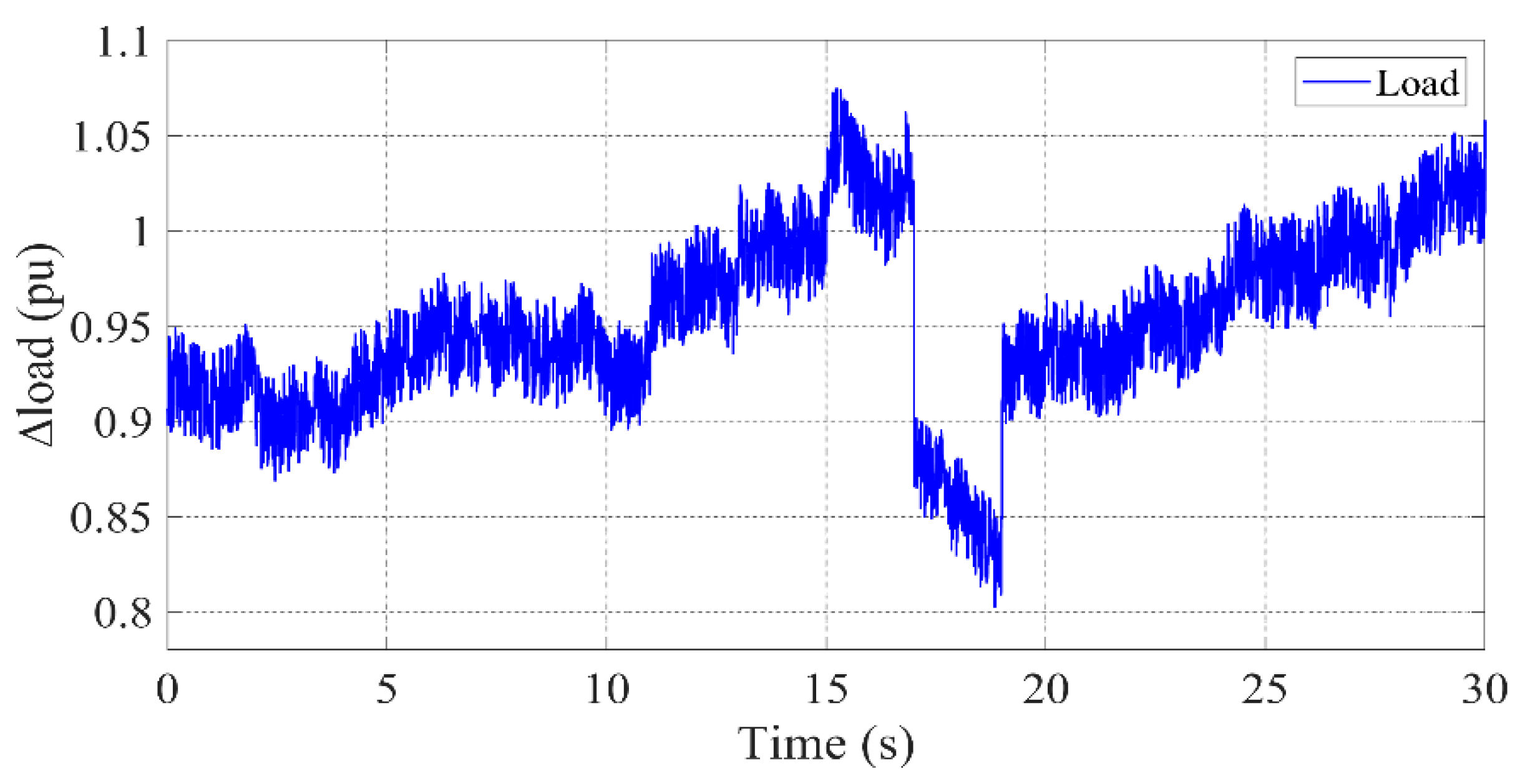
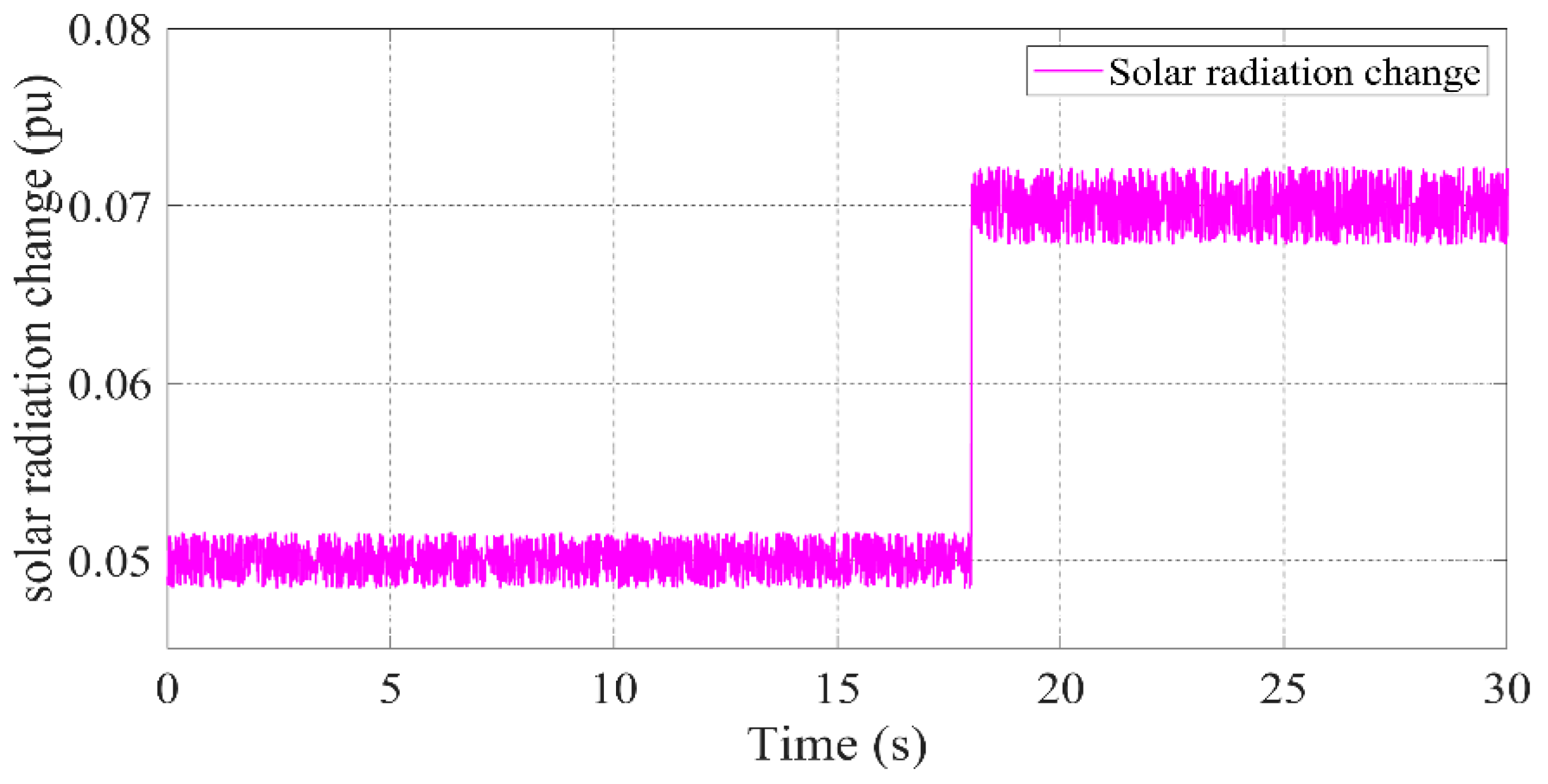
2.3. Stochastics Changes of Wind, Solar, and Load
2.4. Mathematıcal Modeling and Stability Analysis of T3-FLC-Based Microgrid Control
2.4.1. Microgrid State-Space Equations
- is the state vector (e.g., frequency deviation, power deviations in generation units);
- A is the system dynamics matrix;
- B is the input matrix representing external control actions;
- is the control input (e.g., power from renewable sources, battery discharge, etc.).
- Typical state variables include the following:
- Frequency deviation ();
- Power output variations of WTG, PV, BESS, DG, FC, FW;
- Control inputs from T3-FLC;
- Stochastic variations in renewable power and load.
- is the equivalent load power;
- is the actual load;
- and are power contributions from wind and solar, respectively.
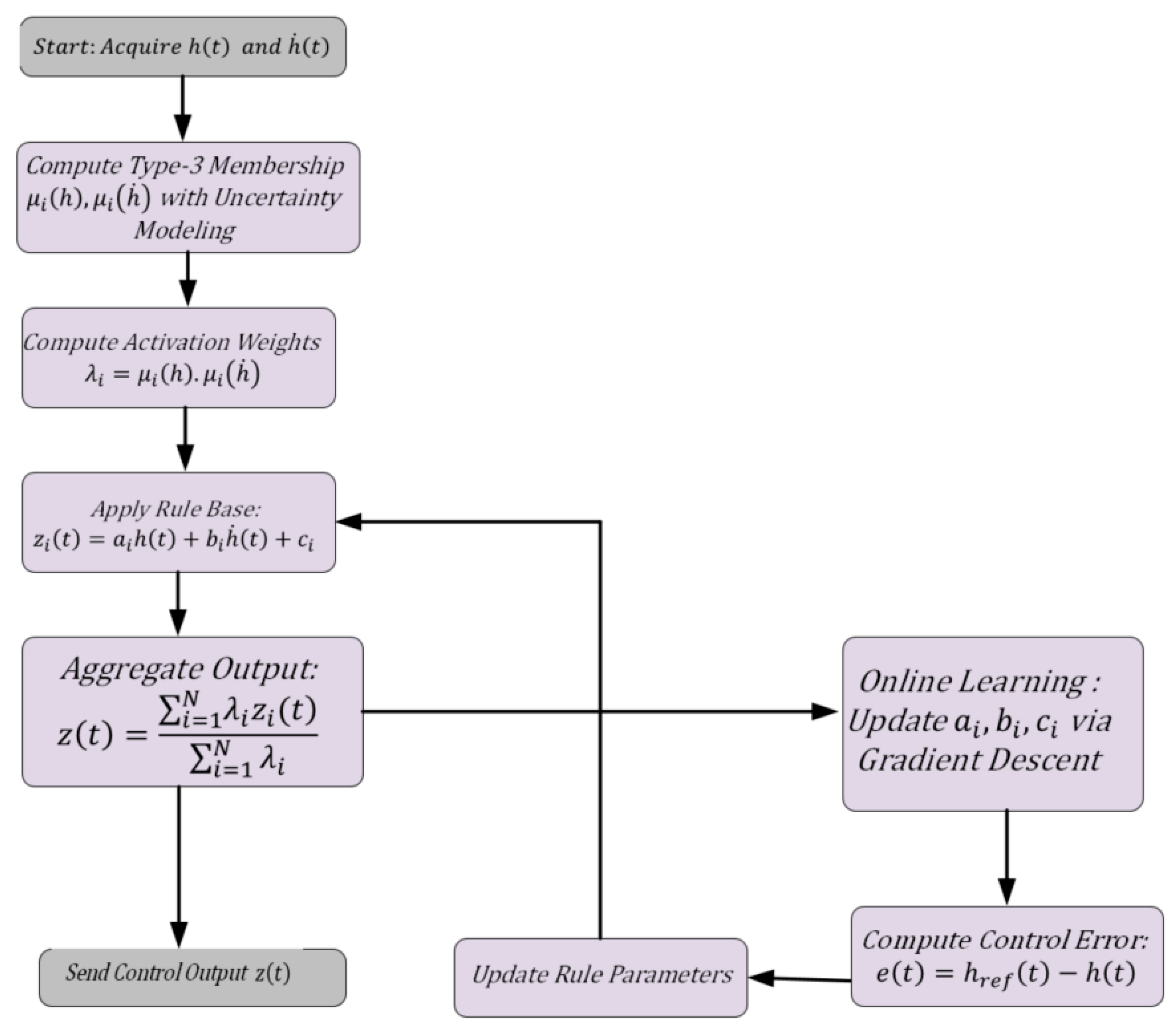
2.4.2. Type-3 Fuzzy Logic Controller (T3-FLC) Equations
- , and are adaptive fuzzy gains;
- is the error signal in LFC.
2.4.3. Stochastic Load and Renewable Energy Modeling
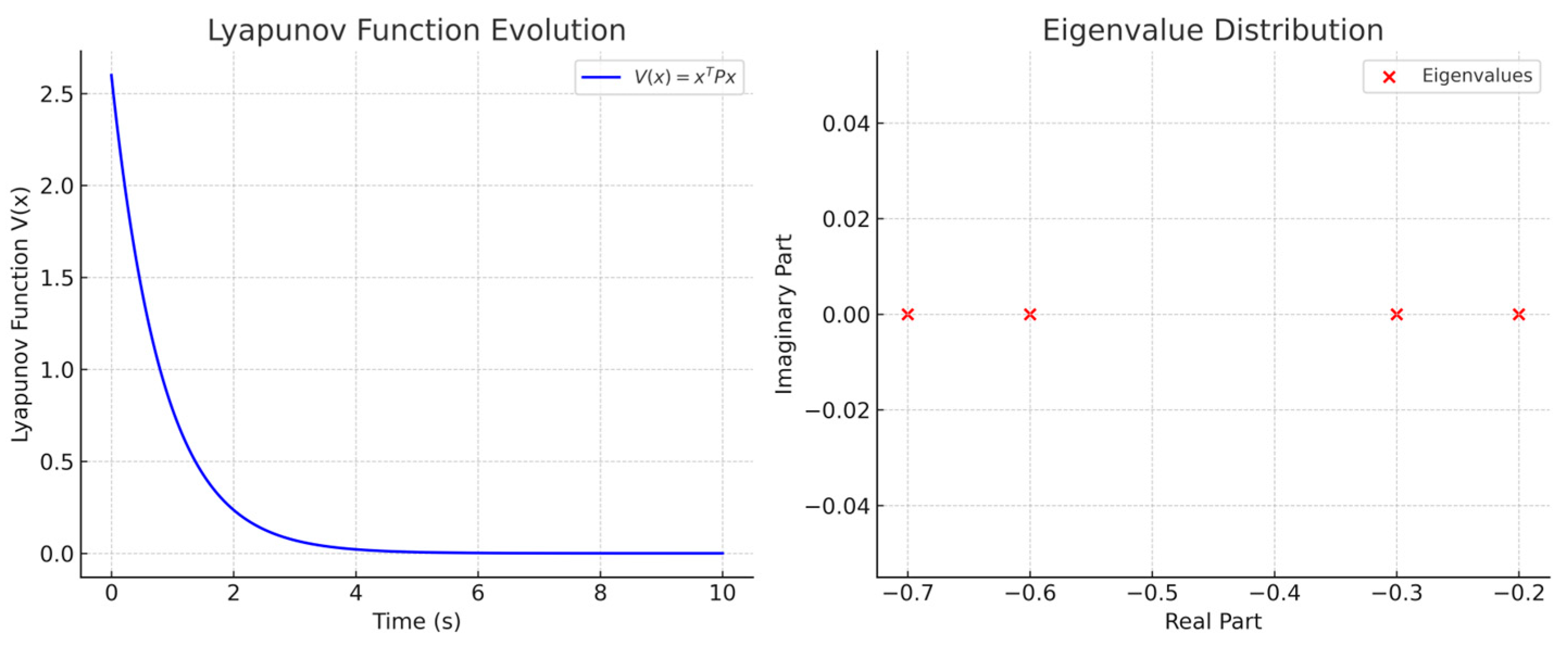
2.4.4. Formal Lyapunov Stability Analysis
3. Finding
3.1. Performance Metrics Across Scenario
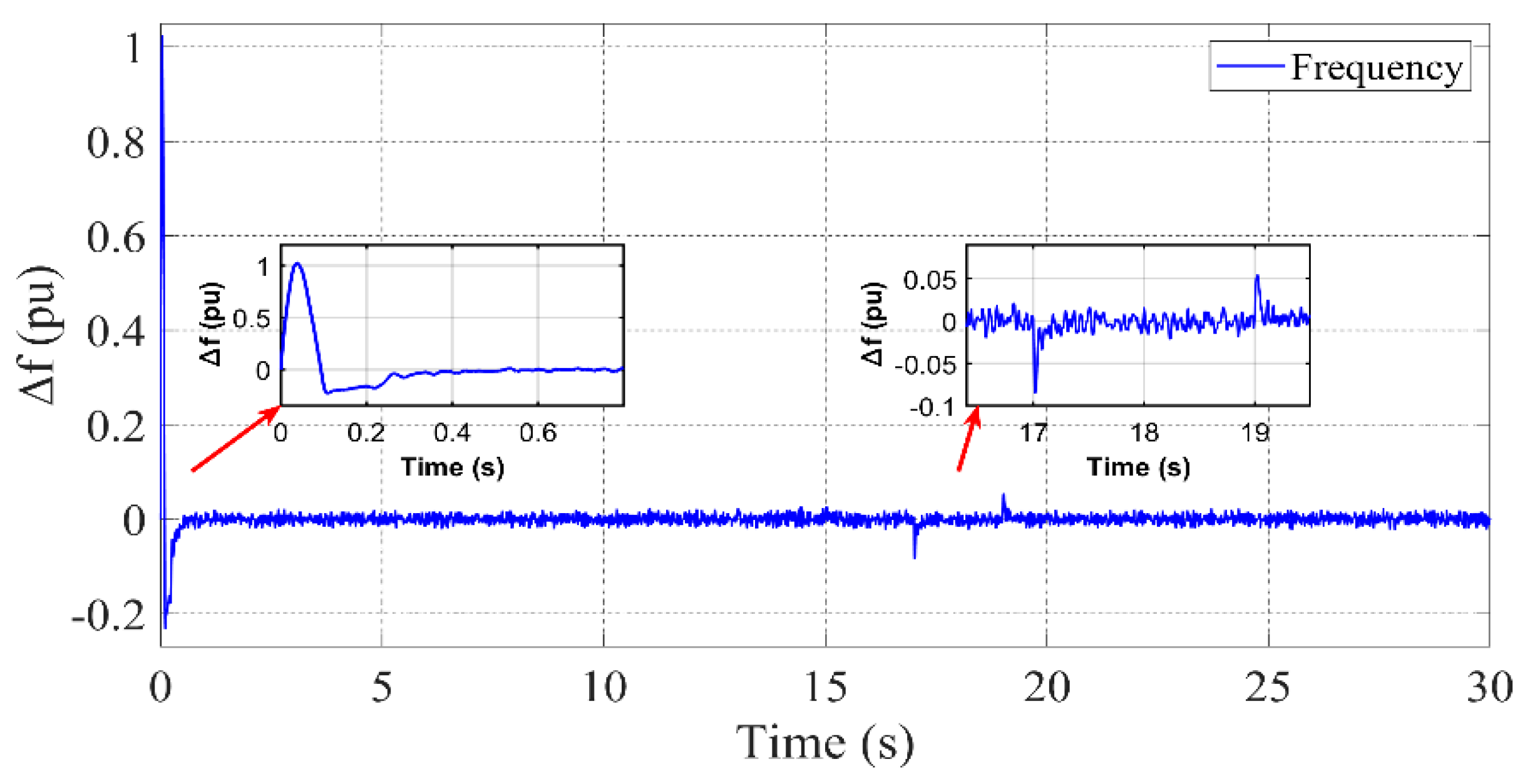
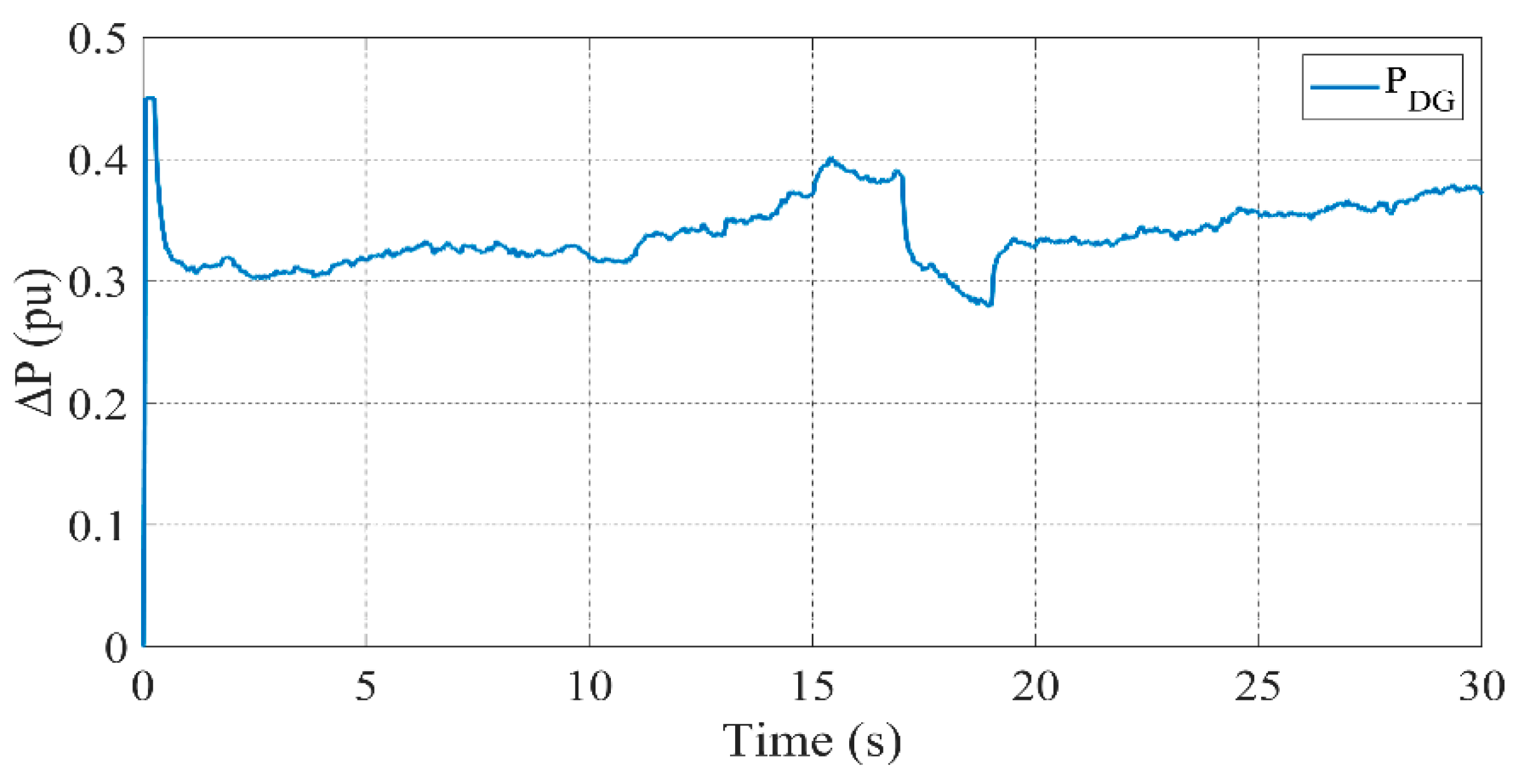
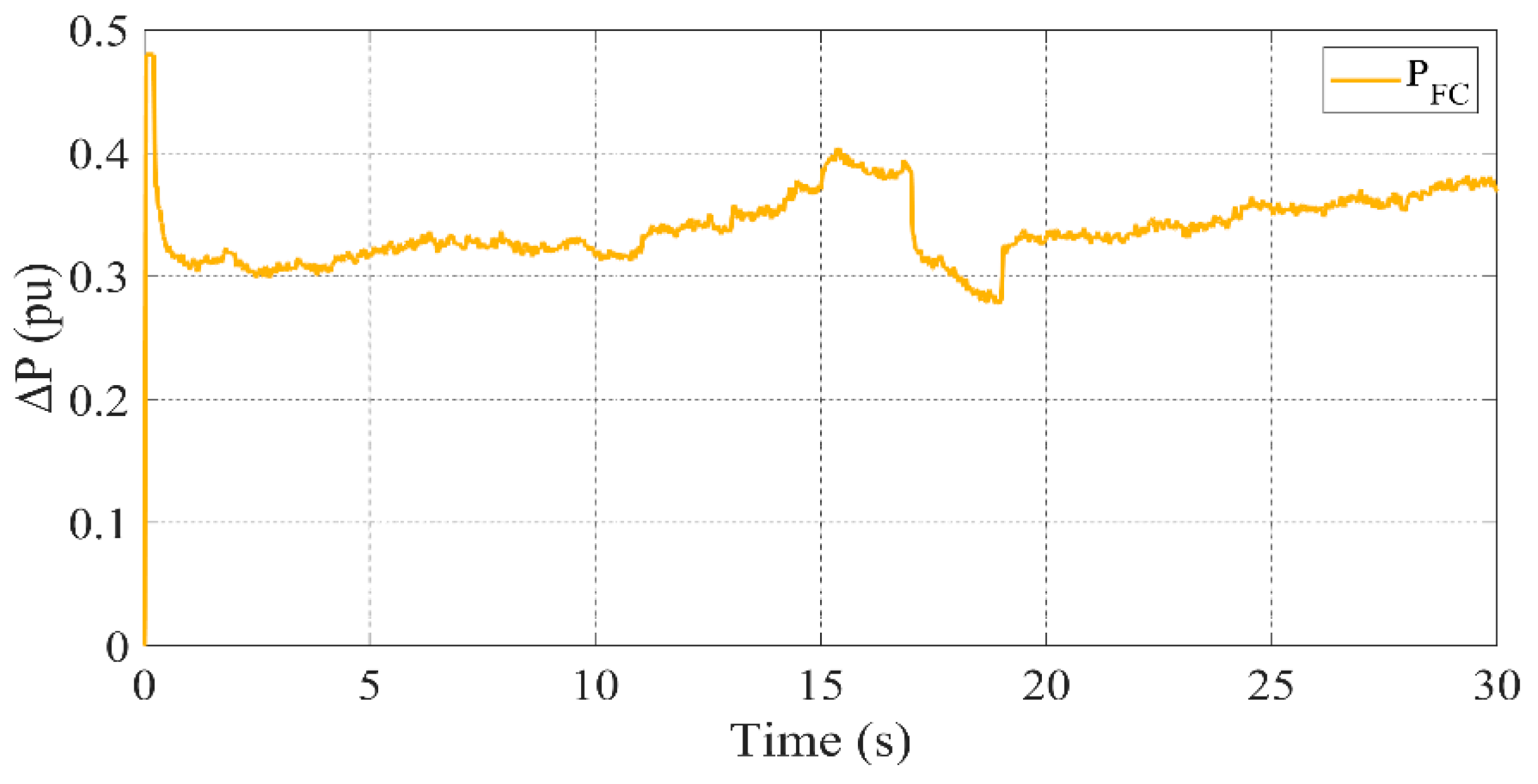
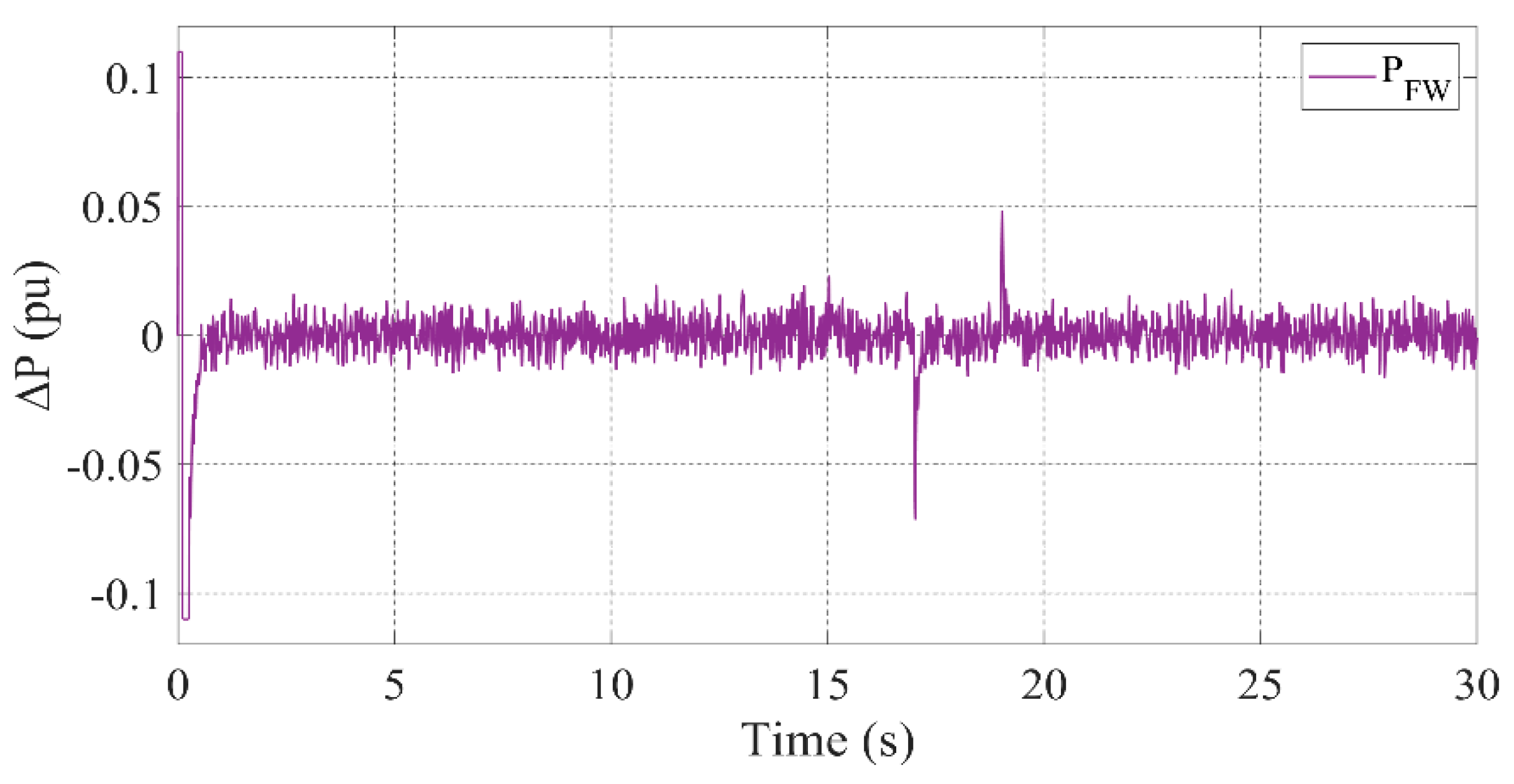
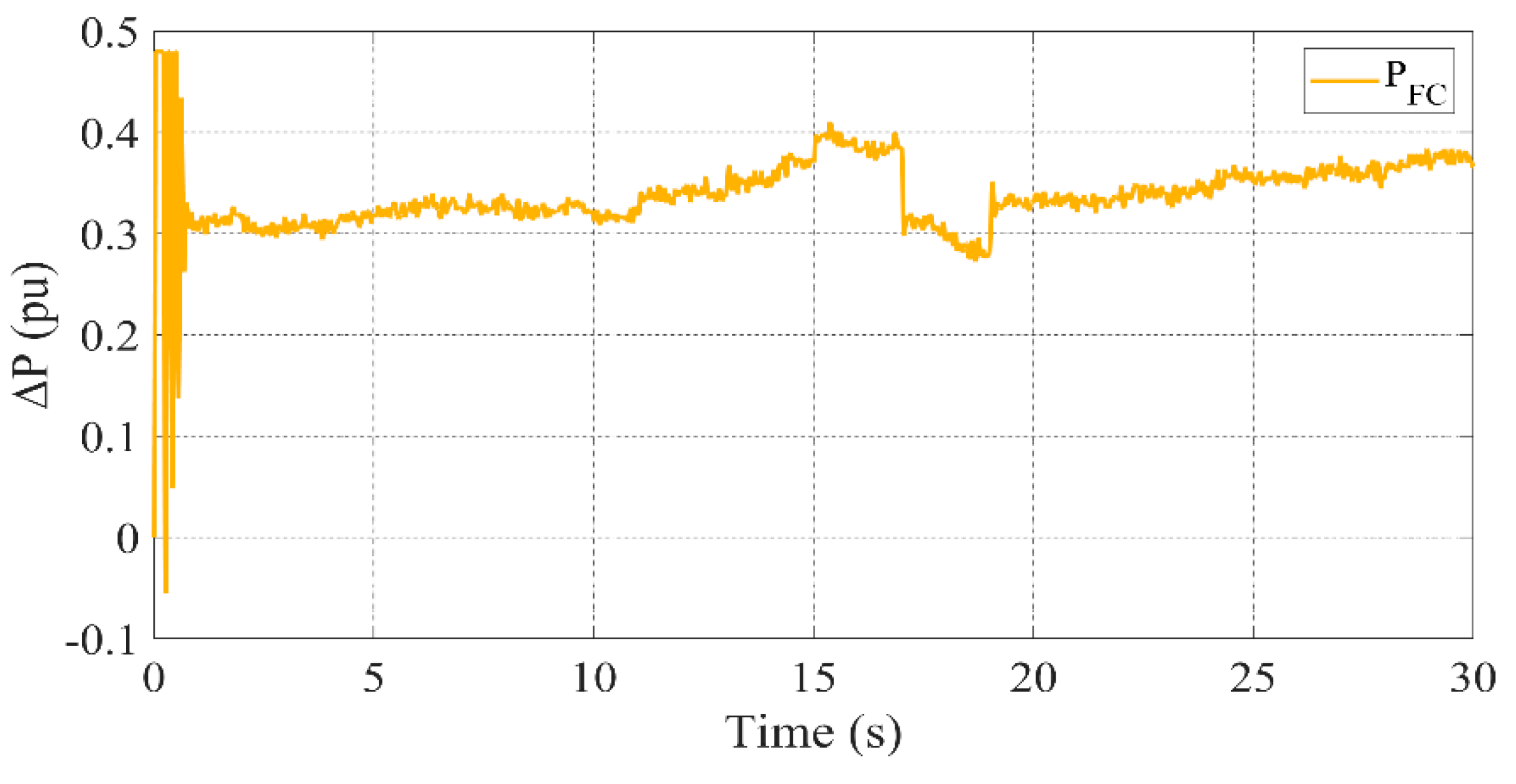
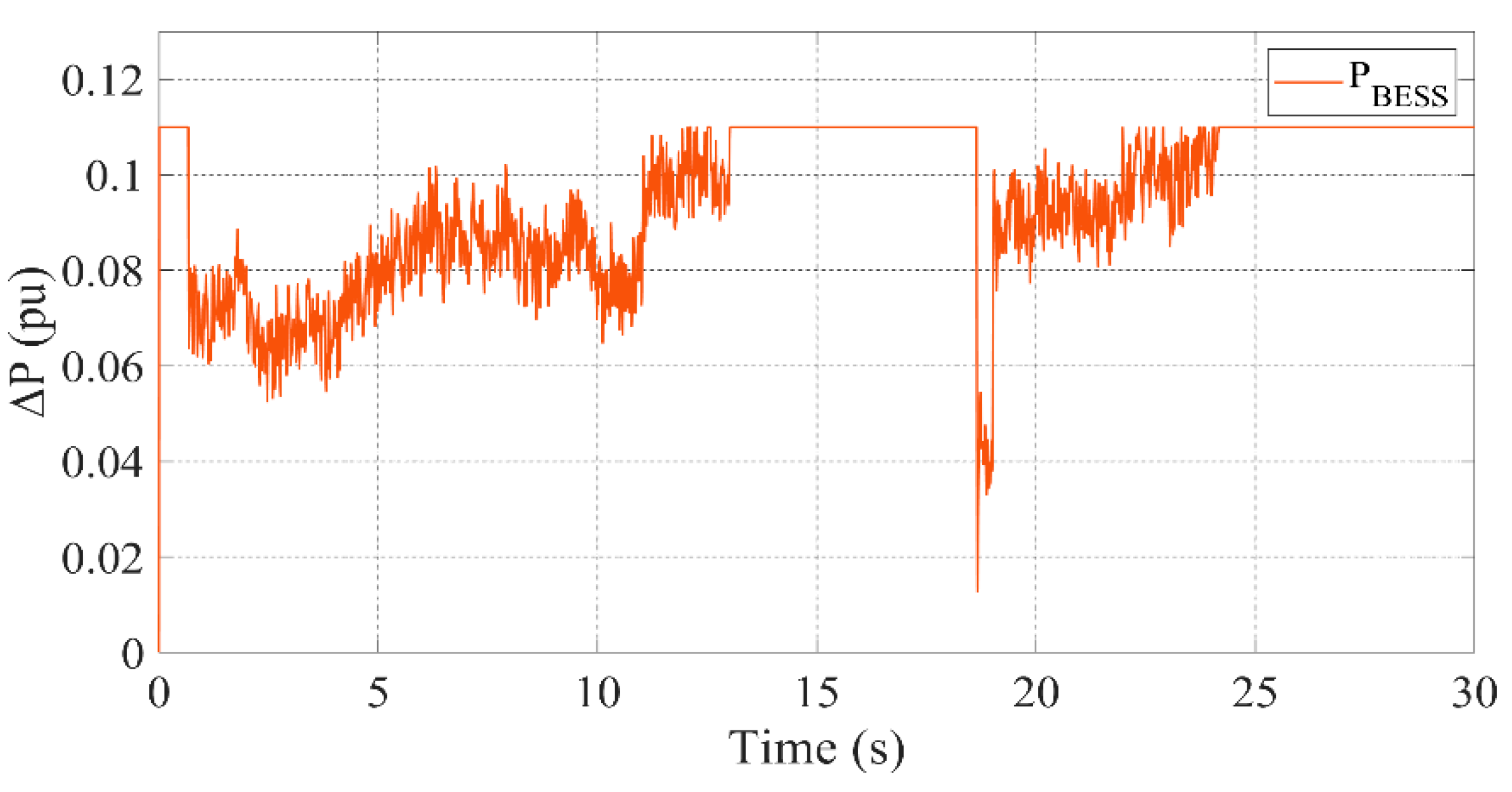
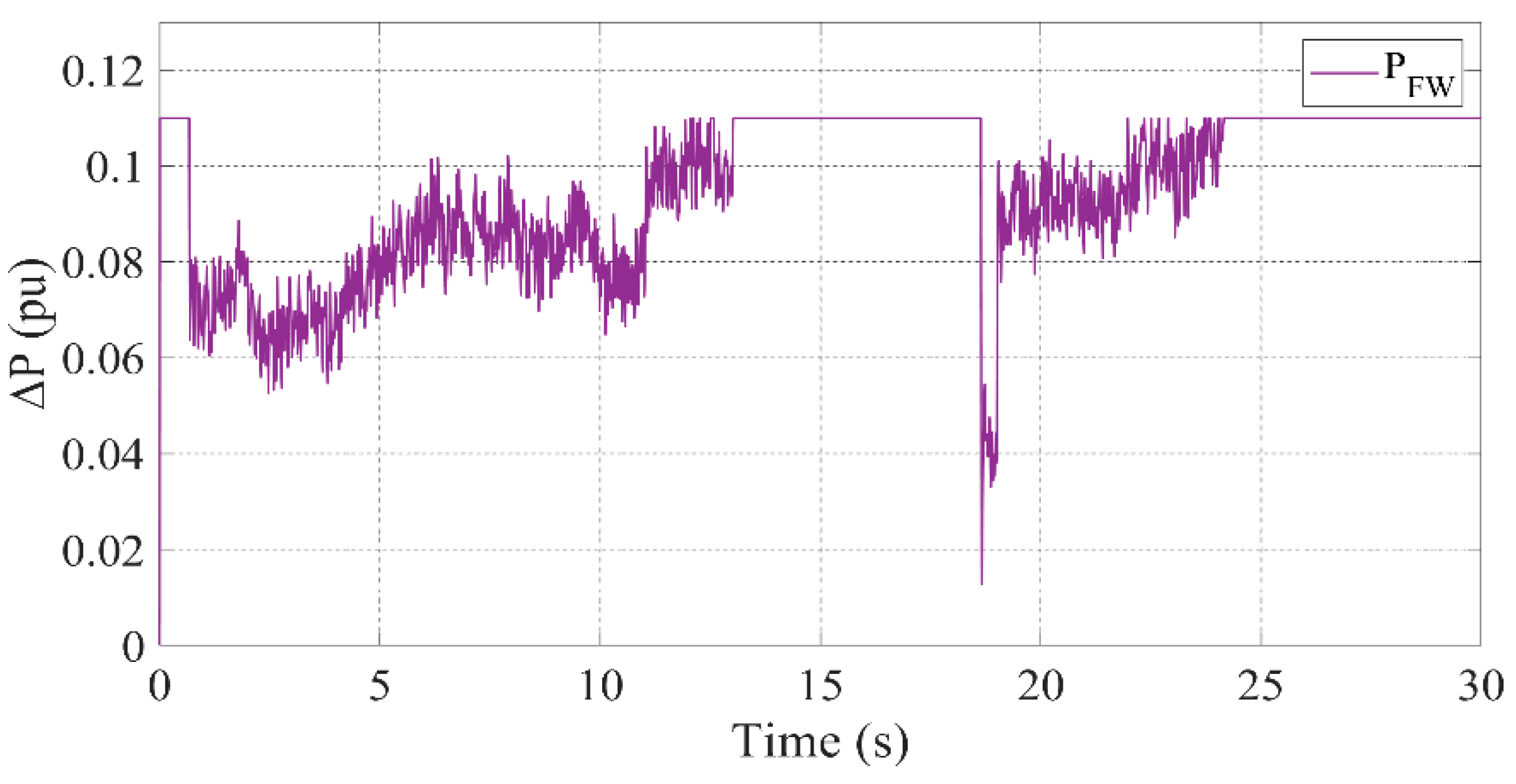
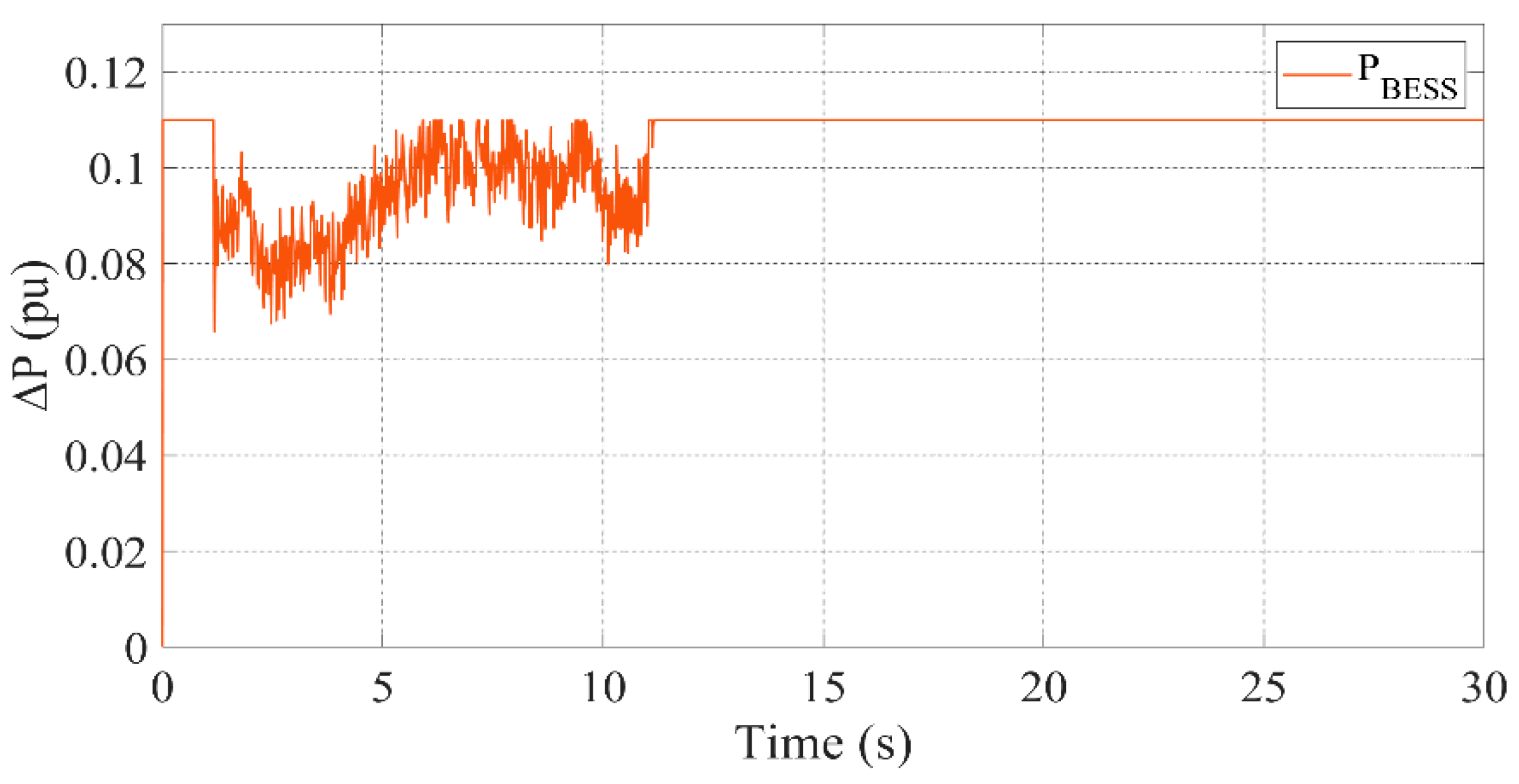
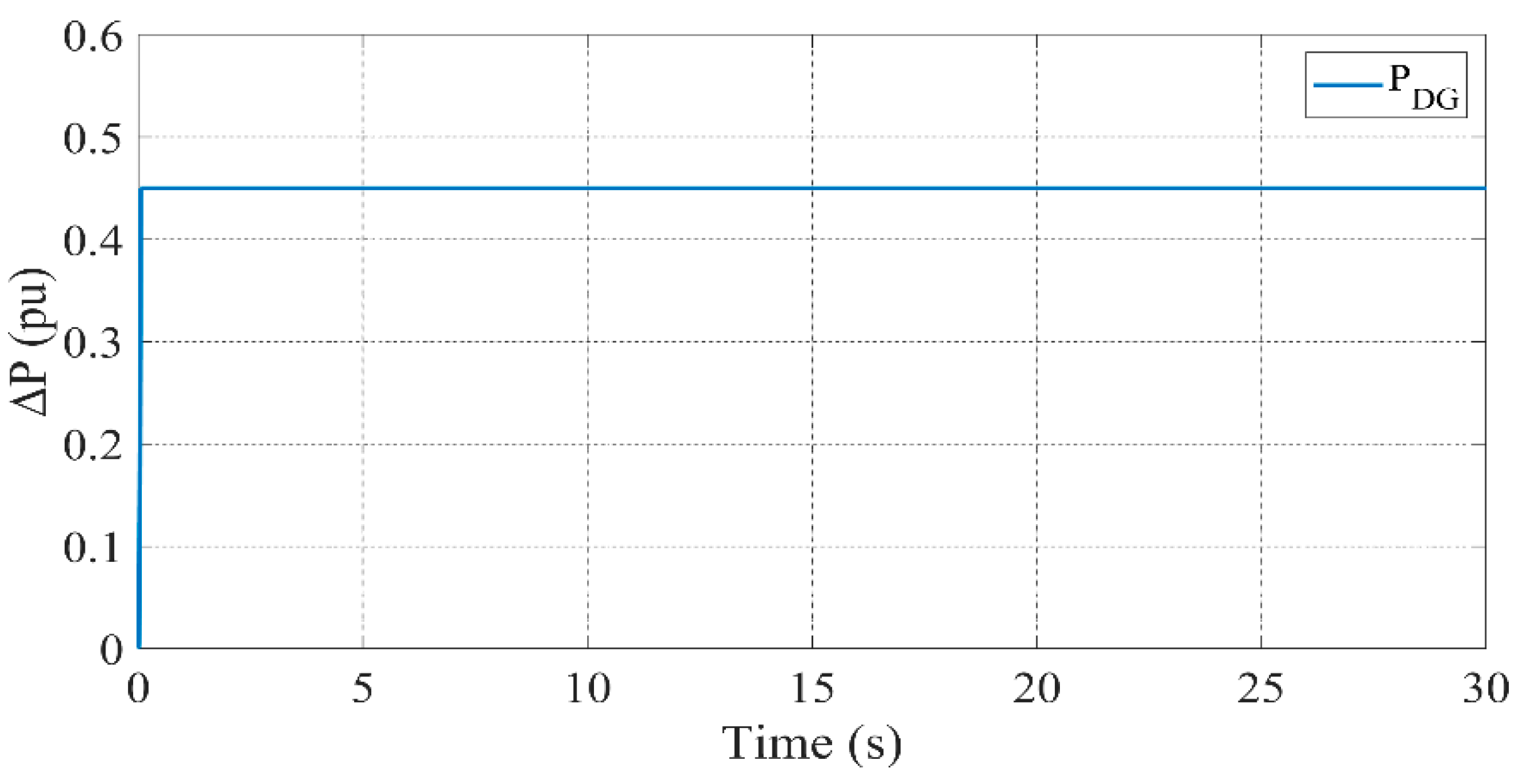
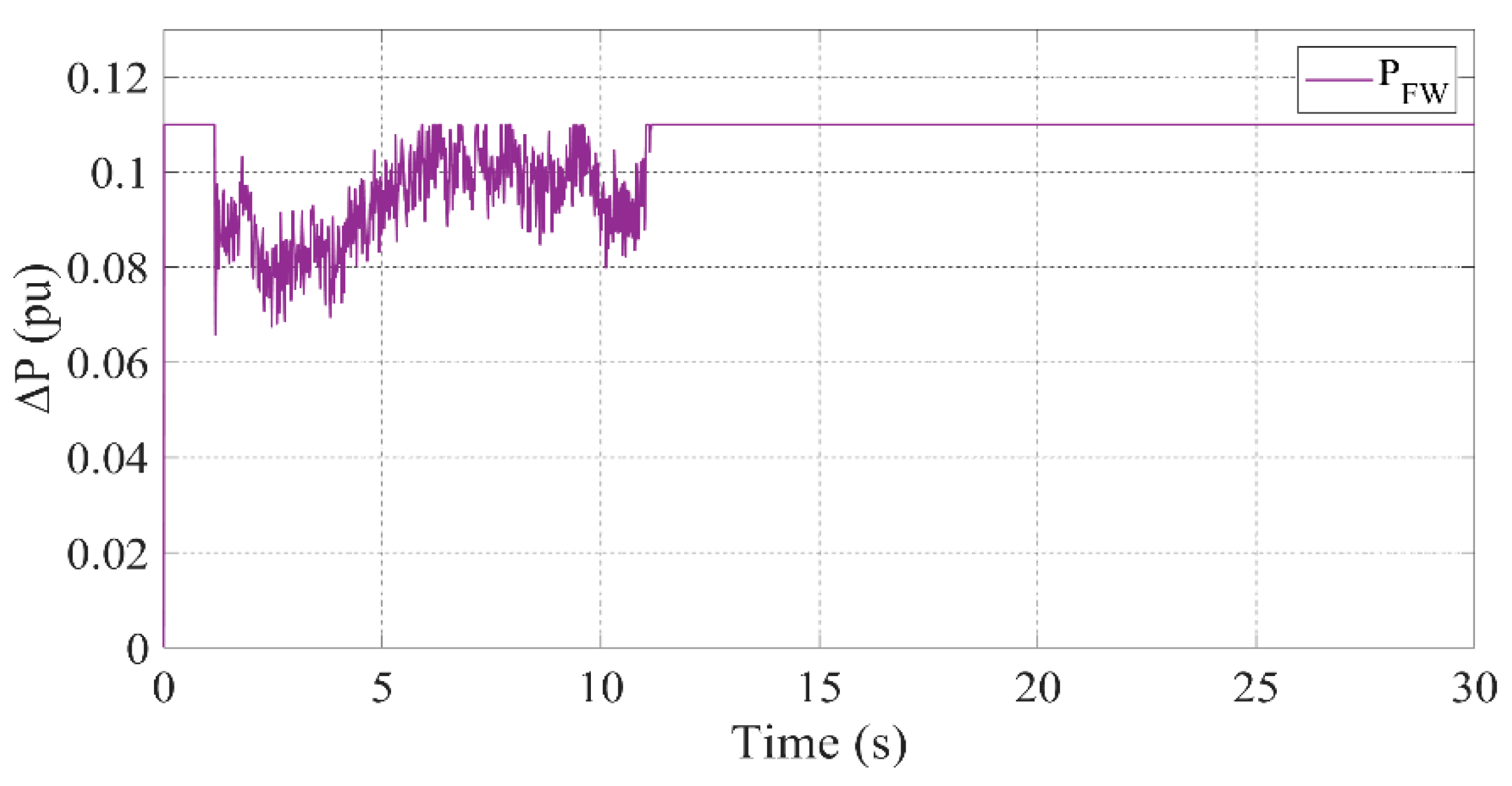
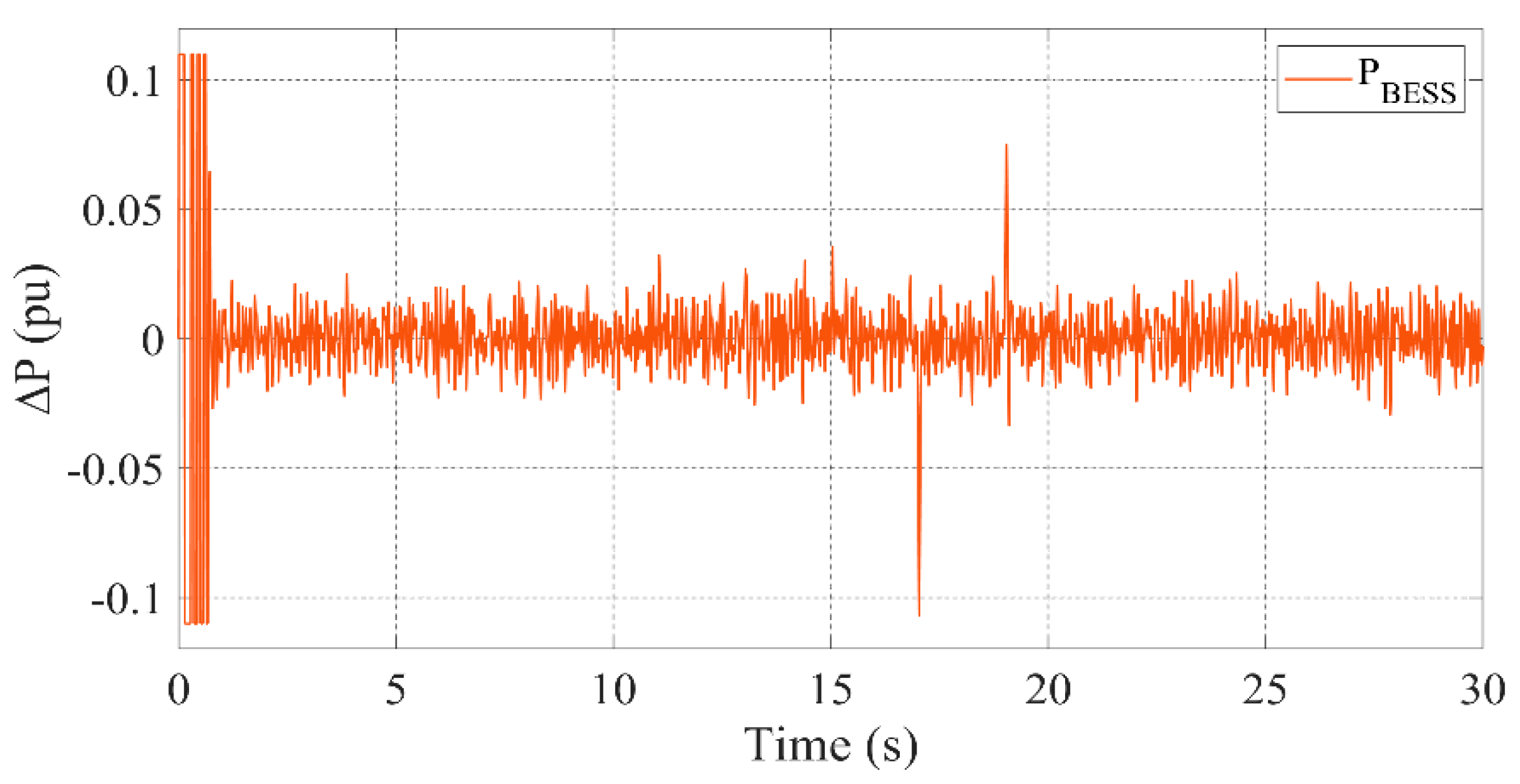
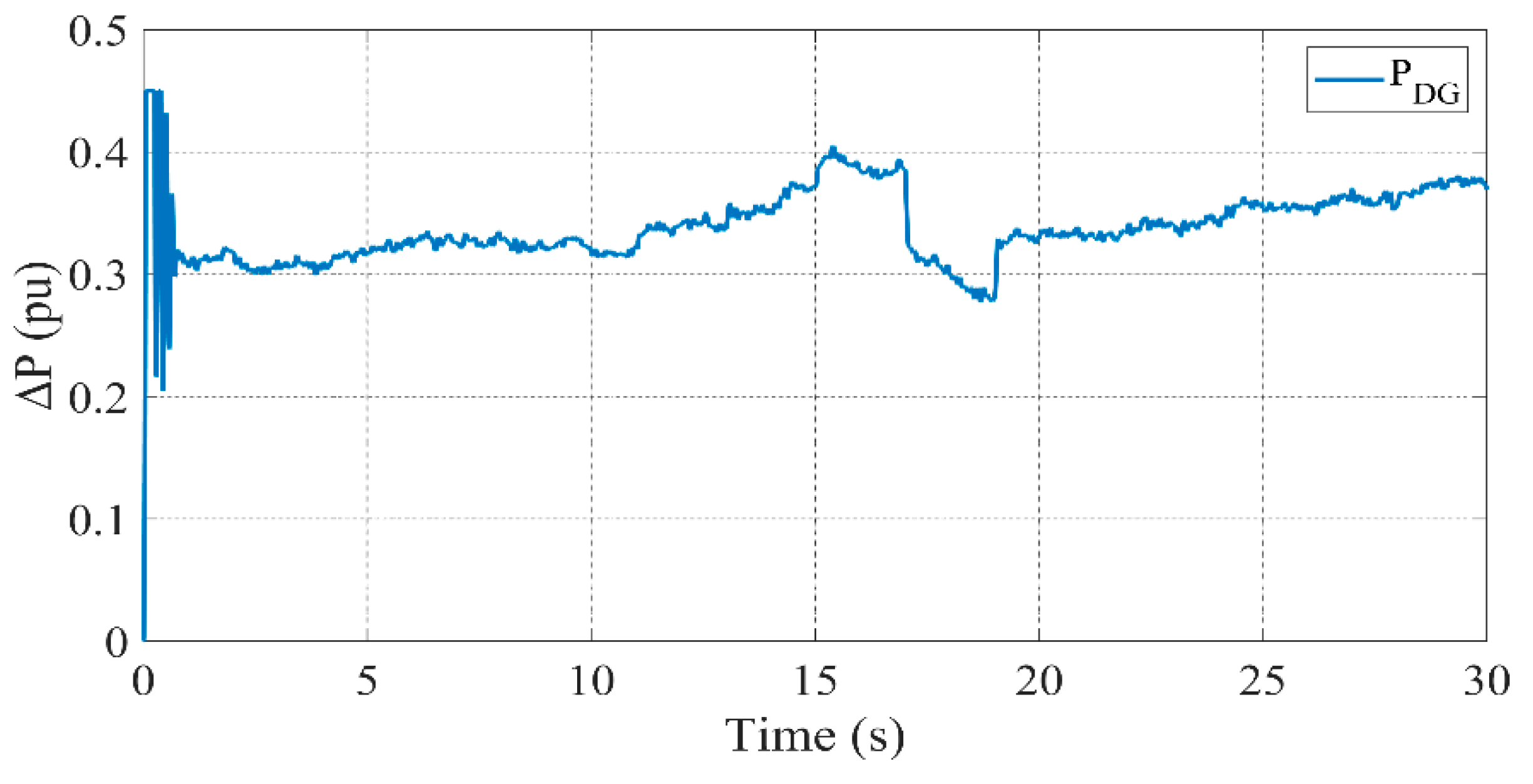
3.2. Scenario 1: All Units Active
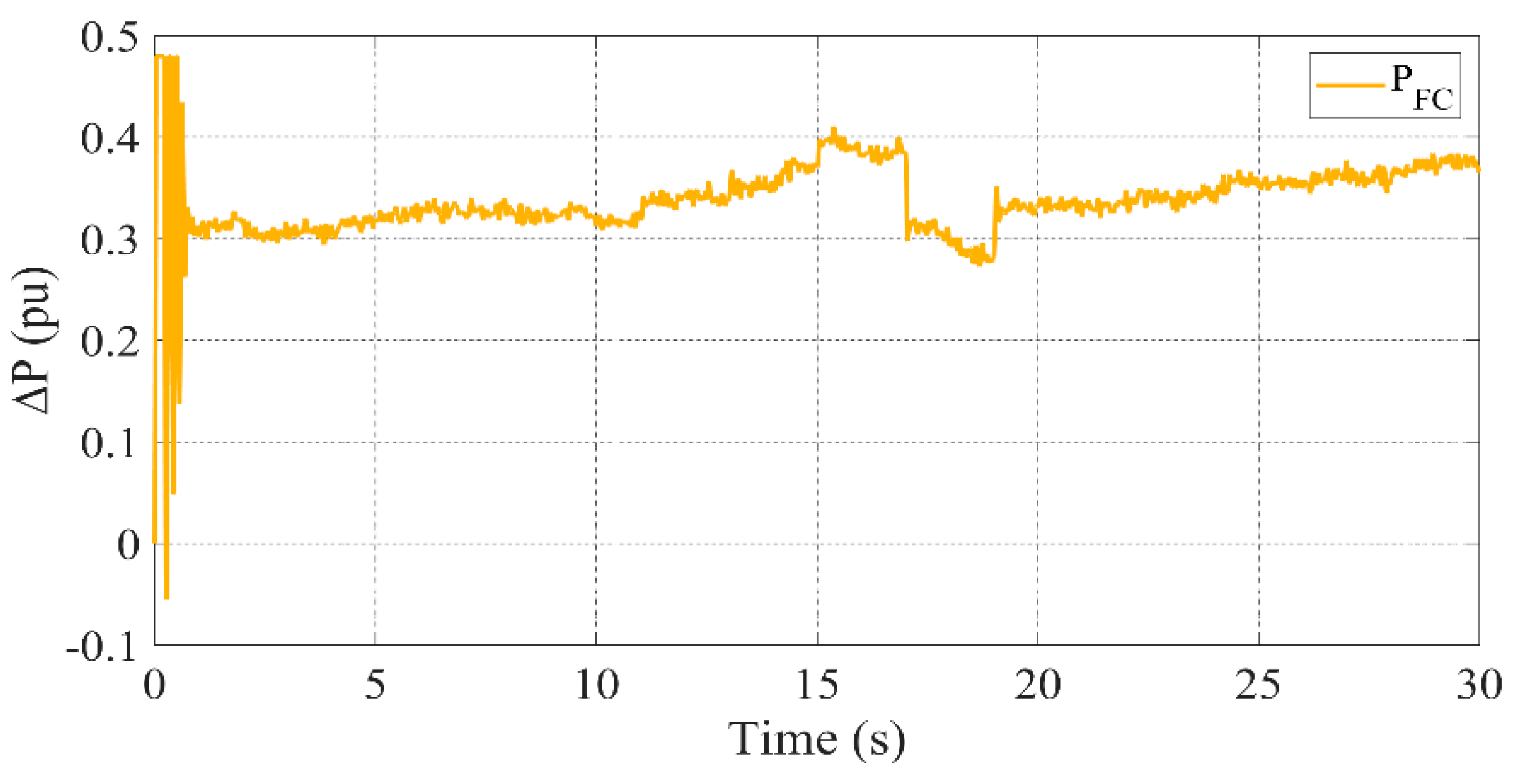
- BESS provides a quick response to power fluctuations by charging or discharging based on energy demand or supply.
- DG ensures stable power generation, particularly when renewable sources experience variability.
- FC contributes steady power to the system, especially when renewable generation is low.
- FW absorbs transient power fluctuations, ensuring smooth frequency regulation.
3.3. Scenario 2: No Battery Energy Storage System
- Impact: Without BESS, the system loses the ability to absorb excess power or provide additional energy quickly during times of high demand, leading to increased frequency deviations.
- Challenges: The absence of BESS leads to greater instability in the system, especially during renewable generation dips (from WTG or PV). The response time of DG and FC, which are not as fast as BESS, is inadequate to stabilize the frequency quickly.
- Example: When there is a sudden decrease in renewable power generation or a load increase, the frequency will drop and take longer to stabilize.
3.4. Scenario 3: No Diesel Generator
- Impact: The system may experience more significant frequency deviations, especially during large fluctuations in load or renewable generation. FC and BESS cannot respond as quickly as DG can to immediate power shortages, which increases the system’s overall sensitivity to rapid changes.
- Challenges: The DG is often a critical backup for grid stabilization in microgrids, and its absence forces the system to depend on slower-to-react components. The FC is steady but not as responsive in short-term frequency regulation, and BESS helps but only has a limited capacity to provide long-term power.
- Example: If the load increases suddenly, the frequency may drop before the FC or BESS can respond.
3.5. Scenario 4: No Fuel Cell
- Impact: Without the FC, the system will face a reduction in steady, reliable power output. While DG and BESS can still provide power, their combined output may not be as consistent as that provided by the FC.
- Challenges: This impacts the system’s ability to maintain a stable output during periods of low renewable generation. Although BESS can charge/discharge to balance the system, its power availability is limited compared to FC.
- Example: In periods when WTG and PV are not generating sufficient power, the absence of the FC means that the system will experience greater frequency variations, especially during peak demand periods.
3.6. Scenario 5: No Flywheel
- Impact: Without the FW, the microgrid system will have a reduced ability to respond to fast variations in load or generation, leading to increased frequency oscillations.
- Challenges: The FW is particularly important for fast frequency stabilization, and its absence will result in larger oscillations, especially when there are sudden changes in generation (e.g., wind gusts or cloud cover affecting renewable sources). The BESS and DG can provide support, but their response times are slower than that of the FW.
- Example: During rapid load shedding or sudden changes in renewable energy output, the system will experience more pronounced oscillations, and the recovery time will be slower.
3.7. Comparative Analysis with Advanced Controllers
3.8. Discussion of Modeling Assumption Accuracy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, G.; Huang, K.; Yang, C.; Xu, J. Day-ahead scheduling of microgrid with hydrogen energy considering economic and environmental objectives. Energy Rep. 2024, 12, 1303–1314. [Google Scholar] [CrossRef]
- Doğan, S.; Haydaroğlu, C.; Gümüş, B.; Mohammadzadeh, A. Innovative fuzzy logic type 3 controller for transient and maximum power point tracking in hydrogen fuel cells. Int. J. Hydrogen Energy 2024, in press. [CrossRef]
- Arsad, A.Z.; Hannan, M.; Al-Shetwi, A.Q.; Mansur, M.; Muttaqi, K.; Dong, Z.; Blaabjerg, F. Hydrogen energy storage integrated hybrid renewable energy systems: A review analysis for future research directions. Int. J. Hydrogen Energy 2022, 47, 17285–17312. [Google Scholar] [CrossRef]
- Wei, Y.-M.; Chen, K.; Kang, J.-N.; Chen, W.; Wang, X.-Y.; Zhang, X. Policy and Management of Carbon Peaking and Carbon Neutrality: A Literature Review. Engineering 2022, 14, 52–63. [Google Scholar] [CrossRef]
- Kilic, H. Improving the performance of microgrid-based Power-to-X systems through optimization of renewable hydrogen generation. Int. J. Hydrogen Energy 2024, 75, 106–120. [Google Scholar] [CrossRef]
- SaberiKamarposhti, M.; Kamyab, H.; Krishnan, S.; Yusuf, M.; Rezania, S.; Chelliapan, S.; Khorami, M. A comprehensive review of AI-enhanced smart grid integration for hydrogen energy: Advances, challenges, and future prospects. Int. J. Hydrogen Energy 2024, 67, 1009–1025. [Google Scholar] [CrossRef]
- Arya, Y.; Dahiya, P.; Çelik, E.; Sharma, G.; Gözde, H.; Nasiruddin, I. AGC performance amelioration in multi-area interconnected thermal and thermal-hydro-gas power systems using a novel controller. Eng. Sci. Technol. Int. J. 2021, 24, 384–396. [Google Scholar] [CrossRef]
- Elkasem, A.H.A.; Khamies, M.; Hassan, M.H.; Agwa, A.M.; Kamel, S. Optimal Design of TD-TI Controller for LFC Considering Renewables Penetration by an Improved Chaos Game Optimizer. Fractal Fract. 2022, 6, 220. [Google Scholar] [CrossRef]
- Heydari, R.; Gheisarnejad, M.; Khooban, M.H.; Dragicevic, T.; Blaabjerg, F. Robust and Fast Voltage-Source-Converter (VSC) Control for Naval Shipboard Microgrids. IEEE Trans. Power Electron. 2019, 34, 8299–8303. [Google Scholar] [CrossRef]
- Suresh, V.; Pachauri, N.; Vigneysh, T. Decentralized control strategy for fuel cell/PV/BESS based microgrid using modified fractional order PI controller. Int. J. Hydrogen Energy 2021, 46, 4417–4436. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Suo, Y.; Song, X.; Ju, Y. Active Disturbance Rejection Control Combined with Improved Model Predictive Control for Large-Capacity Hybrid Energy Storage Systems in DC Microgrids. Appl. Sci. 2024, 14, 8617. [Google Scholar] [CrossRef]
- Saenger, P.; Devillers, N.; Deschinkel, K.; Pera, M.-C.; Couturier, R.; Gustin, F. Optimization of Electrical Energy Storage System Sizing for an Accurate Energy Management in an Aircraft. IEEE Trans. Veh. Technol. 2016, 66, 5572–5583. [Google Scholar] [CrossRef]
- Wu, D.; Guo, F.; Yao, Z.; Zhu, D.; Zhang, Z.; Li, L.; Du, X.; Zhang, J. Enhancing Reliability and Performance of Load Frequency Control in Aging Multi-Area Power Systems under Cyber-Attacks. Appl. Sci. 2024, 14, 8631. [Google Scholar] [CrossRef]
- Shangguan, X.-C.; He, Y.; Zhang, C.-K.; Jin, L.; Yao, W.; Jiang, L.; Wu, M. Control Performance Standards-Oriented Event-Triggered Load Frequency Control for Power Systems Under Limited Communication Bandwidth. IEEE Trans. Control Syst. Technol. 2022, 30, 860–868. [Google Scholar] [CrossRef]
- Zhou, H.; Zhong, Q.; Hu, S.; Yang, J.; Shi, K.; Zhong, S. Dissipative Discrete PID Load Frequency Control for Restructured Wind Power Systems via Non-Fragile Design Approach. Mathematics 2023, 11, 3252. [Google Scholar] [CrossRef]
- Khalil, A.E.; Boghdady, T.A.; Alham, M.H.; Ibrahim, D.K. Enhancing the Conventional Controllers for Load Frequency Control of Isolated Microgrids Using Proposed Multi-Objective Formulation via Artificial Rabbits Optimization Algorithm. IEEE Access 2023, 11, 3472–3493. [Google Scholar] [CrossRef]
- Ahmed, M.; Magdy, G.; Khamies, M.; Kamel, S. Modified TID controller for load frequency control of a two-area interconnected diverse-unit power system. Int. J. Electr. Power Energy Syst. 2022, 135, 107528. [Google Scholar] [CrossRef]
- Abid, S.; El-Rifaie, A.M.; Elshahed, M.; Ginidi, A.R.; Shaheen, A.M.; Moustafa, G.; Tolba, M.A. Development of Slime Mold Optimizer with Application for Tuning Cascaded PD-PI Controller to Enhance Frequency Stability in Power Systems. Mathematics 2023, 11, 1796. [Google Scholar] [CrossRef]
- Kumar, D.; Mathur, H.D.; Bhanot, S.; Bansal, R.C. Forecasting of solar and wind power using LSTM RNN for load frequency control in isolated microgrid. Int. J. Model. Simul. 2021, 41, 311–323. [Google Scholar] [CrossRef]
- Cam, E.; Gorel, G.; Mamur, H. Use of the genetic algorithm-based fuzzy logic controller for load-frequency control in a two area interconnected power system. Appl. Sci. 2017, 7, 308. [Google Scholar] [CrossRef]
- Esfahani, Z.; Roohi, M.; Gheisarnejad, M.; Dragičević, T.; Khooban, M.-H. Optimal non-integer sliding mode control for frequency regulation in stand-alone modern power grids. Appl. Sci. 2019, 9, 3411. [Google Scholar] [CrossRef]
- Alshehri, S.; Wazir, A.B.; Alhussainy, A.A.; Alghamdi, S.; Alobaidi, A.; Rawa, M.; Alturki, Y.A. Impact of Advanced Thyristor Controlled Series Capacitor on Load Frequency Control and Automatic Voltage Regulator Dual Area System with Interval Type-2 Fuzzy Sets-PID Usage. Processes 2024, 12, 2647. [Google Scholar] [CrossRef]
- Xie, Y.; Liao, P.; Liang, Z.; Zhou, D. State of Change-Related Hybrid Energy Storage System Integration in Fuzzy Sliding Mode Load Frequency Control Power System with Electric Vehicles. Machines 2025, 13, 57. [Google Scholar] [CrossRef]
- Ali, G.; Aly, H.; Little, T. Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller. Energies 2024, 17, 2000. [Google Scholar] [CrossRef]
- Qu, Z.; Younis, W.; Wang, Y.; Georgievitch, P.M. A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization. Energies 2024, 17, 517. [Google Scholar] [CrossRef]
- Younis, W.; Yameen, M.Z.; Tayab, A.; Qamar, H.G.M.; Ghith, E.; Tlija, M. Enhancing Load Frequency Control of Interconnected Power System Using Hybrid PSO-AHA Optimizer. Energies 2024, 17, 3962. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Nivolianiti, E. Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Appl. Sci. 2023, 13, 6128. [Google Scholar] [CrossRef]
- Aly, M.; Mohamed, E.A.; Noman, A.M.; Ahmed, E.M.; El-Sousy, F.F.M.; Watanabe, M. Optimized Non-Integer Load Frequency Control Scheme for Interconnected Microgrids in Remote Areas with High Renewable Energy and Electric Vehicle Penetrations. Mathematics 2023, 11, 2080. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Diab, A.A.Z.; Hussein, M.M. Application of linear quadratic Gaussian and coefficient diagram techniques to distributed load frequency control of power systems. Appl. Sci. 2015, 5, 1603–1615. [Google Scholar] [CrossRef]
- YLan, Y.; Illindala, M.S. Robust Distributed Load Frequency Control for Multi-Area Power Systems with Photovoltaic and Battery Energy Storage System. Energies 2024, 17, 5536. [Google Scholar] [CrossRef]
- Zhong, Q.; Yang, J.; Shi, K.; Zhong, S.; Li, Z.; Sotelo, M.A. Event-Triggered H∞Load Frequency Control for Multi-Area Nonlinear Power Systems Based on Non-Fragile Proportional Integral Control Strategy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12191–12201. [Google Scholar] [CrossRef]
- Guo, J. The Load Frequency Control by Adaptive High Order Sliding Mode Control Strategy. IEEE Access 2022, 10, 25392–25399. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, S. A Coordinated Emergency Frequency Control Strategy Based on Output Regulation Approach for an Isolated Industrial Microgrid. Energies 2024, 17, 5217. [Google Scholar] [CrossRef]
- Li, J.; Yu, T.; Zhang, X. Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 2022, 306, 117900. [Google Scholar] [CrossRef]
- Abdelrahim, M.; Almakhles, D. Synthesis of State/Output Feedback Event-Triggered Controllers for Load Frequency Regulation in Hybrid Wind–Diesel Power Systems. Appl. Sci. 2023, 13, 9652. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Turkeri, C.; Ahmad, M.A. Spider Wasp Optimizer-Optimized Cascaded Fractional-Order Controller for Load Frequency Control in a Photovoltaic-Integrated Two-Area System. Mathematics 2024, 12, 3076. [Google Scholar] [CrossRef]
- Kumar, N.; Malik, H.; Singh, A.; Alotaibi, M.A.; Nassar, M.E. Novel Neural Network-Based Load Frequency Control Scheme: A Case Study of Restructured Power System. IEEE Access 2021, 9, 162231–162242. [Google Scholar] [CrossRef]
- Haydaroğlu, C. Chaos-based optimization for load frequency control in Islanded airport microgrids with hydrogen energy and electric aircraft. Int. J. Hydrogen Energy 2025, in press. [CrossRef]
- Xiong, L.; Song, R.; Huang, S.; Ban, C.; Li, P.; Wang, Z.; Khan, M.W.; Niu, T. Markov jump system modeling and control of inverter-fed remote area weak grid via quantized sliding mode. IEEE Trans. Power Syst. 2024, 40, 2091–2105. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, S.; Xiong, L.; Zhou, Y.; Niu, T.; Gao, F.; Khan, M.W.; Wang, Z.; Ban, C.; Song, R. Distributed secondary control based on bi-limit homogeneity for AC microgrids subjected to non-uniform delays and actuator saturations. IEEE Trans. Power Syst. 2024, 40, 820–833. [Google Scholar] [CrossRef]
- Pradhan, C.; Bhende, C.N.; Samanta, A.K. Adaptive virtual inertia-based frequency regulation in wind power systems. Renew. Energy 2018, 115, 558–574. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, Y.; Yu, P.; Li, B.; Yang, Y.; Shi, Y.; Zhao, L. Coordination control of multiple micro sources in islanded microgrid based on differential games theory. Int. J. Electr. Power Energy Syst. 2018, 97, 11–16. [Google Scholar] [CrossRef]
- Abazari, A.; Monsef, H.; Wu, B. Coordination strategies of distributed energy resources including FW, DG, FC and WTG in load frequency control (LFC) scheme of hybrid isolated micro-grid. Int. J. Electr. Power Energy Syst. 2019, 109, 535–547. [Google Scholar] [CrossRef]
- Yildirim, B. Advanced controller design based on gain and phase margin for microgrid containing PV/WTG/Fuel cell/Electrolyzer/BESS. Int. J. Hydrogen Energy 2021, 46, 16481–16493. [Google Scholar] [CrossRef]
- Khokhar, B.; Dahiya, S.; Parmar, K.P.S. Load frequency control of a microgrid employing a 2D Sine Logistic map based chaotic sine cosine algorithm. Appl. Soft Comput. 2021, 109, 107564. [Google Scholar] [CrossRef]
- Yildirim, B.; Gheisarnejad, M.; Khooban, M.H. A Robust Non-Integer Controller Design for Load Frequency Control in Modern Marine Power Grids. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 852–866. [Google Scholar] [CrossRef]
- Yıldız, S.; Gunduz, H.; Yildirim, B.; Özdemir, M.T. An islanded microgrid energy system with an innovative frequency controller integrating hydrogen-fuel cell. Fuel 2022, 326, 125005. [Google Scholar] [CrossRef]
- Türk, İ.; Kılıç, H. Bulanık Mantık Tip-3 Kullanılarak Mikro Şebeke Frekans Regülasyonu. DÜMF Mühendislik Derg. 2023, 3, 421–436. [Google Scholar] [CrossRef]
- Zadeth, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Chen, F.; Zhang, C.; Mohammadzadeh, A. An Applied Type-3 Fuzzy Logic System: Practical Matlab Simulink and M-Files for Robotic, Control, and Modeling Applications. Symmetry 2023, 15, 475. [Google Scholar] [CrossRef]
- Kilic, H.; Asker, M.E.; Haydaroglu, C. Enhancing power system reliability: Hydrogen fuel cell-integrated D-STATCOM for voltage sag mitigation. Int. J. Hydrogen Energy 2024, 75, 557–566. [Google Scholar] [CrossRef]
- Düzdağ, M.S.; Kılıç, H.; Haydaroglu, C. Tip-3 Bulanık Mantık ile Düşüş Kontrollü İnverter Tabanlı Mikro Şebekelerin İkincil Gerilim ve Frekans Restorasyon Kontrolü. Fırat Üniversitesi Mühendislik Bilim. Derg. 2024, 36, 419–435. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, X.; Zhong, C. Model Predictive Secondary Frequency Control for Islanded Microgrid under Wind and Solar Stochastics. Electronics 2023, 12, 3972. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Robust and Optimal Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]







| Ref. | Controller | Power Source | Working Environment | Advantages | Disadvantages |
|---|---|---|---|---|---|
| [41] | adaptive fuzzy | variable speed wind turbine generator | The validation of the method is performed by means of a real-time hardware-in-the-loop (HIL) simulation based on OPAL-RT. | (i) use of fuzzy-based schema (ii) wind turbine stability | (i) Failure to assess the system impacts of other generation sources such as PV |
| [42] | quadratic differential games theory | PV, BESS, WTG | A Matlab/Simulink model of an islanded microgrid model was created. | (i) Consideration of the operating characteristics of each micro-source (ii) Considering the benefit of all components to realize the coordination arrangement of micro DGs in the microgrid system | (i) This method applies only to the decentralized control method |
| [43] | Self-tuning-Adaptive fuzzy controller | FW, DG, FC, and WT | Matlab/Simulink model of an islanded microgrid model was created. | (i) Using the artificial bee colony (ABC) algorithm in a fuzzy logic controller to determine the parameters of membership functions based on a multi-objective function | (i) not addressing the stability and oscillation impact of other distributed resources and storage systems |
| [44] | The stability boundary locus (SBL) | PV/WTG/FC/Electrolyzer/BESS | Matlab/Simulink model of an islanded microgrid model was created. | (i) Use of a fuel cell as a backup generator | (i) frequency distortion when the GPM value exceeds the specified limit in the mathematically based equations. |
| [45] | two dimensional Sine Logistic map-based chaotic sine cosine algorithm (2D-SLCSCA) optimized classical PID | PV/WTG/FC/FW/BESS/DG and microturbine | Matlab/Simulink model of an islanded microgrid model was created. | (i) The use of an optimized classical PID controller with a two-dimensional Sine Logistic map-based chaotic sine cosine algorithm (2D-SLCSCA) | (i) Power output limitations of MG components such as BESS or DG are not taken into account |
| [46] | fuzzy fractional sequential PI controller | shipboard MG with PV/FC/FW/BESS | A Matlab/Simulink model of the microgrid model has been created, and the validation of the method is carried out with OPAL-RT-based real-time hardware-in-the-loop (HIL) simulation. | (i) type-2 fuzzy fractional sequential PI (SIT2-FFOPI) controller | (i) The impact of other distributed resources and storage systems on stability and oscillation is not addressed (ii) not addressing the problems of grid-connectedness in different microgrid organizations |
| [47] | Fuzzy Logic Controller | PV/FC/Electrolyzer/Biodiesel engine generator, Biogaz Turbine Generator | The microgrid model was created in Matlab/Smilunilk model | (i) Cascaded Dual Input Range Type 2 Fuzzy Logic Controller (C-DIT2-FLC) | (i) not using higher-order fuzzy systems |
| Proposed method | TIP-3 Fuzzy Logic Controller | BESS, FW, DG, FC, PV and WTG | Matlab/Simulink model of an islanded microgrid model was created. | (i) Type-3 FLC, model-independent, no membership function limitation (ii) Considered scholastic variations for wind, solar, and load |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1.5 | 0.08 | ||
| 0.1 | 0.4 | ||
| 0.1 | 0.1667 | ||
| 0.04 | 0.0015 | ||
| 0.004 | 0.26 | ||
| 0.004 | 0.04 |
| NB | NM | Z | PM | PB | |
|---|---|---|---|---|---|
| NB | PB | PB | PM | Z | Z |
| NM | PB | PM | Z | Z | NM |
| Z | PM | Z | Z | Z | NM |
| PM | Z | Z | Z | NM | NB |
| PB | Z | NM | NM | NB | NB |
| Matrix | Type | Eigenvalues | Stability Criterion |
|---|---|---|---|
| A | System dynamics | {−2.86, −1.44} | Hurwitz (asymptotically stable) |
| Q | Design parameter | {1, 1} | Positive definite |
| P | Lyapunov matrix | {1.45, 2.82} | Positive definite |
| Controller | Settling Time (s) | Overshoot (%) | Frequency Deviation (Hz) |
|---|---|---|---|
| PID | 15.2 | 12.5 | 0.5 |
| Type-2 FLC | 12.8 | 8.3 | 0.4 |
| Type-3 FLC | 10.4 | 5.2 | 0.2 |
| Scenario | Description | Real-World Justification |
|---|---|---|
| 1 | Sudden load increase/decrease | Simulates real-time fluctuations in residential or industrial demand. Tests load-following and power balance mechanisms. |
| 2 | Step loss of renewable generation (e.g., PV loss) | Represents loss of solar irradiance due to cloud cover or shadowing. Validates renewable intermittency handling. |
| 3 | Grid disturbance (e.g., voltage/frequency dip) | Emulates short-duration fault or transient fault from an upstream network or generation fluctuations. |
| 4 | Communication delay or signal dropout | Reflects latency and instability in the information layer of a cyber–physical system, affecting control coordination. |
| 5 | Compound event (load + PV + noise) | A worst-case scenario combining multiple disturbances to evaluate robustness under compound stress conditions. |
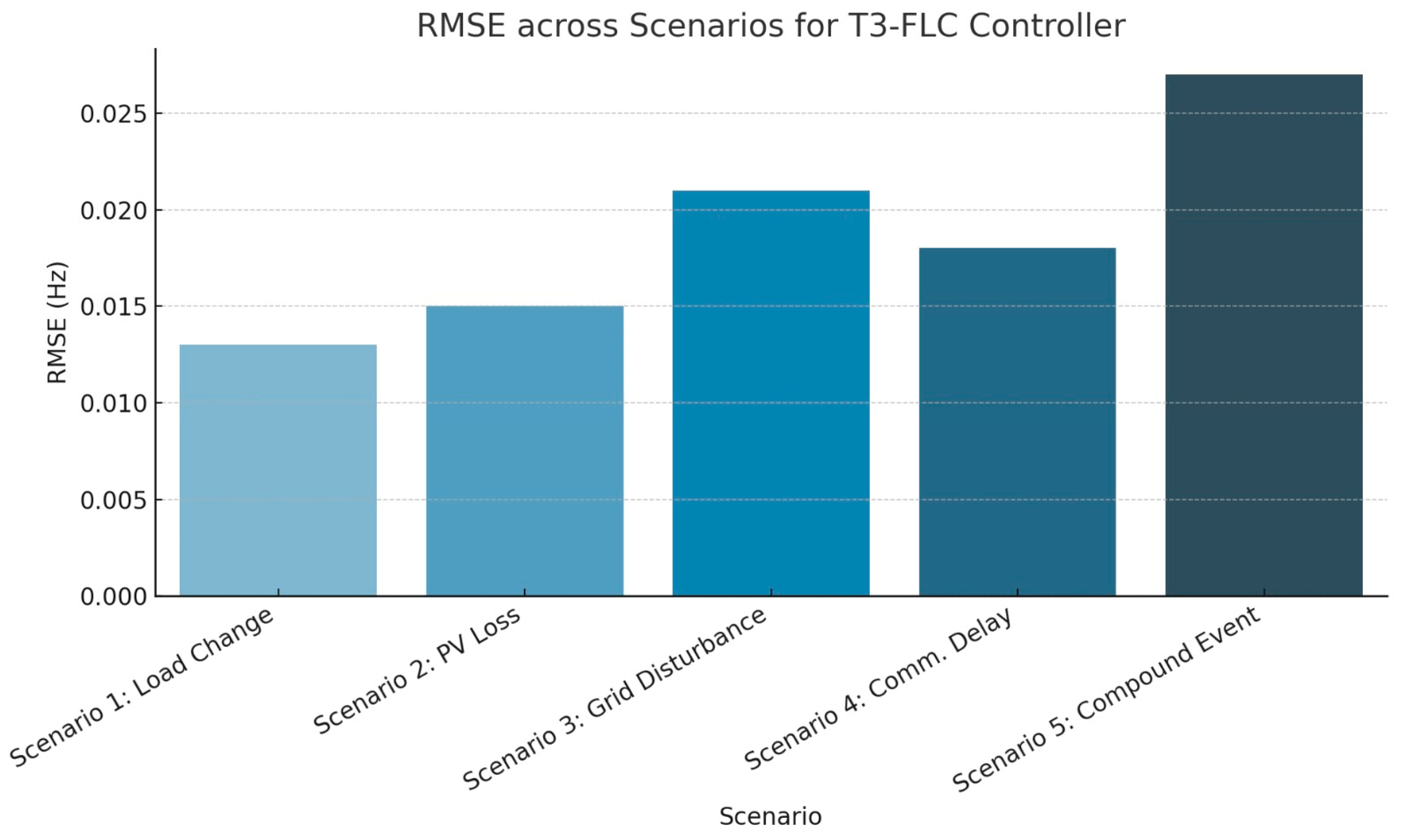
| Scenario | RMSE (Hz) | Overshoot (%) | Settling Time (s) | Control Effort (PU) |
|---|---|---|---|---|
| Scenario 1: Load Change | 0.013 | 2.5 | 1.8 | 0.95 |
| Scenario 2: PV Loss | 0.015 | 3.0 | 2.0 | 1.02 |
| Scenario 3: Grid Disturbance | 0.021 | 4.5 | 2.5 | 1.20 |
| Scenario 4: Communication Delay | 0.018 | 3.8 | 2.3 | 1.10 |
| Scenario 5: Compound Event | 0.027 | 5.5 | 3.1 | 1.35 |
| Controller | Implementation Complexity | Robustness | Real-Time Suitability | Reference |
|---|---|---|---|---|
| PID | Low | Low | High | [54] |
| Type-2 FLC | Moderate | Moderate | Moderate | [55] |
| HOSMC | High | Very High | Moderate | [56] |
| Very High | High | Low | [57] | |
| Proposed T3-FLC | Moderate | High | High | This Work |
| Controller | RMSE (Hz) | Overshoot (%) | Settling Time (s) | Control Effort (PU) |
|---|---|---|---|---|
| PID | 0.039 | 8.2 | 4.0 | 0.88 |
| Type-2 FLC | 0.031 | 6.5 | 3.6 | 1.05 |
| HOSMC | 0.021 | 3.9 | 2.5 | 1.65 |
| Proposed T3-FLC | 0.027 | 5.5 | 3.1 | 1.35 |
| Modeling Approach | RMSE (Hz) | Overshoot (%) | Settling Time (s) | Control Effort (PU) |
|---|---|---|---|---|
| Explicit PV/WTG Modeling | 0.028 | 5.4 | 3.0 | 1.33 |
| Net-Load Abstraction | 0.027 | 5.5 | 3.1 | 1.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Türk, İ.; Kılıç, H.; Haydaroğlu, C.; Top, A. Robust Load Frequency Control in Hybrid Microgrids Using Type-3 Fuzzy Logic Under Stochastic Variations. Symmetry 2025, 17, 853. https://doi.org/10.3390/sym17060853
Türk İ, Kılıç H, Haydaroğlu C, Top A. Robust Load Frequency Control in Hybrid Microgrids Using Type-3 Fuzzy Logic Under Stochastic Variations. Symmetry. 2025; 17(6):853. https://doi.org/10.3390/sym17060853
Chicago/Turabian StyleTürk, İsmail, Heybet Kılıç, Cem Haydaroğlu, and Ahmet Top. 2025. "Robust Load Frequency Control in Hybrid Microgrids Using Type-3 Fuzzy Logic Under Stochastic Variations" Symmetry 17, no. 6: 853. https://doi.org/10.3390/sym17060853
APA StyleTürk, İ., Kılıç, H., Haydaroğlu, C., & Top, A. (2025). Robust Load Frequency Control in Hybrid Microgrids Using Type-3 Fuzzy Logic Under Stochastic Variations. Symmetry, 17(6), 853. https://doi.org/10.3390/sym17060853








