The Mittag-Leffler–Caputo–Fabrizio Fractional Derivative and Its Numerical Approach

Abstract

This study introduces a novel fractional-order derivative, termed the Mittag-Leffler–Caputo–Fabrizio (MLCF) fractional derivative, which is characterized by a singular kernel. Symmetry plays a key role in the structure and behavior of fractional operators, and our formulation reflects this by incorporating symmetric properties of the Mittag-Leffler function and its integral representation. To numerically approximate the MLCF derivative, we apply a two-point finite forward difference scheme to estimate the first-order derivative of the function $u(\lambda )$ within the integral component of the definition. This leads to the construction of a new numerical differentiation scheme. Our analysis demonstrates that the proposed approximation exhibits first-order convergence, with absolute errors decreasing as the time step size h diminishes. These errors are quantified by comparing our numerical results with exact analytical solutions, reinforcing the accuracy of the method.

1. Introduction

Fractional derivatives extend the concept of classical differentiation by allowing the differentiation and integration of non-integer orders. Numerous definitions have been introduced in this field, including the $\psi$-Caputo–Katugampola derivative [1], the weighted Atangana–Baleanu fractional operators [2], the $\mathsf{\Theta }$-fractional operators [3], the $\psi$-proportional fractional operators [4], the $\psi$-weighted fractional operators [5], the $\psi$-Hilfer fractional operators [6], the $\phi$-conformable derivative [7], the nabla fractional operators [8], and the fractal fractional operators [9].

Differential equations involving arbitrary real orders $\nu >0$ serve as essential tools for modeling diverse physical systems across multiple disciplines, including science and engineering. Such equations find applications in areas such as statistical mechanics, Brownian motion, viscoelasticity, continuum and quantum mechanics, biosciences, chemical process engineering, and control systems. In [10], the authors studied the new mathematical model using the Caputo–Fabrizio fractional derivative. In [11], the authors studied the modeling of the dynamics of hepatitis E using the Caputo–Fabrizio derivative. More details on these applications can be found in [12,13,14,15,16,17,18,19,20,21] and related references.

The increasing attention toward fractional calculus (FC) has led to the emergence of multiple approaches for defining fractional integrals and derivatives. In contrast to the Riemann–Liouville fractional integral, derivatives have been formulated in numerous ways, with certain definitions equivalent only under specific conditions of the function being differentiated [22,23,24,25]. Furthermore, three recent classifications of fractional operators were explored in [26].

With the growing role of fractional derivatives in modeling complex physical phenomena, it becomes essential not only to establish a well-defined and widely accepted formulation for these derivatives but also to develop precise and efficient numerical approximations. This is particularly crucial for handling systems characterized by inherent singularities and nonlinearities [27,28,29,30,31]. However, the non-local nature of fractional operators poses challenges in designing computationally efficient algorithms, as they require incorporating all prior system states during simulations. This characteristic, often referred to as persistent memory, significantly increases both computational effort and processing time [32,33].

There are several numerical methods in the literature for Caputo–Fabrizio, such as finite difference methods, trapezoidal methods, and interpolation, among which we mention the two-point finite forward difference formula [34], Simpson’s $1/3$ rule [35], the quadratic interpolation-based $L1-2$ formula [36], and the $L1$ and $L1-2$ formulas using Lagrange interpolation [37].

To address this issue, various short-memory principles have been introduced in recent studies [38,39]. These approaches effectively reduce computational costs and minimize the accumulation of rounding errors when applying numerical methods, making them particularly advantageous for solving fractional initial value problems.

This study introduces a novel fractional derivative, referred to as the MLCF fractional derivative, along with a numerical scheme for its approximation. The proposed method utilizes a two-point finite difference approach to approximate the derivative term $u^{\prime }(\lambda )$. In addition, error analysis of this numerical approximation is presented. Consequently, this work formulates a numerical differentiation formula for the MLCF fractional derivative.

As demonstrated in Section 3, the error analysis reveals that the local truncation error of the proposed approximation contains a positive constant dependent on the fractional order $\nu$, resulting in an error term of $O(h)$. This confirms the first-order accuracy of the developed numerical approach. To enhance precision, the approximation is applied over a continuous temporal mesh, as elaborated in Section 4. Finally, Section 5 presents numerical experiments that validate the efficiency and accuracy of the proposed method.

2. Preliminaries

This section revisits fundamental definitions that are relevant to this study.

Definition 1

([12]). Let $0<\nu <1$. The Caputo fractional derivative for $u(\lambda )$ is defined as

$${}^{C}D_{\lambda }^{\nu }\left[u(\lambda )\right]={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\nu )}}{\int }_0^{\lambda }{(\lambda -\tau )}^{-\nu }{u}^{\prime }(\tau )d\tau ,$$

(1)

where $\lambda >0,u\in C[0,\lambda ]$, with $\mathrm{\Gamma }(.)$ denoting the Gamma function.

Definition 2

([40]). Let $0<\nu <1$. The Caputo–Fabrizio derivative is expressed as follows:

$$\begin{array}{cc}\hfill {}^{CF}D_{\lambda }^{\nu }\left[u(\lambda )\right]& ={\displaystyle \frac{M(v)exp\left[-v\frac{\lambda }{1-\nu }\right]}{1-\nu }}{\int }_0^{\lambda }{u}^{\prime }(\tau )exp\left[\nu {\displaystyle \frac{\tau }{1-\nu }}\right]d\tau ,\hfill \end{array}$$

(2)

with $M(\nu )$ serving as a normalization function—any smoothness. $M(\nu )$ plays a role in the following:

1. 

Ensuring consistency at integer orders:

• When $\nu \to 0^{+}$, the fractional derivative should reduce to the original function $u(\lambda )$.
• When $\nu \to 1^{-}$, it should recover the classical first derivative $u^{\prime }(\lambda )$.
• Thus, $M(\nu )$ must satisfy

  $$M(0)=M(1)=1.$$

2. 

Dimensional analysis:

• The fractional derivative has units dependent on ν.
• $M(\nu )$ adjusts the operator so that both sides of the equation have consistent physical dimensions.

3. 

Kernel Normalization: The term ${\displaystyle \frac{M(\nu )}{1-\nu }}$ normalizes the exponential kernel to ensure proper weighting in the integral.

Additionally, u belongs to the Sobolev space $H^1(a,b)$ with $b>a$. It is worth noting that the given definition does not include a singular kernel. Definition 2 plays a central role in the forthcoming sections of this work.

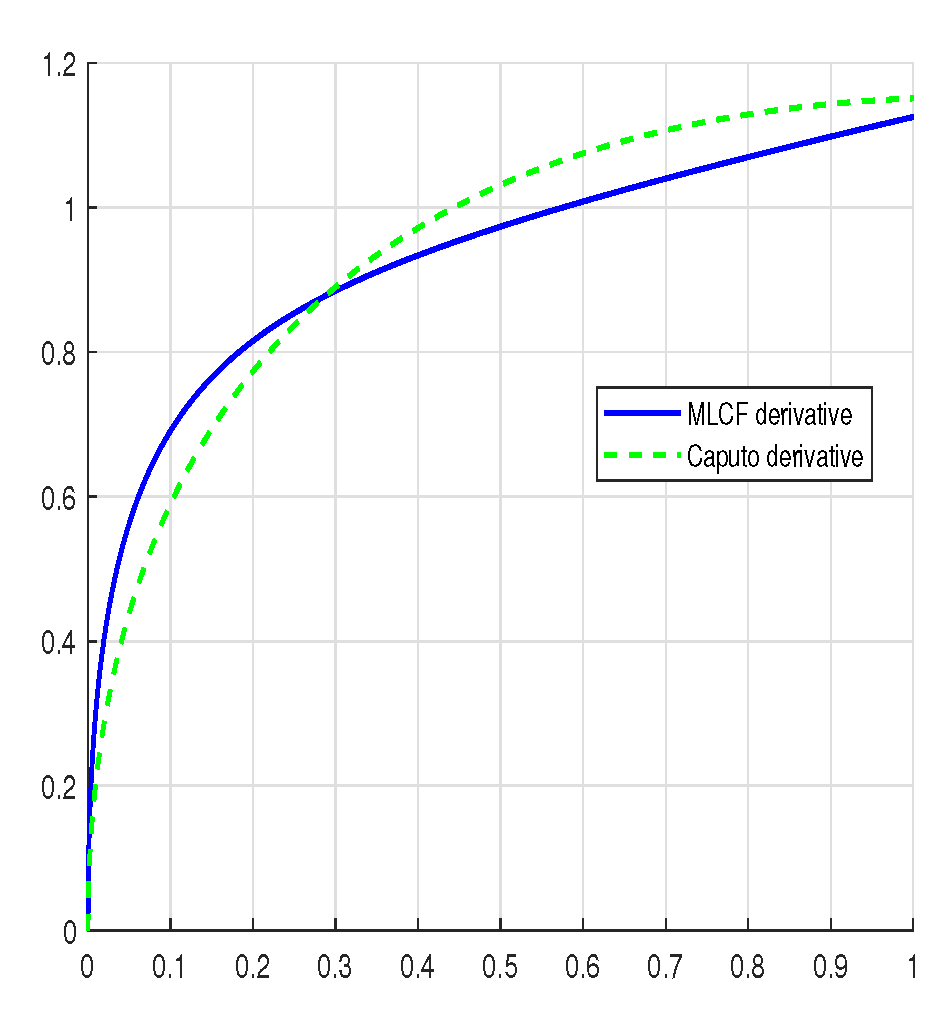
3. The Mittag-Leffler–Caputo–Fabrizio Fractional Derivative

In this section, we present the new fractional derivative termed the Mittag-Leffler–Caputo–Fabrizio fractional derivative. From the Definition 2, we have new definitions:

Definition 3.

Let $0<\nu <1$ and $0<\alpha \le 1$. The Mittag-Leffler–Caputo–Fabrizio fractional derivative is defined as follows:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }u(\lambda )& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }^{\alpha })}^{-1}}{1-\nu }}{\int }_0^{\lambda }{\mathbb{E}}_{\alpha }({\displaystyle \frac{\nu }{1-\nu }}{s}^{\alpha })u^{\prime }(s)ds,\hfill \end{array}$$

(3)

where the one-parameter Mittag-Leffler function is

$${\mathbb{E}}_{\alpha }(\lambda )=\sum _{k=0}^{\infty }{\displaystyle \frac{{\lambda }^k}{\mathrm{\Gamma }(\alpha k+1)}}.$$

There are many uses for the Mittag-Leffler function; see [41,42,43,44,45,46].

Remark 1.

This definition is a generalization of the Caputo–Fabrizio derivative with the flexibility of α and ν. If $\alpha =1$, we obtain the Caputo–Fabrizio fractional derivative in Definition 2.

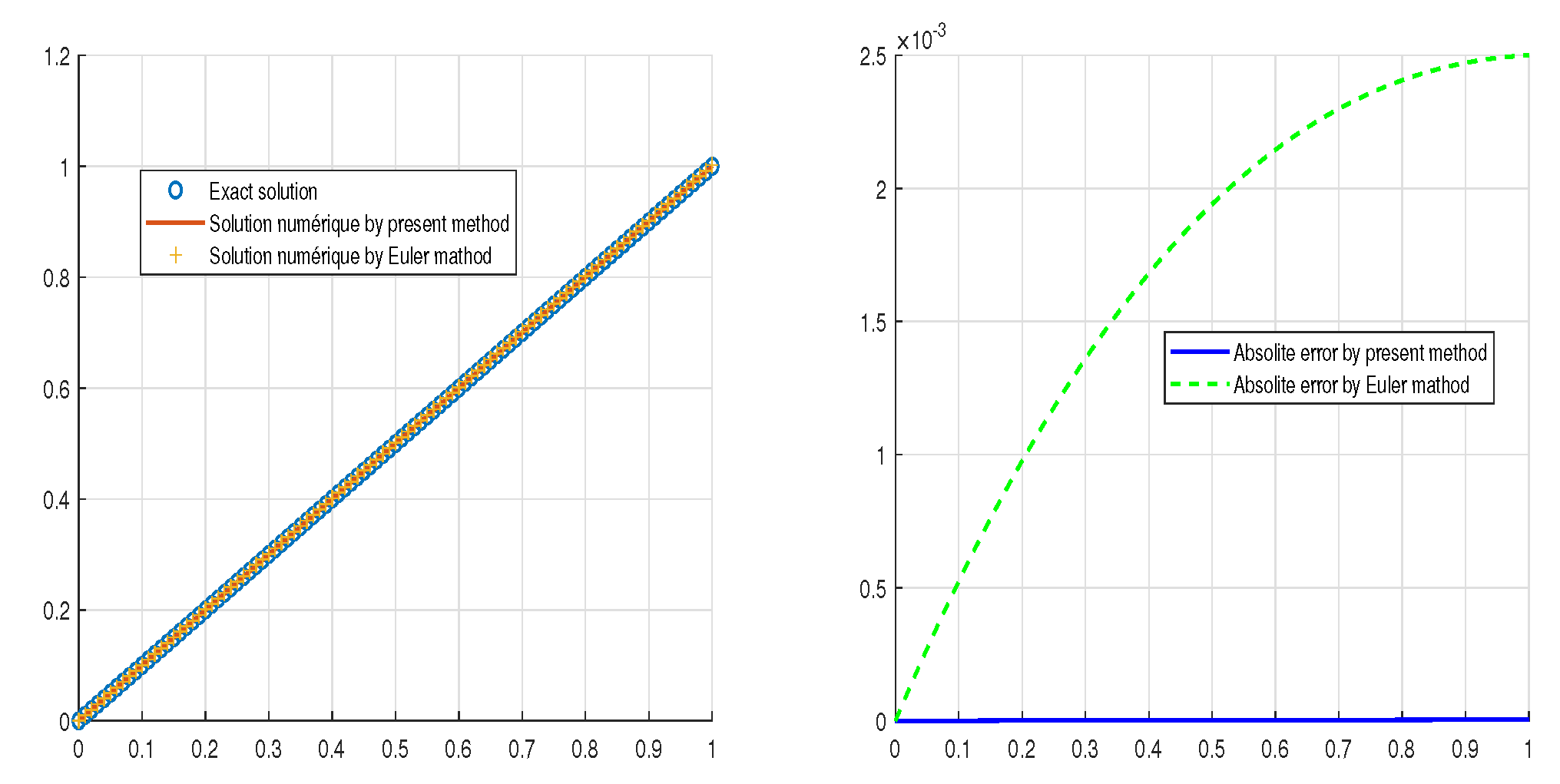
4. Numerical Approximation

In this section, we present the numerical approximation of the MLCF fractional derivative. Consider a function $u(\lambda )\in H^1(a,b)$ and define the interval $J=[0,T]$. Let h be a constant step size given by $h=T/n$ for some $n\in \mathbb{N}$, and set ${\lambda }_k=kh$. Our goal is to derive a numerical approximation for the integral appearing in Equation (3). A straightforward approach is to apply the standard two-point finite forward difference method to approximate the first derivative over the interval J. Evaluating at $\lambda ={\lambda }_n$ for $0<\nu <1$, we obtain the following expression:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_n}& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{1-\nu }}{\int }_0^{{\lambda }_n}{u}^{\prime }(\tau ){\mathbb{E}}_{\alpha }\left(\nu {\displaystyle \frac{{\tau }^{\alpha }}{1-\nu }}\right)d\tau \hfill \\ & \approx {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{1-\nu }}\sum _{k=0}^{n-1}\left[{\displaystyle \frac{u_{k+1}-u_k}{h}}+\mathcal{O}(h)\right]{\int }_{{\lambda }_k}^{{\lambda }_{k+1}}{\mathbb{E}}_{\alpha }\left(\nu {\displaystyle \frac{{\tau }^{\alpha }}{1-\nu }}\right)d\tau ,\hfill \end{array}$$

as the integral is subsequently approximated using the two-point trapezoidal quadrature method

$${\int }_a^{b}g(z)\mathrm{d}z\approx {\displaystyle \frac{b-a}{2}}(g(a)+g(b)),$$

Then,

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_n}& \approx {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{1-\nu }}\sum _{k=0}^{n-1}[{\displaystyle \frac{u_{k+1}-u_k}{h}}\hfill \\ & +\mathcal{O}(h)]{\displaystyle \frac{h}{2}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})\right).\hfill \end{array}$$

For $n=1,2$, and 3, we, respectively, obtain

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_1}& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_1)}^{-1}}{2(1-\nu )}}(u_1-u_0)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_1^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_0^{\alpha }}{1-\nu }})\right)\hfill \\ \hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_2}& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_2)}^{-1}}{2(1-\nu )}}[(u_1-u_0)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_1^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_0^{\alpha }}{1-\nu }})\right)\hfill \\ \hfill & +(u_2-u_1)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_2^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_1^{\alpha }}{1-\nu }})\right)]\hfill \\ \hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_3}& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_3)}^{-1}}{2(1-\nu )}}[(u_1-u_0)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_1^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_0^{\alpha }}{1-\nu }})\right)\hfill \\ \hfill & +(u_2-u_1)({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_2^{\alpha }}{1-\nu }})\hfill \\ \hfill & +{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_1^{\alpha }}{1-\nu }}))+(u_3-u_2)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_3^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_2^{\alpha }}{1-\nu }})\right)].\hfill \end{array}$$

(4)

Continuing in the same way, we obtain

$${}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_n}={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{(1-\nu )2}}\sum _{k=0}^{n-1}(u_{k+1}-u_k)\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})\right).$$

One can replace k with $k-1$ to obtain the following form:

$${}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_n}={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{(1-\nu )2}}\sum _{k=1}^n(u_{n-k+1}-u_{n-k})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right).$$

(5)

Equation (5) represents a first-order time discretization of the MLCF derivative. Based on this, the following theorem is formulated.

Theorem 1.

Consider dividing the interval $[0,T]$ into n equal subintervals, each of width $h=T/n$, using the nodes ${\lambda }_k=kh$ for $k=0,1,\dots ,n$. This leads to the following expression:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }(u,h,\nu )& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{k=1}^n(u_{n-k+1}-u_{n-k})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right)\hfill \\ \hfill & +{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{k=1}^n\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right)\mathcal{O}(h^2),\hfill \end{array}$$

(6)

which is the proposed numerical approximation to the MLCF derivative. In addition, we have

$${}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]{|}_{\lambda ={\lambda }_n}={}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }(u,h,\nu )-E_{MLCF}(u,h,\nu ),{\lambda }_n>0,0<\nu <1.$$

Additionally, if $u(\lambda )\in C^1[0,T]$, there exists a constant $A_{\nu }$ that depends solely on ν, such that the error term $E_{MLCF}(u,h,\nu )$ can be expressed in the following manner:

$$\left|E_{MLCF}(u,h,\nu )\right|\le A_{\nu }{∥u^{\prime }∥}_{\infty }{T}^{\nu }h=\mathcal{O}(h).$$

Proof. 

Based on the previous steps in Section 4, we obtain the following:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }(u,h,\nu )& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{k=1}^n(u_{n-k+1}-u_{n-k})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right)\hfill \\ \hfill & +{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{k=1}^n\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right)\mathcal{O}(h^2),\hfill \end{array}$$

(7)

By considering the third term in Equation (7), we obtain

$${\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_n^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{k=1}^n\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{n-k}^{\alpha }}{1-\nu }})\right)\mathcal{O}(h^2).$$

   □

The next section presents several test cases selected to evaluate the effectiveness of the aforementioned approximations.

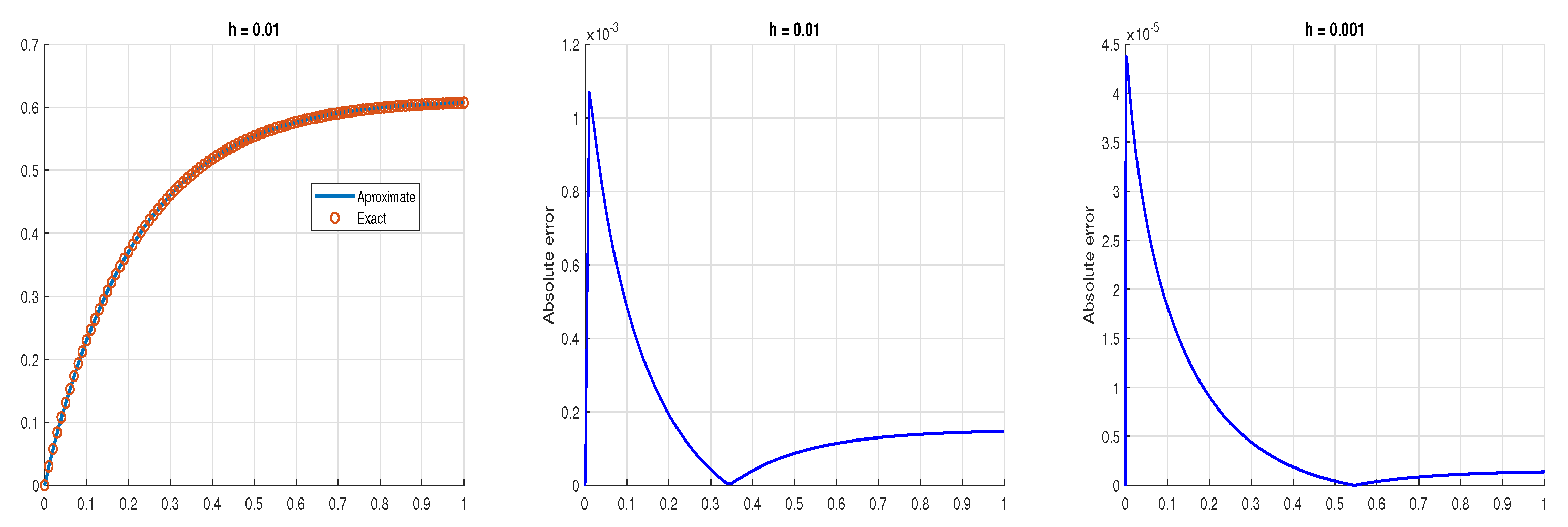
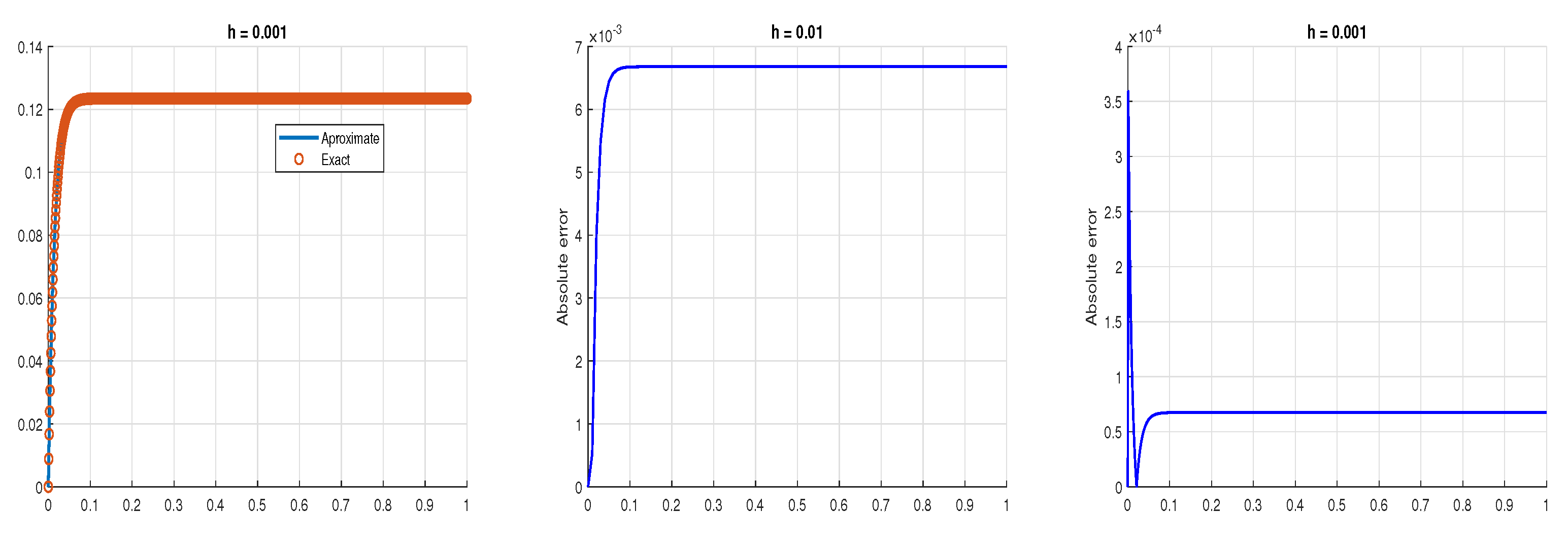
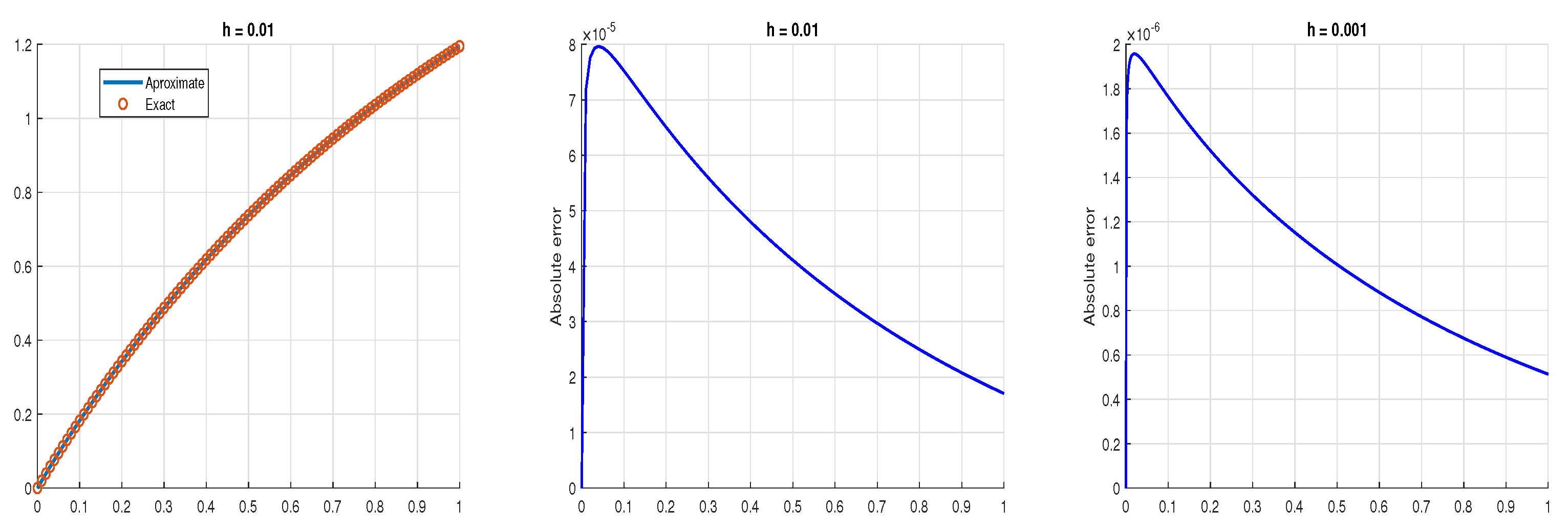
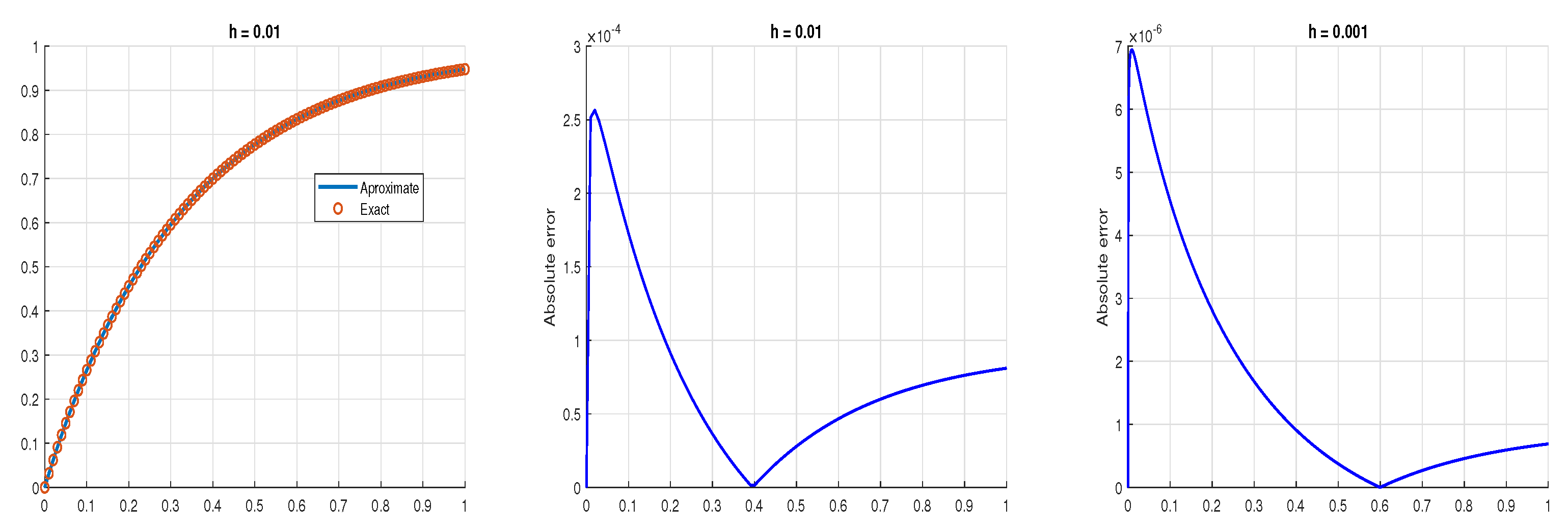
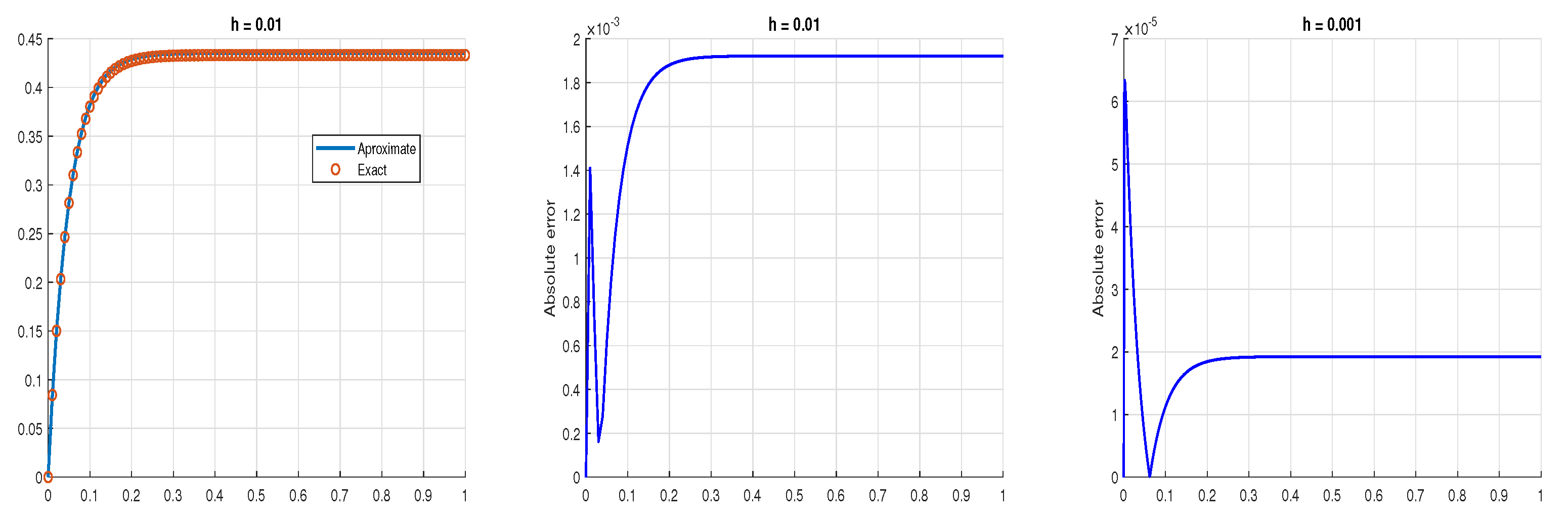
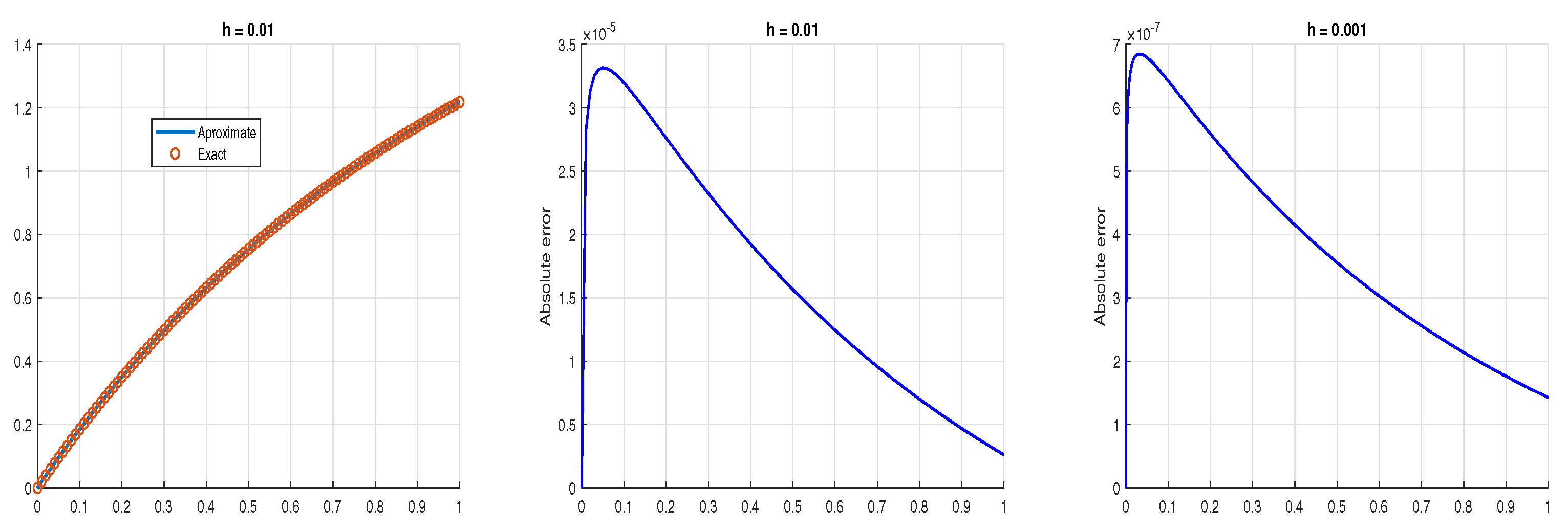
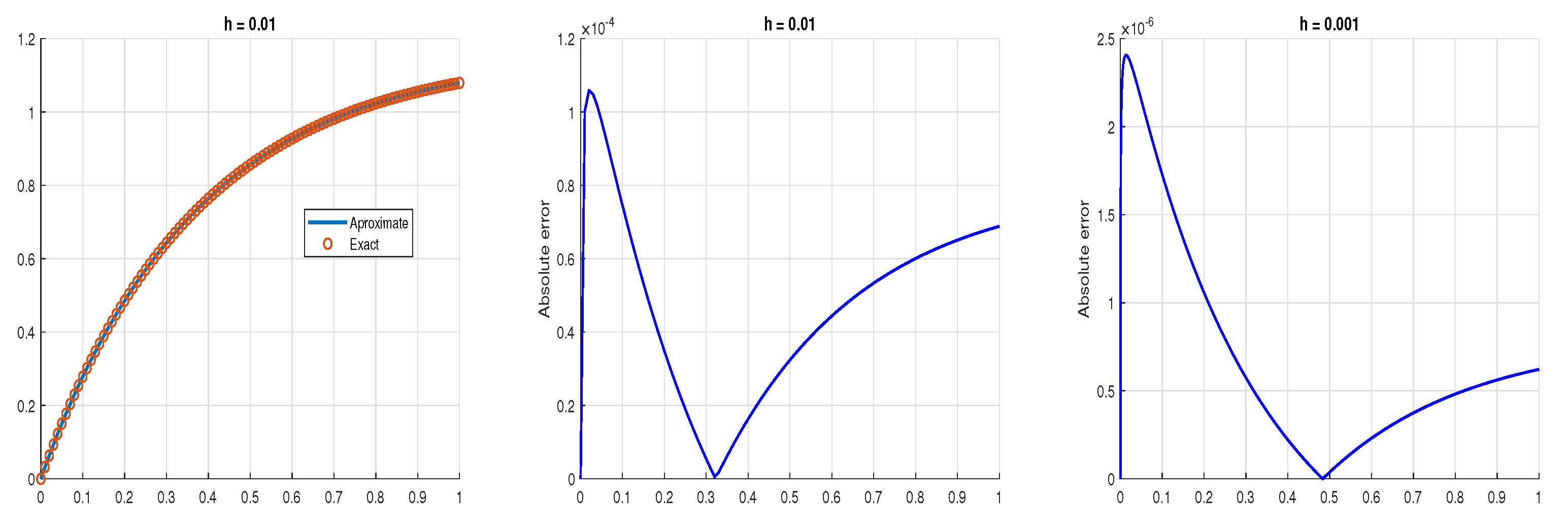
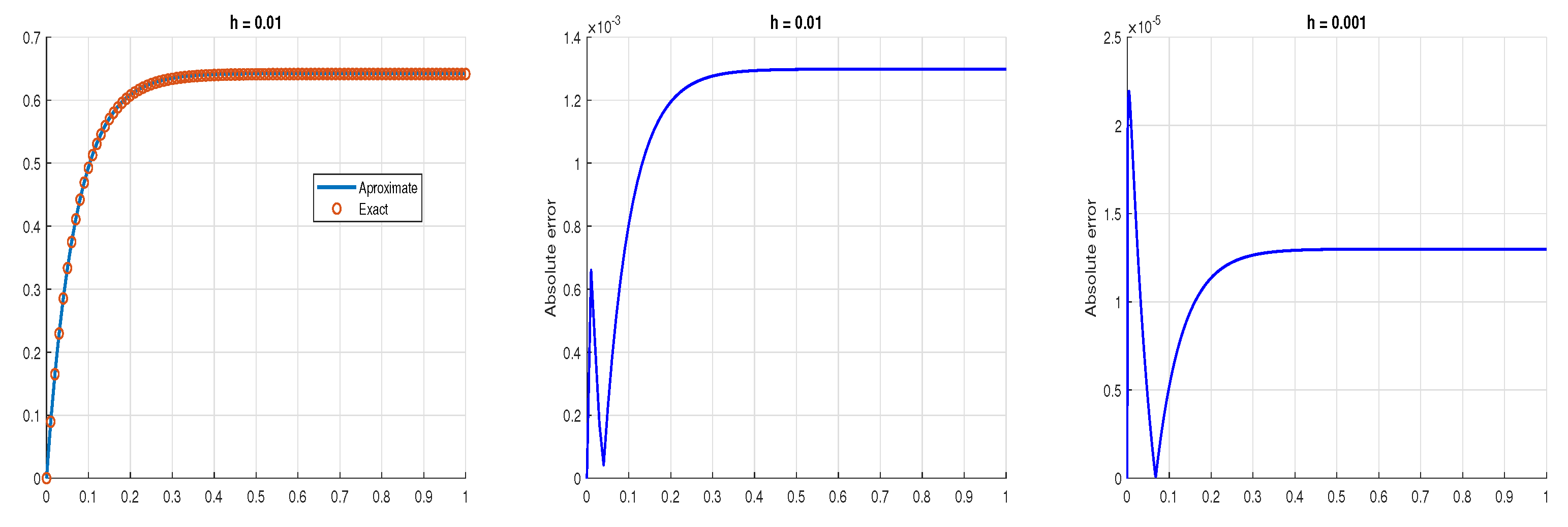
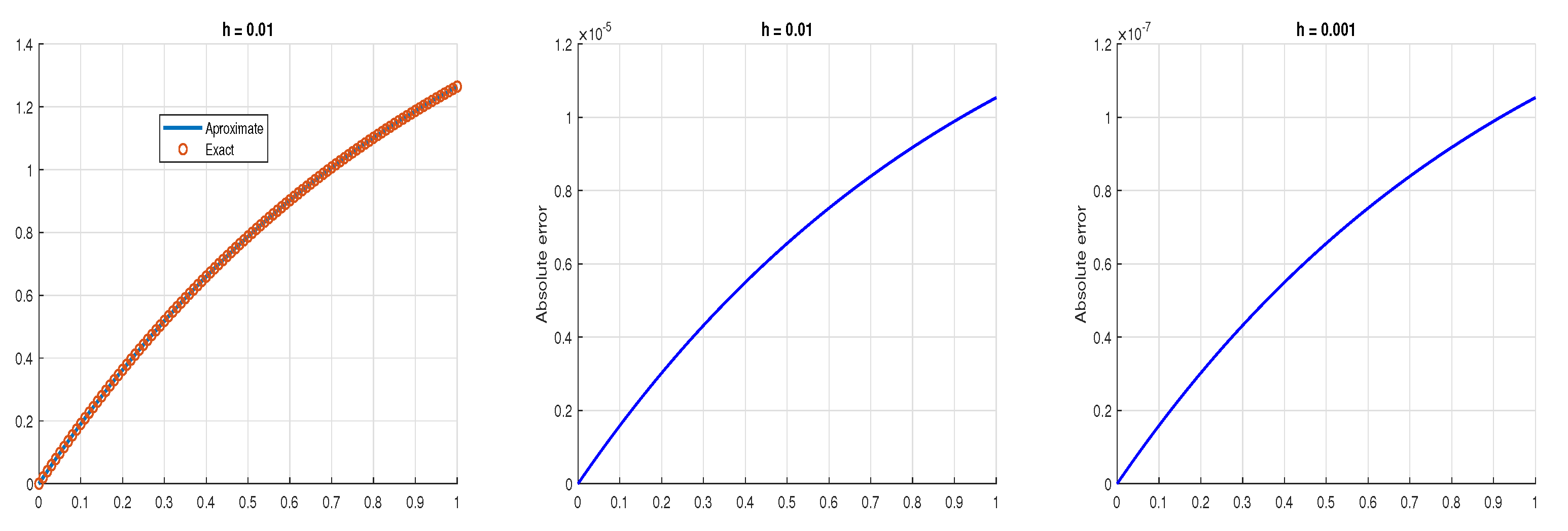
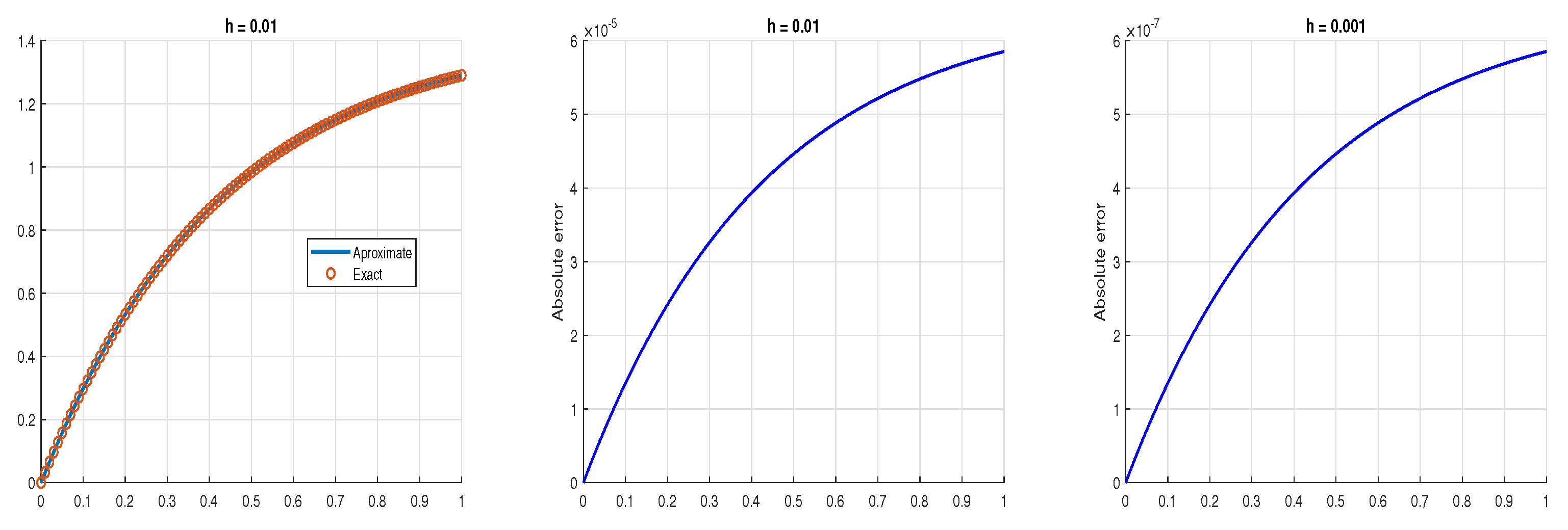
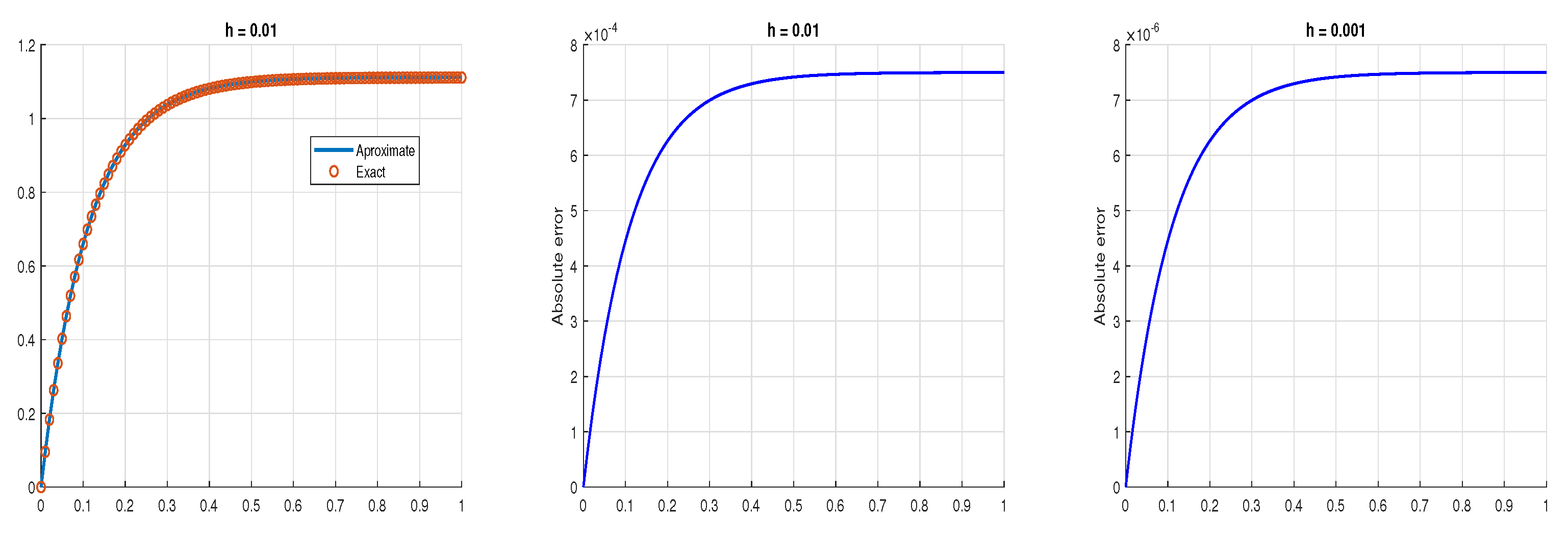
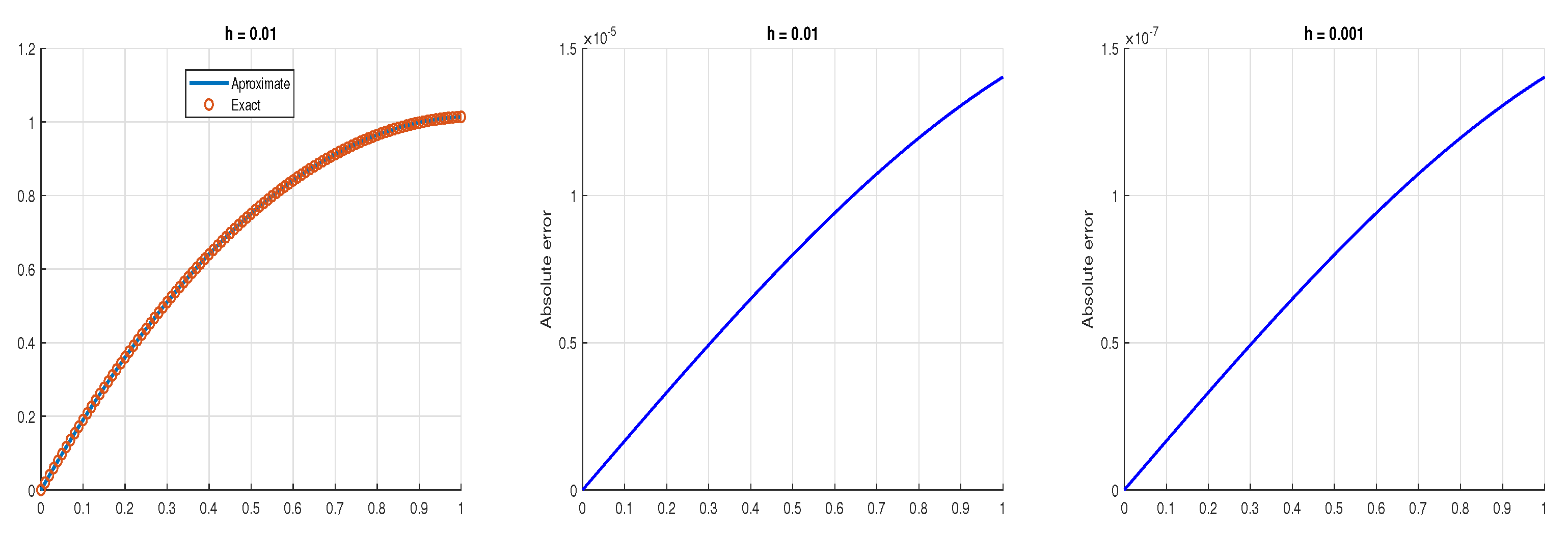
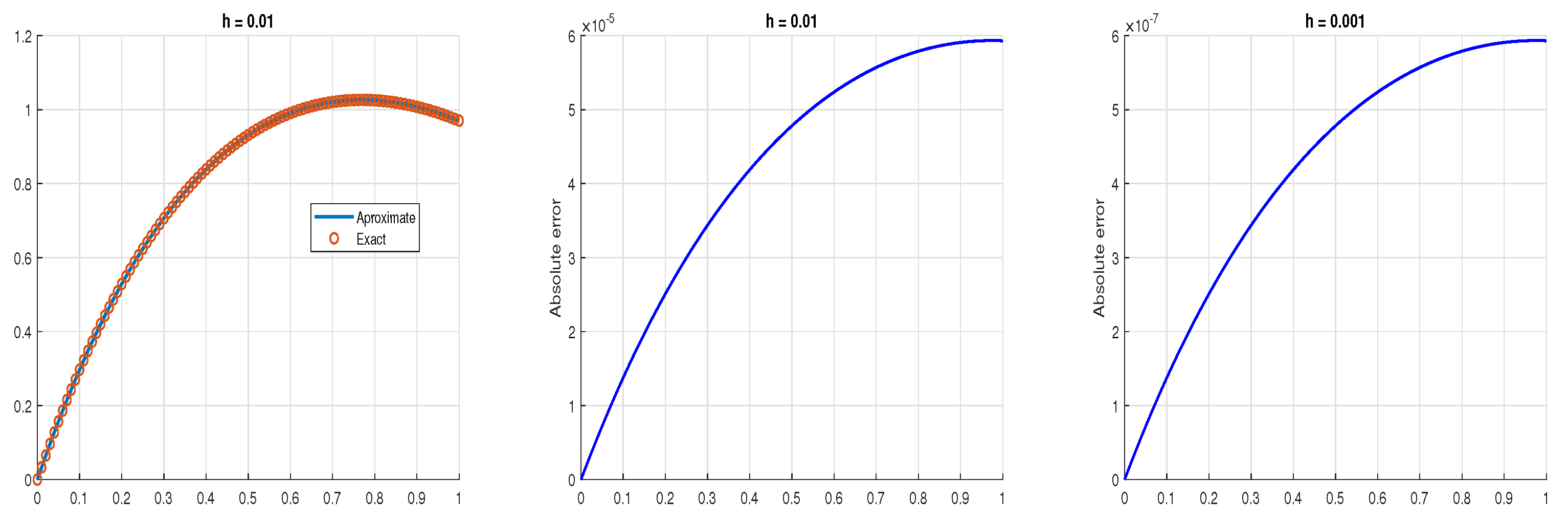
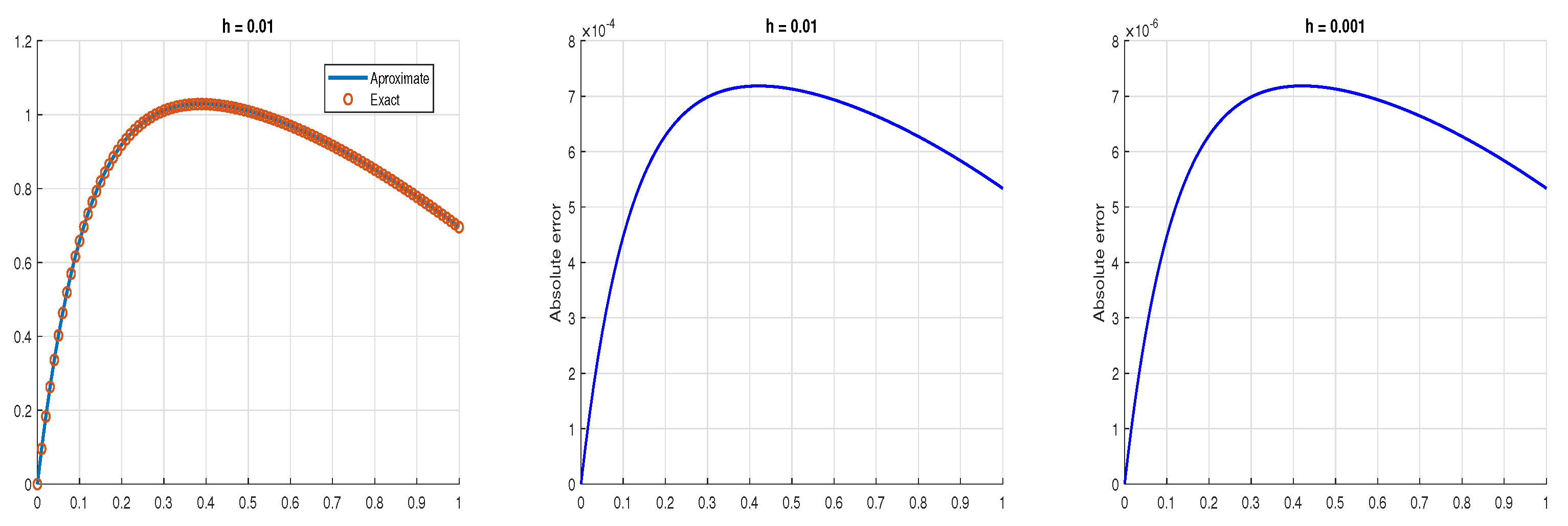
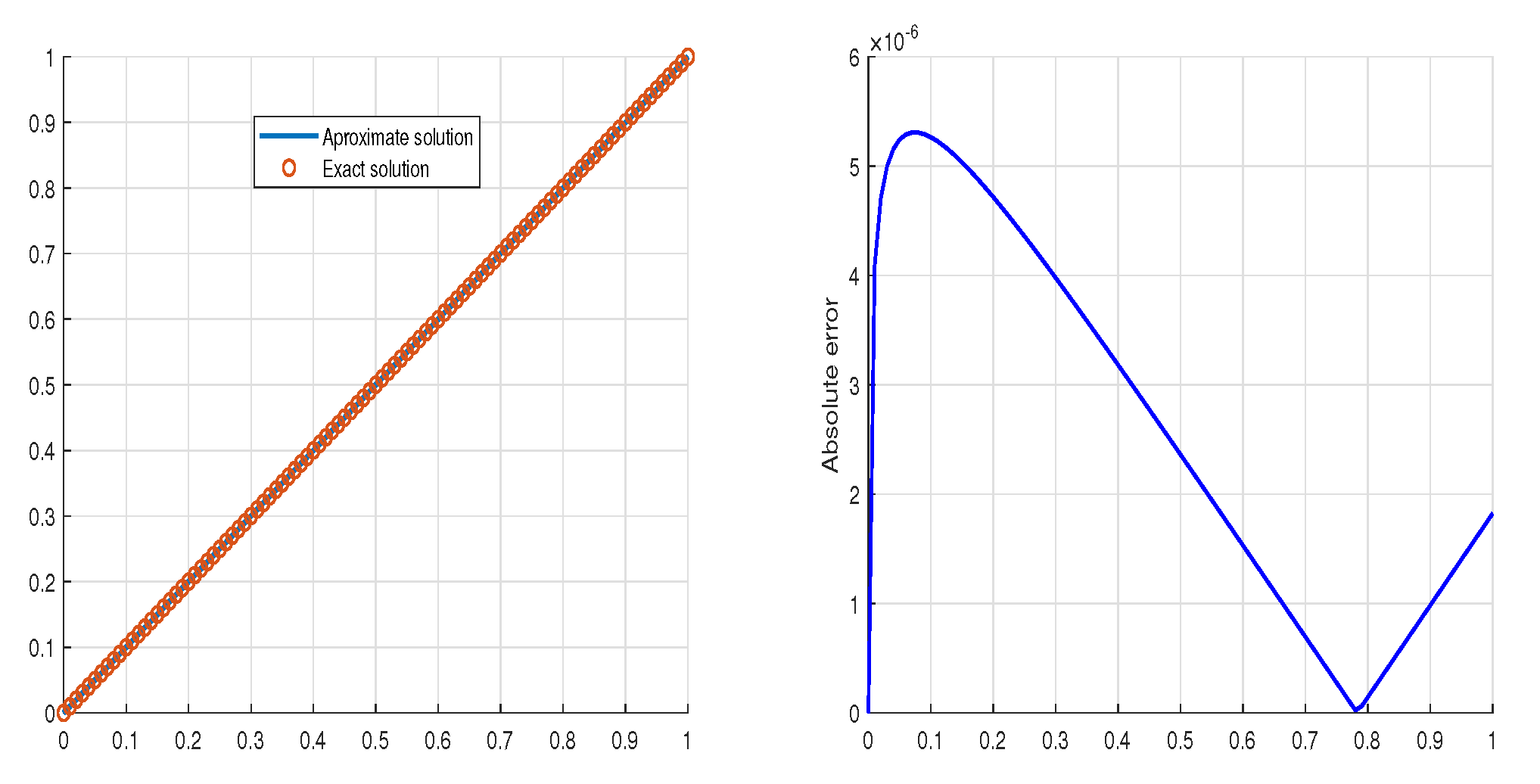
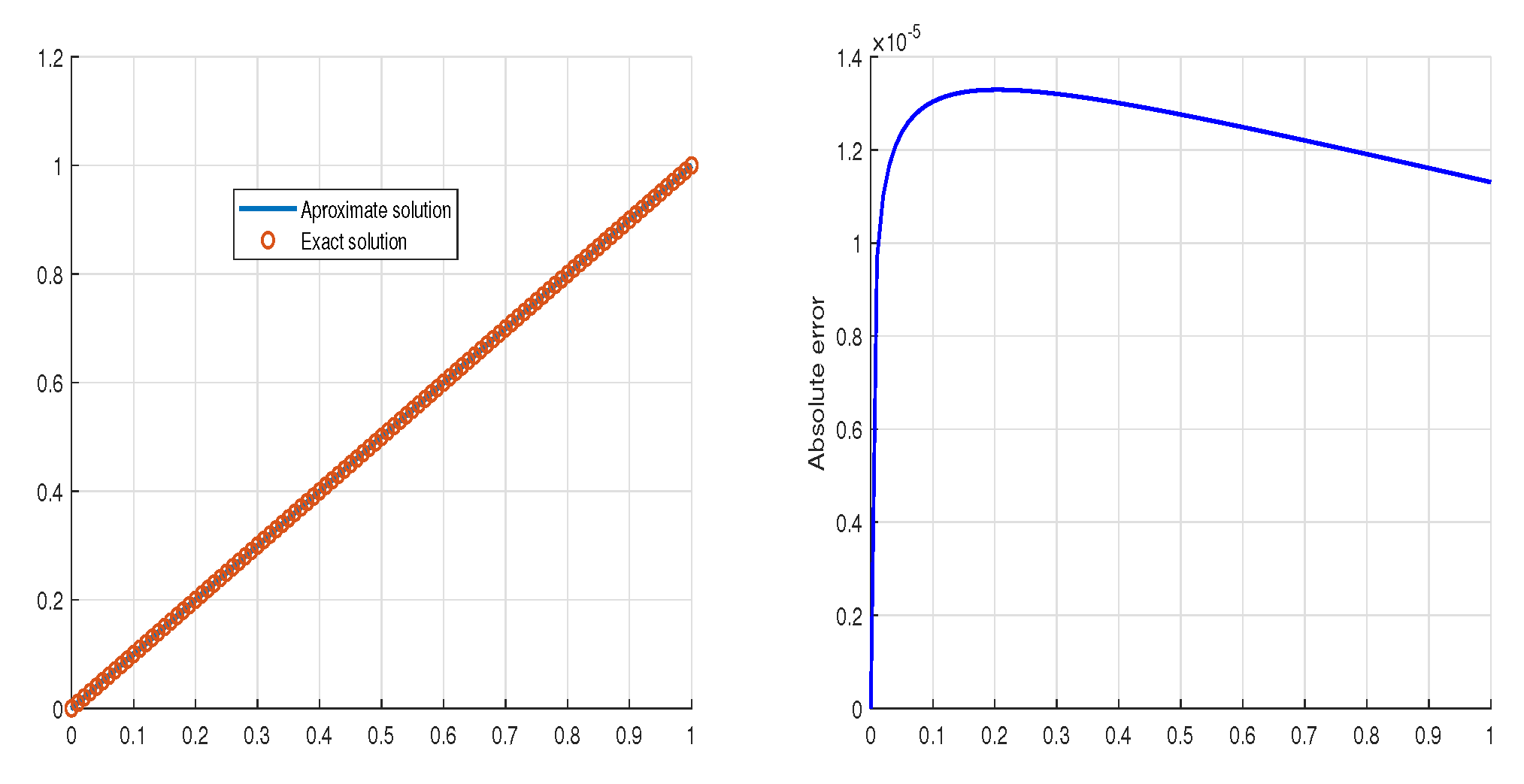
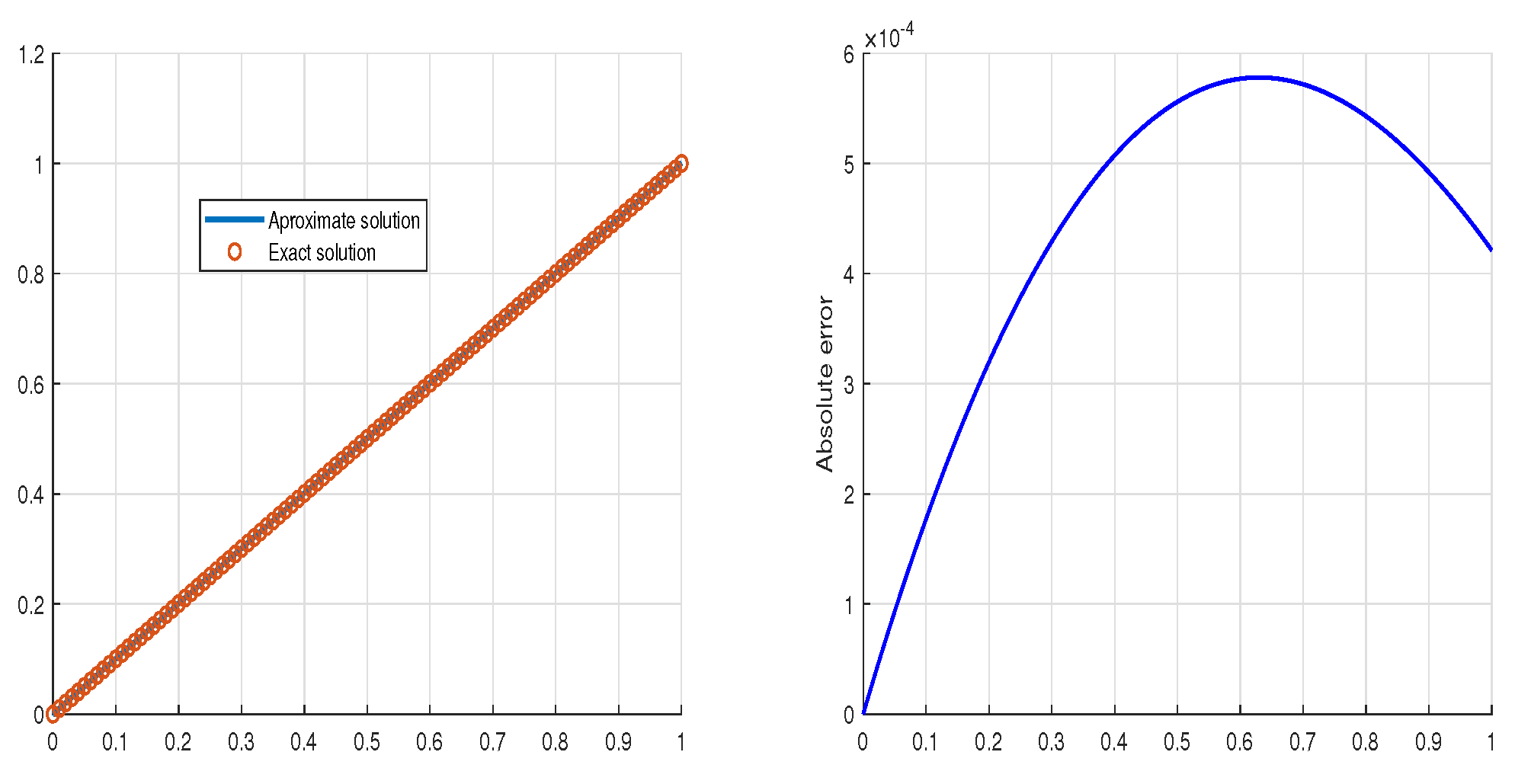
5. Examples

To evaluate the effectiveness of the proposed numerical approximation (5), two distinct mathematical functions were selected for testing and two applications. The computations were conducted for fractional orders $\alpha \in \{0.5,0.7,0.8,0.9,1\}$ and $\nu \in \{0.5,0.7,0.8,0.9\}$, assuming $M(\nu )=1$. The test cases and their corresponding numerical simulations are summarized in

Table 1. The absolute errors for different $\alpha$ and v.

	$\alpha =0.5$		$\alpha =0.7$
$\nu$	$h={10}^{-2}$	$h={10}^{-3}$	$h={10}^{-2}$	$h={10}^{-3}$
$0.5$	$7.8521\times {10}^{-5}$	$2.8099\times {10}^{-6}$	$1.7050\times {10}^{-5}$	$5.1342\times {10}^{-7}$
$0.7$	$1.4702\times {10}^{-4}$	$1.3851\times {10}^{-6}$	$8.1065\times {10}^{-5}$	$6.9029\times {10}^{-7}$
$0.8$	$6.6638\times {10}^{-4}$	$6.6666\times {10}^{-6}$	$3.0124\times {10}^{-4}$	$3.0064\times {10}^{-6}$
$0.9$	$6.6773\times {10}^{-3}$	$6.7493\times {10}^{-5}$	$1.9215\times {10}^{-3}$	$1.9232\times {10}^{-5}$
	$\alpha =0.8$		$\alpha =1$
$\nu$	$h={10}^{-2}$	$h={10}^{-3}$	$h={10}^{-2}$	$h={10}^{-3}$
$0.5$	$2.6185\times {10}^{-6}$	$1.4263\times {10}^{-7}$	$1.0535\times {10}^{-5}$	$1.0535\times {10}^{-7}$
$0.7$	$6.8827\times {10}^{-5}$	$6.2163\times {10}^{-7}$	$5.8529\times {10}^{-5}$	$5.8530\times {10}^{-7}$
$0.8$	$2.3386\times {10}^{-4}$	$2.3281\times {10}^{-6}$	$1.6361\times {10}^{-4}$	$1.6361\times {10}^{-6}$
$0.9$	$1.2985\times {10}^{-3}$	$1.2990\times {10}^{-5}$	$7.4981\times {10}^{-4}$	$7.4991\times {10}^{-6}$

and

Table 2. The absolute errors for different $\nu$ and h.

$\mathit{\nu }$	$\mathit{h}={10}^{-2}$	$\mathit{h}={10}^{-3}$
$0.5$	$1.4024\times {10}^{-5}$	$1.4025\times {10}^{-7}$
$0.7$	$5.9311\times {10}^{-5}$	$5.9311\times {10}^{-7}$
$0.8$	$1.4276\times {10}^{-4}$	$1.4276\times {10}^{-6}$
$0.9$	$5.3376\times {10}^{-4}$	$5.3379\times {10}^{-6}$

. MATLAB R2020b was used to perform the numerical computations.

Example 1.

Let function $u(\lambda ):=\lambda ,\lambda \in [0,1]$. The ${}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }$ of λ is

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }u(\lambda )& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }^{\alpha })}^{-1}}{1-\nu }}{\int }_0^{\lambda }{\mathbb{E}}_{\alpha }({\displaystyle \frac{\nu }{1-\nu }}{s}^{\alpha })ds\hfill \\ & ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }^{\alpha })}^{-1}}{1-\nu }}{\int }_0^{\lambda }{\mathbb{E}}_{\alpha }({\displaystyle \frac{\nu }{1-\nu }}{s}^{\alpha })ds,\hfill \end{array}$$

since

$${\int }_0^z{\mathbb{E}}_{\alpha ,\beta }(c{\lambda }^{\alpha }){\lambda }^{\beta -1}d\lambda =z^{\beta }{\mathbb{E}}_{\alpha ,\beta +1}(c{z}^{\alpha }),$$

so

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }u(\lambda )& ={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }^{\alpha })}^{-1}}{1-\nu }}\lambda {\mathbb{E}}_{\alpha ,2}({\displaystyle \frac{\nu }{1-\nu }}{\lambda }^{\alpha }).\hfill \end{array}$$

In Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, we plot the MLCF of function u, the numerical approximation of the MLCF of u, and absolute errors for deferential v and $\alpha$.

Example 2.

Let $u(\lambda )=sin(\lambda )$. Then, we have

$${}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }\left[u(\lambda )\right]={\displaystyle \frac{-\nu e^{\frac{\nu }{\nu -1}\lambda }+\nu cos(\lambda )+(1-\nu )sin(\lambda )}{1-2\nu +2{\nu }^2}}.$$

In Figure 17, Figure 18, Figure 19 and Figure 20, we plot the MLCF of function u, the numerical approximation of the MLCF of u, and absolute errors for deferential v and $\alpha$.

Application 1

Consider the following fractional problem:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }u(\lambda )& =\lambda f(\lambda ),\lambda \in ]0,1],\hfill \\ \hfill u(0)& =0,\hfill \end{array}$$

(8)

where

$$f(\lambda )={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }^{\alpha })}^{-1}}{1-\nu }}{\mathbb{E}}_{\alpha ,2}({\displaystyle \frac{\nu }{1-\nu }}{\lambda }^{\alpha }).$$

The exact solution is $u(\lambda )=\lambda$. Consider dividing the interval $[0,1]$ into n equal subintervals, each of width $h=1/n$, using the nodes ${\lambda }_k=kh$ for $k=0,1,\dots ,n$. from Equation (8), we have

$$\begin{array}{c}\hfill {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{i=1}^k(u_{k-i+1}-u_{k-i})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right)={\lambda }_{k}f({\lambda }_k),\end{array}$$

for $k=1,\dots ,n$. Then,

$$\begin{array}{cc}& {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}{u}_k\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)={\lambda }_{k}f({\lambda }_k)\hfill \\ & +{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}{u}_{k-1}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)\hfill \\ & -{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{i=2}^k(u_{k-i+1}-u_{k-i})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right).\hfill \end{array}$$

Let

$$\left\{\begin{array}{cc}{a}_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right),\hfill & k=1,\dots ,n,\hfill \\ b_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}},\hfill & k=1,\dots ,n,\hfill \\ c_{k,i}=\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right),\hfill & k=2,\dots ,n,i=2,\dots ,k.\hfill \end{array}\right.$$

Therefore,

$$\left\{\begin{array}{cc}{u}_1={\displaystyle \frac{{\lambda }_{1}f({\lambda }_1)}{a_1}}+u_0,\hfill & \\ u_k={\displaystyle \frac{{\lambda }_{k}f({\lambda }_k)}{a_k}}+u_{k-1}-{\displaystyle \frac{b_k}{a_k}}\sum _{i=2}^k(u_{k-i+1}-u_{k-i})c_{k,i},\hfill & k=2,\dots ,n.\hfill \end{array}\right.$$

In Algorithm 1, we present the numerical method for solving Equation (8).

Algorithm 1 Numerical method for solving Equation (8).

Input: $n\in \mathbb{N}$, $\alpha ,\nu \in [0,1]$.   Set $h={\displaystyle \frac{1}{n}}$.   Set ${\lambda }_k=kh$ for $k=0,1,\dots ,n$.   Compute $a_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right),k=1,\dots ,n$.   Compute $b_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}},k=1,\dots ,n.$   Compute $c_{k,i}=\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right),k=2,\dots ,n,i=2,\dots ,k.$   Compute $u_1={\displaystyle \frac{{\lambda }_{1}f({\lambda }_1)}{a_1}}+u_0.$   Compute $u_k={\displaystyle \frac{{\lambda }_{k}f({\lambda }_k)}{a_k}}+u_{k-1}-{\displaystyle \frac{b_k}{a_k}}{\sum }_{i=2}^k(u_{k-i+1}-u_{k-i})c_{k,i},k=2,\dots ,n.$

Output: The approximate solution $u_k$.

In Figure 21 and Figure 22, we plot the exact solution, numerical solution, and absolute error for different $\nu$ and $\alpha$.

Application 2

Consider the following fractional problem:

$$\begin{array}{cc}\hfill {}^{MLCF}\mathcal{D}_{\lambda }^{\nu ,\alpha }u(\lambda )& =u(\lambda )\left(f(\lambda )+1\right)-{\lambda }^{\alpha },\lambda \in ]0,1],\hfill \\ \hfill u(0)& =0,\hfill \end{array}$$

(9)

where

$$f(\lambda )={\displaystyle \frac{M(\nu )\alpha }{1-\nu }}{\mathbb{E}}_{\alpha }{({\displaystyle \frac{\nu }{1-\nu }}{\lambda }^{\alpha })}^{-1}{\mathbb{E}}_{\alpha ,\alpha +1}({\displaystyle \frac{\nu }{1-\nu }}{\lambda }^{\alpha }).$$

The exact solution is $u(\lambda )={\lambda }^{\alpha }$. Consider dividing the interval $[0,1]$ into n equal subintervals, each of width $h=1/n$, using the nodes ${\lambda }_k=kh$ for $k=0,1,\dots ,n$. From Equation (9), we have

$$\begin{array}{c}\hfill {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{i=1}^k(u_{k-i+1}-u_{k-i})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right)=u_k\left(f({\lambda }_k)+1\right)-{\lambda }_k^{\alpha },\end{array}$$

for $k=1,\dots ,n$. Then,

$$\begin{array}{cc}& {\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}{u}_k\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)=u_k\left(f({\lambda }_k)+1\right)-{\lambda }_k^{\alpha }\hfill \\ & +{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}{u}_{k-1}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)\hfill \\ & -{\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\sum _{i=2}^k(u_{k-i+1}-u_{k-i})\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right).\hfill \end{array}$$

Let

$$\left\{\begin{array}{cc}{a}_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)-\left(f({\lambda }_k)+1\right),\hfill & k=1,\dots ,n,\hfill \\ b_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right),\hfill & k=1,\dots ,n,\hfill \\ d_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}},\hfill & k=1,\dots ,n,\hfill \\ c_{k,i}=\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right),\hfill & k=2,\dots ,n,i=2,\dots ,k.\hfill \end{array}\right.$$

Therefore,

$$\left\{\begin{array}{cc}{u}_1=-{\displaystyle \frac{{\lambda }_1^{\alpha }}{a_1}}+{\displaystyle \frac{b_1}{a_1}}{u}_0,\hfill & \\ u_k=-{\displaystyle \frac{{\lambda }_k^{\alpha }}{a_k}}+{\displaystyle \frac{b_k}{a_k}}{u}_{k-1}-{\displaystyle \frac{d_k}{a_k}}\sum _{i=2}^k(u_{k-i+1}-u_{k-i})c_{k,i},\hfill & k=2,\dots ,n.\hfill \end{array}\right.$$

In Algorithm 2, we present the numerical method for solving Equation (9).

Algorithm 2 Numerical method for solving Equation (9).

Input: $n\in \mathbb{N}$, $\alpha ,\nu \in [0,1]$.   Set $h={\displaystyle \frac{1}{n}}$.   Set ${\lambda }_k=kh$ for $k=0,1,\dots ,n$.   Compute $a_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right)-\left(f({\lambda }_k)+1\right),k=1,\dots ,n$.   Compute $b_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}}\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_k^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-1}^{\alpha }}{1-\nu }})\right),k=1,\dots ,n.$   Compute $d_k={\displaystyle \frac{M(\nu ){\mathbb{E}}_{\alpha }{(\frac{\nu }{1-\nu }{\lambda }_k^{\alpha })}^{-1}}{2(1-\nu )}},k=1,\dots ,n.$   Compute $c_{k,i}=\left({\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i+1}^{\alpha }}{1-\nu }})+{\mathbb{E}}_{\alpha }(\nu {\displaystyle \frac{{\lambda }_{k-i}^{\alpha }}{1-\nu }})\right),k=2,\dots ,n,i=2,\dots ,k.$   Compute $u_1=-{\displaystyle \frac{{\lambda }_1^{\alpha }}{a_1}}+{\displaystyle \frac{b_1}{a_1}}{u}_0.$   Compute $u_k=-{\displaystyle \frac{{\lambda }_k^{\alpha }}{a_k}}+{\displaystyle \frac{b_k}{a_k}}{u}_{k-1}-{\displaystyle \frac{d_k}{a_k}}{\sum }_{i=2}^k(u_{k-i+1}-u_{k-i})c_{k,i},k=2,\dots ,n.$

Output: The approximate solution $u_k$.

In Figure 23, we plot the exact solution, numerical solution, and the absolute error. In Figure 24, we plot the solution obtained using the MLCF derivative and the solution obtained using the Caputo derivative. In Figure 25, we plot the solution obtained using the MLCF derivative and the solution obtained using the fractional Euler method in [47].

6. Conclusions

This study introduces a new definition for the fractional derivative with a numerical approximation. The error analysis demonstrates that the proposed method converges at the first order, as evidenced by the local truncation error term of the form $\mathcal{O}(h)$. This analysis was extended to a continuous temporal mesh to achieve improved accuracy. Test cases 1 and 2 validate the first-order convergence of the numerical approximation, showing a consistent reduction in the computed absolute errors by one order with each corresponding to a decrease in time step h. In the future, we will study other schemes.