Heavy–Heavy and Heavy–Light Mesons in Cold Nuclear Matter

Abstract

We review the in-medium modifications of effective masses (Lorentz scalar potentials or phenomenon of mass shift) of the heavy–heavy and heavy–light mesons in symmetric nuclear matter and their nuclear bound states. We use a combined approach with the quark–meson coupling (QMC) model and an effective Lagrangian. As demonstrated by the cases of pionic and kaonic atoms, studies of the meson–nucleus bound state can provide us with important information on chiral symmetry in a dense nuclear medium. In this review, we examine the mesons, $K,K^{\ast },D,D^{\ast },B,B^{\ast },\eta ,{\eta }^{\prime },\varphi ,{\eta }_c,J/\psi ,{\eta }_b,\mathsf{{\rm Y}}$, and $B_c$, where our emphasis is on the heavy mesons. In addition, we also present some new results for the $B_c$-nucleus bound states.

1. Introduction

Quantum chromodynamics (QCD) is the theory of strong interactions at the fundamental level, namely, at the level of quarks and gluons, which compose the observed hadrons in the standard model (SM) [1,2,3,4,5,6,7]. However, a quantitative understanding of the strong force and strongly interacting matter from the underlying first principles of QCD is still limited, in particular when the hadrons are under the circumstance with many nucleons, such as when emersed in nuclei and dense nuclear medium. The study of the interactions of heavy–heavy and heavy–light mesons with atomic nuclei is an important tool for understanding the properties of strongly interacting matter in vacuum and in extreme conditions of temperature and density based on QCD Refs. [8,9,10,11,12,13,14,15]. In this review, we treat the zero temperature case. An understanding of hadronic interactions with the nuclear medium is imperative for studying the production of heavy mesons in high energy heavy ion collisions [16,17], because the medium modifications of hadron properties may have a significant impact on the experimental results. Decay processes and decay rates involving mesons in a nuclear medium should also be modified. For example, decays of the type $B_c\to D_s{\mathcal{l}}^{+}{\mathcal{l}}^{-}$ involving a flavor-changing neutral-current process are highly suppressed in the Standard Model (SM) [18,19,20,21,22,23,24]; thus, it is very important for investigating the physics beyond the SM. Moreover, the suppression or enhancement in the production of mesons, such as $J/\psi$, $\mathsf{{\rm Y}}$, and $B_c$, makes them interesting probes of quark–gluon plasma (QGP) [25,26,27,28,29,30,31,32,33,34].

To calculate the in-medium (effective) masses of the mesons containing light quarks, including K, $K^{\ast }$, D, $D^{\ast }$, B, $B^{\ast }$, $\eta$, and ${\eta }^{\prime }$, we use the quark–meson coupling (QMC) model [35]. Because of the Okubo–Zweig–Iizuka (OZI) [36,37,38,39,40] rule, the heavy quarkonium–nucleus interaction via the exchange of mesons made of only light quarks is suppressed, so that the quarkonium–nucleus interaction is primarily by a QCD van der Waals type interaction [41]. For the mesons that do not contain light quarks, namely, $\varphi$, ${\eta }_c$, $J/\psi$, ${\eta }_b$, $\mathsf{{\rm Y}}$, and $B_c$, we employ a combined approach in the self energy, in which the mechanism for the meson interact with the nuclear medium through the excitation of the intermediate-state mesons that do contain light quarks. Where the in-medium masses of the intermediate-state mesons are calculated by the QMC model, the meson self-energies are estimated with effective Lagrangians.

Partial restoration of chiral symmetry, and chiral symmetry itself in nuclear medium, are another interesting phenomena that can be studied in an empirical sense, because the (effective) mass reduction of the medium-modified hadron may be associated with a signature of partial restoration of chiral symmetry [42,43,44,45]. This negative mass shift can be regarded as an attractive Lorentz scalar potential, which, if sufficiently attractive, can bind mesons to atomic nuclei. Deeply bound pionic atoms were first discussed in 1985 [46] and later observed in the ²⁰⁸Pb(d, ³He) reaction [47]. In addition, studies of kaonic atoms were performed [48,49,50,51,52]. The studies of the pionic and kaonic atoms can provide us with very important information on chiral symmetry in a dense nuclear medium. Furthermore, other possible meson–nucleus bound states were proposed [53,54,55]. Charmonium–nucleus systems were proposed in 1989 [56] and followed by many predictions [8,10,11,41,42,43,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. Lattice QCD has also predicted such states [73,74,75], as well as $\varphi$-nucleon bound states [76]. In the bottom sector of quarkonia, strong nuclear bound states with various nuclei [77,78,79,80] were predicted for $\mathsf{{\rm Y}}$ and ${\eta }_b$. In this article, we review the downward shift of meson masses in nuclear matter and the meson–nucleus bound states, focusing on the heavy–heavy and heavy–light mesons. We also comment on some new results for the $B_c$-nucleus bound states.

This review is organized as follows. In Section 2, we present the details of the quark–meson coupling (QMC) model needed to better understand most of our results. In Section 3, we present the results for the mass shift of mesons with heavy–light quark content using the quark–meson coupling (QMC) model. Since heavier flavor quarks $Q=s,c,b$ do not directly interact directly with the mean fields in a nuclear medium, we use a combined approach using both the QMC model with and effective Lagrangians to compute the effective masses for the mesons with a (heavy quark)-(heavy antiquark) content.

We describe this in Section 4. In Section 5, we use the calculated amounts of the downward shift of masses for the mesons considered in this work to present our results for the meson–nucleus potentials for various nuclei in a wide range of nuclear masses. In Section 6, we present our results for meson–nucleus bound state energies and widths for some mesons by solving the Klein–Gordon equation, using the meson–nucleus potentials obtained in the previous section. Finally, in Section 7, we present a summary and conclusions.

2. The Quark–Meson Coupling (QMC) Model

The quark–meson coupling (QMC) model, the standard version we use, is a quark-based model for nuclear matter and nuclei that describes the internal structure of the nucleons using the non-overlapping MIT bag model, and the binding of nucleons (nuclear matter) by the self-consistent couplings of the confined light quarks u and d to the Lorentz scalar-$\sigma$, Lorentz-vector-isoscalar-$\omega$ and Lorentz-vector-isovector-$\rho$ meson mean fields generated by the confined light quarks in the nucleons [35].

In a nuclear medium, the hadrons with light quarks are expected to be predominantly modified by their properties, as evidenced by the European Muon Collaboration effect [81,82] and the modifications of bound proton electromagnetic form factors [83,84,85]. Thus, one can expect that the nuclear medium can modify the internal structure of nucleons and hadrons and can affect the interaction with nucleons. Thus, studying such effects due to the hadron internal structure based on the quarks and gluons can make the QMC model a useful phenomenological tool for describing the change in the internal structure of hadrons in a nuclear medium.

The QMC model has been successfully applied for the studies of various properties of infinite nuclear matter and finite (hyper)nuclei [11,86,87,88,89]. Here, we briefly present the necessary details for understanding our results better. For more detailed discussions and some successful features of the model, see Refs. [11,86,87,89], and references therein.

We consider nuclear matter (NM) in its rest frame, where all the scalar and vector mean field potentials, which are responsible for the nuclear many-body interactions, are constants in the Hartree approximation. We assume SU(2) symmetry for the quarks ($m_q=m_u=m_d$ and $q=u$ or d). Note that the heavier quarks $Q=s,c,b$ (hereafter, we will simply denote heavy quarks as Q, including the s quarks) are not affected directly by the mean field potentials in the standard QMC model. Thus, when dealing with mesons composed of valence (heavy quark)-(heavy antiquark) pairs, we will have to proceed in a different manner for hidden flavor heavier mesons with $Q=s,c,b$ and two-heavy-flavored mesons such as $B_c$ and $B_s$ mesons. In this study, we will treat the $B_c$ and $B_c^{\ast }$ mesons only; however, for the other two-heavy-flavored mesons $B_s,B_s^{\ast },D_s$ and $D_s^{\ast }$ mesons, see Ref. [90].

The Dirac equations for the quarks and antiquarks in nuclear matter (neglecting the Coulomb force), in a bag of a hadron, h, ($q=u$ or d, and $Q=s,c$ or b), are given by ($x=(t,\mathbf{r})$ bag radius) [55,91,92,93,94],

$$\begin{array}{ccc}\hfill \left[i\gamma ·{𝜕}_x-(m_q-V_{\sigma }^q)\mp {\gamma }^0\left(V_{\omega }^q+{\displaystyle \frac{1}{2}}{V}_{\rho }^q\right)\right]\left(\begin{array}{c}{\psi }_u\left(x\right)\\ {\psi }_{\overline{u}}\left(x\right)\end{array}\right)& =& 0,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \left[i\gamma ·{𝜕}_x-(m_q-V_{\sigma }^q)\mp {\gamma }^0\left(V_{\omega }^q-{\displaystyle \frac{1}{2}}{V}_{\rho }^q\right)\right]\left(\begin{array}{c}{\psi }_d\left(x\right)\\ {\psi }_{\overline{d}}\left(x\right)\end{array}\right)& =& 0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \left[i\gamma ·{𝜕}_x-m_Q\right]{\psi }_Q\left(x\right)=0,\left[i\gamma ·{𝜕}_x-m_Q\right]{\psi }_{\overline{Q}}\left(x\right)& =& 0,\hfill \end{array}$$

(3)

where the mean field potentials are defined by $V_{\sigma }^q\equiv g_{\sigma }^q\sigma$, $V_{\omega }^q\equiv g_{\omega }^q\omega$, and $V_{\rho }^q\equiv g_{\rho }^{q}b$, with $g_{\sigma }^q$, $g_{\omega }^q$, and $g_{\rho }^q$ being the corresponding quark–meson coupling constants. We assume SU(2) symmetry, $m_q=m_{\overline{q}}\equiv m_{u,\overline{u}}=m_{d,\overline{d}}\equiv m_{q,\overline{q}}$. The Lorentz-scalar “effective quark masses” are defined by, $m_q^{\ast }=m_{u,\overline{u}}^{\ast }=m_{d,\overline{d}}^{\ast }=m_{q,\overline{q}}^{\ast }\equiv m_q-V_{\sigma }^q$, and thus $m_q^{\ast }$ is dominated by $-V_{\sigma }^q$ as baryon density increases, and can be negative, but one should not demand the positivity of usual particle mass, since this is nothing but the reflection of the strong attractive scalar potential. Note that $m_Q=m_Q^{\ast }$, since the $\sigma$ field does not couple to the heavier (“heavy”) quarks $Q=s,c,b$ in the QMC model. Furthermore, when we consider symmetric nuclear matter (SNM) with Hartre approximation, the $\rho$-meson mean field becomes zero, $V_{\rho }^q=0$, in Equations (1) and (2), and we can ignore hereafter. However, when we consider the meson–nucleus bound states, the isospin dependent $\rho$-meson mean field, as well as the Coulomb potential in nuclei, will be included if necessary. In this study, only the Coulomb potentials for the $B_c$-nucleus bound states will be considered.

The static solution for the ground-state quarks (antiquarks) in asymmetric nuclear matter (ANM) with flavor $f(=u,d,s,c,b)$ is written as ${\psi }_f\left(x\right)=N_f{e}^{-i{ϵ}_{f}t/R_h^{\ast }}{\psi }_f\left(\mathbf{r}\right)$, with the $N_f$ being the normalization factor, and ${\psi }_f\left(\mathbf{r}\right)$ the corresponding spin and spatial part of the wave function.

The eigenenergies for the quarks and antiquarks in a hadron h, in units of the in-medium bag radius of hadron h, $1/R_h^{\ast }$, are given by

$$\begin{array}{ccc}& & \left(\begin{array}{c}{ϵ}_u\\ {ϵ}_{\overline{u}}\end{array}\right)={\mathsf{\Omega }}_q^{\ast }\pm R_h^{\ast }\left(V_{\omega }^q+{\displaystyle \frac{1}{2}}{V}_{\rho }^q\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & \left(\begin{array}{c}{ϵ}_d\\ {ϵ}_{\overline{d}}\end{array}\right)={\mathsf{\Omega }}_q^{\ast }\pm R_h^{\ast }\left(V_{\omega }^q-{\displaystyle \frac{1}{2}}{V}_{\rho }^q\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & {ϵ}_Q={ϵ}_{\overline{Q}}={\mathsf{\Omega }}_Q,Q=s,c,b.\hfill \end{array}$$

(6)

The in-medium mass and bag radius of hadron h in the nuclear medium, $m_h^{\ast }$ and $R_h^{\ast }$ respectively, are determined from

$$m_h^{\ast }=\sum _{j=q,\overline{q},Q,\overline{Q}}{\displaystyle \frac{n_j{\mathsf{\Omega }}_j^{\ast }-z_h}{R_h^{\ast }}}+{\displaystyle \frac{4}{3}}\pi R_{\eta }^{\ast 3}{B}_p,{\left.{\displaystyle \frac{d{m}_h^{\ast }}{d{R}_h}}\right|}_{R_h=R_h^{\ast }}=0,$$

(7)

in particular, for the mesons $h=K,K^{\ast },D,D^{\ast },B,B^{\ast }$, while for the $\eta$ and ${\eta }^{\prime }$ mesons, to take into account flavor mixing, these are given by

$$\begin{array}{ccc}\hfill m_{\eta }^{\ast }& =& {\displaystyle \frac{2[a_P^2{\mathsf{\Omega }}_q^{\ast }+b_P^2{\mathsf{\Omega }}_s]-z_{\eta }}{R_{\eta }^{\ast }}}+{\displaystyle \frac{4}{3}}\pi R_{\eta }^{\ast 3}{B}_p,{\left.{\displaystyle \frac{d{m}_h^{\ast }}{d{R}_j}}\right|}_{R_h=R_h^{\ast }}=0,(h=\eta ,{\eta }^{\prime }),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill a_P& \equiv & \sqrt{1/3}cos{\theta }_P-\sqrt{2/3}sin{\theta }_P,b_P\equiv \sqrt{2/3}cos{\theta }_P+\sqrt{1/3}sin{\theta }_P\hfill \\ & & (\mathrm{for}{\eta }^{\prime },\eta \to {\eta }^{\prime },\mathrm{and}{a}_P\leftrightarrow b_P),\hfill \end{array}$$

(9)

where $m_q^{\ast }=m_q-V_{\sigma }^q$, $m_Q^{\ast }=m_Q$ (as already mentioned), ${\mathsf{\Omega }}_q^{\ast }={\mathsf{\Omega }}_{\overline{q}}^{\ast }={\left[x_q^2+{\left(R_h^{\ast }{m}_q^{\ast }\right)}^2\right]}^{1/2}$, ${\mathsf{\Omega }}_Q^{\ast }={\mathsf{\Omega }}_{\overline{Q}}^{\ast }={\left[x_Q^2+{\left(R_h^{\ast }{m}_Q\right)}^2\right]}^{1/2}$, with $x_{q,Q}$ being the lowest mode bag eigenfrequencies; $B_p$ is the bag constant; $n_{q,Q}$ ($n_{\overline{q},\overline{Q}}$) are the lowest mode valence quark (antiquark) numbers for the quark flavors q and Q in the corresponding mesons; and $z_h$ parameterize the sum of the center-of-mass and gluon fluctuation effects and are assumed to be independent of density [95]. The MIT big parameters $z_N$ ($z_h$) and $B_p$ are fixed by fitting the nucleon (hadron) mass in free space.

We choose the values ($m_q,m_s,m_c,m_b=(5,250,1270,4200)$ MeV) for the current quark masses, and $R_N=0.8\mathrm{fm}$ for the free space nucleon bag radius. See Ref. [96] for other values used ($m_q,m_s=(5,93,1270,4180)$ MeV result). The quark–meson coupling constants, $g_{\sigma }^q$, $g_{\omega }^q$ and $g_{\rho }^q$, for the light quarks were determined by the fit to the saturation energy (−15.7 MeV) at the saturation density (${\rho }_0=0.15$ fm⁻³) of symmetric nuclear matter for $g_{\sigma }^q$ and $g_{\omega }^q$, and by the bulk symmetry energy (35 MeV) for $g_{\rho }^q$ [35,86]. The obtained values for the quark–meson coupling constants are ($g_{\sigma }^q$, $g_{\omega }^q$, $g_{\rho }^q$) = (5.69, 2.72, 9.33).

Finally, for the mixing angle ${\theta }_P$ appearing in Equation (9), we use the value ${\theta }_P=-11.3^{\circ }$, neglecting any possible mass dependence and imaginary parts [96,97]. Furthermore, we also assume that the value of the mixing angle does not change in the nuclear medium.

3. Results with the QMC Model

In Figure 1 and Figure 2 we present respectively the QMC model predictions for the effective masses of $B,B^{\ast },D,D^{\ast },K$ and $K^{\ast }$ mesons [90], and the effective masses and the mass shift $\mathsf{\Delta }{m}_h\left({\rho }_B\right)\equiv m_h^{\ast }\left({\rho }_B\right)-m_h$ for $\eta$ and ${\eta }^{\prime }$ mesons with $m_h^{\ast }$ the in-medium meson mass and $m_h$ the vacuum mass [98], in symmetric nuclear matter versus nuclear matter density ${\rho }_0/{\rho }_B$. Clearly, the masses of these mesons decrease in the nuclear medium, and this fact may be regarded as a signature of partial restoration of chiral symmetry in the medium, although the QMC model does not explicitly have a chiral symmetry mechanism. Below, we will discuss and use the results shown in Figure 1 and Figure 2.

4. Combining QMC Model and Effective Lagrangian Approach

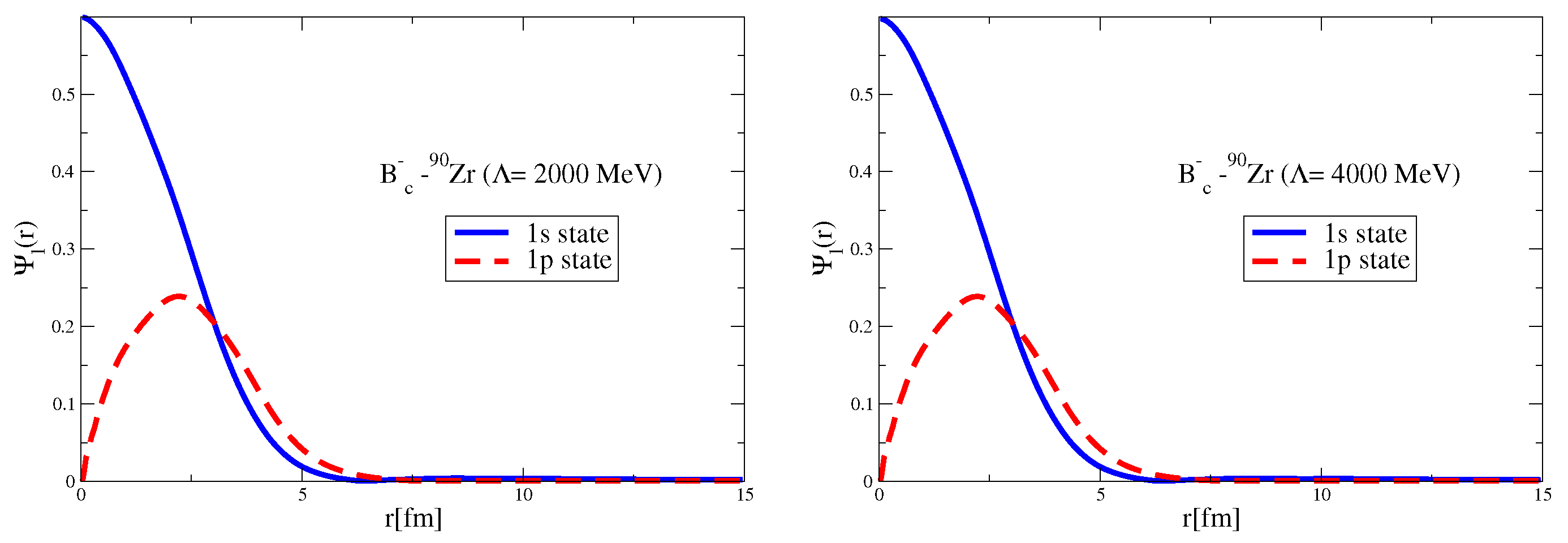
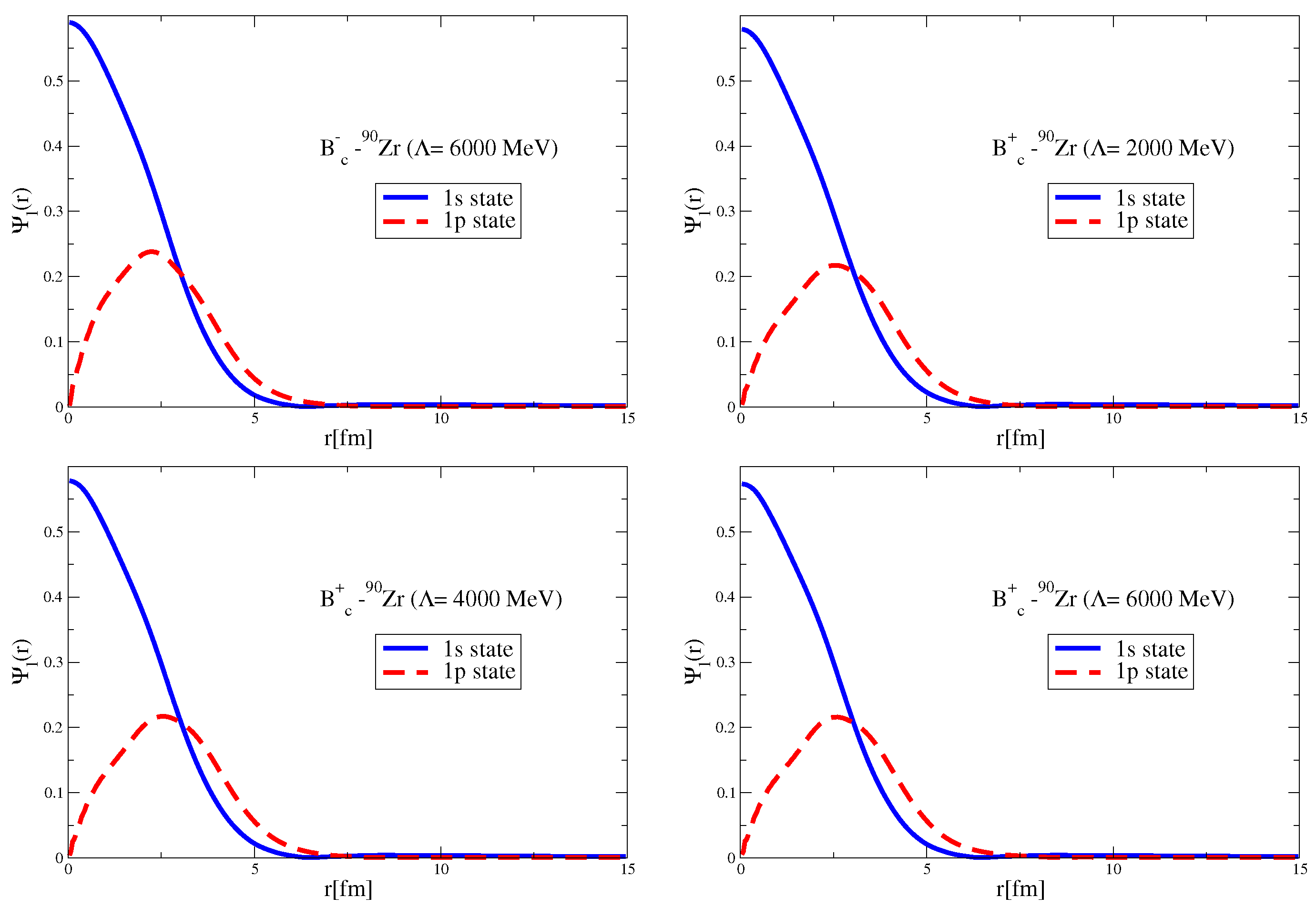
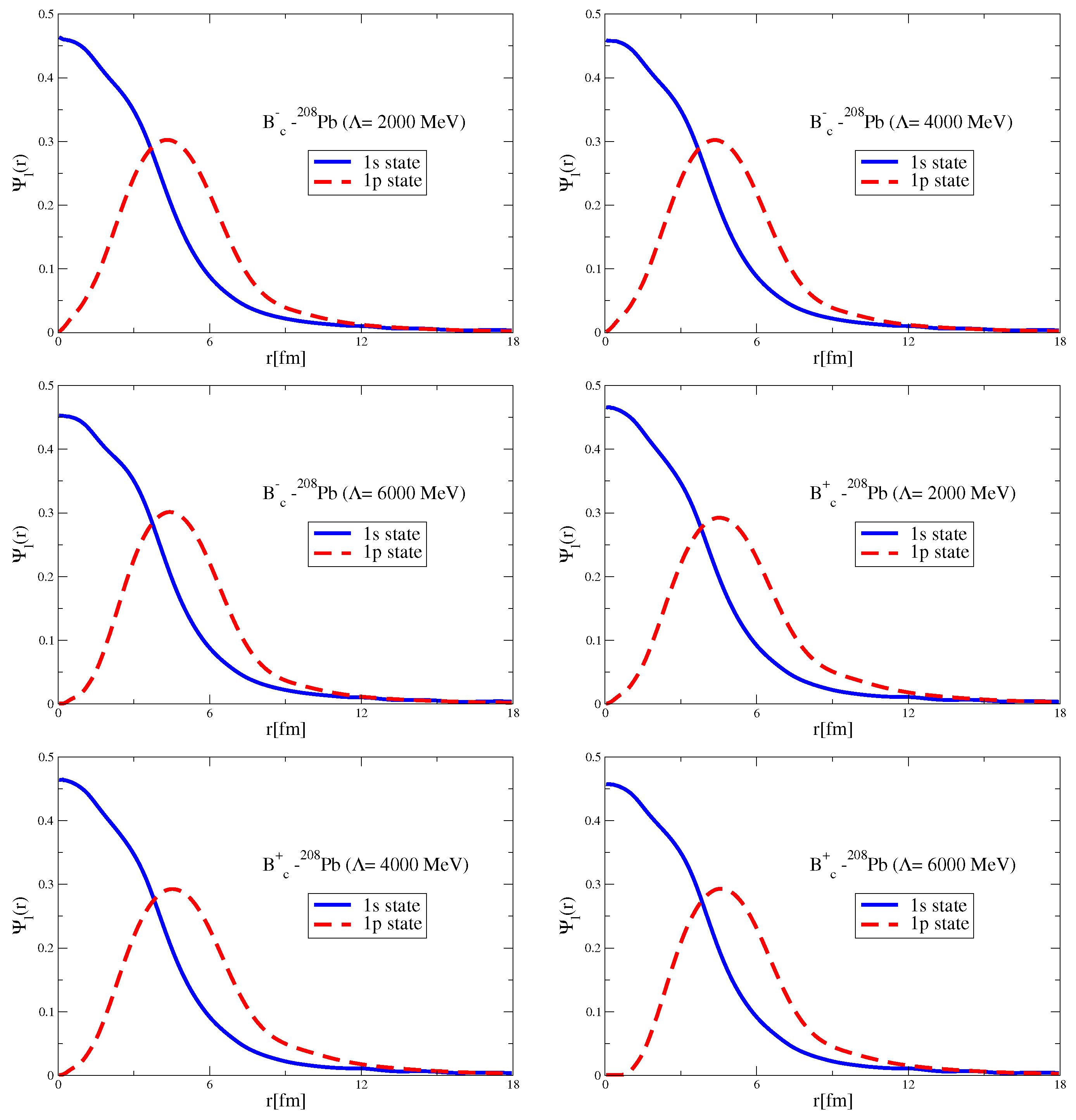
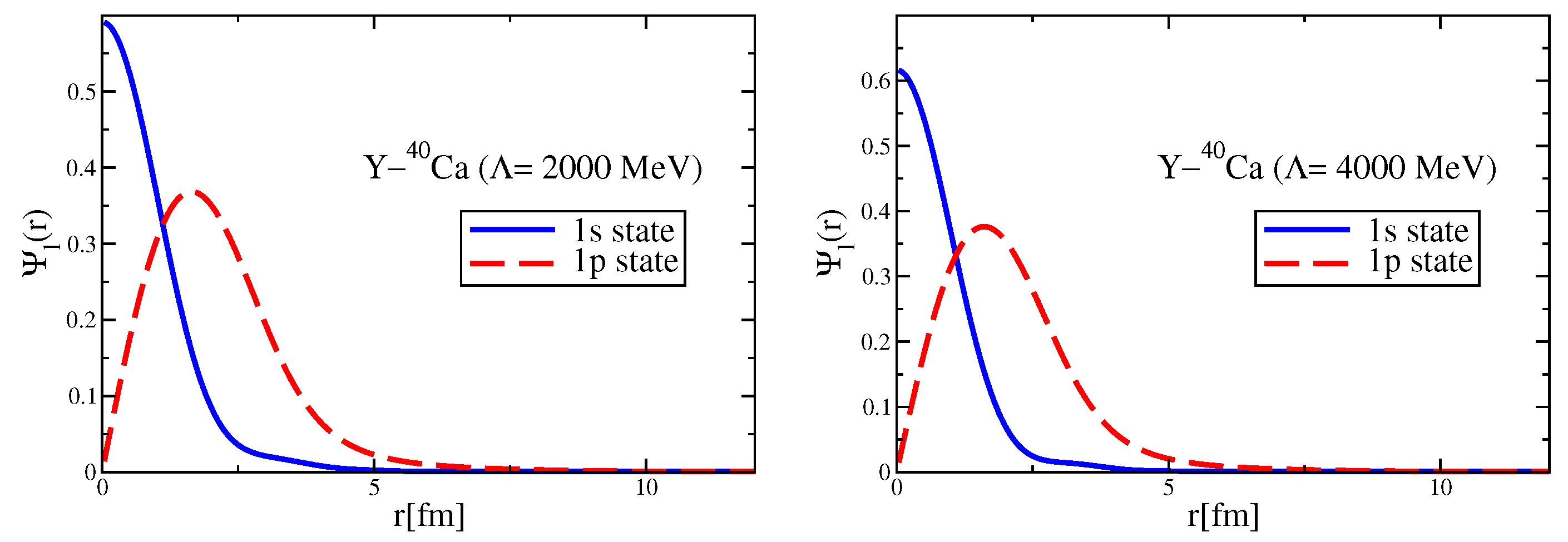
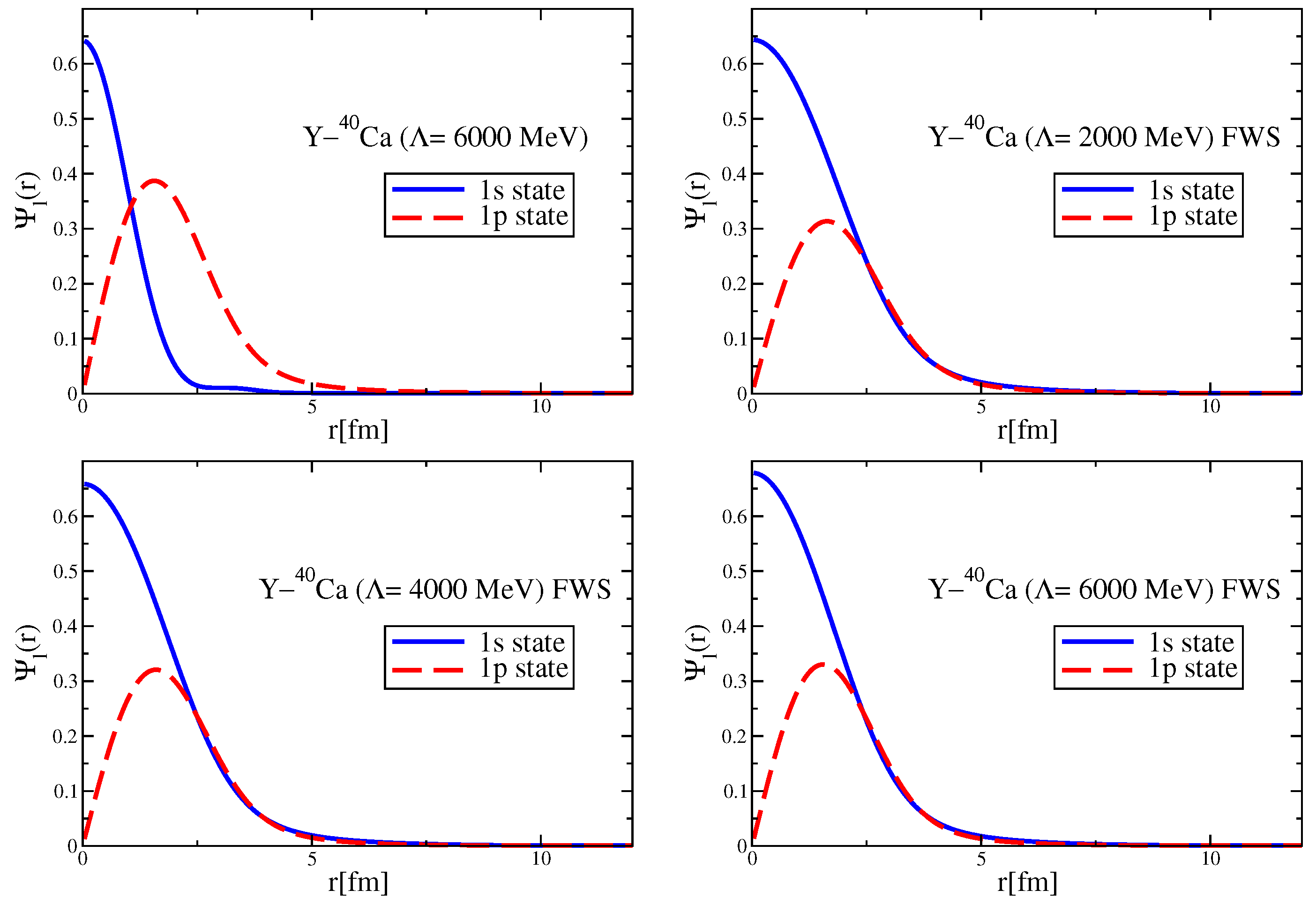
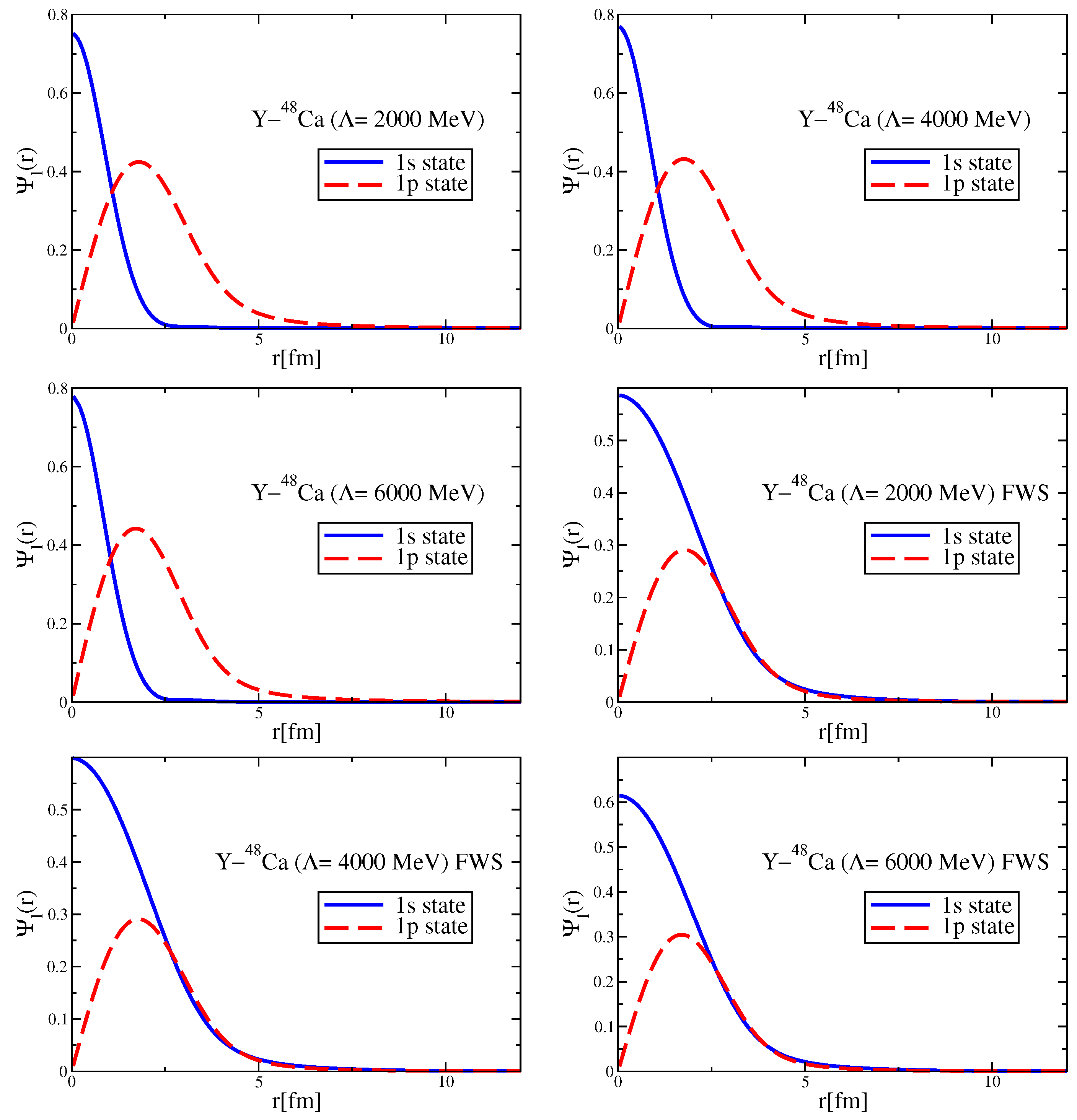
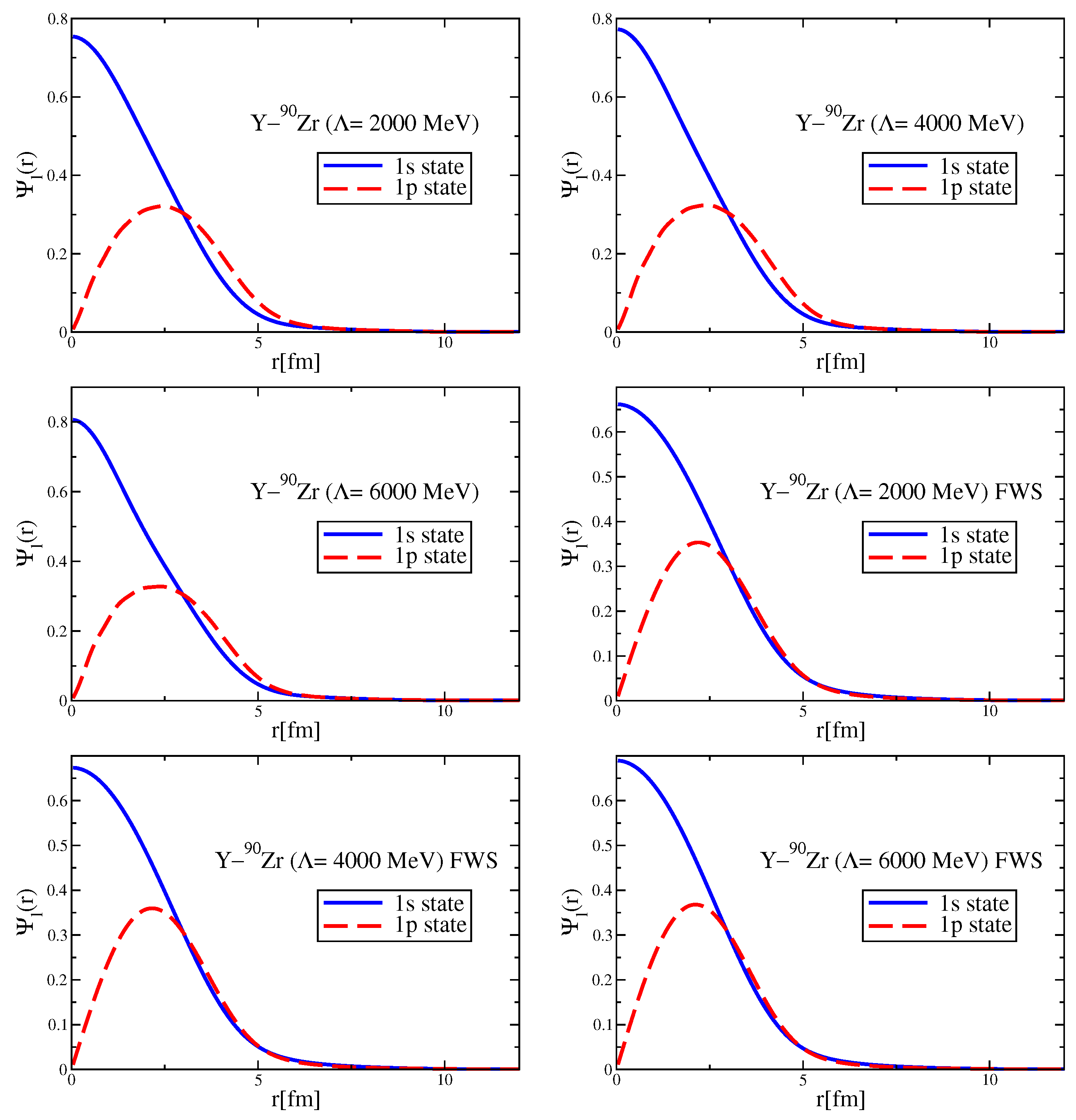
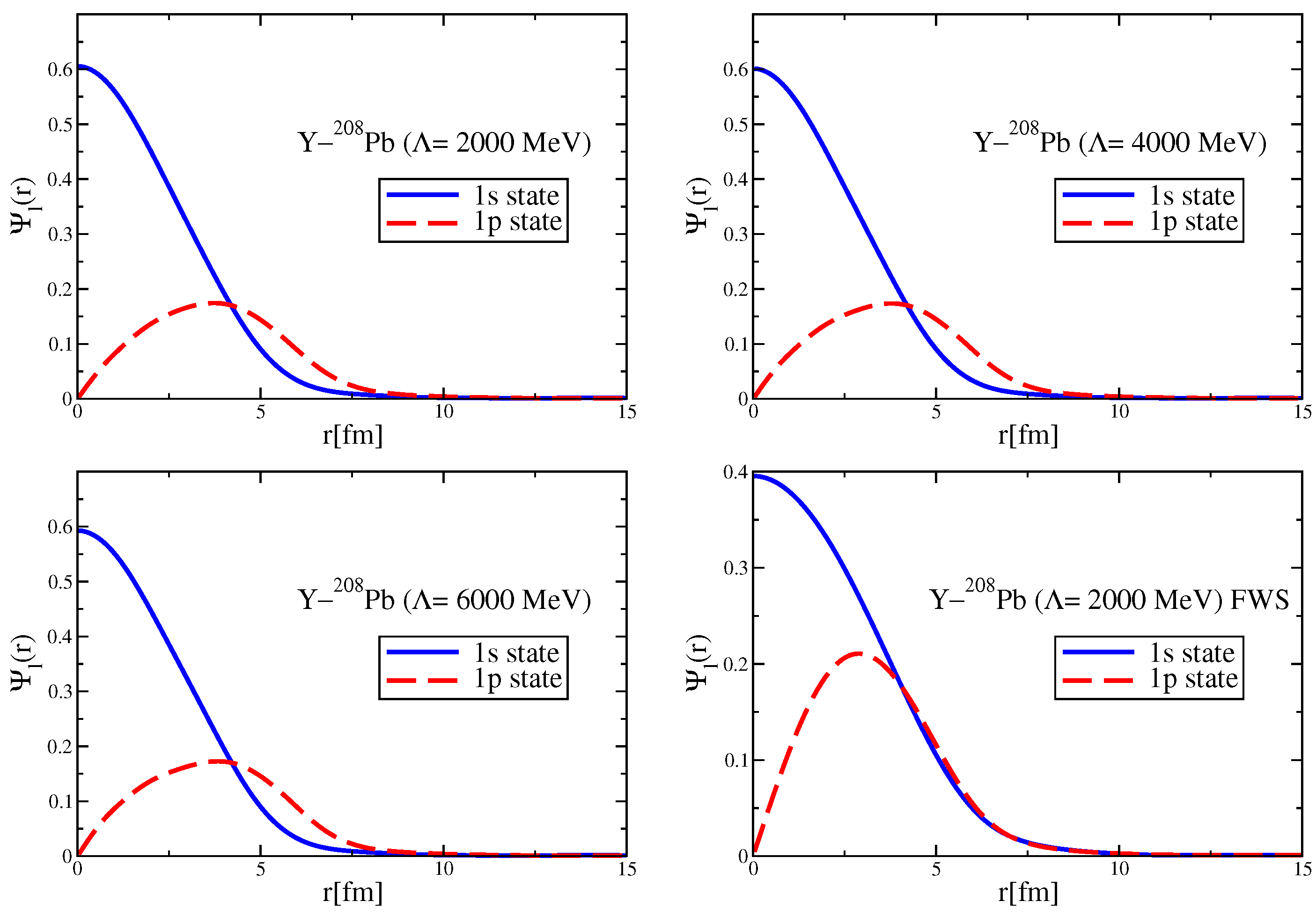
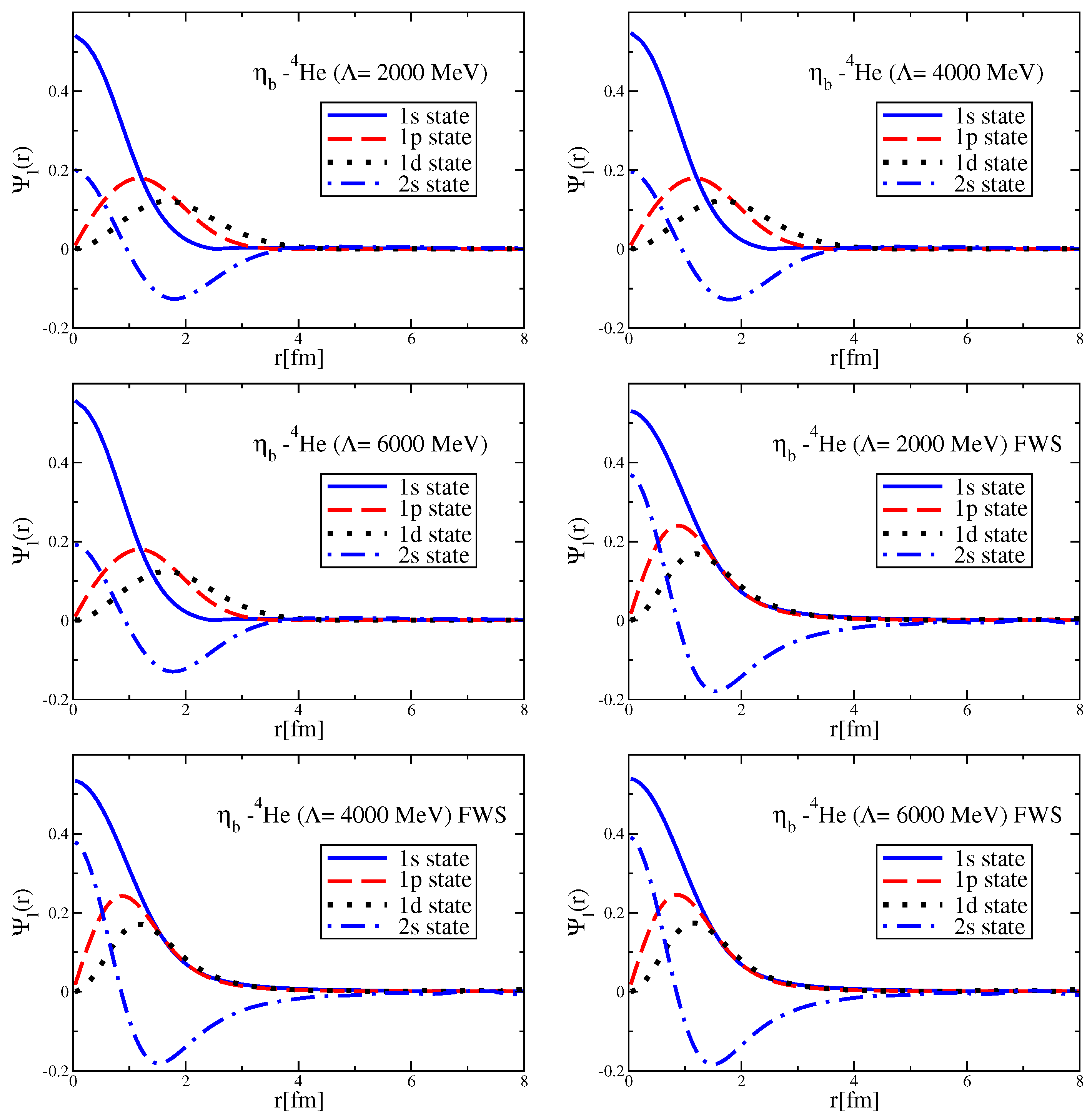
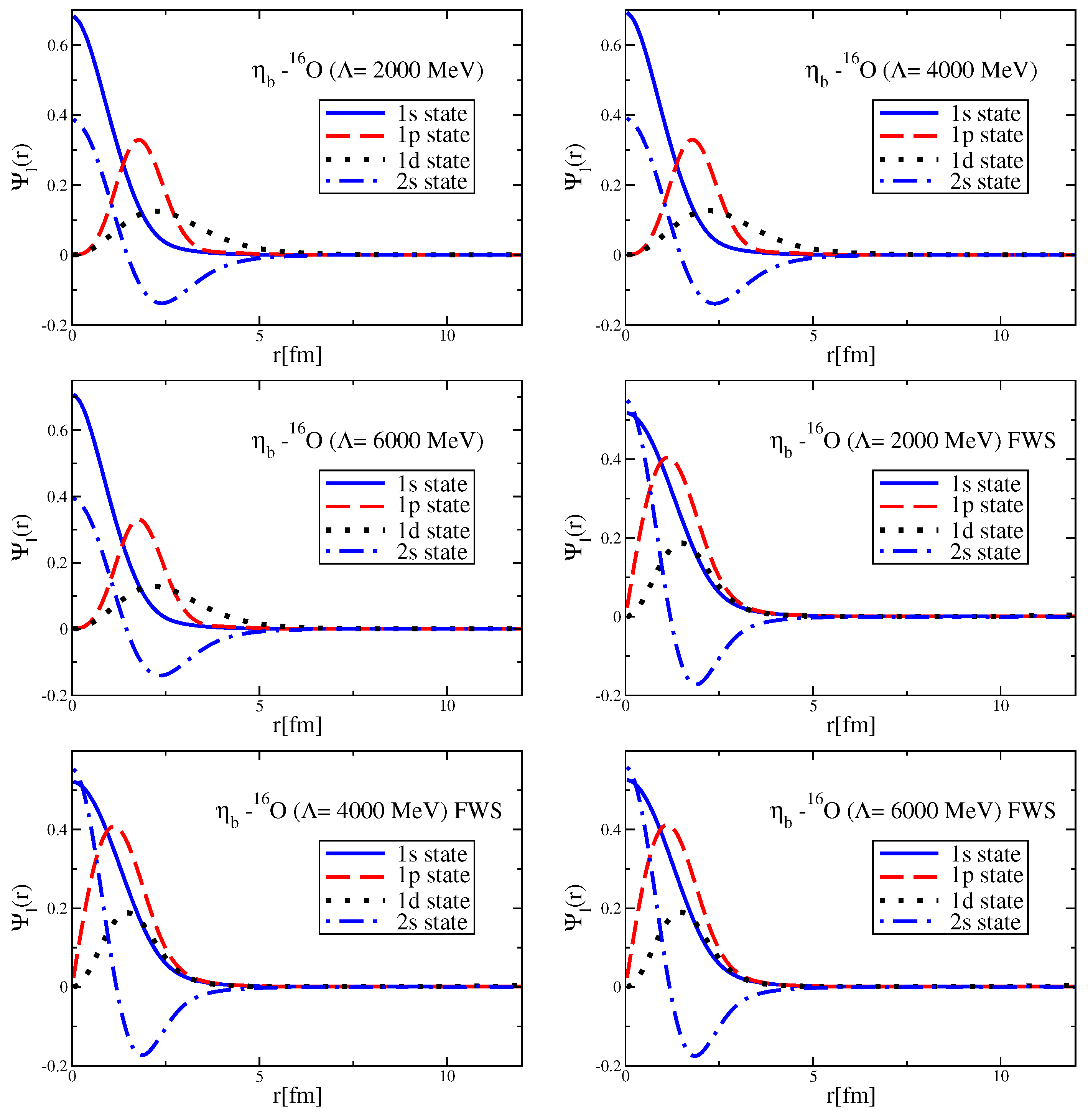
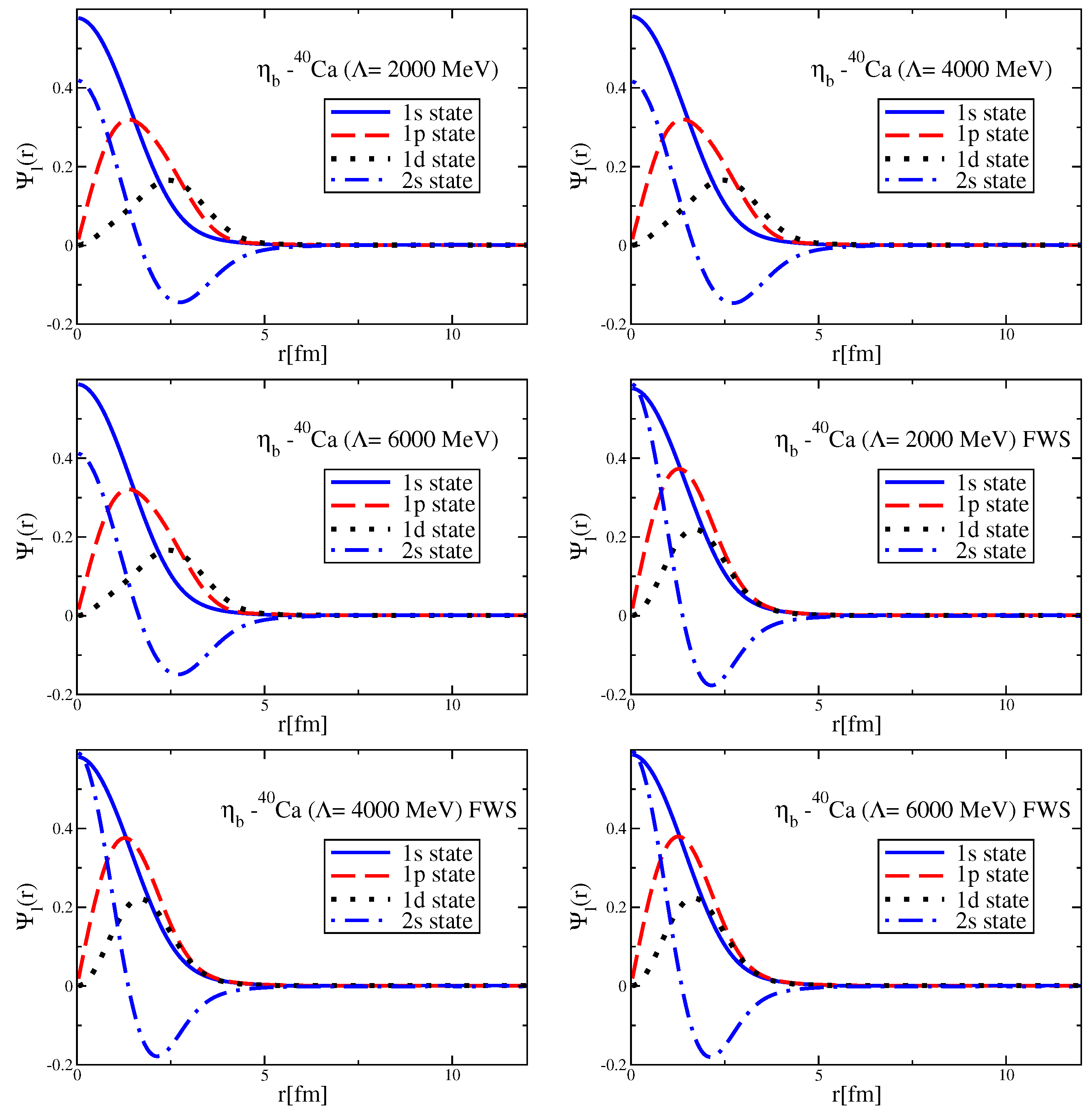
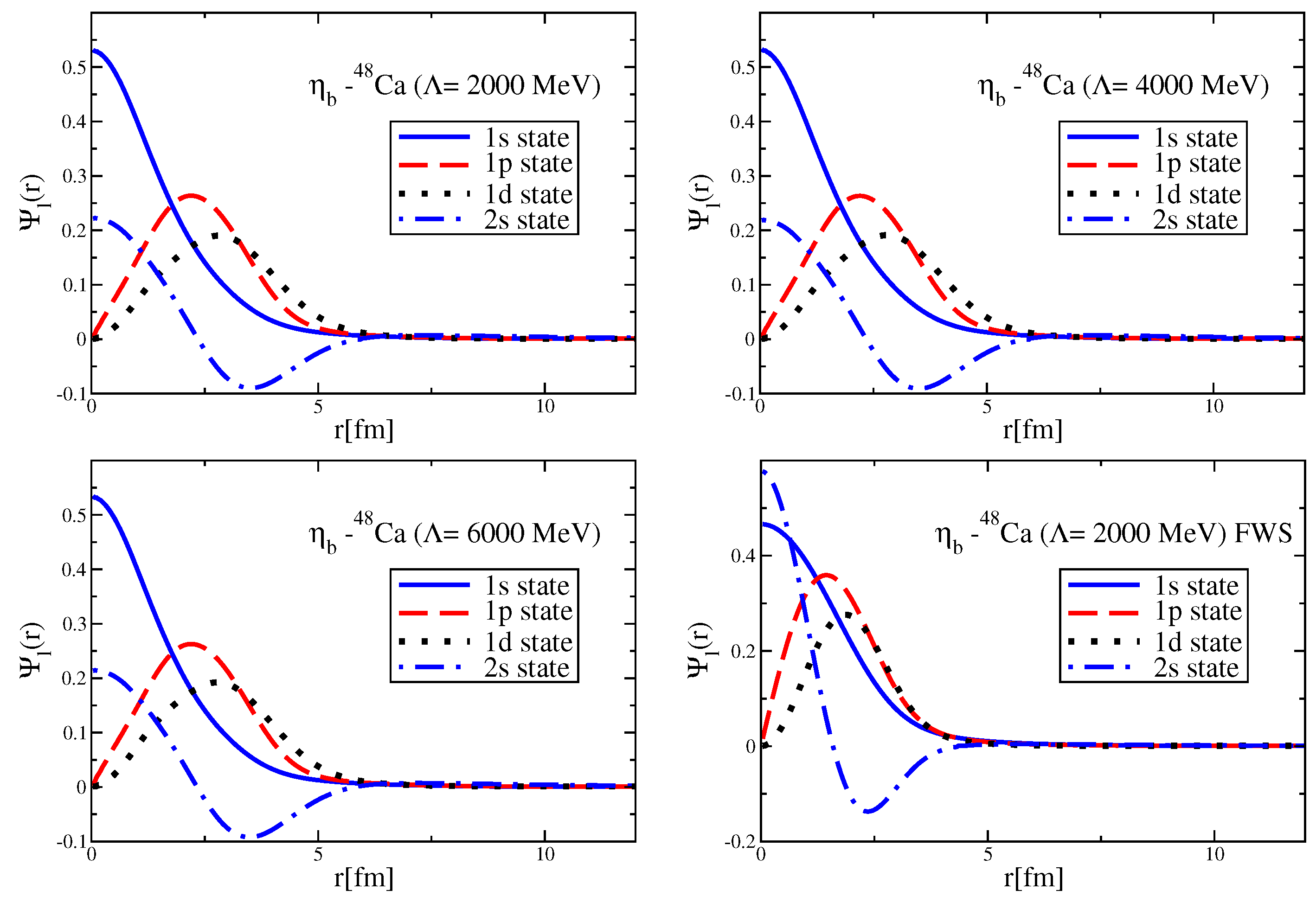
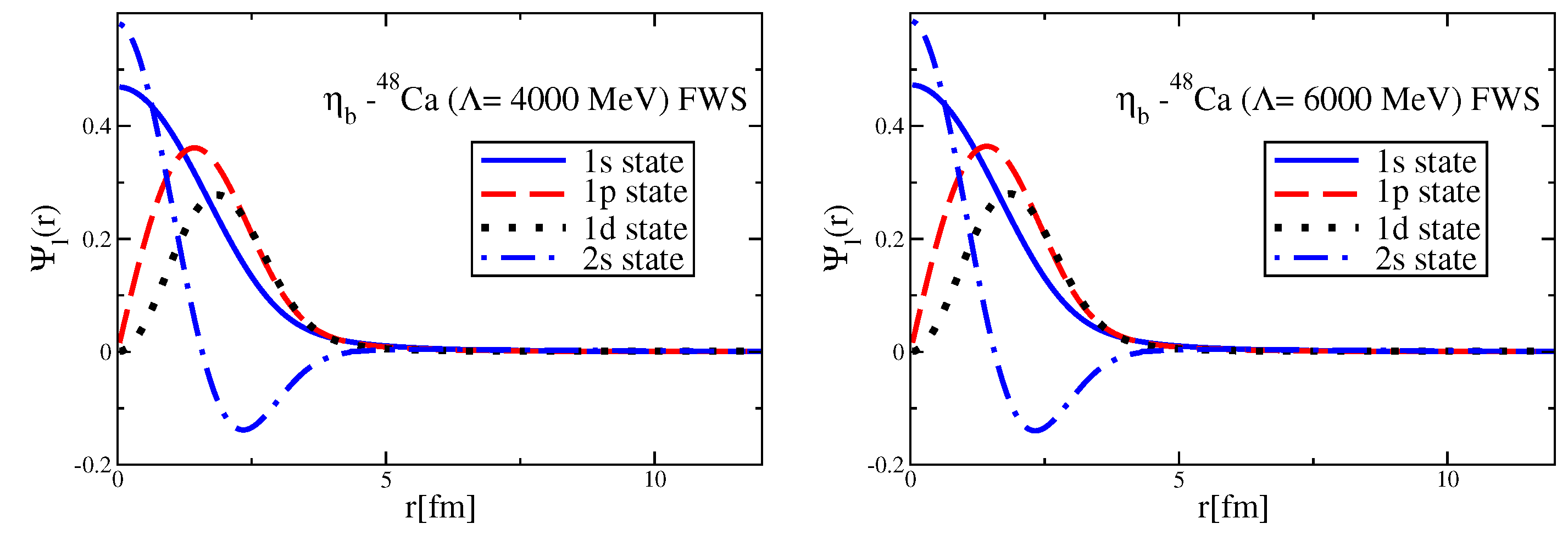
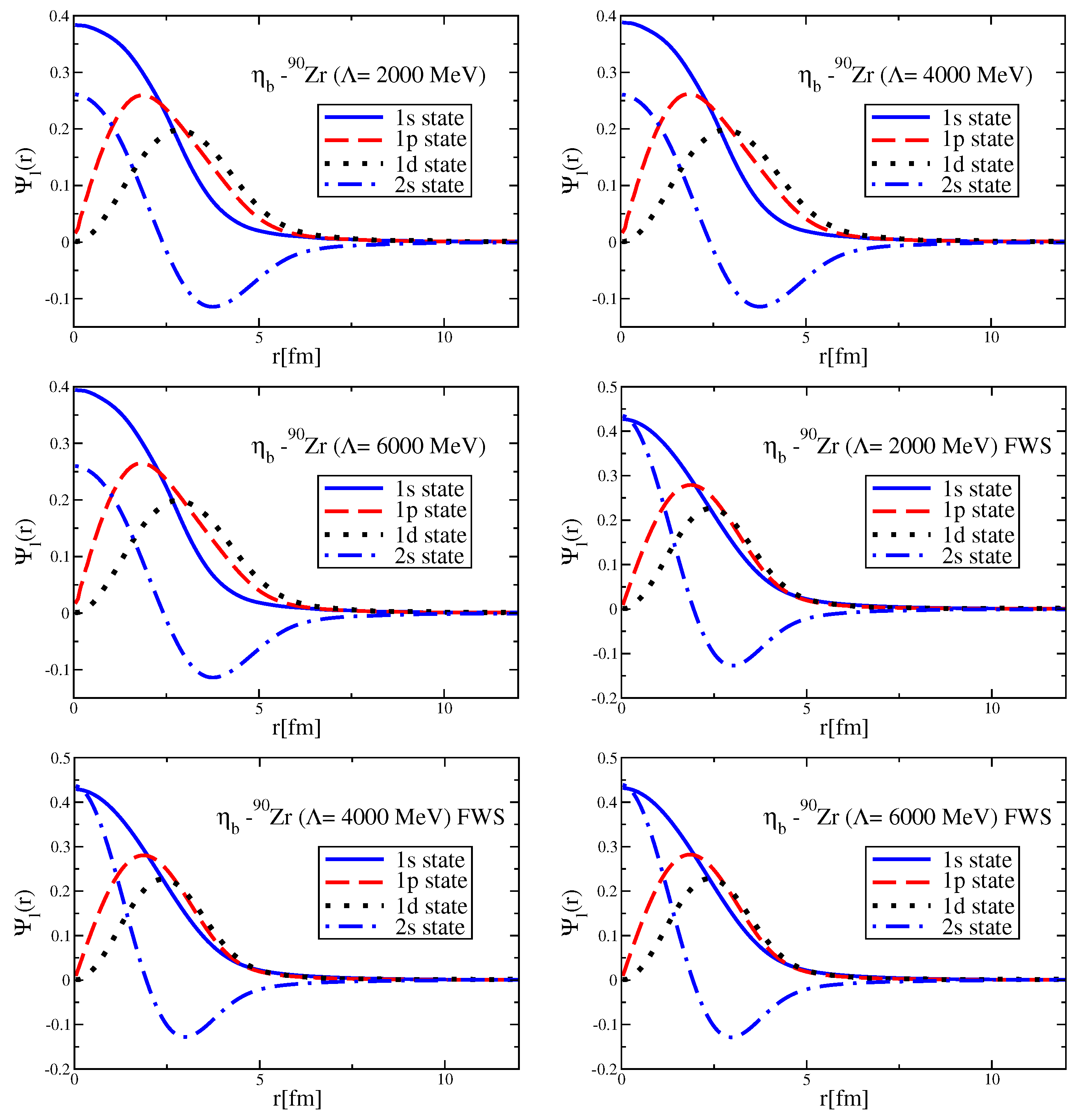
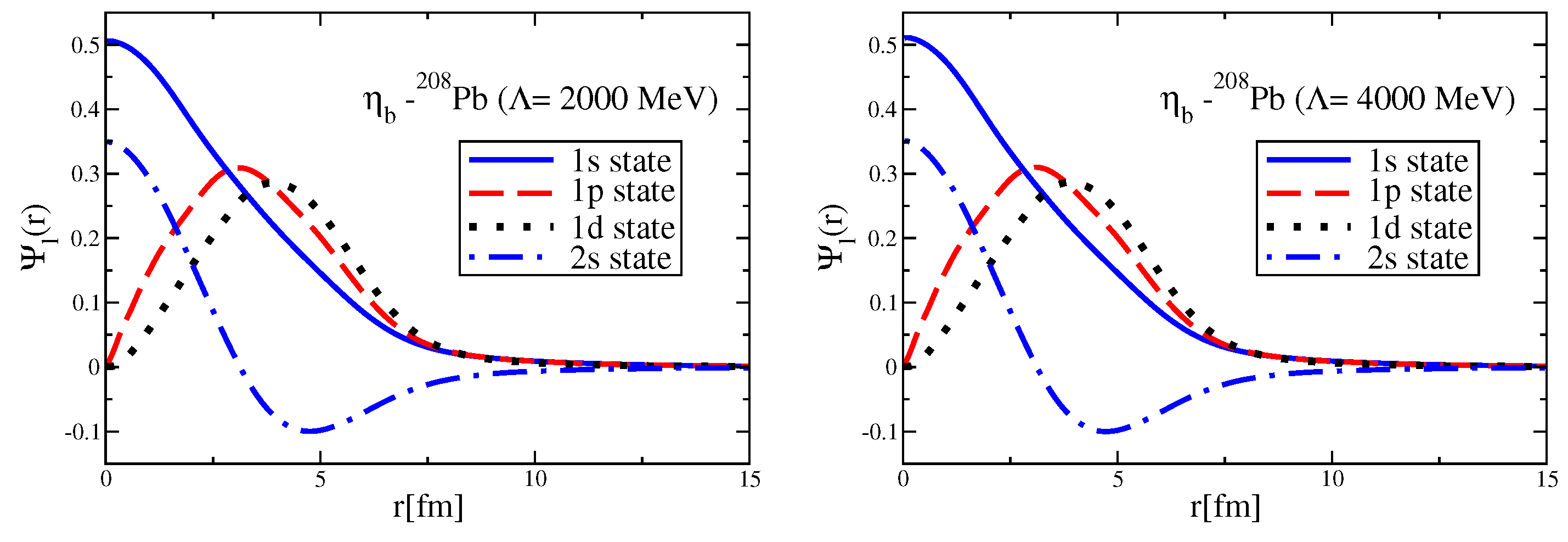
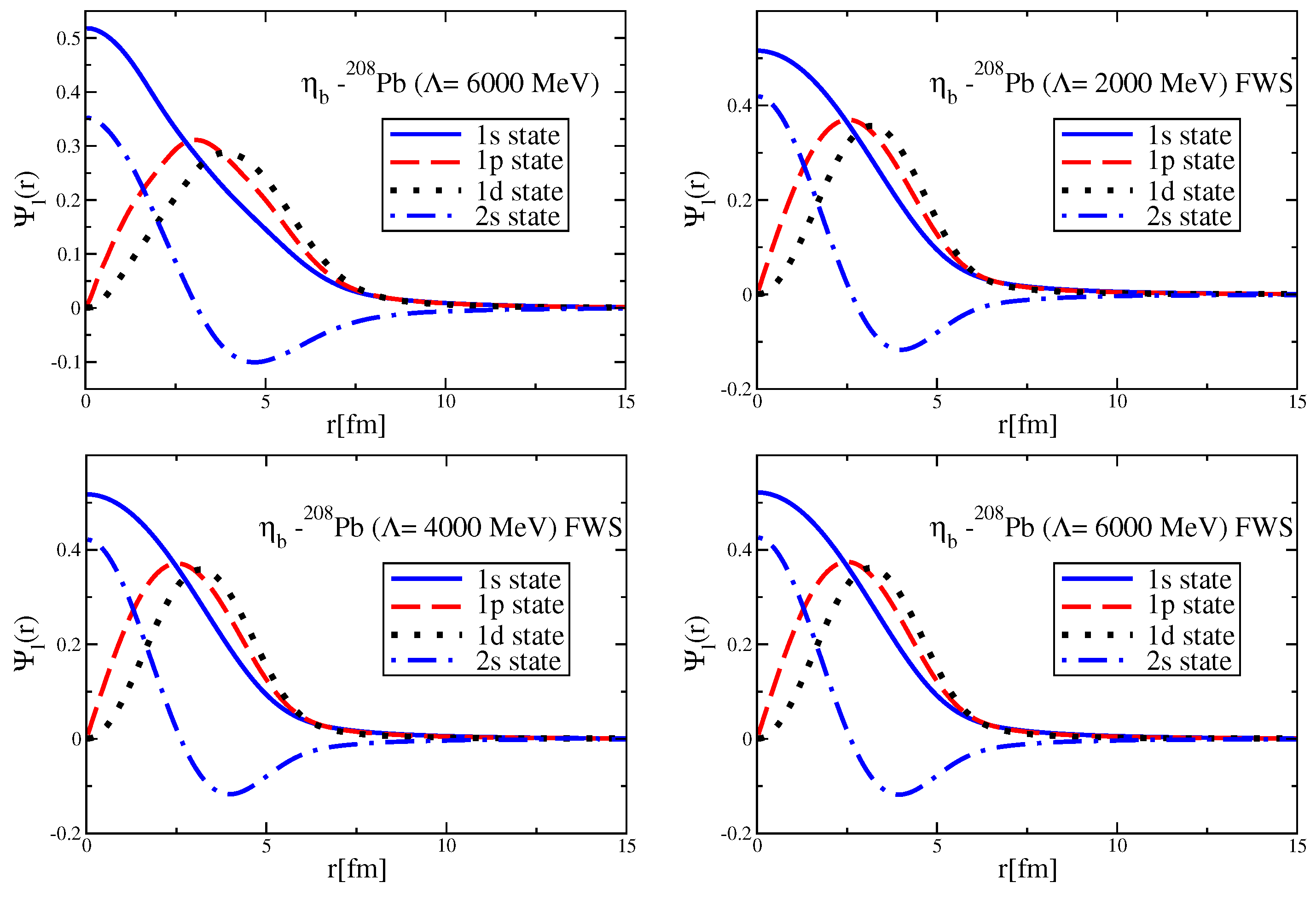
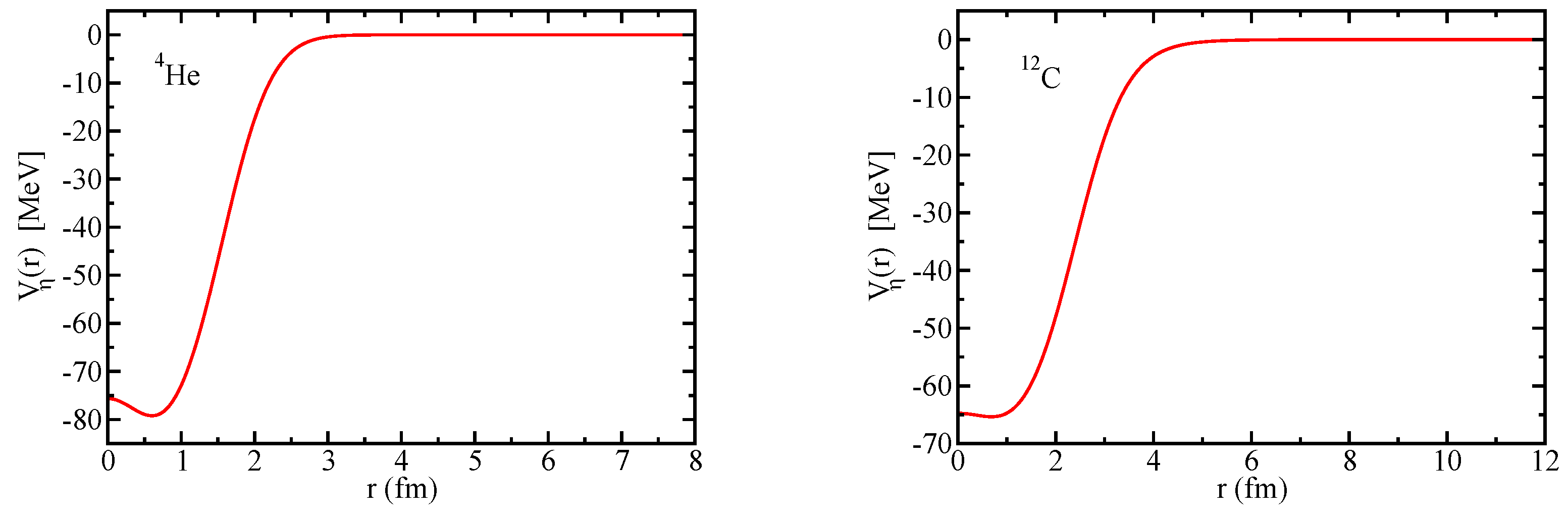
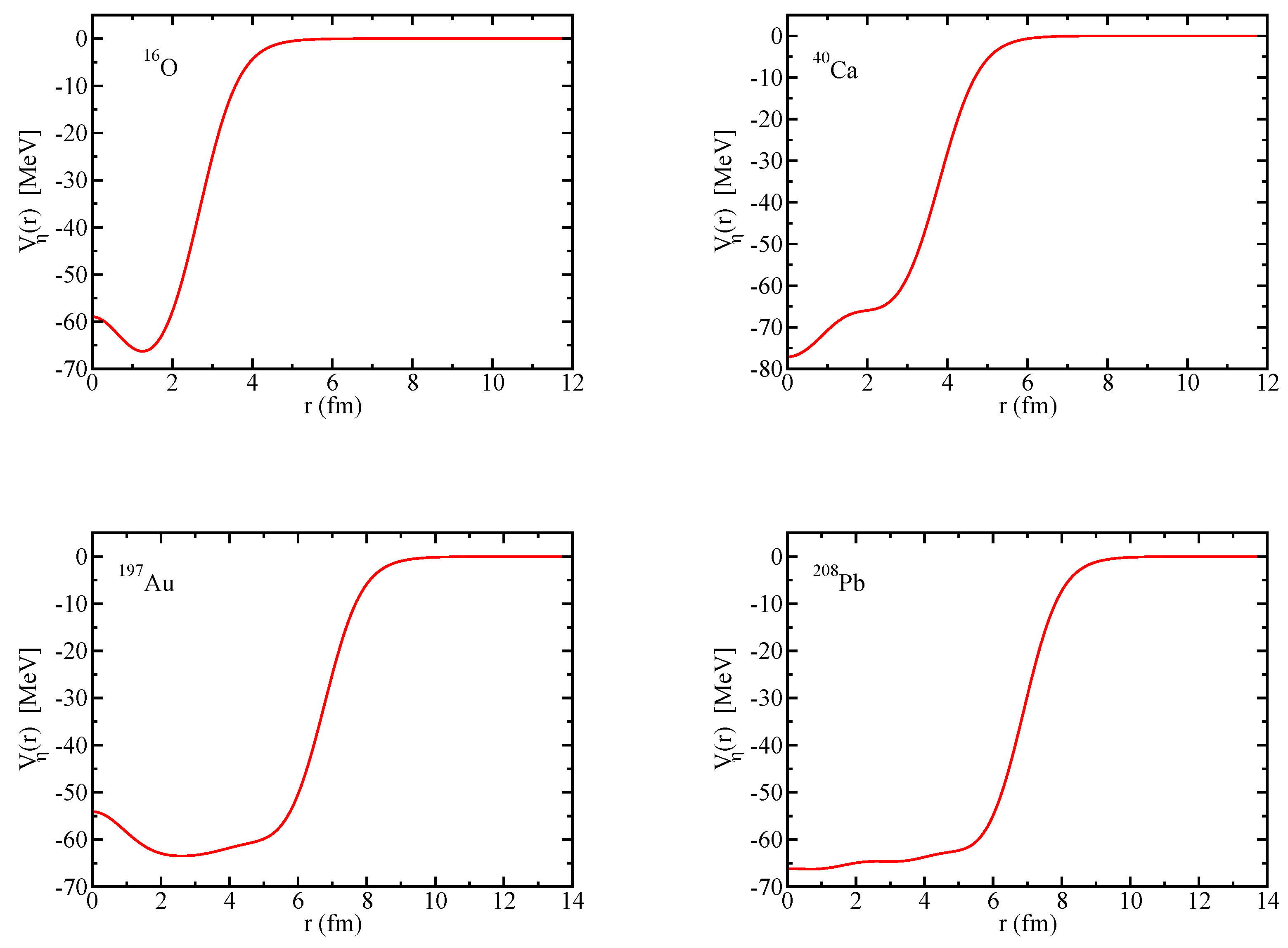
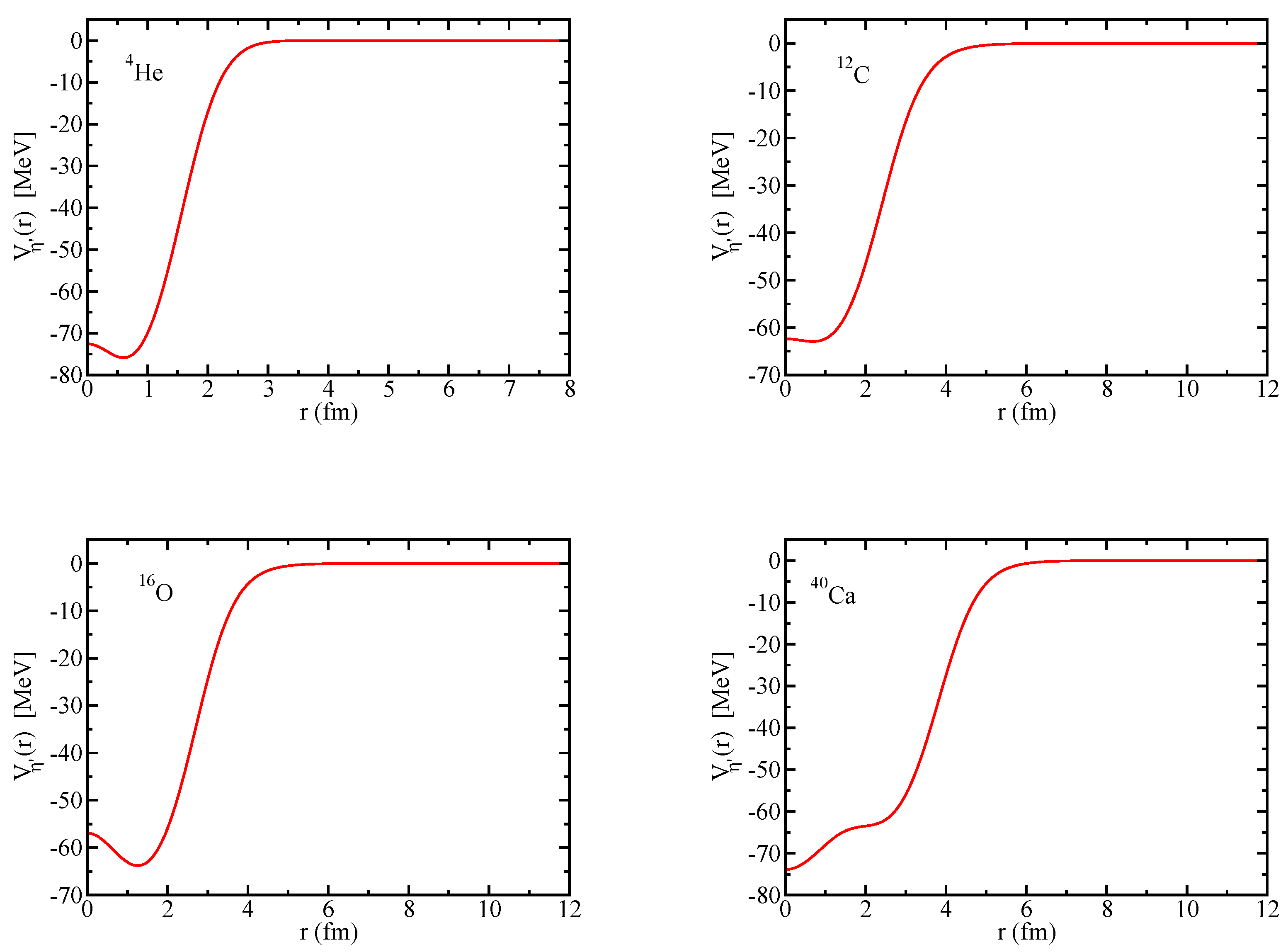
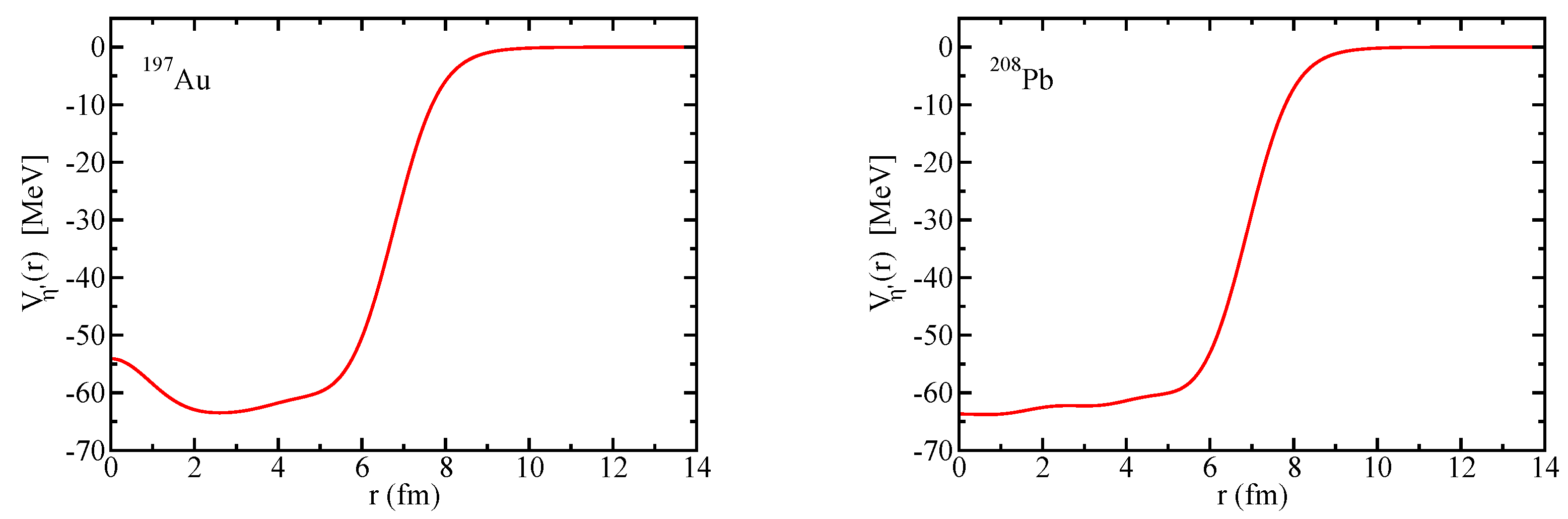
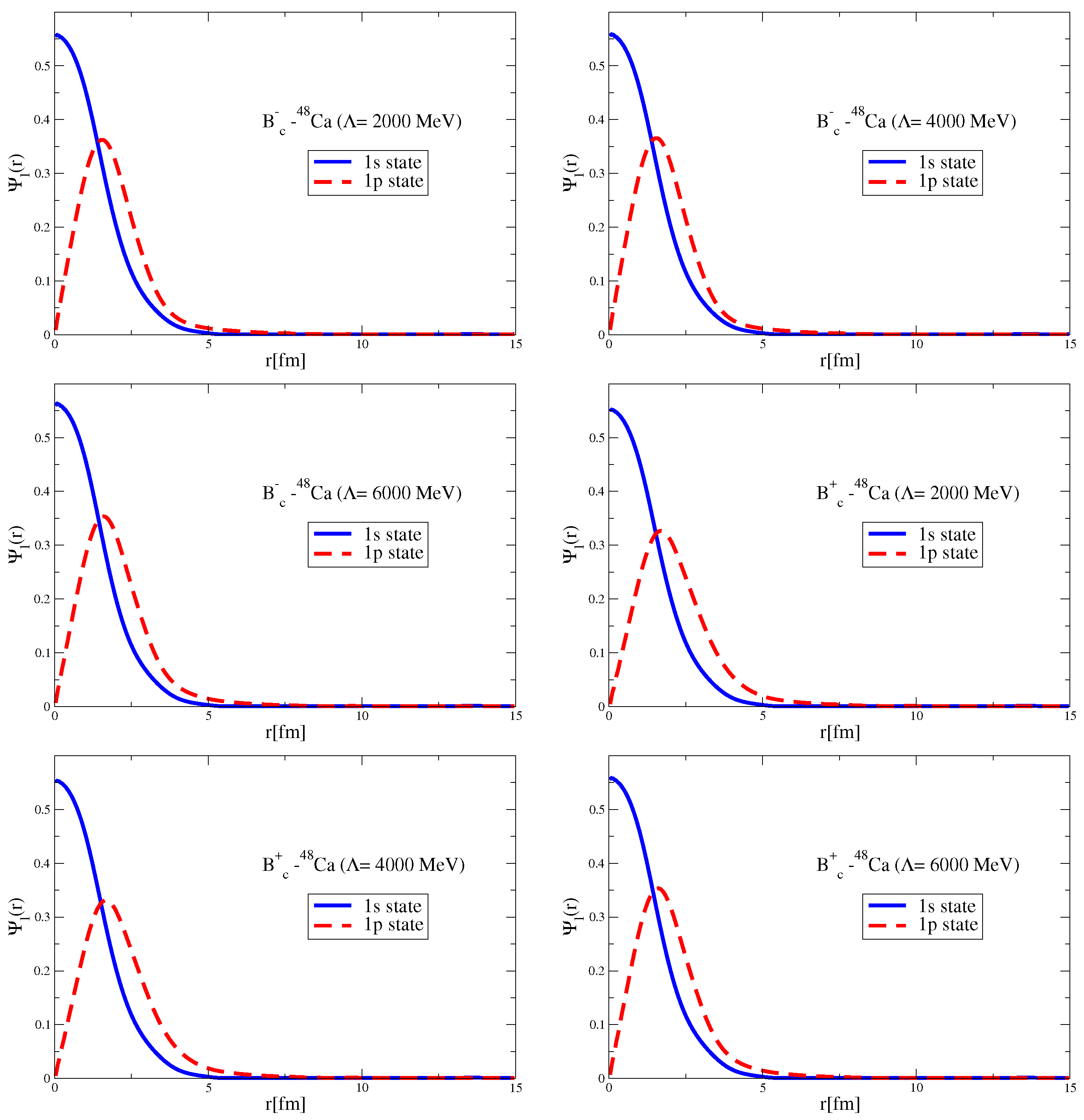Since the Okubo–Zweig–Iizuka rule suppresses the interactions mediated by the exchange of mesons made of light quarks for the case of heavy–heavy mesons, it is therefore necessary to explore other potential sources of attraction, which could potentially lead to the binding of heavy–heavy mesons to atomic nuclei. Furthermore, since the heavy quarks $Q=s,c,b$ do not directly interact with the mean fields in a nuclear medium (see Equation (3)), to compute the effective masses (Lorentz scalar potentials) for the mesons composed of a (heavy quark)-(heavy antiquark) pair, we take a different approach.

This approach consists of the combined treatment with the QMC model and an effective Lagrangian. We have already introduced the QMC model above, so we now describe the effective Lagrangian approach we rely on.

In the effective Lagrangian approach, mesons are treated as structureless point-like particles, whose interactions are dictated by a local gauge symmetry principle. In order to be more explicit, we separate our study according to the different mesons. Part of the descriptions and treatments reviewed here have already been published in journals [72,77,80,98,99,100,101], as well as presented at various conferences [79,102,103,104,105,106].

4.1. The $\varphi$ Vector Meson

The $\varphi$ meson properties in nuclear matter, such as mass and decay width, are strongly correlated to its coupling to the $K\overline{K}$, which is the dominant decay channel in vacuum. 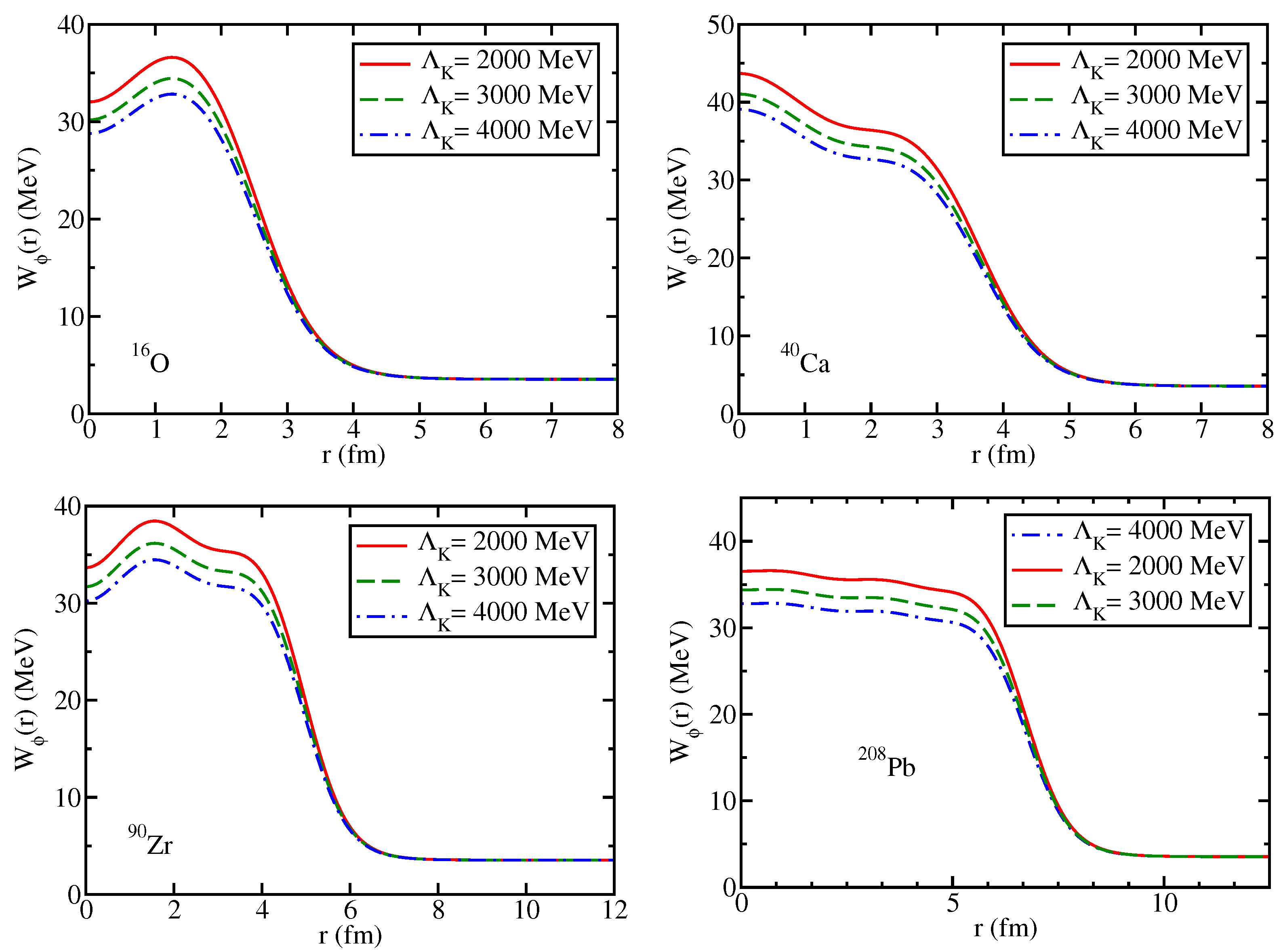Therefore, the density dependence of the $\varphi$ meson self-energy in nuclear matter arises mainly due to interactions of the kaons and antikaons with the nuclear medium, and the kaon and antikaon in-medium properties are calculated in the QMC model [91] (see also Figure 1 for the effective mass of K (=$\overline{K}$) meson). Here we use the effective Lagrangian approach of Ref. [107] to compute the $\varphi$ meson self-energy.

The lowest-order interaction Lagrangian providing the coupling of the $\varphi$ meson to the $K\overline{K}$ pair reads [107]

$${\mathcal{L}}_{\varphi K\overline{K}}=\mathrm{i}{g}_{\varphi }{\varphi }^{\mu }\left[\overline{K}\left({𝜕}_{\mu }K\right)-\left({𝜕}_{\mu }\overline{K}\right)K\right],$$

(10)

where $g_{\varphi }$ is $\varphi K\overline{K}$ coupling constant and we use the convention:

$$K=\left(\begin{array}{c}{K}^{+}\\ K^0\end{array}\right),\overline{K}=\left(K^{-}{\overline{K}}^0\right).$$

(11)

The scalar self-energy for the $\varphi$ meson, ${\mathsf{\Pi }}_{\varphi }\left(p\right)$, is determined from Equation (10). The Feynman diagram contributing to ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ at $\mathcal{O}\left(g_{\varphi }^2\right)$ is depicted in Figure 3. For a $\varphi$ meson at rest, the scalar self-energy is given by

$$\mathrm{i}{\mathsf{\Pi }}_{\varphi }\left(m_{\varphi }^2\right)=-{\displaystyle \frac{8}{3}}{g}_{\varphi }^2\int {\displaystyle \frac{{\mathrm{d}}^{3}q}{{\left(2\pi \right)}^3}}{\mathbf{q}}^2{D}_K\left(q\right)D_K(q-p),$$

(12)

where $D_K\left(q\right)={\left(q^2-m_K^2+\mathrm{i}ϵ\right)}^{-1}$ is the kaon propagator; $p^{\mu }=(p^0=m_{\varphi },\mathbf{0})$ is the $\varphi$ meson four-momentum vector ($\varphi$ at rest), with $m_{\varphi }$ the $\varphi$ meson mass; $m_K(=m_{\overline{K}})$ is the kaon mass. When $m_{\varphi }<2m_K$ the self-energy ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ is real. However, when $m_{\varphi }>2m_K$, which is the case here, ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ acquires an imaginary part.

The mass of the $\varphi$ meson is determined from the real part of ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ (see Equation (17)), while its decay width ${\mathsf{\Gamma }}_{\varphi }$ to a $K\overline{K}$ pair from the imaginary part of ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ through the optical theorem (see Equation (15)). The real and imaginary parts of ${\mathsf{\Pi }}_{\varphi }\left(p\right)$ can be computed as [99]

$$\begin{array}{ccc}\hfill \mathrm{Re}{\mathsf{\Pi }}_{\varphi }& =& -{\displaystyle \frac{2}{3}}{g}_{\varphi }^2\mathcal{P}\int {\displaystyle \frac{{\mathrm{d}}^{3}q}{{\left(2\pi \right)}^3}}{\mathbf{q}}^2{\displaystyle \frac{1}{E_K(E_K^2-m_{\varphi }^2/4)}},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \mathrm{Im}{\mathsf{\Pi }}_{\varphi }& =& -{\displaystyle \frac{g_{\varphi }^2}{3\pi }}{\displaystyle \frac{1}{m_{\varphi }}}{\left[{\displaystyle \frac{m_{\varphi }}{2}}{\left(1-{\displaystyle \frac{4m_K^2}{m_{\varphi }^2}}\right)}^{1/2}\right]}^3,\hfill \end{array}$$

(14)

where $\mathcal{P}$ denotes the Principal Value of the integral and $E_K={({\mathbf{q}}^2+m_K^2)}^{1/2}$. The integral in Equation (13) is divergent, but it will be regulated using a phenomenological form factor, with cutoff parameter ${\mathsf{\Lambda }}_K$, as in Ref. [42].

The decay width ${\mathsf{\Gamma }}_{\varphi }$ for the process $\varphi \to K\overline{K}$ can be obtained from the imaginary part of the $\varphi$ meson self-energy $\mathrm{Im}{\mathsf{\Pi }}_{\varphi }$ through the optical theorem

$${\mathsf{\Gamma }}_{\varphi }=-{\displaystyle \frac{1}{m_{\varphi }}}\mathrm{Im}{\mathsf{\Pi }}_{\varphi },$$

(15)

where $\mathrm{Im}{\mathsf{\Pi }}_{\varphi }$ is given by Equation (14). Thus, one obtains

$${\mathsf{\Gamma }}_{\varphi }={\displaystyle \frac{g_{\varphi }^2}{3\pi }}{\displaystyle \frac{1}{m_{\varphi }^2}}{\left[{\displaystyle \frac{m_{\varphi }}{2}}{\left(1-{\displaystyle \frac{4m_K^2}{m_{\varphi }^2}}\right)}^{1/2}\right]}^3.$$

(16)

The coupling constant $g_{\varphi }$ is determined by the experimental value for the $\varphi \to K\overline{K}$ decay width in vacuum, corresponding to a branching ratio of $83.1\%$ of the total decay width (4.266 MeV) [108]. For the $\varphi$ meson mass $m_{\varphi }$ we use its experimental value in vacuum $m_{\varphi }^{\mathrm{expt}}=1019.461$ MeV [108]. For the kaon mass $m_K$, there is a small ambiguity since $m_{K^{+}}\ne m_{K^0}$ in the real world due to the isospin (or charge) symmetry breaking and electromagnetic interactions. The experimental values for the $K^{+}$ and $K^0$ meson masses in vacuum are $m_{K^{+}}^{\mathrm{expt}}=493.677$ MeV and $m_{K^0}^{\mathrm{expt}}=497.611$ MeV, respectively [108]. For definitiveness, we use the average of $m_{K^{+}}^{\mathrm{expt}}$ and $m_{K^0}^{\mathrm{expt}}$ as the value of $m_K$ in vacuum. (However, the effect of this tiny mass ambiguity on the properties of kaon (antikaon) in medium, to be presented in the next section, is negligible compared with those obtained by using the value $m_{K^{+}}=493.7$ MeV [91]). This gives $g_{\varphi }=4.539$ [99]. The mass of the $\varphi$ meson will be obtained from the solution of

$$m_{\varphi }^2={\left(m_{\varphi }^0\right)}^2+\mathrm{Re}{\mathsf{\Pi }}_{\varphi }\left(m_{\varphi }^2\right)={\left(m_{\varphi }^0\right)}^2-\left|\mathrm{Re}{\mathsf{\Pi }}_{\varphi }\left(m_{\varphi }^2\right)\right|,$$

(17)

where $\mathrm{Re}{\mathsf{\Pi }}_{\varphi }$ is given by Equation (13) and $m_{\varphi }^0$ is the bare $\varphi$ meson mass. In vacuum, Equation (17), together with the value obtained for the coupling constant, actually fixes the bare $\varphi$ meson mass $m_{\varphi }^0$.

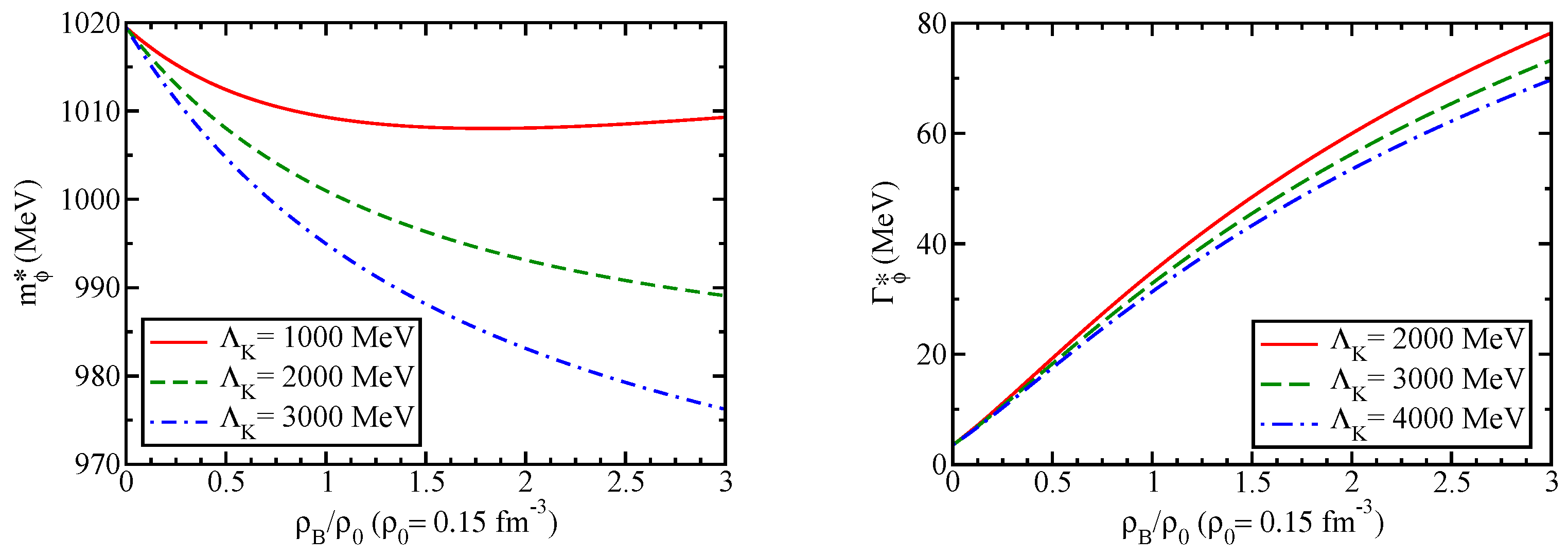
Critical to our results of the in-medium $\varphi$ meson mass $m_{\varphi }^{\ast }$ and decay width ${\mathsf{\Gamma }}_{\varphi }^{\ast }$ at finite baryon density ${\rho }_B$, is the in-medium kaon mass $m_K^{\ast }$. The nuclear (baryon) density dependence of the $\varphi$ meson mass and decay width are driven by the interactions of the kaon with the nuclear medium, which enter through $m_K^{\ast }$ in the kaon propagators in Equation (12). The in-medium kaon mass $m_K^{\ast }$ was calculated previously in the QMC model, and the results are shown in the right panel of Figure 1. We note that the kaon effective mass at normal nuclear density ${\rho }_0=0.15$ fm⁻³ decreases by about $13\%$ [99]. We remind that, to calculate the kaon-antikaon loop contributions to the $\varphi$-meson self-energy in symmetric nuclear matter, the isoscalar-vector $\omega$ mean field potentials arise both for the kaon and antikaon. However, they have opposite signs and cancel each other, or can be eliminated by the variable shift in the loop integral calculation.

To calculate the width and mass of the in-medium $\varphi$ meson, ${\mathsf{\Gamma }}_{\varphi }^{\ast }$ and $m_{\varphi }^{\ast }$, respectively, we solve the corresponding Equations (16) and (17) in symmetric nuclear matter by replacing $m_K$ by $m_K^{\ast }$ and $m_{\varphi }$ by $m_{\varphi }^{\ast }$ in the self-energy of the $\varphi$ meson. In Figure 4, we present our results [99] for the $\varphi$ meson mass (left panel) and decay width (right panel) in nuclear matter up to ${\rho }_B=3{\rho }_0$. As can be seen in Figure 4, the effect of the in-medium change in kaon mass gives a negative change in $\varphi$ meson mass. However, even for the largest value of density considered in this study, the downward mass shift is only a few percent for all values of the cutoff parameter ${\mathsf{\Lambda }}_K$. In

Table 1. $\varphi$ meson mass and width at normal nuclear density, ${\rho }_0$. The $\varphi$ meson mass decreases by a few percent ($1.8\%$ in average), while the decay width increases by an order of magnitude, with respect to the corresponding vacuum values. All quantities are given in MeV.

	${\mathbf{\Lambda }}_{\mathit{K}}=1000$	${\mathbf{\Lambda }}_{\mathit{K}}=2000$	${\mathbf{\Lambda }}_{\mathit{K}}=3000$
$m_{\varphi }^{\ast }$	1009.3	1000.9	994.9
${\mathsf{\Gamma }}_{\varphi }^{\ast }$	37.7	34.8	32.8

, we present the values for $m_{{\varphi }^{\ast }}$ and ${\mathsf{\Gamma }}_{\varphi }^{\ast }$ at normal nuclear density ${\rho }_0$. More quantitatively, from Table 1 we see that the negative kaon mass shift of 13% induces only ≈ 2% downward mass shift of the $\varphi$ meson [99]. On the other hand, from Figure 4 we see that ${\mathsf{\Gamma }}_{\varphi }^{\ast }$ is very sensitive to the change in the kaon mass. It increases rapidly with increasing nuclear density, up to a factor of ∼20 enhancement for the largest nuclear density considered, ${\rho }_B=3{\rho }_0$ [99]. As can be seen from Table 1, the broadening of the $\varphi$ meson decay width becomes an order of magnitude larger than its vacuum value at normal nuclear density.

4.2. ${\eta }_c$ and $J/\psi$ Mesons

The study of interactions of charmonium states, such as ${\eta }_c$ and $J/\psi$, with atomic nuclei offers the opportunity to gain new insights into the properties of the strong force and strongly interacting matter [72]. Because charmonia and nucleons do not share light quarks, the Okubo–Zweig–Iizuka (OZI) rule [36,37,38,39,40] suppresses the interactions mediated by the exchange of mesons composed of light quarks and/or antiquarks. The situation here is similar to the $\varphi$ meson case and also generally for quarkonia and two-heavy-flavor mesons). Thus, it is important and necessary to explore other possible mechanisms, which can provide attractive (repulsive) interactions that could lead to the binding (unbinding) of charmonia to atomic nuclei [72]. For a review on the subject, see Refs. [8,9,10,11]. Here, we employ an effective Lagrangian approach and consider charmed meson loops in the charmonium self-energy [42,43,58,72,109]; that light quark-antiquark pair is created from the vacuum.

Note that, recent lattice study using the HAL QCD method with nearly realistic pion mass of $m_{\pi }=146$ MeV, which was also able to reproduce well the physical hadron masses [110,111], found that the N-$c\overline{c}$ (N-$J\psi$ and N-${\eta }_c$) interactions to be attractive in all distances. They predicted mass reduction of the $J/\psi$-meson at normal nuclear density of 0.17 fm⁻³ of about 19(3) MeV. This is consistent with our prediction made without the “gauge term”, which is to be shown later.

For the computation of the ${\eta }_c$ Lorentz scalar potential in nuclear matter, we use an effective Lagrangian approach at the hadronic level, which is an SU(4)-flavor extension of light-flavor chiral-symmetric Lagrangians of pseudoscalar and vector mesons [107,112]. When we treat the mesons that contain at least one bottom quark (antiquark), we will use an SU(5)-flavor Lagrangian [31]. However, one can expect that the SU(5) flavor symmetry breaking is larger than that of SU(4) due to the current quark mass values of the charm and bottom quarks. Thus, for the SU(4) flavor sector, we use a flavor SU(4) effective Lagrangian, and determine the relevant coupling constants based on the flavor SU(4) symmetry.

We compute the ${\eta }_c$ self-energy in vacuum and symmetric nuclear matter, following our previous works [42,43,58,99,100,102,103,104,109], and consider only the $D{D}^{\ast }$ loop. See Ref. [72] for details. The interaction Lagrangian density for the ${\eta }_{c}D{D}^{\ast }$ vertex is given by

$${\mathcal{L}}_{{\eta }_{c}D{D}^{\ast }}=\mathrm{i}{g}_{{\eta }_{c}D{D}^{\ast }}\left({𝜕}_{\mu }{\eta }_c\right)\left[{\overline{D}}^{\ast \mu }D-\overline{D}{D}^{\ast \mu }\right]-\mathrm{i}{g}_{{\eta }_{c}D{D}^{\ast }}{\eta }_c\left[{\overline{D}}^{\ast \mu }\left({𝜕}_{\mu }D\right)-\left({𝜕}_{\mu }\overline{D}\right)D^{\ast \mu }\right],$$

(18)

where $D^{(\ast )}$ represents the $D^{(\ast )}$-meson field isospin doublet, and $g_{{\eta }_{c}D{D}^{\ast }}$ is the coupling constant. The ${\eta }_c$ self-energy in the rest frame of ${\eta }_c$ meson, $p_{{\eta }_c}^{\mu }=(m_{{\eta }_c},\mathbf{0})$ is given by [72]

$${\Sigma }_{{\eta }_c}\left(m_{{\eta }_c}^2\right)={\displaystyle \frac{8g_{{\eta }_{c}D{D}^{\ast }}^2}{{\pi }^2}}{\int }_0^{\infty }\mathrm{d}q{q}^{2}I\left(q^2\right),$$

(19)

where

$$\begin{array}{cc}\hfill I\left(q^2\right)& ={\left.{\displaystyle \frac{m_{{\eta }_c}^2(-1+q_0^2)/m_{D^{\ast }}^2)}{(q_0+{\omega }_{D^{\ast }})(q_0-{\omega }_{D^{\ast }})(q_0-m_{{\eta }_c}-{\omega }_D)}}\right|}_{q_0=m_{{\eta }_c}-{\omega }_{D^{\ast }}}\hfill \\ \hfill +& {\left.{\displaystyle \frac{m_{{\eta }_c}^2(-1+q_0^2)/m_{D^{\ast }}^2)}{(q_0-{\omega }_{D^{\ast }})(q_0-m_{{\eta }_c}+{\omega }_D)(q_0-m_{{\eta }_c}-{\omega }_D)}}\right|}_{q_0=-{\omega }_{D^{\ast }}},\hfill \end{array}$$

(20)

and ${\omega }_{D^{(\ast )}}={(q^2+m_{D^{(\ast )}}^2)}^{1/2}$, with $q=\left|\mathbf{q}\right|$. The integral in Equation (19) is divergent, and we regularize it with a phenomenological vertex form factor

$$u_{D^{(\ast )}}\left(q^2\right)={\left({\displaystyle \frac{{\mathsf{\Lambda }}_{D^{(\ast )}}^2+m_{{\eta }_c}^2}{{\mathsf{\Lambda }}_{D^{(\ast )}}^2+4{\omega }_{D^{(\ast )}}^2\left(q^2\right)}}\right)}^2,$$

(21)

with cutoff parameter ${\mathsf{\Lambda }}_{D^{(\ast )}}$, as in previous works. See Ref. [72] and references therein. Thus, to regularize Equation (19), we will introduce the form factor $u_D\left(k^2\right)u_{D^{\ast }}\left(k^2\right)$ into the integrand. As before, the cutoff parameter ${\mathsf{\Lambda }}_D^{(\ast )}$ is an unknown input to our calculation (we use ${\mathsf{\Lambda }}_{D^{\ast }}={\mathsf{\Lambda }}_D$). However, it may be fixed phenomenologically, for example, using a quark model. In Ref. [42], the value of ${\mathsf{\Lambda }}_D$ has been estimated to be $\mathsf{\Lambda }\approx 2500$ MeV, and serves as a reasonable guidance to quantify the sensitivity of our results to its value. Therefore, we vary it over the interval 1500–3000 MeV [72].

Because the flavor SU(4) symmetry is strongly broken (though less than that of SU(5),we use the experimental values for the meson masses [108] and known (extracted) empirical values for the coupling constants, as explained in the following. For the D meson mass, we take the averaged masses of the neutral and charged states, and similarly for the $D^{\ast }$. Thus $m_D=1867.2$ MeV and $m_{D^{\ast }}=2008.6$ MeV. For the coupling constants, $g_{{\eta }_{c}D{D}^{\ast }}=0.60g_{\psi DD}$ was obtained in Ref. [113], as the residue at the poles of suitable form factors using a dispersion formulation of the relativistic constituent quark model, where $g_{\psi DD}=7.64$ was estimated in Ref. [114] using the vector meson dominance (VMD) model and isospin symmetry. In this study we use the coupling constant, $g_{{\eta }_{c}D{D}^{\ast }}=(0.60/\sqrt{2})g_{\psi DD}\simeq 0.424g_{\psi DD}$ [72], where the factor ($1/\sqrt{2}$) is introduced to give a larger SU(4) symmetry breaking effect than Ref. [113].

In this subsection, we will show the mass shift of ${\eta }_c$ with the use of both the SU(4) symmetry coupling constant as well as that with the broken SU(4) coupling constant. Furthermore, later we will compare the in-medium masses of ${\eta }_c$ and $J/\psi$ with those of the ${\eta }_b,\mathsf{{\rm Y}},B_c$ and $B_c^{\ast }$, using the coupling constant value $g_{{\eta }_{c}D{D}^{\ast }}=g_{\psi DD}=7.64\to 7.7$, without any symmetry breaking factor, i.e., $g_{{\eta }_{c}D{D}^{\ast }}=(0.60/\sqrt{2})g_{\psi DD}\simeq 0.424g_{\psi DD}$ $\to g_{{\eta }_{c}DD}=g_{\psi DD}=7.7$, where the tiny difference may be ignored. For the $J/\psi$ mass shift in this subsection, after the ${\eta }_c$ mass shift, we will use only the SU(4) symmetric coupling constant, $g_{\psi DD}=7.64$.

We are interested in the difference between the in-medium, $m_{{\eta }_c}^{\ast }$, and vacuum, $m_{{\eta }_c}$, masses of the ${\eta }_c$,

$$\mathsf{\Delta }{m}_{{\eta }_c}=m_{{\eta }_c}^{\ast }-m_{{\eta }_c},$$

(22)

with the masses obtained self-consistently from

$$m_{{\eta }_c}^2={\left(m_{{\eta }_c}^0\right)}^2+{\Sigma }_{{\eta }_c}\left(m_{{\eta }_c}^2\right)={\left(m_{{\eta }_c}^0\right)}^2-\left|{\Sigma }_{{\eta }_c}\left(m_{{\eta }_c}^2\right)\right|,$$

(23)

where $m_{{\eta }_c}^0$ is the bare ${\eta }_c$ mass and the ${\eta }_c$ self-energy in the rest frame of ${\eta }_c$ meson, ${\Sigma }_{{\eta }_c}\left(m_{{\eta }_c}^2\right)$ is given by Equation (19). The ${\mathsf{\Lambda }}_D$-dependent ${\eta }_c$-meson bare mass, $m_{{\eta }_c}^0$, is fixed by fitting the physical ${\eta }_c$-meson mass, $m_{{\eta }_c}=2983.9$ MeV [72].

The in-medium ${\eta }_c$ mass is obtained in a similar way, with the self-energy calculated with the medium-modified D and $D^{\ast }$ meson masses. The nuclear density dependence of the ${\eta }_c$-meson mass is influenced and determined by the intermediate-state D and $D^{\ast }$ meson interactions with the nuclear medium through their medium-modified masses. The in-medium masses $m_D^{\ast }$ and $m_{D^{\ast }}^{\ast }$ are calculated within the quark–meson coupling (QMC) model [42,43], in which effective scalar and vector meson mean fields couple to the light u and d quarks in the charmed mesons [42,43].

In the middle panel of Figure 1 we present the resulting medium-modified masses for the D and $D^{\ast }$ mesons, calculated within the QMC model [42], as a function of ${\rho }_B/{\rho }_0$, where ${\rho }_B$ is the baryon density of nuclear matter and ${\rho }_0=0.15$ fm⁻³ the saturation density of symmetric nuclear matter. The net reductions in the masses of the D and $D^{\ast }$ mesons are nearly the same as a function of density, with each decreasing by about 60 MeV at ${\rho }_0$. The behavior of the D meson mass in medium (finite density and/or temperature) has been studied in a variety of approaches, where some of these [115,116,117] find a decreasing D meson mass at finite baryon density, while others [118,119,120,121,122], interestingly, find the opposite behavior. However, it is important to note that none of the studies in nuclear matter are constrained by the saturation properties of nuclear matter, despite the fact that they are constrained in the present work. Furthermore, some of these works employ a non-relativistic approach, where relativistic effects might be important.

In Figure 5, we present the ${\eta }_c$-meson mass shift, $\mathsf{\Delta }{m}_{{\eta }_c}$, as a function of the nuclear matter density, ${\rho }_B$ (${\rho }_B/{\rho }_0$), for four values of the cutoff parameter ${\mathsf{\Lambda }}_D$ [72]. As can be seen from the figure, the effect of the in-medium D and $D^{\ast }$ mass changes is to shift the ${\eta }_c$ mass downwards. This is because the reduction in the D and $D^{\ast }$ masses enhances the $D{D}^{\ast }$-loop contribution in nuclear matter relative to that in vacuum. This effect increases the larger the cutoff mass ${\mathsf{\Lambda }}_D$ becomes.

The results described above with the two values of the $g_{{\eta }_{c}D{D}^{\ast }}$ coupling constants, both support a small downward mass shift for the ${\eta }_c$ in nuclear matter, and open the possibility to study the binding of ${\eta }_c$ meson to nuclei [72].

We now turn to the discussion of the $J/\psi$ vector meson [105,106], following the same procedure as in the $\varphi$ meson. In Refs. [11,42,43], the $J/\psi$ self-energy intermediate states involved the D, $\overline{D}$, $D^{\ast }$, and $\overline{D^{\ast }}$ mesons. However, it was found that the $J/\psi$ self-energy has larger contributions from the loops involving the $D^{\ast }$ and $\overline{D^{\ast }}$ mesons, which is unexpected; see Refs. [11,42,43] for details on the issues and possible explanations. As explained in Ref. [11], this is related to the divergent behavior of the vector meson propagator. We present results for the $J/\psi$ mass shift in nuclear matter and nuclei considering only the lightest intermediate state mesons in the $J/\psi$ self-energy, namely the $D\overline{D}$ loop [105,106].

We use the following phenomenological effective Lagrangian densities at the hadronic level, which are similar to those used above for the $\varphi$-meson,

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{int}& =& {\mathcal{L}}_{\psi DD}+{\mathcal{L}}_{\psi \psi DD},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\psi DD}& =& i{g}_{\psi DD}{\psi }^{\mu }\left[\overline{D}\left({𝜕}_{\mu }D\right)-\left({𝜕}_{\mu }\overline{D}\right)D\right],\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\psi \psi DD}& =& g_{\psi DD}^2{\psi }_{\mu }{\psi }^{\mu }\overline{D}D.\hfill \end{array}$$

(26)

where $g_{\psi DD}$ is the $J/\psi D\overline{D}$ coupling constant and we use the convention

$$\begin{array}{c}\hfill D=\left(\begin{array}{c}{D}^0\\ D^{+}\end{array}\right),\overline{D}=\left(\overline{D^0}{D}^{-}\right).\end{array}$$

(27)

For notational simplicity, we have written $\psi$ to denote the field representing the $J/\psi$ vector meson. We note that the Lagrangians are an $SU$(4) extension of light-flavor chiral-symmetric Lagrangians of pseudoscalar and vector mesons. In the light flavor sector, they have been motivated by a local gauge symmetry, treating vector mesons either as massive gauge bosons or as dynamically generated gauge bosons. Local gauge symmetry implies the contact interaction in Equation (26) involving two pseudoscalar and two vector mesons.

In view of the fact that $SU$(4) flavor symmetry is strongly broken in nature, and in order to stay as close as possible to phenomenology, we use the experimental values for the charmed meson masses and use the empirically known meson coupling constants. For these reasons, we do not use gauged Lagrangians for the study of $J/\psi$ nuclear bound states—a similar attitude was followed in Ref. [112] in a study of hadronic scattering of charmed mesons. However, in order to compare results with Ref. [57] and assess the impact of a contact term of the form Equation (26), we also present results for the $J/\psi$ mass shift including such a term.

We are interested in the difference of the in-medium, $m_{\psi }^{\ast }$, and vacuum, $m_{\psi }$,

$$\mathsf{\Delta }{m}_{\psi }=m_{\psi }^{\ast }-m_{\psi },$$

(28)

with the masses obtained from

$$m_{\psi }^2={\left(m_{\psi }^0\right)}^2+{\Sigma }_{D\overline{D}}\left(m_{\psi }^2\right)={\left(m_{\psi }^0\right)}^2-\left|{\Sigma }_{D\overline{D}}\left(m_{\psi }^2\right)\right|.$$

(29)

Here $m_{\psi }^0$ is the bare mass and ${\Sigma }_{D\overline{D}}\left(k^2\right)$ is the total $J/\psi$ self-energy obtained from the $D\overline{D}$-loop contribution only. The in-medium mass, $m_{\psi }^{\ast }$, is obtained likewise, with the self-energy calculated with medium-modified D meson mass calculated by the QMC model (see again the middle panel of Figure 1).

The scalar self-energy for the $J/\psi$ meson in the rest frame of $J/\psi$, ${\Sigma }_{D\overline{D}}\left(m_{\psi }^2\right)$, is obtained from Equation (24). The Feynman diagram contributing to $J/\psi$ self-energy $\mathcal{O}\left(g_{\psi }^2\right)$ is identical to the one in Figure 3 with the replacements $\varphi \to J/\psi$, $K\to D$ and $\overline{K}\to \overline{D}$.

For a $J/\psi$ meson at rest, the self-energy is given by

$${\Sigma }_{D\overline{D}}\left(m_{\psi }^2\right)=-{\displaystyle \frac{g_{\psi DD}^2}{3{\pi }^2}}{\int }_0^{\infty }dq{q}^2{F}_{D\overline{D}}\left(q^2\right)K_{D\overline{D}}\left(q^2\right),$$

(30)

where $q=\left|\mathbf{q}\right|$, and $F_{D\overline{D}}\left(q^2\right)=u_D\left(q^2\right)u_{\overline{D}}\left(q^2\right)$ is the product of vertex form-factors with $u_D\left(q^2\right)$ and $u_{\overline{D}}$ given as in Equation (21) with cutoff parameters ${\mathsf{\Lambda }}_D$ and ${\mathsf{\Lambda }}_{\overline{D}}$, respectively (we use ${\mathsf{\Lambda }}_D={\mathsf{\Lambda }}_{\overline{D}}$); and $K_{D\overline{D}}\left(q^2\right)$ for the $D\overline{D}$ loop contribution is given by

$$K_{D\overline{D}}\left(q^2\right)={\displaystyle \frac{q^2}{{\omega }_D}}\left({\displaystyle \frac{q^2}{{\omega }_D^2-m_{\psi }^2/4}}-\xi \right),$$

(31)

where ${\omega }_D={(q^2+m_D^2)}^{1/2}$, $\xi =0$ for the non-gauged Lagrangian of Equation (24) and $\xi =1$ with Equation (26), for the gauged Lagrangian of Ref. [57].

As before, the cutoff parameter ${\mathsf{\Lambda }}_D$ is an unknown input to our calculation. However, it may be fixed phenomenologically. In Ref. [42] the value of ${\mathsf{\Lambda }}_D$ has been estimated to be ${\mathsf{\Lambda }}_D\approx 2500$ MeV, and serves as a reasonable guidance to quantify the sensitivity of our results to its value. Since this is a somewhat rough estimate, and it is made solely to obtain an order of magnitude estimate, we allow the value of ${\mathsf{\Lambda }}_D$ vary in the range $2000\mathrm{MeV}\le {\mathsf{\Lambda }}_D\le 6000\mathrm{MeV}$; see Refs. [11,42,43].

The bare $J/\psi$ mass $m_{\psi }^0$ and the coupling constants remain to be fixed. The bare mass is fixed by fitting the physical mass $m_{J/\psi }=3096.9$ MeV using Equation (29). is strongly broken, we use experimental values for the meson masses and known empirical values for the coupling constants. For the D meson mass, we take the averaged masses of the neutral and charged D mesons. Thus $m_D=1867.2$ MeV [108]. For the coupling constants, we use $g_{\psi DD}=7.64$, which is obtained by the use of isospin symmetry [114]. Note that, for $J/\psi$, we use only the SU(4) coupling constant extracted, different from that of the ${\eta }_c$ case (no extra SU(4) breaking effect on the coupling constant).

The nuclear density dependence of the $J/\psi$-meson mass is influenced and determined by the intermediate-state D and $\overline{D}$ meson interactions with the nuclear medium through their medium-modified masses. The in-medium masses $m_D^{\ast }$ and $m_{{\overline{D}}^{\ast }}^{\ast }=m_{D^{\ast }}^{\ast }$ are calculated within the quark–meson coupling (QMC) model [42,43], in which effective scalar and vector meson mean fields couple to the light u and d quarks in the charmed mesons [42,43]. However, in the self-energy of the $D\overline{D}$ loop, the vector potentials cancel out, and there is no need to consider the effects.

Again, see the middle panel of Figure 1; we present the medium-modified masses for the D and $\overline{D}$ mesons ($m_{{\overline{D}}^{\ast }}^{\ast }=m_D^{\ast }$), calculated within the QMC model [42] as a function of ${\rho }_B/{\rho }_0$. In Figure 6, we show the contribution of the $D\overline{D}$-loop to the $J/\psi$ mass shift for $\xi =0$. As the cutoff mass value increases in the form factor, the $D\overline{D}$-loop contribution obviously becomes larger.

First, from the result shown in the left panel of Figure 6 without the gauge term ($\xi =0$), one can see that the $J/\psi$ obtains the attractive potential for all the values of the cutoff ${\mathsf{\Lambda }}_D$, 2000–6000 MeV [105,106]. In contrast, one can see from the right panel in Figure 6, that the effect of the gauge term tends to oppose the effect (repulsion) of the contribution of the $D\overline{D}$-loop as noticed in Refs. [42,105,106]. When the value of ${\mathsf{\Lambda }}_D$ is smaller, the mass shift actually becomes positive. The results shown in Figure 6 reveal a negative mass shift (attractive potential) for the $J/\psi$ meson in symmetric nuclear matter for all values of the cutoff mass parameter ${\mathsf{\Lambda }}_D$ when $\xi =0$ and, as in the ${\eta }_c$ meson case, open the possibility to study the binding of $J/\psi$ mesons to nuclei [105,106].

4.3. $\mathit{{\rm Y}}$ and ${\eta }_b$ Mesons

First, we discuss the $\mathsf{{\rm Y}}$ (vector) meson. The $\mathsf{{\rm Y}}$ mass shift in nuclear matter originates from the modifications of the $BB$, $B{B}^{\ast }$, and $B^{\ast }{B}^{\ast }$ meson loops contributions to the $\mathsf{{\rm Y}}$ self-energy, relative to those in free space; the lowest order Feynman diagrams associated with these contributions are similar to Figure 3. The $\mathsf{{\rm Y}}$ self-energy is calculated using an effective SU(5)-flavor symmetric Lagrangian at the hadronic level [31,77], where mesons are considered to be point like, for the interaction vertices $\mathsf{{\rm Y}}BB$, $\mathsf{{\rm Y}}{B}^{\ast }{B}^{\ast }$, and $\mathsf{{\rm Y}}B{B}^{\ast }$ neglecting any possible imaginary part. In Ref. [77] we made an extensive analysis of these contributions to the $\mathsf{{\rm Y}}$ self-energy and found that, for example, the $B^{\ast }{B}^{\ast }$ loop gives an unexpectedly large contribution, similar to the case of $J/\psi$. For this reason, and to be consistent with the ${\eta }_b$ case studied below, we consider only the $BB$ loop contribution to the $\mathsf{{\rm Y}}$ self-energy [77], leaving for the future a full study of all three contributions. This treatment is also consistent with the $J/\psi$ self-energy calculation with the lowest $D\overline{D}$ loop contribution, and we can compare the amounts of mass shift for the $\mathsf{{\rm Y}}$ and $J/\psi$ based on a similar footing. The interaction Lagrangian for the $\mathsf{{\rm Y}}BB$ vertex is given by [77]

$${\mathcal{L}}_{\mathsf{{\rm Y}}BB}=i{g}_{\mathsf{{\rm Y}}BB}{\mathsf{{\rm Y}}}^{\mu }\left[\overline{B}{𝜕}_{\mu }B-\left({𝜕}_{\mu }\overline{B}\right)B\right],$$

(32)

where $g_{\mathsf{{\rm Y}}BB}$ is the coupling constant for the vertex $\mathsf{{\rm Y}}BB$ vertex, and the following convention is adopted for the isospin doublets of the B mesons

$$\begin{array}{ccc}\hfill B& =\left(\begin{array}{c}{B}^{+}\\ B^0\end{array}\right),\hfill & \hfill \overline{B}=\left(\begin{array}{cc}{B}^{-}& \overline{B^0}\end{array}\right).\end{array}$$

The coupling constant $g_{\mathsf{{\rm Y}}BB}$ is calculated from the experimental data for $\mathsf{\Gamma }(\mathsf{{\rm Y}}\to e^{+}{e}^{-})$ using the vector meson dominance (VMD) model. This gives $g_{\mathsf{{\rm Y}}BB}=13.2$; see Refs. [31,77] and references therein for details. We note that a similar approach was taken in Refs. [42,114] to determine the coupling constant $g_{J/\psi DD}=7.64$ for the vertex $J/\psi DD$.

Including only the $BB$ loop, Equation (32), the $\mathsf{{\rm Y}}$ self-energy ${\Sigma }_{\mathsf{{\rm Y}}}$ for an $\mathsf{{\rm Y}}$ at rest is given by [77]

$${\Sigma }_{\mathsf{{\rm Y}}}\left(m_{\mathsf{{\rm Y}}}^2\right)=-{\displaystyle \frac{g_{\mathsf{{\rm Y}}BB}^2}{3{\pi }^2}}{\int }_0^{\infty }\mathrm{d}q{q}^{2}I\left(q^2\right)$$

(33)

where

$$I\left(q^2\right)={\displaystyle \frac{1}{{\omega }_B}}\left({\displaystyle \frac{q^2}{{\omega }_B-m_{\mathsf{{\rm Y}}}^2/4}}\right),$$

(34)

with $q=\left|\mathbf{q}\right|$ and ${\omega }_B={\left(q^2+m_B^2\right)}^{1/2}$. As is always the case in an effective Lagrangian approach, when mesons are treated as point-like particles, the self-energy loop integrals like Equation (33) are divergent and therefore need to be regularized. To this end, we introduce into the integrand of Equation (33) a phenomenological vertex form factor $u_B\left(q^2\right)$ with cutoff parameter ${\mathsf{\Lambda }}_B$ [42,43,58,99,100,102,103,104,109], for to each $\mathsf{{\rm Y}}BB$ vertex, as we did in previous cases; see Equation (21). We recall that form factors are necessary to take into account the finite size of the mesons participating in the vertices, while the cutoff ${\mathsf{\Lambda }}_B$, which is an unknown input to our calculation, may be associated with energies needed to probe the internal structure of the mesons. Thus, in order to reasonably include these effects, and to quantify the sensitivity of our results to its value, we vary ${\mathsf{\Lambda }}_B$ over the interval 2000–6000 MeV (roughly up to around the mass of the B meson); see Ref. [77] for a more extensive discussion.

The $\mathsf{{\rm Y}}$ mass shift in nuclear matter, $\mathsf{\Delta }{m}_{\mathsf{{\rm Y}}}$, is calculated from the difference between its mass in the medium, $m_{\mathsf{{\rm Y}}}^{\ast }$, and its value in vacuum, $m_{\mathsf{{\rm Y}}}$, in the rest frame of the $\mathsf{{\rm Y}}$, namely,

$$\mathsf{\Delta }{m}_{\mathsf{{\rm Y}}}=m_{\mathsf{{\rm Y}}}^{\ast }-m_{\mathsf{{\rm Y}}},$$

(35)

where these masses are computed self-consistently from

$$m_{\mathsf{{\rm Y}}}^2={\left(m_{\mathsf{{\rm Y}}}^0\right)}^2+{\Sigma }_{\mathsf{{\rm Y}}}\left(m_{\mathsf{{\rm Y}}}^2\right)={\left(m_{\mathsf{{\rm Y}}}^0\right)}^2-\left|{\Sigma }_{\mathsf{{\rm Y}}}\left(m_{\mathsf{{\rm Y}}}^2\right)\right|,$$

(36)

with $m_{\mathsf{{\rm Y}}}^0$ the bare $\mathsf{{\rm Y}}$ mass and the $\mathsf{{\rm Y}}$ self-energy ${\Sigma }_{\mathsf{{\rm Y}}}\left(m_{\mathsf{{\rm Y}}}^2\right)$ is given in Equation (33). The ${\mathsf{\Lambda }}_B$-dependent $\mathsf{{\rm Y}}$ bare mass, $m_{\mathsf{{\rm Y}}}^0$, is fixed with the physical $\mathsf{{\rm Y}}$ mass, namely $m_{\mathsf{{\rm Y}}}=9640$ MeV.

The in-medium $\mathsf{{\rm Y}}$ mass $m_{\mathsf{{\rm Y}}}^{\ast }$ is obtained by solving Equation (36) with the self-energy calculated with medium-modified B mass. This medium-modified mass was calculated using the quark–meson coupling (QMC) model as a function of the nuclear matter density ${\rho }_B$, and the results are shown in Figure 1 (left panel). From Figure 1, it can be seen that the QMC model gives a similar downward mass shift for the B and $B^{\ast }$ in symmetric nuclear matter. For example, at the saturation density ${\rho }_0=0.15{\mathrm{fm}}^{-3}$, the mass shift for the B and $B^{\ast }$ mesons are respectively, $(m_B^{\ast }-m_B)=-61$ MeV and $(m_{B^{\ast }}^{\ast }-m_{B^{\ast }})=-61$ MeV, where the difference in their mass shift values appears in the decimal place. The values for the masses in vacuum for the B and $B^{\ast }$ mesons used are $m_B=5279$ MeV and $m_{B^{\ast }}=5325$ MeV, respectively.

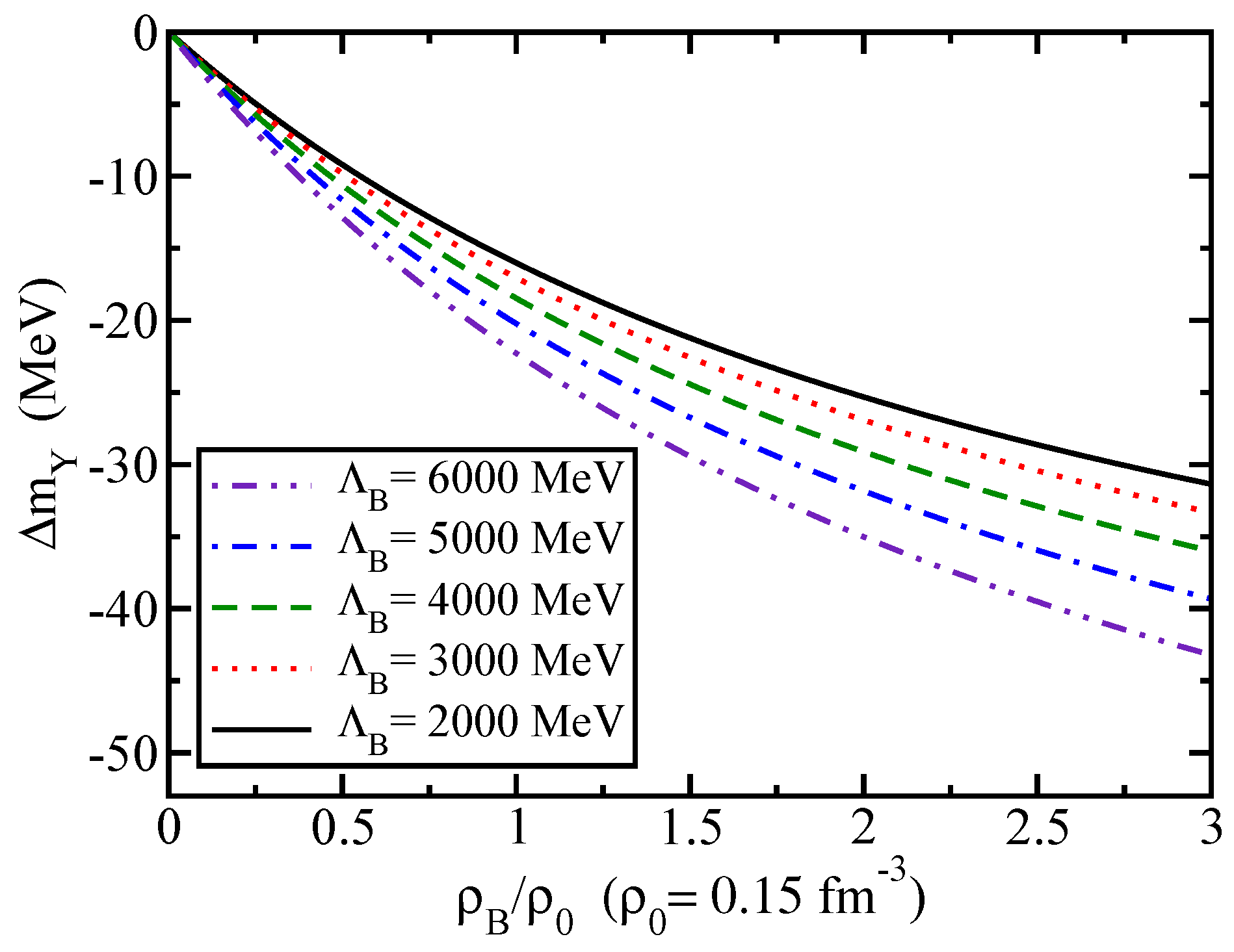
The nuclear density dependence of the $\mathsf{{\rm Y}}$ mass is driven by the intermediate $B\overline{B}$ state interactions with the nuclear medium, where the effective scalar and vector meson mean fields couple to the light u and d quarks in the bottom mesons, B and $B^{\ast }$. In Figure 7 we show the results for the $\mathsf{{\rm Y}}$ mass shift as a function of the nuclear density, ${\rho }_B/{\rho }_0$, for five values of the cutoff parameter ${\mathsf{\Lambda }}_B$. As can be seen in Figure 1 (left panel) and Figure 7, a decrease in the in-medium B meson mass induces a negative mass shift for $\mathsf{{\rm Y}}$. As expected, the mass shift amount of the $\mathsf{{\rm Y}}$ is dependent on the value of the cutoff mass ${\mathsf{\Lambda }}_B$ used, being larger for larger ${\mathsf{\Lambda }}_B$; see Ref. [77] for further details. For example, for the values of the cutoff shown in Figure 7, the $\mathsf{{\rm Y}}$ mass shift amount varies from −16 to −22 MeV, at ${\rho }_B={\rho }_0$.

For the calculation of the ${\eta }_b$ mass shift in nuclear matter, we proceed similarly to the $\mathsf{{\rm Y}}$ case and take into account only the $B{B}^{\ast }$ loop (pseudoscalar-pseudoscalar-vector) contribution to the ${\eta }_b$ self-energy. In Ref. [77], we have also studied the mass shift, including the ${\eta }_b{B}^{\ast }{B}^{\ast }$ interaction in the ${\eta }_b$ self-energy, and found that its contribution to the mass shift amount turned out to be negligible. Thus, in order to be consistent with the $\mathsf{{\rm Y}}$ case above, in both cases we consider only the minimal contribution, and here we only give results for the $B{B}^{\ast }$ loop in the ${\eta }_b$ self-energy. This is also a consistent treatment with the ${\eta }_c$ mass shift calculation, and later we can compare based on a similar footing of the self-energy calculation.

For the calculation of the ${\eta }_b$ mass shift in symmetric nuclear matter, we proceed similarly to the $\mathsf{{\rm Y}}$ and ${\eta }_c$ cases, and take into account only the $B{B}^{\ast }$ loop contribution to the ${\eta }_b$ self-energy. As already mentioned, in Ref. [77], we have also studied including the ${\eta }_b{B}^{\ast }{B}^{\ast }$ interaction in the ${\eta }_b$ self-energy and found that its contribution to the mass shift amount is negligible.

The effective Lagrangian for the ${\eta }_{b}B{B}^{\ast }$ interaction is [77]

$${\mathcal{L}}_{{\eta }_{b}B{B}^{\ast }}=i{g}_{{\eta }_{b}B{B}^{\ast }}\left[\left({𝜕}^{\mu }{\eta }_b\right)\left({\overline{B}}_{\mu }^{\ast }B-\overline{B}{B}_{\mu }^{\ast }\right)-{\eta }_b\left({\overline{B}}_{\mu }^{\ast }\left({𝜕}^{\mu }B\right)-\left({𝜕}^{\mu }\overline{B}\right)B_{\mu }^{\ast }\right)\right],$$

(37)

where $g_{{\eta }_{b}B{B}^{\ast }}$ is the coupling constant for the ${\eta }_{b}B{B}^{\ast }$ vertex. We will use its value in the SU(5) scheme [77], namely $g_{{\eta }_{b}B{B}^{\ast }}=g_{\mathsf{{\rm Y}}BB}=g_{\mathsf{{\rm Y}}{B}^{\ast }{B}^{\ast }}={\displaystyle \frac{5g}{4\sqrt{10}}}$. Using Equation (37), the ${\eta }_b$ self-energy for an ${\eta }_b$ at rest is given by [72]

$${\Sigma }_{{\eta }_b}={\displaystyle \frac{8g_{{\eta }_{b}B{B}^{\ast }}^2}{{\pi }^2}}{\int }_0^{\infty }\mathrm{d}q{q}^{2}I\left(q^2\right),$$

(38)

where

$$\begin{array}{ccc}\hfill I\left(q^2\right)& =& {\left.{\displaystyle \frac{m_{{\eta }_b}^2(-1+q_0^2/m_{B^{\ast }}^2)}{(q_0^2-{\omega }_{B^{\ast }}^2)(q_0-m_{{\eta }_b}-{\omega }_B)}}\right|}_{q_0=m_{{\eta }_b}-{\omega }_B}\hfill \\ & +& {\left.{\displaystyle \frac{m_{{\eta }_b}^2(-1+q_0^2/m_{B^{\ast }}^2)}{(q_0-{\omega }_{B^{\ast }})\left({(q_0-m_{{\eta }_b})}^2-{\omega }_B^2\right)}}\right|}_{q_0=-{\omega }_{B^{\ast }}},\hfill \end{array}$$

(39)

with $q=\left|\mathbf{q}\right|$ and ${\omega }_{B^{\ast }}=\sqrt{q^2+m_{B^{\ast }}^2}$. The mass of the ${\eta }_b$ meson, in vacuum and in nuclear matter, is computed similarly to the $\mathsf{{\rm Y}}$ case [77]. First, we introduce form factors, as in Equation (21), into each ${\eta }_{b}B{B}^{\ast }$ vertex, with ${\mathsf{\Lambda }}_B={\mathsf{\Lambda }}_{B^{\ast }}$, to regularize the divergent integral in the self-energy Equation (38). Second, we fix the value of the ${\eta }_b$ bare mass using the physical (vacuum) mass of the ${\eta }_b$, namely $m_{{\eta }_b}=9399$ MeV, using Equation (36) appropriately written for the ${\eta }_b$ case. Then, for the calculation of the ${\eta }_b$ mass shift in nuclear matter, the self-energy ${\Sigma }_{{\eta }_b}$ is computed using the medium-modified B and $B^{\ast }$ masses calculated with the QMC model and shown in Figure 1 (left panel). The results for the ${\eta }_b$ mass shift behavior in nuclear matter are shown in Figure 8 as a function of the nuclear matter density ${\rho }_B/{\rho }_0$, for the same range of values for the cutoff mass ${\mathsf{\Lambda }}_B$ as for the $\mathsf{{\rm Y}}$ [77]. As can be seen from Figure 8, the mass of the ${\eta }_b$ is shifted downwards in nuclear matter for all values of the cutoff ${\mathsf{\Lambda }}_B$, similarly to the $\mathsf{{\rm Y}}$. For example, at the normal density of symmetric nuclear matter ${\rho }_0$, the mass shift value varies from −75 MeV to −82 MeV when the cutoff varies from ${\mathsf{\Lambda }}_B=2000$ MeV to ${\mathsf{\Lambda }}_B=6000$ MeV. Similarly to the $\mathsf{{\rm Y}}$ mass shift, the dependence of the ${\eta }_b$ mass shift amount on the values of the cutoff is small, for example, just −7 MeV when the cutoff is increased by a factor of 3 at ${\rho }_B={\rho }_0$ [77].

4.4. $B_c$ and $B_c^{\ast }$ Mesons

The $B_c$ ($B_c^{\ast }$) in-medium downwards mass shift comes from the enhanced $B^{\ast }D+B{D}^{\ast }$ ($BD$) loop contribution to the self-energy, relative to those in free space. See Figure 3 but replacing the $K\overline{K}$ loop properly by $B^{\ast }D$ and $B{D}^{\ast }$ loops ($BD$ loop). See Ref. [90] for details. By expanding the SU(5) flavor symmetric effective meson Lagrangian [31] in terms of the components of pseudoscalar (P) and vector (V) $5\times 5$ matrices, we obtain the following Lagrangians for the interactions $B_c{B}^{\ast }D$, $B_{c}B{D}^{\ast }$ and $B_c^{\ast }BD$ [90]:

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{B_c{B}^{\ast }D}& =& i{g}_{B_c{B}^{\ast }D}[\left({𝜕}_{\mu }{B}_c^{-}\right)D-B_c^{-}\left({𝜕}_{\mu }D\right)]B^{\ast \mu }+h.c.,\hfill \\ \hfill {\mathcal{L}}_{B_{c}B{D}^{\ast }}& =& i{g}_{B_{c}B{D}^{\ast }}[\left({𝜕}_{\mu }{B}_c^{+}\right)\overline{B}-B_c^{+}\left({𝜕}_{\mu }\overline{B}\right)]{\overline{D^{\ast }}}^{\mu }+h.c.,\hfill \\ \hfill {\mathcal{L}}_{B_c^{\ast }BD}& =& -i{g}_{B_c^{\ast }BD}{B}_c^{\ast +\mu }[\overline{B}\left({𝜕}_{\mu }\overline{D}\right)-\left({𝜕}_{\mu }\overline{B}\right)\overline{D}]+h.c.,\hfill \end{array}$$

(40)

where the conventions for the $B,D$ and $B^{\ast }$ mesons have been already given.

The SU(5) symmetric universal coupling g yields the relations, $g_{B_c{B}^{\ast }D}=g_{B_{c}B{D}^{\ast }}=g_{B_c^{\ast }BD}$. The value of g is fixed by $g_{\mathsf{{\rm Y}}BB}={\displaystyle \frac{5g}{4\sqrt{10}}}\approx 13.2$ by the $\mathsf{{\rm Y}}$ decay data $\mathsf{\Gamma }(\mathsf{{\rm Y}}\to e^{+}{e}^{-})$ with the vector meson dominance (VMD) model [31,77], and thus we obtain,

$$g_{B_c{B}^{\ast }D}={\displaystyle \frac{2}{\sqrt{5}}}{g}_{\mathsf{{\rm Y}}BB},g_{B_c{B}^{\ast }D}=g_{B_{c}B{D}^{\ast }}=g_{B_c^{\ast }BD}={\displaystyle \frac{g}{2\sqrt{2}}}\approx 11.9.$$

(41)

The in-medium mass shift of the $B_c$ meson, $\mathsf{\Delta }{m}_{B_c}$, is computed by the difference of the in-medium $m_{B_c}^{\ast }$ and the free space $m_{B_c}$ masses

$$\mathsf{\Delta }{m}_{B_c}=m_{B_c}^{\ast }-m_{B_c},$$

(42)

where, the free space mass $m_{B_c}$ (input) is used to determine the bare mass $m_{B_c}^0$ by

$$m_{B_c}^2={\left(m_{B_c}^0\right)}^2+{\Sigma }_{B_c}\left(m_{B_c}^2\right)={\left(m_{B_c}^0\right)}^2-\left|{\Sigma }_{B_c}\left(m_{B_c}^2\right)\right|.$$

(43)

Note that the total self-energy ${\Sigma }_{B_c}$ is calculated by the sum of the $B^{\ast }D$ and $B{D}^{\ast }$ meson loop contributions in free space, ignoring the possible $B_c$ meson as well as all the other meson widths (or imaginary part) in the self-energy. The in-medium $B_c$ mass $m_{B_c}^{\ast 2}$ is similarly calculated, with the same bare mass value $m_{B_c}^0$ determined in free space, and the in-medium masses of the ($B,B^{\ast },D,D^{\ast }$) mesons ($m_B^{\ast },m_{B^{\ast }}^{\ast },m_D^{\ast },m_{D^{\ast }}^{\ast }$), namely,

$$\begin{array}{ccc}\hfill m_{B_c}^2& =& {\left[m_{B_c}^0(B^{\ast }D+B{D}^{\ast })\right]}^2-\left|{\Sigma }_{B_c}\left(B^{\ast }D\right)+{\Sigma }_{B_c}\left(B{D}^{\ast }\right)\right|\left(m_{B_c}^2\right),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill m_{B_c}^{\ast 2}& =& {\left[m_{B_c}^0(B^{\ast }D+B{D}^{\ast })\right]}^2-\left|{\Sigma }_{B_c}^{\ast }\left(B^{\ast }D\right)+{\Sigma }_{B_c}^{\ast }\left(B{D}^{\ast }\right)\right|\left(m_{B_c}^{\ast 2}\right).\hfill \end{array}$$

(45)

We note that, when the self-energy graphs contain different contributions, as ${\Sigma }_{B_c}\left(\mathrm{total}\right)=\Sigma \left(B^{\ast }D\right)+\Sigma \left(B{D}^{\ast }\right)$, $m^0$ depends on both $\Sigma \left(B^{\ast }D\right)$ and $\Sigma \left(B{D}^{\ast }\right)$ to reproduce the physical mass $m_{B_c}$. Thus, one must be careful when discussing the $B_c$ in-medium mass and mass shift of each loop contribution $\Sigma \left(B^{\ast }D\right)$ and $\Sigma \left(B{D}^{\ast }\right)$, since $m^0(B^{\ast }D+B{D}^{\ast })\ne m^0\left(B^{\ast }D\right)\ne m^0\left(B{D}^{\ast }\right)$, and $m^0(B^{\ast }D+B{D}^{\ast })\ne m^0\left(B^{\ast }D\right)+m^0\left(B{D}^{\ast }\right)$. The dominant loop contribution can be known by the decomposition of the self-energy ${\Sigma }_{B_c}^{(\ast )}(B^{\ast }D+B{D}^{\ast })={\Sigma }_{B_c}^{(\ast )}\left(B^{\ast }D\right)+{\Sigma }_{B_c}^{(\ast )}\left(B{D}^{\ast }\right)$. It turned out that the dominant contribution is from the $B{D}^{\ast }$ loop [90]. This is due to the dominant contribution from the lighter vector meson $D^{\ast }$ due to the vector meson propagator Lorentz structure.

As an example, in the case considering solely the $B^{\ast }D$ loop without the $B{D}^{\ast }$ loop, the “in-medium” $B_c$ self-energy in the rest frame of $B_c$ is given by

$${\Sigma }_{B_c}^{B^{\ast }D}\left(m_{B_c}^{\ast }\right)={\displaystyle \frac{-4g_{B_c{B}^{\ast }D}^2}{{\pi }^2}}\int dq{q}^2{I}_{B_c}^{B^{\ast }D}\left(q^2\right)F_{B_c{B}^{\ast }D}\left(q^2\right),$$

(46)

with $q=\left|\mathbf{q}\right|$, and $I_{B_c}^{B^{\ast }D}\left(q^2\right)$ is expressed, after the Cauchy integral with respect to $q^0$ complex plane shifting $q^0$ variable for the vector potentials as,

$$\begin{array}{ccc}\hfill I_{B_c}^{B^{\ast }D}\left(q^2\right)& =& {\left.{\displaystyle \frac{m_{B_c}^{\ast 2}\left(-1+q_0^2/m_{B^{\ast }}^{\ast 2}\right)}{(q_0-{\omega }_{B^{\ast }}^{\ast })(k_0-m_{B_c}^{\ast }+{\omega }_D^{\ast })(q_0-m_{B_c}^{\ast }-{\omega }_D^{\ast })}}\right|}_{q_0=-{\omega }_{B^{\ast }}^{\ast }}\hfill \\ & & {\left.+{\displaystyle \frac{m_{B_c}^{\ast 2}\left(-1+q_0^2/m_{B^{\ast }}^{\ast 2}\right)}{(q_0+{\omega }_{B^{\ast }}^{\ast })(q_0-{\omega }_{B^{\ast }}^{\ast })(q_0-m_{B_c}^{\ast }-{\omega }_D^{\ast })}}\right|}_{q_0=m_{B_c}^{\ast }-{\omega }_D^{\ast }},\hfill \end{array}$$

(47)

where, $F_{B_c{B}^{\ast }D}$ in Equation (46) is the product of vertex form factors in medium to regularize the divergence in the loop integral, $F_{B_c{B}^{\ast }D}\left(q^2\right)=u_{B_c{B}^{\ast }}\left(q^2\right)u_{B_{c}D}\left(q^2\right)$. They are given by using the corresponding meson in-medium masses, $u_{B_c{B}^{\ast }}={\left({\displaystyle \frac{{\mathsf{\Lambda }}_{B^{\ast }}^2+m_{B_c}^{\ast 2}}{{\mathsf{\Lambda }}_{B^{\ast }}^2+4{\omega }_{B^{\ast }}^{\ast 2}\left(q^2\right)}}\right)}^2$ and $u_{B_{c}D}={\left({\displaystyle \frac{{\mathsf{\Lambda }}_D^2+m_{B_c}^{\ast 2}}{{\mathsf{\Lambda }}_D^2+4{\omega }_D^{\ast 2}\left(q^2\right)}}\right)}^2$ with ${\mathsf{\Lambda }}_{B^{\ast }}$ and ${\mathsf{\Lambda }}_D$ being the cutoff masses associated with the $B^{\ast }$ and D mesons, respectively. We use the common value $\mathsf{\Lambda }={\mathsf{\Lambda }}_{B^{\ast }}={\mathsf{\Lambda }}_D$. A similar calculation is performed to obtain the $B{D}^{\ast }$ loop contribution, namely, in Equations (46) and (47), as well as in the form factors, by replacing $(B^{\ast },D)\to (B,D^{\ast })$.

The choice of cutoff value has no negligible impact on the results. We use the common cutoff $\mathsf{\Lambda }\equiv {\mathsf{\Lambda }}_{B,B^{\ast },D,D^{\ast },K,K^{\ast }}$ by varying the $\mathsf{\Lambda }$ value. The $\mathsf{\Lambda }$ value may be associated with the energies to probe the internal structure of the mesons. In the previous study [77], it was observed that when the values of the cutoff become close to the masses of the mesons in calculating the self-energies, a certain larger cutoff mass value range did not make sense to serve as the form factors. This is because the Compton wavelengths of the corresponding cutoff mass values reach values near and/or smaller than those of the meson sizes. Therefore, we need to constrain the cutoff $\mathsf{\Lambda }$ value in such a way that the form factors reflect properly the finite size of the mesons. Based on the heavy quark and heavy meson symmetry, we use the same range of values for $\mathsf{\Lambda }$ as it was practiced for the quarkonia [77]. Thus, we use the values, $\mathsf{\Lambda }$ = 2000, 3000, 4000, 5000, and 6000 MeV.

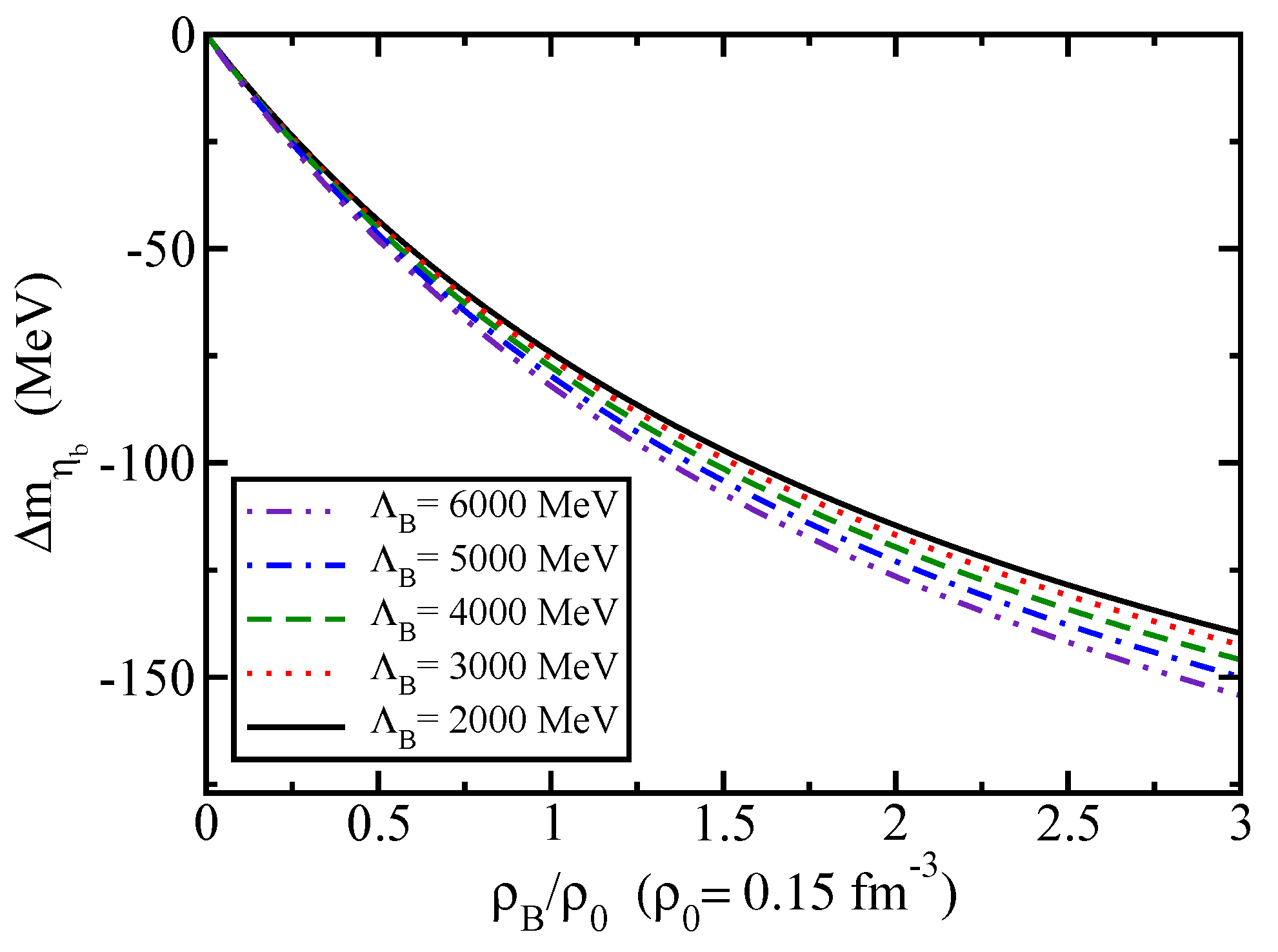
The $B_c$ mass shift amount $\mathsf{\Delta }{m}_{B_c}(B{D}^{\ast }+B^{\ast }D)$ at ${\rho }_0$, which includes the total ($B{D}^{\ast }+B^{\ast }D$) loop contributions, ranges from −90.4 to −101.1 MeV ($m_{B_c}^{\ast }(B{D}^{\ast }+B^{\ast }D)=$ 6184.1 to 6173.4 MeV). Later, we will compare the $B_c$ mass shift and those of the ${\eta }_b$ and ${\eta }_c$.

Next, we study the in-medium mass shift of the $B_c^{\ast }$ meson calculated in the rest frame of $B_c^{\ast }$. For the $B_c^{\ast }$ self-energy, we include only the $BD$ loop contribution, as already commented based on the $\mathsf{{\rm Y}}$ and $J/\psi$ self-energies [77],

$${\Sigma }_{B_c^{\ast }}^{BD}\left(m_{B_c^{\ast }}^{\ast }\right)={\displaystyle \frac{-4g_{B_c^{\ast }BD}^2}{3{\pi }^2}}\int dq{q}^4{I}_{B_c^{\ast }}^{BD}\left(q^2\right)F_{B_c^{\ast }BD}\left(q^2\right),$$

(48)

where $I_{B_c^{\ast }}^{BD}\left(q^2\right)$ is expressed by,

$$\begin{array}{ccc}\hfill I_{B_c^{\ast }}^{BD}\left(q^2\right)& =& {\left.{\displaystyle \frac{1}{(q_0-{\omega }_B^{\ast })(q_0-m_{B_c^{\ast }}^{\ast }+{\omega }_D^{\ast })(q_0-m_{B_c^{\ast }}^{\ast }-{\omega }_D^{\ast })}}\right|}_{q_0=-{\omega }_B^{\ast }}\hfill \\ & & {\left.+{\displaystyle \frac{1}{(q_0+{\omega }_B^{\ast })(q_0-{\omega }_B^{\ast })(q_0-m_{B_c^{\ast }}^{\ast }-{\omega }_D^{\ast })}}\right|}_{q_0=m_{B_c^{\ast }}^{\ast }-{\omega }_D^{\ast }},\hfill \end{array}$$

(49)

with $q=\left|\mathbf{q}\right|$. In Equation (48), $F_{B_c^{\ast }BD}\left(q^2\right)$ is given by the product of the form factors, $F_{B_c^{\ast }BD}\left(q^2\right)=u_{B_c^{\ast }B}\left(q^2\right)u_{B_c^{\ast }D}\left(q^2\right)$, with $u_{B_c^{\ast }B}$ and $u_{B_c^{\ast }B}$ being $u_{B_c^{\ast }B}={\left({\displaystyle \frac{{\mathsf{\Lambda }}_B^2+m_{B_c^{\ast }}^{\ast 2}}{{\mathsf{\Lambda }}_B^2+4{\omega }_B^{\ast 2}\left(q^2\right)}}\right)}^2$ and $u_{B_c^{\ast }B}={\left({\displaystyle \frac{{\mathsf{\Lambda }}_D^2+m_{B_c^{\ast }}^{\ast 2}}{{\mathsf{\Lambda }}_D^2+4{\omega }_D^{\ast 2}\left(q^2\right)}}\right)}^2$. Again we use $\mathsf{\Lambda }={\mathsf{\Lambda }}_B={\mathsf{\Lambda }}_D$ ranging 2000 to 6000 MeV.

4.5. Comparison with Heavy Quarkonia

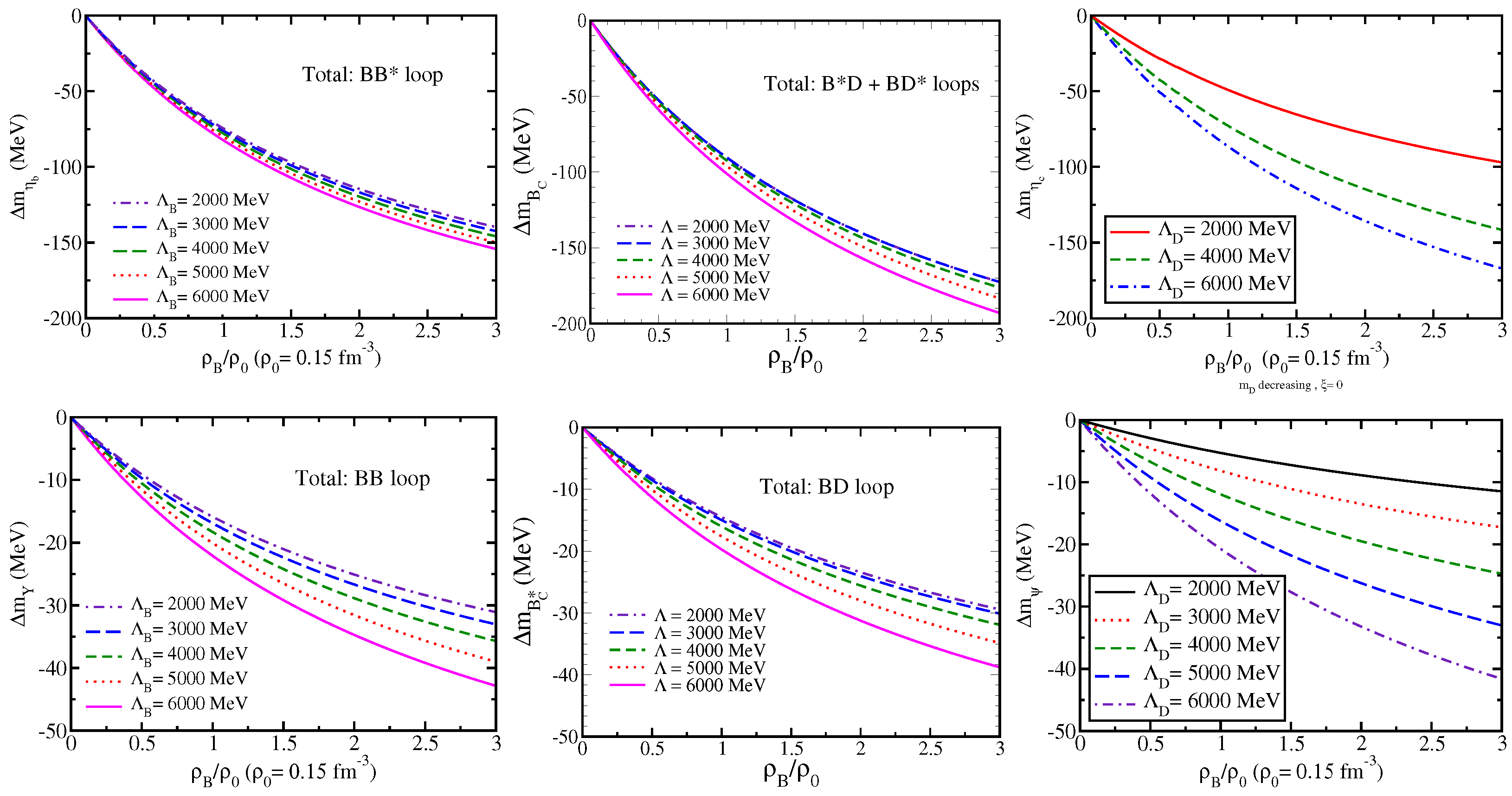
We now compare in Figure 9 the results of $B_c$ and $B_c^{\ast }$ [90], with those of the heavy quarkonia [11,42,72,77]. Since the $B_c$ meson is a pseudoscalar meson, we compare with the bottomonium ${\eta }_b$ and charmonium ${\eta }_c$ (upper panel), while for the $B_c^{\ast }$ meson, we compare with those of the $\mathsf{{\rm Y}}$ and $J/\psi$ (lower panel).

For the comparison, we would like to emphasize that we use the empirically extracted SU(4) sector coupling constants for the charm sector (${\eta }_c$ and $J/\psi$), which would be more reasonable than using the empirically extracted SU(5) sector coupling constant from the $\mathsf{\Gamma }(\mathsf{{\rm Y}}\to e^{+}{e}^{-})$, since the SU(5) flavor symmetry breaking is expected to be much larger than that of the SU(4) based on the quark masses.

The value for the coupling constant of the vertex $J/\psi DD$ used in the calculation of $J/\psi$ mass shift, was obtained from the experimental data for $\mathsf{\Gamma }(J/\psi \to e^{+}{e}^{-})$ by the VMD hypothesis (note that the slight difference, 7.64 → 7.7 below, but the difference is negligible)

$$g_{J/\psi DD}={\displaystyle \frac{g}{\sqrt{6}}}\approx 7.7,$$

(50)

where g is the universal SU(4) coupling constant.

For the coupling constant $g_{{\eta }_{c}D{D}^{\ast }}$ used in the calculation of the ${\eta }_c$ mass shift, we also adopt the SU(4) symmetry for the charm sector, which gives the relation

$$g_{{\eta }_{c}D{D}^{\ast }}=g_{J/\psi DD}={\displaystyle \frac{g}{\sqrt{6}}}\approx 7.7.$$

(51)

A comprehensive list of the values used for the coupling constants is presented in

Table 2. Coupling constant values in SU(4) and SU(5) symmetries.

	SU(5)
g	18.9
$g_{J/\psi DD}$	7.7
$g_{{\eta }_{c}D{D}^{\ast }}$	7.7
	SU(5)
g	33.4
$g_{\mathsf{{\rm Y}}BB}$	13.2
$g_{{\eta }_{b}B{B}^{\ast }}$	13.2
$g_{B_c{B}^{\ast }D}$	11.9
$g_{B_s^{\ast }BD}$	11.9

.

Although we make this comparison, we repeat that this is not made based on a rigorous SU(5) symmetry of the same footing. Namely, the coupling constant g is calculated for the charm sector ($J/\psi$, ${\eta }_c$) based on the SU(4) symmetry, and for the bottom sector ($\mathsf{{\rm Y}}$, ${\eta }_b$) and ($B_c$, $B_c^{\ast }$) based on the SU(5) symmetry. This comparison would make sense based on the fact that SU(5) symmetry is much more broken by the quark masses than that of SU(4).

Note that, although for the mass shift amount $\mathsf{\Delta }{m}_{{\eta }_c}$ [72], the cutoff mass values $\mathsf{\Lambda }={\mathsf{\Lambda }}_D={\mathsf{\Lambda }}_{D^{\ast }}=3000$ and 5000 MeV are missing, it is irrelevant to see the mass shift range for the cutoff range between the 2000 MeV and 6000 MeV.

In the study of the ${\eta }_c$ mass shift, only the $D{D}^{\ast }$ loop contribution was included, and it corresponds to the mass shift value $\mathsf{\Delta }{m}_{{\eta }_c}\left(D{D}^{\ast }\right)$ at ${\rho }_0$ ranges −49.2 to −86.5, for the cutoff mass values ${\mathsf{\Lambda }}_D={\mathsf{\Lambda }}_{D^{\ast }}$ of 2000, 4000, and 6000 MeV. The estimated values for the ${\eta }_b$ mass shift $\mathsf{\Delta }{m}_{{\eta }_b}\left(B{B}^{\ast }\right)$ at ${\rho }_0$ including only the $B{B}^{\ast }$ loop, ranges from −74.2 to −82.0 MeV, where the same range of the cutoff mass value is applied for the present study. The total $B^{\ast }D+B{D}^{\ast }$ loop contributions for the $B_c$ mass shift give a more negative mass shift than those of the ${\eta }_b$ and ${\eta }_c$. This fact indicates that the $B_c$ mass shift value does not show the middle range mass shift value between those of the ${\eta }_c$ and ${\eta }_b$, which may be different from one’s naive expectation.

Next, we compare the mass shift behaviors of $\mathsf{{\rm Y}},B_c^{\ast }$ and $J/\psi$ in Figure 9 (lower panel). The $\mathsf{{\rm Y}}$ and $J/\psi$ mass shift values are calculated by taking, respectively, only the (minimal) $BB$ and $DD$ loop contributions corresponding to the present $B_c^{\ast }$ meson treatment with only the $BD$ loop. The mass shift value $\mathsf{\Delta }{m}_{\mathsf{{\rm Y}}}\left(BB\right)$ at ${\rho }_0$ ranges from −15.9 to −22.1 MeV, while $\mathsf{\Delta }{m}_{J/\psi }\left(DD\right)$ at ${\rho }_0$ ranges from −5.3 to −20.7, when the common range of the $\mathsf{\Lambda }$ (2000 to 6000 MeV) is used. The corresponding $B_c^{\ast }$ mass shift value $\mathsf{\Delta }{m}_{B_c^{\ast }}\left(BD\right)$ at ${\rho }_0$ ranges from −14.5 to −19.7 MeV. The $B_c^{\ast }$ meson in-medium mass shift value is less dependent on the cutoff mass value than that of the $J/\psi$. Although the mass shift behavior depends on the cutoff mass value, the global trend shown in the lower panel of Figure 9 indicates that $\mathsf{\Delta }{m}_{B_c^{\ast }}$ is more or less in the middle of the corresponding $\mathsf{\Delta }{m}_{\mathsf{{\rm Y}}}$ and $\mathsf{\Delta }{m}_{J/\psi }$.

5. Meson–Nucleus Potential

The baryon density dependence of the mass shift behaviors of the $\eta$, ${\eta }^{\prime }$, $\varphi$, ${\eta }_c$, $J/\psi$, ${\eta }_b$, $\mathsf{{\rm Y}},B_c$, and $B_c^{\ast }$ mesons in nuclear matter, shown in Figure 2, Figure 4 (left panel), Figure 5, Figure 6, Figure 7 and Figure 8, Figure 10 and Figure 11 indicate that the nuclear medium provides attraction to these mesons, and opens the possibility for their binding to nuclei.

Therefore, we now consider the nuclear bound states for several of these mesons, which we generally denote the meson as h, when the mesons have been produced nearly at rest inside nucleus A, and study the following nuclei in a wide range of masses, namely ⁴He, ¹²C, ¹⁶O, ⁴⁰Ca, ⁴⁸Ca, ⁹⁰Zr, ¹⁹⁷Au, and ²⁰⁸Pb.

In a local density approximation, the meson h potential within a nucleus A is given by

$$V_{hA}\left(r\right)=U_{hA}\left(r\right)-{\displaystyle \frac{\mathrm{i}}{2}}{W}_{hA}\left(r\right),$$

(52)

where r is the distance from the center of the nucleus; $U_{hA}\left(r\right)=\mathsf{\Delta }{m}_h\left({\rho }_B\left(r\right)\right)$, with $\mathsf{\Delta }{m}_h\left({\rho }_B\right)$ the value of mass shift computed previously for meson h as a function of nuclear density ${\rho }_B$; and ${\rho }_B^A\left(r\right)$ is the baryon density distribution in the nucleus A. The imaginary part of the potential $W_{hA}\left(r\right)$, which is related to the absorption of the meson h in the nuclear medium, is included only for the $\varphi$, $\eta$, and ${\eta }^{\prime }$ mesons in the present study. For the $\varphi$ meson it is given by $W_{\varphi A}\left(r\right)={\mathsf{\Gamma }}_{\varphi }\left({\rho }_B^A\left(r\right)\right)$ where ${\mathsf{\Gamma }}_{\varphi }\left({\rho }_B\right)$ is the $\varphi$ decay width in a nucleus A, Equation (16). For the $\eta$ and ${\eta }^{\prime }$ mesons $W_{hA}\left(r\right)=-\gamma \mathsf{\Delta }{m}_h\left({\rho }_B\left(r\right)\right)+{\gamma }_h^{\mathrm{vac}}$. Here ${\mathsf{\Gamma }}_h^{\mathrm{vac}}$ the meson decay width in vacuum (${\mathsf{\Gamma }}_{\eta }^{\mathrm{vac}}=1.31$ keV and ${\mathsf{\Gamma }}_{{\eta }^{\prime }}^{\mathrm{vac}}=0.188$ MeV [97]), and $\gamma$ is a phenomenological parameter used to simulate the strength of the absorption of the meson in the nuclear medium. The values of the $\gamma$ parameter used below cover the estimated widths of the $\eta$ and ${\eta }^{\prime }$ mesons in the nuclear medium [98]. The nuclear density distributions ${\rho }_B^A\left(r\right)$ for the nuclei listed above are calculated using the QMC model [123], except for ⁴He, which we take from Ref. [124]. Before proceeding, a comment on the use of the local density approximation might be useful, in particular for ⁴He nuclei. At the position r inside nucleus A, the nuclear density is ${\rho }_A\left(r\right)$, and the potentials (effective masses) are taken from the uniform (constant) nuclear density calculation in nuclear matter. For small nuclei, such as ⁴He, this might appear problematic at first sight since for such a nucleus the r-dependence of the nuclear density is expected to be relatively rapid (strong). Because the r-dependence of the nuclear density can be faster than for larger nuclei, depending on the interval value $\mathsf{\Delta }r$, to use the local density approximation, it might not be good enough to assume the uniform nuclear density between the interval $\mathsf{\Delta }r$. However, our calculation uses $\mathsf{\Delta }r=0.04$ fm with the interpolation, and we expect the local density approximation even for the ⁴He nucleus to be sufficiently good. For the ⁴He nucleus, the nuclear density change within the interval 0.04 fm is very small and thus can be regarded as a constant density.

In the following figures, we present the meson–nucleus potentials for some selected nuclei computed using Equation (52).

In Figure 12 and Figure 13, we present the $\varphi$-meson potentials calculated for some nuclei, for three values of the cutoff parameter ${\mathsf{\Lambda }}_K$, $2000,4000$, and 6000 MeV. One can see that the depth of the real part of the potential, $U_{\varphi }\left(r\right)$, is sensitive to the cutoff parameter, from −20 MeV to −35 MeV for ⁴He and from −20 MeV to −30 MeV for ²⁰⁸Pb [100]. In addition, one can see that the imaginary part does not vary much with ${\mathsf{\Lambda }}_K$. Furthermore, note that the imaginary part of the potential is repulsive. This observation may well have consequences for the feasibility of experimental observation of the expected bound states [100].

In Figure 14 and Figure 15, we present, respectively, the ${\eta }_c$-meson potentials for selected nuclei listed above and various values of the cutoff parameter ${\mathsf{\Lambda }}_D$ [72], with the SU(4) breaking parameter of $0.6/\sqrt{2}$ for the coupling constant as explained in Section 4.2. From the figures, one can see that the ${\eta }_c$ and $J/\psi$ potentials in the nuclei are attractive in all cases, but their depth depends on the value of the cutoff parameter, which becomes deeper the larger ${\mathsf{\Lambda }}_D$ becomes. This dependence is, indeed, an uncertainty in the results obtained in our approach when using an effective Lagrangian approach. Note that this is the same conclusion we reached from the mass shift computed in the previous Section 4.2 [72].

In Figure 16 and Figure 17 we present the bottomonium-nucleus potentials for some of the nuclei listed above and the same values of the cutoff parameter ${\mathsf{\Lambda }}_B$ that were used in the computation of the mass shift in the previous Section 4.3 [80]. We can see from Figure 16 and Figure 17 that the $V_{hA}$ potentials, for $h=\mathsf{{\rm Y}}$ and ${\eta }_b$, respectively, are attractive for all nuclei and all values of the cutoff mass parameter used [80]. However, for each nucleus, the depth of the potential depends on the value of the cutoff parameter, being more attractive the larger ${\mathsf{\Lambda }}_B$ becomes. This dependence is expected and is, indeed, an uncertainty in the results obtained in our approach [80].

Next, the calculated potentials for the $\eta$ and ${\eta }^{\prime }$ mesons in nuclei are shown in Figure 18 and Figure 19 [98]. These figures show that all potentials for the $\eta$ and ${\eta }^{\prime }$ in nuclei are attractive. This is so because the corresponding value of the mass shift (in nuclear matter) is negative for both mesons (see Section 2). The differences in the potentials, for a given meson, reflect the differences in the baryon density distributions for the nuclei studied [98]. Furthermore, note that for a given nucleus, the potentials for the $\eta$ and ${\eta }^{\prime }$ are very similar; the reason for this is that the values of the mass shift are very similar, as shown in Figure 2 [98].

Finally, the nuclear strong interaction potentials for the $B_c^{\pm }$-A systems are presented in Figure 20, together with the attractive and repulsive Coulomb potentials, where the Coulomb potentials are not added, but they will be included in calculating the bound state energies in next section.

6. Numerical Results for the Meson–Nucleus Bound State Energies

We now compute the meson h-nucleus A bound state energies, for $h=\eta$, ${\eta }^{\prime }$, $\varphi$, ${\eta }_c$, $J/\psi$, ${\eta }_b$, $\mathsf{{\rm Y}}$ and $B_c^{\pm }$, in a wide range of nuclear masses $A=$ ⁴He, ¹²C, ¹⁶O, ⁴⁰Ca, ⁴⁸Ca, ⁹⁰Zr, ¹⁹⁷Au, and ²⁰⁸Pb by solving the Klein–Gordon equation (KGE)

$$\left(-{\nabla }^2+{(m+V\left(\mathbf{r}\right))}^2\right)\psi \left(\mathbf{r}\right)={\mathcal{E}}^2\psi \left(\mathbf{r}\right)$$

(53)

where $V\left(\mathbf{r}\right)=V\left(r\right)$ is the scalar nuclear potential associated with mass shift, given by Equation (52), $r=\left|\mathbf{r}\right|$ is the distance from the nucleus, and m is the reduced mass of the meson h-nucleus A system $m_h{m}_A/(m_h+m_A)$, in vacuum. The bound state energies E and widths $\mathsf{\Gamma }$ are given by are given by $E=\mathcal{E}-m$ and $\mathsf{\Gamma }=-2\mathrm{Im}\mathcal{E}$, respectively, where $\mathcal{E}$ is the energy eigenvalue in Equation (53). Note that, when the Coulomb or vector potential is relevant, the right hand side of Equation (53) must be modified properly as ${\mathcal{E}}^2\to {(\mathcal{E}-V_{\mathrm{V},\mathrm{Coul}})}^2$ with $V_{\mathrm{V},\mathrm{Coul}}$ being the vector and Coulomb potentials, respectively. See Ref. [101] for details.

Before proceeding to solve Equation (53), we note that we have also solved to approximations of Equation (53), namely the Schrödinger equation and also the KGE dropping the $V^2\left(\mathbf{r}\right)$ term in Equation (53) for some meson–nucleus systems. In all cases, we obtain essentially the same results, which do not change the conclusions about the existence of the bound states.

We solve the Klein–Gordon equation using the momentum space methods [125]. Here, Equation (53) is first converted to momentum space representation via a Fourier transform, followed by a partial wave-decomposition of the Fourier-transformed potential, or we obtain directly the partial wave decomposition in momentum space by a double Spherical Bessel transform. For $\eta$, ${\eta }^{\prime }$, $\varphi$, ${\eta }_c$, and $J/\psi$, the method used is the partial wave-decomposition of the Fourier-transformed potential. For the $B_c^{\pm }$ we employ the direct double Spherical Bessel transform, and for $\mathsf{{\rm Y}}$ and ${\eta }_b$ we use both methods. Then, for a given value of angular momentum ℓ, the eigenvalues of the resulting equation are found by the inverse iteration eigenvalue algorithm. The detailed comparison and discussions were made in Ref. [101], and it turned out that the main conclusions remain valid in both methods. The calculated bound state energies are similar, with, at most, a difference of a few MeV, which we would think is within the desired experimental accuracy for the strong interaction bound state energy measurement.

In

Table 3. $\varphi$-nucleus single-particle energies, E, and half widths, $\mathsf{\Gamma }/2$, obtained with and without the imaginary part of the potential, for three values of the cutoff parameter ${\mathsf{\Lambda }}_K$. When only the real part is included, where the corresponding single-particle energy E is given in parenthesis and $\mathsf{\Gamma }=0$ for all nuclei. “n” indicates that no bound state is found. All quantities are given in MeV.

		${\mathbf{\Lambda }}_{\mathit{K}}=2000$		${\mathbf{\Lambda }}_{\mathit{K}}=3000$		${\mathbf{\Lambda }}_{\mathit{K}}=4000$
		$\mathit{E}$	$\mathsf{\Gamma }/\mathbf{2}$	$\mathit{E}$	$\mathsf{\Gamma }/\mathbf{2}$	$\mathit{E}$	$\mathsf{\Gamma }/\mathbf{2}$
${}_{\varphi }{}^4\mathrm{He}$	1s	n (−0.8)	n	n (−1.4)	n	−1.0 (−3.2)	8.3
${}_{\varphi }{}^{12}\mathrm{C}$	1s	−2.1 (−4.2)	10.6	−6.4 (−7.7)	11.1	−9.8 (−10.7)	11.2
${}_{\varphi }{}^{16}\mathrm{O}$	1s	−4.0 (−5.9)	12.3	−8.9 (−10.0)	12.5	−12.6 (−13.4)	12.4
	1p	n (n)	n	n (n)	n	n (−1.5)	n
${}_{\varphi }{}^{40}\mathrm{Ca}$	1s	−9.7 (−11.1)	16.5	−15.9 (−16.7)	16.2	−20.5 (−21.2)	15.8
	1p	−1.0 (−3.5)	12.9	−6.3 (−7.8)	13.3	−10.4 (−11.4)	13.3
	1d	n (n)	n	n (n)	n	n (−1.4)	n
${}_{\varphi }{}^{48}\mathrm{Ca}$	1s	−10.5 (−11.6)	16.5	−16.5 (−17.2)	16.0	−21.1 (−21.6)	15.6
	1p	−2.5 (−4.6)	13.6	−7.9 (−9.2)	13.7	−12.0 (−12.9)	13.6
	1d	n (n)	n	n (−0.8)	n	−2.1 (−3.6)	11.1
${}_{\varphi }{}^{90}\mathrm{Zr}$	1s	−12.9 (−13.6)	17.1	−19.0 (−19.5)	16.4	−23.6 (−24.0)	15.8
	1p	−7.1 (−8.4)	15.5	−12.8 (−13.6)	15.2	−17.2 (−17.8)	14.8
	1d	−0.2 (−2.5)	13.4	−5.6 (−6.9)	13.5	−9.7 (−10.6)	13.4
	2s	n (−1.4)	n	−3.4 (−5.1)	12.6	−7.4 (−8.5)	12.7
	2p	n (n)	n	n (n)	n	n (−1.1)	n
${}_{\varphi }{}^{208}\mathrm{Pb}$	1s	−15.0 (−15.5)	17.4	−21.1 (−21.4)	16.6	−25.8 (−26.0)	16.0
	1p	−11.4 (−12.1)	16.7	−17.4 (−17.8)	16.0	−21.9 (−22.2)	15.5
	1d	−6.9 (−8.1)	15.7	−12.7 (−13.4)	15.2	−17.1 (−17.6)	14.8
	2s	−5.2 (−6.6)	15.1	−10.9 (−11.7)	14.8	−15.2 (−15.8)	14.5
	2p	n (−1.9)	n	−4.8 (−6.1)	13.5	−8.9 (−9.8)	13.4
	2d	n (n)	n	n (−0.7)	n	−2.2 (−3.7)	11.9

we show our results for the $\varphi$-nucleus bound state energies and half widths, obtained with and without the imaginary part of the potential, for three values of the cutoff parameter [100].

We first analyze the case in which the imaginary part of the $\varphi$-nucleus potential, $W_{\varphi }\left(r\right)$, is set to zero. These results are shown in parentheses in Table 3. From the values shown in parenthesis, we see that the $\varphi$-meson is expected to form bound states with all seven nuclei selected, for all values of the cutoff parameter ${\mathsf{\Lambda }}_K$ studied. However, the bound state energy is obviously dependent on ${\mathsf{\Lambda }}_K$, increasing in magnitude with ${\mathsf{\Lambda }}_K$ [100].

Next, we discuss the results obtained when the imaginary part of the potential is retained. Adding the absorptive part of the potential, the situation changes considerably. From the results presented in Table 3, we note that for the largest value of the cutoff parameter, which yields the deepest attractive potentials, the $\varphi$-meson is expected to form bound states in all the nuclei selected, including the lightest ⁴He nucleus. However, in this case, whether or not the bound states can be observed experimentally is sensitive to the value of the cutoff parameter ${\mathsf{\Lambda }}_K$ [100]. Given that the widths are large, the signal for the formation of the $\varphi$-nucleus bound states may be difficult to identify experimentally.

We also observe that the width of the bound state is insensitive to the values of ${\mathsf{\Lambda }}_K$ for all nuclei. Furthermore, since the so-called dispersive effect of the absorptive potentials is repulsive, the bound states disappear completely in some cases, even though they were found when the absorptive part was set to zero [100]. This feature is obvious for the ⁴He nucleus, making it especially relevant to the future experiments, planned at J-PARC and JLab using light and medium-heavy nuclei [126,127,128,129].

The bound state energies E of the ${\eta }_c$-nucleus system were calculated for four values of the cutoff parameter ${\mathsf{\Lambda }}_D$ and are listed in

Table 4. ${\eta }_c$-nucleus bound state energies for different values of the cutoff parameter ${\mathsf{\Lambda }}_D$. All dimensional quantities are in MeV.

		Bound State Energies
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{D}}=\mathbf{1500}$	${\mathsf{\Lambda }}_{\mathit{D}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{D}}=\mathbf{2500}$	${\mathsf{\Lambda }}_{\mathit{D}}=\mathbf{3000}$
${}_{{\eta }_c}{}^4\mathrm{He}$	1s	−1.49	−3.11	−5.49	−8.55
${}_{{\eta }_c}{}^{12}\mathrm{C}$	1s	−5.91	−8.27	−11.28	−14.79
	1p	−0.28	−1.63	−3.69	−6.33
${}_{{\eta }_c}{}^{16}\mathrm{O}$	1s	−7.35	−9.92	−13.15	−16.87
	1p	−1.94	−3.87	−6.48	−9.63
${}_{{\eta }_c}{}^{40}\mathrm{Ca}$	1s	−11.26	−14.42	−18.31	−22.73
	1p	−7.19	−10.02	−13.59	−17.70
	1d	−2.82	−5.22	−8.36	−12.09
	2s	−2.36	−4.51	−7.44	−10.98
${}_{{\eta }_c}{}^{48}\mathrm{Ca}$	1s	−11.37	−14.46	−18.26	−22.58
	1p	−7.83	−10.68	−14.23	−18.32
	1d	−3.88	−6.40	−9.63	−13.41
	2s	−3.15	−5.47	−8.54	−12.17
${}_{{\eta }_c}{}^{90}\mathrm{Zr}$	1s	−12.26	−15.35	−19.14	−23.43
	1p	−9.88	−12.86	−16.53	−20.70
	1d	−7.05	−9.87	−13.38	−17.40
	2s	−6.14	−8.87	−12.29	−16.24
	1f	−3.90	−6.50	−9.81	−13.65
${}_{{\eta }_c}{}^{197}\mathrm{Au}$	1s	−12.57	−15.59	−19.26	−23.41
	1p	−11.17	−14.14	−17.77	−21.87
	1d	−9.42	−12.31	−15.87	−19.90
	2s	−8.69	−11.53	−15.04	−19.02
	1f	−7.39	−10.19	−13.70	−17.61
${}_{{\eta }_c}{}^{208}\mathrm{Pb}$	1s	−12.99	−16.09	−19.82	−24.12
	1p	−11.60	−14.64	−18.37	−22.59
	1d	−9.86	−12.83	−16.49	−20.63
	2s	−9.16	−12.09	−15.70	−19.80
	1f	−7.85	−10.74	−14.30	−18.37

[72]. Note that the ${\eta }_c$ bound state energies are calculated with the SU(4) broken coupling constant by $(0.6/\sqrt{2})g_{et{a}_{c}DD}$, thus the values shown below are expected to be smaller in magnitude than those calculated with the SU(4) symmetric coupling constant, $g_{et{a}_{c}DD}$ (See Section 4.2). These results show that the ${\eta }_c$-meson is expected to form bound states with all the nuclei studied, and this prediction is independent of the value of the cutoff parameter ${\mathsf{\Lambda }}_D$ [72]. However, the particular values for the bound state energies are clearly dependent on ${\mathsf{\Lambda }}_D$, namely, each of them increases in absolute value as ${\mathsf{\Lambda }}_D$ increases. This was expected from the behavior of the ${\eta }_c$ potentials, since these are deeper for larger values of the cutoff parameter. Note also that the ${\eta }_c$ bounds more strongly to heavier nuclei [72].

We remind that we have ignored the natural width of $\sim 31$ MeV [130] in the free space of the ${\eta }_c$, and this could be an issue related to the observability of the predicted bound states. Furthermore, we have no reason to believe the width will be suppressed in the medium. Thus, even though it could be difficult to resolve the individual states, it should be possible to see that there are bound states, which is the main point here. It remains to be seen how much the inclusion of a repulsive imaginary part will affect the predicted bound states. We believe this can be determined in future work.

The results for the $J/\psi$-nucleus bound states are presented in

Table 5. $J/\psi -$ nucleus bound state energies taking into account the change in the self-energy in medium, calculated with the Schrödinger equation. All dimensioned quantities are given in MeV.

		Bound State Energies
		${\mathsf{\Lambda }}_{\mathbf{D}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathbf{D}}=\mathbf{3000}$	${\mathsf{\Lambda }}_{\mathbf{D}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathbf{D}}=\mathbf{5000}$	${\mathsf{\Lambda }}_{\mathbf{D}}=\mathbf{6000}$
${}_{J/\psi }{}^4\mathrm{He}$	1s	n	n	−0.70	−2.70	−5.51
${}_{J/\psi }{}^{12}\mathrm{C}$	1s	−0.52	−1.98	−4.47	−7.67	−11.26
	1p	n	n	n	−1.38	−3.84
${}_{J/\psi }{}^{16}\mathrm{O}$	1s	−1.03	−2.87	−5.72	−9.24	−13.09
	1p	n	n	−0.94	−3.48	−6.60
${}_{J/\psi }{}^{40}\mathrm{Ca}$	1s	−2.78	−5.44	−9.14	−13.50	−18.12
	1p	−0.38	−2.32	−5.43	−9.32	−13.56
	1d	n	n	−1.52	−4.74	−8.49
	2s	n	n	−1.27	−4.09	−7.60
${}_{J/\psi }{}^{48}\mathrm{Ca}$	1s	−2.96	−5.62	−9.28	−13.55	−18.08
	1p	−0.73	−2.83	−6.03	−9.95	−14.18
	1d	n	n	−2.46	−5.87	−9.73
	2s	n	−0.07	−1.90	−5.00	−8.65
${}_{J/\psi }{}^{90}\mathrm{Zr}$	1s	−3.64	−6.40	−10.12	−14.41	−18.92
	1p	−1.93	−4.42	−7.92	−12.03	−16.40
	1d	−0.03	−2.13	−5.31	−9.18	−13.37
	2s	−0.02	−1.56	−4.51	−8.26	−12.37
	2p	n	n	−1.52	−4.71	−8.45
${}_{J/\psi }{}^{208}\mathrm{Pb}$	1s	−4.25	−7.08	−10.82	−15.11	−19.60
	1p	−3.16	−5.86	−9.52	−13.74	−18.18
	1d	−1.84	−4.38	−7.90	−12.01	−16.37
	2s	−1.41	−3.81	−7.25	−11.30	−15.61
	2p	−0.07	−1.95	−5.10	−8.97	−13.14

. These results show that the $J/\psi$ is expected to form $J/\psi$-nuclear bound states for nearly all the nuclei considered, except some cases for ⁴He, for all values of the cutoff parameter ${\mathsf{\Lambda }}_D$ [105,106]. Therefore, it will be possible to search for the bound states, for example, in a ²⁰⁸Pb nucleus at JLab, the 12 GeV upgraded facility. In addition, one can expect quite rich spectra for medium and heavy mass nuclei. Of course, the main issue is to produce the $J/\psi$ meson with nearly stopped kinematics, or nearly zero momentum relative to the nucleus. Since the present results imply that many nuclei should form $J/\psi$-nuclear bound states, it may be possible to find such kinematics by careful selection of the beam and target nucleus [105,106].

The bound state energies E of the $\mathsf{{\rm Y}}$-nucleus and ${\eta }_b$-nucleus systems are listed in

Table 6. $\mathsf{{\rm Y}}$-nucleus bound state energies obtained by the Woods–Saxon Fourier transform for several nuclei A. All dimensioned quantities are in MeV.

		Bound State Energies
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{3000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{5000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{\mathsf{{\rm Y}}}{}^4\mathrm{He}$	1s	−5.6	−6.4	−7.5	−9.0	−10.8
${}_{\mathsf{{\rm Y}}}{}^{12}\mathrm{C}$	1s	−10.6	−11.6	−12.8	−14.4	−16.3
	1p	−6.1	−6.8	−7.9	−9.3	−10.9
	1d	−1.5	−2.1	−2.9	−4.0	−5.4
	2s	−1.6	−2.1	−2.8	−3.8	−5.1
${}_{\mathsf{{\rm Y}}}{}^{16}\mathrm{O}$	1s	−11.9	−12.9	−14.2	−15.8	−17.8
	1p	−8.3	−9.2	−10.4	−11.9	−13.7
	1d	−4.4	−5.1	−6.2	−7.5	−9.2
	2s	−3.7	−4.4	−5.4	−6.7	−8.3
	1f	n	−0.9	−1.8	−2.9	−4.3
${}_{\mathsf{{\rm Y}}}{}^{40}\mathrm{Ca}$	1s	−15.5	−16.6	−18.2	−20.0	−22.3
	1p	−13.3	−14.4	−15.9	−17.7	−19.8
	1d	−10.8	−11.9	−13.3	−15.0	−17.1
	2s	−10.3	−11.3	−12.7	−14.4	−16.4
	1f	−8.1	−9.1	−10.4	−12.1	−14.0
${}_{\mathsf{{\rm Y}}}{}^{48}C$	1s	−15.3	−16.4	−17.9	−19.7	−21.8
	1p	−13.5	−14.6	−16.0	−17.8	−19.9
	1d	−11.4	−12.4	−13.8	−15.6	−17.6
	2s	−10.8	−11.8	−13.2	−14.9	−16.9
	1f	−9.1	−10.1	−11.4	−13.1	−15.0
${}_{\mathsf{{\rm Y}}}{}^{90}\mathrm{Zr}$	1s	−15.5	−16.6	−18.1	−19.9	−22.0
	1p	−14.5	−15.5	−17.0	−18.8	−20.9
	1d	−13.2	−14.2	−15.7	−17.4	−19.5
	2s	−12.7	−13.8	−15.2	−16.9	−19.0
	1f	−11.7	−12.7	−14.1	−15.9	−17.9
${}_{\mathsf{{\rm Y}}}{}^{197}\mathrm{Au}$	1s	−15.3	−16.3	−17.7	−19.4	−21.5
	1p	−14.7	−15.8	−17.2	−18.9	−20.9
	1d	−14.0	−15.0	−16.4	−18.1	−20.1
	2s	−13.7	−14.7	−16.0	−17.8	−19.8
	1f	−13.2	−14.2	−15.6	−17.3	−19.3
${}_{\mathsf{{\rm Y}}}{}^{208}\mathrm{Pb}$	1s	−15.7	−16.8	−18.2	−20.0	−22.1
	1p	−15.2	−16.2	−17.7	−19.4	−21.5
	1d	−14.5	−15.5	−16.9	−18.7	−20.8
	2s	−14.1	−15.2	−16.6	−18.3	−20.4
	1f	−13.6	−14.7	−16.1	−17.8	−19.9

,

Table 7. $\mathsf{{\rm Y}}$-nucleus bound state energies obtained by the Direct Bessel transform for several nuclei A. All dimensioned quantities are in MeV.

		Bound State Energies (MeV)
		Direct Bessel Transform
	$\mathit{n}\mathcal{\ell }$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{\mathsf{{\rm Y}}}{}^4\mathrm{He}$	1s	−5.93	−6.25	−6.56
${}_{\mathsf{{\rm Y}}}{}^{12}\mathrm{C}$	1s	−13.22	−15.26	−18.41
	1p	−8.30	−9.57	−11.51
${}_{\mathsf{{\rm Y}}}{}^{16}\mathrm{O}$	1s	−14.30	−16.57	−20.06
	1p	−10.81	−12.37	−14.73
${}_{\mathsf{{\rm Y}}}{}^{40}\mathrm{Ca}$	1s	−18.17	−21.63	−23.16
	1p	−15.22	−18.11	−19.58
${}_{\mathsf{{\rm Y}}}{}^{48}\mathrm{Ca}$	1s	−16.74	−19.33	−23.20
	1p	−15.36	−17.76	−21.53
${}_{\mathsf{{\rm Y}}}{}^{90}\mathrm{Zr}$	1s	−15.87	−18.24	−21.89
	1p	−12.52	−14.78	−18.32
${}_{\mathsf{{\rm Y}}}{}^{208}\mathrm{Pb}$	1s	−15.95	−18.41	−22.23
	1p	−13.23	−15.49	−19.91

,

Table 8. ${\eta }_b$-nucleus bound state energies obtained by the Woods–Saxon Fourier transform for several nuclei A. All dimensioned quantities are in MeV.

		Bound State Energies
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{3000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{5000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{{\eta }_b}{}^4\mathrm{He}$	1s	−63.1	−64.7	−66.7	−69.0	−71.5
	1p	−40.6	−42.0	−43.7	−45.8	−48.0
	1d	−17.2	−18.3	−19.7	−21.4	−23.2
	2s	−15.6	−16.6	−17.9	−19.4	−21.1
${}_{{\eta }_b}{}^{12}\mathrm{C}$	1s	−65.8	−67.2	−69.0	−71.1	−73.4
	1p	−57.0	−58.4	−60.1	−62.1	−64.3
	1d	−47.5	−48.8	−50.4	−52.3	−54.4
	2s	−46.3	−47.5	−49.1	−51.0	−53.0
	1f	−37.5	−38.7	−40.2	−42.0	−43.9
${}_{{\eta }_b}{}^{16}\mathrm{O}$	1s	−67.8	−69.2	−71.0	−73.1	−75.4
	1p	−61.8	−63.2	−64.9	−67.0	−69.2
	1d	−54.9	−56.2	−57.9	−59.9	−62.0
	2s	−53.2	−54.6	−56.3	−58.2	−60.3
	1f	−47.3	−48.6	−50.2	−52.1	−54.2
${}_{{\eta }_b}{}^{40}\mathrm{Ca}$	1s	−79.0	−80.6	−82.6	−85.0	−87.5
	1p	−75.4	−77.0	−79.0	−81.4	−83.9
	1d	−71.4	−73.0	−74.9	−77.2	−79.7
	2s	−70.5	−72.0	−74.0	−76.3	−78.8
	1f	−67.0	−68.5	−70.4	−72.7	−75.1
${}_{{\eta }_b}{}^{48}\mathrm{Ca}$	1s	−76.7	−78.2	−80.2	−82.5	−85.0
	1p	−74.0	−75.5	−77.4	−79.7	−82.1
	1d	−70.8	−72.3	−74.2	−76.4	−78.8
	2s	−69.9	−71.4	−73.3	−75.5	−77.9
	1f	−67.2	−68.6	−70.6	−72.8	−75.1
${}_{{\eta }_b}{}^{90}\mathrm{Zr}$	1s	−75.5	−77.0	−78.9	−81.1	−83.5
	1p	−74.1	−75.6	−77.5	−79.7	−82.1
	1d	−72.3	−73.8	−75.7	−77.9	−80.2
	2s	−71.6	−73.0	−74.9	−77.1	−79.5
	1f	−70.2	−71.7	−73.6	−75.8	−78.1
${}_{{\eta }_b}{}^{197}\mathrm{Au}$	1s	−72.8	−74.2	−76.1	−78.2	−80.5
	1p	−72.3	−73.7	−75.6	−77.7	−80.0
	1d	−71.3	−72.8	−74.6	−76.7	−79.0
	2s	−70.7	−72.1	−74.0	−76.1	−78.4
	1f	−70.2	−71.7	−73.5	−75.6	−77.9
${}_{{\eta }_b}{}^{208}\mathrm{Pb}$	1s	−74.7	−76.2	−78.1	−80.3	−82.6
	1p	−74.2	−75.7	−77.5	−79.7	−82.1
	1d	−73.2	−74.7	−76.6	−78.8	−81.1
	2s	−72.7	−74.1	−76.0	−78.2	−80.5
	1f	−72.1	−73.6	−75.5	−77.6	−80.0

and

Table 9. ${}_{{\eta }_b}{}^4\mathrm{A}$ bound state energies obtained by the Direct Bessel transform for several nuclei A. All dimensioned quantities are in MeV.

		Bound State Energies (MeV)
		Direct Bessel Transform
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{{\eta }_b}{}^4\mathrm{He}$	1s	−68.71	−71.59	−75.44
	1p	−39.97	−41.50	−43.54
	1d	−37.73	−39.56	−42.03
	2s	−29.14	−30.09	−31.38
${}_{{\eta }_b}{}^{12}\mathrm{C}$	1s	−63.70	−66.93	−70.27
	1p	−53.17	−55.13	−59.38
	1d	−46.47	−48.50	−51.17
	2s	−34.53	−36.30	−39.43
${}_{{\eta }_b}{}^{16}\mathrm{O}$	1s	−68.37	−71.25	−75.14
	1p	−57.02	−59.58	−63.02
	1d	−47.05	−49.37	−52.50
	2s	−23.18	−25.50	−28.69
${}_{{\eta }_b}{}^{40}\mathrm{Ca}$	1s	−79.11	−82.59	−87.27
	1p	−70.60	−73.86	−78.26
	1d	−53.31	−55.99	−59.61
	2s	−48.35	−51.31	−55.32
${}_{{\eta }_b}{}^{48}\mathrm{Ca}$	1s	−63.94	−66.88	−70.83
	1p	−58.60	−61.10	−64.43
	1d	−34.04	−36.40	−39.60
	2s	−26.35	−28.30	−30.95
${}_{{\eta }_b}{}^{90}\mathrm{Zr}$	1s	−71.32	−74.52	−78.85
	1p	−63.78	−67.03	−71.42
	1d	−57.78	−60.82	−64.93
	2s	−51.53	−54.07	−57.46
${}_{{\eta }_b}{}^{208}\mathrm{Pb}$	1s	−61.44	−64.25	−68.02
	1p	−59.82	−62.95	−67.18
	1d	−51.36	−54.05	−57.65
	2s	−48.71	−51.25	−54.66

, respectively, for all nuclei listed at the beginning of this section and the same range of values for the cutoff mass parameter as used in the mass shift calculation (see Section 4.3) [80]. We note that for the $\mathsf{{\rm Y}}$-nucleus systems, we have only listed a few bound states for each nucleus since that number increases with the mass of the nucleus, and for the heaviest of these, ²⁰⁸Pb, the number of bound states is quite large. For the ²⁰⁸Pb nucleus, we have found ∼70 states [80].

In Table 8 we show the ${\eta }_b$-nucleus bound state energies for the same nuclei and range of values of the cutoff mass parameter as in Table 6 [80]. Furthermore, as in the case of the $\mathsf{{\rm Y}}$-nucleus bound state energies, we have listed only a few bound states for each nucleus. For the ²⁰⁸Pb nucleus, we have ∼ 200 states, and clearly, it is not practical to show them all [80].

These results given in Table 6, Table 7, Table 8 and Table 9 show that the $\mathsf{{\rm Y}}$ and ${\eta }_b$ mesons are expected to form bound states with all the nuclei studied, independent of the value of the cutoff parameter ${\mathsf{\Lambda }}_B$. However, the particular values for the bound state energies are dependent on the cutoff parameter values, increasing in absolute value as the cutoff parameter increases. This dependence was expected from the behavior of the bottomonium-nucleus potentials, since these are more attractive for larger values of the cutoff parameter. Note also that bottomonium (${\eta }_b$ or $\mathsf{{\rm Y}}$) binds more strongly to heavier nuclei; therefore, a richer spectrum is expected for these nuclei [80].

However, from Table 6, Table 7, Table 8 and Table 9, we see that the bound state energies for the ${\eta }_b$ are larger than those of the $\mathsf{{\rm Y}}$ for the same nuclei and range of cutoff values explored. These differences are probably due to two reasons: (a) the couplings $g_{{\eta }_{b}B{B}^{\ast }}$ and $g_{\mathsf{{\rm Y}}BB}$ are very different. Indeed, the results obtained in Ref. [72] on the ${\eta }_c$ nuclear bound state energies are closer to those of the $J/\psi$ when the SU(4) flavor symmetry is broken, such that $g_{{\eta }_{c}D{D}^{\ast }}=(0.6/\sqrt{2})g_{J/\psi DD}\simeq 0.424g_{J/\psi DD}$ [72,113]. Thus, a reduced coupling $g_{{\eta }_{b}B{B}^{\ast }}$ can bring the ${\eta }_b$ nuclear bound state energies closer to those the $\mathsf{{\rm Y}}$, since the ${\eta }_b$ self-energy is proportional to $g_{{\eta }_{b}B{B}^{\ast }}^2$. (b) the form factors are not equal for the vertices $\mathsf{{\rm Y}}BB$ and ${\eta }_{b}B{B}^{\ast }$, and we have to readjust the cutoff values, which means ${\mathsf{\Lambda }}_B\ne {\mathsf{\Lambda }}_{B^{\ast }}$, and the comparisons for the mass shift values and bound state energies have to be made for different values of the cutoff parameters.

The bound-state energies associated with each energy level can be confirmed by analyzing the number of nodes in the corresponding coordinate−space wave function as described in Ref. [101]. We present the wave functions of some meson–nucleus systems and cutoff values in Appendix A, which will help to better understand the meson–nucleus bound systems.

In

Table 10. Bound state energies (E) and full widths ($\mathsf{\Gamma }$) of $\eta$ meson in nucleus of mass number A obtained by solving the Klein–Gordon equation for various values of the parameter $\gamma$.

		$\mathit{\gamma }=0$		$\mathit{\gamma }=0.25$		$\mathit{\gamma }=0.5$		$\mathit{\gamma }=1.0$
	$\mathit{n}\mathcal{l}$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$
${}_{\eta }{}^4\mathrm{He}$	$1s$	−10.99	0	−10.79	8.21	−10.20	16.65	−8.13	34.94
${}_{\eta }{}^{12}\mathrm{C}$	$1s$	−25.25	0	−25.16	10.86	−24.91	21.82	−24.02	44.29
	$1p$	−0.87	0	−0.43	4.97	N	N	N	N
${}_{\eta }{}^{16}\mathrm{O}$	$1s$	−30.78	0	−30.72	12.00	−30.53	24.07	−29.86	48.67
	$1p$	−6.47	0	−6.26	7.84	−5.67	15.99	−3.77	33.80
${}_{\eta }{}^{40}\mathrm{Ca}$	$1s$	−46.93	0	−46.89	15.12	−46.79	30.28	−46.43	60.87
	$1p$	−26.93	0	−26.85	12.67	−26.61	25.44	−25.77	51.59
	$1d$	−6.67	0	−6.47	9.48	−5.91	19.27	−4.15	40.31
	$2s$	−5.43	0	−5.09	7.51	−4.18	15.59	N	N
${}_{\eta }{}^{48}\mathrm{Ca}$	$1s$	−47.78	0	−47.75	14.98	−47.66	30.00	−47.38	60.25
	$1p$	−29.97	0	−29.90	12.99	−29.71	26.06	−29.04	52.71
	$1d$	−11.08	0	−10.93	10.45	−10.51	21.10	−9.15	43.52
	$2s$	−8.7	0	−8.11	8.83	−7.42	18.06	N	N
${}_{\eta }{}^{90}\mathrm{Zr}$	$1s$	−52.56	0	−52.54	15.34	−52.50	30.71	−52.34	61.56
	$1p$	−39.85	0	−39.81	14.17	−39.71	28.40	−39.36	57.11
	$1d$	−25.32	0	−25.25	12.74	−25.06	25.57	−24.40	51.75
	$2s$	−21.04	0	−20.94	11.95	−20.65	24.04	−19.70	49.03
${}_{\eta }{}^{197}\mathrm{Au}$	$1s$	−55.12	0	−55.11	15.20	−55.09	30.41	−55.01	60.89
	$1p$	−47.13	0	−47.11	14.58	−47.06	29.19	−46.90	58.53
	$1d$	−37.60	0	−37.58	13.83	−37.49	27.69	−37.20	55.67
	$2s$	−34.01	0	−33.97	13.45	−33.86	26.96	−33.47	54.31
${}_{\eta }{}^{208}\mathrm{Pb}$	$1s$	−56.85	0	−56.84	15.61	−56.82	31.24	−56.75	62.55
	$1p$	−48.92	0	−48.90	14.99	−48.86	30.01	−48.70	60.17
	$1d$	−39.81	0	−39.45	14.24	−39.37	28.51	−39.09	57.29
	$2s$	−35.95	0	−35.91	13.87	−35.80	27.80	−35.43	55.96

and

Table 11. Bound state energies (E) and full widths ($\mathsf{\Gamma }$) of ${\eta }^{\prime }$ meson in nucleus of mass number A obtained by solving the Klein–Gordon equation for various values of the parameter $\gamma$.

		$\mathit{\gamma }=0$		$\mathit{\gamma }=0.25$		$\mathit{\gamma }=0.5$		$\mathit{\gamma }=1.0$
	$\mathit{n}\mathcal{l}$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$	$\mathit{E}$	$\mathsf{\Gamma }$
${}_{{\eta }^{\prime }}{}^4\mathrm{He}$	$1s$	−22.11	0	−21.96	11.37	−21.55	22.89	−20.06	46.83
${}_{{\eta }^{\prime }}{}^{12}\mathrm{C}$	$1s$	−33.88	0	−33.82	12.30	−33.64	24.66	−33.00	49.73
	$1p$	−12.72	0	−12.57	9.06	−12.15	18.29	−10.67	37.68
${}_{{\eta }^{\prime }}{}^{16}\mathrm{O}$	$1s$	−38.64	0	−38.59	13.06	−38.46	26.17	−38.00	52.65
	$1p$	−19.75	0	−19.65	10.76	−19.34	21.64	−18.28	44.07
	$2s$	−1.39	0	−0.84	4.48	N	N	N	N
	$1d$	−0.33	0	−0.69	7.20	N	N	N	N
${}_{{\eta }^{\prime }}{}^{40}\mathrm{Ca}$	$1s$	−52.38	0	−52.35	15.59	−52.28	31.22	−52.00	62.61
	$1p$	−38.41	0	−38.35	14.18	−38.19	28.41	−37.63	57.22
	$1d$	−23.12	0	−23.02	12.46	−22.74	25.03	−21.75	50.81
	$2s$	−20.38	0	−20.25	11.72	−19.87	23.60	−18.58	48.25
${}_{{\eta }^{\prime }}{}^{48}\mathrm{Ca}$	$1s$	−52.40	0	−52.38	15.29	−52.32	30.60	−52.11	61.35
	$1p$	−40.30	0	−40.26	14.18	−40.13	28.40	−39.68	57.12
	$1d$	−26.68	0	−26.59	12.82	−26.37	25.72	−25.58	52.02
	$2s$	−23.45	0	−23.34	12.19	−23.04	24.51	−22.01	49.85
${}_{{\eta }^{\prime }}{}^{90}\mathrm{Zr}$	$1s$	−55.20	0	−55.19	15.31	−55.16	30.63	−55.04	61.35
	$1p$	−47.05	0	−47.02	14.70	−46.96	29.43	−46.72	59.04
	$1d$	−37.42	0	−37.38	13.96	−37.27	27.96	−36.86	56.22
	$2s$	−34.19	0	−34.14	13.61	−33.99	27.29	−33.47	54.98
${}_{{\eta }^{\prime }}{}^{197}\mathrm{Au}$	$1s$	−56.03	0	−56.03	14.94	−56.01	29.89	−55.96	59.83
	$1p$	−51.12	0	−51.10	14.64	−51.07	29.30	−50.96	58.67
	$1d$	−45.15	0	−45.14	14.27	−45.08	28.56	−44.89	57.26
	$2s$	−42.80	0	−42.78	14.10	−42.71	28.22	−42.47	56.63
${}_{{\eta }^{\prime }}{}^{208}\mathrm{Pb}$	$1s$	−57.65	0	−57.64	15.34	−57.63	30.68	−57.57	61.40
	$1p$	−52.77	0	−52.76	15.03	−52.73	30.07	−52.62	60.23
	$1d$	−46.87	0	−46.85	14.66	−46.80	29.33	−46.61	58.80
	$2s$	−44.56	0	−44.54	14.49	−44.47	29.00	−44.24	58.19

, we show, respectively, the results for the bound state energies (E) and full widths ($\mathsf{\Gamma }$) of the $\eta$- and ${\eta }^{\prime }$-mesic nuclei of mass number A, obtained by solving the Klein–Gordon equation, for various values of the strength of the imaginary part of the potential $\gamma =0.0,0.25,0.5,1.0$ (See below Equation (52) about the $\gamma$). The results for $\gamma =0$, for both the $\eta$ and ${\eta }^{\prime }$ mesons, correspond to the case where the imaginary part of the potential has been ignored. The bound state energies and full widths are obtained from the complex energy eigenvalue $\mathcal{E}$ as $\mathcal{E}=E+m-i\mathsf{\Gamma }/2$. We also note that for each nucleus, we have computed all bound states but have only listed up to four. In fact, the number of bound states increases with the mass of the nucleus in such a way that for the heavier nuclei, we have a richer structure of bound states. Furthermore, we note that the relativistic corrections shallower the bound state energies for the $\eta$ and ${\eta }^{\prime }$ by approximately 2 MeV and 1 MeV, respectively.

From Table 10 and Table 11, (column with $\gamma =0$) we conclude that the $\eta$ and ${\eta }^{\prime }$ are expected to form bound states with all the nuclei considered.

However, the situation changes appreciably once we take into account the absorption effects of these mesons by nuclei, which we simulate with nonzero phenomenological parameter $\gamma$. We study the values $\gamma =0.25,0.5,1.0$, where a larger value means a stronger absorption of the meson by the nuclear medium. When $\gamma \ne 0$, some of the bound states that are present when $\gamma =0$ disappear. The columns with $\gamma =0.25$, $\gamma =0.5$, and $\gamma =1.0$ in Table 10 and Table 11 show the results for the bound state energies E and full widths $\mathsf{\Gamma }$ of the $\eta$- and ${\eta }^{\prime }$-mesic nuclei of mass number A, obtained by solving the Klein–Gordon equation, for some values of the strength of the imaginary part of the potential $\gamma =0.25,0.5,1.0$.

Considering only the ground states, adding and absorbing part of the potential changes the situation appreciably, where the effects are larger the larger $\gamma$ is. Clearly, the imaginary part of the potential is repulsive, being more repulsive for $\gamma =1$. Whether or not the bound states can be observed experimentally is sensitive to the value of the parameter $\gamma$, since $\mathsf{\Gamma }$ increases with increasing $\gamma$. Furthermore, because the so-called dispersive effect of the absorptive potential is repulsive, the binding energies for all nuclei decrease with $\gamma$. However, they decrease very slightly. Even for the largest value of $\gamma$, there is at least one bound state. We have found similar results for the $\varphi$ meson in our past work [100]. Note that the width of the ground state increases with $\gamma$ for all nuclei, as expected, since a larger $\gamma$ means that the strength of the imaginary part of the potential is larger.

Finally, in

Table 12. Bound state energies of $B_c^{-}$ in nucleus of mass number A, obtained by the Direct Bessel transform method. All dimensioned quantities are in MeV.

		Bound State Energies (MeV)
		Direct Bessel Transform
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{B_c^{-}}{}^{12}\mathrm{C}$	1s	−79.12	−80.63	−87.03
	1p	−56.15	−57.53	−63.38
${}_{B_c^{-}}{}^{16}\mathrm{O}$	1s	−75.00	−76.16	−80.94
	1p	−54.86	−56.13	−61.55
${}_{B_c^{-}}{}^{40}\mathrm{Ca}$	1s	−104.27	−105.69	−111.87
	1p	−81.71	−83.51	−91.34
${}_{B_c^{-}}{}^{48}\mathrm{Ca}$	1s	−96.63	−98.37	−105.81
	1p	−72.02	−73.56	−80.24
${}_{B_c^{-}}{}^{90}\mathrm{Zr}$	1s	−96.34	−98.32	−106.82
	1p	−83.82	−85.44	−92.35
${}_{B_c^{-}}{}^{208}\mathrm{Pb}$	1s	−95.88	−97.39	−103.79
	1p	−70.46	−71.76	−77.34

and

Table 13. Bound state energies of $B_c^{+}$ in nucleus of mass number A, obtained by the Direct Bessel transform method. All dimensioned quantities are in MeV.

		Bound State Energies (MeV)
		Direct Bessel Transform
	$\mathit{n}\mathcal{l}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{2000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{4000}$	${\mathsf{\Lambda }}_{\mathit{B}}=\mathbf{6000}$
${}_{B_c^{+}}{}^{12}C$	1s	−71.01	−72.53	−78.94
	1p	−49.11	−50.49	−56.32
${}_{B_c^{+}}{}^{16}O$	1s	−64.64	−65.80	−70.59
	1p	−45.94	−47.22	−52.64
${}_{B_c^{+}}{}^{40}\mathrm{Ca}$	1s	−84.89	−86.31	−92.49
	1p	−62.80	−64.57	−72.23
${}_{B_c^{+}}{}^{48}\mathrm{Ca}$	1s	−77.09	−78.83	−86.26
	1p	−53.64	−55.13	−61.60
${}_{B_c^{+}}{}^{90}\mathrm{Zr}$	1s	−65.51	−67.49	−75.99
	1p	−55.11	−56.75	−63.75
${}_{B_c^{+}}{}^{208}\mathrm{Pb}$	1s	−48.61	−50.13	−56.53
	1p	−29.27	−30.58	−36.22

, we present the $B_c^{\pm }$-nucleus bound state energies for several nuclei restricted to the 1s and 1p states, where we certainly expect shallower bound states. (More detailed results will be presented elsewhere in the near future). For details on the momentum space and the Coulomb potential treatment focusing on the $B_c$¹²C case, see Ref. [101]. From Table 12 and Table 13, we conclude that the $B_c^{\pm }$ are expected to form bound states with all the nuclei studied.

7. Summary and Conclusions

We have computed the mass shift amount $\mathsf{\Delta }{m}_h\equiv m_h^{\ast }-m_h$, with $m_h$ being the meson mass in vacuum and $m_h^{\ast }$ that in nuclear medium, for the mesons $h=\eta$, ${\eta }^{\prime }$, $\varphi$, ${\eta }_c$, $J/\psi$, ${\eta }_b$, $\mathsf{{\rm Y}}$, and $B_c^{\pm }$ in symmetric nuclear matter and nuclei. For this, we have used two approaches for some meson in this study, namely the quark–meson coupling model and a hybrid approach that combines the quark–meson coupling model with an effective Lagrangian.

We found in all cases that the mass shift amount (Lorentz scalar potential) is negative, which means that the nuclear medium provides attraction to these mesons (these mesons do not acquire any repulsive vector potentials) and opens the possibility of their binding to nuclei. Even though the precise values for the negative mass shifts reported in this work are based on the quark–meson coupling model and effective Lagrangian approach, negative mass shifts have also been observed in other approaches and experimental results. Thus, we believe this is a robust prediction of our approach. Using the baryon density distributions of several nuclei calculated in the quark–meson coupling model, we have, except for ⁴He nucleus (taken from Ref. [124]), and the mass shift amount computed previously, calculated the meson–nucleus potentials in a local density approximation for these mesons in nuclei in a wide range of nuclear masses, namely A = ⁴He, ¹²C, ¹⁶O, ⁴⁰Ca, ⁴⁸Ca, ⁹⁰Zr, ¹⁹⁷Au, and ²⁰⁸Pb. In all the nucleus cases selected for each meson, the resulting nuclear potentials have turned out to be attractive, reflecting the characteristics of the mass shift in the nuclear medium.

Finally, we have solved the Schrödinger or Klein–Gordon equation with the calculated nuclear potentials to obtain the meson–nucleus bound state energies and widths when the nuclear potential is complex. Although the details differ for each meson, we have found that all the mesons studied are expected to form bound states with nuclei. For the nuclear potential that is complex, the signal for the formation of the meson–nucleus bound state might be difficult to identify experimentally, depending on the imaginary part of the obtained bound state energy.