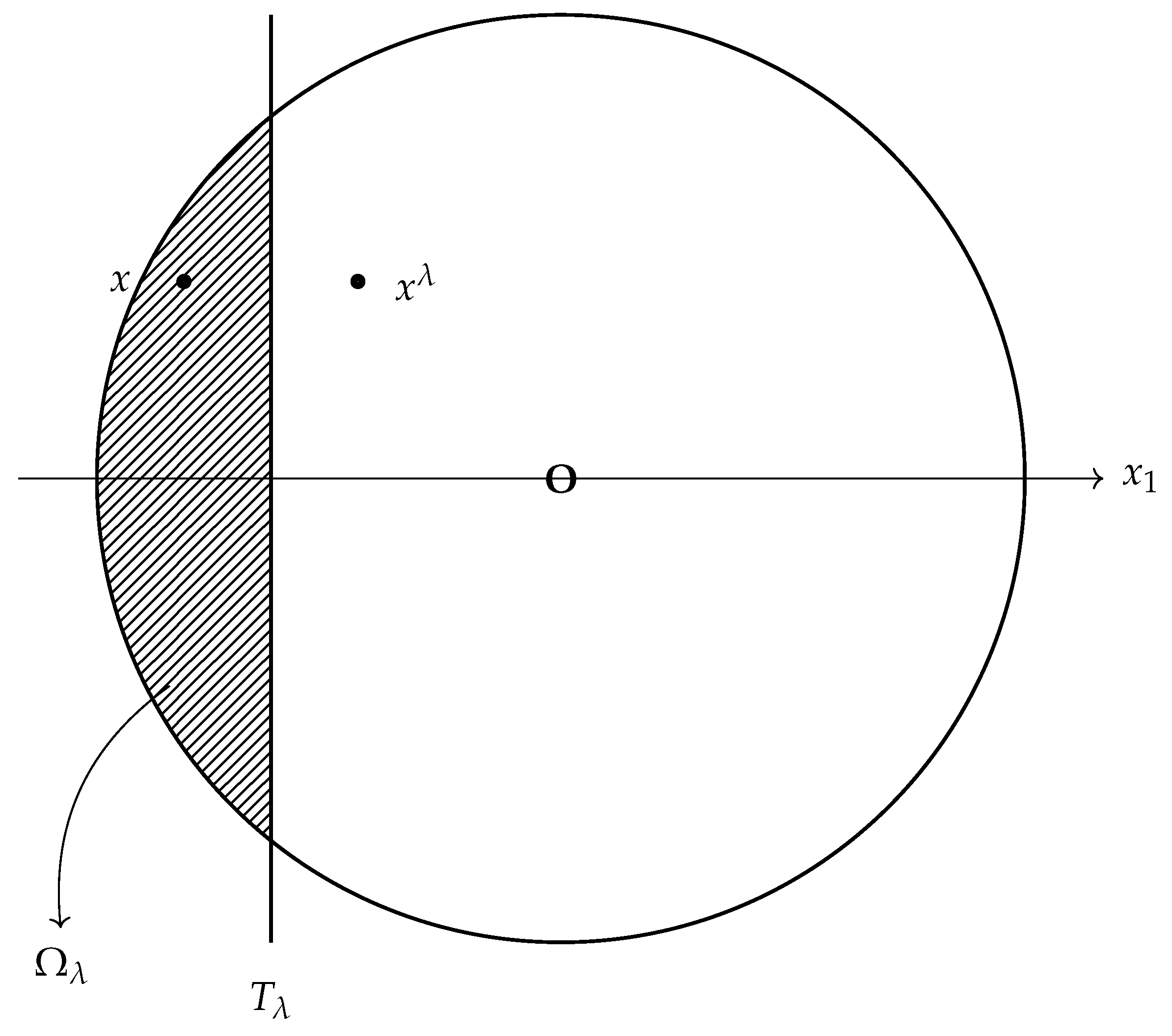1. Introduction
In this paper, we consider nonlinear equations involving the fractional parabolic equation in the unit ball
with
for any real number
, where
is a normalization positive constant depending on
n and
s, and
stands for the Cauchy principal value.
In order to understand the integral in (2), we require that
with
In contrast to the usual differential operators, the fractional Laplacian is a nonlocal operator, meaning that its value at a point depends on the values of the function in the whole space. This nonlocality gives rise to a number of mathematical properties that make the fractional Laplacian an important tool for modeling nonlocal phenomena, and has gained much attention in recent years, with a lot of researchers studying equations involving the fractional Laplacian (e.g., Cabré & Cinti, 2014; Caffarelli & Silvestre, 2007; Felmer & Wang, 2014; Musina & Nazarov, 2014; Chen et al., 2015; Cabré & Sire, 2015 [
1,
2,
3,
4,
5,
6]; and references therein). During the past two decades, researchers have developed several methods for studying the lower-order fractional operators with
. Notably, the extension method (Caffarelli & Silvestre, 2007) [
2] and the integral method (Chen & Li, [
7]) have produced fruitful outcomes. To our knowledge, the extension method cannot be applied to higher-order fractional problems with
due to technical limitations. In contrast, applying the integral method requires imposing additional constraints on the integrability of solutions; consequently, the integral method also loses its effectiveness. In 2017, Chen et al. (2017) [
8] introduced a direct method of moving planes for the fractional Laplacian, to avoid circumventing the issue and investigate nonlocal problems directly, they applied it to obtain the symmetry, existence/nonexistence, and regularity properties of solutions of various problems (e.g., Caffarelli et al., [
9,
10,
11]; and references therein). The method of moving planes was first introduced by A. D. Alexandrov (1950s) to prove the celebrated Soap Bubble Theorem. Since its inception, the method has been refined and extended by numerous mathematicians, including Serrin (1971) [
12], who applied it to establish symmetry results for elliptic equations. In recent years, the method has been adapted for nonlocal problems, such as in the direct method of moving planes (e.g., Chen et al., 2019 [
13]), which arise naturally in models of anomalous diffusion, Lévy flights, and image processing. This adaptation has facilitated the study of nonlinear problems (e.g., Cai & Ma, 2018; Chen & Li, 2018; Chen et al., 2017 [
14,
15,
16]).
In our paper, we use the direct method of moving planes (Chen et al., 2017 [
8]) to study the radial symmetry and monotonicity of solutions of fractional parabolic equations in the unit ball. Du and Wang (2023) [
17] use the direct method of moving planes to prove the monotonicity of solutions of equations involving a nonlocal Monge–Ampère operator; however, they only discuss how to address problems when restricting variables solely to the half-space, since the nonlocal fractional operator generates the semi-group in
. We generalize the variables to the unit ball. When the variables are not restricted to a half-space, ensuring the existence of solutions within this framework requires preserving maximal regularity. To achieve this, we adopt the method proposed by Liu (2024) in [
18], which involves controlling the norm of the spatial operator to be less than 1. However, since the fractional Laplacian is nonlocal, the challenge lies in how to enforce such a norm constraint. Conventionally, one might assume uniform convergence and boundedness of the solution
u (e.g.,
), as in Chen et al. (2020) [
19]. In contrast, our paper boldly relaxes this assumption, requiring only that
u converges almost everywhere—a key innovation that distinguishes our work from the existing literature. Meanwhile, our paper also employs a localization procedure by restricting the problem to specific local subdomains of the domain of interest. This approach transforms a global partial differential equation problem into locally tractable subproblems, thereby simplifying analysis or computation. For instance, in
Section 3 of the paper, we utilize the Fourier transform to decompose the partial differential equation into distinct frequency components and achieve localization by truncating certain frequency ranges. Similarly, in
Section 5, we confine the problem to a specific region using a cut-off function, effectively localizing the analysis.
The fractional Laplacian, as a nonlocal operator, requires values from the entire domain to determine its values on the boundary. Consequently, there is currently a lack of literature addressing boundary-value problems for partial differential equations involving the fractional Laplacian. Although our study incorporates an investigation into maximal regularity, we still adhere to the common assumption, adopted in the majority of existing works, of imposing homogeneous (zero) boundary conditions. If we consider
, we have to consider the boundary conditions
, and the intersection of
with
, which complicates the problem; the detailed process for finding the maximal regularity of complicated half-space problems can be found in Shibata and Shimizu (2007) [
20]. Possible directions for future research can place significant emphasis on the exploration of incorporating boundary conditions into fractional Laplacian equations.
2. Main Results
In our study, we consider nonlinear parabolic equations involving the fractional Laplacian on a parabolic cylinder using the direct method of moving planes, we aim to prove the following main theorems:
Theorem 1. Let be a unit ball. Let ; assume that is a positive bounded classical solution ofThen, the solution of (3) satisfies the - maximal regularity estimate:for any . Since , and is dense in . The proof of Theorem 1 is referred to in [
20]; take the advantage that the heat equation and fractional Laplacian operator have similar Fourier transform structures.
Theorem 2. Let be a unit ball. Let , and suppose that is a positive bounded classical solution ofand assume satisfies the following assumptions: (f1) are decreasing in .
(f2) f is uniformly Lipschitz continuous in u, i.e.:then, is radially symmetric and monotone decreasing about the origin. Remark 1. implies that converges almost everywhere to when . Specifically in our case, on a measure space , where , there exists a sequence of functions and a function u, such that for any positive number ε, there exists a set with , and for all , , which means the sequence of functions converges to u at all points except for those in a set of measure zero. The reason why this condition is imposed is expatiated in Section 3. Theorem 2 is referred to in [
21]; compared to the version in [
21], Theorem 2 has undergone updates that add convergent conditions on
u.
In the process of proving Theorem 2, we will develop a systematic approach to carry out the method of moving planes for nonlocal problems, see the
Figure 1. The main theorems and how they fit in the framework of the method of moving planes are illustrated in the following.
For any given
let
be the moving planes,
be the region to the left of the plane, and
be the reflection of
x about the plane
is the reflection region of the plane, and
is the intersection of
and
.
Assume that
is a positive solution of Equation (
5). We compare the values of
with
and we denote
The main part of the proof is to show that
This provides a starting point to move the plane. Then, in the second step, we move the plane to the right as long as inequality (6) holds to its limiting position to show that
u is symmetric about the limiting plane. A maximum principle is usually used to prove (6). Since
is an anti-symmetric function:
for simplicity of notation, in the following, we denote
by
w,
by
, and
by
. We first prove the following; Theorem 3 is referred to in [
21].
Theorem 3. (The maximum principle for the anti-symmetric functions on a parabolic cylinder) We add a time dimension on the unit ball with lower edge and higher edge ; denote this thin cylinder as to be the narrow region in . Assume that and is lower semi-continuous on . Ifwhere is bounded from below in ; denotethen In
Section 3, we present proofs of Theorem 1. In
Section 4, we present proofs of Theorem 3. In
Section 5, we present proofs of Theorem 2, and therefore we obtain the radial symmetry and monotonicity of solutions of fractional parabolic equations. We hold a strong conviction that the ideas and methods presented here can be readily employed to investigate diverse nonlocal problems that involve more comprehensive operators and nonlinearities. Notice in
Section 3,
is used to denote eigenvalues; in the
Section 4 and
Section 5,
is used to denote the reflection variable.
3. Proof of Theorem 1
Lemma 1. The nonlocal fractional Laplacian operator defined by Equation (2) generates the semi-group in .
Proof. The resolvent for the fractional Laplacian
is
Since is the integration variable and the integral is taken over all , the poles are actually the values of z in the complex plane, such that there exists some such that . These values correspond to the positive real part of the complex plane, where with . The set is dense in ; for any , we can find a such that is arbitrarily close to z. Therefore, the fractional Laplacian operator generates the semi-group in . □
Lemma 2. The nonlocal fractional Laplacian operator defined by Equation (2) is a self-adjoint and dense operator.
Proof. Consider the fractional Laplacian operator
defined on an appropriate function space
H; we will show that for all
, we have
Let
be a Fourier transform representation of the fractional Laplacian applied to
, where
the fractional Laplacian can be represented in Fourier space as
where
denotes the Fourier transform.
Consider the inner product
. Using Parseval’s identity, we have
Since
for all
, we conclude that
is a self-adjoint operator; therefore, the nonlocal fractional Laplacian operator is also a self-adjoint operator.
The domain of the fractional Laplacian , which is , typically includes functions that are smooth or at least have some regularity properties, belonging to a Sobolev space . In , smooth functions are dense in various function spaces, including Sobolev spaces ; this means that for any , there exists a sequence such that in the norm. Since is a subset of and is dense therein, and the fractional Laplacian is well defined on , we can apply to each in the sequence; the resulting sequence converges to as . Therefore, the domain of the fractional Laplacian is dense in . □
Now, we will prove Theorem 1. First of all, we show the
-
maximal regularity of solutions to the model problems in the whole space according to reference [
20]:
Let
; we would like to show that the solution of (10) satisfies the
-
maximal regularity estimate:
for any
. We may assume that
, because
is dense in
.
To obtain the solution formula of (10), we first consider the resolvent problem corresponding to (10):
apply the Laplace transform, we have
solving for
U, we have
To obtain the exact formula of solutions of (10), we consider the equivalent homogeneous equation:
Apply the Fourier transform to the problem related to
x; we have
where
combine (14) and (15); we have
Solve (14); we have
where
is the initial value, and take
as the eigenvalues so that (17) generates a semi-group.
Therefore, we obtain the solution formula of (10):
where
and
denote the Fourier–Laplace transform and its inverse, defined by
respectively. In particular,
is given by the formula:
Set
Then, we have
Employing the same arguments and process in [
20], only different in the denominator in the solution formula (26), by the
-boundedness of the families
and
, we obtain
We can also see that in [
20]:
Combining (20) with (21), we obtain (11).
Since we have proved the maximal
-
regularity of the model equation (10), to apply the result on proving the maximal
-
regularity of the nonlocal parabolic fractional Laplacian equations (1), use the following procedure, since
where
is the Fourier transform of
u, i.e.,
The Fourier transform of homogeneous equation
is
we derive
for some constant
, and take
as the eigenvalues so that (23) generates a semi-group. Therefore, the above process of finding the maximal regularity of the model problem could be applied to the nonlocal parabolic fractional Laplacian equations.
In this paper, we consider the case where the boundary condition is zero, in which . Therefore, the maximal regularity of nonlocal parabolic fractional Laplacian equations in the whole space can be applied to our problem, which proves the Theorem 1.
In [
18], the author briefly elucidates the underlying logic and principles governing the existence of maximal regularity for parabolic and hyperbolic differential equations. Based on this reference, we can verify that the prerequisite for the existence of maximal regularity for parabolic differential equations is that the eigenvalues of the operator related to spatial variables must be less than 1. In (11), we observe that as
and
,
could be bounded by 1; however, when
is not sufficiently large or
, to ensure that the eigenvalues of the nonlocal fractional Laplacian operator remain less than 1, we impose the condition
for
in Theorem 2, where we take the measure space
as the following:
therefore, we have
for all
to control the growth of
on those uncountable sets where the eigenvalues of
could be defined, by the definition of fractional Laplacian operator, since we take the integration variable
, the eigenvalue of
could be controlled less than 1.
5. Proof of Theorem 2
Step 1: Begin moving the plane from near the left end of along the axis, but do not reach origin,
so then
we derive
We deduce from the Equation (
5) and
,
that
satisfies
where
is bounded.
We first prove that for
sufficiently close to
, we have:
Let
be
w in Theorem 3, we have
according to Theorem 3, we conclude that for
sufficiently close to
when
is narrow,
Let
from (27), we derive
with
is still bounded.
Suppose otherwise that (
28) does not hold, then
is negative somewhere; hence, there exists an
and
such that
If
,
. If
,
Combine with (
29), we derive
from (26), we also have
where
; then, we derive
which is a contradiction for
d sufficiently small. Thus,
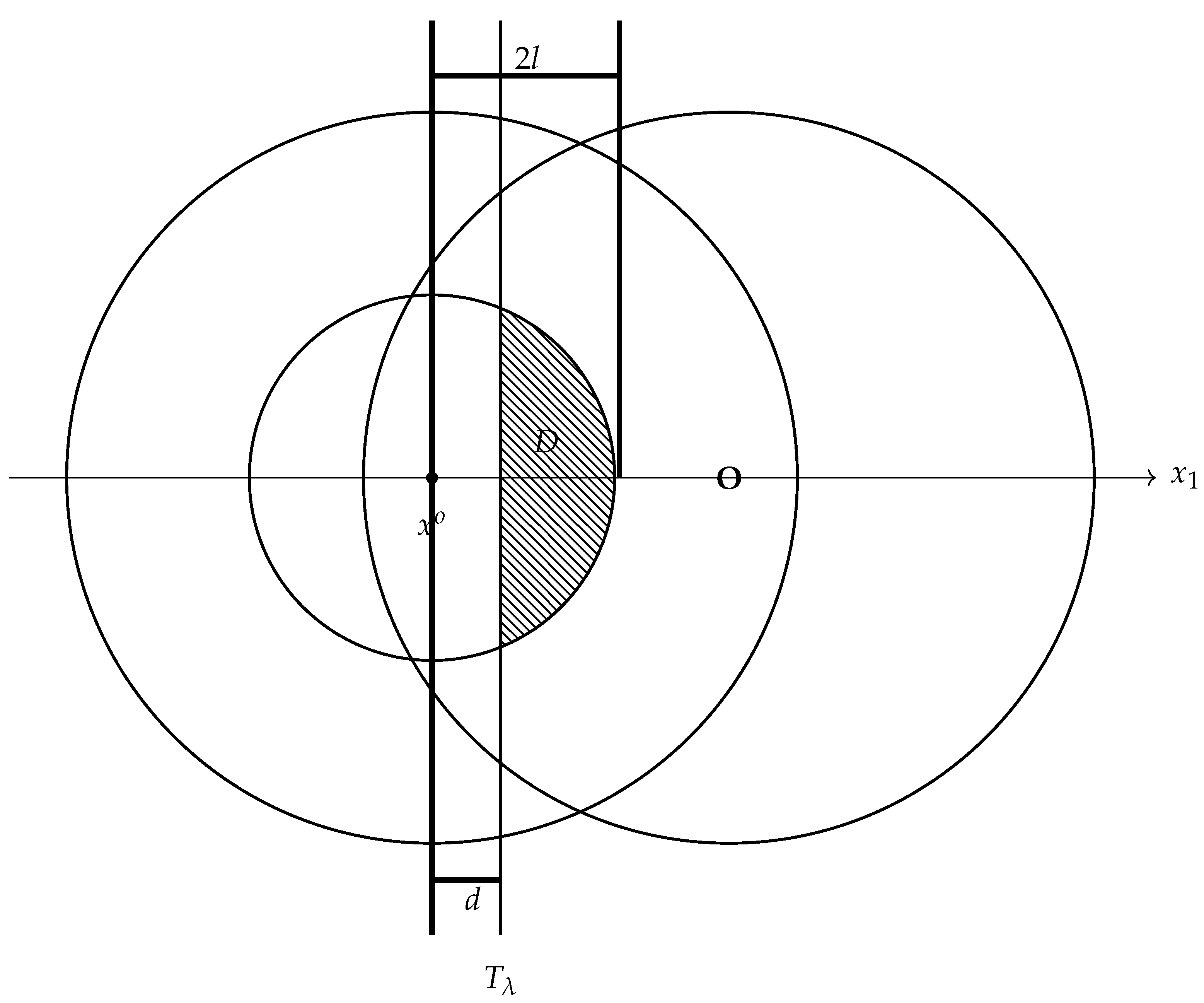
is bounded from below. Let , .
Therefore, (28) is proved if is narrow.
Step 2: The inequality (28) provides a starting point, from which we can carry out the moving. Now, we move the plane continuously to the right until its limiting position, as long as (28) holds.
Define
we will prove
.
Otherwise, if
, we will show that
can be moved further to the right and we will have
Suppose
; we want to first show
Suppose otherwise, (31) does not hold, then there exists
such that
. Since
inside
as step 1 has proved,
is the minimum point, thus
; following from (27), we derive
so that
It follows that
since
this implies that
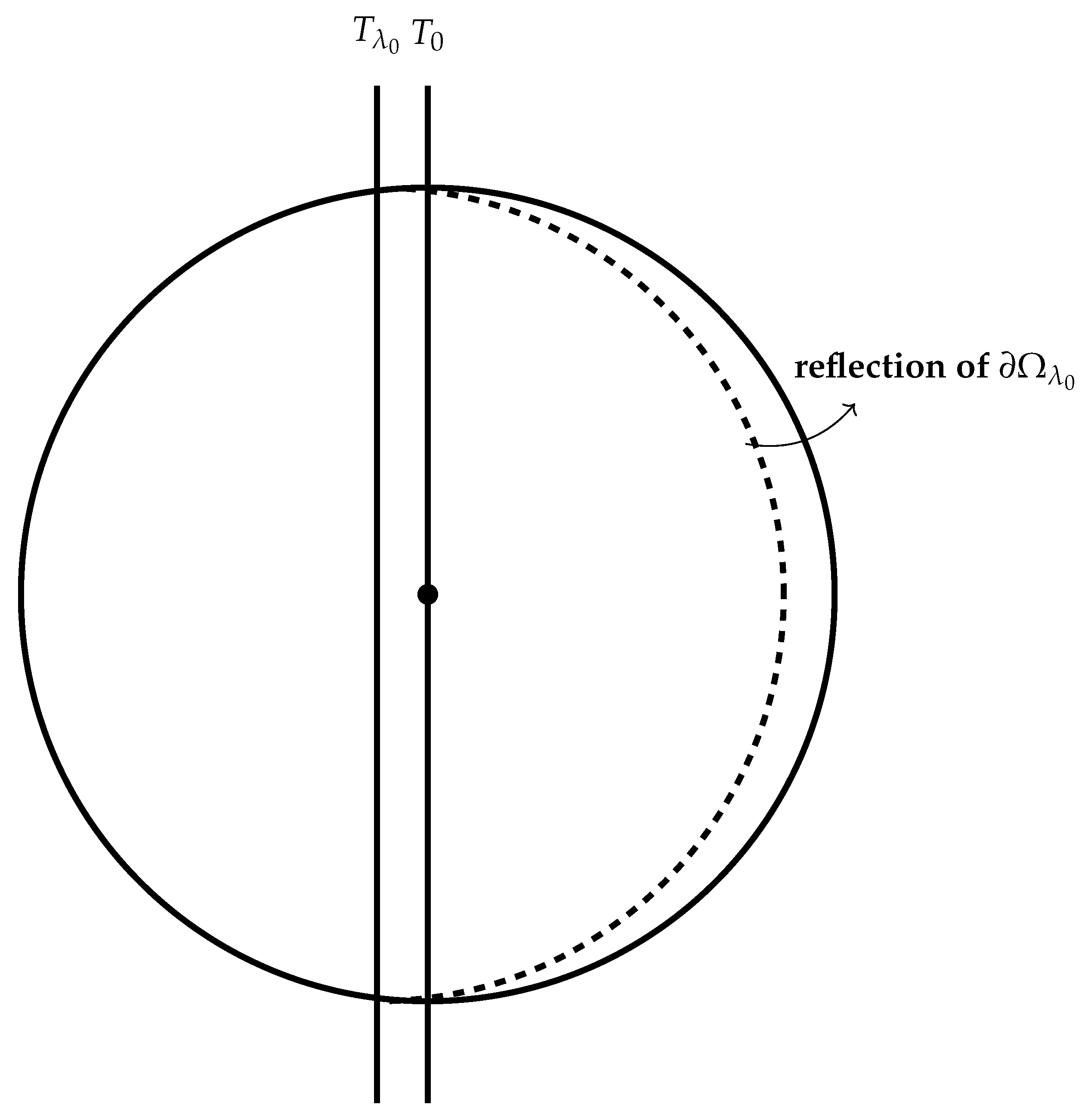
we derive a contradiction, since the plane
did not reach the origin. If we take a point
on the curved part
, then its reflection point
is in the interior of the ball,
,
, which contradicts (33). Therefore, (31) is proved.
However, since for all
,
, we proceed to establish
is bounded away from 0:
Suppose (
34) is violated, then there exists
such that
. Without loss of generality, by the Bolzano–Weierstrass theorem, there exist some subsequences of
(here, we still denote this subsequence by
for convenience) such that
in
.
Let
We rewrite Lemma 3.1 from [
22] as the following, as we will use it later:
Lemma 3. Let , and let be a sequence of nonlocal fractional Laplacian operators. Let and be sequences of functions satisfying in the weak sensefor a given bounded interval and a bounded domain . Assume that have spectral measures converging to a spectral measure μ. Let L be the operator associated with μ (weak limit of ), and suppose that, for some functions, u and f, the following hypotheses hold: - 1.
uniformly in compact sets of
- 2.
uniformly in ,
- 3.
for some , and for all .
Then, u satisfiesin the weak sense. By the assumption that
for some
, and given that
satisfies a certain compactness property, the compactness is derived from the Arzelà–Ascoli theorem, which guarantees that if
is bounded in a suitable fractional Sobolev space, then it converges locally uniformly in
for
. Therefore,
converges locally uniformly to
and
. It follows that,
We also have
which forces
Let ; suppose there are some sequences such that converges uniformly to , and converges uniformly to .
By a Strong Maximum principle:
Lemma 4. Assume that satisfieswe have eitheror If
,
somewhere, but we already derive
in (37), see
Figure 3, then we must have
,
. Thus,
converges to 0 uniformly in
. Until now, the hypotheses in Lemma 3 have been satisfied; then, we can guarantee the equation of the form
could converge to the form
in the weak sense. In the context of weak sense, the equation is understood in the distributional sense, meaning that the equation holds in the limit after multiplication by a test function and subsequent integration. For an arbitrary test function
, the following holds:
Furthermore, as the limit is taken,
w fulfills the weak formulation
for all test functions
, where
in (41) and
L in (42) are fractional Laplacian operators. We can also guarantee the equation of the form
could converge to the form
in the weak sense. For an arbitrary test function
, the following holds:
as the limit is taken,
u fulfills the weak formulation
Notice that we use the Lemma 3 to verify the weak convergence; however, by regularity theory for parabolic equations in [
22], it is easy to check that (39) converges to (40) uniformly and (43) converges to (44) uniformly. More content related to the regularity of fractional function could refer to [
23].
In order to derive a contradiction for large
k in (41), let
which converges to 0 uniformly.
Let
where
is a cut-off function such that
and
attains its minimum at some point, say
in
; this implies
Combining (48) and (49), it also implies
and
Combining (
47) and (
48), it is easy to deduce
thus
Since we have
where
, which is a contradiction. Hence, we have proved (34).
Since
depends on
continuously, there exists
and
, such that for all
, we have
Now apply the Maximum principle 3 and, in our case, the narrow region is
by the narrow region theorem, we derive
Combining (51) and (52), we conclude that for all
this contradicts the definition of
. Therefore, we must have
and
Similarly, one can move the plane
from
to the left and show that
Combining (
53) and (
54), we have shown that
and
This completes step 2.
So far, we have proved that u is symmetric about the plane . Since the direction can be chosen arbitrarily, we have actually shown that u is radially symmetric about origin.
Since
,
,
, if there exists
such that
is the minimum point, from the above process, on one hand,
on the other hand,
this forces
which is a contradiction. Therefore,
u is monotone decreasing about the origin. We have proved Theorem 2.