Abstract
Existing remote sensing scene classification (RSSC) models mainly rely on convolutional neural networks (CNNs) to extract high-level features from remote sensing images, while neglecting the importance of low-level features. To address this, we propose a novel RSSC framework, LGNet, a lightweight model with a symmetric dual-branch architecture that combines Lie group-based feature extraction with an innovative multi-dimensional cross-attention mechanism. By utilizing the Lie group feature covariance matrix in one branch, the model captures the low-level features of the image while extracting the high-level semantic information using CNNs in the parallel branch. The dynamic fusion of these multi-scale features using the attention mechanism optimizes the classification accuracy and computational efficiency. Extensive experiments on three standard datasets (AID, UC Merced, and NWPU-RESISC45) show that LGNet outperforms current state-of-the-art models, providing superior classification performance with significantly fewer parameters. Verified on publicly available challenging datasets, LGNet achieves a classification accuracy of 96.50% with 4.71M parameters on AID. Compared with other state-of-the-art models, it has certain advantages regarding classification accuracy and parameter count. These results highlight the efficiency and effectiveness of LGNet in complex remote sensing scenarios, making it a promising solution for large-scale high-resolution remote sensing images (HRSSI) tasks.
1. Introduction
With the widespread application of HRRSI and the rapid development of related technologies, an increasing amount of HRRSI data have become available [1,2]. HRRSI can effectively represent the texture, geometric structure, and spatial distribution relationships of ground objects within a scene [3], providing essential data support to identify the features of the object accurately. In this context, RSSC, as a key technology for analyzing and processing HRRSI, has become a fundamental tool in multiple fields such as urban planning [4]. However, HRRSI typically exhibits significant intra-class and small inter-class differences [5]; moreover, characteristics such as complex backgrounds, multi-scale features, and scene similarity considerably increase the difficulty of classification tasks. Especially when images contain a large amount of detailed information, distinguishing objects of different categories effectively has become a core issue in current research.
RSSC methods are primarily categorized into approaches based on low-level, mid-level, and high-level features [6]. Methods based on low-level features mainly depend on the spectral, texture, and shape features of images [7], such as color histogram (CH) [8], local binary pattern (LBP) [9], and scale-invariant feature transform (SIFT) [10]. Although these methods are computationally simple, their capacity for abstract representation is insufficient. Mid-level feature-based methods aggregate low-level features through approaches such as the bag-of-visual-words model (BoVW) [11], Fisher encoding [12], and spatial pyramid matching (SPM) [13], compensating for the deficiencies of low-level features in capturing global semantic information and complex scene structures, thus improving the accuracy of scene classification. High-level feature-based methods mainly use convolution operations to extract high-level semantic features from HRSSI. Due to their capability to automatically extract scene features, they have become one of the main models today [14,15]. In recent years, the introduction of the attention mechanism has further enhanced the network’s ability to focus on key feature regions, effectively reducing interference from irrelevant information [16,17]. These developments have made significant progress in RSSC applications from low-level to high-level features, demonstrating stronger performance in classifying complex scenes in remote sensing images.
Despite the advancements in RSSC driven by the techniques mentioned above, several challenges remain:
- Insufficient utilization of low-level features in HRRSI: Many current RSSC models primarily use convolution operations to extract high-level semantic features from scenes, neglecting low-level features [18], which results in the model’s inability to effectively capture small but essential local texture structures in complex scenes, leading to decreased classification performance. Additionally, the fixed receptive fields commonly used in CNNs are difficult to adapt to multi-scale feature representations, limiting the model’s potential in extracting local information [2].
- Limitations of attention mechanisms in low-level feature learning: Although attention mechanisms have played an essential role in improving the performance of RSSC models, most existing attention mechanisms are designed to optimize high-level features, with little consideration given to the role of low-level features [19]. Due to the neglect of low-level features in existing models, the model struggles to comprehensively understand the multi-layered information in images, leading to suboptimal performance in complex backgrounds or multi-object scenarios.
- High complexity and large parameter count in existing models: Most existing RSSC models are based on deep learning frameworks and typically rely on multiple convolutional and fully connected layers, leading to a sharp increase in the model’s parameter count, which significantly raises the computational overhead and storage requirements. During remote sensing data processing, such high-complexity models increase training and inference time and make efficient deployment difficult in resource-constrained environments. As scene complexity increases, traditional models struggle to strike a balance between high performance and high efficiency, especially when processing HRRSI, where the model’s consumption of computational resources becomes a major bottleneck in practical applications, limiting its feasibility for widespread use.
To address the abovementioned challenges, we propose an RSSC model based on a Lie group multi-dimensional cross-attention mechanism. To address the first challenge, our model supplements the low-level features of the scene and integrates high-level semantic features, enhancing feature learning. For the second challenge, we design a novel cross-attention mechanism module that considers both high-level semantic features and low-level features of images, enabling the model to learn global and local features of scenes better. For the third challenge, we adopt a lightweight design. The model uses Lie group feature covariance matrix for representation, reducing the computational demands of high-dimensional feature matrices, and effectively decreases parameter count and computational complexity through depthwise separable convolution. Furthermore, introducing the cross-attention mechanism enables the model to associate relationships between multi-level features and focus on key regions, thereby improving classification accuracy and adaptability.
Overall, the contributions of this paper are as follows:
- We propose LGNet, a RSSC model based on Lie group feature extraction and the cross-attention mechanism. It improves the classification performance by extracting the low-level and high-level features of remote sensing scenes and fusing them effectively.
- We propose a multi-dimensional cross-attention mechanism (MD-CAM). This attention mechanism fully considers the correlations between features by capturing the relationships among low-level, high-level, and fused features of images.
- The model adopts a lightweight design. Using Lie group feature covariance matrix and depthwise separable convolutions reduces computational complexity, while the proposed MD-CAM focuses on key region features, enhancing the model’s computational efficiency.
The remainder of this paper is organized as follows. Section 2 reviews related work on RSSC, LGML, and attention mechanisms. Section 3 presents the proposed LGNet model in detail, including the overall architecture, LGML branch, deep learning branch, MD-CAM, and experimental setup. Section 4 demonstrates experimental results and analysis on three standard datasets, as well as ablation studies to validate the effectiveness of each module. Section 5 discusses the limitations of our approach and potential future work directions. Finally, Section 6 concludes this paper and summarizes our contributions.
2. Related Work
This section reviews key developments in RSSC research across three domains: scene classification methods, LGML techniques, and attention mechanisms. By examining the strengths and limitations of existing approaches, we establish the theoretical foundation for our proposed LGNet model and highlight its innovative contributions to the field.
2.1. Scene Classification Models
In the early stages, scholars primarily used methods based on low-level features for scene classification. For example, Swain and Ballard [8] proposed a method for image retrieval and matching based on color distribution using color histograms (CH). Ojala et al. [9] introduced Local Binary Patterns (LBP), which analyze the texture features of an image, particularly the grayscale variations and rotation invariance at different scales, achieving more accurate image classification. Additionally, Lowe’s [10] Scale-Invariant Feature Transform (SIFT) identifies prominent feature points in images across multiple scales, providing strong stability and robustness when processing image matching and classification tasks. These features effectively represent remote sensing images’ texture, color, and edge information and possess some degree of rotational and translational invariance. However, these features primarily describe the visual surface properties of the image, lacking an abstract representation of high-level semantics, and rely mainly on a single feature for learning. As a result, their generalization ability is insufficient when handling complex scenes or images with high inter-class similarity [20].
To compensate for the shortcomings of low-level feature learning, scholars have proposed scene classification methods based on mid-level features. The Bag of Visual Words (BoVW) method was first proposed by Sivic and Zisserman [21] and was applied to RSSC in the research by Zhu et al. [22]. This method classifies images by extracting visual features from local regions and constructing frequency histograms. Additionally, probabilistic topic models (PTM) [23], such as Probabilistic Latent Semantic Analysis (PLSA) [24] and Latent Dirichlet Allocation (LDA) [23], further extract image information by capturing latent topics in features, improving scene classification accuracy and robustness. Through these methods, the model adds more abstract expressions at the feature level, enabling it to capture local structural information in images better. However, mid-level feature models still have limitations in representing the spatial relationships of different regions in images. For example, they struggle to fully utilize the complex geometric structures and rich semantic information in HRRSI, thus limiting their effectiveness in recognizing diverse ground object targets.
With the rapid development of deep learning, RSSC technology has made significant progress [14,15]. As early as 1998, LeCun et al. [25] proposed CNN, laying the foundation for image recognition. Krizhevsky et al. [26] used deep CNN (AlexNet) to achieve unprecedentedly efficient image classification, promoting the application of deep learning in computer vision. The Generative Adversarial Network (GAN) proposed by Goodfellow et al. [27], through adversarial training between the generator and discriminator, can generate high-quality data, effectively alleviating the difficulty of acquiring remote sensing data. The deep autoencoder proposed by Hinton and Salakhutdinov [28] uses neural networks for nonlinear dimensionality reduction, effectively extracting the latent high-level features of the data. These typical models have laid a solid foundation for the application of deep learning in RSSC. In recent years, HRRSI classification methods combining CNN have been widely applied. Zhu et al. [29] proposed a classification method based on deep residual networks (ResNet), which effectively alleviates the vanishing gradient problem in deep networks by introducing residual modules, improving classification performance. The deep residual learning framework proposed by He et al. [30] has been widely applied in RSSC, significantly increasing the depth and complexity of the model while maintaining training stability.
2.2. LGML
As a mathematical tool that combines group structure and differential manifold properties, Lie groups can effectively capture the geometric information of data through their manifold attributes, exhibiting excellent rotation, scaling, and affine invariance, making them particularly suitable for RSSC tasks [31]. LGML overcomes the limitations of Euclidean methods in processing complex geometric features by mapping data to Lie group space and using covariance matrices and kernel functions to explore intrinsic relationships. Xu et al. [32] first proposed the intrinsic mean model of Lie groups and introduced Lie group kernel functions applicable to matrices and vector samples, achieving significant results in RSSC. They further optimized the algorithm, reducing model parameters and improving classification accuracy [33]. In addition, Xu et al. [19] proposed a classification model combining Lie groups with CNNs, which retains low-level detail information and integrates high-level semantic features. Lin et al. [34] verified the robustness of LGML in dealing with directional changes using Lie group algebra methods, further proving its advantages in handling geometric transformations. In recent years, LGML combined with deep learning models has been widely applied to tasks such as object detection [35], pedestrian recognition [36], and 3D object classification [37], further enhancing multi-level feature expression and classification performance, making it an ideal tool for handling complex HRRSI classification.
2.3. Attention Mechanism
By adjusting the focus on features from different regions, the introduction of attention mechanisms enables models to concentrate on key areas or important features, thereby enhancing discriminative capabilities in complex scenes. For example, the Convolutional Block Attention Module (CBAM) proposed by Woo et al. [38] combines channel and spatial attention, and its lightweight design has brought significant performance improvements in applications across various computer vision tasks, such as image classification. The SENet model designed by Hu et al. [39] innovatively recalibrates convolutional feature maps through significant channel attention mechanisms, effectively enhancing feature representation and achieving good results in RSSC tasks. Additionally, context-related attention mechanisms further strengthen the model’s understanding of complex objects and backgrounds. Wang et al. [40] proposed a recursive attention-based model that captures the spatial relationships between features through a multi-level structure, enhancing the model’s feature representation and robustness.
In recent years, with the tremendous progress of the Transformer architecture in computer vision, researchers have proposed various attention mechanisms to improve the performance of visual task processing [41,42]. As one of the key developments, cross-attention mechanisms have demonstrated good application value and performance advantages in the RSSC field. Cross-attention mechanisms establish interactive relationships between multi-level features, enabling a multi-directional information flow of features, which effectively improves the model’s ability to understand complex scenes. For example, the DMINet model proposed by Feng et al. [43] significantly improves remote sensing image detection accuracy by designing a joint module of self-attention and cross-attention. Yang et al. [44] further designed the SF-MSFormer framework, which improves the classification capability of diversified ground objects in complex scenes by introducing spatial and frequency domain multi-scale Transformers. Additionally, the MGSNet model proposed by Wang et al. [40] enhances feature diversity between network branches using target-background separation strategies and contrastive regularization, thereby improving classification performance. Meanwhile, the cross-attention and graph convolution combined algorithm proposed by Cai and Wei [45] effectively optimizes remote sensing images’ feature extraction and classification performance through a horizontal and vertical joint weight allocation strategy.
In summary, existing RSSC methods have made significant progress in feature extraction and attention mechanisms. Based on the review of existing methods, we present a qualitative comparison in Table 1 that highlights the key differences between our approach and representative RSSC methods. As shown in the table, while existing approaches employ various advanced network architectures and attention strategies, they predominantly focus on optimizing high-level semantic features, neglecting the importance of low-level features. This common limitation can lead to insufficient feature learning when processing scenes with complex backgrounds or subtle inter-class differences. In contrast, our proposed LGNet uniquely addresses this challenge through a symmetric dual-branch architecture that effectively integrates both low-level features via LGML and high-level features through an optimized deep learning branch, further enhanced by our novel MD-CAM that enables effective cross-layer information flow.

Table 1.
Qualitative comparison of LGNet and representative RSSC methods.
3. Method
In this section, we present the proposed LGNet architecture, which addresses key challenges in RSSC through Lie group feature extraction and MD-CAM. First, we provide an overview of the overall model structure, followed by comprehensive explanations of the LGML branch, deep learning branch, MD-CAM, and feature fusion strategy design principles and implementation details. Finally, we describe our experimental setup, including datasets, implementation environment, and parameter configurations, establishing the foundation for subsequent results analysis and discussion.
3.1. Overall Model Architecture
Figure 1 illustrates our proposed RSSC framework based on Lie group multi-dimensional cross-attention mechanisms. The symmetric dual-branch architecture consists of: (1) an LGML branch for extracting low-level features (), (2) a deep learning branch for capturing high-level semantic features (), (3) a feature-level fusion module that combines both feature types into fused features (), and (4) the MD-CAM that processes these three feature streams to highlight key information. The final classification is performed using a Softmax function applied to the enhanced features.
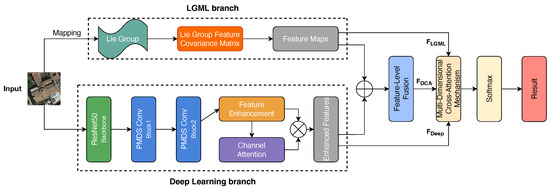
Figure 1.
Architecture of our proposed model.
Before feeding images into the model, we performed systematic preprocessing and data augmentation operations on the input HRSSI to improve training sample quality and model generalization capabilities. First, all remote sensing images were resampled to a standard size of pixels to ensure data format consistency. Subsequently, we applied normalization using the canonical ImageNet dataset mean and standard deviation , accelerating model convergence and significantly enhancing training stability.
For the training dataset, we implemented diverse data augmentation techniques to enrich sample diversity: we introduced random horizontal and vertical flipping to enhance the model’s invariance to directional changes; carefully designed random rotation strategies ( degrees) to cultivate the model’s ability to recognize rotation-invariant features; adjusted brightness, contrast, and saturation (each ) to enable robust performance under varying illumination conditions; and incorporated subtle random affine transformations (translation range ) to strengthen the model’s adaptability to object position shifts. This enhancement protocol was specifically optimized for HRSSI-specific characteristics such as multi-angle views, complex illumination conditions, and temporal variations, effectively improving the model’s classification performance and generalization capabilities when confronting diverse and complex scenes.
3.2. LGML Branch
Based on our team’s previous research in the field of Lie group feature extraction [1,2,51], we first map the samples to the Lie group manifold space to obtain the Lie group samples, and the formula is as follows:
In this context, represents the j-th sample within the i-th class of the dataset, while corresponds to the sample in the Lie group manifold space. The subsequent operations will be based on these processed Lie group samples.
Through extensive comparative experiments, we found that different scene classes often have similarities in texture and color, making it difficult to effectively distinguish these classes by relying only on single shallow features. To extract the low-level features of the image more comprehensively and avoid the limitations and errors caused by a single feature, building upon our previous research [2,19], we introduce the Lie group feature covariance matrix to capture multiple low-level features in the image jointly, thus improving the characterization ability of the features in different scenes. After numerous experimental optimizations, our determined feature vector expression is as follows:
where x and y are the pixel position coordinates, which are mainly used to preserve the spatial distribution information of the features. For the color features, through experimental comparisons of RGB, YCbCr, and Lab spaces, we ultimately selected the , , and components of the Lab color space, which represent the luminance, green-red, and blue-yellow color contrasts, respectively. Experiments have shown that the Lab space, based on a human vision model, has better color consistency under lighting changes and can reflect color differences more naturally [52]. represents the average color of a local image block, which is used to summarize the overall color distribution of the region, and is advantageous for identifying areas of uniform color (e.g., grass, rivers, etc.).
Local Binary Patterns (LBP) [53] encode the grayscale variations around pixels to generate binary texture features, effectively reflecting the local texture patterns of images. Histogram of Oriented Gradients (HOG) [54] computes the gradient directions of pixels within a local region and constructs a directional histogram, capturing edge and contour information of the image. Based on previous research [19,51], we employed Gabor [55] filters to extract spatial and directional information from the image through filtering operations at multiple scales and directions.
Our feature covariance matrix also integrates the extraction of image shape features, including area S, compactness , and aspect ratio . Area S reflects the size of the feature and is an important feature for distinguishing objects at different scales. To describe the complexity of shadowed objects, we incorporate the compactness metric proposed in previous studies [56]:
where P is the perimeter of the object’s silhouette. Specifically, objects with high structural regularity, such as buildings and roads, tend to have higher , while natural elements like forests and lakes exhibit lower . The elongation measures the extent of an object’s shape, making it useful for distinguishing elongated features such as rivers and roads from more compact objects, thereby enhancing the accuracy and efficiency of geographical object classification in HRRSI.
By extracting texture, color, shape, and other features described above, our model can obtain more low-level features from images, thereby acquiring multi-scale remote sensing image information and more accurate classification results. Based on these feature vectors, we calculate the Lie group feature covariance matrix C:
where represents the i-th feature vector, is the mean of all feature vectors, and n is the total number of feature vectors.
Compared with traditional feature extraction methods, our Lie group feature covariance matrix has three key advantages: (1) low matrix dimensionality, effectively reducing redundancy in the feature space; (2) high computational performance, suitable for real-time or large-scale data processing; and (3) strong noise resistance, providing robust performance against noise and distortions in images. This method can effectively capture low-level features in HRRSI and significantly reduce computational complexity during subsequent feature fusion and classification processes. For additional details on the Lie group feature covariance matrix, please refer to [35].
3.3. Deep Learning Branch
In the RSSC task, HRRSI has rich texture and multi-scale target features, which place higher demands on the model’s feature extraction capability. However, traditional deep neural networks often result in a sharp increase in computational complexity while improving classification performance, leading to reduced inference efficiency and making it difficult to meet the demands of large-scale remote sensing data processing [57,58].
To address the challenges mentioned above, we designed an innovative deep learning branch (Figure 2). In this study, ResNet50 [30] serves as the backbone network of our deep learning branch. While maintaining high accuracy and significantly reducing computational complexity, we implemented key optimizations to the ResNet50 architecture: (1) a lightweight network structure that preserves only the initial convolution layer, max-pooling layer, and first three residual blocks, substantially reducing parameters while retaining essential feature extraction capabilities; (2) transfer learning with pre-trained weights to efficiently capture high-level semantic features in remote sensing images.
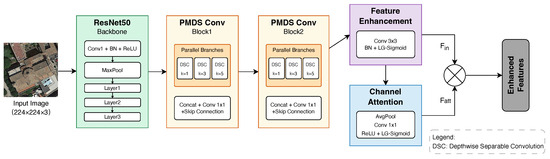
Figure 2.
Architecture of our deep learning branch.
Based on this optimized architecture, we innovatively introduced depthwise separable convolution to replace standard convolutions, reducing computation by 8–9 times while preserving feature representation ability [59]. More importantly, we designed a novel parallel multi-scale depthwise separable convolution module (PMDS Conv, Figure 3) that processes three different dimensional convolution operations in parallel and decomposes standard convolution into a combination of depthwise convolution and pointwise convolution (), effectively expanding the feature extraction range while reducing computational overhead.
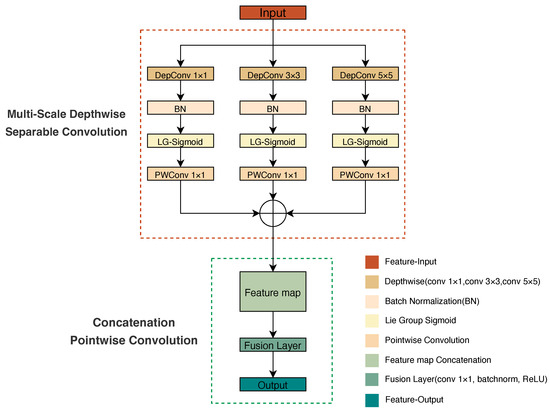
Figure 3.
Detailed architecture of the proposed parallel multi-scale depthwise separable convolution module (PMDS Conv) showing both the multi-scale feature extraction branches and the feature fusion process.
Specifically, PMDS Conv consists of three parallel branches, employing , , and convolutions respectively to extract multi-scale features. Among them, the convolution quickly integrates channel information; the convolution is used for extracting local features; while the convolution expands the receptive field to capture larger-scale spatial contextual information. This parallel structural design enables the model to simultaneously process features at different scales, making it suitable for extracting complex and diverse ground object features in HRRSI.
After the convolution operations in each branch, we introduce the Lie group Sigmoid (LG-Sigmoid) activation function [1]:
where represents the matrix trace calculation, c denotes a constant (), and is the Hermitian transpose matrix of y. This activation function is based on Lie group manifold space, providing a smooth normalization and probabilistic mapping of processed matrix samples, thus facilitating the model to obtain a more balanced, continuous, and interpretable feature distribution in subsequent feature decision processes [60,61]. Subsequently, we fuse features of different scales obtained from the three channels to capture multi-scale receptive field information. Direct concatenation would significantly increase the number of channels and reduce computational efficiency. Therefore, we employ pointwise convolution for feature refinement, combined with Batch Normalization (BN) [62] and the ReLU activation function [63] to stabilize feature distributions and enhance the model’s nonlinear representation capability.
Despite PMDS Conv’s effective capture of multi-scale features in remote sensing images, our experimental analysis revealed room for improvement in distinguishing complex scenes. To address this limitation, we developed two complementary innovative modules that further enhance model performance.
The Feature Enhancement Module was designed based on the complex relationship between targets and backgrounds in remote sensing images. This module employs a standard convolution combined with the BN and LG-Sigmoid activation function to highlight key target characteristics while effectively suppressing background interference. After comparative experimentation, we selected the convolution kernel as the optimal solution, achieving an ideal balance between effective local receptive field coverage and computational efficiency.
Remote sensing images typically exhibit distinctive channel-wise feature distributions in different categories. Based on this observation, we developed a lightweight Channel Attention Mechanism (CAM) that adaptively adjusts the importance of different channels. Unlike traditional SENet [39], which requires a complete Multilayer Perceptron for feature transformation, our approach efficiently employs a single convolution, significantly reducing computational load while maintaining robust feature modeling capability. The mechanism initially performs Global Average Pooling (GAP) on input features to obtain global channel response, then processes it through ReLU and LG-Sigmoid activation functions, enabling the network to focus precisely on the most discriminative feature channels for classification tasks. The channel attention calculation process is expressed as
where represents the calculated channel attention weights, denotes the input features, and are the two convolution kernels in the attention mechanism, and represents the LG-Sigmoid activation function. Finally, these attention weights are used to recalibrate the input features to enhance important information:
To further enhance the representational capacity of the model and accelerate training convergence, we also introduce residual connections in the deep learning branch. By adding skip connections, the residual structure effectively addresses the degradation problem in deep networks and promotes the learning of deep features, thereby improving the stability of training [30]. Additionally, for the feature maps obtained from the LGML branch and the deep learning branch after processing, we adopt the feature-level fusion method proposed by Xu et al. [2,33], fusing the two branch-derived feature maps to obtain a processed fusion feature map , thereby enabling the feature map to have better representational capacity and lower dimensionality for subsequent processing.
3.4. MD-CAM
Traditional self-attention mechanisms generate attention weights by calculating dot products between input features. Despite remarkable success in various vision tasks, these approaches still face challenges of computational overhead and insufficient information fusion when processing multi-dimensional features or high-resolution images [64].
To overcome these limitations, we propose an innovative multi-dimensional cross-attention mechanism (MD-CAM) as shown in Figure 4. This mechanism enhances RSSC performance through two key innovations: first, employing a local block self-attention strategy instead of traditional global dot-product attention schemes, calculating interrelationships between features within local regions; second, implementing multi-dimensional interaction among low-level features, high-level features, and fused features, addressing the insufficient fusion of different-level features in existing methods.
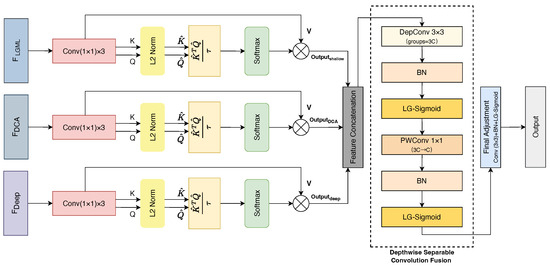
Figure 4.
Architecture of the proposed multi-dimensional cross-attention mechanism (MD-CAM) with feature fusion strategy. The diagram shows (a) parallel cross-attention processing for three feature types (, , and ), (b) attention computation with query–key interactions and L2 normalization, and (c) feature fusion through the depthwise separable convolution pathway.
In our model design, we simultaneously input the feature map obtained from feature-level fusion, as well as the feature maps and from the LGML branch and deep learning branch, respectively, into the MD-CAM for processing. For each feature map, we generate separate Query (Q), Key (K), and Value (V) matrices through three independent convolution operations. Unlike traditional attention mechanisms, our design ensures that matrices generated from each feature layer effectively capture information at various levels without mutual interference, while reducing feature dimensionality and lowering the complexity of subsequent computations [65,66]:
where , , and are independent convolution kernels that serve as learnable projection matrices in our multi-dimensional attention framework.
Subsequently, within each feature layer, the key matrix K and query matrix Q generate the attention weight matrix through dot product operations. To ensure numerical stability and accelerate model convergence, we perform L2 normalization [67] on K and Q before calculating the attention weights. Specifically, we normalize K and Q along the dimension of the channels, making the norm of each channel vector equal to 1, thereby constraining the dot product results within the range of [−1, 1]. The normalization method is expressed as
The normalized and calculate similarity through the dot product, thereby generating the attention weight matrix
where is a learnable parameter that determines the sharpness of the attention weight distribution. When is smaller, the attention weights tend toward a sharper distribution, focusing on fewer important features; when is larger, the attention distribution becomes more uniform, attending to more feature channels. We initialize to 1 and allow it to adjust during the training process adaptively.
Using the attention weight matrix calculated in the previous step, we perform weighted summation with the value matrix V, allowing the model to generate the final fused feature representation:
This weighted summation operation implements efficient information fusion through the attention mechanism performed along the channel dimension. It enables the model to focus more on key relationships between features, reduces computational complexity, and significantly enhances the feature dependency modeling capability.
3.5. Feature Fusion Strategy
After obtaining the cross-attention enhanced representations from each feature stream, this study proposes a hierarchical feature fusion strategy to maximally preserve complementary information from multiple sources while enhancing the model’s ability to comprehend multi-scale features. Unlike the simple additive fusion methods widely adopted in existing research, we first employ feature concatenation as the initial fusion step:
where B represents the batch size, C represents the number of channels in a single feature stream, and H and W represent the height and width of the feature map, respectively. This concatenation operation preserves the complete information from all three feature streams but simultaneously introduces issues of redundancy and increased channel dimensionality. To address this issue, we design an efficient feature fusion module composed of depthwise separable convolution and standard convolution:
where represents the depthwise separable convolution operation, specifically implemented as
Inspired by MobileNet V2 [68], we choose a depthwise separable convolution. Here, represents depthwise convolution using a kernel, PWConv represents pointwise convolution used to reduce channel dimensionality from to C, represents the LG-Sigmoid activation function, and BN represents the batch normalization operation.
To further ensure feature space consistency and enhance contextual modeling capability, we apply the final convolution operation :
The innovation of this hierarchical feature fusion strategy is mainly reflected in three aspects: (1) the connection operation preserves the integrity of the original information in different feature streams, avoiding information loss that may result from simple addition fusion; (2) depthwise separable convolutions reduce computational complexity while providing a wide receptive field by separating convolution operations across channels and spatial dimensions; and (3) the standard convolution, as the final fusion layer, strengthens the spatial consistency and contextual correlation of features, enabling the model to more accurately capture complex spatial relationships of ground objects in remote sensing images.
After obtaining the fused features, we adopt a simple and efficient classification strategy by compressing the feature map into a fixed-dimensional feature vector through GAP, followed by applying a single-layer linear mapping to project the feature vector into the classification space:
The model finally applies the Softmax function to generate class probability distributions. This classification architecture not only reduces the parameter count and lowers the risk of overfitting but also simplifies the computational process while enhancing the model’s generalization capability.
Table 2 compares computational complexity across different attention mechanisms. Traditional self-attention mechanisms have a time complexity of in HRRSI [69] (where N represents the number of tokens in the image). In contrast, the MD-CAM proposed in this study successfully reduces the overall complexity to (where d represents the number of feature channels after dimensionality reduction) by constraining global attention calculations within fixed-size local blocks. This design significantly reduces the computational overhead and preserves the independent semantic expression capability of different feature layers, enhancing cross-layer feature fusion effects while effectively avoiding the information interference between feature layers. Experimental results demonstrate that MD-CAM exhibits significant advantages in multi-feature layer fusion and dynamic attention to key regions, while notably reducing the overall computational complexity.

Table 2.
Comparison of computational complexity and cross-layer fusion capability among different attention mechanisms.
3.6. Experimental Setup
To evaluate the proposed LGNet model for RSSC tasks, we design a comprehensive experimental framework. In this section, we introduce three representative public datasets with varying complexities and scales, followed by implementation details and parameter settings.
3.6.1. Experimental Datasets
In this study, we select three representative publicly available RSSC datasets: AID [48], UC Merced [70], and NWPU-RESISC45 [71]. The relevant information of the three datasets is shown in Table 3. By conducting experiments on the datasets in Table 3, we compare the proposed model with several classical and state-of-the-art models to evaluate its performance under different scene complexities, resolution differences, and category numbers.

Table 3.
Comparison of NWPU-RESISC45, AID and UC Merced datasets.
3.6.2. Experimental Setup
Based on previous research and experimental foundations [1,2,19], this study adopts the experimental parameters shown in Table 4. We use overall accuracy (OA) and confusion matrices (CMs) to evaluate the model’s performance. For the AID, UC Merced, and NWPU-RESISC45 datasets, we set up different training ratios: 20% and 50% for AID, 50% and 80% for UC Merced, and 10% and 20% for NWPU-RESISC45.

Table 4.
Experimental environment and training parameters.
To ensure the reliability and stability of experimental results, we implement a rigorous validation strategy. We employ stratified random sampling for all three datasets to divide each dataset into training and testing sets according to the specified ratios while maintaining balanced class distributions. To comprehensively evaluate model performance and minimize the impact of random variations, we conduct ten independent experiments for each dataset at each training ratio. In each experiment, we perform a new random data split while keeping the same hyperparameter settings, only changing the random seeds to ensure consistency and comparability across experiments.
4. Results and Analysis
This section presents comprehensive experimental results and in-depth analysis to evaluate the effectiveness and computational efficiency of our proposed LGNet model for RSSC tasks. Based on the experimental setup detailed in Section 3.6, we conduct systematic comparative experiments on three standard datasets with varying complexities and scales. Our analysis encompasses classification accuracy comparisons with both classical models and state-of-the-art methods, visualization analysis of feature representations and attention mechanisms, computational efficiency evaluation regarding parameter count and inference speed, and ablation studies validating the contributions of key components such as the LGML branch and MD-CAM. These experimental results comprehensively demonstrate the superiority of our approach in integrating low-level features with high-level features, while showcasing LGNet’s capability to achieve high classification accuracy while maintaining a lightweight structure.
4.1. Experimental Results on AID
To verify the effectiveness of the proposed model, we conduct a systematic performance comparison with current mainstream models. Table 5 shows the performance of various models on the AID dataset with training ratios of 20% and 50%.

Table 5.
OA (%) and parameters (M) on AID dataset with 20% and 50% training ratios.
Experimental results indicate that our model achieves superior classification accuracy with identical environmental settings compared to some classic models and current state-of-the-art models. Specifically, compared to lightweight CNN models such as MobileNet [72], EfficientNet [47], and GoogLeNet [48], our model achieves an accuracy of 95.06% with only 20% of the training data, significantly surpassing MobileNet [72] (87.91%), EfficientNet [47] (87.37%), and GoogLeNet [48] (83.27%). This result indicates that although lightweight CNN structures have higher computational efficiency, their ability to extract features from complex remote sensing images is limited, especially in adequately capturing the associations between low-level and high-level features, resulting in restricted classification performance.
While more advanced deep learning models in the table, such as MDRCN [49], HFAM [46], and DCNNet [50], exhibit relatively high classification performance with 20% training data, they primarily focus on optimizing high-level features while lacking the effective utilization of low-level features. In contrast, our approach achieves the joint optimization of low-level and high-level features through a cross-attention mechanism, reaching 95.06% with 20% training data, outperforming all comparative models. With 50% training data, our model still outperforms MDRCN [49] (95.66%) and DCNNet [50] (96.23%), indicating that the feature fusion strategy plays a crucial role in improving classification performance.
Figure 5 presents the CM for our proposed model on the AID dataset with 50% training data, further demonstrating the robust classification capabilities across various scene categories.
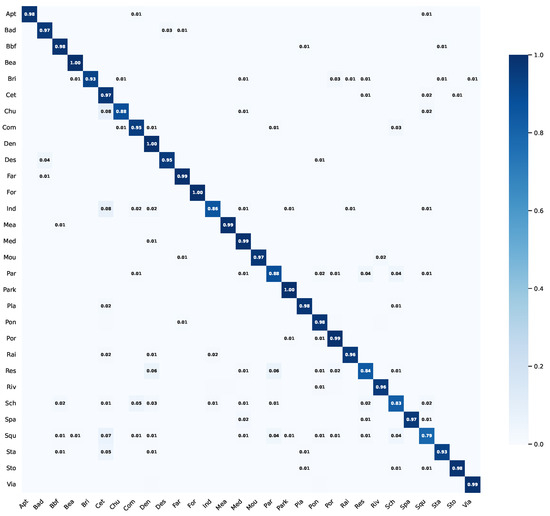
Figure 5.
CM of the proposed model on the AID dataset with 50% training data.
4.2. Experimental Results on UC Merced
To further validate the performance of our proposed model, we conduct extensive experiments on the UC Merced dataset, with the results presented in Table 6. The UC Merced dataset features a balanced distribution of class samples, making it suitable for the comprehensive evaluation of model generalization ability and classification accuracy. Analysis of the experimental results is as follows.
In comparison with traditional models, GoogLeNet [48] (92.70%), CaffeNet [48] (93.98%), and VGG16 [46] (94.14%) primarily rely on CNNs for high-level feature extraction, but these models neglect shallow texture and local structural information in HRRSI, resulting in limited classification accuracy. In contrast, our model achieves 98.79% accuracy with 50% training data, outperforming these methods that rely solely on CNN-based high-level feature extraction. Methods such as T2T-ViT-12 [76] (95.68%) and RS-DBNet [77] (97.90%) incorporate Transformer architectures and deep belief networks (DBNs), which enhance classification capability to some extent. However, these approaches primarily depend on large-scale high-level extraction while still insufficiently utilizing low-level features, particularly when processing scenes with subtle class differences, which can impact their classification effectiveness. Our model thoroughly integrates low-level and high-level features during the feature fusion stage, further improving classification accuracy. With 80% training data, our model achieves 99.76%, surpassing all comparison models.
Furthermore, regarding the more advanced deep learning methods shown in the table, such as PSCL1-TF [78], MDRCN [49], and LDBST [79], although these models demonstrate relatively high classification performance under the 80% training data ratio, their primary improvements focus on optimizing deep features, while their capture of superficial information remains limited. In comparison, our approach extracts low-level features through the Lie group feature covariance matrix and combines them with MD-CAM for cross-layer feature fusion, enabling the model to not only precisely capture local detail information in remote sensing images but also fully leverage the representational capacity of high-level semantic features, resulting in superior performance across various classification tasks.
The CM results further verify our model’s superiority. As shown in Figure 6, our proposed model achieves near-perfect classification effects across almost all categories. The deep blue regions along the diagonal of the confusion matrix indicate that the model’s recognition accuracy for most categories approaches 100%, outperforming existing methods. The experimental results fully demonstrate the effectiveness of our proposed low-level and high-level feature fusion strategy and showcase the model’s outstanding performance in RSSC tasks.
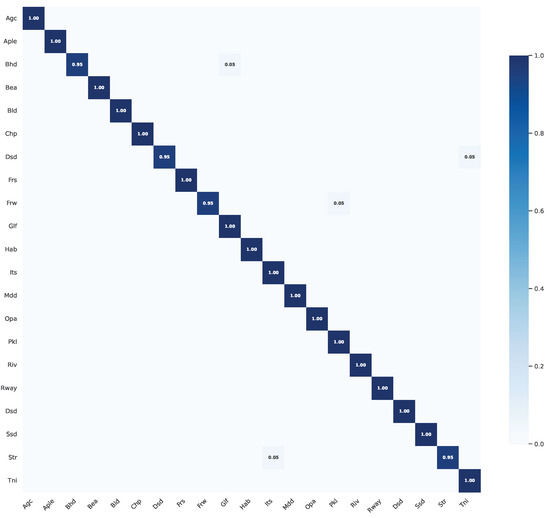
Figure 6.
CM of the proposed model on the UC Merced dataset with 50% training data.

Table 6.
OA (%) and parameters (M) on UC Merced dataset with 50% and 80% training ratios.
Table 6.
OA (%) and parameters (M) on UC Merced dataset with 50% and 80% training ratios.
| Models | Training Ratios | Parameters (M) | |
|---|---|---|---|
| 50% | 80% | ||
| GoogLeNet [48] | 92.70 ± 0.60 | 94.31 ± 0.89 | 7.00 |
| CaffeNet [48] | 93.98 ± 0.67 | 95.02 ± 0.81 | 60.97 |
| VGG16 [46] | 94.14 ± 0.69 | 95.21 ± 1.20 | 138.36 |
| TAKD [74] | 95.41 ± 0.18 | 97.33 ± 0.22 | – |
| T2T-VIT-12 [76] | 95.68 ± 0.61 | 97.81 ± 0.49 | 6.9 |
| DCLSSF+DCA [80] | 96.81 ± 0.21 | 99.10 ± 0.27 | – |
| GLR-CNN [75] | 97.52 ± 0.33 | 99.14 ± 0.26 | – |
| RS-DBNet [77] | 97.90 ± 0.15 | 99.21 ± 0.14 | – |
| LSMNet [81] | 97.71 ± 0.14 | 99.29 ± 0.15 | 2.15 |
| LG-Sigmoid [32] | 98.32 ± 0.13 | 98.92 ± 0.35 | – |
| LDBST [79] | 98.76 ± 0.29 | 99.52 ± 0.24 | 9.3 |
| PSCL1-TF [78] | 98.70 ± 0.17 | 99.62 ± 0.19 | 23.8 |
| MDRCN [49] | 98.57 ± 0.19 | 99.64 ± 0.12 | – |
| Proposed | 98.79 ± 0.15 | 99.76 ± 0.12 | 4.71 |
4.3. Experimental Results on NWPU-RESISC45
The NWPU-RESISC45 dataset contains a variety of scene categories, encompassing more complex and diverse remote sensing images, which poses higher demands on the classification capability of the model. As shown in Table 7, the experimental results demonstrate that our proposed model exhibits outstanding classification performance across different training data ratios, with significant advantages over existing methods in terms of generalization capability and robustness.
When compared with deep learning models incorporating attention mechanisms such as VGG16+CBAM [46] and ResNet50+CBAM [46], these approaches optimize the representational capacity of high-level features through channel and spatial attention, enabling the model to focus more on important regions in images. However, since CBAM primarily operates on high-level features without effectively integrating shallow information at the feature extraction stage, its classification performance remains limited. Experimental results show that under the 10% training data condition, ResNet50+CBAM [46] achieves an accuracy of 88.11%, while our method reaches 91.74%, fully validating the importance of low-level and high-level feature fusion in RSSC tasks. Under the 20% training data condition, our method further improves to 93.87%, still outperforming ResNet50+CBAM [46] and VGG16+CBAM [46]. These results indicate that single-dimensional attention mechanisms have limited feature modeling capability in complex scenarios, whereas the MD-CAM establishes deeper interactions between different scales and feature layers, enabling full integration of shallow detail information and high-level semantic features, thereby effectively enhancing classification performance.
Compared to recently proposed advanced deep learning methods such as MDRCN [49], SAF-Net [82], and SAGN [83], these models have further optimized feature extraction and fusion processes in their structural design, improving classification accuracy to some extent. However, these methods primarily rely on complex deep learning structures for feature modeling without effectively integrating low-level features, which can lead to insufficient feature learning when training data are limited. Experimental results show that under the 10% training data condition, MDRCN [49], SAF-Net [82], and SAGN [83] achieve classification accuracies of 91.59%, 90.94%, and 91.73%, respectively, showing improvement compared to ResNet50+CBAM [46] but still lower than our proposed method. The LG-Sigmoid [32] model also considers the extraction and utilization of low-level features in RSSC, but its feature fusion approach is relatively simplistic, lacking the deep modeling of multi-scale information. In contrast, our MD-CAM enables efficient feature interaction across channel, spatial, and layer dimensions, allowing low-level features and high-level semantic features to integrate, thereby improving classification accuracy fully. Additionally, using ResNet50 as the backbone network provides a stronger generalization ability and deep feature extraction capability compared to the simpler convolutional structure used by LG-Sigmoid [32], further enhancing the model’s performance in complex scenarios.
Figure 7 shows the confusion matrix at a 20% training ratio on the NWPU-RESISC45 dataset. Compared to the previous datasets, the NWPU-RESISC45 dataset presents even greater challenges as evidenced by the model’s generally lower classification accuracy across scene categories. Further analysis of the easily confused scenes reveals that some categories exhibit strong visual similarities. For instance, Church and Palace scenes may contain architectural elements such as towers, domes, or stone decorative features, making it difficult for the model to distinguish between them during feature extraction. The high degree of visual feature overlap between these categories leads the model to occasionally classify them as the same category during the learning process, resulting in a certain level of classification confusion. This phenomenon demonstrates that in HRRSI classification tasks, relying solely on high-level features has inherent limitations, while multi-scale, multi-level feature fusion is crucial for improving classification accuracy and enhancing generalization capability.

Figure 7.
CM of the proposed model on the NWPU-RESISC45 dataset with 20% training data.

Table 7.
OA (%) and parameters (M) on the NWPU-RESISC45 dataset with 10% and 20% training ratios.
Table 7.
OA (%) and parameters (M) on the NWPU-RESISC45 dataset with 10% and 20% training ratios.
| Models | Training Ratios | Parameters (M) | |
|---|---|---|---|
| 10% | 20% | ||
| GoogLeNet [48] | 76.19 ± 0.38 | 78.48 ± 0.26 | 7.00 |
| ResNet50 [46] | 87.43 ± 0.29 | 88.93 ± 0.12 | 25.61 |
| VGG16 [46] | 86.44 ± 0.41 | 88.57 ± 0.16 | 138.36 |
| VGG16+CBAM [46] | 86.84 ± 0.24 | 89.32 ± 0.15 | 135.13 |
| ResNet50+CBAM [46] | 88.11 ± 0.39 | 90.27 ± 0.15 | 26.29 |
| TAKD [74] | 87.96 ± 0.22 | 91.96 ± 0.24 | – |
| GLR-CNN [75] | 89.35 ± 0.25 | 92.11 ± 0.22 | – |
| DCLSSF+DCA [80] | 88.10 ± 0.35 | 93.10 ± 0.54 | – |
| LSMNet [81] | 90.80 ± 0.15 | 93.16 ± 0.13 | 2.15 |
| LG-Sigmoid [32] | 90.19 ± 0.11 | 93.21 ± 0.12 | – |
| SAGN [83] | 91.73 ± 0.18 | 93.49 ± 0.10 | – |
| SAF-Net [82] | 90.94 ± 0.08 | 93.62 ± 0.10 | 23.75 |
| MDRCN [49] | 91.59 ± 0.29 | 93.82 ± 0.17 | – |
| Proposed | 91.74 ± 0.14 | 93.87 ± 0.16 | 4.71 |
4.4. Feature Visualization Analysis
To deeply explore how the model captures and processes different levels of features in the remote sensing scene, we visualize and analyze the feature activation maps in the model.
As shown in Figure 8, we show the feature activation maps of a BaseballField selected from the AID dataset. The low-level feature activation map (top left) mainly captures the edge, texture, and local structure information of the scene, especially the round-like contour of the BaseballField and the square structure of the center region, which exemplifies the effectiveness of the Lie group feature covariance matrix that we adopt in extracting low-level features. In contrast, the high-level feature activation map (top right) presents a more abstract semantic representation, reflecting the advantages of CNNs in extracting high-level semantic features. Through the action of MD-CAM, the fused feature activation map (bottom left) exhibits a balanced response to the entire scene, while retaining the highlighted areas of key structural information. This balanced distribution indicates that the model can effectively integrate low-level and high-level features of the image. When the fused features are superimposed on the original image (bottom right), we can clearly observe the model’s strong response to the BaseballField’s key structures while maintaining a semantic understanding of the overall scene. This effective fusion of multi-level features provides the model with a more comprehensive representation of the scene, allowing it to focus on both local details and global semantics, thus achieving higher accuracy in classification tasks.
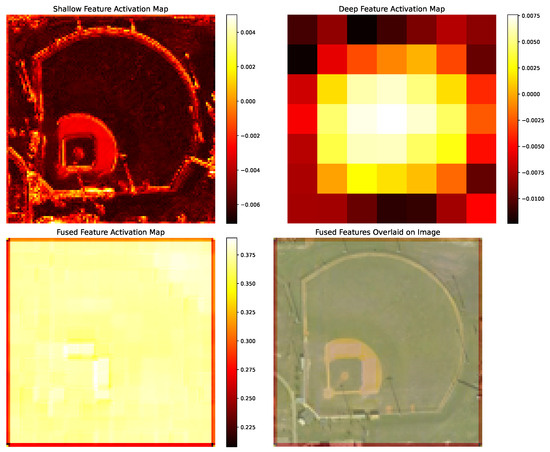
Figure 8.
Feature activation maps of a BaseballField from the AID dataset. Top left: low-level feature activation map highlighting edges and local structures. Top right: high-level feature activation map showing semantic representation. Bottom left: fused feature activation map with balanced distribution. Bottom right: fused features overlaid on the original image.
4.5. Comparison of Model Parameters and Computational Efficiency
To more directly demonstrate the lightweight design of our proposed model, we select a series of representative models for detailed comparison. We compare the classification accuracy, model parameters, inference speed, and total test time of various models. The experimental results are presented in Table 8. Compared to traditional deep networks, our method employs depthwise separable convolution and Lie group feature covariance matrix, effectively reducing feature dimensionality and parameter count while maintaining strong feature representation capability. Experimental results show that our method uses only 4.71 M parameters, and even with this significant reduction in computational requirements, it still achieves an accuracy of 96.50% on the AID dataset with a 50% training ratio, surpassing methods such as ResNet50 [46] (95.51%, 25.58 M), ResNet50+SE [46] (95.84%, 26.28 M), and ResNet50+CBAM [46] (95.38%, 26.29 M), demonstrating the model’s high feature extraction capability and the effectiveness of the optimization strategy.

Table 8.
Comparison of accuracy, parameters, inference speed, and running time on AID dataset with 50% training ratio.
Furthermore, compared to high-complexity models such as VGG-VD-16 [48] (138.36 M), SPG-GAN [84] (87.36 M), and TSAN [85] (381.67 M), our method achieves a significant reduction in parameters while maintaining high classification accuracy, indicating that the rational compression of feature dimensionality not only reduces computational cost but also improves the generalization capacity of the model. In terms of inference speed and test time, our method reaches 45.00 samples/s. It processes the entire test set in 111.11 s, significantly faster than ResNet50 and its derivative models (131.58 s) and substantially more efficient than high-complexity models like SPG-GAN (172.41 s). Compared to lightweight models such as MobileNetV3-Small [86] and GhostNet [87], although our LGNet shows a slight increase in parameter count and test time, it achieves considerably higher classification accuracy, striking a favorable balance between accuracy and computational efficiency. The above experimental results quantitatively verify that LGNet maintains the advantages of lightweight design while achieving superior scene classification performance, providing a practical solution for HRRSI classification tasks that maintains high accuracy even in resource-constrained environments.
4.6. Ablation Experiments
To verify the impact of each module in the model on the overall classification accuracy, we design a series of ablation experiments using the AID (50%) dataset. The experimental details and results are as follows.
4.6.1. Evaluation of LGML Branch
To verify the contribution of low-level features to model classification accuracy, we design ablation experiments for the low-level feature extraction module. As shown in Table 9, the results indicate that incorporating low-level features significantly improves classification performance. Compared to traditional deep learning models that only focus on high-level semantic features, our approach integrating LGML achieves a 3.46% improvement in classification accuracy. This result strongly confirms the importance of low-level features in RSSC.

Table 9.
Ablation study of LGML module on AID dataset.
Furthermore, we analyze the specific contributions of various low-level features to classification performance, with the results presented in Table 10. The average color feature (), Local Binary Patterns (LBPs), Histogram of Oriented Gradients (HOG), and Gabor features capture color distribution, texture patterns, edge contours, and multi-scale directional information, respectively. Shape features including area S, compactness , and aspect ratio are employed to distinguish the geometric characteristics of different geographical objects.

Table 10.
Feature ablation analysis: incremental impact of individual features on classification accuracy for AID dataset.
The ablation experiments demonstrate that HOG features contribute the most significant gain (+1.11%) when added first, highlighting the importance of edge and contour information in remote sensing scene classification. The experiments confirm that optimal performance (96.50%) is achieved when all low-level features work in conjunction, validating the effectiveness of the LGML module and indicating that the fusion of low-level features with high-level features represents a key pathway to improve the classification performance of remote sensing scenes.
4.6.2. Evaluation of Different Backbone Networks
To investigate the impact of different backbone networks on model performance and computational efficiency, we compare our original optimized ResNet50 with more lightweight architectures: MobileNetV3-Small and EfficientNet-B1. Table 11 presents a comprehensive comparison of the performance of LGNet when integrated with different backbone networks on the AID dataset with a 50% training ratio.

Table 11.
Ablation study of different backbone networks on AID dataset with a 50% training ratio.
As shown in Table 11, our optimized ResNet50 backbone achieves the highest classification accuracy (96.50%) among the three evaluated architectures, but this performance advantage comes at the cost of higher computational demands, requiring 4.71 M parameters and 14.31 GFLOPs of computational resources. In contrast, EfficientNet-B1 provides a more balanced solution, achieving a competitive accuracy of 95.21% while consuming only 3.80 M parameters and 11.28 GFLOPs. MobileNetV3-Small further reduces the resource requirements to 3.72 M parameters and 10.50 GFLOPs, though with a corresponding decrease in classification performance to 93.41%.
These results of the ablation study reveal the trade-off between resource efficiency and classification performance in the current LGNet design. Although the optimized ResNet50 offers advantages in classification accuracy, its relatively higher computational complexity can become a bottleneck in resource-constrained scenarios, indicating that our current backbone network selection still has room for improvement in terms of computational efficiency.
In future work, we plan to investigate more lightweight backbone alternatives for LGNet that can further reduce computational complexity while maintaining high classification performance. Future iterations of LGNet could benefit from exploring more advanced, efficient architectures or hybrid designs that better preserve high classification accuracy while approaching the efficiency of lightweight models such as EfficientNet.
4.6.3. Evaluation of MD-CAM
To validate the effectiveness of our proposed MD-CAM, we conduct a series of ablation experiments. Table 12 shows the comparison of different attention mechanisms and their performance.

Table 12.
Ablation study of different attention mechanisms on AID dataset.
As shown in the table, our proposed attention mechanism achieves a 96.50% accuracy, outperforming all other comparison methods. Compared to the baseline model without attention (93.04%), our method improves by 3.46 percentage points, a significant increase that fully validates the effectiveness of our designed attention mechanism.
In Figure 9, the redder areas indicate regions where the model pays more attention, while bluer areas receive less attention. As shown in the visualization, our method more accurately focuses on discriminative regions specific to each scene category. For example, in the Airport scene, our method concentrates more precisely on the runway and terminal structures; in the Bridge scene, it highlights the bridge structure and its connections more distinctly; and in the Center scene, it captures the unique circular architecture with greater precision. These results demonstrate that our attention mechanism can better identify key features that differentiate between scene categories.

Figure 9.
Visualization comparison of different attention mechanisms on the AID dataset using Grad-CAM.
To understand the internal mechanisms behind our model’s superior classification accuracy, we conduct an in-depth comparative analysis between our proposed attention mechanism and existing methods. Our MD-CAM has unique advantages in feature cross-construction. This mechanism optimizes the interaction between multilayer and multi-type features in complex remote sensing scenes, effectively capturing low-level features and high-level semantic features while modeling the key relationships between features across channel dimensions, significantly enhancing the model’s ability to recognize scene-related discriminative features. In contrast, although traditional self-attention mechanisms can also establish links between features, they lack the clear modeling of interactions between multilayer features, leading to weaker performance in complex scene understanding. Compared to CBAM, our method overcomes the optimization difficulties and computational redundancy caused by simultaneously processing spatial and channel attention. By focusing on key feature cross-interactions and integrating depthwise separable convolution’s lightweight design, our approach not only maintains powerful feature representation capabilities but also significantly reduces computational complexity, substantially improving accuracy and efficiency.
4.6.4. Feature Space Visualization Analysis
To validate the feature representation capabilities of our proposed model, we conduct t-SNE visualization analysis on different feature spaces using the AID dataset as illustrated in Figure 10. The low-level feature space (top left) shows considerable mixing between different categories. This confirms our understanding that while low-level features capture rich details, they lack the discriminative power needed for effective scene classification. The high-level feature space (top right) begins to show some category clustering, though the boundaries remain fuzzy with many overlapping regions between classes.
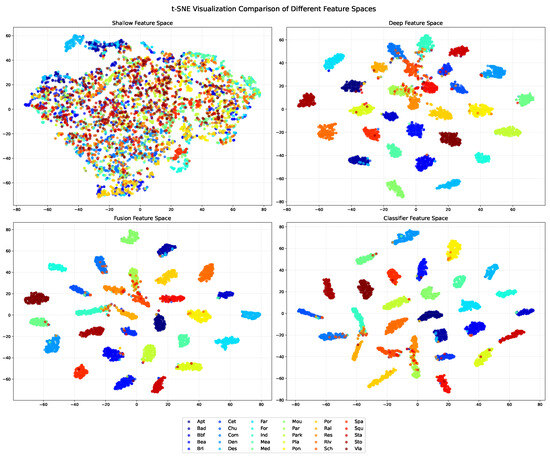
Figure 10.
The t-SNE visualization of different feature spaces on the AID dataset: low-level feature space (top left) showing high inter-class mixing, high-level feature space (top right) with preliminary clustering, fused feature space after feature-level fusion (bottom left) demonstrating enhanced discriminability, and feature space after applying MD-CAM (bottom right) exhibiting clear category boundaries and high intra-class consistency.
The feature fusion process implemented in our model significantly improves this situation as seen in the fused feature space visualization (bottom left), where samples form tighter, more distinct clusters with more apparent separation between categories. When our proposed MD-CAM is applied to these fused features as shown in the classifier feature space (bottom right), the improvement is even more pronounced, with well-defined category boundaries and strong intra-class consistency. This visual progression from mixed to well-organized feature distributions provides compelling evidence for the effectiveness of both our feature fusion approach and the attention mechanism. The results clearly show that our model successfully combines the detailed textural information from low-level features with the semantic understanding from high-level features, with the MD-CAM further enhancing the discriminative power of the fused representations, resulting in substantially improved scene classification capabilities.
5. Limitations and Future Work
Despite the superior performance of our proposed LGNet model on three standard datasets, several noteworthy limitations remain that warrant further exploration and improvement in future work.
5.1. Domain Knowledge Requirements
The construction of the LGML branch in our LGNet model relies heavily on domain expertise in remote sensing, particularly during low-level feature selection and the construction of Lie group feature covariance matrices. The optimal feature set utilized in this study was obtained through extensive preliminary experiments, which may present challenges for non-specialists attempting to understand and reproduce our approach. Furthermore, adapting feature extraction strategies for specific application scenarios requires users to possess relevant domain knowledge, potentially limiting broader adoption.
5.2. Computational Efficiency Optimization
Although our LGNet demonstrates significantly reduced parameter counts compared to traditional deep learning models, substantial room for optimization remains regarding computational efficiency. When processing large-scale HRRSI as shown in Table 8, the LGNet inference speed, while superior to several complex models, still lags behind ultra-lightweight networks such as MobileNetV3-Small. This limitation primarily stems from our pursuit of high classification accuracy, where the multi-dimensional cross-attention mechanism requires considerable computational resources during feature fusion, and the comprehensive processing of multi-dimensional features increases computational complexity. Additionally, despite our lightweight improvements to the ResNet backbone, its inherent deep structure continues to impose computational efficiency constraints. On severely resource-constrained edge devices, these computational demands may present significant challenges for our model.
5.3. Real-Time Performance Challenges
While our model achieves promising experimental results across three standard datasets, our late-stage real-time computation tests reveal opportunities for optimization in real-time processing capabilities. This is primarily because actual application environments, particularly when handling non-standard datasets, often require additional data preprocessing operations such as geometric correction and spectral analysis, which introduce extra computational parameters and processing time. Moreover, when applying the model to remote sensing imagery acquired under varying conditions, environmental factors (e.g., illumination variations and atmospheric conditions) may impact processing effectiveness, necessitating adaptive adjustments. Consequently, the LGNet performance in real-time computing scenarios has considerable potential for enhancement, especially in applications requiring rapid response, and these factors must be addressed in future work.
5.4. Future Work
Based on the aforementioned limitations, our future research will focus on addressing these challenges: regarding computational efficiency, we plan to optimize the implementation of the multi-dimensional cross-attention mechanism while investigating more lightweight backbone network alternatives to reduce computational complexity without compromising classification accuracy; to address real-time processing challenges, we aim to develop integrated end-to-end processing pipelines that incorporate preprocessing steps into the model architecture, thereby reducing processing latency.
6. Conclusions
This paper presents LGNet, a novel RSSC model based on the Lie group multi-dimensional cross-attention mechanism. The proposed approach effectively addresses the limitations of existing RSSC methods, including the insufficient utilization of low-level features, over-reliance on high-level semantic features, and high computational complexity. Through a dual-branch architecture that integrates Lie group feature covariance matrix with lightweight multi-dimensional depthwise separable convolutions, our model successfully achieves an effective combination of low-level and high-level features. The proposed MD-CAM further enhances classification performance by efficiently capturing dependencies between cross-level features. Experimental results on three authoritative remote sensing datasets demonstrate that our proposed method exhibits excellent classification accuracy while significantly reducing parameter counts. However, the model still has certain limitations in computational efficiency for real-time remote sensing data processing and resource-constrained environments. In future work, we will focus on optimizing MD-CAM, researching more efficient attention design schemes, and exploring the integration of LGML with lighter-weight models to enhance model performance further.
Author Contributions
Conceptualization, H.Z., C.Y. and S.Z.; methodology, H.Z. and S.Z.; software, S.Z.; validation, H.Z. and C.Y.; formal analysis, S.Z.; investigation, H.Z.; resources, H.Z. and C.Y.; data curation, S.Z. and C.X.; writing—original draft preparation, H.Z. and C.X.; writing—review and editing, H.Z. and C.Y.; visualization, S.Z.; supervision, S.Z.; project administration, S.Z.; funding acquisition, C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Natural Science Foundation of China, No. 42261068.
Data Availability Statement
The datasets used in this study are publicly accessible. The UC Merced land use dataset can be obtained from http://weegee.vision.ucmerced.edu/datasets/landuse.html (accessed on 12 December 2024). The NWPU-RESISC45 dataset is available at https://gcheng-nwpu.github.io/#Datasets (accessed on 12 December 2024). The Aerial Image Dataset (AID) can be accessed via https://captain-whu.github.io/AID/ (accessed on 13 December 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AID | Aerial Image Dataset |
| BN | Batch Normalization |
| BoVW | Bag-of-Visual-Words |
| CAM | Channel Attention Module |
| CBAM | Convolutional Block Attention Module |
| CH | Color Histogram |
| CM | Confusion Matrix |
| CNN | Convolutional Neural Network |
| DepConv | Depthwise Separable Convolutions |
| GAP | Global Average Pooling |
| HFAM | Harmonic Feature Attention Module |
| HRRSI | High-Resolution Remote Sensing Images |
| LBP | Local Binary Pattern |
| LGML | Lie Group Machine Learning |
| MD-CAM | Multi-Dimensional Cross-Attention Mechanism |
| MLP | Multilayer Perceptron |
| MSFE | Multi-Scale Feature Extraction |
| MSFF | Multi-Scale Feature Fusion |
| OA | Overall Accuracy |
| PMDS Conv | Parallel Multi-scale Depthwise Separable Convolution |
| PWConv | Pointwise Convolutions |
| RSSC | Remote Sensing Scene Classification |
| ReLU | Rectified Linear Unit |
| SA | Spatial Attention |
| SE | Squeeze and Excitation |
| SIFT | Scale-Invariant Feature Transform |
| SPM | Spatial Pyramid Matching |
References
- Xu, C.; Shu, J.; Zhu, G. Adversarial Remote Sensing Scene Classification Based on Lie Group Feature Learning. Remote Sens. 2023, 15, 914. [Google Scholar] [CrossRef]
- Xu, C.; Shu, J.; Zhu, G. Scene Classification Based on Heterogeneous Features of Multi-Source Data. Remote Sens. 2023, 15, 325. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Y.; Zhang, L.; Xu, Y. Blind Hyperspectral Unmixing Considering the Adjacency Effect. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6633–6649. [Google Scholar] [CrossRef]
- Zhao, B.; Zhong, Y.; Zhang, L. Hybrid Generative/Discriminative Scene Classification Strategy Based on Latent Dirichlet Allocation for High Spatial Resolution Remote Sensing Imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 196–199. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, X.; Sun, J.; Wang, L. Remote Sensing Scene Image Classification Based on Self-Compensating Convolution Neural Network. Remote Sens. 2022, 14, 545. [Google Scholar] [CrossRef]
- Xu, C.; Shu, J.; Wang, Z.; Wang, J. A Scene Classification Model Based on Global-Local Features and Attention in Lie Group Space. Remote Sens. 2024, 16, 2323. [Google Scholar] [CrossRef]
- dos Santos, J.A.; Penatti, O.A.B.; da, S.; Torres, R. Evaluating the Potential of Texture and Color Descriptors for Remote Sensing Image Retrieval and Classification. In Proceedings of the International Conference on Computer Vision Theory and Applications—Volume 2: VISAPP, (VISIGRAPP 2010), Angers, France, 17–21 May 2010; pp. 203–208. [Google Scholar] [CrossRef][Green Version]
- Swain, M.J.; Ballard, D.H. Indexing via Color Histograms. In Active Perception and Robot Vision; Springer: Berlin/Heidelberg, Germany, 1992; pp. 261–273. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Li, F.-F.; Perona, P. A Bayesian Hierarchical Model for Learning Natural Scene Categories. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 524–531. [Google Scholar] [CrossRef]
- Zhao, Y.; Wan, S.; Wu, Z.; Yin, B.; Yue, L. Multi-Scale and Multi-GMM Pooling Based on Fisher Kernel for Image Representation. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP 2016), Chengu, China, 20–22 May 2016; Falco, C.M., Jiang, X., Eds.; SPIE: Bellingham, WA, USA, 2016; p. 100334V. [Google Scholar] [CrossRef]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2169–2178. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Zhang, Y.; Chen, W. RS-DARTS: A Convolutional Neural Architecture Search for Remote Sensing Image Scene Classification. Remote Sens. 2021, 14, 141. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, X.; Wang, L. A Lightweight Convolutional Neural Network Based on Channel Multi-Group Fusion for Remote Sensing Scene Classification. Remote Sens. 2021, 14, 9. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A Model of Saliency-Based Visual Attention for Rapid Scene Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Wei, L.; Geng, C.; Yin, Y. Remote Sensing Image Scene Classification Based on Head-Tail Global Joint Dual Attention Discrimination Network. IEEE Access 2023, 11, 88305–88316. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, L.; Xu, H.; Wen, X. CSDS: End-to-end Aerial Scenes Classification with Depthwise Separable Convolution and an Attention Mechanism. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10484–10499. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A Combination of Lie Group Machine Learning and Deep Learning for Remote Sensing Scene Classification Using Multi-Layer Heterogeneous Feature Extraction and Fusion. Remote Sens. 2022, 14, 1445. [Google Scholar] [CrossRef]
- Chen, W.; Ouyang, S.; Tong, W.; Li, X.; Zheng, X.; Wang, L. GCSANet: A Global Context Spatial Attention Deep Learning Network for Remote Sensing Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1150–1162. [Google Scholar] [CrossRef]
- Sivic.; Zisserman. Video Google: A Text Retrieval Approach to Object Matching in Videos. In Proceedings of the Proceedings Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 2, pp. 1470–1477. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhong, Y.; Zhao, B.; Xia, G.S.; Zhang, L. Bag-of-Visual-Words Scene Classifier with Local and Global Features for High Spatial Resolution Remote Sensing Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 747–751. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Hofmann, T. Unsupervised Learning by Probabilistic Latent Semantic Analysis. Mach. Learn. 2001, 42, 177–196. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of Their Applications; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Xu, C.; Zhu, G.; Shu, J. Robust Joint Representation of Intrinsic Mean and Kernel Function of Lie Group for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 796–800. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A Lightweight Intrinsic Mean for Remote Sensing Classification with Lie Group Kernel Function. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1741–1745. [Google Scholar] [CrossRef]
- Liao, D.; Liu, G. Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution. Remote Sens. 2023, 15, 3758. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Region Covariance: A Fast Descriptor for Detection and Classification. In Computer Vision—ECCV 2006; Leonardis, A., Bischof, H., Pinz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3952, pp. 589–600. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Human Detection via Classification on Riemannian Manifolds. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Finzi, M.; Stanton, S.; Izmailov, P.; Wilson, A.G. Generalizing Convolutional Neural Networks for Equivariance to Lie Groups on Arbitrary Continuous Data. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; III, H.D., Singh, A., Eds.; PMLR, Proceedings of Machine Learning Research. JMLR, Inc.: Cambridge, MA, USA, 2020; Volume 119, pp. 3165–3176. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. arXiv 2018, arXiv:1807.06521. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2017, arXiv:1709.01507. [Google Scholar] [CrossRef]
- Wang, J.; Li, W.; Zhang, M.; Tao, R.; Chanussot, J. Remote-Sensing Scene Classification via Multistage Self-Guided Separation Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5615312. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Feng, Y.; Jiang, J.; Xu, H.; Zheng, J. Change Detection on Remote Sensing Images Using Dual-Branch Multilevel Intertemporal Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4401015. [Google Scholar] [CrossRef]
- Yang, Y.; Jiao, L.; Liu, F.; Liu, X.; Li, L.; Chen, P.; Yang, S. An Explainable Spatial–Frequency Multiscale Transformer for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5907515. [Google Scholar] [CrossRef]
- Cai, W.; Wei, Z. Remote Sensing Image Classification Based on a Cross-Attention Mechanism and Graph Convolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8002005. [Google Scholar] [CrossRef]
- Wan, Q.; Xiao, Z.; Yu, Y.; Liu, Z.; Wang, K.; Li, D. A Hyperparameter-Free Attention Module Based on Feature Map Mathematical Calculation for Remote-Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5600318. [Google Scholar] [CrossRef]
- Momeni Pour, A.; Seyedarabi, H.; Abbasi Jahromi, S.H.; Javadzadeh, A. Automatic Detection and Monitoring of Diabetic Retinopathy Using Efficient Convolutional Neural Networks and Contrast Limited Adaptive Histogram Equalization. IEEE Access Pract. Innov. Open Solut. 2020, 8, 136668–136673. [Google Scholar] [CrossRef]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A Benchmark Data Set for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Dai, W.; Shi, F.; Wang, X.; Xu, H.; Yuan, L.; Wen, X. A Multi-Scale Dense Residual Correlation Network for Remote Sensing Scene Classification. Sci. Rep. 2024, 14, 22197. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Cheng, P.; Xu, G.; Sun, X. DCNNet: A Distributed Convolutional Neural Network for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5603618. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A Lightweight and Robust Lie Group-Convolutional Neural Networks Joint Representation for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501415. [Google Scholar] [CrossRef]
- Wu, N.; Jiang, M. An Improved Shadow Compensation Algorithm Based on Lab Color Space. In Proceedings of the AOPC 2022: Advanced Laser Technology and Applications, Beijing, China, 18–20 December 2022; Bai, Z., Chen, Q., Tan, Y., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 37. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, L.; Zhang, D. A Completed Modeling of Local Binary Pattern Operator for Texture Classification. IEEE Trans. Image Process. 2010, 19, 1657–1663. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar] [CrossRef]
- Pang, Y.; Yuan, Y.; Li, X. Gabor-Based Region Covariance Matrices for Face Recognition. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 989–993. [Google Scholar] [CrossRef]
- Jiao, L.; Liu, Y. Analyzing The Shape Characteristics Of Land Use Classes In Remote Sensing Imagery. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-7, 135–140. [Google Scholar] [CrossRef]
- Cui, B.; Dong, X.M.; Zhan, Q.; Peng, J.; Sun, W. LiteDepthwiseNet: A Lightweight Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5502915. [Google Scholar] [CrossRef]
- Yu, D.; Xu, Q.; Guo, H.; Zhao, C.; Lin, Y.; Li, D. An Efficient and Lightweight Convolutional Neural Network for Remote Sensing Image Scene Classification. Sensors 2020, 20, 1999. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, Y.; Zheng, Z.; Ma, A.; Zhang, L. RSNet: The Search for Remote Sensing Deep Neural Networks in Recognition Tasks. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2520–2534. [Google Scholar] [CrossRef]
- Alhichri, H. RS-DeepSuperLearner: Fusion of CNN Ensemble for Remote Sensing Scene Classification. Ann. GIS 2023, 29, 121–142. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. Lie Group Spatial Attention Mechanism Model for Remote Sensing Scene Classification. Int. J. Remote Sens. 2022, 43, 2461–2474. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; Bach, F., Blei, D., Eds.; Proceedings of Machine Learning Research. JMLR, Inc.: Cambridge, MA, USA, 2015; Volume 37, pp. 448–456. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; Gordon, G., Dunson, D., Dudík, M., Eds.; Proceedings of Machine Learning Research. JMLR, Inc.: Cambridge, MA, USA, 2011; Volume 15, pp. 315–323. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Bello, I.; Zoph, B.; Vaswani, A.; Shlens, J.; Le, Q.V. Attention Augmented Convolutional Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Shen, Z.; Zhang, M.; Zhao, H.; Yi, S.; Li, H. Efficient Attention: Attention with Linear Complexities. arXiv 2018, arXiv:1812.01243. [Google Scholar] [CrossRef]
- Tarzanagh, D.A.; Li, Y.; Zhang, X.; Oymak, S. Max-Margin Token Selection in Attention Mechanism. arXiv 2023, arXiv:2306.13596. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv 2018, arXiv:1801.04381. [Google Scholar] [CrossRef]
- Duman Keles, F.; Wijewardena, P.M.; Hegde, C. On the Computational Complexity of Self-Attention. In Proceedings of the 34th International Conference on Algorithmic Learning Theory, Singapore, 20–23 February 2023; Agrawal, S., Orabona, F., Eds.; PMLR, Proceedings of Machine Learning Research. JMLR, Inc.: Cambridge, MA, USA, 2023; Volume 201, pp. 597–619. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Pan, H.; Pang, Z.; Wang, Y.; Wang, Y.; Chen, L. A New Image Recognition and Classification Method Combining Transfer Learning Algorithm and MobileNet Model for Welding Defects. IEEE Access Pract. Innov. Open Solut. 2020, 8, 119951–119960. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of High-Spatial-Resolution Remote Sensing Scenes Method Using Transfer Learning and Deep Convolutional Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Yue, J. TAKD: Target-Aware Knowledge Distillation for Remote Sensing Scene Classification. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 8188–8200. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Peng, J.; Zhang, L. GLR-CNN: CNN-Based Framework With Global Latent Relationship Embedding for High-Resolution Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5633913. [Google Scholar] [CrossRef]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.; Tay, F.E.; Feng, J.; Yan, S. Tokens-to-Token ViT: Training Vision Transformers from Scratch on ImageNet. arXiv 2021, arXiv:2101.11986. [Google Scholar] [CrossRef]
- Waqas Ahmed, M.; Alshahrani, A.; Almjally, A.; Al Mudawi, N.; Algarni, A.; Al Nowaiser, K.; Jalal, A.; Park, J. Remote Sensing Image Interpretation: Deep Belief Networks for Multi-Object Analysis. IEEE Access Pract. Innov. Open Solut. 2024, 12, 142360–142379. [Google Scholar] [CrossRef]
- Li, D.; Liu, R.; Tang, Y.; Liu, Y. PSCLI-TF: Position-sensitive Cross-Layer Interactive Transformer Model for Remote Sensing Image Scene Classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5001305. [Google Scholar] [CrossRef]
- Zheng, F.; Lin, S.; Zhou, W.; Huang, H. A Lightweight Dual-Branch Swin Transformer for Remote Sensing Scene Classification. Remote Sens. 2023, 15, 2865. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.; Yuan, B. A Deep Curriculum Learning Semi-Supervised Framework for Remote Sensing Scene Classification. Appl. Sci. 2025, 15, 360. [Google Scholar] [CrossRef]
- Zhang, K.; Cui, T.; Wu, W.; Zheng, X.; Cheng, G. Large Kernel Separable Mixed ConvNet for Remote Sensing Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4294–4303. [Google Scholar] [CrossRef]
- Song, W.; Zhang, Y.; Wang, C.; Jiang, Y.; Wu, Y.; Zhang, P. Remote Sensing Scene Classification Based on Semantic-Aware Fusion Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 2505805. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, X.; Cheung, Y.M.; Zhang, X.; Jiao, L. SAGN: Semantic-aware Graph Network for Remote Sensing Scene Classification. IEEE Trans. Image Process. 2023, 32, 1011–1025. [Google Scholar] [CrossRef] [PubMed]
- Ma, A.; Yu, N.; Zheng, Z.; Zhong, Y.; Zhang, L. A Supervised Progressive Growing Generative Adversarial Network for Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5618818. [Google Scholar] [CrossRef]
- Zheng, J.; Wu, W.; Yuan, S.; Zhao, Y.; Li, W.; Zhang, L.; Dong, R.; Fu, H. A Two-Stage Adaptation Network (TSAN) for Remote Sensing Scene Classification in Single-Source-Mixed-Multiple-Target Domain Adaptation (S2M2T DA) Scenarios. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5609213. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. GhostNet: More Features From Cheap Operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).