Revisiting the Contact Model with Diffusion Beyond the Conventional Methods
Abstract
1. Introduction
- When a healthy (susceptible) site has two infected nearest neighbors, the probability of infection is: ;
- If only one nearest neighbor is infected, the probability is halved: ;
- Regardless of the neighboring states, an infected site recovers with probability ;
- (a)
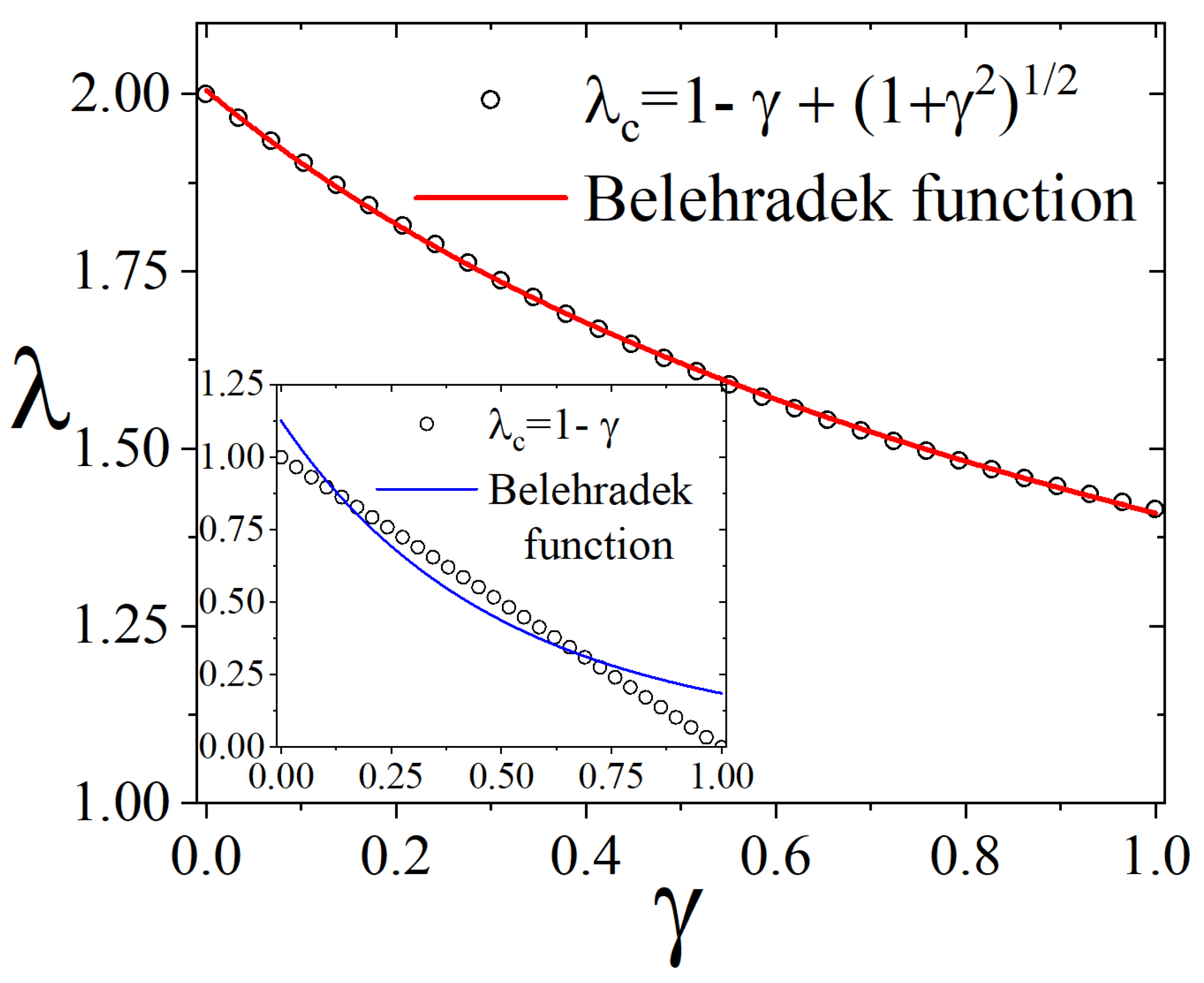
- Absorbing phase: For , , indicating that the system falls into an absorbing state where the entire population remains healthy and the dynamics cease;
- (b)
- Active phase: For , the system reaches an active phase characterized by .
2. Mean-Field Approximation and Pedagogical Arguments
3. Simulation and Methods
3.1. First Method: Optimization of Power Laws by the Coefficient of Determination
3.2. Second Method: Spectral Analysis of Correlation Matrices
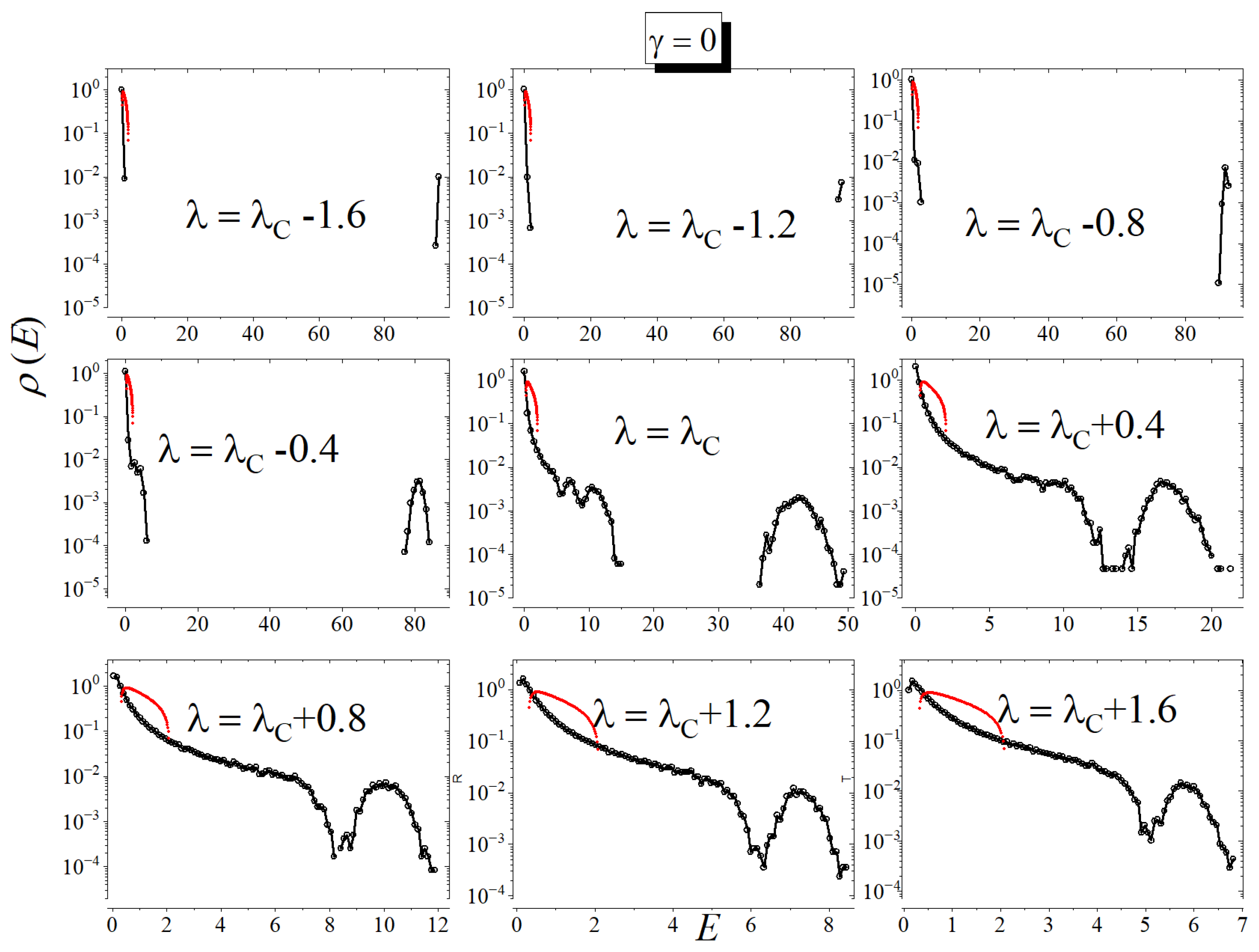
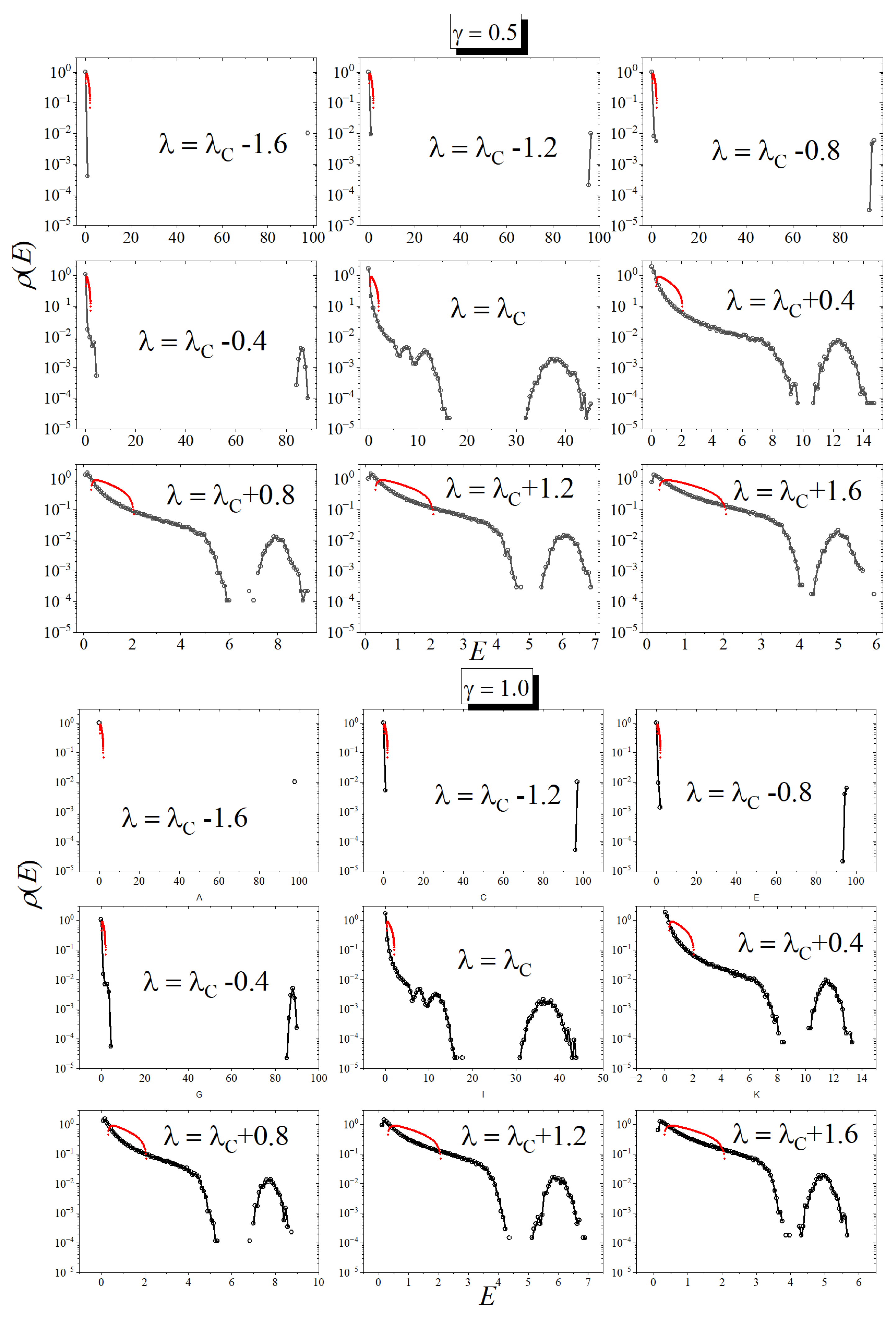
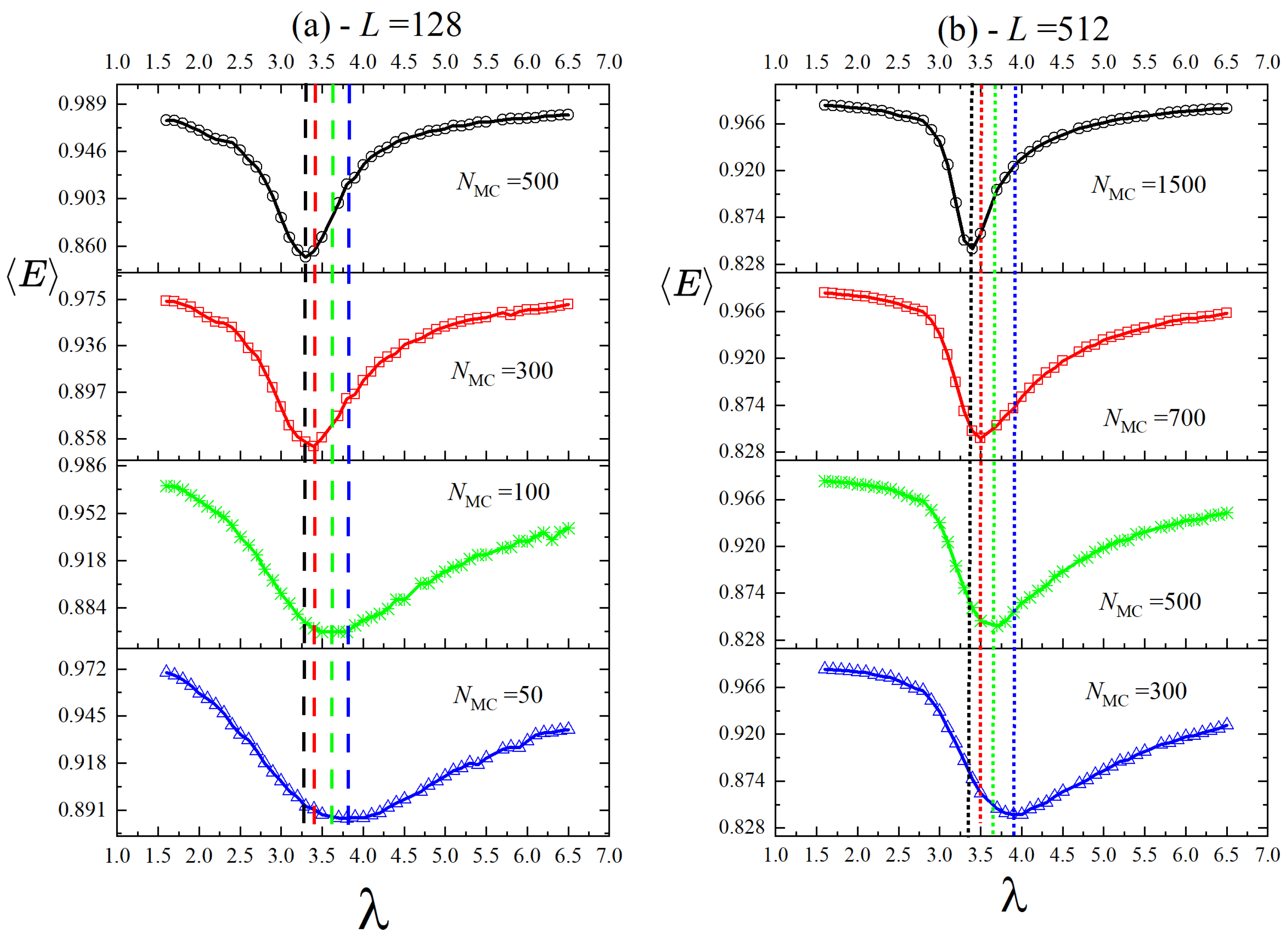
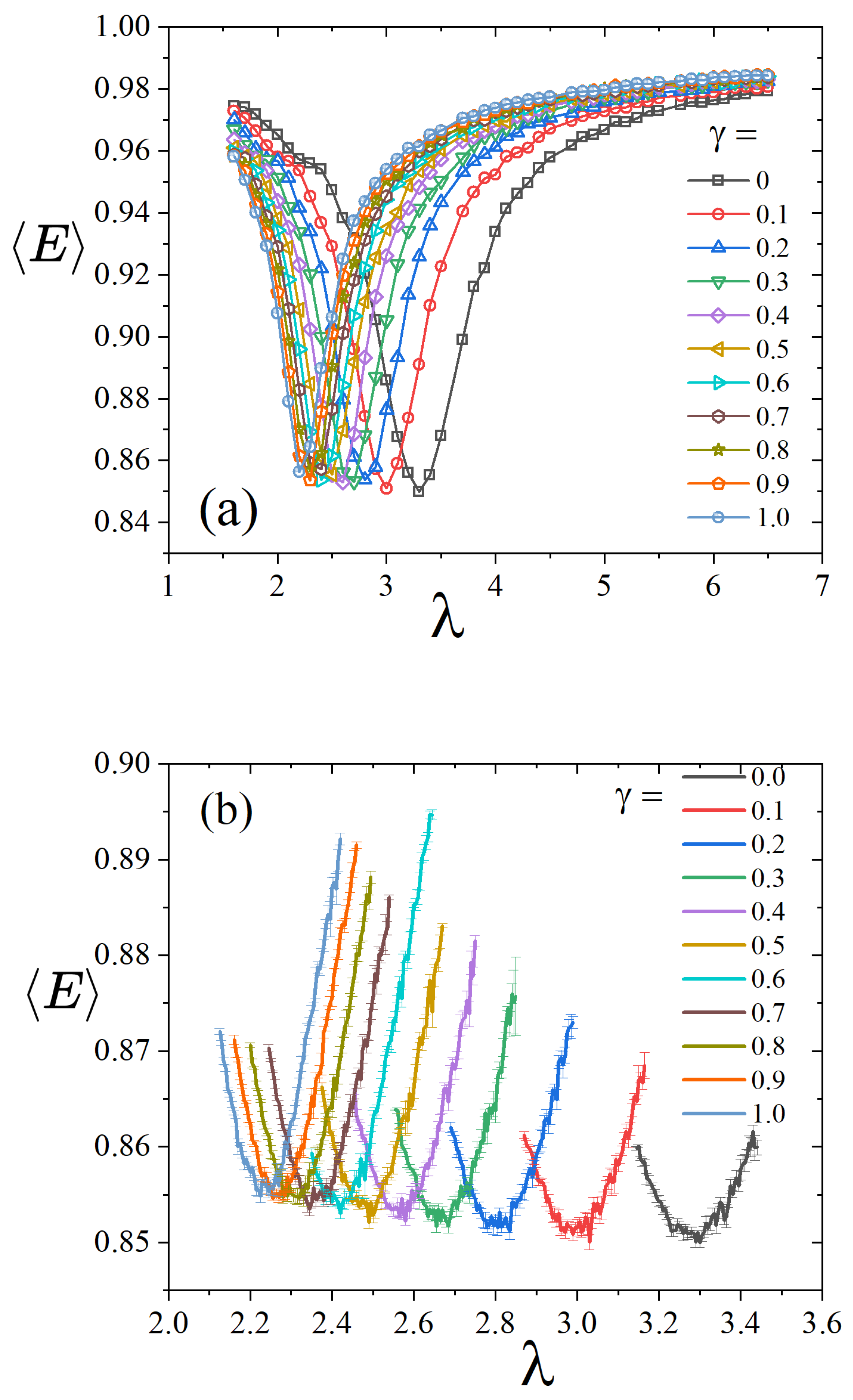
4. Results
4.1. Method 1
4.2. Method 2
4.3. Comparison Between the Methods
4.4. Brief Discussion About the Computational Complexity of the Methods
- Sampling: The analysis requires independent realizations of the order parameter’s time evolution (e.g., the density of active sites);
- Time Evolution: Each realization comprises a time series of MC steps;
- System Operations: Each MC step involves elementary operations, where L represents the system size.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, T.E. Contact interactions on a lattice. Ann. Prob. 1974, 2, 969. [Google Scholar] [CrossRef]
- Ligget, T.M. Interacting Particle Systems; Springer: New York, NY, USA, 1995. [Google Scholar]
- Marro, J.; Dickman, R. Nonequilibrium Phase Transitions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 2000, 49, 815. [Google Scholar] [CrossRef]
- Henkel, M.; Pleimling, M. Non-Equilibrium Phase Transitions, Volume 2: Ageing and Dynamical Scaling Far from Equilibrium; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Dickman, R. Nonequilibrium lattice models: Series analysis of steady states. J. Stat. Phys. 1989, 55, 997–1026. [Google Scholar] [CrossRef]
- Böttcher, L.; Herrmann, H.J.; Henkel, M. Dynamical universality of the contact process. J. Phys. A Math. Theor. 2018, 51, 125003. [Google Scholar] [CrossRef]
- da Silva, R.; Dickman, R.; Drugowich de Felício, J.R. Critical behavior of nonequilibrium models in short-time Monte Carlo simulations. Phys. Rev. E 2004, 70, 067701. [Google Scholar] [CrossRef]
- Dantas, W.G.; de Oliveira, M.J.; Stilck, J.F. Revisiting the one-dimensional diffusive contact process. J. Stat. Mech. 2007, P08009. [Google Scholar] [CrossRef]
- Dantas, W.G.; de Oliveira, M.J.; Stilck, J.F. Dependence of the crossover exponent with the diffusion rate in the generalized contact process model. Braz. J. Phys. 2008, 38, 94–96. [Google Scholar] [CrossRef]
- Fiore, C.; de Oliveira, M.J. Phase transition in conservative diffusive contact processes. Phys. Rev. E 2004, 70, 046131. [Google Scholar] [CrossRef]
- Shen, J.; Li, W.; Deng, S.; Xu, D.; Chen, S.; Liu, F. Machine learning of pair-contact process with diffusion. Sci. Rep. 2022, 12, 19728. [Google Scholar] [CrossRef]
- da Silva, R.; de Felício, J.R.D.; Martinez, A.S. Generalized Metropolis dynamics with a generalized master equation: An approach for time-independent and time-dependent Monte Carlo simulations of generalized spin systems. Phys. Rev. E 2012, 85, 066707. [Google Scholar] [CrossRef]
- da Silva, R. Random matrices theory elucidates the nonequilibrium critical phenomena. Int. J. Mod. Phys. C 2023, 34, 2350061. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M. Stochastic Dynamics and Irreversibility; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Stock, E.V.; da Silva, R. Chaos Solit. Fractals 2023, 168, 113117. [Google Scholar] [CrossRef]
- Trivedi, K.S. Probability and Statistics with Realiability, Queuing, and Computer Science and Applications, 2nd ed.; John Wiley and Sons: Chichester, UK, 2002. [Google Scholar]
- da Silva, R.; Fernandes, H.A.; de Felício, J.R.D. Nonequilibrium scaling explorations on a two-dimensional Z (5)-symmetric model. Phys. Rev. E 2014, 90, 042101. [Google Scholar] [CrossRef] [PubMed]
- Vinayak, T.; Prosen, T.; Buca, B.; Seligman, T.H. Spectral analysis of finite-time correlation matrices near equilibrium phase transitions. EPL 2014, 108, 20006. [Google Scholar] [CrossRef]
- Biswas, S.; Leyvraz, F.; Castillero, P.M.; Seligman, T.H. Rich structure in the correlation matrix spectra in non-equilibrium steady states. Sci. Rep. 2017, 7, 40506. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.N.; Stanley, H. Universal and nonuniversal properties of cross correlations in financial time series. Phys. Rev. Lett. 1999, 83, 1471–1474. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.N.; Stanley, H. A random matrix theory approach to financial cross-correlations. Physica A 2000, 287, 374–382. [Google Scholar] [CrossRef]
- Stanley, H.E.; Gopikrishnan, P.; Plerou, V.; Amaral, L.A.N. Quantifying fluctuations in economic systems by adapting methods of statistical physics. Physica A 2000, 287, 339–361. [Google Scholar] [CrossRef]
- Laloux, L.; Cizeau, P.; Potters, M.; Bouchaud, J.-P. Random matrix theory and financial correlations. Int. J. Theor. Appl. Financ. 2000, 3, 391. [Google Scholar] [CrossRef]
- Bouchaud, J.-P.; Potters, M. Theory of Finantial Risks. In From Statistical Physics to Risk Management; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wishart, J. The generalised product moment distribution in samples from a normal multivariate population. Biometrika 1928, 20, 32–52. [Google Scholar] [CrossRef]
- Wigner, E.P. On the Distribution of the Roots of Certain Symmetric Matrices. Ann. Math. 1958, 67, 325. [Google Scholar] [CrossRef]
- Dyson, F.J. Statistical theory of the energy levels of complex systems. I. J. Math. Phys. 1962, 3, 140. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Academic Press: Boston, MA, USA, 1991. [Google Scholar]
- Vinayak, T.H. Seligman, Time series, correlation matrices and random matrix models. AIP Conf. Proc. 2014, 1575, 196–217. [Google Scholar]
- Livan, G.; Novaes, M.; Vivo, P. Introduction to Random Matrices, Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Marcenko, V.A.; Pastur, L.A. Distribution of eigenvalues for some sets of random matrices. Math. USSR Sb. 1967, 1, 457. [Google Scholar] [CrossRef]
- Sengupta, A.M.; Mitra, P.P. Distributions of singular values for some random matrices. Phys. Rev. E 1999, 60, 3389. [Google Scholar] [CrossRef]
- da Silva, R.; Prado, S.D. Exploring Transition from Stability to Chaos through Random Matrices. Dynamics 2023, 3, 777–792. [Google Scholar] [CrossRef]
- Ross, T. Bělehrádek-type models. J. Ind. Microbiol. 1993, 12, 180–189. [Google Scholar] [CrossRef]
- ben-Avraham, D.; Köhler, J. Mean-field (n, m)-cluster approximation for lattice models. Phys. Rev. A 1992, 45, 8358. [Google Scholar] [CrossRef]
- da Silva, R.; Filho, E.V.; Prado, S.D.; de Felício, J.R.D. Efficient computational method using random matrices describing critical thermodynamics. Int. J. Mod. Phys. C 2024, 37, 1–30. [Google Scholar] [CrossRef]
- da Silva, R.; Prado, S.D. Identifying patterns using cross-correlation random matrices derived from deterministic and stochastic differential equations. Chaos 2025, 35, 033147. [Google Scholar] [CrossRef]
- da Silva, R.; Tomé, T.; de Oliveira, M.J. Numerical exploration of the aging effects in spin systems. Phys. Lett. A 2023, 489, 129148. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, R.; Filho, E.V.; Fernandes, H.A.; Gomes, P.F. Revisiting the Contact Model with Diffusion Beyond the Conventional Methods. Symmetry 2025, 17, 774. https://doi.org/10.3390/sym17050774
da Silva R, Filho EV, Fernandes HA, Gomes PF. Revisiting the Contact Model with Diffusion Beyond the Conventional Methods. Symmetry. 2025; 17(5):774. https://doi.org/10.3390/sym17050774
Chicago/Turabian Styleda Silva, Roberto, Eliseu Venites Filho, Henrique A. Fernandes, and Paulo F. Gomes. 2025. "Revisiting the Contact Model with Diffusion Beyond the Conventional Methods" Symmetry 17, no. 5: 774. https://doi.org/10.3390/sym17050774
APA Styleda Silva, R., Filho, E. V., Fernandes, H. A., & Gomes, P. F. (2025). Revisiting the Contact Model with Diffusion Beyond the Conventional Methods. Symmetry, 17(5), 774. https://doi.org/10.3390/sym17050774






