Abstract
Challenges are brought to high impedance fault (HIF) line selection in traditional distribution networks by the fault signals with short windows and weak characteristics provided by new energy power sources. A new method driven by the symmetry of current traveling wave spectrum is proposed in this paper. Frequency-domain features are extracted by using Pisarenko spectral decomposition, and the differences in amplitude, frequency, and polarity between faulted and healthy feeders are analyzed. A similarity matrix is constructed with the help of Manhattan distance, and an improved density-based spatial clustering of application with noise (DBSCAN) clustering is adopted to achieve intelligent fault line selection. Experimental results show that compared with the steady state component method and the transient component method, the accuracy of this method is increased to 97.5%, with an improvement of more than 12.5%. Quantitative thresholds are replaced by qualitative spectrum differences, and this method is not affected by weak signals, thus solving the problem of threshold setting caused by the access of new energy. The accuracy of this method under different fault types, phases, and resistances is verified by simulation, ensuring easy engineering implementation.
1. Introduction
New distribution networks are of critical importance to the stability of power systems. However, severe challenges in high impedance fault (HIF) line detection are introduced by the high penetration of distributed energy resources (DERs). These challenges include weak transient characteristics and extremely short data windows. To address these challenges, a fault line selection method driven by the symmetry difference of current traveling wave (CTW) spectrum is proposed in this paper. High-reliable fault identification without threshold setting is achieved by exploiting the inherent frequency-domain characteristic differences between faulted and healthy lines. The motivations of this paper are introduced in this section, including the background and challenges, distinctions from existing research techniques, and primary focuses and contributions.
1.1. Background and Challenge
Global climate change, rapid urbanization, and rapid economic development have brought many threats and challenges to mankind and increased the demand for sustainable development. The construction of new power systems dominated by renewable energy (e.g., solar and wind) has emerged as the primary paradigm for future energy development. Modern distribution networks integrated with distributed generation (DG) are characterized by wide spatial distribution and complex operating environments [1]. Initial fault impedance may exceed tens of kilohms, while fault currents can be as low as 0.1 ampere (0.01% of normal current). Accurate fault line detection is significantly challenged by the coupling effects of distributed power sources and power electronic devices [2]. HIFs often remain undetected in distribution networks. If not promptly addressed, these faults may escalate into widespread equipment damage, wildfires, or even fatal electric shock incidents [3,4].
1.2. Existing Research and Comparison
Currently, extensive research has been conducted globally on high-impedance fault line selection techniques. The mainstream technologies are classified into steady-state component methods [5], transient component methods [6,7], and traveling wave methods [8,9]. In recent years, stringent requirements on fault ride-through capabilities for DER grid-connected systems have been imposed by international standards such as IEEE-1547–2018. Existing line selection methods based on power frequency components or transient energy comparison face numerous challenges in addressing high-resistance grounding faults. For example, the steady-state component-based method in Reference [10], although unaffected by transition resistance and fault types, is characterized by weak steady-state component features, low detection signal reliability, and low line selection accuracy. The transient component method in Reference [11], despite having more obvious signals and improving line selection accuracy to some extent, is vulnerable to system operation modes and parameter variations in fault line determination. The method in Reference [12], which relies on the amplitude ratio characteristics of zero-sequence currents between the neutral point, healthy lines, and faulted lines for line selection, requires additional detection of neutral point current, increasing system complexity. The fifth harmonic-based method in Reference [13] struggles to achieve stable and accurate line selection in practice due to harmonic signal interference from load fluctuations. The segment localization method in Reference [14] identifies fault segments by comparing the matching degree of amplitude characteristics at both ends of feeder segments with set thresholds. However, artificially set thresholds in high-resistance grounding faults of new distribution networks are prone to insufficient line selection margin.
Traveling wave methods have become research hotspots in the relay protection field due to advantages such as immunity to transition resistance, current transformer (CT) saturation, system oscillations, and long-line distributed capacitance [15,16]. Numerous studies have shown that the symmetry-breaking features of high-resistance grounding traveling wave signals in the frequency-domain provide new insights for solving existing technical challenges [17]. The high-impedance fault line selection method driven by CTW spectrum symmetry proposed in this paper possesses unique advantages compared with existing traveling wave methods and other techniques. Existing traveling wave methods mostly focus on time-domain features or simple frequency-domain characteristics. However, this method deeply exploits frequency-domain symmetry-breaking features. It is unaffected by weak fault signals with short data windows caused by renewable energy integration, suitable for various neutral grounding modes and renewable energy operation scenarios, and eliminates the need for complex operations such as additional neutral point current detection. This approach avoids the problem of insufficient line selection margin caused by artificially set thresholds. By using Manhattan distance and DBSCAN clustering algorithm, qualitative differences in spectrum waveform features are employed to replace quantitative threshold calculations. This fundamentally solves the threshold-setting challenges under renewable energy integration and high-impedance conditions, achieving the unity of high sensitivity and high reliability. The establishment of a fault detection theoretical system based on symmetry analysis holds significant scientific value and engineering significance for enhancing the fault defense capability of smart distribution networks [18].
1.3. Primary Focus and Contributions
A novel fault line selection method for high-resistance grounding faults in new distribution networks is proposed in this paper. This method achieves fault line selection by utilizing the differences in CTW spectrum waveforms between faulted and healthy feeders and addresses issues in existing research.
- New paradigm of spectrum waveform: This approach differs from traditional methods relying on steady-state components, transient signals, or harmonic thresholds. The amplitude–frequency–polarity asymmetry of fault CTW spectra is first used for line selection. Qualitative difference features are extracted via Pisarenko spectral decomposition, eliminating the need for quantitative threshold setting. This solves the sensitivity issues caused by short data windows of new energy and weak fault characteristics.
- Threshold-free clustering mechanism: A spectrum similarity matrix based on Manhattan distance and an improved DBSCAN clustering algorithm are innovatively designed. No empirical thresholds or neutral point current detection are required, achieving 97.5% accuracy under complex grid topologies and new energy fluctuations.
The remainder of this paper is organized as follows: Section 2 introduces the new distribution network CTW spectrum line selection principle. Section 3 presents the multi-feature difference analysis of the CTW spectrum waveform. Section 4 describes the spectrum feature-driven fault line detection algorithm. Simulation analyses are conducted in Section 5. Section 6 provides a conclusion of the paper.
2. CTW Spectrum Fault Line Detection Principle for New Distribution Network
2.1. Generation Mechanism of Fault CTW in New Distribution Network
When a fault occurs at feeder f in, the new distribution network, the fault point potential is observed to undergo abrupt collapse. This transient process induces electromagnetic coupling effects, which generate traveling wave signals propagating as electromagnetic waves. The generation mechanism is illustrated in Figure 1. The original fault distribution network is depicted in Figure 1a. Based on the circuit superposition theorem, the fault system is decoupled into a linear superposition of the normal operating system and the fault-induced subsystem. The equivalent process is shown in Figure 1b. This decomposition demonstrates that the fault signal is essentially a time-domain superposition of power–frequency steady-state components and high-frequency transient components [19]. Further decomposition yields the normal operation subsystem shown in Figure 1c and the fault-induced subsystem presented in Figure 1d. The instantaneous potential at fault point f during normal operation is defined as eF. Upon fault occurrence, the fault point potential is forced to zero relative to ground. According to Thevenin’s equivalence theorem, an equivalent voltage source with magnitude −eF is required to be injected at node f in, the fault-induced subsystem. This equivalent voltage excitation generates initial traveling waves at the fault point. Wave propagation paths are established through line surge impedances, causing traveling wave signal transmission and reflection phenomena in the multi-terminal network.
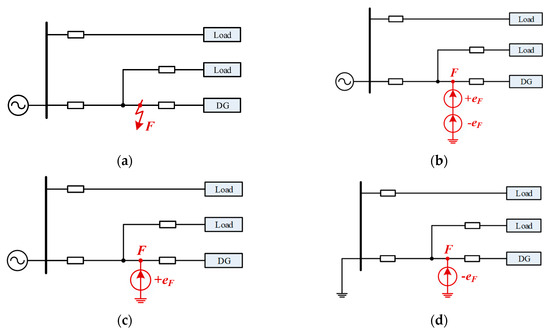
Figure 1.
Fault traveling wave generation mechanism diagram. (a) represents the original fault system diagram. (b) represents the fault superposition system diagram. (c) represents the normal operation state. (d) represents fault additional state.
Fault impedance is considered as a non-negligible physical characteristic at fault points in practical fault conditions. The typical fault f is selected as the research object. A traveling wave propagation path model is established based on traveling wave propagation theory, as shown in Figure 2. According to transient circuit analysis principles, the amplitude characteristics of initial voltage traveling wave Uτ and CTW Iτ excited at the fault point are determined by Equations (1)–(3).
In Equations (1)–(3), Uτ is defined as the fault voltage potential; θ denotes the fault inception angle; RF is referred to as the transition impedance of fault F; IF represents the fault current flowing through RF at the moment of fault occurrence; ZC indicates the line surge impedance, whose magnitude is determined by line parameters and system operating conditions. As indicated by Equations (2) and (3), θ, RF, and ZC are identified as the three primary factors influencing the amplitude of initial traveling wave fronts. These parameters are, therefore, recognized as critical elements for distinguishing between fault and non-fault lines at the mechanism level.

Figure 2.
Line fault traveling wave transmission diagram.
2.2. Traveling Wave Modulus Selection
When a line fault occurs, traveling waves propagate along the line from the fault point. Due to electromagnetic coupling between phases, the propagation characteristics of traveling waves in each phase cannot be analyzed independently. Therefore, the Karenbauer transformation is employed for decoupling. The A, B, and C phase components are transformed into independent zero-mode, α-mode, and β-mode components [20]. This paper utilizes the zero-mode component of CTWs for fault line detection in new distribution networks. The specific rationale is analyzed as follows.
(1) Based on Kirchhoff’s current law and combined with Equations (2) and (3), the zero-mode component U0 and line-mode components Uα and Uβ can be calculated.
In Equation (4), Z0 and Z1 represent the zero-mode and line-mode impedances, respectively. Since the zero-mode impedance is larger than the line-mode impedance, the zero-mode voltage exceeds the line-mode voltage. Although the zero-mode component decays faster than the line-mode component, the zero-mode voltage traveling wave at the bus remains larger than the line-mode component due to the shorter length of distribution lines [21]. Similarly, the same pattern is observed in CTWs.
(2) In the zero-sequence channel of distribution networks, no significant fault or load power–frequency currents are present. This ensures higher resolution of the zero-mode traveling wave component, which is easier to extract and more suitable for constructing fault line detection criteria.
(3) The zero-sequence network of the system remains unchanged when Δ or Y connection configurations are adopted on the grid-connected side of DG. After fault occurrence, the current circulation path between DG and the main grid is interrupted. The distribution of zero-mode CTW components remains unaffected in the network. Consequently, fault line detection methods utilizing zero-mode CTW components remain applicable.
(4) When capacitor banks are installed on the bus, the line-mode component forms a loop between two phases and is influenced by the compensation capacitance. The compensation capacitor is modeled as 1/(ωC). Since the line-mode CTW contains significant high-frequency components, the parallel capacitor acts as a short circuit to these components. Thus, the line-mode CTW predominantly exists on the faulted line and capacitor, while the signal detected on non-fault lines is weak. Since capacitor banks are typically configured in Δ or Y, the zero-mode CTW cannot form a closed loop within the capacitor, and its influence is negligible [22]. Simulation results are shown in Figure 3.
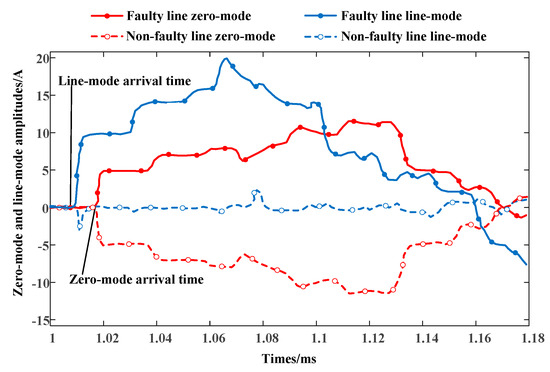
Figure 3.
Faulted and sound lines in the presence of busbar shunt capacitors: zero-mode and line-mode waveforms.
Based on the comprehensive analysis above, it is concluded that the zero-mode CTW component is more suitable for fault line detection in new distribution networks.
2.3. Symmetry Analysis of Operating Conditions
Under normal operation conditions of the distribution network, three-phase parameters and load distribution of the system exhibit symmetric characteristics. The CTW spectrum of lines demonstrates frequency-domain symmetry due to the balance of electromagnetic coupling. This is specifically reflected in the following: the energy of traveling wave spectra in each phase is uniformly distributed within fundamental frequency and characteristic harmonic frequency bands, and the phase polarity of positive and negative half-cycles is strictly symmetric [23]. However, when a high-resistance grounding fault occurs in the system, asymmetric wave impedance boundary conditions are formed at the fault point. This leads to fundamental differences in traveling wave propagation paths and spectral characteristics between faulted and healthy lines [24]. The specific analysis is as follows:
2.3.1. Analysis of Balance Parameters Under Symmetric Operating Conditions
In normal operation of distribution networks, the three-phase system parameters are characterized by symmetrical characteristics and balanced load distribution, while the CTW spectra exhibit frequency-domain symmetry due to balanced electromagnetic coupling. Specifically, the spectral energy of each phase is uniformly distributed across fundamental and characteristic harmonic frequencies, with strictly symmetrical phase polarities observed in positive and negative half-cycles. However, when HIF occurs, asymmetric wave impedance boundary conditions are formed at the fault point, resulting in fundamental differences in CTW propagation paths and spectral characteristics between fault and non-fault lines. Specifically, analysis proceeds as follows:
Under symmetric operating conditions, the balanced parameters of distribution network phases are maintained. The terminal load impedance also exhibits symmetry, resulting in strict frequency-domain symmetry in CTW spectra. Under symmetric operating conditions, the balanced parameters of distribution network phases are maintained. The spectral energy density function for each phase can be expressed as follows:
In Equation (5), Sg(f) represents the power spectral density function of the g-phase CTW. T denotes the sampling time window width, and ig(t) is the time-domain signal of the g-phase CTW. Under normal operation, the spectral energy is uniformly distributed across the fundamental and harmonic frequency bands. The phase also satisfies the conjugate symmetry condition:
In Equation (6), Sa(f), Sb(f), and Sc(f) are defined as the complex spectra of three-phase CTW signals ia(t), ib(t), and ic(t), respectively, which are obtained through PHD (detailed in Section 4.1). The phase angle of spectrum Sa(f) is denoted as ∠Sa(f), and h represents an integer parameter for phase symmetry evaluation. When an HIF occurs, asymmetric wave impedance boundary conditions are formed at the fault point (labeled as point f in in Figure 1), and its reflection coefficient is defined as follows:
In Equation (7), ΓF is defined as the CTW reflection coefficient. When metallic grounding occurs, RF is approximated to zero, and ΓF approaches −1. This results in full reflection of CTWs on the fault line, and resonance is excited at characteristic frequencies.
In Equation (8), fn is defined as the CTW resonant frequency, v represents the wave propagation velocity, and l corresponds to the electrical distance (propagation distance) from the measurement point to the fault location. Under this condition, the spectral energy density of the fault phase is significantly enhanced, while the non-fault phases retain their original distribution patterns. The symmetry breaking is quantified as follows:
In Equation (9), ΔA(f) is termed the spectral asymmetry index. Ag(f) is defined as the spectral magnitude of the CTW at frequency f for phase g, where g = 1, 2, 3 corresponds to phases A, B, and C. This parameter quantifies the frequency-domain energy distribution imbalance caused by faults.
Under normal operating conditions, three-phase electromagnetic coupling symmetry is maintained, causing Ag(f) to approximate Ag(f) while ΔS(f) approaches zero. During fault conditions, abrupt boundary condition variations at the fault phase (e.g., asymmetric wave reflection coefficients caused by fault impedance RF) result in significant deviation of Sfault-phase(f) from A (f). This leads to a sharp increase in ΔA(f). Statistical analyses demonstrate that ΔA(f) values of fault lines in resonant frequency bands Δf reach 5–10 times those of non-fault lines. Consequently, CTW spectral characteristics are proposed as critical indicators for fault line detection from the perspective of modern distribution network symmetry. These spectral features inherently reflect the essential characteristics of fault transients.
2.3.2. Analysis of Unbalance Parameters Under Symmetric Conditions
When the distribution of line to ground capacitance is uneven or there is asymmetric access of DG, the symmetry of the zero-mode component of the CTW is disrupted. As a result, the amplitude difference is reduced, and the sensitivity significantly decreases, especially when the transition resistance is relatively high (>1 kΩ). At this time, the parameters of each phase line in the distribution network no longer meet the balance conditions [25], and the symmetry of the load impedance at the line terminal is also broken. This imbalance causes the frequency-domain symmetry of the CTW spectrum to be damaged. The energy of the traveling wave spectrum of each phase is no longer evenly distributed in the fundamental frequency and characteristic harmonic frequency bands, and the strict symmetry of the phase polarity in the positive and negative half cycles is also broken [26]. For the spectrum amplitude, an unbalanced degree index is defined as follows:
Under balanced conditions, Δunbalance(f) ≈ 0. Under unbalanced conditions, Δunbalance(f) increases significantly, indicating that the spectral amplitude symmetry is disrupted.
In terms of phase–frequency characteristics, the Equation (6) originally holds under balanced conditions. However, this phase symmetry condition is broken under unbalanced conditions, and the phase relationships of each phase’s spectrum no longer satisfy the above formula, further damaging the original frequency-domain symmetry of the CTW spectrum. Furthermore, unbalanced load impedances in each phase lead to different reflection coefficients. Assuming the load impedance of phase a is Za and that of phase b is Zb (Za ≠ Zb), then , , . Such differences in reflection coefficients affect traveling wave propagation and spectral energy distribution, making high-impedance fault detection more complex.
However, the method proposed in this paper, driven by CTW spectrum symmetry, does not rely on a strict balance of system three-phase parameters. Regardless of the distribution of line-to-ground capacitance or the asymmetric integration of DG, its core lies in utilizing the variation law of CTW spectra during fault transients. For example, in distribution networks with DG, the integration of renewable energy alters system power flow and fault characteristics. The CTW spectral waveform focuses on the abrupt change characteristics of the traveling wave spectrum at the fault instant rather than system steady-state balance parameters. This direct utilization of fault transient spectral characteristics enables it to adapt to various unbalanced operating conditions, ensuring the effectiveness of high-impedance fault feeder selection in complex distribution network environments.
2.4. CTW Spectrum Waveform
From the perspective of CTW spectrum analysis in the frequency-domain, the CTW spectrum is determined jointly by the broadband characteristics of sudden voltage excitation at the fault point and the frequency response characteristics of the transmission network. The spectral magnitude can be expressed as follows:
In Equation (11), H(f) is defined as the network transfer function, and ∂ (f) is termed the line attenuation coefficient.
The spectral characteristics of CTWs are influenced by multiple factors, including fault types, initial fault phase angles, line parameters, and monitoring point locations. Particularly, high-frequency components are significantly attenuated by line parameters, thus resulting in band-limited characteristics in measured spectra. To quantitatively analyze these features, PHD is applied to CTWs within the detection window T (detailed in Section 4.1). The amplitude–frequency characteristic curve is plotted, as shown in Figure 4. This waveform characterizes the energy distribution of CTWs across different frequency bands.
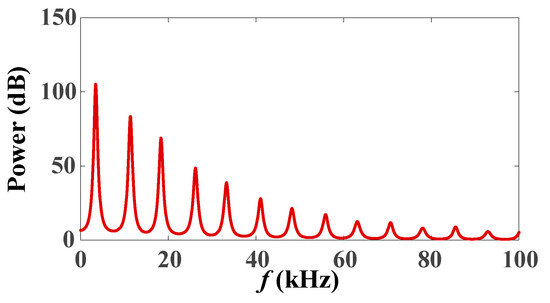
Figure 4.
CTW spectrum diagram.
As shown in Figure 4, abundant frequency-domain information is embedded in CTW signals, from which fault-related parameters such as fault location, system topology, and fault characteristics (including fault impedance and initial phase angle) can be extracted. CTW spectra exhibit varying degrees of spectral similarity and divergence between fault and non-fault lines. By investigating transmission characteristics of broadband spectral waveforms, key parameters, including amplitude, frequency, and polarity variations, are extracted. Through analyzing these parameter variations under different fault locations (at busbars or along lines) and fault conditions, novel distribution network fault line detection is achieved based on CTW spectral characteristics.
3. Multi-Feature Difference Analysis of CTW Spectrum Waveform
3.1. Spectrum Waveform Amplitude Characteristics
To further analyze spectral amplitude differences between non-fault and fault line CTWs, Figure 5 is taken as an illustrative case where a single-phase grounding fault occurs in modern distribution networks. Consequently, the phase-to-ground voltage of the fault phase is reduced to zero, while non-fault phase voltages are elevated to line-to-line levels. In distribution system circuits, numerous power devices are present, which can be modeled as distributed inductance and capacitance components. When faults occur, abrupt voltage variations at fault points initiate multiple charging–discharging transients, thus generating CTWs. These transients are illustrated in Figure 5.
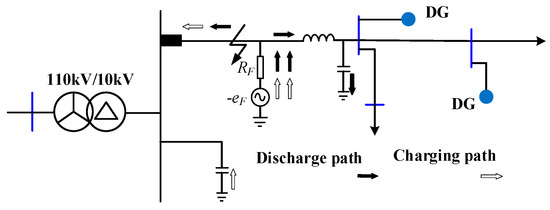
Figure 5.
The charge–discharge model of fault.
As shown in Figure 5, CTWs generated at the fault point propagate along the fault line toward non-fault lines. The wave propagation process is essentially composed of discharge and charge cycles of distributed parameters (capacitance and inductance). Two distinct characteristics are observed: During discharge cycles, current paths are formed between the fault line capacitance and ground, where low loop inductance causes rapid signal attenuation. During charge cycles, current paths are established through the bus system (buses, transformers, and directly connected high-voltage equipment) and non-fault line capacitance to ground, with high loop inductance leading to slow signal attenuation.
Therefore, the CTW spectral amplitude of fault lines is observed to be significantly higher than that of non-fault lines.
3.2. Frequency Characteristics of Spectrum Waveform
The distribution network bus system is composed of buses, transformers, and directly connected high-voltage equipment such as instrument transformers, disconnectors, and circuit breakers. By analyzing the amplitude–frequency transmission characteristics of CTW spectral waveforms within the bus system, spectral differences between CTW signals transmitted on fault and non-fault lines can be derived.
The CTW reflection and refraction through the bus-to-ground capacitance system is illustrated in Figure 6a, where two uniform lossless lines with surge impedances Z11 and Z22 are connected at impedance discontinuity point K. Current wave I1b is injected as the incident wave propagating from line Z11 toward line Z22. Partial reflection occurs at point K, generating reflected wave I1f on line Z11. Simultaneously, refracted wave I2f is produced on line Z22. Assuming both lines are infinitely long, Peterson’s theorem is applied by introducing a 2U1b voltage source into line Z11, yielding the equivalent circuit shown in Figure 6b. The refracted current wave I2f(s) is derived as follows:
In Equation (12), G(s) is defined as the CTW refraction transfer function (also termed the refraction coefficient), whose magnitude is determined by Z22 and Zcs. By applying Laplace transform, the complex frequency-domain variable s is converted to the frequency-domain variable jω. Consequently, the frequency-domain transmission characteristic (refraction coefficient) G(s) is obtained. In the literature [27], the bus system capacitance to ground (CS) is modeled within 100–9000 pF. Assuming Z11 = Z22 = 350 Ω, the amplitude–frequency characteristic of the refraction coefficient is plotted as shown in Figure 7.
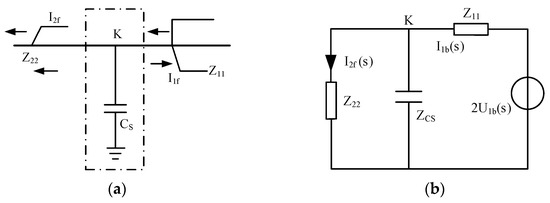
Figure 6.
CTW passing through bus-to-ground. (a) represents the reflection of CTWs. (b) represents the Peterson equivalent circuit.
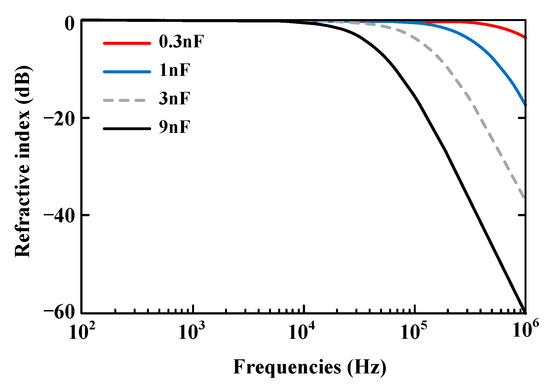
Figure 7.
Amplitude–frequency characteristics of refractive index.
As shown in Figure 7, high-frequency signals above 10 kHz are significantly attenuated by the bus system, with the attenuation effect intensified by increased capacitance values. Consequently, CTWs detected on fault lines exhibit nearly full-bandwidth waveforms, while those observed on non-fault lines exhibit severe attenuation in high-frequency components. Additionally, CTW propagation involves distinct discharge and charge cycles: during discharge cycles, smaller loop inductance leads to rapid signal attenuation and higher oscillation frequencies; during charge cycles, larger loop inductance results in slower attenuation and lower oscillation frequencies.
Therefore, the CTW signal frequency of fault lines is observed to be significantly higher than that of non-fault lines.
3.3. Spectrum Waveform Polarity Characteristics
In power systems, the positive current direction is defined as flowing from buses to lines. On non-fault lines, CTW propagation directions are aligned with the positive direction (from buses to lines), while on fault lines, these directions are reversed (from lines to buses). Consequently, the polarities of CTW signals between fault and non-fault lines are observed to be completely opposite.
Based on the above analysis, significant differences in CTW amplitude, frequency, and polarity are observed between fault and non-fault lines during faults in modern distribution networks. Consequently, the exploitation of multi-dimensional spectral features of CTWs is expected to enhance the reliability of fault line detection.
4. Spectrum Feature-Driven Fault Line Detection Algorithm
4.1. Spectrum Waveform Extraction Method
The PHD method, as a spectrum estimation technique based on eigen-space decomposition, is implemented through the construction of signal autocorrelation matrices and their eigenvalue decomposition. This process enables precise extraction of frequency components from noise-contaminated signals [28]. This method is particularly advantageous due to its capability to segment weak CTW spectral signals, generated during HIFs in modern distribution networks, into smaller data blocks. The approach enhances the utilization efficiency of short-duration signals produced by renewable energy integrated system faults and is specifically applicable for spectral symmetry identification of weak fault signatures. For CTW signals in modern distribution networks, the implementation procedure is described as follows:
(1) The zero-mode CTW signal ik(t), represented in the time-domain, is sampled to obtain the discrete signal ik(p), where p denotes discrete sampling points. The autocorrelation function Rk [q] of the discrete signal is then calculated as follows:
In Equation (13), N is defined as the length of the zero-mode CTW signal ik(t), and q is denoted as the time delay. The subscript k represents the signal detected by the k-th feeder (k = 1, 2,···, n). This sampling method effectively mitigates spectral aliasing in short-time data windows under renewable energy integrated systems, thereby avoiding energy leakage caused by data truncation in conventional approaches.
(2) The autocorrelation matrix Rk is constructed based on the autocorrelation function Rk [q] of the discrete signal.
(3) The autocorrelation matrix is subjected to eigenvalue decomposition.
In Equation (15), Vk is defined as the eigenvector matrix, and Λk is termed the eigenvalue matrix. Subsequently, the largest m eigenvalues (λ1, λ2,…, λm) are selected, and their corresponding eigenvectors (λ1, λ2,…, λm) are extracted. The conjugate transpose of the matrix is denoted as H.
(4) The selected eigenvalues and eigenvectors are utilized to construct a high-frequency spectral vector Sk (f) with m sampling points. This approach effectively addresses challenges posed by short-time data windows in renewable energy systems, weak fault signal interference, and high-frequency signal extraction.
In Equation (16), vm(f) is defined as the eigenvector.
The spectral energy coefficient pk for line k is established.
The algorithm separates the signal subspace from the noise subspace by constructing an autocorrelation matrix with specific dimensions. The eigenvectors corresponding to the smallest eigenvalues of the matrix are then solved, and a frequency estimation polynomial is constructed based on these eigenvectors to extract dominant frequency components. The horizontal axis of the resulting spectral matrix represents the distribution characteristics of different frequency components, while the vertical axis reflects the energy amplitudes of these components. This enables precise identification of fault characteristics, as illustrated in Figure 4. Compared to conventional spectral transformation methods (e.g., Fourier transform), the resolution and noise immunity are significantly enhanced.
4.2. Improved DBSCAN Clustering Algorithm Based on Manhattan Distance Symmetry
The symmetry of Manhattan distance matrices is inherently endowed with mathematical properties, which are assigned distinct physical significance in fault line detection scenarios. For non-fault feeders, Manhattan distances between CTW spectra approach zero, indicating symmetrical consistency of feeder characteristics under normal operating conditions. In contrast, distances between fault and non-fault feeders approach unity due to significant spectral distortion differences, demonstrating symmetrical opposition between faulted and normal states.
Based on the detected zero-mode CTW spectra S1(f), S2(f), …, Sk(f), …, Sn(f) of n feeders in a modern distribution network, the Manhattan distances between these spectral vectors are calculated. By leveraging the cumulative difference characteristics of Manhattan distances and combining them with high-resolution spectral vectors Sk(f), spectral energy leakage caused by short-time data windows is mitigated. The utilization efficiency of limited sampled data is thereby improved. Taking feeders k and j as an example, the similarity distance between their CTW spectral vectors Sk(f) and Sj(f) is expressed as follows:
Accordingly, an n × n Manhattan distance matrix M for feeder CTWs is obtained.
In Equation (19), the matrix element Mkj is defined as the similarity distance between the CTW spectral vectors Sk(f) and Sj(f) of feeders k and j, respectively. A larger value of Mkj is observed to correspond to greater spectral differences between the CTWs of the feeders.
The n × n feeder CTW similarity distance matrix M is input into the DBSCAN clustering algorithm. As a representative density-based clustering method, DBSCAN fundamentally differs from algorithms such as K-means and fuzzy C-means, which rely on preset cluster numbers. Its innovations are demonstrated through three aspects: (1) Cluster structures are autonomously identified via dynamic neighborhood density thresholds, eliminating the need for preset cluster numbers. This enables adaptation to multi-modal distribution characteristics of fault features in renewable energy integration scenarios while suppressing short-duration weak signal interference. (2) A noise filtering mechanism is established based on density-reachability criteria. Effective fault features are accurately distinguished from random noise under weak fault signal interference in renewable energy short-time data windows, thus preventing misjudgments caused by signal amplitude fluctuations in conventional threshold methods. (3) High-frequency transient component extraction capabilities are enhanced through adaptive parameter tuning. Combined with the time–frequency correlation characteristics of CTW similarity distance matrices, high-frequency signal features in fault CTWs are precisely captured.
In parameter configuration, a parameter set [Eps,MinPts] is utilized to characterize the density distribution of all element values in the Manhattan distance matrix M. Here, Eps is defined as the radius of elements, and Eps specifies the minimum number of elements required within neighborhood this radius. For the k-th row element array Mk in M, elements with Manhattan distances smaller than Eps are labeled as X(Mk ):
In Equation (20), ‖Mj,Mk‖ represents the radius distance between arrays Mj and Mk. If the number of elements in X(Mk) is greater than or equal to MinPts, Mk and its neighboring elements are clustered into one category, where Mk is identified as the core point of the cluster.
In data clustering, elements of the n × n dimensional feeder CTW Manhattan distance matrix M are treated as n2 sample data. The specific procedure is described as follows:
a. All n2 sample data are initially marked as unvisited.
b. An unvisited element array Mk is randomly selected as the data sample Q. It is then marked as visited.
c. The number of samples Δ within Eps for sample Q is calculated using Equation (4). If Δ ≥ MinPts, sample Q is recorded as a core sample P. If Δ < MinPts, sample Q is marked as a suspected sample, and the process returns to step b.
d. A new non-fault feeder cluster N is created with core sample P. If other core samples R are contained within the neighborhood of sample P, the density-reachable neighborhoods of R and P are merged. Samples within the neighborhood of R are then added to cluster N. The process returns to step b.
e. After all n2 sample data in matrix M are processed, suspected samples not assigned to any cluster are categorized into the fault feeder outlier cluster F. The line detection clustering process is thus completed.
f. The entire element dataset of the feeder CTW Manhattan distance matrix is partitioned through density-based clustering. All elements are classified into fault and non-fault categories. If all feeder element values are clustered into a single category, the feeders are determined to be normal, and a busbar fault is identified.
In HIF selection for modern distribution networks, the DBSCAN algorithm yields a maximum of two clusters: one non-fault feeder cluster and one fault feeder cluster. Since the number of non-fault feeders generally exceeds two during HIFs, MinPts is set to 2. The optimal Eps parameter is calculated based on the mean value of all similarity distances. This parameter selection strategy is adopted to ensure adaptability to varying fault scenarios.
Clustering performance, namely clustering quality, can be quantified by the silhouette coefficient. For each sample i in the dataset, a(i) is first calculated, which is the average distance from sample i to all other samples in its cluster. This measures the compactness within the cluster; a smaller a(i) indicates a higher degree of aggregation of the sample within its cluster. Next, b(i) is calculated, which is the average distance from sample i to all samples in the nearest other cluster. This reflects the dissimilarity between clusters.
In Equation (22), S(i) represents the silhouette coefficient. When S(i) approaches 1, it indicates that sample i is closely connected to samples in its cluster and well-distinguished from other clusters, implying good clustering performance. When S(i) approaches −1, it suggests that sample i may be incorrectly assigned to the current cluster. When S(i) approaches 0, it indicates that sample i is at the boundary of clusters and difficult to classify clearly. Finally, the average of S(i) for all samples in the dataset is computed to obtain the overall silhouette coefficient.
This coefficient comprehensively considers the compactness within the same cluster and the dissimilarity between different clusters, where a larger value indicates better clustering performance. In this way, the silhouette coefficient can effectively quantify clustering quality and provide a powerful basis for performance evaluation of different clustering algorithms.
4.3. High Impedance Grounding Fault Line Detection Process of New Distribution Network
A novel HIF line detection method for modern distribution networks is driven by CTW spectral symmetry. The implementation process is described as follows, algorithm flow chart as shown in Figure 8:
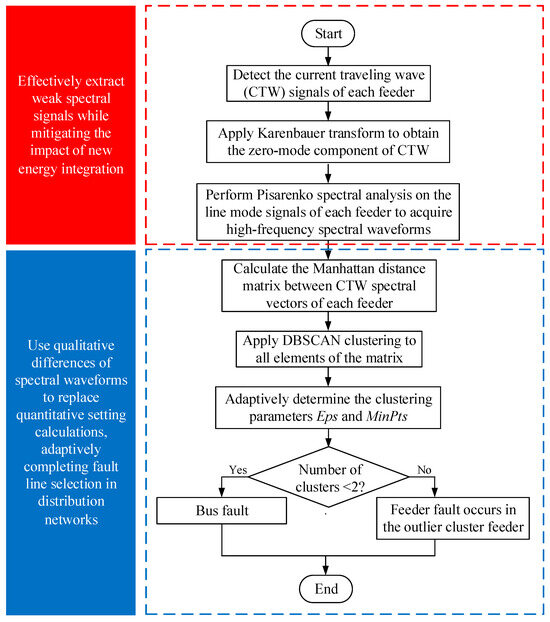
Figure 8.
Algorithm flow chart of fault line detection based on CTW spectrum.
Step 1. CTW detection devices are installed at the busbar outlet of each line. The sampling frequency of the devices is set to 100 kHz. Time-domain fault CTW line-mode signals ik(t) within a 1 ms window are captured.
Step 2. The CTW signals of each feeder are transformed via the Karenbauer transformation, where the zero-mode component i0 is derived.
Step 3. The zero-mode components i0 of CTWs from all feeders are subjected to spectral analysis using PHD. Corresponding spectral vectors Sk(f) are obtained, and the frequency window is configured in the high-frequency band (20–100 kHz). This configuration is designed to mitigate interference from low-frequency harmonics generated by nonlinear characteristics of power electronic devices in renewable energy systems, thereby enhancing the robustness of the proposed method in modern distribution networks.
Step 4. Manhattan distances between the CTW spectral vectors of all feeders are calculated. A Manhattan distance matrix M is thus generated.
Step 5. Density-based clustering (DBSCAN) is applied to all elements in the Manhattan distance matrix of feeder CTWs. Parameters Eps and MinPts are adaptively determined based on the data distribution characteristics. Clustering labels for each line are generated by the algorithm. Fault lines are identified through analysis of these clustering labels.
Step 6. If all feeder elements are clustered into a single category, the feeders are determined to be normal, and a busbar fault is identified. When two clusters are formed with outlier feeders, feeders in the outlier cluster or smaller cluster are classified as having an HIF, thus concluding the line detection process.
5. Simulation Analysis
5.1. Simulation Model
A 10 kV modern distribution network simulation model is constructed in the PSCAD/EMTDC environment, as shown in Figure 9. Five feeder lines (L1–L5) with distinct supply configurations are implemented, including two hybrid overhead-cable lines with branches, one branched overhead line, one 14 km overhead line, and one 15 km underground cable line. Parameters of each feeder are detailed in Table 1, while line lengths and terminal labels (E1~E17) are annotated in the diagram. Distributed renewable energy sources DG1–DG3 are integrated with capacities of 4 MW, 8 MW, and 8 MW, respectively. The maximum output current is set to 1.5 times the rated current. The control strategy is configured as conventional PQ control, incorporating low-voltage ride-through (LVRT) capability. The equivalent grounding capacitance CS of the bus system is specified as 1 μF [29].
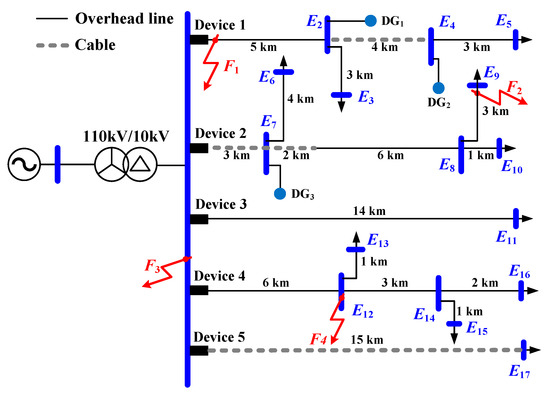
Figure 9.
Simulation structure of 10 kV power distribution system.

Table 1.
Parameters of 10 kV line in new distribution network.
5.2. Analysis of Line Detection Results
Four HIFs are configured at distinct locations in Figure 9: Fault F1 is set on feeder L1 at 1.2 km from the E1 terminal in the E1E2 section; Fault F2 is set on feeder L2 at 2.7 km from the E8 terminal in the E8E9 section; Fault F3 is set at the busbar; Fault F4 is set at the E12 terminal of feeder L4. All faults are phase-A grounding faults with a fault impedance of 5 kΩ. CTW detection devices installed at the head ends of feeders acquire zero-mode CTW spectral waveforms. The spectral energy coefficient pk of each feeder is calculated after fault occurrence. Results in Figure 10 demonstrate that the spectral energy coefficients of faulted feeders significantly exceed those of non-fault lines under all fault scenarios.
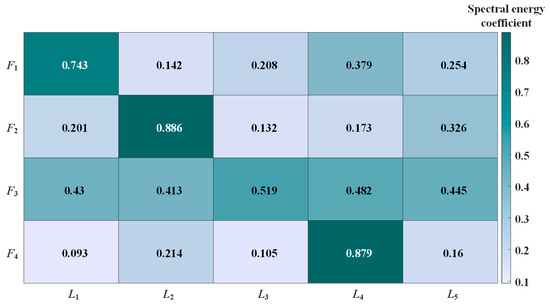
Figure 10.
Spectral energy coefficients for each line at different fault positions.
Spectral waveform dissimilarity analysis is performed between all feeder lines. Manhattan distances between each pair of lines are calculated to construct a Manhattan distance matrix. The element data in this matrix are clustered using DBSCAN to determine fault line locations. During the testing process, CTW detection devices are triggered upon capturing CTW signals from all feeders. The line detection process is then initiated, and test results are summarized in Table 2.

Table 2.
The results of HIF line detection in different fault locations.
Taking the first case of fault F1 as an example, the calculated similarity distance matrix MF1 is shown in Equation (21). The matrix elements in Equation (21) are clustered using DBSCAN, and the clustering results are plotted in Figure 11 (horizontal and vertical axes have no physical significance). The clustering results in Figure 11 demonstrate that the algorithm successfully partitions the fault data into two categories: a “fault cluster” and a “non-fault cluster”. Feeders L2, L3, L4, and L5 are grouped into the same cluster based on their similarity distance data, while feeder L1 is isolated into the outlier cluster. Feeder L1 is thus identified as experiencing an HIF. As indicated in Table 2, fault line determination is achieved through clustering analysis, confirming the feasibility of the proposed method for fault line detection.
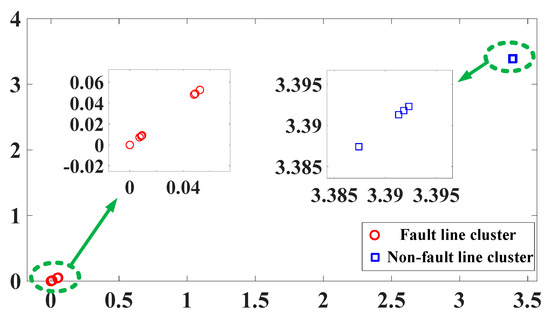
Figure 11.
Scatter Plot of Fault and Non-Fault Line Clusters in Distribution Network.
5.3. Adaptability Analysis of Line Detection Method
Four HIFs with varying fault impedances and types are configured at the locations described in Section 5.2. The fault types include phase-A, phase-B, and phase-C grounding faults, with fault impedances of 5 kΩ, 8 kΩ, and 10 kΩ, respectively. Line detection results are summarized in Table 3. Further analyses are conducted to evaluate the impact of DRE types, capacities, and noise interference on the proposed method. The capacity and type of DG3 are modified, and a phase-A grounding fault with 8 kΩ fault impedance at location F2 is analyzed. Corresponding line detection results are provided in Table 4.

Table 3.
HIF line detection results of different fault types and impedances.

Table 4.
HIF line detection results of different new energy and noise interference.
As shown in Table 1 and Table 2, the proposed method reliably achieves accurate fault line detection in modern distribution networks with HIFs. This robustness is attributed to two key factors: (1) Variations in fault types, fault impedances, and noise primarily affect the amplitude of CTWs but minimally alter their waveform shapes. Consequently, the similarity distance calculations for spectral waveforms are slightly perturbed without compromising the final selection results. (2) High-frequency CTW spectral components inherently suppress low-frequency harmonic interference caused by renewable energy integration. Changes in renewable energy capacities and types do not significantly influence similarity distance metrics or line detection outcomes. Extensive simulation tests demonstrate that the method simplifies fault identification by replacing quantitative threshold calculations with qualitative waveform dissimilarity analysis. It accurately identifies fault lines under diverse conditions, including varying fault locations, fault types, fault impedances, and noise levels. This approach fundamentally resolves the threshold-setting challenges induced by renewable energy integration and high-impedance conditions, enabling both high sensitivity and reliability in fault line detection.
5.4. Comparative Analysis of Fault Line Selection Effect by Different Methods
In order to comprehensively evaluate the performance of the proposed HIF line detection method, a comparative analysis with other existing methods is conducted [30]. This comparison focuses on key aspects such as the percentage of success, advantages, and disadvantages of each method. By doing so, we can clearly demonstrate the superiority and innovation of the proposed method in addressing high-impedance fault line selection challenges in new distribution networks.
5.5. Comparative Analysis of Line Detection Effect of Different Clustering Algorithms
A comparative analysis is conducted among K-means clustering [31], fuzzy C-means clustering, hierarchical clustering, spectral clustering, and DBSCAN to evaluate their line detection performance. Two metrics are selected to assess clustering algorithm performance: clustering quality and line detection accuracy. Clustering quality is quantified using the silhouette coefficient, which comprehensively evaluates intra-cluster compactness and inter-cluster separation. Higher values of this coefficient indicate superior clustering effectiveness. Simulation data are processed through the five clustering algorithms, and their clustering outcomes are analyzed. The line detection accuracy rates and silhouette coefficients are summarized in Table 5.

Table 5.
Comparison of line selection effects for different methods.
As shown in Table 6, the DBSCAN clustering algorithm demonstrates superior performance compared to other clustering algorithms. Both line detection accuracy and clustering quality are significantly improved.

Table 6.
Comparison of evaluation indicators for different clustering algorithms.
6. Conclusions
This paper proposes an HIF fault line selection method driven by the symmetry of the CTW spectrum. Innovatively, CTW spectral waveforms are utilized for feeder selection in distribution networks. The method remains unaffected by weak fault signals within short data windows caused by renewable energy integration and is applicable to common neutral-grounding methods and renewable energy operation scenarios, facilitating direct implementation in engineering applications with renewable energy integration. Based on Manhattan distance and the DBSCAN clustering algorithm, a fast, simple, and intuitive line selection principle is formed. By using the qualitative dissimilarity of spectral waveform characteristics to replace quantitative threshold calculations, it can accurately identify the feeders of modern distribution networks under different fault locations, fault types, fault resistances, and noise interferences. This fundamentally solves the problem of difficult threshold setting for fault line selection, caused by renewable energy integration and high resistance conditions, and realizes high-sensitivity, high-reliability, and high-impedance grounding fault line selection for modern distribution networks simultaneously.
However, there are still some limitations. Currently, the performance of this method in extremely complex scenarios with multiple simultaneous HIFs and strong noise interference has not been fully verified. Although it works well in common cases, these extreme situations may pose challenges to its accuracy and reliability. This limitation indicates that while the method is effective for typical HIF detections in new distribution networks, its robustness in ultra-complex scenarios needs further exploration. For future research, we plan to expand the research to include such extreme fault scenarios. We will also explore the integration of this method with other advanced smart grid technologies, such as real-time big data analytics for grid operations, to enhance its applicability and accuracy.
Author Contributions
Conceptualization, M.X. and J.Z.; methodology, M.X.; software, J.Z.; validation, M.X., J.Z. and Z.Z.; formal analysis, M.X.; investigation, Q.Z.; resources, L.D.; data curation, F.P.; writing—original draft preparation, M.X.; writing—review and editing, M.X.; visualization, J.Z.; supervision, J.Z.; project administration, J.Z.; funding acquisition, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meng, L.; Yang, X.; Zhu, J.; Wang, X.; Meng, X. Network Partition and Distributed Voltage Coordination Control Strategy of Active Distribution Network System Considering Photovoltaic Uncertainty. Appl. Energy 2024, 362, 122846. [Google Scholar] [CrossRef]
- Xiaotian, L.U.; Jinrui, T.; Xin, Y.I.N.; Yunhui, H.; Keliang, Z.; Chengqing, Y. Single-phase-to-ground Fault Section Location in New-type Distribution System Based on Multidimensional Time-frequency Distribution Characteristics. High Volt. Eng. 2025, 51, 903–914. [Google Scholar]
- Galvez, C.; Abur, A. Fault Location in Active Distribution Networks Containing Distributed Energy Resources (DERs). IEEE Trans. Power Deliv. 2021, 36, 3128–3139. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, S.; Li, Z.; Ren, J.; Geng, S. A Novel Steady-State-Component-Based Current Differential Protection Scheme for Petal-Shaped Distribution Network with Inverter-Interfaced Distributed Generators. CSEE J. Power Energy Syst. 2022, 8, 1–11. [Google Scholar]
- Han, X.; Yan, X.; Ma, C.; Han, H. Fault Line Selection Method Based on Steady-State Zero-Sequence Voltage. In Proceedings of the International Conference on Energy Technology and Electrical Power (ETEP 2024), Guangzhou, China, 20–22 December 2024; SPIE: Bellingham, WA, USA; Volume 13566, pp. 384–389. [Google Scholar]
- Liang, Y.; Chen, H.; Ding, J.; Xu, Z.; Li, H.; Wang, G. Transient Analytical Method for Single-Ended Fault Location of AC Transmission Lines Considering Fuzzy Constraints of Fault Features. J. Mod. Power Syst. Clean Energy 2024, 10, 1–13. [Google Scholar]
- Tang, Y.; Chang, Y.; Tang, J.; Xu, B.; Ye, M.; Yang, H. A Novel Faulty Phase Selection Method for Single-Phase-to-Ground Fault in Distribution System Based on Transient Current Similarity Measurement. Energies 2021, 14, 4695. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, T.; Wang, Y. A Novel Fault Location Method for Distribution Networks with Distributed Generations Based on the Time Matrix of Traveling-Waves. Prot. Control. Mod. Power Syst. 2022, 7, 46. [Google Scholar] [CrossRef]
- Liu, F.; Xie, L.; Yu, K.; Wang, Y.; Zeng, X.; Bi, L.; Liu, F.; Tang, X. A Novel Fault Location Method Based on Traveling Wave for Multi-Branch Distribution Network. Electr. Power Syst. Res. 2023, 224, 109753. [Google Scholar] [CrossRef]
- Wang, S.; Liu, C.; Wei, S. Research on Fault Line Selection Method Based on Steady State Variables. AIP Adv. 2024, 14, 075112. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, W. Fault Line Selection of Resonant Grounding System Using Transient Zero-Sequence Current Waveform Characteristics. In Proceedings of the 2022 International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 23–25 September 2022; pp. 278–283. [Google Scholar]
- Guang, F.; Tinglong, G.; Lei, W.; Yongduan, X.U.E.; Xiaoyong, Y.U.; Bingyin, X.U. Grounding Fault Line Selection of Non-solidly Grounding System Based on Linearity of Current and Voltage Derivative. Power Syst. Technol. 2019, 45, 302–311. [Google Scholar]
- Wei, L.; Jia, W.; Jiao, Y. Single-Phase Fault Line Selection Scheme of a Distribution System Based on Fifth Harmonic and Admittance Asymmetry. Power Syst. Prot. Control. 2020, 48, 77–83. [Google Scholar]
- Li, Z.; Wan, J.; Wang, P.; Weng, H.; Li, Z. A Novel Fault Section Locating Method Based on Distance Matching Degree in Distribution Network. Prot. Control. Mod. Power Syst. 2021, 6, 1–11. [Google Scholar] [CrossRef]
- Xia, Y.; Li, Z.; Wang, S.; Sun, J.; Guo, X. Traveling Wave Inversion Method of Power Line Faults. Int. J. Electr. Power Energy Syst. 2023, 149, 109025. [Google Scholar] [CrossRef]
- Wang, Z.; Razzaghi, R.; Paolone, M.; Rachidi, F. Electromagnetic Time Reversal Similarity Characteristics and Its Application to Locating Faults in Power Networks. IEEE Trans. Power Deliv. 2020, 35, 1735–1748. [Google Scholar] [CrossRef]
- Yang, D.; Lu, B.; Lu, H. High-Resistance Grounding Fault Detection and Line Selection in Resonant Grounding Distribution Network. Electronics 2023, 12, 4066. [Google Scholar] [CrossRef]
- Deng, F.; Zu, Y.; Mao, Y.; Zeng, X.; Li, Z.; Tang, X.; Wang, Y. A Method for Distribution Network Line Selection and Fault Location Based on a Hierarchical Fault Monitoring and Control System. Int. J. Electr. Power Energy Syst. 2020, 123, 106061. [Google Scholar] [CrossRef]
- Tang, L.; Dong, X.; Luo, S.; Shi, S.; Wang, B. A New Differential Protection of Transmission Line Based on Equivalent Travelling Wave. IEEE Trans. Power Deliv. 2017, 32, 1359–1369. [Google Scholar] [CrossRef]
- Angrisani, L.; D’Apuzzo, M.; Grillo, D.; Pasquino, N.; Schiano Lo Moriello, R. A New Time-Domain Method for Frequency Measurement of Sinusoidal Signals in Critical Noise Conditions. Measurement 2014, 49, 368–381. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Zeng, D.; Li, H. High-Impedance Ground Faulted Line-Section Location Method for a Resonant Grounding System Based on the Zero-Sequence Current’s Declining Periodic Component. Int. J. Electr. Power Energy Syst. 2020, 119, 105910. [Google Scholar] [CrossRef]
- Jiang, B.; Dong, X.; Shi, S. A Method of Single Phase to Ground Fault Feeder Selection Based on Single Phase Current Traveling Wave for Distribution Lines. Proc. CSEE 2014, 34, 6216–6227. [Google Scholar]
- Zichang, L.; Yadong, L.; Yingjie, Y.; Peng, W.; Xiuchen, J. An Identification Method for Asymmetric Faults With Line Breaks Based on Low-Voltage Side Data in Distribution Networks. IEEE Trans. Power Deliv. 2021, 36, 3629–3639. [Google Scholar] [CrossRef]
- Yalçın, F.; Yıldırım, Y. A Study of Symmetrical and Unsymmetrical Short Circuit Fault Analyses in Power Systems. Sak. Univ. J. Sci. 2019, 23, 879–895. [Google Scholar] [CrossRef]
- Wang, W.; Gao, X.; Fan, B.; Zeng, X.; Yao, G. Faulty Phase Detection Method Under Single-Line-to-Ground Fault Considering Distributed Parameters Asymmetry and Line Impedance in Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 1513–1522. [Google Scholar] [CrossRef]
- Guo, M.-F.; Cai, W.-Q.; Zheng, Z.-Y.; Wang, H. Fault Phase Selection Method Based on Single-Phase Flexible Arc Suppression Device for Asymmetric Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 4548–4558. [Google Scholar] [CrossRef]
- Jankovski, M.; Popov, M.; Godefrooi, J.; Parabirsing, E.; Wierenga, E.; Lekić, A. Novel Busbar Protection Scheme for Impedance-Earthed Distribution Networks. Electr. Power Syst. Res. 2023, 223, 109569. [Google Scholar] [CrossRef]
- Mousaviyan, I.; Seifossadat, S.G.; Saniei, M. Traveling Wave-Based Algorithm for Fault Detection, Classification, and Location in STATCOM-Compensated Parallel Transmission Lines. Electr. Power Syst. Res. 2022, 210, 108118. [Google Scholar] [CrossRef]
- Kersting, W.H. Distribution System Modeling and Analysis. In Electric Power Generation, Transmission, and Distribution; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-315-22242-4. [Google Scholar]
- Wang, Y.; Feng, C.; Liu, J.; Dong, X.; Yuan, J.; Jiao, Z. Faulty Line Detection for Cross-line Same-phase Successive Ground Faults in Distribution Network Based on Transient Characteristics. IET Gener. Transm. Distrib. 2024, 18, 1624–1640. [Google Scholar] [CrossRef]
- Ni, Y.; Zeng, X.; Liu, Z.; Yu, K.; Xu, P.; Wang, Z.; Zhuo, C.; Huang, Y. Faulty Feeder Detection of Single Phase-to-Ground Fault for Distribution Networks Based on Improved K-Means Power Angle Clustering Analysis. Int. J. Electr. Power Energy Syst. 2022, 142, 108252. [Google Scholar] [CrossRef]
- Wenjun, G.; Heng, W.; Ying, Z. Fault Line Selection of Small Current Grounding System Research Based on Zero Sequence Circuit Current Phase. J. Phys. Conf. Ser. 2024, 2872, 012049. [Google Scholar] [CrossRef]
- Xie, L.; Luo, L.; Ma, J.; Li, Y.; Zhang, M.; Zeng, X.; Cao, Y. A Novel Fault Location Method for Hybrid Lines Based on Traveling Wave. Int. J. Electr. Power Energy Syst. 2022, 141, 108102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).