Stochastic Programming-Based Annual Peak-Regulation Potential Assessing Method for Virtual Power Plants
Abstract
1. Introduction
1.1. Background
1.2. Recent Works
1.3. Motivations and Contributions
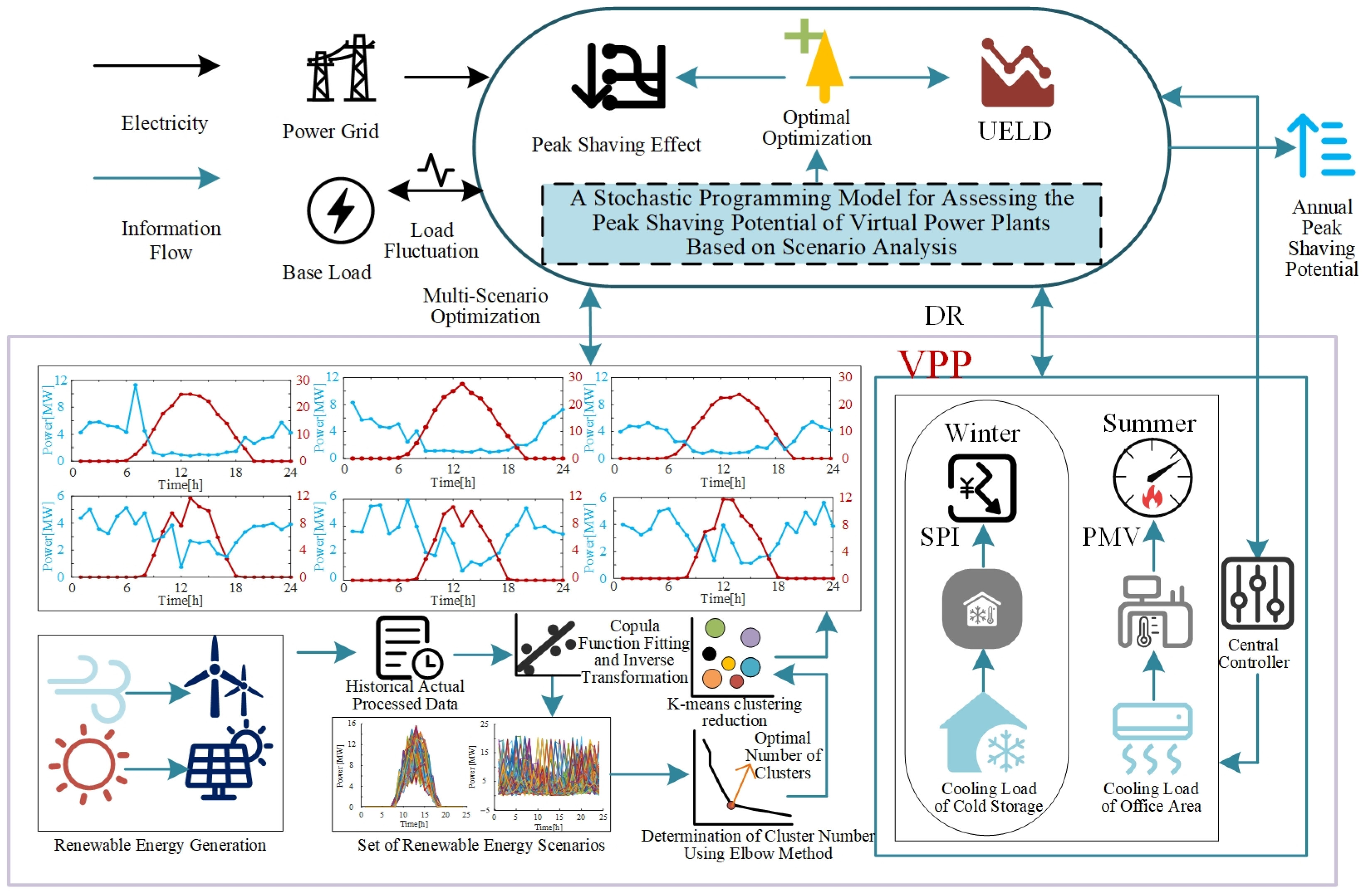
2. Basic Structure of the VPP
Total Framework with Diverse Cooling Loads
3. Scene Construction Considering Scenery Uncertainty and Correlation
3.1. Density Estimation
3.2. Calculation of the Joint Distribution Function of Scenery
3.3. K-Means Clustering Reduction
4. Stochastic Programming Model of a Multi-Scenario-Based VPP
4.1. Objective Function
4.2. Flexible Load Model
4.2.1. Human Comfort Indicators
4.2.2. Selling Pressure Indicator
4.2.3. Constraint Conditions
- (1)
- Electric power balance constraint:
- (2)
- Cold equilibrium constraint:
- (3)
- Refrigerator output constraint:
- (4)
- Constraints on electricity purchase from the grid:
4.3. Indicators for Peak-Regulation Potential
4.4. Solving the Model
5. Case Studies
5.1. Case Overview
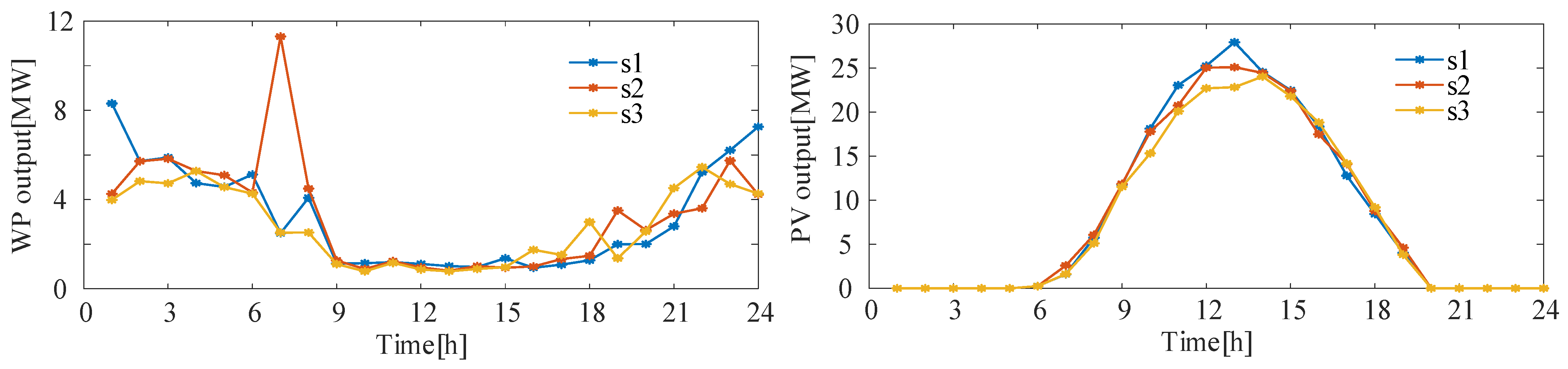
5.2. Generation of Typical Output Scenarios of New Energy
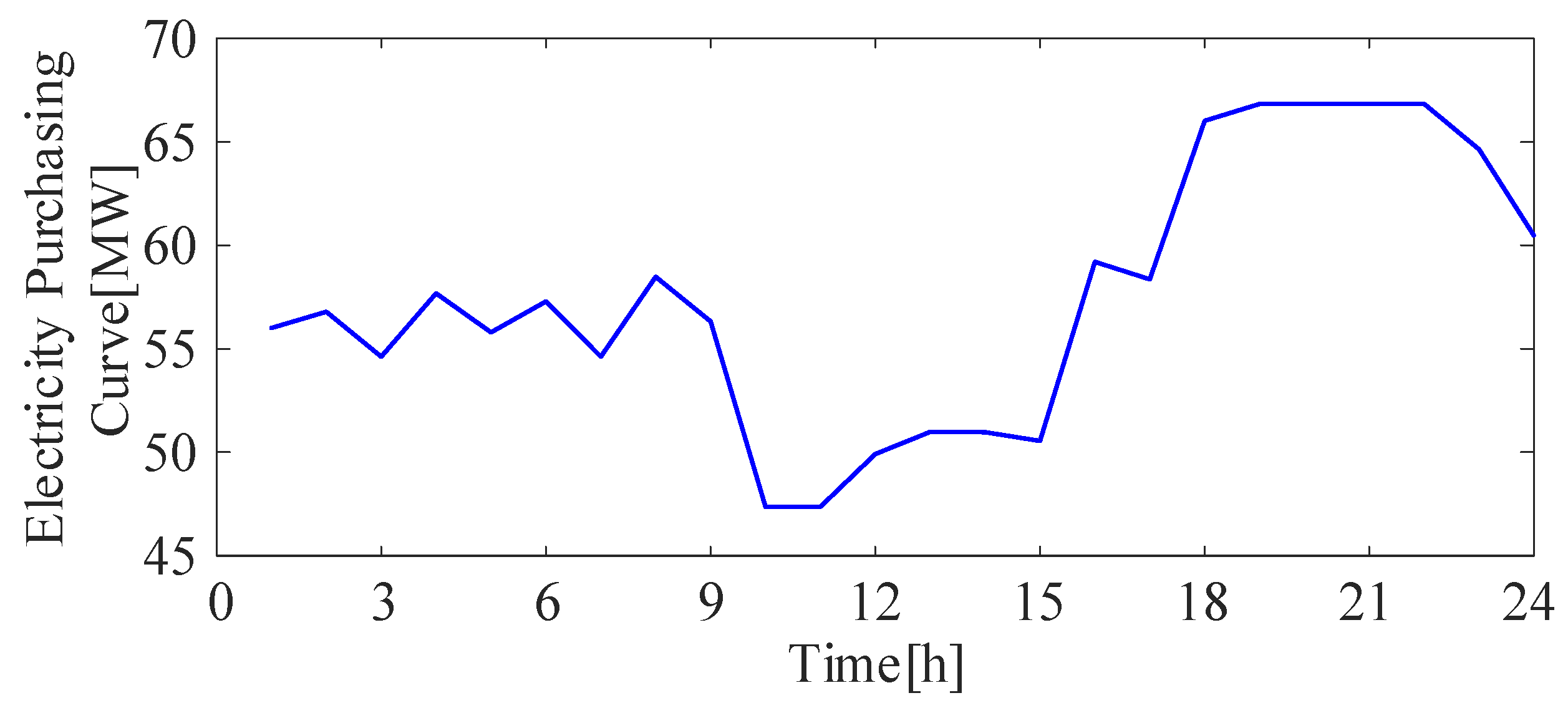
5.3. Planning Results
5.4. Validation of Indicator Nondominations
5.4.1. Validation of the Nondomination of Indicators
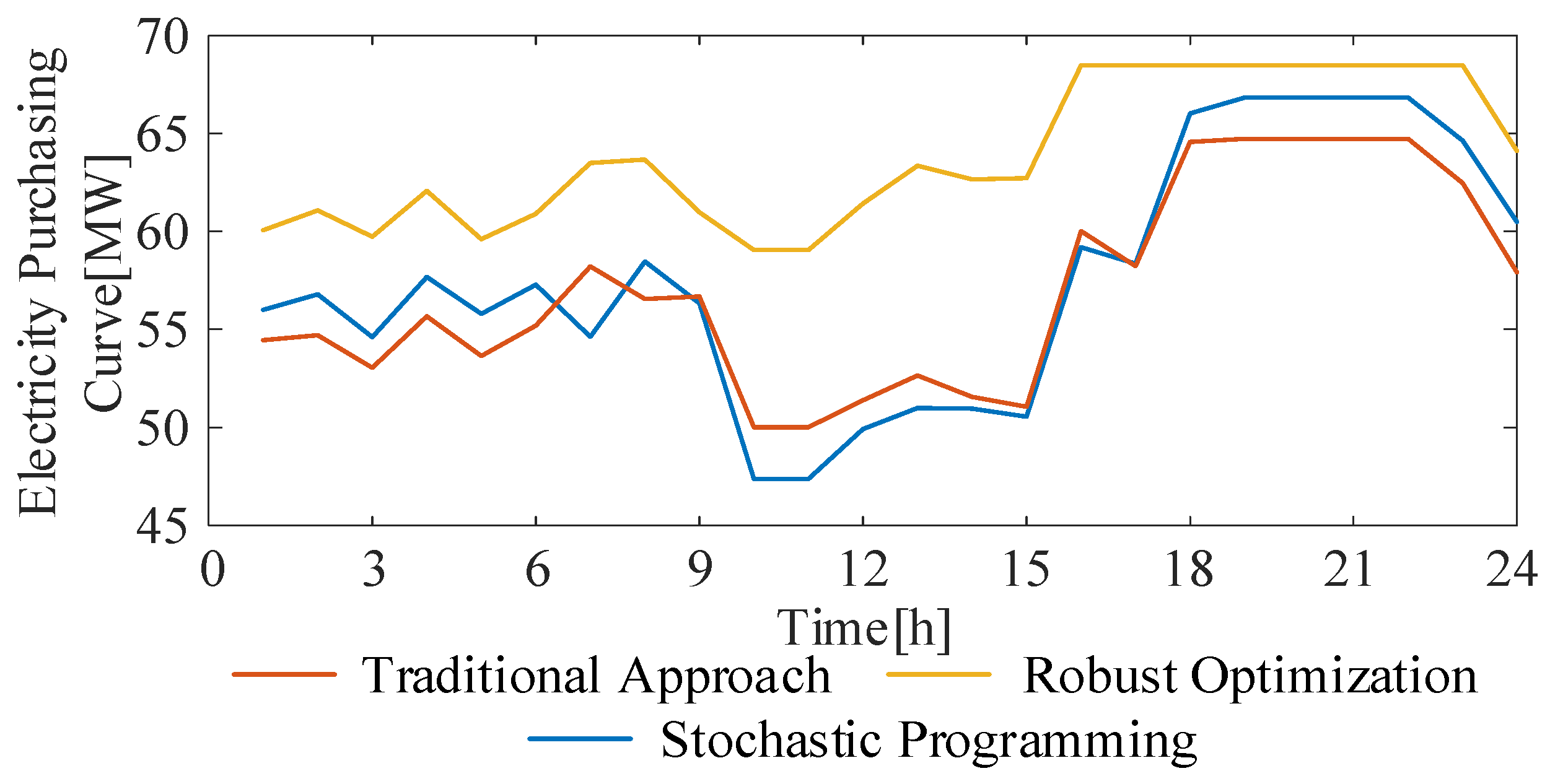
5.4.2. Comparison and Validation of the Planning Methods
5.5. Effect of Temperature-Controlled Flexible Load Change on Peak-Shaving Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-Timescale Security Evaluation and Regulation of Integrated Electricity and Heating System. IEEE Trans. Smart Grid 2025, 16, 1088–1099. [Google Scholar] [CrossRef]
- Qiu, W.; Yin, H.; Dong, Y.; Wei, X.; Liu, Y.; Yao, W. Synchro-Waveform-Based Event Identification Using Multi-Task Time-Frequency Transform Networks. IEEE Trans. Smart Grid 2025, 16, 2647–2658. [Google Scholar] [CrossRef]
- Arteconi, A.; Polonara, F. Assessing the Demand Side Management Potential and the Energy Flexibility of Heat Pumps in Buildings. Energies 2018, 11, 1846. [Google Scholar] [CrossRef]
- Navesi, R.B.; Naghibi, A.F.; Zafarani, H.; Tahami, H.; Pirouzi, S. Reliable operation of reconfigurable smart distribution network with real-time pricing-based demand response. Electr. Power Syst. Res. 2025, 241, 111341. [Google Scholar] [CrossRef]
- Vanhoudt, D.; Geysen, D.; Claessens, B.; Leemans, F.; Jespers, L.; Van Bael, J. An actively controlled residential heat pump: Potential on peak shaving and maximization of self-consumption of renewable energy. Renew. Energy 2014, 63, 531–543. [Google Scholar] [CrossRef]
- Sæther, G.; Granado, P.C.D.; Zaferanlouei, S. Peer-to-peer electricity trading in an industrial site: Value of buildings flexibility on peak load reduction. Energy Build. 2021, 236, 110737. [Google Scholar] [CrossRef]
- Zheng, M.; Meinrenken, C.J.; Lackner, K.S. Agent-based model for electricity consumption and storage to evaluate economic viability of tariff arbitrage for residential sector demand response. Appl. Energy 2014, 126, 297–306. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, R.; Kong, D.; Guo, H. Coordinated Operation Strategy for Equitable Aggregation in Virtual Power Plant Clusters with Electric Heat Demand Response Considered. Energies 2024, 17, 2640. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Huang, M.; Yang, S.; Zhu, J.; Zhang, M.; Chen, D. Research on day-ahead optimal dispatching of virtual power plants considering the coordinated operation of diverse flexible loads and new energy. Energy 2024, 297, 131235. [Google Scholar] [CrossRef]
- Luo, Z.; Hong, S.; Ding, Y. A data mining-driven incentive-based demand response scheme for a virtual power plant. Appl. Energy 2019, 239, 549–559. [Google Scholar] [CrossRef]
- Li, D.; Wang, M.; Shen, Y.; Li, F.; Lin, S.; Zhou, B. Low-carbon operation strategy of virtual power plant considering progressive demand response. Int. J. Electr. Power Energy Syst. 2024, 161, 110176. [Google Scholar] [CrossRef]
- Su, S.; Hu, G.; Li, X.; Li, X.; Xiong, W. Electricity-Carbon Interactive Optimal Dispatch of Multi-Virtual Power Plant Considering Integrated Demand Response. Energy Eng. 2023, 120, 2343–2368. [Google Scholar] [CrossRef]
- Mei, S.; Tan, Q.; Liu, Y.; Trivedi, A.; Srinivasan, D. Optimal bidding strategy for virtual power plant participating in combined electricity and ancillary services market considering dynamic demand response price and integrated consumption satisfaction. Energy 2023, 284, 128592. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Tang, L.; Sun, W.; Li, B. A Wasserstein based two-stage distributionally robust optimization model for optimal operation of CCHP micro-grid under uncertainties. Int. J. Electr. Power Energy Syst. 2020, 119, 105941. [Google Scholar] [CrossRef]
- Parvar, S.S.; Nazaripouya, H. Optimal Operation of Battery Energy Storage Under Uncertainty Using Data-Driven Distributionally Robust Optimization. Electr. Power Syst. Res. 2022, 211, 108180. [Google Scholar] [CrossRef]
- Aghdam, F.H.; Javadi, M.S.; Catalão, J.P.S. Optimal stochastic operation of technical virtual power plants in reconfigurable distribution networks considering contingencies. Int. J. Electr. Power Energy Syst. 2023, 147, 108799. [Google Scholar] [CrossRef]
- Wang, J.; Lei, T.; Qi, X.; Zhao, L.; Liu, Z. Chance-constrained optimization of distributed power and heat storage in integrated energy networks. J. Energy Storage 2022, 55, 105662. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Mallik, A. A two-stage stochastic programming approach for electric energy procurement of EV charging station integrated with BESS and PV. Electr. Power Syst. Res. 2024, 232, 110411. [Google Scholar] [CrossRef]
- Al-Lawati, R.A.H.; Faiz, T.I.; Noor-E-Alam, M. A nationwide multi-location multi-resource stochastic programming based energy planning framework. Energy 2024, 295, 130898. [Google Scholar] [CrossRef]
- Ebeed, M.; Alhejji, A.; Kamel, S.; Jurado, F. Solving the Optimal Reactive Power Dispatch Using Marine Predators Algorithm Considering the Uncertainties in Load and Wind-Solar Generation Systems. Energies 2020, 13, 4316. [Google Scholar] [CrossRef]
- Lin, S.; Liu, C.; Shen, Y.; Li, F.; Li, D.; Fu, Y. Stochastic Planning of Integrated Energy System via Frank-Copula Function and Scenario Reduction. IEEE Trans. Smart Grid 2022, 13, 202–212. [Google Scholar] [CrossRef]
- Wan, Q.; Yu, Y. Power load pattern recognition algorithm based on characteristic index dimension reduction and improved entropy weight method. Energy Rep. 2020, 6, 797–806. [Google Scholar] [CrossRef]
- Ismkhan, H. I-k-means−+: An iterative clustering algorithm based on an enhanced version of the k-means. Pattern Recognit. 2018, 79, 402–413. [Google Scholar] [CrossRef]
- Onumanyi, A.J.; Molokomme, D.N.; Isaac, S.J.; Abu-Mahfouz, A.M. AutoElbow: An Automatic Elbow Detection Method for Estimating the Number of Clusters in a Dataset. Appl. Sci. 2022, 12, 7515. [Google Scholar] [CrossRef]
- Duan, C.; Ding, X.; Shi, F.; Xiao, X.; Duan, P. PMV-based fuzzy algorithms for controlling indoor temperature. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 1492–1496. [Google Scholar]
- Donaisky, E.; Oliveira, G.H.C.; Freire, R.Z.; Mendes, N. PMV-Based Predictive Algorithms for Controlling Thermal Comfort in Building Plants. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 182–187. [Google Scholar]
- Gormley, R.; Walshe, T.; Hussey, K.; Butler, F. The Effect of Fluctuating vs. Constant Frozen Storage Temperature Regimes on Some Quality Parameters of Selected Food Products. LWT—Food Sci. Technol. 2002, 35, 190–200. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, J.; Qiu, Z.; Yu, Z.; Cui, Q.; Tong, X. Two-Stage Robust Optimization for Large Logistics Parks to Participate in Grid Peak Shaving. Symmetry 2024, 16, 949. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Z.; Meng, Q.; Wang, Y.; Li, Y. Reinforcement learning of room temperature set-point of thermal storage air-conditioning system with demand response. Energy Build. 2022, 259, 111903. [Google Scholar] [CrossRef]

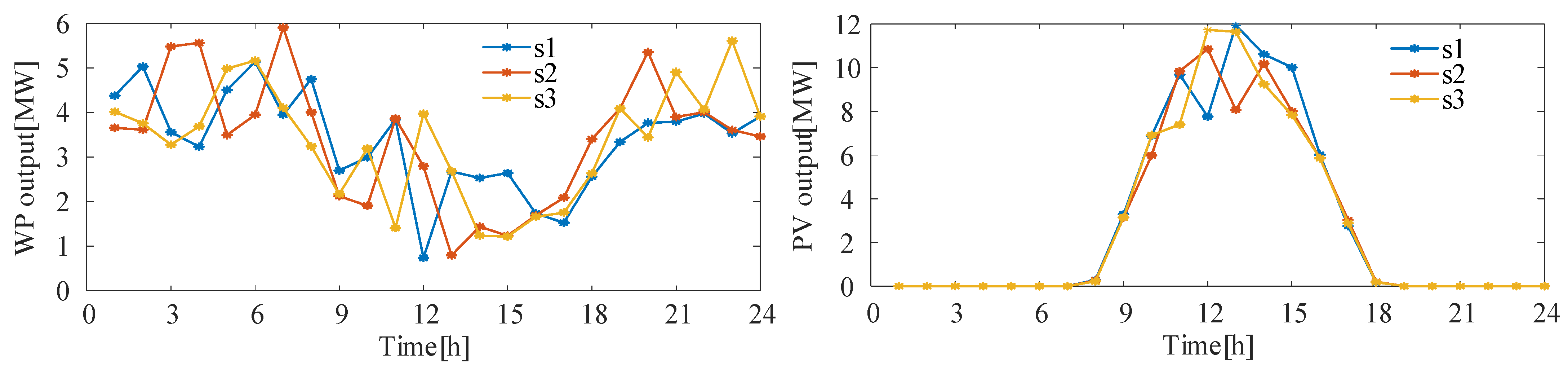

| Fields | Contributions | |
|---|---|---|
| Demand Response | Thermal flexibility | Heat pump flexibility potential assessed [3] Peak-shaving participation studied [5] |
| Dynamic pricing | Distribution network peak shaving via pricing [4] | |
| Energy storage | Industrial storage sharing proposed [6] Residential storage economics analyzed [7] | |
| VPP | Cluster operation | Multi-VPP cost–potential optimization modeled [8] |
| Energy aggregation | Renewable–storage–pumped hydro coordination [9] Gas turbine integration studied [11] | |
| Incentive design | Adaptive pricing schemes developed [10] | |
| Integrated dispatch | Electricity–carbon–user satisfaction model [12] | |
| Pricing strategy | Dynamic pricing–satisfaction framework [13] | |
| Uncertainty Management | Robust optimization | Wasserstein-based DRO method developed [14] |
| Chance constraints | Probabilistic constraints applied [16,17] | |
| Scenario generation | Renewable-load uncertainty scenarios created [18,19,20] |
| PMV Value | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| Thermal sensation | Cold | Cool | Slightly cool | Neutral | Slightly warm | Warm | Hot |
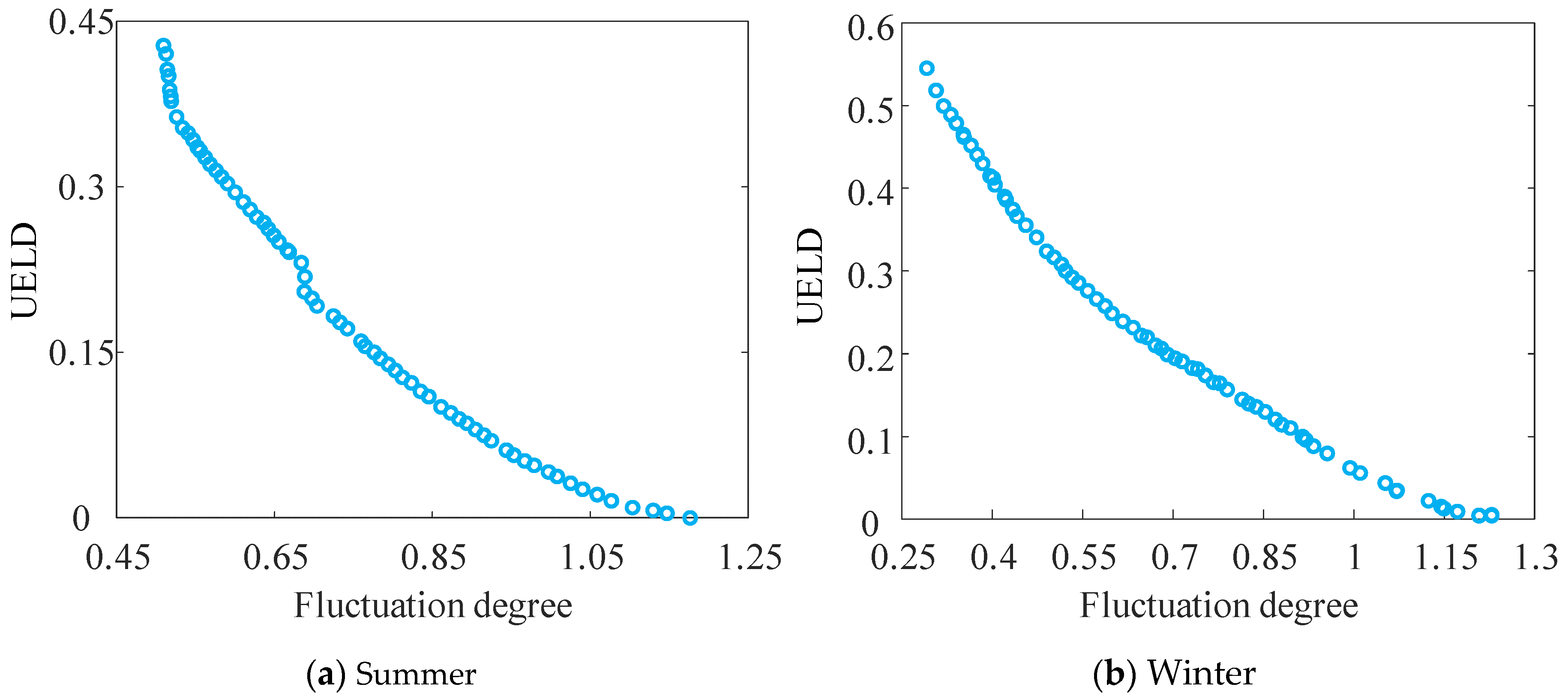
| Scenario | Daily Cumulative Power Generation [MW] | FSD Optimization Effect | PVD Optimization Effect | UELD | |
|---|---|---|---|---|---|
| WP | PV | ||||
| 1 | 77.65 | 204.30 | 28.78% | 35.01% | 0.238 |
| 2 | 80.31 | 201.18 | 23.35% | 28.24% | 0.150 |
| 3 | 68.34 | 191.21 | 21.49% | 25.66% | 0.224 |
| Scenario | Daily Cumulative Power Generation [MW] | FSD Optimization Effect | PVD Optimization Effect | UELD | |
|---|---|---|---|---|---|
| WP | PV | ||||
| 1 | 80.79 | 69.42 | 17.06% | 34.65% | 0.226 |
| 2 | 81.42 | 65.44 | 9.71% | 34.92% | 0.235 |
| 3 | 80.18 | 67.05 | 8.97% | 19.28% | 0.229 |
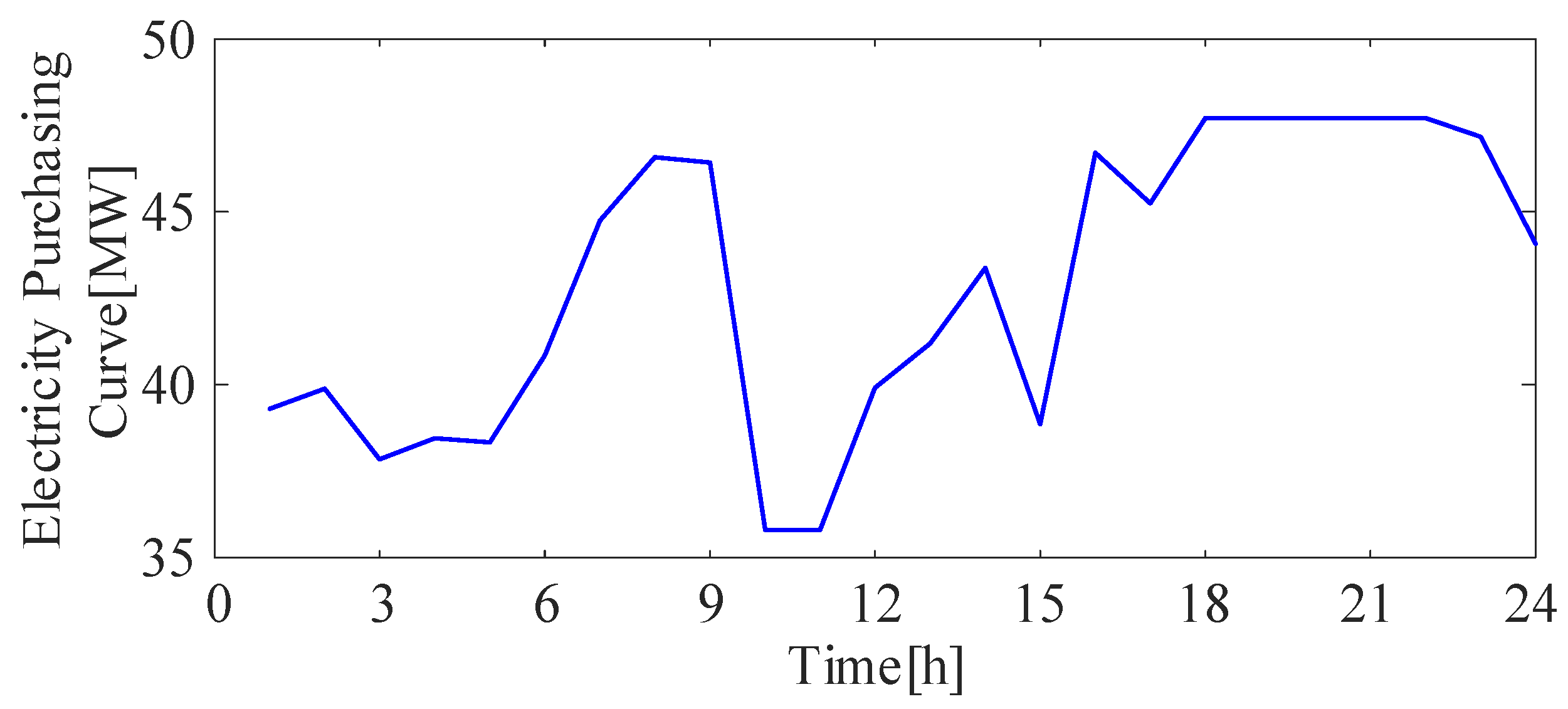
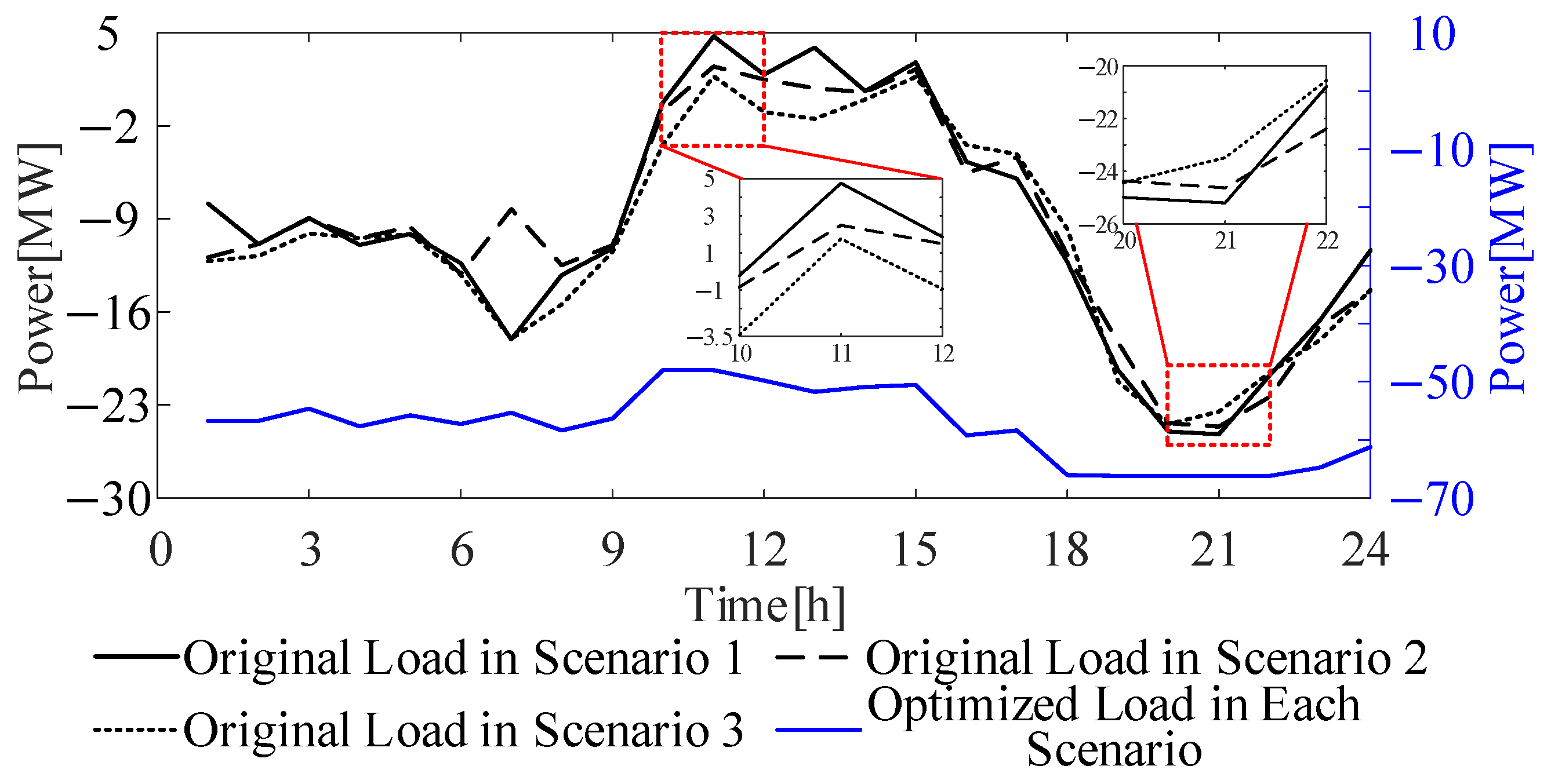
| Planning Methods | Proportion of Load Drop During Peak Hour | Proportion of Load Increase During Trough Hours | Daily Electricity Purchase [MW] | UELD |
|---|---|---|---|---|
| SP | 23.87% | 22.88% | 1380.76 | 0.209 |
| DO | 25.19% | 23.63% | 1366.94 | 0.125 |
| RO | 10.63% | 10.21% | 1531.82 | 0.199 |
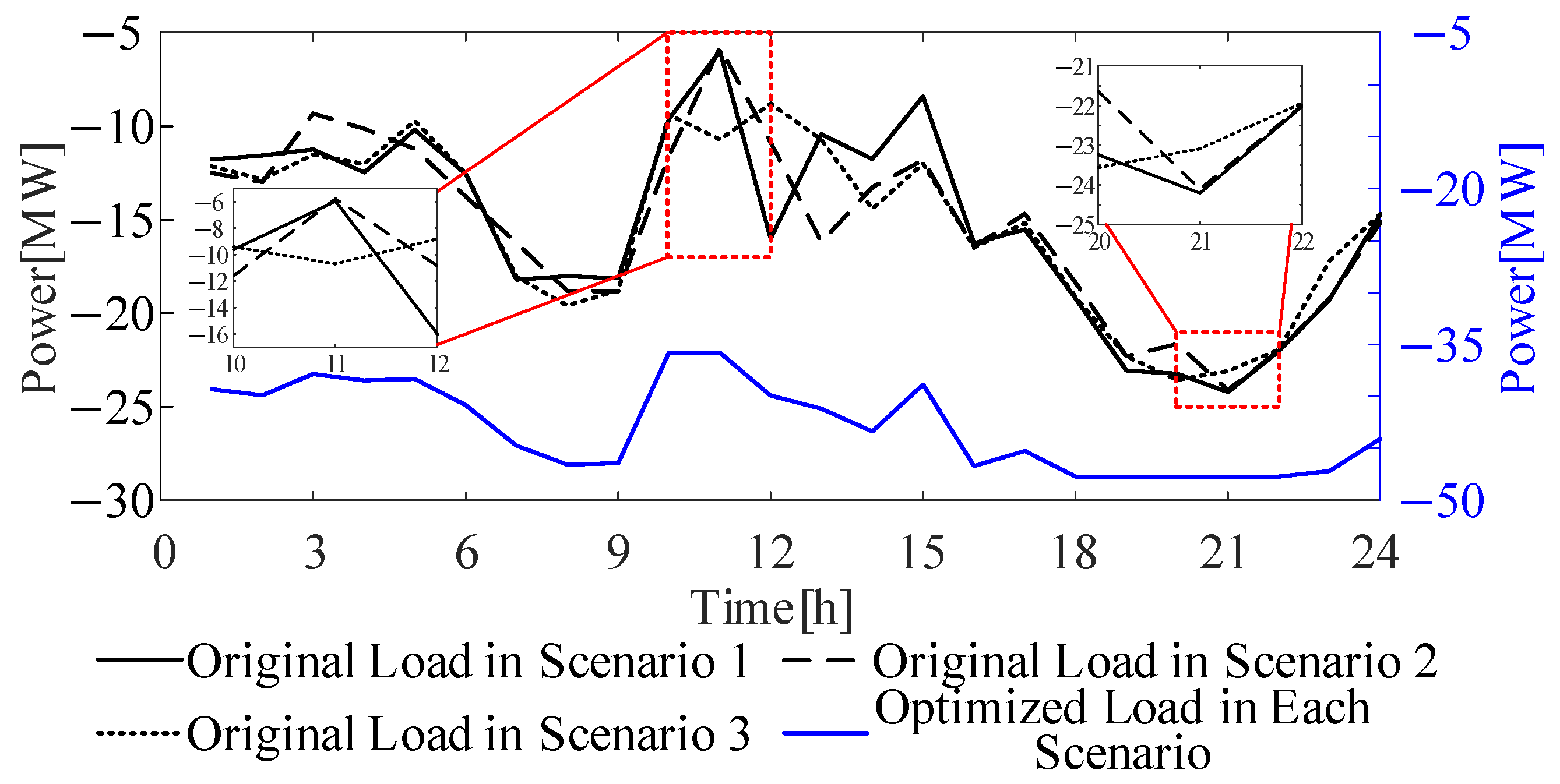
| Planning Methods | Peak Hour Share Load Reduction Ratio | Share of Trough Time Load Increase Ratio | Daily Electricity Purchase [MW] | UELD |
|---|---|---|---|---|
| SP | 8.08% | 8.01% | 1029.13 | 0.167 |
| DO | 9.61% | 9.68% | 1012.94 | 0.142 |
| RO | 5.02% | 4.52% | 1147.93 | 0.169 |
| Planning Methods | Proportion of Load Drop During Peak Hour | Proportion of Load Increase During Trough Hours |
|---|---|---|
| SP | 18.61% | 17.92% |
| DO | 20.00% | 18.98% |
| RO | 8.76% | 8.31% |
| Scenario | Comprehensive Optimization Effect | ||
|---|---|---|---|
| FSD Optimization Effect | PVD Optimization Effect | UELD | |
| Scenario I | 22.74% | 26.90% | 0.206 |
| Scenario II | 24.57% | 29.66% | 0.209 |
| Scenario III | 26.54% | 32.41% | 0.217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Y.; Liu, C.; Tong, X.; Xie, Y. Stochastic Programming-Based Annual Peak-Regulation Potential Assessing Method for Virtual Power Plants. Symmetry 2025, 17, 683. https://doi.org/10.3390/sym17050683
Qu Y, Liu C, Tong X, Xie Y. Stochastic Programming-Based Annual Peak-Regulation Potential Assessing Method for Virtual Power Plants. Symmetry. 2025; 17(5):683. https://doi.org/10.3390/sym17050683
Chicago/Turabian StyleQu, Yayun, Chang Liu, Xiangrui Tong, and Yiheng Xie. 2025. "Stochastic Programming-Based Annual Peak-Regulation Potential Assessing Method for Virtual Power Plants" Symmetry 17, no. 5: 683. https://doi.org/10.3390/sym17050683
APA StyleQu, Y., Liu, C., Tong, X., & Xie, Y. (2025). Stochastic Programming-Based Annual Peak-Regulation Potential Assessing Method for Virtual Power Plants. Symmetry, 17(5), 683. https://doi.org/10.3390/sym17050683






