Abstract
In the research and practice of integrated scheduling problems, the tree structure of complex products usually presents an asymmetric and complex form. This asymmetry is mainly reflected in the hierarchical relationship between the various components of the product, the degree of dependence, and the sequence of production processes. Existing studies often neglect that leaf nodes with the lowest layer priority can be scheduled at any moment, leading to underutilization of parallelism potential under symmetric structures and exacerbation of critical path delays under asymmetric structures. Aiming at solving this kind of problem, an integrated scheduling algorithm based on the improved Floyd algorithm (ISA-IFA) is proposed. According to the improved Floyd algorithm, the algorithm proposed a path-weighted strategy, which constructs the vertical path value according to the processing time of the process itself. Combined with the proposed process scheduling advantage strategy, the leaf node process is especially emphasized as the priority scheduling object, which makes the connection between the processes more closely, and then significantly reduces the idle time of the equipment. The empirical results show that the ISA-IFA algorithm shortens the completion time of complex products and simultaneously improves the equipment utilization rate to 55.9%, verifying its effectiveness in dynamic scheduling and resource co-optimization.
1. Introduction
Intelligent manufacturing is the core technology and strategic main line that is leading the transformation of the manufacturing industry from large to strong and shoulders the heavy responsibility of building manufacturing power. In recent years, countries have been committed to accelerating the comprehensive integration of digital technology, digital economy, information technology, artificial intelligence, and manufacturing, and these strategic measures have effectively accelerated enterprises to embark on a new journey of digital innovation and intelligence [1,2,3,4,5,6,7,8]. Vigorously developing the intelligent manufacturing industry is the core action to implement the strategy of manufacturing power, and it is also a critical path to comply with the global development trend and achieve the goal of transformation and upgrading.
To better solve the needs of the production and manufacturing of the products with strict constraints and tree-like structures (essentially a hierarchical acyclic topology based on a unique root node and strict unidirectional timing constraints between parent and child tasks), no matter whether the order is the single complex or small-batch variety, some experts have innovatively proposed integrated scheduling; that is, the processing and assembly are handled collaboratively, which breaks the limitation of the separation of traditional processes and achieves considerable research results [9,10,11,12,13,14,15,16,17,18,19,20,21]. In this model, symmetric tree structures exhibit uniformity in hierarchical relationships and process distribution, whereas asymmetric structures often arise from personalized design or complex constraints, leading to irregular layouts and dynamic resource allocation requirements. Traditional scheduling theory contrasts Flow-shop [22,23,24,25,26,27]—a rigid linear assembly line with fixed sequences for standardized mass production—against Job-shop [28,29,30,31,32], which adapts to multi-species small-batch needs via heterogeneous process paths but suffers from resource conflicts and exponential complexity. In comparison, integrated scheduling only focuses on complex products with a tree-like structure in both processing and assembly stages. Integrated scheduling is dedicated to solving a series of key scheduling problems in collaborative processing, involving the reasonable allocation and scheduling of limited resources (including equipment, personnel, etc.), aiming to optimize time efficiency and improve equipment utilization so as to achieve efficient production activities.
Despite advancements in existing research, integrated scheduling still faces key challenges: insufficient dynamic modeling of process dependencies, limited horizontal/vertical collaborative optimization in multi-level process trees, and inefficient equipment resource scheduling. These bottlenecks directly constrain production efficiency and socio-economic benefits, demanding urgent algorithmic innovations to bridge the current gaps. To solve the above problems, especially for the problem of asymmetric structure process trees in which there is the advantage that leaf node processes with low layer priority can be scheduled at any moment, this paper proposes a general integrated scheduling algorithm based on the improved Floyd algorithm (ISA-IFA). The main contributions are as follows:
- (1)
- The Floyd algorithm was improved to establish the scheduling sequence by taking the processing time of the immediate successor process as the path value of its adjacent processes;
- (2)
- In the aspect of vertical optimization, the path-weighted strategy is designed based on the improved Floyd algorithm, and the effect of horizontal and vertical optimization is improved by combining the position advantage of the leaf node process;
- (3)
- The scheduling advantage strategy is proposed. All devices are scheduled from the starting point, dynamically adjusting idle time for symmetric stability and asymmetric flexibility, and the utilization rate of the equipment is further improved.
This paper is structured as follows: Section 2 reviews related work; Section 3 proposes the integrated scheduling model based on an improved Floyd algorithm; Section 4 details the algorithm design; Section 5 conducts multi-dimensional simulation experiments and comparative analyses; Section 6 discusses the algorithm of this study in terms of previous experiments; and Section 7 condenses the findings and outlines future research directions.
2. Related Work
Within the domain of integrated scheduling of complex products, current research has conducted an in-depth study of the tree structure of complex products through computational complexity analysis and operations research methods, and scholars have achieved a large number of rigorous research results. For example, Zhang et al. [9] enhance horizontal parallelism via dynamic reorganization of adjacent processes, but their local neighborhood operations lack mechanisms for non-adjacent process synergy and vertical priority constraints, failing to address global dependencies in tree-like workflows. Zhang et al. [10] integrate supply chain and production scheduling using Q-learning-driven algorithms to improve local search, yet their framework struggles with multi-objective dynamic adjustments and supply chain disruption responses. Xie et al. [11] propose the tight workgroup linkage method to reduce equipment interference and avoid chain effects by balancing workloads incrementally. However, when the predecessor process is not unique, vertical serial process articulation weakens, increasing resource fragmentation risks. Xie et al. [12] introduce the reverse time-selection vertical optimization method. However, it ignores cross-hierarchical leaf-node scheduling advantages and generates excessive idle time when scheduling vertical serial processes with higher priority in the layer, thereby significantly lowering equipment utilization. Xie et al. [13] proposed the layer prioritization method but overemphasized the role of horizontal layer prioritization and weakened the tightness of the vertical which can be decomposed into subtrees for scheduling. Table 1 provides a comparative analysis of the above articles.

Table 1.
Comparison of related works.
References [9,10,11,12,13] enhance scheduling efficiency but face bottlenecks like limited local adaptability, poor dynamic responsiveness, and excessive equipment idling. Our algorithm achieves breakthroughs via triple innovations, offering a globally robust solution for complex tree-process scheduling.
3. Problem Analysis and Mathematical Modeling
The Floyd algorithm is an exact approach that employs the dynamic programming strategy to compute the shortest paths between all pairs of vertices in a weighted graph. The algorithm inherently accommodates asymmetric graphs characterized by directional edge weight discrepancies, wherein the weight of an edge from vertex A to vertex B may differ from its counterpart in the reverse direction. It can take a given starting vertex as the origin and describe the optimal path topology in the process of extending to other vertices. On the one hand, for any two vertices in a given weighted graph, the Floyd algorithm leads a logical and rigorous algorithm flow, and accurately solves the shortest path between them at one time, efficiently handling asymmetric edge weights to accurately solve the shortest path between them at one time, laying a solid foundation for subsequent applications. On the other hand, focusing on a single vertex and relying on the efficient iterative characteristics of dynamic planning, the Floyd algorithm quickly finds the way in the complex network maze, even in highly asymmetric environments, quickly calculates the shortest path from the vertex to all other vertices, and effectively solves the path planning problems in logistics distribution, network communication, and other fields. In addition, it can also reverse solve the shortest path from each vertex to a particular vertex, breaking the one-way limitation of the traditional algorithm and addressing asymmetry in graph topology, so it has been widely used in many fields [33,34,35,36,37,38].
3.1. Floyd Algorithm Weight Matrix
Let be a weighted digraph, where, is the weight of arc when there is no arc directly connected between and , . Then, the weight matrix, , of the network is constructed, where .
Take the Floyd algorithm network structure diagram shown in Figure 1 as an example, and its weight matrix is shown in Formula (1):
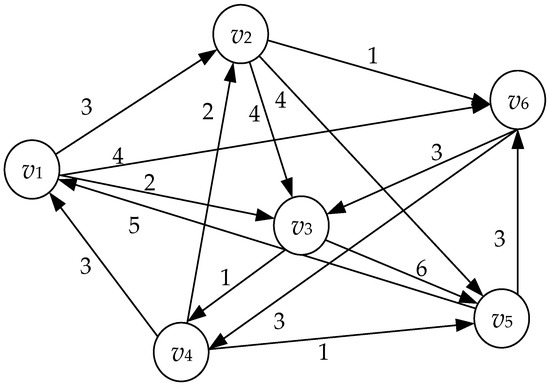
Figure 1.
Network structure diagram of Floyd algorithm.
3.2. Unidirectional Weighted Digraph
In the integrated scheduling, the tree structure of complex products includes a symmetric tree structure with a uniform layout and regular structure, which is used to reflect the balance and regularity of the product process in some aspects, as well as an asymmetric tree structure with obvious differences and irregular structure, which is used to express the uniqueness and complexity of the product process. Therefore, in the improved Floyd algorithm, the two-way weighted directed graph of traditional Floyd algorithm is optimized to unidirectional graph, as shown in Figure 2a. The structure diagram adjusted according to the tree structure is shown in Figure 2b, and the corresponding one-way weight matrix is shown in Formula (2). This structural adjustment strictly follows the process flow of “parent node child node”. It effectively avoids the invalid calculation of the reverse path in the tree structure and lays a structural foundation for the implementation of the subsequent dynamic pruning strategy.
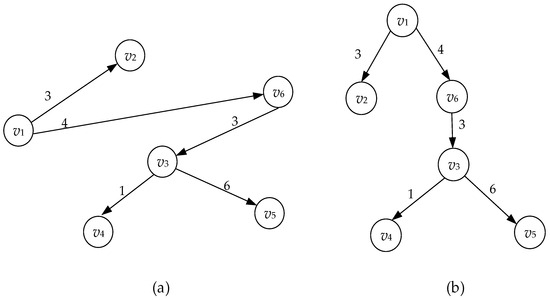
Figure 2.
Comparison of structural optimization of improved one-way Floyd algorithm: (a) Improved unidirectional structure diagram; (b) Improved unidirectional tree structure diagram.
3.3. Integrated Scheduling Analysis
Assume that there are m machines in the integrated scheduling system, and a tree-structured complex product with n processes needs to be the product. The specific requirements are as follows:
- (1)
- Each process contains a series of attributes: process numbers, machine numbers, and processing time. Additionally, the corresponding machine of each process is known, and the compulsory relationships between processes are known;
- (2)
- When the equipment executes the process processing, its operation time is clear, and once the processing begins, the continuous processing process will be maintained until the process is completed;
- (3)
- In addition to the process in the position of the leaf node, the sufficient and necessary condition for any other process to enter the processing stage is that in the processing sequence, all of its predecessor processes are completed;
- (4)
- When the final process on all the equipment has been completed, the time point at this time marks the end of the entire product processing cycle, that is, the total processing time of the product, the makespan.
In order to further optimize the overall processing time of a complex product, it is particularly important to plan the initial processing time of each process. However, in the integrated scheduling, whether dealing with process trees with mirrored hierarchies or process trees with irregular branches, the dependency constraints follow a universal pattern, except that the leaf node process located at the last end of the complex process tree is restricted by the immediate successor processes and the root node process located at the beginning position of the process tree is restricted by its immediate predecessor process, all the rest of the node processes are facing the double-constraint fetters built by the immediate predecessor and successor processes. In the process tree with symmetrical structure, these dual constraints form balanced parallelism opportunities, while in the process tree with asymmetric structure, they require dynamic scheduling to resolve conflicting resource demands. Symmetric structures are essentially degenerate forms of asymmetric topologies. And only when its immediate predecessor process (group) has successfully completed the processing can it start processing.
Multilevel dependence, resource competition, and dynamic constraints of complex product processes implement orderly and reasonable scheduling through dynamic priority scheduling and multi-constraint co-optimization to determine the optimal processing time nodes of each process in order to minimize the total processing time of the complex product and to ensure that the scheduling scheme has both global and local efficiency. Accordingly, the model of related problems is established as follows:
Model symbol definition:
- (1)
- Indices
: Process index, which represents the ith process;
: Device index, representing the jth device;
- (2)
- Sets
: Process set, ;
M: Equipment set, ;
- (3)
- Parameters
: Machining hours of process on ;
- (4)
- Decision Variables
: At machines, the start processing time of the th process;
: End processing time of the th process at machines;
: The moment when the th process starts;
: The moment when the th process starts;
: The total time required for the complex product to complete all the machining processes.
Objective function:
s.t.
where Formula (3) denotes the optimization objective of this study: minimizing the maximum completion time of the complex product; Formula (4) strictly limits all process machining times to positive real numbers; Formula (5) shows that on the same processing equipment , the starting processing time of the (i + 1)th process is later than the end processing time of the ith process; Formula (6) represents the constraint condition of the pre-tightening and post-tightening process, and the (i + 1)th process needs to start processing after the ith process is finished; and Formula (7) indicates that the total processing time of a complex product is equal to the largest completion time of all processes.
4. Algorithm Design and Analysis
The complexity of process tree scheduling arises from multilevel constraints and dynamic resource interactions. We proposed a comprehensive algorithm that integrates dynamic pruning and an enhanced Floyd method for complex product scheduling. This section details the design principles, core definitions, and optimization strategies of the algorithm, and its effectiveness is validated through complexity analysis and flowcharts.
4.1. Definitions and Policies
Definition 1.
Path-weighted strategy. The basic principle of the Floyd algorithm is to calculate the shortest path from a certain point to a certain point . Define as the shortest path for the root node to reach the node with lower priority through g nodes. represents the shortest path of the node to itself. Accordingly, the path weight value of the improved Floyd algorithm strategy is defined as the reverse order of the path value from the process tree node to the leaf node with lower layer priority, that is:
At the same time, it is stipulated that when the path values are the same, the path with more processes is preferentially scheduled.
Definition 2.
Scheduling advantage. The earliest time point at which a process can be started on the equipment under the premise of meeting the process constraints.
Definition 3.
Audit strategy. On the basis of the scheduling advantage strategy, according to the hierarchy division, starting from the layer with the highest priority, in the order of the leaf node process followed by the non-leaf-node process, the initial processing time of the process is checked successively to ensure that it is not earlier than the completion time of the predecessor process (group) to avoid any possible time conflict or delay.
Because the leaf node process is at the end of the process tree and there are no time constraints imposed by the predecessor process, the leaf node process has greater time freedom on the equipment and can start processing at any relatively early time; thus, its subsequent processes are encouraged to start processing as soon as possible.
If there are processes with the same priority, in order to optimize the scheduling process and improve the overall efficiency, the leaf node processes are preferentially arranged to enter the scheduling process. If there are nodes on the same layer, the node process with the shortest processing time is preferentially selected for scheduling.
The process constraint relationship audit strategy algorithm flowchart is shown in Figure 3.
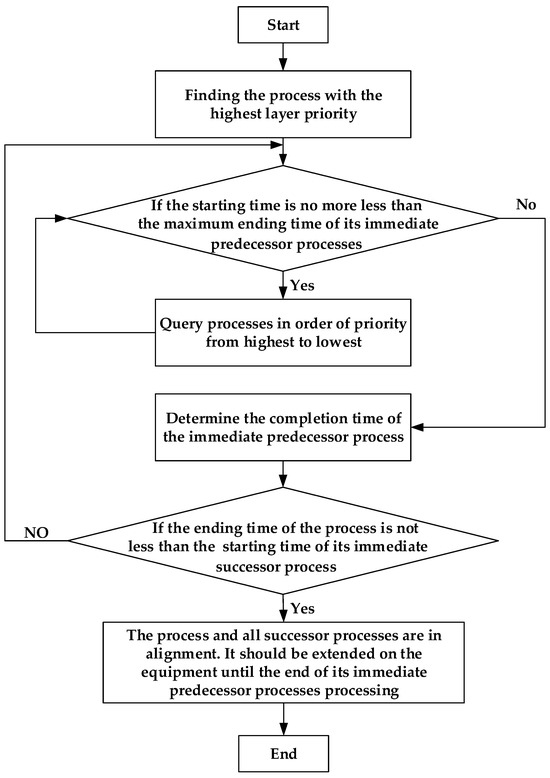
Figure 3.
Flowchart of audit strategy.
4.2. Analysis of Algorithm Design
In the integrated scheduling optimization of complex products, the processing time and other attributes of leaf node processes in the directed graph corresponding to the complex process tree are crucial to improving the overall scheduling efficiency. Therefore, the proposed algorithm sets the processing time of the processes as the path weight of processes with constraints and achieves global resource balance by dynamically adapting to the parallelism of symmetric paths and the heterogeneity of asymmetric paths.
The proposed algorithm first constructs the unidirectional path process tree of complex products according to the Floyd algorithm and sets the processing time of the immediate process as the path weight between the adjacent nodes, that is, the weight value of the adjacent nodes on the unidirectional path. Then, taking the root node of the unidirectional path process tree as the starting point, the path from the root node to the leaf node with lower layer priority is established. For symmetric process trees, the algorithm preferentially selects the shortest path in parallel branches to enhance parallelism. For asymmetric process tree, the cross-layer resource conflict is solved by dynamic weight adjustment. When there are multiple leaf nodes with lower layer priority, the leaf node with shorter processing time is selected to establish the path.
The algorithm flowchart is shown in Figure 4. The specific steps are as follows:
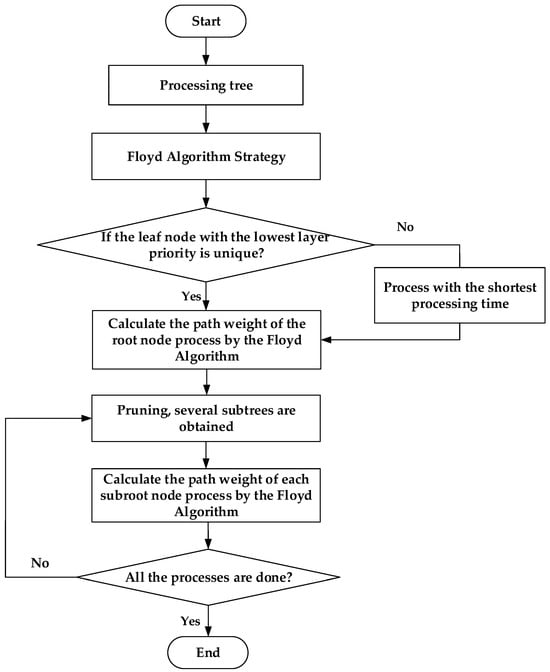
Figure 4.
Flowchart of the proposed algorithm.
Step 1: According to the Floyd algorithm strategy, the processing time of the process is taken as the path weight of its adjacent process, and the shortest path weight from the node process at the root of the process to the node process with lower priority is calculated.
Step 2: Determine whether the node process with the lowest priority is unique. If it is unique, establish the shortest path. If it is not unique, select the node with lower priority in the layer with less processing time to establish the shortest path;
Step 3: Prune, that is, cut off the nodes on the established shortest path from the original process tree, and establish the shortest path weight of several process sub-root node processes to the node processes with lower priority in the layer;
Step 4: Repeat Step 3 until all process path weights have been calculated;
Step 5: Arrange each group of paths according to the descending order of the weight value of each path;
Step 6: Scheduling advantage strategy;
Step 7: Constraint relationship audit strategy;
Step 8: Dynamically adjust the scheduling advantage strategy;
Step 9: End, exit.
4.3. Algorithm Code
Algorithm 1 presents the pseudo-code of the proposed algorithm.
| Algorithm 1 Hierarchical pruning optimization algorithm |
| BEGIN Initialize ComplexProductProcessTree() Apply FloyedAlgorithmStrategy() WHILE NOT AllProcessNodesComputed() IF IsLeafNodeProcessUnique(low_priority_layer) THEN Calculate RootNodeFloyedWeight() ELSE Select ShorterProcessingTimeProcess() Calculate RootNodeFloyedWeight() END IF PruneAndCreateSubProcessTrees() FOR EACH sub_tree IN sub_process_trees Calculate SubTreeRootFloyedWeight(sub_tree) END FOR END WHILE END |
4.4. Algorithm Complexity
The integrated scheduling method proposed in this study significantly reduces the time complexity of the traditional Floyd algorithm from O(n3) to O(n2) through multi-strategy co-optimization. The improved Floyd algorithm employs dynamic path compression with a one-way constraint mechanism to perform cyclic pruning operations with O(n2) complexity on the process tree. Building on this foundation, the scheduling dominance strategy leverages the tree structure’s unidirectional timing constraints to determine the earliest start time of processes in linear time O(n), while the constraint auditing strategy ensures temporal feasibility through O(nlogn) conflict detection based on hierarchical division and prioritization (leaf-node first, shortest-processing-time first). Ultimately, the overall time complexity of the algorithm remains O(n2).
5. Comparative Analysis Experiment
In order to strictly verify the performance of the ISA-IFA algorithm proposed in this paper, this section will make a multi-dimensional comparison with the three scheduling methods of ISA-NWCOG, TISA-CCSP, and RCISA-CHSO.
5.1. Random Scheduling Case Analysis
The algorithm proposed in this paper is aimed at the field of general integrated scheduling. It is universal for any tree structure product process tree with symmetrical or asymmetrical structure. Therefore, in order to better verify the applicability of the algorithm in this paper, the process tree A randomly generated by MATLAB R2021b software is used as an example, as shown in Figure 5. Each piece of equipment is idle in the initial stage of processing, and there is no processing time constraint. The appropriate processing equipment is selected for the process with the goal of minimizing the total processing time of the product. Process tree A comprises 22 processes and four pieces of equipment. Each node includes three elements: process/equipment processed by process/corresponding processing time; for example, the processing time of process A1 on equipment M1 is 2 working hours. Arrows denote temporal constraints between adjacent operations, with directed edges from current nodes to direct successors defining dependencies. Next, taking the randomly generated complex product A as an example, starting from the scheduling requirements of the product, the detailed process of using the improved Floyed algorithm for scheduling is elaborated in detail according to each link. The specific contents are as follows:
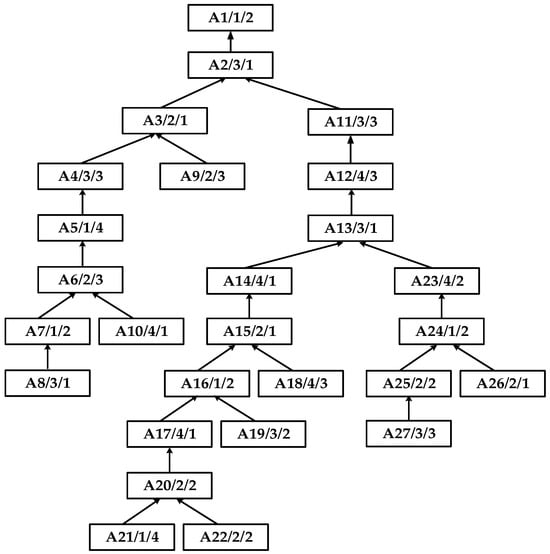
Figure 5.
Process tree of complex product A.
Step 1: According to the weights in the improved Floyd algorithm, as shown in the node path marked in red in Figure 6, establish the path from the root node to the leaf node with the lowest priority in the layer: {A1, A2, A3, A9};
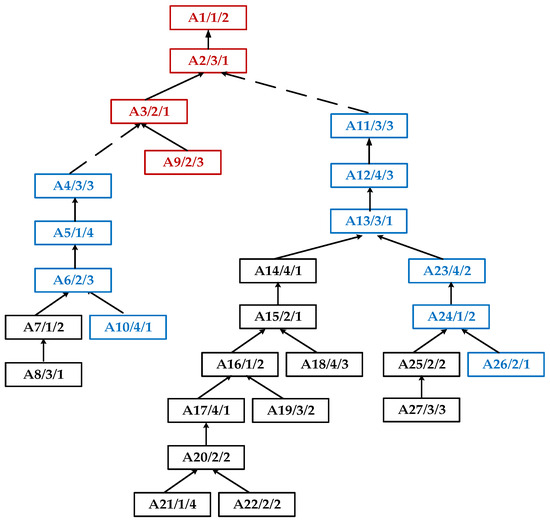
Figure 6.
Path weight diagram from root node to leaf node process with the lowest priority in layer.
Step 2: Conduct the first pruning on the basis of Step 1, generate several subtrees (see the blue part in Figure 6), and establish the process path from each subtree root node to the leaf node with the lowest priority in the new subtree layer: {A4, A5, A6, A10}, {A11, A12, A13, A23, A24, A26};
Step 3: On the basis of Step 2, prune the second time to generate several subtrees, as shown in the purple part in Figure 7, and then establish the process path from the sub-root node to the leaf node with the lowest priority in the new subtree layer: {A7, A8}, {A14, A15, A18}, {A25, A27};
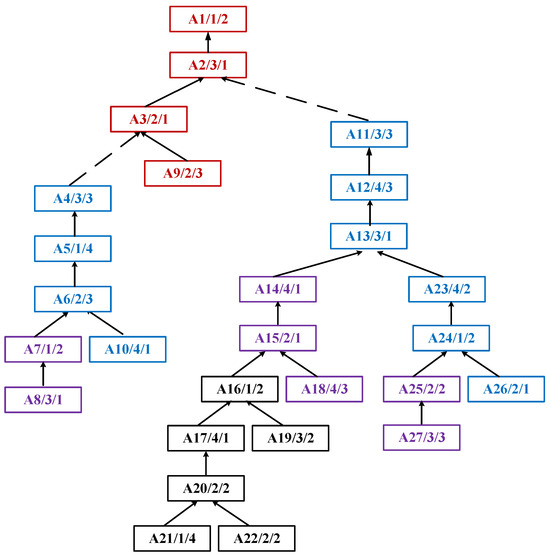
Figure 7.
The path weight diagram of the sub-root node to the leaf node process with the lowest priority in the subtree is established after the second pruning.
Step 4: In this cycle, after the third, the fourth, and the fifth pruning, the path weights of the sub-root node to the leaf node with the lowest priority in the sub-tree layer are shown in the green, orange, and black parts of Figure 8, which are {A16, A19}, {A17, A20, A22}, and {A21}, respectively. At this point, all process paths are established.
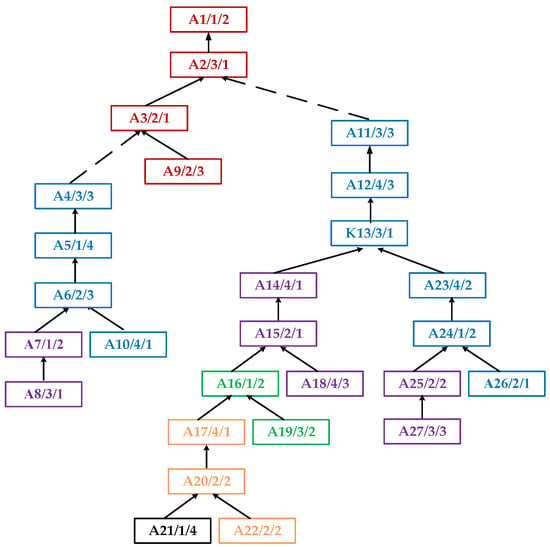
Figure 8.
After the third, the fourth, and the fifth pruning of complex product A, the path weight value of the sub-root node to the leaf node process with the lowest level priority in the sub-tree.
Step 5: According to the improved Floyd algorithm strategy, arrange the weight values of each group of paths successively.
- (1)
- {A11, A12, A13, A23, A24, A26},
- (2)
- {A4, A5, A6, A10},
- (3)
- {A1, A2, A3, A9},
- (4)
- {A14, A15, A18}, {A17, A20, A22}, {A25, A27},
- (5)
- {A16, A19}, {A21},
- (6)
- {A7, A8}.
Step 6: Establish the initial scheduling scheme according to the scheduling advantage strategy, as shown in Figure 9.
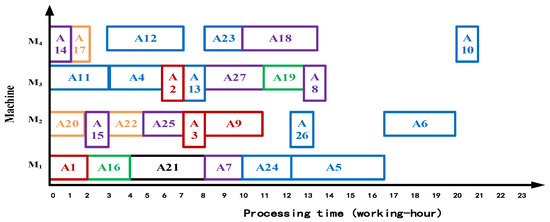
Figure 9.
The Gantt chart of the initial scheduling by ISA-IFA algorithm with 22 working hours.
Step 7: Optimize the initial scheduling scheme according to the constraint relationship audit strategy and scheduling advantage strategy. As shown in Figure 10, the entire processing time of complex product A is 27 working hours.
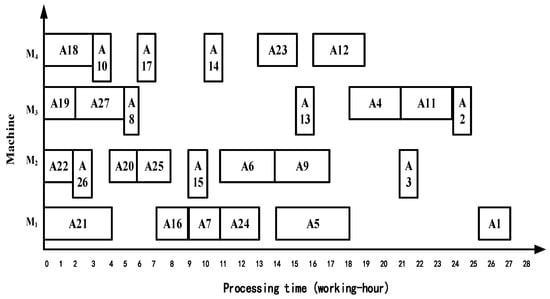
Figure 10.
The Gantt chart of the constraint relationship audit strategy with 27 man-hours.
5.2. Comparison and Analysis of Asymmetric Complex Product Scheduling
In order to highlight the unique advantages of the proposed algorithm, ISA-IFA, in a more comprehensive and intuitive way, in-depth and thorough comparative experiments and analysis are carried out between the ISA-IFA and the algorithms in the same research field in Reference [11], Reference [12], and Reference [13].
Taking asymmetric complex product A as the scheduling case, the processing time of the ISA-NWCOG [11], the TISA-CCSP [12], and the RCISA-CHSO [13] was 28 working hours, 31 working hours, and 28 working hours, respectively. The Gantt charts are shown in Figure 11, Figure 12 and Figure 13, respectively.
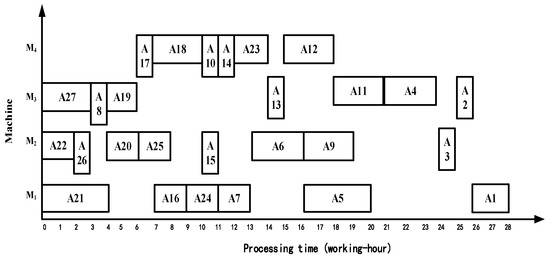
Figure 11.
The Gantt chart obtained by the algorithm ISA-NWCOG.
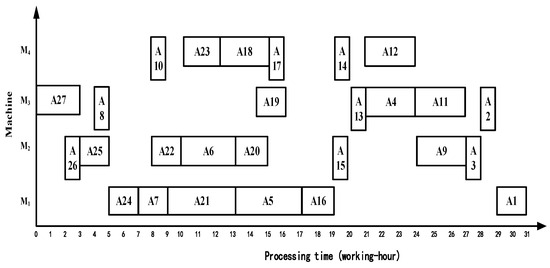
Figure 12.
The Gantt chart obtained by the algorithm TISA-CCSP.
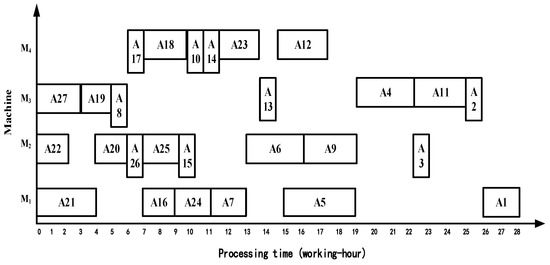
Figure 13.
The Gantt chart obtained by the algorithm RCISA-CHSO.
In the experimental framework of asymmetric process trees, the overall utilization of equipment of the above four algorithms is shown in Table 2. From the overall utilization of equipment in the scheduling system, the ISA-IFA is 2.3%, 9.5%, and 0.6% higher than the other three algorithms, respectively. Therefore, the proposed algorithm not only takes less time for processing but also has a higher overall utilization rate of equipment. It effectively balances workloads in asymmetric process trees, avoiding the unbalanced state of long-term idle or being over-busy. It achieves a better scheduling effect and demonstrated its ability to handle the challenges of heterogeneous resource allocation.

Table 2.
Equipment utilization.
5.3. Data Set Scheduling Instance Analysis
To validate the performance of ISA-IFA and its adaptability to different structured products in the context of multi-variety and small-batch complex processes, four sets of 40 product process trees with varying scales and structures were randomly generated. We are still conducting experiments using Matlab R2021b on the same PC.
The number of processes in the four groups was 20, 50, 100, and 200, respectively, and each group had ten different instances. For products with symmetric tree-like structures owing to their regular and balanced component distribution, most algorithms can achieve relatively efficient scheduling. However, in the case of asymmetric structures, where non-uniform component distribution poses more complex challenges, the performance differences among the algorithms become more pronounced. Figure 14 compares the total processing time of product flow trees scheduled by four algorithms—ISA-IFA, ISA-NWCOG, TISA-CCSP, and RCISA-CHSO—across 40 product instances with varying operation scales: (a) 20 operations, (b) 50 operations, (c) 100 operations, and (d) 200 operations. From Figure 15, it can be seen that ISA-IFA always spends the least amount of time in the 40 product instances, followed by RCISA-CHSO, and then ISA-NWCOG, while TISA-CCSP takes the most time, except for a few instances.
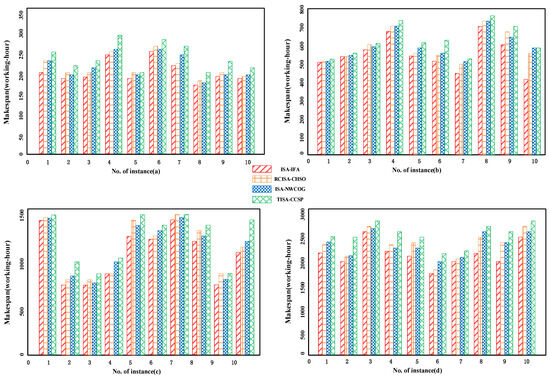
Figure 14.
Performance comparison of four integrated scheduling algorithms across varying operation scales.
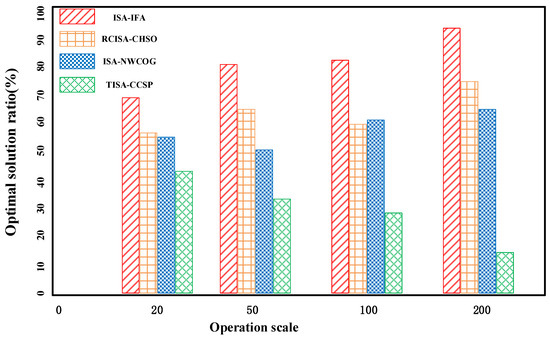
Figure 15.
Optimal solution ratio of the ISA-IFA, the ISA-NWCOG, the TISA-CCSP, and the RCISA-CHSO for integrated scheduling of 40 product instances.
To compare these four algorithms more intuitively, the optimal solution ratio and variance curves are plotted in Figure 15 and Figure 16, respectively.
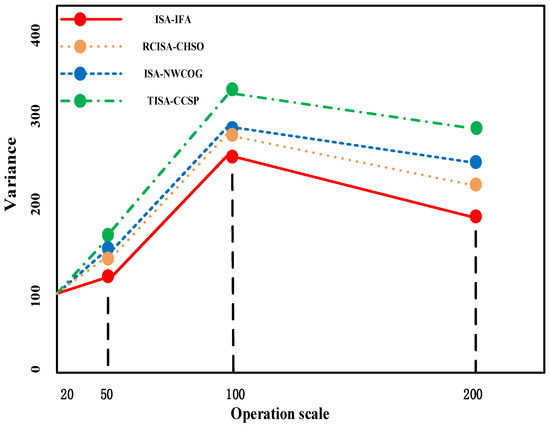
Figure 16.
Variance curves of the ISA-IFA, the ISA-NWCOG, the TISA-CCSP, and the RCISA-CHSO for integrated scheduling 40 product instance.
As shown in Figure 15, it can be seen from the comparative analysis of the optimal solution ratio that ISA-IFA always maintains a higher ratio across both symmetric hierarchies and asymmetric fragmented topologies, and the result is superior to the other three algorithms.
As shown in Figure 16, when dealing with complex products featuring both symmetric and asymmetric tree-like structures, the ISA-IFA also has the best stability among the four algorithms. For products with symmetric tree-like structures, despite the seemingly more straightforward scheduling owing to regular component arrangements, the variance curve of ISA-IFA remained consistently at a lower level. In contrast, for products with asymmetric tree structures, where the non-uniform component distribution poses complex challenges in resource allocation and processing sequence determination, ISA-IFA still manages to adapt well, maintaining its low-variance performance, which is more stable than the other three algorithms. This suggests that the solution obtained by the ISA-IFA may be closer to the best solution, as it dynamically balances resource allocation in symmetric subtrees while resolving fragmented dependencies unique to asymmetric workflows.
6. Discussion
In real-world manufacturing scenarios, complex products often exhibit symmetric hierarchies with uniform dependencies or asymmetric fragmented branches with irregular constraints, both of which pose different scheduling challenges. Symmetric layouts require efficient parallelism, whereas asymmetric workflows require dynamic conflict resolution and adaptive resource allocation to minimize the idle time and processing latency. The main reasons for the superior algorithm in this paper are as follows:
- (1)
- In terms of vertical and horizontal bidirectional optimization, compared with ISA-NWCOG, ISA-IFA addresses vertical articulation weakening in multi-preprocessor scenarios via dynamic pruning, reducing the machining time by 1 working hour. In contrast, TISA-CCSP overlooks leaf-node scheduling advantages, whereas ISA-IFA innovatively introduces leaf node optimization with two-dimensional priorities, reducing the 4 working hours. For example, with the ISA-IFA, the starting time of all the equipment is set to be t = 0, and in terms of the working state of M4, the other three algorithms have idle time of 7 working hours, 13 working hours, and 7 working hours, respectively.
- (2)
- In terms of equipment utilization, the ISA-IFA adopts the scheduling advantage strategy, which addresses the key shortcoming of ignoring the scheduling potential of unconstrained leaf nodes in References [11,12,13], and reduces the idle time of the equipment. Compared with the other three algorithms, it improves the overall utilization rate of the equipment system by 2.3%, 9.5%, and 0.6%, respectively. For example, judging from the working state of M2, the total idle time of the ISA-IFA is 6 working hours, while the total idle time of the other three algorithms on the same equipment is 10 working hours, 12 working hours, and 8 working hours, respectively.
- (3)
- In terms of algorithmic time complexity, the algorithm can give the scheduling scheme within the quadratic complexity, which indicates that the algorithm is simple, feasible, and breaks through the computational bottleneck of traditional scheduling algorithms in large-scale complex product scenarios.
In addition, despite the high efficiency in small-and medium-scale scenarios, the ISA-IFA algorithm has limitations: significant escalation of processing time at ultra-large scales, sensitivity to the initialization of sparse process trees (optimal solution ratio: 68%), and a lack of integration with multi-dimensional constraints (e.g., personnel and materials), restricting generalization to industrial scenarios.
In summary, the algorithm in this paper shows significant adaptability in actual production, although there are some limitations. In order to systematically improve the scheduling performance of intelligent manufacturing, it is suggested that the management dimension builds an elastic resource pool architecture based on dynamic prioritization to optimize the efficiency of resource spatial and temporal allocation; the institutional dimension promotes the standardization of a hybrid scheduling paradigm and multilevel emergency response process and establishes a synergistic mechanism of “dynamic pruning, hierarchical constraints, and algorithmic iteration” to ultimately form an intelligent scheduling system with autonomous decision-making and generalization capabilities.
7. Summary and Outlook
In integrated scheduling, the tree structure of complex products clearly presents symmetric and asymmetric structural layouts through its hierarchical relationships and node distributions, thus providing a structured basis for differentiated optimization of resource allocation and scheduling timing. In this paper, we propose an integrated scheduling algorithm based on the improved Floyd algorithm to address the potential problem that traditional methods ignore, the advantage that leaf node processes with low hierarchical priority can be scheduled at any time in the scheduling of complex product tree-like process trees. ISA-IFA significantly shortens the machining time and reduces the equipment idle time cost by means of the vertical and horizontal bi-directional equilibrium framework, dynamic pruning-path optimization mechanism, and leaf node-driven parallel scheduling strategy. Experimental results show that the algorithm achieves better scheduling results in the field of integrated scheduling of complex products, provides a new methodology for process tree scheduling, and helps enterprises to shorten the production cycle. However, the algorithm still has limitations in the real time of extreme asymmetric structures and the distributed scalability of ultra-large-scale symmetric trees. In the future, based on this study, we will integrate heterogeneous resources, such as personnel skills and material supply, construct a multi-objective co-optimization model, and explore the trade-off mechanism between green scheduling objectives and efficiency.
Author Contributions
Conceptualization, Y.W. and W.Z.; methodology, Z.T.; software, Y.W. and Z.X.; data curation, M.S.; writing—original draft preparation, Y.W.; writing—review and editing, W.C. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Natural Science Foundation of China (61772160, Funder: Z.X.); the National Social Science Foundation of China (20BZS058, Funder: M.S.); the Heilongjiang Natural Science Foundation project (LH2024F045, Funder: W.C.); the Key Project of the Department of Education of Jilin Province (JJKH20250946KJ, Funder: W.Z.); and the Jilin Normal University Doctoral Program (2022014, Funder: W.Z.).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shi, G.D.; Wu, G.; Huang, J.J. Digitalization Transformation and ESG Performance of Manufacturing Enterprises—From the ESG Segmentation Perspective. Statist. Decis. 2025, 05, 166–171. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Liu, Y.; Meng, L.J. Construction of Quality Infrastructure and Upgrading of Manufacturing Foreign Trade: Theoretical Mechanism and Experimental Evidence. Int. Bus. Res. 2025, 46, 48–62. [Google Scholar] [CrossRef]
- Wang, X.; Mao, X.M.; Liu, M. The Coupling and Coordination Relationship between Digital Economy and Manufacturing Industry in China: A High-quality Development Perspective. Stat. Inf. Forum 2024, 39, 41–55. [Google Scholar] [CrossRef]
- Zhu, G.P.; Wang, K. Artificial Intelligence Applications and Green Innovation in Manufacturing Firms. J. Ind. Technol. Econ. 2024, 43, 73–81. [Google Scholar] [CrossRef]
- Gao, Y.; Song, Y. Research on the interactive relationship between information communication technology and manufacturing industry. Clust. Comput. 2019, 22, 5719–5729. [Google Scholar] [CrossRef]
- Ji, K.; Liu, X.; Xu, J. Digital Economy and the Sustainable Development of China’s Manufacturing Industry: From the Perspective of Industry Performance and Green Development. Sustainability 2023, 15, 5121. [Google Scholar] [CrossRef]
- Kovič, K.; Ojsteršek, R.; Palčič, I. Simultaneous Use of Digital Technologies and Industrial Robots in Manufacturing Firms. Appl. Sci. 2023, 13, 5890. [Google Scholar] [CrossRef]
- Xie, W.H.; Zheng, D.W.; Li, Z.S.; Wang, Y.J.; Wang, L.G. Digital technology and manufacturing industrial change: Evidence from the Chinese manufacturing industry. Comput. Ind. Eng. 2024, 187, 109825. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, Z.; Zhang, D.; Xu, T.; Jiang, H. An Improved Intelligent Optimization Algorithm for Small-Batch Order Production Scheduling. Sci. Rep. 2024, 14, 21394. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.X.; Deng, Q.W.; Luo, Q.; Wang, Z.; Zhuang, H.N.; Huang, Y.T. A Double-Layer Q-Learning Driven Memetic Algorithm for Integrated Scheduling of Procurement, Production and Maintenance with Distributed Resources. Appl. Soft Comput. 2024, 165, 112110. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Teng, Y.Z.; Yang, J. Integrated Scheduling Algorithm with No-wait Constraint Operation Group. Acta Autom. Sin. 2011, 37, 371–379. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhang, X.H.; Gao, Y.L.; Xin, Y. Time-selective Integrated Scheduling Algorithm Considering The Compactness of Serial Processes. J. Mech. Eng. 2018, 54, 191–202. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhou, W.; Yang, J. Resource cooperative integrated scheduling algorithm considering hierarchical scheduling order. Comput. Integr. Manuf. Syst. 2022, 28, 3391–3402. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Xin, Y.; Yang, J. Integrated Scheduling Algorithm Based on Event-driven by Machines’ Idle. J. Mech. Eng. 2018, 54, 191–202. [Google Scholar] [CrossRef]
- Xie, Z.Q. Study on Operation Scheduling of Complex Product with Constraint among Jobs. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, 2009. [Google Scholar]
- Wang, J.R.; Li, Y.; Zhang, Z.W.; Wu, Z.Y.; Wu, L.H.; Jia, S.; Peng, T. Dynamic Integrated Scheduling of Production Equipment and Automated Guided Vehicles in a Flexible Job Shop Based on Deep Reinforcement Learning. Processes 2024, 12, 2423. [Google Scholar] [CrossRef]
- Yang, D.; Xie, Z.Q.; Zhang, C. Multi-flexible integrated scheduling algorithm for multi-flexible integrated scheduling problem with setup times. Math. Biosci. Eng. 2023, 20, 9781–9817. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Xie, Z.Q.; Liu, Q.; Yu, X. Asignal-driven based flexible integrated scheduling algorithm with bidirectional coordination mechanism. Multimed. Tools Appl. 2023, 82, 34029–34051. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Zou, Y.; Guo, W.; Wang, Y. Integrated scheduling algorithm for multiple complex products with due date constraints. J. Phys. Conf. Ser. 2021, 1748, 032030. [Google Scholar] [CrossRef]
- Ding, X.Y.; Xie, Z.Q.; Zhou, W.; Tan, Z.J.; Sun, M. Flexible Integrated Scheduling Considering Periodic Maintenance. Electronics 2024, 13, 3730. [Google Scholar] [CrossRef]
- Ding, X.Y.; Zhou, W.; Xie, Z.Q.; Sun, M.; Tan, Z.J.; Cao, W.C. Integrated Scheduling Algorithm Based on Improved Semi-Numerical Algorithm. Symmetry 2025, 17, 434. [Google Scholar] [CrossRef]
- Xia, B.L.; Ma, Y.Z. Optimization of Distributed Flow Shop Scheduling Problem Based on Deep Q-network. Mach. Des. Res. 2025, 41, 311–319. [Google Scholar] [CrossRef]
- Han, J.H.; Lee, J.Y. Genetic algorithm-based approach for makespan minimization in a flow shop with queue time limits and skipping jobs. Adv. Prod. Eng. Manag. 2023, 18, 152–162. [Google Scholar] [CrossRef]
- Su, J.T.; Dong, S.H.; Zhu, S.M. Research on Machine Fault Rescheduling Problem of Multi Objective Hybrid Flow Shop Based on Intelligent Manufacturing. J. Mech. Eng. 2024, 60, 438–448. [Google Scholar]
- Badri, H.; Bahreini, T.; Grosu, D. Parallel shifting bottleneck algorithms for non-permutation flow shop scheduling. Ann. Oper. Res. 2024, 343, 39–65. [Google Scholar] [CrossRef]
- Hidri, L.; Elsherbeeny, A.M. Optimal Solution to the two-stage hybrid flow shop scheduling problem with removal and transportation times. Symmetry 2022, 14, 1424. [Google Scholar] [CrossRef]
- Ge, Z.P.; Wang, H.F. Integrated Optimization of Blocking Flowshop Scheduling and Preventive Maintenance Using a Q-Learning-Based Aquila Optimizer. Symmetry 2023, 15, 1600. [Google Scholar] [CrossRef]
- Li, Z.H.; Tang, H.T.; Zhang, W. Solving the Scheduling of Flexible Assembly Workshops with Outsourcing Cooperation Based on Improving Whale Dynamic Scheduling Algorithm. Mach. Tool Hydraul. 2024, 52, 1–9. [Google Scholar] [CrossRef]
- Momenikorbekandi, A.; Abbod, M. Intelligent Scheduling Based on Reinforcement Learning Approaches: Applying Advanced Q-Learning and State–Action–Reward–State–Action Reinforcement Learning Models for the Optimisation of Job Shop Scheduling Problems. Electronics 2023, 12, 4752. [Google Scholar] [CrossRef]
- Xu, G.D.; Chen, Y.F. Petri-net-based scheduling of flexible manufacturing systems using an estimate function. Symmetry 2022, 14, 1052. [Google Scholar] [CrossRef]
- Ding, L.S.; Guan, Z.L.; Luo, D.; Rauf, M.; Fang, W.K. An Adaptive Search Algorithm for Multiplicity Dynamic Flexible Job Shop Scheduling with New Order Arrivals. Symmetry 2024, 16, 641. [Google Scholar] [CrossRef]
- Yang, Z.; Bi, L.; Jiao, X. Combining Reinforcement Learning Algorithms with Graph Neural Networks to Solve Dynamic Job Shop Scheduling Problems. Processes 2023, 11, 1571. [Google Scholar] [CrossRef]
- He, Y.R.; Pang, J.M.; Xu, J.L.; Zhu, Y.; Tao, X.H. Implementation and Optimization of Floyd Parallel Algorithm Based on Sunway Platform. Comput. Sci. 2021, 48, 34–40. [Google Scholar] [CrossRef]
- Emara, S.F.; Abdelhady, S.; Zaki, M. A novel traceback model for DDoS attacks using modified Floyd-Warshall algorithm. Int. J. Inf. Comput. Secur. 2023, 20, 84–103. [Google Scholar]
- Xu, E. Strategic Evaluation and Optimization of Clan Sides Based on Floyd Algorithm. Adv. Comput. Signals Syst. 2023, 7, 105–112. [Google Scholar] [CrossRef]
- Lyu, D.S.; Chen, Z.W.; Cai, Z.S.; Piao, S.H. Robot path planning by leveraging the graph-encoded Floyd algorithm. Comput. Syst. 2021, 122, 204–208. [Google Scholar] [CrossRef]
- Li, N.; Xin, C.Y. Urban Logistics Distribution Routing Optimization of “Vehicle-Drone” Based on Clustering-Floyd-Genetic Algorithm. Sci. Technol. Engng. 2024, 24, 9186–9193. [Google Scholar]
- Habib, S.; Majeed, A.; Akram, M.; Ali Al-Shamiri, M.M. Floyd-Warshall Algorithm Based on Picture Fuzzy Information. CMES-Comput. Model. Eng. Sci. 2023, 136, 2873–2894. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).