Two High-Accuracy Linear Finite Difference Schemes for Rosenau–KdV–RLW Equation
Abstract
1. Introduction
2. The First Method: A Two-Level Linearized Finite Difference Scheme
2.1. Preliminaries
2.2. The Two-Level Numerical Scheme and the Conservative Law
2.3. The Convergence and Stability of Scheme (21)–(23)
3. The Second Method: The Three-Level Linear Finite Difference Scheme
3.1. The Numerical Scheme and the Truncation Error
3.2. The Convergence and Stability of Scheme (53)–(55)
4. Numerical Experiments
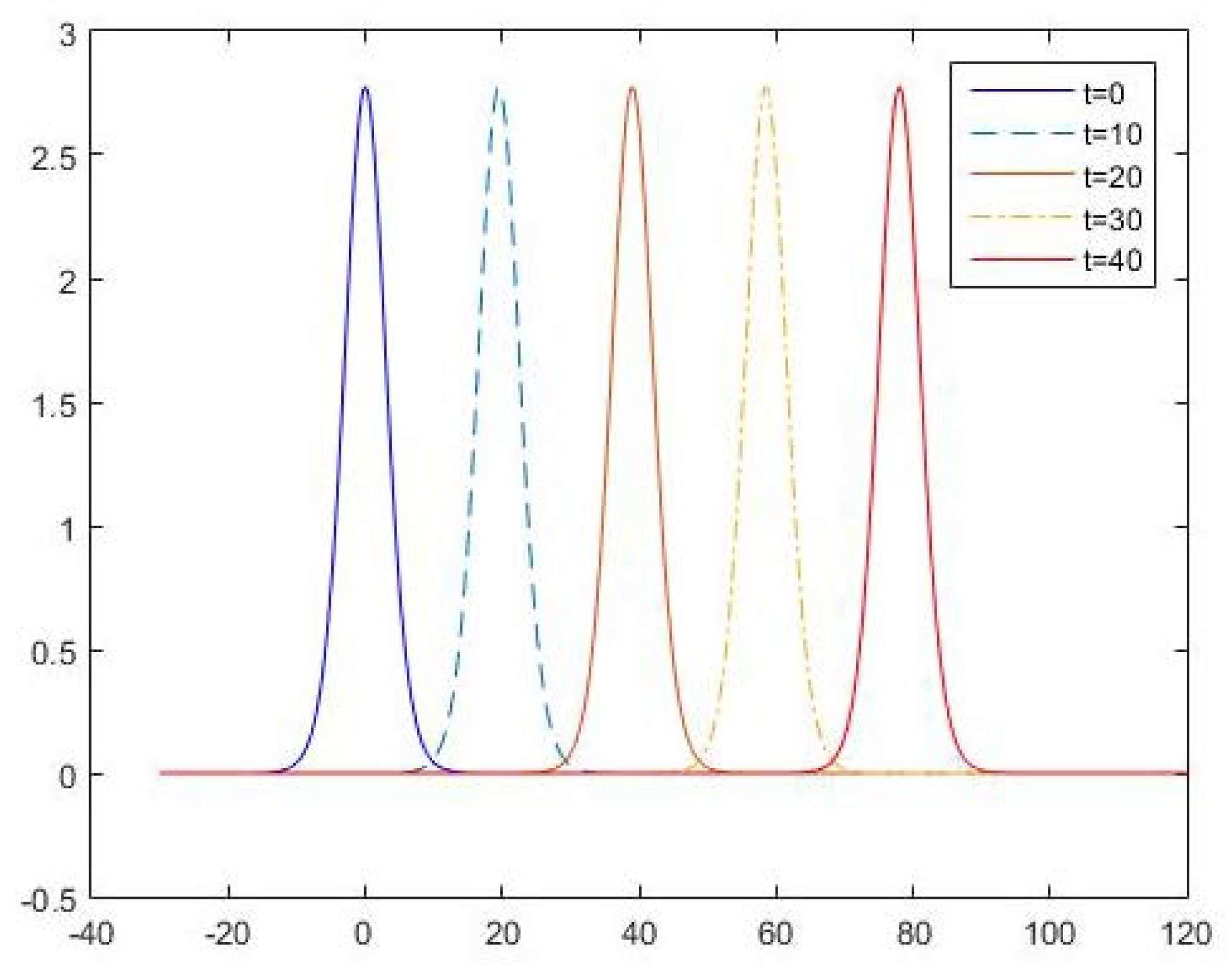
4.1. The Numerical Results of Scheme (21)–(23)
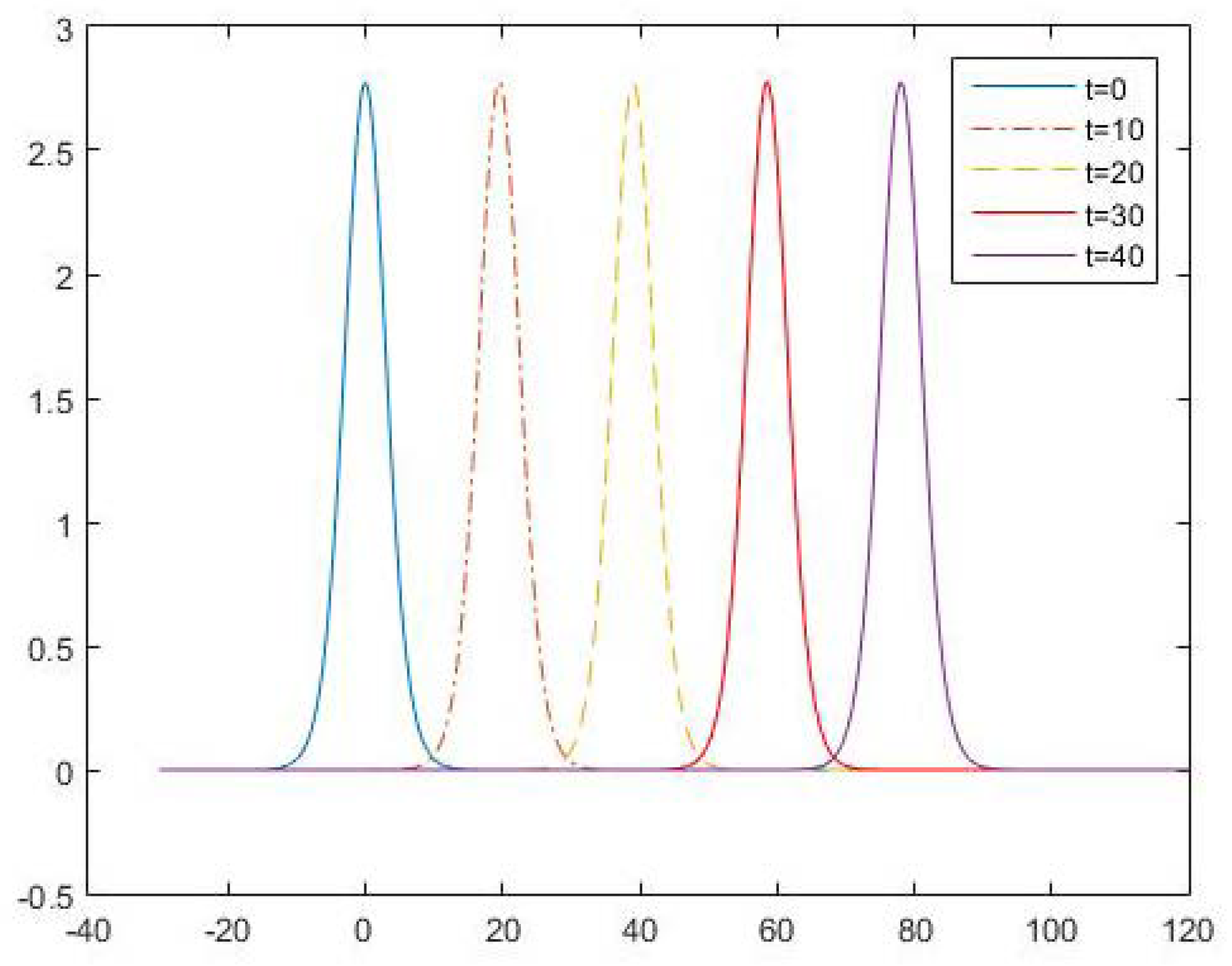
4.2. The Numerical Results of Scheme (53)–(55)
4.3. Comparison of the Numerical Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korteweg, D.J.; de Vires, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar]
- Rosenau, P. A quasi-continuous description of a nonlinear transmission line. Phys. Scr. 1986, 34, 827–829. [Google Scholar]
- Rosenau, P. Dynamics of dense discrete systems: High order effects. Prog. Theor. Phys. 1988, 79, 1028–1042. [Google Scholar]
- Kim, Y.D.; Lee, H.Y. The convergence of finite element Galerkin solution for the Rosenau equation. Korean J. Comput. Appl. Math. 1998, 5, 171–180. [Google Scholar]
- Chung, S.K.; Pani, A.K. Numerical methods for the Rosenau equation. Appl. Anal. 2001, 77, 351–369. [Google Scholar]
- Hu, J.S.; Zheng, K.L. Two conservative difference schemes for the generalized Rosenau equation. Bound. Value Probl. 2010, 2010, 543503. [Google Scholar] [CrossRef]
- Özer, S. Numerical solution of the Rosenau-KdV-RLW equation by operator splitting techniques based on B-spline collocation method. Numer. Methods Partial Differ. Equ. 2019, 35, 1928–1943. [Google Scholar]
- Özer, S. Two efficient numerical methods for solving Rosenau-KdV-RLW equation. Kuwait J. Sci. 2021, 48, 14–24. [Google Scholar]
- Razborova, P.; Moraru, L.; Biswas, A. Perturbation of dispersive shallow water waves with Rosenau-KdV-RLW equation and power law nonlinearity. Rom. J. Phys. 2014, 59, 658–676. [Google Scholar]
- Razborova, P.; Ahmed, B.; Biswas, A. Solitons, shock waves and conservation laws of Rosenau-KdV-RLW equation with power law nonlinearity. Appl. Math. Inform. Sci. 2014, 8, 485–491. [Google Scholar]
- Razborova, P.; Kara, A.H.; Biswas, A. Additional conservation laws for Rosenau-KdV-RLW equation with power law nonlinearity by Lie symmetry. Nonlin. Dyn. 2015, 79, 743–748. [Google Scholar]
- Ak, T.; Karakoc, S.B.G.; Biswas, A. Numerical scheme to dispersive shallow water waves. J. Comput. Theor. Nanos. 2016, 13, 7084–7092. [Google Scholar]
- Kaur, A.; Kanwar, V.; Ramos, H. A conservative algorithm based on a hybrid block method and tension B-spline differential quadrature method for Rosenau–KdV–RLW equation. Math. Meth. Appl. Sci. 2024, 47, 8638–8650. [Google Scholar]
- Korkmaz, B.; Dereli, Y. Numerical solution of the Rosenau-KdV-RLW equation by using RBFs collocation method. Int. J. Mod. Phys. C 2016, 27, 1650117. [Google Scholar]
- Ahmat, M.; Qiu, J. Compact ETDRK scheme for nonlinear dispersive wave equations. Comput. Appl. Math. 2021, 40, 286. [Google Scholar]
- Shallu; Kukreja, V.K. An efficient collocation algorithm with SSP-RK43 scheme to solve Rosenau-KdV-RLW equation. Int. J. Appl. Comput. Math. 2021, 7, 161. [Google Scholar]
- Pan, X.T.; Wang, Y.J.; Zhang, L.M. Numerical analysis of a pseudo-compact C-N conservative scheme for the Rosenau-KdV equation coupling with the Rosenau-RLW equation. Bound. Value Probl. 2015, 2015, 65. [Google Scholar]
- Wongsaijai, B.; Poochinapan, K. A three-level average implicit finite difference scheme to solve equation obtained by coupling the Rosenau-KdV equation and the Rosenau-RLW equation. Appl. Math. Comput. 2014, 245, 289–304. [Google Scholar]
- Ghiloufi, A.; Omrani, K. New conservative difference schemes with fourth-order accuracy for some model equation for nonlinear dispersive waves. Numer. Methods Partial. Differ. Equ. 2018, 34, 451–500. [Google Scholar]
- Labidi, S.; Rahmeni, M.; Omrani, K. Numerical approach of dispersive shallow water waves with Rosenau-KdV-RLW equation in (2 + 1)-dimensions. Discret. Cont. Dyn.-S 2023, 16, 2157–2176. [Google Scholar] [CrossRef]
- Wang, X.F.; Dai, W.Z. A three-level linear implicit conservative scheme for the Rosenau-KdV-RLW equation. J. Comput. Appl. Math. 2018, 330, 295–306. [Google Scholar]
- Verma, A.K.; Rawani, M.K. Numerical solutions of generalized Rosenau-KDV-RLW equation by using Haar wavelet collocation approach coupled with nonstandard finite difference scheme and quasilinearization. Numer. Methods Partial Differ. Equ. 2023, 39, 1085–1107. [Google Scholar] [CrossRef]
- Zhou, Y.L. Application of Discrete Functional Analysis to the Finite Difference Method; International Academic Publishers: Beijing, China, 1990. [Google Scholar]
- Zheng, K.L.; Hu, J.S. High-order conservative Crank-Nicolson scheme for regularized long wave equation. Adv. Differ. Equ. 2013, 2013, 287. [Google Scholar]
- Shumoua, F.A.; Fatimah, A.A.; Hany, N.H. An efficient numerical technique for investigating the generalized Rosenau-KDV-RLW equation by using the Fourier spectral method. AIMS Math. 2024, 9, 8661–8688. [Google Scholar]
- Li, S.; Kravchenko, O.V.; Qu, K. On the L∞ convergence of a novel fourth-order compact and conservative difference scheme for the generalized Rosenau-KdV-RLW equation. Numer. Algorithms 2023, 94, 789–816. [Google Scholar] [CrossRef]
- Aydin, A. A convergent two-level linear scheme for the generalized Rosenau-KdV-RLW equation. Turk. J. Math. 2019, 43, 2226–2245. [Google Scholar] [CrossRef]
- Cai, J.X.; Hong, Q.; Yang, B. Local structure-preserving methods for the generalized Rosenau-RLW-KdV equation with power law nonlinearity. Chin. Phys. B 2017, 26, 100202. [Google Scholar]
- Wang, X.F.; Dai, W.Z. A new conservative finite difference scheme for the generalized Rosenau-KdV-RLW equation. Comput. Appl. Math. 2020, 39, 237. [Google Scholar]
- Nas, M.; Yalçın, S.; Bayram, H. A class of analytic functions defined by a second order differential inequality and error function. Int. J. Appl. Comput. Math. 2024, 10, 42. [Google Scholar] [CrossRef]
| t = 10 | 2.63467 × 10−2 | 1.65735 × 10−3 | 9.94049 × 10−5 | 7.00687 × 10−2 | 4.40715 × 10−3 | 2.54754 × 10−4 |
| t = 20 | 5.05143 × 10−2 | 3.17890 × 10−3 | 1.75745 × 10−4 | 1.35375 × 10−1 | 8.51817 × 10−3 | 4.51715 × 10−4 |
| t = 30 | 7.45117 × 10−2 | 4.69031 × 10−3 | 2.37401 × 10−4 | 2.00088 × 10−1 | 1.25923 × 10−2 | 6.08385 × 10−4 |
| t = 40 | 9.84930 × 10−2 | 6.20064 × 10−3 | 2.84942 × 10−4 | 2.64761 × 10−1 | 1.66644 × 10−2 | 7.27054 × 10−4 |
| t = 10 | – | 3.99067 | 4.05942 | – | 3.99085 | 4.11267 |
| t = 20 | – | 3.99009 | 4.17697 | – | 3.99027 | 4.23706 |
| t = 30 | – | 3.98971 | 4.30429 | – | 3.99002 | 4.37191 |
| t = 40 | – | 3.98953 | 4.44368 | – | 3.98985 | 4.51856 |
| t = 0 | 21.67925836181 | 21.67925836040 | 21.67925835969 |
| t = 10 | 21.67925803228 | 21.67925803744 | 21.67931092312 |
| t = 20 | 21.67925095503 | 21.67925849815 | 21.67936576362 |
| t = 30 | 21.67900791772 | 21.67924382931 | 21.67941983441 |
| t = 40 | 21.67952193450 | 21.67927604434 | 21.67947672631 |
| t = 10 | 9.35198 × 10−2 | 5.35165 × 10−3 | 3.35914 × 10−4 | 2.49529 × 10−1 | 1.36134 × 10−2 | 8.49912 × 10−4 |
| t = 20 | 2.20014 × 10−1 | 1.00773 × 10−2 | 6.24682 × 10−4 | 5.68603 × 10−1 | 2.66997 × 10−2 | 1.64330 × 10−3 |
| t = 30 | 3.84552 × 10−1 | 1.52808 × 10−2 | 9.34444 × 10−4 | 9.87308 × 10−1 | 4.10605 × 10−2 | 2.49280 × 10−3 |
| t = 40 | 5.86758 × 10−1 | 2.10901 × 10−2 | 1.26603 × 10−3 | 1.50784 × 100 | 5.67519 × 10−2 | 3.40179 × 10−3 |
| t = 10 | – | 4.12722 | 3.99382 | – | 4.19611 | 4.00157 |
| t = 20 | – | 4.44841 | 4.01184 | – | 4.41253 | 4.02216 |
| t = 30 | – | 4.65339 | 4.03147 | – | 4.58752 | 4.04191 |
| t = 40 | – | 4.79813 | 4.05818 | – | 4.73167 | 4.06030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Zheng, K.; Chen, Z. Two High-Accuracy Linear Finite Difference Schemes for Rosenau–KdV–RLW Equation. Symmetry 2025, 17, 566. https://doi.org/10.3390/sym17040566
Hu J, Zheng K, Chen Z. Two High-Accuracy Linear Finite Difference Schemes for Rosenau–KdV–RLW Equation. Symmetry. 2025; 17(4):566. https://doi.org/10.3390/sym17040566
Chicago/Turabian StyleHu, Jinsong, Kelong Zheng, and Zhong Chen. 2025. "Two High-Accuracy Linear Finite Difference Schemes for Rosenau–KdV–RLW Equation" Symmetry 17, no. 4: 566. https://doi.org/10.3390/sym17040566
APA StyleHu, J., Zheng, K., & Chen, Z. (2025). Two High-Accuracy Linear Finite Difference Schemes for Rosenau–KdV–RLW Equation. Symmetry, 17(4), 566. https://doi.org/10.3390/sym17040566