A Privacy-Enhancing Mechanism for Federated Graph Neural Networks

Abstract

In recent years, with the rapid development of the internet, the accumulation of massive data has significantly propelled the advancement of artificial intelligence. Graphs, as an important data structure for representing relationships between entities, are widely used in various real-world scenarios such as social networks and e-commerce platforms. Graph Neural Networks (GNNs) have emerged as a popular research topic, capable of learning information from neighborhoods and extracting features from graph-structured data to solve tasks like graph classification, node classification, and link prediction. However, the centralized training of GNNs often faces challenges due to data isolation and privacy concerns. Federated Learning (FL) has been proposed as a solution to these issues, allowing multiple users to collaboratively train models without sharing raw data. This paper introduces a privacy-preserving mechanism based on Local Differential Privacy (LDP) to enhance the security of Federated Graph Neural Networks (FedGNNs) against inference attacks while maintaining model performance.

1. Introduction

In recent years, with the rapid development of the internet, massive data accumulated across various sectors have significantly advanced artificial intelligence. As an important data structure for representing relationships between entities, graphs have broad applications in real-world scenarios, such as social relationship graphs in social networks, as shown in Figure 1, and user–item graphs in e-commerce networks. Graph data mining and analysis have critical significance, and GNNs have emerged as a prominent research focus. GNNs can learn neighborhood-related information, extract features from graph-structured data, and solve tasks such as graph classification, node classification, and link prediction.

Current research on GNN models focuses primarily on centralized training scenarios. However, real-world data are often fragmented in isolated silos owned by independent entities. In addition, growing concerns about information security and frequent reports of privacy breaches have heightened public awareness of personal data protection. Governments around the world have enacted data privacy regulations requiring internet companies to safeguard user information, leading to increasingly comprehensive and stringent data governance. Against this backdrop, a crucial challenge arises: how to effectively mine the value of data scattered across silos while ensuring privacy protection and meeting the demand for high-performance graph data training.

In 2017, Google introduced FL as a solution to data silo challenges. As research progresses, FL has been widely adopted for machine learning training in diverse scenarios. FL trains machine learning models without collecting raw data from participating clients. Instead, users locally train their graph data and send model parameters to a server for aggregation. The server then distributes the updated global parameters back to users for local model updates, iterating until convergence. This approach achieves privacy preservation and data security to some extent.

By integrating federated learning with graph neural networks, researchers proposed FedGNNs, offering a viable framework for multiuser collaborative GNN training. Although this method enables information fusion across users to enhance algorithm performance without compromising privacy, attackers may still launch inference attacks by intercepting client–server communication parameters to deduce private data. Consequently, securing client privacy through encrypted communication between servers and clients has become a pressing issue. Among various privacy-preserving techniques, differential privacy stands out and has been widely adopted in FL. Its application ensures that client privacy is protected against inference attacks during FedGNN training.

Balancing privacy preservation with model performance remains a key research focus in federated learning. Notably, FL scenarios often involve Non-Independently Identically Distributed (Non-IID) data due to inherent data fragmentation. Training models with Non-IID data create significant parameter discrepancies among clients, which further degrade global model performance during aggregation. Therefore, developing suitable privacy-preserving methods to protect sensitive data in federated GNN-based link prediction tasks holds both theoretical significance and practical value. This challenge underscores the need for innovative approaches that reconcile privacy constraints with model efficacy in distributed graph learning environments.

This paper aims to achieve resistance against inference attacks in federated graph neural networks. Building upon existing federated graph neural network frameworks, we propose improvements by introducing a local differential privacy-based privacy protection mechanism. This mechanism involves clipping client model gradients, controlling gradient clipping thresholds, and adding noise to the clipped gradients to generate encrypted model parameters. These measures prevent attackers from stealing model parameters through compromised client–server communication channels and thereby obtaining client privacy data, ultimately enhancing the model’s anti-attack capabilities.

The main innovations of this paper are as follows.

• We propose a privacy protection mechanism based on local differential privacy technology, which is applied during the gradient descent process of client-side backpropagation to ensure the security of private data. The feasibility of this method is verified on the CoraML dataset.
• We further investigate the issue of performance degradation in models due to the application of local differential privacy technology. By conducting additional experiments and adjusting parameters, it provides specific hyperparameters that can maintain prediction accuracy while ensuring privacy protection.

2. Related Work

Link prediction and node classification tasks are considered classic examples of node-level tasks in graph neural network (GNN) models, which are of significant importance in the field of data mining. Scholars around the world have proposed theories to further explore these tasks. For example, link prediction refers to predicting the probability of future connections between nodes based on graph-structured data, which is widely applied in social network analysis, recommendation systems, and other domains. Node classification, on the other hand, assigns nodes to different categories or labels, such as grouping users on social networks into distinct communities, helping to understand user behavior and social relationships. Research on these tasks not only enhances the effectiveness of GNN models, but also provides critical references and practical foundations for advancing data mining. For example, Ding Shifei’s team proposed a node classification method based on the theory and algorithms of the support vector machine [1], while Li Jiawei’s team introduced a key node and edge identification method using particle swarm optimization [2]. Currently, machine learning-based node classification methods have been applied in various fields, such as influence node identification on Twitter [3] and key node classification on social networks [4].

In recent years, the rapid development of graph data mining technologies has led scholars to explore how to leverage graph data to solve real-world challenges. There is an urgent societal need for novel methods to analyze and predict the structural features of graphs using GNNs, enabling precise extraction of label information. For example, GNN-based analysis of social network data allows researchers to efficiently identify hidden key individuals, community structures, and even infer user relationships, offering significant support for social media operations and relationship management. In addition, GNNs are applied in bioinformatics to uncover molecular interaction networks, advancing research on disease mechanisms and drug development. Kipf’s team trained models using labeled nodes in graph data through graph convolutional networks (GCNs) and classified unlabeled nodes [5]. Velikovi’s team introduced a self-attention mechanism in GCNs, proposing graph-attention networks (GATs), which reduce computational costs while assigning dynamic weights to neighbor nodes [6]. To address the “flatness” issue in GNNs, researchers like Ying et al. of Stanford University proposed differentiable grouping, mapping nodes into clusters across GNN layers for hierarchical graph representation [7]. Furthermore, Yang’s team proposed a Graph Variational Generative Adversarial Network (GVGAN) to improve flexible graph generation [8], enhancing the adaptability of GNNs in real-world scenarios. Although GNNs excel at linking prediction with rich node features and neighborhood information, real-world data often reside in isolated silos across institutions due to privacy concerns and competition, posing unresolved challenges.

To address data isolation, FL has been integrated into traditional GNN frameworks, forming FedGNNs. Lalitha’s team pioneered this integration by treating each client as a graph node [9]. Wang’s team proposed a meta-learning-based FL framework for semi-supervised node classification [10], while Meng’s team developed a federated GNN between nodes that encodes the underlying graph structures [11]. Existing research on FedGNN classification includes Yang’s comprehensive taxonomy [12], which categorizes FedGNNs into intergraph FL (collaboration in multiple distinct graphs) and intragraph FL (collaboration within a single graph). Intragraph FL is further divided into horizontal FedGNNs (shared feature spaces across nodes) and vertical FedGNNs (shared node IDs with different features).

Intergraph FL enables collaboration among data owners with distinct graph structures, learning shared patterns to enhance model generalization. Intragraph FL focuses on federated learning within a single graph, where data are distributed across nodes/edges. Horizontal intragraph FL addresses cross-graph topology learning, while vertical intragraph FL targets feature alignment under shared topologies. These approaches balance privacy preservation with collaborative learning, but remain vulnerable to inference and data leakage attacks. Recent studies highlight that despite its advantages, FedGNN still faces significant challenges in maintaining both model performance and data privacy, necessitating further research on secure aggregation techniques.

As discussed earlier, federated learning (FL) allows multiple users to collaboratively train models without sharing raw data. This approach has been widely adopted in various scenarios, providing an efficient method to train graph neural networks while preserving privacy. This ensures that data remain local throughout the process, providing an efficient method to train graph neural networks. McMahan’s team proposed the Federated Averaging (FedAvg) algorithm, which reduces communication costs by averaging local client models [13]. Unlike traditional machine learning, FL does not require centralized data storage for training, thus mitigating the risks and costs associated with the systemic privacy of centralized approaches [14]. However, challenges such as system heterogeneity and non-IID data distribution remain unresolved, affecting the generalization ability of FL models. FL generates high-quality shared models that preserve privacy through collaborative client training, making it highly impactful across various domains.

In an ideal FL framework, users train models locally, upload parameters to a server for aggregation, and receive updated global parameters for iterative training. However, in real-world scenarios, client–server data exchanges face threats such as inference attacks and poisoning attacks, which means that FL alone cannot fully ensure data privacy. For example, Carlini’s team extracted sensitive data (e.g., credit card numbers) from a neural network trained on user language data [15]. Fredrikson’s team stole patient privacy information through model inversion attacks [16], and Hitaj’s team used generative adversarial networks (GANs) to compromise user-sensitive data [17]. Geiping et al. demonstrated that deep learning models remain vulnerable to gradient-based input recovery [18]. Existing research suggests that integrating adversarial training and secure multi-party computation (MPC) could further enhance privacy protection in FL. Current research focuses on integrating differential privacy (DP) and homomorphic encryption (HE) into FL frameworks to protect user privacy. These technologies, including DP-based noise addition and HE-based encryption, effectively safeguard individual data while enabling model training in FL.

Inference attacks involve attackers extracting critical model information (e.g., parameters, training data, or outputs) to infer model behavior on specific tasks or data. These attacks do not directly compromise model integrity or availability, but aim to gain insight or information beneficial to the attacker. As a distributed learning method, FL aims to achieve a collective model improvement while maintaining data privacy and security. However, inference attacks have raised significant concerns about data privacy and model safety. Attackers may use techniques such as model reverse engineering, parameter inference, or output analysis to obtain sensitive information about FL participants or the system. The goal of inference attacks is often to uncover data distributions or specific training samples, which can be valuable for analyzing model performance, generalization, or behavior. Melis’s team proposed and evaluated several inference attacks on collaborative learning [19]. Nasr’s team designed a novel white-box membership inference attack targeting deep learning algorithms [20]. Zhang’s team introduced a membership inference attack that causes severe privacy leaks in FL [21]. Liu’s team used a node embedding stealing method based on generative regression networks and inferred privacy attribute information of target graph data in FedGNNs by training shadow models [22]. Countermeasures include encrypting model parameters, designing stronger access control policies, applying DP, and adding noise to model output. These methods help reduce the likelihood of successful inference attacks, thereby protecting the security of the FL system and the integrity of the model.

In summary, while FL presents a promising solution for privacy-preserving machine learning, challenges remain in balancing model utility, security, and efficiency. DP, with its low communication cost and effective privacy protection, is a promising solution. However, excessive noise, while enhancing privacy, can significantly degrade the accuracy of the model. Therefore, balancing noise intensity and model precision is a critical research challenge. This paper explores how to integrate DP into federated graph neural networks to defend against inference attacks while preserving data privacy and maintaining model accuracy.

3. Relevant Technology

3.1. Graph Neural Networks

As previously mentioned in Section 1, graph-structured data are essential for representing relationships between entities. In each network layer, GNNs update node features by aggregating the information of each node’s neighbors with the current node’s information. Graph-structured data can effectively represent the attributes of objects and the relationships between them, thus achieving significant importance in various fields. The feature information of the nodes is of various types, whereas the structural information of the graph represents the connectivity between the nodes. Due to its unique topological relationships, it has broad applications in real life. However, the irregularity of graph data structures poses significant challenges to traditional deep learning methods. For instance, convolutional operations can adeptly handle issues on image data, but these problems have not been well resolved for graph data. GNNs, as an emerging deep learning approach, can effectively process graph-structured data and perform graph-related tasks. This method aims to model network models with topological relationships, thus effectively addressing network topology issues in complex networks, such as node classification and link prediction. The input to GNNs models is graph-structured data that include feature information and structural information in the form of adjacency matrices. In each network layer, GNNs update node features by aggregating the information of each node’s neighbors with the current node’s information. By stacking multiple layers of networks and applying a non-linear activation function to the aggregated information, the characteristics of nodes within the corresponding hop count are encompassed in the features of each node. To obtain the characteristics of this layer, each node, during each iteration, collects information from adjacent nodes and aggregates the characteristics of these adjacent nodes from the previous layer. Using the similarity of the adjacency relationships enables this method to update nodes in the network with more accuracy. When GNNs aggregate neighborhood nodes, they employ an averaging method and use neural networks for the aggregation operation, as shown in the following formula (1).

$$H_v^{l+1}=\sigma (w_{l+1}\sum _{u\in N\left(v\right)}{\displaystyle \frac{H_u^l}{\left|N\right(v\left)\right|}}+B_{l+1}{H}_v^l),\forall k>0$$

(1)

where $H_v^{l+1}$ represents the updated node embedding of node v, $W_{i+1}$ and $B_{i+1}$ denote the weights and biases of the current layer, $\sigma (·)$ represents the non-linear activation function, and the summation formula represents the sum of the features of different neighbor nodes u of node v at layer 1. Further, $\left|N\right(v\left)\right|$ denotes the total number of neighbor nodes of v, $H_v^l$ represents the characteristic of the node of node v in layer 1, $H_u^{\prime }$ represents the characteristic of the neighbor node u in layer 1, and the input vector $x_v$ is the characteristic of the node $H_v^0$ in layer 0.

3.2. Graph Neural Networks for Link Prediction Tasks

Given a simple undirected graph with a node set V and an edge set E, which does not contain self-loops or multiple edges, M is the adjacency matrix of graph G. If $(i,j\in E)$, then $M_{i,j}=1$; otherwise, $M_{i,j}=0$. U represents all possible ${\displaystyle \frac{\left|V\right|·\left(\right|V|-1)}{2}}$ links between nodes, where $\left|V\right|$ is the number of nodes in the set V. Then, $U-E$ represents all currently non-existent links. If certain connections may emerge in the future, the task of link prediction is to identify these potential links—for example, links between users on social networks. Traditional deep learning systems only utilize individual attributes without considering relationships between entities, whereas graph neural networks can fully integrate data attributes and structures to build more powerful predictive models.

The key to the link prediction task lies in how to aggregate the feature information of neighboring nodes in the network through an aggregator function. Graph neural networks achieve this goal by training implicit vector representations for each node in the graph, ensuring that the vectors fully encapsulate the classification information of the nodes. Currently, various graph neural networks based on convolution, gating, and attention mechanisms have been proposed.

The link prediction task ultimately outputs the predicted edge relationships. Graph neural networks utilize graph structures and node attributes to train vector representations for each node, enabling more accurate classification. This process relies on the design of the aggregator function, with the key being the effective extraction of feature information from node neighbors.

Graph neural network models treat the features on each node in the topological graph as a signal and accept two types of input: a feature matrix X with N nodes, where each node’s feature description vector has a dimension of d, and the structural description information of the topological graph, typically represented by the adjacency matrix A. In each layer of the convolutional neural network, the non-linear function is (2).

$$H^{l+1}=f(H^l,A)$$

(2)

where $H^0=X$, where l represents the number of layers in the model, and H denotes the features of the sample data in the hidden layer. There are differences between the various models. This paper focuses on link prediction tasks based on GAT, GCN, and GraphSAGE.

3.3. Federated Learning

Existing graph learning methods are typically applied in centralized learning scenarios, where graph data are stored centrally and models are trained centrally, as shown in Figure 2. However, many industries face significant data silos, with graph data often scattered across various domains. Particularly in sensitive fields such as healthcare and finance, the privacy breaches resulting from centralized learning of graph data can lead to severe societal consequences. High-performance graph neural network models usually require rich node features and adjacency information between nodes. Therefore, how to collaboratively train high-quality graph models while ensuring data privacy is a critical and meaningful challenge.

In the federated learning framework, there are mainly two types of entities: clients and servers. Local clients hold local training and testing data and perform model training, testing, and storage locally. The server is responsible for distributing the initial model and aggregating the local model parameters uploaded by the clients to generate a new global model, as shown in Figure 3.

In a federated learning framework, the initial creation of the model begins on the server side, where the overall model undergoes preliminary training. Afterward, the initial global model is broadcast in a federated learning environment involving N clients. Each client learns from this overall model and processes its own local data. During the local model update phase, users utilize local samples to train the initial model and generate local models, which they return to the server as modified model parameters. The server then aggregates these updates to form a new global model, which is broadcast to all participating clients. This marks the end of one cycle, and the process is repeated until a predetermined accuracy or a specified number of iterations is reached. Assuming there are i clients, let $w_i$ denote the model parameters of the i-th client, $D_i$ represent the local dataset on the client, and $w_t$ represent the global model dispatched by the server during the t-th round of training. A complete federated learning process can be described through these steps.

• Problem Definition and Model Selection: Identify the problem to be solved and select an appropriate machine learning model that will be used for training and inference on distributed data.
• Identifying Participants: Various data holders (such as devices, companies, or individuals) are invited to participate in federated learning. Each participant possesses its own data, which are often not shareable for privacy or security reasons.
• Initialization: At the start of federated learning, either an empty model is initialized or a pre-trained model is used. The initial parameters of this model are typically obtained from a central server.
• Local Training: Each selected participant locally trains the model using its own data. During local training, participants can conduct multiple training rounds as needed to ensure optimal performance of the model on their data. For a participating client i in the federated learning process, the formula for the t-th model update can be expressed as (3).

  $$w_{(t+1)}=w_t+\alpha \nabla L_{\left(D_i\right)}\left(w_t\right)$$

  (3)

  and the current model update parameters are calculated via (4).

  $$\Delta w=w_{(t+1)}-w_t$$

  (4)
• Aggregation of Updates: After the central server or coordinator node receives updates from participants, it performs the aggregation of model parameters. This operation typically involves averaging or weighted averaging to combine updates from various participants to generate new parameters for the global model.
• Evaluation: The new global model is evaluated, usually using a validation dataset or a hold-out dataset to assess the model’s performance and generalization capability.
• Iteration: The training, updating, and evaluation processes are repeated until a predetermined stopping condition is met, such as a specified number of training rounds or convergence in model performance.
• Final Model Release: After the whole federated learning process is complete, the final global model can be released for actual inference or application scenarios. Throughout the training process, federated learning does not require transmitting data to a central server or exposing it to other clients, effectively protecting users’ data privacy.

3.3.1. Federated Learning Inference Attacks

Although federated learning was initially designed to protect user privacy during the model building process, current implementations have not fully achieved this goal. During the federated learning training process, such as GNN training, the model parameters transmitted between the server and the clients may contain private information, and attackers can perform inference attacks by stealing these parameters. Depending on the attack objectives, inference attacks can be categorized into Property Inference Attacks and Membership Inference Attacks. The goal of Property Inference Attacks is to infer the fundamental properties of the target graph. Formally, a Property Inference Attack can be defined as (5).

$$F_{AP}:H_{\left(G_T\right)}\to \{\mathrm{graph} \mathrm{properties}\}$$

(5)

Given the embedding of the target graph $H_{\left(G_T\right)}$, the objective of the Property Inference Attack is to infer fundamental properties of the target graph $G_T$, such as the number of nodes, the number of edges, and the density. To train the attack model, we require a set of graph embeddings $H_{\left(G_T\right)}$ and a set of properties of interest P. The attacker can access an auxiliary dataset D that shares the same distribution as $H_{\left(G_T\right)}$. The attacker can query the target embedding model to obtain the auxiliary graph $G\in D$ and its corresponding auxiliary graph embedding $H_G$. Finally, the graph properties of G can be used to label $H_G$. The attack model $F_{AP}$ is a combination of a feature extractor E and several prediction layers M, which can be trained using the following Formula (6).

$$\underset{G\in D}{min}E\left[\sum _{p\in P}L[M^p\left(E\left(H_G\right)\right),p]\right]$$

(6)

where P is the set of properties of interest to the attacker, p is an individual property in P, and L is the cross-entropy loss.

3.3.2. Federated Learning Privacy Protection Methods

Differential privacy ensures that attackers cannot deduce specific datasets from the output of a function, providing a reasonable information security solution for privacy protection. Differential privacy techniques can effectively resist membership inference attacks based on proxy relationships, with the aim of determining whether a specific sample exists within a given collection of test samples.

The core idea of differential privacy is to add random noise to the data, thereby obtaining a noise-processed sample. This approach reduces the success rate of attackers during inference attacks while also maintaining a certain level of accuracy in database queries, thereby protecting privacy while satisfying statistical properties. Unlike traditional global differential privacy techniques, local differential privacy computes privacy-preserving data at the local level without having to rely on a trusted third-party data center. In a local differential privacy mechanism, users apply local differential privacy noise addition to their data before sending them to an untrusted server. As a result, when the server performs statistical queries on the input data, a certain level of accuracy can still be guaranteed. Moreover, as the number of users n increases, and each user independently perturbs their input, the total variance also increases.

Assume that there exists a randomized algorithm M, and let S be the set of all possible outputs of M. The probability Pr denotes the probability. For any two neighboring datasets D and $D^{\prime }$ that differ by only one record, if the condition holds

$$Pr[M\left(D\right)\in S]\le e^{ϵ}Pr[M\left(D^{\prime }\right)\in S]+\delta$$

(7)

then the algorithm M is said to satisfy $ϵ$-differential privacy, where $ϵ$ is the privacy budget used to ensure consistency of the output of the randomized algorithm M when a record is added or removed. The value $\delta$ serves as a relaxation factor; when $\delta =0$, the output of algorithm M achieves exact $ϵ$-differential privacy. Rearranging Equation (8) gives the following:

$$ϵ=ln\left({\displaystyle \frac{Pr\left[M\right(D)\in S]}{Pr[M\left(D^{\prime }\right)\in S]}}\right)$$

(8)

Thus, $ϵ$ is also referred to as privacy loss. Due to the strict nature of the privacy of $ϵ$-differentiation, it is often challenging to fully apply in practical scenarios, which is why a relaxation factor $\delta$ is typically included.

In differential privacy, there are two types of sensitivity: global sensitivity and local sensitivity. Global sensitivity refers to a function $f:D\to {\mathbb{R}}^d$ for any two neighboring datasets D and $D^{\prime }$, with the global sensitivity defined as (9):

$$G{S}_f=\underset{(D,D^{\prime })}{max}{\parallel f\left(D\right)-f\left(D^{\prime }\right)\parallel }_1$$

(9)

Local sensitivity pertains to a given dataset D and its neighboring dataset $D^{\prime }$ for a function $f:D\to {\mathbb{R}}^d$, defined as (10):

$$L{S}_f=\underset{D^{\prime }}{max}{\parallel f\left(D\right)-f\left(D^{\prime }\right)\parallel }_1$$

(10)

Local sensitivity can reflect the distributional characteristics of the samples. Generally, local sensitivity is much smaller than global sensitivity, thereby reducing the amount of noise added and improving the effectiveness of the data.

Gaussian Mechanism: For a dataset D with global sensitivity $G{S}_f$, if there exists a function $f:D\to {\mathbb{R}}^d$ such that the randomized function $M_G\left(D\right)$ satisfies

$$M_G\left(D\right)=f\left(D\right)+N(0,{\sigma }^2)$$

(11)

and meets the condition $\sigma \ge {\displaystyle \frac{G{S}_f}{ϵ}}\sqrt{2ln\left({\displaystyle \frac{1.25}{\delta }}\right)}$, then $M_G\left(D\right)$ is said to satisfy $(ϵ,\delta )$-differential privacy, where $N(0,{\sigma }^2)$ represents noise with mean 0 and variance ${\sigma }^2$. The Gaussian mechanism is a commonly used noise addition method in differential privacy, which enhances the overall privacy of the model by clipping gradients and adding Gaussian noise.

3.4. Federated Graph Neural Network Model

Traditional graph-based neural network learning often requires centralized data. However, due to many factors such as data silos and privacy protection, it is challenging to integrate vast amounts of information from multiple institutions and entities into a unified platform. If this information is used directly for distributed training, it may render the information transmission mechanisms in graph neural networks ineffective, thereby affecting their performance. Consequently, it is crucial to solve the problem of cross-institutional and cross-entity collaboration without requiring raw data. Federated learning has been proposed to address model training challenges in a distributed data environment. In this context, the research field of federated graph learning has emerged, with the aim of exploring the training issues of graph neural networks in a federated learning environment.

3.4.1. GCN Model

The GCN was introduced by Kipf and Welling [5] ref and further simplified based on the Chebyshev network (ChebNet) [23] proposed by Defferrard. GCN incorporates self-loops into the adjacency matrix, allowing nodes to better retain their own information during each information aggregation.

In GCN, the graph convolution operation at each layer can be defined as follows in (12):

$$H^{(l+1)}=f(H^l,A)=\sigma \left(\widehat{A}{H}^l{W}^l\right)$$

(12)

where $H^l$ is the node representation vector at layer l, $W^l$ is the parameters at layer l, and $\widehat{A}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{1/2}$ is the symmetric normalized adjacency matrix, where $D_{ii}={\sum }_j{\tilde{A}}_{ij}$ and $\tilde{A}=A+I_n$.

Therefore, for a graph $G=\{v,E,X\}$, a two-layer Graph Convolutional Neural Network can be represented as (13):

$$\widehat{Y}=f(X,A)=\mathrm{Softmax}\left(\widehat{A}\mathrm{ReLU}\left(\widehat{A}X{W}^0\right)W^1\right)$$

(13)

where $\widehat{Y}$ represents the predicted labels. Compared to SCNN, the GCN exhibits more flexible characteristics and achieves significant improvements in computational speed.

3.4.2. GAT Model

GAT was proposed by Velickovic [6]. In GAT, different weights are assigned to neighbor nodes on the basis of their feature differences. For nodes i and j, an attention mechanism is applied through a function att that maps the embedding vectors of the nodes to an attention weight (14):

$$e_{ij}=\mathrm{att}(W{h}_i,W{h}_j)$$

(14)

where $h_i\in {\mathbb{R}}^d$ is the embedding vector of node i, and $W\in {\mathbb{R}}^{d^{\prime }\times d}$ is a weight matrix.

In GAT, the authors use a single-layer neural network and the LeakyReLU function as the attention function as in (15):

$$e_{ij}=\mathrm{LeakyReLU}\left(a[W{h}_i\parallel W{h}_j]\right)$$

(15)

where || denotes concatenation and a is a parameter.

For a node v in the graph, considering its graph structure information, attention needs to be calculated for its neighbor nodes $N_i$ and normalized as in (16):

$$a_{ij}={\mathrm{Softmax}}_j\left(e_{ij}\right)={\displaystyle \frac{exp\left(\mathrm{LeakyReLU}\left(a[W{h}_i\parallel W{h}_j]\right)\right)}{{\sum }_{k\in N_i}exp\left(\mathrm{LeakyReLU}\left(a[W{h}_i\parallel W{h}_k]\right)\right)}}$$

(16)

After obtaining the normalized attention $a_{ij}$, the adjacent information from neighboring nodes can be aggregated based on this attention weight to update the vector representation of the node:

$$h_i^{\prime }=\sigma \left(\sum _{j\in N_i}{a}_{ij}W{h}_j\right)$$

(17)

3.4.3. GraphSAGE Model

GraphSAGE is an inductive framework that generates embeddings by sampling and aggregating features from a node’s local neighborhood, unlike transductive models like GCN, GraphSAGE can generate embeddings for previously unseen data.

In GraphSAGE, the node embedding at each layer can be computed as follows:

$$h_v^{(l+1)}=\sigma (W^{\left(l\right)}·{\mathrm{AGG}}^{\left(l\right)}(\left\{h_v^{\left(l\right)}\right\}\cup \{h_u^{\left(l\right)},\forall u\in \mathcal{N}\left(v\right)\}\left)\right)$$

(18)

where $h_v^{\left(l\right)}$ is the embedding of node v at layer l, $\mathcal{N}\left(v\right)$ denotes the set of neighbors of node v, ${\mathrm{AGG}}^{\left(l\right)}$ is a differentiable aggregator function such as mean, LSTM, or pooling, and $W^{\left(l\right)}$ is the trainable weight matrix. $\sigma (·)$ is a non-linear activation function.

For a classification task on graph $G=\{V,E,X\}$, the final prediction can be represented as follows:

$${\widehat{y}}_v=\mathrm{Softmax}\left(W^{\left(K\right)}{h}_v^{\left(K\right)}\right)$$

(19)

where ${\widehat{y}}_v$ is the predicted label for node v, and K is the total number of GraphSAGE layers. Compared to GCN, GraphSAGE allows more scalable and generalizable training by enabling inductive learning on large-scale and dynamic graphs.

4. Privacy-Enhanced Mechanisms for Federated Graph Neural Networks

In a federated environment, the neural network training model consists of i clients, one server, and one attacker. Each client has a local dataset $D_i$ for local training. The goal is to achieve protection against inference attacks by the attacker while ensuring the accuracy of the locally trained model during the federated learning process. In this paper, the traditional GCN model, the GAT model, and the GraphSAGE model are placed in a federated environment for training datasets in clients. Four clients are set up locally for training, and the training model is shown in Figure 4.

In the federated learning training process, users upload the updated model parameters to the server after completing the local model training, and the server subsequently generates a new global model. However, even with federated learning, there remains a risk of privacy leakage. For instance, during the communication process of uploading model parameters, an attacker can still perform inference attacks and deduce user privacy information contained in the gradients from the obtained information.

4.1. Overall Algorithm Framework

As discussed earlier, local differential privacy can effectively address the issue of privacy leakage in federated graph neural networks. In the following, we detail the implementation algorithm of the proposed privacy protection mechanism based on local differential privacy.

• Server Initialization: Before each training round begins, the server randomly generates a flag value of either 0 or 1 for all participating clients and sends it along with the global model parameters $w_t$ to the clients. $w_t$ may be the initial model parameters or the model parameters updated by the server after aggregating the previous round of training.
• Client Model Training: After receiving the flag and global model from the server, the client performs judgment and transformation operations on the flag. The client trains the model based on the received global model and decides whether to perform noise addition based on the flag value.
• Gradient Clipping: If the client decides to apply local differential privacy noise, they first clip the model gradients during the convergence process. A clipping threshold $\eta$ is set, specifically by performing the operation $g_i=\mathrm{clip}(g_i,\eta )$.
• Adding Noise: Once gradient clipping is complete, to achieve privacy protection, noise is added to the clipped gradients, specifically by performing the operation $g_i=g_i+N(0,{\sigma }^2)$.
• Local Model Update and Upload: During each round of training, regardless of whether noise addition is performed, the client must update the local model, generating the model update parameter $\Delta w_i$ to upload to the server.
• Model Parameter Aggregation: Upon receiving the model update parameters from each client, the server uses the federated averaging algorithm to perform a weighted average operation on the model update parameters collected, generating new global model parameters $w_t$.

The algorithm then enters a loop, continuously updating and iterating the model until convergence is achieved or a predetermined number of rounds is completed.

4.2. Server-Side Algorithm Implementation

The main function of the server is to perform model aggregation operations and to randomly generate flags for all clients. The server employs the Federated Averaging algorithm to update the global model parameters. Federated averaging is a distributed machine learning algorithm primarily used to train machine learning models across different devices or nodes. The core idea of this algorithm is to decentralize the model-training process among multiple participants, thereby achieving data privacy protection and optimizing the use of computational resources.

First, an initial base model is initialized on the central server. This model is then distributed to various participants for further training. Each participant uses their own dataset to train the model, resulting in a set of local model parameters. This step can be completed independently on the participants’ local devices without the need to upload data to the central server. The participants then upload their locally trained model parameters to the central server. The central server uses the Federated Averaging algorithm to perform a weighted average on these parameters, resulting in an updated global model. Finally, the central server sends the updated global model back to each participant, preparing for the next round of training iterations.

The advantages of this approach are primarily as follows:

• Participants do not need to upload their raw data to the central server; they only need to upload the locally trained model parameters, effectively protecting data privacy.
• The model training process is decentralized across multiple participating devices, significantly improving the efficiency of computational resource utilization.
• Since participants train models using their own data, the model can better adapt to different data distributions, thereby improving generalization capabilities.
• The Federated Average algorithm can be applied to various machine learning tasks, such as image classification, natural language processing, and speech recognition.

The specific process is as follows: First, the server collects all the uploaded model update parameters $w_i$ from the clients. These parameters may contain the most recent model weights obtained during local training by each client. The server then performs a weighted average of these parameters based on the amount of data on each client to ensure that each client’s contribution is considered when updating the global model. After calculating the new parameters for the global model, the server sends these parameters back to each client as the starting point for their next round of training. This process continues iteratively until the global model converges or reaches a predetermined number of training rounds.

The aggregation process can be expressed as follows in (20):

$$w_{(t+1)}=w_t+{\displaystyle \frac{1}{k}}\sum _{i=1}^4\Delta w_i$$

(20)

Through the Federated Averaging algorithm, the server can effectively integrate model updates from distributed clients, thereby optimizing and learning the global model while protecting data privacy. The specific server-side algorithm description is shown in Algorithm 1.

Algorithm 1 Server Algorithm

Input: Initial client model parameters $w_0$ Output: Global client model parameters $w_T$ Initialize: Input initial model parameters from clients; For $t=0$ to $T-1$ do: (a) Randomly generate $fla{g}_i=1$ or 0; (b) For $i=0$ to 4 do: // Set up four local clients i.  Client receives $fla{g}_i$ and global model $w_t$; ii. Client model returns model update parameters $\Delta w_i$; // see Algorithm 2 (c) End for; (d) $w_{(t+1)}=w_t+{\displaystyle \frac{1}{k}}{\sum }_{i=1}^4\Delta w_i$; (e) Distribute $w_{(t+1)}$ to clients; End for; Return $w_T$;

4.3. Client Algorithm Implementation

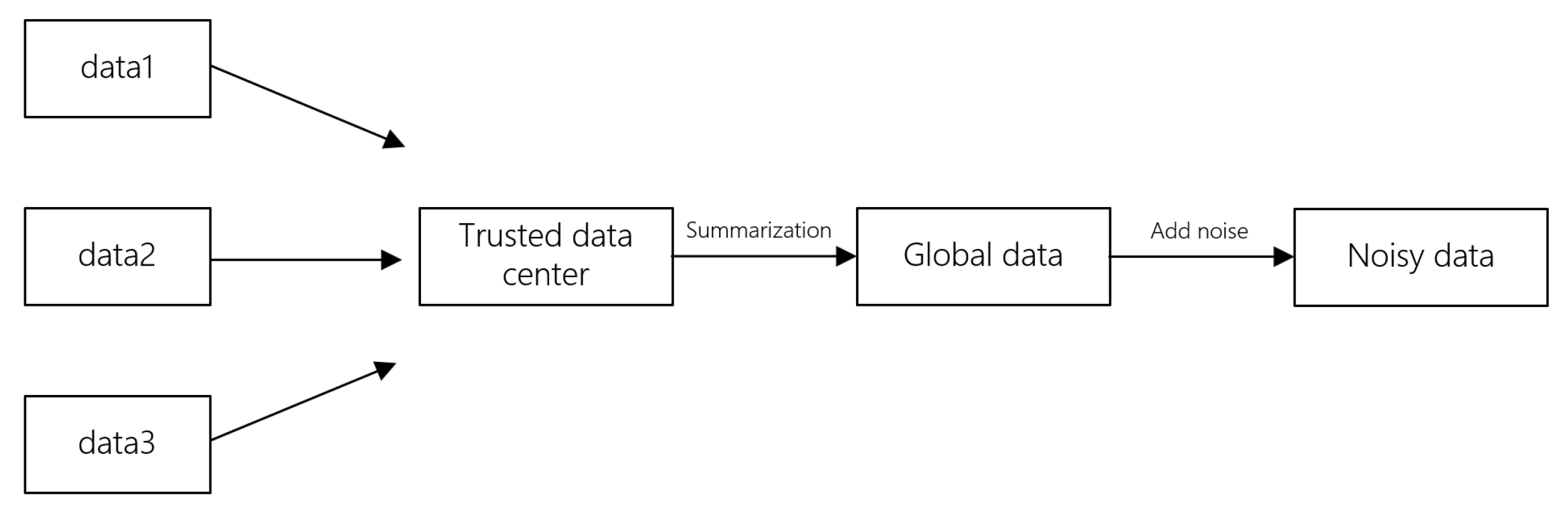
Traditional global differential privacy techniques rely on a trusted data center to collect local data from each client and add noise to the entire dataset for global model training. This method is known as centralized differential privacy. However, in practice, it is challenging to find a trusted third-party data center. This creates a data isolation problem similar to that of traditional centralized graph neural network models. Therefore, researchers have proposed local differential privacy, which shifts the data privacy steps to each client participating in model training. Each client adds noise locally and then sends the noisy data to the third party. Since the data sent is not the original data, it solves the main challenge of traditional global differential privacy. The specific client-side algorithm description is shown in Algorithm 2.

Algorithm 2 Client Algorithm

Input: Global model parameters $w_t$, model gradient $g_i$, gradient clipping threshold $\eta$, flag Output: Model update parameters $\Delta w_i$ Initialize: Receive global model parameters $w_t$ and flag from the server; If $flag=1$: (a) $g_i=\mathrm{clip}(g_i,\eta )+N(0,{\sigma }^2)$; // Clip the gradient and add noise (b) $w_{(t+1)}=w_t+\alpha (\mathrm{clip}(\nabla L\left(w_t\right),\eta )+N(0,{\sigma }^2));$// Update local model with the noisy gradient (c) $\Delta w=w_{(t+1)}-w_t;$// Generate model update parameters Else: Change the flag randomly to $flag=1$ or 0; (a) If $flag=1$: i.  Repeat steps 3–6 of the algorithm; (b) Else: i.  $w_{(t+1)}=w_t+\alpha \nabla L_{D_i}\left(w_t\right);$// No local differential privacy noise added ii. $\Delta w_i=w_{(t+1)}-w_t;$ Return $\Delta w_i$;

We choose to apply local differential privacy techniques to federated learning due to the similarities between the local differential privacy generation mechanism and the independent training characteristic of clients in federated learning, thus achieving user privacy protection. Each user independently generates differential privacy at the local level before uploading model parameters, ensuring that the model parameters cannot be inferred through attacks. Federated differential privacy places dual requirements on attackers: on the one hand, they should not be able to infer whether a particular client participated in the current training when receiving the local model from the client; on the other hand, they should not be able to identify the client who uploaded the parameters. This ensures both the information security between clients and the local privacy security of each client’s data, as shown in Figure 5.

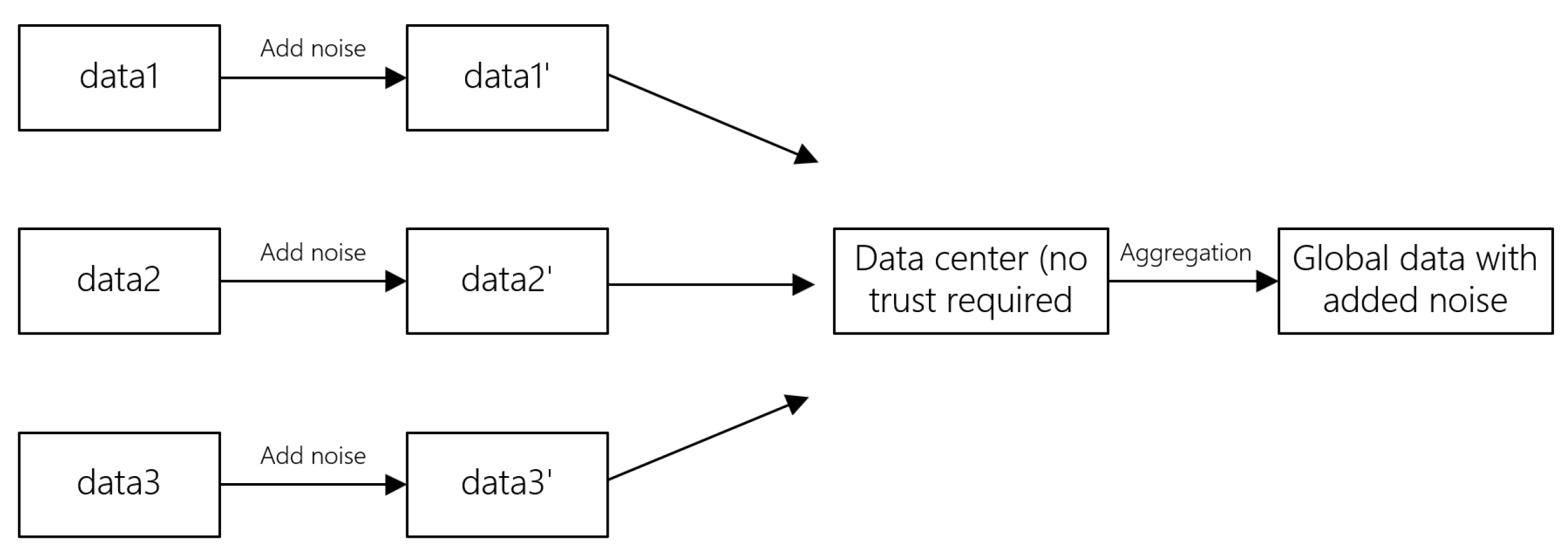
LDP distributes the task of adding noise to the data among each user, which further enhances the security of private data. Using differential privacy techniques, noise is added to the data in such a way that it becomes difficult for attackers to deduce personal privacy from the obtained parameters. The implementation of differential privacy consists of two steps: gradient smear and noise addition, as shown in Figure 6.

Each client employs graph attention models and graph convolutional neural networks to train local data, apply gradient clipping to the samples, and process the added noise using local differential privacy methods. First, a gradient threshold $\eta$ is set to reduce the gradient. Based on this threshold, each user generates a differential privacy parameter $ϵ$, which is determined by the personal privacy needs of each user. The higher the value, the lower the privacy security. Mussian noise is then added to the clipped gradient, expressed as follows in (21):

$$g_i=\mathrm{clip}(g_i,\eta )+N(0,{\sigma }^2)$$

(21)

where $\eta$ is the gradient clipping threshold and ${\sigma }^2$ is the variance of the Gaussian noise.

The protected gradient $g_i$ is then used for local model update iterations:

$$w_{(t+1)}=w_t+\alpha (\mathrm{clip}(\nabla L\left(w_t\right),\eta )+N(0,{\sigma }^2))$$

(22)

where $\alpha$ is the learning rate, and $\nabla L\left(w_t\right)$ represents the current gradient value. Model update parameters can be generated using the following formula (23):

$$\Delta w=w_{(t+1)}-w_t$$

(23)

After the user completes local model training, the trained model update parameters are uploaded to the server. The server then constructs an overall model based on the parameters uploaded by each user and broadcasts the updated model to users. This process continues iteratively until the gradient approaches zero.

4.4. Attack Model

In machine learning, the goal of membership inference attacks is to infer whether a particular sample was used in training by analyzing the behavior of the model. Attackers typically do not have direct access to the training data, but can obtain information through interaction with the model. The potential consequences of such attacks include user privacy violations and exposure of sensitive information, which is especially critical in sectors like healthcare and finance where data privacy needs to be protected. The attack model training algorithm is described in Algorithm 3.

Algorithm 3 Attacker Algorithm

Input: Global client model parameters $w_t$, target data x Output: Determine whether the target data exists in the training dataset of another client Initialize: Input global client model parameters $w_t$ and target data x; $w_{(t+1,A)}\leftarrow w_t+\gamma ·{\displaystyle \frac{\partial L^x}{\partial w_t}}$; // The attacker generates global model parameters based on target data $\Delta w_i=w_{(t+1,A)}-w_t$; // Output model update parameters and upload to the server Compare $w_{(t+1)}$ with $w_t$ to determine if x is in a certain client’s training dataset; Return the judgment result;

The attack model in this paper employs the GradAscent method to carry out membership inference attacks. The core idea of this method is to utilize the gradient information of the target data during the training process to infer whether the target data exists in a specific training dataset.

In GradAscent, the successful conduct of a membership inference attack is achieved through the following steps:

• Select Model: The attacker needs an already trained model, usually publicly available or obtained from some service.
• Generate Samples: The attacker can randomly generate candidate samples or draw samples from a specific distribution. These samples may resemble the training data.
• Calculate Loss Function: For each candidate sample x, the attacker inputs it into the model and computes the loss function L. The loss function is typically represented as follows in (24):

  $$L(y,f(x\left)\right)=-log\left(f\right(x\left)\right)$$

  (24)

  where y is the true label, and $f\left(x\right)$ is the predicted probability output by the model.
• Compute Gradient: Through backpropagation, the attacker can obtain the gradient of the loss function with respect to the input sample $\nabla L$:

  $$\nabla L={\displaystyle \frac{\partial L}{\partial x}}$$

  (25)
• Gradient Ascent: The attacker uses the gradient ascent algorithm to adjust the input sample, maximizing the value of the loss function. The update rule can be expressed as (26):

  $$x^{\prime }=x+\gamma ·\nabla L$$

  (26)

  where $x^{\prime }$ is the updated sample, and $\gamma$ is the learning rate.
• Determine Membership: By comparing the loss of the adjusted sample with that of the original sample, the attacker can infer whether the sample belongs to the training set. Generally, the loss for training samples is higher, whereas the loss for unseen samples is lower.

The specific attack process is as follows: First, the attacker selects one or more target data samples x that may be part of the model’s training dataset or data from other sources. Next, the attacker utilizes the trained target model to compute the gradient of the loss function concerning the model parameters while inputting these target data samples x. This gradient information reveals the model’s sensitivity and response to the target data.

Subsequently, the attacker uses the gradient ascent method to adjust the model parameters according to the gradient information of the target data samples. By updating the model parameters based on (28), the attacker attempts to maximize the loss function of the model on the target data samples x, thus inferring whether the data sample was ever used to train the model.

The effectiveness of this membership inference attack method depends on the attacker’s access to the target model and the selection of target data samples. By analyzing the gradient information, the attacker can determine whether the target data samples possess “memorability” indicating whether they were ever used for model training, thus threatening the privacy protection capabilities of the model, as shown in (27).

$$w\leftarrow w+\gamma ·\left({\displaystyle \frac{\partial L^x}{\partial w}}\right)$$

(27)

where w are the model parameters, and $L^x$ is the loss function for the target data. If the target data x exists in another client’s training dataset, it will significantly update the model parameters w, as its optimizer will suddenly reduce the gradient of the loss function $L^x$.

5. Experimental Validation and Result Analysis

The experiments were conducted using the PyTorch framework and Python version 3.9. The specifications of the other software and hardware parameters are shown in

Table 1. Configuration table.

Configuration	Parameter
Operating System	Windows 10
CPU	AMD Ryzen 9 7940H w/Radeon 780 M Graphics 4.00 GHz
GPU	NVIDIA GeForce RTX 4060 Laptop GPU
Memory	16 GB

:

The experimental dataset used in this paper is the CoraML dataset, which is an extended version of the Cora dataset. The CoraML dataset contains link information between nodes, allowing the construction of a graph structure to train on graph link prediction tasks. Dataset is divided according to the standard federated learning setting—80% of the nodes are used as training sets and 20% as global test sets. The data between clients is randomly sampled to achieve non-independent and identically distributed (Non-IID) simulation. The node labels in the dataset correspond to the fields of the papers, divided into seven categories, where each node represents a research paper, and the edges represent the citation relationships between papers. The properties of the dataset are shown in

Table 2. CoraML attribute table.

Dataset	Edges	Nodes	Features	Classes
CoraML	6783	2810	1433	7

.

5.1. Experimental Settings

Classic graph neural network models gather training samples and testing samples from each user, and then input these samples into a model for unified training, followed by evaluation on a global test set. However, such an ideal approach is often impractical in real-world scenarios due to various reasons, such as privacy protection and industry competition, making it unrealistic to aggregate data.

In this paper, we use Graph Attention Network (GAT), Graph Convolutional Network (GCN), and Graph Sample and Aggregator (GraphSAGE) as client training models. The federated learning process is optimized using the Stochastic Gradient Descent (SGD) algorithm, with a learning rate set to 0.01. After applying a privacy protection mechanism based on local differential privacy, we compare the changes in model accuracy under different differential privacy parameters to analyze the impact of privacy mechanisms on model performance.

The hyperparameter settings for the models are shown in

Table 3. Model training parameters.

Parameter Name	Parameter Value
Local Training Epochs	400
Global Training Epochs	150
Learning Rate	0.01
Optimization Algorithm	SGD

.

In order to achieve local differential privacy, the experiment adds Gaussian noise to the gradients at the client side, sets different gradient clipping thresholds, and configures different noise intensities for the clients. This setup trains the federated graph neural network model to validate the effects of varying gradient clipping thresholds and noise intensities on model performance.

Accuracy is commonly used to evaluate the global accuracy of the trained model, with the specific calculation formula as follows in (28).

$$\mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(28)

where $TP$ (True Positive) and $TN$ (True Negative) indicate correctly predicted samples, while $FP$ (False Positive) and $FN$ (False Negative) indicate incorrectly predicted samples.

The F1 score is the harmonic mean of precision and recall, with a maximum value of 1 and a minimum value of 0. A higher value indicates a better model accuracy. Its specific calculation formulas are given as follows:

$$\mathrm{precision}={\displaystyle \frac{TP}{TP+FP}}$$

(29)

$$\mathrm{recall}={\displaystyle \frac{TP}{TP+FN}}$$

(30)

$$F_1={\displaystyle \frac{2\times (\mathrm{precision}\times \mathrm{recall})}{\mathrm{precision}+\mathrm{recall}}}$$

(31)

This paper selects accuracy as the metric for assessing model prediction performance and the F1 score as the metric for evaluating the accuracy of the attack model.

5.2. Experimental Result Analysis

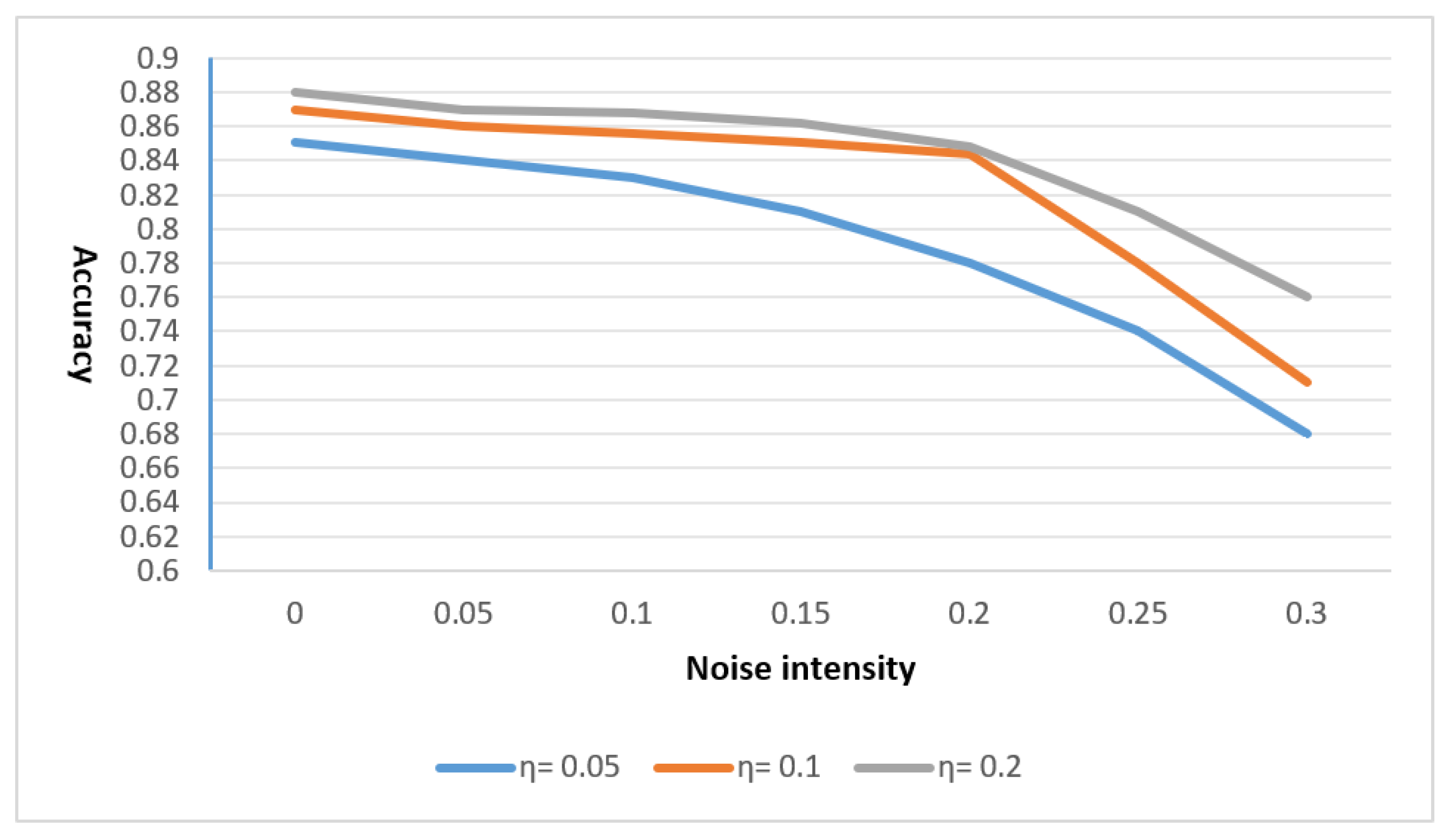
The experiment analyzes the impact of different noise intensities on the performance of the model at the same gradient clipping threshold. This paper fixes the gradient clipping thresholds at three different values, 0.05, 0.1, and 0.2, and then sets different noise intensities to conduct multiple experiments. The average accuracy of these multiple experiments is used as the standard to compare and derive the experimental results.

The results obtained from training the two models under different gradient clipping thresholds and noise intensities are shown in Figure 7, Figure 8 and Figure 9. In these figures, the vertical axis represents accuracy, while the horizontal axis represents noise intensity. It can be observed that at the same noise intensity, a larger gradient clipping threshold corresponds to a higher accuracy in model prediction. When the gradient clipping threshold is set to $\eta =0.1$ or $0.2$, the prediction accuracy of the model shows little difference, while a smaller gradient clipping threshold of 0.05 leads to a significant drop in accuracy. On the other hand, under the same gradient clipping threshold, as the noise intensity increases, the model’s performance declines accordingly.

However, it is important to note that the proposed privacy method may struggle or underperform in certain edge cases. For instance, when dealing with extremely high noise intensities or very small gradient clipping thresholds, the model’s prediction accuracy might be severely impacted, leading to a trade-off between privacy protection and model performance. Additionally, in situations where the data are highly sparse or have a large number of outliers, the effectiveness of the privacy-preserving technique could be diminished. These limitations should be taken into consideration when applying the method to specific real-world scenarios.

Based on this comparison, this paper recommends training the GCN model with a gradient clipping threshold of 0.1 and a noise intensity of 0.2, training the GAT model with a gradient clipping threshold of 0.1 and a noise intensity of 0.15, and training the GraphSAGE model with a gradient clipping threshold of 0.1 and a noise intensity of 0.2, to achieve a good balance between privacy protection and model accuracy.

Based on the conclusions above, this paper continues to add attackers on the client side to compare the F1 scores of the attack model after applying the proposed local differential privacy-based federated graph neural network privacy enhancement mechanism and using traditional federated aggregation algorithms (Fed-Avg) in the face of inference attacks. The results are shown in

Table 4. F1 score of inference attacks under different models.

Model	Mechanism	F1 Score
GCN	Ours	0.39
	Fed-Avg	0.94
GAT	Ours	0.41
	Fed-Avg	0.92
GraphSAGE	Ours	0.44
	Fed-Avg	0.87

:

After applying the proposed privacy enhancement mechanism, the accuracy of the attack model decreased significantly, demonstrating that the privacy enhancement mechanism of the federated graph neural network based on local differential privacy proposed in this paper can effectively defend against inference attacks.

6. Conclusions and Future Work

This paper addresses the privacy leakage issue inherent in traditional link prediction methods for graph neural networks from the perspective of local differential privacy technology, aiming to resolve the privacy leakage and security risks present in existing link prediction models and to protect users’ private data. The model proposed in this paper achieves high performance while protecting private data. The proposed method shows promising results in reducing privacy leakage while maintaining high prediction performance, which is a significant contribution to enhancing the security of graph-based models. For example, in online social networks or recommendation systems, where user privacy is critical, this approach can significantly reduce the risks associated with data exposure. In the future, exploring the integration of other privacy-preserving mechanisms, such as homomorphic encryption, with graph neural networks could further improve data security and lead to more robust models. However, there are still some aspects that need improvement. Many graph neural network models are currently capable of performing link prediction tasks. The model presented in this paper is based primarily on GCN and GAT. More research is needed to explore how other graph neural network models can be applied to federated learning techniques, compared, and selected for greater prediction accuracy, for example, research on the following:

• Optimizing Noise Addition Strategies**: Future efforts could focus on developing more refined noise addition methods aimed at minimizing the impact on model accuracy while ensuring higher levels of privacy protection. By adjusting parameters or employing different noise distributions, it might be possible to find a better balance between privacy and utility.
• Integrating Advanced Security Techniques Such as Homomorphic Encryption (HE)**: In addition to LDP, integrating homomorphic encryption or other advanced secure computation techniques into the FedGNN framework could provide stronger data security for users. This not only prevents the leakage of model parameters but also protects participant data throughout the training process.
• Addressing Challenges Posed by Non-IID Datasets**: Current research indicates that Non-IID data lead to significant parameter discrepancies among clients, thereby affecting the performance of the global model. Developing new algorithms and strategies to better handle such datasets is crucial for improving overall model performance.
• Exploring the Impact of Different Graph Structures on FedGNNs**: Various types and scales of graph structures can significantly influence the performance of FedGNNs. Conducting in-depth studies on how these factors affect performance and designing corresponding optimization schemes represent another important research direction.

By combining different privacy-preserving mechanisms, such as differential privacy with homomorphic encryption, we can build more robust systems that ensure high levels of security and effectiveness across various application scenarios. These suggestions not only help address current challenges but also drive innovation in distributed graph learning environments.