Multi-Keyword Ranked Search on Encrypted Cloud Data Based on Snow Ablation Optimizer

Abstract

The idea of multi-keyword ranked search over encrypted cloud data has attracted considerable attention in recent studies, as it allows users to securely and efficiently retrieve highly relevant results. Traditional methods improve search efficiency by incorporating the K-means clustering algorithm. However, when applied to large-scale datasets, K-means can become computationally expensive. This paper introduces a multi-keyword ranked search method, SAO-KRS, which leverages the snow ablation optimizer (SAO) to enhance clustering performance. The approach begins with principal component analysis (PCA) to reduce the dimensionality of high-dimensional data, followed by clustering the reduced data using SAO, which reduces clustering overhead massively. By incorporating a heuristic best-first search algorithm over index trees, the scheme achieves reduced computational cost with high retrieval accuracy. In the best-case scenario, the proposed method achieves up to 21 times faster clustering and 2.7 times faster searching compared to the traditional K-means approach. Extensive experimental results verify that this method significantly improves clustering efficiency while ensuring both search speed and accuracy.

1. Introduction

Cloud computing offers significant potential by providing cost-effective, flexible, and scalable resources over the Internet. These advantages motivate individuals and organizations to move applications and services to the cloud, especially for scenarios involving long-term storage and retrieval of large datasets, such as digital archives, scientific repositories, and enterprise data management systems [1]. In such contexts, efficient data processing during the archiving phase is critical, as large volumes of data need to be indexed and stored with minimal computational overhead. On the other hand, retrieval operations can tolerate more flexible search strategies, as immediate responses are not always required.

While cloud computing offers many benefits, outsourcing data to third-party cloud service providers (CSPs) raises significant privacy concerns. Since CSPs control the stored data, unauthorized access or actions could occur out of curiosity or interest [2]. As a result, sensitive data must be encrypted before being outsourced. However, encryption makes traditional plaintext-based keyword searches unusable. Downloading the entire encrypted dataset for local decryption and search is impractical, particularly for large-scale storage. Therefore, developing an efficient keyword search approach for encrypted data is crucial in cloud-based archival systems and similar applications where data retrieval needs to balance security, accuracy, and computational efficiency.

Due to growing security concerns, the ability to perform secure searches on encrypted data has become a focal point in academic research. Among the various techniques, searchable encryption (SE) has emerged as a prominent solution due to its efficiency, functionality, and security. SE allows clients to keep encrypted data on the cloud and carry out keyword searches directly on the ciphertext. Various search functionalities, including single-keyword search [3,4], multi-keyword Boolean search [5], and multi-keyword ranked search [6,7], have been presented under different threat models. Multi-keyword ranked search has drawn particular interest because it enhances practicality. Users may swiftly obtain the most pertinent data via ranked search, which is able to lessen network traffic by returning only the top results. In contrast, single-keyword searches often provide coarse results, whereas multi-keyword searches improve search accuracy. This makes multi-keyword search especially important in cloud environments, where efficient searching of large datasets must be balanced with data security.

Researchers have not only explored various search functionalities but also focused on enhancing the effectiveness of multi-keyword search. Cao et al. adopted inverted index structures for search [7], while Xia et al. employed balanced binary tree index structures [8], achieving superior sublinear search efficiency compared to inverted indices. Moreover, machine learning algorithms have been applied to keyword-ranked searches to further boost efficiency. Systems can learn from data and carry out tasks based on this learning process via machine learning. Traditional methods for encrypted cloud data retrieval rely primarily on encrypted indexing and keyword matching. However, as data volumes increase and user demands diversify, methods based solely on statistical weights struggle to meet the need for high-accuracy and efficient search. Miao et al. addressed this by incorporating K-means clustering [9], which optimizes index structures to improve search efficiency. However, K-means clustering can be computationally expensive for large datasets and is sensitive to initial centroid selection, impacting overall efficiency.

To address these challenges, this paper presents a multi-keyword ranked search scheme based on a balanced binary tree search structure, integrating snow ablation optimizer (SAO) and principal component analysis (PCA) to enhance both clustering and searching effectiveness in large-scale data environments, thereby optimizing system efficiency.

The following are the main contributions of this paper:

(1)

We propose a multi-keyword ranked search scheme that efficiently returns the top k most relevant results.

(2)

We apply PCA for dimensionality reduction and introduce SAO-based clustering to construct optimized index structures. This combination preserves key document features, simplifies data representation, and significantly improves clustering efficiency and query performance over traditional methods.

(3)

We design a heuristic best-first search algorithm over an index tree to efficiently retrieve the top k relevant documents. By combining vector similarity estimation with priority-based traversal and adaptive pruning, the method achieves high retrieval accuracy with reduced computational cost.

The remainder of this paper is organized as follows: Section 2 reviews related work, Section 3 presents the notation and preliminary concepts, Section 4 outlines the system model, threat model, and design objectives, Section 5 elaborates on the proposed scheme, Section 6 evaluates its performance, and Section 7 provides the conclusion.

2. Related Work

SE allows clients to securely keep encrypted data on the cloud and carry out keyword searches directly on the ciphertext, without requiring decryption. SE can be created with either symmetric-key or public-key cryptography, depending on the cryptographic primitives used. Song et al. introduced the searchable symmetric encryption (SSE) model [3], which ensures data security and privacy while enabling efficient keyword searches. Boneh et al. subsequently presented the public-key encryption with keyword search (PEKS) scheme [4]. These early models, however, were restricted to single-keyword Boolean searches, which often lack accuracy. In contrast, multi-keyword Boolean search enables users to query documents using multiple keywords. Golle et al. proposed an encrypted retrieval scheme supporting multi-keyword conjunctive queries (i.e., documents must contain all queried keywords) [5], enabling accurate document searches using multiple keywords.

However, these approaches obtain results based solely on the presence of keywords, without considering document relevance, making them functionally simple. Ranked search, on the other hand, facilitates fast retrieval of the most relevant documents, significantly reducing network traffic by returning only the top k results. Wang et al. introduced a ranked search scheme that sorts matching files based on relevance score before returning results [6], achieving ranked keyword search. However, this scheme is limited to supporting only single-keyword ranked searches. To address this limitation, Cao et al. later introduced the first multi-keyword ranked search scheme [7], which avoids irrelevant results. However, this scheme only supports exact keyword searches and uses an inverted index, making search efficiency linearly dependent on the number of documents. Sun et al. introduced a secure multi-keyword ranked search based on similarity ranking [10]. By using an index tree structure, Sun’s search algorithm achieved sublinear search efficiency but sacrificed accuracy. Yu et al. introduced a two-round searchable encryption scheme supporting multi-keyword retrieval [11], incorporating vector space models and homomorphic encryption to enhance security. Despite performance optimizations, computational complexity remained high for large-scale datasets and multi-keyword queries.

In addition, efforts are being made to expand the functionalities of multi-keyword search schemes. Fu et al. introduced a solution that supports multi-keyword ranking searches and synonym queries for semantic-based retrieval [12]. This solution designed a synonym expansion module, allowing the user’s query keywords to automatically expand into semantically related terms, thereby improving the coverage and accuracy of search results. Li et al. introduced a scheme supporting verifiable fuzzy multi-keyword ranking search [13], which enables efficient fuzzy matching, multi-keyword retrieval, and result ranking on encrypted data. Additionally, this scheme allows users to testify to the correctness and completeness of the search results. Meanwhile, Joshi et al. introduced a ranking search scheme based on multi-keyword synonym support and greedy depth-first search [14], which prioritizes accessing documents with higher relevance within the search space, thereby improving retrieval efficiency.

Several recent works have further advanced multi-keyword ranked search in encrypted settings. Hu and Zhang [15] proposed a semantic-based multi-keyword ranked search scheme with enhanced relevance and efficiency. Zhao et al. [16] introduced a forward-privacy design that supports ranked search over dynamic datasets. The MUSES platform by Le et al. [17] improves multi-user encrypted search with minimized leakage and significantly enhanced performance. Lin et al. [18] presented an attribute-based searchable encryption framework supporting flexible multi-keyword ranking. Furthermore, Xu et al. [19] leveraged blockchain and bitmap indexing to build a verifiable and efficient multi-keyword search system.

Researchers have also explored enhanced multi-keyword search efficiency. Miao et al. combined K-means clustering to propose a ranked keyword search scheme based on machine learning [9], leveraging clustering to improve retrieval efficiency. Liu et al. proposed a privacy-preserving, semantic-aware, multi-keyword ranked search scheme [20], using optimized index structures and lightweight encryption techniques to reduce computational and communication overhead.

3. Notations and Preliminaries

3.1. Notation

This paper uses many symbols. For convenience, a summary is provided as follows:

• $\mathcal{W}$—The keyword list, which is a collection of plaintext keywords $\mathcal{W}=\left\{w_1,w_2,\cdots ,w_l\right\}$.
• $l$—The overall scale of keywords throughout all documents.
• $\mathcal{D}$—The collection of encrypted documents $\mathcal{D}=\left\{d_1,d_2,\cdots ,d_n\right\}$.
• $n$—The sum of the documents in the collection.
• ${\mathcal{W}}_Q$—A subset of $\mathcal{W}$, representing the set of keywords to be searched.
• $Q$—The query vector corresponding to ${\mathcal{W}}_Q$ with a dimension of $l$.
• $\widehat{Q}$—The encrypted form of $Q$.
• ${\mathcal{V}}_u$—The index vector of tree node $u$, also with a dimension of $l$.
• ${\widehat{\mathcal{V}}}_u$—The encrypted form of ${\mathcal{V}}_u$.

3.2. TF-IDF Model

Multi-keyword ranked search is successfully supported by the incorporation of the vector space model and the TF-IDF model, which is frequently utilized in plaintext information retrieval [21]. In the TF-IDF model, “TF” indicates term frequency, which refers to the frequency of a keyword’s occurrence in a document, while “IDF” indicates inverse document frequency. IDF, which measures a word’s importance over the whole document set, is commonly computed by dividing the total number of documents by the number of documents that contain the keyword. In this paper, each document is formatted as an index vector, with each element of the vector corresponds to a normalized TF value. The query vector’s elements represent normalized IDF values, with the IDF values for irrelevant keywords set to 0. Both the index and query vectors have the same dimensionality, and the elements within the vectors must align with the corresponding keywords in the set. The evaluation of the relevance score is described as follows:

• $m_{i,j}$—The sum of occurrences of the keyword $w_j$ in the document $d_i$.
• $n_j$—The sum of documents that contain the keyword $w_j$.
• $T{F}_{i,j}$—The TF value of the keyword $w_j$ in the document $d_i$.
• ${\overline{TF}}_{i,j}$—The normalized TF value of the keyword $w_j$ in the document $d_i$.
• $ID{F}_j$—The IDF value of the keyword $w_j$ in the entire document collection.
• ${\overline{IDF}}_j$—The normalized IDF value of the keyword $w_j$ in the entire document collection.

The relevance score calculation is defined as follows:

$$R\left({\mathcal{V}}_u,Q\right)={\mathcal{V}}_u\cdot Q={\displaystyle \sum _{w_j\in {\mathcal{W}}_Q}{\overline{TF}}_{u,j}\times {\overline{IDF}}_j}$$

(1)

For node $u$, its normalized TF value is calculated by its child nodes. If $u$ is a leaf node, i.e., it represents a specific document $d_i$, then the normalized TF value of $d_i$ is calculated as follows:

$${\overline{TF}}_{i,j}={\displaystyle \frac{T{F}_{i,j}}{\sqrt{{\displaystyle {\sum }_{w_j\in {\mathcal{W}}_Q}{\left(T{F}_{i,j}\right)}^2}}}}$$

(2)

where $T{F}_{i,j}=1+\ln m_{i,j}$ represents the term frequency of $w_j$ in document $d_i$.

For keyword $w_j$, its normalized IDF value is calculated as follows:

$${\overline{IDF}}_j={\displaystyle \frac{ID{F}_j}{\sqrt{{\displaystyle {\sum }_{w_j\in {\mathcal{W}}_Q}{\left(ID{F}_j\right)}^2}}}}$$

(3)

where $ID{F}_j=\ln \left(1+n/n_j\right)$ represents the inverse document frequency of $w_j$ in the document collection.

3.3. Snow Ablation Optimizer (SAO)

Deng et al. presented the snow ablation optimizer (SAO) [22], a novel swarm intelligence optimization algorithm. Inspired by the physical phenomenon of high-altitude snow gradually melting under the influence of solar radiation and temperature changes in natural environments, the algorithm simulates the dynamic processes of snow particle ablation, flow, and recrystallization to achieve global optimization in the solution space. SAO operates by simulating three core natural processes inspired by the melting and flow of snow:

Ablation Phase. Each solution, represented as a “snow particle,” undergoes local perturbations that mimic the gradual melting caused by environmental factors. This phase enhances local exploration by slightly adjusting particle positions to refine solutions.

Migration Phase. The melted snow flows towards regions of lower potential energy, analogous to moving solutions toward globally promising areas in the search space. This phase promotes global exploitation by guiding particles towards the current best solution(s).

Recrystallization Phase. To prevent premature convergence and maintain population diversity, some particles are randomly reinitialized, simulating the natural recrystallization process that occurs due to environmental cooling.

By iteratively applying these phases, SAO balances exploration and exploitation effectively, enabling it to efficiently search complex, high-dimensional, and multimodal optimization landscapes.

3.4. Principal Component Analysis (PCA)

PCA is a commonly adopted technique for dimensionality reduction and feature extraction [23]. It is often used to simplify datasets, eliminate redundant information, and retain as much of the original data’s variability as possible. PCA operates by transforming the data from its original coordinate system into a new one, identifying the “principal components,” which are the direction vectors. These components correspond to the directions of maximum variance in the data within the new space. The primary objective of PCA is to reduce the dimensionality of high-dimensional data while retaining the most significant features during the compression process.

4. Problem Definition

4.1. System Model

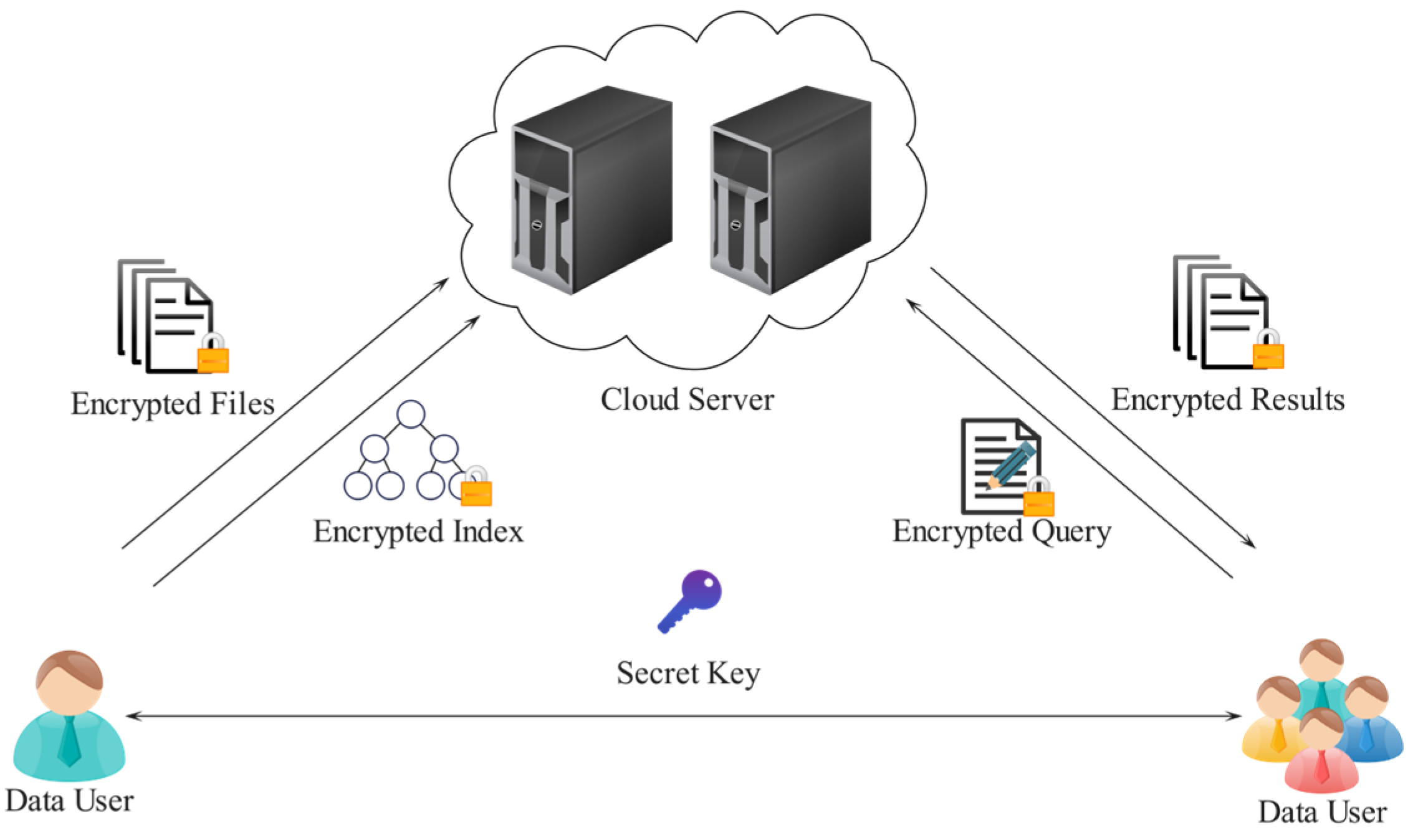
This paper introduces a system model comprising three main entities, as depicted in Figure 1: the data owner, the data user, and the cloud server.

Data Owner. The data owner manages the storage of all documents intended for outsourcing to the cloud server. This entity is responsible for generating a private key, constructing an encrypted index tree for the document set, and encrypting the documents themselves. Once these steps are completed, the data owner securely transmits the necessary key information to authorized data users via a protected communication channel.

Data User. Given a query consisting of several keywords, an authorized user generates a trapdoor based on the predefined search control mechanism. This trapdoor enables the user to retrieve the top-k most relevant encrypted documents from the cloud server. Once retrieved, the documents can be decrypted locally using the shared secret key.

Cloud Server. The cloud server is responsible for storing both the encrypted document collection and the encrypted searchable tree indexes, both generated by the data owner. Upon receiving the trapdoor from the data user, the server performs a search over the index and identifies the k most relevant encrypted documents based on the encrypted relevance scores computed from the TF-IDF-based vector representations. These documents are then returned to the data user without revealing any content or keyword information.

Initially, the data owner computes the normalized TF vector for each document in the collection and subsequently performs clustering on the resulting vector set. For each cluster, an encrypted index tree is constructed, and the associated documents are encrypted. These encrypted index trees and documents are uploaded to the cloud server. In addition, the data owner generates a private key along with the complete IDF vector for the document set.

If an authorized data user wishes to execute a query, they first obtain the necessary key information and the IDF vector from the data owner via a secure communication channel. According to the query requirements, the data user constructs an encrypted query token and transmits it to the cloud server. The most pertinent encrypted documents are then returned by the server once it has computed relevance scores from the query token. Finally, the data user decrypts the received documents using the private key to retrieve the original information.

4.2. Threat Model

As with most keyword ranked search schemes [8,9], this model implies that both the data owner and the data user are fully trusted entities, whereas the cloud server is considered honest but curious. That is, while the server honestly carries out search operations, it may also try to extract sensitive data from the stored documents or user queries. This paper considers two specific types of threat models:

Known Ciphertext Model. In the known ciphertext model, the cloud server can access solely encrypted data—such as the encrypted documents, index structures, and query vectors—without any exposure to plaintext content. Under this threat model, the server may attempt a ciphertext-only attack to infer information from the encrypted data.

Known Background Model. This more advanced threat model assumes that the cloud server has access not only to encrypted data but also to auxiliary information, such as statistical distributions of term frequencies, keyword co-occurrence patterns, or public background knowledge about the dataset. With this knowledge, the server may launch statistical attacks, which involve analyzing access patterns, frequency similarities, or repeated query behaviors to infer or even accurately identify specific query keywords. Such attacks exploit the correlation between encrypted query structures and the statistical features of the underlying plaintext data, posing a significant risk to keyword privacy.

4.3. Key Management and Security Enhancement

To support the privacy protection objectives, the scheme includes a secure key management mechanism. The data owner is responsible for generating and managing the secret key materials, which are used for encrypting the index and query vectors. These keys are securely distributed to authorized data users through authenticated and encrypted communication channels. In practice, this can be implemented using standard key exchange protocols such as Diffie–Hellman or public key infrastructure (PKI), depending on the system’s security requirements.

Moreover, under the known background model, where the cloud server may possess auxiliary statistical information, the scheme incorporates perturbation elements to prevent statistical inference attacks. These perturbations introduce controlled noise into encrypted vectors, making it significantly more difficult for the server to reverse-engineer sensitive query terms. Together, the encryption and obfuscation mechanisms form a robust security foundation for the proposed searchable encryption system.

4.4. Design Goals

The proposed scheme accomplishes three key objectives: it enables multi-keyword ranked search, ensures privacy protection, and enhances clustering efficiency. Specifically, the scheme offers an advanced search functionality by ranking results based on relevance, unlike traditional Boolean search methods. It also addresses critical privacy concerns by protecting sensitive data from the cloud server, such as keyword indices, query terms, and term frequencies. In terms of efficiency, the scheme focuses on optimizing clustering performance through a combination of dimensionality reduction and clustering techniques. These objectives are designed to work together seamlessly to provide a robust and efficient solution.

Multi-keyword Search: This scheme enables multi-keyword searches and ranks the search results by relevance scores, unlike Boolean search schemes that only return undifferentiated search results.

Privacy Protection: The primary goal of the scheme is the prevention of the cloud server from gaining any further insights into the encrypted document collection, the encrypted index tree, or the encrypted query vectors. To achieve this, the scheme is made to meet the following specific privacy requirements:

(1)

Index and Query Confidentiality. Both the keywords contained in the index and query, along with the TF values kept in the index and the IDF values associated with the query keywords, are treated as sensitive information. These elements must be securely protected to prevent any disclosure to the cloud server.

(2)

Trapdoor Unlinkability. To prevent the cloud server from identifying if two encrypted query trapdoors originate from the identical search input, the trapdoor generation mechanism must be randomized. A deterministic approach would allow the server to observe repeated patterns and track keyword frequency across multiple queries. Therefore, to achieve trapdoor unlinkability, it is essential to incorporate adequate randomness into the trapdoor generation process, ensuring that each query appears distinct even if the same keywords are used.

(3)

Keyword Privacy. Since users typically do not want their search queries to be exposed to others, the main concern is concealing the specific keywords being searched, as represented by the trapdoor. While encrypting trapdoors can protect the content of the query, the cloud server can still apply statistical analysis techniques to make educated guesses. Document frequency, which indicates how many documents contain a keyword, is often enough to identify high-probability keywords [24]. With access to some background knowledge about the dataset, the cloud server could reverse-engineer the keywords using these specific features. Therefore, keyword privacy seeks to prevent the server from uncovering keyword identities within queries, indexes, or documents by defending against statistical inference attacks based on frequency analysis.

Clustering and Searching Efficiency: The proposed scheme uses a balanced binary tree index structure and improves clustering efficiency by combining PCA for dimensionality reduction and SAO for clustering. This approach enhances clustering efficiency significantly. By introducing a heuristic best-first search algorithm, the method enhances performance in the searching process, with reduced computational cost and high retrieval accuracy.

5. Proposed Methodology

Combining PCA techniques, this paper proposes a multi-keyword ranked search scheme utilizing SAO, namely SAO-KRS. SAO-KRS first uses PCA to perform dimensionality reduction on the document TF vectors in the dataset. Then, SAO is used to cluster the document collection, and a balanced binary tree index is constructed for each cluster. The final result is a search forest. After the user uploads a query, the relevance score is computed through this search forest, and the results are retrieved through a heuristic best-first search algorithm.

5.1. Constructing Keyword Balanced Binary Tree

We choose a balanced binary tree as the basic index structure, and a forest is constructed by combining clustering algorithms. The process is as follows:

The construction process begins with each document in the collection being represented by a normalized TF vector, forming a set of unencrypted normalized TF vectors, denoted as $\mathcal{V}=\left\{{\mathcal{V}}_{d_1},{\mathcal{V}}_{d_2},\cdots ,{\mathcal{V}}_{d_n}\right\}$. Then, a clustering algorithm is applied to the vector set $\mathcal{V}$ to form y clusters. For each cluster, a balanced binary tree is constructed to achieve sub-linear search time. Since the elements within each cluster have similar features, for a specific query vector, the most relevant documents are likely to be found within the same cluster (i.e., within the same balanced binary tree), thus saving a significant amount of query time.

In the unencrypted case, let $n_p$ be the sum of documents in the p-th cluster, with the document set of the cluster being $\left\{d_1,d_2,\cdots ,d_{n_p}\right\}$ and the corresponding vector set being $\left\{{\mathcal{V}}_{d_1},{\mathcal{V}}_{d_2},\cdots ,{\mathcal{V}}_{d_{n_p}}\right\}$. For the j-th keyword $w_j$ of document $d_i$ in the cluster, the normalized TF value in the vector is denoted as ${\mathcal{V}}_{d_i}\left[j\right]$.

The process of constructing the unencrypted balanced binary tree is as follows:

(1)

The document vector set $\left\{{\mathcal{V}}_{d_1},{\mathcal{V}}_{d_2},\cdots ,{\mathcal{V}}_{d_{n_p}}\right\}$ of the cluster is considered as the leaf nodes of the tree.

(2)

The intermediate nodes and root node of the balanced binary tree are iteratively generated from the bottom up. For an intermediate node ${\mathcal{V}}_u$, it is generated by its left child node ${\mathcal{V}}_{left}$ and right child node ${\mathcal{V}}_{right}$, such that ${\mathcal{V}}_u\left[j\right]=\max \left\{{\mathcal{V}}_{left}\left[j\right],{\mathcal{V}}_{right}\left[j\right]\right\}$. All intermediate nodes and the root node are iteratively generated following the above process.

5.2. Heuristic Best-First Search Algorithm

This balanced binary tree structure allows for efficient search and retrieval of relevant documents within each cluster. During the retrieval phase, we adopt a heuristic best-first search strategy that evaluates node-level semantic relevance scores and uses a priority-based traversal mechanism to minimize redundant computation while maintaining retrieval accuracy.

As defined in Equation (1), the algorithm begins at the root node of each tree in the forest. It computes the relevance scores between the query vector and the left and right child nodes of the current node. The child node with the higher score is prioritized for expansion. This process continues recursively: at each level, the algorithm evaluates the children of the most relevant unvisited node and selects the next best candidate for exploration. This guided traversal proceeds until a leaf node is reached, at which point the corresponding document is treated as a candidate result.

Throughout the traversal, the algorithm maintains a dynamic top k result list sorted by relevance scores. If a newly encountered document has a higher relevance than the current k-th ranked document, it is inserted into the result list, and the list is updated accordingly.

In parallel, the search is applied to other trees in the forest. To avoid unnecessary computation, a global pruning criterion is enforced: if the root node of a tree yields a relevance score lower than the lowest score in the current top k list, the entire tree is skipped. Otherwise, the same heuristic search process is performed on that tree, and the result list is updated if more relevant documents are found.

This optimization not only preserves the accuracy of the search results but also significantly reduces the search space and computation time, especially when dealing with large-scale document sets distributed across multiple clusters.

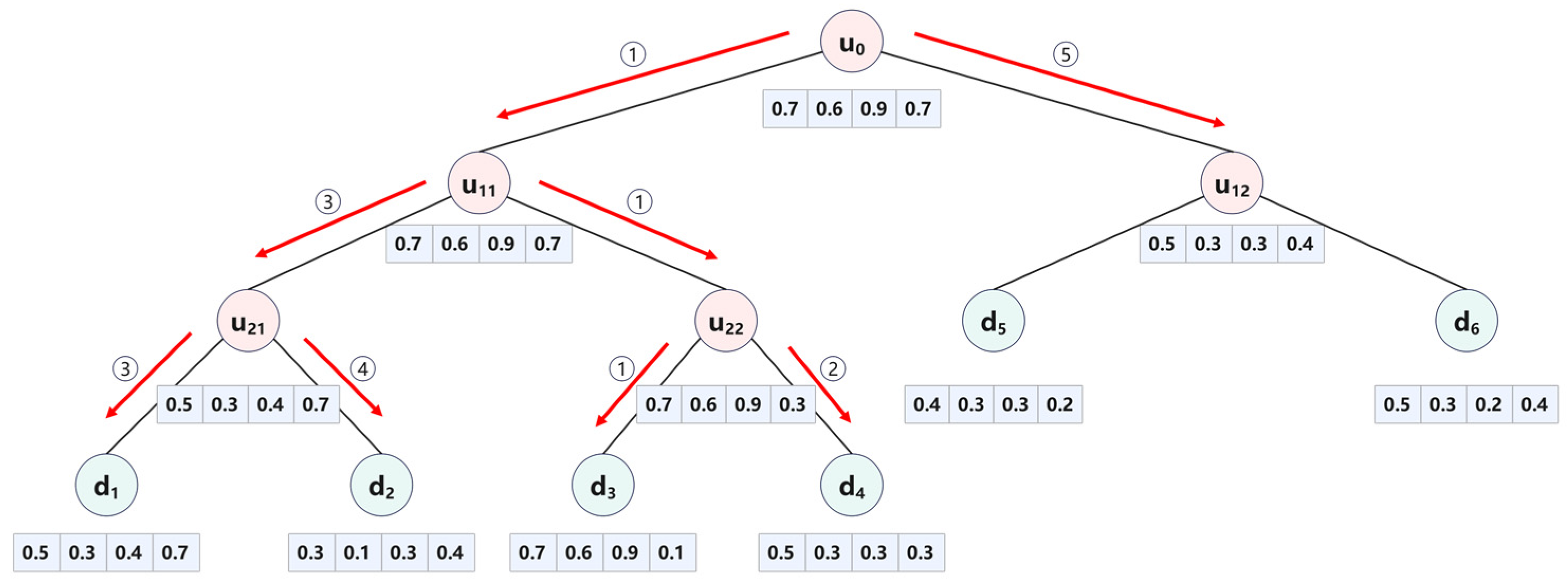
The search process for a single tree is illustrated in Figure 2. Let the query vector be $Q=\left(1,0,1,0\right)$, and the two documents with the highest relevance scores in the query document collection are as follows:

(1)

Starting from the root node, based on Equation (1), we calculate the relevance scores. Since $R\left({\mathcal{V}}_{u_{11}},Q\right)>R\left({\mathcal{V}}_{u_{12}},Q\right)$, we proceed to query the left subtree. Subsequently, we compare the relevance scores of the child nodes and the unexplored node $u_{12}$. Since $R\left({\mathcal{V}}_{u_{22}},Q\right)>R\left({\mathcal{V}}_{u_{21}},Q\right)>R\left({\mathcal{V}}_{u_{12}},Q\right)$, we need to query the node $u_{22}$.

(2)

We compare the corresponding relevance scores of $d_3$ and $d_4$. Based on Equation (1), we get $R\left({\mathcal{V}}_{d_3},Q\right)=1.6$, and $R\left({\mathcal{V}}_{d_4},Q\right)=0.8$. Let the two most relevant documents in the set be $d_3$ and $d_4$, where $d_4$ is the document with the lowest score.

(3)

Notice that $R\left({\mathcal{V}}_{u_{21}},Q\right)=0.9>0.8=R\left({\mathcal{V}}_{d_4},Q\right)=R\left({\mathcal{V}}_{u_{12}},Q\right)$, so there may exist a document with a higher relevance score in the subtree rooted at ${\mathcal{V}}_{u_{21}}$. Therefore, we need to search the subtree rooted at ${\mathcal{V}}_{u_{21}}$. After calculating, we get $R\left({\mathcal{V}}_{d_1},Q\right)=0.9$, and $R\left({\mathcal{V}}_{d_2},Q\right)=0.6$. So, we replace $d_4$ with $d_1$, and $d_1$ becomes the document with the lowest score among the relevant documents.

(4)

At this point, $u_{12}$ is the only unexplored node. Since $R\left({\mathcal{V}}_{u_{12}},Q\right)=0.8<0.9=R\left({\mathcal{V}}_{d_1},Q\right)$, no higher-scoring documents exist in this subtree, and the recursive search concludes. The two most relevant documents are $d_1$ and $d_3$.

The specific algorithm is outlined below, where Algorithm 1 is the index tree construction function, and Algorithm 2 is the search function.

Algorithm 1 $\mathrm{Build}\_\mathrm{Index}\_\mathrm{Tree}\left(\mathcal{V}\right)$

Input: A normalized TF vector set $\mathcal{V}=\left\{{\mathcal{V}}_{d_1},{\mathcal{V}}_{d_2},\cdots ,{\mathcal{V}}_{d_n}\right\}$, document labels $\mathcal{I}\mathcal{D}=\left\{ID\left|1,2,\cdots ,n\right.\right\}$ Output: A balanced binary tree index$\mathcal{T}$ Initialize $\mathrm{NodeSet}$ as an empty list # Load term frequency vector: For each vector in $\mathcal{V}$ do     Create leaf node $u$ with $u.D\left[i\right]={\mathcal{V}}_{d_{ID}}\left[i\right]$, $u.ID=ID$     Append leaf node $u$ to $\mathrm{NodeSet}$ # Build the index tree: While $\mathrm{NodeSet}$ has more than one node do     Initialize $\mathrm{TempSet}$ as an empty list     If $\mathrm{NodeSet}$ has an even number of nodes then         For every pair $\left(u_1, u_2\right)$ in $\mathrm{NodeSet}$ do             Create parent node $u$ with $u.D\left[i\right]=\max \left(u_1.D\left[i\right], u_2.D\left[i\right]\right)$.             Append $u$ to $\mathrm{TempSet}$     Else         # Handle the case where the number of nodes is odd:         For every pair $\left(u_1, u_2\right)$ except last three nodes do             Create parent node $u$ with $u.D\left[i\right]=\max \left(u_1.D\left[i\right], u_2.D\left[i\right]\right)$             Append $u$ to $\mathrm{TempSet}$         # For the last three nodes, merge the first two into an intermediate node:         Create an intermediate node $u_t$ with $u_t.D\left[i\right]=\max \left(u_1.D\left[i\right], u_2.D\left[i\right]\right)$         Create a parent node $u$ with $u.D\left[i\right]=\max \left(u_t.D\left[i\right], u_3.D\left[i\right]\right)$         Append $u$ to $\mathrm{TempSet}$     Set $\mathrm{NodeSet}$ to $\mathrm{TempSet}$ Return the last remaining node in $\mathrm{NodeSet}$ as the root of index tree $\mathcal{T}$

Algorithm 2 $\mathrm{Find}\_\mathrm{Docs}\left(\mathcal{T},Q,k\right)$

Input: The balanced binary tree index structure $\mathcal{T}$, query vector $Q$, and the number of documents to retrieve, k Output: The top k most relevant document results $\mathrm{RList}$ Initialize the priority queue $\mathrm{node}\_\mathrm{heap}$ Compute relevance of root node $\mathrm{score}\leftarrow R\left(\mathrm{root}.D, Q\right)$ Push $\left(\mathrm{score}, \mathrm{root}\right)$ into $\mathrm{node}\_\mathrm{heap}$ while $\mathrm{node}\_\mathrm{heap}$ is not empty do     $\left(\mathrm{score}, \mathrm{node}\right)\leftarrow \mathrm{node}\_\mathrm{heap}.pop\_max()$     if $\mathrm{score}<\mathrm{benchmark}$ then         break     if $\mathrm{node}$ is an internal node then         Compute $\mathrm{left}\_\mathrm{score}\leftarrow R\left(\mathrm{node}.left.D, Q\right)$         Compute $\mathrm{right}\_\mathrm{score}\leftarrow R\left(\mathrm{node}.right.D, Q\right)$         if $\mathrm{left}\_\mathrm{score}\ge \mathrm{benchmark}$ then             Push $\left(\mathrm{left}\_\mathrm{score},\mathrm{node}.left\right)$ into $\mathrm{node}\_\mathrm{heap}$         if $\mathrm{right}\_\mathrm{score}\ge \mathrm{benchmark}$ then             Push $\left(\mathrm{right}\_\mathrm{score}, \mathrm{node}.right\right)$ into $\mathrm{node}\_\mathrm{heap}$     else         $\mathrm{relevance}\leftarrow R\left(\mathrm{node}.D, Q\right)$         if $\mathrm{relevance}\ge \mathrm{benchmark}$ then             Append $\left(\mathrm{relevance}, \mathrm{node}.ID\right)$ to $\mathrm{RList}$             Sort $\mathrm{RList}$ in descending order of score             if length of $\mathrm{RList}$ > k then                 Trim $\mathrm{RList}$ to top k elements                 Update $\mathrm{benchmark}$ to the score of the k-th document in $\mathrm{RList}$ Return $\mathrm{RList}$, $\mathrm{benchmark}$

5.3. SAO Clustering

In existing solutions [9], pre-clustering document TF vectors using the K-means algorithm is a widely adopted approach to enhance the overall efficiency of the search scheme. By organizing documents into clusters beforehand, the system can significantly reduce the search space during query processing, thereby improving response time and computational performance. However, K-means is sensitive to the initial centroid selection, and since document TF vectors are typically high-dimensional and sparse, the clustering algorithm’s efficiency may be impacted when the document collection is large.

To address the above issues, this scheme combines PCA to perform dimensionality reduction on the document TF vectors while retaining the primary characteristics of the original documents. Given that the reduced data may still differ from the original data, this scheme uses SAO to cluster the reduced document TF vectors, replacing the K-means algorithm, which may be inefficient on large-scale data. This is because SAO generally converges quickly to a global optimum and is less influenced by the initial centroid choice, thus minimizing the error caused by other factors during clustering.

The steps for SAO clustering are as follows:

Initialization. First, initialize SAO by setting key parameters: the number of clusters to generate, denoted as k, the number of snow particles, denoted as $\rho$, where each particle represents a candidate solution (i.e., a set of k cluster centers). Each particle is initialized with random cluster centers within the search space. Define the maximum number of iterations denoted as $iter$, after which the optimization process will terminate.

Fitness Evaluation. In each iteration, the fitness of every particle is evaluated based on the clustering quality. Specifically, for each document sample, the cosine distance to each of the current cluster centers in the particle is computed. Each sample is assigned to its nearest cluster center. The sum of these minimum cosine distances across all samples is calculated as the particle’s fitness value. Lower fitness values indicate better clustering solutions, as they represent tighter and more coherent clusters.

Search and Update. SAO applies three main operators inspired by natural snow ablation dynamics. (1) Ablation (local perturbation): each particle undergoes local perturbations to simulate partial melting, enabling fine-grained exploration near its current solution. (2) Migration (guided search): melted particles “flow” toward better solutions, i.e., the current global best position, by adjusting their positions in the direction of high-quality clustering configurations. (3) Recrystallization (diversity enhancement): with a certain probability, a subset of particles is randomly reinitialized to explore new regions of the search space and maintain population diversity.

After applying these mechanisms, each particle’s new fitness value is recalculated. If a particle’s new position yields better fitness than its previous position, the update is retained. Moreover, if this new solution surpasses the current global best fitness, the global best position and fitness are updated accordingly.

Main Loop Optimization. The optimization process repeats for $iter$ iterations. In each iteration, all particles perform the ablation, migration, and recrystallization steps, followed by fitness evaluation and global best updating. Once the maximum number of iterations is reached, the algorithm returns the global best set of cluster centers along with the final clustering result list $CTR$ for all document samples.

5.4. Specific Scheme Construction

The secure K-nearest neighbors (KNN) algorithm is considered secure under the known ciphertext model because, not knowing the encryption matrix, an adversary cannot derive the original data from the observed ciphertext. The encryption matrix serves as a critical component in obfuscating the relationship between plaintext and ciphertext, thereby preventing meaningful inference attacks based solely on the encrypted content. However, in the stronger known background model, the adversary can launch statistical attacks and even infer certain keywords. Therefore, this scheme introduces $U$ perturbation elements, combined with random values, to prevent the attacker from inferring whether the encrypted query vectors were generated from the same query based on their relationship. The proposed SAO-based multi-keyword ranking search scheme (SAO-KRS) is as follows:

(1)

$Setup\left( \right)\to SK$: The data owner constructs a private key $SK=\left(A_1,A_2,B\right)$. $A_1$ and $A_2$ are two invertible matrices of size $\left(l+U+1\right)\times \left(l+U+1\right)$, and $B$ is a random vector of size $\left(l+U+1\right)$.

(2)

$MetaData\left(\mathcal{D}\right)\to \mathcal{V},IDF$: According to Formula (2), for each document $d_i$ in the set, generate a normalized TF vector $\left(v_{i,1},v_{i,2},\cdots ,v_{i,l}\right)$, then generate $U$ perturbation elements $\left({\epsilon }_{i,1},{\epsilon }_{i,2},\cdots ,{\epsilon }_{i,U}\right)$ and append a fixed element 1 at the end. Thus, document $d_i$ can be represented as $\left(v_{i,1},v_{i,2},\cdots ,v_{i,l},{\epsilon }_{i,1},{\epsilon }_{i,2},\cdots ,{\epsilon }_{i,U},1\right)$. These vectors are collected as $\mathcal{V}$. Additionally, according to Formula (3), generate a global normalized IDF vector $\mathcal{A}$.

(3)

$SAO\_Cluster\left(\mathcal{V},y,iter,pca\right)\to CTR$: The SAO algorithm is called with the sum of the minimum cosine distances as the optimization goal. Based on the number of clusters y, iteration count $iter$, and PCA data dimensions $pca$, the document normalized TF vectors are first reduced in dimension and then clustered. The clustering result $CTR$ is returned. The dimensionality reduction is performed only during clustering, and the original data is used when calculating relevance scores.

(4)

$GenForest\left(CTR,SK\right)\to FRT$: First, based on the clustering results, an unencrypted balanced binary index tree is constructed for each cluster, and the root nodes of these trees are used as markers, forming the search forest. Then, each node must be encrypted to form the encrypted search forest $FRT$. For each node u, based on $B$, the data owner constructs two random vectors $\left\{{\mathcal{V}}_{u,1},{\mathcal{V}}_{u,2}\right\}$ for index vector ${\mathcal{V}}_u$. In detail, if $B\left[j\right]=0$, then ${\mathcal{V}}_{u,1}\left[j\right]={\mathcal{V}}_{u,2}\left[j\right]={\mathcal{V}}_u\left[j\right]$; if $B\left[j\right]=1$, then ${\mathcal{V}}_{u,1}\left[j\right]+{\mathcal{V}}_{u,2}\left[j\right]={\mathcal{V}}_u\left[j\right]$. The final encrypted node is constructed as ${\widehat{\mathcal{V}}}_u=\left\{A_1^T{\mathcal{V}}_{u,1},A_2^T{\mathcal{V}}_{u,2}\right\}$.

(5)

$GenTrap\left({\mathcal{W}}_Q,SK\right)\to \widehat{Q}$: The data user, based on the search request, first constructs an unencrypted query vector $Q=\left(q_1,q_2,\cdots ,q_l\right)$ based on $\mathcal{A}$. If $w_j\in {\mathcal{W}}_Q$, then $q_j={\mathcal{A}}_j$; otherwise, $q_j=0$. Next, expand $Q$ to $\left(l+U\right)$-dimensional space. For the $U$ extra elements, randomly choose $X$ elements to set as 1, and set the remaining elements as 0. Then, select a random positive number $r$ to scale the vector $Q$. Finally, append a random number $t$ to the end of the vector. Thus, the query vector is expanded to a $\left(l+U+1\right)$-dimensional vector, represented as $Q=\left(r{q}_1,r{q}_2,\cdots ,r{q}_l,r,r,0,\cdots r,0,t\right)$. The encryption process is similar to the encryption of the search tree nodes but with slight differences. Specifically, if $B\left[j\right]=0$, then $Q_1\left[j\right]+Q_2\left[j\right]=Q\left[j\right]$; if $B\left[j\right]=1$, then $Q_1\left[j\right]=Q_2\left[j\right]=Q\left[j\right]$. The final encrypted query token is represented as $\widehat{Q}=\left\{A_1^{-1}{Q}_1,A_2^{-1}{Q}_2\right\}$.

(6)

$R\left(FRT,\widehat{Q}\right)\to Result$: Based on the encrypted search forest $FRT$ and the encrypted query vector presented by the data user $\widehat{Q}$, the cloud server can compute the relevance scores for each node. Verification shows that the results of calculating the encrypted vector at each node match the results of the unencrypted vector calculation:

$$\begin{array}{c}{\widehat{\mathcal{V}}}_u\cdot \widehat{Q}\hfill \\ =\left(A_1^T{\mathcal{V}}_{u,1}\right)\cdot \left(A_1^{-1}{Q}_1\right)+\left(A_2^T{\mathcal{V}}_{u,2}\right)\cdot \left(A_2^{-1}{Q}_2\right)\hfill \\ ={\left(A_1^T{\mathcal{V}}_{u,1}\right)}^T\left(A_1^{-1}{Q}_1\right)+{\left(A_2^T{\mathcal{V}}_{u,2}\right)}^T\left(A_2^{-1}{Q}_2\right)\hfill \\ ={\mathcal{V}}_{u,1}^T{A}_1{A}_1^{-1}{Q}_1+{\mathcal{V}}_{u,2}^T{A}_2{A}_2^{-1}{Q}_2\hfill \\ ={\mathcal{V}}_{u,1}^T{Q}_1+{\mathcal{V}}_{u,2}^T{Q}_2\hfill \\ ={\mathcal{V}}_u\cdot Q\hfill \\ =r\left({\displaystyle \sum v_{u,j}{q}_j+{\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}}\right)+t\hfill \end{array}$$

(4)

This scheme employs symmetric encryption to protect document vectors during indexing and querying. The encryption is designed to preserve inner product operations, ensuring that the encrypted vectors behave equivalently to unencrypted vectors during relevance computation.

During the search, the cloud server must dynamically maintain the top k most relevant documents. Each time a newly identified document has a higher relevance score than the least relevant document in the current top k set, it replaces the latter. Following this replacement, the server reorders the updated set and designates the document with the lowest relevance score as the new threshold for subsequent comparisons. If the root node relevance score of the next unvisited tree in the forest is lower than the current lowest relevance score, the server will not search this tree; otherwise, the server proceeds to search this tree.

Once all the search trees in the forest have been traversed, the query process is considered complete. The cloud server then sends the final results to the data user, as well as the associated encrypted documents.

5.5. Computational Cost Analysis

5.5.1. Index Tree Construction and Trapdoor Generation

The construction of a single index tree structure first requires building a keyword balanced binary tree, followed by encryption through matrix multiplication and splitting operations using matrices of size $\left(l+U+1\right)\times \left(l+U+1\right)$. As described in Section 5.1, the balanced binary tree index structure is constructed recursively from the document set, normally resulting in $\left(2n-1\right)$ nodes. Since each node has a size of l, generating each node incurs a computational cost of $O\left(l\right)$, while the matrix-vector multiplication requires a cost of $O\left(l^2\right)$. Therefore, the total computational cost for constructing the index tree is $O\left(n\cdot l^2\right)$. Clearly, the computational cost of index tree construction is mainly determined by the document set size n and the keyword set size l.

Trapdoor generation mainly involves a vector splitting operation and a matrix multiplication using a matrix of size $\left(l+U+1\right)\times \left(l+U+1\right)$, with a computational cost of $O\left(l^2\right)$. Since each query typically includes only a small number of keywords, the computational overhead of trapdoor generation is generally low.

5.5.2. Search Process

In the proposed search algorithm, the use of a balanced binary tree search structure allows for pruning during the search process. As a result, many nodes do not need to be visited during actual execution, saving computational resources.

Let the number of leaf nodes that involve one or more query keywords be denoted as $\theta$, the number of documents contained in each cluster as $n_p$, and the global word table length as $l$. It can be concluded that, since documents are always located at leaf nodes in each search tree, the height of the tree is $\log n_p$. Furthermore, because each node consumes $O\left(l\right)$ computational resources for evaluation, the time complexity of the search can be expressed as $O\left(\theta l\log n_p\right)$. This structure ensures efficient search by reducing the number of nodes visited and thereby improving both the accuracy and efficiency of the search process.

5.6. Security Analysis

5.6.1. Index and Query Confidentiality

In this proposed scheme, both the encrypted index ${\widehat{\mathcal{V}}}_u$ and encrypted query $\widehat{Q}$ are represented as random vectors. As a result, without access to the secret key set $SK$, the cloud server is unable to reconstruct or infer the original index and query information. Additionally, since the private key $A_1$ and $A_2$ are random matrices, based on [25], an attacker using only the ciphertext cannot calculate the matrix. Therefore, the proposed scheme effectively guarantees the confidentiality of both the index and the query, safeguarding sensitive information from potential inference attacks by the cloud server.

5.6.2. Query Unlinkability

The query vector’s trapdoor is generated through random splitting, meaning that identical search requests will transform into varied query trapdoors. Furthermore, by incorporating perturbation elements and random numbers, identical search requests will produce varied query vectors, resulting in varied relevance score distributions. This ensures that the cloud server cannot associate identical search requests based on access patterns or relevance scores, thus protecting query unlinkability. However, the perturbation vectors will inevitably reduce the precision of the search results. Therefore, the data user can adjust the value of ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$ to control the degree of unlinkability. This requires the user to balance precision and privacy.

5.6.3. Keyword Privacy

The proposed scheme guarantees keyword privacy within the known ciphertext model by safeguarding the confidentiality of both the index and query vectors using the secret key set $SK$. During the ciphertext search process, the cloud server only performs dot product calculations and cannot access any specific keyword information. In a more advanced known background model, where the cloud server has access to additional contextual information, keyword privacy cannot be fully guaranteed unless perturbation elements are incorporated. Without these perturbations, the server could exploit the extra background knowledge to potentially deduce the keywords, undermining the privacy of the query.

It can be observed that the change in the relevance score before and after adding perturbation elements only comes from ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$. Therefore, as we get more different values of ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$, the confusion effect brought by the perturbation elements becomes stronger. Suppose the probability of two ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$ being identical is $1/2^{\alpha }$, i.e., ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$ takes at least $2^{\alpha }$ distinct choices. It is crucial to notice that the number of distinct ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$ cannot exceed $\left(\begin{array}{c}U\\ X\end{array}\right)$, and when this number is maximized, we have $U/X=2$. Furthermore, according to the mathematical relationship $\left(\begin{array}{c}U\\ X\end{array}\right)\ge {\left(U/X\right)}^X=2^X$, we have $X=\alpha$, and $U=2\alpha$. That means for each query vector, a random selection of half of these perturbation elements will be involved in the relevance score calculation.

Additionally, for each perturbation element in the index, ${\epsilon }_j$ follows a uniform distribution $U\left({\mu }^{\prime }-\delta ,{\mu }^{\prime }+\delta \right)$, with a mean of ${\mu }^{\prime }$ and variance of ${{\sigma }^{\prime }}^2={\delta }^2/3$. Based on the Central Limit Theorem, the sum of ${\epsilon }_j$, denoted as ${\displaystyle \sum {\epsilon }_{u,j}^{\left(X\right)}}$, will approximate a normal distribution $N\left(\mu ,{\sigma }^2\right)$. Hence, the mean of the sum is $\mu =\alpha {\mu }^{\prime }$, and the variance is ${\sigma }^2=\alpha {{\sigma }^{\prime }}^2=\alpha {\delta }^2/3$. Therefore, we have ${\mu }^{\prime }=\mu /\alpha$ and $\delta =\sqrt{3/\alpha }\sigma$. By adjusting the parameters $\alpha$ and $\sigma$, users can effectively control the distribution of the perturbations, thus balancing the trade-off between search precision and privacy protection.

In summary, the proposed approach impacts query words by transforming them into encrypted vectors with added perturbation elements, while preserving their semantic intent. These perturbation elements—comprising random binary values and a scaling factor—introduce controlled randomness into the relevance score calculation. This mechanism is essential for protecting keyword privacy in stronger threat models.

While these perturbations effectively prevent the cloud server from inferring sensitive query information, they inevitably introduce noise into the similarity computation. As analyzed, the sum of perturbation elements follows an approximate normal distribution, which may slightly distort the final ranking of documents. Consequently, this can lead to a minor decrease in search precision. To address this, users can adjust the number and range of perturbation elements, as well as corresponding parameters to balance between privacy protection and search precision, depending on application requirements.

6. Tests and Results

We conducted tests on the SAO-KRS scheme using real-world plain-text datasets [26,27,28], comparing it with the scheme using K-means clustering with greedy depth-first search [9]. The main evaluation focuses on the following:

(1)

Search precision of the proposed SAO-KRS scheme at different privacy levels.

(2)

Clustering efficiency comparison between the proposed SAO-KRS scheme and the K-means scheme.

(3)

Search accuracy and efficiency comparison between the proposed SAO-KRS scheme and the K-means scheme.

The experimental environment consists of an Intel(R) Core (TM) i9-12900H @ 2.50 GHz processor, 16 GB of RAM, and Windows 11 operating system, with implementation in Python 3.11. Following the setting in [9], in this paper, the number of clusters is set to five in our scheme. To support cluster visualization and retain as much original feature information as possible, the PCA dimension is set to three. Additionally, through preliminary testing, we observed that under the current dataset, the optimization results of the SAO algorithm tend to converge and stabilize when the number of iterations reaches around 200. Therefore, the iteration count is set to 200 in our experiments.

6.1. Precision and Privacy

The inclusion of perturbation elements in the scheme leads to a trade-off between precision and privacy. Specifically, while the perturbations ensure the protection of keyword privacy, they also introduce slight inaccuracies in the document relevance scores. As a result, when the cloud server returns the top k documents based on these perturbed scores, some documents that would have been the most relevant may be excluded. This requires the user to balance the need for privacy with the potential loss in search precision.

In the test, we selected a dataset containing 1000 documents, and the query length was set to five, meaning the query contained five keywords. The test compared precision and privacy levels under different settings of perturbation elements.

In this work, we adopt the definition of precision provided by Cao et al. [7]: $P_k=k^{\prime }/k$. where $k^{\prime }$ represents the sum of documents that are in the search results both before and after the addition of perturbation elements. Clearly, when the standard deviation $\sigma$ of ${\epsilon }_j$ is smaller, the search precision is higher, and the search results are more precise.

However, when the standard deviation $\sigma$ is set too small, the user may inadvertently leak privacy. While the search results themselves cannot be protected, perturbation elements can still obscure document ranking, thus protecting user privacy. In this scheme, privacy level is defined as ${\tilde{P}}_k={\displaystyle \sum \left|r_i-{r^{\prime }}_i\right|}/k^2$. The ranking of document $d_i$ in the search results returned during the operation of the proposed scheme is represented by $r_i$, while ${r^{\prime }}_i$ represents the ranking of document $d_i$ in the search results before the inclusion of the perturbation elements.

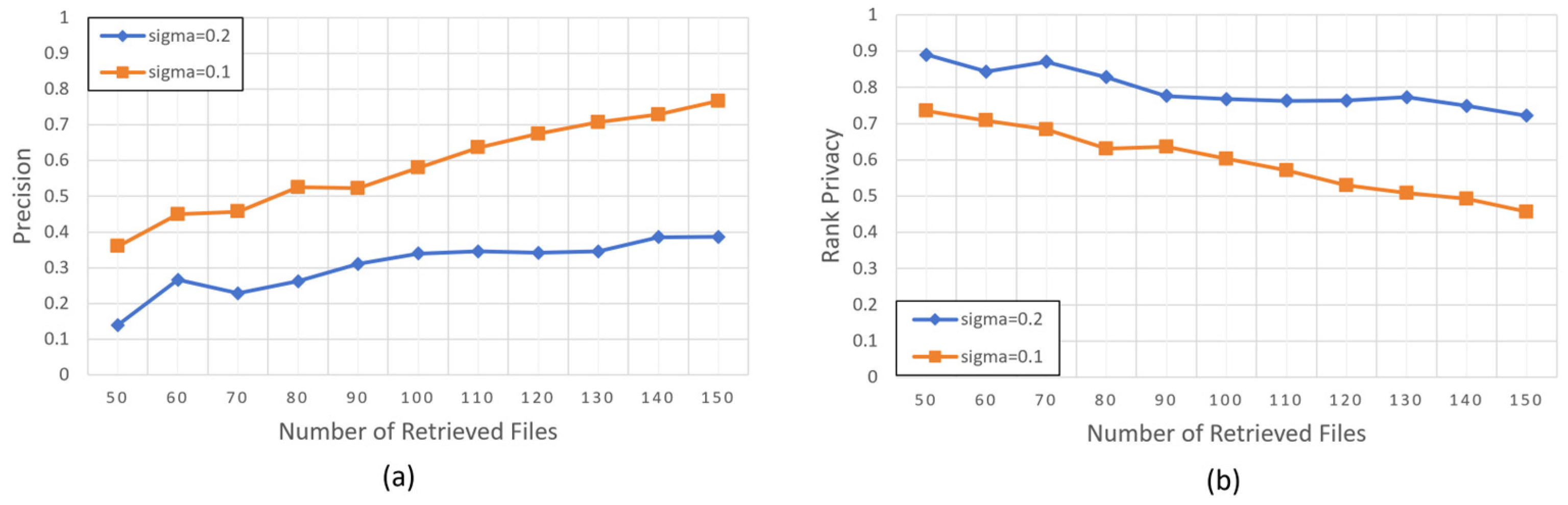
As shown in Figure 3, when $\sigma$ is set smaller, the search precision of the scheme is higher, but the privacy level is low. When $\sigma$ is set closer to 0, the perturbation effect decreases, causing the document relevance scores to approach their true values, which improves precision but lowers the level of privacy protection. Therefore, users need to tune the parameter based on their specific privacy and precision requirements.

For instance, in privacy-sensitive scenarios such as medical record retrieval, higher perturbation levels are recommended, whereas applications that prioritize precision, such as academic literature search, may benefit from smaller perturbations.

6.2. Clustering Efficiency

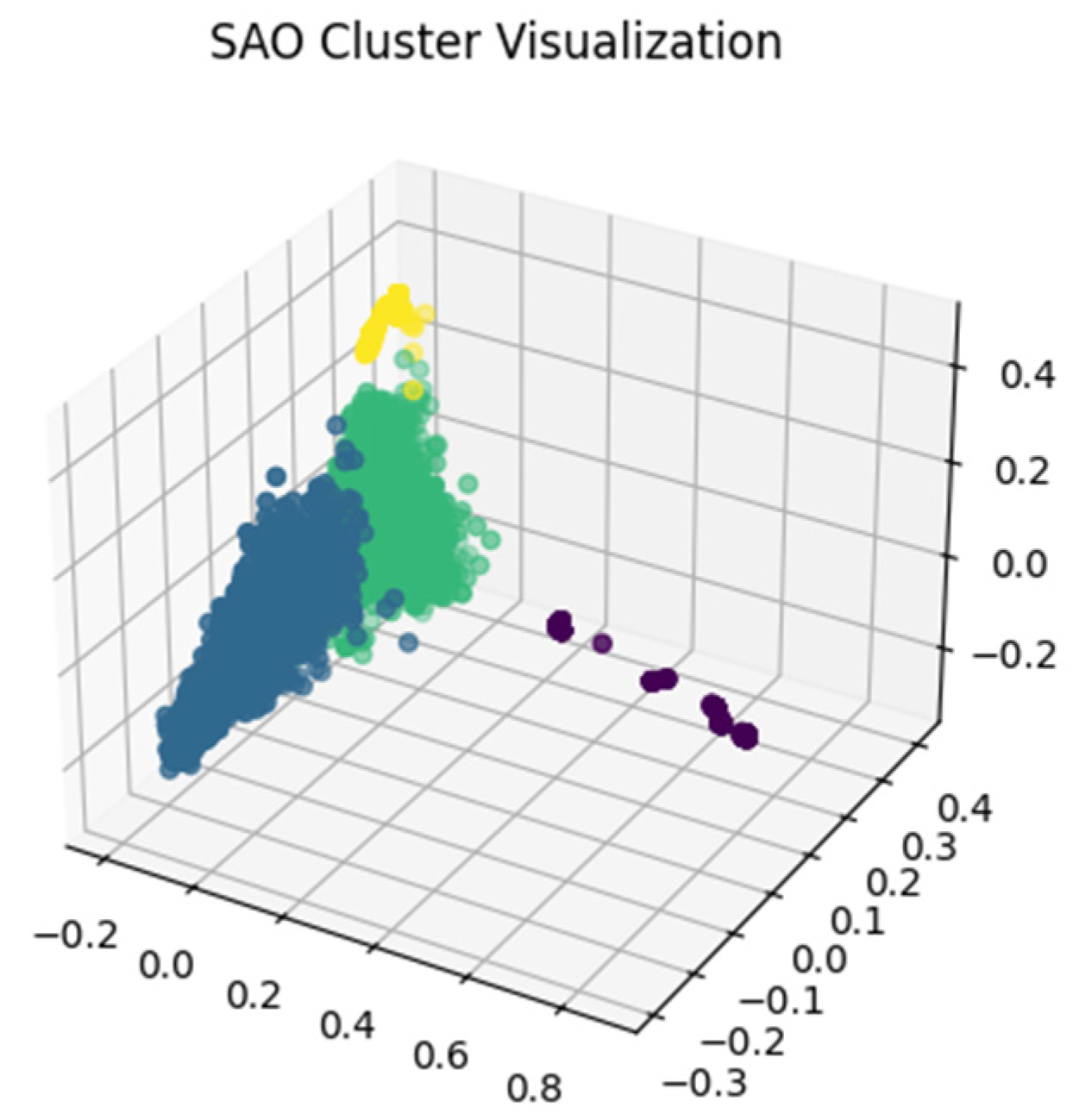
In such large-scale datasets, the TF vectors of documents are usually high-dimensional sparse vectors, so clustering directly might not be efficient. The SAO-KRS scheme combines PCA to reduce the dimensionality of the original high-dimensional sparse vectors before performing clustering. By using PCA for dimensionality reduction, SAO-KRS’s clustering results can be visualized. Figure 4 demonstrates the visualized clustering results of SAO-KRS. While reducing the dimensionality, PCA can still retain the main features of the original data, and since SAO has strong global search capabilities, we can conclude that the clustering results of the scheme are reliable. Moreover, by applying PCA for dimensionality reduction, the document’s TF vectors become fixed low-dimensional vectors after the transformation, regardless of the dataset’s size. Therefore, the impact of the dataset size on clustering will be significantly reduced after PCA operation.

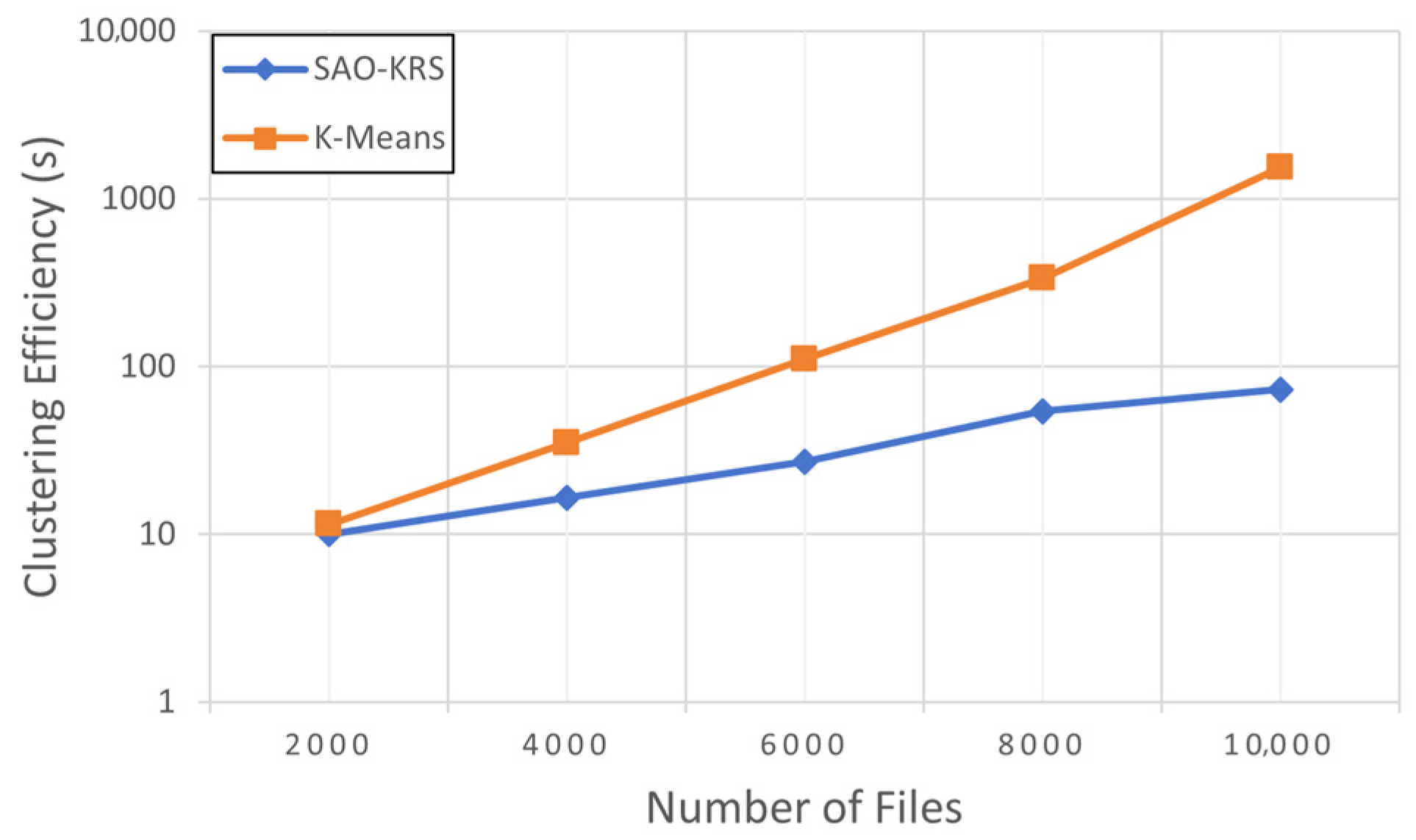
We set up datasets with varying numbers of documents to test the SAO-KRS and K-means clustering methods, using the time cost for clustering to represent clustering efficiency. Figure 5 shows that, compared to the traditional K-means clustering method, SAO-KRS significantly outperforms in clustering speed across different datasets. As the dataset size increases, the computational time of the K-means method increases exponentially, while the time cost of SAO-KRS stabilizes. When the size of documents reached 10,000, SAO-KRS was nearly 21 times faster in terms of clustering efficiency.

6.3. Search Accuracy and Efficiency

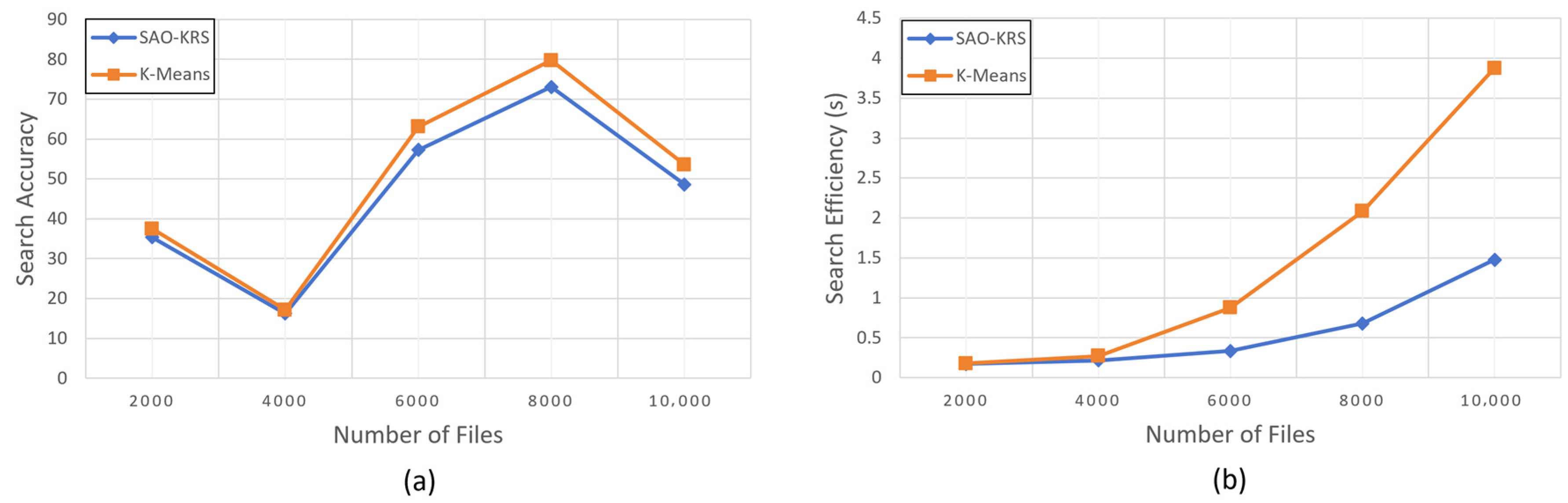
We simulated user behavior by randomly selecting 100 documents from the dataset and generating a fixed number of query keywords for each document. These 100 queries were then processed using both the SAO-KRS and K-means methods. We use mean square error to represent search accuracy and the time cost for searching to represent search efficiency.

Figure 6a shows that in actual operation, the search accuracy of SAO-KRS is slightly higher than that of the K-means method. The best performance showed that SAO-KRS’s search accuracy was about 9.2% better than the K-means method. Since both methods use the same index structure, the accuracy difference arises from documents with the same relevance score. The results in Figure 6a indicate that when relevance scores are the same, the documents returned by SAO-KRS are ranked higher in the search results, which means more accurate search results. This also reflects that the features of elements within clusters in SAO clustering are more similar, making its clustering performance superior to K-means, thus improving search accuracy.

Figure 6b shows that in actual operation, when the number of documents is 2000, the search speed of the SAO-KRS scheme is slightly higher than that of the K-means scheme. However, as the size of the document collection increases, the SAO-KRS scheme—benefiting from the integration of the heuristic best-first search algorithm—demonstrates significantly faster search performance compared to the K-means scheme, which relies on the greedy depth-first search. When the test set reaches its maximum size of 10,000 documents, the search speed of the SAO-KRS scheme is approximately 2.7 times that of the K-means scheme.

7. Conclusions

This paper presents an efficient multi-keyword ranked search scheme, SAO-KRS, by integrating the snow ablation optimizer (SAO) and principal component analysis (PCA) techniques. By leveraging the TF-IDF model and vector space model, the scheme constructs a balanced binary tree index structure that enhances both search efficiency and accuracy. The SAO-based clustering significantly reduces the clustering time compared to the K-means algorithm, making it particularly suitable for large-scale data archiving and retrieval applications, where indexing and storage efficiency are crucial. PCA-based dimensionality reduction preserves clustering performance while improving efficiency and enabling the visualization of clustering results. Additionally, the heuristic best-first search algorithm helps to efficiently retrieve top k relevant documents with minimal computation.

Moreover, the proposed scheme provides flexibility in balancing privacy levels and search precision through parameter adjustments, making it adaptable to different application requirements. Experimental evaluations on a real dataset demonstrate that SAO-KRS significantly improves both clustering efficiency and search performance, making it a promising solution for secure and efficient multi-keyword ranked search in cloud-based long-term storage systems.

However, deploying the scheme in real-world cloud environments may encounter certain practical challenges. For instance, the perturbation mechanism, while effective in preserving keyword privacy, introduces additional computation overhead and may slightly degrade search accuracy. Key management at scale, including secure distribution and revocation of keys among multiple authorized users, also requires careful coordination. Moreover, the parameters must be appropriately tuned based on specific privacy and performance requirements, which may vary across heterogeneous cloud applications. These aspects can complicate practical deployment, particularly in dynamic or high-throughput environments.

In future work, we plan to prototype and evaluate support for dynamic datasets, as real-world cloud data changes continuously over time. This enhancement will address practical needs for real-time indexing and search. Additionally, we will explore adaptive parameter tuning mechanisms and lightweight privacy-preserving techniques to further improve the system’s usability and security in realistic deployment scenarios.