Research on Sliding Mode Control of Robot Fingers Driven by Tendons Based on Nonlinear Disturbance Observer
Abstract
1. Introduction
- (I)
- The system modeling takes into account the influence of disturbances on the control system. The unknown disturbance is accurately estimated by using a nonlinear disturbance observer, and the estimated value is used as a feedback signal to provide compensation for the sliding mode controller, effectively restraining the trajectory tracking error caused by the disturbance and improving the anti-interference ability of the system.
- (II)
- A nonsingular fast terminal sliding mode controller based on nonlinear disturbance observer compensation is proposed for dexterous robot finger control. The nonlinear hyperbolic tangent function is used to replace the symbolic function, which further weakens the chattering problem. Fast and high-precision tracking of the expected trajectory in joint space is achieved.
- (III)
- Parameter optimization of the control system is implemented using the PSO algorithm, which improves the overall performance of the controller.
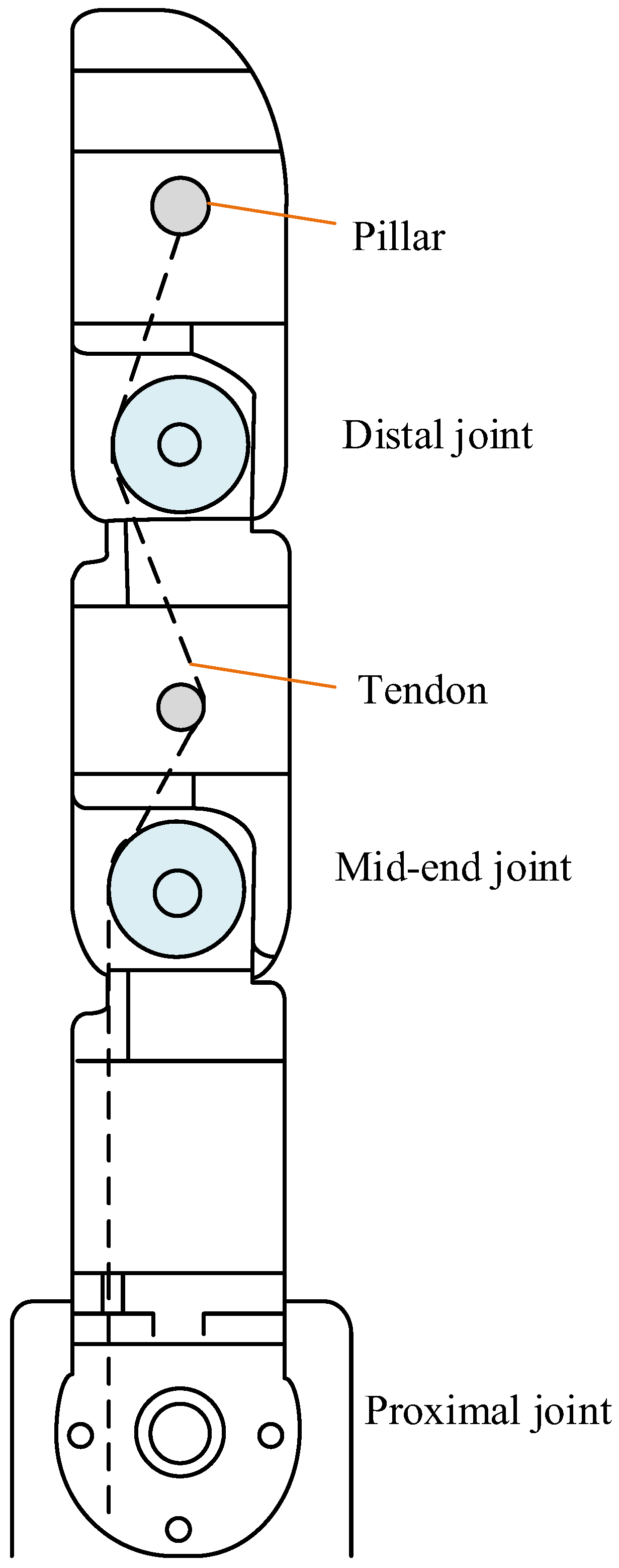
2. System Description
3. Controller Design
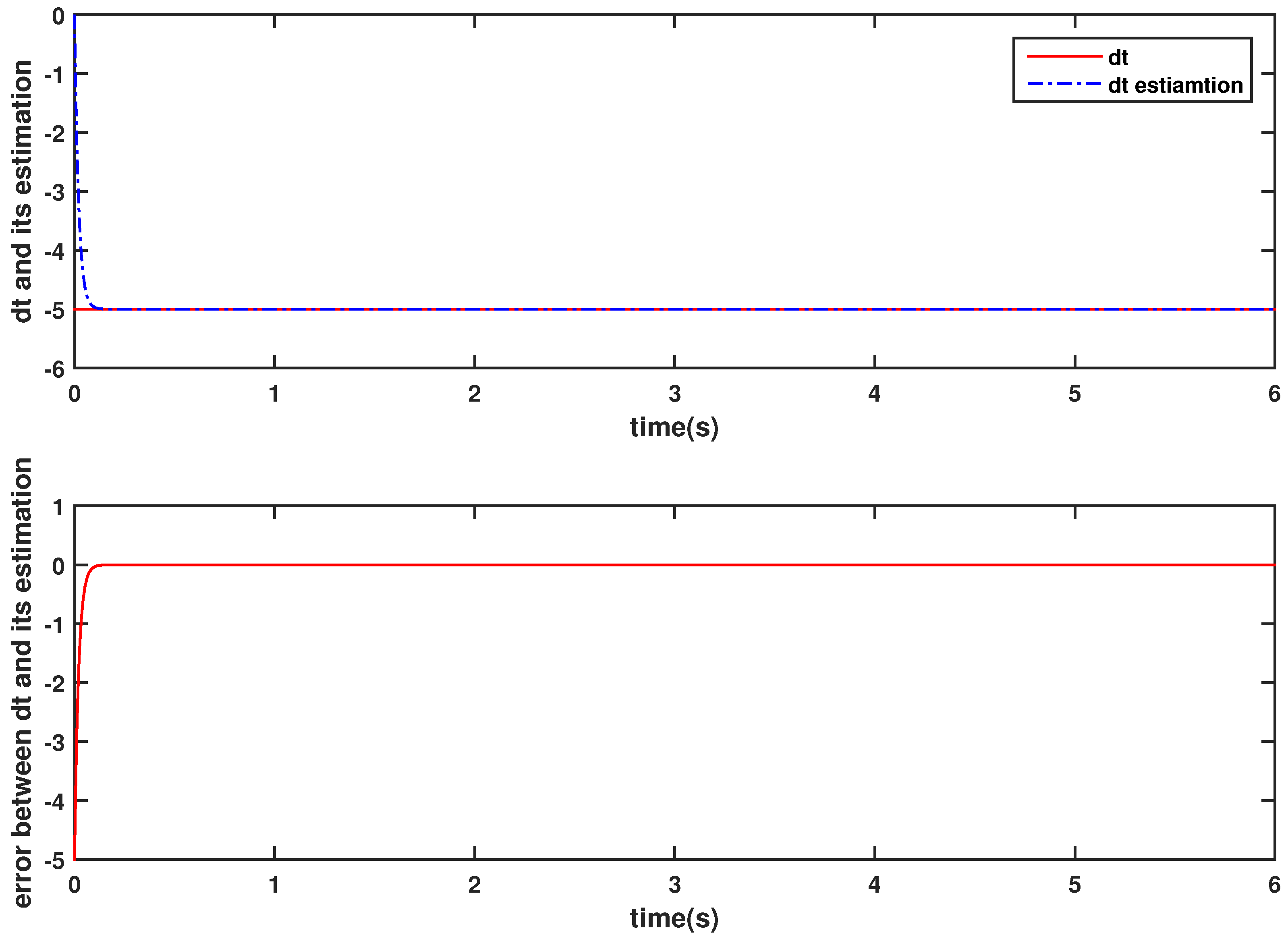
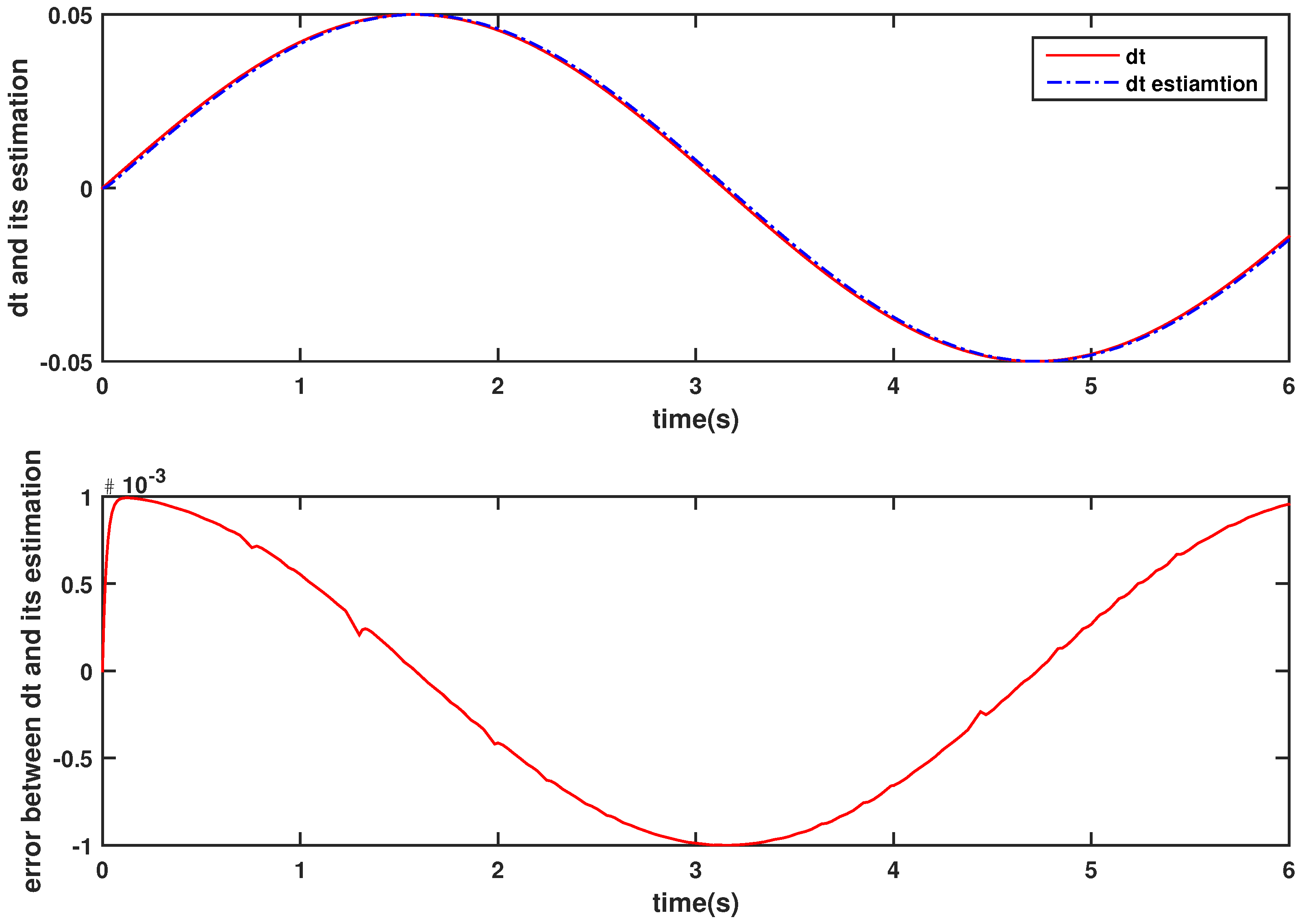
3.1. Design of Nonlinear Disturbance Observer
3.1.1. Observer Structure Design
3.1.2. Estimation Error Dynamics
3.1.3. Convergence of Error
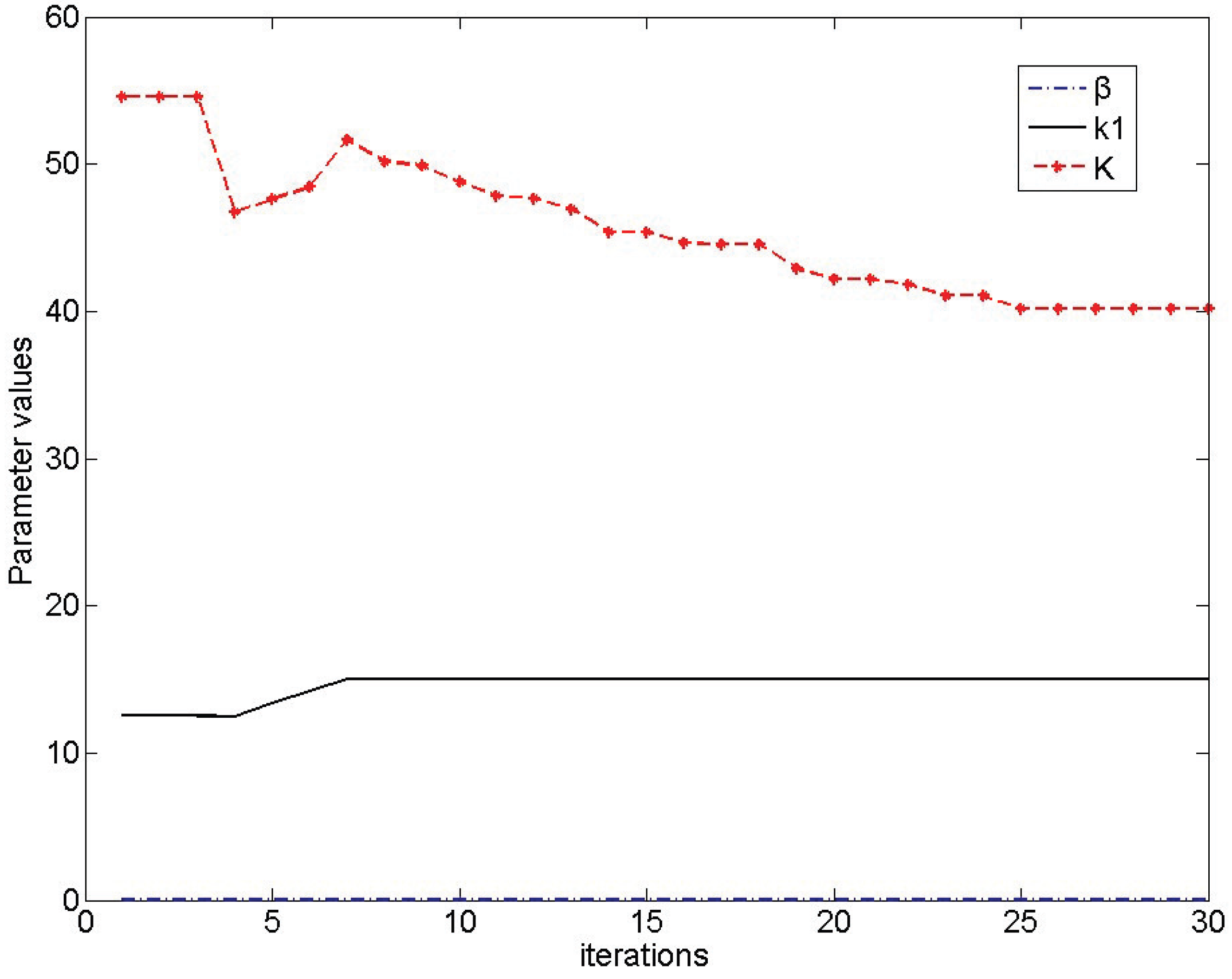
3.1.4. Selection of Parameter K
- Depending on the dynamic characteristics of the system, an initial value is selected;
- We tune the parameter K using simulation or experimental methods, so that the convergence speed of the observer meets the requirements.
- We consider the accuracy of the system and the energy efficiency of particle swarm optimization parameter K, as shown in Section 3.3.
3.1.5. Proof of Stability of Observer
3.2. Design of Fast Continuous Nonsingular Terminal Sliding Mode Controller
3.2.1. Control Input
3.2.2. Proof of Stability and Convergence of Sliding Mode
3.2.3. The Proof of the Convergence of the Tracking Error and the First Derivative of the Tracking Error
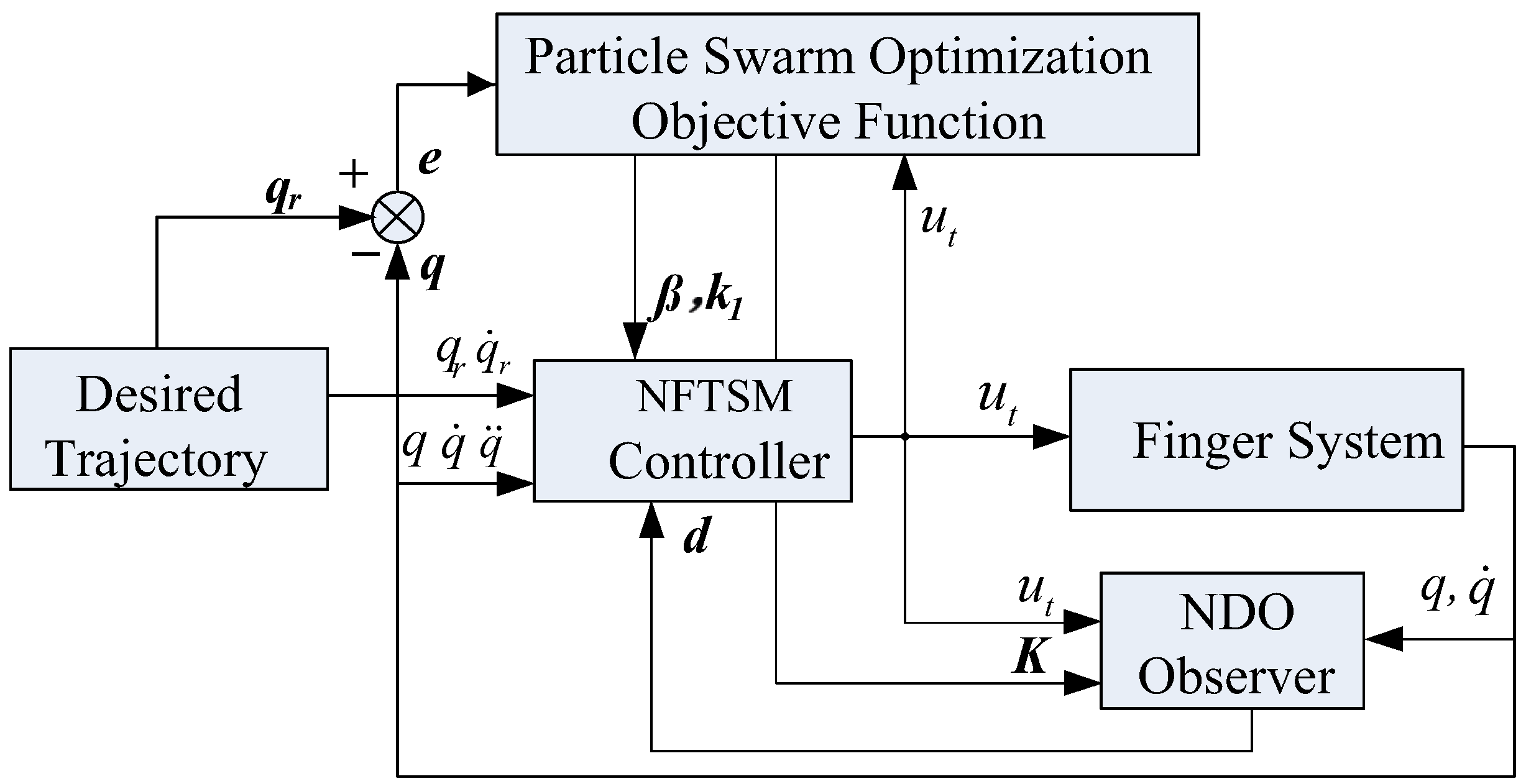
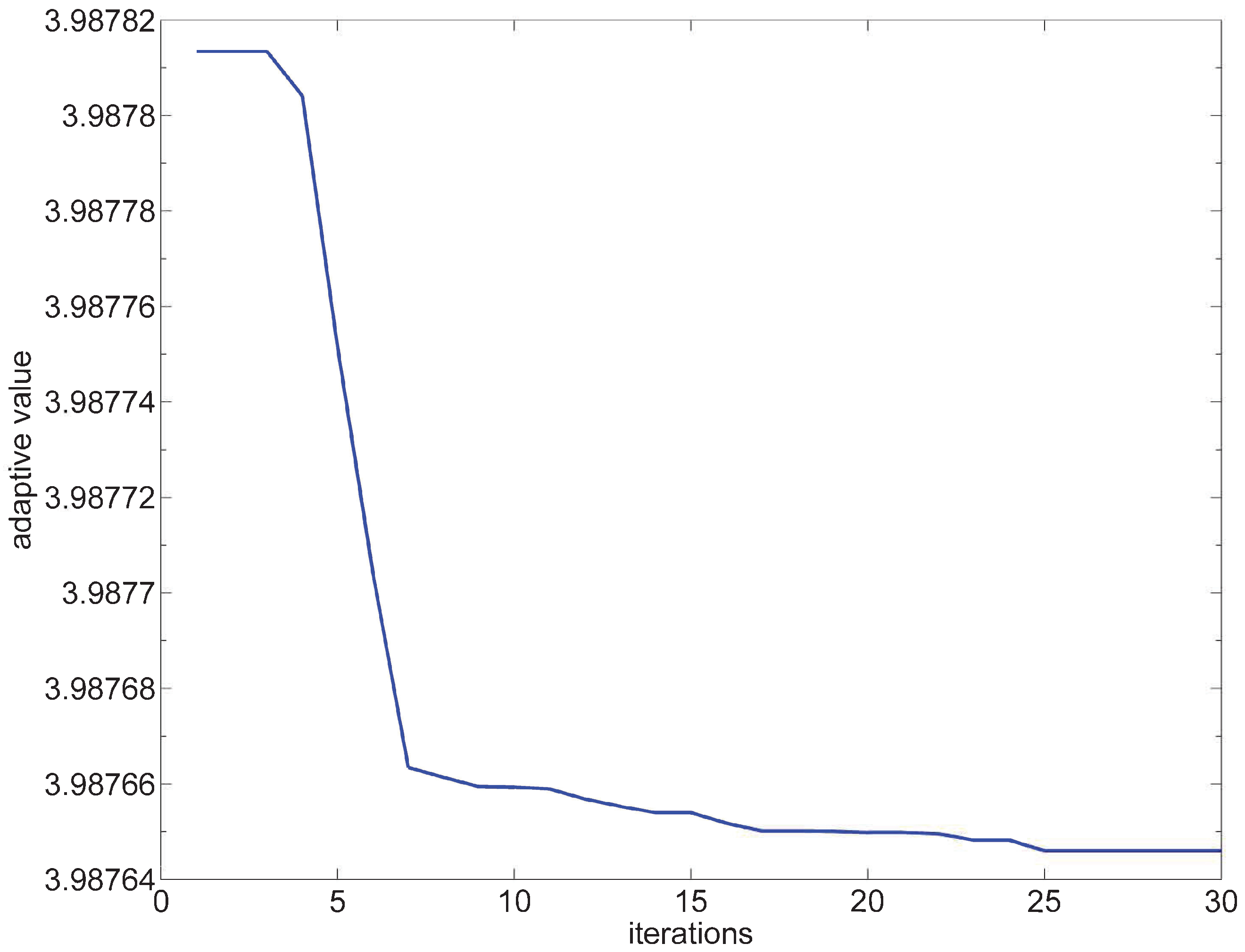
3.3. Parameter Tuning of NDO-NFTSM Based on PSO Algorithm
3.3.1. Selection of Evaluation Function
3.3.2. System Structure of NDO-NFTSM Control
3.3.3. NDO-NFTSM Process Based on PSO Algorithm
4. Numerical Simulations
5. Conclusions
- (1)
- A dynamic model of a dexterous cable-driven robot finger was established by equating the flexibility effect of rope drive with the joint, and the simulation results also proved the effectiveness of the model.
- (2)
- Utilizing NDOB to estimate unknown interference online and compensating for interference in the control system effectively suppresses the chattering of the system.
- (3)
- By tuning the controller parameters using the PSO algorithm, it makes parameter adjustment more convenient and improves the performance of the control system.
- (4)
- FNTSMC is introduced to accelerate the rate of convergence of the control law, so that the system tracking error can converge to the specified region in a finite time. The simulation results show that the control algorithm in this paper has a faster convergence rate and higher tracking accuracy than the others.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NFTSM | nonsingular fast terminal sliding mode |
| ERLSMC | exponent reaching law sliding mode control |
| PID | Proportional Integral Differential |
| NA-SMC | neural network adaptive sliding mode control |
| NDO | nonlinear disturbance observer |
| PSO | particle swarm optimization |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
References
- Yoshikawa, T. Multifingered robot hands: Control for grasping and manipulation. Annu. Rev. Control. 2010, 34, 199–208. [Google Scholar] [CrossRef]
- Ozawa, R.; Tahara, K. Grasp and dexterous manipulation of multi-fingered robotic hands: A review from a control view point. Adv. Robot. 2017, 31, 1030–1050. [Google Scholar] [CrossRef]
- Grebenstein, M.; Albu-Schäffer, A.O.; Bahls, T.; Chalon, M.; Eiberger, O.; Friedl, W.; Gruber, R.; Haddadin, S.; Hagn, U.; Haslinger, R.; et al. The DLR hand arm system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3175–3182. [Google Scholar] [CrossRef]
- King, J.P.; Bauer, D.; Schlagenhauf, C.; Chang, K.H.; Moro, D.; Pollard, N.S.; Coros, S. Design. Fabrication, and Evaluation of Tendon-Driven Multi-Fingered Foam Hands. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Shadow Robot Company. Shadow Dexterous Hand Technical Specification; Shadow Robot Company: London, UK, 2022; Available online: https://www.shadowrobot.com/wp-content/uploads/2024/06/20240610-UPDATED-shadow_dexterous_hand_e_technical_specification.pdf (accessed on 1 January 2025.).
- Fan, S.; Gu, H.; Zhang, Y.; Jin, M.H.; Liu, H. Research on adaptive grasping with object pose uncertainty by multi-fingered robot hand. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418766783. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Ma, C. Optimal grasp force for robotic grasping and in-hand manipulation with impedance control. Assem. Autom. 2021, 41, 208–220. [Google Scholar] [CrossRef]
- Shahriari, E.; Birjandi, S.A.B.; Haddadin, S. Passivity-based Adaptive Force-Impedance Control for Modular Multi-Manual Object Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 2194–2201. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, L.; Fan, S.; Wu, X.; Feng, W. Development and experimental evaluation of multi-fingered robot hand with adaptive impedance control for unknown environment grasping. Robotica 2014, 34, 1168–1185. [Google Scholar] [CrossRef]
- Jalani, J.; Mahyuddin, M.N.; Herrmann, G.; Melhuish, C. Active robot hand compliance using operational space and Integral Sliding Mode Control. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 1749–1754. [Google Scholar] [CrossRef]
- Herrmann, G.; Jalani, J.; Mahyuddin, M.N.; Herrmann, G.; Melhuish, C. Robotic hand posture and compliant grasping control using operational space and integral sliding mode control. Robotica 2016, 34, 2163–2185. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Robust Speed Control of PMSM Using Sliding Mode Control (SMC)—A Review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Jung, S. Improvement of Tracking Control of a Sliding Mode Controller for Robot Manipulators by a Neural Network. Int. J. Control. Autom. Syst. 2018, 16, 937–943. [Google Scholar] [CrossRef]
- Man, Z.; Paplinski, A.P.; Wu, H.R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control. 1994, 39, 2464–2469. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control and its application for robot manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.S.; Wang, X.S.; Cheng, Y.H. Considering disturbance and input saturation of the manipulator continuous nonsingular fast terminal sliding mode control. Control. Decis. 2022, 37, 903–912. [Google Scholar]
- Yi, S.; Zhai, J. Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators. ISA Trans. 2019, 90, 41–51. [Google Scholar] [CrossRef]
- Ma, X.; Xu, Y.; Zhang, L.; Bai, J. Model-Free Generalized Super-Twisting Fast Terminal Sliding Mode Control for Permanent Magnet Synchronous Motors. Symmetry 2025, 17, 18. [Google Scholar] [CrossRef]
- Yao, Y.; Ding, L.; Ma, R.; Wang, Y.Y. Robust Control for a Cable-driven Aerial Manipulator with Joint Flexibility in Joint Space. Control. Decis. 2023, 38, 9–17. [Google Scholar] [CrossRef]
- Sun, G.F.; Zhao, E.Q.; Zhang, G.J.; Huang, M. Non-singular fast terminal sliding mode control of manipulator based on disturbance observe compensation. Control. Theory Appl. 2022, 39, 1506–1515. [Google Scholar] [CrossRef]
- Zhao, Z.; He, X.; Ki, A.C. Boundary Disturbance Observer-Based Control of a Vibrating Single-Link Flexible Manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2382–2390. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, C.; Zhang, C.; Lu, Y.; Xu, G.; Shang, Y. Differential Flatness Based Unmanned Surface Vehicle Control: Planning and Conditional Disturbance-Compensation. Symmetry 2024, 16, 1118. [Google Scholar] [CrossRef]
- Bu, X.; Xiaoyan, W.; Yongxing, C.; Ruiyang, B. Nonlinear-disturbance-observer-based sliding mode backstepping control of hypersonic vehicles. Control. Theory Appl. 2015, 31, 1473–1479. [Google Scholar] [CrossRef]
- Yu, J.; Chen, M.; Jiang, C.S. Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer. Control. Theory Appl. 2014, 31, 993–999. [Google Scholar]
- Wang, X.; Guo, W.; Wei, M. Parameter Tuning of Fractional-Order PID Sliding Mode Control Based on Particle Swarm Optimization. Meas. Control. Technol. 2017, 36, 63–66. [Google Scholar]
- Duan, X.J.; Zhu, F.Y.; Liu, X.Q. Fuzzy Neural Network Sliding Mode Anti-swing Control for Tower Crane Based on PSO. Mach. Tool Hydraul. 2016, 44, 155–159. [Google Scholar]
- Nekoukar, V.; Erfanian, A. Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems. Fuzzy Sets Syst. 2011, 179, 34–49. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, K.; Chen, B.; Jin, M. Model-free continuous nonsingular fast terminal sliding mode control for cable-driven manipulators. ISA Trans. 2020, 98, 483–495. [Google Scholar] [CrossRef]
- Liu, J. Sliding Mode Variable Structure Control MATLAB Simulation, 3rd ed.; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
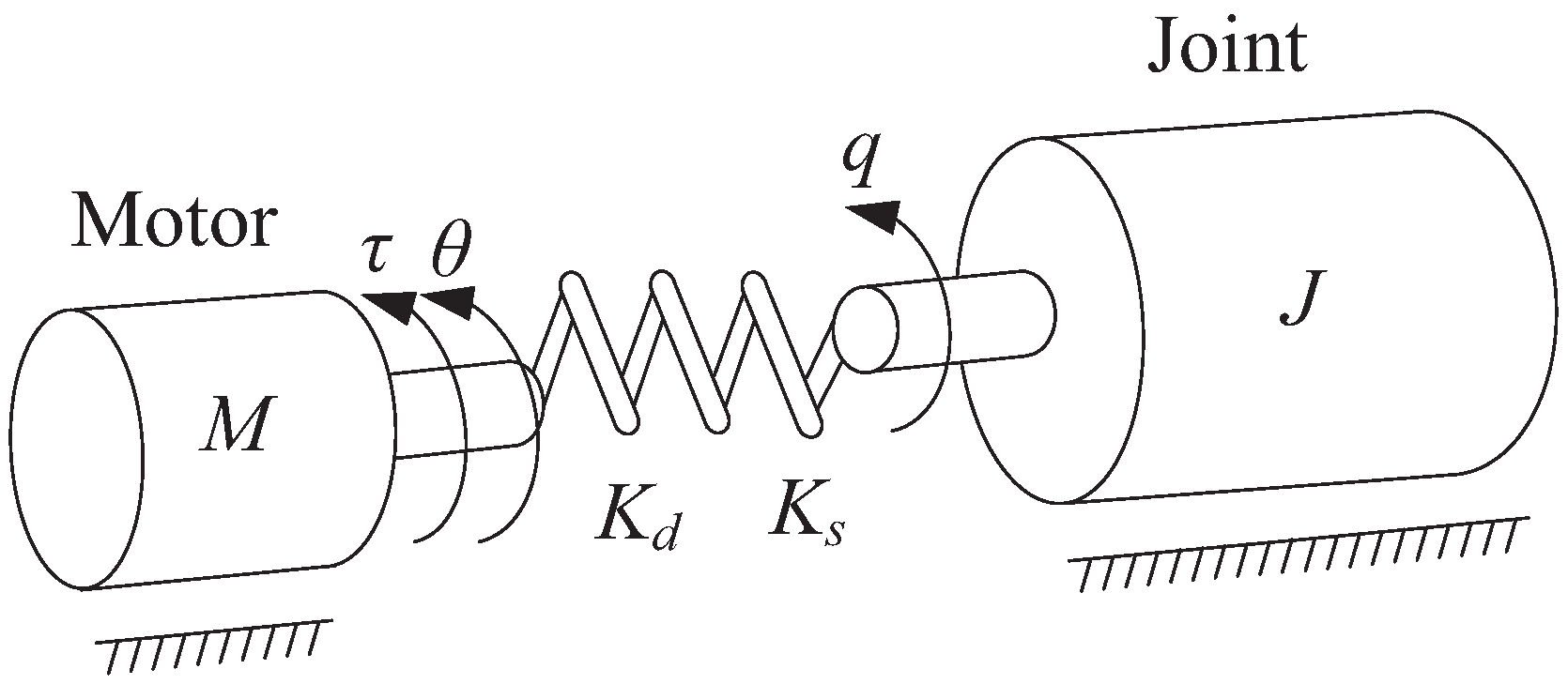

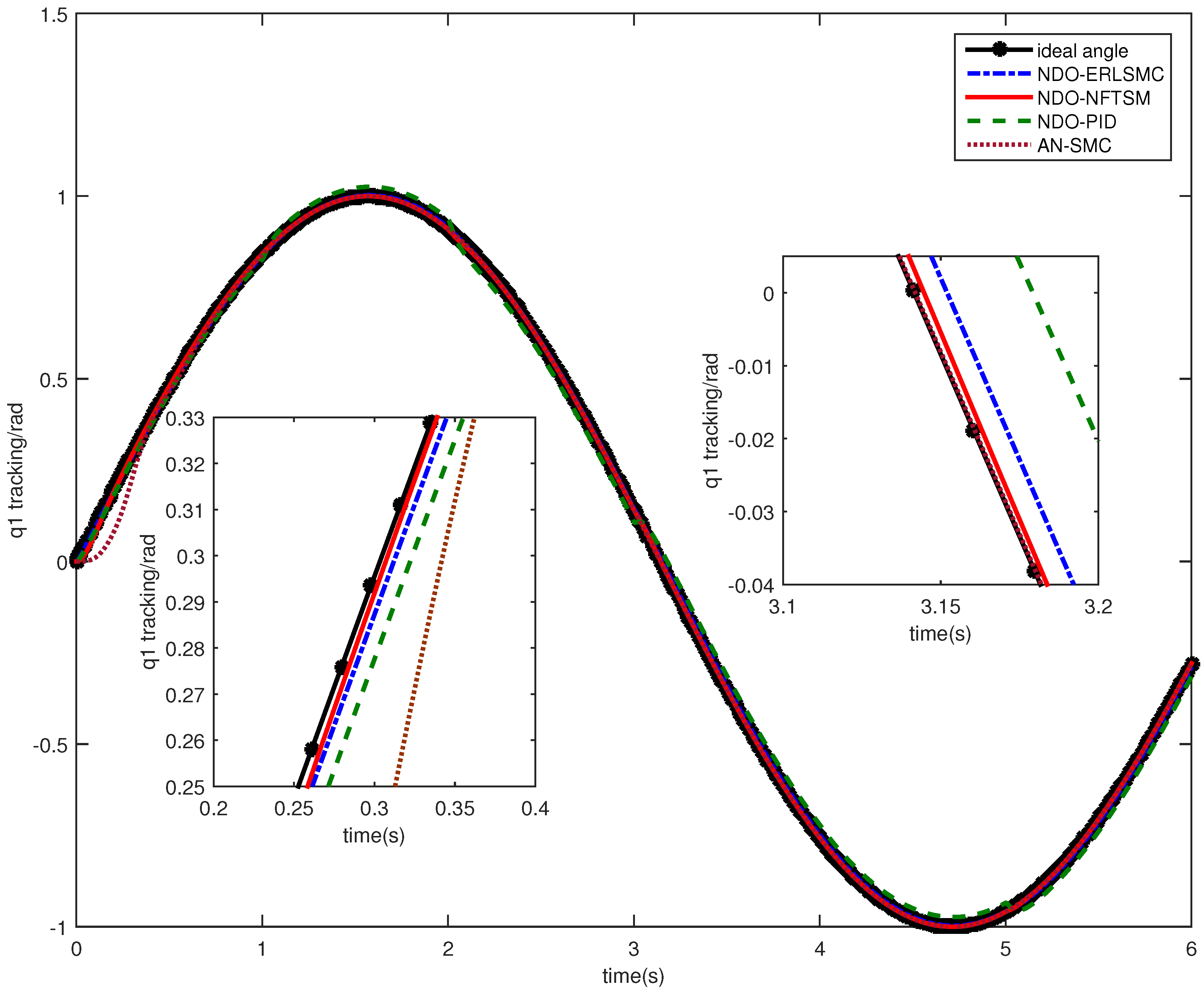
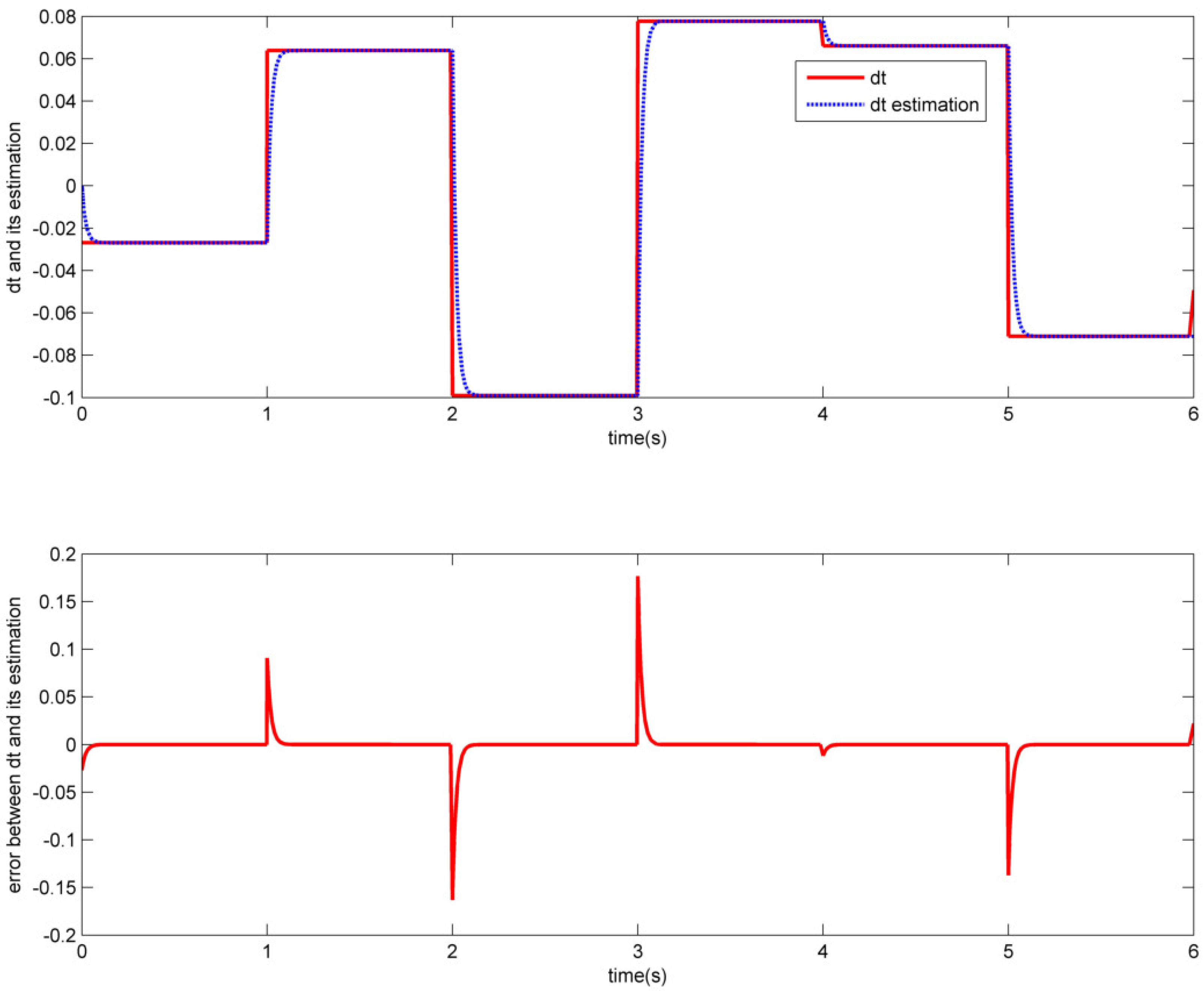
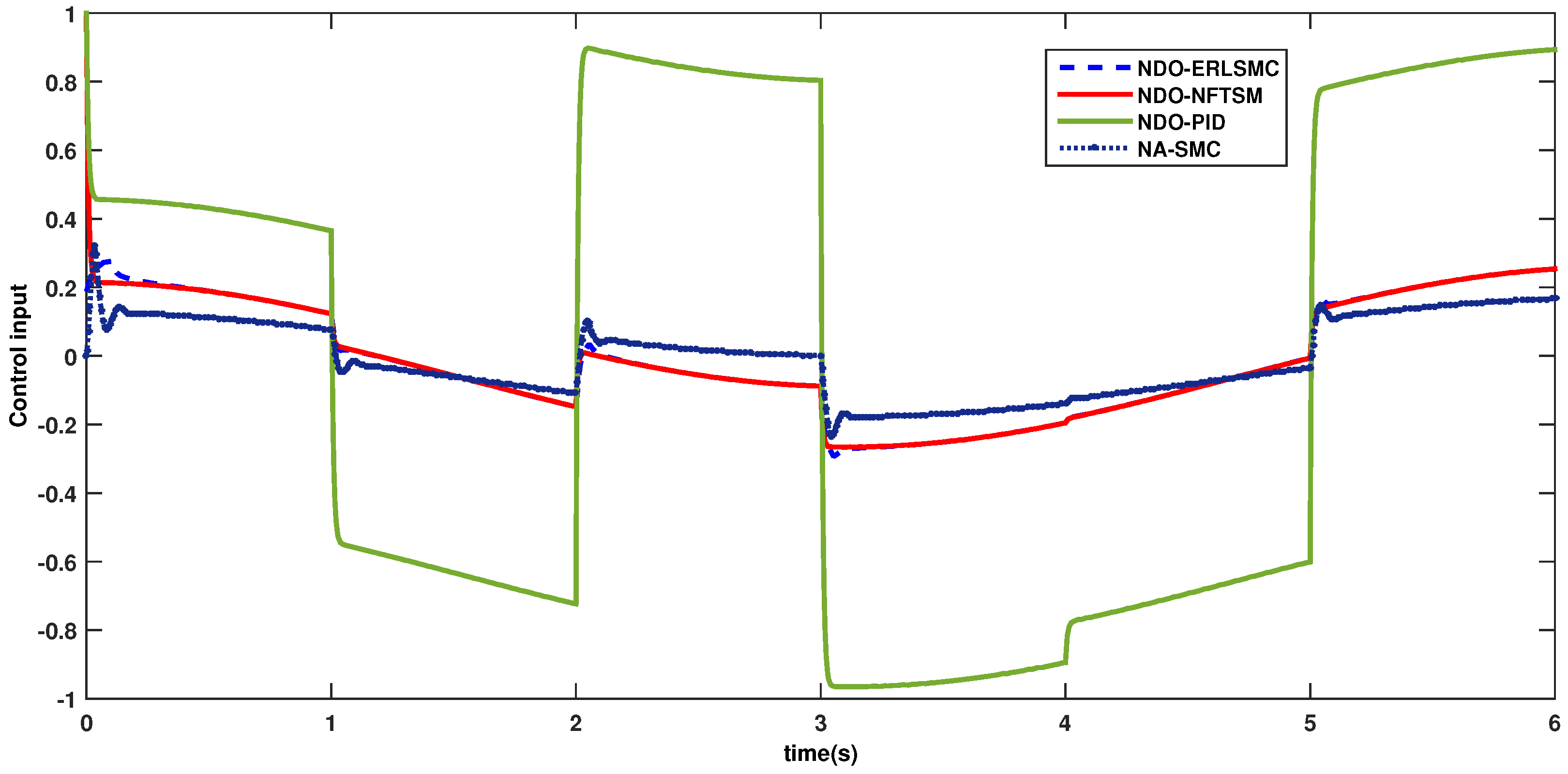
| Controller | Parameters |
|---|---|
| NDO-NFTSM (the proposed controller) | = 0.01, K = 40.205, = 1.5, p = 0.1, = 15, = 400 |
| NDO-ERLSMC | c = 15, K = 40.205 |
| NA-SMC | c = 15, = 0.05, = 0.1 |
| NDO-PID | = 50, = 0.5, = 2 |
| Error Indicator | |||
|---|---|---|---|
| MSE | 0.0523 | 0.0479 | 0.0446 |
| MAE | 0.0942 | 0.0873 | 0.0784 |
| Error Indicator | NDO-NFTSM | NDO-ERLSMC | NA-SMC | NDO-PID |
|---|---|---|---|---|
| MSE | 1.4417 × 10−4 | 1.8118 × 10−4 | 2.5063 × 10−4 | 2.2701 × 10−4 |
| MAE | 0.0088 | 0.0102 | 0.0127 | 0.0091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, J.; Cheng, J. Research on Sliding Mode Control of Robot Fingers Driven by Tendons Based on Nonlinear Disturbance Observer. Symmetry 2025, 17, 560. https://doi.org/10.3390/sym17040560
Pei J, Cheng J. Research on Sliding Mode Control of Robot Fingers Driven by Tendons Based on Nonlinear Disturbance Observer. Symmetry. 2025; 17(4):560. https://doi.org/10.3390/sym17040560
Chicago/Turabian StylePei, Jiufang, and Jinshi Cheng. 2025. "Research on Sliding Mode Control of Robot Fingers Driven by Tendons Based on Nonlinear Disturbance Observer" Symmetry 17, no. 4: 560. https://doi.org/10.3390/sym17040560
APA StylePei, J., & Cheng, J. (2025). Research on Sliding Mode Control of Robot Fingers Driven by Tendons Based on Nonlinear Disturbance Observer. Symmetry, 17(4), 560. https://doi.org/10.3390/sym17040560






