Abstract
We describe the quark substructure of hadrons and the equation of state of high-density neutron star matter by using the Nambu–Jona-Lasinio (NJL) model, which is an effective quark theory based on QCD. The interaction between quarks fully respects the chiral and flavor symmetries. Guided by the success of various low-energy theorems, we assume that the explicit breaking of these symmetries occurs only via the current quark masses, and all other symmetry breakings are of dynamical nature. In order to take into account the effects of the finite quark core sizes of the baryons on the equation of state, we make use of an excluded volume framework that respects thermodynamic consistency. The effects generated by the swelling quark cores generally act repulsively and lead to an increase in the pressure with increasing baryon density. On the other hand, in neutron star matter, these effects also lead to a decrease in the density window where hyperons appear because it becomes energetically more favorable to convert the faster moving nucleons into hyperons. Our quantitative analysis shows that the net effect of the excluded volume is too small to solve the long-standing “hyperon puzzle”, which is posed by the large observed masses of neutron stars. Thus, the puzzle persists in a relativistic effective quark theory which takes into account the short-range repulsion between baryons caused by their finite and swelling quark core sizes in a phenomenological way.
1. Introduction
The properties of strongly interacting hadronic systems like nucleons, nuclei, nuclear matter, and neutron stars reflect the basic quark substructure of their constituents. At very high densities but low temperatures, such as in the interior of neutron stars, new states of matter such as color superconducting quark matter [1] or various kinds of coexisting phases of hadrons and quarks [2] are expected to play important roles, and understanding their structures is a fascinating field of current research. Besides the familiar blocks of nuclear systems—protons and neutrons made of up (u) and down (d) quarks—baryons and quarks with strangeness are receiving much attention experimentally as well as theoretically. The current s quark mass () is still small enough to assume the full symmetry of QCD for the effective hadronic interactions from intermediate to high energies. Thus, can be viewed as the principal source of explicit chiral and flavor symmetry breakings; all other symmetry breaking patterns, including the more familiar vector [3] and axial-vector [4] cases, must be of dynamical origin. This way of thinking, which is supported by phenomenological as well as theoretical considerations [5,6,7], puts strong constraints on the hadronic interactions involving strangeness. Any theoretical model which aims to describe hyperons in nuclei and nuclear matter, or strange quarks in hadrons and highly compressed neutron star matter, has to comply with these constraints.
An important test stone for theoretical models was provided by the observation of heavy neutron stars with about 2 solar masses [8,9,10,11], and more recently, up to 2.35 solar masses [12]. (For a recent analysis of independent data from the NICER collaboration, including star radii, see Ref. [13].) Because the onset of hyperons usually leads to a softening of the equation of state (EOS) of neutron star matter [14], it is still a major difficulty for many models to reproduce such heavy stars. This problem, which is commonly called the “hyperon puzzle” [15], has triggered an extensive amount of research (see, for example, Ref. [16]). Here, we can mention only a few more recent examples: Lattice QCD calculations, which have been very useful to study the hyperon–nucleon interactions [17,18], begin to provide new bounds on the pressure and the maximum mass of neutron stars [19,20]. Nuclear density functional theory, based on available empirical information on the interaction between hyperons [21], relativistic mean field theories with novel momentum-dependent interactions [22], and studies of three-body forces involving hyperons [23,24], is making important contributions to understand the stiffening of the EOS of neutron star matter. On the other hand, quark matter cores may exist in massive neutron stars under certain stability conditions [25], and their evidence has been supported by model-independent analyses [26]. In fact, detailed model calculations have shown that phase transitions to normal [27] or color superconducting quark matter [28,29] may be strong candidates to describe heavy neutron stars, if a vector-type repulsion between the quarks in the core of the star is also taken into account.
Quarkyonic matter, which was originally motivated by the expansion [30,31] and hadron–quark continuity [32,33], is receiving more and more interest recently because it may provide a solution to the hyperon puzzle based on the Pauli blocking of d quarks in neutron star matter before the onset of hyperons [34,35,36]. This is particularly interesting because the role of short-range repulsions arising from the Pauli principle on the quark level in systems with strangeness has also been suggested by recent group theoretical methods [37] and analysis of scattering experiments [38]. A more phenomenological method to include short-range repulsions is based on the excluded volume effects (EVEs) of the van der Waals type, as used in previous studies of relativistic heavy-ion collisions [39,40]. This method, which assumes that the finite sizes of quark cores in baryons give rise to important short-range repulsions, was used recently in Ref. [41] in the framework of the quark–meson coupling (QMC) model [42,43], where it was claimed that those effects are strong enough to sustain heavy neutron stars. A closer investigation of this point in a framework that respects the basic symmetries of QCD is the principal aim of our present investigation.
Nowadays, it is well established that the Nambu–Jona-Lasinio (NJL) model [44,45,46,47] is one of the most useful effective quark theories of QCD. A fully relativistic Faddeev approach [48,49] has opened the door to describe baryons in this model, and the inclusion of confinement effects in a phenomenological way via an infrared cut-off [50] was the starting point for many applications to nuclear systems [51,52,53]. Despite quite different model assumptions, the QMC model and the NJL model share many points in common: in the present context, most notably, the important role of the scalar polarizability of the nucleon to describe saturation and induce many-body forces [54,55], and the enhancement of spin–spin correlations between light quarks in the nuclear medium which leads to an increase in the mass difference in nuclear matter [56,57]. In view of the results presented in Ref. [41] for the QMC model, it is therefore of interest to see whether the NJL model can describe heavy neutron stars in a similar way without invoking a phase transition to quark matter.
The purposes of our present work can therefore be summarized as follows: First, we wish to base the description of excluded volumes on the actual quark core sizes, calculated consistently in the NJL model for each baryon and each density separately, without introducing any new free parameters. It is well known that by assuming a common quark core radius for all baryons in the system, a thermodynamically consistent description can be achieved [58] that satisfies the requirements of causality up to very high densities. In view of our successful NJL model description of the properties of free octet baryons [59], like their sizes, magnetic moments, and electromagnetic form factors, it is desirable to describe the radii of in-medium quark cores and their effects on restricting the volumes available for the Fermi motion of baryons in a consistent way. Because EVEs reflect the short-range repulsion between nucleons in a phenomenological way, they will certainly stiffen the nuclear matter EOS. However, it is well known that if this stiffening affects only baryons in motion, i.e., mainly the neutrons, it becomes easier for them to reach the hyperon thresholds, which leads to the unwanted effect of lowering the onset of hyperons [60]. Therefore, it is important to also take into account the effects of finite—actually swelling—quark core radii of hyperons before their onset. For the nucleons, a moderate swelling is known to be important in describing the EMC effect [51], the Coulomb sum rule [53], and the reduction in the in-medium ratio of electric to magnetic nucleon form factors [61]. Therefore, in this work we would like to consistently take into account the swelling of the quark cores of all in-medium baryons as a function of baryon density.
Second, we wish to examine the effects of this extended description of EVE on the EOS of nuclear matter, neutron star matter, and the properties of neutron stars in the framework of the mean field approximation to the NJL model. The EOS and all numerical results of our present paper agree with our earlier work [57] using the standard four-Fermi interactions in the NJL model [57], as soon as we switch off the EVEs which arise from the finite quark core sizes. The basic physical picture is therefore the same, i.e., it can be visualized by composite baryons moving in self-consistent scalar and vector mean fields on the background of the constituent quark vacuum. Using concepts of the Fermi liquid theory [62,63], it has been shown that this picture can be translated into a model of baryons interacting via the exchange of composite neutral scalar and vector mesons [50,57]. In other words, the overlap of the meson clouds of the baryons leads to the meson exchange interactions, and it is natural to identify the distance at which the relative wave function of interacting baryons is strongly suppressed with the quark core radii, i.e., the sizes of the baryons without their meson clouds. Because we will calculate the quark core radii in our model without assuming any new parameters, we can investigate their effects on the EOS in a parameter-free way. Because our previous NJL calculations [57] have shown that six-Fermi and eight-Fermi interactions—with coupling constants chosen so as not to spoil the saturation properties of normal nuclear matter—cannot solve the hyperon puzzle, we limit ourselves to the standard four-Fermi interactions in this work.
The outline of the paper is as follows: Section 2 discusses our extended EOS in the NJL model and demonstrates that thermodynamic consistency can be achieved in the case where each member of the baryon octet has their independent quark core size. Section 3 presents our results for the EOS of nuclear matter, neutron star matter, and the properties of neutron stars, with particular emphasis on the EVEs on the onset of hyperons, the role of the in-medium swellings of baryons, and the resulting volume fractions occupied by the quark cores at very high baryon densities. Section 4 gives a summary of our results.
2. NJL Model and Excluded Volume Effects
Our work is based on the following three-flavor NJL Lagrangian with 4-Fermi interactions in the channels [46,47]:
where is the quark field, the current quark mass matrix with diagonal elements , and () are the Gell-Mann flavor matrices plus . The 4-Fermi coupling constants in the scalar–pseudoscalar and the vector–axial-vector channels are denoted by and , respectively. The interaction Lagrangian in Equation (1) has the symmetry of QCD, which contains the familiar flavor as a subgroup. In our previous work [57], we have shown that the 6-Fermi (determinant) interaction [4], which breaks the symmetry, and chiral invariant 8-Fermi interactions [64] have only moderate effects on the EOS of neutron star matter if their strengths are restricted so as not to spoil the saturation properties of isospin symmetric nuclear matter. Therefore, in this work, we will consider only the 4-Fermi interactions for simplicity. Following the successes of various low-energy theorems and mass formulas, we will assume that current quark masses are the only sources of explicit breaking of the flavor and chiral symmetries, and all other symmetry breakings are of a dynamical nature.
In order to construct the octet baryons as quark–diquark bound states, we also need the interaction Lagrangian in the channels with the same symmetries. This Lagrangian, which involves the 4-fermi coupling constants and in the scalar and axial-vector channels, respectively, together with details of the quark–diquark description of octet baryons based on the Faddeev framework, was presented in our previous work (Appendix A of Ref. [57]) and will not be repeated here. In a vacuum, isospin symmetry is assumed to be intact, i.e., we use throughout this work. In neutron star matter, the isospin asymmetry will be fully taken into account by solving the bound state equations with independent constituent quark masses , , and defined by Equation (3) below.
In order to construct the EOS, we will use the mean field approximation, which can be visualized by composite baryons moving in self-consistent scalar and vector fields on the background of the constituent quark vacuum. We will take into account three scalar fields and the time components of three 4-vector fields , where . Their definitions are as follows:
where denotes the expectation value in the ground state of the medium under consideration (vacuum, nuclear matter, or neutron star matter). The scalar fields lead to the spontaneous breaking of the chiral symmetry and give rise to the effective quark masses:
The vector fields lead to shifts in the energies of the baryons in the system. As a result, the energy of a baryon with flavor b and 3-momentum is obtained from the pole of the quark–diquark equation in the variable as follows:
Here, is the number of quarks with flavor in the baryon b with mass . (A comment on our notation: A summation over multiple flavor indices— for quarks, for octet baryons, ℓ for leptons, and i for both baryons and leptons—in a product, including squares like , is implied if those indices appear only on one side of an equation. As usual, the same convention is used for the Lorentz indices . The Fermi momentum of particle i will be denoted as .)
The mean field approximation is implemented into the Lagrangian (1) in the standard way by decomposing the various quark bilinears into classical (c-number) parts and quantum (normal-ordered) parts. We will assume that the only non-vanishing classical parts are the mean fields given in Equation (2). The normal-ordered parts, together with the interaction parts given in Equation (A1) of Ref. [57], are used to calculate bound state masses of pseudoscalar mesons and octet baryons, as well as the pion decay constant.
2.1. Mean Field Approximation Without EVEs
In our model defined above, the energy density of neutron star matter has the form
Here,
is the energy density of the baryons, where denotes a given set of octet baryon densities, denotes the Fermi distributions with Fermi momenta , and the single baryon energies are given in Equation (4). (We attach a superscript to those quantities which, in the next subsection, will become effective quantities if their argument is the set of effective baryon densities , defined by Equation (11) of the next subsection.) The total baryon density will be denoted as . in Equation (5), which is the (Mexican hat-shaped) contribution of the constituent quark vacuum to the energy density, expressed in its unregularized form by
where a sum over the quark flavors is implied, and the sub-index 0 refers to the vacuum with zero baryon densities. The label in Equation (5) denotes the contributions from the Fermi gas of leptons in chemical equilibrium with the baryons.
The stationary conditions for the vector fields for fixed gives , and therefore, the total contribution of the vector fields to the energy density becomes . The corresponding requirement on the scalar fields, , is equivalent to the in-medium gap equations. The energy density is then stationary with respect to all mean fields, and the chemical potential of baryon b simply becomes the Fermi energy :
Because the model is thermodynamically consistent, the pressure can be calculated either from the first law of thermodynamics () or by direct calculation. The resulting expression is
where the contribution from the baryons is given by
2.2. EVEs for Baryons with Different Quark Core Sizes
In order to take into account the EVEs, we define the effective baryon densities by , where are true baryon numbers in the volume V, and is the volume occupied by the quark cores of all baryons. These effective baryon densities are considered as functions of the true baryon densities according to the relation
where is the volume of the quark core of baryon b, which will be defined more precisely in the next section, and therefore, is the volume fraction () occupied by the quark cores of all baryons.
Let us first consider the pressure. To take into account the EVEs, we follow previous works [39,40,41,58] and replace the explicit dependence on the baryon densities in the last form of (10) by the effective baryon densities , i.e., we use
with the effective Fermi momenta defined by . The total pressure as a function of the true baryon densities then follows from Equation (9) as
The effective baryon energy density is defined as the energy of the baryons per volume available for their motion, i.e.,
The baryon energy density including the EVEs is then expressed as , where is given by the original NJL model expression (6) after the replacement :
We therefore arrive at the following expression for the total energy density including the EVEs:
(We note that the factor in Equation (15) does not mean that only the contributions from outside the quark cores are taken into account, as can be seen, for example, by the correct zero-density limit .) The mean fields including the EVEs are determined for fixed true baryon densities by the stationarity conditions applied to (15). By using the spectrum (4) for the vector fields, this condition leads to
which shows that the vector fields are unchanged by the EVEs: . The total vector contribution to the energy density (15) is then the same as in the previous subsection, namely . For the scalar fields, the gap equations
have to be solved numerically to obtain the quark and baryon masses as functions of the true baryon densities. Because, from Equations (16) and (17), the energy density is stationary with respect to all mean fields, the baryon chemical potential can be obtained from , i.e., only the explicit dependence on , which resides in the first term of (15), needs to be taken into account. A simple calculation, using the relation and the thermodynamic consistency relation of the original NJL model (), gives
where, in the last step, we used the form of as given by the last form in Equation (8) after the replacement , and the relation according to Equation (12). From Equation (18), we see that the EVEs led to an increase in the Fermi momenta of baryons and to a volume term in the chemical potentials.
We can now confirm the thermodynamic consistency of the approach, that is, the first law of thermodynamics,
as follows: For the leptonic contributions, it is obvious, and for the other contributions, we use the form (13) for and (15) for , as well as Equation (18) and the aforementioned thermodynamic consistency relation of the original NJL model for the baryon contributions. Leaving out the leptonic contributions for simplicity, we obtain
which becomes
Compared to previous works on EVEs in effective quark theories [41,58], the important new point here is that the thermodynamic consistency can be satisfied for the case where each baryon has its own quark core radius, which can be calculated consistently in the same model framework, as will be explained in the next section. We finally note that the formulas given in this subsection can be used to derive the following simple and instructive relation for the change in the energy density with respect to the quark core volume of a baryon b:
3. Results
In this section, we present our results on EVEs in symmetric nuclear matter, neutron star matter, and neutron stars. The EVEs in our model arise from the finite rms radii of the baryon density distributions of the quark cores of octet baryons in the medium, which are calculated by using the quark–diquark model based on the Faddeev equation for each baryon separately, as will be explained below.
3.1. Model Parameters and Results for Single Baryons
The model parameters used in the present numerical calculations are the same as in our previous work [57] and are summarized in Table 1. Besides the model parameters , , m, and , which appear in the Lagrangian of Equation (1), other parameters necessary to define the model are the infrared (IR) and ultraviolet (UV) cut-offs and , which are used with the proper-time regularization scheme [65,66] (also see Appendix C of Ref. [57]). While the UV cut-off is necessary to give finite integrals, the IR cut-off eliminates unphysical decay thresholds of hadrons into quarks, thereby simulating one important aspect of confinement. It should be similar to , and because our results are rather insensitive to its precise value as long as , we choose GeV. (A recent study [67] of in the scheme for two active flavors gave GeV, which encompasses our assumed value.) The parameters , m, and are determined so as to give a constituent light quark mass in a vacuum of GeV via the gap equation (see Equations (3) and (17)), the pion decay constant GeV, and pion mass GeV via the standard Bethe–Salpeter equation in the pionic channel [46,47]. The strange quark mass is determined so that the gap equation gives a constituent s quark mass in a vacuum of GeV, which reproduces the observed mass of the baryon GeV by using the quark–diquark bound state equations. The vector coupling is determined from the binding energy per nucleon in symmetric nuclear matter ( MeV) at the saturation density ( ). (See Refs. [68,69] for recent precision studies of and at of symmetric nuclear matter.) As will be seen in the next subsection, the EVEs lead to a slight shift in the saturation point of symmetric nuclear matter which, however, is completely unimportant for neutron star matter at high densities, so we will keep the value of determined in our previous work [57]. As explained in Appendix A of Ref. [57], the coupling constants in the scalar and axial-vector channels, and , are fixed to the free nucleon and delta masses ( GeV and GeV). Except for , the resulting free masses of octet baryons are then predictions of the model and are summarized in Table 2 together with the observed values. The good agreement with the observed values may be taken as an a posteriori justification of our choice GeV.

Table 1.
Values for the model parameters which are determined in the vacuum, single hadron, and nuclear matter sectors. The regularization parameters, constituent quark masses in the vacuum (sub-index 0), and current quark masses are given in units of GeV, and the coupling constants are given in units of Ge.

Table 2.
Masses of octet baryons (in units of GeV up to 3 significant figures) calculated in the vacuum (sub-index 0) by using the coupling constants Ge and Ge in the scalar and axial-vector diquark channels fitted to the standard vacuum masses of the nucleon ( GeV) and the baryon ( GeV), in comparison to the isospin-averaged observed values [70].
By using the solutions of the quark–diquark bound state equations as described in Appendix A of Ref. [57], we can calculate the quark core (qc) contribution to the form factor corresponding to the distribution of baryon charge from the Feynman diagrams shown in Figure 1, which represent the baryon current associated with “bare” constituent quarks, i.e., constituent quarks without their meson clouds. Each operator insertion in these diagrams is therefore given by , where the factor is the baryon number of a quark.

Figure 1.
Feynman diagrams representing the quark core contributions to the baryon current. The ovals (circles) are the vertex functions of the quark–diquark (quark–quark) bound state as given in Refs. [57,59,71], and the crosses stand for the external field which transfers a 4-momentum q to the baryon and couples it to the constituent quarks via the elementary vertex . A single (double) solid line stands for the quark (diquark) propagator, and the external lines represent a given member of the baryon octet.
Similar to the more familiar electric form factor, the baryon current represented by Figure 1 can be parametrized by the Dirac–Pauli form factors and , which give the desired form factor as and the associated rms radius . Our results for these radii in the vacuum (zero baryon density), where isospin symmetry is assumed to be intact, are shown in the second column of Table 3. It is important to note that it is these baryon radii of quark cores without meson cloud effects that are responsible for the EVEs in our model, and which precisely agree with the notion of “hard core radii” of Ref. [33]. The physical reason is simply that the overlap of the meson clouds gives rise to the meson exchange interaction and should not be counted as an excluded volume effect. Indeed, by using familiar relations of the Fermi liquid theory, one can verify that our effective baryon–baryon interaction takes into account the direct terms of neutral scalar and vector meson exchanges (see Appendix A). They mediate the interactions between the baryons by generating the mean fields and do not restrict the volume available for their motion in any way. It is interesting to observe that our values of are similar to the radii used in previous works on EVEs [41,58], where they were used as free parameters common to all baryons.

Table 3.
Baryon radii of single (free) baryons (in units of fm up to 2 significant figures). The second column shows the quark core (qc) results, which are used to assess the EVEs on the EOS in this work. The third and fourth columns, which are taken from our earlier calculations [59] in the same model, also include the effects of the vector meson (vm) and the pion () cloud for those cases where the baryon radii can be related to the electric radii, as explained in the main text. For those cases, the last column shows the observed values [70] where available. For the , where no observed value is available, we quote the results of a recent calculation in nonlocal chiral effective theory [72].
Although the meson cloud effects, a part of which is incorporated automatically in our effective interaction, should not be included in the definition of hard core radii, they are of course very important to explain the physical sizes of single baryons. For the case of the baryon radii , the vector mesons are of particular importance, as one can expect from the vector meson dominance model, but also the pion cloud gives some contributions. For illustrative purposes, we therefore quote the results from Table VI of our previous work [59] on baryon octet form factors, which was performed within the same model, in the third and fourth columns of Table 3. (For the nucleon, the relation between the baryon radius and the electric charge radii of protons and neutrons is . For the and , the corresponding relations are simply and because and consist only of d and s quarks with the same electric charge of . No such relation exists for .)
Because, in the following discussions, the term “baryon radius” always refers to the quark core radius , we return to the simplified notations of the previous section, i.e., we use for the radius and for volume. The values of in the vacuum, given in the second column of Table 3, will be denoted by .
3.2. Symmetric Nuclear Matter
Figure 2 shows the results for the binding energy per nucleon and the pressure in isospin symmetric nuclear matter as functions of the baryon density. Each figure shows our previous results [57] without EVEs (dotted lines): the results where the EVEs are evaluated by using the radius of free nucleons, fm, as given in the second column of Table 3, for all densities (dashed lines), and our full results, which include the density dependence (swelling) of the nucleon radius, which arises via its dependence on the mean scalar field (solid lines).
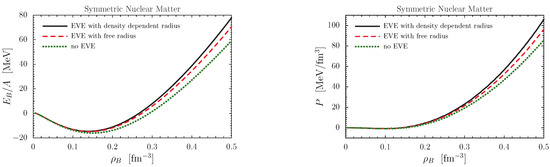
Figure 2.
Binding energy per nucleon (left panel) and pressure (right panel) in symmetric nuclear matter. Dotted lines: results without EVEs (); dashed lines: results obtained with the free (zero baryon density) nucleon radius ; solid lines: results obtained with our calculated density-dependent nucleon radius .
We see that, at normal nuclear matter density, the EVEs have little effect on the EOS. The left panel of Figure 2 shows that the saturation density is shifted from 0.15 (dotted line) to 0.14 (solid line), with a corresponding shift in the binding energy per nucleon from MeV to MeV. Although it is possible to readjust model parameters to keep the saturation point unchanged, we keep the same parameters for clarity, because such small changes would not affect our main results and conclusions in any way. Also, the other results given in Ref. [57] at the saturation point, like the incompressibility ( MeV), the symmetry energy ( MeV), the effective quark mass (325 MeV), and the effective nucleon mass (756 MeV), change by less than when the EVEs are included.
On the other hand, at densities of about 3 times the normal nuclear matter density, both the energy per nucleon and the pressure increase appreciably when the EVEs are included. For the energy, about 30% of the repulsive contributions come from the swelling of the nucleons in the medium, while for the pressure, the swelling effects make up 50% of the total EVEs. Because typical values of the central baryon densities in massive neutron stars are about , one may naively expect from these figures that the EVEs may have a large effect on heavy neutron stars.
Figure 3 shows the results for the nucleon radius () and the corresponding volume fraction occupied by the quark cores in the medium () as functions of the baryon density. The modest swelling of about at normal densities plays an important role in describing several nuclear phenomena, as mentioned in Section 1. At the highest density shown in Figure 2, which is about 3.3 times the normal nuclear matter density, the swelling of the nucleon radius is about and indicates a kind of plateau, which reflects our phenomenological implementation of confinement effects via the infrared cut-off (). The volume fraction occupied by the quark cores at this density is about 33%, indicating that the physical picture of the mean field approximation is not unreasonable, although it leaves room for effects from the Pauli principle on the level of quarks, which is an important subject of current research as mentioned in Section 1.

Figure 3.
Nucleon hard core radius (left panel) and corresponding volume fractions occupied by the quark cores (right panel) in symmetric nuclear matter as a function of the baryon density.
3.3. Neutron Star Matter
In order to calculate the EOS of neutron star matter, the basic formalism explained in Section 2.2 must be supplemented by the conditions for chemical equilibrium and charge neutrality, which can be expressed by
Here, the chemical potentials of baryons are given by Equation (18), and for the leptons (), we assume the non-interacting Fermi gas expression . The Fermi momenta of baryons () and leptons () are related to their number densities by . In Equation (23), denotes the electric charges of baryons and leptons. The numerical calculation is then carried out as follows: The vector fields can be eliminated from the outset in favor of the baryon densities by using Equation (16). Then, for a given baryon density , we solve the set of Equation (23) for the number densities of the particles in the system on a grid of scalar fields , which in turn is determined by minimizing the energy density (15), see Equation (17). The solutions of these equations can be used to calculate the EOS and chemical composition of the system, together with other physical quantities like the effective masses of quarks and baryons, the radii of the baryons, and the volume fraction occupied by the quark cores of baryons.
In Figure 4, we compare the results for the chemical potentials and the ratios of the number densities of baryons and leptons to the baryon density, for the case where the EVEs are neglected (panels on the left) to the case where the EVEs are included (panels on the right). The chemical potentials of the hyperons below their threshold densities, where they touch one of the three solid lines representing and from above according to the equilibrium conditions (see Equation (23)), are given by Equation (18) for . They can be visualized as hyperons immersed in the nuclear medium without forming a nonzero macroscopic number density.
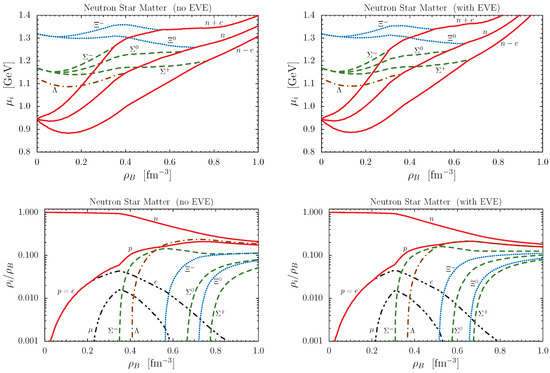
Figure 4.
Chemical potentials of octet baryons (upper panels) and the ratio of number densities of baryons and leptons to the baryon density (lower panels) in neutron star matter as a function of the baryon density. The results for (no EVEs) are shown by the left panels, while those on the right refer to the case of our calculated density-dependent baryon radii (with EVEs).
A comparison of the two upper panels of Figure 4 shows that, with EVEs, the nucleon chemical potentials (solid lines) increase faster with density, partially because of their larger effective Fermi momenta ( in Equation (18)) and partially because of their volume terms in (18), while the chemical potentials of the hyperons below their thresholds increase only slightly from their values. This is because for (case of hyperons dispersed in the nuclear medium), the difference between the chemical potentials for and comes, besides small differences in effective masses, only from the volume term in Equation (18), which is quite small in the density region of the hyperon onset. (For example, the value of at , including the EVEs, is GeV/, which is about of the total pressure at this density, see Figure 5. Then, a typical hadron size of fm gives a contribution GeV to the chemical potential, which is small on the scale of Figure 4.) Thus, the crossing between the steeper solid lines and the almost unchanged hyperon lines in Figure 4 is shifted to smaller densities when the EVEs are included, and as a result, the onset of hyperons occurs in a more narrow window of densities, as shown in the right panels of Figure 4. Because the presence of hyperons generally tends to soften the EOS, we can therefore expect that the repulsion induced by the EVEs will be much less effective in neutron star matter than in nuclear matter.

Figure 5.
The pressure (upper left panel) and the energy density (upper right panel) as a function of the baryon density and the pressure as a function of energy density (lower panel) for neutron star matter. In each panel, the upper (lower) three lines show the results obtained without (with) hyperons, and for each case, we show the results without EVEs (dotted lines), with EVEs calculated with the free baryon radii (dashed lines), and with our calculated density-dependent baryon radii (solid lines). The velocity of sound () does not exceed the velocity of light for the range of densities shown in all figures of this paper. The gray area in the lower panel reproduces the posterior credible band shown in Figure 2 of Ref. [13] from a Bayesian inference analysis of NICER data on neutron stars.
The pressure and the energy density in neutron star matter are shown in Figure 5 for the following six cases: the upper three lines show the results without hyperons (only nucleons and leptons in chemical equilibrium), and the lower three lines show the results including the hyperons. For each case, we show the results obtained without EVEs (, dotted lines), with EVEs calculated by using the free baryon radii (, dashed lines), and with our calculated density-dependent baryon radii (, solid lines).
Because the energy density is determined mainly by the number densities and the effective masses of the baryons, the EVEs on the energy density are generally small. Concerning the pressure, as can be expected from the results of Section 3.2 and the discussions presented above, the EVEs are very large in the region of high densities if only nucleons and leptons are considered, but become much smaller when the hyperons are also included. A comparison of the solid lines in the left panel of Figure 5 demonstrates the enormous reduction in the pressure by almost a factor of 3 in the region . A comparison of the dashed and solid lines shows that, for the case without hyperons, the swelling of nucleons contributes roughly 50% to the total EVEs for the pressure, which is similar to the case of symmetric nuclear matter shown in Figure 2, while for the case including the hyperons, the swelling effects are dominant. The comparison with the posterior credible band [13] in the lower panel of Figure 5 clearly rules out the presence of hyperons in our EOS for , demonstrating the hyperon puzzle in an impressive way.
The calculated quark core radii of octet baryons and the corresponding volume fraction occupied by the quark cores are shown in Figure 6. In the left panel, the density dependence of the radii of hyperons below their onsets simply reflects the action of the scalar fields produced by other baryons with finite density on the quarks inside the hyperon at rest. In the right panel, the volume fraction naturally includes only those baryons that exist in the system with a finite number density.
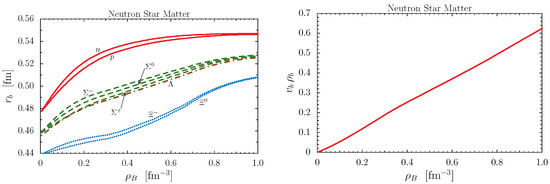
Figure 6.
The calculated radii of octet baryons (left panel) and the corresponding volume fraction occupied by the quark cores (right panel) in neutron star matter as a function of the baryon density.
From the left panel of Figure 6, we see that the swelling of baryons in the medium, which is caused by the decreasing quark masses, is at most and—in particular for the nucleons—tends to saturate at high densities. As mentioned already in Section 3.2, this reflects our phenomenological implementation of confinement effects via the infrared cut-off (). The splittings of radii within the isospin multiplets (N, , ) of the baryon octet shown in the left panel of Figure 6 are caused by in a medium that contains more d quarks than u quarks. This effect, which gives a small negative contribution to the symmetry energy in normal nuclear matter, is caused by our scalar isovector part of the effective baryon–nucleon interaction, which is positive but small at high densities [57], and which corresponds to the effect of the meson exchange in baryon–meson theories [73]. The radius of the baryon stays below the radii of the baryons for all densities. This can be traced back to the additional attraction in the from the scalar diquark made of u and d quarks (antisymmetric flavor combination ), which is not present in the baryon, and which becomes more pronounced at finite density because the mass of this light scalar diquark decreases more rapidly with density than the mass of the other (heavy scalar and axial vector) diquarks.
The right panel of Figure 6 shows that for baryon densities less than , which, in our calculation, is the highest density in stable neutron stars including hyperons, the volume fraction occupied by the quark cores is at most . Because this is still well below the closest packing fraction ( for spheres of similar radii), it may give us some confidence that the overall physical picture of the mean field approximation of three-quark bound states moving in self-consistent scalar and vector fields does not break down at such high densities, but it can be used as a starting point for corrections and improvements, taking into account the effects of the Pauli principle on the level of quarks.
3.4. Neutron Stars
By using our EOS as input to the Tolman–Oppenheimer–Volkoff (TOV) equations [74,75], we can calculate the properties of neutron stars. Our results for the star masses and radii based on the EOS discussed in the previous subsection are collected in Figure 7.
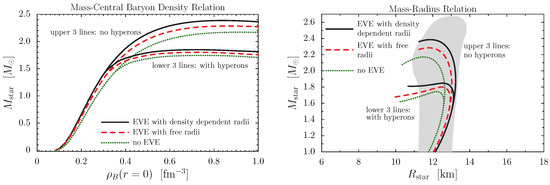
Figure 7.
Neutron star mass as a function of the central baryon density (left panel) and the relation between the mass and the radius of the stars (right panel). In both figures, the upper (lower) three lines show the results obtained without (with) hyperons, and for each case, we show the results without EVEs (dotted lines), with EVEs calculated by using the free baryon radii (dashed lines), and by using our calculated density-dependent radii (solid lines). The gray area in the right panel reproduces the posterior credible band shown in Figure 5 of Ref. [13] from a recent Bayesian inference analysis of NICER data on neutron stars.
Both figures demonstrate a reduction in neutron star masses caused by a reduction in pressure in the high-density region when the hyperons are included (Figure 5). The two groups of lines shown in Figure 7 clearly separate from each other in the density region of the onset of hyperons. The repulsive EVEs increase the maximum masses of stable stars consisting only of nucleons and leptons by up to , which is larger than the value reported recently for the heaviest observed neutron star [12]. On the other hand, because of the reasons discussed in the previous subsection, the repulsive EVEs become suppressed very much when the hyperons are included and increase the maximum mass of stable stars by only up to . This surprisingly small change is explained by the fact that the EVEs, in spite of introducing repulsion into the system, narrow the region of densities for the onset of hyperons, where the direct effect of the finite baryon volumes is too small to balance the gain of energy when a neutron, which obtains more kinetic energy as the available volume shrinks, is transformed to a hyperon at rest by the weak interactions. We also mention that the swelling of baryons makes up of the total EVEs on the maximum star masses in all cases shown in Figure 7. The comparison with the posterior credible band [13] in the right panel of Figure 7 shows that our stars with masses in the range tend to have radii that are too large when the EVEs are included. This is because the inner crust of the stars, typically in the density range of to , is not included in our calculation. Its effects can decrease the radius of the stars in this mass region by roughly 1 km [76].
To summarize, we obtain the following results for the maximum central baryon density which gives stable stars and the corresponding maximum star mass and radius at maximum mass for the case when the EVEs are taken into account with our calculated density-dependent baryon radii:
for the case of no hyperons, and
for the case with hyperons. We therefore conclude that the long-standing “hyperon puzzle” persists in our relativistic effective quark theory which takes into account the repulsive EVEs caused by the finite quark core sizes of the baryons.
Here, we wish to emphasize again the important role of symmetries which has lead us to this conclusion: Our model is based on the chiral and flavor symmetries of the interaction Lagrangians, given in Equation (1) for the channels and in Equation (A1) of Ref. [57] for the channels, following the well established paths in hadronic physics which lead to many successful low-energy theorems and mass formulas. The essential assumption here is that explicit breakings of these symmetries are allowed to arise only from the current quark masses, and all other breakings must be of dynamical origin. Because chiral symmetric six-Fermi and eight-Fermi interactions do not solve the hyperon puzzle [57], and our aim was to see how far we can go without invoking a phase transition to quark matter, we were left with just eight model parameters (four coupling constants, two cut-offs, and two current quark masses). If these are fixed as explained in Section 2, we do not have any free parameters to solve disagreements with observations. If we would allow for symmetry breaking interactions, modifications of the basic model equations, etc., there would be many ways to “resolve” the problem and obtain neutron star masses as large as needed. To us, however, it seems more important to respect the basic symmetries observed in nature than to reproduce observations by force.
Based on our results, we expect that the solution of the hyperon puzzle may be difficult to achieve on the level of composite baryons with short-range repulsions. Still, the possibility of strong three-body forces involving strangeness on the level of baryons is the subject of intensive theoretical and experimental investigations [23], but to us, it seems that some kind of strongly interacting quark matter will emerge as the solution, either by invoking a phase transition to color superconducting quark matter [29,77], or by exploring the possibilities created by recent work on quarkyonic matter [34,35,36], which is a new form of high-density matter based on the hadron–quark continuity.
4. Summary
Strongly interacting baryonic systems are fascinating objects of current research in hadronic physics because they relate the basic symmetries of microscopic nuclear systems to macroscopic astrophysical objects. In our work, we used the NJL model as an effective quark theory of QCD to describe constituent quarks, relativistic bound states forming hadrons, and the equations of state for nuclear and neutron star matter. This model has the basic chiral and flavor symmetries of QCD, which must be respected by all models for the hadronic interactions. Our basic assumption was that the current quark masses are the only sources of explicit symmetry breakings, while all other mechanisms of symmetry breaking must be of dynamical origin. This basic assumption leads to very strong restrictions on the model parameters, which have to be respected irrespective of agreement or disagreement with observations.
The new point of our work was to achieve a consistent description of excluded volume effects (EVEs) in the NJL model by identifying the quark core radii of each baryon in the system with the hard distance scale at which the relative wave function of interacting baryons becomes strongly suppressed. For this purpose, we reformulated the EOS including EVEs such that each baryon can have its own quark core size, which we calculated consistently within our model. We have shown that this description of EVEs, which does not introduce any new parameters, satisfies the requirements of thermodynamic consistency in general and of causality up to densities more than 6 times the normal nuclear matter density, which exceeds the range that is relevant for the cores of heavy neutron stars. By solving the three independent gap equations for the u, d, and s quarks, we were able to dynamically include the effects of in-medium hadron swelling, which are known to be important for the case of the nucleon on the EOS at high baryon densities. Our main motivation to re-examine the role of EVEs was to investigate their effects on the long-standing hyperon puzzle.
Our findings can be summarized as follows: For symmetric nuclear matter, the mechanism of volume exclusion by the swelling quark cores leaves the saturation properties almost unchanged, but at about 3 times the normal density, it increases both the energy per nucleon and the pressure by about 30%, while increasing the quark core size of the nucleons modestly by 10% and keeping the volume fraction occupied by the quark cores below 30%. These results reflect our phenomenological implementation of confinement effects into the model. A stable neutron star made only of nucleons and leptons can then be as heavy as solar masses, without any violation of causality. However, the direct repulsive effects coming from the quark core sizes are too small to balance the increased energy gain from the conversion of fast nucleons into hyperons at rest by the weak interactions. This effect decreases the density window where hyperons appear by , which is enough to cancel most of the direct repulsive EVEs on the pressure at high densities and the maximum mass of stable neutron stars. The result that we obtained of stable stars of only up to solar masses if the hyperons and EVEs are included together leads us to expect that the hyperon puzzle may be difficult to solve on the level of composite baryons with short-range repulsions.
Besides further investigations on strong three-body forces involving strange baryons, there are a number of ways to proceed by exploiting explicit quark degrees of freedom. One natural way might be to connect our NJL EOS with a color superconducting three-flavor quark EOS calculated in the same model by the usual Maxwell or Gibbs constructions. However, there are also other possibilities as reported recently. For example, in Ref. [33], it was argued that the hard cores should be replaced by continuous distributions, i.e., by the radial variable of the density, energy, and pressure profiles of a single baryon. In this way, it was observed that the resulting EOS, based on a closest packing of nucleons with variable radial size variables, becomes similar to empirical EOSs from other approaches. Another line proposed in the same paper is based on quantum percolation and hadron–quark continuity, where the quark wave functions become delocalized without a phase transition. It was pointed out, and supported by recent work based on schematic forms for the quark momentum distribution in baryons [34,35], that this mechanism could lead to a solution of the hyperon puzzle. The fascination of studying strongly interacting matter at high baryon densities is continuing and will increase our knowledge about the basic building blocks of nature.
Author Contributions
All authors have equally contributed to the conceptualization, numerical calculation, writing and editing of this article. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, contract no. DE-AC02-06CH11357.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Effective Interaction Between Baryons
By using Landau’s Fermi liquid theory [62,63], the effective interaction between two baryons (b and ) at their respective Fermi surfaces, denoted by , can be obtained from Equation (18) of the main text as follows:
where is the density of states per volume of baryon b at its Fermi surface, and the first term in (A1) refers to the volume available for the Fermi motion, .
To calculate the derivative from (18), it is convenient to separate the term depending explicitly on the density from the terms depending implicitly on the density via the mean fields and :
The explicit density dependence in (18) comes from the effective Fermi momentum in and the baryon pressure , while the baryon mass , the vector potential contribution, and the quark core volume can be considered as functions of the mean fields. The evaluation of the first term in (A2) is straightforward, and for the other terms, it is convenient to note that the energy density is minimized with respect to the mean fields at each set of baryon densities separately, i.e.,
where we used the fact that there is no mixing between scalar and vector mean fields in our energy density (15).
We obtain the following result for the effective interaction:
Here, we defined the generalized scalar and vector meson propagators for zero momentum by the inverse of the flavor matrices:
The term (A4) is the repulsive interaction arising directly from the finite quark core sizes. The two terms in (A5) correspond to the direct terms arising from the exchange of neutral scalar and vector mesons, as illustrated by Figure A1.
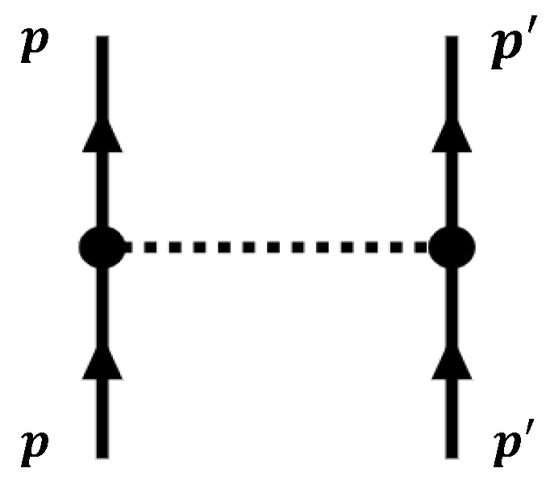
Figure A1.
Graphical representation of the meson exchange contribution to the effective baryon–baryon interaction (Equation (A5)). The magnitudes of the 3-momenta indicated in this figure are the Fermi momenta of the baryons b and , i.e., and .
The vector meson exchange term in Equation (A5) is the same as without EVEs and is simply given by . The scalar meson exchange term is more complicated than the form without EVEs given in Ref. [57]). The square of the coupling constant between a scalar meson made of () and the baryon b is expressed by
where the first term has a familiar form [50], but the second term could only be assessed numerically because of the dependence of on the scalar fields. For the same reason, the scalar meson propagator is also more complicated because of the dependence of the energy density (15) on the quark core radii. The , , and components of the exchanged scalar meson could be disentangled by an orthogonal transformation to diagonalize S at a fixed baryon density. Although further numerical analyses may be interesting, we do not go into more detail in this work.
References
- Alford, M.G.; Rajagopal, K.; Wilczek, F. QCD at finite baryon density: Nucleon droplets and color superconductivity. Phys. Lett. 1998, 422, 247–256. [Google Scholar] [CrossRef]
- Heiselberg, H.; Hjorth-Jensen, M. Phases of dense matter in neutron stars. Phys. Rep. 2000, 328, 237–327. [Google Scholar] [CrossRef]
- Weinberg, S. Superconductivity for Particular Theorists. Prog. Theor. Phys. Suppl. 1986, 86, 43. [Google Scholar] [CrossRef]
- ’t Hooft, G. Computation of the Quantum Effects Due to a Four-Dimensional Pseudoparticle. Phys. Rev. D 1976, 14, 3432–3450, Erratum in Phys. Rev. D 1978, 18, 2199. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetries of baryons and mesons. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef]
- Okubo, S. Note on unitary symmetry in strong interactions. Prog. Theor. Phys. 1962, 27, 949–966. [Google Scholar] [CrossRef]
- Pagels, H. Departures from Chiral Symmetry: A Review. Phys. Rep. 1975, 16, 219. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Brandes, L.; Weise, W. Constraints on Phase Transitions in Neutron Star Matter. Symmetry 2024, 16, 111. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Bombaci, I. The Hyperon Puzzle in Neutron Stars. JPS Conf. Proc. 2017, 17, 101002. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Vidana, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Beane, S.R.; Chang, E.; Cohen, S.D.; Detmold, W.; Lin, H.W.; Luu, T.C.; Orginos, K.; Parreno, A.; Savage, M.J.; Walker-Loud, A. Hyperon-Nucleon Interactions and the Composition of Dense Nuclear Matter from Quantum Chromodynamics. Phys. Rev. Lett. 2012, 109, 172001. [Google Scholar] [CrossRef]
- Inoue, T. Strange Nuclear Physics from QCD on Lattice. AIP Conf. Proc. 2019, 2130, 020002. [Google Scholar] [CrossRef]
- Abbott, R.; Detmold, W.; Illa, M.; Parreño, A.; Perry, R.J.; Romero-López, F.; Shanahan, P.E.; Wagman, M.L. QCD Constraints on Isospin-Dense Matter and the Nuclear Equation of State. Phys. Rev. Lett. 2025, 134, 011903. [Google Scholar] [CrossRef]
- Moore, G.D.; Gorda, T. Bounding the QCD Equation of State with the Lattice. JHEP 2023, 12, 133. [Google Scholar] [CrossRef]
- Choi, S.; Hiyama, E.; Hyun, C.H.; Cheoun, M.K. ΛΛ Interaction in a Nuclear Density Functional Theory and Hyperon Puzzle of the Neutron Star. arXiv 2023, arXiv:2309.01348. [Google Scholar]
- Chorozidou, A.; Gaitanos, T. Momentum dependence of in-medium potentials: A solution to the hyperon puzzle in neutron stars. Phys. Rev. C 2024, 109, L032801. [Google Scholar] [CrossRef]
- Tamura, H. How can we solve the hyperon puzzle?—Introduction to “topical session on ΛNN three-body force”. EPJ Web Conf. 2022, 271, 06001. [Google Scholar] [CrossRef]
- Jinno, A.; Murase, K.; Nara, Y.; Ohnishi, A. Repulsive Λ potentials in dense neutron star matter and binding energy of Λ in hypernuclei. Phys. Rev. C 2023, 108, 065803. [Google Scholar] [CrossRef]
- Eslam Panah, B.; Yazdizadeh, T.; Bordbar, G.H. Contraction of cold neutron star due to in the presence a quark core. Eur. Phys. J. C 2019, 79, 815. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Ferreira, M.; Câmara Pereira, R.; Providência, C. Neutron stars with large quark cores. Phys. Rev. D 2020, 101, 123030. [Google Scholar] [CrossRef]
- Contrera, G.A.; Blaschke, D.; Carlomagno, J.P.; Grunfeld, A.G.; Liebing, S. Quark-nuclear hybrid equation of state for neutron stars under modern observational constraints. Phys. Rev. C 2022, 105, 045808. [Google Scholar] [CrossRef]
- Tanimoto, T.; Bentz, W.; Cloët, I.C. Massive Neutron Stars with a Color Superconducting Quark Matter Core. Phys. Rev. C 2020, 101, 055204. [Google Scholar] [CrossRef]
- McLerran, L.; Pisarski, R.D. Phases of cold, dense quarks at large N(c). Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
- Jeong, K.S.; McLerran, L.; Sen, S. Dynamically generated momentum space shell structure of quarkyonic matter via an excluded volume model. Phys. Rev. C 2020, 101, 035201. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K.; Kojo, T.; Weise, W. Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter. Phys. Rev. D 2020, 102, 096017. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kojo, T.; McLerran, L. Quarkyonic matter pieces together the hyperon puzzle. arXiv 2024, arXiv:2410.22758. [Google Scholar]
- Kojo, T. Stiffening of matter in quark-hadron continuity: A mini-review. arXiv 2024, arXiv:2412.20442. [Google Scholar]
- Xia, C.J. Extended NJL model for baryonic matter and quark matter. Phys. Rev. D 2024, 110, 014022. [Google Scholar] [CrossRef]
- Oka, M. Spin-Flavor SU(6) Symmetry for Baryon-Baryon Interactions. arXiv 2023, arXiv:2301.06026. [Google Scholar]
- Nanamura, T.; Miwa, K.; Ahn, J.K.; Akazawa, Y.; Aramaki, T.; Ashikaga, S.; Callier, S.; Chiga, N.; Choi, S.W.; Ekawa, H.; et al. Measurement of differential cross sections for Σ + p elastic scattering in the momentum range 0.44–0.80 GeV/c. PTEP 2022, 2022, 093D01. [Google Scholar] [CrossRef]
- Rischke, D.H.; Gorenstein, M.I.; Stoecker, H.; Greiner, W. Excluded volume effect for the nuclear matter equation of state. Z. Phys. C 1991, 51, 485–490. [Google Scholar] [CrossRef]
- Yen, G.D.; Gorenstein, M.I.; Greiner, W.; Yang, S.N. Excluded volume hadron gas model for particle number ratios in A+A collisions. Phys. Rev. C 1997, 56, 2210–2218. [Google Scholar] [CrossRef]
- Leong, J.; Thomas, A.W.; Guichon, P.A.M. Excluded volume effects on cold neutron star phenomenology. Nucl. Phys. A 2024, 1050, 122928. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A Possible Quark Mechanism for the Saturation of Nuclear Matter. Phys. Lett. B 1988, 200, 235–240. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Vogl, U.; Weise, W. The Nambu and Jona Lasinio model: Its implications for hadrons and nuclei. Prog. Part. Nucl. Phys. 1991, 27, 195–272. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Ishii, N.; Bentz, W.; Yazaki, K. Baryons in the NJL model as solutions of the relativistic Faddeev equation. Nucl. Phys. A 1995, 587, 617–656. [Google Scholar] [CrossRef]
- Ishii, N. Goldberger-Treiman relation and g pi N N from the three quark BS/Faddeev approach in the NJL model. Nucl. Phys. A 2001, 689, 793–845. [Google Scholar] [CrossRef]
- Bentz, W.; Thomas, A.W. The Stability of nuclear matter in the Nambu-Jona-Lasinio model. Nucl. Phys. 2001, A696, 138–172. [Google Scholar] [CrossRef]
- Cloet, I.C.; Bentz, W.; Thomas, A.W. EMC and polarized EMC effects in nuclei. Phys. Lett. B 2006, 642, 210–217. [Google Scholar] [CrossRef]
- Cloët, I.C.; Bentz, W.; Thomas, A.W. Parity-violating DIS and the flavour dependence of the EMC effect. Phys. Rev. Lett. 2012, 109, 182301. [Google Scholar] [CrossRef] [PubMed]
- Cloët, I.C.; Bentz, W.; Thomas, A.W. Relativistic and Nuclear Medium Effects on the Coulomb Sum Rule. Phys. Rev. Lett. 2016, 116, 032701. [Google Scholar] [CrossRef] [PubMed]
- Birse, M.C. Low-energy theorem for a composite particle in mean scalar and vector fields. Phys. Rev. C 1995, 51, R1083–R1085. [Google Scholar] [CrossRef] [PubMed]
- Wallace, S.J.; Gross, F.; Tjon, J.A. Low-energy theorem for scalar and vector interactions of a composite spin 1/2 system. Phys. Rev. Lett. 1995, 74, 228–230. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Thomas, A.W.; Tsushima, K. Binding of hypernuclei in the latest quark-meson coupling model. Nucl. Phys. A 2008, 814, 66–73. [Google Scholar] [CrossRef][Green Version]
- Noro, K.; Bentz, W.; Cloët, I.C.; Kitabayashi, T. Composite octet baryons in a relativistic mean field description of nuclear and neutron star matter. Phys. Rev. C 2024, 109, 025205. [Google Scholar] [CrossRef]
- Panda, P.K.; Bracco, M.E.; Chiapparini, M.; Conte, E.; Krein, G. Excluded volume effects in the quark meson coupling model. Phys. Rev. C 2002, 65, 065206. [Google Scholar] [CrossRef]
- Carrillo-Serrano, M.E.; Bentz, W.; Cloët, I.C.; Thomas, A.W. Baryon Octet Electromagnetic Form Factors in a confining NJL model. Phys. Lett. 2016, B759, 178–183. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F.; Schulze, H.J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801. [Google Scholar] [CrossRef]
- Lu, D.H.; Thomas, A.W.; Tsushima, K.; Williams, A.G.; Saito, K. In-medium electron-nucleon scattering. Phys. Lett. B 1998, 417, 217–223. [Google Scholar] [CrossRef]
- Negele, J.; Orland, H. Quantum Many-particle Systems; Westview Press: Boulder, CO, USA, 1998. [Google Scholar]
- Shankar, R. Renormalization group approach to interacting fermions. Rev. Mod. Phys. 1994, 66, 129–192. [Google Scholar] [CrossRef]
- Osipov, A.A.; Hiller, B.; Blin, A.H.; da Providencia, J. Effects of eight-quark interactions on the hadronic vacuum and mass spectra of light mesons. Ann. Phys. 2007, 322, 2021–2054. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Hellstern, G.; Alkofer, R.; Reinhardt, H. Diquark confinement in an extended NJL model. Nucl. Phys. 1997, A625, 697–712. [Google Scholar] [CrossRef]
- Kneur, J.L.; Neveu, A. from Renormalization Group Optimized Perturbation. Phys. Rev. D 2012, 85, 014005. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J.; Reed, B. Insights into nuclear saturation density from parity violating electron scattering. Phys. Rev. C 2020, 102, 044321. [Google Scholar] [CrossRef]
- Wang, N.; Liu, M.; Wu, X.; Meng, J. Surface diffuseness correction in global mass formula. Phys. Lett. B 2014, 734, 215–219. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.; Patrignani, C.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Carrillo-Serrano, M.E.; Cloët, I.C.; Thomas, A.W. SU(3)-flavor breaking in octet baryon masses and axial couplings. Phys. Rev. C 2014, 90, 064316. [Google Scholar] [CrossRef]
- Yang, M.; Wang, P. Electromagnetic form factors of octet baryons with the nonlocal chiral effective theory. Phys. Rev. D 2020, 102, 056024. [Google Scholar] [CrossRef]
- Ulrych, S.; Muther, H. Relativistic structure of the nucleon selfenergy in asymmetric nuclei. Phys. Rev. C 1997, 56, 1788–1794. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Rather, I.A.; Usmani, A.A.; Patra, S.K. Effect of Inner Crust EoS on Neutron star properties. Nucl. Phys. A 2021, 1010, 122189. [Google Scholar] [CrossRef]
- Lastowiecki, R.; Blaschke, D.; Grigorian, H.; Typel, S. Strangeness in the cores of neutron stars. Acta Phys. Polon. Supp. 2012, 5, 535–540. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).