Impact of Stochastic Atmospheric Density on Satellite Orbit Stability
Abstract
1. Introduction
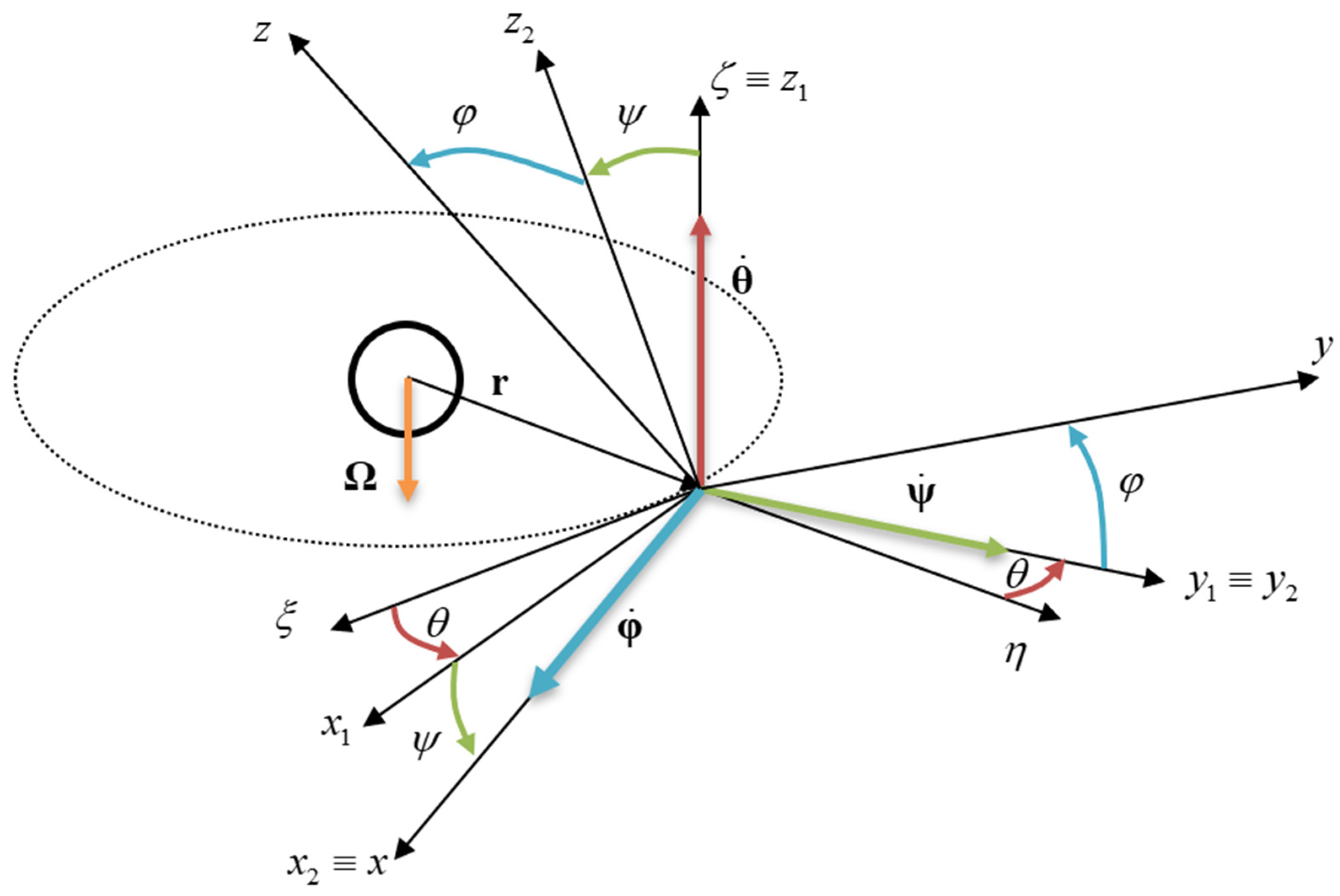
2. Short Review of the Mechanical Aspects of the Satellite
- Reference system Ox1y1z1 is obtained by rotating Oξηζ around axis Oζ with the angular displacement θ.
- Reference system Ox2y2z2 is obtained by further rotating Ox1y1z1 around Oy1 with the angular displacement ψ.
- Principal reference system Oxyz is obtained by rotating Ox2 around with the angular displacement φ; the final axis Ox is the symmetry axis of the satellite.
3. Stochastic Numerical Methods
- -
- Strong convergence:
- -
- Weak convergence:
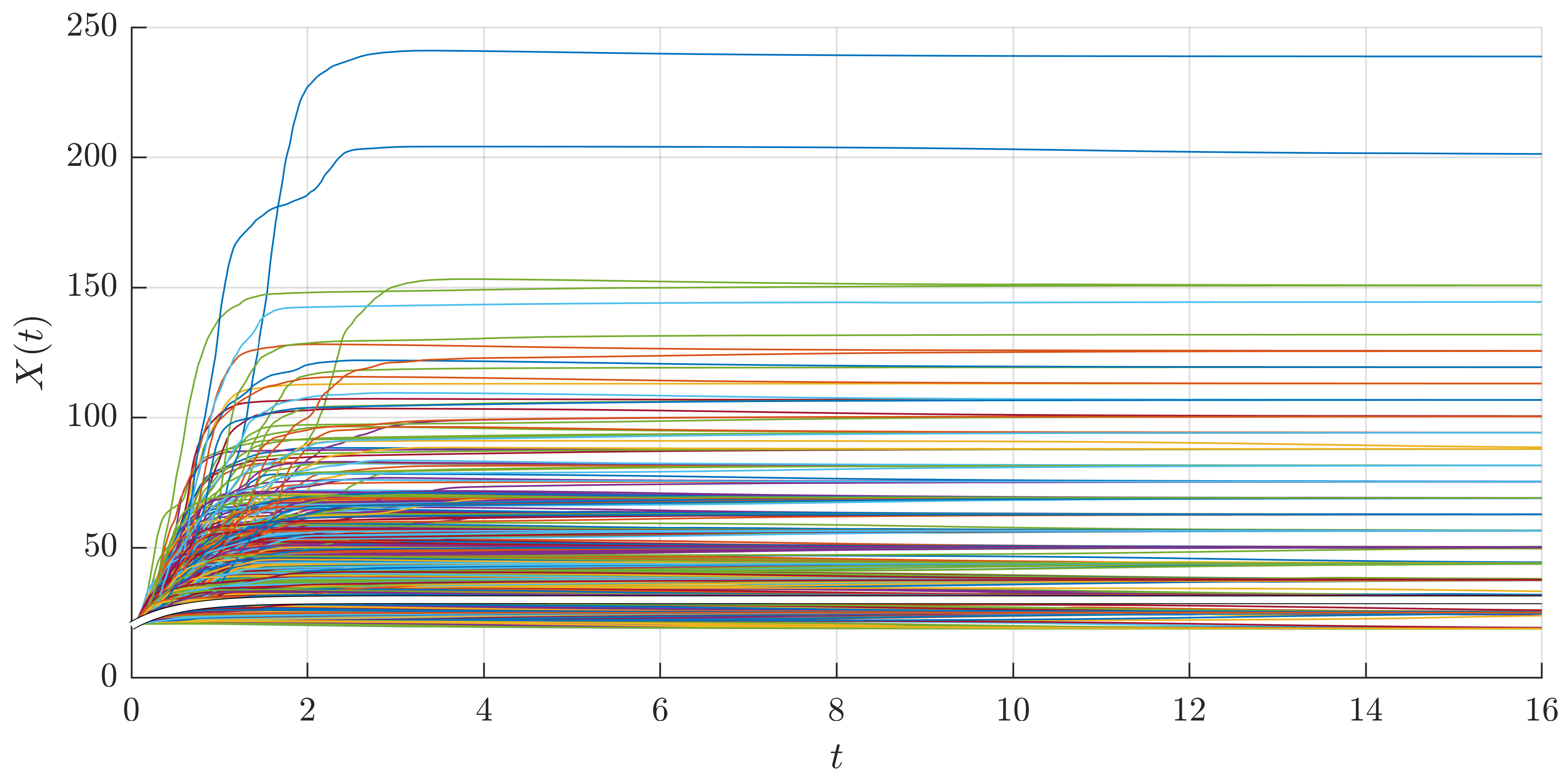
4. Numerical Simulations
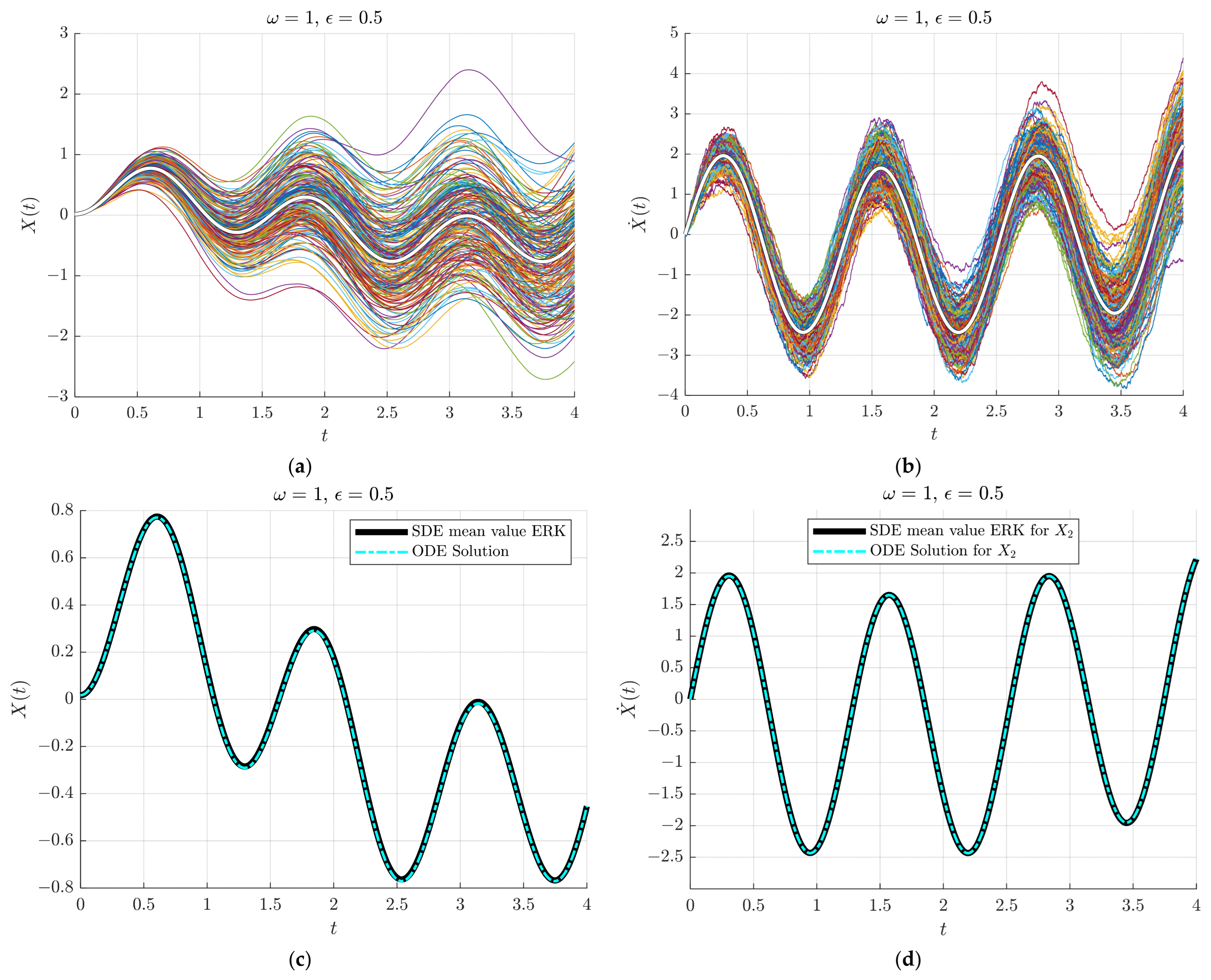
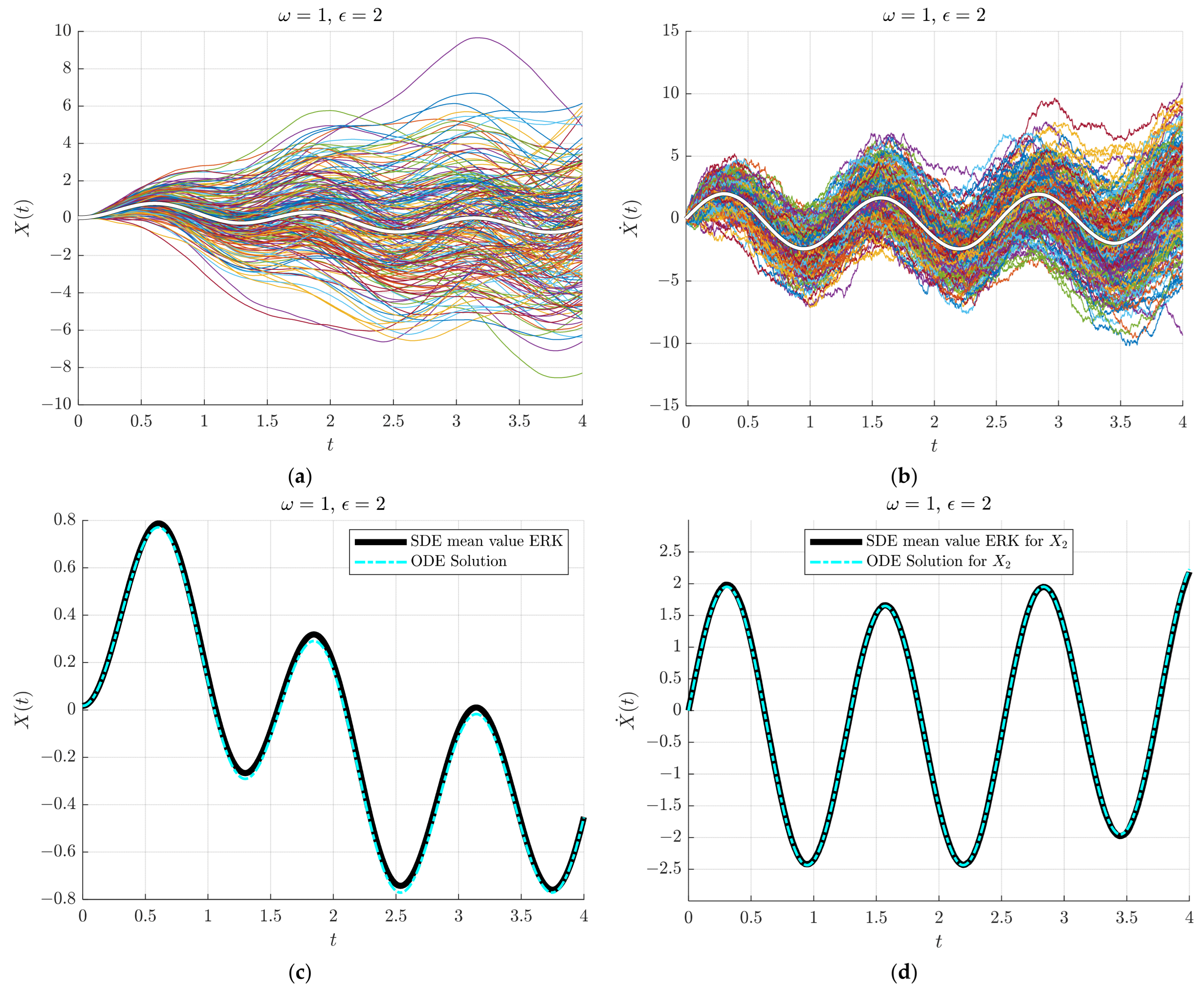
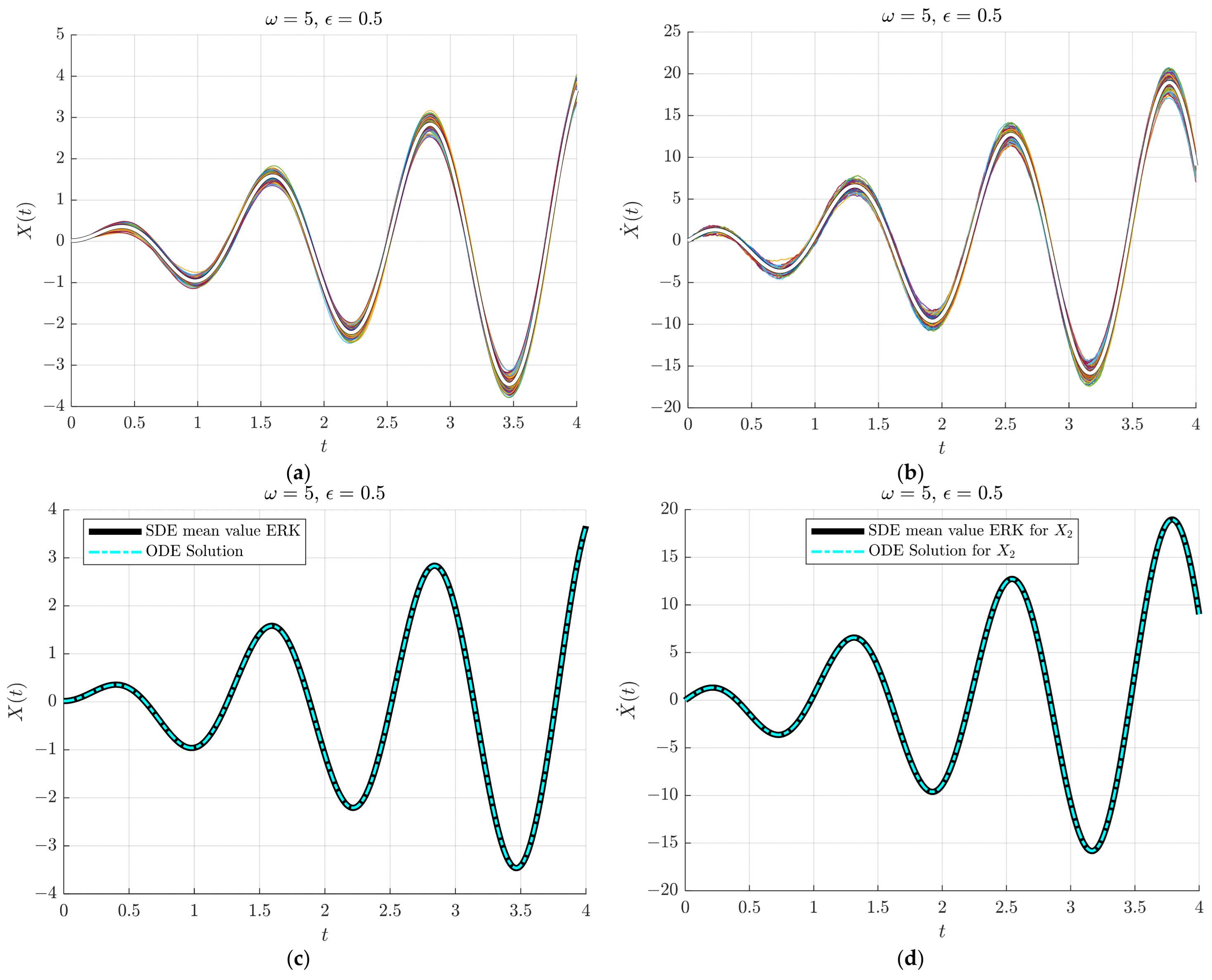
4.1. Test 1. The SDE of a Forced Undamped Oscillator with Exterior Stochastic Disturbance
- A.
- Non-resonant case .
- B.
- Resonant case .
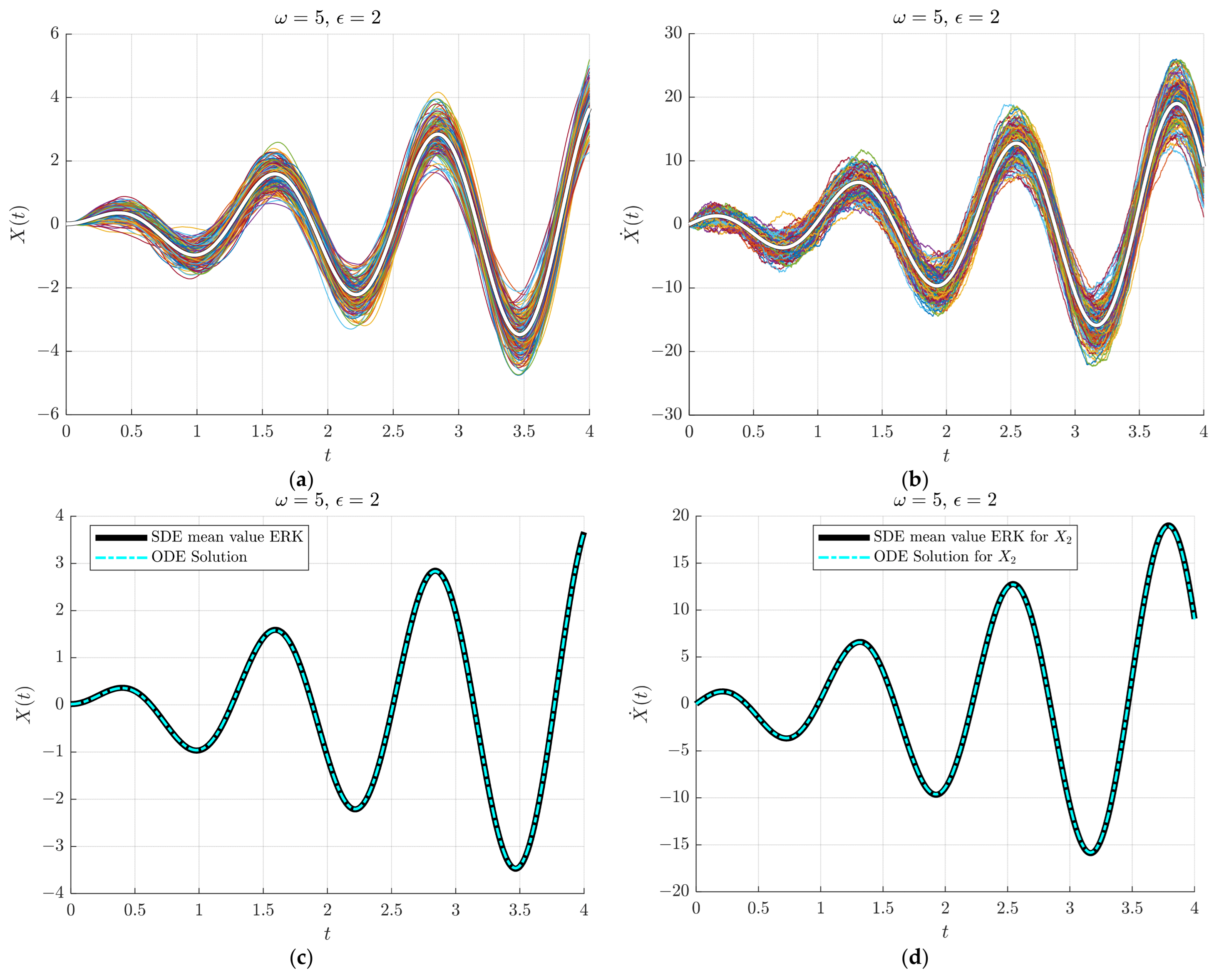
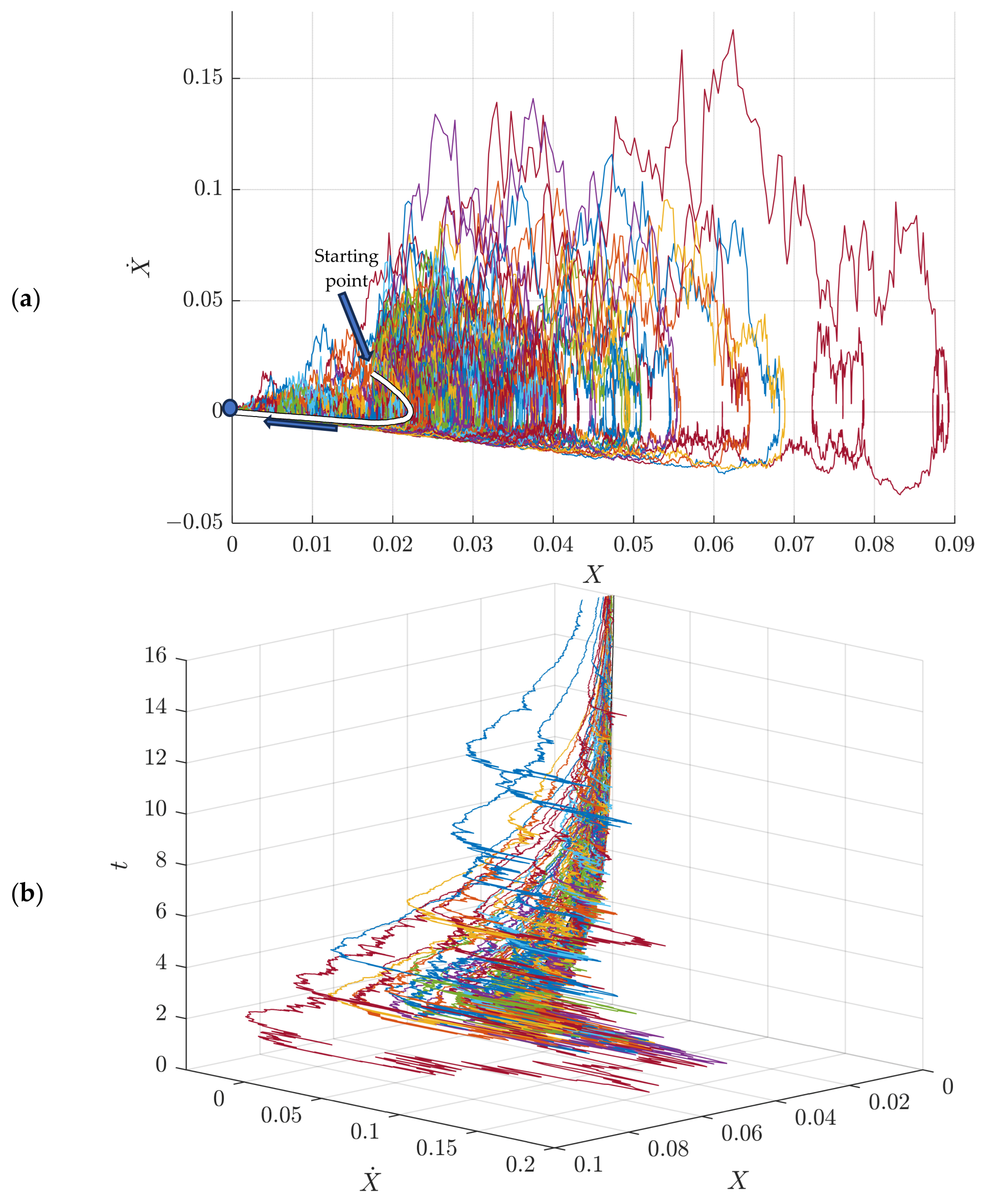
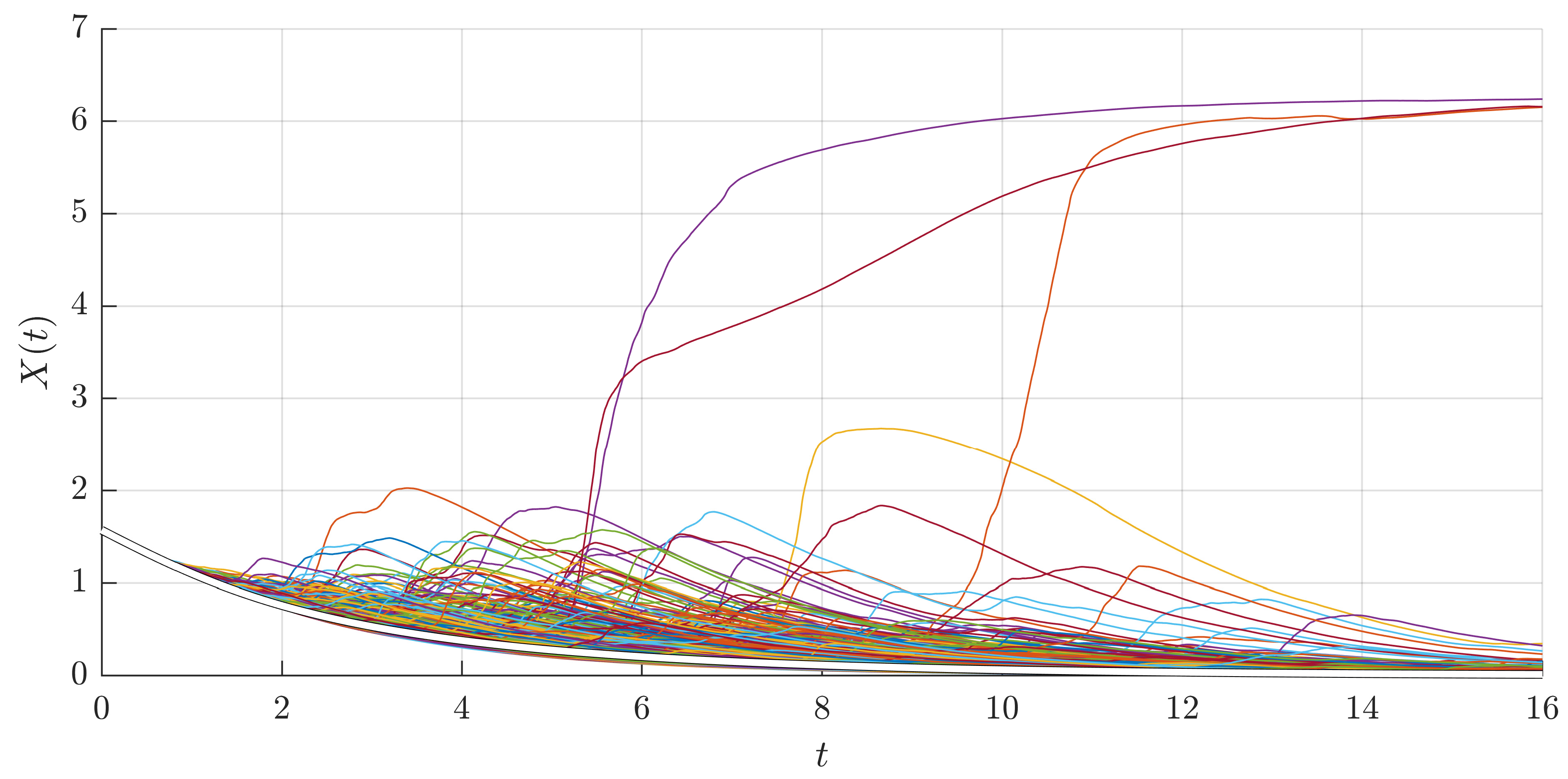
4.2. The Dimensionless SDE of the Pitch Angle of the Satellite
4.2.1. Case 1
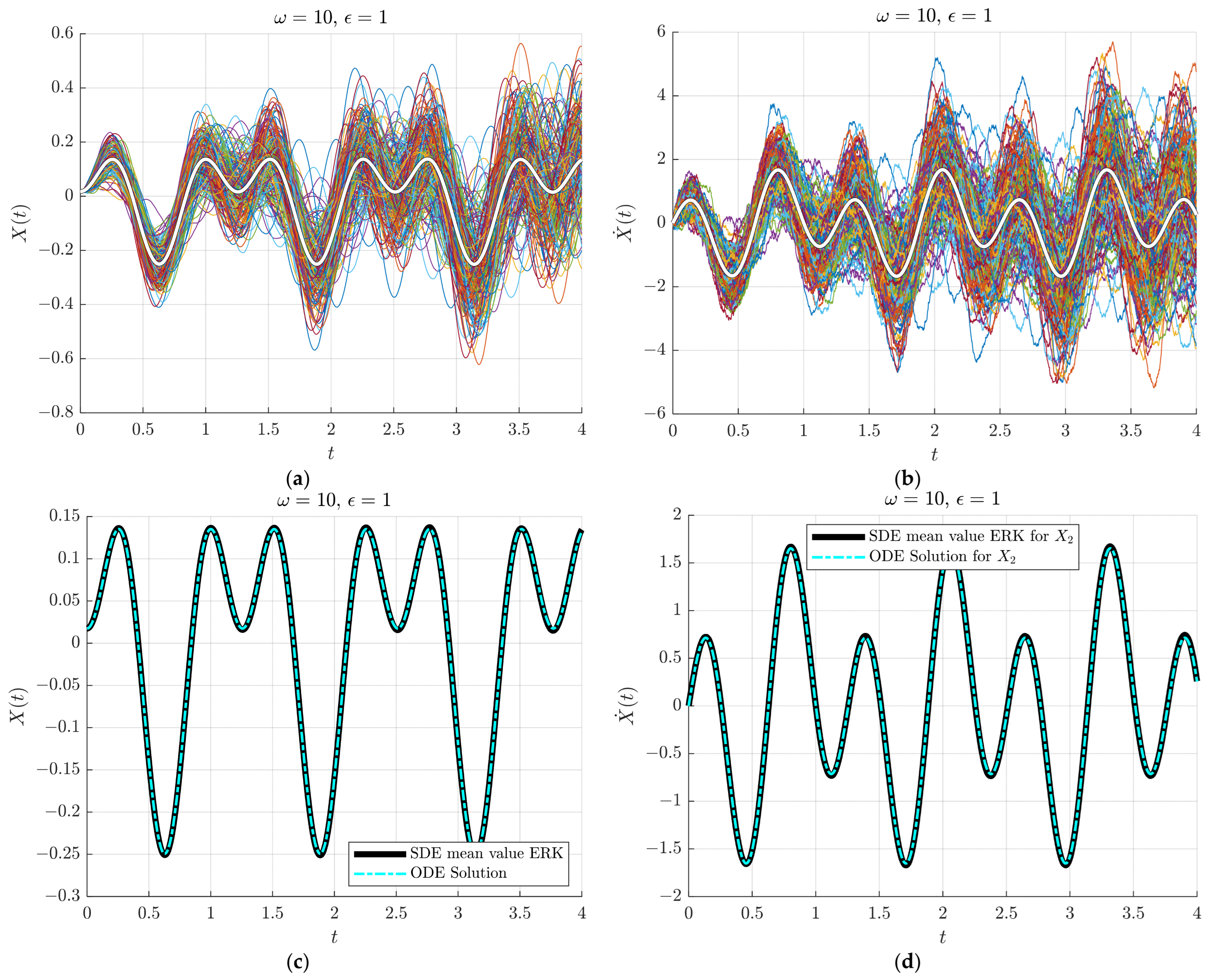
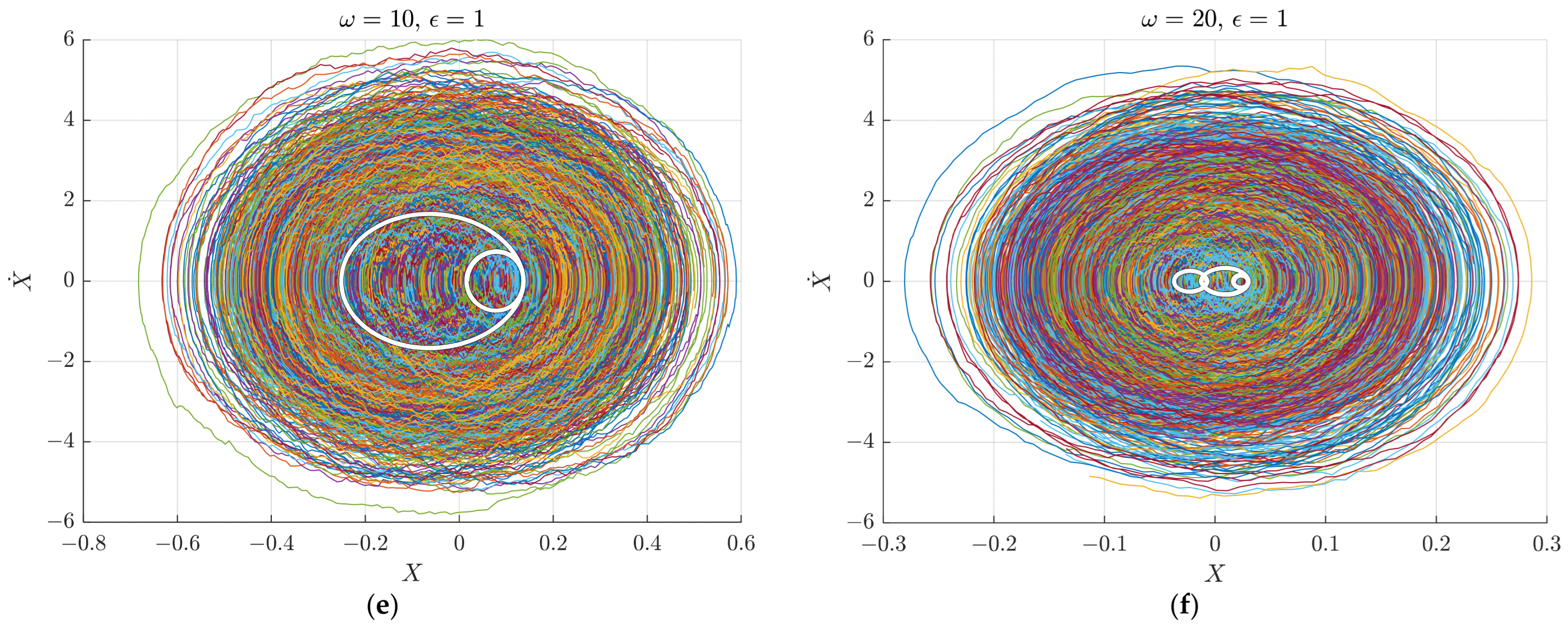
4.2.2. Case 2
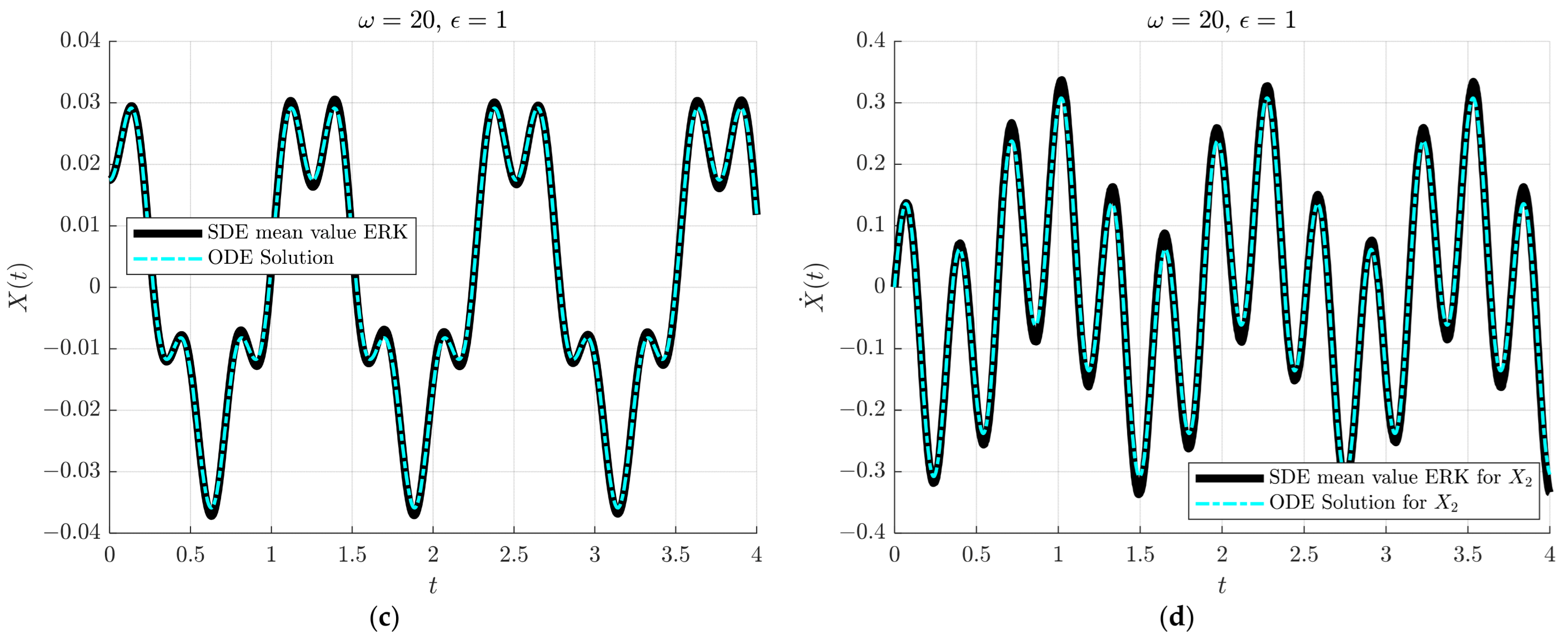
4.2.3. Case 3
4.2.4. Case 4
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sagirow, P. (Ed.) Stochastic Dynamical Systems. In Stochastic Methods in the Dynamics of Satellites: Course Held at the Department for General Mechanics; Springer: Vienna, Austria, 1970; pp. 8–47. [Google Scholar] [CrossRef]
- Beletskii, V.V. Motion of an Artificial Satellite About Its Center of Mass. In Mechanics of Space Flight; Israel Program for Scientific Translation: Jerusalem, Israel, 1966. [Google Scholar]
- Toral, R.; Colet, P. Introduction to Stochastic Processes. In Stochastic Numerical Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 167–190. [Google Scholar] [CrossRef]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Society: Providence, RI, USA, 2012; ISBN 1470410540. [Google Scholar]
- Itô, K. Stochastic integral. Proc. Jpn. Acad. Ser. Math. Sci. 1944, 20, 519–524. [Google Scholar] [CrossRef]
- Capasso, V.; Bakstein, D. An introduction to continuous-time stochastic processes: Theory, models, and applications to finance, biology, and medicine. In Modeling and Simulation in Science, Engineering and Technology; Birkhäuser: Boston, MA, USA; Basel, Switzerland; Berlin, Germany, 2005. [Google Scholar]
- Dupačová, J.; Hurt, J.; Štěpán, J. Stochastic modeling in economics and finance. In Applied Optimization; No. 75; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; New York, NY, USA; London, UK; Moscow, Russia, 2002. [Google Scholar]
- Andersson, H.; Britton, T. Stochastic epidemic models and their statistical analysis. In Lecture Notes in Statistics; No. 151; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Voinea, R.; Stroe, I.V.; Predoi, M.V. Technical Mechanics; Politehnica Press: Bucureşti, Romania, 2010. [Google Scholar]
- Rao, A.V. Dynamics of Particles and Rigid Bodies: A Systematic Approach; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2006. [Google Scholar]
- Bogoi, A.; Dănăilă, S.; Isvoranu, D. Ecuații Generale de Transport ale Dinamicii Fluidelor; Monitorul Official: București, Romania, 2021. [Google Scholar]
- Gillies, G.T. The Newtonian gravitational constant: Recent measurements and related studies. Rep. Prog. Phys. 1997, 60, 151–225. [Google Scholar] [CrossRef]
- Li, Q.; Xue, C.; Liu, J.-P.; Wu, J.-F.; Yang, S.-Q.; Shao, C.-G.; Quan, L.-D.; Tan, W.-H.; Tu, L.-C.; Liu, Q.; et al. Measurements of the gravitational constant using two independent methods. Nature 2018, 560, 582–588. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley Series in Physics; Addison-Wesley: Reading, MA, USA; Menlo Park, CA, USA; London, UK, 1981. [Google Scholar]
- Schrello, D.M. Dynamic Stability of Aerodynamically Responsive Satellites. J. Aerosp. Sci. 1962, 29, 1145–1155. [Google Scholar] [CrossRef]
- Sheporaitis, L.P. Stochastic stability of a satellite influenced by aerodynamic and gravity gradient torques. AIAA J. 1971, 9, 218–222. [Google Scholar] [CrossRef]
- Mostaza-Prieto, D. Characterisation and Applications of Aerodynamic Torques on Satellites. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2017. [Google Scholar]
- Kutiev, I.; Tsagouri, I.; Perrone, L.; Pancheva, D.; Mukhtarov, P.; Mikhailov, A.; Lastovicka, J.; Jakowski, N.; Buresova, D.; Blanch, E.; et al. Solar activity impact on the Earth’s upper atmosphere. J. Space Weather Space Clim. 2013, 3, A06. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar] [CrossRef]
- Durrett, R. Probability: Theory and Examples, 5th ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Mörters, P.; Peres, Y.; Schramm, O.; Werner, W. Brownian motion. In Cambridge Series in Statistical and Probabilistic Mathematics; No. 30; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bogoi, A.; Dan, C.-I.; Strătilă, S.; Cican, G.; Crunteanu, D.-E. Assessment of Stochastic Numerical Schemes for Stochastic Differential Equations with “White Noise” Using Ito’s Integral’. Symmetry 2023, 15, 2038. [Google Scholar] [CrossRef]
- Saito, Y.; Mitsui, T. Stability Analysis of Numerical Schemes for Stochastic Differential Equations. SIAM J. Numer. Anal. 1996, 33, 2254–2267. [Google Scholar] [CrossRef]
- Milʹshteĭn, G.N. Numerical Integration of Stochastic Differential Equations; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Saito, Y.; Mitsui, T. Discrete approximations for stochastic differential equations. Trans. Jpn. SIAM 1992, 746, 1–16. [Google Scholar]
- Bogoi, A.; Cican, G.; Daniel-Eugeniu, C. Fundamentals of Acoustics; Lecture Notes for Engineers; Editura Monitorul Official: Bucureşti, Romania, 2024. [Google Scholar]
- Bacalu, I.; Şerbănescu, C. Ecuaţii Diferenţiale: Culegere de Probleme: Compendiu; Printech: Bucureşti, Romania, 2013. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 8th ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Leipholz, H. Stability Theory, 2nd ed.; Vieweg+Teubner Verlag: Weisbaden, Germany, 1987. [Google Scholar]
- Tunç, O.; Tunç, C. On the asymptotic stability of solutions of stochastic differential delay equations of second order. J. Taibah Univ. Sci. 2019, 13, 875–882. [Google Scholar] [CrossRef]
- Zouine, A.; Imzegouan, C.; Bouzahir, H.; Tunç, C. General decay stability of nonlinear delayed hybrid stochastic system with switched noises. Appl. Set-Valued Anal. Optim. 2024, 6, 157–177. [Google Scholar] [CrossRef]




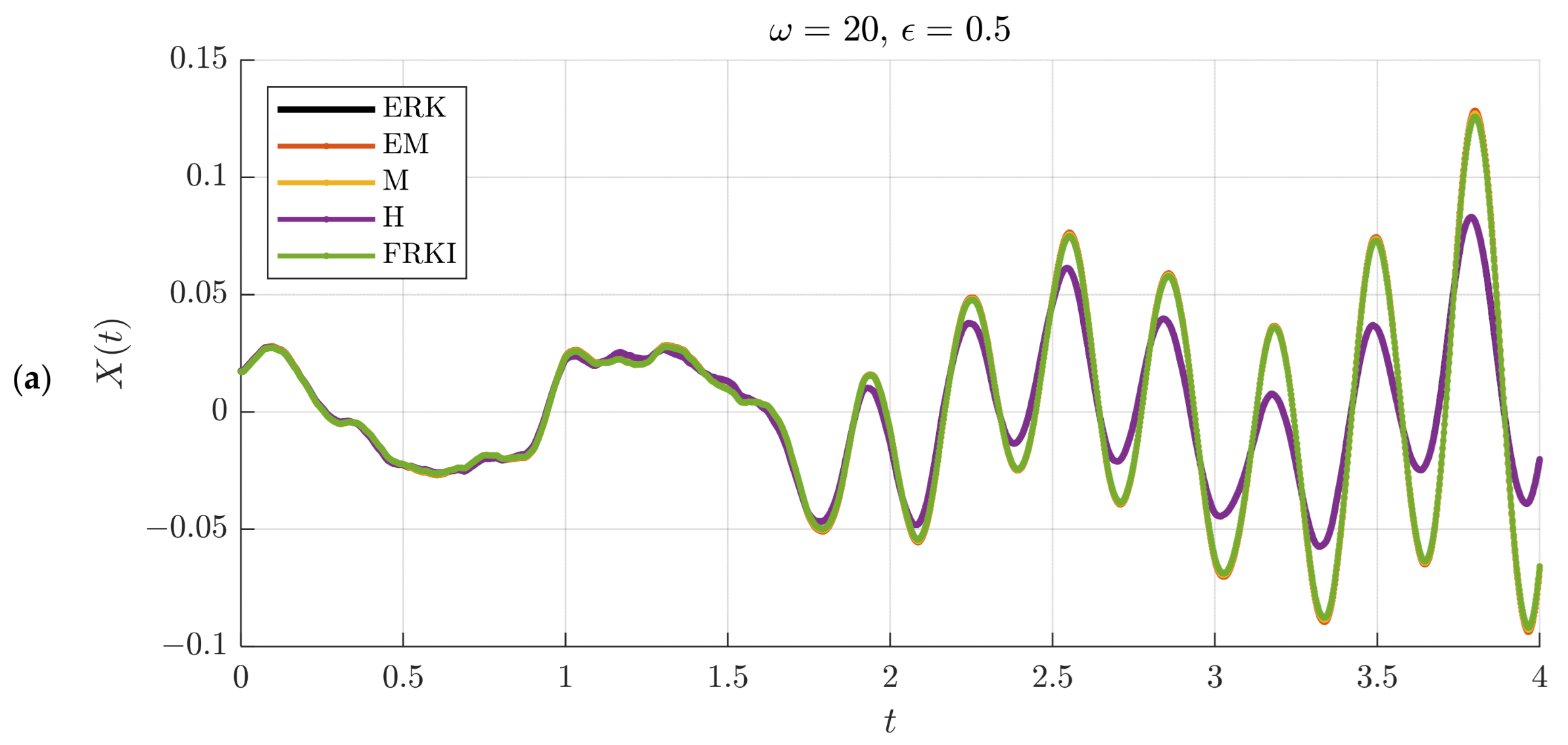
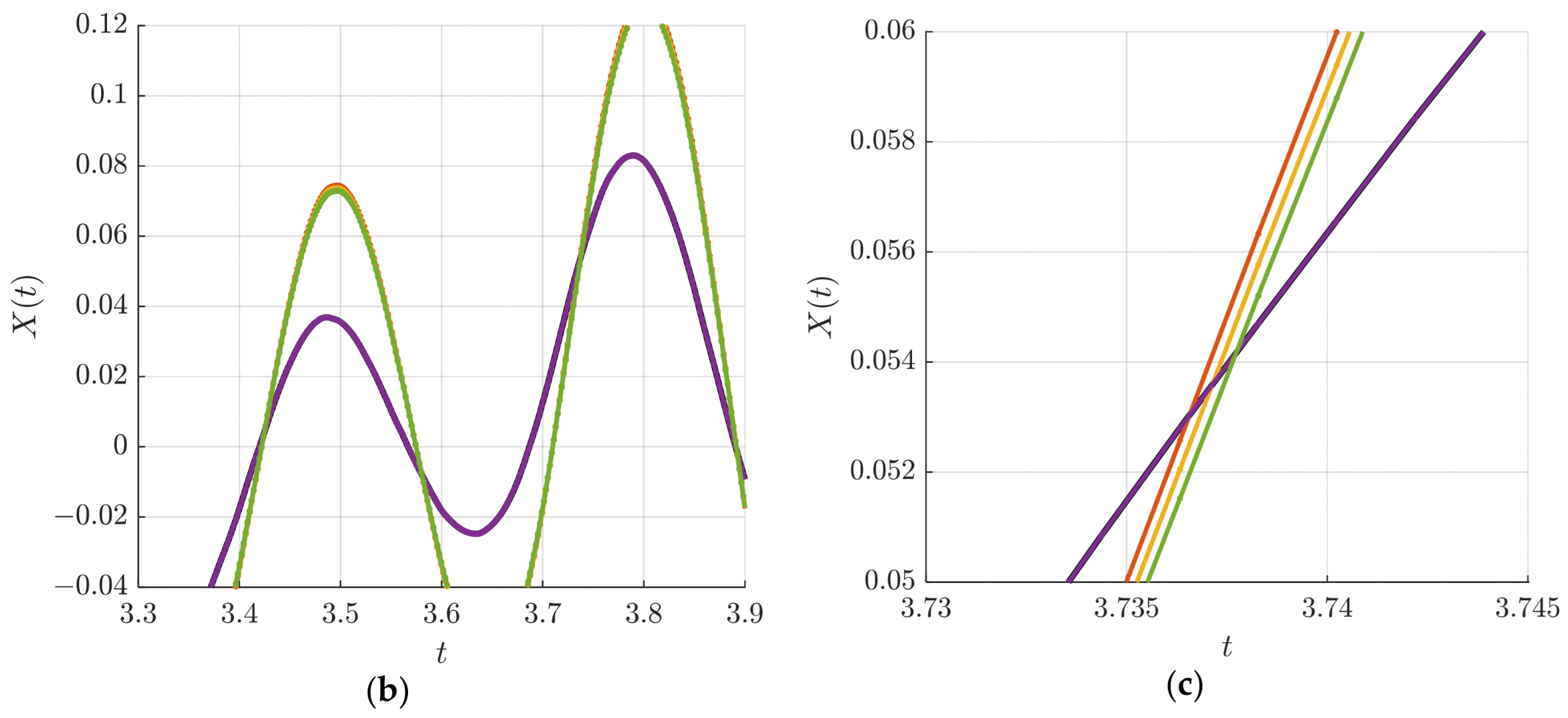


| Name of the Scheme | Additive Noise | Multiplicative Noise | ||
|---|---|---|---|---|
| Weak Order | Strong Order | Weak Order | Strong Order | |
| Euler–Maruyama | 1 | 1 | 1 | 0.5 |
| Milshtein | 1 | 1 | 1 | 1 |
| Stochastic Heun | 2 | 2 | 1 | 1 |
| FRKI | 1 | 1 | 1 | 1 |
| ERK | 1 | 1 | 1.5 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogoi, A.; Strătilă, S.; Cican, G.; Crunțeanu, D.-E.; Levențiu, C. Impact of Stochastic Atmospheric Density on Satellite Orbit Stability. Symmetry 2025, 17, 402. https://doi.org/10.3390/sym17030402
Bogoi A, Strătilă S, Cican G, Crunțeanu D-E, Levențiu C. Impact of Stochastic Atmospheric Density on Satellite Orbit Stability. Symmetry. 2025; 17(3):402. https://doi.org/10.3390/sym17030402
Chicago/Turabian StyleBogoi, Alina, Sergiu Strătilă, Grigore Cican, Daniel-Eugeniu Crunțeanu, and Constatin Levențiu. 2025. "Impact of Stochastic Atmospheric Density on Satellite Orbit Stability" Symmetry 17, no. 3: 402. https://doi.org/10.3390/sym17030402
APA StyleBogoi, A., Strătilă, S., Cican, G., Crunțeanu, D.-E., & Levențiu, C. (2025). Impact of Stochastic Atmospheric Density on Satellite Orbit Stability. Symmetry, 17(3), 402. https://doi.org/10.3390/sym17030402






