Integrated Scheduling Algorithm for No-Wait Network Flexible Based on Idle-Time Optimization and Process Rescheduling

Abstract

To address the integrated scheduling problem involving no-wait constraints between processes in the actual production of complex products with both symmetric and asymmetric branches, and the need for cross-workshop equipment network collaboration and equipment flexibility, a no-wait network flexible integrated scheduling algorithm based on idle-time optimization and process rescheduling is proposed (ITPR-NFIS). Based on the concepts of non-terminal flexible process groups, terminal flexible process groups, and virtual no-wait flexible process groups, the algorithm first determines the scheduling sequence for non-terminal flexible process groups and virtual no-wait flexible process groups using the reverse layer priority strategy and the average reverse subsequent path strategy. Then, the no-wait earliest completion strategy, the optimal completion-semi-idle triggered insertion rescheduling strategy, and the optimal completion-full-idle adaptive insertion scheduling strategy are proposed to determine the processing machine and processing time for the target process. Finally, for terminal flexible process groups, the scheduling sequence is determined based on the completion time of their reverse preceding process, and the processing machine and processing time of the terminal flexible process groups are determined by the no-wait earliest completion strategy and the optimal completion-full-idle adaptive insertion scheduling strategy. The example shows that the algorithm can effectively solve the integrated scheduling problem with no-wait constraints in cross-workshop equipment networks, whether applied to symmetric, asymmetric, or mixed-structure complex products. It significantly reduces the total processing time and enhances production efficiency.

1. Introduction

With the rise of Industry 4.0, the progress of science and technology, and the transformation of consumers’ concepts, people have more and more demands for products with multiple varieties and small batches. In order to meet the demand of today’s society for multi-variety and small batch products, unlike job shop scheduling [1,2,3,4] and flow shop scheduling [5,6,7,8], which process and assemble separately, Xie et al. proposed the third type of product manufacturing mode, namely an integrated scheduling mode that processes and assembles products together [9,10,11,12,13,14,15,16]. In recent years, with the development of processing technology, flexible manufacturing has become an important trend in the development of the manufacturing industry. The processing machine for processes in flexible manufacturing is flexible, which is more in line with actual production requirements. Research on flexible manufacturing scheduling problems has been increasing, and many experts and scholars have achieved certain results. To address the problem, forward scheduling of the flexible integrated scheduling algorithm needs to consider the constraints of the multiple tight previous processes of the target process, which makes it difficult to reasonably arrange the relevant processes, thus affecting the product completion time. Xie et al. [17] proposed a flexible machine-network-integrated scheduling algorithm that considers the same layer after process, in response to the problem of difficult selection of processing equipment and related processes that affect product completion time in flexible device network integrated scheduling algorithms. Li et al. [18] proposed an improved dueling double deep Q-network algorithm to solve the flexible integrated scheduling problem under random working hours. Yang et al. [19] proposed a flexible integrated scheduling algorithm with a bidirectional coordination mechanism to solve the problem that the flexible integrated scheduling algorithm ignores the bidirectional selection relationship between machine and process. The machine-process coordination mechanism designed in this algorithm can allocate the choice between machine and processes based on the actual scheduling status at the driving moment and adopt the optimal combination strategy to resolve conflicts when they arise. Gui et al. [20] proposed a flexible integrated scheduling algorithm for reverse-scheduling processes. In response to the fact that most existing flexible integrated scheduling algorithms forward schedule processes and select processing equipment for processes based on short-term strategies, forward scheduling needs to consider the possibility of multiple preceding processes of the process causing serial processing of the same equipment process and prolonging product completion time. Xie et al. [21] proposed a flexible integrated scheduling algorithm based on reverse layer priority to solve the problem. Considering the previous flexible integrated scheduling algorithms that consider forward scheduling, it is necessary to consider the predecessors’ multiple constraints of the target operation, which makes it difficult to rationally arrange the relevant operations and affects the product completion time. Zhou et al. [22] proposed an integrated scheduling algorithm that considers the processing capability of flexible equipment in response to the lack of consideration for the collaborative processing capability of equipment systems in existing flexible integrated scheduling research, which reduces the high-density and fast processing capabilities of equipment systems. Although the above methods have effectively solved problems related to the integrated scheduling of flexible machines, none of them consider the no-wait constraints between processes.

In the actual production of complex products, when the start time of the subsequent process is required to be the same as the end time of the previous process, it indicates that there are no-wait constraints between processes. The most common example in actual production is mixing and batching in the chemical industry. Once a certain batching is processed, it must immediately enter the next process, and there should be no time gap between processes to prevent the deterioration of the chemical batching [23]. At present, the no-wait integrated scheduling problem is divided into two categories: no-wait with a single preceding process and no-wait with non-single preceding processes. Guo et al. [24] proposed a no-wait constraint integrated scheduling algorithm for complex products based on design structure matrix and genetic algorithm. This algorithm—the integrated scheduling algorithm of complex products with no-wait constraint based on virtual component—solves the non-flexible integrated scheduling problem involving no-wait constraints between processes in the actual production of complex products. To address the scheduling problem of complex products with no-wait constraints between processes in actual production, Xie et al. [25] proposed a study on the complex product scheduling problem with no-wait constraint between operations (O-NPS). The method involves virtualizing the processes with no-wait constraints into a single process and using the mobile exchange algorithm to separate and schedule the virtual process on the corresponding machine, thereby solving the non-flexible no-wait constrained integrated scheduling problem for complex products. However, this research only considered the scenario of a single preceding tight connection where no-wait exists between two processes. Xie et al. [26] proposed the integrated scheduling algorithm with no-wait constraint operation group (OG-NIS). This method introduced the concept of a no-wait process group, prioritizing the scheduling of processes within the no-wait process group and the immediately preceding processes of the process group. The process groups with the no-wait constraint are uniformly linked using the process-group-first-adaptation scheduling algorithm, and the standard processes are scheduled according to the quasi-critical path method. This achieves optimization for the non-flexible integrated scheduling of complex products with no-wait constraints between processes. Nevertheless, it ignores the significant impact of processes on long paths on scheduling results. Guo et al. [27] proposed an integrated scheduling algorithm of complex products with a no-wait constraint based on reversed virtual components. This algorithm uses a genetic algorithm based on reverse virtual components to solve the non-flexible integrated scheduling problem of complex products with no-wait constraints. In view of the situation that the no-wait scheduling algorithm in the previous integrated scheduling could only handle a single preceding process, which made the algorithm limited. Xie et al. [28] proposed a no-wait integrated scheduling algorithm based on reversed order signal-driven (ROSD-NIS). This algorithm achieved solutions for non-flexible no-wait-constrained complex product integrated scheduling problems, which did not consider the demand for flexible scheduling in actual production. Xie et al. [29] proposed the integrated flexible scheduling algorithm of complex products with no-wait constraint between procedures (P-NIFS), which combines processes with no-wait constraints and their preceding processes into a virtual node set but fails to consider the idle time on the machine. Although these studies have considered no-wait constraints, most of the current research focuses on non-flexible integrated scheduling problems and does not consider the demand for machine flexibility in actual production.

To summarize, the shortcomings of the current research are as follows: First, most studies only focus on a single aspect of flexible machine-integrated scheduling or no-wait integrated scheduling. They rarely consider the two key factors of machine flexibility and no-wait constraints simultaneously, which cannot meet the comprehensive needs of machine flexibility and tight connection constraints between processes in actual production. Second, although a few studies have considered both machine flexibility and no-wait constraints, they have not optimized machine idle time, making it difficult to improve scheduling efficiency. This paper considers both machine flexibility and no-wait constraints and optimizes machine idle time. Based on the existing research on integrated scheduling problems considering no-wait constraints, this paper proposes an integrated scheduling algorithm for the no-wait flexible network based on idle-time optimization and process rescheduling (ITPR-NFIS). This algorithm proposes concepts such as non-terminal flexible process groups, terminal flexible process groups, and virtual no-wait flexible process groups. It prioritizes the use of the reverse layer priority strategy, average reverse subsequent path strategy, no-wait earliest completion strategy, optimal completion-semi-idle triggered insertion rescheduling strategy, and optimal completion-full-idle adaptive insertion scheduling strategy to determine the processing machine and processing time for non-terminal flexible process groups and virtual no-wait flexible process groups. This algorithm achieves effective utilization of idle time. Finally, for terminal flexible process groups, the scheduling sequence is determined based on the completion time of their reverse preceding processes, and the processing machine and processing time of the terminal flexible processes are determined by the no-wait earliest completion strategy and the optimal completion-full-idle adaptive insertion scheduling strategy. The optimization effect of the algorithm is verified through a case study. For clarity, the algorithm abbreviations and their full names used in this study are provided in

Table 1. Abbreviations–full names correspondence table.

Abbreviation	Full Name
O-NPS	Study on the complex product scheduling problem with no-wait constraint between operations
OG-NIS	Integrated scheduling algorithm with no-wait constraint operation group
ROSD-NIS	No-wait integrated scheduling algorithm based on reversed order signal-driven
P-NIFS	The integrated flexible scheduling algorithm of complex products with no-wait constraint between procedures
ITPR-NFIS	Integrated scheduling algorithm for no-wait network flexible based on idle-time optimization and process rescheduling

.

2. Problem Description and Mathematical Model

2.1. Problem Description

In the network flexible integrated scheduling algorithm with no-wait constraints, the layout of the machine network is known, the workpiece processes are known, and the constraint relationships between processes cannot be changed. The processing time of each process of each workpiece on different processing machines is known. In network flexible integrated scheduling, the processing procedures of complex products with both symmetric and asymmetric branches present a tree-like structure, which is called the product processing process tree, and the directed edges between procedures represent the partial order relationship of product processing. The processing and assembly of the process are unified as processing. The processing machine and assembly machine in the machine network are unified as processing machine. The network flexible integrated scheduling considering no-wait constraints meets the following requirements:

(1)

The processing machine in the machine network can only process one process at a time.

(2)

Each process can only be processed by one processing machine, and once a process starts, it cannot be interrupted.

(3)

Each process can only start processing after all its preceding procedures have been completed. For processes with no-wait constraints, the completion time of the preceding process is the start time of this process.

(4)

There are no identical machines in the machine network, and the processing machine is in a discrete distribution state. To simplify the model and emphasize the optimization of process sequencing and machine idle time, the transportation time between processing machines is not considered in this model. This assumption is reasonable in scenarios where the machine layout is extremely compact or transportation time is much shorter than processing time.

(5)

The completion time of the last process of the product is the total processing time of the product.

To simplify the network flexible integrated scheduling problem with no-wait constraints between processes, an analysis of the constraints in the production process of complex products with no-wait processes is conducted. The definitions are as follows:

Definition 1. 

Reverse virtual flexible processing process tree: In the processing flow of complex products, a tree structure is formed by reversing the directed edges of the processing process tree based on the processing process constraints between non-terminal flexible process groups, terminal flexible process groups, and virtual no-wait flexible process groups.

Definition 2. 

Reverse preceding process: In the reverse virtual flexible processing process tree, the subsequent process of a certain process in the original processing process tree becomes the preceding process of this process, which is called a reverse preceding process.

Definition 3. 

Reverse subsequent process: In the reverse virtual flexible processing process tree, the preceding process of a certain process in the original processing process tree becomes the subsequent process of this process, which is called a reverse subsequent process.

Definition 4. 

Non-terminal flexible process group: In the reverse virtual flexible processing process tree, a process that has reverse subsequent processes and no no-wait constraints is called a non-terminal flexible process group.

Definition 5. 

Terminal flexible process group: In the reverse virtual flexible processing process tree, a process that has no no-wait constraints and no reverse subsequent processes is called a terminal flexible process group.

Definition 6. 

Virtual no-wait flexible process group: Virtualize flexible processes with no-wait constraints between processes into a process group. Although there are no-wait flexible processes that are virtualized as a process group, these processes are still processed on the original machine, but there is no time interval between processes.

Definition 7. 

Idle start time: The starting point of the idle time from the completion of the previous process by the processing machine to the actual start of the next process is called the idle start time.

Definition 8. 

Idle end time: The time point at which a processing machine ends its idle time and starts the next process after completing the previous process, known as the idle end time.

Definition 9. 

Effective start time: The maximum value of the idle start time and the completion time of all the reverse preceding processes is called the effective start time of the process.

Definition 10. 

Effective Idle time: The remaining time from the effective start time to the idle end time of the process is obtained by subtracting the effective start time from the idle end time, which is called the effective idle time.

2.2. Mathematical Model

The mathematical symbols and their definitions in the constructed mathematical model of the network flexible integrated scheduling problem are shown in

Table 2. Definition of mathematical symbols.

Symbol	Definition
n	total number of processes
m	total number of processing machines
Ai	the i-th process of the product, i = 1, 2, …, n
Mj	the j-th device, j = 1, 2, …, m
si	start processing time of process Ai
fi	completion time of process Ai
ti	processing time of process Ai
AFTij	actual completion time of process Ai on processing machine Mj
tij	processing time of process Ai on processing machine Mj
Hij	decision variable, whether process Ai is processed on processing machine Mj

.

The objective of network flexible integrated scheduling is to minimize the maximum completion time. Therefore, the mathematical model of the network flexible integrated scheduling problem can be described as:

Objective function:

$$T=\min \left\{\max AF{T}_{ij}\right\}$$

(1)

Constraint conditions:

$${\displaystyle \sum _{j=1}^m{H}_{ij}}=1$$

(2)

$$t_i={\displaystyle \sum _{j=1}^m{H}_{ij}{t}_{ij}}$$

(3)

$$f_i=s_i+t_i$$

(4)

$$s_i\ge \max \left\{f_x\right\},x\in \mathrm{pred}(i),\min (s_i)$$

(5)

$$f_i\le \min \left\{s_y\right\},y\in \mathrm{succ}(i)$$

(6)

$$f_i\le s_i,H_{ij}=1,H_{il}=1$$

(7)

$$s_z-f_v=0,v\in pred(z)$$

(8)

Equation (1) indicates the objective function, which aims to minimize the maximum completion time. Equation (2) indicates that each process can only be processed by one processing machine. Equation (3) represents the processing time of process $A_i$. Equation (4) is the completion time of the process $A_i$. Equation (5) indicates that the start time of the process $A_i$ must be greater than or equal to the completion time of its reverse preceding process and the process $A_i$ should start processing as early as possible. $x\in \mathrm{pred}(i)$ indicates that the process $A_x$ is the reverse sequence of the preceding process $A_i$. Equation (6) indicates that the completion time of the process $A_i$ must be less than or equal to the minimum start time of its reverse subsequent process. $y\in \mathrm{succ}(i)$ indicates that the process $A_y$ is the reverse sequence of the subsequent process $A_i$. Equation (7) indicates that if the process $A_i$ and the process $A_l$ are processed on the same processing machine, the start time of the latter process must be greater than or equal to the completion time of the previous process. Equation (8) indicates that the process $A_z$ and the process $A_v$ have a no-wait relationship.

3. Strategy Analysis

When solving the network flexible integrated scheduling problem with no-wait constraints, according to the characteristics of the reverse virtual flexible processing process tree, it is known that the partial order relationship between processes must be strictly followed when scheduling each process. In addition, in the network flexible integrated scheduling problem with no-wait constraints, it is also very important to reasonably select the processing machine and determine the start time of the virtual no-wait flexible process groups. If the processing machine cannot be reasonably selected and the processing time of virtual no-wait flexible process groups cannot be determined, it will affect the product completion time. To minimize the product completion time as much as possible, this paper proposes an integrated scheduling algorithm for no-wait network flexible based on idle-time optimization and process rescheduling. First, according to the extended processing process tree [25], the flexible processes with no-wait relationships are transformed into virtual no-wait flexible process groups. The directed edges of the processing process tree are reversed to obtain a reverse virtual flexible processing process tree composed of non-terminal flexible process groups, terminal flexible process groups, and virtual tight connection flexible process groups. Then, for non-terminal flexible process groups and virtual no-wait flexible process groups, the processes are sorted, and their processing machine and processing time are determined using the reverse layer priority strategy, average reverse subsequent path strategy, no-wait earliest completion strategy, optimal completion-semi-idle triggered insertion rescheduling strategy, and optimal completion-full-idle adaptive insertion scheduling strategy. Finally, for terminal flexible process groups, the scheduling sequence is determined based on the completion time of their reverse preceding processes, and the processing machine and processing time of the terminal flexible processes are determined by the no-wait earliest completion strategy and the optimal completion-full-idle adaptive insertion scheduling strategy. Ultimately, the product scheduling scheme is generated.

3.1. Reverse Layer Priority Strategy

The reverse layer priority strategy [21] divides the reverse virtual flexible processing process tree into layers. First, the division is carried out layer by layer starting from the root node. That is, the root node is the first layer, the layer of its reverse order subsequent processes is the second layer, and so on. Then, the processes of each layer are put into the reverse-sequence layer to-be-scheduled process set. Finally, the processes of each layer are scheduled in sequence, starting from the first layer. The advantages of the reverse layer priority strategy include the following: (1) Scheduling by layer improves the parallel processing of processes in the same layer. (2) It is very easy to determine the earliest processing start time and the earliest end time of the root node. At the same time, in the reverse virtual flexible processing process tree, each process has only one reverse preceding process, which solves the problem that it is difficult to determine the processing start time of the process.

3.2. Average Reverse Subsequent Path Strategy

The average reverse subsequent path strategy [17] determines the scheduling sequence of processes within the set of processes to be scheduled in each reverse layer. The process scheduling sequence is sorted in descending order according to the average reverse subsequent path value of each process. When the average reverse subsequent path values are the same, prioritize scheduling the process with the highest number of reverse subsequent processes. If the number of reverse subsequent processes is also the same, a process is selected randomly. The average reverse subsequent path value is the sum of the maximum value of all reverse subsequent processes of the target process to the leaf node and the average processing time of the target process on flexible machines. This formula is shown in Equation (9). The advantage of the average reverse subsequent path strategy is that it improves the tightness of vertical processing processes.

$$T(A_i)=\overline{t_i}+\underset{A_j\in \mathrm{succ}(A_i)}{\max }\{T(A_j)\}$$

(9)

where $\overline{t_i}$ is the average processing time of the process on flexible machines. The process $A_j$ is the reverse subsequent process of process $A_i$. $T(A_i)$ is the average reverse subsequent path of process $A_i$.

3.3. No-Wait Earliest Completion Strategy

In the network flexible integrated scheduling problem, due to the non-uniqueness of processing machines, it is important to select a suitable processing machine for the process and shorten the completion time of the product. The ITPR-NFIS algorithm proposes the no-wait earliest completion strategy based on the HEFT algorithm [30], which determines the processing machine and processing time for the target process. Select a machine that enables the process to achieve a shorter completion time and considers that virtual no-wait flexible process group’s need to meet no-wait constraints, as well as processing machines for subsequent processes in the same layer. The no-wait earliest completion strategy selects processing machine for each process, giving priority to the machine with an earlier completion time. If the completion time of the target process is the same on different processing machines, the processing machine with the shorter processing time should be given priority. If the processing time on different processing machines is also the same, it gives priority to the processing machine that is different from the short-time machine of subsequent processes in the same layer. If the processing machine is different from the short-time machine of the subsequent processes on the same level, the processing machine will be randomly selected. The earliest completion time for tight connection is the sum of the earliest start time of the process on the corresponding machine and its processing time on the corresponding machine. Its formula is shown in Equation (10). At the same time, the process in the virtual no-wait flexible process groups needs to meet the no-wait constraint, as shown in Equation (11). The advantage of the no-wait earliest completion strategy is to ensure that the processes are fully parallel.

$$\begin{array}{l}EF{T}_{jk}=ES{T}_{jk}+t_{jk}\\ ES{T}_{jk}=\max \left\{T_{available}(M_k),\underset{A_i\in \mathrm{pred}(A_j)}{\max }\{AF{T}_{iw}\}\right\}\end{array}$$

(10)

$$AS{T}_{jk}=AF{T}_{iw}$$

(11)

where $EF{T}_{jk}$ is the earliest completion time of the process $A_j$ on the processing machine $M_k$. $ES{T}_{jk}$ is the earliest start time of the process $A_j$ on the processing machine $M_k$. $AF{T}_{iw}$ is the actual completion time of the process $A_i$ on the processing machine $M_w$. $t_{jk}$ is the processing time for the process $A_j$ on the processing machine $M_k$. $T_{available}(M_k)$ is the earliest ready time of Machine $M_k$. $AS{T}_{jk}$ is the actual start time of the process $A_j$ on the processing machine $M_k$, where the process $A_i$ is the reverse preceding process of the process $A_j$, and the process $A_i$ and the process $A_j$ belong to the virtual no-wait flexible process group.

3.4. Optimal Completion-Semi-Idle Triggered Insertion Rescheduling Strategy

In order to improve machine utilization and shorten product completion time, the ITPR-NFIS algorithm proposes the optimal completion-semi-idle triggered insertion rescheduling strategy based on the backward movement strategy [13]. The conditions that must be met for optimizing machine idle time in the target process are that the effective idle time on the processing machine of the target process is greater than half of the processing time of the target process on the machine and less than the processing time of the target process on the machine. Additionally, the average reverse subsequent path of the target process must be greater than the average reverse subsequent of the first affected process inserted into the machine, and the completion time of the target process on the inserted machine must be the shortest, as shown in Equation (14). The idle time on the processing machine is shown in Equation (12). The completion time of the target process on the inserted machine is shown in Equation (13). After the insertion of the target process, identify the types of processes affected by it and process them separately: If the affected process is a non-terminal flexible process group, reschedule it to re-determine the processing machine and processing time. If new conflicts arise, multiple layers of conflict handling will be carried out, the new conflict will be rescheduled, and the processing machine and processing time will be re-determined. If it is a virtual no-wait flexible process group, it needs to meet the virtual no-wait constraints between processes when rescheduling, which can be divided into two situations: the first situation is that the process is the first virtual no-wait constraint process, which will generate new conflicts during the scheduling process. The new conflict is the rescheduling of the reverse subsequent process. When rescheduling the new conflict, ensure that its start time is equal to the completion time of the reverse preceding process. In the second situation, when the process is not the first no-wait constraint process, check whether there exists a processing machine whose start time is equal to the completion time of its reverse predecessor process. If it exists, reschedule the process by selecting the machine that has the same start time as the completion time of the reverse preceding process and requires the shortest processing time. If new conflicts arise, multiple layers of conflict handling will be carried out, and the new conflict will be rescheduled. If no such machine exists, first adjust the reverse preceding process to make the completion time of the reverse preceding process equal to the start time of the process. If there are available machines, select the machine with the shortest processing time, and the processing machine selected for this process remains unchanged. If there are no available devices, the start time of the reverse preceding process on different machines will be set as the completion time of the last process on the corresponding device for scheduling, and any new conflicts arising from it will be rescheduled. The optimal completion-semi-idle triggered insertion rescheduling strategy reduces machine idle time and shortens product completion time.

$$I{T}_{wr}=\left\{\begin{array}{l}IE{T}_{wr}-IS{T}_{wr}\hspace{1em}IS{T}_{wr}>AF{T}_{ik}\\ IE{T}_{wr}-AF{T}_{ik}\hspace{1em}IS{T}_{wr}\le AF{T}_{ik}\end{array}\right.$$

(12)

$$\begin{array}{l}F{T}_{jw}=S{T}_{jw}+t_{jw}\\ S{T}_{jw}=\max \left\{IS{T}_{wr},AF{T}_{ik}\right\}\end{array}$$

(13)

$$\left\{t_{jw}>I{T}_{wr}\ge {\displaystyle \frac{1}{2}}{t}_{jw}\right\}\wedge \left\{T(A_j)>T(A_z)\right\}\wedge \left\{F{T}_{jw}<\min (EF{T}_{jk}),\forall w\ne k\right\}$$

(14)

where $I{T}_{wr}$ is the r-th effective idle time on the corresponding processing machine $M_w$. $IE{T}_{wr}$ is the idle end time of the r-th idle time on the corresponding processing machine $M_w$. $IS{T}_{wr}$ is the idle start time of the r-th idle time on the corresponding processing machine $M_w$. ${\mathrm{t}}_{jw}$ is the processing time of the process $A_i$ on the corresponding processing machine. $F{T}_{jw}$ is the completion time of the process $A_j$ on the inserted processing machine $M_w$. $S{T}_{jw}$ is the effective start time of the process $A_j$ on the inserted processing machine $M_w$. $T(A_j)$ is the average reverse subsequent path value of the process $A_j$. $T(A_z)$ is the average reverse subsequent path value of the first affected process on the inserted machine, and the process $A_i$ is the reverse preceding process of the process $A_j$.

3.5. Optimal Completion-Full-Idle Adaptive Insertion Scheduling Strategy

In order to improve machine utilization and shorten product completion time, the ITPR-NFIS algorithm proposes the optimal completion-full-idle adaptive insertion scheduling strategy. The condition for optimizing machine idle time in the target process is that the effective idle time on the processing machine of the target process is greater than or equal to the processing time of the target process on the machine. And the completion time of the target process on the inserted machine is the shortest, as shown in Equation (15). Insert the target process when the above conditions are met. The optimal completion-full-idle adaptive insertion scheduling strategy reduces machine idle time and shortens product completion time.

$$\left\{I{T}_{wr}\ge t_{jw}\right\}\wedge \left\{F{T}_{jw}<\min (EF{T}_{jk}),\forall w\ne k\right\}$$

(15)

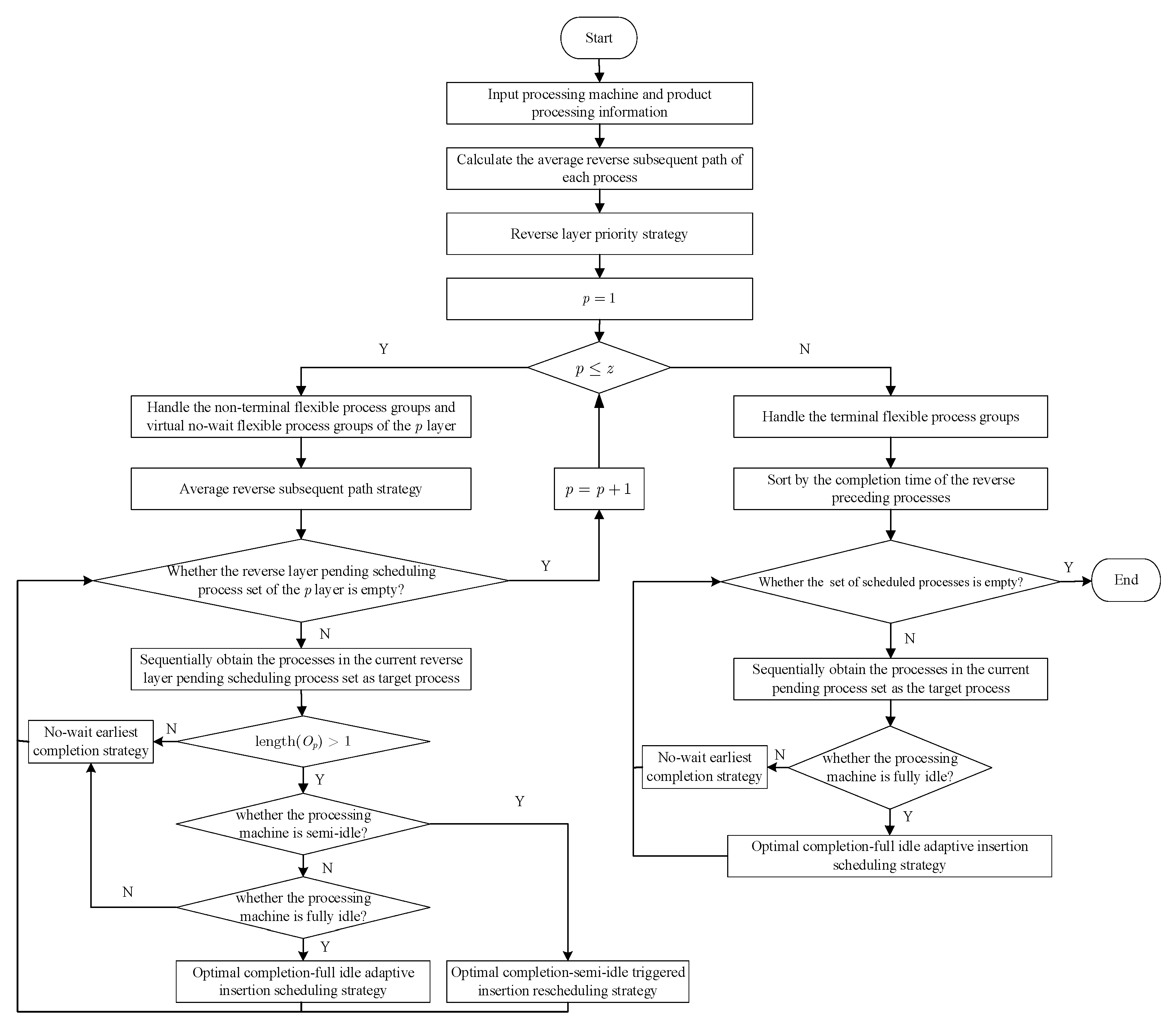
4. Algorithm Design and Complexity Analysis

4.1. Algorithm Design

The implementation steps of the integrated scheduling algorithm for no-wait network flexible based on idle-time optimization and process rescheduling are as follows, and the algorithm flowchart is shown in Figure 1.

Step 1: Input the processing machine and product process tree information, calculate the average processing time and the average reverse subsequent path of each process, and calculate the number of terminal flexible processes $F(F<n)$ in the reverse virtual flexible processing process tree.

Step 2: Implement the reverse layer priority strategy, allocating each process to different reverse layer sets of processes to be scheduled according to the number of layers it is located in. Schedule the processes layer by layer starting from the first layer. Assume there are a total of $z$ layers, with the first layer being $p=1$.

Step 3: Determine if $p$ is less than or equal to $z$. If yes, proceed to step 4. Otherwise, proceed to step 15.

Step 4: Calculate the average reverse subsequent path values of non-terminal flexible process groups and virtual no-wait flexible process groups in the $p$ layer. Implement the average reverse subsequent path strategy to sort the non-terminal flexible process groups and virtual no-wait flexible process groups in the $p$ layer in descending order.

Step 5: Determine whether the current reverse layer pending scheduling process set is empty. If it is empty, execute $p=p+1$ and proceed to step 3. Otherwise, proceed to step 6.

Step 6: Sequentially obtain the processes in the current reverse layer pending scheduling process set as target process.

Step 7: Determine whether the work sequence number of the current reverse layer pending scheduling process set is greater than one and whether the current pending scheduling process is the first process. If it is greater than one, proceed to step 9. Otherwise, proceed to step 8.

Step 8: Implement the no-wait earliest completion strategy. If the target process can be fully scheduled on all machines, calculate the earliest completion time of the target process on the flexible machine. Otherwise, proceed to step 5

Step 9: Determine whether the processing machine $M_w$ of the target process is semi-idle. If it is semi-idle, proceed to step 10. Otherwise, proceed to step 12.

Step 10: If machine $M_w$ has already scheduled process $A_z$, the effective idle time of the target process $A_i$ on the processing machine is greater than or equal to half of the processing time of the target process on the machine and less than the processing time of the target process on the machine $t_{iw}>I{T}_{wr}\ge {\displaystyle \frac{1}{2}}{t}_{iw}$. The average reverse subsequent path $T(A_i)$ of the target process $A_i$ is greater than the average reverse subsequent path $T(A_z)$ of the inserted process $A_z$, that is $T(A_i)>T(A_z)$. And its completion time on this machine is the shortest $F{T}_{iw}<\min (EF{T}_{ik}),\forall w\ne k$. Then proceed to step 11. Otherwise, proceed to step 12.

Step 11: Implement the optimal completion-semi-idle triggered insertion rescheduling strategy to determine the processing start time and end time of the target process and the selected processing machine, and jump to step 5.

Step 12: Determine whether the processing machine $M_w$ of the target process is fully idle. If it is fully idle, proceed to step 13. Otherwise, proceed to step 8.

Step 13: If machine $M_w$ has already scheduled process $A_z$, the effective idle time on the processing machine of target process $A_i$ is greater than or equal to the processing time of the target process on this machine $I{T}_{wr}\ge t_{iw}$, and its completion time on this machine is the shortest $F{T}_{iw}<\min (EF{T}_{ik}),\forall w\ne k$. Then proceed to step 14. Otherwise, proceed to step 8.

Step 14: Execute the optimal completion-full-idle adaptive insertion scheduling strategy, determine the target process processing start time and end time, as well as the selected processing machine, and jump to step 5.

Step 15: Calculate the completion time of the reverse preceding processes of the terminal flexible processes in each layer. Schedule the processes with the shorter completion time of the reverse preceding processes first, and so on. Sort each process and place the sorted processes in the set of processes to be scheduled.

Step 16: Determine whether the current set of scheduled processes is empty. If it is empty, proceed to step 22. Otherwise, proceed to step 17.

Step 17: Sequentially obtain the processes in the current pending process set as the target process.

Step 18: Determine whether the processing machine $M_w$ of the target process is full-idle. If it is full-idle, then proceed to step 19. Otherwise, proceed to step 21.

Step 19: If machine $M_w$ has already scheduled process $A_z$, the effective idle time of the target process $A_i$ on the processing machine is greater than or equal to the processing time of the target process $A_i$ on this machine, and its completion time on this machine is the shortest $F{T}_{iw}<\min (EF{T}_{ik}),\forall w\ne k$. Then proceed to step 20. Otherwise, proceed to step 21.

Step 20: Execute the optimal completion-full-idle adaptive insertion scheduling strategy, determine the processing start time and end time of the target process and the selected processing machine, and jump to step 16.

Step 21: Implement the no-wait earliest completion strategy. If the target process can be fully scheduled on all machines, calculate the earliest completion time of the target process on the flexible machine. Otherwise, proceed to step 16.

Step 22: End.

4.2. Algorithm Pseudo-Code

The pseudo-code of the ITPR-NFIS algorithm is shown in Algorithm 1.

Algorithm 1 ITPR-NFIS
Input: product process tree and processing machine information
Output: process scheduling plan and makespan
1:	Calculate the average reverse subsequent path of each process
2:	Calculate the number of terminal flexible processes F
3:	Perform reverse layering on the process tree, calculate the total number of layers z, and assign the processes to the corresponding set of scheduled processes Op in the reverse layer. The first layer is p = 1
4:	While p <= z
5:	Obtain the non-terminal flexible process groups and virtual no-wait flexible process groups in the current layer, and sort them in descending order according to the average reverse subsequent path value
6:	if Op is empty
7:	p = p + 1, continue
8:	end
9:	for i = 1 to length(Op)
10:	Sequentially obtain the processes in the current reverse layer pending scheduling process set as target process.
11:	if length(Op) > 1
12:	if tiw > ITwr and T(Ai) > T(Az) and FTiw < min(EFTik)
13:	Implement the optimal completion-semi-idle triggered insertion rescheduling strategy to determine the processing start time and end time of the target process and the selected processing machine, continue
14:	else if ITwr > = tiw and FTiw < min(EFTik)
15:	Execute the optimal completion-full-idle adaptive insertion scheduling strategy, determine the target process processing start time and end time, as well as the selected processing machine, continue
16:	else
17:	Implement the no-wait earliest completion strategy. If the target process can be fully scheduled on all machines, calculate the earliest completion time of the target process on the flexible machine, continue
18:	end if
19:	end if
20:	end for
21:	p = p + 1
22:	end while
23:	Calculate the completion time of the reverse preceding processes of the terminal flexible processes in each layer. Schedule the processes with shorter completion times of the reverse preceding processes first, and so on. Sort each process and place the sorted processes in the set of processes to be scheduled.
24:	if the current set of scheduled processes is not empty
25:	if ITwr > = tiw and FTiw < min(EFTik)
26:	Execute the optimal completion-full-idle adaptive insertion scheduling strategy, determine the target process processing start time and end time, as well as the selected processing machine, continue
27:	else
28:	Implement the no-wait earliest completion strategy. If the target process can be fully scheduled on all machines, calculate the earliest completion time of the target process on the flexible machine, continue
29:	end if
30:	end if
end procedure

4.3. Complexity Analysis

Assuming that the number of processing processes for a complex product is $n$ and the number of processing machine is $m$, the main operations of this algorithm are as follows:

Assuming that the number of processing processes for a complex product is $n$ and the number of processing machine is $m$. The main operations of this algorithm are as follows:

(1) Reverse layer priority strategy. According to the partial order relationship of the processes in the reverse virtual flexible processing process tree, the nodes of each layer in the reverse virtual flexible processing process tree are sequentially determined and placed into the reverse layer pending scheduling step set. This needs to be executed n times. The time complexity of the reverse layer priority strategy is $O(n)$.

(2) Average reverse subsequent path strategy. First, calculate the average processing time of each process on the flexible machine. This step needs to be executed $m$ times, involving a total of n processes. The time complexity for calculating the average processing time of each process is $O(n\times m)$. Calculate the average reverse subsequent path for each process. With $n$ processes in total, the time complexity for this step is $O(n)$. Finally, the processes in the reverse order layer to be scheduled are sorted according to the average reverse subsequent path values, with a time complexity of $O(n{\log }_2^n)$. The time complexity of the average reverse subsequent path strategy is $O(n{\log }_2^n)$.

(3) No-wait earliest completion strategy. Since each process can be processed on at most m machines, selecting the machine with the earliest completion time requires at most m processes. Therefore, the time complexity of the no-wait earliest completion strategy is $O(n\times m)$.

(4) Optimal completion-semi-idle triggered insertion rescheduling strategy. Determine that the effective idle time of the corresponding processing machine for the process is greater than or equal to half of the processing time of the process on the machine and less than the processing time of the process on the machine. Additionally, check if the process’s average reverse subsequent path is greater than that of the first affected process on the machine and if the completion time on the machine is the shortest. If the insertion conditions are met, the process will be inserted to reschedule the affected process. The time complexity of this strategy is $O(n\times m\times l)$, where $l$ is the number of processes already scheduled on the machine. In the worst case scenario, $l=n$, but since m (the number of machine) is usually much smaller than $n$, the time complexity is $O(n^2)$. If $m$ and $l$ are very small, they can be treated as constants, and the time complexity is $O(n)$.

(5) Optimal completion-full-idle adaptive insertion scheduling strategy. Determine that the effective idle time of the corresponding processing machine for the process is greater than or equal to the processing time of the target process on the machine, and that the completion time of the target process on the inserted machine is the shortest. If the insertion conditions are met, the process will be inserted. The time complexity of this strategy is $O(n\times m)$, where m (number of machines) is typically much smaller than n, so the time complexity is $O(n)$.

In summary, the maximum time complexity of the ITPR-NFIS algorithm is $O(n^2)$.

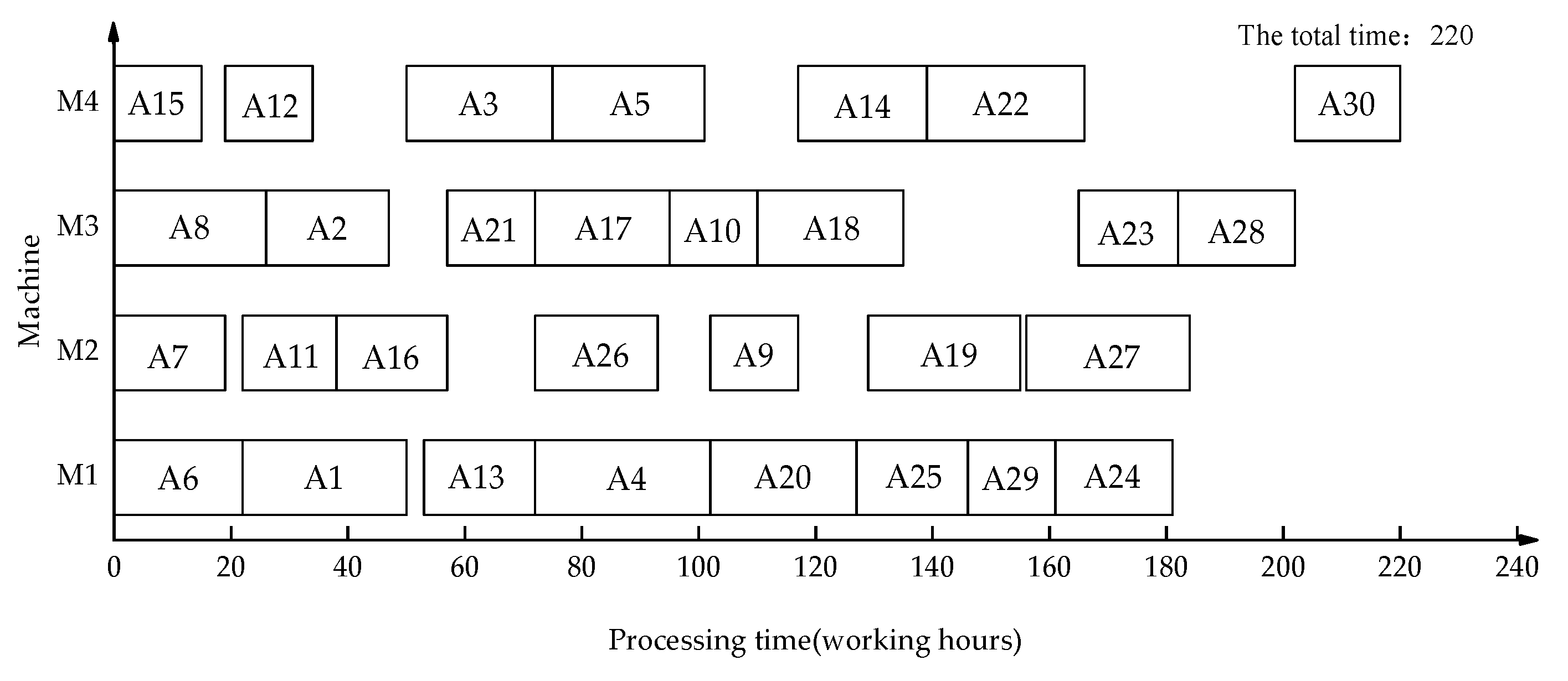
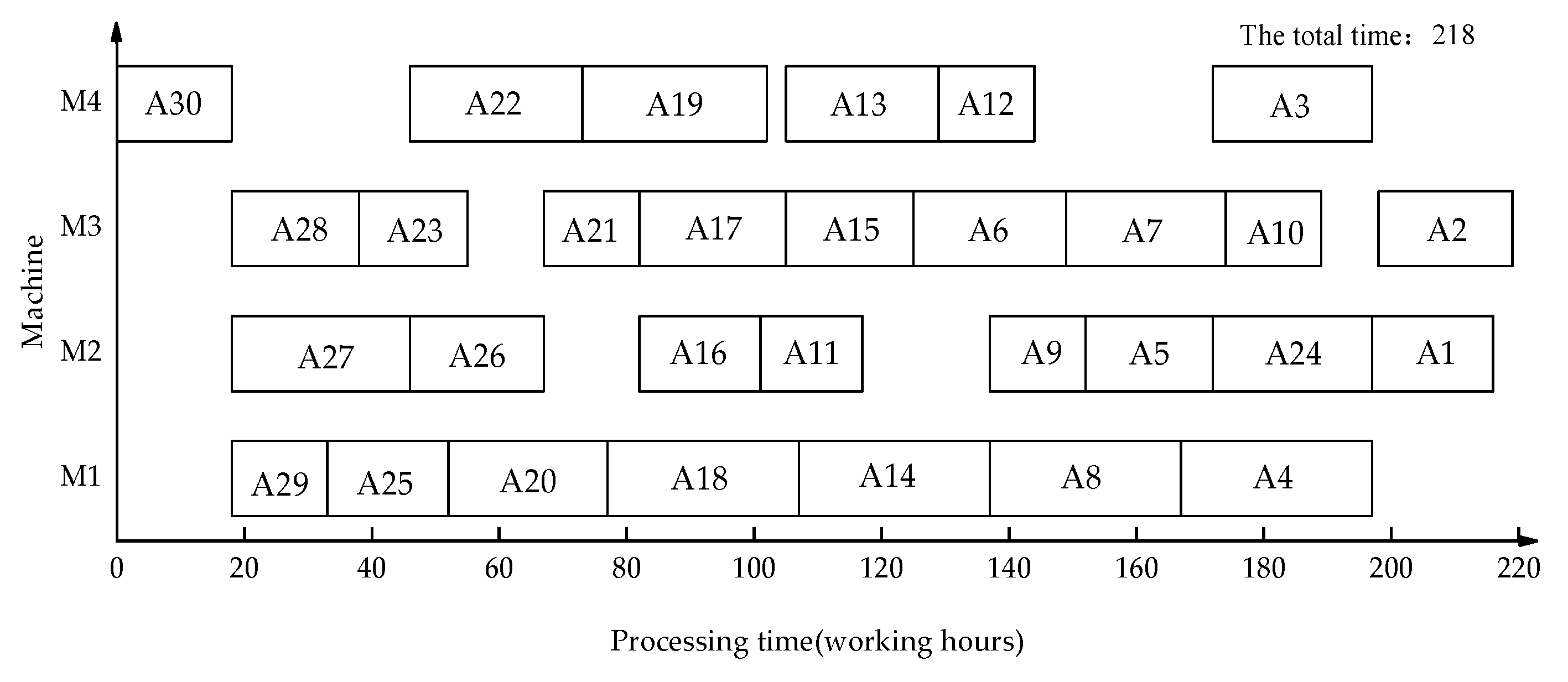
5. Comparative Analysis of Example

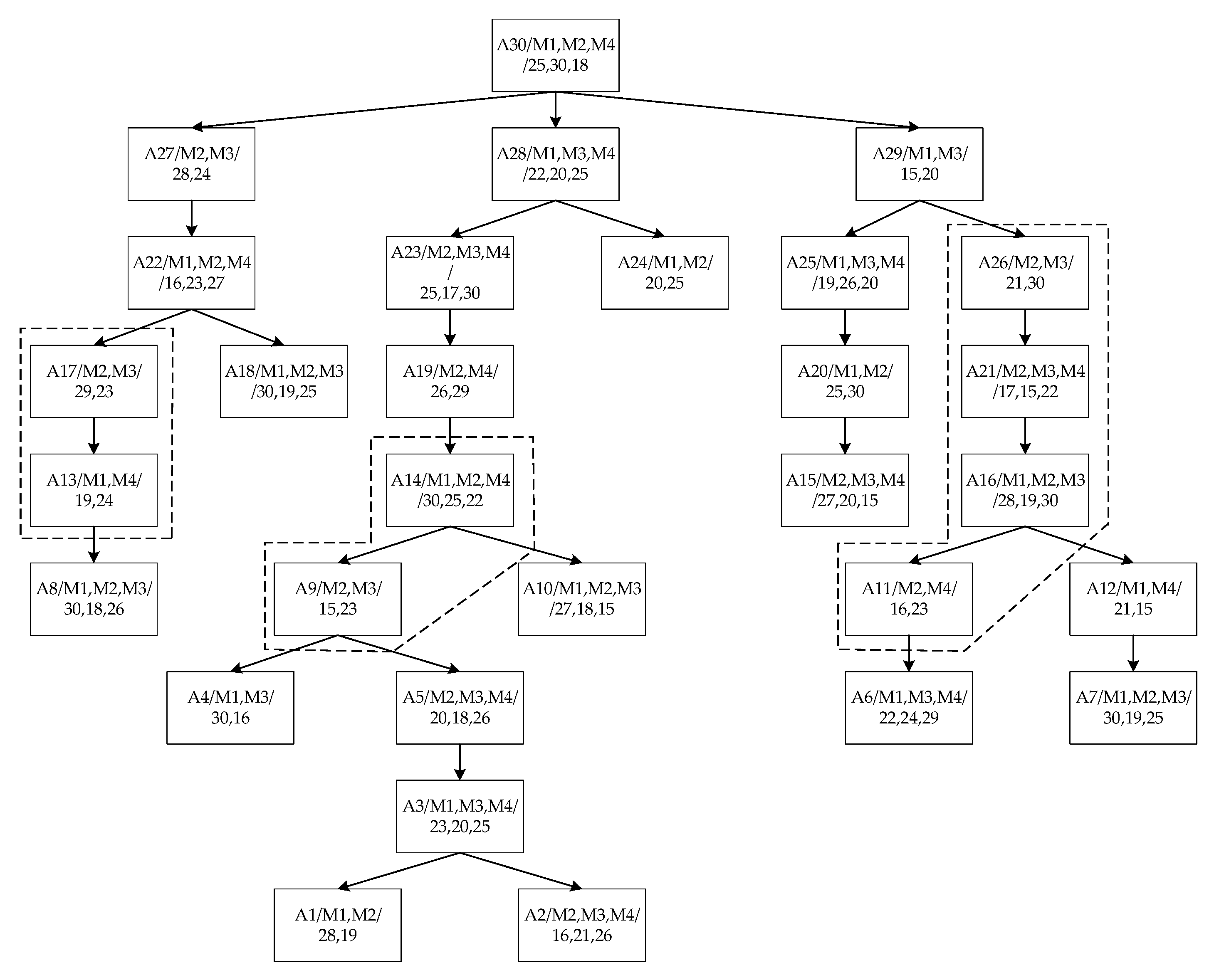
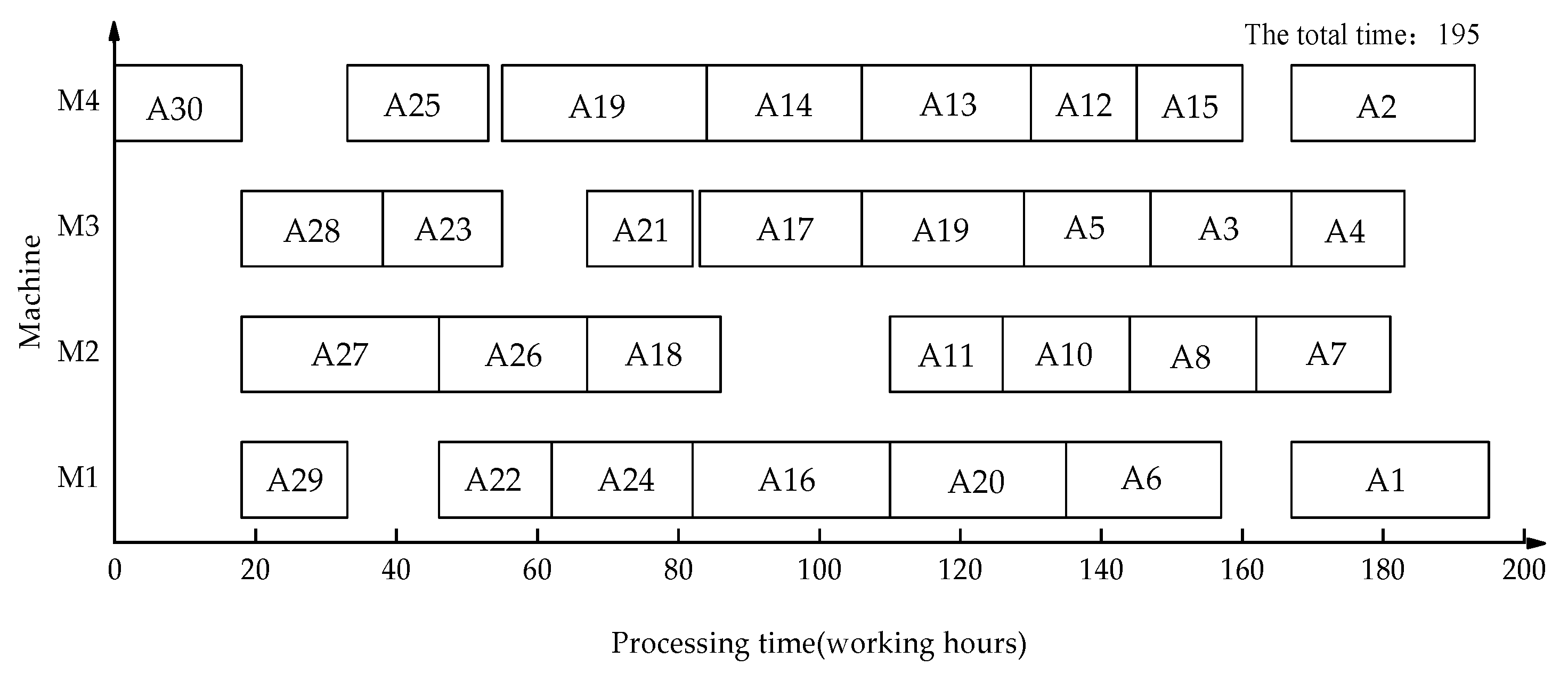
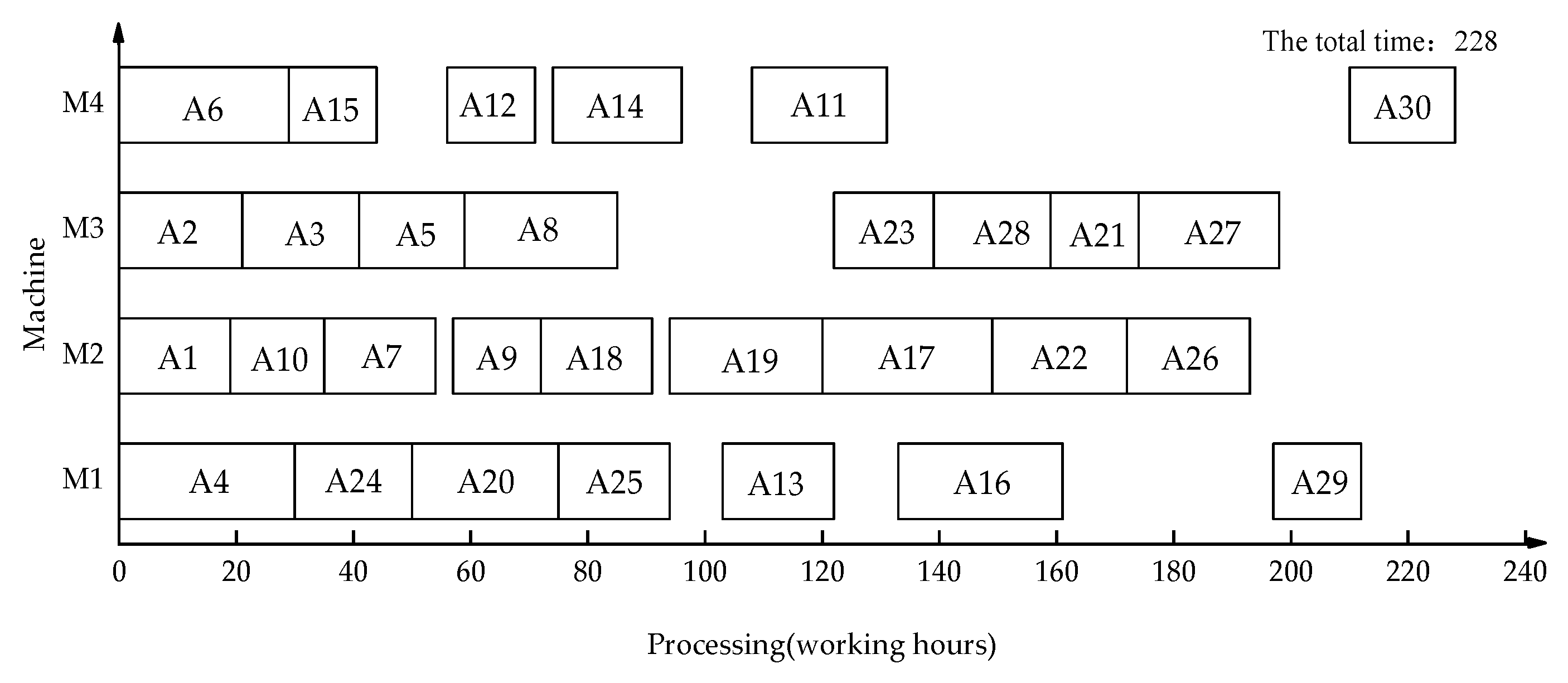
5.1. Example Analysis

Product A is a complex product composed of 30 processes with constraint relationships, which can be processed on 4 flexible processing machines. Due to processing requirements, there are no-wait constraints between process A17 and process A13, process A14 and process A9, process A26, process A21, process A16, and process A11 in the processing of Product A. The flexible processes with no-wait constraints are enclosed by dashed box. The reverse expansion processing process tree of Product A is shown in Figure 2.

The scheduling process of Product A scheduled by the ITPR-NFIS algorithm is as follows:

Step 1. First, determine the non-terminal flexible process groups {A30, A29, A28, A27, A25, A23, A22, A20, A19, A12, A11, A5, A3}, the no-wait flexible process groups {{A26, A21, A16, A11}, {A17, A13}, {A14, A9}}, and the terminal flexible process groups {A24, A18, A15, A10, A8, A7, A6, A4, A2, A1}. Calculate the average processing time and average reverse subsequent path value for each process in Product A by converting the flexible processes with no-wait constraints in the reverse extended processing process tree into virtual no-wait flexible process groups as proposed in this paper. The reverse virtual flexible processing process tree is composed of non-terminal flexible process groups, terminal flexible process groups, and virtual no-wait flexible process groups. The average processing time of each process and the average reverse subsequent path value was obtained. The reverse virtual flexible processing process tree of Product A is shown in Figure 3, where NF_i denotes non-terminal flexible process groups, F_i denotes terminal flexible process groups, and V_i denotes virtual no-wait flexible process groups.

Step 2. Determine the scheduling sequence of non-terminal flexible process groups and virtual no-wait flexible process groups in each layer based on the reverse layer priority strategy and the average reverse subsequent path strategy. The scheduling sequence allocates each process to the reverse layer’s process set to be scheduled. Product A has a total of seven reverse layer process sets to be scheduled. The scheduling sequence of processes in the first layer is {NF₁}. The scheduling sequence of processes in the second layer is {NF₃, NF₄, NF₂}. The scheduling sequence of processes in the third layer is {NF₆, V₉, NF₅, NF₈}. The scheduling sequence of processes in the fourth layer is {NF₁₂, V₁₀, NF₁₃, NF₁₅}. The scheduling sequence of processes in the fifh layer is {V₁₇}. The scheduling sequence of processes in the sixth layer is {NF₂₁}, and the scheduling sequence of processes in the seventh layer is {NF₂₃}.

Step 3. Determine the processing machine and processing time for non-terminal flexible process groups and virtual no-wait flexible process groups based on the no-wait earliest completion strategy, the optimal completion-semi-idle triggered insertion rescheduling strategy, and the optimal completion-full-idle adaptive insertion scheduling strategy. Then, determine the scheduling sequence of terminal flexible process groups based on the completion time of their reverse preceding processes. The scheduling sequence of terminal flexible process groups is {F7, F11, F22, F14, F20, F16, F18, F19, F24, F25}. Determine the processing machine and processing time for the terminal flexible process groups based on the no-wait earliest completion strategy and the optimal completion-full-idle adaptive insertion scheduling strategy. The scheduling scheme of Product A was formed, as shown in

Table 3. Scheduling process of ITPR-NFIS algorithm for Product A.

Process Set	Process	EST				EFT				Selected Processing
		M1	M2	M3	M4	M1	M2	M3	M4	Machine
NF1	A30	0	0	-	0	25	30	-	18	M4
NF3, NF4, NF2	A28	18	-	18	18	40	-	38	43	M3
	A29	18	-	38	-	33	-	58	-	M1
	A27	-	18	38	-	-	46	52	-	M2
NF6, V9, NF5, NF8	A23	-	46	38	38	-	71	55	68	M3
	A26	-	46	55	-	-	67	85	-	M2 (A26 meets no-wait constraints.)
	A21	-	67	67	67	-	84	82	89	M3 (A21 meets no-wait constraints.)
	A16	82	82	82	-	110	101	112	-	M2 (A16 meets no-wait constraints.)
	A11	-	101	-	101	-	117	-	124	M2 (A11 meets no-wait constraints.)
	A22	46	67	-	46	62	90	-	73	M1
	A25	62	-	82	33	81	-	108	53	M4
NF12, V10, NF13, NF15	A19	-	67	-	55	-	93	-	84	M4
	A17	-	67	82	-	-	96	105	-	M2 (A17 meets the semi-idle insertion condition on machine M2 and is inserted. A17 meets no-wait constraints. The affected processes are A16 and A11.)
	A13	96	-	-	96	115	-	-	120	M1 (A13 meets no-wait constraints.)
	A16	82	96	82	-	110	115	112	-	M1 (A16 rescheduling. A16 meets the semi-idle insertion condition on machine M1 and is inserted. A16 meets no-wait constraints. The affected process is A13.)
	A11	-	110	-	110	-	126	-	133	M2 (A11 rescheduling. A11 meets no-wait constraints.)
	A13	110	-	-	96	129	-	-	120	M4 (A13 rescheduling. A13 meets no-wait constraints.)
	A20	110	126	-	-	135	156	-	-	M1
	A12	135	-	-	120	156	-	-	135	M4
V17	A14	135	96	-	84	165	121	-	106	M4 (A14 meets the semi-idle insertion condition on machine M4 and is inserted. A14 meets no-wait constraints. The affected process is A13.)
	A9	-	126	106	-	-	141	129	-	M3 (A9 meets no-wait constraints.)
	A13	135	-	-	106	154	-	-	130	M4 (A13 rescheduling. A13 meets the semi-idle insertion condition on machine M4 and is inserted. A13 does not meet the no-wait constraint. Reschedule A17 to ensure that A13 meets the no-wait constraint. The affected processes are A12 and A17.)
	A17	-	77	83	-	-	106	106	-	M3 (A17 rescheduling. The completion time of A17 on M2 and M3 is the same, but the processing time on M3 is shorter, so M3 is chosen. A17 meets the full-idle insertion condition on machine M3 and is inserted. A17 and A13 meet no-wait constraints.)
	A12	135	-	-	130	156	-	-	145	M4 (A12 rescheduling.)
NF21	A5	-	129	129	145	-	159	147	171	M3
NF23	A3	147	-	147	147	170	-	167	172	M3
F7, F11, F22, F14, F20, F16, F18, F19, F24, F25	A24	62	67	-	-	82	92	-	-	M1 (A24 meets the full-idle insertion condition on machine M1 and is inserted. No affected processes.)
	A18	135	67	167	-	165	86	192	-	M2 (A18 meets the full-idle insertion condition on machine M2 and is inserted. No affected processes.)
	A10	135	126	167	-	162	144	182	-	M2
	A6	135	-	167	145	157	-	191	174	M1
	A4	157	-	167	-	187	-	183	-	M3
	A8	157	144	183	-	187	162	209	-	M2
	A15	-	162	183	145	-	189	203	160	M4
	A7	157	162	183	-	187	181	208	-	M2
	A1	167	181	-	-	195	200	-	-	M1
	A2	-	181	183	167	-	197	205	193	M4

.

The ITPR-NFIS algorithm final scheduling sequence is as follows: A30, A28, A29, A27, A23, A26, A21, A22, A25, A19, A16, A11, A20, A14, A9, A13, A12, A17, A5, A3, A24, A18, A10, A6, A4, A8, A15, A7, A1, A2. The corresponding processing machine for the above processes in sequence is as follows: M4, M3, M1, M2, M3, M2, M3, M1, M4, M3, M1, M2, M1, M4, M3, M4, M4, M3, M3, M1, M2, M2, M1, M3, M3, M1, M2, M2, M1, M3. The Gantt chart of the ITPR-NFIS algorithm scheduling is shown in Figure 4; the total processing time is 195 working hours.

5.2. Performance Comparison Analysis

To further verify the optimization effect of the ITPR-NFIS algorithm, the O-NPS algorithm [25], OG-NIS algorithm [26], ROSD-NIS algorithm [28], and P-NIFS [29] algorithm are respectively used to schedule Product A. As the O-NPS algorithm, OG-NIS algorithm, and ROSD-NIS algorithm did not consider the no-wait constraint problem of flexible machine, the O-NPS algorithm, OG-NIS algorithm, and ROSD-NIS algorithm were improved. The O-NPS algorithm is integrated with the average processing time and the no-wait earliest completion strategy proposed in this paper, resulting in the IO-NPS algorithm. The IO-NPS algorithm adopts the average allied critical path method, best fit scheduling method, movement and exchange algorithm, and no-wait earliest completion strategy. The OG-NIS algorithm, combined with the average processing time and the no-wait earliest completion strategy proposed in this paper, constitutes the IOG-NIS algorithm. This algorithm utilizes the first fit scheduling method for unified linkage of no-wait process groups, the average allied critical path method, and the no-wait earliest completion strategy. The ROSD-NIS algorithm, combined with the average processing time proposed in this paper, constitutes the IROSD-NIS algorithm that adopts the biggest parallelism chosen policy, the frontier greedy policy, and the reverse order signal-driven policy. These four improved algorithms are then compared with the ITPR-NFIS algorithm.

Table 4. Comparison of characteristics of five algorithms.

Algorithm	Scheduling Strategy	Optimization Objective	No-Wait Constraints	Idle Time
IO-NPS	average allied critical path method, best fit scheduling method, movement and exchange algorithm, and no-wait earliest completion strategy	Minimize makespan	Yes	Not optimized
IOG-NIS	first fit scheduling method for unified linkage of no-wait process groups, average allied critical path method, and no-wait earliest completion strategy	Minimize makespan	Yes	Not optimized
IROSD-NIS	biggest parallelism chosen policy, frontier greedy policy, and reverse order signal-driven	Minimize makespan	Yes	Not optimized
P-NIFS	allied critical path method, adaptive flexible scheduling strategy, equipment balanced strategy, optimization strategy of procedure scheduling	Minimize makespan	Yes	Not optimized
ITPR-NFIS	reverse layer priority strategy, average reverse subsequent path strategy, no-wait earliest completion strategy, optimal completion-semi-idle triggered insertion rescheduling strategy, optimal completion-full-idle adaptive insertion scheduling strategy	Minimize makespan	Yes	Optimized

compares and analyzes the proposed algorithm and the comparative algorithm in terms of core strategies, optimization objectives, and other aspects. Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the Gantt chart obtained from scheduling Product A using various algorithms.

The scheduling sequence of the IO-NPS algorithm is as follows: A1, A2, A3, A5, A4, A10, A9, A14, A19, A23, A24, A28, A6, A7, A12, A11, A16, A21, A26, A15, A20, A25, A29, A8, A13, A17, A18, A22, A27, A30. The corresponding processing machine for each process is as follows: M2, M3, M3, M3, M1, M2, M2, M4, M2, M3, M1, M3, M4, M2, M4, M4, M1, M3, M2, M4, M1, M1, M1, M3, M1, M2, M2, M2, M3, M4. The Gantt chart of the IO-NPS algorithm scheduling is shown in Figure 5, and the total processing time is 228 working hours.

The scheduling sequence of the IOG-NIS algorithm is as follows: A6, A7, A12, A11, A16, A21, A26, A8, A13, A17, A1, A2, A3, A5, A4, A10, A9, A14, A15, A20, A25, A29, A19, A23, A24, A28, A18, A22, A27, A30. The corresponding processing machine for each process is as follows: M1, M2, M4, M2, M2, M3, M2, M3, M1, M3, M3, M3, M2, M4, M1, M1, M1, M2, M3, M1, M3, M4, M2, M4. The Gantt chart of the IOG-NIS algorithm scheduling is shown in Figure 6, and the total processing time is 220 working hours.

The scheduling sequence of the IROSD-NIS algorithm is as follows: A30, A28, A23, A29, A19, A27, A26, A21, A16, A11, A14, A9, A22, A25, A17, A13, A5, A12, A3, A20, A6, A8, A7, A18, A1, A4, A24, A2, A15, A10. The corresponding processing machine for each process is: M4, M3, M3, M1, M4, M2, M2, M3, M2, M2, M1, M2, M4, M1, M3, M4, M2, M4, M1, M3, M1, M3, M1, M3, M1, M2, M1, M2, M3, M3. The Gantt chart scheduled by the IROSD-NIS algorithm is shown in Figure 7, and the total processing time is 218 working hours.

The scheduling sequence of the P-NIFS algorithm is as follows: A6, A11, A7, A12, A16, A21, A26, A8, A13, A17, A1, A2, A3, A5, A4, A9, A10, A14, A15, A20, A25, A29, A19, A23, A24, A28, A18, A22, A27, A30. The corresponding processing machine for each process is: M1, M2, M2, M4, M2, M3, M2, M3, M1, M3, M3, M4, M4, M1, M2, M3, M4, M4, M1, M1, M1, M2, M2, M3, M3, M4, M1, M1, M1, M2, M3, M3, M3, M4, M2, M4. The Gantt chart scheduled by the P-NIFS algorithm is shown in Figure 8, and the total processing time is 220 working hours.

The makespan of the ITPR-NFIS algorithm, IO-NPS algorithm, IOG-NIS algorithm, IROSD-NIS algorithm, and P-NIFS algorithm, as well as the relative reduction rate of makespan of the ITPR-NFIS algorithm, are shown in

Table 5. Comparison of makespan for five algorithms.

Algorithm	Makespan (Working Hours)	Relative Reduction Ratio of Makespan of ITPR-NFIS Algorithm
IO-NPS	228	14.47%
IOG-NIS	220	11.36%
IROSD-NIS	218	10.55%
P-NIFS	220	11.36%
ITPR-NFIS	195	-

. In Table 5, it can be seen that the ITPR-NFIS algorithm has a shorter completion time for scheduling product A. The relative reduction rates of makespan of the ITPR-NFIS algorithm compared to IO-NPS algorithm, IOG-NIS algorithm, IROSD-NIS algorithm, and P-NIFS algorithm are 14.47%, 11.36%, 10.55%, and 11.36%, respectively. Compared with the IO-NPS algorithm, IOG-NIS algorithm, IROSD-NIS algorithm, and P-NIFS algorithm, the ITPR-NFIS algorithm has a shorter completion time for scheduling Product A. The scheduling result of the IO-NPS algorithm is not ideal because the average pseudo critical path method adopted by the IO-NPS algorithm uses vertical optimization. It fully considers the scheduling of vertical processes but ignores the parallelism of horizontal processes, resulting in more idle-time periods, ultimately leading to unsatisfactory scheduling results. The reason why the scheduling result of the IOG-NIS algorithm is not ideal is that the IOG-NIS algorithm determines the scheduling order of the process group on the path based on the number of processes belonging to the process group on the path. This causes the path with the fewest no-wait processes to be scheduled last, hindering parallel processing between some operations on this path and already scheduled operations, thereby adversely affecting the scheduling result. The reason why the scheduling results of the IROSD-NIS algorithm are not ideal is that the IROSD-NIS algorithm only focuses on the idle and busy status of processing machines and the critical path length of processes, without comprehensively considering the processing time of processes on flexible machines and their relative positions in the process tree, ultimately resulting in unsatisfactory scheduling results. The scheduling result of the P-NIFS algorithm is not ideal because the P-NIFS algorithm determines the scheduling sequence of the path based on the number of real nodes on the path, overly relying on the short-time machine of the process and not making full use of the flexible machine, ultimately resulting in an unsatisfactory scheduling result. Compared with the IO-NPS algorithm, IOG-NIS algorithm, IROSD-NIS algorithm, and P-NIFS algorithm, the ITPR-NFIS algorithm comprehensively considers the relative position of processes in the process tree and optimizes the idle time of machine. It enhances both the parallel processing of parallel processes and the compactness of sequential processes. The ITPR-NFIS algorithm fully utilizes machines to reduce idle time and makes subsequent processes occur as early as possible, shortening completion time. The ITPR-NFIS algorithm effectively reduces the product’s completion time.

6. Conclusions and Prospects

In network flexible integrated scheduling with no-wait constraint relationships, with the goal of minimizing the product completion time, based on a comprehensive consideration of many factors such as processing processes, process constraint relationships, and machine operation conditions in the manufacturing system, a no-wait network flexible integrated scheduling algorithm based on idle-time optimization and process rescheduling is proposed. The ITPR-NFIS algorithm divides complex product processes into non-terminal flexible process groups, terminal flexible process groups, and virtual no-wait flexible process groups. For non-terminal flexible process groups and virtual no-wait flexible process groups, the scheduling sequence of each process is determined by the reverse layer priority strategy and the average reverse subsequent path strategy. The processing machine and processing time for each process are determined by the no-wait earliest completion strategy, the optimal completion-semi-idle triggered insertion rescheduling strategy, and the optimal completion-full-idle adaptive insertion scheduling strategy. For terminal flexible process groups, the scheduling sequence is determined by the completion time of their reverse preceding processes, and the processing machine and processing time of each process are determined based on the no-wait earliest completion strategy and the optimal completion-full-idle adaptive insertion scheduling strategy. The ITPR-NFIS algorithm achieves optimization effects in both vertical and horizontal directions. The ITPR-NFIS algorithm provides a new method and expands new ideas for solving the problem of no-wait network flexible integrated scheduling for complex products and has certain theoretical and practical significance.

In future work, more constraints that exist in actual production, such as transportation time and equipment failures, can be considered in mathematical models, and robust optimization methods can be used to solve constraints such as equipment failures and non-zero transportation times to enhance the practicality of the algorithm.