Skeleton Information-Driven Reinforcement Learning Framework for Robust and Natural Motion of Quadruped Robots

Abstract

Legged robots have great potential in complex environments, but achieving robust and natural locomotion remains difficult due to challenges in generating smooth gaits and resisting disturbances. This article presents a novel reinforcement learning framework that integrates a skeleton-aware graph neural network (GNN), a single-stage teacher–student architecture, a system-response model, and a Wasserstein Adversarial Motion Priors (wAMP) module. The skeleton-aware GNN enriches observations by encoding key node information and link properties, providing structured body information and better spatial awareness on irregular terrains. Unlike conventional two-stage approaches, this method jointly trains teacher and student policies to accelerate learning and improve sim-to-real transfer using hybrid advantage estimation (HAE). The system-response model further enhances robustness by predicting future observations from historical states via contrastive learning, enabling the policy to anticipate terrain variations and external disturbances. Finally, wAMP provides a more stable adversarial imitation method for fitting expert datasets of both flat ground and stair locomotion. Experiments on quadruped robots demonstrate that the proposed approach achieves more natural gaits and stronger robustness than existing baselines.

1. Introduction

In the field of legged robot locomotion, traditional control algorithms face significant challenges in achieving robust performance [1,2]. Particularly in complex terrains, these methods typically rely on intricate finite-state machines to coordinate basic motion primitives and reflex controllers [1,2]. Critical tasks such as ground contact detection and slip estimation often depend on empirically tuned thresholds, which are highly sensitive to unmodeled environmental factors like mud, snow, or vegetation [3,4,5]. Additionally, while foot-mounted contact sensors are widely used, their reliability in real-world scenarios is often limited. As operational scenarios expand, the complexity of traditional control systems grows exponentially, making them not only difficult to develop and maintain, but also prone to failure in edge cases [6].

In contrast, model-free reinforcement learning (RL) offers a more streamlined alternative [7]. By optimizing reward functions through autonomous data collection, RL significantly simplifies the design process of locomotion controllers [8], reducing reliance on manual parameter tuning and expert knowledge while automating many aspects of the development pipeline. This approach enables robots to acquire movement capabilities that are difficult to achieve with traditional methods. However, despite the significant advantages of RL in legged robot applications, the generated motion patterns often appear unnatural, characterized by stiff, jerky movements rather than the fluid, biologically-inspired gaits seen in animals. This lack of natural motion characteristics remains a major limitation of current RL approaches in legged locomotion.

Researchers have explored integrating predefined gait priors into RL training to guide convergence towards natural gaits [9,10,11]. Imitation learning [12,13,14], where robots mimic expert reference motions using phase variables, accelerates training but struggles to scale across diverse motion types [15,16]. Alternatively, action spaces such as central pattern generators (CPGs) or policies-modulating trajectory generators (PMTG) impose constraints that limit complex movement generation [17]. Although promising, these approaches often restrict behavior flexibility.

A notable advancement is Adversarial Motion Priors (AMP) [18]. Unlike direct imitation learning, AMP leverages style rewards to encourage the agent to produce desired locomotion behaviors while maintaining natural motion characteristics. This approach provides greater flexibility, enabling robots to learn diverse and complex gait patterns without imposing restrictive action constraints [19]. However, AMP is inherently based on a Generative Adversarial Network (GAN) framework, and thus suffers from a similar drawback: mode collapse. When the training dataset contains multiple types of locomotion behaviors, such as flat-ground walking and stair climbing, AMP tends to capture only one dominant mode of motion, leading to monotonous outputs and reduced generalization to diverse scenarios.

To address this issue, this article proposes Wasserstein Adversarial Motion Priors (wAMP) [20], which replaces the standard loss of GAN in AMP with a loss of Wasserstein divergence (WGAN-div) [21,22]. WGAN-div provides a smoother and more informative gradient signal, even when generated actions deviate significantly from expert demonstrations. This mitigates mode collapse by encouraging the generator to explore a broader distribution of locomotion behaviors. As a result, wAMP produces more diverse and natural gait patterns, enabling quadrupedal robots to learn both regular flat ground walking and complex skills such as stair climbing within a unified reinforcement learning framework.

Two-stage teacher–student frameworks have been developed to enable blind locomotion and reduce the sim-to-real gap [9,11]. In this paradigm, a teacher policy is first trained in simulation with access to privileged information, such as terrain friction or elevation maps, that is unavailable in the real world. A proprioceptive student policy is then trained to mimic the teacher, relying solely on onboard sensors such as IMUs and joint encoders. This approach allows the student to operate without privileged information, thereby bridging the sim-to-real gap and enabling blind locomotion.

However, the two-stage process is often cumbersome and time-consuming, as it requires training and distillation in two separate phases. To overcome this limitation, a single-stage teacher–student training framework is proposed [23]. Instead of training policies sequentially, the teacher and student are optimized jointly, with their relative contributions controlled by hybrid advantage estimation (HAE). In the early stages of training, the teacher dominates both action generation and representation encoding, providing strong guidance. Over time, the proportion of student contributions gradually increases until the student ultimately takes full control of the training process. This progressive strategy accelerates training while retaining the benefits of teacher–student transfer, leading to more efficient sim-to-real adaptation.

A Graph Neural Network (GNN) module enhances imitation learning and blind locomotion tasks, such as climbing stairs, by encoding robot skeletal information, specifically joint positions relative to body in Cartesian coordinates and the length and mass of the parent link of each joint. Representing the kinematic structure as a graph with joints as nodes and links as edges, the GNN captures spatial relationships and constraints in multiple consecutive states [24,25,26,27,28]. These embeddings, integrated into a reinforcement learning (RL) policy, support faster convergence during imitation learning by providing a concise kinematic representation, aiding adaptation to expert demonstrations. For blind staircase climbing, where tactile feedback (for example, front foot contact) guides navigation, the module improves spatial awareness, contributing to robust terrain perception.

Furthermore, a system-response model [29] is incorporated to enhance robustness against external disturbances. By modeling robot responses to environmental variations through proprioceptive feedback, the system-response model enables the policy to better anticipate and compensate for unexpected perturbations, thus improving stability and adaptability in real-world deployments. See Figure 1 for a side-by-side comparison with prior approaches.

The main contributions of this work are summarized as follows:

• A novel reinforcement learning (RL) framework is proposed, driven by skeletal information. Joint positions relative to the body and parent link lengths and masses are encoded using a graph neural network (GNN), enriching observations and accelerating the convergence of both reinforcement and imitation learning. This enables fast, robust, and regular blind locomotion, such as climbing stair, without relying on navigation or external perception.
• The framework integrates a single-stage teacher–student approach and a system-response model. The single-stage strategy jointly optimizes both teacher and student policies, improving the efficiency of sim-to-real transfer, while the system-response model enhances adaptability to environmental disturbances by predicting future states from historical observations.
• The proposed approach leverages Wasserstein-based Adversarial Motion Priors (wAMP) to address the mode collapse issue that arises when training on multi-terrain datasets. By replacing the standard GAN loss with Wasserstein divergence, wAMP stabilizes adversarial imitation learning, promotes diverse gait generation, and prevents collapse on unseen terrains. This enables quadrupedal robots to efficiently learn from mixed datasets containing both flat-ground walking and complex stair locomotion. As a result, the training process achieves faster convergence across varied terrains, while the learned policies exhibit smoother and more adaptive transitions, such as ascending and descending stairs.

2. Materials and Methods

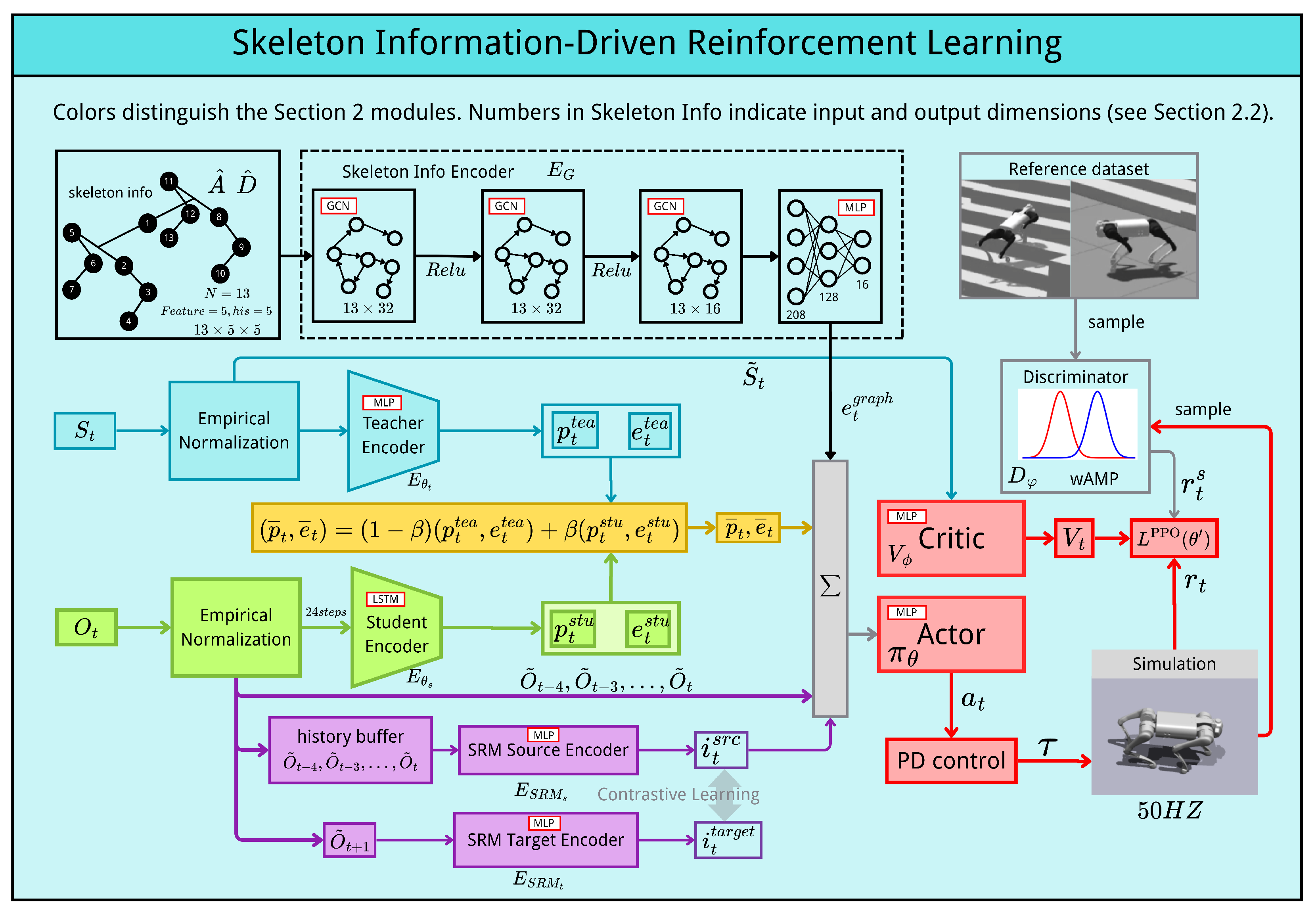
Figure 2 illustrates the overall architecture of our framework, which integrates four key components to achieve robust and natural quadrupedal locomotion. First, the skeleton-aware Graph Convolutional Network (GCN) encoder (Section 2.2) processes skeletal information from 13 nodes representing the robot’s kinematic structure. Each node is characterized by 25 features across 5 consecutive time steps, capturing joint positions, link lengths, and masses. The GCN produces a 16-dimensional embedding $e_t^{graph}$ that encodes spatial relationships and body awareness. Second, the teacher–student framework (Section 2.3 and Section 2.4) enables efficient sim-to-real transfer. The teacher encoder receives privileged information ($S_t^p$ and $S_t^e$), while the student encoder processes 24 steps of proprioceptive observation history ($O_{24steps}$). Their outputs are adaptively aggregated using coefficient $\beta$, controlled by hybrid advantage estimation (HAE). Third, the system-response model (Section 2.5) enhances robustness by predicting future robot states from historical observations. Using contrastive learning, it aligns past observations ${\tilde{o}}_{t-5:t}$ with future states ${\tilde{o}}_{t+1}$, generating implicit response features $i_t^{src}$ that capture system dynamics. Finally, the actor network combines all embeddings to generate actions $a_t$, optimized via Proximal Policy Optimization (PPO) with style rewards from the Wasserstein Adversarial Motion Priors (wAMP) discriminator (Section 3.5).

2.1. Reinforcement Learning Problem Formulation

The locomotion control of the legged robot is modeled as a partially observable Markov decision process $\mathcal{P}=(\mathcal{S},\mathcal{O},\mathcal{A},p,r,\gamma )$ [34], where state, observation, and action are denoted as $s\in \mathcal{S}$, $o\in \mathcal{O}$, and $a\in \mathcal{A}$. The state transition probability is defined as $p(s_{t+1}\mid s_t,a_t)$. The policy $\pi$ selects actions based on H steps of historical observations $a_t\sim \pi (·\mid o_t^H)$. The reward function is $r_t=r(s_t,a_t)$ with a discount factor $\gamma \in [0,1)$, while the objective is to maximize cumulative discounted rewards:

$$J\left(\pi \right)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)\right].$$

(1)

Table 1. Components of partial observations $O_t$ and states $S_t$, $S_t^p,S_t^e\in S_t$.

Name	Dimension	Noise Level	Category
Command	3	0	$O_t$
Base Angular Velocity	3	±0.2 rad/s	$O_t$
Projected Gravity	3	±0.05 rad/s2	$O_t$
DoF Position	12	±0.01 rad	$O_t$
DoF Velocity	12	±1.5 rad/s	$O_t$
DoF Action	12	0	$O_t$
$O_t$ (Without noise)	45	–	$S_t$
Terrain Information	187	–	$S_t^e$
base linear velocity	3	–	$S_t^p$
Base Height	1	–	$S_t^p$
ground friction coefficients	1	–	$S_t^p$
ground restitution coefficients	1	–	$S_t^p$
foot contact forces	12	–	$S_t^p$
external forces and their positions	6	–	$S_t^p$
collision states (trunk, thigh, shank)	12	–	$S_t^p$

summarizes the construction and physical meaning of observations and states. The noise levels are adopted from [35].

2.2. Skeleton Information Encoder

In this paper, the Unitree GO1 quadruped robot is modeled with 13 nodes: one base node, eight joint nodes, and four foot nodes. The adjacency matrix is constructed based on the physical connectivity of these nodes. The ordering of the nodes, along with the corresponding adjacency matrix $\widehat{A}$ and the degree matrix $\widehat{D}$ are illustrated in Figure 3. It is worth noting that for the two closely adjacent joints on the shoulder of the Unitree robot, the proposed method has selected only the HIP joint for modeling.

The output feature matrix $Y\in {\mathbb{R}}^{N\times F^{\prime }}$ for a graph convolutional layer is computed as:

$$Y={\widehat{D}}^{-1/2}\widehat{A}{\widehat{D}}^{-1/2}X\Theta$$

(2)

where the input is the feature matrix $X\in {\mathbb{R}}^{N\times F}$ (representing N nodes, each with F input features) and the trainable weight matrix $\Theta \in {\mathbb{R}}^{F\times F^{\prime }}$. This operation aggregates and transforms node features based on the graph structure encoded in the renormalized adjacency matrix ${\widehat{D}}^{-1/2}\widehat{A}{\widehat{D}}^{-1/2}$, producing an output where each node is now represented by $F^{\prime }$ new features. Subsequent layers propagate features iteratively as:

$$H^{l+1}=\sigma \left({\widehat{D}}^{-1/2}\widehat{A}{\widehat{D}}^{-1/2}{H}^l{W}^l\right)$$

(3)

where the input is the feature matrix $H^l$ from the l-th layer and the layer-specific trainable weight matrix $W^l$. The output $H^{l+1}$ is the updated feature matrix for the next layer, with $\sigma (·)$ being the ReLU activation function [25].

The proposed graph neural network (GNN) encoder architecture is illustrated in Figure 2. Each node in a state is characterized by a 5-D input feature vector, including its position in the body coordinate system, as well as the length and mass of the previous link. By stacking the five most recent consecutive states, each node obtains 25 features in total, resulting in an input dimension of $E_G$ of (13, 25). After three layers of the GCN with the number of hidden features 32, 32 and 16, respectively, each node will be represented by a 16-features vector, these features represent the relationships between the nodes that affect each other. Then, the features of thirteen nodes are flattened into a 208-dimensional vector before passing through fully connected layers to encode them into a 16-dimensional embedding $e_t^{graph}$, which is input to actor networks.

Through domain randomization of physical parameters during training, the GCN learns to extract structural features that remain stable across different dynamic conditions. This allows the skeleton encoding to provide a reliable morphological representation that works with varying contact dynamics, friction coefficients, and external disturbances, making it robust to diverse physical environments encountered during deployment.

2.3. Teacher and Student Encoder Networks

To simplify the learning process and mitigate training challenges, a latent representation is created by implicitly reducing the dimensionality of the privileged state. For successful sim-to-real transfer, the proposed approach employs a teacher encoder (TE) and a student encoder (SE), which are parameterized by ${\theta }_t$ and ${\theta }_s$ respectively. The TE is designed to function as an environmental factor network, taking as input privileged information $S_t^p$ along with terrain details $S_t^e$. In contrast, the SE, which acts as an adaptation network, receives only historical information $O_{24steps}$. Both encoders generate a set of latent feature vectors. This approach allows the student to acquire a policy that is suitable for real-world deployment, as it learns from non-privileged sensor data.

The specifics of the TE and SE are described below:

$$p_t^{tea},e_t^{tea}=E_{{\theta }_t}(S_t^p,S_t^e)$$

(4)

$$p_t^{stu},e_t^{stu}=E_{{\theta }_s}\left(O_{24steps}\right)$$

(5)

The proposed framework enables single-stage training of the entire teacher–student network. Drawing inspiration from adaptive asymmetric DAgger (A2D) [36], an adaptive coefficient $\beta$ is introduced for each agent. This coefficient dynamically adjusts the mixture between the teacher’s encoding of environmental information and the student’s encoding of historical proprioceptive observations, as defined by the following equation:

$$({\overline{p}}_t,{\overline{e}}_t)=(1-\beta )(p_t^{tea},e_t^{tea})+\beta (p_t^{stu},e_t^{stu})$$

(6)

$${\mathcal{L}}_{\mathrm{distill}}=\mathrm{MSE}(p_t^{\mathrm{stu}},p_t^{\mathrm{tea}})+\mathrm{MSE}(e_t^{\mathrm{stu}},e_t^{\mathrm{tea}})$$

(7)

The teacher–student framework serves two main purposes. First, it helps reduce the sim-to-real gap by allowing the student to learn a deployable policy using only onboard sensors. Second, it enables blind locomotion by teaching the student to infer surrounding terrain from proprioceptive signals alone. The mechanism works by having the student encoder approximate both the privileged information encoding $p_t^{tea}$ and the terrain encoding $e_t^{tea}$ that the teacher obtains only in simulation. Through processing 24-step historical proprioceptive observations with LSTM, the student learns to reconstruct these features from motion patterns, enabling terrain-aware control without external sensors.

2.4. Hybrid Advantage Estimation (HAE) and Adaptive Aggregation

Traditional A2D methods often link $\beta$ updates to a fixed number of training iterations, a strategy that can introduce instability. To overcome this, a novel hybrid advantage estimation method (HAE) [23] is introduced, which provides a reliable metric (Equation (8)) to evaluating policy improvement. HAE determines whether a policy update from ${\pi }_{\theta }$ to ${\pi }_{{\theta }^{\prime }}$ results in an increased reward advantage.

$$A^{{\pi }_{\theta }}=E_{s\sim D^{{\pi }_{\theta }}}{E}_{a\sim {\pi }_{\theta }}\left[{\tilde{A}}_R^{{\pi }_{\theta }}(s,a)\right]$$

(8)

This metric is then used to intelligently govern the adjustment of $\beta$ according to this rule:

$$\beta \leftarrow \beta +\delta ·B_{p^{mtl-TE}\ge 1}·B_{A^{{\pi }_{\theta }^{\prime }}-A^{{\pi }_{\theta }}>0}$$

(9)

Here, B denotes the indicator function and $p^{mtl-TE}$ indicates whether the agent, following the teacher’s policy, has reached an average terrain difficulty level of 5.

The curriculum learning strategy is fully detailed in Section 3.1. Initially, $\beta$ is set to 0. The teacher’s latent representation is considered sufficiently accurate once the agent reaches an average terrain difficulty level of 5. At this point, the teacher encoder’s parameters are frozen, and the student encoder begins to actively participate in RL training. As $\beta$ increases by $\delta$ based on the change in HAE, the influence of student gradually increases until $\beta$ reaches 1, signifying a full transition where the student alone interacts with the environment. Guided by HAE, this adaptive aggregation strategy enables the student to reliably imitate the teacher while mitigating over-reliance.

2.5. System-Response Model

To enhance robustness against external disturbances, a system-response model [29] is incorporated. The principle follows Internal Model Control (IMC) [37], which suggests that robust control can be achieved by simulating system responses instead of directly modeling disturbances. In legged locomotion, disturbances such as terrain elevation, friction, and restitution are difficult to model explicitly. Instead, the system-response module predicts the robot’s reaction to implicit stability requirements.

In concrete terms, a history of proprioceptive observations ${\tilde{o}}_{t-5:t}$ is encoded by an encoder $E_{SR{M}_s}$ into a latent embedding, represented as the implicit response feature $i_t^{src}$.The training objective is to ensure that the embedding accurately represents the successor state of the robot ${\tilde{o}}_{t+1}$. The implicit response $i_t^{src}$ is optimized with contrastive learning. Specifically, pairs of $({\tilde{o}}_{t-5:t},{\tilde{o}}_{t+1})$ sampled from the same trajectory are treated as positive pairs, while pairs from different trajectories are negative. Setting positive and negative pairs allows the system-response model to learn discriminative representations: Positive pairs encourage the embedding to capture consistent dynamics between past observations and their true successor state, while negative pairs push apart embeddings from unrelated trajectories. A source encoder $E_{SR{M}_s}$ processes ${\tilde{o}}_{t-5:t}$ and a target encoder $E_{SR{M}_t}$ processes ${\tilde{o}}_{t+1}$, producing normalized latent features $i_t^{\mathrm{src}}$ and $i_t^{\mathrm{target}}$. Cluster assignment probabilities are computed via:

$$p_t^{\mathrm{src}}={\displaystyle \frac{exp\left(\frac{1}{\tau }{i}_t^{\mathrm{src}\top }{e}_k\right)}{{\sum }_{k^{\prime }}exp\left(\frac{1}{\tau }{i}_t^{\mathrm{src}\top }{e}_{k^{\prime }}\right)}}\mathrm{and}{p}_t^{\mathrm{target}}={\displaystyle \frac{exp\left(\frac{1}{\tau }{i}_t^{\mathrm{target}\top }{e}_k\right)}{{\sum }_{k^{\prime }}exp\left(\frac{1}{\tau }{i}_t^{\mathrm{target}\top }{e}_{k^{\prime }}\right)}}$$

(10)

where $\left\{e_k\right\}$ are normalized prototypes and $\tau$ is a temperature parameter. The representation learning objective is to minimize the following loss function:

$${\mathcal{L}}_{\mathrm{SwAV}}=-{\displaystyle \frac{1}{2H}}\sum _{t=1}^H\left(q_t^{\mathrm{src}}log{p}_t^{\mathrm{target}}+q_t^{\mathrm{target}}log{p}_t^{\mathrm{src}}\right).$$

(11)

where q represents the target assignments obtained by the Sinkhorn-Knopp algorithm [38], which helps to avoid trivial solutions. This optimization framework enables the implicit response model to learn a meaningful representation of the robot’s dynamics, which is important for handling external disturbances.

The System-Response Model helps the robot handle external disturbances and dynamic uncertainties. By learning to predict the robot’s future state from historical observations through contrastive learning, the SRM captures how the robot responds to disturbances such as terrain variations, friction changes, and external forces without explicitly modeling these factors. The learned response embedding $i_t^{src}$ is integrated into the actor network, providing the policy with system dynamics information.

2.6. Network Architecture Details

Our framework integrates multiple network modules with different architectures.

Table 2. Details of network architecture.

Module	Inputs	Architecture	Outputs
Skeleton Info Encoder *	skeleton info	GCN + MLP *	$e_t^{graph}$
Teacher Encoder	${\tilde{S}}_t^p,{\tilde{S}}_t^e$	[256, 128]	$p_t^{tea},e_t^{tea}$
Student Encoder *	${\tilde{O}}_{24steps}$	LSTM + MLP *	$p_t^{stu},e_t^{stu}$
SRM Source Encoder	${\tilde{O}}_{t-4:t}$	[128, 64]	$i_t^{src}$
SRM Target Encoder	${\tilde{O}}_{t+1}$	[128, 64]	$i_t^{target}$
Actor Network	${\tilde{O}}_{5steps},i_t^{src},{\overline{p}}_t,{\overline{e}}_t,e_t^{graph}$	[512, 256, 128]	$a_t$
Critic Network	${\tilde{S}}_t$	[512, 256, 128]	$v_t$
wAMP Discriminator	$M_t,M_{t+1}$	[1024, 512]	$R_t^s$

An asterisk (*) denotes a non-MLP specialized architecture. Details are provided in the main text.

provides an overview of all components, where standard MLP modules list their hidden layer dimensions in the “Architecture” column, and the specialized architectures are marked with asterisks.

The Skeleton Info Encoder employs a 3-layer Graph Convolutional Network with channel dimensions [N × 32, N × 32, N × 16], where N is the number of skeleton nodes. The GCN output is then processed through an MLP with layers [N × 16, 128, 16] to produce the final graph embedding $e_t^{graph}$. The Student Encoder consists of a 3-layer LSTM with hidden size 256 that processes the 24-step observation history, followed by an MLP with layers [256, 64, 16] to extract the information embedding $p_t^{stu}$ and the environment embedding $e_t^{stu}$.

All networks are optimized using the Adam optimizer with default learning rates, except for the wAMP Discriminator which uses the RMSProp optimizer.

3. Training Process

3.1. Training Curriculum

A total of 4096 parallel agents were trained on different types of terrain using the IsaacGym simulator [35], which supports NVIDIA RTX 30-series GPUs (NVIDIA Corporation, Santa Clara, CA, USA) [39]. The teacher and student policies were trained simultaneously in a single stage with a total of 800 simulated time steps. The total training time for this process was 7 h of wall-clock time. Each RL episode lasts for a maximum of 1000 steps, equivalent to 20 s, and terminates early if it reaches the termination criteria. The control frequency of the policy is 50 Hz in the simulation. All trainings were performed on a single NVIDIA RTX 4090 GPU. The primary memory requirement stems from our 24-step LSTM encoder; for resource-constrained settings, lightweight alternatives such as GRU units can be adopted to reduce memory footprint [11].

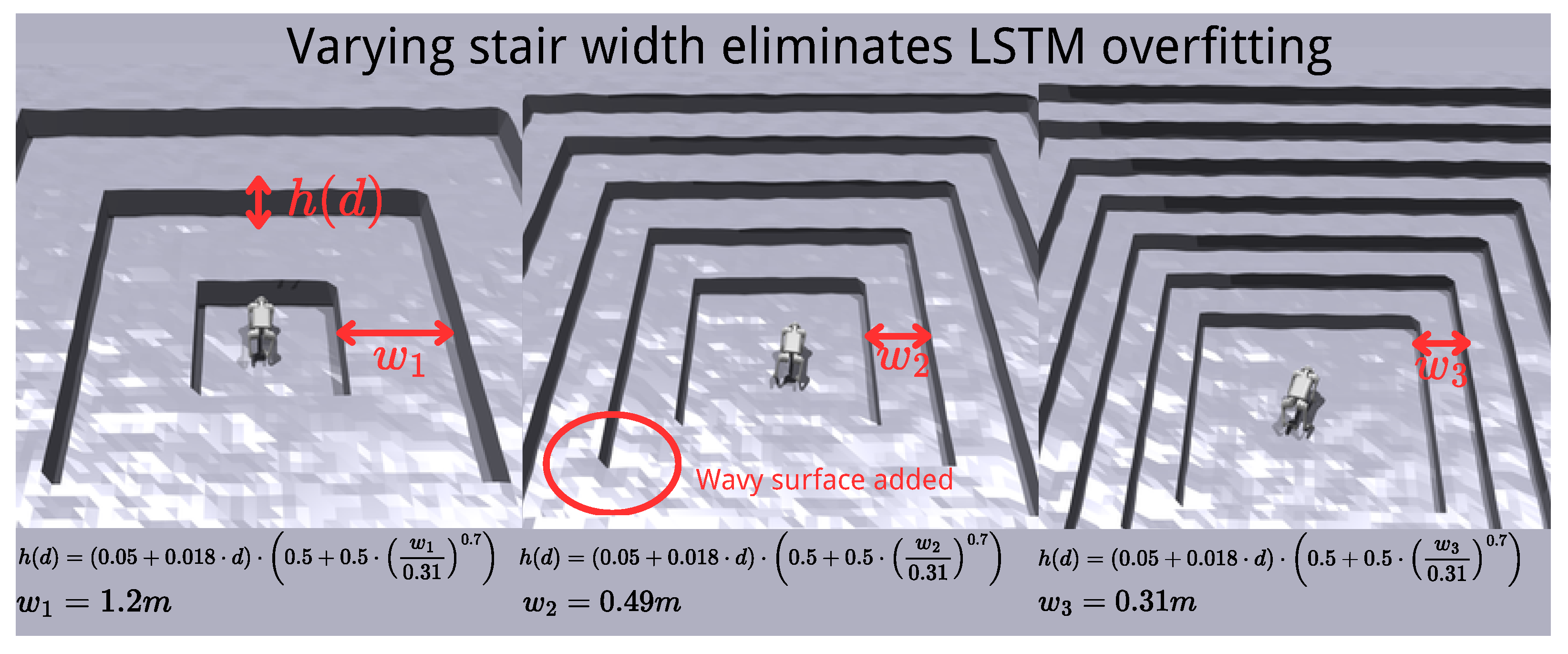
To address the overfitting issue of the LSTM encoder caused by repetitive terrain patterns, especially the false identification of flat ground as stairs, a diverse set of stairs terrains was designed with varying step widths and heights (Figure 4). Specifically, the step width is randomly sampled from a range between 0.31 and 1.2 m, allowing the robot to experience transitions where the entire base can stand on a single step. This increases the diversity of terrain transitions and improves the policy’s ability to distinguish between flat surfaces and obstacles, thereby enhancing deployment stability in real-world scenarios.

The terrain setup included four procedurally generated types as [35]: smooth slopes, rough slopes, stairs, and discrete obstacles. A height field map comprising 100 terrain segments was arranged in a grid $20\times 10$, each row representing a specific terrain type and the difficulty progressively increasing from left to right. All terrains maintained a uniform size of $8\mathrm{m}\times 8\mathrm{m}$.

Smooth sloped terrains are generated with inclinations gradually increasing from 0° to 45°. Rough slopes use the same slope range but include surface irregularities by adding elevation noise with a maximum amplitude of $5\mathrm{cm}$. The stairs consist of four types with step widths of $0.31\mathrm{m}$, $0.40\mathrm{m}$, $0.49\mathrm{m}$, and $1.2\mathrm{m}$; wider stairs are associated with higher maximum step heights to enrich terrain diversity. Discrete terrains feature obstacles with two height levels, progressively increasing from $\pm 5\mathrm{cm}$ to $\pm 15\mathrm{cm}$.

At the beginning of training, all robots are randomly initialized on terrains with difficulty levels ranging from 0 to 4 (with a maximum difficulty of 9). During each reset, if the robot moves beyond half of the terrain width, it will progress to a higher difficulty level. Conversely, if the robot fails to cover at least half of the expected distance based on its commanded velocity, the difficulty level will be reduced. To prevent skill forgetting, robots that reach the highest difficulty are reset to a randomly selected difficulty within the current terrain type.

A command-conditioned policy was trained using velocity tracking. Each episode began with a desired command comprising longitudinal, lateral, and yaw velocities in the base frame. Two command curricula were employed: heading commands (60% probability) facilitated rapid terrain navigation by guiding yaw alignment before forward movement, while randomly sampled commands (40% probability) fixed the yaw axis within a command cycle and varied forward velocities. This design allowed the agent to practice in-place rotation more frequently, thus preventing unnatural spinning behaviors.

Episodes ended after meeting failure criteria including trunk-ground collisions, excessive body inclination, or prolonged immobilization.

3.2. Dynamics Randomization

To enhance policy robustness and support sim-to-real transfer, domain randomization is applied during training by varying several dynamic properties at the beginning of each episode (

Table 3. Dynamic parameters and the range of their randomization values used during training.

Parameters	Range [Min, Max]	Unit
Link Mass	[0.8, 1.2] × nominal value	kg
Payload Mass	[0, 3]	kg
Payload Position	[−0.1, 0.1] relative to base	m
Ground Friction	[0.05, 2.75]	-
Ground Restitution	[0.0, 1.0]	-
Motor Strength	[0.8, 1.2] × motor torque	Nm
Joint $K_p$	[0.8, 1.2] × 20	-
Joint $K_d$	[0.8, 1.2] × 0.5	-
Initial Joint Positions	[0.5, 1.5] × nominal value	rad

). These include the mass of the robot’s trunk and limbs, the payload’s mass and location on the body, ground friction and restitution coefficients, actuator strength, joint-level proportional-derivative (PD) gains, and initial joint configurations. A subset of these randomized parameters is treated as a privileged state $s_p$ to assist in training the teacher policy. Additionally, observation noise is injected following the same scheme as described in [35].

3.3. Motion Capture Data Preprocessing

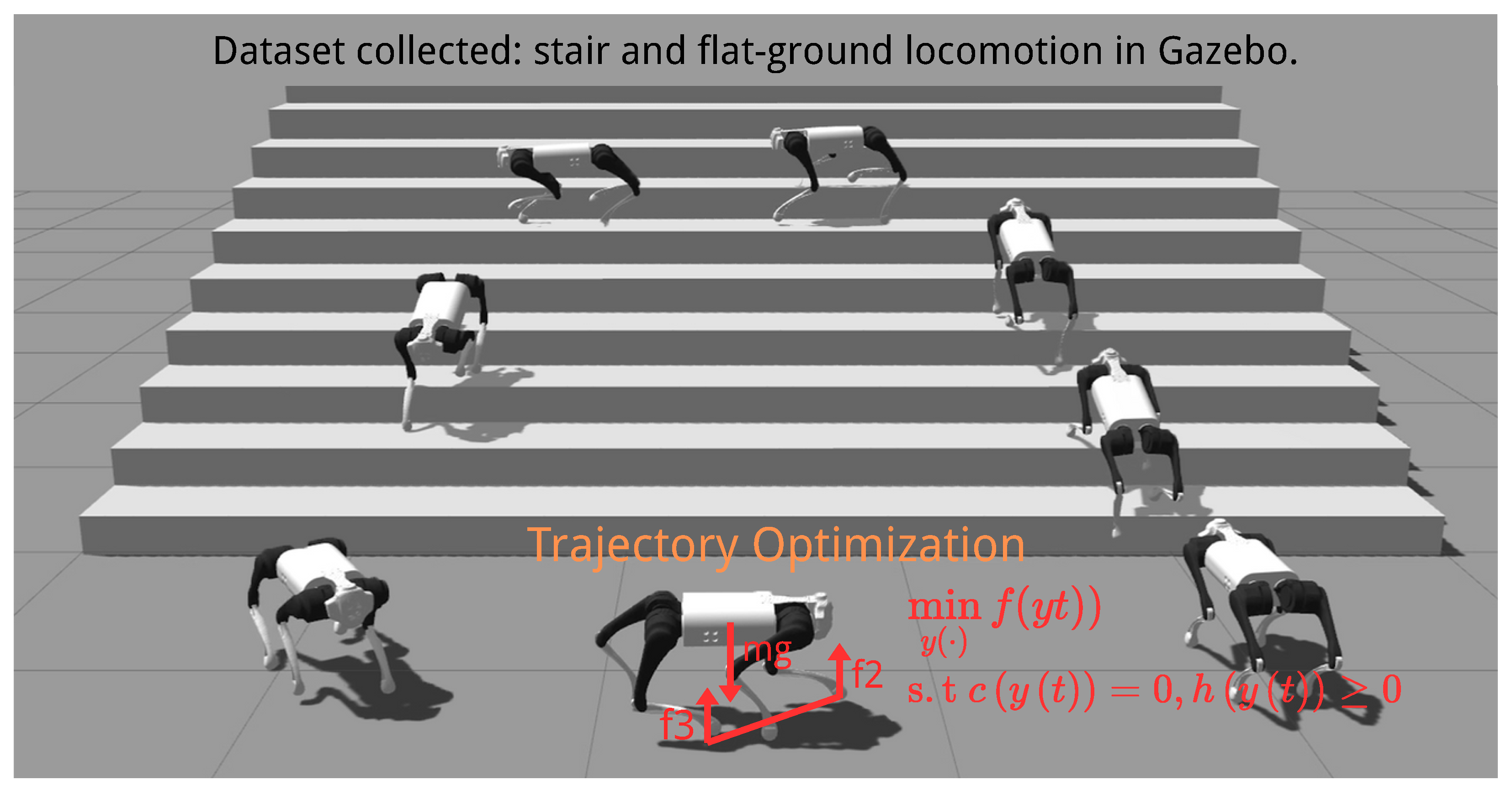
Since only state transitions are required to construct the motion dataset D, this article adopts a trajectory optimization (TO) approach [40] based on centroidal dynamics to generate quadrupedal locomotion trajectories with a trotting gait on flat terrain. Specifically, the OCS2 framework is used [41,42] to solve the TO problem, which explicitly enforces friction cone constraints and kinematic constraints.

To collect motion data, a traditional control simulation of the Unitree Go2 quadrupedal robot is deployed in the Gazebo 11 environment (Figure 5). During the simulation, state transitions are recorded at a frequency of 50 Hz. Each recorded frame consists of joint positions, joint velocities, base linear velocity, base angular velocity, and base height. The dataset D includes trajectories of forward, backward, lateral left, lateral right, left steering, right steering, and combined locomotion, with a total duration of approximately 30 s.

3.4. Reward Terms Design

In this work, the overall reward function is composed of four components: a task term $r_t^g$, a regularization term $r_t^l$, a contact term $r_t^c$, and a style term $r_t^s$. The total reward is given by:

$$r_t=r_t^g+r_t^l+r_t^c+r_t^s.$$

(12)

To encourage accurate tracking behavior, the task reward focuses on minimizing the error between the commanded and actual linear and angular velocities.

Regularization terms are introduced to promote smooth joint motion, consistent gait patterns, and base stability.

The contact reward helps the robot move more smoothly when stepping over obstacles by reducing undesired foot collisions and promoting cleaner foot placement during contact transitions.

Finally, the style reward measures how well the agent’s behavior matches expert motion patterns from a reference dataset $\mathcal{D}$. It is computed using an wAMP discriminator that assigns high scores to agent behaviors resembling those in the demonstration set. This reward term encourages natural and smooth trotting gaits.

To ensure training stability and handle the unbounded output of the Wasserstein discriminator, the style reward $r_t^s$ is normalized using running statistics. The exponential moving average of the mean $\mu$ and variance ${\sigma }^2$ of the discriminator’s outputs over recent batches is maintained. The reward is then calculated as:

$$r_t^s={\displaystyle \frac{D_{\varphi }(s_t,s_{t+1})-\mu }{\sqrt{{\sigma }^2+ϵ}}}$$

(13)

This normalization scheme centers the reward around zero and maintains a consistent scale, which significantly improves the stability of the reinforcement learning process.

The details of the reward functions are shown in

Table 4. Design of reward functions.

Term	Equation	Weight
Task Reward $r^g$	$exp\left(-{\displaystyle \frac{\parallel v_{t,xy}^{\mathrm{des}}-v_{t,xy}{\parallel }_2}{0.25}}\right)$	1.3
	$exp\left(-{\displaystyle \frac{\parallel {\omega }_{t,z}^{\mathrm{des}}-{\omega }_{t,z}{\parallel }_2}{0.25}}\right)$	0.65
Regularization Reward $r^l$	$-{\parallel \tau \parallel }_2$	$1\times {10}^{-4}$
	$-\parallel \ddot{q}{\parallel }_2$	$2.5\times {10}^{-7}$
	$-\parallel q_{t-1}-q_t{\parallel }_2$	$0.1$
	${\sum }_{i=0}^{4}min\left(t_{\mathrm{air},i}-0.35,0\right)$	$1.0$
	$-\parallel v_{t,z}{\parallel }_2^2$	2
	$-\sum \parallel {\omega }_{t,xy}{\parallel }_2^2$	0.05
	$-{\left(h_{\mathrm{base}}-h_{\mathrm{target}}\right)}^2$	1
Contact Reward $r^c$	$-n_{\mathrm{collision}}$	0.1
	$-\parallel {\mathbf{f}}_{xy}{\parallel }_2>5\left|{\mathbf{f}}_z\right|$	0.6
Style Reward $r^s$	$r_t^s={\displaystyle \frac{D_{\varphi }(s_t,s_{t+1})-\mu }{\sqrt{{\sigma }^2+ϵ}}}$	0.5

.

3.5. Adversarial Motion Priors with Wasserstein Divergence

Following [18], a discriminator $D_{\varphi }$ is defined as a neural network with parameters $\varphi$, which predicts whether a state transition $(s_t,s_{t+1})$ is a real sample from the dataset $\mathcal{D}$ or a fake sample produced by the agent $\mathcal{A}$.

Each state $s_t^{\mathrm{AMP}}\in {\mathbb{R}}^{35}$ consists of joint positions, joint velocities, base linear velocity, base angular velocity, foot positions, and base height relative to terrain. The inclusion of foot positions is crucial to ensuring that the learned motion does not cause excessive foot dragging. Moreover, in the reference dataset, when executing a stop command, the robot comes to a halt with all four feet grounded, ensuring that the learned policy stabilizes the feet in place when stopping. This design helps prevent unintended foot movements and improves the naturalness of stopping behaviors.

The conventional GAN-based discriminator, trained solely on flat-terrain motion data, utilizes a Least-Squares GAN (LSGAN) objective with a gradient penalty term. However, this approach is prone to mode collapse when the agent’s policy explores motions that are valid but fall outside the narrow distribution of the flat-terrain dataset, leading to vanishing gradients and hindering the learning of diverse, adaptive locomotion skills.

To overcome these limitations, a Wasserstein-based objective is adopted to train the discriminator $D_{\varphi }$. This formulation provides smoother gradients and prevents mode collapse by maximizing the Wasserstein distance between the distributions of agent motions and reference demonstrations. The discriminator is optimized using RMSProp with the following update rule:

$$\widehat{\mathit{S}}\leftarrow ϵS_{\mathcal{A}}+(1-ϵ)S_{\mathcal{D}},\mathrm{a}\mathrm{random}\mathrm{number}ϵ\sim U[0,1]$$

(14)

$${\mathcal{L}}_{\mathrm{wAMP}}={\displaystyle \frac{1}{m}}\sum _{i=1}^m{D}_{\phi }\left(s_{\mathcal{A}}^{\left(i\right)}\right)-{\displaystyle \frac{1}{m}}\sum _{i=1}^m{D}_{\phi }\left(s_{\mathcal{D}}^{\left(i\right)}\right)+\lambda (\parallel {\nabla }_{\widehat{\mathit{S}}}{D}_{\phi }\left(\widehat{\mathit{S}}\right){{\parallel }_2-1)}^2$$

(15)

3.6. Training Pipeline

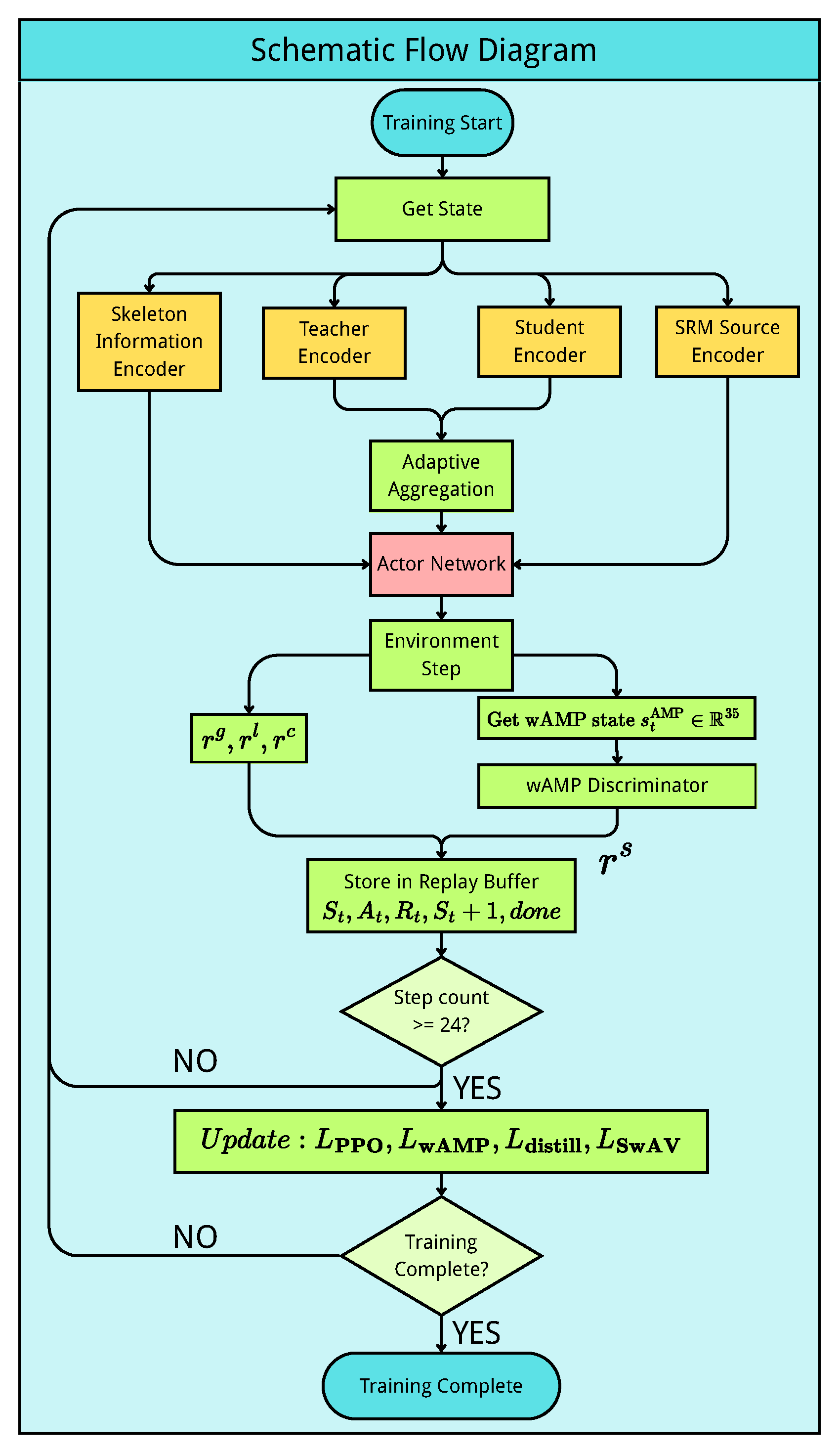
Figure 6 illustrates the complete training workflow of our framework. The training process follows a standard reinforcement learning loop with multiple specialized components working together.

Environment Initialization and State Acquisition. At the beginning of each episode, the environment is reset and the initial state $S_t$ is obtained from the simulation. This state contains observations $O_t$ (proprioceptive information), privileged states $S_t^p$ (simulation-only information such as base linear velocity and contact forces), terrain information $S_t^e$ (height map), and skeleton information (robot morphology).

Encoder Processing. Different components of the state are processed by their respective encoders. The Student Encoder processes 24-step observation history through LSTM and MLP to produce embeddings $p_t^{stu}$ and $e_t^{stu}$. The Teacher Encoder processes privileged and terrain information to generate $p_t^{tea}$ and $e_t^{tea}$. The SRM Source Encoder processes 5-step observation history to extract dynamics embedding $i_t^{src}$. The Skeleton Encoder uses GCN and MLP to encode the robot’s morphology into $e_t^{graph}$.

Adaptive Fusion and Action Generation. The teacher and student embeddings are adaptively fused using coefficient $\beta$ as described in Equation (6). The Actor Network integrates multiple inputs including 5-step observations, SRM embedding $i_t^{src}$, fused embeddings ${\overline{p}}_t$ and ${\overline{e}}_t$, and skeleton embedding $e_t^{graph}$ to generate action $a_t$.

Environment Interaction and Reward Calculation. The action is executed in the simulation environment, yielding the next state $S_{t+1}$ and a done flag. The total reward $R_t$ is computed as the sum of task reward and style reward. The style reward is provided by the wAMP discriminator evaluating motion features $s_t^{AMP}$ extracted from the current state.

Experience Collection. The tuple $(S_t,A_t,R_t,S_{t+1},\mathrm{done})$ is stored in the replay buffer. This process repeats for 24 time steps to accumulate sufficient experience for network updates.

Network Update. After collecting 24 steps of experience, all networks are updated. The PPO loss ${\mathcal{L}}_{\mathrm{PPO}}$ consists of three components:

• Surrogate Loss:

  $${\mathcal{L}}_{\mathrm{surrogate}}={\mathbb{E}}_t\left[max\left(-A_t·r_t,-A_t·\mathrm{clip}(r_t,1-ϵ,1+ϵ)\right)\right]$$

  (16)

  where $r_t=exp(log{\pi }_{\theta }\left(a_t\right|s_t)-log{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t\right|s_t))$ is the probability ratio, $A_t$ is the advantage, and $ϵ=0.2$ is the clipping parameter.
• Value Loss (with clipping):

  $${\mathcal{L}}_{\mathrm{value}}={\mathbb{E}}_t\left[max\left({(V_{\theta }\left(s_t\right)-R_t)}^2,{(\mathrm{clip}(V_{\theta }\left(s_t\right),V_{\mathrm{old}}-ϵ,V_{\mathrm{old}}+ϵ)-R_t)}^2\right)\right]$$

  (17)

  where $R_t$ is the return and $V_{\mathrm{old}}\left(s_t\right)$ is the previous value estimate.
• Entropy Loss:

  $${\mathcal{L}}_{\mathrm{entropy}}=-{\mathbb{E}}_t\left[\mathcal{H}\left({\pi }_{\theta }(·|s_t)\right)\right]$$

  (18)

  which encourages exploration by maximizing policy entropy.

• The complete PPO loss is:

  $${\mathcal{L}}_{\mathrm{PPO}}={\mathcal{L}}_{\mathrm{surrogate}}+1.0·{\mathcal{L}}_{\mathrm{value}}-0.01·{\mathcal{L}}_{\mathrm{entropy}}$$

  (19)
• The total training loss combines PPO with auxiliary losses:

  $${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{PPO}}+{\mathcal{L}}_{\mathrm{SwAV}}+{\mathcal{L}}_{\mathrm{distill}}+{\mathcal{L}}_{\mathrm{AMP}}$$

  (20)

  where ${\mathcal{L}}_{\mathrm{SwAV}}$, ${\mathcal{L}}_{\mathrm{distill}}$, and ${\mathcal{L}}_{\mathrm{AMP}}$ are the contrastive loss, distillation loss, and discriminator loss as described in their respective subsections.

4. Results

4.1. Hardware

The controller is deployed on the Unitree Go1 Air robot (Unitree Robotics Co., Ltd., Hangzhou, China), which stands 33 cm tall and weighs 13 kg. The sensors used on the robot consist of joint position encoders and an IMU. The trained student policy is optimized by using the ONNX framework to improve inference speed and runs on a laptop with a Ryzen 7 5800H CPU (Advanced Micro Devices, Inc., Santa Clara, CA, USA). For deployment, the control frequency is 50 Hz. As shown in Figure 7, the trained policy enables the robot to perform various locomotion tasks, including obstacle crossing, stair climbing, recovery from missteps, and payload balancing. A demonstration of the quadruped robot locomotion and additional experiments are provided in the Supplementary Materials (Videos S1–S6).

4.2. Long-Distance Locomotion and Torque Analysis Under Extreme Conditions

Figure 8 provides visual and data analysis illustrating the quadruped robot’s performance across diverse challenging scenarios. The curves represent the motor torque trajectories during different test conditions, offering insight into how the policy adapts to varying terrains and disturbances.

The experiment begins with a long-distance stability test in a park environment covering approximately 300 m, which includes steep slopes, consecutive steps, and dense vegetation. This extended traverse validates the policy’s ability to maintain consistent locomotion over prolonged periods while handling terrain variations. The torque measurements during this phase reveal how the robot continuously adjusts joint actuation to accommodate surface changes.

Subsequently, the robot is tested under two extreme conditions: slippery surfaces and heavy payload (10 kg). Figure 8 highlights torque data from four representative scenarios: continuous stairs, steep slope, 10 kg payload, and oil-contaminated slippery surfaces. When ascending continuous stairs, torque spikes correspond to the moment when the swing leg lifts to clear each step height, with the stance legs providing increased support. On steep slope, sustained elevated torque is observed in the hip and knee joints to counteract gravitational pull. Under 10 kg payload (approaching the robot’s own body weight), the torque profiles exhibit uniformly higher magnitudes across all joints throughout the gait cycle as the actuators compensate for the additional mass. On oil-contaminated slippery surfaces, torque fluctuations become more frequent as the policy continuously adjusts to maintain traction and balance, with the reduced ground friction forcing more conservative torque modulation to prevent excessive foot slipping.

These torque measurements serve as direct indicators of the policy’s internal decision-making process. Unlike kinematic variables such as joint angles or angular velocities, torque reflects the actual control effort required under varying physical constraints. The consistent and adaptive torque profiles across all test scenarios demonstrate the robustness and effectiveness of our skeleton information-driven reinforcement learning framework.

4.3. Evaluation of Training Efficiency and Terrain Adaptation

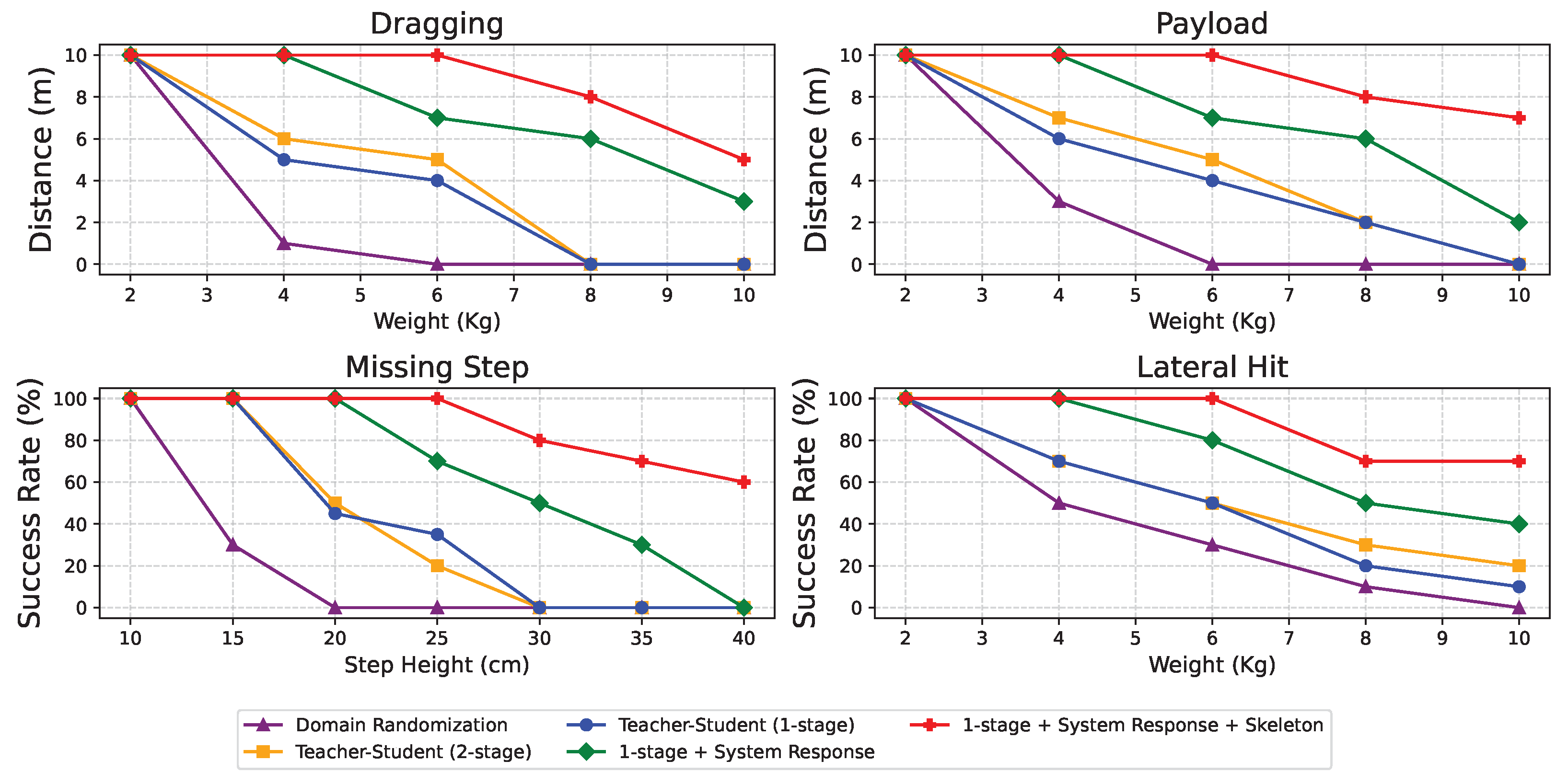
The training efficiency and terrain level of five representative strategies are analyzed. Domain Randomization (DR), Teacher–Student (2-stage), Teacher–Student (1-stage), 1-stage + System Response, and 1-stage + System Response + Skeleton. The evaluation metrics include: (i) the progression of cumulative rewards during training, which reflects the learning efficiency of each method, and (ii) the terrain level achieved during curriculum training, which indicates the adaptability to increasingly complex terrains.

As shown in Figure 9, the two-stage Teacher–Student framework benefits from the teacher policy’s access to terrain information, resulting in faster improvement compared to domain randomization alone. When the average difficulty in the terrain reaches level 5, the student training phase begins, causing the yellow curve to restart from zero. The student policy converges to the optimal performance in approximately 12,000 steps.

The single-stage Teacher–Student framework gradually mixes the student encoder once the teacher reaches terrain level 5. This design avoids the discontinuity of two-stage training and allows the policy to converge to the optimal value in about 10,000 steps. The final reward and terrain level achieved are higher than those of the two-stage framework.

Adding a system-response model and skeletal information encoding on top of the single-stage framework leads to faster convergence and higher performance. The system-response model enables anticipation and compensation for external disturbances, while the skeletal representation accelerates convergence of imitation learning convergence and enhances adaptability to challenging terrains such as stair environments, resulting in consistently superior outcomes.

4.4. Robustness on Large Obstacles and Unseen Terrains

The robustness of the robot is measured by its ability to handle challenging obstacles. As shown in Figure 10, the robot successfully steps over a 25 cm high obstacle, which is close to its own standing height of 33 cm. This obstacle height is significantly larger than the 8 cm foot clearance present in the AMP demonstration dataset. The policy, trained purely on proprioceptive observations without any exteroceptive sensors, exhibits emergent behaviors such as trunk lifting and foot raising after detecting a head collision, allowing for successful traversal. Additionally, the method is further evaluated against several baselines using only proprioception inputs.

• RMA [9]: A teacher–student framework with a 1D CNN adaptation module.
• Concurrent [31]: A jointly trained policy with a learned state estimator.
• Domain Randomization: A policy trained without privileged information.
• Built-in MPC: A model predictive controller (MPC) implemented on Unitree Go1.

All RL methods above were trained using the same curriculum strategy detailed in Section 3.1, the same reward functions detailed in Section 3.4 and the same random seed. For a fair comparison, the same low-level network architecture detailed in Table 2 is used for all RL methods. The CNN input sequence length for the RMA baseline was 50, with access to the same memory length as the LSTM encoder.

Each controller was evaluated in a single-step task using a remote-control command of 0.4 m/s. For each height of the step, the robot attempted to ascend or descend one step from the starting point, and a trial was considered successful if it completed the motion without falling. Each height was tested 10 times and the success rate was recorded. These experiments were carried out on the physical robot, and the results are reported in Figure 11.

To further evaluate the limits of the proposed method (1-stage + System Response + Skeleton), additional tests are conducted in simulation using Isaac Gym. In this setting, the environment consisted of ten parallel stair setups, each composed of five consecutive steps with varying heights. For each step height, 10 trials were performed in parallel, and the success rate was measured. As shown in Figure 12, the proposed method demonstrates enhanced robustness in simulation, successfully navigating step heights up to 35 cm.

4.5. Evaluation of Anti-Disturbance Capability

To examine the controller’s robustness against external perturbations, several physical disturbance tests are conducted on the Unitree Go1 robot, including dragging interference, payload loading, missing step, and lateral hit. All evaluations are performed in real-world scenarios using only proprioceptive observations:

• Dragging: To assess robustness against pulling disturbances, the robot is commanded to move forward at 0.4 m/s while dragging a pair of dumbbells. The maximum straight-line distance it can travel without falling is measured over 3 trials, with a maximum distance of 10 m.
• Payload: This test evaluates the robot’s ability to handle additional static loads. A dumbbell payload is fixed on the robot’s torso and is commanded to walk forward at 0.4 m/s. Performance is assessed by the maximum distance the robot can travel stably without falling, measured in 3 trials.
• Missing Step: The robot’s recovery from an unexpected drop is tested as it is commanded to walk forward at 0.4 m/s and step off a platform. The success rate of this maneuver is recorded over 10 trials.
• Lateral Hit: To evaluate the robot’s capability to recover push, a dumbbell attached to a pendulum is raised to 15° from the vertical and released from a height of 100 cm, with the robot positioned directly beneath the rope so that the mass delivers a lateral impact. The success rate for maintaining balance is recorded on 10 trials.

The method is first compared with several representative baselines to demonstrate its overall performance in handling these disturbances. The methods considered for this study include:

• RMA [9]: A teacher–student framework with a 1D CNN adaptation module.
• MoB [43]: A multi-behavioral controller trained for terrain generalization.
• Built-in MPC: The MPC controller provided by the factory on Unitree Go1.

As summarized in Figure 13, the approach demonstrates significantly improved robustness, outperforming all baseline methods against external perturbations. Although domain randomization allows other methods to handle payload and lateral impacts effectively, our approach demonstrates superior performance in dragging and missing-step scenarios. This is primarily attributed to the method’s ability to utilize skeletal information, allowing the robot to better detect when its rear feet are being dragged or its front feet miss a step.

To further validate the contribution of each component within the framework, an ablation study is conducted. This comparison includes the following training strategies:

• Domain Randomization (DR): The baseline approach where the agent is trained with domain randomization alone and deployed directly.
• Teacher-Student (2-stage): A two-stage framework where a teacher policy is first trained and then distilled to a student.
• Teacher-Student (1-stage): A single-stage framework where both teacher and student are trained jointly.
• 1-stage + System Response: The single-stage framework with the addition of the system-response model.
• 1-stage + System Response + Skeleton: The full proposed method, which includes both the system-response model and skeletal information encoding.

As shown in Figure 14, the method’s superior performance is a result of the effective integration of its core components. The system-response model allows the robot to proactively anticipate and compensate for external forces, making it exceptionally robust against payload and lateral hit disturbances. For the dragging test, the Graph Neural Network (GNN) encodes skeletal information, providing the policy with a deeper awareness of its own physical state under tension. Finally, success in the missing step test is a direct result of the specialized terrain curriculum, which trains the robot to handle complex vertical transitions by distinguishing between different ground surfaces and obstacles. This combination of proactive control, enhanced body awareness, and specialized training enables the method to consistently outperform other approaches.

5. Discussion

This work introduces a skeleton information-driven reinforcement learning framework that integrates a Graph Convolutional Network (GCN), a single-stage teacher–student architecture, a system-response model, and Wasserstein Adversarial Motion Priors (wAMP). The GCN encodes relative joint and foot positions, enriching the observation space and enabling more reliable gait generation on irregular terrains. Compared with previous two-stage methods such as RMA, single-stage training accelerates convergence and simplifies deployment. The system-response model further improves stability by implicitly encoding dynamic reactions, while wAMP mitigates mode collapse on multi-terrain datasets, allowing smoother transitions such as stair climbing. Together, these components produce robust and natural quadrupedal locomotion in diverse environments.

5.1. Constraints and Assumptions

While our experimental validation focuses on the Unitree GO1 quadruped, the framework is designed to be generalizable across different platforms. The skeleton-based encoding via Graph Convolutional Networks naturally adapts to different morphologies [25], and the teacher–student learning paradigm has shown consistent effectiveness across diverse quadruped platforms [9,17,33]. Our System-Response Model employs contrastive learning to capture system dynamics, a technique successfully applied across quadrupeds and humanoids [29,32,44]. Similarly, our AMP-based imitation learning has demonstrated effectiveness in both quadruped [39] and humanoid control [20,44]. Our current implementation deliberately focuses on proprioceptive feedback to establish robust blind locomotion capabilities [17,23,39]. However, the framework can be extended with exteroceptive sensing, as demonstrated by recent successful integrations of LiDAR [45] and vision [46] in legged robots. The framework supports diverse motion prior sources including motion capture data [20,30,44] and traditional control datasets [39]. These design choices position our framework for broader application beyond the GO1 platform, though comprehensive validation across multiple robots and sensing modalities remains important future work.

Table 5. Framework requirements and constraints by module.

Module	Robot Platform	Sensing	Motion Dataset	GPU Memory Overhead
Skeleton Info Encoder	–	Proprioceptive	–	+1 GB (GCN)
Teacher Encoder	–	Privileged state	–	+1 GB (MLP)
Student Encoder	–	Proprioceptive	–	+12 GB (LSTM)
System-Response Model	–	Proprioceptive	–	+1 GB (MLP)
AMP Discriminator	–	Proprioceptive	Motion priors (sim/mocap)	+1 GB (MLP)
Baseline (4096 envs IsaacGym): 6 GB GPU Memory
Our Framework: 22 GB GPU Memory

summarizes the requirements and constraints of our framework by module.

Table 5 presents the GPU memory requirements for each module in our framework. The baseline IsaacGym environment with 4096 parallel agents occupies approximately 6 GB of GPU memory. Each module adds additional memory overhead, with the Student Encoder’s LSTM contributing the largest increase (+12 GB). The complete framework requires approximately 22 GB total GPU memory for training. For resource-constrained settings, the LSTM in the Student Encoder can be replaced with Gated Recurrent Units (GRU) to reduce memory consumption.

Our framework uses proprioceptive sensing to validate the feasibility of blind locomotion, which does not imply that it is restricted to proprioceptive-only configurations. For vision-based training, the framework can be extended by removing the environment encoding components from the teacher and student encoders and replacing them with depth camera encoders to process visual information.

5.2. Future Work

Despite these advances, limitations remain. The framework has been validated primarily on a quadruped platform without exteroceptive sensing. Future work may extend skeleton-aware representations with visual or tactile input and validate the approach across different robot platforms. Exploring integration with high-level planning or multi-robot coordination could further broaden its applicability in unstructured environments.