1. Introduction
Power systems often face challenges in ensuring the desired supply of quality electricity to consumer centers [
1]. Variability in energy demand, the interconnection of large generation centers by long transmission lines, the incorporation of new energy sources, and the increasing number of faults and incidents are some of the current operational challenges of modern power systems. Therefore, control projects are frequently proposed and implemented to improve the dynamic performance of power systems [
1]. Xiong et al. [
2] developed a control scheme to ensure the stability of power systems in major emergencies. Huang et al. [
3] developed a hierarchical robustness strategy to address voltage and frequency deviation in islanded AC microgrids. Liu et al. [
4] developed a technique using fault current limiters to treat commutation failure in power systems. Huang et al. [
5] developed a new sliding mode controller to ensure stability and good transient stability indices of power systems. Song et al. [
6] developed a new control to suppress low-frequency oscillations in power systems with wind generation. Ban et al. [
7] propose a new control strategy for bus voltage regulation and SoC balance in microgrids.
Damping controller design is one of the most common control projects in small-signal angular stability studies of power systems. Oscillation modes associated with the electromechanical variables of power systems are in the frequency range of 0.1 to 2 Hz and, in most cases, have low damping ratios. The lower these damping ratios, the greater the oscillations in the system’s electrical quantities and the greater the system’s vulnerability to instability in the event of contingencies [
8].
Power system stabilizers (PSSs) are traditional oscillation mode damping controllers designed and implemented to send control signals to automatic voltage regulators (AVRs) of synchronous generators [
8]. A variety of PSS design techniques are presented in the literature, and their performance in improving signal damping is remarkable. De Campos et al. [
9] develop a technique based on Linear Matrix Inequalities (LMIs) to obtain PSS parameters. Abido [
10] presents a method based on Particle Swarm Optimization (PSO) for the robust design of a PSS. Bento et al. [
11] propose a PSS design by a method based on the linear quadratic regulator (LQR). Metaheuristics such as genetic algorithm [
12], bat algorithm [
13], ant colony optimization [
14], and marine predator algorithm [
15] are recommended by the authors in the design of PSS, and the reported results are well detailed and satisfactory. PSSs have proven effective for many years but have shown limited effect in recent years in modern systems due to several factors. The expansion of the interconnection of large power systems has increased the number of inter-area oscillation modes with very low damping ratios, and PSSs are not effective for these inter-area modes due to the low observability of the system since PSSs receive and send control signals only to the synchronous generator to which they are connected.
The increased use of phasor measurement units (PMUs) due to technological advances has brought various benefits to the monitoring [
16] and control [
17] of power systems. PMUs collect voltage and current measurements in real time at impressive sampling rates, thus providing a snapshot of the system’s dynamics [
18]. Furthermore, this PMU data can be acquired from different points of the system where the PMU is installed, facilitating increased system observability [
19].
The benefits of PMUs have also extended to power system control due to improved observability and high data transmission rates. Researchers have developed wide-area damping controllers (WADCs), which utilize data from PMUs at different locations in the system and produce control signals for the AVRs [
20]. Various techniques have been presented by the scientific community for the design of a WADC [
21]. Zhang and Bose [
17] presented a method based on LMIs. Bento [
22] proposes an LQR-based technique for the design of a robust WADC. Mukherjee et al. [
23] proposed the design of a WADC using reinforcement learning. Gupta et al. [
24] proposed using reinforcement learning and deep neural networks to design a WADC. Ranjbar et al. [
25] developed a method using Thevenin impedance and the CART technique for the design of a WADC. Metaheuristics such as PSO [
26,
27], greylag goose optimization [
28], firefly algorithm [
29], genetic algorithm [
30,
31], grey wolf optimizer [
32], mountain gazelle optimizer [
33], African vultures optimization [
34], marine predators algorithm [
35], and crow search algorithm [
36] are also widely used in the design of this controller. Researchers have shown that WADCs can significantly increase the damping ratios of inter-area oscillation modes. Thus, the combined use of PSSs and a WADC can improve system performance requirements in small-signal stability studies. Furthermore, a well-defined optimization model can be solved by any metaheuristic.
Although the benefits of the WADC are notable and well documented, implementation challenges arise due to the vulnerability of communication channels to cyberattacks or communication failures. False data injection (FDI) attacks and denial-of-service attacks are a concern in operation centers that rely on PMU data for various applications. WADCs, for example, can malfunction or even destabilize a power system. There is some promising work addressing cyberattacks on WADC channels. Zhang and Vittal [
37] propose turning off the WADC when a communication failure is identified, and thus the system operates only with local controls. Naguru [
38] proposes a detection and correction matrix so that the WADC is able to tolerate different communication failures. Sarkar et al. [
39] propose a dual input and single output for the operation of the WADC, and when a communication failure occurs, the WADC operates as a single input and single output. Bento [
40] proposed a technique to address permanent failures in a WADC. Yao et al. [
41] developed a WADC capable of handling deception attacks. Patel et al. [
42] proposed a WADC with a dynamic loop where the input and output signals are dynamically changed to deal with cyberattacks. Zhang and Vittal [
43] propose a structure of redundancy of communication channels to deal with communication failures. A relevant group of researchers have developed WADC control strategies to deal with FDI attacks. Liu et al. [
44] developed a Markov game to deal with FDI attacks. Zhao et al. [
45] combined goal representation heuristic dynamic programming and a linear state estimator to develop a resilient adaptive WADC capable of tolerating FDI attacks. Sun et al. [
46] proposed a mechanism for WADC’s resilience to FDI attacks through a non-intrusive data verification technique that uses a deep convolutional neural network and an adaptive variational autoencoder. Vavdareh et al. [
47] proposed and compared two tools to mitigate FDI attacks: (i) a multi-agent control strategy and (ii) a neural-network-based autoencoder. Kumar et al. [
48] proposed applying a random forest classifier to detect and mitigate FDI attacks in the operation of a WADC. Saini and Bhui [
49] developed a technique using a support vector machine and semi-supervised generative adversarial network to guarantee the security of a WADC against cyberattacks. Saini et al. [
50] developed a technique using an unscented Kalman filter and autoencoder to detect dynamic attacks in WADCs. Zhao et al. [
51] proposed mitigating strong attacks through a multiple-controller switching technique. Li et al. [
52] developed a stochastic game theoretic framework to address cyberattacks on WADC channels. Zhao et al. [
53] developed a robust subspace tracking to mitigate sparse attack in WADCs. Zhao et al. [
54] developed a method to quantify the resilience of WADCs to cyberattacks. These studies are interesting, but the researchers still identified limitations that require further research.
In LMI-based damping control designs, the search for a symmetric, positive-definite matrix ensures the stability of the dynamic system. Various LMI-based techniques are available in the literature for damping control design [
55,
56]. However, one of the difficulties reported by the authors is determining this symmetric, positive-definite matrix and meeting the system’s dynamic performance requirements.
This paper presents the design of a WADC robust to communication failures through the solution of a multi-objective optimization model. Linearized power system models are employed. Constraints are incorporated into the optimization model, such as the requirement for the existence of a positive-definite symmetric matrix from an LMI formulation. Limiting the variables’ boundary values of the WADC has been shown to facilitate the obtainment of this positive-definite symmetric matrix. The stellar oscillation optimizer [
57] and particle swarm optimization [
58] metaheuristics are applied and compared in the multiobjective optimization model. In addition, modal and time domain analyses are presented to evaluate the benefits of the WADC in the operation of the power system. The main contributions of this article are as follows:
A multi-objective approach to designing a WADC resilient to communication failures is developed and discussed.
The control objective is to ensure that the WADC provides high damping rates for the three lowest damping modes of the system even when a single permanent communication failure occurs in the communication channels.
The convergence of the proposed method provides symmetric and positive-definite matrices to guarantee the stability of the closed-loop system.
Bio-inspired algorithms such as the stellar oscillation optimizer and particle swarm optimization are applied and compared to evolve the optimization model with constraints and a multi-objective function.
The remainder of the paper presents the following framework for understanding and evaluating the contributions of this research.
Section 2 discusses the control structure and how the WADC operates in the control loop.
Section 3 describes the system model, the WADC model, the time delay model, the closed-loop model, and the stability criterion using LMIs.
Section 4 presents in detail the optimization model for the design of a WADC, describing the variables, objective function, and constraints.
Section 5 evaluates the proposed method through case studies with modal analysis and time-domain analysis.
Section 6 concludes the paper with the main evaluations.
5. Case Studies and Discussion
The proposed method, composed of the optimization model and different metaheuristics for the design of a resilient WADC, was applied to the IEEE 68-bus to increase the damping ratios of multiple oscillation modes at multiple operating points. This test system consists of 68 buses and 16 generators and is a test system developed for stability studies in [
59,
65]. There is only one operating condition available and detailed in [
59,
65]. Three new operating points were obtained from this nominal operating point (C0): an operating point with a 1% load increase (C1), an operating point with a 2% load increase (C2), and an operating point with a 3% load increase (C3).
Table 1 presents a modal analysis of these four operating points. The oscillation modes of the four operating points have damping ratios below 5%. It is important to note that this system already has PSSs designed and implemented in generators 1 through 12, but these existing PSSs are not sufficient to effectively improve oscillation modes. Therefore, an appropriate WADC design could be beneficial and necessary for these operating points.
Once the oscillation modes with the lowest damping ratios have been identified, the next step is to select the WADC input and output signals. The selection will be made based on geometric measures of observability and controllability. The generators at buses 12, 13, 14, 15, and 16 were selected to have their velocity signals estimated by PMUs and sent as input to the WADC. The generators at buses 5, 9, 10, 11, and 12 were selected to receive control signals generated by the WADC output. Thus, the WADC to be designed can be formulated as
Now, the proposed method will be applied to design a fault-resilient WADC for these four operating points. The codes were implemented in MATLAB version 2016a [
66]. Time-domain analyses with the application of contingencies were performed in ANATEM version 12.5.1 [
67]. The population of both metaheuristics was chosen as 20, and the maximum number of epochs was chosen as 1000. The minimum damping rates were set as
,
, and
. The weights
,
, and
were also chosen as 1. The minimum and maximum values of the time constants associated with the WADC poles were chosen as 0.01 and 0.1, respectively. Thus,
,
,
,
,
, and
. The choice of minimum and maximum values for the time constants associated with the zeros of the WADC deserves special attention. The time constants could assume values between 0 and 1, but initial simulations showed that high time constant values made it difficult to determine the symmetric matrices
P,
Q, and
R and to satisfy the inequalities of the constraints that make up the optimization model. Convergence and satisfaction of the inequalities were guaranteed when the minimum and maximum bounds were set to 0 and 0.5, respectively. Thus,
,
,
, and
. In addition to evaluating the proposed optimization model, the metaheuristics’ performance was also evaluated. To evaluate how random initialization of variables and metaheuristic operators affects the convergence of the optimization model, 100 simulations of each of the two metaheuristics were performed, and the objective function results are reported in
Table 2. These results allow the following evaluations:
Both methods converged with low multi-objective function values, indicating that the minimum damping ratios achieved are close to the desired damping ratios of , , and .
The SOO method provided the lowest multi-objective function values compared to the PSO method.
The SOO method also presents a much lower standard deviation when compared to the PSO method. Thus, the SSO method converges to low multi-objective function values regardless of the simulations performed.
The WADCs that achieved the lowest multi-objective function values for each metaheuristic were chosen to evaluate the closed-loop control system subject to contingencies and communication failures.
Table 3 and
Table 4 present the WADC(SOO) and WADC(PSO) parameters that yielded the lowest multi-objective function values for the SOO and PSO algorithms, respectively.
A comparative analysis was performed with another WADC design technique based on LQR, available in [
40]. This technique aims to minimize control effort but does not necessarily increase the damping ratios of the oscillation modes. Furthermore, this technique considers uncertainties that can be modeled as a variation of the state matrix of the linearized system. The method was applied to this test system, and the parameters of this WADC(LQR) are available in
Table 5, considering that the poles were fixed at −25 and −25, and thus the denominator is
.
The oscillation modes of cases C0, C1, C2, and C3 with WADC(SSO) and WADC(PSO) can also be evaluated.
Table 6,
Table 7,
Table 8 and
Table 9 present the three oscillation modes with the lowest damping ratios for cases C0, C1, C2, and C3 with WADC(SOO), respectively.
Table 10,
Table 11,
Table 12 and
Table 13 present the three oscillation modes with the lowest damping ratios for cases C0, C1, C2, and C3 with WADC(PSO), respectively.
Table 14,
Table 15,
Table 16 and
Table 17 present the three oscillation modes with the lowest damping ratios for cases C0, C1, C2, and C3 with WADC(LQR), respectively. These results provide the following assessments:
Operating points C0, C1, C2, and C3 with WADC(SOO) and WADC(PSO) exhibit oscillation modes with higher damping ratios than those without WADC, even in scenarios with signal loss. Therefore, proper WADC design ensures good damping ratios for the closed-loop system.
The operating points C0, C1, C2, and C3 with WADC(SOO) presented higher damping ratios than the cases with WADC(PSO). This result is consistent with the fact that WADC(SOO) provided the lowest objective function value.
The guarantee of obtaining symmetric and positive-definite matrices (, , and ) in the linearized models was beneficial for ensuring the stability of the system.
The strategy of working by zeroing columns of and rows of to represent communication losses was beneficial in the WADC project because it only required working with different closed-loop matrices.
WADC(SOO) provided higher damping rates for the system than WADC(LQR) obtained by applying the technique [
40].
The results presented so far are a modal analysis of the system using linearized models. Therefore, a dynamic analysis of the system subject to contingencies was conducted. System bus 40 was chosen to experience a three-phase fault starting at 1 s and ending 100 ms later for cases C0, C1, C2, and C3, considering the WADCs operating normally and operating with the loss of the speed signal from generator 15, and operating with the loss of the WADC control signal that would go to the AVR of generator 11.
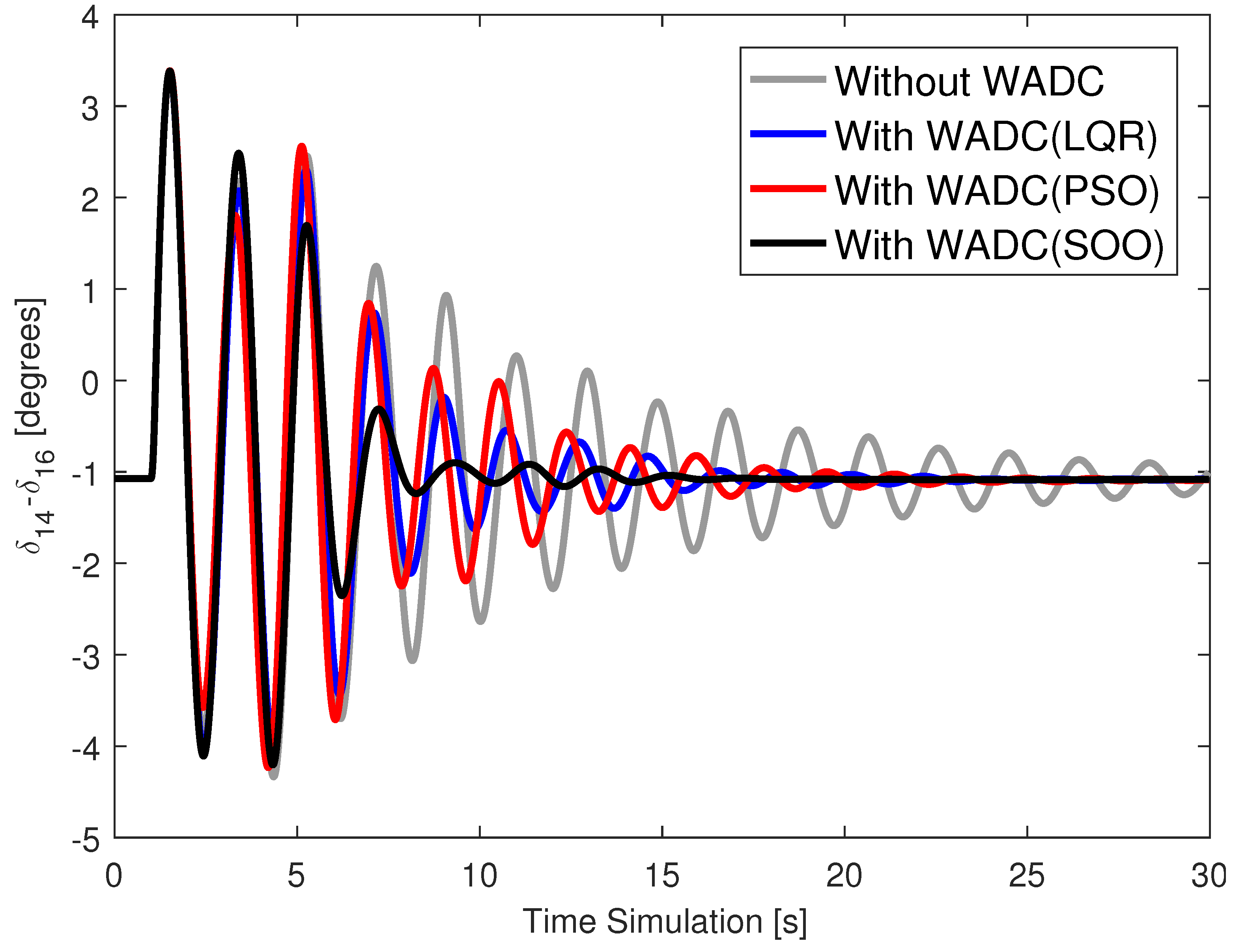
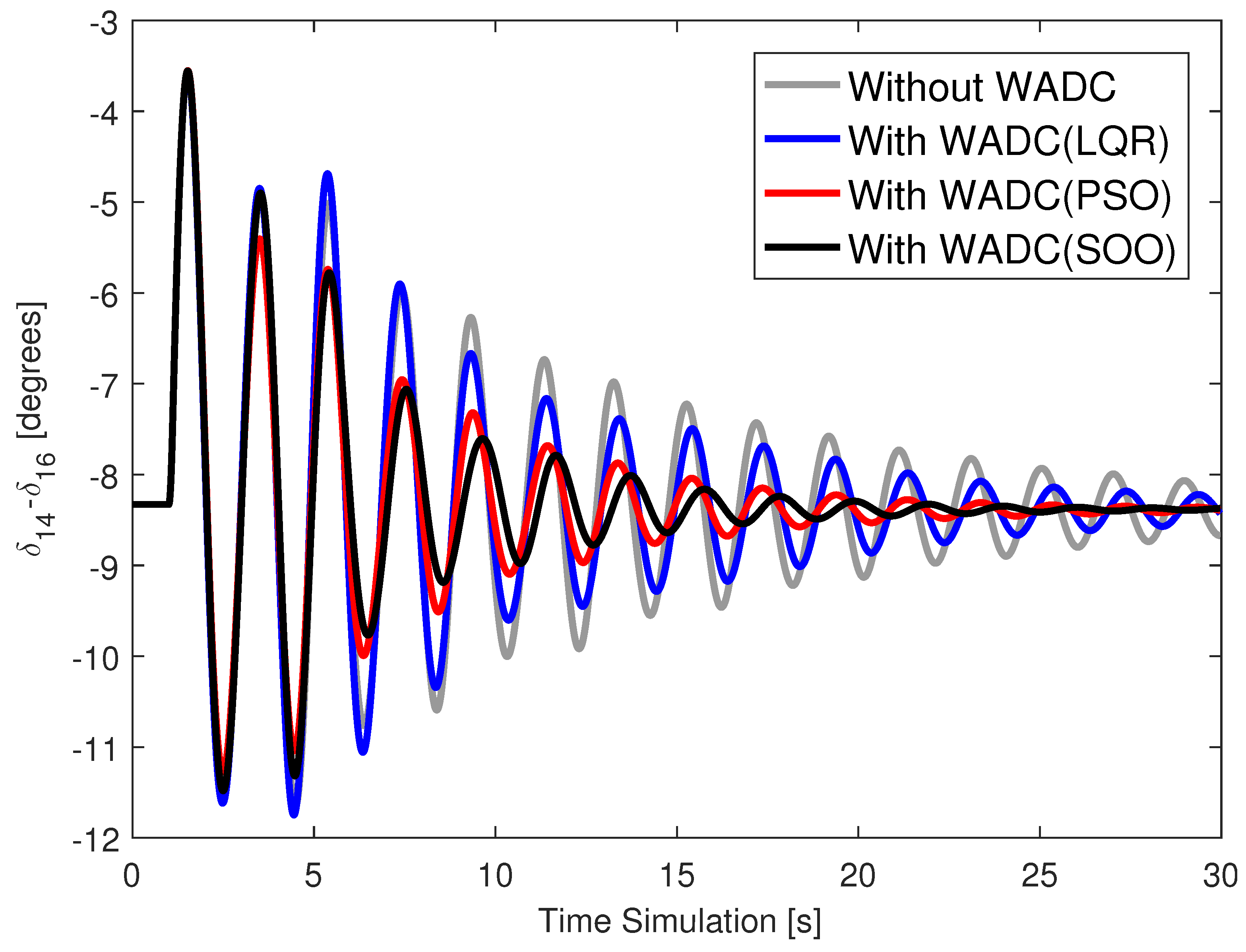
Figure 2,
Figure 3,
Figure 4 and
Figure 5 show the angle of generator 14 for cases C0, C1, C2, and C3 for this contingency scenario and with the WADC operating normally.
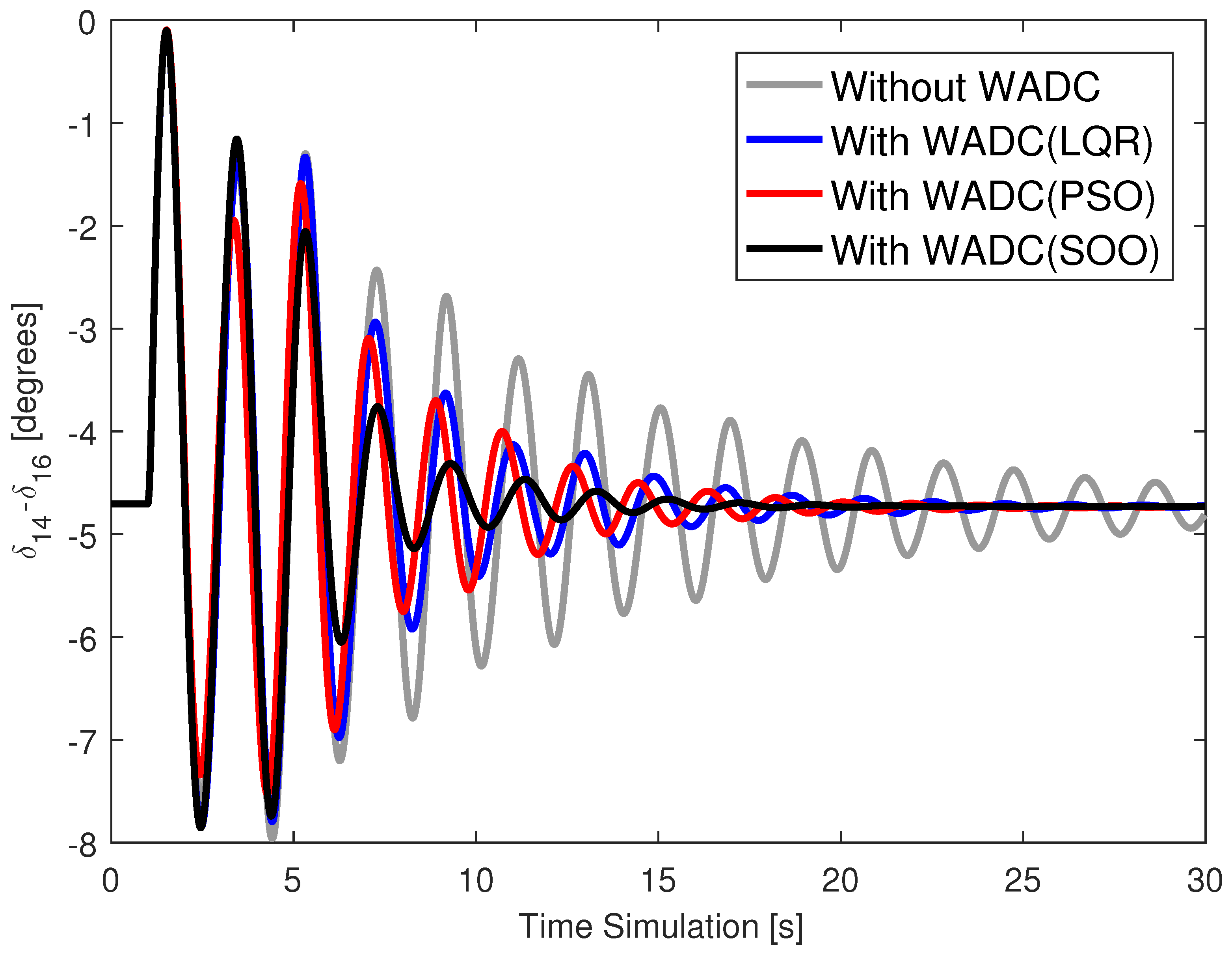
Figure 6,
Figure 7,
Figure 8 and
Figure 9 present the angle of generator 14 for cases C0, C1, C2 and C3 for this contingency scenario and with the WADC operating with the loss of the WADC control signal that would go to the AVR of generator 11.
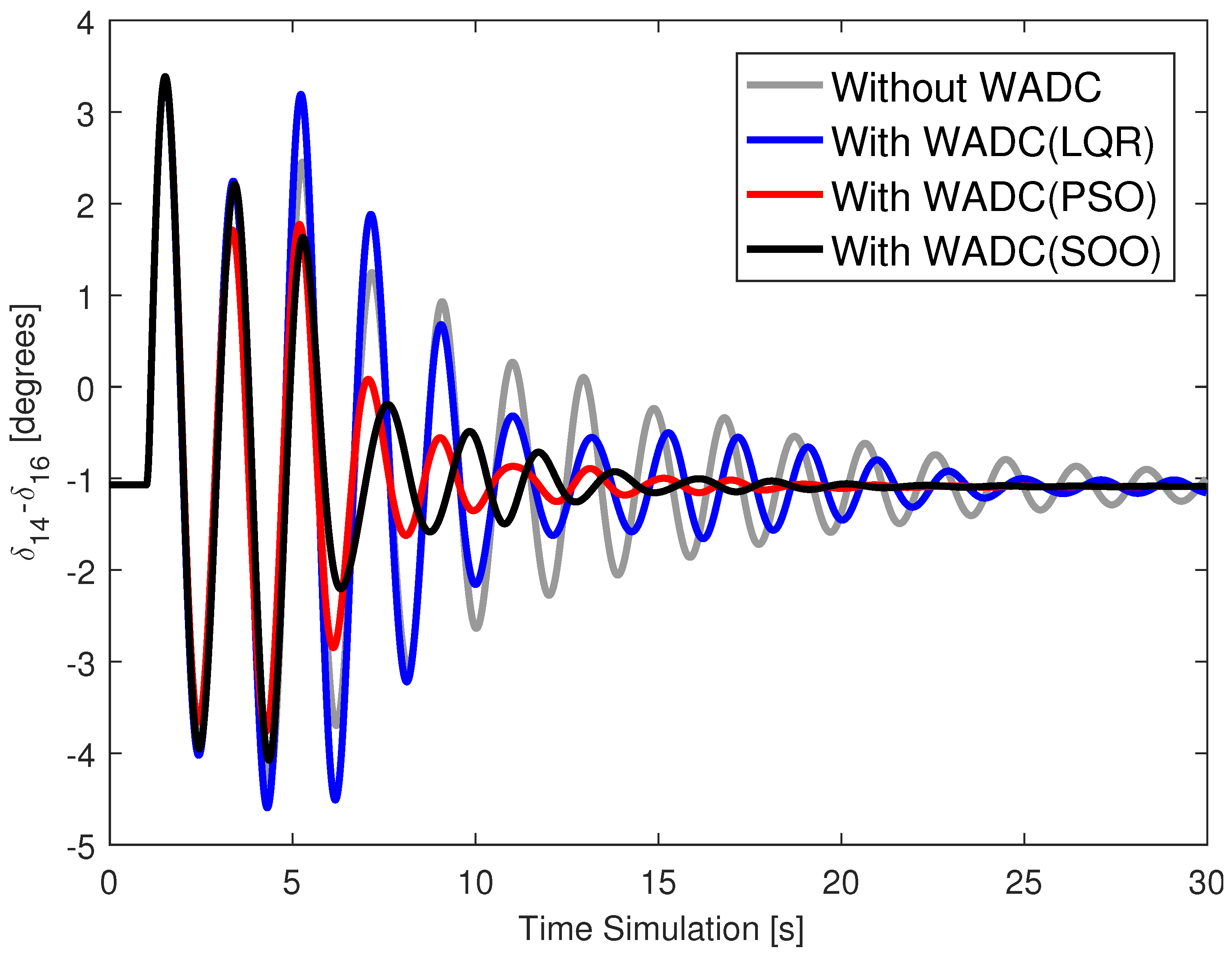
Figure 10,
Figure 11,
Figure 12 and
Figure 13 present the angle of generator 14 for cases C0, C1, C2, and C3 for this contingency scenario and with the WADC operating with the loss of the speed signal from generator 15. These results provide the following observations:
The angular responses are well damped for the system operating with a WADC compared to the system without a WADC.
Angular responses are well damped for all operating cases, even in the event of a communication failure at the WADC input or output.
WADC(SOO) provided slightly better performance than WADC(PSO) in improving the damping of the angular response.
The WADC(SOO) provided better damped angular responses than the WADC(LQR) obtained by applying the technique [
40].
6. Conclusions
This work proposed an optimization model for the design of a WADC resilient to communication failures. To ensure quadratic stability of the closed-loop control system, the optimization model required finding symmetric and positive-definite matrices that satisfied a set of inequalities. This requirement required that the minimum and maximum bounds of the WADC numerator time constants be between 0 and 0.5 to guarantee convergence. This is important because the SeDuMi solver may have difficulty solving LMIs and finding these symmetric and positive-definite matrices. The SOO and PSO methods were applied and compared to find the WADC parameters in the optimization model. The SOO method achieved a desired minimum value of , while the PSO method achieved a minimum value of . Comparative analyses with the LQR-based technique already existing in the literature showed the difficulty of this existing method in achieving high damping ratios for the oscillation modes, a desirable control objective for the system. Time-domain simulations with contingency and communication channel loss application showed well-damped angular responses with a WADC in the power system, especially for the WADC obtained by the SOO algorithm.
One of the most significant drawbacks of the proposed method is that the symmetric and positive-definite matrices have the same order as those in closed-loop control systems. Therefore, large power systems would have high-dimensional matrices in the linearized model, and thus the variable matrices would have high dimensions. The SeDuMi solver may present convergence problems, hindering the design of a fault-resilient WADC. Another drawback observed during the simulations is the initialization of the variables that define the WADC. In this study, the initialization was random, and different initial values may result in different WADCs with different objective function values.
The successful results of this research have opened new directions for future research, such as the development of WADC design strategies to deal with false data injection attacks. Furthermore, new strategies can be developed to deal with variations in time delays and uncertainties in power system operation. New bio-inspired algorithms can be applied in the future to the proposed multi-objective model, and the results can be compared and analyzed.