Hurwicz-Type Optimal Control Problem for Uncertain Singular Non-Causal Systems
Abstract
1. Introduction
2. Preliminaries
2.1. Uncertainty Theory
2.2. Optimal Control Problem
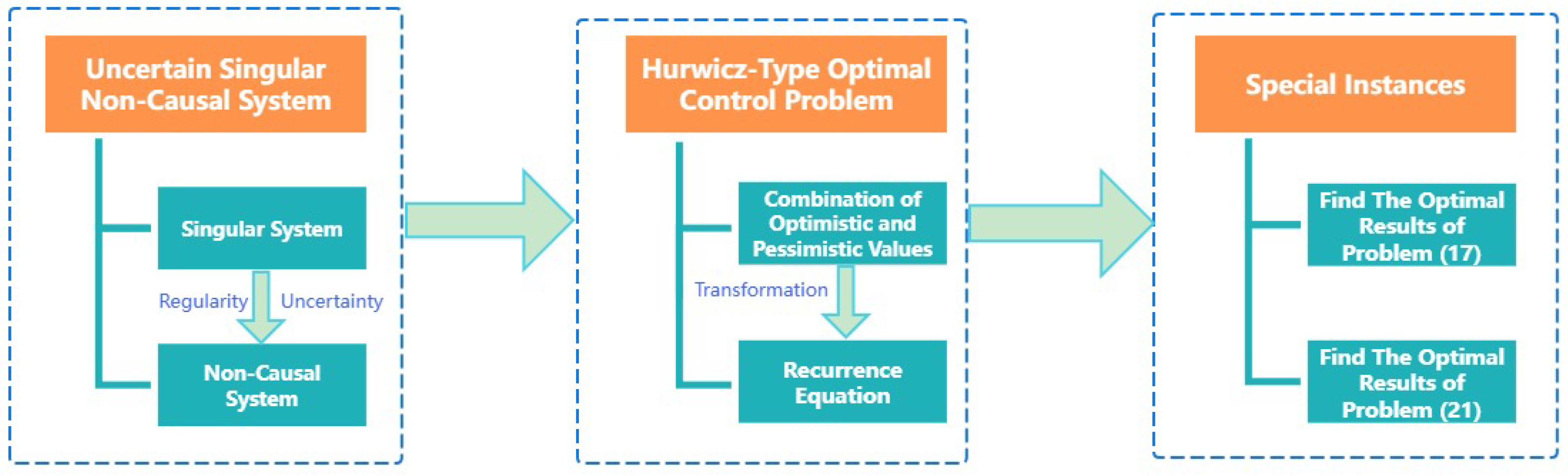
3. Uncertain Singular Non-Causal System
4. Optimal Control Problem Based on the Hurwicz Criterion
5. Special Instances
| Algorithm 1 Find the optimal results of problem (17) |
|
| Algorithm 2 Find the optimal results of problem (25) |
|
6. Numerical Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosenbrock, H.H. Structural properties of linear dynamical systems. Int. J. Control 1974, 20, 191–202. [Google Scholar] [CrossRef]
- Luenberger, D.G.; Arbel, A. Singular dynamic Leontief systems. Econometrica 1977, 45, 991–995. [Google Scholar] [CrossRef]
- Cobb, D. Controllability, observability, and duality in singular systems. IEEE Trans. Autom. Control 1984, 29, 1076–1082. [Google Scholar] [CrossRef]
- Dai, L. Singular Control Systems; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Lukashiv, T.; Malyk, I.V.; Hemedan, A.A.; Satagopam, V.P. Optimal control of stochastic dynamic systems with semi-Markov parameters. Symmetry 2025, 17, 498. [Google Scholar] [CrossRef]
- Shu, Y.; Li, B. Linear-quadratic optimal control for discrete-time stochastic descriptor systems. J. Ind. Manag. Optim. 2022, 18, 1583–1602. [Google Scholar] [CrossRef]
- Vlasenko, L.A.; Rutkas, A.G.; Semenets, V.V.; Chikrii, A.A. Stochastic optimal control of a descriptor system. Cybern. Syst. Anal. 2020, 56, 204–212. [Google Scholar] [CrossRef]
- Li, Y.; Ma, S. Finite and infinite horizon indefinite linear quadratic optimal control for discrete-time singular Markov jump systems. J. Frankl. Inst. 2021, 358, 8993–9022. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, B. Uncertainty Theory, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Li, B.; Zhang, R.; Sun, Y. Multi-period portfolio selection based on uncertainty theory with bankruptcy control and liquidity. Automatica 2023, 147, 110751. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, L. Modeling RL electrical circuit by multifactor uncertain differential equation. Symmetry 2021, 13, 2103. [Google Scholar] [CrossRef]
- Mohammed, P.O. A generalized uncertain fractional forward difference equations of Riemann-Liouville type. J. Math. Res. 2019, 11, 43–50. [Google Scholar] [CrossRef]
- Zhu, Y. Uncertain Optimal Control; Springer Nature: Singapore, 2019. [Google Scholar]
- Shu, Y.; Zhu, Y. Optimistic value based optimal control for uncertain linear singular systems and application to a dynamic input-output model. ISA Trans. 2017, 71, 235–251. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; You, Z.; Chen, Y. Optimistic value model of multidimensional uncertain optimal control with jump. Eur. J. Control 2018, 39, 1–7. [Google Scholar] [CrossRef]
- Yang, X.; Gao, J. Linear-quadratic uncertain differential games with application to resource extraction problem. IEEE Trans. Fuzzy Syst. 2016, 24, 819–826. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y. Optimal control for uncertain random singular systems with multiple time-delays. Chaos Solitons Fractals 2021, 152, 111371. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y.; Sheng, L. Optimal control for uncertain stochastic dynamic systems with jump and application to an advertising model. Appl. Math. Comput. 2021, 407, 126337. [Google Scholar] [CrossRef]
- Latunde, T.; Bamigbola, O.M. Uncertain optimal control model for management of net risky capital asset. IOSR J. Math. 2016, 12, 22–30. [Google Scholar]
- Shu, Y.; Zhu, Y. Stability analysis of uncertain singular systems. Soft Comput. 2018, 22, 5671–5681. [Google Scholar] [CrossRef]
- Shu, Y.; Li, B.; Zhu, Y. Optimal control for uncertain discrete-time singular systems under expected value criterion. Fuzzy Optim. Decis. Mak. 2021, 20, 331–364. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, Y. Stability and optimal control for uncertain continuous-time singular systems. Eur. J. Control 2017, 34, 16–23. [Google Scholar] [CrossRef]
- Chen, X.; Cao, Z.; Zhang, Z. Linear quadratic optimal control and zero-sum game for uncertain time-delay systems based on pessimistic value. Eur. J. Control 2025, 84, 101224. [Google Scholar] [CrossRef]
- Shu, Y.; Sheng, L. Hurwicz criterion based optimal control model for uncertain descriptor systems with an application to industrial management. J. Ind. Manag. Optim. 2023, 19, 6054–6081. [Google Scholar] [CrossRef]
- Shu, Y. Optimal control for discrete-time descriptor noncausal systems. Asian J. Control 2021, 23, 1885–1899. [Google Scholar] [CrossRef]
- Hurwicz, L. Some specification problems and application to econometric models. Econometrica 1951, 19, 343–344. [Google Scholar]
- Pierre, D.A. A perspective on adaptive control of power systems. IEEE Trans. Power Syst. 2007, 2, 387–395. [Google Scholar] [CrossRef]
- Kwatny, H.G.; Miu-Miller, K. Power System Dynamics and Control; Springer: New York, NY, USA, 2016. [Google Scholar]
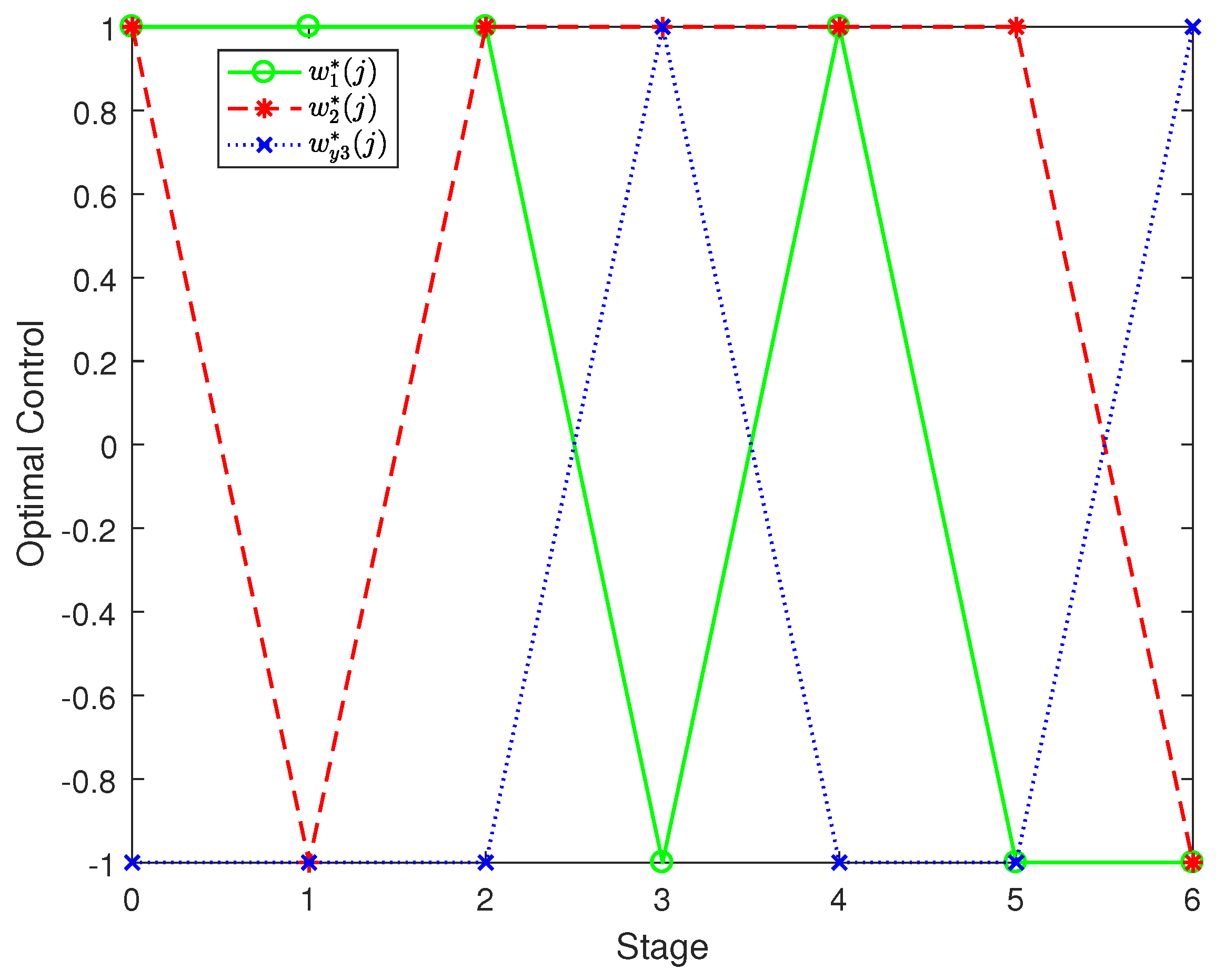
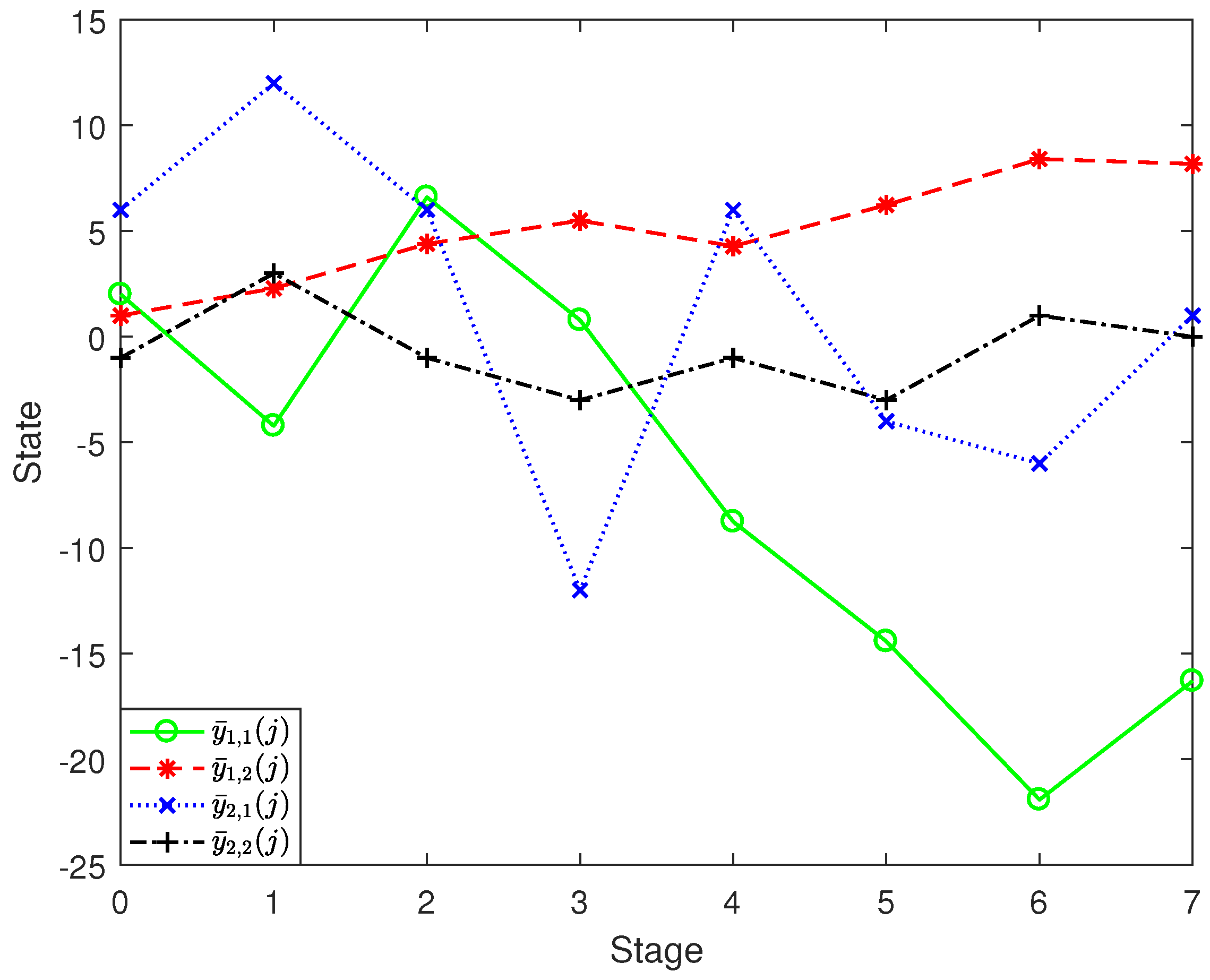
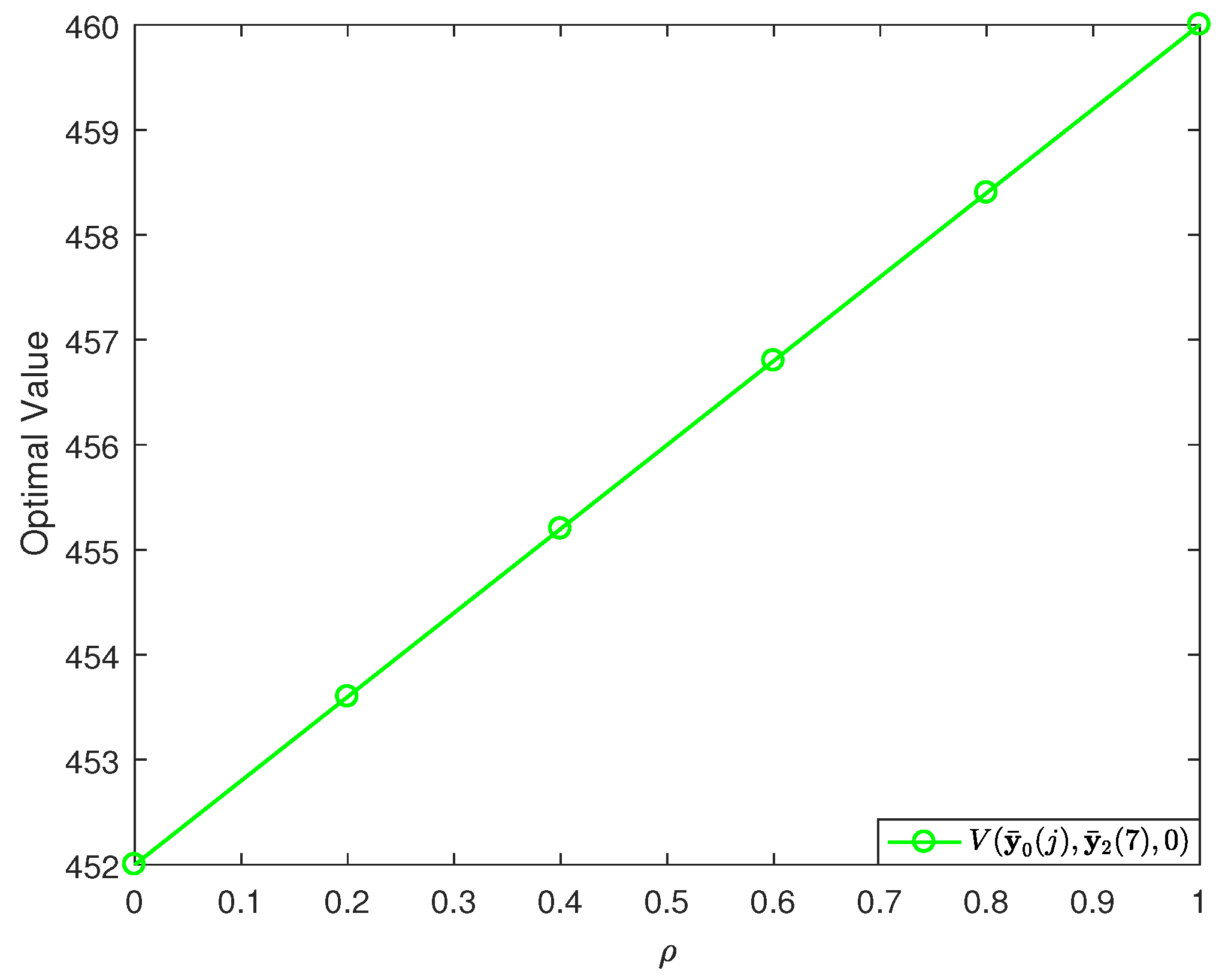
| Stage | ||||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 |
| 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | |
|---|---|---|---|---|---|---|
| 452 | 453.6000 | 455.2000 | 456.8000 | 458.4000 | 460.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Chen, X. Hurwicz-Type Optimal Control Problem for Uncertain Singular Non-Causal Systems. Symmetry 2025, 17, 1130. https://doi.org/10.3390/sym17071130
Chen Y, Chen X. Hurwicz-Type Optimal Control Problem for Uncertain Singular Non-Causal Systems. Symmetry. 2025; 17(7):1130. https://doi.org/10.3390/sym17071130
Chicago/Turabian StyleChen, Yuefen, and Xin Chen. 2025. "Hurwicz-Type Optimal Control Problem for Uncertain Singular Non-Causal Systems" Symmetry 17, no. 7: 1130. https://doi.org/10.3390/sym17071130
APA StyleChen, Y., & Chen, X. (2025). Hurwicz-Type Optimal Control Problem for Uncertain Singular Non-Causal Systems. Symmetry, 17(7), 1130. https://doi.org/10.3390/sym17071130







