Exceptional Point Engineering and Optical Transport in Coupled Double Waveguides
Abstract
1. Introduction
2. Model
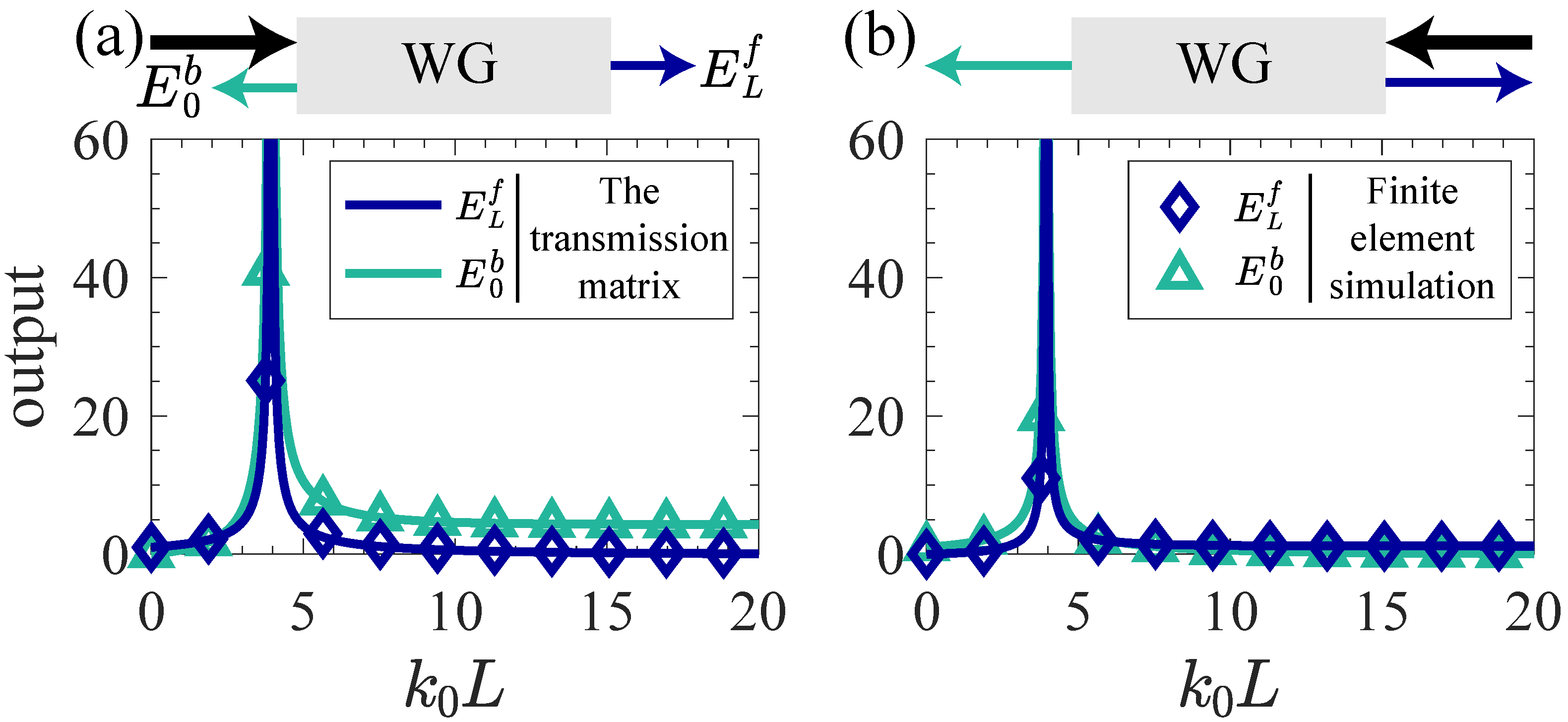
2.1. Single-Waveguide System
2.2. Double-Waveguide System
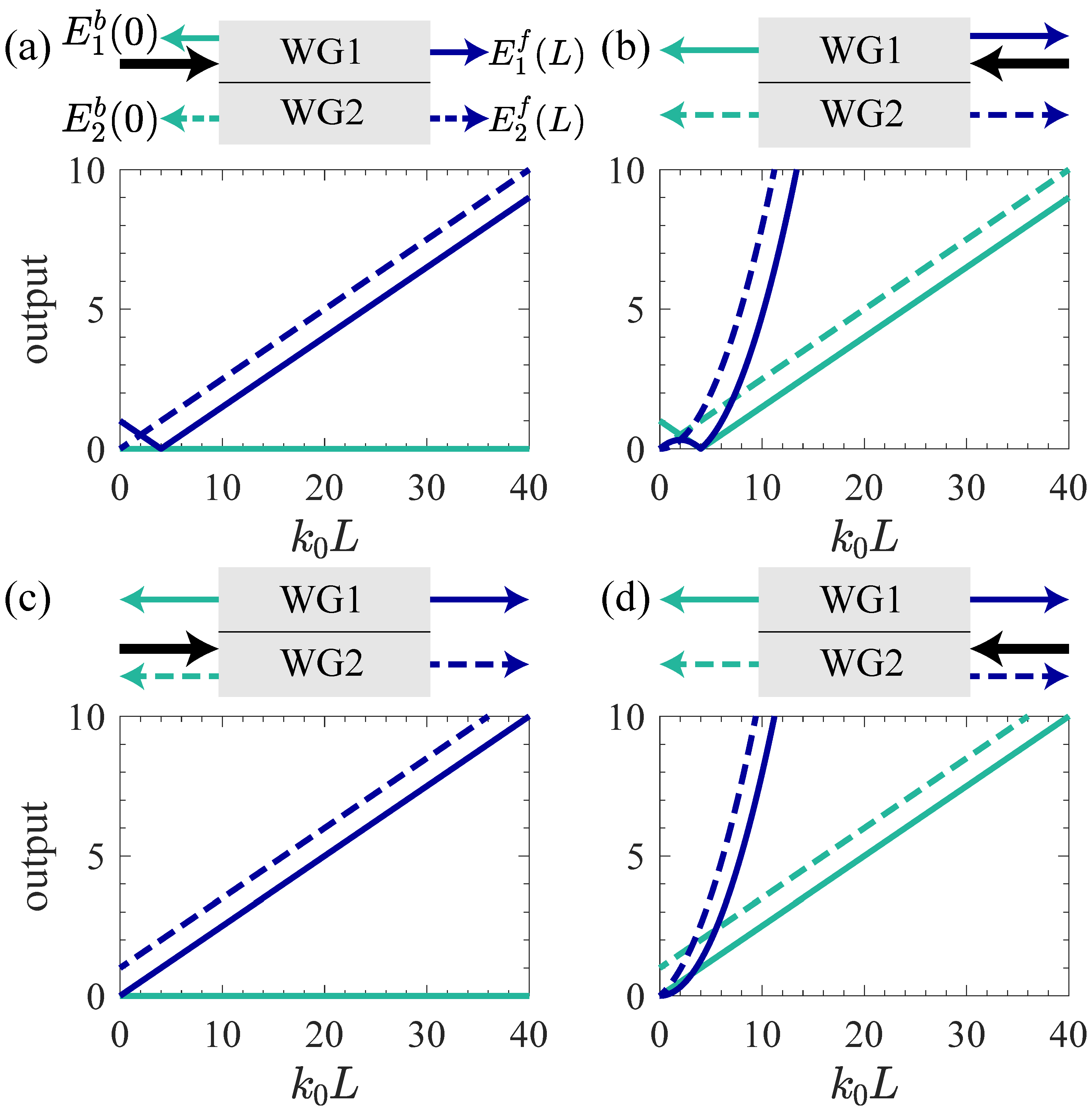
3. Light Transmission
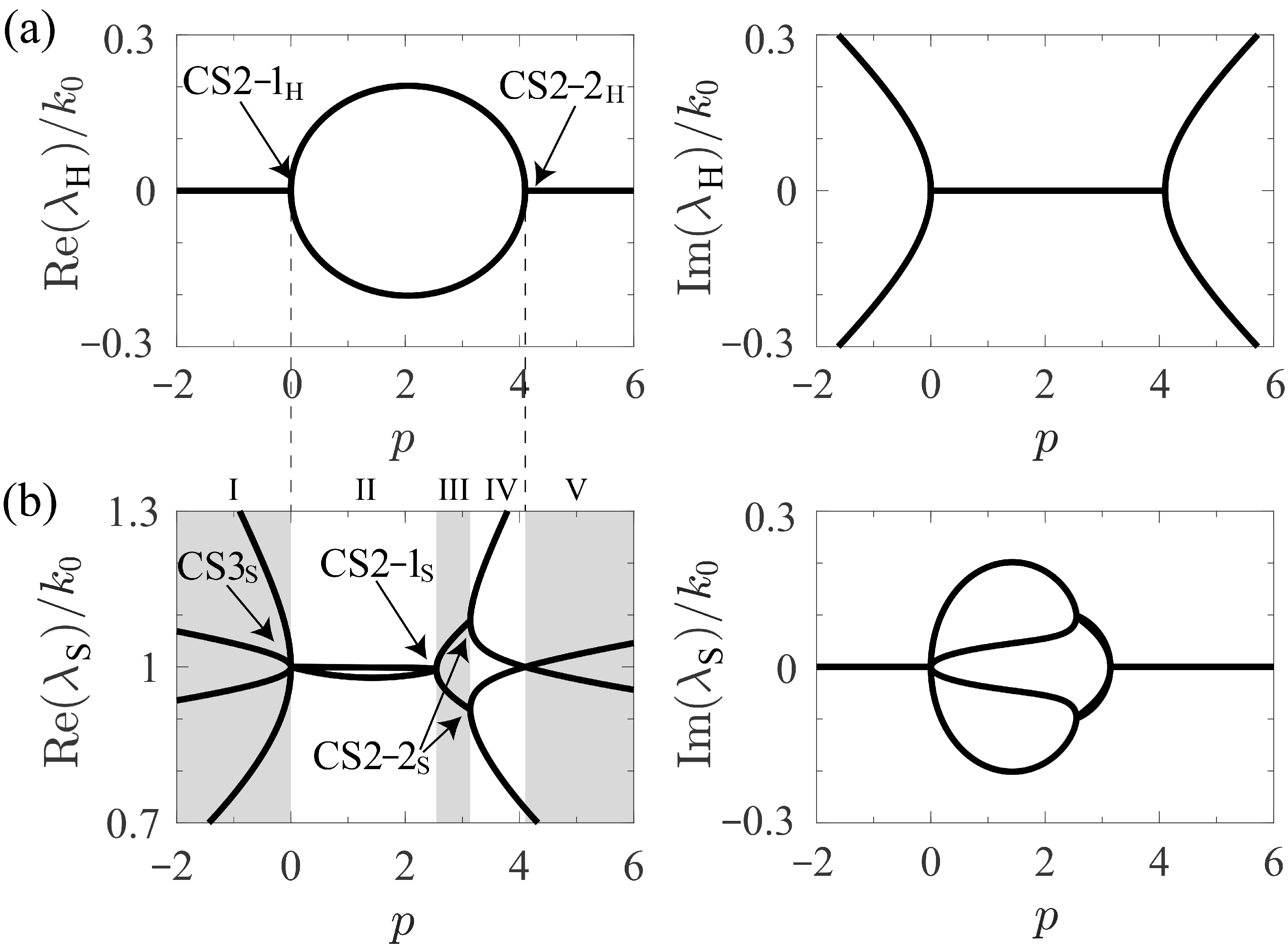
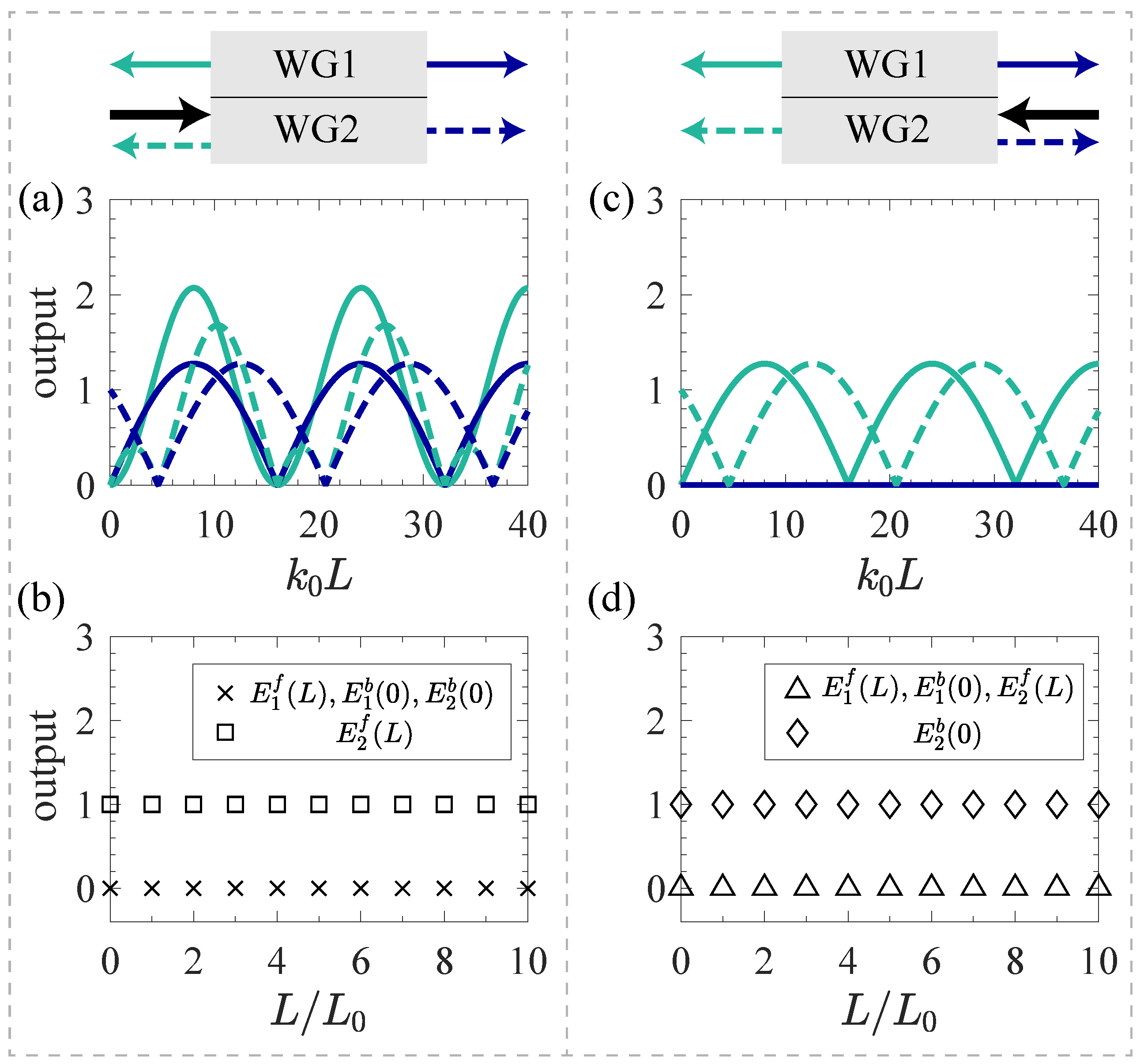
3.1. CS2-1H (CS3S)
3.2. CS2-1S
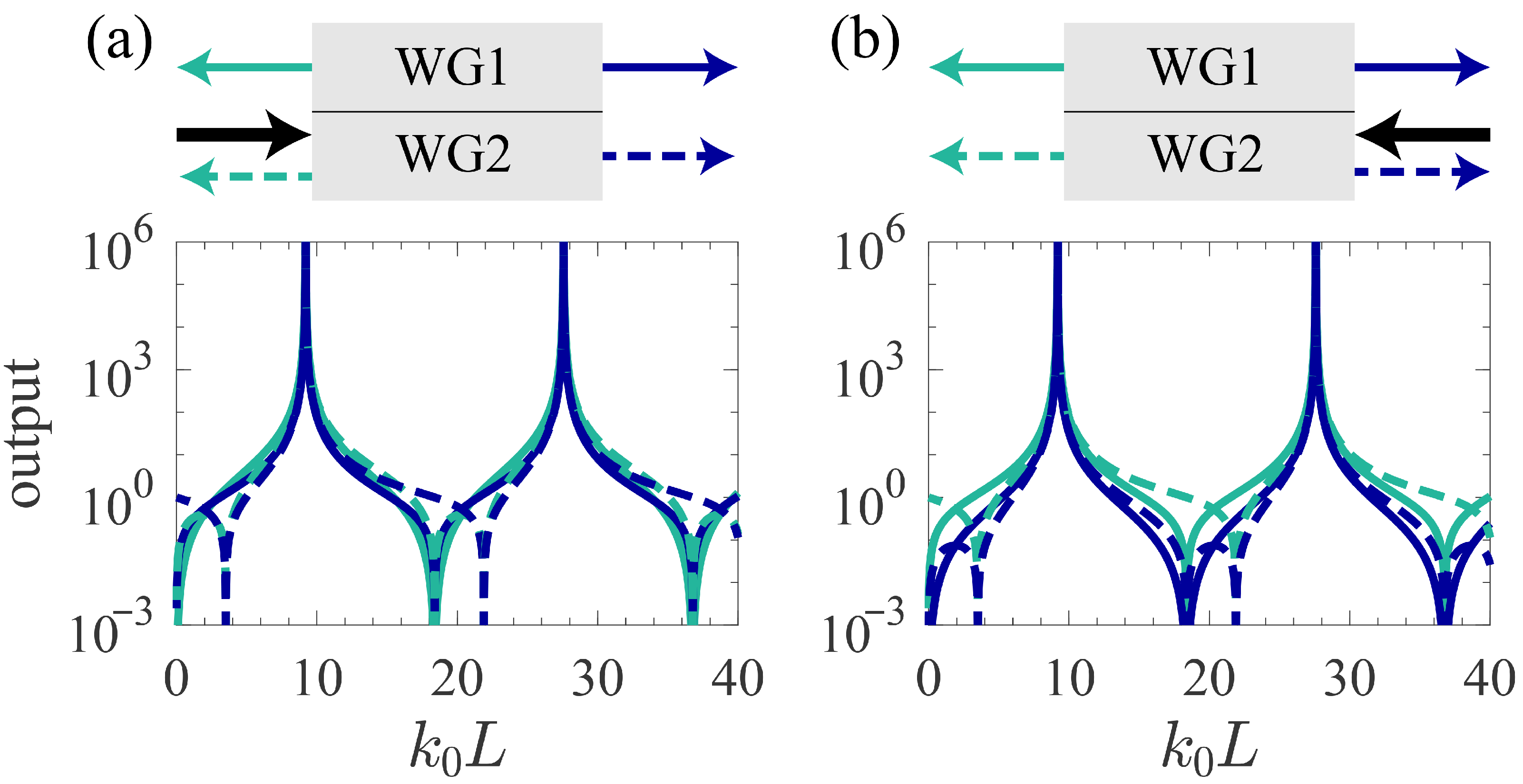
3.3. CS2-2S
3.4. CS2-2H)
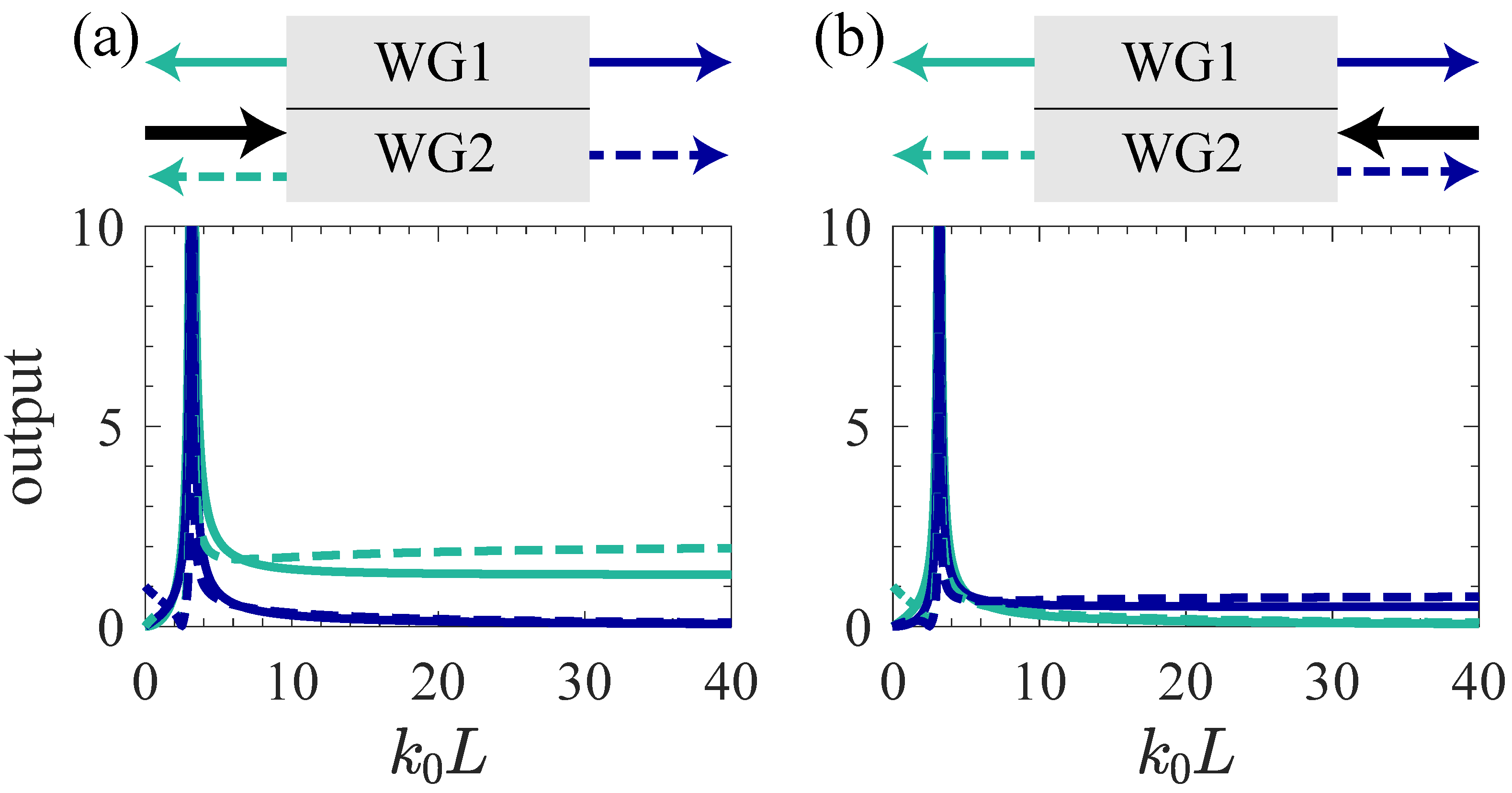
3.5. Out of EPs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heiss, W.D. Repulsion of Resonance States and Exceptional Points. Phys. Rev. E 2000, 61, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Heiss, W.D. The Physics of Exceptional Points. J. Phys. A Math. Theor. 2012, 45, 444016. [Google Scholar] [CrossRef]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-Hermitian Physics. Adv. Phys. 2020, 69, 249–435. [Google Scholar] [CrossRef]
- Bergholtz, E.J.; Budich, J.C.; Kunst, F.K. Exceptional Topology of Non-Hermitian Systems. Rev. Mod. Phys. 2021, 93, 015005. [Google Scholar] [CrossRef]
- Ding, K.; Fang, C.; Ma, G. Non-Hermitian Topology and Exceptional-point Geometries. Nat. Rev. Phys. 2022, 4, 745–760. [Google Scholar] [CrossRef]
- Ding, K.; Ma, G.; Xiao, M.; Zhang, Z.Q.; Chan, C.T. Emergence, Coalescence, and Topological Properties of Multiple Exceptional Points and Their Experimental Realization. Phys. Rev. X 2016, 6, 021007. [Google Scholar] [CrossRef]
- Ding, K.; Zhang, Z.Q.; Chan, C.T. Coalescence of Exceptional Points and Phase Diagrams for One-dimensional PT-symmetric Photonic Crystals. Phys. Rev. B 2015, 92, 235310. [Google Scholar] [CrossRef]
- San-Jose, P.; Cayao, J.; Prada, E.; Aguado, R. Majorana Bound States from Exceptional Points in Non-topological Superconductors. Sci. Rep. 2016, 6, 21427. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-Induced Suppression and Revival of Lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef]
- Wang, K.; Xiao, L.; Lin, H.; Yi, W.; Bergholtz, E.J.; Xue, P. Experimental Simulation of Symmetry-protected Higher-order Exceptional Points with Single Photons. Sci. Adv. 2023, 9, eadi0732. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, I.I.; Miranowicz, A.; Minganti, F.; Özdemir, K.; Nori, F. Dynamically Crossing Diabolic Points while Encircling Exceptional Curves: A Programmable Symmetric-Asymmetric Multimode Switch. Nat. Commun. 2023, 14, 2076. [Google Scholar] [CrossRef]
- Dembowski, C.; Gräf, H.D.; Harney, H.L.; Heine, A.; Heiss, W.D.; Rehfeld, H.; Richter, A. Experimental Observation of the Topological Structure of Exceptional Points. Phys. Rev. Lett. 2001, 86, 787–790. [Google Scholar] [CrossRef]
- Sayyad, S.; Kunst, F.K. Realizing Exceptional Points of any Order in the Presence of Symmetry. Phys. Rev. Res. 2022, 4, 023130. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Open Quantum Systems and Dicke Superradiance. Eur. Phys. J. D 2014, 68, 74. [Google Scholar] [CrossRef]
- Peng, P.; Cao, W.; Shen, C.; Qu, W.; Wen, J.; Jiang, L.; Xiao, Y. Anti-parity–time Symmetry with Flying Atoms. Nat. Phys. 2016, 12, 1139–1145. [Google Scholar] [CrossRef]
- Li, J.; Harter, A.K.; Liu, J.; de Melo, L.; Joglekar, Y.N.; Luo, L. Observation of Parity-time Symmetry Breaking Transitions in a Dissipative Floquet System of Ultracold Atoms. Nat. Commun. 2019, 10, 855. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Liu, D.; Zhao, E.; He, C.; Pak, K.K.; Li, J.; Jo, G.B. Chiral Control of Quantum States in Non-Hermitian Spin–orbit-coupled Fermions. Nat. Phys. 2022, 18, 385–389. [Google Scholar] [CrossRef]
- Liang, C.; Tang, Y.; Xu, A.N.; Liu, Y.C. Observation of Exceptional Points in Thermal Atomic Ensembles. Phys. Rev. Lett. 2023, 130, 263601. [Google Scholar] [CrossRef]
- Ding, L.; Shi, K.; Zhang, Q.; Shen, D.; Zhang, X.; Zhang, W. Experimental Determination of PT-symmetric Exceptional Points in a Single Trapped Ion. Phys. Rev. Lett. 2021, 126, 083604. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, W.; Geng, J.; Song, X.; Ye, X.; Duan, C.K.; Rong, X.; Du, J. Observation of Parity-time symmetry Breaking in a Single-spin System. Science 2019, 364, 878–880. [Google Scholar] [CrossRef]
- Choi, Y.; Kang, S.; Lim, S.; Kim, W.; Kim, J.R.; Lee, J.H.; An, K. Quasieigenstate Coalescence in an Atom-cavity Quantum Composite. Phys. Rev. Lett. 2010, 104, 153601. [Google Scholar] [CrossRef] [PubMed]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Delgado, F.; Muga, J.G. Physical Realization of PT-symmetric Potential Scattering in a Planar Slab Waveguide. J. Phys. A Math. Gen. 2005, 38, L171. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of Coupled Optical PT-symmetric Structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of PT-symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of Parity-time Symmetry in Optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Feng, L.; Ayache, M.; Huang, J.; Xu, Y.L.; Lu, M.H.; Chen, Y.F.; Fainman, Y.; Scherer, A. Nonreciprocal Light Propagation in a Silicon Photonic Circuit. Science 2011, 333, 729–733. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian Photonics Based on Parity–time Symmetry. Nat. Photonics 2017, 11, 752–762. [Google Scholar] [CrossRef]
- Bender, N.; Factor, S.; Bodyfelt, J.D.; Ramezani, H.; Christodoulides, D.N.; Ellis, F.M.; Kottos, T. Observation of Asymmetric Transport in Structures with Active Nonlinearities. Phys. Rev. Lett. 2013, 110, 234101. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, H.; Luo, B.; Guo, H. Parity-time Symmetric Bragg Structure in Atomic Vapor. Opt. Express 2014, 22, 25120–25127. [Google Scholar] [CrossRef]
- Zhu, X.; Ramezani, H.; Shi, C.; Zhu, J.; Zhang, X. PT-symmetric Acoustics. Phys. Rev. X 2014, 4, 031042. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-mode Laser by Parity-time Symmetry Breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric Whispering-gallery Microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Nazari, F.; Abdollahi, S.; Samsami-Khodadad, F. On-chip Magnetic-free Optical Multi-port Circulator Based on a Locally Linear Parity-time Symmetric System. Appl. Opt. 2019, 58, 2867–2872. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Miri, M.A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time–symmetric Microring Lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Liu, F.; Li, J. Effective Spontaneous PT-symmetry Breaking in Hybridized Metamaterials. Phys. Rev. A 2013, 87, 053824. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveira, J.E.B.; Almeida, V.R.; Chen, Y.F.; Scherer, A. Experimental Demonstration of a Unidirectional Reflectionless Parity-time Metamaterial at Optical Frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef]
- Lee, J.Y.; Chen, P.Y. Generalized Parametric Space, Parity Symmetry of Reflection, and Systematic Design Approach for Parity-time-symmetric Photonic Systems. Phys. Rev. A 2021, 104, 033510. [Google Scholar] [CrossRef]
- Boucher, Y.G.; Féron, P. Parity-time Symmetry in Laterally Coupled Bragg Waveguides. IEEE J. Quantum Electron. 2019, 55, 1–9. [Google Scholar] [CrossRef]
- Shu, X.; Zhong, Q.; Hong, K.; You, O.; Wang, J.; Hu, G.; Alù, A.; Zhang, S.; Christodoulides, D.N.; Chen, L. Chiral Transmission by an Open Evolution Trajectory in a Non-Hermitian System. Light Sci. Appl. 2024, 13, 65. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional Invisibility Induced by PT-symmetric Periodic Structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [PubMed]
- Novitsky, A.; Lyakhov, D.; Michels, D.; Pavlov, A.A.; Shalin, A.S.; Novitsky, D.V. Unambiguous Scattering Matrix for Non-Hermitian Systems. Phys. Rev. A 2020, 101, 043834. [Google Scholar] [CrossRef]
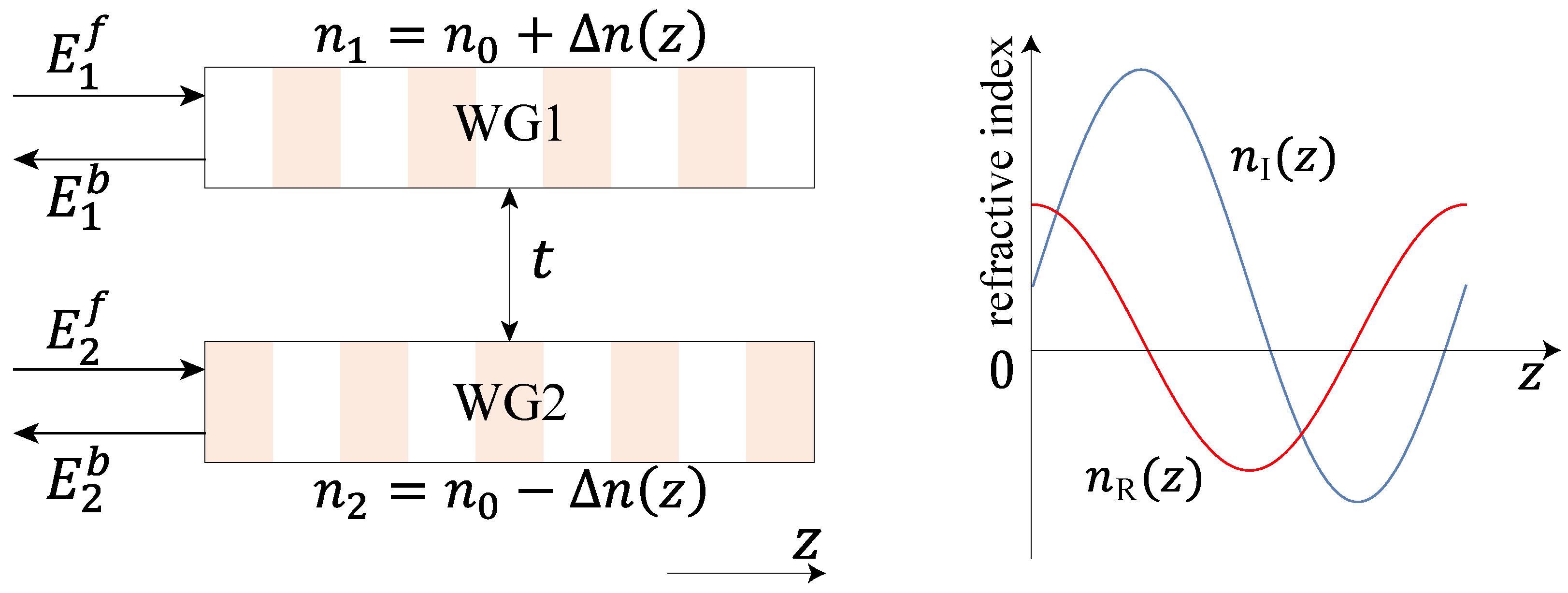

| The amplitude of the forward propagating modes | |
| The amplitude of the backward propagating modes | |
| The refractive index of the waveguide | |
| The refractive index of the homogeneous medium | |
| The modulated refractive index of the waveguide | |
| A constant used to coupling two modes | |
| The wave vector in the homogeneous medium | |
| the wave vector in vacuum | |
| p, g and m | The parameters of modulated refractive index |
| t | The coupling coefficient between two waveguides |
| Hamiltonian of single waveguide | |
| Hamiltonian of double waveguide | |
| , and | The parameters of Hamiltonian in waveguide system |
| , and | Pauli matrices |
| I | Identity matrix |
| T | The transmission matrix |
| S | The scattering matrix |
| The eigenvalues of the Hamiltonian matrix | |
| The eigenvalues of the scattering matrix | |
| a, , b, c, d, e and f | The parameters of the scattering matrix |
| Region | Key Behavior |
|---|---|
| I | Appear a divergent point, and then tend towards a finite value when |
| II | Periodic amplitude oscillations |
| III | Periodic amplitude oscillations |
| IV | Periodic amplitude oscillations and divergent responses |
| V | Appear a divergent point, and then tend towards a finite value when |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Wang, Z.; Hu, Y.; Sun, Y. Exceptional Point Engineering and Optical Transport in Coupled Double Waveguides. Symmetry 2025, 17, 1748. https://doi.org/10.3390/sym17101748
Yue Y, Wang Z, Hu Y, Sun Y. Exceptional Point Engineering and Optical Transport in Coupled Double Waveguides. Symmetry. 2025; 17(10):1748. https://doi.org/10.3390/sym17101748
Chicago/Turabian StyleYue, Yang, Ziyu Wang, Ying Hu, and Yue Sun. 2025. "Exceptional Point Engineering and Optical Transport in Coupled Double Waveguides" Symmetry 17, no. 10: 1748. https://doi.org/10.3390/sym17101748
APA StyleYue, Y., Wang, Z., Hu, Y., & Sun, Y. (2025). Exceptional Point Engineering and Optical Transport in Coupled Double Waveguides. Symmetry, 17(10), 1748. https://doi.org/10.3390/sym17101748






