Modified Soft Margin Optimal Hyperplane Algorithm for Support Vector Machines Applied to Fault Patterns and Disease Diagnosis
Abstract
1. Introduction
2. Materials and Methods
- 1.
- First Stage: Data Classification and Heart Disease Diagnosis with MSMOH Method.
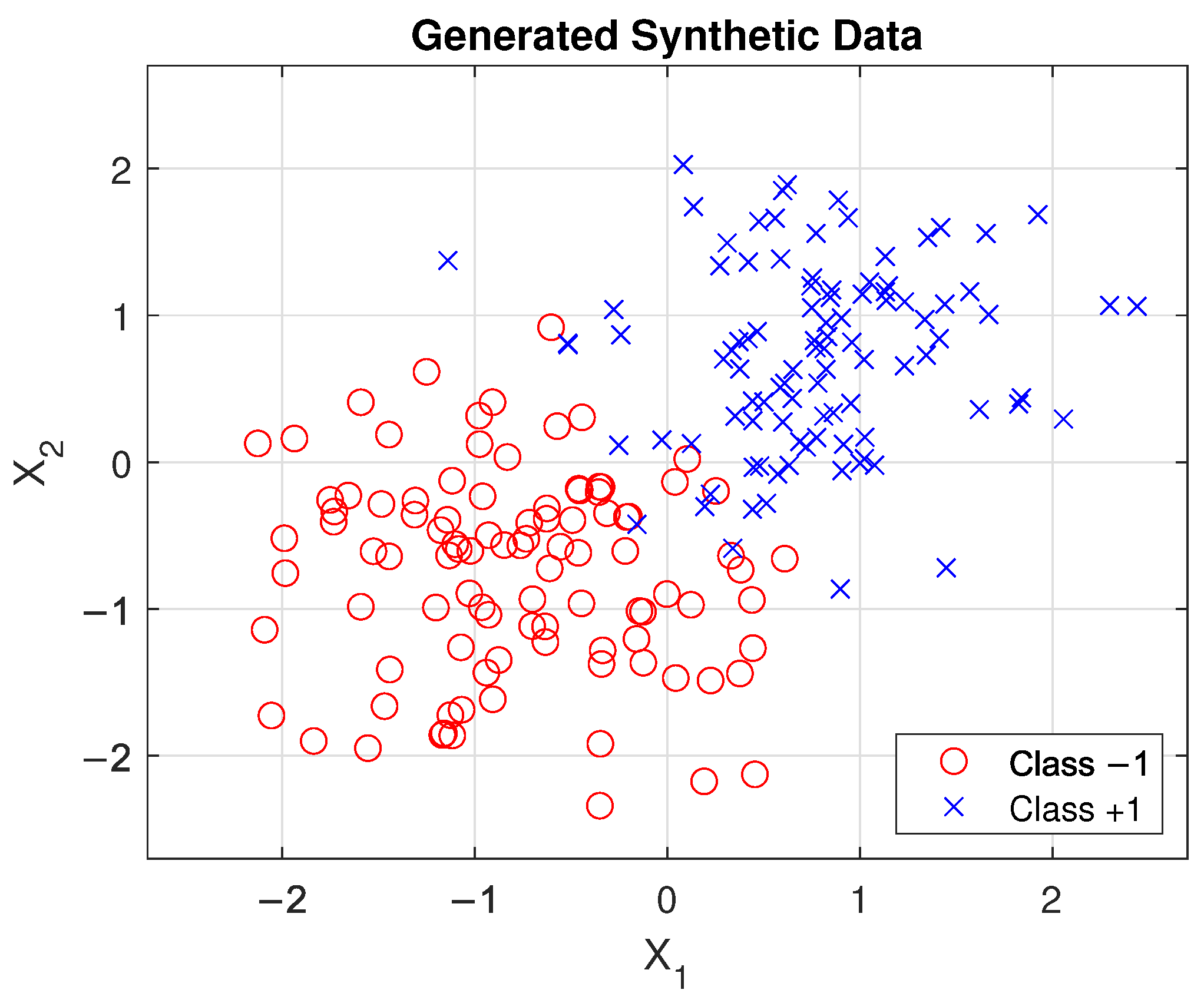
- Following the description of MSMOH in Section 4, two different datasets are employed to illustrate the superiority of the new method. The first is a two-dimensional synthetic dataset with balanced distribution (symmetric), which allows for a visual comparison of the margin maximization offered by the constructed MSMOH versus SMOH.
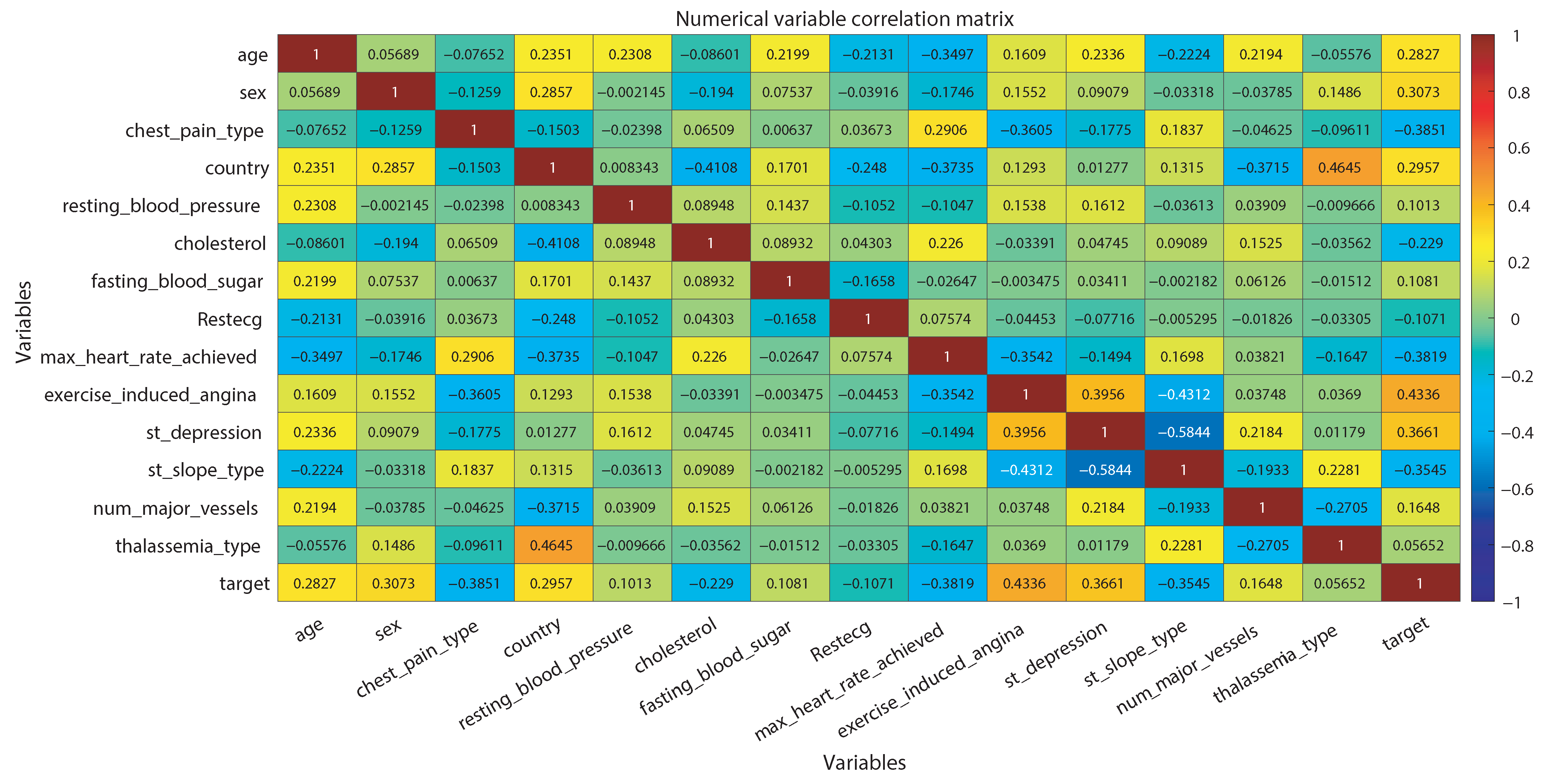
- The heart disease database [21], sourced from the UCI repository, constitutes the second dataset with unbalanced data distribution (asymmetric). Prior to classification, this database underwent imputation, codification, and correlation analysis to optimize its representation. Subsequent analysis, encompassing performance metrics such as accuracy, precision, and confusion matrix, among others, are detailed in Section 5.
- 2.
- Second Stage: Fault Pattern Diagnosis.
- Section 6 details the acquisition of fault patterns in fossil electric power plants, along with the procedures employed for codifying the measured patterns.
- Subsequent to the codification of fault patterns into bipolar vectors, a NAM is trained using the novel MSMOH synthesis to facilitate fault pattern diagnosis.
- An analysis of the results obtained from the trained NAM is presented, showcasing its significant advantages when compared to conventional training algorithms such as perceptron, OH, and SMOH.
- Furthermore, the convergence properties—including convergence, non-convergence, and spurious memories—were analyzed and compared for each training algorithm across all 1024 possible element combinations ().
3. Mathematical Preliminaries
3.1. Optimal Hyperplane of SVM
3.2. Soft Margin Optimal Hyperplane
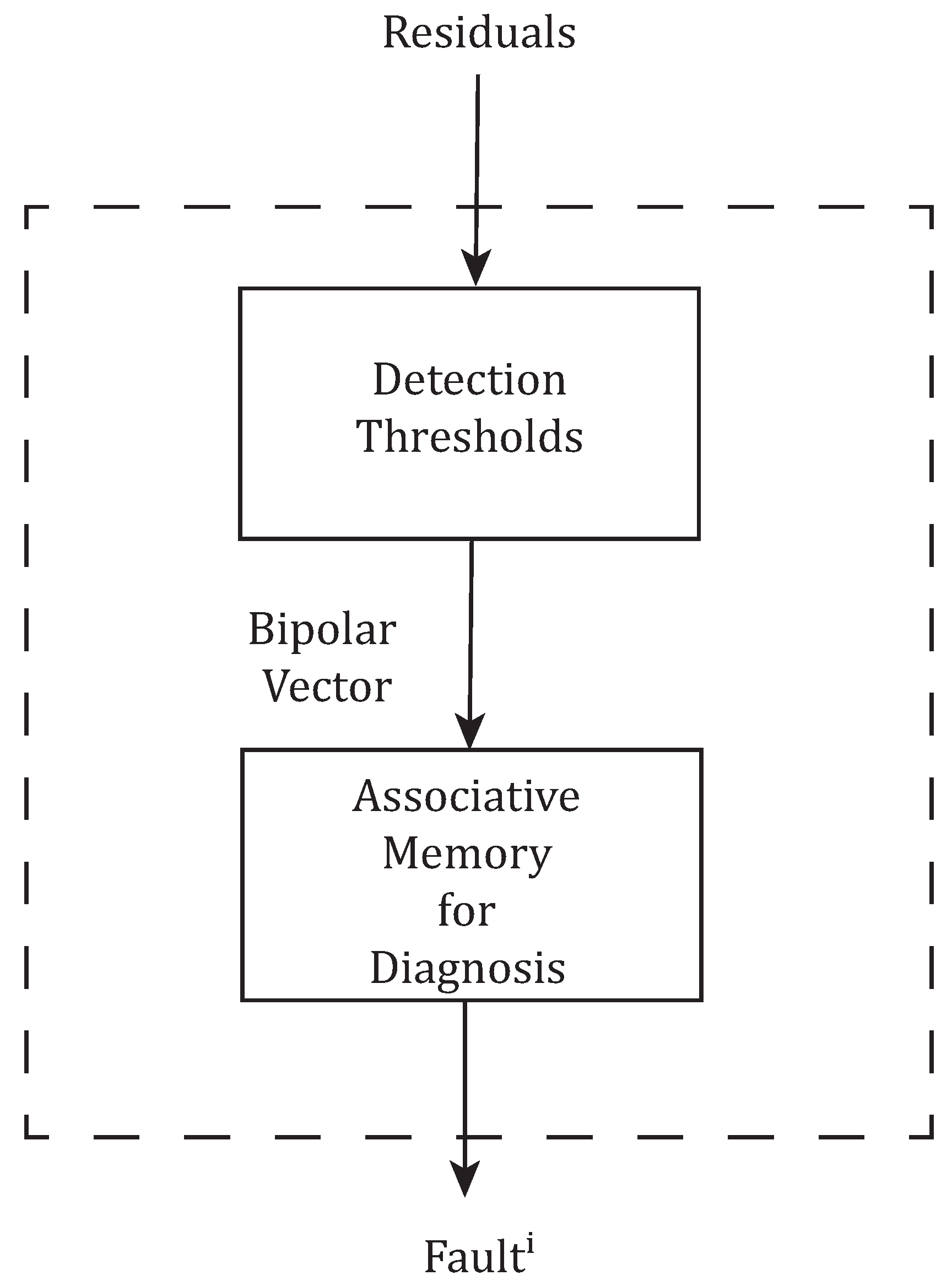
3.3. Neural Associative Memory Based on Recurrent Neural Network
- 1.
- Each of the given vectors becomes a stable memory vector for the system in Equation (22);
- 2.
- The number of undesirable or ”spurious” memory vectors is minimized, and the basin of attraction for each of the desired memory vectors is maximized. This means that even a noisy or incomplete version of a desired vector can still successfully converge to the correct stored memory.
Training Algorithms for NAM
- 1.
- Perceptron training algorithmThe perceptron has the following equation:where Z is the perceptron output, is the input vector, is the weight vector, andThe perceptron training finds the weight vector W with the following steps considering and the patterns when and when .
- (a)
- Initialize the weight vector for .
- (b)
- For
- i.
- If and , then update;
- ii.
- If and , then update;
- iii.
- Otherwise, , where for some , and is the perceptron learning rate.
- (c)
- The training stops when no more updates for the weight vector W are needed.
The search of W weight values are presented as follows:such thatfor , andchoose with . For choose if . with and . - 2.
- Optimal hyperplane algorithmThis training is based on the equations described in Section 3.1, where W values are obtained finding the Lagrange multipliers and the b value using the support vectors selected in the optimal hyperplane construction. However, the selection of and I are subject to the following equation:and the vector is defined exactly as in (30). A notable distinction exists between the selection of NAM parameters and perceptron training regarding the determination of T and I. This process requires that with . For choose if . with and .
- 3.
- Soft Margin Training AlgorithmSimilar to the OH training, this training employs the equations presented in Section 3.2 for the search of optimal values to construct the SMOH. In this case, a hyperparameter C is introduced and must be correctly selected for the efficient training of the NAM. Once the weight vector is computed, the following condition must be accomplishedwhere the vector is again considered and defined as in (30), letting the NAM parameters be chosen with the same requirements as in the OH training algorithm where with . For choose if . with and .Despite the selection of the and I parameters being similar to the OH training algorithm, the main difference is that obtaining the W and b parameters is based on the SMOH construction and hinge loss function. Further and deep analysis of the training algorithms for the NAM can be consulted in [17].
4. Proposed Soft Margin Optimal Hyperplane Modification
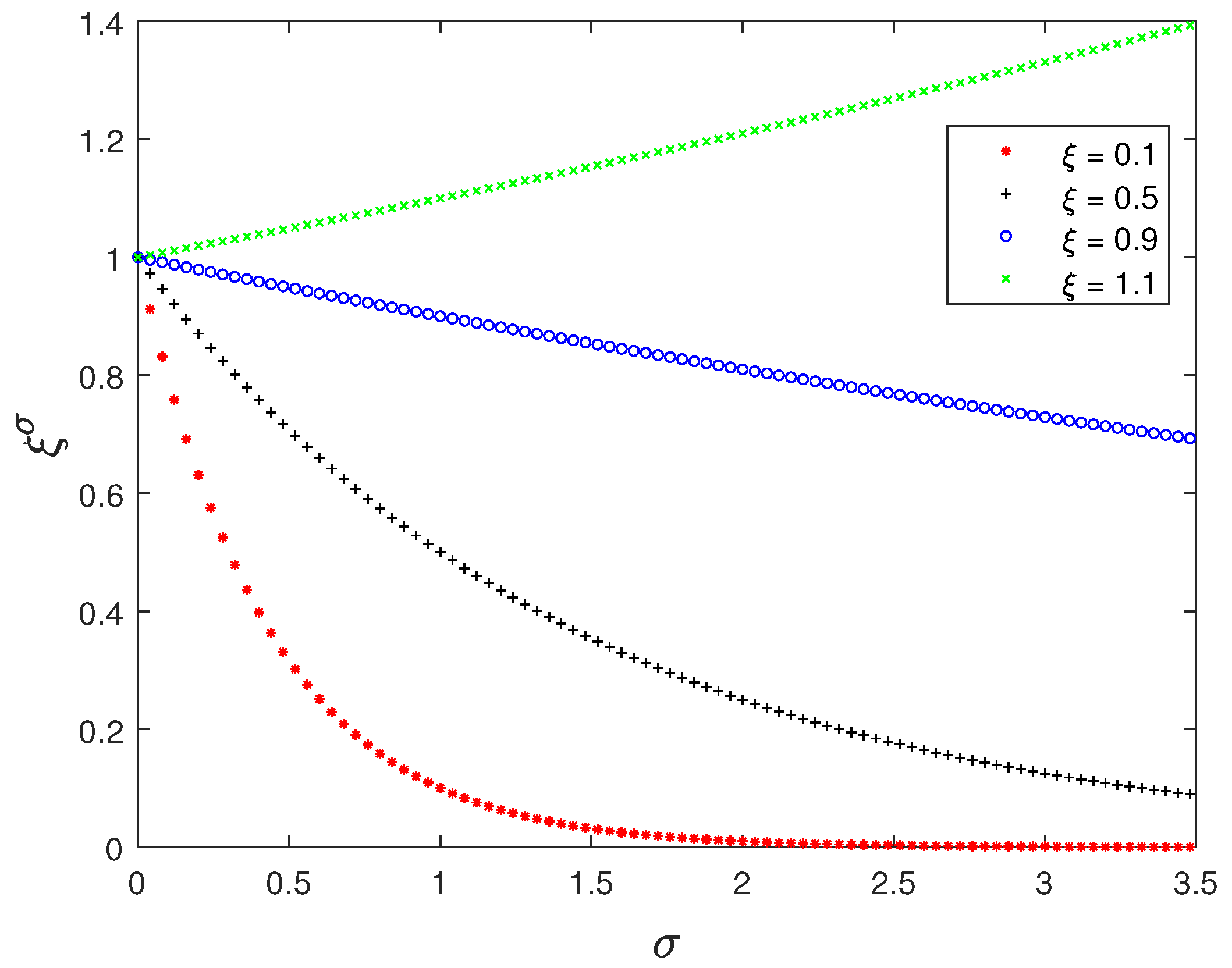
4.1. First Case of the Proposed Modification, p = 1
4.2. Second Case of the Proposed Modification, p = 2
4.3. Third Case of the Proposed Modification, p = 3
4.4. Forth Case of the Proposed Modification, p = 4
5. Data Classification with MSMOH Synthesis for Support Vector Machines
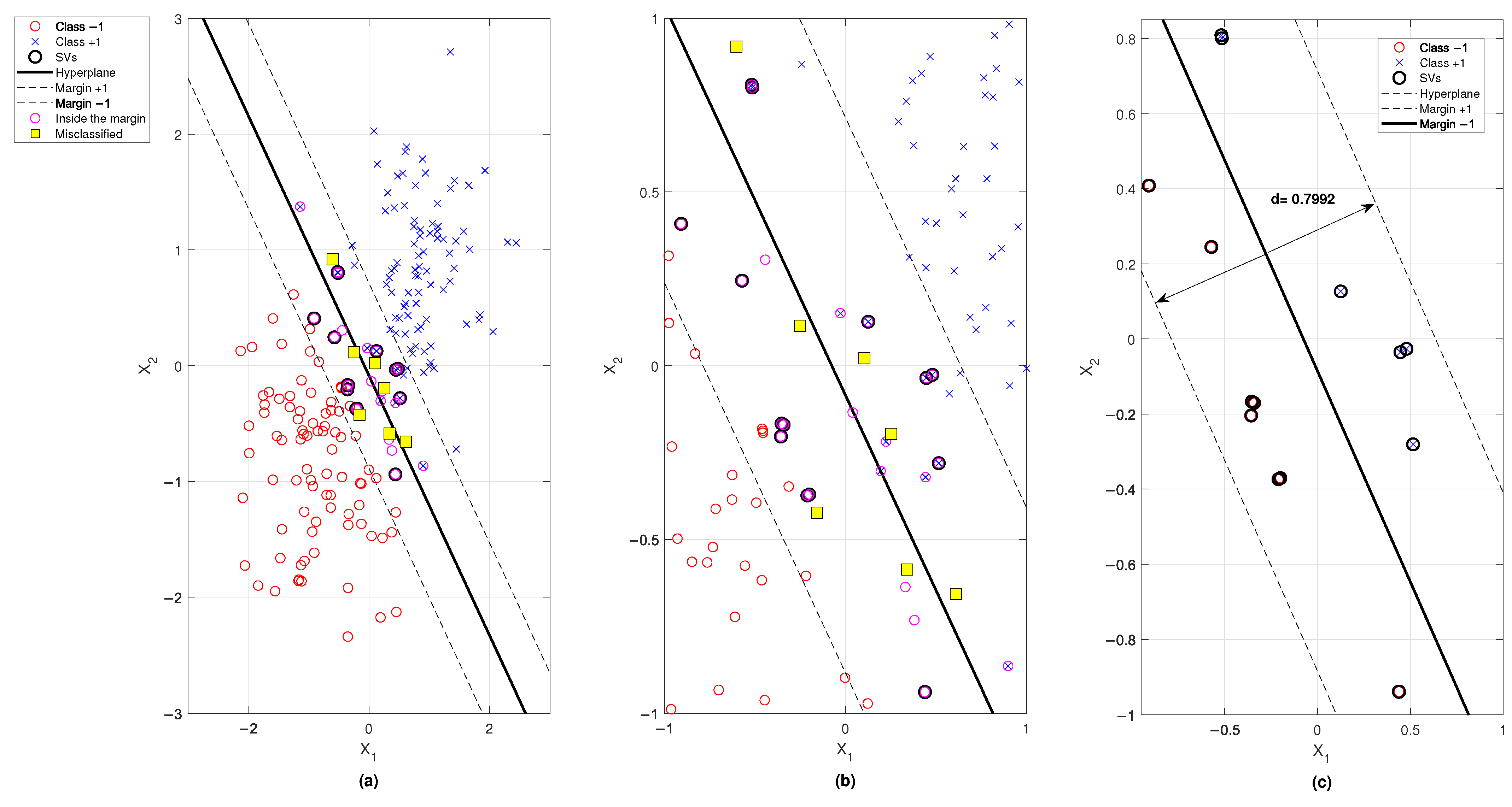
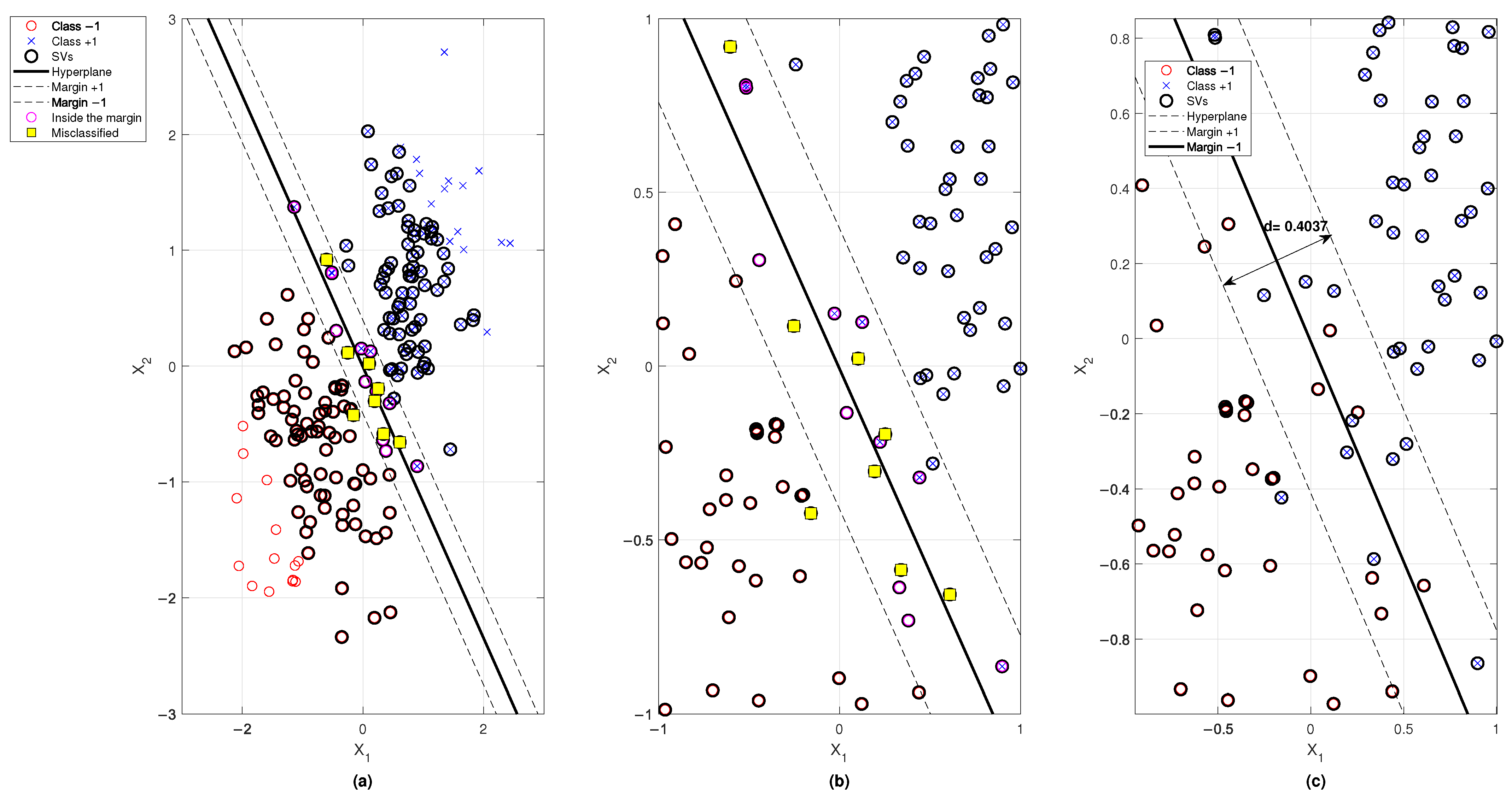
5.1. Classification of Synthetic Data with MSMOH
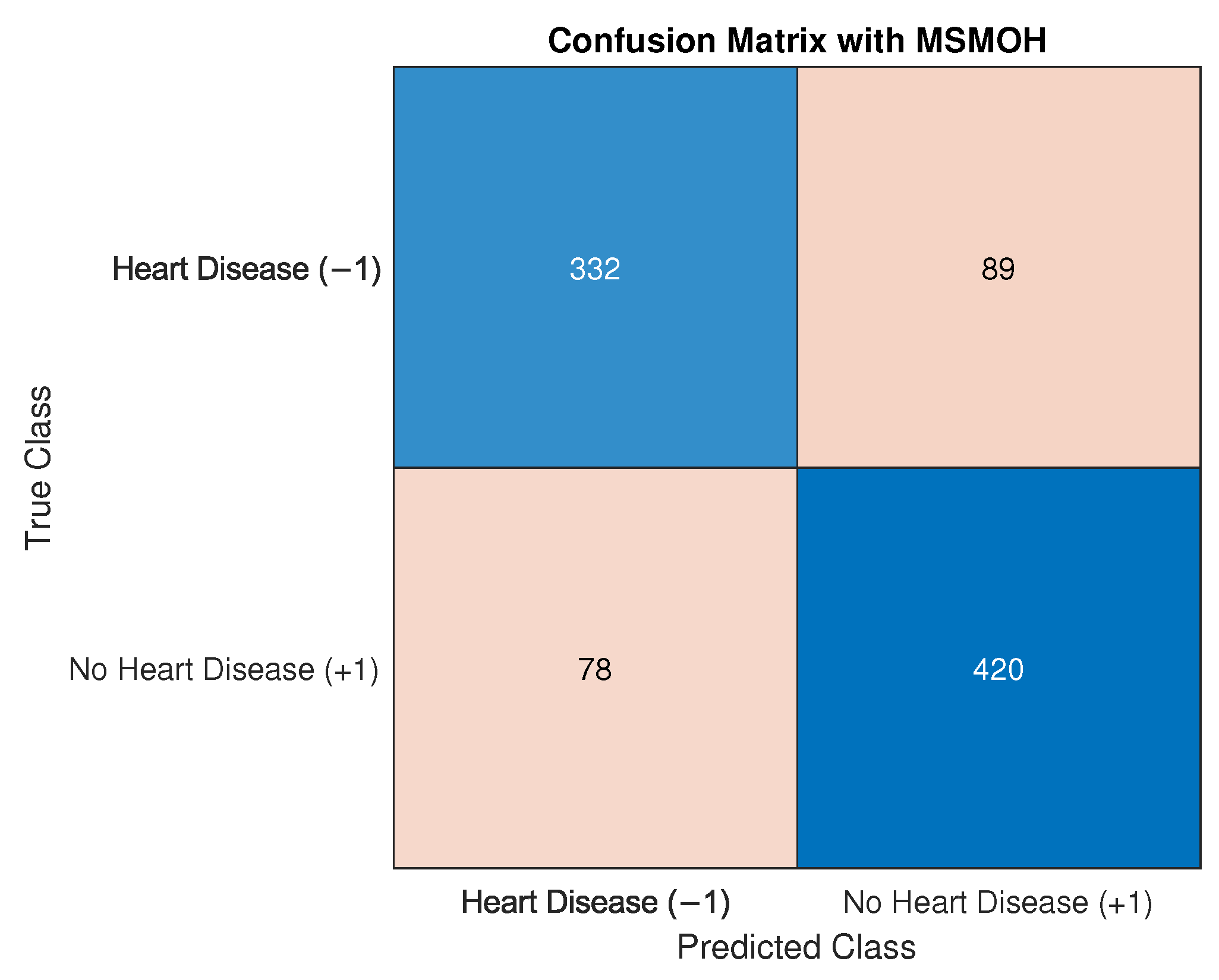
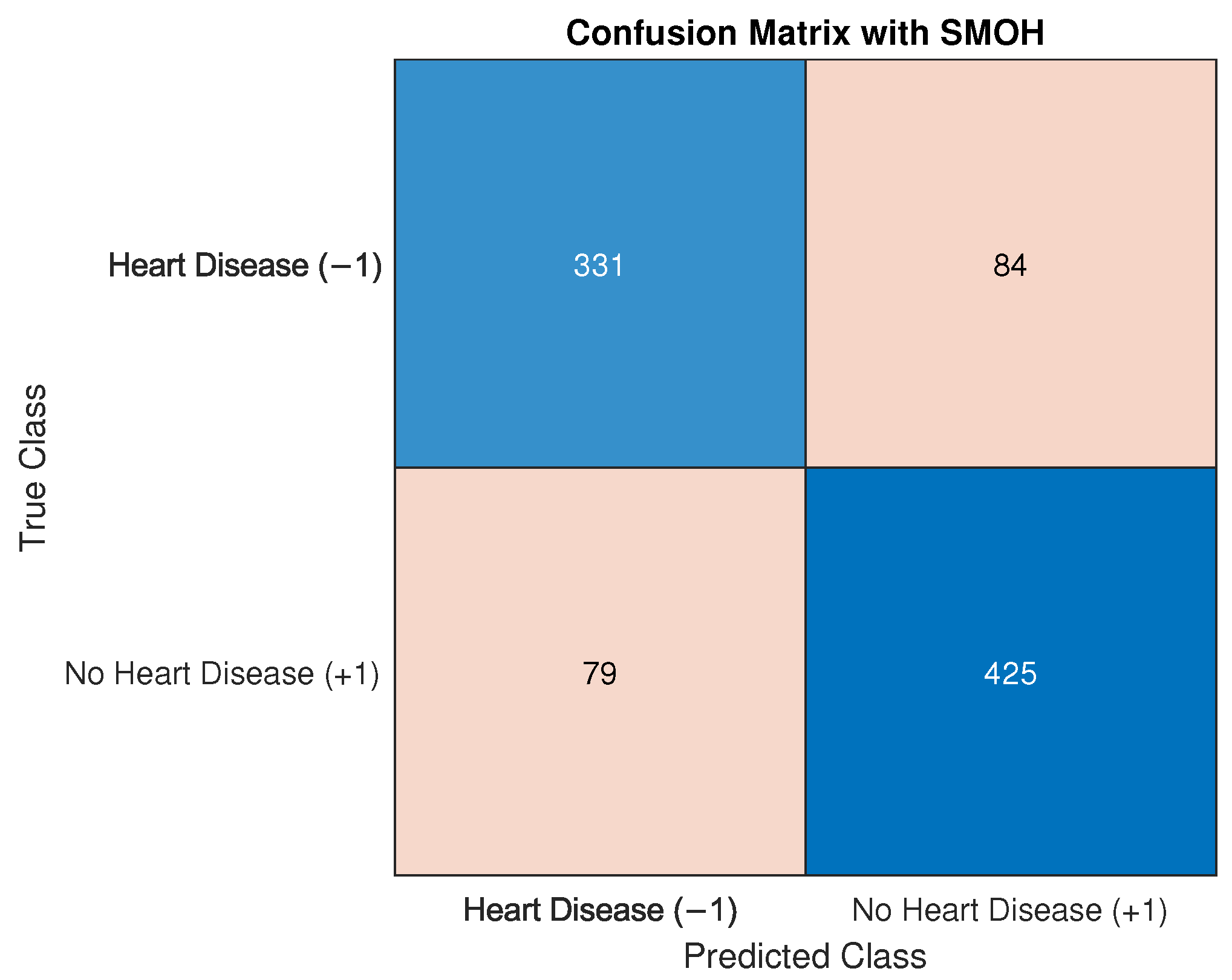
5.2. Heart Diseases Diagnosis with MSMOH
5.2.1. UCI Heart Disease Database Preprocessing
5.2.2. Heart Disease Diagnosis with SVM-MSMOH Classification
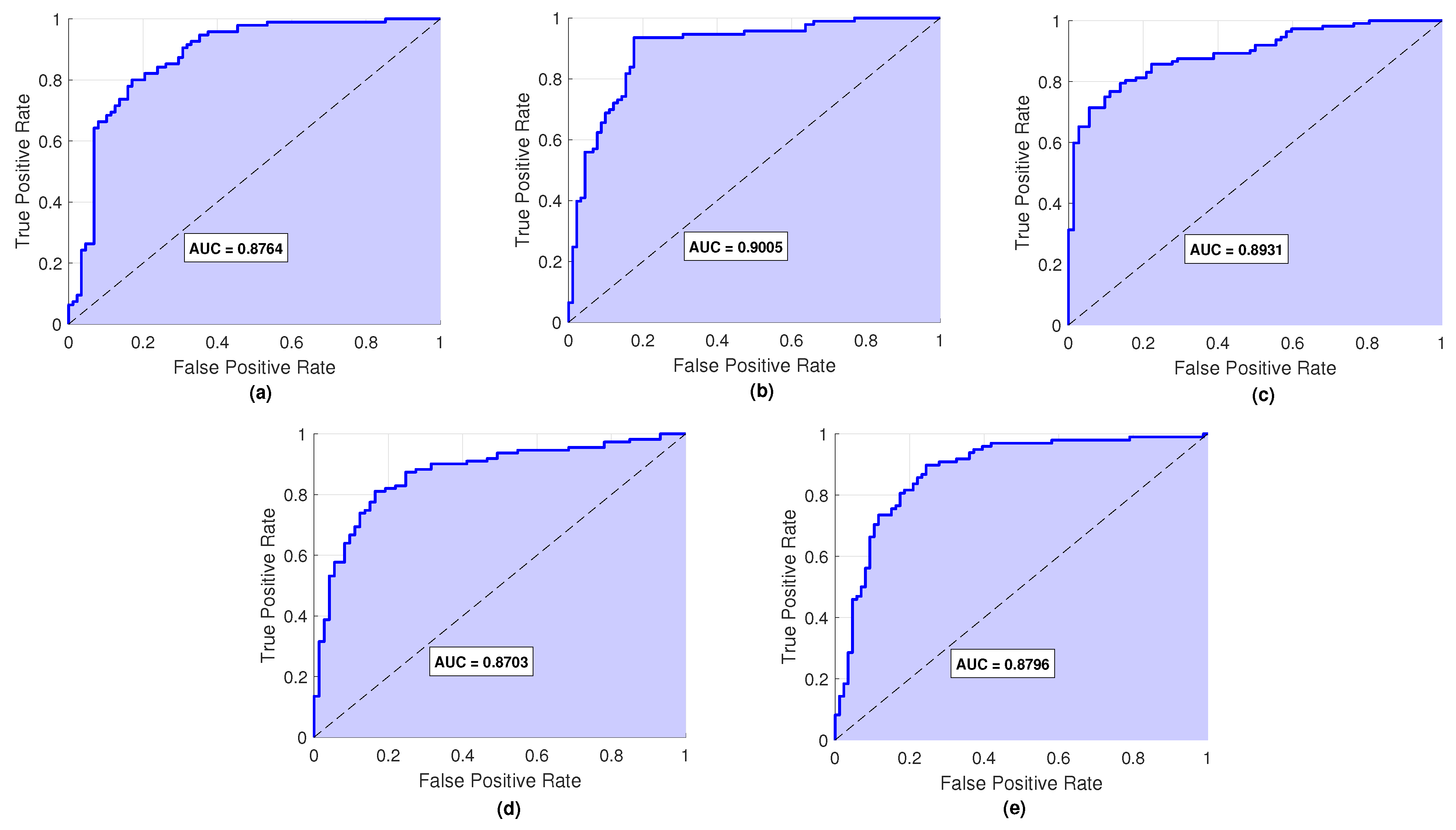
5.2.3. Heart Disease Diagnosis with Cross-Validation
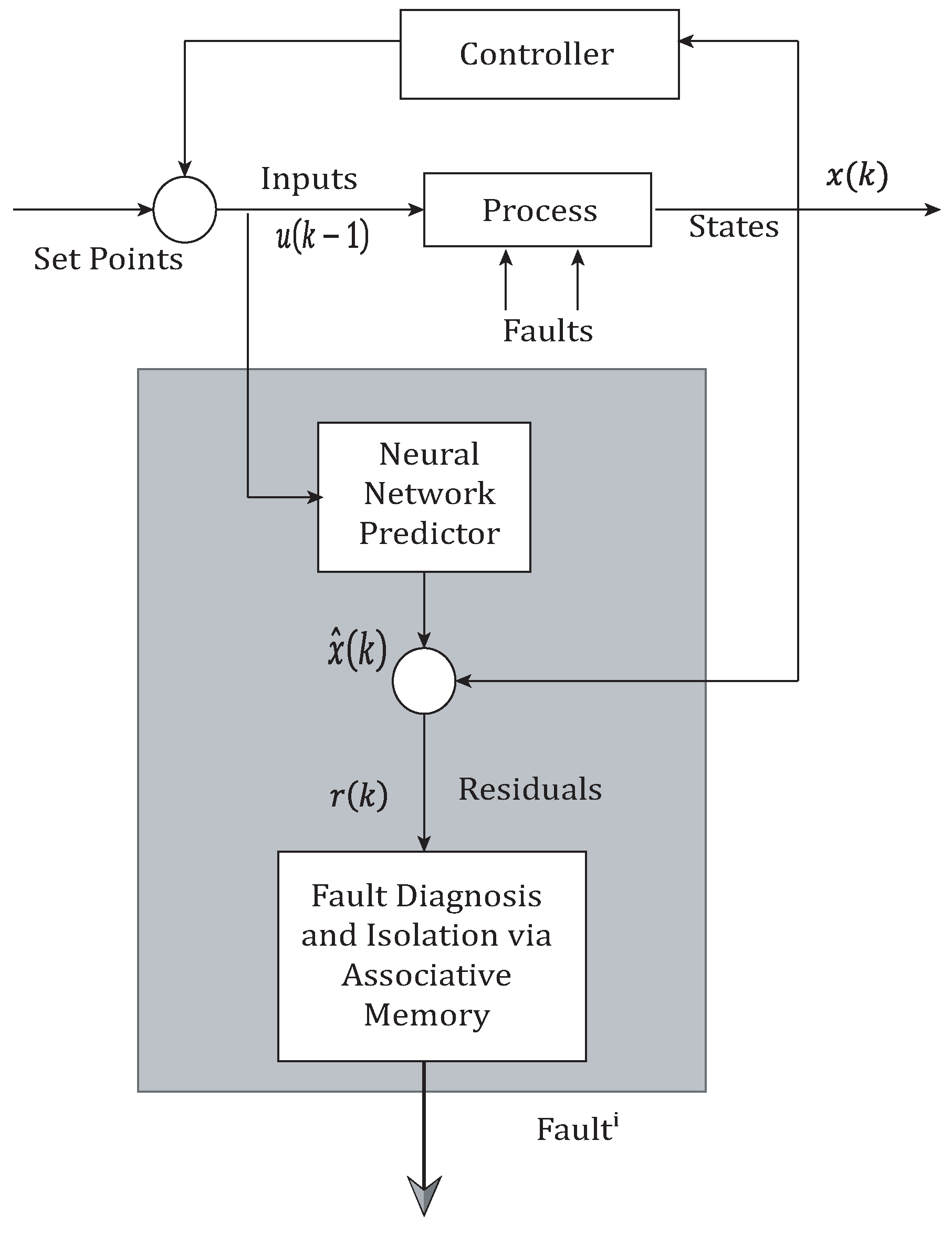
6. Neural Associative Memory with MSMOH Training for Fault Diagnosis in Fossil Electric Power Plants
- : Normal Operating Conditions;
- : Water Wall Tube Rupture;
- : Superheater Tube Rupture;
- : Superheated Steam Temperature Control Failure;
- : Fouled Regenerative Preheater;
- : Feedwater Pump Variable Speed Drive Operating at Maximum;
- : Stuck Fuel Valve.
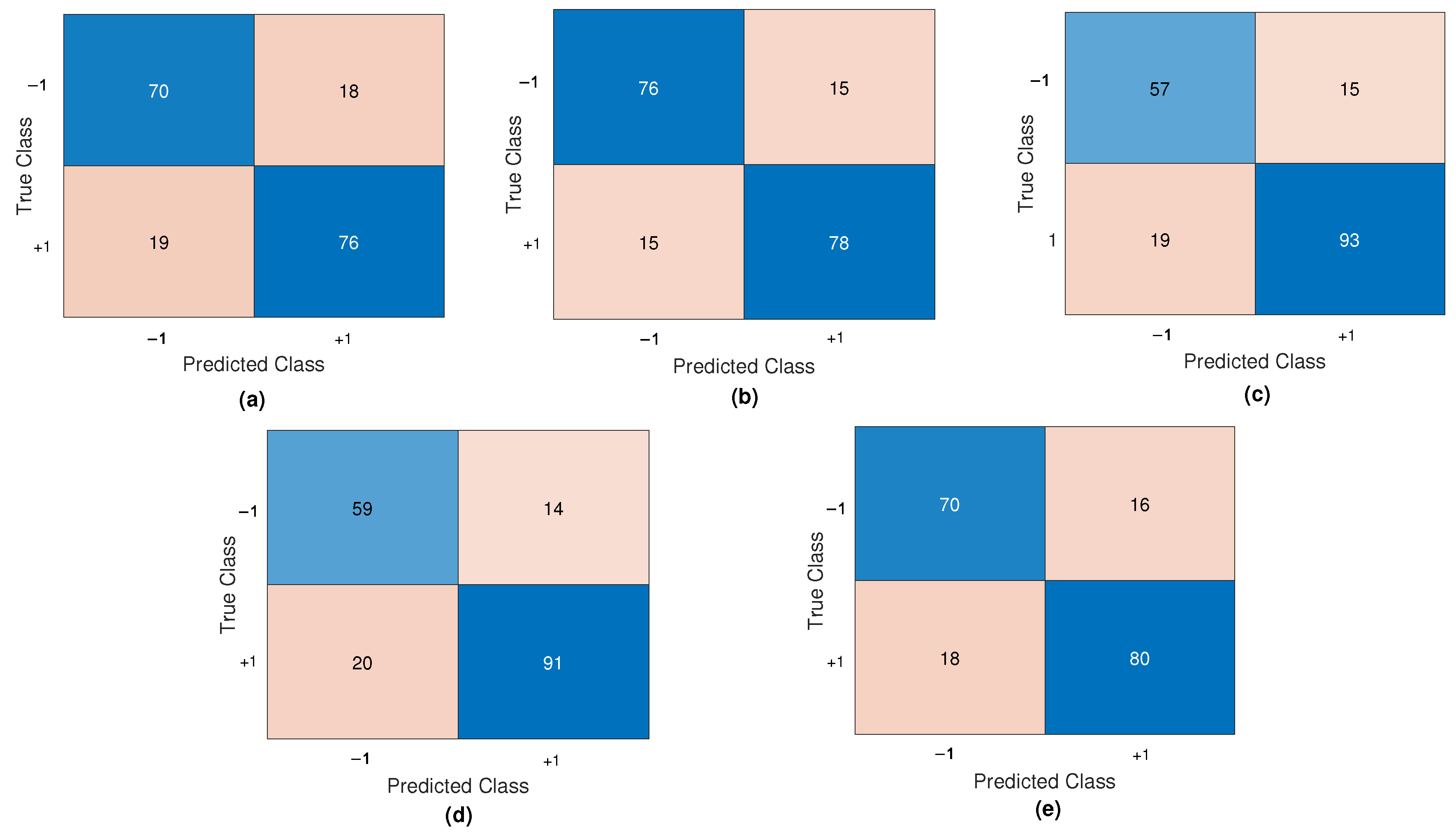
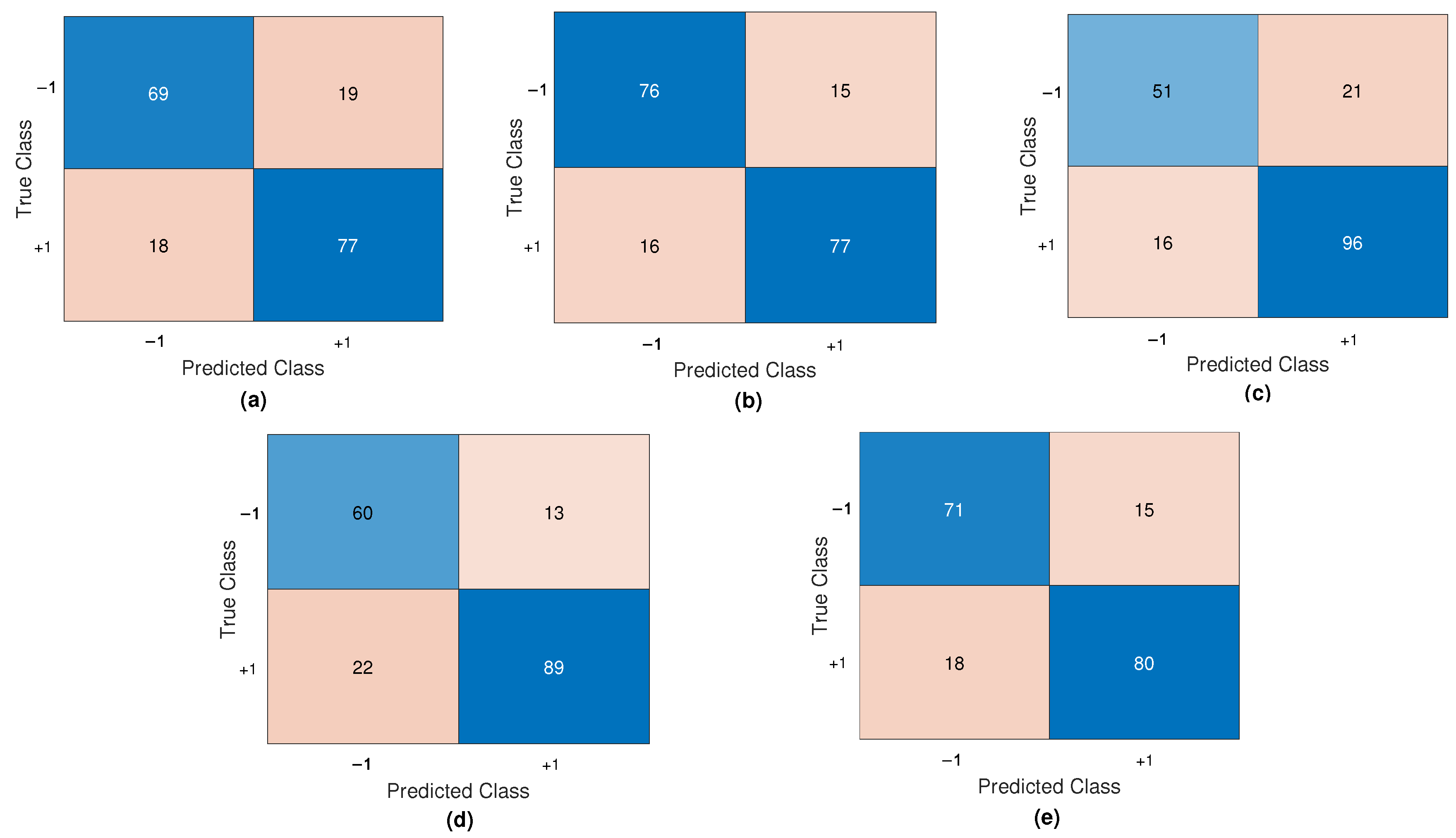
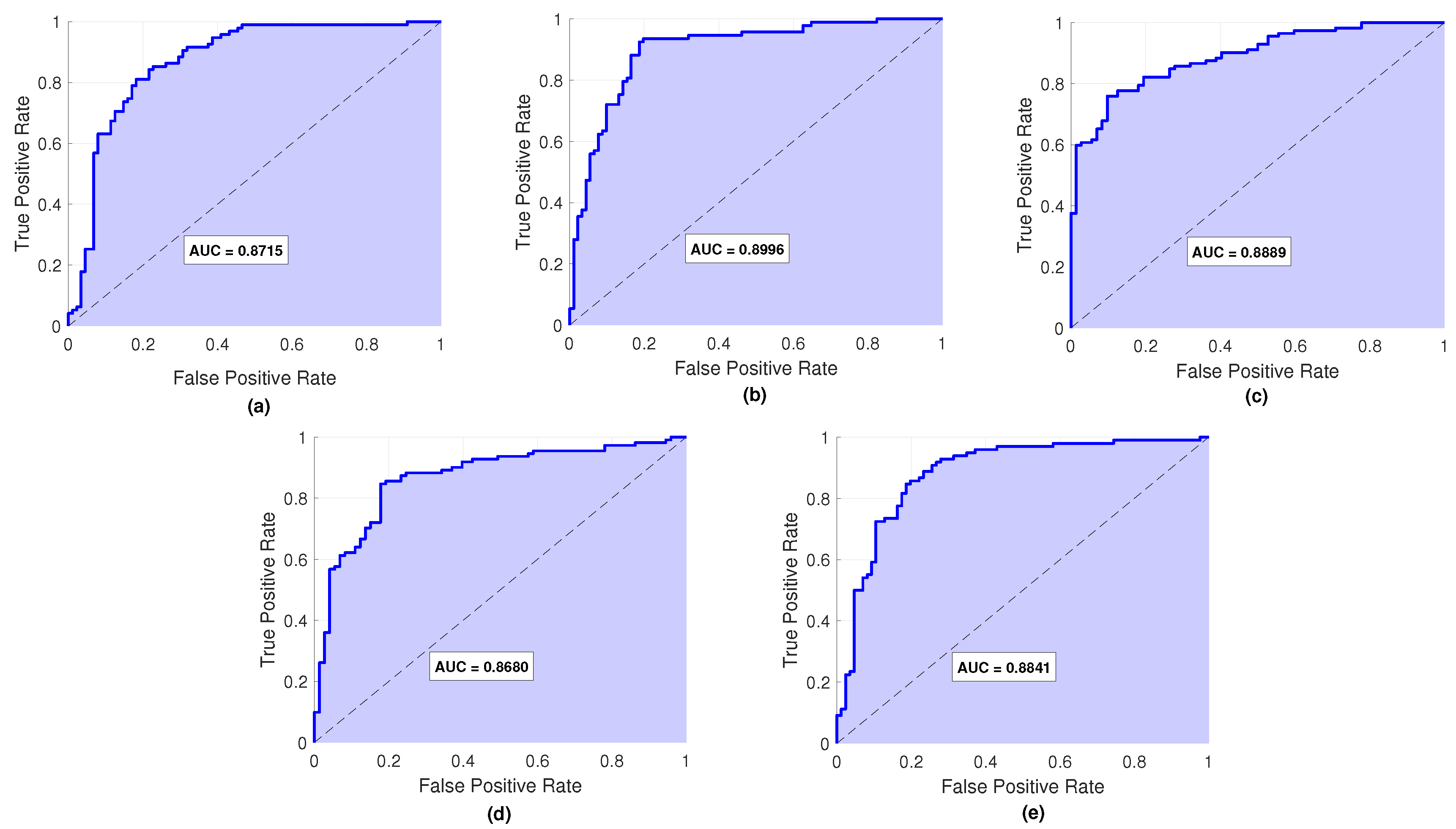
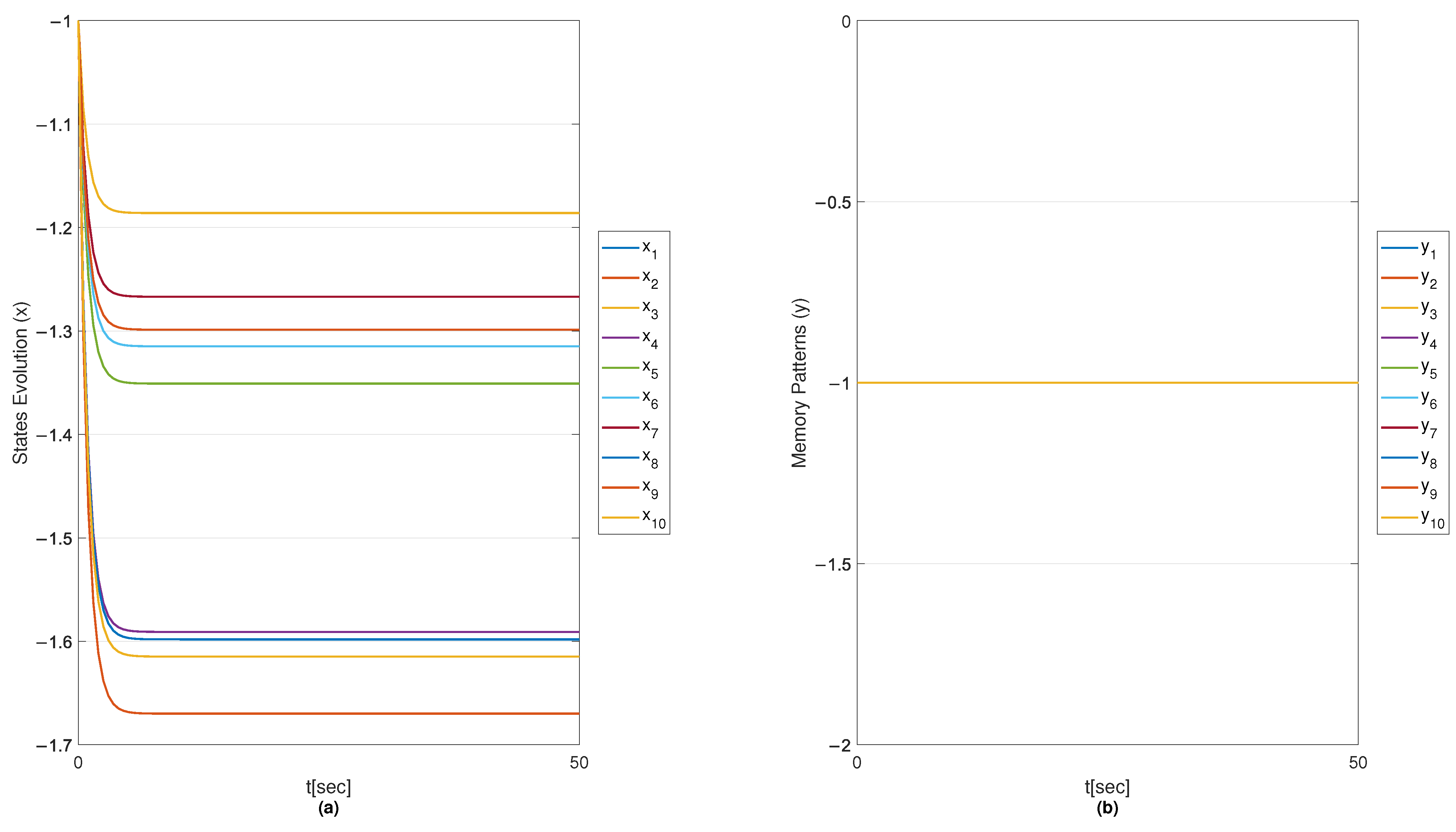
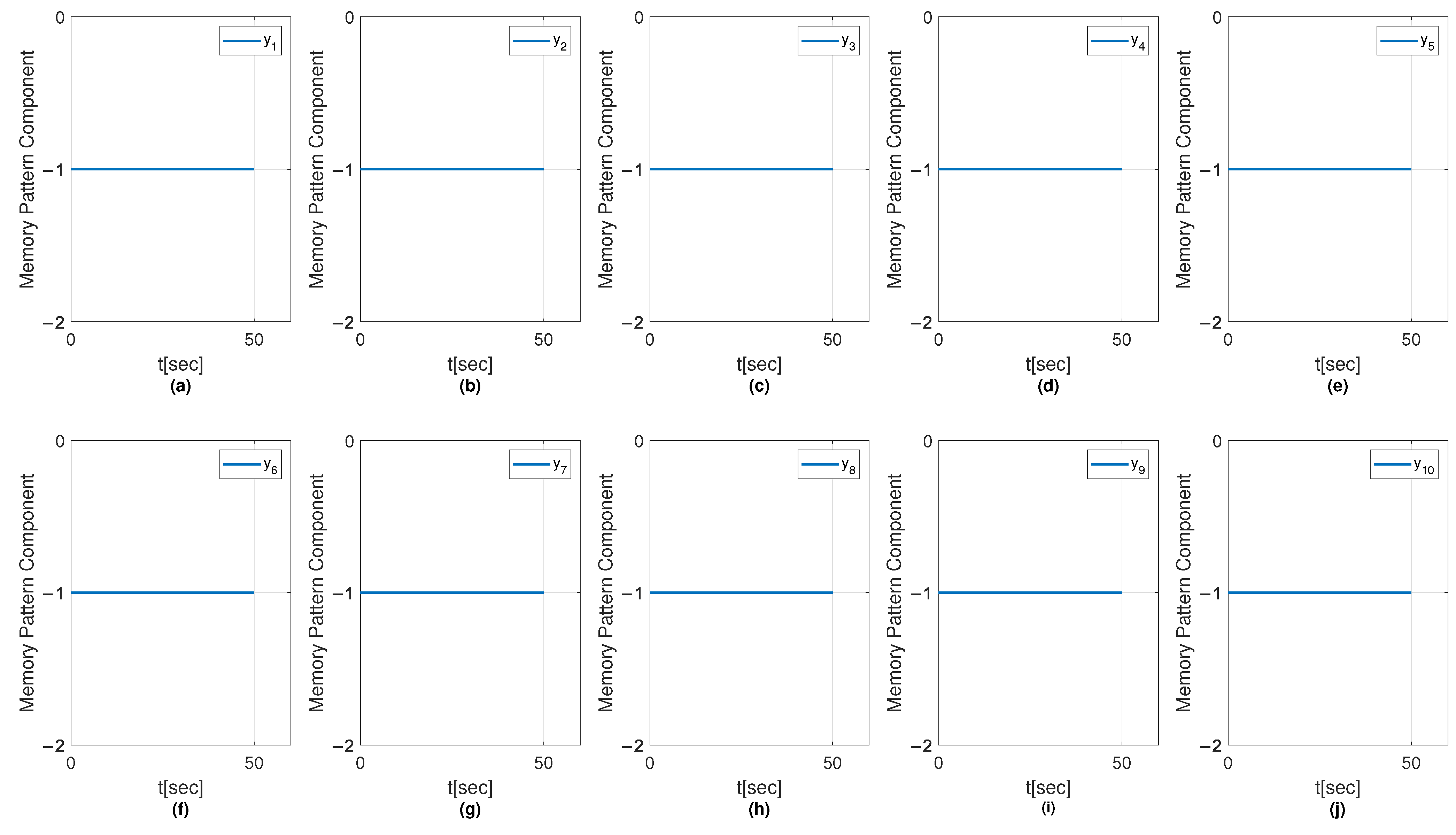
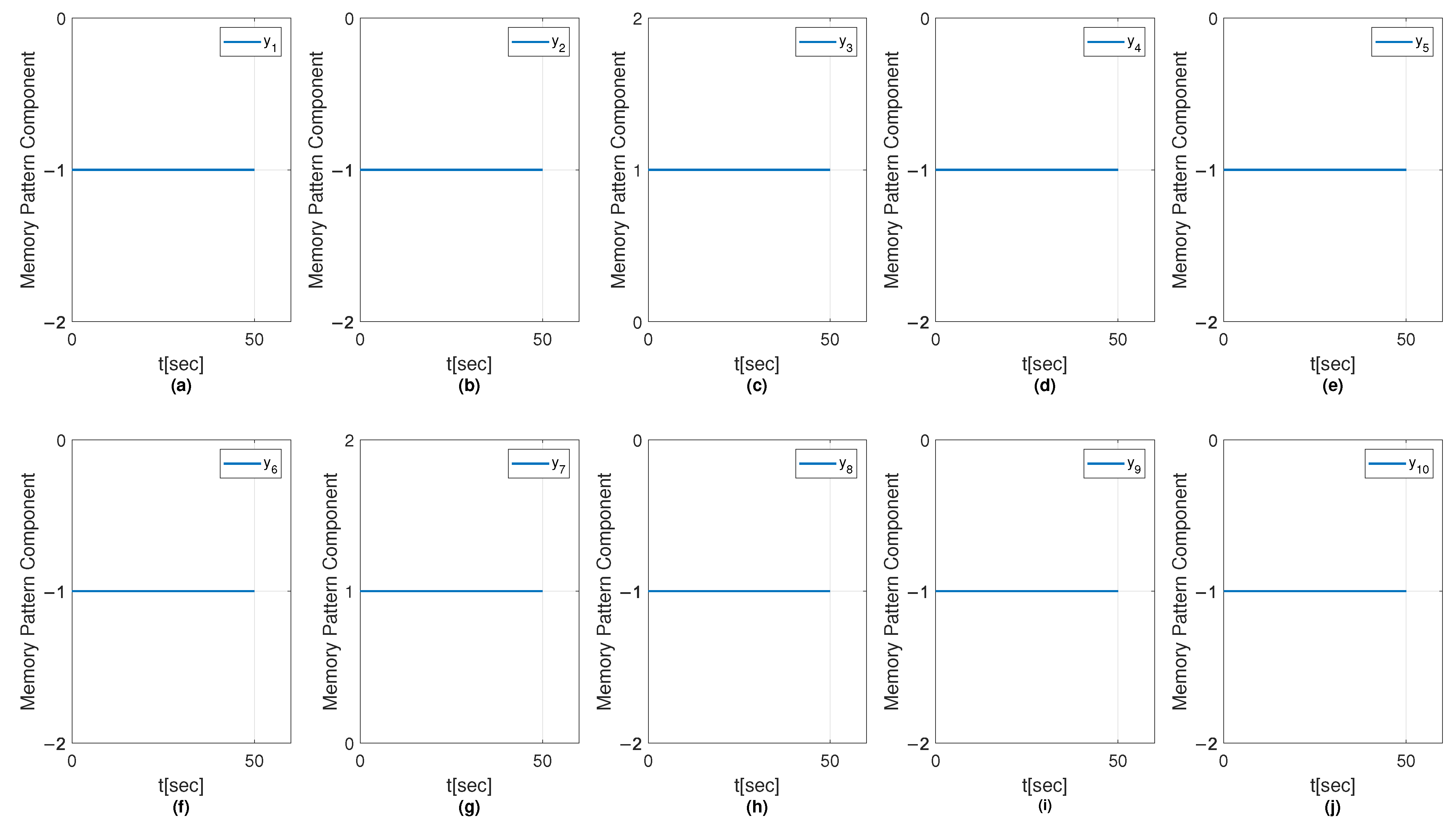
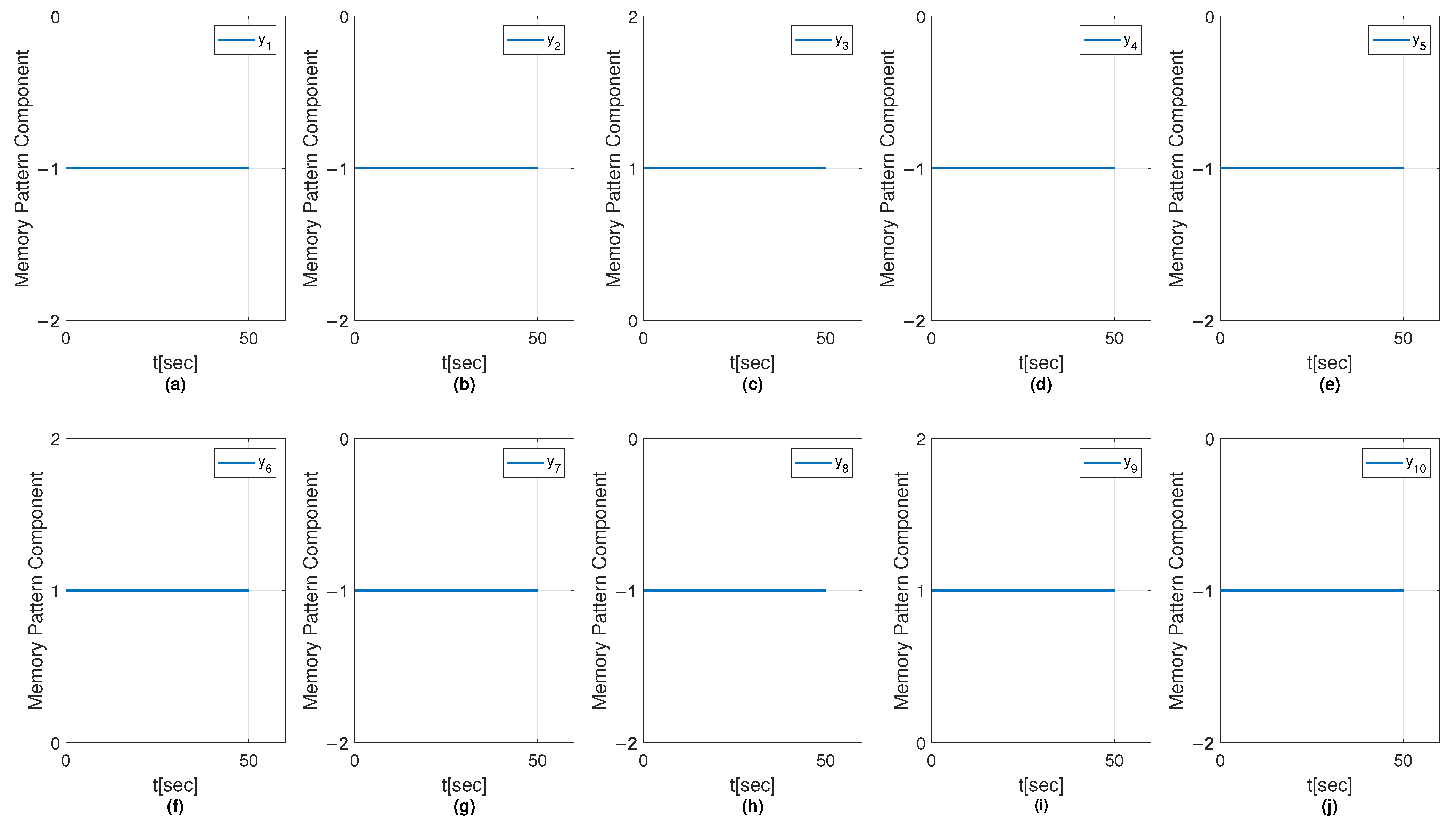
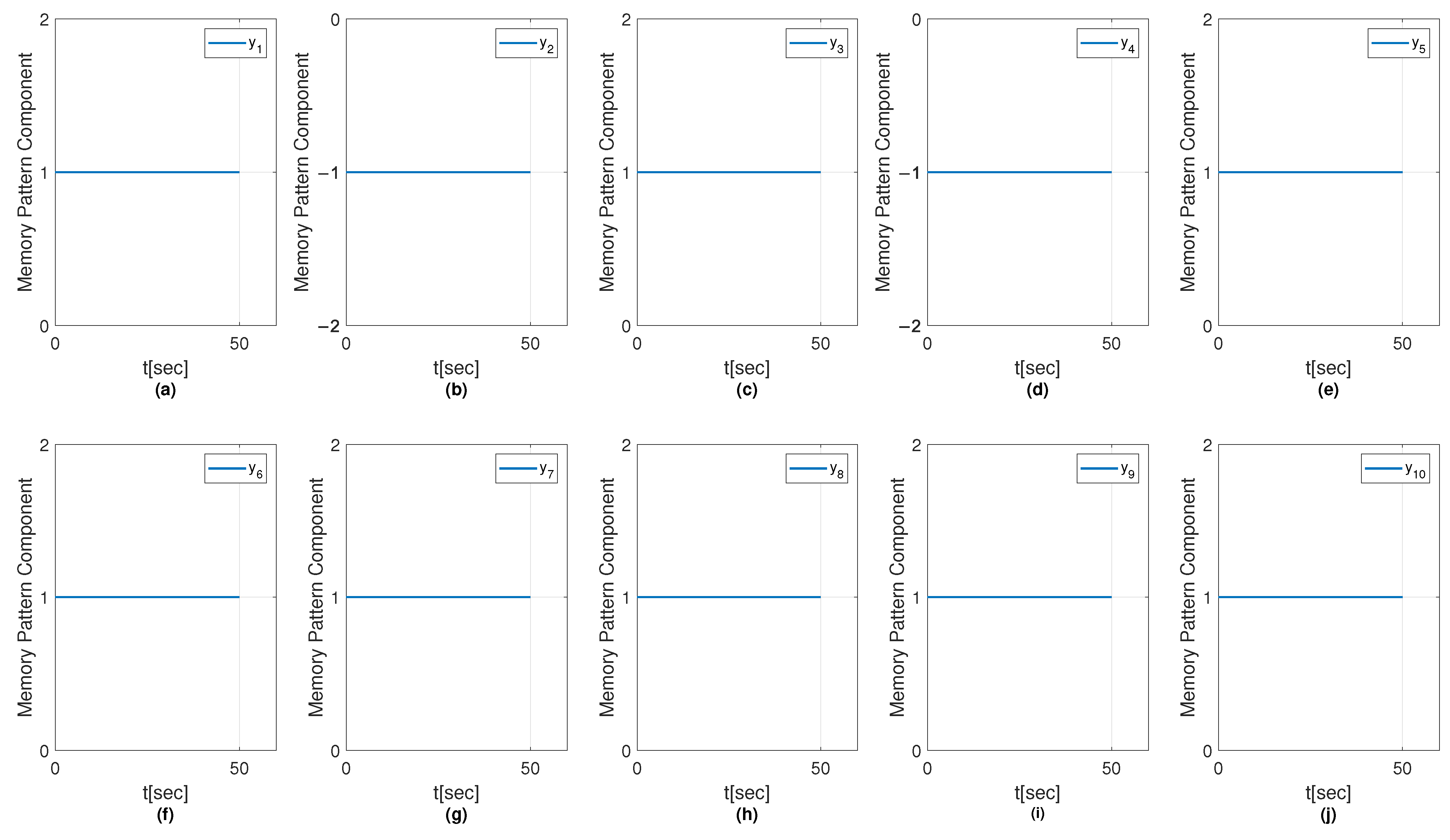
6.1. Results on Fault Diagnosis
6.1.1. Results with Perceptron Training Algorithm
6.1.2. Results with OH Training Algorithm
6.1.3. Results with SMOH Training Algorithm
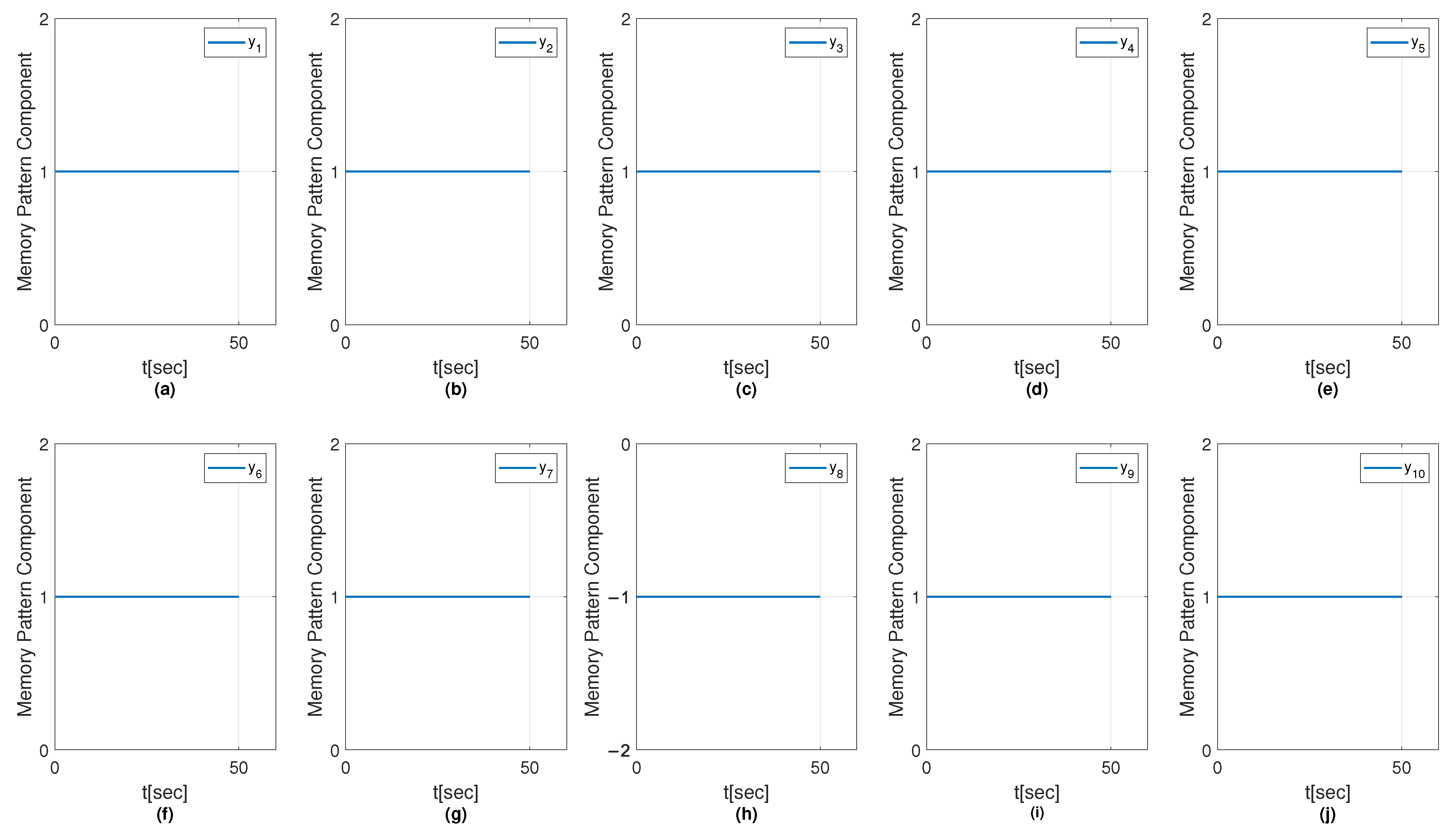
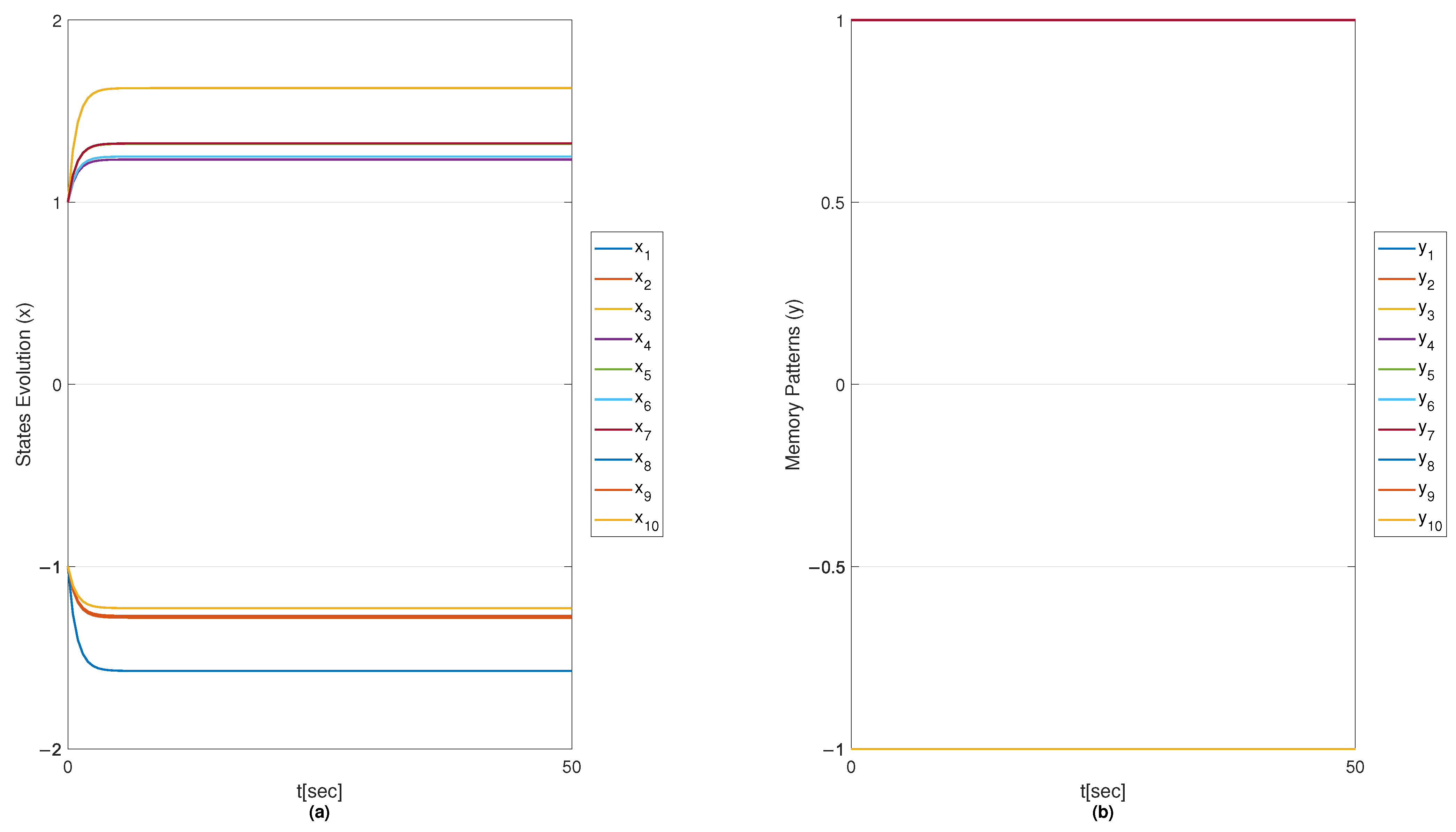
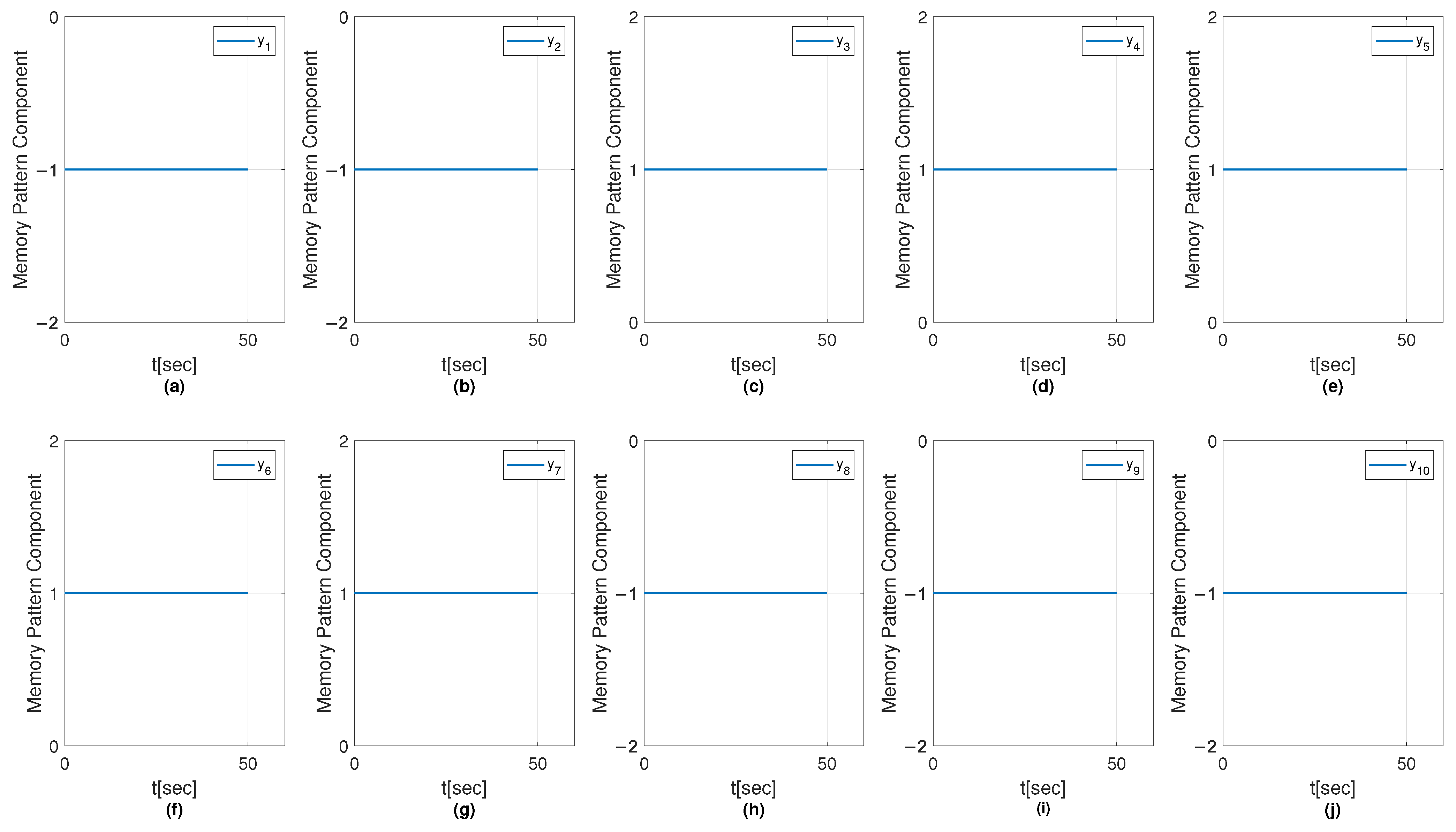
6.1.4. Results with MSMOH Training Algorithm
6.2. Convergence Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SVM | Support Vector Machine |
| OH | Optimal Hyperplane |
| SMOH | Soft Margin Optimal Hyperplane |
| MSMOH | Modified Soft Margin Optimal Hyperplane |
| NAM | Neural Associative Memory |
| RNN | Recurrent Neural Network |
| SVs | Support Vectors |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under Curve |
| QP | Quadratic Programmatic |
References
- Abe, S. Support Vector Machines for Pattern Classification; Springer: Berlin/Heidelberg, Germany, 2005; Volume 2. [Google Scholar]
- Chandra, M.A.; Bedi, S. Survey on SVM and their application in image classification. Int. J. Inf. Technol. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Lo, C.S.; Wang, C.M. Support vector machine for breast MR image classification. Comput. Math. Appl. 2012, 64, 1153–1162. [Google Scholar] [CrossRef]
- Homaeinezhad, M.; Tavakkoli, E.; Atyabi, S.; Ghaffari, A.; Ebrahimpour, R. Synthesis of multiple-type classification algorithms for robust heart rhythm type recognition: Neuro-svm-pnn learning machine with virtual QRS image-based geometrical features. Sci. Iran. 2011, 18, 423–431. [Google Scholar] [CrossRef][Green Version]
- Bansal, M.; Goyal, A.; Choudhary, A. A comparative analysis of K-nearest neighbor, genetic, support vector machine, decision tree, and long short term memory algorithms in machine learning. Decis. Anal. J. 2022, 3, 100071. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Y.; Yang, X.; Zhou, R. A firefly algorithm modified support vector machine for the credit risk assessment of supply chain finance. Res. Int. Bus. Financ. 2021, 58, 101482. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wang, H.; Leng, G.; Wang, L.; Liang, H. A hybrid VMD-SVM model for practical streamflow prediction using an innovative input selection framework. Water Resour. Manag. 2021, 35, 1321–1337. [Google Scholar] [CrossRef]
- Divya, P.; Devi, B.A. Hybrid metaheuristic algorithm enhanced support vector machine for epileptic seizure detection. Biomed. Signal Process. Control 2022, 78, 103841. [Google Scholar] [CrossRef]
- Laxmi, S.; Gupta, S.; Kumar, S. Intuitionistic fuzzy least square twin support vector machines for pattern classification. Ann. Oper. Res. 2024, 339, 1329–1378. [Google Scholar] [CrossRef]
- Wang, H. A novel feature selection method based on quantum support vector machine. Phys. Scr. 2024, 99, 056006. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Van Schrick, D. Remarks on terminology in the field of supervision, fault detection and diagnosis. IFAC Proc. Vol. 1997, 30, 959–964. [Google Scholar] [CrossRef]
- Çira, F.; Arkan, M.; Gümüş, B. A new approach to detect stator fault in permanent magnet synchronous motors. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 316–321. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Liu, W.; Chen, Z.; Li, Y.; Yang, J. A Fault Pattern and Convolutional Neural Network Based Single-phase Earth Fault Identification Method for Distribution Network. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 838–843. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; John Wiley and Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Ruz-Hernandez, J.A.; Suarez, D.A.; Garcia-Hernandez, R.; Sanchez, E.N.; Suarez-Duran, M.U. Optimal training algorithm application to design an associative memory for fault diagnosis at a fossil electric power plant. IFAC Proc. Vol. 2012, 45, 756–762. [Google Scholar] [CrossRef]
- Ruz-Hernandez, J.A.; Sanchez, E.N.; Suarez, D.A. Soft Margin Training for Associative Memories: Application to Fault Diagnosis in Fossil Electric Power Plants. In Soft Computing for Hybrid Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 205–230. [Google Scholar] [CrossRef]
- Liu, D.; Lu, Z. A new synthesis approach for feedback neural networks based on the perceptron training algorithm. IEEE Trans. Neural Netw. 1997, 8, 1468–1482. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, A.S.; Valle, M.E. Max-C and Min-D Projection Auto-Associative Fuzzy Morphological Memories: Theory and an Application for Face Recognition. Appl. Math. 2023, 3, 989–1018. [Google Scholar] [CrossRef]
- Janosi, A.; Steinbrunn, W.; Pfisterer, M.; Detrano, R. Heart Disease Data Set. 1989. Available online: https://archive.ics.uci.edu/ml/datasets/heart+Disease (accessed on 1 July 2025).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ruz-Hernandez, J.A.; Sanchez, E.N.; Suarez, D.A. Fault Detection and Diagnosis for Fossil Electric Power Plants via Recurrent Neural Networks. Dyn. Continous Discret. Impuls. Syst. Ser. B 2008, 15, 219. [Google Scholar]
- Aoki, M. Introduction to Optimization Techniques: Fundamentals and Applications of Nonlinear Programming; Macmillan: New York, NY, USA, 1971. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]

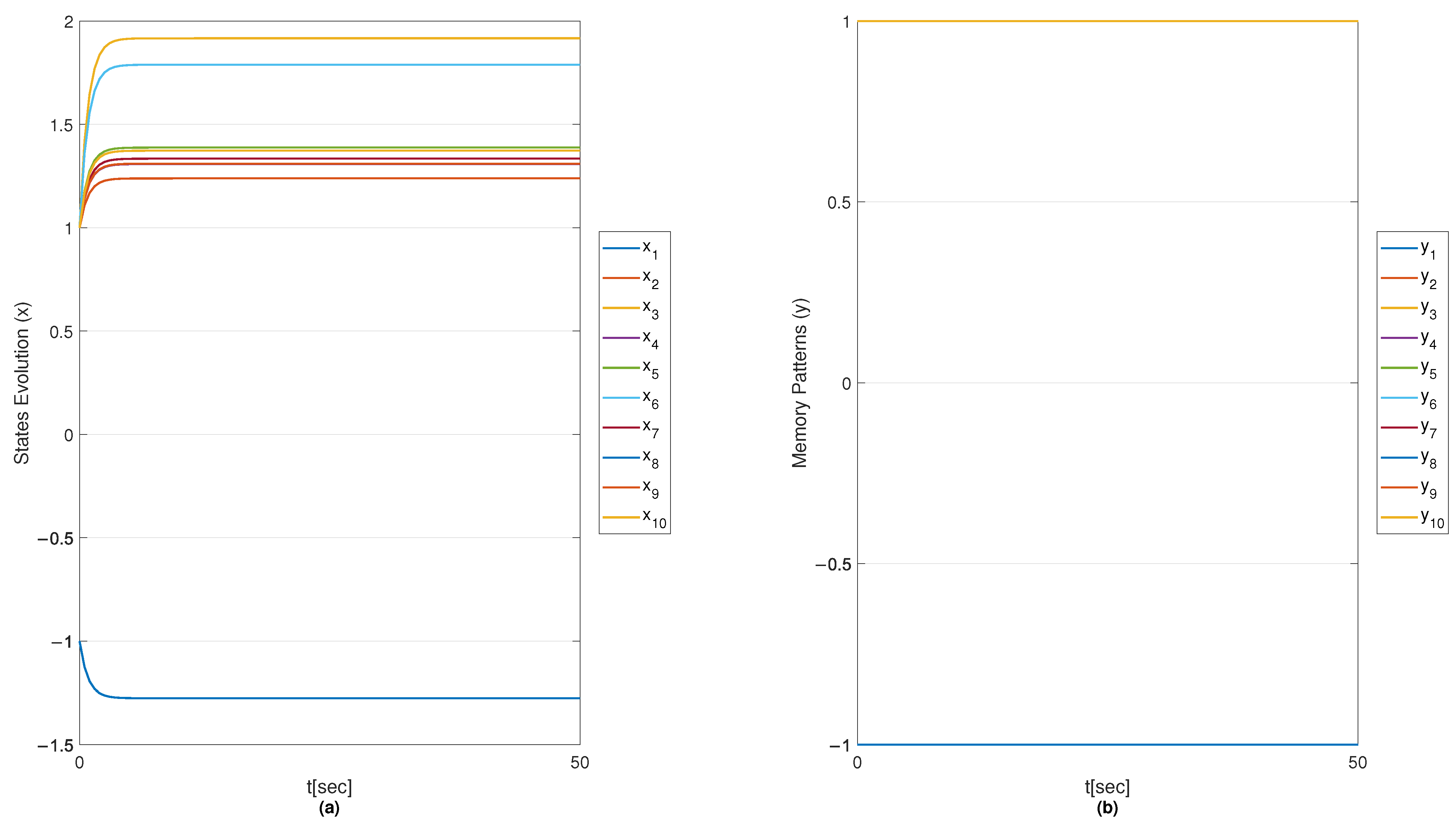
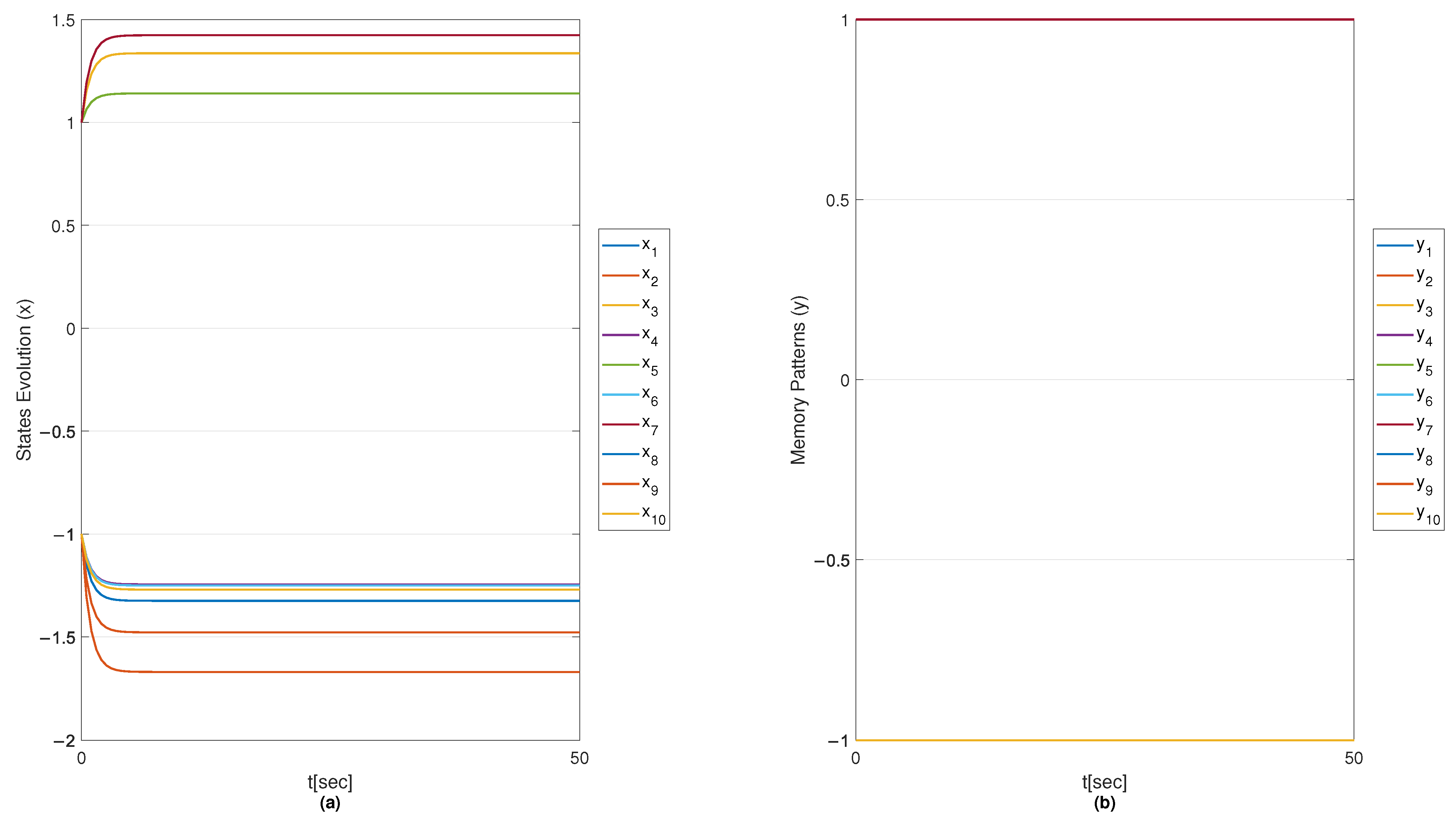



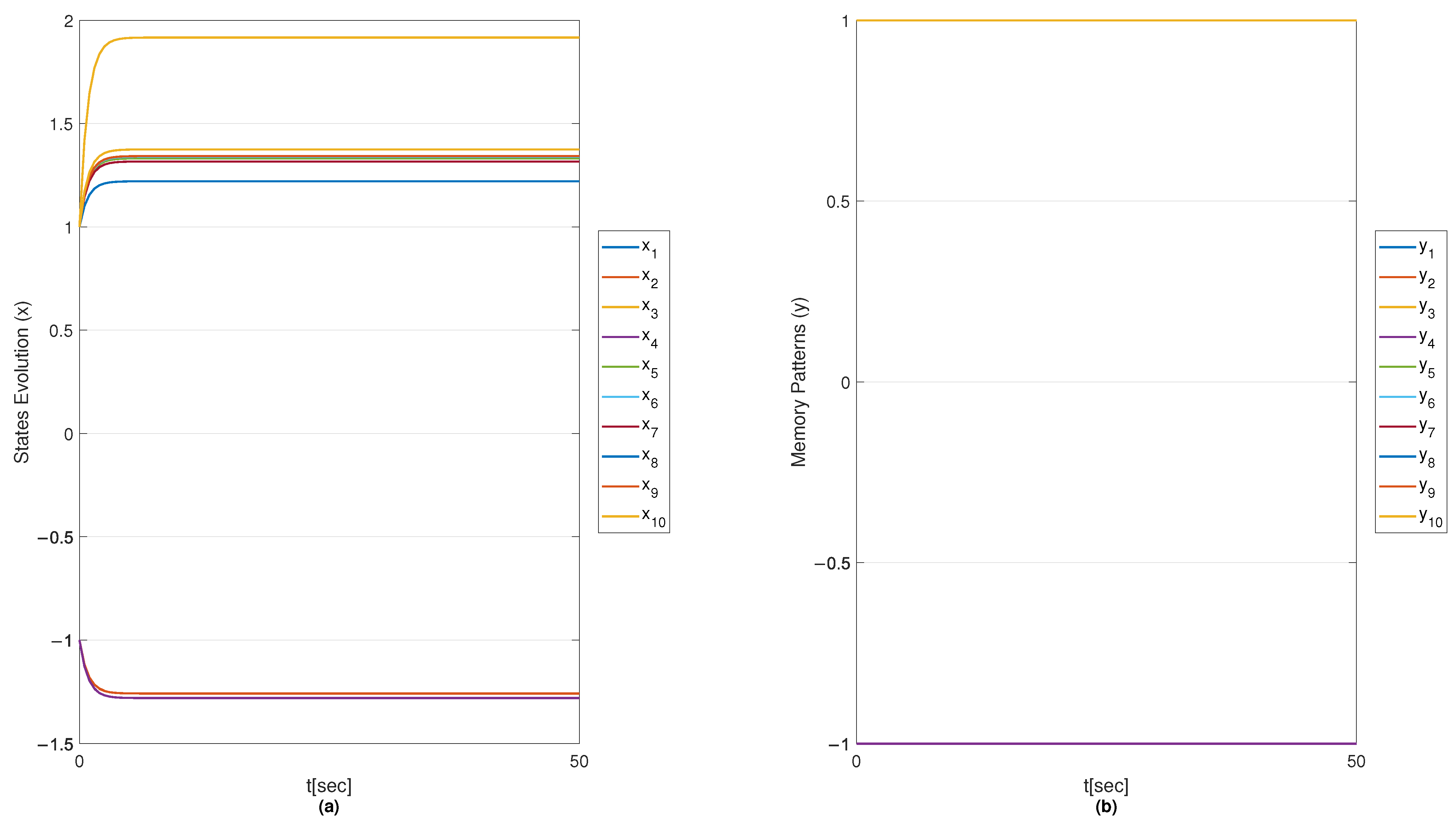
| Hyperparameter | Range | Grid Size | Scale Type |
|---|---|---|---|
| C | 700 | Logarithmic |
| Method | Accuracy | Sensitivity | Specificity | Precision | SVs |
|---|---|---|---|---|---|
| MSMOH | 14 | ||||
| SMOH | 171 |
| Method | 1 Time | 10 Times | 100 Times | 500 Times | 1000 Times |
|---|---|---|---|---|---|
| MSMOH | |||||
| SMOH |
| Attribute | Description | Non-Null Count 1 | Data Type 1 |
|---|---|---|---|
| ID | Unique for each patient | 920 non-null | int64 |
| Age | Age of patients in years | 920 non-null | int64 |
| Origin | Place of study | 920 non-null | object |
| Sex | Male/Female | 920 non-null | object |
| cp | Chest Pain Type | 920 non-null | object |
| trestbps | Resting Blood Pressure | 861 non-null | float64 |
| chol | Serum Cholesterol (in mg/dL) | 890 non-null | float4 |
| fbs | Indicates if Fasting blood sugar mg/dL | 830 non-null | object |
| restecg | resting electrocardiographic results (normal, Stt abnormality, lv hypertrophy) | 918 non-null | object |
| thalch | Maximum Heart rate achieved | 868 non-null | float64 |
| exang | Exercise-induced angina (True/False) | 865 non-null | object |
| oldpeak | ST depression induced by exercise relative to test | 858 non-null | float64 |
| slope | The slope of the peak exercise ST segment | 611 non-null | object |
| ca | Number of major vessels (0–3) colored by fluoroscopy | 309 non-null | float64 |
| thal | Thalassemia (normal; fixed defect; reversible defect) | 434 non-null | object |
| num | The predicted attribute (0 = heart disease; 1, 2, 3, 4 = Stages of heart disease) | 920 non-null | int64 |
| Sex | Dataset | cp | restecg | exang |
|---|---|---|---|---|
| Male | Cleveland | typical angina | lv hypertrophy | False |
| Male | Cleveland | asymptomatic | lv hypertrophy | True |
| Male | Cleveland | asymptomatic | lv hypertrophy | True |
| Male | Cleveland | non-anginal | normal | False |
| Female | Cleveland | atypical angina | lv hypertrophy | False |
| Sex | Dataset | cp | restecg | exang |
|---|---|---|---|---|
| 1 | 0 | 3 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 2 | 2 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| Attribute | Description | Non-Null Count 1 | Data Type 1 |
|---|---|---|---|
| ID | Unique for each patient | 920 non-null | int64 |
| Age | Age of patients in years | 920 non-null | int64 |
| Origin | Place of study (0–3) | 920 non-null | int64 |
| Sex | Male/Female | 920 non-null | int64 |
| cp | Chest Pain Type | 920 non-null | int64 |
| trestbps | Resting Blood Pressure | 920 non-null | float64 |
| chol | Serum Cholesterol (in mg/dL) | 920 non-null | float4 |
| fbs | Indicates if Fasting blood sugar mg/dL | 920 non-null | int64 |
| restecg | Resting electrocardiographic results (normal, Stt abnormality, lv hypertrophy) | 920 non-null | int64 |
| thalch | Maximum Heart rate achieved | 920 non-null | float64 |
| exang | Exercise-induced angina (True/False) | 920 non-null | int64 |
| oldpeak | ST depression induced by exercise relative to test | 920 non-null | float64 |
| slope | The slope of the peak exercise ST segment | 920 non-null | int64 |
| ca | Number of major vessels (0–3) colored by fluoroscopy | 920 non-null | float64 |
| thal | Thalassemia (normal; fixed defect; reversible defect) | 920 non-null | int64 |
| num2 | The predicted attribute (−1 = no heart disease; 1 = Heart disease) | 920 non-null | int64 |
| Method | Accuracy | Sensitivity | Specificity | Precision | F1-Score | Support Vectors | Margin |
|---|---|---|---|---|---|---|---|
| MSMOH | 327 | ||||||
| SMOH | 403 |
| Fold | Accuracy in Training | Sensitivity in Training | Specificity in Training | Precision in Training | F1-Score in Training | SVs | Margin |
|---|---|---|---|---|---|---|---|
| 1 | 261 | 3.7324 | |||||
| 2 | 270 | 3.9522 | |||||
| 3 | 281 | 3.9357 | |||||
| 4 | 265 | 3.7586 | |||||
| 5 | 251 | 3.8735 | |||||
| Mean | 81.9911% | 82.9949% | 80.7062% | 84.2516% | 0.8361 | 265.6 | 3.8504 |
| Standard Deviation | 0.4287% | 0.7404% | 1.4511% | 0.5790% | 0.0044 | 11.0815 | 0.1006 |
| Fold | Accuracy in Test | Sensitivity in Test | Specificity in Test | Precision in Test | F1-Score in Test |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| Mean | 81.6084% | 82.1042% | 80.8891% | 84.1666% | 0.8311 |
| Standard Deviation | 1.3889% | 1.4709% | 1.7274% | 2.3348% | 0.0170 |
| Fold | Accuracy in Training | Sensitivity in Training | Specificity in Training | Precision in Training | F1-Score in Training | SVs | Margin |
|---|---|---|---|---|---|---|---|
| 1 | 319 | 1.7052 | |||||
| 2 | 377 | 1.8417 | |||||
| 3 | 431 | 1.7455 | |||||
| 4 | 316 | 1.6508 | |||||
| 5 | 323 | 1.8170 | |||||
| Mean | 81.9639% | 84.8515% | 80.8471% | 84.3017% | 0.8356 | 353.2 | 1.7520 |
| Standard Deviation | 0.1637% | 0.7144% | 0.6117% | 0.5810% | 0.0049 | 50.2116 | 0.0787 |
| Fold | Accuracy in Test | Sensitivity in Test | Specificity in Test | Precision in Test | F1-Score in Test |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| Mean | 81.1736% | 82.2750% | 79.5017% | 83.4841% | 0.8283 |
| Standard Deviation | 1.4431% | 2.1445% | 5.2209% | 2.6256% | 0.0129 |
| Metric | Training (MSMOH) | Test (MSMOH) | Training (SMOH) | Test (SMOH) |
|---|---|---|---|---|
| Accuracy (%) | 81.9911 | 81.6084 | 81.9639 | 81.1736 |
| Sensitivity (%) | 82.9949 | 82.1042 | 84.8515 | 82.2750 |
| Specificity (%) | 80.7062 | 80.8891 | 80.8471 | 79.5017 |
| Precision (%) | 84.2516 | 84.1666 | 84.3017 | 83.4841 |
| F1-Score | 0.8361 | 0.8311 | 0.8356 | 0.8409 |
| MAGG | 0.3092 | 1.1070 | ||
| i | Variables | |
|---|---|---|
| 1 | MW | Load power |
| 2 | Pa | Boiler pressure |
| 3 | m | Drum level |
| 4 | Reheated steam temperature | |
| 5 | Superheated steam pressure | |
| 6 | ±20,000 Pa | Reheated steam pressure |
| 7 | ±42,000 Pa | Drum pressure |
| 8 | Differential pressure (spray steam-fossil oil flow) | |
| 9 | Fossil oil temperature to burners | |
| 10 | Feed-water Temperature |
| −1 | 1 | −1 | −1 | −1 | −1 | 1 |
| −1 | 1 | −1 | −1 | −1 | −1 | −1 |
| −1 | 1 | 1 | 1 | 1 | 1 | 1 |
| −1 | 1 | −1 | 1 | −1 | −1 | −1 |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 |
| −1 | 1 | −1 | 1 | −1 | 1 | 1 |
| −1 | 1 | 1 | 1 | 1 | −1 | 1 |
| −1 | −1 | −1 | −1 | −1 | −1 | 1 |
| −1 | 1 | −1 | −1 | −1 | 1 | 1 |
| −1 | 1 | −1 | −1 | −1 | −1 | 1 |
| Training Algorithm | Number of Convergent Elements | Number of Not Convergent Elements | Spurious Memories | C | A | |
|---|---|---|---|---|---|---|
| Perceptron | 991 | 33 | 22 | 7 | - | 1 |
| OH | 797 | 227 | 9 | 1.6486 | - | 1.22 |
| SMOH | 780 | 244 | 11 | 1.6486 | 0.6322 | 1.22 |
| MSMOH | 1019 | 5 | 2 | 1.6486 | 0.6322 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruz Canul, M.A.; Ruz-Hernandez, J.A.; Alanis, A.Y.; Gonzalez Gomez, J.C.; Gálvez, J. Modified Soft Margin Optimal Hyperplane Algorithm for Support Vector Machines Applied to Fault Patterns and Disease Diagnosis. Symmetry 2025, 17, 1749. https://doi.org/10.3390/sym17101749
Ruz Canul MA, Ruz-Hernandez JA, Alanis AY, Gonzalez Gomez JC, Gálvez J. Modified Soft Margin Optimal Hyperplane Algorithm for Support Vector Machines Applied to Fault Patterns and Disease Diagnosis. Symmetry. 2025; 17(10):1749. https://doi.org/10.3390/sym17101749
Chicago/Turabian StyleRuz Canul, Mario Antonio, Jose A. Ruz-Hernandez, Alma Y. Alanis, Juan Carlos Gonzalez Gomez, and Jorge Gálvez. 2025. "Modified Soft Margin Optimal Hyperplane Algorithm for Support Vector Machines Applied to Fault Patterns and Disease Diagnosis" Symmetry 17, no. 10: 1749. https://doi.org/10.3390/sym17101749
APA StyleRuz Canul, M. A., Ruz-Hernandez, J. A., Alanis, A. Y., Gonzalez Gomez, J. C., & Gálvez, J. (2025). Modified Soft Margin Optimal Hyperplane Algorithm for Support Vector Machines Applied to Fault Patterns and Disease Diagnosis. Symmetry, 17(10), 1749. https://doi.org/10.3390/sym17101749








