Quench Dynamics and Stability of Dark Solitons in Exciton–Polariton Condensates
Abstract
1. Introduction
2. The Theoretical Model
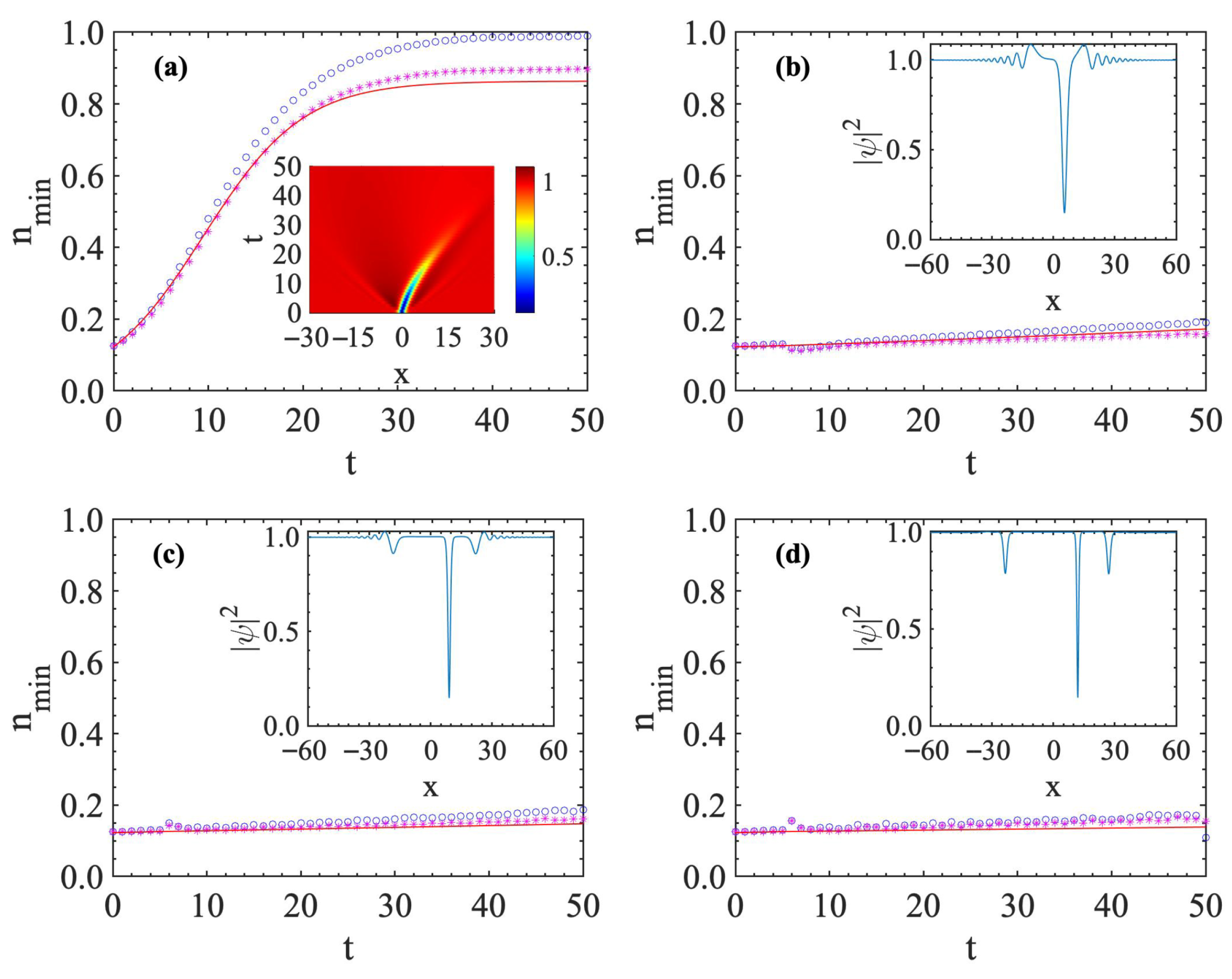
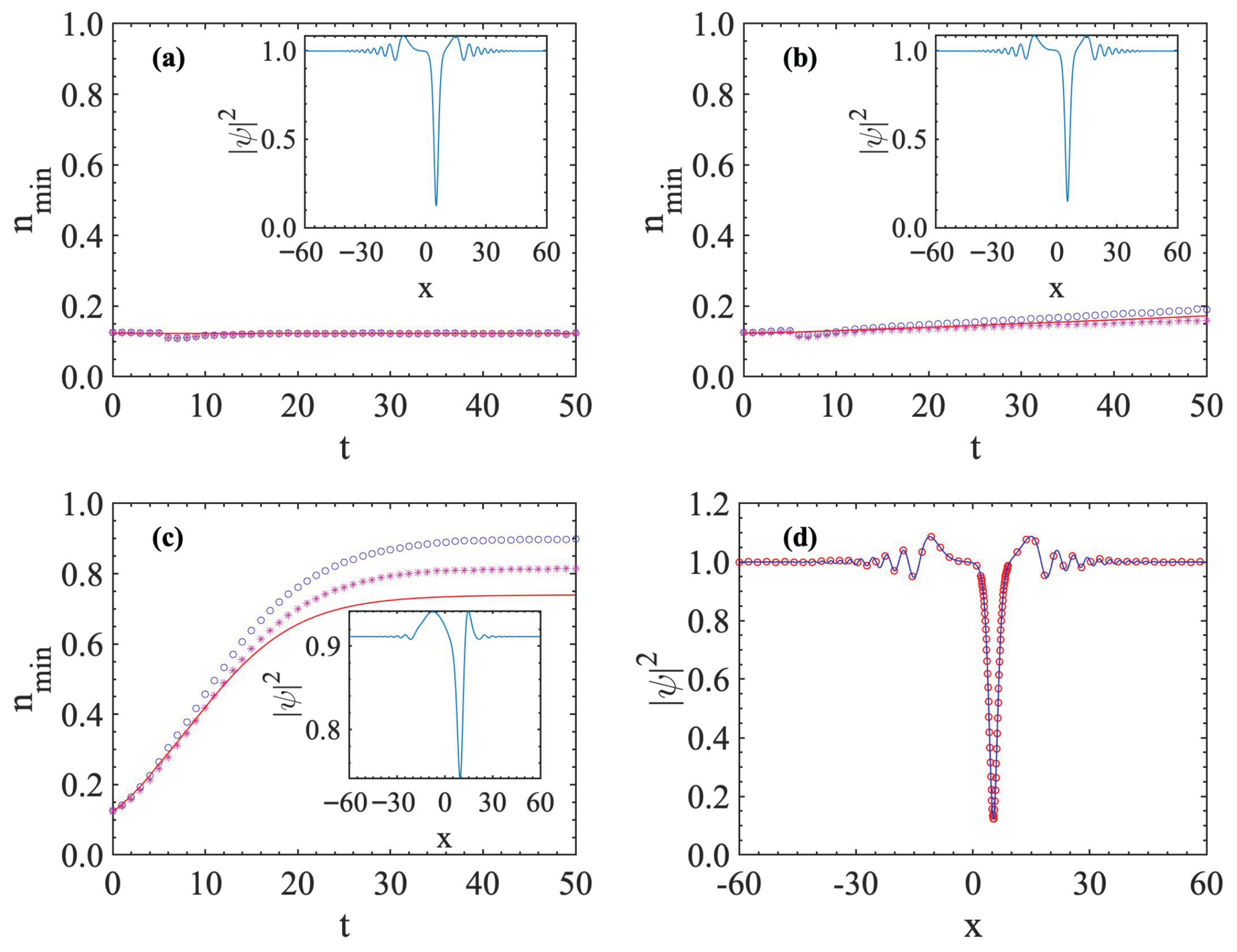
3. The Hamiltonian Approach and Dynamics of the Dark Soliton Induced by the Quenched Interaction
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baumberg, J.J.; Kavokin, A.V.; Christopoulos, S.; Grundy, A.J.D.; Butté, R.; Christmann, G.; Solnyshkov, D.D.; Malpuech, G.; Baldassarri Höger von Högersthal, G.; Feltin, E.; et al. Spontaneous Polarization Buildup in a Room-Temperature Polariton Laser. Phys. Rev. Lett. 2008, 101, 136409. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, C.; Liang, Z. Dynamics of Two Dark Solitons in a Polariton Condensate. Chin. Phys. Lett. 2022, 39, 020501. [Google Scholar] [CrossRef]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.J.; Marchetti, F.M.; Szymańska, M.H.; André, R.; Staehli, J.L.; et al. Bose–Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar] [CrossRef]
- Balili, R.; Hartwell, V.; Snoke, D.; Pfeiffer, L.; West, K. Bose-Einstein Condensation of Microcavity Polaritons in a Trap. Science 2007, 316, 1007–1010. [Google Scholar] [CrossRef]
- Deng, H.; Solomon, G.S.; Hey, R.; Ploog, K.H.; Yamamoto, Y. Spatial Coherence of a Polariton Condensate. Phys. Rev. Lett. 2007, 99, 126403. [Google Scholar] [CrossRef]
- Amo, A.; Sanvitto, D.; Laussy, F.P.; Ballarini, D.; Valle, E.d.; Martin, M.D.; Lemaître, A.; Bloch, J.; Krizhanovskii, D.N.; Skolnick, M.S.; et al. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 2009, 457, 291–295. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.; Rahimi-Iman, A.; Kim, N.Y.; Fischer, J.; Savenko, I.G.; Amthor, M.; Lermer, M.; Wolf, A.; Worschech, L.; Kulakovskii, V.D.; et al. An electrically pumped polariton laser. Nature 2013, 497, 348–352. [Google Scholar] [CrossRef] [PubMed]
- Christopoulos, S.; von Högersthal, G.B.H.; Grundy, A.J.D.; Lagoudakis, P.G.; Kavokin, A.V.; Baumberg, J.J.; Christmann, G.; Butté, R.; Feltin, E.; Carlin, J.F.; et al. Room-Temperature Polariton Lasing in Semiconductor Microcavities. Phys. Rev. Lett. 2007, 98, 126405. [Google Scholar] [CrossRef] [PubMed]
- Ruprecht, P.A.; Holland, M.J.; Burnett, K.; Edwards, M. Time-dependent solution of the nonlinear Schrödinger equation for Bose-condensed trapped neutral atoms. Phys. Rev. A 1995, 51, 4704–4711. [Google Scholar] [CrossRef]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose-Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Zhang, W.; Rao, Y. Coupled polariton solitons in semiconductor microcavities with a double-well potential. Chaos Solitons Fractals 2012, 45, 373–377. [Google Scholar] [CrossRef]
- Xue, Y.; Matuszewski, M. Creation and Abrupt Decay of a Quasistationary Dark Soliton in a Polariton Condensate. Phys. Rev. Lett. 2014, 112, 216401. [Google Scholar] [CrossRef]
- Sich, M.; Skryabin, D.V.; Krizhanovskii, D.N. Soliton physics with semiconductor exciton–polaritons in confined systems. Comptes Rendus Phys. 2016, 17, 908–919. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Skryabin, D.V. Two-dimensional lattice solitons in polariton condensates with spin-orbit coupling. Opt. Lett. 2016, 41, 5043–5046. [Google Scholar] [CrossRef] [PubMed]
- Walker, P.M.; Tinkler, L.; Royall, B.; Skryabin, D.V.; Farrer, I.; Ritchie, D.A.; Skolnick, M.S.; Krizhanovskii, D.N. Dark Solitons in High Velocity Waveguide Polariton Fluids. Phys. Rev. Lett. 2017, 119, 097403. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, L.; Zhang, Z.; Liang, Z. Dark–bright solitons in spinor polariton condensates under nonresonant pumping. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 025303. [Google Scholar] [CrossRef]
- Septembre, I.; Foudjo, I.; Develay, V.; Guillet, T.; Bouchoule, S.; Zúñiga Pérez, J.; Solnyshkov, D.D.; Malpuech, G. Soliton formation in an exciton-polariton condensate at a bound state in the continuum. Phys. Rev. B 2024, 109, 205302. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, K.; Idrees, M.; Li, H.J.; Lin, J.; Kavokin, A. Dark soliton cloning in exciton-polariton condensates. Phys. Rev. B 2024, 110, 155112. [Google Scholar] [CrossRef]
- Krizhanovskii, D.N.; Whittaker, D.M.; Bradley, R.A.; Guda, K.; Sarkar, D.; Sanvitto, D.; Vina, L.; Cerda, E.; Santos, P.; Biermann, K.; et al. Effect of Interactions on Vortices in a Nonequilibrium Polariton Condensate. Phys. Rev. Lett. 2010, 104, 126402. [Google Scholar] [CrossRef]
- Lagoudakis, K.G.; Wouters, M.; Richard, M.; Baas, A.; Carusotto, I.; André, R.; Dang, L.S.; Deveaud-Plédran, B. Quantized vortices in an exciton–polariton condensate. Nat. Phys. 2008, 4, 706–710. [Google Scholar] [CrossRef]
- Ma, X.; Egorov, O.A.; Schumacher, S. Creation and Manipulation of Stable Dark Solitons and Vortices in Microcavity Polariton Condensates. Phys. Rev. Lett. 2017, 118, 157401. [Google Scholar] [CrossRef]
- Rubo, Y.G. Half Vortices in Exciton Polariton Condensates. Phys. Rev. Lett. 2007, 99, 106401. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.; Rodrigues, A.S.; Carretero-González, R.; Kevrekidis, P.G.; Frantzeskakis, D.J. Nonlinear excitations, stability inversions, and dissipative dynamics in quasi-one-dimensional polariton condensates. Phys. Rev. B 2011, 83, 245140. [Google Scholar] [CrossRef]
- Pinsker, F. Approximate solutions for half-dark solitons in spinor non-equilibrium Polariton condensates. Ann. Phys. 2015, 362, 726–738. [Google Scholar] [CrossRef]
- Wang, S.J.; Jia, C.L.; Zhao, D.; Luo, H.G.; An, J.H. Dark and bright solitons in a quasi-one-dimensional Bose-Einstein condensate. Phys. Rev. A 2003, 68, 015601. [Google Scholar] [CrossRef]
- Timmermans, E. Feshbach resonances in atomic Bose–Einstein condensates. Phys. Rep. 1999, 315, 199–230. [Google Scholar] [CrossRef]
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose–Einstein condensate. Nature 1998, 392, 151–154. [Google Scholar] [CrossRef]
- Gamayun, O.; Bezvershenko, Y.V.; Cheianov, V. Fate of a gray soliton in a quenched Bose-Einstein condensate. Phys. Rev. A 2015, 91, 031605. [Google Scholar] [CrossRef]
- Chen, C.A.; Hung, C.L. Observation of Universal Quench Dynamics and Townes Soliton Formation from Modulational Instability in Two-Dimensional Bose Gases. Phys. Rev. Lett. 2020, 125, 250401. [Google Scholar] [CrossRef]
- Drescher, M.; Salmhofer, M.; Enss, T. Real-space dynamics of attractive and repulsive polarons in Bose-Einstein condensates. Phys. Rev. A 2019, 99, 023601. [Google Scholar] [CrossRef]
- Deng, T.S.; Zhang, W.; Yi, W. Tuning Feshbach resonances in cold atomic gases with interchannel coupling. Phys. Rev. A 2017, 96, 050701. [Google Scholar] [CrossRef]
- Hatami-Hanza, H.; Chu, P.; Malomed, B.A.; Peng, G. Soliton compression and splitting in double-core nonlinear optical fibers. Opt. Commun. 1997, 134, 59–65. [Google Scholar] [CrossRef]
- Porsezian, K.; Raja, R.V.J. Soliton fission and supercontinuum generation in photonic crystal fibre for optical coherence tomography application. Pramana 2015, 85, 993–1007. [Google Scholar] [CrossRef]
- Wales, O.J.; Rakonjac, A.; Billam, T.P.; Helm, J.L.; Gardiner, S.A.; Cornish, S.L. Splitting and recombination of bright-solitary-matter waves. Commun. Phys. 2020, 3, 51. [Google Scholar] [CrossRef]
- Li, X.; Gao, P.; Yang, Z.Y.; Yang, W.L. Merging and splitting dynamics between two bright solitons in dipolar Bose–Einstein condensates. Chin. Phys. B 2021, 30, 120501. [Google Scholar] [CrossRef]
- Simmons, S.A.; Bayocboc, F.A.; Pillay, J.C.; Colas, D.; McCulloch, I.P.; Kheruntsyan, K.V. What is a Quantum Shock Wave? Phys. Rev. Lett. 2020, 125, 180401. [Google Scholar] [CrossRef] [PubMed]
- Jia, R.Y.; Fang, P.P.; Gao, C.; Lin, J. Quenched solitons and shock waves in Bose-Einstein condensates. Acta Phys. Sin. 2021, 70, 180303. [Google Scholar] [CrossRef]
- Wang, J.L.; Zhang, K.; Lin, J.; Li, H.J. Generation and modulation of shock waves in two-dimensional polariton condensates. Acta Phys. Sin. 2024, 73, 119601. [Google Scholar] [CrossRef]
- Kulikov, I.; Zak, M. Shock waves in a Bose-Einstein condensate. Phys. Rev. A 2003, 67, 063605. [Google Scholar] [CrossRef][Green Version]
- Damski, B. Formation of shock waves in a Bose-Einstein condensate. Phys. Rev. A 2004, 69, 043610. [Google Scholar] [CrossRef][Green Version]
- Kamchatnov, A.M.; Gammal, A.; Kraenkel, R.A. Dissipationless shock waves in Bose-Einstein condensates with repulsive interaction between atoms. Phys. Rev. A 2004, 69, 063605. [Google Scholar] [CrossRef]
- Hoefer, M.A.; Ablowitz, M.J.; Coddington, I.; Cornell, E.A.; Engels, P.; Schweikhard, V. Dispersive and classical shock waves in Bose-Einstein condensates and gas dynamics. Phys. Rev. A 2006, 74, 023623. [Google Scholar] [CrossRef]
- Wan, W.; Jia, S.; Fleischer, J.W. Dispersive superfluid-like shock waves in nonlinear optics. Nat. Phys. 2007, 3, 46–51. [Google Scholar] [CrossRef]
- Ghofraniha, N.; Gentilini, S.; Folli, V.; DelRe, E.; Conti, C. Shock Waves in Disordered Media. Phys. Rev. Lett. 2012, 109, 243902. [Google Scholar] [CrossRef]
- Nuño, J.; Finot, C.; Xu, G.; Millot, G.; Erkintalo, M.; Fatome, J. Vectorial dispersive shock waves in optical fibers. Commun. Phys. 2019, 2, 138. [Google Scholar] [CrossRef]
- Jang, H.; Song, H.; Koh, H.S.; Yoon, T.; Kwon, Y.J. Shock wave generation in water by nanosecond pulse laser irradiation with 1064 and 2940 nm wavelengths. Opt. Laser Technol. 2023, 167, 109670. [Google Scholar] [CrossRef]
- Yin, C.; Yu, H.; Jin, Z.; Liu, J.; Huang, W.; Wu, S. Investigation of shock wave propagation and water cavitation in a water-filled double plate subjected to underwater blast. Int. J. Mech. Sci. 2023, 253, 108400. [Google Scholar] [CrossRef]
- Hang, C.; Bai, Z.; Li, W.; Kamchatnov, A.M.; Huang, G. Accessing and manipulating dispersive shock waves in a nonlinear and nonlocal Rydberg medium. Phys. Rev. A 2023, 107, 033503. [Google Scholar] [CrossRef]
- Qin, L.; Hang, C.; Huang, G.; Li, W. Shock-wave generation and propagation in dissipative and nonlocal nonlinear Rydberg media. Phys. Rev. A 2024, 110, 013703. [Google Scholar] [CrossRef]
- Wouters, M.; Carusotto, I. Excitations in a Nonequilibrium Bose-Einstein Condensate of Exciton Polaritons. Phys. Rev. Lett. 2007, 99, 140402. [Google Scholar] [CrossRef]
- Carretero-González, R.; Cuevas-Maraver, J.; Frantzeskakis, D.; Horikis, T.; Kevrekidis, P.; Rodrigues, A. A Korteweg–de Vries description of dark solitons in polariton superfluids. Phys. Lett. A 2017, 381, 3805–3811. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Wertz, E.; Ferrier, L.; Solnyshkov, D.D.; Johne, R.; Sanvitto, D.; Lemaître, A.; Sagnes, I.; Grousson, R.; Kavokin, A.V.; Senellart, P.; et al. Spontaneous formation and optical manipulation of extended polariton condensates. Nat. Phys. 2010, 6, 860–864. [Google Scholar] [CrossRef]
- Cao, X.; Jia, C.; Hu, Y.; Liang, Z. Nonlinear Thouless pumping of solitons across an impurity. Phys. Rev. A 2024, 110, 013305. [Google Scholar] [CrossRef]
- Cao, X.; Jia, C.; Lyu, H.; Hu, Y.; Liang, Z. Transport of vector solitons in spin-dependent nonlinear Thouless pumps. Phys. Rev. A 2025, 111, 023329. [Google Scholar] [CrossRef]
- Smirnov, L.A.; Smirnova, D.A.; Ostrovskaya, E.A.; Kivshar, Y.S. Dynamics and stability of dark solitons in exciton-polariton condensates. Phys. Rev. B 2014, 89, 235310. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Liang, Z. Quench Dynamics and Stability of Dark Solitons in Exciton–Polariton Condensates. Symmetry 2025, 17, 1482. https://doi.org/10.3390/sym17091482
Jia C, Liang Z. Quench Dynamics and Stability of Dark Solitons in Exciton–Polariton Condensates. Symmetry. 2025; 17(9):1482. https://doi.org/10.3390/sym17091482
Chicago/Turabian StyleJia, Chunyu, and Zhaoxin Liang. 2025. "Quench Dynamics and Stability of Dark Solitons in Exciton–Polariton Condensates" Symmetry 17, no. 9: 1482. https://doi.org/10.3390/sym17091482
APA StyleJia, C., & Liang, Z. (2025). Quench Dynamics and Stability of Dark Solitons in Exciton–Polariton Condensates. Symmetry, 17(9), 1482. https://doi.org/10.3390/sym17091482



