A Comprehensive Review on the Generalized Sylvester Equation AX − YB = C
Abstract
| Contents | ||
| 1. | Introduction................................................................................................................................................................................................. | 3 |
| 2. | Preliminaries............................................................................................................................................................................................... | 4 |
| 3. | Roth’s Equivalence Theorem...................................................................................................................................................................................................... | 6 |
| 4. | Different Methods on GSE............................................................................................................................................................................................................... | 7 |
| 4.1. Method by Linear Transformations and Subspace Dimensions................................................................................................ | 7 | |
| 4.2. Method by Generalized Inverses................................................................................................................................................... | 8 | |
| 4.3. Method by Singular Value Decompositions................................................................................................................................. | 10 | |
| 4.4. Method by Simultaneous Decompositions................................................................................................................................... | 12 | |
| 4.5. Method by Real (Complex) Representations................................................................................................................................ | 13 | |
| 4.6. Method by Determinable Representations................................................................................................................................... | 15 | |
| 4.7. Method by Semi-Tensor Products.................................................................................................................................................. | 20 | |
| 5. | Constrained Solutions of GSE.................................................................................................................................................................. | 24 |
| 5.1. Chebyshev Solutions and lp-Solutions.......................................................................................................................................... | 25 | |
| 5.2. ★-Congruent Solutions................................................................................................................................................................... | 26 | |
| 5.3. (Minimum-Norm Least-Squares) Symmetric Solutions............................................................................................................... | 27 | |
| 5.4. Self-Adjoint and Positive (Semi)Definite Solutions...................................................................................................................... | 28 | |
| 5.5. Per(Skew)Symmetric and Bi(Skew)Symmetric Solutions............................................................................................................. | 29 | |
| 5.6. Maximal and Minimal Ranks of the General Solution.................................................................................................................. | 31 | |
| 5.7. Re-(Non)negative and Re-(Non)positive Definite Solutions......................................................................................................... | 32 | |
| 5.8. η-Hermitian and η-Skew-Hermitian Solutions.............................................................................................................................. | 35 | |
| 5.9. ϕ-Hermitian Solutions...................................................................................................................................................................... | 37 | |
| 5.10. Equality-Constrained Solutions....................................................................................................................................................... | 38 | |
| 6. | Various Generalizations of GSE................................................................................................................................................................. | 40 |
| 6.1. Generalizing RET over Different Rings........................................................................................................................................... | 40 | |
| 6.1.1. Generalizing RET over Unit Regular Rings...................................................................................................................... | 40 | |
| 6.1.2. Generalizing RET over Principal Ideal Domains.............................................................................................................. | 41 | |
| 6.1.3. Generalizing RET over Division and Module-Finite Rings........................................................................................... | 42 | |
| 6.1.4. Generalizing RET over Commutative Rings................................................................................................................... | 43 | |
| 6.1.5. Generalizing RET over Artinian and Noncommutative Rings..................................................................................... | 44 | |
| 6.2. Generalizing RET to a Rank Minimization Problem.................................................................................................................... | 45 | |
| 6.3. GSE over Dual Numbers and Dual Quaternions.......................................................................................................................... | 46 | |
| 6.4. Linear Operator Equations on Hilbert Spaces............................................................................................................................... | 49 | |
| 6.5. Tensor Equations............................................................................................................................................................................... | 52 | |
| 6.6. Polynomial Matrix Equations.......................................................................................................................................................... | 56 | |
| 6.6.1. By the Divisibility of Polynomials..................................................................................................................................... | 56 | |
| 6.6.2. By Skew-Prime Polynomial Matrices................................................................................................................................ | 57 | |
| 6.6.3. By the Realization of Matrix Fraction Descriptions......................................................................................................... | 58 | |
| 6.6.4. By the Unilateral Polynomial Matrix Equation................................................................................................................ | 59 | |
| 6.6.5. By the Equivalence of Block Polynomial Matrices........................................................................................................... | 61 | |
| 6.6.6. By Jordan Systems of Polynomial Matrices...................................................................................................................... | 62 | |
| 6.6.7. By Linear Matrix Equations............................................................................................................................................... | 63 | |
| 6.6.8. By Root Functions of Polynomial Matrices...................................................................................................................... | 65 | |
| 6.7. Sylvester-Polynomial-Conjugate Matrix Equations....................................................................................................................... | 66 | |
| 6.8. Generalized Forms of GSE................................................................................................................................................................ | 70 | |
| 7. | Iterative Algorithms.................................................................................................................................................................................... | 75 |
| 8. | Applications to GSE.................................................................................................................................................................................... | 83 |
| 8.1. Theoretical Applications.................................................................................................................................................................. | 84 | |
| 8.1.1. Solvability of Matrix Equations......................................................................................................................................... | 84 | |
| 8.1.2. UTV Decomposition of Dual Matrices............................................................................................................................ | 85 | |
| 8.1.3. Microlocal Triangularization of Pseudo-Differential Systems...................................................................................... | 85 | |
| 8.2. Practical Applications......................................................................................................................................................................... | 86 | |
| 8.2.1. Calibration Problems........................................................................................................................................................... | 86 | |
| 8.2.2. Encryption and Decryption Schemes for Color Images................................................................................................... | 87 | |
| 9. | Conclusions........................................................................................................................................................................................................ | 89 |
| 10. | References.......................................................................................................................................................................................................... | 91 |
1. Introduction
2. Preliminaries
- (1)
- The selection of references follows the core principle of focusing on the theoretical research and practical applications of GSE, with specific criteria as follows:
- (i)
- Time frame: It covers 19th-century foundational studies to 2025’s latest achievements. It includes classic works like Hamilton’s quaternion research (1844) and Sylvester’s matrix equation study (1884), and emphasizes 2015–2025 recent studies (over 30% of total);
- (ii)
- Publication venues: Priority is given to peer-reviewed works, including top journals (e.g., SIAM J. Matrix Anal. Appl.), authoritative monographs (e.g., by Gohberg), and key conference papers (e.g., from IEEE ICMA);
- (iii)
- Content types: Original research is the main focus, with a small number of GSE-related review literature included. Only a few preprints/arXiv works are selected, due to their significance for subsequent research.
- (iv)
- Relevance scope: Though some research does not focus directly on GSE itself, its traces of relevance to GSE are easily detectable. Thus, we regard such content as an integral part of GSE-related research.
- (2)
- Results closely related to the theme are rigorously presented as theorems, while less relevant conclusions are briefly summarized narratively. Furthermore, the proofs of these theorems are omitted here.
- (3)
- The remarks in this paper include comments and suggestions on relevant results, encompassing both previous researchers’ views and our reflections, questions, and prospects.
3. Roth’s Equivalence Theorem
4. Different Methods on GSE
4.1. Method by Linear Transformations and Subspace Dimensions
- Step 1:
- Define by
- Step 2:
- Let
- Step 3:
- Since with , there also exists such in . Therefore, , i.e., (3) holds.
- (1)
- In [11], Flanders and Wimmer mentioned that, by making small modifications to the above proof, one can similarly obtain the proof of RET under the condition of rectangular matrices A, B, and C.
- (2)
4.2. Method by Generalized Inverses
4.3. Method by Singular Value Decompositions
4.4. Method by Simultaneous Decompositions
4.5. Method by Real (Complex) Representations
4.6. Method by Determinable Representations
- (1)
- For , the i-th row determinant of A is defined bywhere , and for and .
- (2)
- For , the j-th column determinant of A is defined bywhere and for and .
- (1)
- Equation (22) is solvable;
- (2)
- ;
- (3)
- ;
- (1)
- The restricted Equation (25) is solvable if and only ifin which case,whereand , , , , , and are arbitrary matrices over with appropriate dimensions.
- (2)
- Let , and be full column rank matrices such thatDenote and . If Equation (25) is solvable, thenwith is the j-th column ofand is the i-th row ofwhere , , , , and and are arbitrary matrices over with appropriate orders.
4.7. Method by Semi-Tensor Products
- (1)
- It is applied to any two matrices;
- (2)
- It has certain commutative properties;
- (3)
- It inherits all properties of the conventional matrix product;
- (4)
- It enables easy expression of multilinear functions (mappings);
- (1)
- Then, Equation (26) is consistent if and only if
- (2)
- LetThen,
- (3)
- If satisfiesthen
5. Constrained Solutions of GSE
5.1. Chebyshev Solutions and -Solutions
- (1)
- The matrices and are the -solution of Equation (5);
- (2)
- The following equalities hold:
- (3)
- The columns of are the -solutions of the linear systemsand the columns of are the -solutions of the linear systemswhere , , , , and are the appropriate columns of C, B, , and , respectively.
5.2. ★-Congruent Solutions
5.3. (Minimum-Norm Least-Squares) Symmetric Solutions
- (1)
- LetThen, if and only ifin which case
- (2)
- If satisfiesthen is unique and
- (3)
- LetThen,
- (4)
- If satisfiesthen is unique and
5.4. Self-Adjoint and Positive (Semi)Definite Solutions
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
5.5. Per(Skew)Symmetric and Bi(Skew)Symmetric Solutions
- (1)
- (2)
- (3)
- (4)
- (1)
- (2)
- (3)
- (4)
5.6. Maximal and Minimal Ranks of the General Solution
- (1)
- Then,
- (2)
- Let
- (3)
- Let
5.7. Re-(Non)negative and Re-(Non)positive Definite Solutions
- (1)
- X is re-positive definite if and only if
- (2)
- X is re-negative definite if and only if
- (3)
- X is re-nonnegative definite if and only if
- (4)
- X is re-nonpositive definite if and only if
- (5)
- Y is re-positive definite if and only if
- (6)
- Y is re-negative definite if and only if
- (7)
- Y is re-nonnegative definite if and only if
- (8)
- Y is re-nonpositive definite if and only if
5.8. -Hermitian and -Skew-Hermitian Solutions
- (1)
- Equation (46) has an η-Hermitian solution pair ;
- (2)
- and ;
- (3)
- and .
- (1)
- The statement (47) holds.
- (2)
- There exist the matrices and over such that
- (3)
- There exist the matrices and over such that
- (1)
- There exists a matrix pair such thatif and only if there exist the matrices , , and such that
- (2)
- (1)
- Equation (46) has an η-skew-Hermitian solution pair ;
- (2)
- and ;
- (3)
- and ;
5.9. -Hermitian Solutions
- (1)
- We call ϕ an anti-endomorphism if for any , ϕ satisfiesAn anti-endomorphism ϕ is called an involution if is the identity map.
- (2)
- Let ϕ be a nonzero involution. Then, ϕ can be represented as a matrix in with respect to the basis , i.e.,where either (in which case ϕ is called a standard involution), or is an orthogonal symmetric matrix with the eigenvalues (in which case ϕ is called a nonstandard involution).
- (3)
- Let ϕ be a nonstandard involution and . DefineIf with , then A is called a ϕ-Hermitian matrix.
- (1)
- The system (50) has a solution such that .
- (2)
- The following rank equalities hold:
- (3)
- The following equations hold:
- (1)
- When , Theorem 27 yields the result forwhich can be regarded as Equation (1) under the constrain that X is ϕ-Hermitian, i.e.,
- (2)
- (3)
- By the same method as in Remark 30, we can also discuss the following problem:
5.10. Equality-Constrained Solutions
- (1)
- (2)
- The following rank equations hold:
- (3)
- The following equations hold:
6. Various Generalizations of GSE
6.1. Generalizing RET over Different Rings
6.1.1. Generalizing RET over Unit Regular Rings
- (1)
- M has an inner inverse with the form of ;
- (2)
- has a solution pair ;
- (3)
- for all and ;
- (4)
- , where and ;
- (5)
- , where are invertible;
- (6)
- for all and ;
- (7)
- is a reflexive inverse of M.
- (5a)
- ;
- (5b)
- .
6.1.2. Generalizing RET over Principal Ideal Domains
- (1)
- Let , , and . Then, the matrix equationis consistent if and only ifare equivalent.
- (2)
- Let for . Then,are equivalent if and only if there exist such thatfor .
6.1.3. Generalizing RET over Division and Module-Finite Rings
6.1.4. Generalizing RET over Commutative Rings
- (i)
- , , and are unknown;
- (ii)
- For , the symbol denotes the matrix transpose and for the complex number field, also the matrix conjugate transpose ,
- (i)
- Of complex matrix equations, in which and is the complex conjugate of X;
- (ii)
- Of quaternion matrix equations, in which and is the quaternion conjugate transpose of X,
6.1.5. Generalizing RET over Artinian and Noncommutative Rings
- (1)
- A semisimple Artinian ring has the equivalence property.
- (2)
- An Artinian principal ideal ring has the equivalence property.
6.2. Generalizing RET to a Rank Minimization Problem
6.3. GSE over Dual Numbers and Dual Quaternions
- (1)
- Equation (1) has a solution pair and ;
- (2)
- and ;
- (3)
- The following rank equations hold:
6.4. Linear Operator Equations on Hilbert Spaces
- (1)
- If the spectra of A and B are contained in the open right half-plane and the open left half-plane, respectively, then the operator Equation (1) has the solution pair
- (2)
- Suppose that A and B are Hermitian operators such thatwhere α and β are eigenvalues of A and B, respectively. Assume that, for an absolutely integrable function f defined on , its Fourier transform satisfieswhere . Then, the operator Equation (1) has the solution pair
6.5. Tensor Equations
- (1)
- Theorem 49 is a direct corollary of Theorem 5.1 of [191], which establishes the solvability conditions and the general solution for the following quaternion tensor equation:where and are unknown and other tensors are given over .
- (2)
- Inspired by the transformation between tensors and matrices over (see (Definition 2.8, [194])), He et al. [191,195] defined an analogous transformation over , i.e., the transformation f is a map defined aswhere the components of A are given byLemma 2.2 of [191] shows that the transformation f is a bijection satisfyingfor and . The transformation f ingeniously bridges quaternion tensors under the Einstein product and quaternion matrices under the ordinary product. By virtue of its isomorphism property, f serves as a powerful tool for studying problems related to quaternion tensors under the Einstein product.
- (3)
- (1)
- Then,where is arbitrary with appropriate dimensions.
- (2)
- If satisfiesthen is unique and
6.6. Polynomial Matrix Equations
6.6.1. By the Divisibility of Polynomials
6.6.2. By Skew-Prime Polynomial Matrices
6.6.3. By the Realization of Matrix Fraction Descriptions
- (1)
- Under the hypotheses of Theorem 53, letIn terms of Lemma 2.2 of [218], Emre and Silverman have shown thatwhere . This implies that, to characterize , it is sufficient to characterize .
- (2)
- In Section 3, [218], Equation (70) is further generalized to the case where Q is a general polynomial matrix. In fact, for , there exist unimodular polynomial matrices and such thatwhere is the nonsingular polynomial matrix. LetThen,
6.6.4. By the Unilateral Polynomial Matrix Equation
- (1)
- and are relatively left prime;
- (2)
- is nonsingular and satisfies that is strictly proper;
- (3)
- is the right coprime factorization of , where is row reduced.
6.6.5. By the Equivalence of Block Polynomial Matrices
6.6.6. By Jordan Systems of Polynomial Matrices
- (1)
- Equation (79) is consistent;
- (2)
- There exists a pair of Jordan systems of with property for each ;
- (3)
- All pairs of Jordan systems of have property for each .
6.6.7. By Linear Matrix Equations
- (1)
- Let . If Equation (82) is solvable, then .
- (2)
- Let . There exists satisfying if and only ifwhere
- (3)
- Let . There exists satisfying if and only ifwhere , , and .
- (1)
- For , letand . Then,
- (2)
- The explicit solutions to Equations (84) and (85) have been studied in [229,230], which also serve as a starting point of Section 6.7 in this paper.
- (3)
- Moreover, Sheng and Tian [228] mentioned that Theorem 59 still holds when the field is extended to a commutative ring with identity.
6.6.8. By Root Functions of Polynomial Matrices
- (1)
- For each satisfying , if is a right root function of at of order s and is a left root function of at of order t, then has a zero at of order at least ;
- (2)
- If is a right root function of at zero of order and is a left root function of at zero of order , then has a zero of order at least .
6.7. Sylvester-Polynomial-Conjugate Matrix Equations
- (1)
- Theorem 9 in ref. [239] guarantees the existence of the polynomial matrix in Theorem 62.
- (2)
- TakingEquation (90) over reduces towhere , , and . Clearly, Theorem 62 is also a generalization of RET over .
- (3)
- In Theorem 1 of [241], Wu et al. characterized the homogeneous case of Equation (90) more specifically via a pair of right coprime polynomial matrices. Moreover, in Remark 4 of [241], they utilized the same method to discuss a more general form of Equation (90), i.e.,where are unknown and others are given.
- (4)
- It can be observed that Lemmas 11 and 12 of [241] are crucial for proving Theorem 62 and Theorem 1 of [239]. Meanwhile, it should be noted that Lemmas 11 and 12 of [241] provide only necessary conditions for left and right coprimeness, respectively. Thus, we contend that exploring the converse problems of these two lemmas is interesting.
- (5)
- (1)
- for , , and ;
- (2)
- for , , , and ;
- (3)
- for , , , and .
- (i)
- for any ;
- (ii)
- for any ,;
- (iii)
- for any .
6.8. Generalized Forms of GSE
7. Iterative Algorithms
| Algorithm 1 Algorithm [96] for the -solution of Equation (5) over |
|
| Algorithm 2 Algorithm T [95] for the Chebyshev Solution of Equation (5) over |
|
- (1)
- (2)
| Algorithm 3 Extended CGLSA [276] for the real symmetric solution of Equation (5) |
|
| Algorithm 4 ADM [279] for the nonnegative solution of Equation (5) over |
|
- (I)
- (II)
- The condition number is an important topic in numerical analysis, characterizing the worst-case sensitivity of problems to input data perturbations. A large condition number indicates an ill-posed problem. Consider the following matrix equation:where X and Y are unknown.
- (i)
- (ii)
- (iii)
- In 2013, Diao et al. [283] developed the small sample statistical condition estimation algorithm to evaluate the normwise, mixed, and componentwise condition numbers of Equation (109) over . In [283], they also investigated the effective condition number for Equation (109) and derived sharp perturbation bounds using this condition number.
- (III)
- (IV)
- In 2010, Dehghan and Hajarian [285] presented an iterative algorithm for solving the generalized bisymmetric solutions of the generalized coupled Sylvester matrix equation over :where X and Y are unknown generalized bisymmetric matrices.
- (V)
- (VI)
- In 2018, inspired by [288,289], Lv and Ma (Section 3, [290]) proposed a parametric iterative algorithm for Equation (109) over . Moreover, in (Section 4, [290]), they developed an accelerated iterative algorithm based on this parametric approach. Note that Ref. [289] is a monograph on iterative algorithms for the constrained solutions of matrix equations.
- (VII)
- Interestingly, in 2024, Ma et al. [291] proposed a Newton-type splitting iterative method for the coupled Sylvester-like absolute value equation :where X and Y are unknown. Here, means that each component of a matrix A is absolute-valued.
- (VIII)
- (A)
- In 2005–2006, using the hierarchical identification principle, Ding and Chen [293,294] presented a large family of iterative methods for the more general form of Equation (5) over , i.e.,where are unknown. These iterative methods subsume the well-known Jacobi and Gauss–Seidel iterations. Subsequent scholars have conducted more extensive research on numerical algorithms for Equation (111).
- (a)
- (b)
- (c)
- (d)
- (e)
- In 2017, based on the Hestenes–Stiefel version of the biconjugate residual (BCR) algorithm, Hajarian [300] solved the generalized Sylvester matrix equationover with the generalized reflexive solutions . In 2018, Lv and Ma [301] introduced another Hestenes–Stiefel version of BCR method for computing the centrosymmetric or anti-centrosymmetric solutions of Equation (111) over .
- (f)
- In 2018, inspired by [302], Sheng [292] proposed a relaxed gradient-based iterative (abbreviated as RGI) algorithm to solve Equation (109), and further generalized this algorithm to Equation (111). Moreover, numerical examples in [292] demonstrate that the RGI algorithm outperforms the iterative algorithm in [294] in terms of speed, elapsed time, and iterative steps.
- (g))
- In 2018, Hajarian [303] extended the Lanczos version of BCR algorithm to find the symmetric solutions of the matrix equation over :
- (B)
- In 2009, from an optimization perspective, Zhou et al. [305] developed a novel iterative method for solving Equation (111) over and its more general form, i.e.,with unknown , which contains iterative methods in [293,294] as special cases. In 2015, by extending the generalized product biconjugate gradient algorithms, Hajarian gave [306] four effective matrix algorithms for the coupled matrix equation over :where are unknown.
- (C)
- In 2011, Wu et al. [307] constructed an iterative algorithm to solve the coupled Sylvester-conjugate matrix equation over :where are unknown. In 2021, inspired by [307], Yan and Ma [308] proposed an iterative algorithm for the generalized Hamiltonian solutions of the generalized coupled Sylvester-conjugate matrix equations over :where , and and () are unknown generalized Hamiltonian matrices.
- (D)
- In 2015, inspired by [309,310], Hajarian [311] obtained an iterative method for the coupled Sylvester-transpose matrix equations over :with unknown X and Y, by developing the biconjugate A-orthogonal residual and the conjugate A-orthogonal residual squared methods. Based on this developed method, Hajarian [311] also considered the coupled periodic Sylvester matrix equations over :where and are unknown periodic matrices with a period.
- (E)
- Discrete-time periodic matrix equations are an important tool for analyzing and designing periodic systems [312]. More related studies are as follows:
- (a)
- In 2017, Hajarian [313] introduced a generalized conjugate direction method for solving the general coupled Sylvester discrete-time periodic matrix equations over :where and are unknown periodic matrices with a period.
- (b)
- In 2022, Ma and Yan [314] proposed a modified conjugate gradient algorithm for solving the general discrete-time periodic Sylvester matrix equations over :where and are unknown periodic matrices of period T.
- (F)
- Interestingly, in 2014, Dehghani-Madiseh and Dehghan [315] presented the generalized interval Gauss–Seidel iteration method for the outer estimation of the AE-solution set of the interval generalized Sylvester matrix equation over :where () and () are unknown interval matrices.
- (G)
- In 2018, Hajarian [316] established the biconjugate residual algorithm for solving the matrix equation over :where X and Y are the unknown generalized reflexive and anti-reflexive matrices, respectively.
- (H)
8. Applications to GSE
8.1. Theoretical Applications
8.1.1. Solvability of Matrix Equations
8.1.2. UTV Decomposition of Dual Matrices
8.1.3. Microlocal Triangularization of Pseudo-Differential Systems
- (1)
- In Sections 3.3 and 3.4 of [321], Kiran showed that the triangularization scheme in Theorem 75 can also be applied to symbolic hierarchies.
- (2)
- Lemma 2.5 of [321] shows that Equation (1) over has a unique solution X if and only if A or B is nonsingular. However, there is a simple counterexample to its sufficiency. Indeed, if both A and B are identity matrices (and thus nonsingular), the solution X of Equation (1) is obviously not unique for a given C. For instance, take and , or and . This minor error, however, does not affect the existence of solutions to Equation (1).
8.2. Practical Applications
8.2.1. Calibration Problems
- (i)
- is the known homogeneous transformation from end effector pose measurements,
- (ii)
- is derived from the calibrated manipulator internal-link forward kinematics;
- (iii)
- is the unknown transformation from the tool frame to the flange frame;
- (iv)
- is the unknown transformation from the world frame to the base frame.
8.2.2. Encryption and Decryption Schemes for Color Images
| Algorithm 5 Color image encryption scheme |
|
| Algorithm 6 Color image decryption scheme |
|
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sylvester, J.J. Sur l’équation en matrices px = xq. C. R. Acad. Sci. Paris 1884, 99, 67–71, 115–116. (In French) [Google Scholar]
- Bhatia, R.; Rosenthal, P. How and why to solve the operator equation AX − XB = Y. Bull. Lond. Math. Soc. 1997, 29, 1–21. [Google Scholar]
- Wang, Q.W.; Xie, L.M.; Gao, Z.H. A survey on solving the matrix equation AXB=C with applications. Mathematics 2025, 13, 450. [Google Scholar] [CrossRef]
- Wang, Q.W.; Gao, Z.H.; Gao, J. A comprehensive review on solving the system of equations AX = C and XB = D. Symmetry 2025, 17, 625. [Google Scholar]
- Wang, Q.W.; Gao, Z.H.; Li, Y.F. An overview of methods for solving the system of matrix equations A1XB1=C1 and A2XB2=C2. Symmetry 2025, 17, 1307. [Google Scholar] [CrossRef]
- Roth, W.E. The equations AX − YB = C and AX − XB = C in matrices. Proc. Am. Math. Soc. 1952, 3, 392–396. [Google Scholar]
- Rodman, L. Topics in Quaternion Linear Algebra; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Horn, R.A.; Zhang, F. A generalization of the complex Autonne-Takagi factorization to quaternion matrices. Linear Multilinear Algebra 2012, 60, 1239–1244. [Google Scholar] [CrossRef]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N.E. Generalized Inverses: Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Flanders, H.; Wimmer, H.K. On the matrix equations AX − XB = C and AX − YB = C. SIAM J. Appl. Math. 1977, 32, 707–710. [Google Scholar]
- Dmytryshyn, A.; Kågström, B. Coupled Sylvester-type matrix equations and block diagonalization. SIAM J. Matrix Anal. Appl. 2015, 36, 580–593. [Google Scholar] [CrossRef]
- Dmytryshyn, A.; Futorny, V.; Klymchuk, T.; Sergeichuk, V.V. Generalization of Roth’s solvability criteria to systems of matrix equations. Linear Algebra Appl. 2017, 527, 294–302. [Google Scholar] [CrossRef]
- Rao, C.R.; Mitra, S.K. Generalized Inverse of Matrices and Its Applications; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Wang, G.; Wei, Y.; Qiao, S. Generalized Inverses: Theory and Computations; Springer: Singapore, 2018. [Google Scholar]
- Cvetković-Ilixcx, D.S.; Wei, Y. Algebraic Properties of Generalized Inverses; Springer: Singapore, 2017. [Google Scholar]
- Zhang, D.; Zhao, Y.; Mosić, D. The generalized Drazin inverse of the sum of two elements in a Banach algebra. J. Comput. Appl. Math. 2025, 470, 116701. [Google Scholar] [CrossRef]
- Gao, Z.H.; Wang, Q.W.; Xie, L.M. A novel Moore–Penrose inverse to dual quaternion matrices with applications. Appl. Math. Lett. 2026, 172, 109727. [Google Scholar] [CrossRef]
- Baksalary, J.K.; Kala, R. The matrix equation AX − YB = C. Linear Algebra Appl. 1979, 25, 41–43. [Google Scholar] [CrossRef]
- Marsaglia, G.; Styan, G.P.H. Equalities and inequalities for ranks of matrices. Linear Multilinear Algebra 1974, 2, 269–292. [Google Scholar] [CrossRef]
- van der Woude, J.W. Almost non-interacting control by measurement feedback. Syst. Control Lett. 1987, 9, 7–16. [Google Scholar] [CrossRef]
- Olshevsky, V. Similarity of block diagonal and block triangular matrices. Integral Equ. Oper. Theory 1992, 15, 853–863. [Google Scholar] [CrossRef]
- Meyer, C.D., Jr. Generalized inverses of block triangular matrices. SIAM J. Appl. Math. 1970, 19, 741–750. [Google Scholar] [CrossRef]
- Golub, G.H.; Loan, C.F.V. Matrix Computations; The Johns Hopkins University Press: Baltimore, MD, USA, 1983. [Google Scholar]
- Chu, K.E. Singular value and generalized singular value decompositions and the solution of linear matrix equations. Linear Algebra Appl. 1987, 88–89, 83–98. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. Towards a generalized singular value decomposition. SIAM J. Numer. Anal. 1981, 18, 398–405. [Google Scholar] [CrossRef]
- Xu, G.; Wei, M.; Zheng, D. On solutions of matrix equation AXB + CYD = F. Linear Algebra Appl. 1998, 279, 93–109. [Google Scholar] [CrossRef]
- Golub, G.H.; Zha, H. Perturbation analysis of the canonical correlations of matrix pairs. Linear Algebra Appl. 1994, 210, 3–28. [Google Scholar] [CrossRef]
- Wang, Q.W.; van Woude, J.W.; Yu, S.W. An equivalence canonical form of a matrix triplet over an arbitrary division ring with applications. Sci. China-Math. 2011, 54, 907–924. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W.; Zhang, Y. A simultaneous decomposition for seven matrices with applications. J. Comput. Appl. Math. 2019, 349, 93–113. [Google Scholar] [CrossRef]
- He, Z.H.; Agudelo, O.M.; Wang, Q.W.; Moor, B.D. Two-sided coupled generalized Sylvester matrix equations solving using a simultaneous decomposition for fifteen matrices. Linear Algebra Appl. 2016, 496, 549–593. [Google Scholar] [CrossRef]
- Gustafson, W.H. Quivers and matrix equations. Linear Algebra Appl. 1995, 231, 159–174. [Google Scholar] [CrossRef]
- Gabriel, P. Unzerlegbare Darstellungen I. Manuscripta Math. 1972, 6, 71–103. [Google Scholar] [CrossRef]
- He, Z.H.; Dmytryshyn, A.; Wang, Q.W. A new system of Sylvester-like matrix equations with arbitrary number of equations and unknowns over the quaternion algebra. Linear Multilinear Algebra 2025, 73, 1269–1309. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhang, X.; Woude, J.W.v. A new simultaneous decomposition of a matrix quaternity over an arbitrary division ring with applications. Commun. Algebra 2012, 40, 2309–2342. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W.; Zhang, Y. The complete equivalence canonical form of four matrices over an arbitrary division ring. Linear Multilinear Algebra 2018, 66, 74–95. [Google Scholar] [CrossRef]
- He, Z.H.; Xu, Y.Z.; Wang, Q.W.; Zhang, C.Q. The equivalence canonical forms of two sets of five quaternion matrices with applications. Math. Meth. Appl. Sci. 2025, 48, 5483–5505. [Google Scholar]
- Huo, J.W.; Xu, Y.Z.; He, Z.H. A simultaneous decomposition for a quaternion tensor quaternity with applications. Mathematics 2025, 13, 1679. [Google Scholar] [CrossRef]
- Flaut, C.; Shpakivskyi, V. Real matrix representations for the complex quaternions. Adv. Appl. Clifford Algebras 2013, 23, 657–671. [Google Scholar] [CrossRef]
- Liu, Y.H. Ranks of solutions of the linear matrix equation AX + YB = C. Comput. Math. Appl. 2006, 52, 861–872. [Google Scholar] [CrossRef]
- Zhang, F.; Mu, W.; Li, Y.; Zhao, J. Special least squares solutions of the quaternion matrix equation AXB + CXD = E. Comput. Math. Appl. 2016, 72, 1426–1435. [Google Scholar] [CrossRef]
- Yuan, S. Least squares pure imaginary solution and real solution of the quaternion matrix equation AXB + CXD = E with the least norm. J. Appl. Math. 2014, 2014, 857081. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y. Matrices over quaternion algebras. In Matrix and Operator Equations and Applications; Moslehian, M.S., Ed.; Springer: Cham, Switzerland, 2023; pp. 139–183. [Google Scholar]
- Wang, G.; Guo, Z.; Zhang, D.; Jiang, T. Algebraic techniques for least-squares problem over generalized quaternion algebras: A unified approach in quaternionic and split quaternionic theory. Math. Meth. Appl. Sci. 2020, 43, 1124–1137. [Google Scholar] [CrossRef]
- Yu, C.; Liu, X.; Zhang, Y. The generalized quaternion matrix equation AXB + CX★D = E. Math. Meth. Appl. Sci. 2020, 43, 8506–8517. [Google Scholar] [CrossRef]
- Ren, B.Y.; Wang, Q.W.; Chen, X.Y. The η-anti-Hermitian solution to a constrained matrix equation over the generalized segre quaternion algebra. Symmetry 2023, 15, 592. [Google Scholar] [CrossRef]
- Wei, M.S.; Li, Y.; Zhang, F.; Zhao, J. Quaternion Matrix Computations; Nova Science Publishers: New York, NY, USA, 2018. [Google Scholar]
- Stanimirovic, P.S. General determinantal representation of pseudoinverses of matrices. Mat. Vesn. 1996, 48, 1–9. [Google Scholar]
- Kyrchei, I.I. Analogs of the adjoint matrix for generalized inverses and corresponding Cramer rules. Linear Multilinear Algebra 2008, 56, 453–469. [Google Scholar] [CrossRef]
- Drazin, M.P. Pseudo-inverses in associative rings and semigroups. Am. Math. Mon. 1958, 65, 506–514. [Google Scholar] [CrossRef]
- Aslaksen, H. Quaternionic determinants. Math. Intell. 1996, 18, 57–65. [Google Scholar] [CrossRef]
- Cohen, N.; Leo, S.D. The quaternionic determinant. Electron. J. Linear Algebra 2000, 7, 100–111. [Google Scholar] [CrossRef]
- Kyrchei, I.I. Cramer’s rule for quaternionic systems of linear equations. J. Math. Sci. 2008, 155, 839–858. [Google Scholar] [CrossRef]
- Kyrchei, I.I. The theory of the column and row determinants in a quaternion linear algebra. In Advances in Mathematics Research; Baswell, A.R., Ed.; Nova Science Publisher: New York, NY, USA, 2012; Volume 15, pp. 301–358. [Google Scholar]
- Kyrchei, I.I. Cramer’s rule for some quaternion matrix equations. Appl. Math. Comput. 2010, 217, 2024–2030. [Google Scholar] [CrossRef]
- Song, G.J.; Wang, Q.W.; Yu, S.W. Cramer’s rule for a system of quaternion matrix equations with applications. Appl. Math. Comput. 2018, 336, 490–499. [Google Scholar] [CrossRef]
- Kyrchei, I.I. Determinantal representations of the Moore-Penrose inverse matrix over the quaternion skew field. J. Math. Sci. 2012, 180, 23–33. [Google Scholar] [CrossRef]
- Kyrchei, I. Cramer’s rules for Sylvester quaternion matrix equation and its special cases. Adv. Appl. Clifford Algebr. 2018, 28, 90. [Google Scholar] [CrossRef]
- Kyrchei, I. Explicit representation formulas for the minimum norm least squares solutions of some quaternion matrix equations. Linear Algebra Appl. 2013, 438, 136–152. [Google Scholar] [CrossRef]
- Kyrchei, I.I. Explicit determinantal representation formulas for the solution of the two-sided restricted quaternionic matrix equation. J. Appl. Math. Comput. 2018, 58, 335–365. [Google Scholar] [CrossRef]
- Kyrchei, I. Determinantal representations of solutions to systems of quaternion matrix equations. Adv. Appl. Clifford Algebr. 2018, 28, 23. [Google Scholar] [CrossRef]
- Song, G.J.; Dong, C.Z. New results on condensed Cramer’s rule for the general solution to some restricted quaternion matrix equations. J. Appl. Math. Comput. 2017, 53, 321–341. [Google Scholar] [CrossRef]
- Song, G.J.; Wang, Q.W. Condensed Cramer rule for some restricted quaternion linear equations. Appl. Math. Comput. 2011, 218, 3110–3121. [Google Scholar] [CrossRef]
- Song, G.J.; Wang, Q.W.; Chang, H.X. Cramer rule for the unique solution of restricted matrix equations over the quaternion skew field. Comput. Math. Appl. 2011, 61, 1576–1589. [Google Scholar] [CrossRef]
- Song, G.J. Determinantal expression of the general solution to a restricted system of quaternion matrix equations with applications. Bull. Korean Math. Soc. 2018, 55, 1285–1301. [Google Scholar]
- Cheng, D. Semi-tensor product of matrices and its application to Morgan’s problem. Sci. China 2001, 44, 195–212. [Google Scholar]
- Cheng, D. From Dimension-Free Matrix Theory to Cross-Dimensional Dynamic Systems; Elsevier: London, UK, 2019. [Google Scholar]
- Cheng, D. Matrix and Polynomial Approach to Dynamic Control Systems; Science Press: Beijing, China, 2002. [Google Scholar]
- Cheng, D.; Qi, H.; Xue, A. A survey on semi-tensor product of matrices. J. Syst. Sci. Complex. 2007, 20, 304–322. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H. Semi-Tensor Product of Matrices—Theory and Applications, 2nd ed.; Science Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Cheng, D.; Qi, H.; Li, Z. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach; Springer: London, UK, 2011. [Google Scholar]
- Yao, J.; Feng, J.; Meng, M. On solutions of the matrix equation AX = B with respect to semi-tensor product. J. Franklin Inst. 2016, 353, 1109–1131. [Google Scholar] [CrossRef]
- Wang, J. Least squares solutions of matrix equation AXB = C under semi-tensor product. Electron. Res. Arch. 2024, 32, 2976–2993. [Google Scholar] [CrossRef]
- Jaiprasert, J.; Chansangiam, P. Solving the Sylvester-transpose matrix equation under the semi-tensor product. Symmetry 2022, 14, 1094. [Google Scholar] [CrossRef]
- Wang, N. Solvability of the Sylvester equation AX − XB = C under left semi-tensor product. Math. Model. Control 2022, 2, 81–89. [Google Scholar] [CrossRef]
- Ji, Z.; Li, J.; Zhou, X.; Duan, F.; Li, T. On solutions of matrix equation AXB = C under semi-tensor product. Linear Multilinear Algebra 2021, 69, 1935–1963. [Google Scholar] [CrossRef]
- Li, J.; Tao, L.; Li, W.; Chen, Y.; Huang, R. Solvability of matrix equations AX = B, XC = D under semi-tensor product. Linear Multilinear Algebra 2017, 65, 1705–1733. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.; Huang, H. Solvability of the matrix equation AX2 = B with semi-tensor product. Electron. Res. Arch. 2020, 29, 2249–2267. [Google Scholar] [CrossRef]
- Cheng, D.; Liu, Z. A new semi-tensor product of matrices. Control Theory Technol. 2019, 17, 4–12. [Google Scholar] [CrossRef]
- Cheng, D.; Xu, Z.; Shen, T. Equivalence-based model of dimension-varying linear systems. IEEE Trans. Autom. Control 2020, 65, 5444–5449. [Google Scholar] [CrossRef]
- Wang, J. On solutions of the matrix equation A∘l X = B with respect to MM-2 semitensor product. J. Math. 2021, 2021, 6651434. [Google Scholar]
- Ding, W.; Li, Y.; Wang, D.; Wei, A. Constrained least squares solution of Sylvester equation. Math. Model. Control 2021, 1, 112–120. [Google Scholar] [CrossRef]
- Ding, W.; Li, Y.; Wang, D. A real method for solving quaternion matrix equation based on semi-tensor product of matrices. Adv. Appl. Clifford Algebr. 2021, 31, 78. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Ding, W.X. Several kinds of special least squares solutions to quaternion matrix equation AXB = C. J. Appl. Math. Comput. 2022, 68, 1881–1899. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Ding, W.; Tao, R. A real method for solving octonion matrix equation AXB = C based on semi-tensor product of matrices. Adv. Appl. Clifford Algebr. 2024, 34, 12. [Google Scholar] [CrossRef]
- Chen, W.; Song, C. STP method for solving the least squares special solutions of quaternion matrix equations. Adv. Appl. Clifford Algebr. 2025, 35, 6. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.W.; Zhang, Y. Consistency of quaternion matrix equations AX★ − XB = C and X − AX★B = C★. Electron. J. Linear Algebra 2019, 35, 394–407. [Google Scholar] [CrossRef]
- Fan, X.; Li, Y.; Liu, Z.; Zhao, J. Solving quaternion linear system based on semi-tensor product of quaternion matrices. Symmetry 2022, 14, 1359. [Google Scholar] [CrossRef]
- Fan, X.; Li, Y.; Liu, Z.; Zhao, J. The (anti)-η-Hermitian solution of quaternion linear system. Filomat 2024, 38, 4679–4695. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y.; Sun, J.; Fan, X.; Wei, A. A new method based on the semi-tensor product of matrices for solving communicative quaternion matrix equation and its application. Bull. Sci. Math. 2025, 199, 103576. [Google Scholar] [CrossRef]
- Fan, X.; Li, Y.; Sun, J.; Zhao, J. Solving quaternion linear system AXB = E based on semi-tensor product of quaternion matrices. Banach J. Math. Anal. 2023, 17, 25. [Google Scholar] [CrossRef]
- Xi, Y.; Liu, Z.; Li, Y.; Tao, R.; Wang, T. On the mixed solution of reduced biquaternion matrix equation with sub-matrix constraints and its application. AIMS Math. 2023, 8, 27901–27923. [Google Scholar] [CrossRef]
- Fan, X.; Li, Y.; Zhang, M.; Zhao, J. Solving the least squares (anti)-Hermitian solution for quaternion linear systems. Comput. Appl. Math. 2022, 41, 371. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Fan, X.; Ding, W. A new method of solving special solutions of quaternion generalized Lyapunov matrix equation. Symmetry 2022, 14, 1120. [Google Scholar] [CrossRef]
- Ziętak, K. The Chebyshev solution of the linear matrix equation AX + YB = C. Numer. Math. 1985, 46, 455–478. [Google Scholar] [CrossRef]
- Ziętak, K. The lp-solution of the linear matrix equation AX + YB = C. Computing 1984, 32, 153–162. [Google Scholar] [CrossRef]
- Liao, A.P.; Bai, Z.Z.; Lei, Y. Best approximate solution of matrix equation AXB + CYD = E. SIAM J. Matrix Anal. Appl. 2005, 27, 675–688. [Google Scholar] [CrossRef]
- Wimmer, H.K. Roth’s theorems for matrix equations with symmetry constraints. Linear Algebra Appl. 1994, 199, 357–362. [Google Scholar] [CrossRef]
- Terán, F.D.; Dopico, F.M. Consistency and efficient solution of the Sylvester equation for ★-congruence. Electron. J. Linear Algebra 2011, 22, 849–863. [Google Scholar] [CrossRef]
- Byers, R.; Kressner, D. Structured condition numbers for invariant subspaces. SIAM J. Matrix Anal. Appl. 2006, 28, 326–347. [Google Scholar] [CrossRef]
- Kressner, D.; Schröder, C.; Watkins, D.S. Implicit QR algorithms for palindromic and even eigenvalue problems. Numer. Algor. 2009, 51, 209–238. [Google Scholar] [CrossRef]
- Cvetković-Ilixcx, D.S. The solutions of some operator equations. J. Korean Math. Soc. 2008, 45, 1417–1425. [Google Scholar] [CrossRef]
- Chang, X.W.; Wang, J.S. The symmetric solution of the matrix equations AX + YA = C, AXAT + BYBT = C, and (ATXA, BTXB) = (C, D). Linear Algebra Appl. 1993, 179, 171–189. [Google Scholar] [CrossRef]
- Jameson, A.; Kreindler, E. Inverse problem of linear optimal control. SIAM J. Control 1973, 11, 1–19. [Google Scholar] [CrossRef]
- Jameson, A.; Kreindler, E.; Lancaster, P. Symmetric, positive semidefinite, positive definite real solutions of AX = XAT and AX = YB. Linear Algebra Appl. 1992, 160, 189–215. [Google Scholar] [CrossRef]
- Dobovišek, M. On minimal solutions of the matrix equation AX − YB=0. Linear Algebra Appl. 2001, 325, 81–99. [Google Scholar] [CrossRef]
- Cantoni, A.; Butler, P. Eigenvalues and eigenvectors of symmetric centrosymmetric matrices. Linear Algebra Appl. 1976, 13, 275–288. [Google Scholar] [CrossRef]
- Reid, R.M. Some eigenvalues properties of persymmetric matrices. SIAM Rev. 1997, 39, 313–316. [Google Scholar] [CrossRef]
- Andrew, A.L. Centrosymmetric matrices. SIAM Rev. 1998, 40, 697–698. [Google Scholar] [CrossRef]
- Weaver, J.R. Centrosymmetric (cross-symmetric) matrices, their basic properties, eigenvalues, eigenvectors. Am. Math. Mon. 1985, 92, 711–717. [Google Scholar] [CrossRef]
- Draxl, P.K. Skew Field; Cambridge University Press: London, UK, 1983. [Google Scholar]
- Wang, Q.W.; Li, S.Z. Persymmetric and perskewsymmetric solutions to sets of matrix equations over a finite central algebra. Acta Math. Sin. 2004, 47, 27–34. (In Chinese) [Google Scholar]
- Wang, Q.W.; Sun, J.H.; Li, S.Z. Consistency for bi(skew)symmetric solutions to systems of generalized Sylvester equations over a finite central algebra. Linear Algebra Appl. 2002, 353, 169–182. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhang, H.S.; Song, G.J. A new solvable condition for a pair of generalized Sylvester equations. Electron. J. Linear Algebra 2009, 18, 289–301. [Google Scholar] [CrossRef]
- Wang, Q.W.; He, Z.H. Some matrix equations with applications. Linear Multilinear Algebra 2012, 60, 1327–1353. [Google Scholar] [CrossRef]
- Took, C.C.; Mandic, D.P. Augmented second-order statistics of quaternion random signals. Signal Process. 2011, 91, 214–224. [Google Scholar] [CrossRef]
- Took, C.C.; Mandic, D.P.; Zhang, F. On the unitary diagonalisation of a special class of quaternion matrices. Appl. Math. Lett. 2011, 24, 1806–1809. [Google Scholar] [CrossRef]
- Yuan, S.F.; Wang, Q.W. Two special kinds of least squares solutions for the quaternion matrix equation AXB + CXD = E. Electron. J. Linear Algebra 2012, 23, 257–274. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W. A real quaternion matrix equation with applications. Linear Multilinear Algebra 2013, 61, 725–740. [Google Scholar] [CrossRef]
- Baksalary, J.K.; Kala, R. The matrix equation AXB + CYD = E. Linear Algebra Appl. 1980, 30, 141–147. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W. A pair of mixed generalized Sylvester matrix equations. J. Shanghai Univ. Nat. Sci. 2014, 20, 138–156. [Google Scholar]
- Kyrchei, I. Cramer’s rules of η-(skew-)Hermitian solutions to the quaternion Sylvester-type matrix equations. Adv. Appl. Clifford Algebras 2019, 29, 56. [Google Scholar] [CrossRef]
- He, Z.H.; Liu, J.; Tam, T.Y. The general ϕ-Hermitian solution to mixed pairs of quaternion matrix Sylvester equations. Electron. J. Linear Algebra 2017, 32, 475–499. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Q.; He, Z. The common solution of some matrix equations. Algebra Colloq. 2016, 23, 71–81. [Google Scholar] [CrossRef]
- Wang, Q.W.; Lv, R.Y.; Zhang, Y. The least-squares solution with the least norm to a system of tensor equations over the quaternion algebra. Linear Multilinear Algebra 2022, 70, 1942–1962. [Google Scholar] [CrossRef]
- Guralnick, R.M. Roth’s theorems and decomposition of modules. Linear Algebra Appl. 1980, 39, 155–165. [Google Scholar] [CrossRef]
- Hartwig, R.E. Roth’s equivalence problem in unit regular rings. Proc. Am. Math. Soc. 1976, 59, 39–44. [Google Scholar] [CrossRef]
- Newman, M. The Smith normal form of a partitioned matrix. J. Res. Nat. Bur. Stand.-B. Math. Sci. 1974, 78B, 3–6. [Google Scholar] [CrossRef]
- Feinberg, R.B. Equivalence of partitioned matrices. J. Res. Nat. Bur. Stand.-B. Math. Sci. 1976, 80B, 89–97. [Google Scholar] [CrossRef]
- Gustafson, W.H.; Zelmanowitz, J.M. On matrix equivalence and matrix equations. Linear Algebra Appl. 1979, 27, 219–224. [Google Scholar] [CrossRef]
- Gustafson, W.H. Roth’s theorems over commutative rings. Linear Algebra Appl. 1979, 23, 245–251. [Google Scholar] [CrossRef]
- Guralnick, R.M. Roth’s theorems for sets of matrices. Linear Algebra Appl. 1985, 71, 113–117. [Google Scholar] [CrossRef]
- Lee, S.G.; Vu, Q.P. Simultaneous solutions of matrix equations and simultaneous equivalence of matrices. Linear Algebra Appl. 2012, 437, 2325–2339. [Google Scholar] [CrossRef]
- Miyata, T. Note on direct summands of modules. J. Math. Kyoto Univ. 1967, 7, 65–69. [Google Scholar] [CrossRef]
- Guralnick, R.M. Matrix equivalence and isomorphism of modules. Linear Algebra Appl. 1982, 43, 125–136. [Google Scholar] [CrossRef]
- Özgüler, A.B. The matrix equation AXB + CYD = E over a principal ideal domain. SIAM J. Matrix Anal. Appl. 1991, 12, 581–591. [Google Scholar] [CrossRef]
- Huang, L.; Zeng, Q. The matrix equation AXB + CYD = E over a simple artinian ring. Linear Multilinear Algebra 1995, 38, 225–232. [Google Scholar]
- Wang, Q.W. A system of matrix equations and a linear matrix equation over arbitrary regular rings with identity. Linear Algebra Appl. 2004, 384, 43–54. [Google Scholar] [CrossRef]
- Dajić, A. Common solutions of linear equations in a ring, with applications. Electron. J. Linear Algebra 2015, 30, 66–79. [Google Scholar] [CrossRef]
- Lin, M.; Wimmer, H.K. The generalized Sylvester matrix equation, rank minimization and Roth’s equivalence theorem. Bull. Aust. Math. Soc. 2011, 84, 441–443. [Google Scholar] [CrossRef]
- Ito, N.; Wimmer, H.K. Rank minimization of generalized Sylvester equations over Bezout domains. Linear Algebra Appl. 2013, 439, 592–599. [Google Scholar] [CrossRef]
- Hamilton, W.R. Lectures on Quaternions; Hodges and Smith: Dublin, Ireland, 1853. [Google Scholar]
- Voight, J. Quaternion Algebras; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Adler, S.L. Quaternionic Quantum Mechanics and Quantum Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Girard, P.R. Quaternions, Clifford Algebras and Relativistic Physics; Birkhäuser: Basel, Switzerland, 2007. [Google Scholar]
- Li, W. Quaternion Matrices; National University of Defense Technology Press: Changsha, China, 2002. (In Chinese) [Google Scholar]
- Clifford, M.A. Preliminary sketch of biquaternions. Proc. Lond. Math. Soc. 1873, 4, 381–395. [Google Scholar] [CrossRef]
- Wei, T.; Ding, W.; Wei, Y. Singular value decomposition of dual matrices and its application to traveling wave identification in the brain. SIAM J. Matrix Anal. Appl. 2024, 45, 634–660. [Google Scholar] [CrossRef]
- Fischer, I. Dual-Number Methods in Kinematics, Statics and Dynamics; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Condurache, D.; Burlacu, A. Dual tensors based solutions for rigid body motion parameterization. Mech. Mach. Theory 2014, 74, 390–412. [Google Scholar] [CrossRef]
- Gu, Y.L.; Luh, J.Y.S. Dual-number transformations and its applications to robotics. IEEE J. Robot. Autom. 1987, 3, 615–623. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Pennestri, E.; de Falco, D. Do all dual matrices have dual Moore-Penrose inverses? Mech. Mach. Theory 2020, 151, 103878. [Google Scholar] [CrossRef]
- Udwadia, F.E. Dual generalized inverses and their use in solving systems of linear dual equations. Mech. Mach. Theory 2021, 156, 104158. [Google Scholar] [CrossRef]
- Fan, R.; Zeng, M.; Yuan, Y. The solutions to some dual matrix equations. Miskolc Math. Notes 2024, 25, 679–691. [Google Scholar] [CrossRef]
- Farias, J.G.; Pieri, E.D.; Martins, D. A review on the applications of dual quaternions. Machines 2024, 12, 402. [Google Scholar] [CrossRef]
- Kenwright, B. A beginner’s guide to dual-quaternions: What they are, how they work, how to use them for 3D character hierarchies. In Proceedings of the 20th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Pilsen, Czech Republic, 25–28 June 2012. [Google Scholar]
- Mukundan, R. Quaternions: From classical mechanics to computer graphics, and beyond. In Proceedings of the 7th Asian Technology Conference in Mathematics, Melaka, Malaysia, 17–21 December 2002; pp. 97–106. [Google Scholar]
- Xie, L.M.; Wang, Q.W.; He, Z.H. The generalized hand-eye calibration matrix equation AX − YB = C over dual quaternions. Comput. Appl. Math. 2025, 44, 137. [Google Scholar] [CrossRef]
- Xie, L.M.; Wang, Q.W. A generalized Sylvester dual quaternion matrix equation with applications. Authorea 2025. [Google Scholar] [CrossRef]
- Duan, G.R. Generalized Sylvester Equations: Unified Parametric Solutions; Taylor and Francis Group: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Hamilton, W.R., II. On quaternions; or on a new system of imaginaries in algebra. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1844, 25, 10–13. [Google Scholar] [CrossRef]
- Cockle, J. On systems of algebra involving more than one imaginary and on equations of the fifth degree. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1849, 35, 434–437. [Google Scholar] [CrossRef]
- Segre, C. The real representations of complex elements and extension to bicomplex systems. Math. Ann. 1892, 40, 413–467. (In Italian) [Google Scholar] [CrossRef]
- Tian, Y.; Liu, X.; Zhang, Y. Least-squares solutions of the generalized reduced biquaternion matrix equations. Filomat 2023, 37, 863–870. [Google Scholar] [CrossRef]
- Yaglom, I.M. Complex Numbers in Geometry; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Lam, T.Y. Introduction to Quadratic Forms over Fields; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Pottmann, H.; Wallner, J. Computational Line Geometry; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Kandasamy, W.B.V.; Smarandache, F. Dual Numbers; Zip Publishing: Columbus, OH, USA, 2012. [Google Scholar]
- Lance, E.C. Hilbert C*-Modules: A Toolkit for Operator Algebraists; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Fang, X.; Yu, J.; Yao, H. Solutions to operator equations on Hilbert C*-modules. Linear Algebra Appl. 2009, 431, 2142–2153. [Google Scholar] [CrossRef]
- Xu, Q. Common Hermitian and positive solutions to the adjointable operator equations AX = C, XB = D. Linear Algebra Appl. 2008, 429, 1–11. [Google Scholar] [CrossRef]
- Dajić, A.; Koliha, J.J. Positive solutions to the equations AX = C and XB = D for Hilbert space operators. J. Math. Anal. Appl. 2007, 333, 567–576. [Google Scholar] [CrossRef]
- Douglas, R.G. On majorization, factorization and range inclusion of operators on Hilbert space. Proc. Am. Math. Soc. 1966, 17, 413–416. [Google Scholar] [CrossRef]
- Mousavi, Z.; Eskandari, R.; Moslehian, M.S.; Mirzapour, F. Operator equations AX + YB = C and AXA* + BYB* = C in Hilbert C*-modules. Linear Algebra Appl. 2017, 517, 85–98. [Google Scholar] [CrossRef]
- Karizaki, M.M.; Hassani, M.; Amyari, M.; Khosravi, M. Operator matrix of Moore-Penrose inverse operators on Hilbert C*-modules. Colloq. Math. 2015, 140, 171–182. [Google Scholar] [CrossRef]
- Moghani, Z.N.; Karizaki, M.M.; Khanehgir, M. Solutions of the Sylvester equation in C*-Modular operators. Ukr. Math. J. 2021, 73, 354–369. [Google Scholar] [CrossRef]
- An, I.J.; Ko, E.; Lee, J.E. On the generalized Sylvester operator equation AX − YB = C. Linear Multilinear Algebra 2022, 72, 585–596. [Google Scholar] [CrossRef]
- Jo, S.; Kim, Y.; Ko, E. On Fuglede-Putnam properties. Positivity 2015, 19, 911–925. [Google Scholar] [CrossRef]
- Bhatia, R. Matrix Analysis; Springer: New York, NY, USA, 1997. [Google Scholar]
- Lim, L.H. Tensors in computations. Acta Numer. 2021, 30, 555–764. [Google Scholar] [CrossRef]
- Qi, L.; Luo, Z. Tensor Analysis: Spectral Theory and Special Tensors; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar]
- Ding, W.; Wei, Y. Theory and Computation of Tensors: Multi-Dimensional Arrays; Elsevier: Amsterdam, The Netherlands; Academic Press: London, UK, 2016. [Google Scholar]
- Che, M.; Wei, Y. Theory and Computation of Complex Tensors and its Applications; Springer: Singapore, 2020. [Google Scholar]
- Wu, F.; Li, C.; Li, Y. Manifold regularization nonnegative triple decomposition of tensor sets for image compression and representation. J. Optim. Theory Appl. 2022, 192, 979–1000. [Google Scholar] [CrossRef]
- Savas, B.; Eldén, L. Handwritten digit classification using higher order singular value decomposition. Pattern Recognit. 2007, 40, 993–1003. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, G.; Chen, M. Tensor extreme learning design via generalized Moore-Penrose inverse and triangular type-2 fuzzy sets. Neural Comput. Appl. 2019, 31, 5641–5651. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; Lathauwer, L.D.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Qi, L.; Chen, H.; Chen, Y. Tensor Eigenvalues and Their Applications; Springer: Singapore, 2018. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- He, Z.H.; Navasca, C.; Wang, Q.W. Tensor decompositions and tensor equations over quaternion algebra. arXiv 2017, arXiv:1710.07552v1. [Google Scholar] [CrossRef]
- Einstein, A. The foundation of the general theory of relativity. In The Collected Papers of Albert Einstein; Kox, A.J., Klein, M.J., Schulmann, R., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; Volume 6, pp. 146–200. [Google Scholar]
- Sun, L.; Zheng, B.; Bu, C.; Wei, Y. Moore-Penrose inverse of tensors via Einstein product. Linear Multilinear Algebra 2016, 64, 686–698. [Google Scholar] [CrossRef]
- Brazell, M.; Li, N.; Navasca, C.; Tamon, C. Solving multilinear systems via tensor inversion. SIAM J. Matrix Anal. Appl. 2013, 34, 542–570. [Google Scholar] [CrossRef]
- He, Z.H.; Navasca, C.; Wang, X.X. Decomposition for a quaternion tensor triplet with applications. Adv. Appl. Clifford Algebras 2022, 32, 9. [Google Scholar] [CrossRef]
- Wang, Q.W.; Wang, X. A system of coupled two-sided Sylvester-type tensor equations over the quaternion algebra. Taiwan J. Math. 2020, 24, 1399–1416. [Google Scholar] [CrossRef]
- Mehany, M.S.; Wang, Q.; Liu, L. A system of Sylvester-like quaternion tensor equations with an application. Front. Math. 2024, 19, 749–768. [Google Scholar] [CrossRef]
- Wang, Q.W.; Wang, X.; Zhang, Y. A constraint system of coupled two-sided Sylvester-like quaternion tensor equations. Comput. Appl. Math. 2020, 39, 317. [Google Scholar] [CrossRef]
- Qin, J.; Wang, Q.W. Solving a system of two-sided Sylvester-like quaternion tensor equations. Comput. Appl. Math. 2023, 42, 232. [Google Scholar] [CrossRef]
- He, Z.H. The general solution to a system of coupled Sylvester-type quaternion tensor equations involving η-Hermicity. Bull. Iran. Math. Soc. 2019, 45, 1407–1430. [Google Scholar] [CrossRef]
- Xie, M.; Wang, Q.W. Reducible solution to a quaternion tensor equation. Front. Math. China 2020, 15, 1047–1070. [Google Scholar] [CrossRef]
- Xie, M.; Wang, Q.W.; Zhang, Y. The minimum-norm least squares solutions to quaternion tensor systems. Symmetry 2022, 14, 1460. [Google Scholar] [CrossRef]
- Jia, Z.R.; Wang, Q.W. The general solution to a system of tensor equations over the split quaternion algebra with applications. Mathematics 2025, 13, 644. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.W.; Kou, Z. A system of tensor equations over the dual split quaternion algebra with an application. Mathematics 2024, 12, 3571. [Google Scholar] [CrossRef]
- Bader, B.W.; Kolda, T.G. Algorithm 862: Matlab tensor classes for fast algorithm prototyping. ACM Trans. Math. Softw. 2006, 32, 635–653. [Google Scholar] [CrossRef]
- Kilmer, M.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Qin, Z.; Ming, Z.; Zhang, L. Singular value decomposition of third order quaternion tensors. Appl. Math. Lett. 2022, 123, 107597. [Google Scholar] [CrossRef]
- Shao, J.Y. A general product of tensors with applications. Linear Algebra Appl. 2013, 439, 2350–2366. [Google Scholar] [CrossRef]
- Kernfeld, E.; Kilmer, M.; Aeron, S. Tensor-tensor products with invertible linear transforms. Linear Algebra Appl. 2015, 485, 545–570. [Google Scholar] [CrossRef]
- Kilmer, M.; Horesh, L.; Avron, H.; Newman, E. Tensor-tensor products for optimal representation and compression. arXiv 2019, arXiv:2001.00046v1. [Google Scholar] [CrossRef]
- Jin, H.; Xu, S.; Wang, Y.; Liu, X. The Moore-Penrose inverse of tensors via the M-product. Comput. Appl. Math. 2023, 42, 294. [Google Scholar] [CrossRef]
- Kučera, V. Algebraic approach to discrete stochastic control. Kybernetika 1975, 11, 114–147. [Google Scholar]
- Bengtsson, G. Output regulation and internal models–a frequency domain approach. Automatica 1977, 13, 333–345. [Google Scholar] [CrossRef]
- Cheng, L.; Pearson, J. Frequency domain synthesis of multivariable linear regulators. IEEE Trans. Autom. Control 1978, 23, 3–15. [Google Scholar] [CrossRef]
- Wolovich, W.A. Skew prime polynomial matrices. IEEE Trans. Autom. Control 1978, 23, 880–887. [Google Scholar] [CrossRef]
- Wolovich, W.A. Linear Multivariable Systems; Springer: New York, NY, USA, 1974. [Google Scholar]
- Fuhrmann, P.A. Algebraic system theory: An analyst’s point of view. J. Franklin Inst. 1976, 301, 521–540. [Google Scholar] [CrossRef]
- Emre, E.; Silverman, L.M. The equation XR + QY = Φ: A characterization of solutions. SIAM J. Control Optim. 1981, 19, 33–38. [Google Scholar] [CrossRef]
- Emre, E. The polynomial equation QQc + RPc = Φ with application to dynamic feedback. SIAM J. Control Optim. 1980, 18, 611–620. [Google Scholar] [CrossRef]
- Żak, S.H. On the polynomial matrix equation AX + YB = C. IEEE Trans. Autom. Control 1985, 30, 1240–1242. [Google Scholar] [CrossRef]
- Feinstein, J.; Bar-Ness, Y. The solution of the matrix polynomial A(s)X(s) + B(s)Y(s) = C(s). IEEE Trans. Autom. Control 1984, 29, 75–77. [Google Scholar] [CrossRef]
- Wimmer, H.K. Consistency of a pair of generalized Sylvester equations. IEEE Trans. Autom. Control 1994, 39, 1014–1016. [Google Scholar] [CrossRef]
- Wimmer, H.K. The matrix equation X − AXB = C and an analogue of Roth’s theorem. Linear Algebra Appl. 1988, 109, 145–147. [Google Scholar] [CrossRef]
- Wimmer, H.K. The generalized Sylvester equation in polynomial matrices. IEEE Trans. Autom. Control 1996, 41, 1372–1376. [Google Scholar] [CrossRef]
- Wimmer, H.K. The structure of nonsingular polynomial matrices. Math. Syst. Theory 1981, 14, 367–379. [Google Scholar] [CrossRef]
- Barnett, S. Regular polynomial matrices having relatively prime determinants. Proc. Camb. Philos. Soc. 1969, 65, 585–590. [Google Scholar] [CrossRef]
- Feinstein, J.; Bar-Ness, Y. On the uniqueness minimal solution of the matrix polynomial equation A(λ)X(λ) + Y(λ)B(λ) = C(λ). J. Franklin Inst. 1980, 310, 131–134. [Google Scholar] [CrossRef]
- Chen, S.; Tian, Y. On solutions of generalized Sylvester equation in polynomial matrices. J. Franklin Inst. 2014, 351, 5376–5385. [Google Scholar] [CrossRef]
- Wimmer, H.K. Explicit solutions of the matrix equation AiXDi = C. SIAM J. Matrix Anal. Appl. 1992, 13, 1123–1130. [Google Scholar] [CrossRef]
- Huang, L. The explicit solutions and solvability of linear matrix equations. Linear Algebra Appl. 2000, 311, 195–199. [Google Scholar] [CrossRef]
- Gohberg, I.; Kaashoek, M.A.; Lerer, L. On a class of entire matrix function equations. Linear Algebra Appl. 2007, 425, 434–442. [Google Scholar] [CrossRef]
- Gohberg, I.; Kaashoek, M.A.; Schagen, F. Partially Specified Matrices and Operators: Classification, Completion, Applications; Birkhäuser Verlag: Basel, Switzerland, 1995. [Google Scholar]
- Kaashoek, M.A.; Lerer, L. On a class of matrix polynomial equations. Linear Algebra Appl. 2013, 439, 613–620. [Google Scholar] [CrossRef]
- Gohberg, I.; Kaashoek, M.A.; Lerer, L. The resultant for regular matrix polynomials and quasi commutativity. Indiana Univ. Math. J. 2008, 57, 2793–2813. [Google Scholar] [CrossRef]
- Huang, L. The solvability of linear matrix equation over a central simple algebra. Linear Multilinear Algebra 1996, 40, 353–363. [Google Scholar] [CrossRef]
- Huang, L. The quaternion matrix equation . Acta Math. Sin. New Ser. 1998, 14, 91–98. [Google Scholar]
- Huang, L.; Liu, J. The extension of Roth’s theorem for matrix equations over a ring. Linear Algebra Appl. 1997, 259, 229–235. [Google Scholar] [CrossRef]
- Wu, A.G.; Duan, G.R.; Xue, Y. Kronecker maps and Sylvester-polynomial matrix equations. IEEE Trans. Autom. Control 2007, 52, 905–910. [Google Scholar] [CrossRef]
- Wu, A.G.; Liu, W.; Duan, G.R. On the conjugate product of complex polynomial matrices. Math. Comput. Model. 2011, 53, 2031–2043. [Google Scholar] [CrossRef]
- Wu, A.G.; Duan, G.R.; Feng, G.; Liu, W. On conjugate product of complex polynomials. Appl. Math. Lett. 2011, 24, 735–741. [Google Scholar] [CrossRef]
- Wu, A.G.; Feng, G.; Liu, W.; Duan, G.R. The complete solution to the Sylvester-polynomial-conjugate matrix equations. Math. Comput. Model. 2011, 53, 2044–2056. [Google Scholar] [CrossRef]
- Bevis, J.H.; Hall, F.J.; Hartwig, R.E. Consimilarity and the matrix equation AX − XB = C. In Current Trends in Matrix Theory; Uhlig, F., Grone, R., Eds.; North-Holland: New York, NY, USA, 1987; pp. 51–64. [Google Scholar]
- Bevis, J.H.; Hall, F.J.; Hartwig, R.E. The matrix equation and its special cases. SIAM J. Matrix Anal. Appl. 1988, 9, 348–359. [Google Scholar] [CrossRef]
- Wu, A.G.; Duan, G.R.; Yu, H.H. On solutions of the matrix equations XF − AX = C and . Appl. Math. Comput. 2006, 183, 932–941. [Google Scholar]
- Jiang, T.; Wei, M. On solutions of the matrix equations X − AXB = C and . Linear Algebra Appl. 2003, 367, 225–233. [Google Scholar] [CrossRef]
- Wu, A.G.; Wang, H.Q.; Duan, G.R. On matrix equations X − AXF = C and . J. Comput. Appl. Math. 2009, 230, 690–698. [Google Scholar] [CrossRef]
- Wu, A.G.; Fu, Y.M.; Duan, G.R. On solutions of matrix equations V − AVF = BW and . Math. Comput. Model. 2008, 47, 1181–1197. [Google Scholar] [CrossRef]
- Wu, A.G.; Feng, G.; Hu, J.; Duan, G.R. Closed-form solutions to the nonhomogeneous Yakubovich-conjugate matrix equation. Appl. Math. Comput. 2009, 214, 442–450. [Google Scholar] [CrossRef]
- Wu, A.G.; Zhang, Y. Complex Conjugate Matrix Equations for Systems and Control; Springer: Singapore, 2017. [Google Scholar]
- Mazurek, R. A general approach to Sylvester-polynomial-conjugate matrix equations. Symmetry 2024, 16, 246. [Google Scholar] [CrossRef]
- Lam, T.Y. A First Course in Noncommutative Rings; Springer: New York, NY, USA, 1991. [Google Scholar]
- Wu, A.G.; Liu, W.; Li, C.; Duan, G.R. On j-conjugate product of quaternion polynomial matrices. Appl. Math. Comput. 2013, 219, 11223–11232. [Google Scholar] [CrossRef]
- Futorny, V.; Klymchuk, T.; Sergeichuk, V.V. Roth’s solvability criteria for the matrix equations over the skew field of quaternions with an involutive automorphism q ↦ . Linear Algebra Appl. 2016, 510, 246–258. [Google Scholar] [CrossRef]
- Jiang, T.; Ling, S. On a solution of the quaternion matrix equation and its applications. Adv. Appl. Clifford Algebras 2013, 23, 689–699. [Google Scholar] [CrossRef]
- Song, C.; Chen, G. On solutions of matrix equation XF − AX = C and over quaternion field. J. Appl. Math. Comput. 2011, 37, 57–68. [Google Scholar] [CrossRef]
- Jiang, T.S.; Wei, M.S. On a solution of the quaternion matrix equation and its application. Acta Math. Sin. Engl. Ser. 2005, 21, 483–490. [Google Scholar] [CrossRef]
- Song, C.; Chen, G.; Liu, Q. Explicit solutions to the quaternion matrix equations X − AXF = C and . Int. J. Comput. Math. 2012, 89, 890–900. [Google Scholar] [CrossRef]
- Song, C.; Feng, J.; Wang, X.; Zhao, J. A real representation method for solving Yakubovich-j-conjugate quaternion matrix equation. Abstr. Appl. Anal. 2014, 2014, 285086. [Google Scholar] [CrossRef]
- Yuan, S.; Liao, A. Least squares solution of the quaternion matrix equation with the least norm. Linear Multilinear Algebra 2011, 59, 985–998. [Google Scholar] [CrossRef]
- Song, C.; Feng, J. On solutions to the matrix equations XB − AX = CY and . J. Franklin Inst. 2016, 353, 1075–1088. [Google Scholar] [CrossRef]
- Song, C.; Chen, G. Solutions to matrix equations X − AXB = CY + R and XB − AX = CY and . J. Comput. Appl. Math. 2018, 343, 488–500. [Google Scholar] [CrossRef]
- Moor, B.D.; Zha, H. A tree of generalization of the ordinary singular value decomposition. Linear Algebra Appl. 1991, 147, 469–500. [Google Scholar] [CrossRef]
- He, Z.H. Pure PSVD approach to Sylvester-type quaternion matrix equations. Electron. J. Linear Algebra 2019, 35, 266–284. [Google Scholar] [CrossRef]
- Xie, M.Y.; Wang, Q.W.; He, Z.H.; Saad, M.M. A system of Sylvester-type quaternion matrix equations with ten variables. Acta Math. Sin. Engl. Ser. 2022, 38, 1399–1420. [Google Scholar] [CrossRef]
- Mehany, M.S.; Wang, Q.W. Three symmetrical systems of coupled Sylvester-like quaternion matrix equations. Symmetry 2022, 14, 550. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W.; Zhang, Y. A system of quaternary coupled Sylvester-type real quaternion matrix equations. Automatica 2018, 87, 25–31. [Google Scholar] [CrossRef]
- Rehman, A.; Wang, Q.W.; Ali, I.; Akram, M.; Ahmad, M.O. A constraint system of generalized Sylvester quaternion matrix equations. Adv. Appl. Clifford Algebr. 2017, 27, 3183–3196. [Google Scholar] [CrossRef]
- Wang, Q.W.; He, Z.H. Solvability conditions and general solution for mixed Sylvester equations. Automatica 2013, 49, 2713–2719. [Google Scholar] [CrossRef]
- Wang, Q.W.; He, Z.H. Systems of coupled generalized Sylvester matrix equations. Automatica 2014, 50, 2840–2844. [Google Scholar] [CrossRef]
- Wang, Q.W.; Rehman, A.; He, Z.H.; Zhang, Y. Constraint generalized Sylvester matrix equations. Automatica 2016, 69, 60–64. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W. A system of periodic discrete-time coupled Sylvester quaternion matrix equations. Algebra Colloq. 2017, 24, 169–180. [Google Scholar] [CrossRef]
- Kågström, B. A perturbation analysis of the generalized Sylvester equation (AR − LB, DR − LE) = (C, F). SIAM J. Matrix Anal. Appl. 1994, 15, 1045–1060. [Google Scholar] [CrossRef]
- Ziętak, K. The properties of the minimax solution of a non-linear matrix equation XY = A. IMA J. Numer. Anal. 1983, 3, 229–244. [Google Scholar] [CrossRef]
- Yang, X.; Huang, W. Backward error analysis of the matrix equations for Sylvester and Lyapunov. J. Sys. Sci. Math. Scis. 2008, 28, 524–534. (In Chinese) [Google Scholar]
- Sun, J.G.; Xu, S.F. Perturbation analysis of the maximal solution of the matrix equation X + A*X−1 = P. II. Linear Algebra Appl. 2003, 362, 211–228. [Google Scholar] [CrossRef]
- Li, J.F.; Hu, X.Y.; Duan, X.F. A symmetric preserving iterative method for generalized Sylvester equation. Asian J. Control 2011, 13, 408–417. [Google Scholar] [CrossRef]
- Rockafellar, R.T. The multiplier method of Hestenes and Powell applied to convex programming. J. Optim. Theory Appl. 1973, 12, 555–562. [Google Scholar] [CrossRef]
- Hartwig, R.E. A note on light matrices. Linear Algebra Appl. 1987, 97, 153–169. [Google Scholar] [CrossRef]
- Ke, Y.; Ma, C. An alternating direction method for nonnegative solutions of the matrix equation AX + YB = C. Comp. Appl. Math. 2017, 36, 359–365. [Google Scholar] [CrossRef]
- Peng, Z.; Peng, Y. An efficient iterative method for solving the matrix equation AXB + CYD = E. Numer. Linear Algebra Appl. 2006, 13, 473–485. [Google Scholar] [CrossRef]
- Kågström, B.; Poromaa, P. Lapack-style algorithms and software for solving the generalized Sylvester equation and estimating the separation between regular matrix pairs. ACM Trans. Math. Softw. 1996, 22, 78–103. [Google Scholar] [CrossRef]
- Lin, Y.; Wei, Y. Condition numbers of the generalized Sylvester equation. IEEE Trans. Autom. Control 2007, 52, 2380–2385. [Google Scholar] [CrossRef]
- Diao, H.; Shi, X.; Wei, Y. Effective condition numbers and small sample statistical condition estimation for the generalized Sylvester equation. Sci. China-Math. 2013, 56, 967–982. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. An iterative algorithm for the reflexive solutions of the generalized coupled Sylvester matrix equations and its optimal approximation. Appl. Math. Comput. 2008, 202, 571–588. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. An iterative method for solving the generalized coupled Sylvester matrix equations over generalized bisymmetric matrices. Appl. Math. Modell. 2010, 34, 639–654. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Li, S.K.; Huang, T.Z. LSQR iterative method for generalized coupled Sylvester matrix equations. Appl. Math. Modell. 2012, 36, 3545–3554. [Google Scholar] [CrossRef]
- Huang, J. On parameter iteration method for solving the mixed-type Lyapunov matrix equation. Math. Numer. Sinica 2007, 29, 285–292. (In Chinese) [Google Scholar]
- Zhang, K. Iterative Algorithms for Constrained Solutions of Matrix Equations; National Defense Industry Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Lv, C.; Ma, C. Two parameter iteration methods for coupled Sylvester matrix equations. East Asian J. Appl. Math. 2018, 8, 336–351. [Google Scholar] [CrossRef]
- Ma, C.; Wu, Y.; Xie, Y. The Newton-type splitting iterative method for a class of coupled Sylvester-like absolute value equation. J. Appl. Anal. Comput. 2024, 14, 3306–3331. [Google Scholar] [CrossRef]
- Sheng, X. A relaxed gradient based algorithm for solving generalized coupled Sylvester matrix equations. J. Franklin Inst. 2018, 355, 4282–4297. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Iterative least-squares solutions of coupled Sylvester matrix equations. Syst. Control Lett. 2005, 54, 95–107. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. On iterative solutions of general coupled matrix equations. SIAM J. Control Optim. 2006, 44, 2269–2284. [Google Scholar] [CrossRef]
- Shirilord, A.; Dehghan, M. Gradient descent-based parameter-free methods for solving coupled matrix equations and studying an application in dynamical systems. Appl. Numer. Math. 2025, 212, 29–59. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. The general coupled matrix equations over generalized bisymmetric matrices. Linear Algebra Appl. 2010, 432, 1531–1552. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. Iterative algorithms for the generalized centro-symmetric and central anti-symmetric solutions of general coupled matrix equations. Eng. Comput. 2012, 29, 528–560. [Google Scholar] [CrossRef]
- Hajarian, M. Matrix form of the CGS method for solving general coupled matrix equations. Appl. Math. Lett. 2014, 34, 37–42. [Google Scholar] [CrossRef]
- Hajarian, M. Generalized conjugate direction algorithm for solving the general coupled matrix equations over symmetric matrices. Numer. Algor. 2016, 73, 591–609. [Google Scholar] [CrossRef]
- Hajarian, M. Convergence of HS version of BCR algorithm to solve the generalized Sylvester matrix equation over generalized reflexive matrices. J. Franklin Inst. 2017, 354, 2340–2357. [Google Scholar] [CrossRef]
- Lv, C.Q.; Ma, C.F. BCR method for solving generalized coupled Sylvester equations over centrosymmetric or anti-centrosymmetric matrix. Comput. Math. Appl. 2018, 75, 70–88. [Google Scholar] [CrossRef]
- Niu, Q.; Wang, X.; Lu, L.Z. A relaxed gradient based algorithm for solving Sylvester equations. Asian J. Control 2011, 13, 461–464. [Google Scholar] [CrossRef]
- Hajarian, M. Computing symmetric solutions of general Sylvester matrix equations via Lanczos version of biconjugate residual algorithm. Comput. Math. Appl. 2018, 76, 686–700. [Google Scholar] [CrossRef]
- Yan, T.; Ma, C. The BCR algorithms for solving the reflexive or anti-reflexive solutions of generalized coupled Sylvester matrix equations. J. Franklin Inst. 2020, 357, 12787–12807. [Google Scholar] [CrossRef]
- Zhou, B.; Duan, G.R.; Li, Z.Y. Gradient based iterative algorithm for solving coupled matrix equations. Syst. Control Lett. 2009, 58, 327–333. [Google Scholar] [CrossRef]
- Hajarian, M. Matrix GPBiCG algorithms for solving the general coupled matrix equations. IET Control Theory Appl. 2015, 9, 74–81. [Google Scholar] [CrossRef]
- Wu, A.G.; Li, B.; Zhang, Y.; Duan, G.R. Finite iterative solutions to coupled Sylvester-conjugate matrix equations. Appl. Math. Modell. 2011, 35, 1065–1080. [Google Scholar] [CrossRef]
- Yan, T.; Ma, C. An iterative algorithm for generalized Hamiltonian solution of a class of generalized coupled Sylvester-conjugate matrix equations. Appl. Math. Comput. 2021, 411, 126491. [Google Scholar] [CrossRef]
- Carpentieri, B.; Jing, Y.F.; Huang, T.Z. The BiCOR and CORS iterative algorithms for solving nonsymmetric linear systems. SIAM J. Sci. Comput. 2011, 33, 3020–3036. [Google Scholar] [CrossRef]
- Jing, Y.F.; Huang, T.Z.; Zhang, Y.; Li, L.; Cheng, G.H.; Ren, Z.G.; Duan, Y.; Sogabe, T.; Carpentieri, B. Lanczos-type variants of the COCR method for complex nonsymmetric linear systems. J. Comput. Phys. 2009, 228, 6376–6394. [Google Scholar] [CrossRef]
- Hajarian, M. Developing BiCOR and CORS methods for coupled Sylvester-transpose and periodic Sylvester matrix equations. Appl. Math. Modell. 2015, 39, 6073–6084. [Google Scholar] [CrossRef]
- Bittanti, S.; Colaneri, P. Periodic Systems: Filtering and Control; Springer: London, UK, 2009. [Google Scholar]
- Hajarian, M. Convergence analysis of generalized conjugate direction method to solve general coupled Sylvester discrete-time periodic matrix equations. Int. J. Adapt. Control Signal Process. 2017, 31, 985–1002. [Google Scholar] [CrossRef]
- Ma, C.; Yan, T. A finite iterative algorithm for the general discrete-time periodic Sylvester matrix equations. J. Franklin Inst. 2022, 359, 4410–4432. [Google Scholar]
- Dehghani-Madiseh, M.; Dehghan, M. Generalized solution sets of the interval generalized Sylvester matrix equation and some approaches for inner and outer estimations. Comput. Math. Appl. 2014, 68, 1758–1774. [Google Scholar] [CrossRef]
- Hajarian, M. Convergence properties of BCR method for generalized Sylvester matrix equation over generalized reflexive and anti-reflexive matrices. Linear Multilinear Algebra 2018, 66, 1975–1990. [Google Scholar]
- Li, T.; Wang, Q.W.; Zhang, X.F. A modified conjugate residual method and nearest Kronecker product preconditioner for the generalized coupled Sylvester tensor equations. Mathematics 2022, 10, 1730. [Google Scholar] [CrossRef]
- Varga, A. A numerically reliable approach to robust pole assignment for descriptor systems. Futur. Gener. Comp. Syst. 2012, 19, 1221–1230. [Google Scholar] [CrossRef]
- Trinh, H.; Tran, T.D.; Nahavandi, S. Design of scalar functional observers of order less than (ν − 1). Int. J. Control 2006, 79, 1654–1659. [Google Scholar] [CrossRef]
- Jin, L.; Yan, J.; Du, X.; Xiao, X.; Fu, D. RNN for solving time-variant generalized Sylvester equation with applications to robots and acoustic source localization. IEEE Trans. Ind. Inform. 2020, 16, 6359–6369. [Google Scholar] [CrossRef]
- Kiran, N.U. Simultaneous triangularization of pseudo-differential systems. J. Pseudo-Differ. Oper. Appl. 2013, 4, 45–61. [Google Scholar]
- Gu, D.; Zhang, D.; Liu, Q. Parametric control to permanent magnet synchronous motor via proportional plus integral feedback. Trans. Inst. Meas. Control 2021, 43, 925–932. [Google Scholar]
- Song, W.; Jin, A. Observer-based model reference tracking control of the Markov jump system with partly unknown transition rates. Appl. Sci. 2023, 13, 914. [Google Scholar] [CrossRef]
- Xu, R.; Wei, T.; Wei, Y.; Yan, H. UTV decomposition of dual matrices and its applications. Comput. Appl. Math. 2024, 43, 41. [Google Scholar] [CrossRef]
- Radjavi, H.; Rosenthal, P. Simultaneous Triangularization; Springer: New York, NY, USA, 2000. [Google Scholar]
- Taylor, M. Pseudo Differential Operators; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Mooring, B.W.; Roth, Z.S.; Driels, M.R. Fundamentals of Manipulator Calibration; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Shiu, Y.C.; Ahmad, S. Calibration of wrist-mounted robotic sensors by solving homogeneous transformation equations of the form AX = XB. IEEE Trans. Robot. Autom. 1989, 5, 16–29. [Google Scholar] [CrossRef]
- Zhuang, H.; Roth, Z.S. Comments on “Calibration of wrist-mounted robotic sensors by solving homogeneous transformation equations of the form AX = XB”. IEEE Trans. Robot. Autom. 1991, 7, 877–878. [Google Scholar] [CrossRef]
- Zhuang, H.; Roth, Z.S.; Sudhakar, R. Simultaneous robot/world and tool/flange calibration by solving homogeneous transformation equations of the form AX = YB. IEEE Trans. Robot. Autom. 1994, 10, 549–554. [Google Scholar] [CrossRef]
- Qi, L. Standard dual quaternion optimization and its applications in hand-eye calibration and SLAM. Commun. Appl. Math. Comput. 2023, 5, 1469–1483. [Google Scholar] [CrossRef]
- Li, A.; Wang, L.; Wu, D. Simultaneous robot-world and hand-eye calibration using dual-quaternions and Kronecker product. Int. J. Phys. Sci. 2010, 5, 1530–1536. [Google Scholar]
- Chen, Z.; Ling, C.; Qi, L.; Yan, H. A regularization-patching dual quaternion optimization method for solving the hand-eye calibration problem. J. Optim. Theory Appl. 2024, 200, 1193–1215. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Song, H. Simultaneous robot-world and hand-eye calibration based on a pair of dual equations. Measurement 2021, 181, 109623. [Google Scholar] [CrossRef]
- Daniilidis, K. Hand-eye calibration using dual quaternions. Int. J. Robot. Res. 1999, 18, 286–298. [Google Scholar] [CrossRef]
- Wang, J.; Qu, D.; Xu, F. A new hybrid calibration method for extrinsic camera parameters and hand-eye transformation. Preoceedings of the IEEE International Conference on Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; Volume 4, pp. 1981–1985. [Google Scholar]
- Ernst, F.; Richter, L.; Matthäus, L.; Martens, V.; Bruder, R.; Schlaefer, A.; Schweikard, A. Non-orthogonal tool/flange and robot/world calibration. Int. J. Med. Robotics Comput. Assist. Surg. 2012, 8, 407–420, Erratum in Int. J. Med. Robotics Comput. Assist. Surg. 2017, 13, e1883. [Google Scholar] [CrossRef]
- Shah, M. Solving the robot-world/hand-eye calibration problem using the Kronecker product. J. Mech. Robot. 2013, 5, 031007. [Google Scholar] [CrossRef]
- Wu, L.; Ren, H. Finding the kinematic base frame of a robot by hand-eye calibration using 3D position data. IEEE Trans. Autom. Sci. Eng. 2017, 14, 314–324. [Google Scholar] [CrossRef]
- Tan, N.; Gu, X.; Ren, H. Simultaneous robot-world, sensor-tip, kinematics calibration of an underactuated robotic hand with soft fingers. IEEE Access 2018, 6, 22705–22715. [Google Scholar] [CrossRef]
- Shah, M.; Bostelman, R.; Legowik, S.; Hong, T. Calibration of mobile manipulators using 2D positional features. Measurement 2018, 124, 322–328. [Google Scholar] [CrossRef]
- Condurache, D.; Ciureanu, I.A. A novel solution for AX = YB sensor calibration problem using dual Lie algebra. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT’19), Paris, France, 23–26 April 2019; pp. 302–307. [Google Scholar]
- Wu, J.; Liu, M.; Zhu, Y.; Zou, Z.; Dai, Z.M.; Zhang, C.; Jiang, Y.; Li, C. Globally optimal symbolic hand-eye calibration. IEEE-ASME Trans. Mechatron. 2021, 26, 1369–1379. [Google Scholar] [CrossRef]
- Pan, J.; Fu, Z.; Yue, H.; Lei, X.; Li, M.; Chen, X. Toward simultaneous coordinate calibrations of AX = YB problem by the LMI-SDP optimization. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2445–2453. [Google Scholar] [CrossRef]
- Ha, J. Probabilistic framework for hand-eye and robot-world calibration AX = YB. IEEE Trans. Robot. 2023, 39, 1196–1211. [Google Scholar] [CrossRef]
- Wang, X.; Song, H. One-step solving the robot-world and hand-eye calibration based on the principle of transference. J. Mech. Robot. 2024, 17, 031014. [Google Scholar]
- Xie, L.M.; Wang, Q.W. Some novel results on a classical system of matrix equations over the dual quaternion algebra. Filomat 2025, 39, 1477–1490. [Google Scholar] [CrossRef]
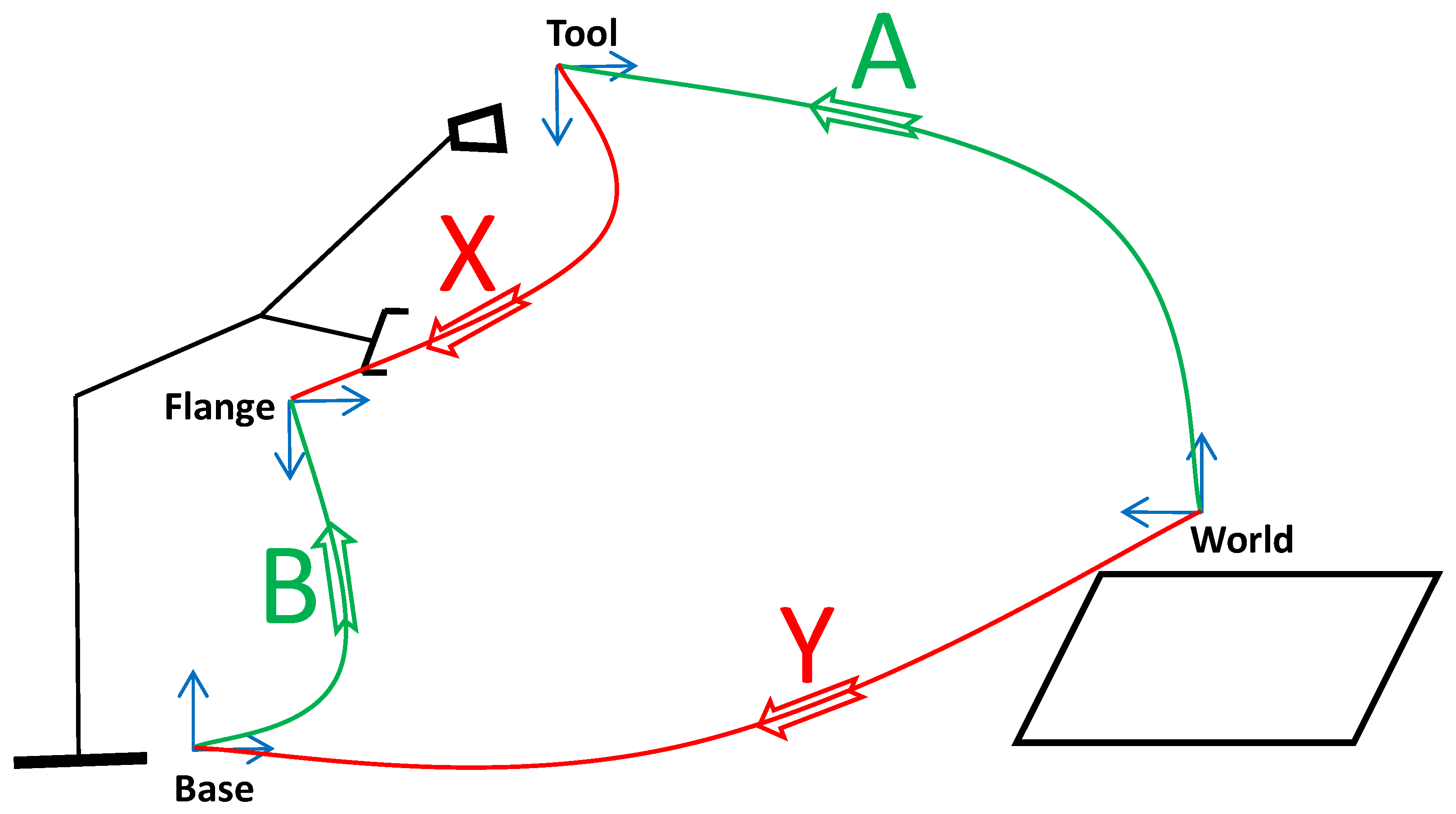




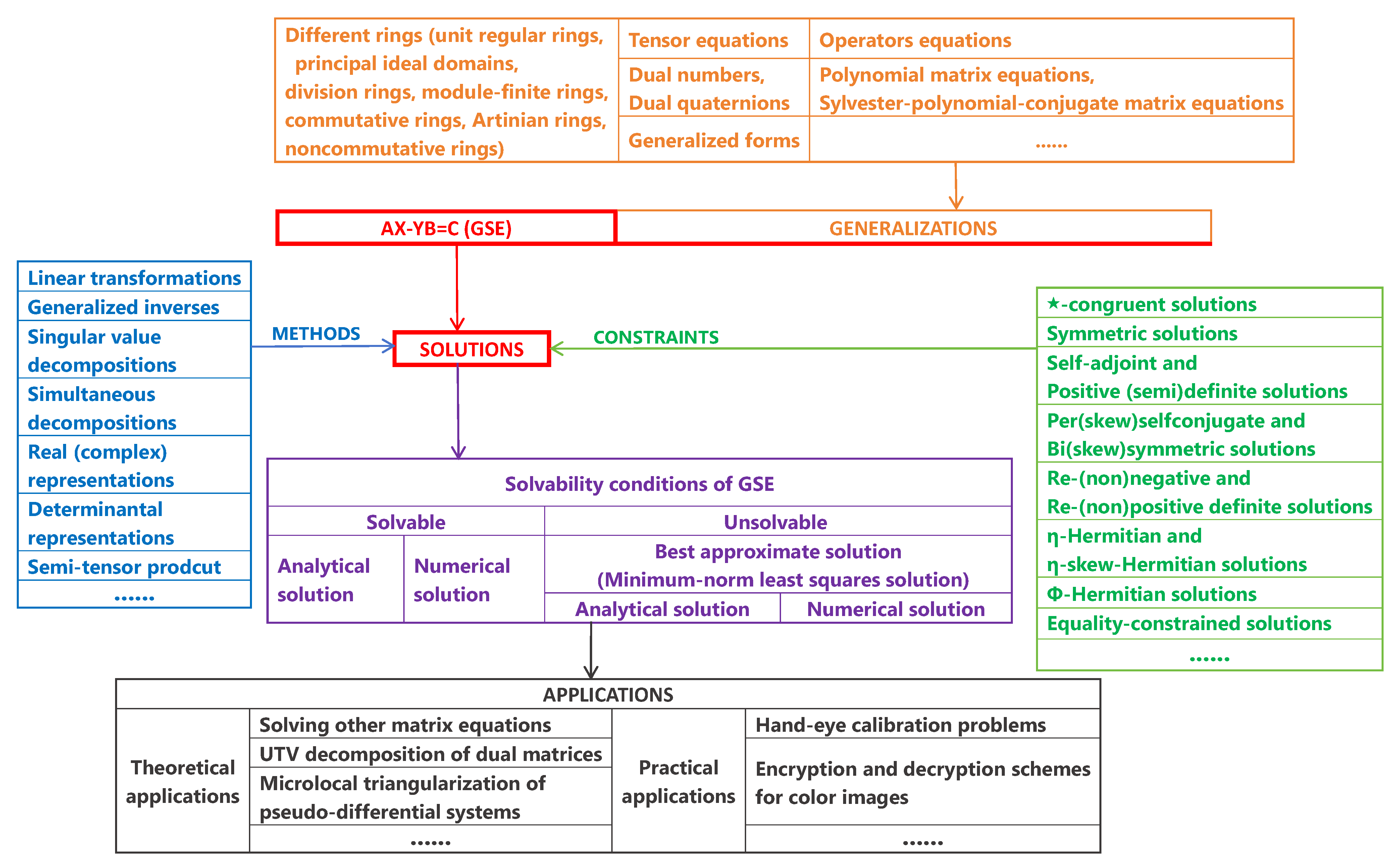
| Full Name | Abbreviation |
|---|---|
| Generalized Sylvester equation | GSE |
| Roth’s equivalence theorem | RET |
| Moore–Penrose inverse | MP inverse |
| Singular value decomposition | SVD |
| Generalized singular value decomposition | GSVD |
| Canonical correlation decomposition | CCD |
| Semi-tensor product | STP |
| Second matrix–matrix semi-tensor product | MM-2 STP |
| Conjugate gradient least-squares algorithm | CGLSA |
| Alternating direction method | ADM |
| Relaxed gradient-based iterative algorithm | RGI algorithm |
| Color Image | SSIM |
|---|---|
| Bike 1 | 0.99 |
| Bike 2 | 0.99 |
| Number | Remark Number | Open Problem |
|---|---|---|
| 1 | Remarks 15 and 16 | Cramer’s rule for GSE only through coefficient matrices (partially solved) |
| 2 | Remark 18 | Solving GSE under STP (or MM-2 STP) |
| 3 | Remark 22 | Solving the GSE via -representation, -representation, -representation, and vectorization properties of STP, respectively, |
| 4 | Remark 35 | Discussing RET from a single common property of Euclidean domains and unit regular rings (partially solved) |
| 5 | Remark 43 | Research on the fundamental properties and applications of combinations of different types of quaternions and dual numbers |
| 6 | Remark 47 | Investigating GSE tensor equations under different tensor products and quaternion algebras. |
| 7 | Remark 60 (4) | Exploring converse problems for Lemmas 11 and 12 of [241] |
| 8 | Remark 63 | Solving the restricted system (101) |
| 9 | Remark 64 | Solving the system (104) (partially solved) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.-W.; Gao, J. A Comprehensive Review on the Generalized Sylvester Equation AX − YB = C. Symmetry 2025, 17, 1686. https://doi.org/10.3390/sym17101686
Wang Q-W, Gao J. A Comprehensive Review on the Generalized Sylvester Equation AX − YB = C. Symmetry. 2025; 17(10):1686. https://doi.org/10.3390/sym17101686
Chicago/Turabian StyleWang, Qing-Wen, and Jiale Gao. 2025. "A Comprehensive Review on the Generalized Sylvester Equation AX − YB = C" Symmetry 17, no. 10: 1686. https://doi.org/10.3390/sym17101686
APA StyleWang, Q.-W., & Gao, J. (2025). A Comprehensive Review on the Generalized Sylvester Equation AX − YB = C. Symmetry, 17(10), 1686. https://doi.org/10.3390/sym17101686







