Abstract
Symmetry is an essential characteristic in both solution spaces and cloud task scheduling loads, as it reflects a structural balance that can be exploited to enhance algorithmic efficiency and robustness. In recent years, with the rapid development of 6G networks, the number of tasks requiring computation in the cloud has surged, prompting an increasing number of researchers to focus on how to efficiently schedule these tasks to idle computing nodes at low cost to enhance system resource utilization. However, developing reliable and cost-effective scheduling schemes for cloud computing tasks in real-world environments remains a significant challenge. This paper proposes a method for cloud computing task scheduling in real-world environments using an improved dhole optimization algorithm (IDOA). First, we enhance the quality of the initial population by employing a uniform distribution initialization method based on the Sobol sequence. Subsequently, we further improve the algorithm’s search capabilities using a sine elite population search method based on adaptive factors, enabling it to more effectively explore promising solution spaces. Additionally, we propose a random mirror perturbation boundary control method to better address individual boundary violations and enhance the algorithm’s robustness. By explicitly leveraging symmetry characteristics, the proposed algorithm maintains balanced exploration and exploitation, thereby improving convergence stability and scheduling fairness. To evaluate the effectiveness of the proposed algorithm, we compare it with nine other algorithms using the IEEE CEC2017 test set and assess the differences through statistical analysis. Experimental results demonstrate that the IDOA exhibits significant advantages. Finally, to verify its applicability in real-world scenarios, we applied IDOA to cloud computing task scheduling problems in actual environments, achieving excellent results and successfully completing cloud computing task scheduling planning.
Keywords:
cloud computing; task scheduling; dhole optimization algorithm; IEEE CEC2017; cost optimization MSC:
68W50
1. Introduction
With the rapid development of cloud computing technology, an increasing number of computing tasks are being scheduled to cloud platforms for processing [1]. In many task scheduling problems, symmetry naturally exists in different forms, such as tasks with similar computational characteristics, resources with equivalent capabilities, or inter-changeable execution orders. Recognizing and exploiting such symmetrical structures can reduce redundant computations, simplify the scheduling search space, and provide new perspectives for designing efficient scheduling strategies. Cloud task scheduling is a core issue in cloud computing resource management. Its essence lies in using reasonable algorithms and strategies to efficiently map heterogeneous, dynamic tasks submitted by users to computing, storage, and network resources in the cloud environment, thereby achieving predetermined optimization objectives. Efficient cloud task scheduling not only directly impacts the utilization rate of computing resources and task execution efficiency but also affects system energy consumption, response time, and service quality assurance. Given the heterogeneous nature of computing resources, the diverse and dynamically changing task types in cloud environments, reasonable task scheduling strategies are of great significance for enhancing the overall performance of cloud platforms, reducing operational costs, and supporting large-scale complex applications. Therefore, research on cloud task scheduling has become a current research hotspot.
Currently, researchers mainly use reinforcement learning algorithms and intelligent optimization algorithms to solve cloud task scheduling problems. For example, Wang et al. proposed a real-time performance-aware task scheduling method based on reinforcement learning, which optimizes task load variance within service quality constraints by simultaneously considering load fluctuations and response times to minimize response times [2]. Zhu et al. also used reinforcement learning algorithms for cloud task scheduling, which made more effective use of the computing power of edge nodes, significantly reduced average energy consumption and latency, and improved the energy efficiency of edge cloud systems [3]. To advance the resolution of resource instance scheduling problems and enhance solution quality, Shu et al. proposed a novel hybrid algorithm named DWOA [4], building upon Whale Optimization Algorithm (WOA) and Deep Reinforcement Learning (DRL). This approach trains a model to learn exploration and exploitation insights from historical data within the WOA search process, thereby guiding the algorithm’s exploration and exploitation phases to accelerate convergence speed and improve solution quality. Zhang et al. proposed a multi-objective edge cloud resource scheduling model based on four objectives: task completion time, cost, energy consumption, and re- liability [5]. They introduced a hybrid approach combining deep reinforcement learning (DRL) and multi-objective optimization. Using three real-world datasets, they demonstrated that the proposed hybrid DRL and multi-objective optimization design outperforms existing design methods. However, due to the fact that reinforcement learning relies on a large number of interactions with the environment during training, it incurs high computational costs and converges slowly. In high-dimensional states, the model is prone to getting stuck in local optima and has high requirements for environment modelling and reward function design. Therefore, many researchers are considering using intelligent optimization algorithms as the primary research algorithm for cloud task scheduling.
In terms of using intelligent optimization algorithms to solve cloud task scheduling problems, Qin et al. improved the RTH algorithm and applied it to solve task scheduling problems in real cloud environments. Experiments showed that the improved RTH algorithm performed well in terms of task completion time, resource utilization, and system load balancing [6]. Wu et al. combined RNN with PSO to convert online task scheduling into offline scheduling, effectively reducing the average task completion time and demonstrating the superiority of optimization algorithms in solving cloud task scheduling problems [7]. Chowdhary et al. addressed the issue that traditional task scheduling algorithms often struggle to handle the complexity and volatility of cloud computing environments by employing an enhanced bald eagle optimization algorithm to schedule tasks on selected virtual machines. Performance comparisons were conducted across two distinct scenarios, evaluating load balancing, cost, resource utilization, and makespan metrics against existing methods. The results demonstrated superior performance compared to existing methods, establishing it as an efficient task scheduling method for cloud computing [8]. To address complex user requirements in cloud service composition problems, Hong et al. proposed a novel Mutation-Wavelet-Optimization Algorithm (MWOA) based on uniform mutation and eagle strategies for solving the QoS-CSC problem [9]. The algorithm employs the Eagle strategy to balance MWOA’s global and local search capabilities, utilizes Levy flight to enhance WOA’s global search ability, and achieved significant results on the QoS-CSC problem. In addition, Fractional Grey wolf Multi-objective optimization-based Task Scheduling strategy [10], Collision-Avoid based on Cloud task Scheduling [11], and improved version of the Harris Hawk optimization algorithm [12] are algorithms developed based on intelligent optimization algorithms for cloud computing task scheduling.
Although significant research progress has been made in cloud task scheduling, several challenging issues remain unresolved. First, the heterogeneous and dynamic nature of resources in cloud environments makes it difficult for scheduling strategies to adapt in real time to changes in resource states. Second, the diversity of task types and their interdependencies pose a significant challenge in optimizing overall performance while ensuring task completion deadlines are met. Furthermore, as cloud platforms continue to expand in scale, task scheduling problems exhibit highly complex combinatorial optimization characteristics, making it difficult for traditional algorithms to obtain global optimal solutions within an acceptable timeframe. Additionally, the scheduling process must also consider multiple objective constraints such as system energy consumption, cost, and service quality, further increasing the complexity of the problem. Therefore, designing efficient, intelligent, and scalable scheduling methods remains a critical issue that requires urgent attention in current research.
DOA is a novel meta-heuristic algorithm proposed by Mohammed et al. in 2025 for solving optimization problems. It draws inspiration from the social and hunting activities of dholes, particularly their vocal communication and coordination techniques. DOA simulates this sound-driven adaptive decision-making behavior, improving the balance between exploration and exploitation in optimization algorithms, thereby achieving better performance. Experimental evaluations show that compared to other optimization algorithms, DOA has significant advantages in terms of convergence time and robustness. In particular, the advantages of DOA are more evident for high-dimensional complex problems. Since the cloud task scheduling problem addressed in this paper also belongs to the category of high-dimensional complex problems, DOA is selected as the basic solution in this paper.
However, NFL’s theorem states that every algorithm has its own scope of application, and no single algorithm can be applied to all problems with good results. Therefore, when using intelligent optimization algorithms to solve their own problems, many researchers usually make targeted improvements. For example, to solve the problem of three-dimensional drone path planning, Xie et al. proposed three improvement strategies for the original RIME algorithm to make it more suitable for solving three-dimensional drone path planning problems [13]. In order to assess the value of data assets, Zhou et al. addressed the shortcomings of DBO and improved it using Levy’s strategy, making the algorithm more suitable for the problems they needed to solve [14].
Based on the above research, this paper proposes an improved DOA (IDOA) for global optimization and cloud task scheduling problem. The specific contributions are as follows.
- A uniform initialization method based on the Sobol sequence is utilized to enhance the quality of the population, allowing the algorithm to explore more promising spaces.
- Propose a sine elite dholes swarm search method based on adaptive factors to enable the algorithm to better utilize the current high-quality solution, rather than being limited to the current optimal solution, thereby enhancing the algorithm’s ability to escape local optima and strengthen its ability to solve high-dimensional complex problems.
- A boundary control method based on random mirror disturbance is proposed, enabling individuals that have crossed the boundary to be better mapped to the search space, thereby enhancing the algorithm’s exploration capabilities.
- The algorithms were qualitatively analyzed using 30 test functions from the IEEE CEC2017 test set and compared with 9 other algorithms to obtain competitive results. Most importantly, the algorithms were statistically analyzed to fully analyze the superior performance of IDOA.
- Apply IDOA to solve cloud computing task scheduling problems in real environments to prove its engineering applicability.
The next part of this paper is organized as follows: Section 2 gives a brief introduction of the original DOA; Section 3 gives a detailed introduction of the three improvement strategies proposed in this paper; Section 4, we apply the IDOA in global optimization experiments and analyze the experimental results in detail; Section 5, we apply the algorithm to the real environment cloud computing task scheduling problems and provide a comprehensive analysis of its advantages and disadvantages; in Section 6, we summarize and outlook the work in this paper to clarify the direction of future work.
2. Dhole Optimization Algorithm (DOA)
In this section, since the algorithm proposed in this paper is an improvement on the DOA, we provide a brief introduction of the DOA [15]. The DOA is inspired by the hunting behaviour of the Dhole. The Dhole is a social animal that typically communicates through vocalizations to hunt. The DOA is modelled primarily on the vocalization behaviour of the dhole to produce an efficient optimization algorithm, the details of which are as follows.
2.1. Algorithm Initialization
Similarly to most meta-heuristic algorithms, DOA uses random initialization of the population. The population matrix of DOA is represented by Equation (1).
where represents the Dhole population, represents -th dhole, which is the candidate solution, represents the population size, which is the number of Dhole, and represents the problem dimension.
2.2. Searching Stage
Dholes are social animals that hunt to sustain themselves. When searching for prey, they first need to define their prey. The mathematical modelling formula is shown below:
Among them, indicates the optimal position of the dhole in the current population, and indicates the optimal position of the dhole throughout the entire iteration process. After identifying prey, dholes decide whether to hunt based on the number of members in their group. Since the number of dholes in a pack is random, the number of dhole members is defined as follows:
where represents a random value between 0 and 1. When the number of members is less than 10 and the vocalization of dholes is less than 0.5, dholes are obliged to approach the prey and decide whether to hunt it. This behavioural mechanism can be expressed as:
where the vocalization of dholes is a random value between 0 and 1, represents the current iteration number, represents the current iteration position of the dhole, and represents the decreasing slope, which can be expressed as:
where represents the maximum number of iterations. The ultimate goal of the dhole is to hunt its prey. At this stage, the dhole first searches for prey, then surrounds it once it has been located, and finally attacks and kills it.
2.3. Encircling Stage
After searching for prey, dholes will work together to surround it, using their agility and vocal communication to encircle the prey. This vocal communication allows them to block the prey’s escape routes as much as possible. When the vocalization is less than 0.5 and the number of members is greater than 10, dholes begin to surround their prey. The mathematical model is shown below:
where represents a random individual in Dholes, which can be expressed as:
2.4. Attacking Stage
After dholes surround their prey, they look for opportunities to attack. During the attack phase, dholes first assess the size of their prey. If the prey is too large to be killed with a single strike, they will attack multiple times until it is dead. Otherwise, a single attack will suffice. The dholes’ attack behaviour varies depending on the size of the prey, which can be defined as:
where represents the prey factor, with a constant value of 3, indicates the largest prey. represents the fitness value of the position of the -th dhole, and represents the fitness value of the position of the prey. When dholes surround their prey, they assess its size. If , it means that the prey is too large, and the dholes will slowly injure it in order to kill it. This behaviour mechanism can be modelled as follows:
where indicates weak prey, and dholes will kill the prey on the second or third attack. The cosine and sine functions are used to simulate this process as follows:
where indicates the appropriate time for hunting, which can be expressed as:
where indicates the optimal number of members to hunt, indicates external environmental factors, with values ranging from 0 to 1, indicates hunting efficiency, and indicates control over prey size in different situations. If , dholes can kill it with a single blow. This process can be modelled as follows:
The pseudocode of the DOA is outlined in Algorithm 1.
| Algorithm 1: The pseudo-code of the DOA |
| 1: Begin |
| 2: Initialize: the relevant parameters and Dholes population. |
| 3: Calculate fitness value and get the best solutions. |
| 4: While do |
| 5: Define PMN and prey by Equations (2) and (3) |
| 6: Searching stage: |
| 7: Update the population by Equation (4) |
| 8: Encircling stage: |
| 9: Update the population by Equation (6) |
| 10: Attacking stage: |
| 11: If |
| 12: Update the population by Equation (10) |
| 13: else |
| 14: Update the population by Equation (12) |
| 15: |
| 16: End while |
| 17: return best solution |
| 18: end |
3. Proposed IDOA
The original DOA has good performance and a simple structure; however, when faced with complex cloud task scheduling problems, it is prone to local optima and other difficulties. To solve these problems, we propose an improved version of the DOA. The details are as follows.
3.1. A Uniform Initialization Method Based on the Sobol Sequence
In the original DOA, conventional random initialization is used to obtain the initial population. Although this method is simple and easy to implement, it often results in uneven distribution of initial solutions in the search space, which may lead to sparse or even missing samples in certain regions, thereby causing the algorithm to easily get stuck in local optima. In contrast, in 1967, Russian mathematician Ilya M. Sobol proposed a sequence of random numbers with uniform distribution properties that can generate more uniformly distributed sample points in high-dimensional spaces, enabling the initial population to cover the search space more comprehensively. This low-variance sequence initialization method not only enhances the global nature of the search but also improves the algorithm’s exploration efficiency in the early stages, providing a better starting point for subsequent iterative optimization and thereby enhancing the overall performance of the intelligent optimization algorithm. The Sobol sequence matrix can be represented as follows [16]:
where indicates sample points generated by the Sobol sequence. Then, map it onto search space , which can be represented as follows:
where and represent the lower bound and upper bound of the problem, respectively. Finally, the population was initialized with a uniform distribution based on the Sobol sequence, as shown below. Figure 1 shows the initial population distribution in two-dimensional and three-dimensional spaces for two scenarios: random initialization of DOA and uniform initialization of IDOA based on the Sobol sequence. As can be seen from the figure, the population distribution based on uniform initialization using the Sobol sequence is more uniform, providing a better initial population for subsequent population exploration and development.
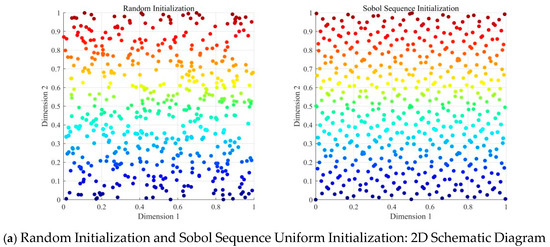
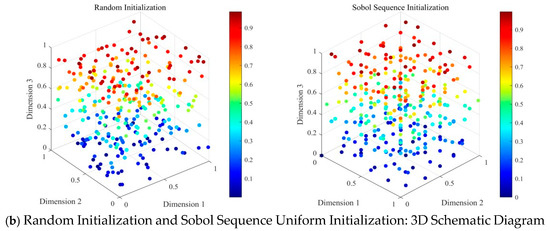
Figure 1.
Graphical description of uniform initialization method based on the Sobol sequence.
3.2. A Sine Elite Dholes Swarm Search Method Based on Adaptive Factors
In the original DOA, during the exploration phase, the position of the new Dhole is mainly updated based on the current optimal solution and the optimal solution to date. Although this update method can converge quickly, there is a high possibility of getting stuck in a local optimal solution during the exploration phase. Therefore, in this subsection, we propose a sine elite Dholes search method based on adaptive factors. This method retains the idea of the original DOA using the optimal solution for updating, participates in position updating by obtaining the mean of the current five optimal solutions, and better avoids the algorithm falling into local optimal solutions by controlling the scale of position updating based on adaptive sine parameters. The specific position updating method is shown below:
where represents the mean of the five optimal solutions, calculated using Equation (17); grants elite Dholes the ability to fly, enabling them to explore more effectively during the exploration phase, as expressed by Equation (18); and is the sine exploration step size based on the adaptive factor, used to control the movement step size of position updates in each iteration, calculated using Equation (19).
where indicates the position of the Dhole with fitness value ranking in the iteration. represents the shape function of the step size distribution. Referring to the values typically used in papers, we set it to 1.5 in this paper. v is a random variable that follows a standard normal distribution of . is a random variable that follows a standard normal distribution of . is calculated using Equation (20).
where is the gamma function. Figure 2 shows a schematic diagram of the elite Dholes population search method, which shows that the update of new individuals is influenced by the mean of the five optimal solutions, the current position, and the prey position, and through Levy flight, it has randomness of exploration and can better perform exploration.
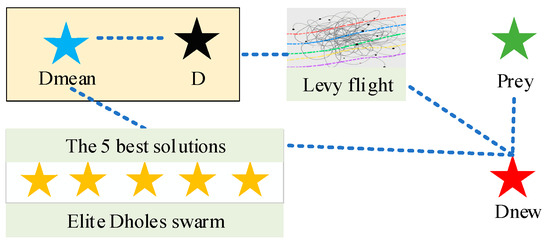
Figure 2.
Elite dholes swarm search method Diagram.
3.3. Boundary Control Method Based on Random Mirror Image Perturbation
For an optimization algorithm, boundary control is an indispensable part and is very important for ensuring that the obtained solution is feasible. A good boundary control method can greatly improve the stability of algorithm convergence. In DOA, the truncation method is used for boundary control, i.e., when the obtained solution exceeds the boundary, it is set equal to the boundary value. Although this method is simple, it is very limited in terms of algorithm performance. Therefore, in this subsection, we propose a boundary control method based on random mirror image perturbation to control the position boundaries of Dholes during the position update process of the algorithm.
Random mirror perturbations can mirror solutions that exceed the boundaries back into the feasible domain and add perturbations to prevent individuals from concentrating at boundary points, thereby greatly improving the algorithm’s global optimization performance and convergence robustness. The specific mirror perturbations are represented by Equation (21).
where represents the mirror image solution of the outlier, which is calculated using Equation (22).
Figure 3 shows a schematic diagram of the random mirror perturbation strategy. When an individual crosses the boundary, instead of using the truncation method to return it to the boundary, the mirror method is used to return the individual to the search space. To increase the randomness of the algorithm and enable it to explore better, random perturbations are added so that even individuals that cross the boundary at the same position can be mapped to different positions in the search space, thereby ensuring the diversity of the algorithm’s population. Figure 4 depicts the flowchart of the IDOA.
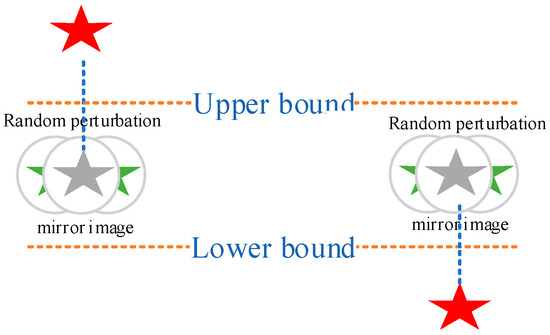
Figure 3.
Boundary control method based on random mirror image perturbation Diagram.
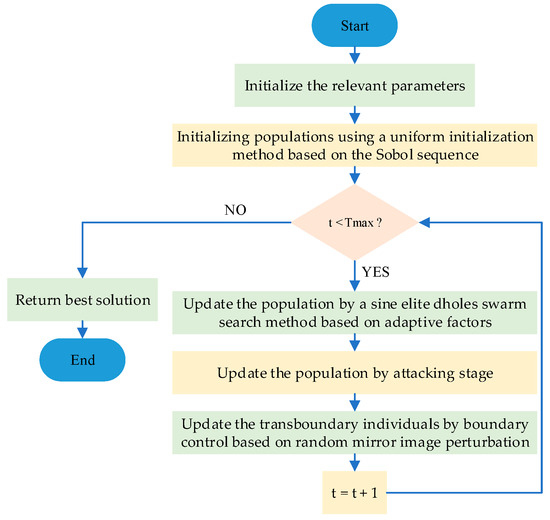
Figure 4.
Flowchart of IDOA.
3.4. Computational Complexity Analysis
For an algorithm, discussing performance gaps without considering computational cost is not advisable. Typically, we need to strike an acceptable balance between computational cost and performance. Therefore, this subsection analyzes the computational complexity of the proposed IDOA. In IDOA, computational complexity primarily stems from population initialization and position update iterations. During population initialization, the computational complexity is. For position updates within the population, the computational complexity is also . In summary, IDOA exhibits a computational complexity of . Similarly to the DOA, our improvements do not increase the computational complexity of DOA by an order of magnitude.
4. Experimental Results and Detailed Analyses
In this section, to evaluate the performance of the IDOA proposed in this paper, we conduct a global optimization test using the CEC2017 test set [17]. First, we provide a brief introduction to the test set functions and detail the settings for the comparison algorithms and parameters; then, we conduct qualitative and quantitative analyses of the IDOA; finally, to fully validate the superior performance of the IDOA, we perform statistical analyses. To ensure the fairness of the experiments, we set the population size for all comparison algorithms to 50 and the maximum number of iterations to 1000 for experimental analysis. All experiments in this paper were conducted on a 12th Gen Intel® Core™ i9-12900KF processor running at 3.20 GHz, using MATLAB 2023a on Windows 11 Professional.
4.1. Benchmark Test Functions
The CEC2017 test set is a standard set of test functions commonly used by researchers to evaluate algorithm performance. It consists of 30 test functions, which are categorized into four major types based on their characteristics: 3 single-peak functions, 7 multi-peak functions, 10 mixed functions, and 10 composite functions. Single-peak functions are primarily used to test the convergence speed of algorithms, multi-peak functions are primarily used to test the ability of algorithms to escape local optima, mixed functions are primarily used to test the robustness and complex search capabilities of algorithms, and composite functions are primarily used for comprehensive testing of global performance. Overall, the CEC2017 test set serves as a benchmark platform closely aligned with real- world complex optimization problems, encompassing single-peak, multi-peak, mixed, and composite functions. It comprehensively evaluates an optimization algorithm’s convergence speed, ability to escape local optima, robustness, and global performance. Therefore, this paper selects CEC2017 as the test set for global optimization.
4.2. Competitor Algorithms and Parameters Setting
In this section, we compare the algorithm proposed in this paper with nine other optimization algorithms to evaluate the performance of IDOA. The algorithms used for comparison include Particle Swarm Optimization (PSO), Snake Optimizer (SO), Artificial Gorilla Troops Optimizer (GTO), Dwarf Mongoose Optimization Algorithm (DMO), Gold Rush Optimizer (GRO), Enterprise development-inspired metaheuristic (ED), Genghis Khan Shark Optimizer (GKSO), Improved Grey Wolf Optimizer (IGWO), and Dhole Optimization Algorithm (DOA). Table 1 summarizes the parameter settings of these algorithms for easier reading.

Table 1.
Parameter settings of the comparison algorithms.
4.3. Qualitative Analysis
4.3.1. The Analysis of Population Diversity
In this subsection, we conduct a qualitative analysis of the proposed IDOA [26]. We analyzed the population diversity of IDOA and DOA. Population diversity can effectively prevent individuals in the population from converging too early on local optima, thereby enhancing the algorithm’s global search capability. Therefore, maintaining the diversity of the algorithm population is a very important factor in ensuring the performance of the algorithm. In this subsection, we assess the population diversity of the IDOA, which is calculated using Equation (23).
where denotes the population diversity, denotes the value of the individual in the dimension at the iteration. reflects the degree of dispersion of the entire population relative to the center of mass at the iteration. calculation through Equation (24).
Figure 5 shows the changes in population diversity across three different dimensions on the CEC2017 test set for the two algorithms. From the experimental results, it can be seen that after improving the algorithm using the Sobol sequence uniform distribution method, population diversity shows a significant improvement. In DOA, population diversity decreases rapidly with the number of iterations and eventually stabilizes at a low level. While IDOA also sometimes decreases rapidly, the final diversity it maintains is always higher than that of DOA. This demonstrates that the Sobol sequence uniform distribution method effectively improves the population diversity of the algorithm.
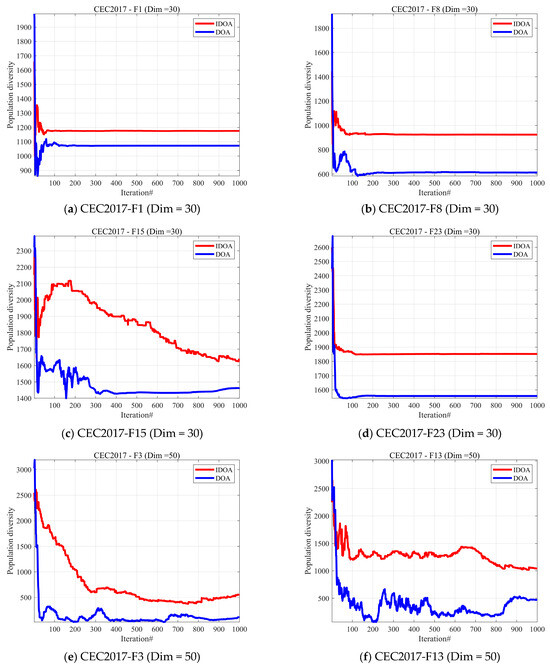
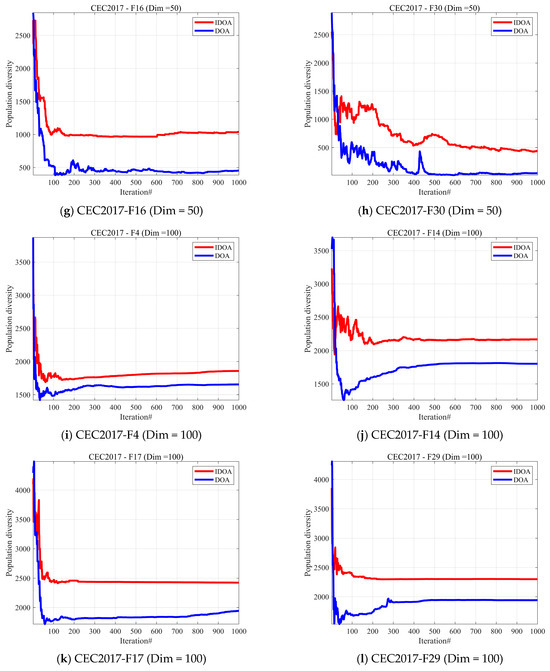
Figure 5.
The analysis of the population diversity of IDOA and DOA.
4.3.2. The Analysis of Parameter Sensitivity
Due to the sensitivity of heuristic algorithms to parameter settings, parameter configuration significantly impacts algorithm performance. Therefore, in this subsection, we conduct a sensitivity analysis on parameter using the CEC2017 test set. We set to values of 0.5, 1, 1.5, 2, and 2.5 for experimental analysis. Figure 6 presents the experimental results under these five parameter configurations.
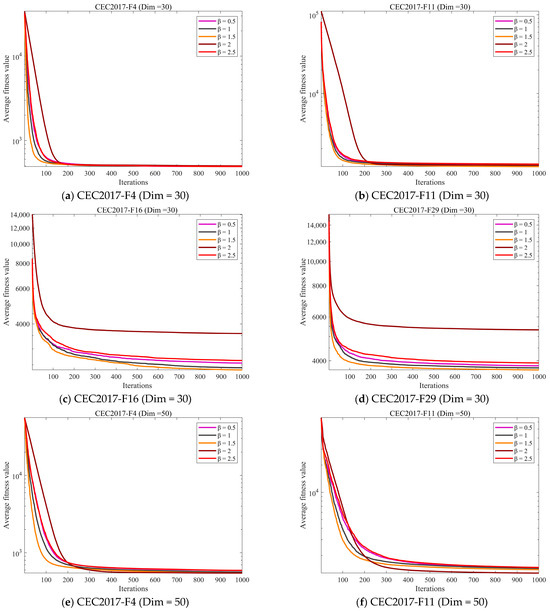
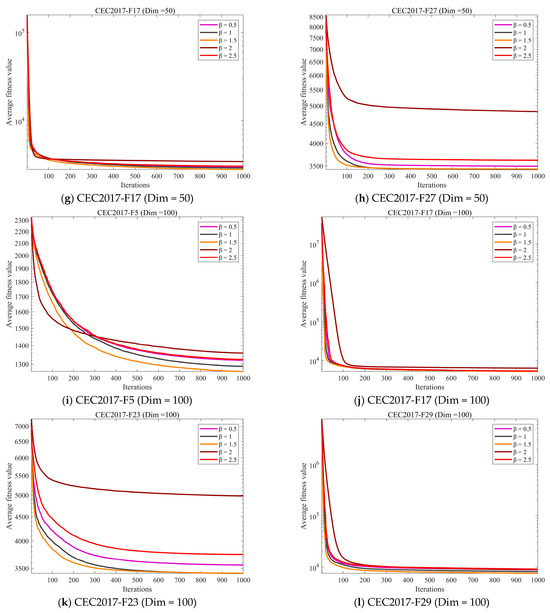
Figure 6.
The analysis of the Parameter Sensitivity of β.
The experimental results demonstrate that for most functions, the algorithm converges regardless of parameter settings, with minimal variation in convergence speed and accuracy. However, for the F16, F23, F27, and F29 functions, the algorithm exhibits poor performance when is set to 2, indicating that the algorithm performs poorly on composite functions when is set to 2. Overall, the algorithm performs optimally when is set to 1.5. Therefore, to better address cloud task scheduling challenges, subsequent experiments will analyze the algorithm with set to 1.5.
4.3.3. The Analysis of Strategy Effectiveness
To investigate whether the three strategies proposed in this paper effectively enhance algorithm performance, this subsection analyzes their efficacy. By comparing the DOA with the original approach and the three enhanced strategies, we demonstrate the validity of the proposed methods. Figure 7 presents the experimental results obtained using the CEC2017 test set. Here, DOA denotes the original algorithm without any enhancement strategies, DOA1 represents the algorithm incorporating the uniform initialization method based on the Sobol sequence, DOA2 denotes the algorithm incorporating the sine elite swarm search method based on adaptive factors, and IDOA denotes the algorithm combining all three strategies.
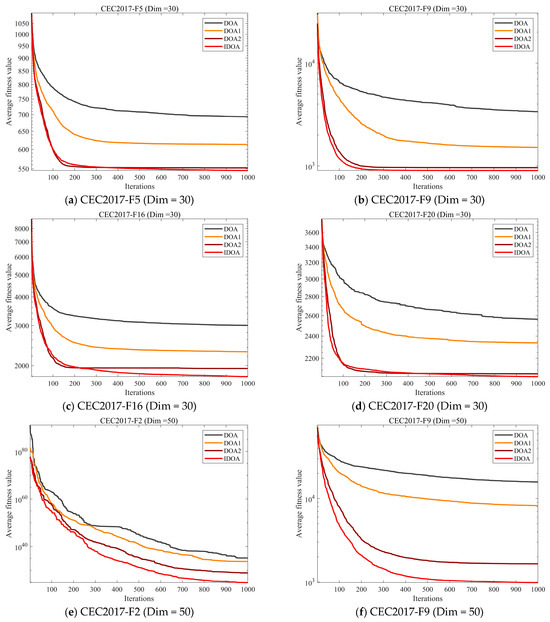
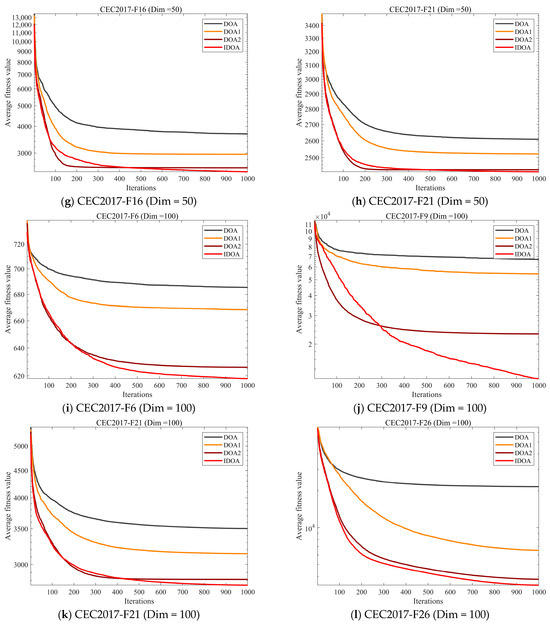
Figure 7.
The analysis of the Strategy Effectiveness.
The experimental results demonstrate that as our improvement strategies are incorporated into the DOA, its performance progressively increases across various functions, confirming the effectiveness of each strategy for DOA. This improvement is particularly pronounced on high-dimensional complex functions. Given that the problem addressed in this paper—cloud task scheduling—also falls under high-dimensional complex problems, IDOA shows great promise for solving cloud task challenges.
4.4. Compare Using CEC 2017 Test Functions
In this section, we evaluate the performance of the IDOA using the CEC2017 test set and compare it with nine other algorithms. The experimental results are shown in Table 2, Table 3 and Table 4. To visualize the convergence speed of the algorithms during the convergence process, the convergence speeds of the 10 algorithms across three dimensions are shown in Figure 6. To further assess the stability of the algorithms when executed multiple times, the box plots of the 10 algorithms after 30 runs are shown in Figure 7.

Table 2.
Results of various algorithms tested on the CEC 2017 benchmark. (dim = 30).

Table 3.
Results of various algorithms tested on the CEC 2017 benchmark. (dim = 50).

Table 4.
Results of various algorithms tested on the CEC 2017 benchmark. (dim = 100).
Figure 8 shows the convergence curves of 10 comparison algorithms across three dimensions on the CEC2017 test set. To avoid experimental randomness, each algorithm was run independently 30 times, and the experimental results were averaged over the 30 runs. From the experimental results, it can be seen that although the average convergence values of many algorithms are comparable to those of IDOA on the 30-dimensional F29 and 100-dimensional F16 and F27, their convergence speeds are slower than those of the IDOA. More importantly, in many test functions, IDOA demonstrates significant performance advantages over all comparison algorithms in terms of both convergence speed and convergence accuracy.
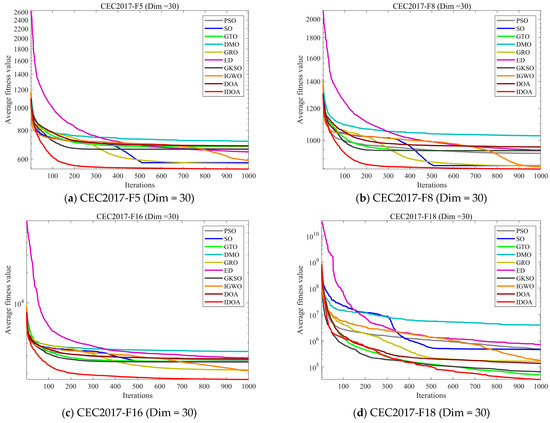
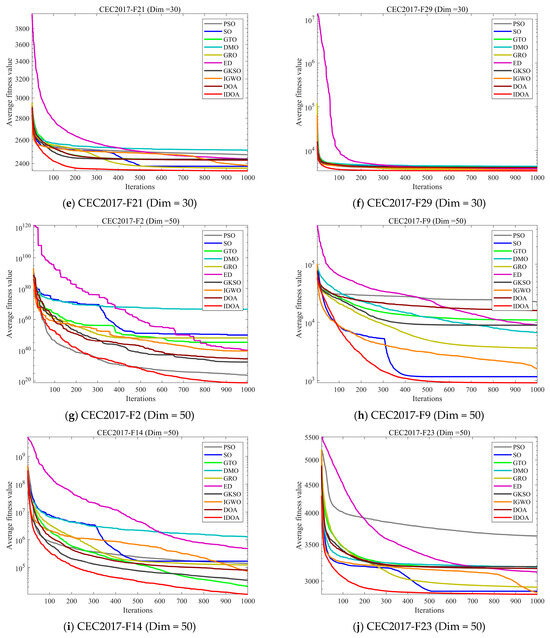
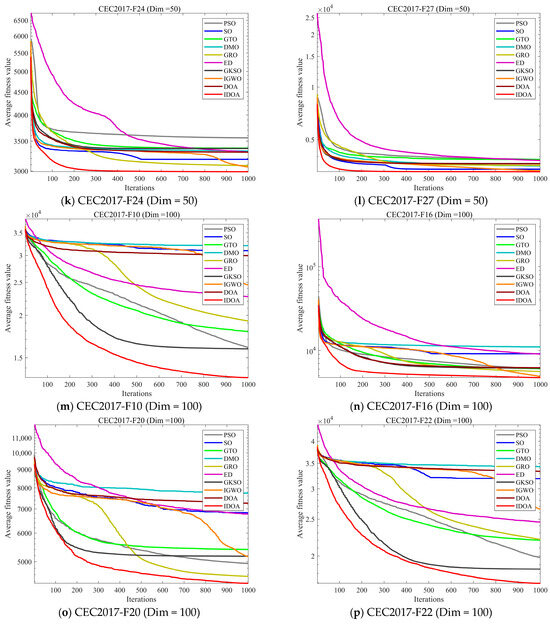
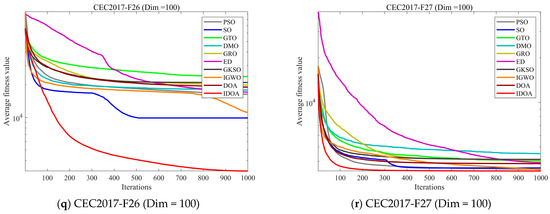
Figure 8.
Comparison of convergence speed of different algorithms on CEC2017 test set.
Figure 9 shows the box plots of 10 algorithms running independently 30 times. From the experimental results, it can be seen that although IDOA does not obtain the optimal value in some cases, it is the most stable, with the smallest fluctuation in 30 runs, demonstrating that IDOA has extremely strong stability.
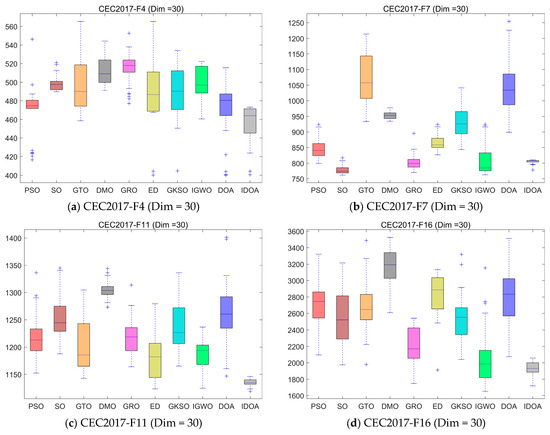
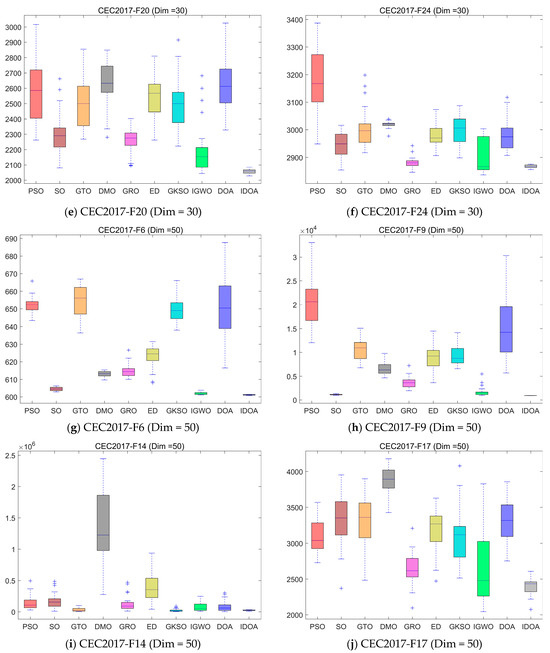
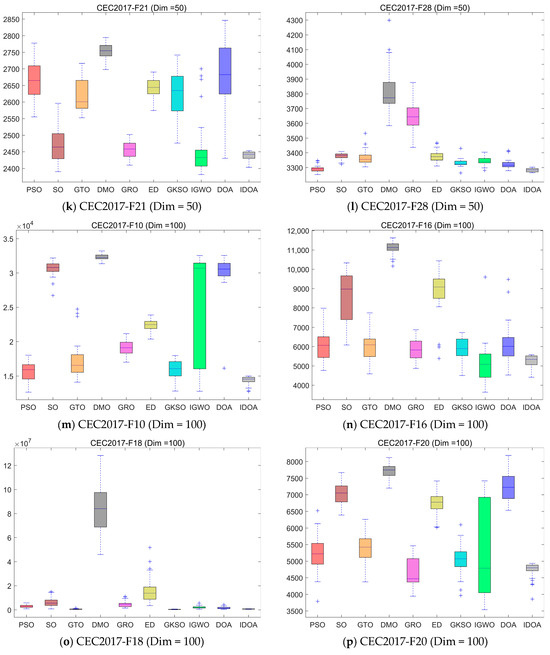
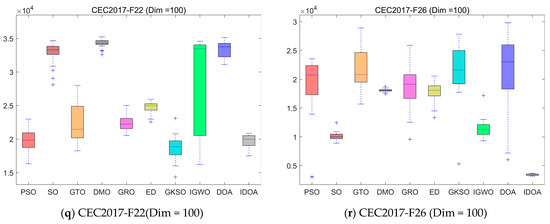
Figure 9.
Boxplot analysis for different algorithms on the CEC2017 test set.
Table 2, Table 3 and Table 4 show the mean and standard deviation of fitness for each algorithm running independently 30 times in three dimensions, where mean represents the average value of 30 runs and std represents the standard deviation of 30 runs. The experimental results show that although IDOA cannot achieve good results in some functions, its results are still among the top of all comparison algorithms and its standard deviation is relatively small, indicating that although IDOA sometimes cannot find the optimal solution, its performance is very stable, which is very important when we deal with practical problems.
4.5. Statistical Analysis
In order to determine whether the differences in performance between the various algorithms are statistically significant, in this subsection, we conducted statistical analysis on IDOA, performing Wilcoxon rank sum test [27] and Friedman mean rank test [28]. The details are as follows:
4.5.1. Wilcoxon Rank Sum Test
In this subsection, we conducted Wilcoxon rank sum test on the IDOA. It is a non-parametric test method that compares the ranks of two independent samples to determine whether there is a significant difference in their distributions. Its advantage lies in the fact that it does not require strict assumptions about the data distribution, making it robust and widely applicable. We set the significance level at 0.05. When p < 0.05, the null hypothesis is rejected, indicating a significant difference between the two algorithms. Otherwise, the null hypothesis is accepted, indicating no significant difference between the two algorithms. The p-value statistics for the 10 algorithms across the three dimensions are presented in Table 5, Table 6 and Table 7. The experimental results show that the IDOA proposed in this paper has significant advantages over other comparison algorithms.

Table 5.
p-values for various algorithms on the CEC 2017 (dim = 30).

Table 6.
p-values for various algorithms on the CEC 2017 (dim = 50).

Table 7.
p-values for various algorithms on the CEC 2017 (dim = 100).
4.5.2. Friedman Mean Rank Test
In this subsection, we performed the Friedman Mean Rank Test on IDOA. The Friedman Mean Rank Test is a non-parametric statistical test method primarily used to compare whether there are significant differences between multiple samples. We can judge the relative performance of algorithms based on their F-ranks obtained on various test functions.
Figure 10 shows the final rankings of the 10 algorithms on the CEC2017 test set. The experimental results show that IDOA ranks lowest on average in all three dimensions of the CEC2017 test set, meaning that IDOA ranks first among all comparison algorithms. Among them, in the case of 30 dimensions, IDOA ranked first, while DOA only ranked seventh, proving that the improved strategy proposed in this paper has a significant effect. In the case of 50 and 100 dimensions, the DOA ranking is 8th, indicating that the DOA performs poorly in high dimensions, while the IDOA performs well not only in low dimensions but also in high dimensions.
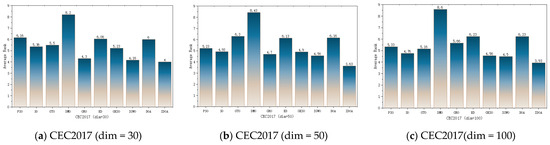
Figure 10.
The ranking of different algorithms on CEC2017.
5. IDOA for Cloud Task Scheduling
To address the issue of cloud task scheduling, this section first models the multi-objective task scheduling problem and then conducts simulation experiments using IDOA. The details are as follows.
5.1. Cloud Computing Task Scheduling Model
Cloud task scheduling is a core issue in cloud computing resource management [29]. It refers to the process of mapping tasks submitted by users to computing resources in the cloud computing environment through certain scheduling strategies and algorithms to ensure that tasks are processed in a timely manner.
In this subsection, we are given a set of n tasks and assign them to m available virtual machines, where represents computing resource nodes, represents n computing tasks, and . Task scheduling under cloud computing can be represented by the following matrix.
In matrix , when , it indicates that task is executed on virtual machine . This section defines the attributes of each resource node, including processing capacity, initial memory, and resource bandwidth. Without loss of generality, the resources of a virtual machine can be represented as processing capacity , load capacity , and resource bandwidth . The computational requirements, size, and resource bandwidth requirements of each task can be expressed as . In summary, time costs, load costs, and price costs can be expressed as follows:
Among them, represents the value of the -th task, represents the value of the -th virtual machine, represents the value of the -th task, represents the value of the -th virtual machine, represents the value of the -th task, and represents the value of the -th virtual machine. Since the values of the three indicators vary greatly, they need to be normalized when used in the fitness function. The normalization of the above three objective functions can be expressed as:
In summary, the objective function in this section can be expressed as:
where , , and represent the weight values of , , and , respectively, and . Therefore, is the optimal scheme for cloud computing task scheduling.
5.2. Experimental Parameter Settings
In this subsection, to ensure fair comparisons among experiments, we provide a detailed introduction to the experimental parameters for the cloud task scheduling problem. We conducted experimental simulations using MATLAB 2023a. Performance analysis encompassed evaluation metrics including time, load, and price cost, with the comprehensive cost calculated via weighted summation of these three indicators. Parameter configurations for virtual machines and tasks are specified in Table 8, where all task and virtual machine settings were randomly selected within the ranges defined in this table. Additionally, the population size for each method was uniformly set to 50, and the number of virtual machines was fixed at 40. Given the significant impact of iteration count on cloud task performance, a consistent iteration count was required across tests. Therefore, referencing the research by Qin et al., the iteration count was uniformly fixed at 100.

Table 8.
Experimental Parameter Settings.
5.3. Analysis of Experimental Results
In this section, we evaluate the performance of IDOA and compare it with some current methods based on a set of simulation experiments. The metrics we use to evaluate algorithm performance include three metrics: time cost, load cost, and price cost. Finally, the total cost is calculated based on these three costs. The details are as follows:
5.3.1. Weight Sensitivity Analysis
In this section, to assess the impact of each cost component on total costs, we conducted a parameter sensitivity analysis based on weighting. We set the weights for the three cost components to 0.8, 0.1, 0.1; 0.7, 0.2, 0.1; 0.6, 0.2, 0.2; 0.5, 0.3, 0.2; and 0.33, 0.33, 0.33, respectively, for experimental analysis. The results are shown in Figure 11.
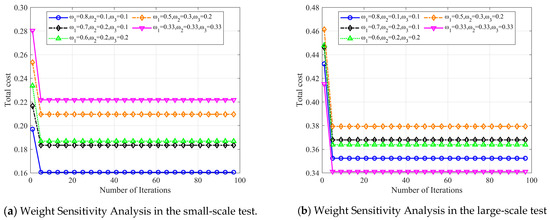
Figure 11.
Weight Sensitivity Analysis.
Figure 11a illustrates how the total cost varies with the number of iterations when the task count is 100. Figure 11b shows how the total cost changes with iterations when the task count is 1000. The experimental results demonstrate that the algorithm converges effectively under various weighting conditions, whether the task count is 100 or 1000. Since cloud computing task scheduling requires comprehensive consideration of multiple factors, we set all three weight values to 0.33 in subsequent experiments.
5.3.2. Comparison with Small-Scale Tasks
In this section, we conduct a detailed evaluation of the algorithm’s performance in small-scale tasks, analyzing the convergence of the algorithm and comparing the costs of dynamic changes in the number of tasks. The details are as follows.
Convergence behavior analysis: In this section, we analyze the convergence of the algorithms. To ensure fairness in the comparison, we fix the number of tasks at 100 and set the maximum number of iterations to 100. We then compare the convergence of IDOA with six other algorithms. The experimental results are shown in Figure 9.
Figure 12a–d show the changes in total cost, time cost, load cost, and price cost as the number of iterations increases, with 100 tasks. The experimental results show that although IDOA achieved a poor result in terms of time cost, it achieved a very good result in terms of total cost. In particular, the load was well balanced, ultimately giving it a significant advantage in terms of total cost among all the algorithms compared.
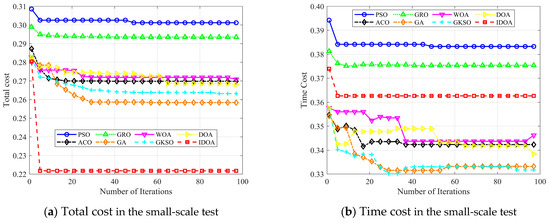
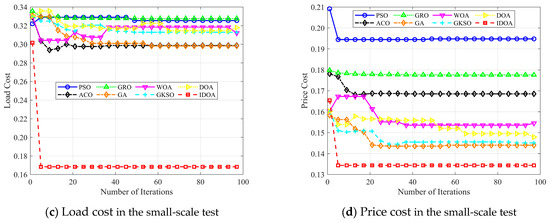
Figure 12.
Best performance achieved by increasing the number of iterations in the small-scale test.
Comparing the costs of dynamic changes in the number of tasks: In this section, we conducted experiments by varying the number of tasks. Figure 13 illustrates the changes in the four metrics of each algorithm as the number of cloud computing tasks increases from 100 to 1000. Figure 13a shows the variation in total cost with changes in the number of tasks. The experimental results indicate that IDOA achieves a significant advantage in 10 out of 10 cases, demonstrating its ability to effectively reduce system costs for small-scale tasks in cloud computing. As shown in Figure 13b–d, all three costs increase with the number of tasks, which is reasonable since an increase in task count leads to higher system workload. All these results indicate that IDOA can significantly improve system memory utilization in a cloud computing environment and achieves the best performance compared to the other six algorithms.
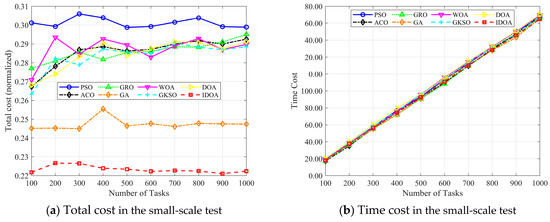
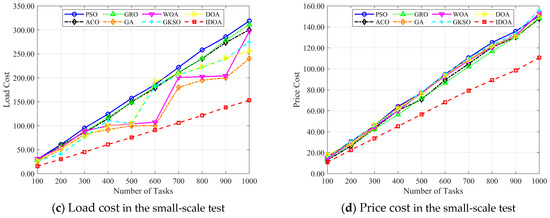
Figure 13.
Best performance achieved of each approach in the small-scale test.
5.3.3. Comparison with Large-Scale Tasks
In this section, we conduct a detailed evaluation of the algorithm’s performance in large-scale tasks, analyzing the convergence of the algorithm and comparing the costs of dynamic changes in the number of tasks. The details are as follows.
Convergence behavior analysis: In this section, we analyze the convergence of the algorithms. To ensure fairness in the comparison, we fix the number of tasks at 100 and set the maximum number of iterations to 100. We then compare the convergence of IDOA with six other algorithms. The experimental results are shown in Figure 14.
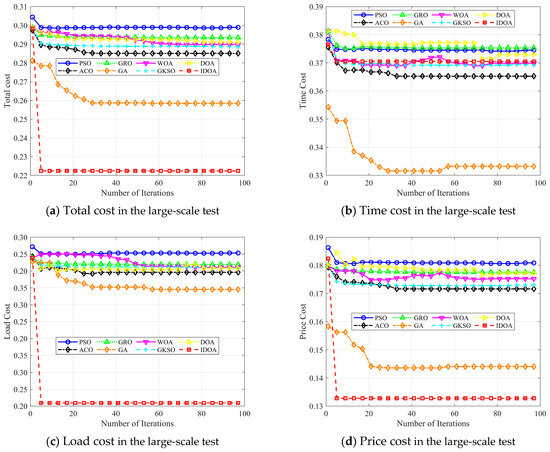
Figure 14.
Best performance achieved by increasing the number of iterations in the large-scale test.
Figure 14 shows the changes in four metrics for seven algorithms as the number of iterations increases when the number of tasks is 1000. From the experimental results, it can be seen that in terms of total cost, IDOA converges quickly and has the lowest convergence rate, achieving the best results. Although its convergence accuracy is relatively low in terms of time cost, it has a significant advantage in terms of load cost and price cost, resulting in a substantial advantage in total cost. Overall, the substantial advantages in terms of load cost and price cost outweigh the disadvantages associated with time cost, thereby neutralizing their impact.
Comparing the costs of dynamic changes in the number of tasks: In this section, we conduct a large-scale experiment by increasing the number of tasks from 1000 to 10,000. Figure 12 shows the changes in four metrics for 10 algorithms in 10 cases.
Figure 15a–d, respectively, show the changes in the four metrics as the number of tasks varies in a large-scale task quantity experiment. From the experimental results, it can be seen that the total scheduling cost of the IDOA is superior to that of the comparison algorithms. Although the time cost is similar to that of other algorithms, its load cost and price cost are significantly lower than those of other algorithms. More importantly, as the number of tasks increases, the gap between the cost of the IDOA and that of other algorithms becomes increasingly larger, further highlighting the superiority of IDOA in addressing large-scale problems.
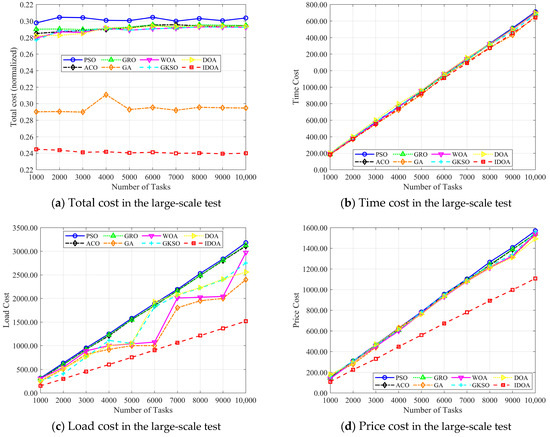
Figure 15.
Best performance achieved of each approach in the large-scale test.
Additionally, in cloud computing task scheduling, task reliability and fairness are also critical considerations. Algorithmic decisions may lead to task starvation or resource imbalance. In this paper, we strive to ensure all resource nodes process every task within a specified timeframe. Thus, task fairness can be considered negligible. However, in practical business scenarios, the reliability and fairness of cloud computing scheduling remain essential concerns. We will incorporate these factors into future research.
6. Conclusions
In this paper, we propose an improved DOA task scheduling method. First, we enhance the quality of the initial population through a uniform distribution initialization method based on the Sobol sequence, laying a solid foundation for the algorithm’s subsequent exploration and development. We also improve the algorithm’s ability to escape local optima and solve high-dimensional complex problems through an elite population update strategy and a random mirror perturbation control strategy. Then, to test the performance of IDOA, we conduct a detailed qualitative and quantitative analysis of the algorithm using the CEC2017 test set. The experimental results demonstrate that the algorithm achieves significant advantages on the test set. Finally, we applied the proposed IDOA to cloud computing task scheduling research. The experimental results indicate that IDOA is indeed efficient in searching for optimal scheduling plans. Compared with some commonly used heuristic algorithms, it can significantly improve the efficiency of cloud computing systems in terms of system load and resource utilization.
In the future, based on IDOA’s outstanding performance, we plan to apply it to more complex cloud computing task scheduling research. Our long-term goal is to develop a highly adaptable and efficient cloud computing scheduling system for situations where tasks have varying degrees of complexity. Moreover, the proposed method provides new insights into how symmetry and structural properties within scheduling problems can be exploited to further improve optimization efficiency. By integrating IDOA with other intelligent optimization frameworks and real-time adaptive scheduling mechanisms, the approach has the potential to support large-scale, heterogeneous, and dynamic cloud environments, contributing to both theoretical research and practical applications in next-generation cloud computing.
Author Contributions
Conceptualization, S.X. and W.Z.; methodology, S.X. and W.Z.; software, S.X. and W.Z.; validation, S.X. and W.Z.; formal analysis, S.X. and W.Z.; investigation, S.X. and W.Z.; resources, S.X. and W.Z.; data curation, S.X. and W.Z.; writing—original draft preparation, S.X. and W.Z.; writing—review and editing, S.X. and W.Z.; visualization, S.X. and W.Z.; supervision, S.X. and W.Z.; funding: acquisition, S.X. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Natural Science Foundation of China (52302408), Technology cooperation program of Henan (252102240129), and The Open Project Funding of State Key Laboratory for High Performance Tools (GXNGJSKL202416). Research and Development of Thermal Protection Technology for Hypersonic Vehicles Based on Ultra-High Temperature Composites (Supported by Sichuan Railway College), (Project Number: XZD202403).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abraham, O.; Ngadi, M.; Sharif, J.; Sidik, M. Multi-Objective Optimization Techniques in Cloud Task Scheduling: A Systematic Literature Review. IEEE Access 2025, 13, 12255–12291. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Zhang, X.; Zhu, K.; Xie, C.; Wu, F. Deep Reinforcement Learning Task Scheduling Method for Real-Time Perfor-mance Awareness. IEEE Access 2025, 13, 31385–31400. [Google Scholar] [CrossRef]
- Zhu, K.; Li, S.; Zhang, X.; Wang, J.; Xie, C.; Wu, F.; Xie, R. An Energy-Efficient Dynamic Offloading Algorithm for Edge Computing Based on Deep Reinforcement Learning. IEEE Access 2024, 12, 127489–127506. [Google Scholar] [CrossRef]
- Shu, T.; Pan, Z.; Ding, Z.; Zu, Z. Resource Scheduling Optimization for Industrial Operating System Using Deep Reinforcement Learning and WOA Algorithm. Expert Syst. Appl. 2024, 255, 124765. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, Z.; Waqas, M.; Alasmary, H.; Tu, S.; Chen, S. Hybrid Edge-Cloud Collaborator Resource Scheduling Approach Based on Deep Reinforcement Learning and Multiobjective Optimization. IEEE Trans. Comput. 2024, 73, 192–205. [Google Scholar] [CrossRef]
- Qin, X.; Li, S.; Tong, J.; Xie, C.; Zhang, X.; Wu, F.; Xie, Q.; Ling, Y.; Lin, G. ERTH Scheduler: Enhanced Red-Tailed Hawk Algorithm for Multi-Cost Optimization in Cloud Task Scheduling. Artif. Intell. Rev. 2024, 57, 328. [Google Scholar] [CrossRef]
- Wu, H.; Shen, W.; Lin, W.; Li, W.; Li, K. End-Edge-Cloud Heterogeneous Resources Scheduling Method Based on RNN and Particle Swarm Optimization. IEEE Trans. Netw. Serv. Manag. 2025, 22, 1664–1676. [Google Scholar] [CrossRef]
- Chowdhary, S.; Rao, A. QoS and Reliability Aware Matched Bald Eagle Task Scheduling Framework Based on IoT-Cloud in Educational Applications. Clust. Comput. J. Netw. Softw. Tools Appl. 2024, 27, 8141–8158. [Google Scholar] [CrossRef]
- Jin, H.; Lv, S.; Yang, Z.; Liu, Y. Eagle Strategy Using Uniform Mutation and Modified Whale Optimization Algorithm for QoS- Aware Cloud Service Composition. Appl. Soft Comput. 2022, 114, 108053. [Google Scholar] [CrossRef]
- Sreenu, K.; Malempati, S. FGMTS: Fractional Grey Wolf Optimizer for Multi-Objective Task Scheduling Strategy in Cloud Computing. J. Intell. Fuzzy Syst. 2018, 35, 831–844. [Google Scholar] [CrossRef]
- Chongdarakul, W.; Aunsri, N. Heuristic Scheduling Algorithm for Workflow Applications in Cloud-Fog Computing Based on Realistic Client Port Communication. IEEE Access 2024, 12, 134453–134485. [Google Scholar] [CrossRef]
- Jafari, Z.; Navin, A.; Zamanifar, A. Task Scheduling Approach in Fog and Cloud Computing Using Jellyfish Search (JS) Opti- mizer and Improved Harris Hawks Optimization (IHHO) Algorithm Enhanced by Deep Learning. Clust. Comput. J. Netw. Softw. Tools Appl. 2024, 27, 8939–8963. [Google Scholar] [CrossRef]
- Xie, C.; Li, S.; Qin, X.; Fu, S.; Zhang, X. Multiple Elite Strategy Enhanced RIME Algorithm for 3D UAV Path Planning. Sci. Rep. 2024, 14, 21734. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Li, S.; Xie, C.; Yuan, P.; Liao, Z. SLPDBO-BP: An Efficient Valuation Model for Data Asset Value. PeerJ Comput. Sci. 2025, 11, e2813. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, B.; Aghdasi, H.; Salehpour, P. Dhole Optimization Algorithm: A New Metaheuristic Algorithm for Solving Op-timization Problems. Clust. Comput. J. Netw. Softw. Tools Appl. 2025, 28, 430. [Google Scholar] [CrossRef]
- Dige, N.; Diwekar, U. Efficient Sampling Algorithm for Large-Scale Optimization under Uncertainty Problems. Comput. Chem. Eng. 2018, 115, 431–454. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.; Suganthan, P.N.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013; Volume 201212, pp. 281–295. [Google Scholar]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Hashim, F.; Hussien, A. Snake Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Knowl. BASED Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.; Mirjalili, S. Artificial Gorilla Troops Optimizer: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Agushaka, J.; Ezugwu, A.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Zolfi, K. Gold Rush Optimizer: A New Population-Based Metaheuristic Algorithm. Oper. Res. Decis. 2023, 33, 113–150. [Google Scholar] [CrossRef]
- Truong, D.-N.; Chou, J.-S. Metaheuristic Algorithm Inspired by Enterprise Development for Global Optimization and Struc- tural Engineering Problems with Frequency Constraints. Eng. Struct. 2024, 318, 118679. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Wei, G.; Abualigah, L. Genghis Khan Shark Optimizer: A Novel Nature-Inspired Algorithm for Engineering Optimization. Adv. Eng. Inform. 2023, 58, 102210. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Ito, H.; Ogden, R.; Langenhorst, T.; Inoue-Murayama, M. Contrasting Results From Molecular and Pedigree-Based Population Diversity Measures in Captive Zebra Highlight Challenges Facing Genetic Management of Zoo Populations. Zoo Biol. 2017, 36, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Glynn, R. Power and Sample Size Estimation for the Wilcoxon Rank Sum Test with Application to Comparisons of C Statistics from Alternative Prediction Models. Biometrics 2009, 65, 188–197. [Google Scholar] [CrossRef] [PubMed]
- Fang, D.; Yan, J.; Zhou, Q. Channa Argus Optimizer for Solving Numerical Optimization and Engineering Problems. Sci. Rep. 2025, 15, 21502. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, L.; Liu, C.; Liu, Q.; Liu, J.; Mao, Y.; Murphy, J. A WOA-Based Optimization Approach for Task Scheduling in Cloud Computing Systems. IEEE Syst. J. 2020, 14, 3117–3128. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).