Abstract
We investigate how simultaneous mass and radius measurements of massive neutron stars can help constrain the properties of dark matter possibly admixed in them. Within a fermionic dark matter model that interacts only through gravitation, along with a well-constrained nuclear matter equation of state, we show that the simultaneous mass and radius measurement of PSRJ0740+6620 reduces the uncertainty of dark matter central energy density by more than 50% compared to the results obtained from using the two observables independently, while other dark matter parameters remain unconstrained. Additionally, we find that the dark matter fraction should be smaller than 2% when constrained by the observed neutron star maximum mass alone, and it could be even smaller than 0.3% with the simultaneous measurement of mass and radius, supporting the conclusion that only a small amount of dark matter exists in dark matter admixed neutron stars (DANSs).
1. Introduction
The existence of dark matter has been widely supported through observations across multiple cosmic scales, such as galactic rotation curves [1], gravitational lensing [2], cosmic microwave background anisotropies [3], and large-scale structure formation [4]. The considerable fraction of dark matter, approximately 26.8% of the total energy content of the universe, undoubtedly plays a crucial role in shaping the large-scale structure of the universe [5]. However, despite its prevalence, the properties of dark matter remain elusive. Various models and candidates have been proposed, spanning a vast mass range from eV to eV [6]. These include weakly interacting massive particles (WIMPs) [7,8,9], axions [10,11,12], dark photons [13], sterile neutrinos [14], and mirror matter [15,16,17], etc.
Direct detection experiments have attempted to constrain the properties of dark matter, with significant contributions from detectors like XENON1T [18,19,20,21,22,23], DAMA/LIBRA [24], LUX-ZEPLIN [25], CRESST [26,27], CDMSLite [28,29], CYGNUS [30], and PANDAX-II [31]. However, no conclusive results have been obtained at present.
Alternatively, dark matter properties can be constrained indirectly. Neutron stars, the densest visible objects in the universe, provide an ideal environment to study the fundamental physics of supradense matter, including the effects of dark matter. As dark matter particles pass through a neutron star, their interactions with the dense core can lead to the capture of dark matter, forming a dark matter admixed neutron star (DANS). The presence of dark matter may modify various neutron star properties and influence the gravitational wave signatures produced during binary neutron star mergers. These effects can potentially be identified through neutron star observations (see a recent review in ref. [32]). The amount of dark matter in a neutron star depends on the star’s evolutionary history and its location throughout its life. Depending on the quantity of dark matter, it may accumulate in the core of the neutron star, forming a dark matter core, or it may distribute itself within and outside the star’s baryonic radius, forming a dark matter halo.
With the accumulation of more neutron star observation data, constraints on dark matter properties have become increasingly possible. For instance, the mass of the massive neutron star, PSR J0740+6620, has been constrained to [33,34], with its radius constrained to km [35] and km [36] by the Neutron Star Interior Composition Explorer (NICER) Collaboration. Additionally, the tidal deformability of a canonical neutron star has been extracted from the binary neutron star merger event GW170817, yielding at the 90% confidence level [37]. Combining results from NICER and GW170817, ref. [38] constrained the dark matter mass to the range MeV, while ref. [39] proposed an upper limit of 60 GeV.
Significant attention has been devoted to studying how dark matter can affect the properties of DANSs. The existence of dark matter can substantially alter the spacetime around a neutron star, impacting observable quantities such as gravitational wave signals after mergers, mass–radius profiles, tidal deformabilities, and thermal evolution [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. The transition between a dark matter core and halo depends on the dark matter particle mass and mass fraction [66]. The dark matter halos can be categorized into two types, namely a compact halo with the same order of nuclear matter radius or a diffuse halo with a radius of up to hundreds of kilometers [54]. Among these, only compact halos with large can significantly alter the radius of nuclear matter, as most of dark matter mass resides within the radius of nuclear matter, exerting a substantial inward gravitational pull on the nuclear matter. Other halo types have limited effects on the radius of nuclear matter.
In ref. [48], the authors found that a dark matter halo forms when is in the range of 105∼200 MeV, while a dark matter core forms if exceeds 200 MeV. Similarly, other studies [39,51] confirmed that a dark matter halo is present for dark matter masses in the range of a few hundred MeV. Moreover, the presence of a dark matter core could result in observable features in gravitational wave signals, such as an additional peak or an increased likelihood of prompt collapse within the first 2 ms after a merger [43,65]. More importantly, dark matter halos can modify the pulse profiles of neutron stars, which in turn affects the interpretation of NICER observations. Given that our study employs simultaneous mass–radius constraints from NICER to constrain dark matter properties, we focus on dark matter cores to ensure self-consistency in our analysis.
In this study, we focus on fermionic dark matter, where gravity is the only interaction between the dark matter and nuclear matter [41,43,66,67,68,69,70,71]. The equation of state (EOS) for nuclear matter is taken from ref. [72]. It satisfies all the current observational constraints on the neutron star maximum mass as well as the radii and masses of several neutron stars by NICER and GW170817 results. Unlike previous studies, we systematically vary dark matter EOS parameters and examine how the simultaneous measurements of the neutron star mass and radius of PSRJ0740+6620 can help constrain the properties of fermionic dark matter. The rest of the paper is organized as follows: in Section 2, we introduce the nuclear matter and dark matter EOSs; in Section 3, we discuss in detail how the simultaneous measurement of neutron star mass and radius can constrain dark matter properties; and in Section 4, we summarize our findings.
2. Theoretical Framework
The EOS for both high-density nuclear matter and dark matter remains highly uncertain. For instance, refs. [32,73] summarize the possible EOSs for both nuclear matter and dark matter. All the dark matter candidates could in principle be employed to study DANSs, and none can be ruled out with existing observational evidence. In the present study, we assume the dark matter to be fermionic dark matter. We use the same meta-model EOS for nuclear matter as in ref. [72]. Once the EOSs are determined, the properties of DANSs can be obtained by solving the traditional Tolman–Oppenheimer–Volkov (TOV) equations or the two fluid TOV equations. The effects of dark matter on the properties of DANSs can be analyzed either through Bayesian methods [56,74], which can handle statistically many parameters and provide insights into their interrelations, or by selecting representative parameter sets to model DANSs directly [41,66,71]. The Bayesian analysis approach allows for a probabilistic view of the parameter space, while the use of representative parameter sets offers a direct connection between the observational data and specific model parameters.
2.1. The EOS of Nuclear Matter
In ref. [75], we constructed a parameterized EOS to describe the matter at -equilibrium in neutron stars. This was achieved by separately parameterizing the EOS for symmetric nuclear matter (SNM) and nuclear symmetry energy as follows:
where , , and are the binding energy, incompressibility, and skewness of SNM at the saturation density , while , L, , and are the magnitude, slope, curvature, and skewness of symmetry energy at .
For more details on this model, the reader can refer to our previous publications [72,76,77,78,79,80]. In ref. [72], we used an EOS for nuclear matter in which all parameters were constrained based on current terrestrial nuclear experiments and neutron star observations. Specifically, the most probable values of these parameters are determined to be MeV, MeV, Mev, MeV, MeV, MeV, and MeV. This EOS, labeled as PEOS in the following discussions, features a maximum mass of and radii for stars with masses of and given by km and km, respectively. In this study, we utilize the PEOS to reduce the complexity arising from the uncertainties in the nuclear matter EOS.
2.2. The EOS of Dark Matter
As mentioned earlier, numerous models and candidates have been proposed to explain the nature of dark matter. In this study, we treat the dark matter particles as fermions that primarily interact through gravity. Both vector and scalar fields are considered, with a neutral scalar meson coupling to the dark matter particles as and a neutral vector meson coupling to the conserved dark matter current as , where represents the coupling constants between dark matter and the mediator. Thus, similar to the potential for baryons, one can define an effective Yukawa potential for dark matter with the exchange of bosons [81]:
The above potential is governed by the coupling constants and the masses of the mediators . With appropriate coupling constants and masses, this potential can be attractive at large distances and repulsive at short distances.
The full Lagrangian value, including both attractive and repulsive interactions, is given by ref. [41] as
where is the strength tensor for the vector meson.
Within the relativistic mean field approximation, the vector and scalar field operators are replaced by their ground state expectation values: and . The energy density and pressure for dark matter can then be calculated as
where is the effective mass of dark matter and is the number density of dark matter.
In this dark matter model, it is found that the dark matter EOS depends only on the ratio of and . There are no reliable constraints on the model parameters, and it is only required that to ensure that the potential is attractive at large distances and repulsive at short distances [41,70]. Consequently, the parameters that affect the EOS are , , and . The typical values of and range from 0 to 20 . For example, ref. [70] suggests that and . Additionally, several representative combinations of and are often chosen to study the effects of dark matter on the properties of DANSs. For instance, combinations like and and and have been used in refs. [41,71]. The mass of dark matter is crucial for determining the formation of the dark matter core or halo. Ref. [48] found that a dark matter halo forms when MeV, and a dark matter core forms if MeV. The effects of varying are explored in ref. [71]. In this study, since reliable constraints on are lacking and given our focus on the study of the dark matter core, we select values in the range from 500 MeV to 2000 MeV. Dark matter with MeV would lead to a dark matter halo for DANSs.
2.3. Two-Fluid TOV Equations
Once the EOSs for nuclear matter and dark matter are prepared, the properties of DANSs are determined by solving the two-fluid TOV equations, given by [82]
where r is the radial coordinate from the center of the star and and represent the pressure and energy density of nuclear matter or dark matter, respectively. The total pressure and energy density are given by and .
To solve the above equations, initial conditions and boundary conditions must be specified. In the center of the star (), we set . For the central densities of nuclear matter and dark matter, there are no reliable constraints on the central density of dark matter as of now. Therefore, we set the ratio of the energy densities between nuclear matter and dark matter, i.e., , as a parameter. This method is similar to those used in ref. [58] and other studies. The radii of nuclear matter or dark matter are determined by the boundary condition of or . If , a dark matter core forms. A dark matter halo forms for .
In short, four parameters describing dark matter can vary in this model, namely , , , and . For a selected value, by constructing a three-dimensional (3D) parameter space of , we can constrain these parameters simultaneously based on current observations of neutron stars, particularly the simultaneous observation of the mass and radius of PSRJ0740+6620.
The 3D parameter space method used in this study and the well-known Bayesian analysis approach are two distinct methods for extracting observational constraints on the properties of nuclear matter or dark matter. Both are rigorous, but each has its own advantages and disadvantages. The 3D parameter space method systematically explores the parameter space without any prior assumptions, thus avoiding the exclusion of potentially valid parameter sets. It directly links the parameters to observational data, offering clearer insights into the effects of dark matter on the properties of DANSs. The resulting data are both informative and straightforward. However, this method faces challenges in quantifying uncertainties and struggles with models that contain numerous parameters. In this study, there are only four free parameters in the dark matter model, making the 3D parameter space method adequate for the analysis.
3. Results and Discussions
The mass of PSR J0740+6620 is constrained to be [33,34], making it the most massive neutron star observed so far. In 2021, NICER obtained simultaneously the mass and radius of PSR J0740+6620 as km [35] and km [36] from two independent analyses of their observational data using somewhat different techniques. Information about both the mass and the radius of a massive neutron star provides tighter constraints on both the EOS of the nuclear matter and the dark matter.
In the present study, we are interested in how the simultaneous measurement of mass and radius of PSR J0740+6620 can help constrain the parameters , , , and the dark matter fraction in a DANS. To achieve this goal, we calculate the constraints based on the upper and lower limits of NICER observations and find that only the lower limit of km provides additional constraints on the properties of dark matter. A similar situation arises in analyzing other NICER and GW170817 observations. This is because the nuclear matter EOS used in the present work already describes well the current astrophysical observations within their uncertain ranges without considering dark matter, namely, and km. To satisfy the constraints of and km in DANS, we only need to include a small amount of dark matter. This would cause only a slight change in the M-R curves, ensuring that the selected constraints are still satisfied. Thus, both and km can be used to constrain the properties of dark matter.
However, for another alternative constraint from NICER, such as km from ref. [35], we find that this condition is always satisfied, regardless of how the dark matter parameters are varied. This is because the inclusion of dark matter tends to reduce the nuclear matter radius as the dark matter core exerts an inward force, pulling the nuclear matter inward. A similar situation arises for other NICER constraints and even tidal deformability. All these constraints are satisfied regardless of changes in the dark matter parameters. Therefore, and km are the only two constraints that can effectively constrain the properties of dark matter.
The effects of dark matter mass (left panel), (middle panel), and (right panel) on the dark matter EOS are shown in Figure 1. The black dashed line, labeled as PEOS, is the nuclear matter EOS mentioned in Section 2.1 and is given for comparison. Note that the dark matter EOS is independent of . As clearly shown, increasing results in a softer dark matter EOS. This behavior can be explained by the equations of dark matter EOS, specifically the last terms in Equations (5) and (6). An increase in leads to a larger energy density but a smaller pressure p, resulting in a softer EOS. Compared to the PEOS of nuclear matter, the dark matter EOS becomes softer at high densities, except for the EOS corresponding to MeV. The contributions of and to the EOS are opposite, as they have opposite effects on the potential, as shown in Equation (3). In addition, we can see that the EOS for and 15 cross around 700 MeV·. This is because the changes in affect both the first and third terms of Equations (5) and (6). More specifically, also influences the effective mass of dark matter. As the first term plays an increasingly dominant role in determining EOS stiffness at high densities and it contributes positively to the dark matter EOS, the EOS for becomes stiffer at high densities.
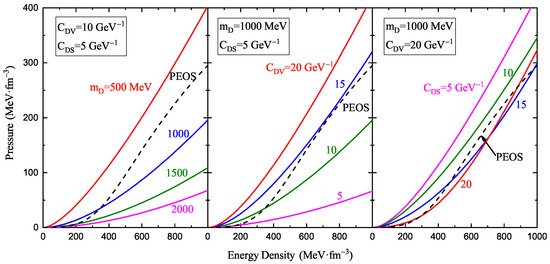
Figure 1.
The effects of dark matter mass (left panel), (middle panel), and (right panel on the EOS of dark matter. The black dashed line, labeled as PEOS, is the neutron star EOS mentioned in Section 2.1 and is given for comparison.
After understanding how each parameter affects the EOS, we can now constrain these parameters based on astrophysical observations. The constant surfaces of (blue surfaces) and km (pink surfaces) in the 3D parameter space of for , 1000, 1500, and 2000 MeV are shown in Figure 2. All surfaces end at . The red arrows indicate the directions that satisfy the corresponding observation, while the black arrow points to the corresponding surface. Note that the ranges of the axis differ across the four panels and the two surfaces do not intersect in each plot. The constant surfaces mean that any point selected from the surface corresponds to a parameter set that satisfies the corresponding observation. For example, any point on the constant surface of corresponds to a parameter set (, , ) that leads to an EOS of DANSs with a maximum mass of . Therefore, the constant surfaces in the 3D parameter space help constrain the parameters.
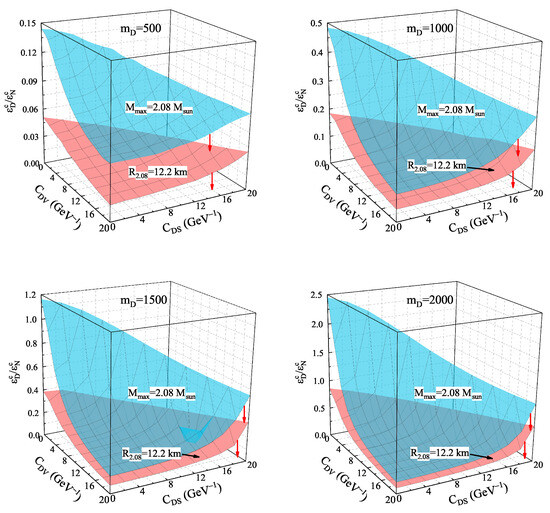
Figure 2.
The constant surfaces of (blue surfaces) and km (pink surfaces) in the 3D parameter space of for , 1000, 1500, and 2000 MeV, respectively. The red arrows indicate the directions that satisfy the corresponding observation, while the black arrow points to the surface of km.
From Figure 2, we can see that the observed mass of PSR J0740+6620 can significantly constrain the parameter space, and the simultaneous measurement of its mass and radius provides even tighter constraints. However, only the parameter can be directly constrained, while and remain unconstrained. This is because there is no direct constraint on at present. For instance, for MeV, if is constrained to be less than 1, we can plot a horizontal constant surface of to intersect other parameter surfaces in the space. The crossline between and provides a projection onto the plane, which helps constrain or . Despite and being unconstrained by the current observations, we obtain a reliable constraint on . The upper limit for increases from 0.15 to 2.45 as increases from 500 to 2000 MeV for . This is because the dark matter EOS becomes softer for larger , requiring more dark matter and thus a larger to support a DANS with . Additionally, all constant surfaces of provide the strictest constraints on at and . This is consistent with Figure 1, where the combination of and results in the hardest dark matter EOS, requiring the least dark matter to support a DANS with .
A similar trend is observed when the mass and radius of PSR J0740+6620 are measured simultaneously ( km), as shown in Figure 2. However, the constant surface of km reduces the upper limit of by more than 50% for any . The upper limit decreases to only 0.05 for MeV and 0.86 for MeV. Using the constraints from [70] for and , we find , 0.17, 0.26, and 0.37 for , 1000, and 2000 MeV, respectively. This suggests that lighter dark matter mass corresponds to a smaller in DANSs. However, lighter dark matter mass leads to a larger dark matter fraction, as discussed below.
For both and km, represents the upper boundary for the constant surfaces. Therefore, by projecting the line of along each surface to the plane, we can better visualize the constraints on . Note that the projections to the or plane are equivalent, as is satisfied for any surface. To make the constraints on clearer, the projection of onto the plane is shown for (red lines), 1000 (blue lines), 1500 (green lines), and 2000 (orange lines) MeV. These projections are presented for the surfaces of (solid lines) and km (dashed lines) in Figure 3.
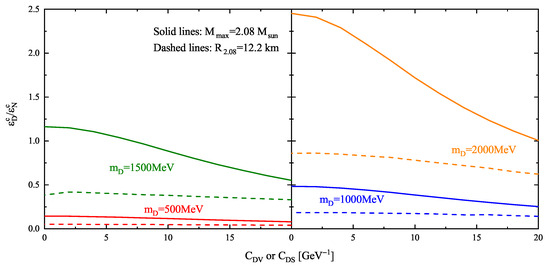
Figure 3.
The projection of to the or plane with = 500 (red lines), 1000 (blue lines), 1500 (green lines), and 2000 (orange lines) MeV for the surfaces of (solid lines) and km (dashed lines).
For the solid lines corresponding to , the dependence of on or exists for and 1500 MeV but decreases as decreases. This dependence disappears as the lines become much flatter for and 500 MeV. This behavior can be explained from Figure 2. Since the maximum mass of the PEOS is 2.13 and the existence of dark matter reduces the maximum mass, a small amount of dark matter must be introduced to obtain a star with . Based on the stiffness of the dark matter EOS, dark matter with smaller requires a smaller central density to contribute similarly to dark matter with larger . Therefore, tighter constraints on are obtained for smaller .
However, when considering the constraint of km, we observe that the density of dark matter must always be smaller than that of nuclear matter for different values of . Furthermore, all the dashed lines appear horizontal, indicating that is independent of or for any value of . Meanwhile, the constrained value of decreases with decreasing . This suggests that we cannot obtain additional constraints on and through the simultaneous measurement of the mass and radius of DANSs. Therefore, the simultaneous measurement of the mass and radius of DANSs can help constrain but not and , even if tighter constraints are obtained in the future.
In the previous discussions, we showed how observations can constrain the properties of dark matter. However, the amount of dark matter in a DANS cannot be determined solely by knowing the central density. Thus, a profile of the density as a function of the distance from the center of the star is needed. To plot this profile, we select three representative parameter sets from Figure 3, specifically , 10, and 20 , to illustrate the possible effects of varying and on the density profile. Since the projections in Figure 3 are monotonic or relatively flat, these three combinations of and capture the main features of the dark matter properties. The energy density profile as functions of distance r for and km, with , 10, and 20 , are shown in Figure 4. The red and green lines represent the profiles of nuclear matter, while the blue and orange lines represent the dark matter profiles. Note that the profiles are displayed for stars with .
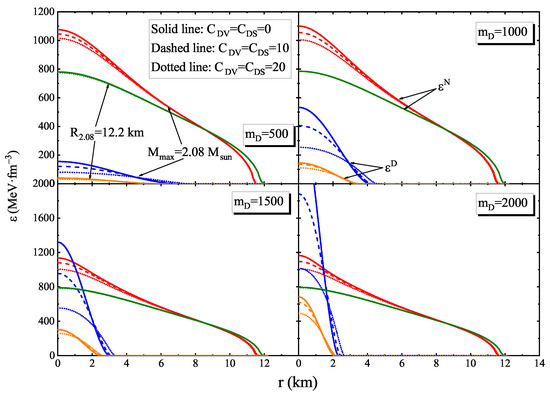
Figure 4.
The profile of energy density as functions of distance r for and km and = 0, 10, 20 , respectively. The red and green lines correspond to the profiles of nuclear matter, while the blue and orange lines correspond to the profile of dark matter.
As expected, only the dark matter core exists for the selected values of . We observe that the effects of and on the profile are noticeable only for but disappear for km. For , and affect only the central part of the star, while they have almost no effect on the core for km. This is because the central density remains the same for different values of and for km, as shown in Figure 3; therefore, they do not impact the density profiles.
In addition, the size of the dark matter core decreases as increases. For , the size of the dark matter core decreases from 8.00 km to 2.41 km as increases from 500 MeV to 2000 MeV when . The change in and from 0 to 20 leads to a correction of less than 1 km but significantly alters the values of and . Although can exceed 2000 MeV·, the small size of the dark matter core may suppress the total amount of dark matter in the DANS. In other words, the competition between the core’s size and the central density determines the amount of dark matter in the DANS.
To quantify the amount of dark matter in the DANS, we define the fraction of dark matter as
where is the total mass of dark matter and is the total mass of the DANS within distance r. Currently, is not well constrained. Bayesian analyses, such as ref. [74], found that ∼7.9%, while other studies [70,83] propose ranges of ∼5.9% and ∼11%. Additionally, ref. [84] found ∼25% with the constraint of , and refs. [43,48] report .
To constrain based on the present observations of and km, the profiles of dark matter fraction (left panel, red and blue lines) and total star mass (right panel, green and orange lines) as functions of distance r for , 10, and 20 are shown in Figure 5. Note that the ranges of the axis differ for different values of . It is clear that decreases with distance r. For MeV, the largest is 12.6% for and 4.8% for km when . Again, the effects of are visible only in the central region of the star. Although is relatively large at the center of the star, it drops to lower values when km, where the star’s mass is still less than 0.5 . Therefore, the total is not expected to be large for the entire star. At , quickly decreases to 1.96% for and 0.3% for km, and the effects of on disappear. For MeV, is constrained to be 1.4% for and 0.3% for km.
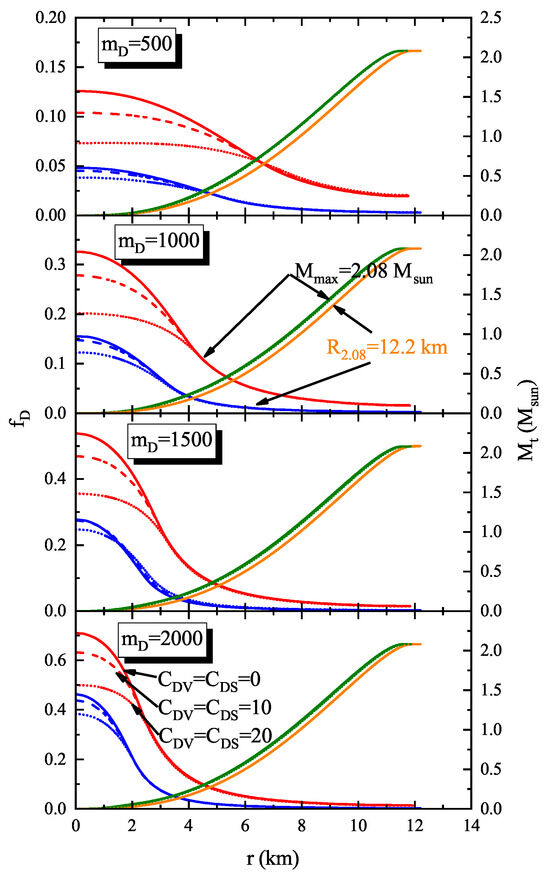
Figure 5.
The profile of dark matter fraction (left title, red and blue lines) and total mass (right title, green and orange lines) as functions of distance r for and km and = 0, 10, 20 , respectively.
Thus, we conclude that the simultaneous measurement of the mass and radius of PSRJ0740+6620 can constrain the dark matter fraction to around 0.3%. Tighter constraints may support smaller values of and, consequently, a smaller dark matter fraction .
4. Conclusions
In this study, we investigate how the observations from NICER can help constrain the properties of dark matter in DANSs. We assume the dark matter to be fermionic dark matter, where dark matter interacts exclusively via gravity. Both vector and scalar fields are considered in the fermionic dark matter. For the nuclear matter in DANSs, we adopt a parameterized EOS from ref. [75]. All parameters have been constrained based on current terrestrial nuclear experiments and neutron star observations. We only utilize this EOS to describe nuclear matter to reduce the complexity arising from the uncertainties in the nuclear matter EOS. We compare the constraints on dark matter properties within the DANS by considering both the observed neutron star maximum mass ( ) and the simultaneous measurement of mass and radius ( km) for PSRJ0740+6620 in the 3D parameter space of . The nuclear matter EOS selected in this study satisfies all relevant observational constraints, including the maximum neutron star mass as well as the masses and radii of several neutron stars observed by NICER and GW170817 by LIGO/VIRGO.
Our results indicate that the simultaneous measurement of the mass and radius can reduce uncertainty in by more than 50%. However, the parameters and remain unconstrained, even with the potential for tighter constraints from future measurements. To better constrain these parameters, new kinds of observation will be essential. Although the central energy density of dark matter can be much larger than that of nuclear matter, the dark matter fraction in the star should remain below 2% with the constraint and could be as low as 0.3% with the km constraint. This suggests that only a small amount of dark matter is present in the DANS.
The nuclear matter EOS we selected is consistent with all existing astrophysical constraints, making it relatively easy for DANSs to satisfy these conditions, as the needed changes from dark matter EOS to the nuclear matter EOS are minimal. Essentially, there is a degeneracy between the EOS of nuclear matter and that of dark matter because the TOV equations are composition-blind. Namely, different combinations of nuclear matter and dark matter can lead to the same pressure and energy density necessary to describe the observations. Naturally, other choices of nuclear matter EOSs could lead to more stringent constraints on dark matter properties. The inclusion of new particles, such as hyperons and mesons, or the consideration of a phase transition from nuclear matter to quark matter could also modify the nuclear matter EOS. Additionally, we focused on the lower limit km constraint derived from the simultaneous measurement of mass and radius. We did not discuss the corresponding upper limit of km or the analysis from Ref. [36], as these are satisfied by almost all EOS parameter combinations within our model framework. Therefore, tighter constraints on the masses and especially radii of massive neutron stars are crucial to deepen our understanding of dark matter properties in DANSs.
Author Contributions
Writing—original draft, N.Z. and B.-A.L.; writing—review and editing, N.Z., B.-A.L., J.Z., W.S., and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
B.-A.L. is supported in part by the U.S. Department of Energy, Office of Science, under Award Number DE-SC0013702, the CUSTIPEN (China-U.S. Theory Institute for Physics with Exotic Nuclei) under the US Department of Energy Grant No. DE-SC0009971. N.Z. is supported in part by the National Natural Science Foundation of China under Grant No. 12375120 and the Zhishan Young Scholar of Southeast University under Grant No. 2242024RCB0013. J.Z., W.S., and H.Z. are supported by the National College Students’ Innovation and Entrepreneurship Training Program.
Data Availability Statement
Data will be made available upon reasonable request.
Acknowledgments
We would like to thank Wei-Zhou Jiang for helpful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Douglas, C.; Marusa, B.; Anthony, H.G.; Maxim, M.; Scott, W.R.; Christine, J.; Dennis, Z. A direct empirical proof of the existence of dark matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Miville-Deschênes, M.A.; Pettorino, V.; Bucher, M.; Delabrouille, J.; Ganga, K.; Le Jeune, M.; Patanchon, G.; Rosset, C.; Roudier, G.; Fantaye, Y.; et al. Planck 2018 results. VI. cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- White, S.D.M.; Rees, M.J. Core condensation in heavy halos: A two-stage theory for galaxy formation and clustering. Mon. Not. R. Astron. Soc. 1978, 183, 341–358. [Google Scholar] [CrossRef]
- Jarosik, N.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Halpern, M.; Hill, R.S.; Hinshaw, G.; Kogut, A.; Komatsu, E.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results. Astrophys. J. Suppl. Ser. 2011, 192, 14. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Caputo, R.; Croon, D.; Perez, K.; Berti, E.; Bramante, J.; Buschmann, M.; Brito, R.; Chen, T.Y.; Cole, P.S.; et al. Dark Matter In Extreme Astrophysical Environments. arXiv 2022, arXiv:2203.07984. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P. Constraining asymmetric dark matter through observations of compact stars. Phys. Rev. D 2011, 83, 083512. [Google Scholar] [CrossRef]
- Steigman, G.; Dasgupta, B.; Beacom, J.F. Precise Relic WIMP Abundance and its Impact on Searches for Dark Matter Annihilation. Phys. Rev. D 2012, 86, 023506. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M.P. A new era in the search for dark matter. Nature 2018, 562, 51. [Google Scholar] [CrossRef]
- Duffy, L.D.; Bibber, K.V. Axions as dark matter particles. New J. Phys. 2009, 11, 105008. [Google Scholar] [CrossRef]
- Olive, K.A. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics: Particle data groups. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- An, H.; Pospelov, M.; Pradler, J.; Ritz, A. Direct Detection Constraints on Dark Photon Dark Matter. Phys. Lett. B 2015, 747, 331–338. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Khlopov, M.Y. On the possible signatures of mirror particles. Sov. J. Nucl. Phys. 1982, 36, 472–474. [Google Scholar]
- Blinnikov, S.I.; Khlopov, M.Y. Possible astronomical effects of mirror particles. Astron. Zhurnal 1983, 27, 371–375. [Google Scholar]
- Khlopov, M.Y.; Beskin, G.M.; Bochkarev, N.G.; Pustilnik, L.A.; Pustilnik, S.A. Observational physics of mirror world. Sov. Astron. 1991, 35, 21–30. [Google Scholar]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Baudis, L.; Bauermeister, B.; et al. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Antochi, V.C.; Arneodo, F.; Baudis, L.; et al. Constraining the spin-dependent WIMP-nucleon cross sections with XENON1T. Phys. Rev. Lett. 2019, 122, 141301. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Antochi, V.C.; Angelino, E.; Arneodo, F.; Barge, D.; et al. Light Dark Matter Search with Ionization Signals in XENON1T. Phys. Rev. Lett. 2019, 123, 251801. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Antochi, V.C.; Angelino, E.; Arneodo, F.; Barge, D.; et al. Search for Light Dark Matter Interactions Enhanced by the Migdal Effect or Bremsstrahlung in XENON1T. Phys. Rev. Lett. 2019, 123, 241803. [Google Scholar] [CrossRef] [PubMed]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Antochi, V.C.; Angelino, E.; Angevaare, J.R.; Arneodo, F.; et al. Projected WIMP sensitivity of the XENONnT dark matter experiment. J. Cosmol. Astropart. Phys. 2020, 11, 031. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Ahmed Maouloud, S.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Andaloro, S.; Antochi, V.C.; Angelino, E.; et al. Search for Coherent Elastic Scattering of Solar 8B Neutrinos in the XENON1T Dark Matter Experiment. Phys. Rev. Lett. 2021, 126, 091301. [Google Scholar] [CrossRef] [PubMed]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.J.; d’Angelo, A.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, X.H.; et al. New results from DAMA/LIBRA. Eur. Phys. J. C 2010, 67, 39–49. [Google Scholar] [CrossRef]
- Akerib, D.S.; Araùjo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Bedikian, S.; Bernard, E.; Bernstein, A.; Bolozdynya, A.; Bradley, A.; et al. First results from the LUX dark matter experiment at the Sanford Underground Research Facility. Phys. Rev. Lett. 2014, 112, 091303. [Google Scholar] [CrossRef]
- Angloher, G.; Bento, A.; Bucci, C.; Canonica, L.; Defay, X.; Erb, A.; von Feilitzsch, F.; Iachellini, N.F.; Gorla, P.; Gütlein, A.; et al. Results on light dark matter particles with a low-threshold CRESST-II detector. Eur. Phys. J. C 2016, 76, 25. [Google Scholar] [CrossRef]
- Abdelhameed, A.H.; Angloher, G.; Bauer, P.; Bento, A.; Bertoldo, E.; Bucci, C.; Canonica, L.; D’Addabbo, A.; Defay, X.; Di Lorenzo, S.; et al. First results from the CRESST-III low-mass dark matter program. Phys. Rev. D 2019, 100, 102002. [Google Scholar] [CrossRef]
- Agnese, R.; Anderson, A.J.; Asai, M.; Balakishiyeva, D.; Basu Thakur, R.; Bauer, D.A.; Beaty, J.; Billard, J.; Borgl, A.; Bowles, M.A.; et al. Search for Low-Mass Weakly Interacting Massive Particles with SuperCDMS. Phys. Rev. Lett. 2014, 112, 241302. [Google Scholar] [CrossRef]
- Agnese, R.; Anderson, A.J.; Aralis, T.; Aramaki, T.; Arnquist, I.J.; Baker, W.; Balakishiyeva, D.; Barker, D.; Basu Thakur, R.; Bauer, D.A.; et al. Low-mass dark matter search with CDMSlite. Phys. Rev. D 2018, 97, 022002. [Google Scholar] [CrossRef]
- Vahsen, S.E.; O’Hare, C.A.J.; Lynch, W.A.; Spooner, N.J.C.; Baracchini, E.; Barbeau, P.; Battat, J.B.R.; Crow, B.; Deaconu, C.; Eldridge, C.; et al. CYGNUS: Feasibility of a nuclear recoil observatory with directional sensitivity to dark matter and neutrinos. arXiv 2020, arXiv:2008.12587. [Google Scholar] [CrossRef]
- Wang, Q.; Abdukerim, A.; Chen, W.; Chen, X.; Chen, Y.H.; Cheng, C.; Cui, X.Y.; Fan, Y.J.; Fang, D.Q.; Fu, C.B.; et al. Results of dark matter search using the full PandaX-II exposure. Chin. Phys. C 2020, 44, 125001. [Google Scholar] [CrossRef]
- Grippa, F.; Lambiase, G.; Kumar, T. Poddar Searching for New Physics in an Ultradense Environment: A Review on Dark Matter Admixed Neutron Stars. Universe 2025, 11, 74. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined mass and geometric measurements of the high-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The radius of PSR J0740+ 6620 from NICER and XMM-Newton data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER view of the massive pulsar PSR J0740+6620 informed by radio timing and XMM-Newton spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Guha, A.; Sen, D. Constraining the mass of fermionic dark matter from its feeble interaction with hadronic matter via dark mediators in neutron stars. Phys. Rev. D 2024, 109, 043038. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Sagun, V.; Lopes, I. Neutron stars: New constraints on asymmetric dark matter. Phys. Rev. D 2020, 102, 063028. [Google Scholar] [CrossRef]
- Li, A.; Huang, F.; Xu, R.X. Too massive neutron stars: The role of dark matter? Astropart. Phys. 2012, 37, 70–74. [Google Scholar] [CrossRef]
- Xiang, Q.F.; Jiang, W.Z.; Zhang, D.R.; Yang, R.Y. Effects of fermionic dark matter on properties of neutron stars. Phys. Rev. C 2014, 89, 025803. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Dark matter effect on realistic equation of state in neutron stars. Phys. Rev. D 2017, 96, 083004. [Google Scholar] [CrossRef]
- Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark matter effects on neutron star properties. Phys. Rev. D 2018, 97, 123007. [Google Scholar] [CrossRef]
- Nelson, A.E.; Reddy, S.; Zhou, D. Dark halos around neutron stars and gravitational waves. J. Cosmol. Astropart. Phys. 2019, 07, 012. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Patra, S.K. Dark matter admixed neutron star as a possible compact component in the GW190814 merger event. Phys. Rev. D 2021, 104, 063028. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Biswal, S.K.; Patra, S.K. Impacts of dark matter on the f-mode oscillation of hyperon star. Phys. Rev. D 2021, 104, 123006. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Kumar, B.; Patra, S.K. Dark Matter Effects on the Compact Star Properties. Galaxies 2022, 10, 14. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Barbat, M.F.; Schaffner-Bielich, J.; Tolos, L. Comprehensive study of compact stars with dark matter. Phys. Rev. D 2024, 110, 023013. [Google Scholar] [CrossRef]
- Flores, C.V.; Lenzi, C.H.; Dutra, M.; Lourenço, O.; Arbanil, J.D.V. Gravitational wave asteroseismology of dark matter hadronic stars. Phys. Rev. D 2024, 109, 083021. [Google Scholar] [CrossRef]
- Giangrandi, E.; Ávila, A.; Sagun, V.; Ivanytskyi, O.; Providência, C. The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars. Particles 2024, 7, 179. [Google Scholar] [CrossRef]
- Konstantinou, A. The Effect of a Dark Matter Core on the Structure of a Rotating Neutron Star. Astrophys. J. 2024, 968, 83. [Google Scholar] [CrossRef]
- Kumar, A.; Sotani, H. Constraints on the parameter space in dark matter admixed neutron stars. Phys. Rev. D 2024, 110, 063001. [Google Scholar] [CrossRef]
- Shawqi, S.; Morsink, S.M. Interpreting Mass and Radius Measurements of Neutron Stars with Dark Matter Halos. Astrophys. J. 2024, 975, 123. [Google Scholar] [CrossRef]
- Shirke, S.; Pradhan, B.K.; Chatterjee, D.; Sagunski, L.; Schaffner-Bielich, J. Effects of dark matter on f-mode oscillations of neutron stars. Phys. Rev. D 2024, 110, 063025. [Google Scholar] [CrossRef]
- Rutherford, N.; Prescod-Weinstein, C.; Watts, A. Probing fermionic asymmetric dark matter cores using global neutron star properties. Phys. Rev. D 2025, 111, 123034. [Google Scholar] [CrossRef]
- Thakur, P.; Kumar, A.; Thapa, V.B.; Parmar, V.; Sinha, M. Exploring non-radial oscillation modes in dark matter admixed neutron stars. J. Cosmol. Astropart. Phys. 2024, 12, 042. [Google Scholar] [CrossRef]
- Kumar, A.; Girmohanta, S.; Sotani, H. Multi-Messenger and Cosmological Constraints on Dark Matter through Two-Fluid Neutron Star Modeling. arXiv 2025, arXiv:2501.16829. [Google Scholar]
- Miao, Z.Q.; Zhu, Y.F.; Li, A.; Huang, F. Dark Matter Admixed Neutron Star Properties in the Light of X-Ray Pulse Profile Observations. Astrophys. J. 2022, 936, 69. [Google Scholar] [CrossRef]
- Shakeri, S.; Karkevandi, D.R. Bosonic dark matter in light of the NICER precise massradius measurements. Phys. Rev. D 2024, 109, 043029. [Google Scholar] [CrossRef]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shahrbaf, M.; Shakeri, S.; Typel, S. Exploring the Distribution and Impact of Bosonic Dark Matter in Neutron Stars. Particles 2024, 7, 201–213. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Huertas-Roldan, T.; Santos, D. Neutron decay anomaly, neutron stars, and dark matter. Phys. Rev. D 2024, 110, 083003. [Google Scholar] [CrossRef]
- Scordino, D.; Bombaci, I. Dark matter admixed neutron stars with a realistic nuclear equation of state from chiral nuclear interactions. J. High Energy Astrophys. 2025, 45, 371–381. [Google Scholar] [CrossRef]
- Giangrandi, E.; Rüter, H.R.; Kunert, N.; Emma, M.; Abac, A.; Adhikari, A.; Dietrich, T.; Sagun, V.; Tichy, W.; Providência, C. Numerical Relativity Simulations of Dark Matter Admixed Binary Neutron Stars. arXiv 2025, arXiv:2504.20825. [Google Scholar] [CrossRef]
- Grippa, F.; Lambiase, G.; Poddar, T.K. Constraints on scalar and vector dark matter admixed neutron stars with linear and quadratic couplings. arXiv 2024, arXiv:2407.16386. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer Science & Business Media: Berlin, Germany, 1997. [Google Scholar]
- Collier, M.; Croon, D.; Leane, R.K. Tidal Love numbers of novel and admixed celestial objects. Phys. Rev. D 2022, 106, 123027. [Google Scholar] [CrossRef]
- Das, A.; Malik, T.; Nayak, A.C. Dark matter admixed neutron star properties in light of gravitational wave observations: A two fluid approach. Phys. Rev. D 2022, 105, 123034. [Google Scholar] [CrossRef]
- Routaray, P.; Mohanty, S.R.; Das, H.C.; Ghosh, S.; Kalita, P.J.; Parmar, V.; Kumar, B. Investigating dark matter-admixed neutron stars with NITR equation of state in light of PSR J0952-0607. J. Cosmol. Astropart. Phys. 2023, 10, 073. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Impact of the nuclear equation of state on the formation of twin stars. Euro. Phys. J. A 2025, 61, 31. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Vidana, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Liu, X.Z.; Mahapatra, P.; Huang, C.; Hazarika, A.; Singha, C.; Das, P.K. Revealing Dark Matter’s Role in Neutron Stars Anisotropy: A Bayesian Approach Using Multi-messenger Observations. arXiv 2025, arXiv:2506.08376. [Google Scholar]
- Zhang, N.B.; Li, B.A.; Xu, J. Combined constraints on the equation of state of dense neutron-rich Matter from terrestrial nuclear experiments and observations of Neutron Stars. Astrophys. J. 2018, 859, 90. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Delineating effects of nuclear symmetry energy on the radii and tidal polarizabilities of neutron stars. J. Phys. G Nucl. Part. Phys. 2019, 46, 014002. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Implications of the mass M= M⊙ of PSR J0740+6620 on the equation of state of super-dense neutron-rich nuclear matter. Astrophys. J. 2019, 879, 99. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Constraints on the Muon Fraction and Density Profile in Neutron Stars. Astrophys. J. 2020, 893, 61. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Impact of symmetry energy on sound speed and spinodal decomposition in dense neutron-rich matter. Eur. Phys. J. A 2023, 59, 86. [Google Scholar] [CrossRef]
- Xie, W.J.; Li, B.A.; Zhang, N.B. Impact of the newly revised gravitational redshift of X-ray burster GS 1826-24 on the equation of state of supradense neutron-rich matter. Phys. Rev. D 2024, 110, 043025. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; McGraw-Hill: Boston, MA, USA, 1971. [Google Scholar]
- Ciarcellut, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19. [Google Scholar] [CrossRef]
- Arvikar, P.; Gautam, S.; Venneti, A.; Banik, S. Exploring Fermionic Dark Matter Admixed Neutron Stars in the Light of Astrophysical Observations. arXiv 2025, arXiv:2506.20736. [Google Scholar] [CrossRef]
- Thakur, P.; Malik, T.; Das, A.; Jha, T.K.; Providência, C.M.C. Exploring robust correlations between fermionic dark matter model parameters and neutron star properties: A two-fluid perspective. Phys. Rev. D 2024, 109, 043030. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).