Design and Finite Element Analysis of Reducer Housing Based on ANSYS
Abstract
1. Introduction
2. Finite Element Modeling of Reducer Housing
2.1. Basic Theory of the Finite Element Method
2.2. The Structure and Working Principle of the Reducer
2.3. Structural Design of the Reducer Housing
2.3.1. Design Requirements for the Shell
2.3.2. Design Guidelines for the Shell
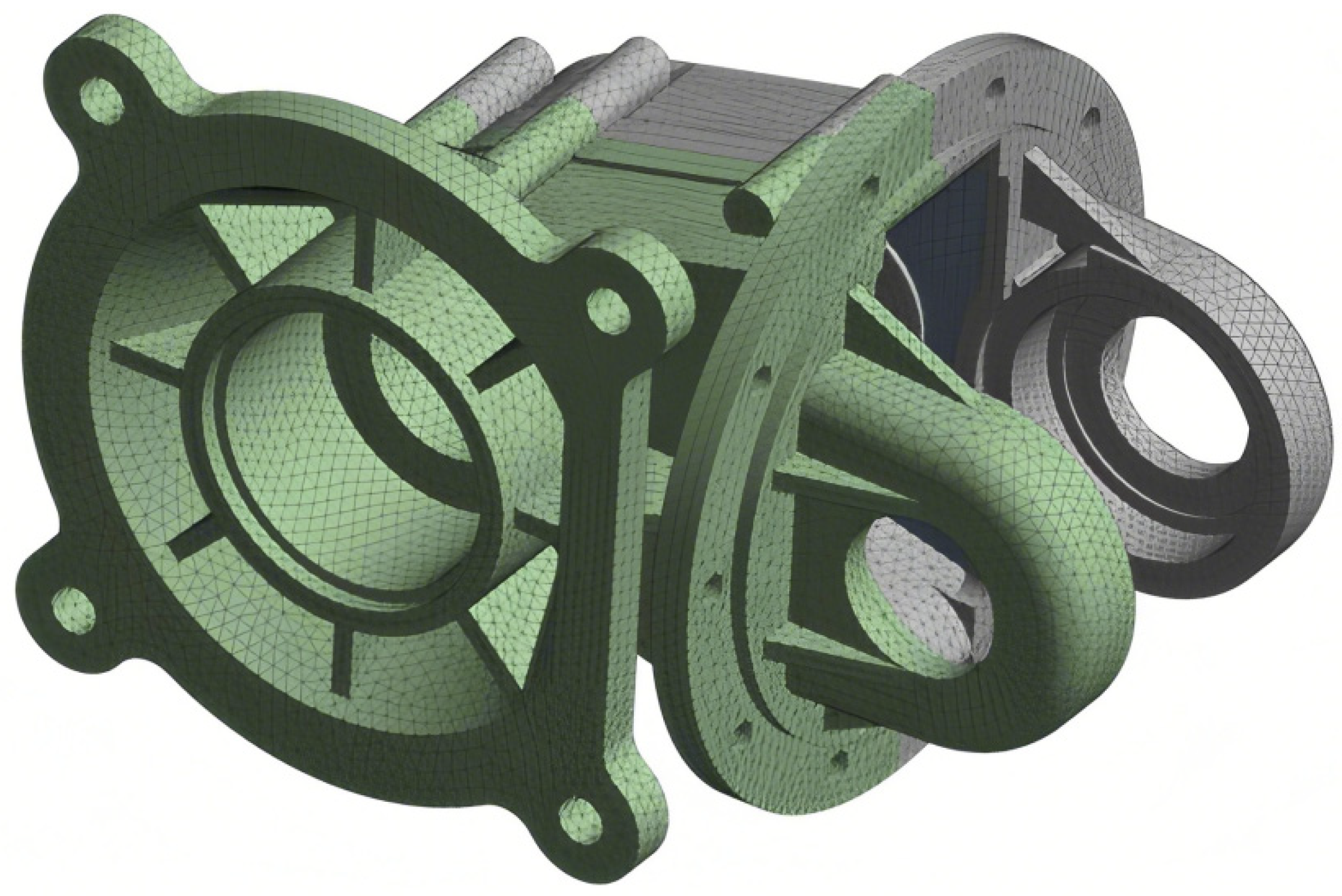
2.3.3. Establishment of the Housing Mode
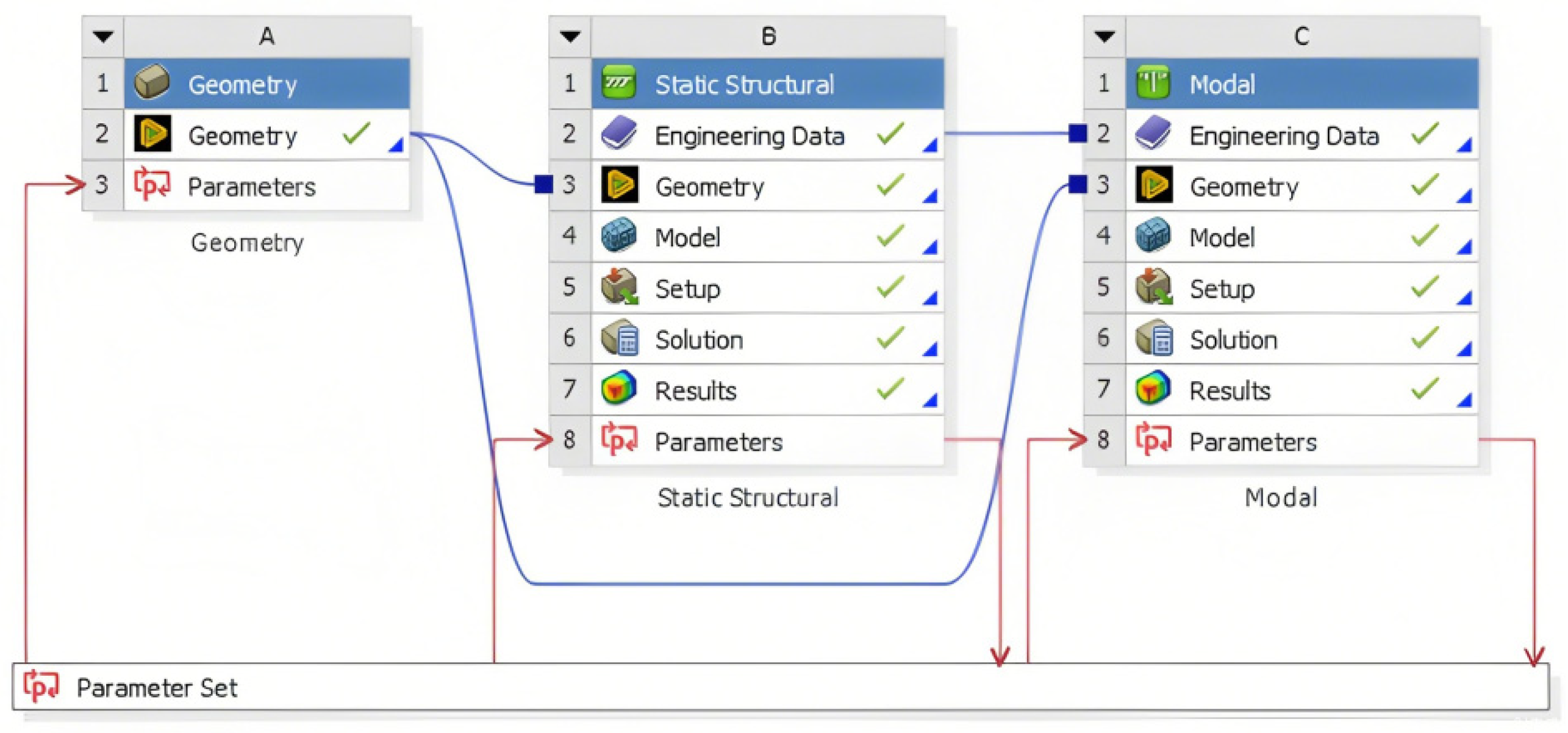
2.4. Finite Element Modeling of the Reducer Housing
3. Finite Element Analysis of Reducer Housing
3.1. Static Analysis of the Shell
3.1.1. Theory and Procedure of Static Analysis
- (1)
- Theory of Static Analysis
- (2)
- The static analysis process of the shell
3.1.2. Dynamic Modeling of the Transmission System Inside the Shell
- (1)
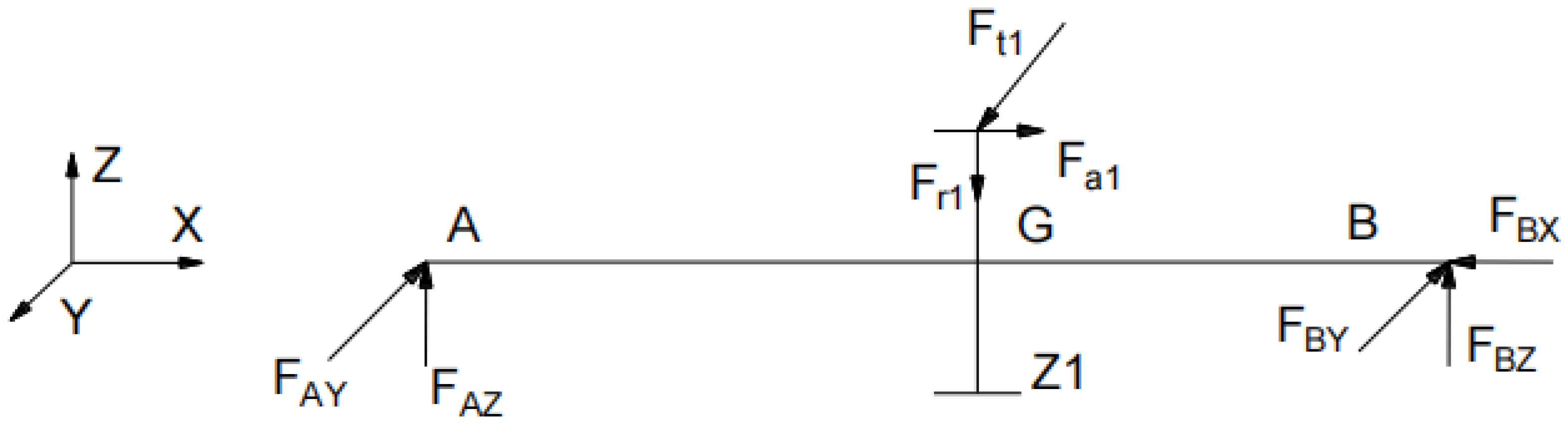
- Force analysis of the transmission system
- (2)
- Dynamic Modeling and Results
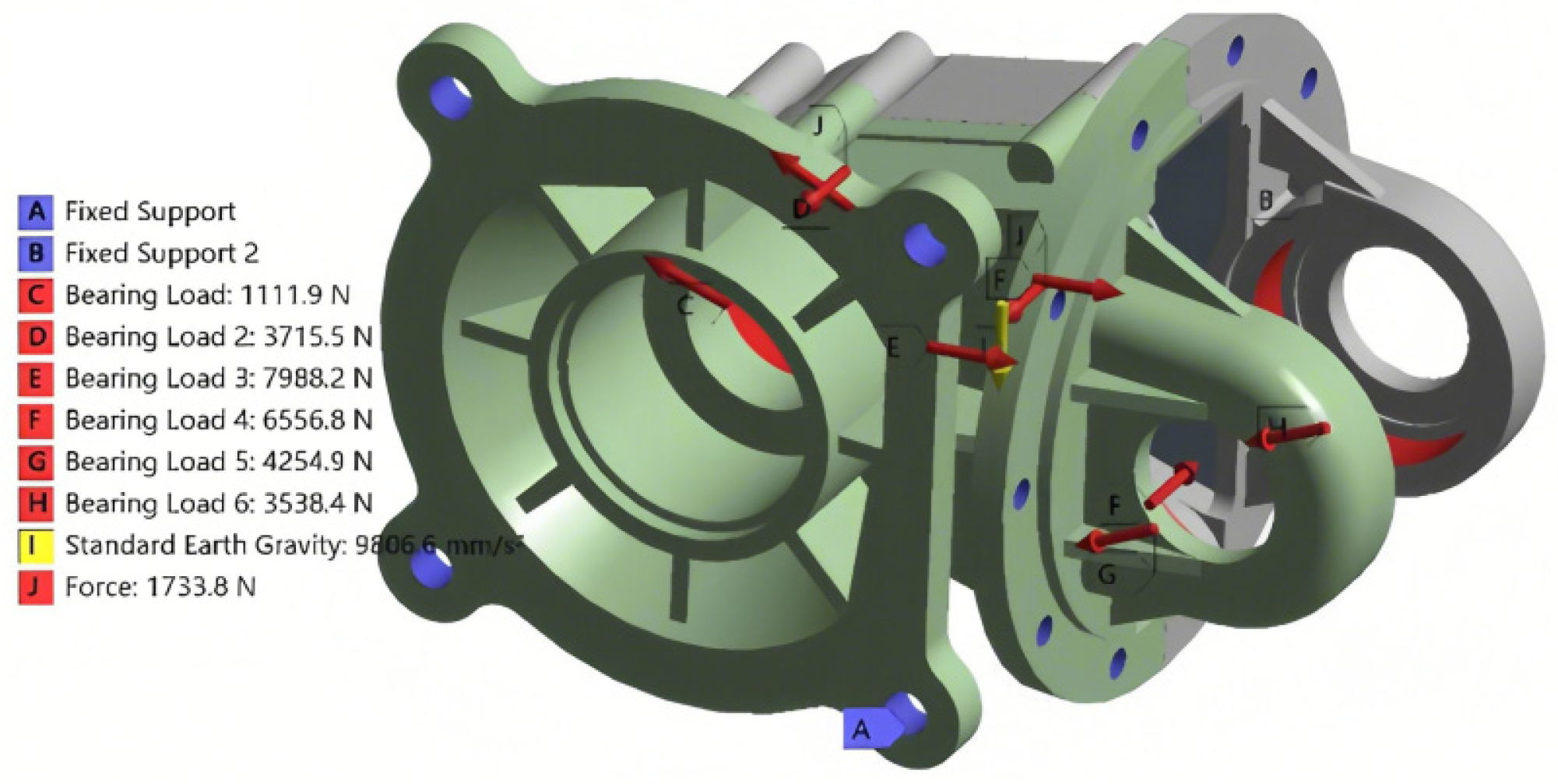
3.1.3. The Setting of Shell Boundary Conditions
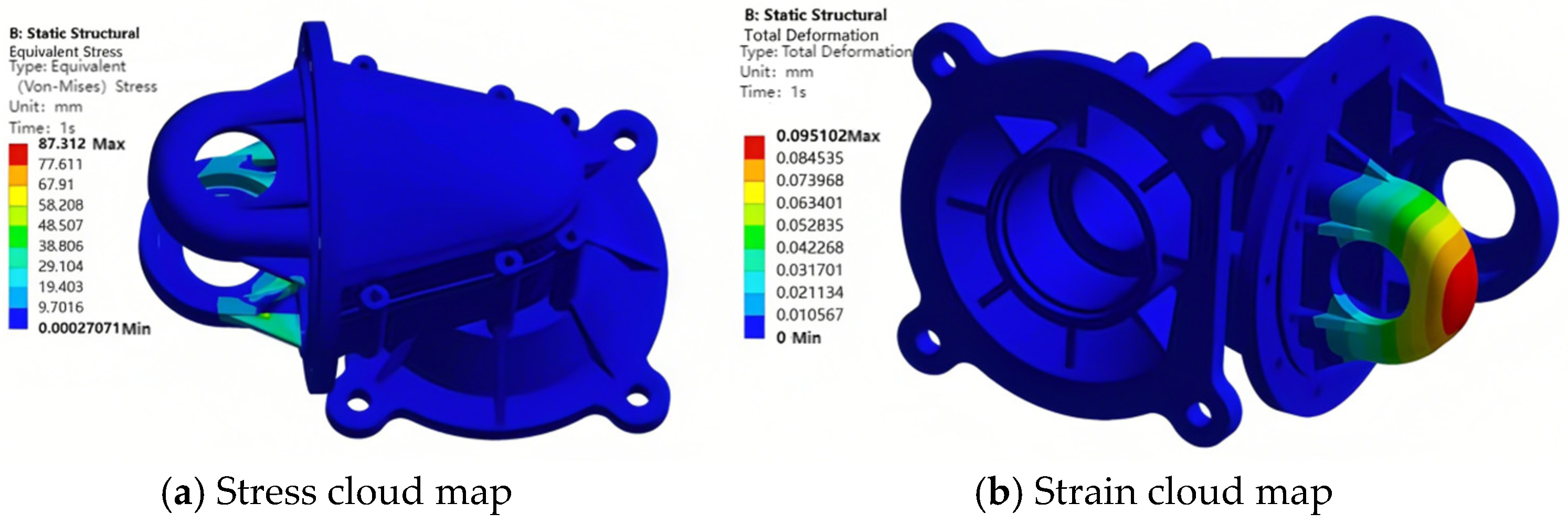
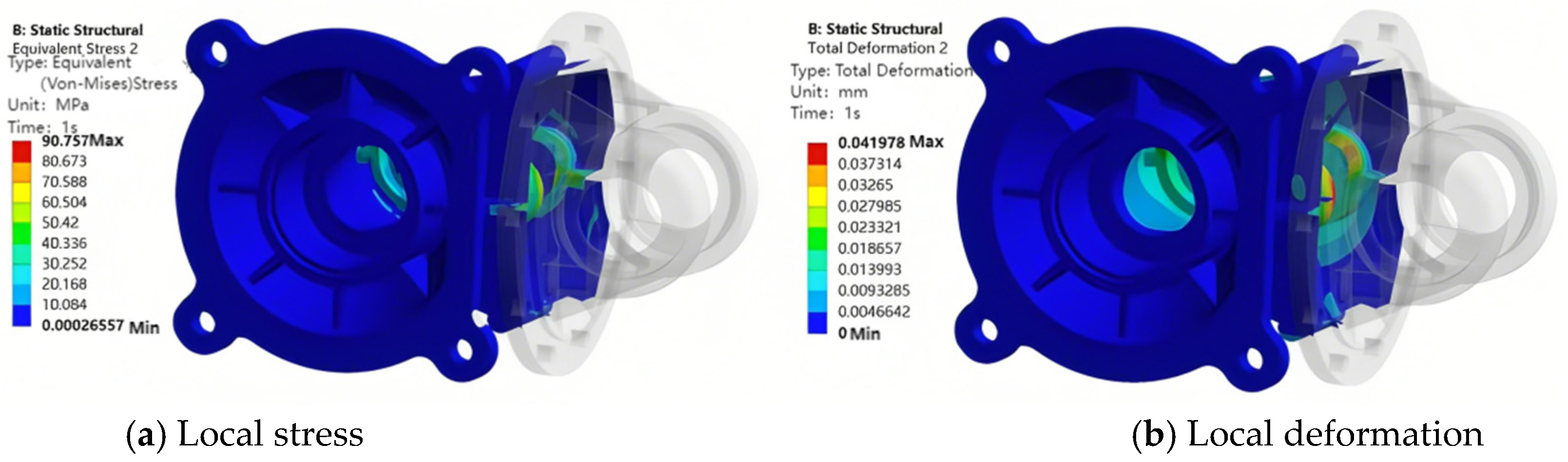
3.1.4. Evaluation of the Static Analysis Results of the Shell
3.2. Shell Constraint Mode Analysis
3.2.1. Modal Analysis Theory and Process
- (1)
- Modal Analysis Theory
- (2)
- Modal Analysis Procedure for the Housing
3.2.2. Analysis Results of Shell Constraint Mode
3.2.3. Evaluation of Shell Constraint Modal Analysis Results
- (1)
- Excitation Frequency of Internal Gear Shaft Self-Rotation, fx:
- (2)
- Motor shaft rotational excitation frequency fn
- (3)
- Gear meshing frequency ft
4. Multi-Objective Optimization of Reducer Housing Based on Approximate Model
4.1. Optimization Process of Reducer Housing Size
4.2. Dimensional Optimization of the Reducer Housing
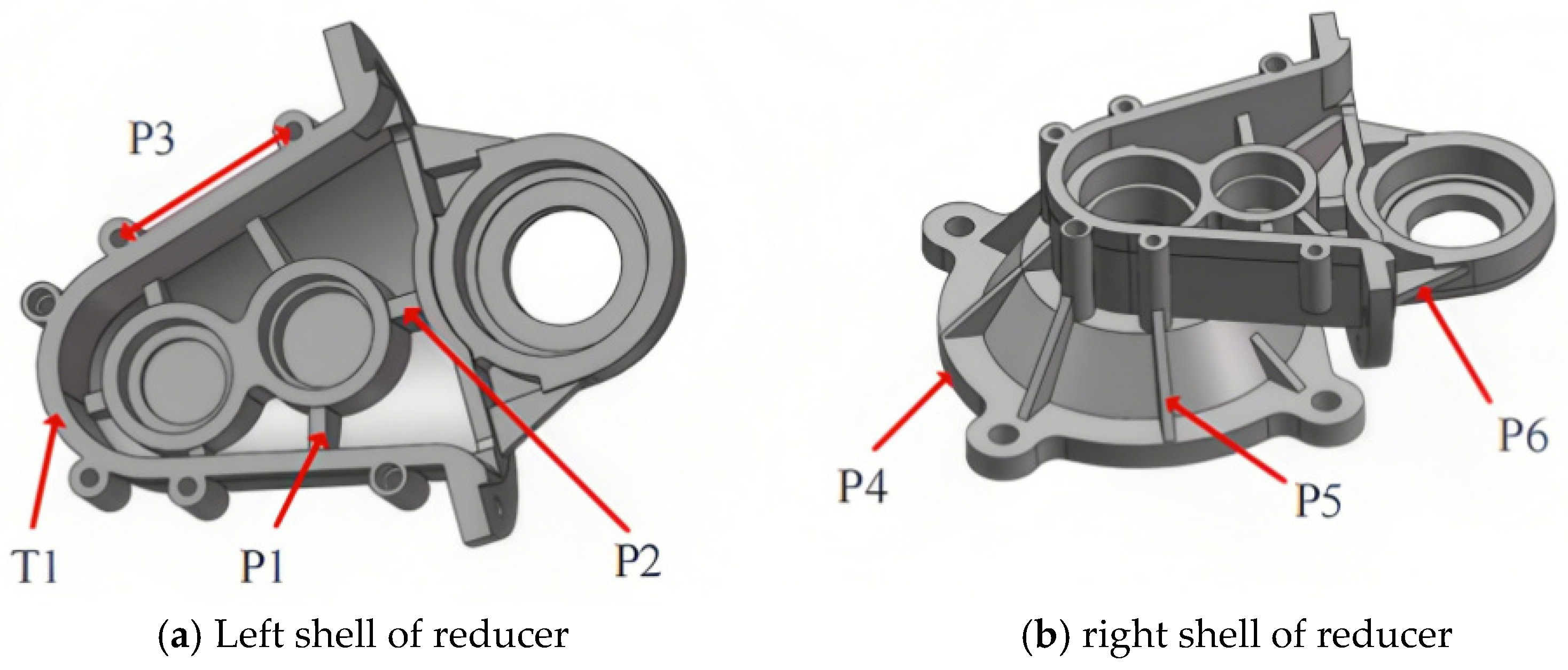
4.2.1. Selection of Design Variables
4.2.2. Experimental Design
- (1)
- Full Factorial Experimental Design
- (2)
- Orthogonal Experimental Design
- (3)
- Latin Hypercube Experimental Design
4.2.3. Screening of Design Variables
- (1)
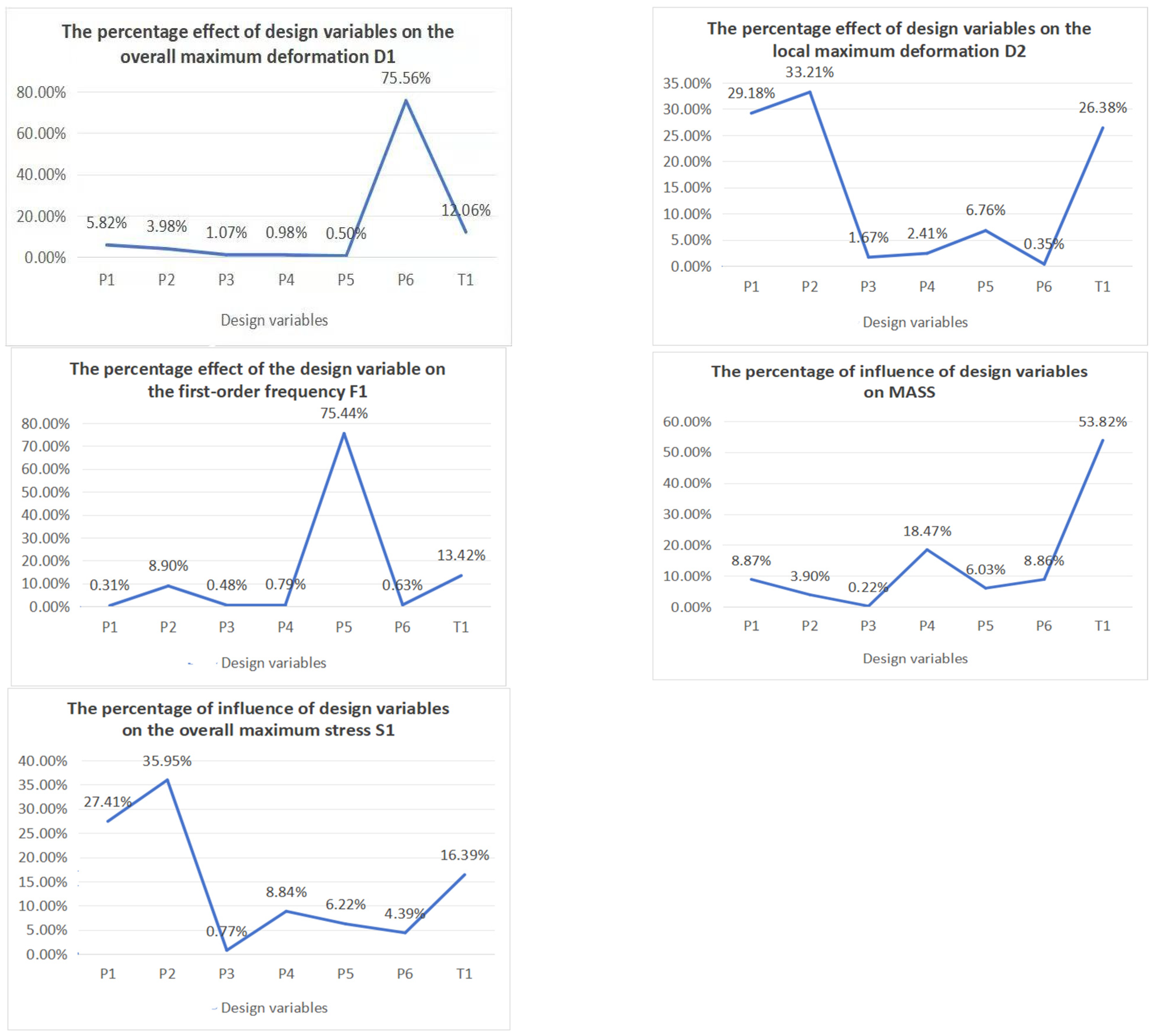
- Analysis of the Pareto Contribution of Design Variables to Output Responses
- (2)
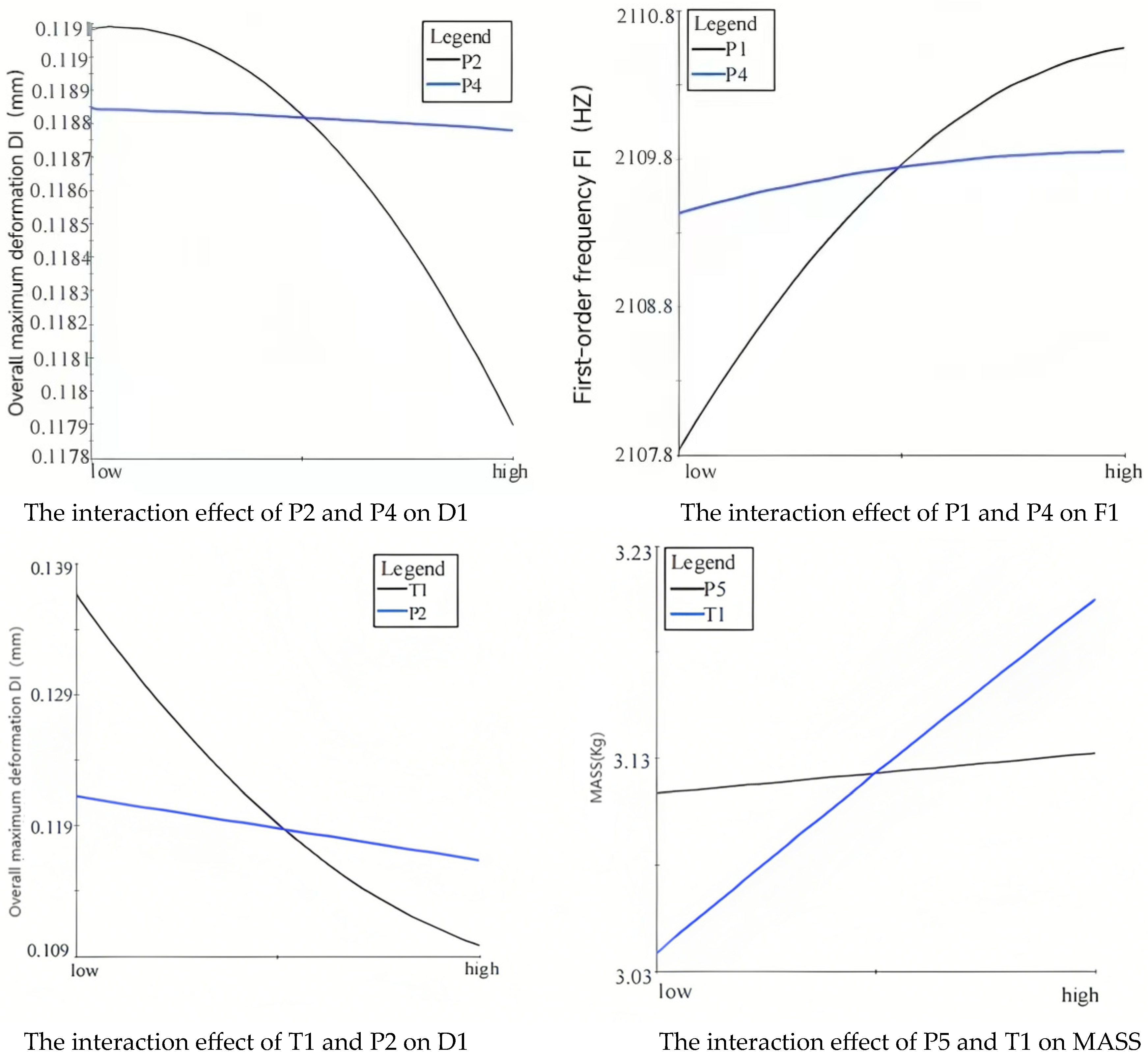
- Analysis of Interaction Effects between Partial Design Variables on Output Responses
4.2.4. Establishment of the Approximate Model of the Shell Response Surface
- (1)
- Surrogate Model Methods
- (2)
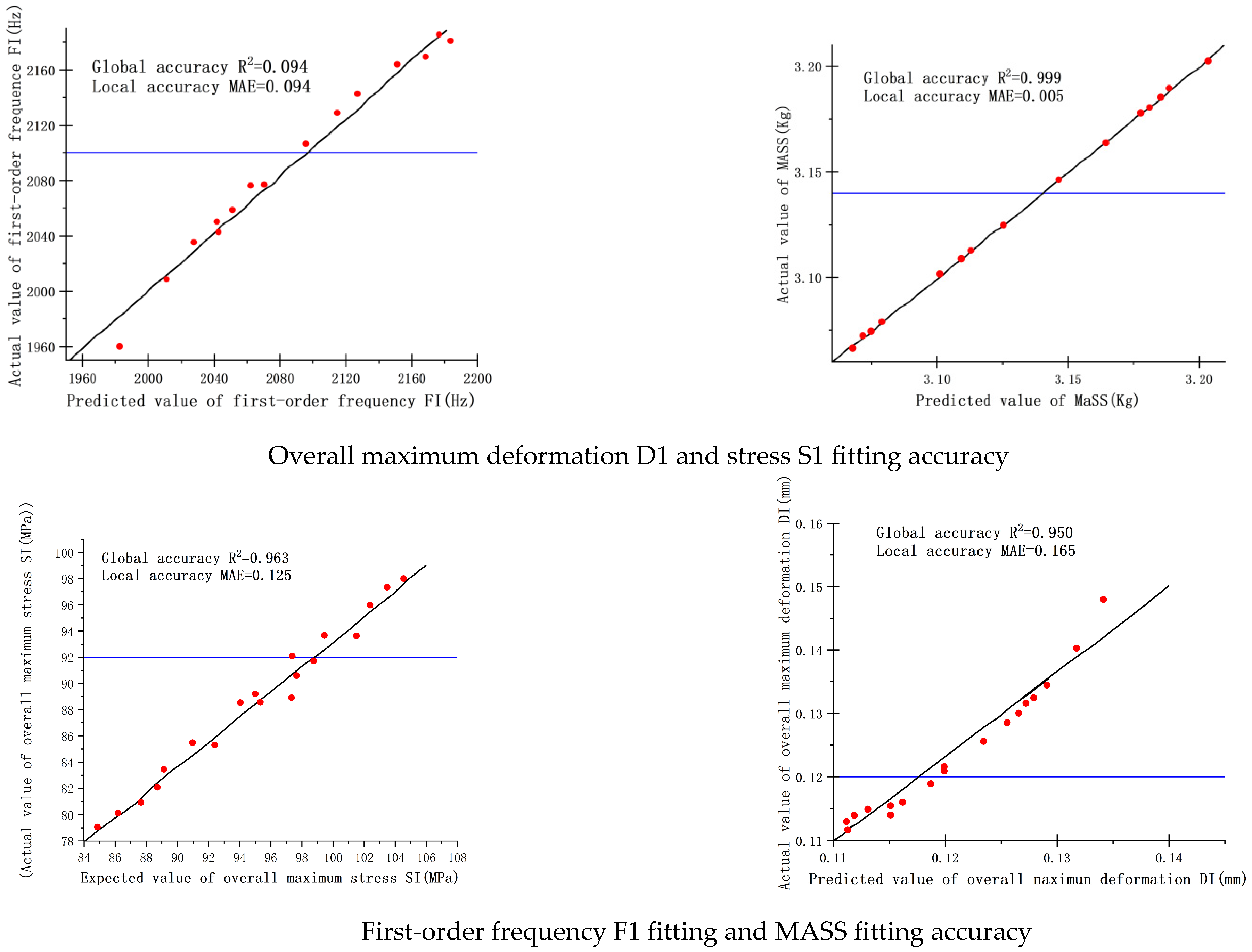
- Error Analysis of Shell Response Surface Surrogate Models
4.2.5. Multi-Objective Optimization of the Shell
- (1)
- Multi-Objective Optimization Methods
- Objective Function Setting:
- Constraint Condition Setting:
- (2)
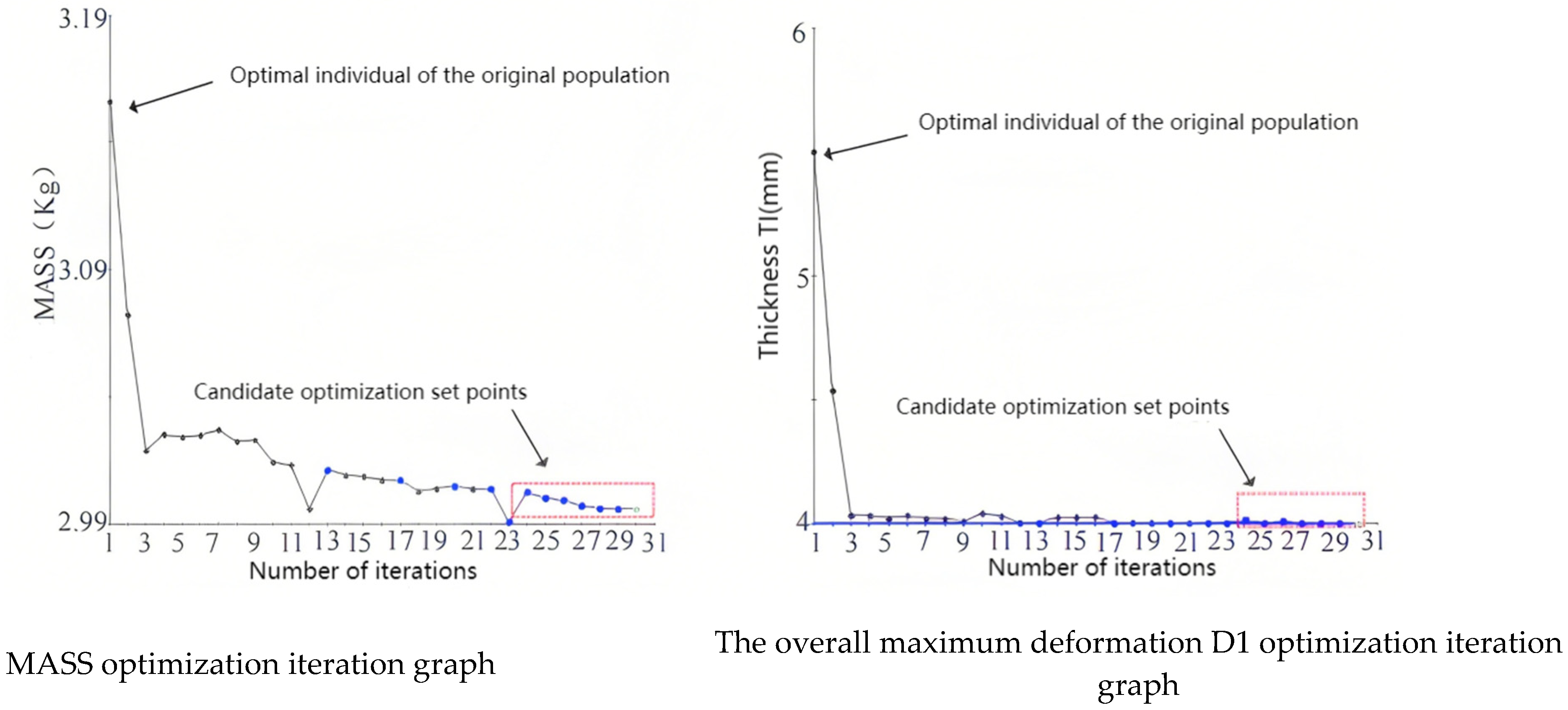
- Analysis of Multi-Objective Optimization Results for the Housing
4.3. Performance Analysis of the Reducer Housing After Size Optimization
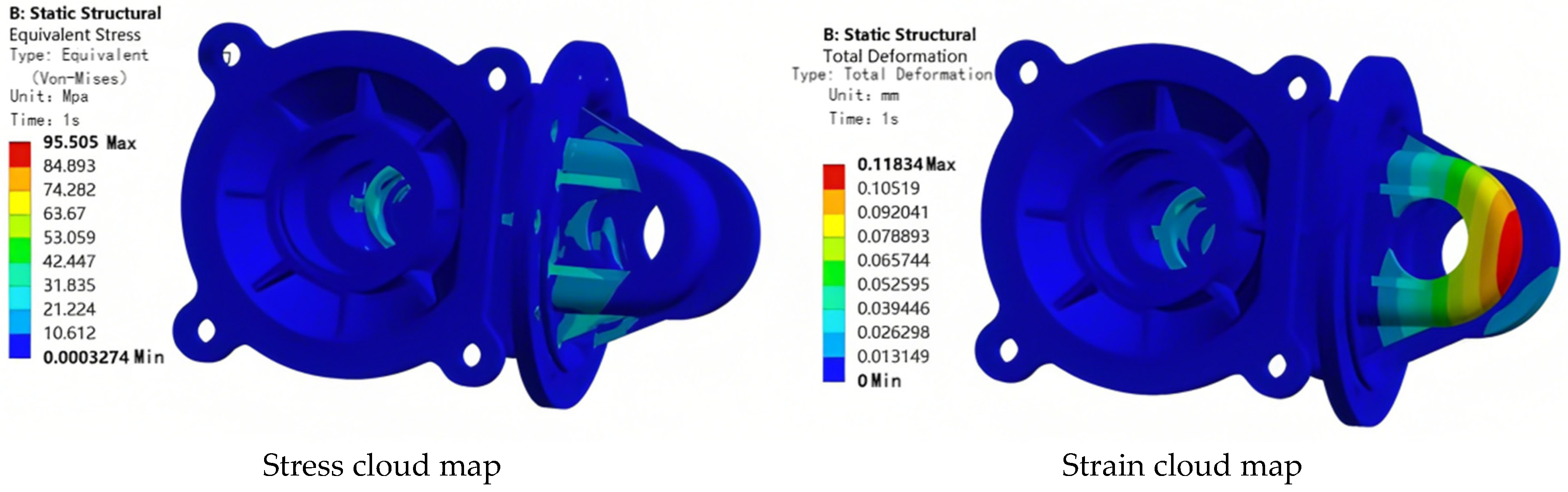
4.3.1. Static Analysis of the Optimized Shell Size
4.3.2. Constrained Modal Analysis After Shell Size Optimization
4.4. The Assembly Model of the Reducer After Size Optimization
4.5. Summary of This Chapter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, H.S. The lightweighting of automobile main reducer. Automot. Eng. 2010, 7, 3. [Google Scholar]
- Pinto, D.V.; Rosa, J.S.; Wander, P.R. Thermal and electrical performance analysis of a lightweight micro CHP system for recreational vehicles. Appl. Therm. Eng. 2024, 257, 124173. [Google Scholar] [CrossRef]
- Tian, G.; Lu, W.; Zhang, X.; Zhan, M.; Dulebenets, M.A.; Aleksandrov, A.; Fathollahi-Fard, A.M.; Ivanov, M. A survey of multi-criteria decision-making techniques for green logistics and low-carbon transportation systems. Environ. Sci. Pollut. Res. 2023, 30, 57279–57301. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Li, F.; Chen, L. Simulation Analysis of the Performance of New Energy Commercial Vehicle Chassis. Automob. New Power 2024, 7, 36–39. [Google Scholar]
- Wheatley, G.; Popoola, S.; Collins, J. Design, Optimization, and Analysis of the Chassis of a Racecar; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Chawla, T.S.; Leonhardt, E. Two Approaches to Optimize Formula SAE Chassis Design Using Finite Element Analysis. In Proceedings of the 2018 ASEE Annual Conference & Exposition, Salt Lake City, UT, USA, 23–27 July 2018. [Google Scholar]
- Gawande, S.H.; Muley, A.A.; Yerrawar, R.N. Optimization of torsional stiffness for heavy commercial vehicle chassis frame. Automot. Innov. 2018, 1, 352–361. [Google Scholar] [CrossRef]
- Pilley, S.; Morkos, B.; Alfalahi, M. Integration and Modularity Analysis for Improving Hybrid Vehicles Battery Pack Assembly; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Topac, M.M.; Karaca, M.; Aksoy, B.; Deryal, U.; Bilal, L. Lightweight design of a rear axle connection bracket for a heavy commercial vehicle by using topology optimisation: A case study. Mechanics 2020, 26, 64–72. [Google Scholar] [CrossRef]
- Tian, G.D.; Cheng, Z.; Amir, M. An enhanced social engineering optimizer for solving an energy-efficient disassembly line balancing problem based on bucket brigades and cloud theory. IEEE Trans. Ind. Inform. 2022, 19, 7148–7159. [Google Scholar]
- Sun, Z.; Siringoringo, D.M.; Fujino, Y. Load-carrying capacity evaluation of girder bridge using moving vehicle. J. Eng. Struct. 2021, 229, 111645. [Google Scholar] [CrossRef]
- Galos, J.; Sutcliffe, M. Material selection and structural optimization for lightweight truck trailer design. SAE Int. J. Commer. Veh. 2020, 12, 281–297. [Google Scholar] [CrossRef]
- Ding, X.; Liu, X. Modal Analysis of Automobile Wheels based on Lightweight Technology. J. Electr. Syst. 2024, 20, 353–364. [Google Scholar] [CrossRef]
- Bian, J. Optimum Design and Modal Analysis of Reducer Worm Drive for Belt Conveyor by Matlab and ANSYS. PLoS ONE 2019, 10, e0136706. [Google Scholar]
- Yang, X.; Tartakovsky, G.; Tartakovsky, A.M. Physics information aided kriging using stochastic simulation models. SIAM J. Sci. Comput. 2021, 43, A3862–A3891. [Google Scholar] [CrossRef]
- Zhao, P.; Xue, L. Variable selection for semiparametric varying coefficient partially linear errors-in-variables models. J. Multivar. Anal. 2010, 101, 1872–1883. [Google Scholar] [CrossRef]
- Li, J.; Tan, J.; Dong, J. Lightweight Design of front suspension upright of electric formula car based on topology optimization method. World Electr. Veh. J. 2020, 11, 15. [Google Scholar] [CrossRef]
- Yang, Q.; Youli, L. Lightweight Design and Production Practice of the Heavy Truck Drive Axle. Automob. Des. 2023, 47, 148–152. [Google Scholar]
- Junk, S.; Rothe, N. Lightweight design of automotive components using generative design with fiber-reinforced additive manufacturing. Procedia CIRP 2022, 109, 119–124. [Google Scholar] [CrossRef]
- Xu, W.; Ma, X.; Jin, Y. A Modular Mathematical Modeling Method for Smart Design and Manufacturing of Automobile Driving Axles. J. Circuits Syst. Comput. 2024, 33, 2450115. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Tian, G.; Ke, H.; Fu, Y. Efficient multi-objective metaheuristic algorithm for sustainable harvest planning problem. Comput. Oper. Res. 2023, 158, 106304. [Google Scholar] [CrossRef]
- Nwe, T.; Tantrapiwat, A.; Pimsarn, M. Multi-Objective Optimization of Lightweight Inboard Bearing Design for High-Speed Railway Axle. J. Res. Appl. Mech. Eng. 2024, 12, 1–9. [Google Scholar]
- Shi, D.; Ye, Y.; Gillwald, M.; Hecht, M. Designing a lightweight 1D convolutional neural network with Bayesian optimization for wheel flat detection using carbody accelerations. Int. J. Rail Transp. 2021, 9, 311–341. [Google Scholar] [CrossRef]
- Zhao, F. Finite-Element Analysis on Lightweight Material of Drive Axle Housin. J. Compos. Adv. Mater./Rev. Des Compos. Des Matériaux Avancés 2021, 31, 41–49. [Google Scholar]












| Rated Power /kW | Peak Power /kW | Peak Torque /Nm | Rated Speed /r/min | Frequency /Hz |
|---|---|---|---|---|
| 4 | 6 | 65 | 3000 | 102 |
| Elastic Model/GPa | Poison by | Density/Kg·m−3 | Tensile Strength/MPa | Yield Strength/MPa |
|---|---|---|---|---|
| 70 | 0.33 | 2700 | 230 | 170 |
| Project | Input Shaft Gear Z1 | Intermediate Shaft Gear Z2 | Intermediate Shaft Gear Z3 | Output Shaft Gear Z4 |
|---|---|---|---|---|
| Normal modulus m | 1.5 | 1.5 | 1.75 | 1.75 |
| Number of teeth Z | 18 | 46 | 18 | 73 |
| Tooth profile Angle α | 20° | 20° | 20° | 20° |
| Helix angle β | 20° | 20° | 20° | 20° |
| Rotation direction | Left rotation | Right rotation | Right rotation | Left rotation |
| Project | FX (N) | FY (N) | FZ (N) |
|---|---|---|---|
| Bearing at input shaft A | 0 | 1075.2 | 283.5 |
| Bearing at input shaft B | 1733.8 | 3456.4 | 1363.3 |
| Bearing at intermediate shaft C | 0 | 7925.4 | 999.7 |
| Bearing at intermediate shaft D | 2201 | 6486 | 960.7 |
| Bearing at output shaft E | 2656.2 | 3755.1 | 2000.9 |
| Bearing at output shaft F | 0 | 3152.8 | 1606.3 |
| Order | Modal Frequency/Hz | Vibration Mode Performance |
|---|---|---|
| 1 | 2480.6 | Bend locally along the Y direction |
| 2 | 2506.6 | Bend locally along the Y direction |
| 3 | 3228.5 | Bend locally along the Y direction |
| 4 | 3685.7 | Bend locally along the Y direction |
| 5 | 3979.3 | Local distortion along the X direction |
| 6 | 4021.6 | Local distortion along the Y direction |
| 7 | 4443.7 | Stretch locally along the Z direction |
| 8 | 4675.7 | Stretch locally along the Z direction |
| 9 | 5021.7 | Stretch locally along the X direction |
| 10 | 5754.1 | Local distortion along the Z direction |
| Code Name | The Meaning of Design Variables | Initial Value/mm | Value Range/mm |
|---|---|---|---|
| T1 | The wall thickness of the left and right shells | 6 | 4–7 |
| P1 | The widths of the reinforcing ribs on both sides of the bearing housings of the left and right shells | 6 | 4–7 |
| P2 | The width of the reinforcing ribs along the axis of the bearing housing of the left and right shells | 7 | 4–8 |
| P3 | The distance between the centers of the two bolt holes on the left and right shells | 72 | 65–75 |
| P4 | The thickness of the flange end face | 12 | 9–13 |
| P5 | The width of the reinforcing ribs on the flange plate of the left shell | 5 | 2–6 |
| P6 | The widths of the reinforcing ribs on both sides of the output shafts of the left and right shells | 5 | 2–6 |
| Serial Number | P1 | P2 | P3 | P4 | P5 | P6 | T1 |
|---|---|---|---|---|---|---|---|
| 1 | 4.045 | 4.020 | 68.065 | 12.538 | 3.910 | 3.568 | 4.693 |
| 2 | 4.164 | 5.447 | 73.392 | 9.643 | 3.166 | 4.653 | 5.327 |
| 3 | 4.221 | 7.638 | 65.905 | 10.608 | 4.231 | 2.060 | 5.116 |
| 4 | 4.287 | 4.161 | 73.894 | 11.593 | 5.698 | 6.000 | 5.402 |
| 5 | 4.402 | 4.985 | 73.794 | 11.492 | 2.241 | 3.266 | 4.106 |
| … | … | … | … | … | … | … | … |
| 33 | 6.754 | 4.804 | 74.648 | 12.940 | 3.628 | 4.090 | 4.980 |
| 34 | 6.810 | 6.915 | 71.231 | 11.312 | 5.658 | 2.623 | 5.342 |
| 35 | 6.874 | 5.648 | 73.090 | 9.497 | 2.864 | 5.136 | 4.965 |
| 36 | 6.930 | 6.935 | 70.528 | 12.859 | 4.010 | 2.020 | 4.829 |
| Serial Number | First-Order Frequency F1/Hz | Quality MASS/Kg | Overall Maximum Deformation D1/mm | Overall Maximum Stress S1/MPa | Local Maximum Deformation D2/mm | Local Maximum Stress S2/mm |
|---|---|---|---|---|---|---|
| 1 | 2053.233 | 3.097 | 0.125 | 115.815 | 0.045 | 115.815 |
| 2 | 2145.596 | 3.114 | 0.116 | 106.943 | 0.044 | 106.943 |
| 3 | 1969.593 | 3.113 | 0.136 | 89.192 | 0.041 | 89.192 |
| 4 | 2202.912 | 3.170 | 0.110 | 117.601 | 0.045 | 117.601 |
| 5 | 2028.189 | 3.025 | 0.128 | 106.042 | 0.042 | 106.042 |
| … | … | … | … | … | … | … |
| 33 | 1959.316 | 3.079 | 0.134 | 98.976 | 0.040 | 98.976 |
| 34 | 2023.987 | 3.175 | 0.128 | 101.595 | 0.041 | 101.595 |
| 35 | 2187.239 | 3.137 | 0.111 | 89.596 | 0.040 | 89.596 |
| 36 | 1957.392 | 3.143 | 0.136 | 91.744 | 0.040 | 91.744 |
| Number | The Meaning of Design Variables | Before Optimization/mm | After Optimization/mm | After Rounding/mm |
|---|---|---|---|---|
| T1 | The wall thickness of the left and right shells | 6 | 4.0008 | 4 |
| P1 | The widths of the reinforcing ribs on both sides of the bearing housings of the left and right shells | 6 | 4.0103 | 4 |
| P2 | The width of the reinforcing ribs along the axis of the bearing housing of the left and right shells | 7 | 7.3126 | 7.5 |
| P3 | The distance between the centers of the two bolt holes on the left and right shells | 72 | 74.914 | 75 |
| P4 | The thickness of the flange end face | 12 | 9.0004 | 9 |
| P5 | The width of the reinforcing ribs on the flange plate of the left shell | 5 | 2.0269 | 2 |
| P6 | The widths of the reinforcing ribs on both sides of the output shafts of the left and right shells | 5 | 5.9517 | 6 |
| First-Order Frequency F1/Hz | Quality MASS/Kg | Overall Maximum Deformation D1/mm | Overall Maximum Stress S1/MPa |
|---|---|---|---|
| 2205.4 | 2.99 | 0.110 | 97.364 |
| Maximum Stress/MPa | Maximum Deformation/mm | |
|---|---|---|
| Before size optimization | 90.757 | 0.109 |
| After size optimization | 95.505 | 0.118 |
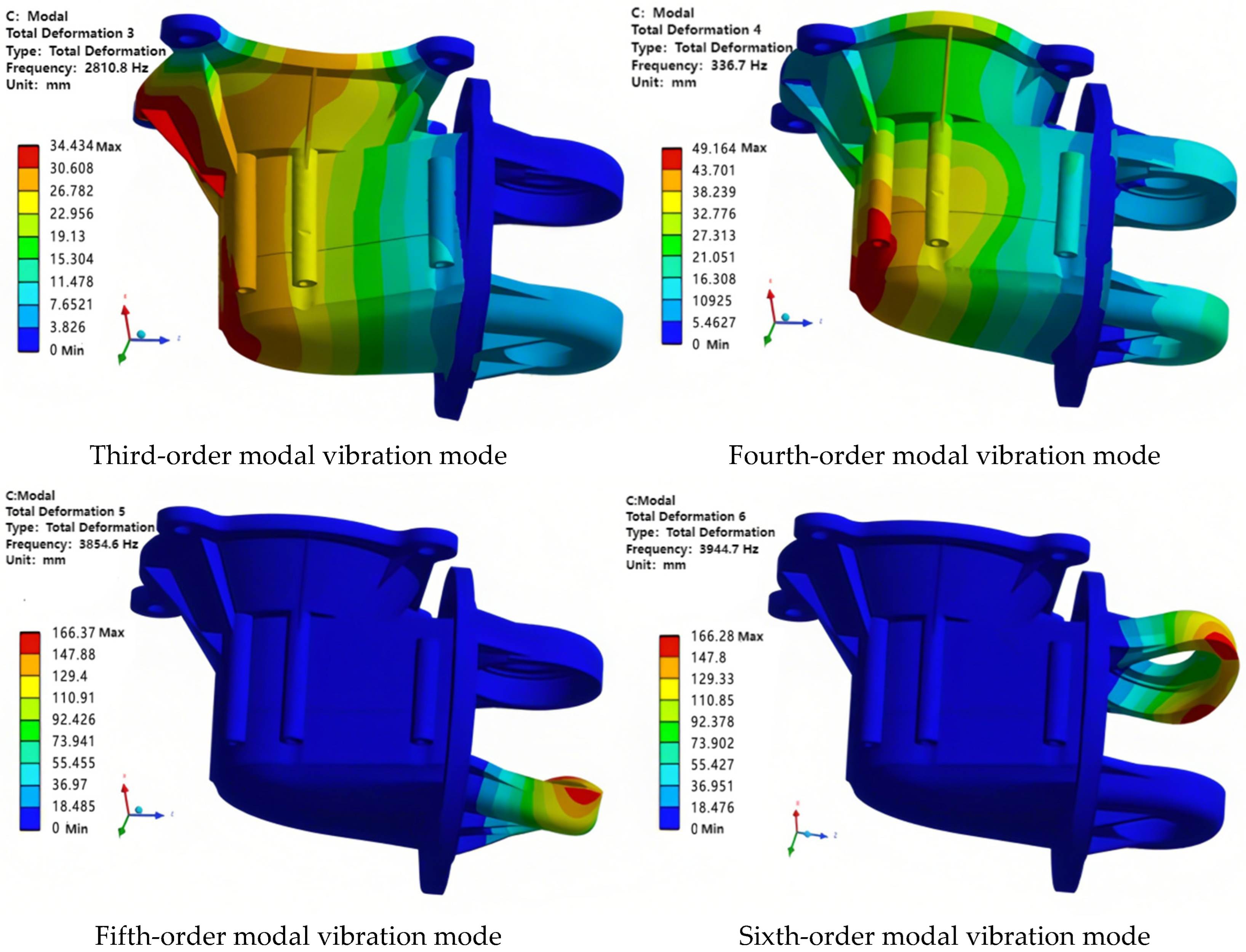
| Order | Before Size Optimization/Hz | After Size Optimization/Hz | Rate of Change |
|---|---|---|---|
| 1 | 2177.2 | 2194.8 | Rise 0.80% |
| 2 | 2349.1 | 2347.6 | Decline 0.08% |
| 3 | 3144.6 | 2810.8 | Decline 10.61% |
| 4 | 3557.7 | 3365.7 | Decline 5.39% |
| 5 | 3790.0 | 3854.6 | Rise 1.70% |
| 6 | 3894.4 | 3944.7 | Rise 1.29% |
| 7 | 4454.8 | 4390.6 | Decline 1.44% |
| 8 | 4650.9 | 4544.5 | Decline 2.28% |
| 9 | 4837.5 | 4701.8 | Decline 0.28% |
| 10 | 4998.1 | 4841.6 | Decline 3.13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gao, X.; Huang, H.; Tan, J. Design and Finite Element Analysis of Reducer Housing Based on ANSYS. Symmetry 2025, 17, 1663. https://doi.org/10.3390/sym17101663
Liu Y, Gao X, Huang H, Tan J. Design and Finite Element Analysis of Reducer Housing Based on ANSYS. Symmetry. 2025; 17(10):1663. https://doi.org/10.3390/sym17101663
Chicago/Turabian StyleLiu, Yingshuai, Xueming Gao, Hao Huang, and Jianwei Tan. 2025. "Design and Finite Element Analysis of Reducer Housing Based on ANSYS" Symmetry 17, no. 10: 1663. https://doi.org/10.3390/sym17101663
APA StyleLiu, Y., Gao, X., Huang, H., & Tan, J. (2025). Design and Finite Element Analysis of Reducer Housing Based on ANSYS. Symmetry, 17(10), 1663. https://doi.org/10.3390/sym17101663








