HGAA: A Heterogeneous Graph Adaptive Augmentation Method for Asymmetric Datasets

Abstract

Edge intelligence plays an increasingly vital role in ensuring the reliability of distributed microservice-based applications, which are widely used in domains such as e-commerce, industrial IoT, and cloud-edge collaborative platforms. However, anomaly detection in these systems encounters a critical challenge: labeled anomaly data are scarce. This scarcity leads to severe class asymmetry and compromised detection performance, particularly under the resource constraints of edge environments. Recent approaches based on Graph Neural Networks (GNNs)—often integrated with DeepSVDD and regularization techniques—have shown potential, but they rarely address this asymmetry in an adaptive, scenario-specific way. This work proposes Heterogeneous Graph Adaptive Augmentation (HGAA), a framework tailored for edge intelligence scenarios. HGAA dynamically optimizes graph data augmentation by leveraging feedback from online anomaly detection. To enhance detection accuracy while adhering to resource constraints, the framework incorporates a selective bias toward underrepresented anomaly types. It uses knowledge distillation to model dataset-dependent distributions and adaptively adjusts augmentation probabilities, thus avoiding excessive computational overhead in edge environments. Additionally, a dynamic adjustment mechanism evaluates augmentation success rates in real time, refining the selection processes to maintain model robustness. Experiments were conducted on two real-world datasets (TraceLog and FlowGraph) under simulated edge scenarios. Results show that HGAA consistently outperforms competitive baseline methods. Specifically, compared with the best non-adaptive augmentation strategies, HGAA achieves an average improvement of 4.5% in AUC and 4.6% in AP. Even larger gains are observed in challenging cases: for example, when using the HGT model on the TraceLog dataset, AUC improves by 14.6% and AP by 18.1%. Beyond accuracy, HGAA also significantly enhances efficiency: compared with filter-based methods, training time is reduced by up to 71% on TraceLog and 8.6% on FlowGraph, confirming its suitability for resource-constrained edge environments. These results highlight the potential of adaptive, edge-aware augmentation techniques in improving microservice anomaly detection within heterogeneous, resource-limited environments.

1. Introduction

Microservice architecture has emerged as a leading paradigm for building scalable, modular, and maintainable distributed systems [1,2]. By decomposing monolithic applications into loosely coupled, independently deplorably services, microservices enable rapid development and continuous delivery. However, the dynamic and heterogeneous nature of these systems makes ensuring reliability a complex challenge [3]. Detecting anomalies in service call patterns is crucial, as these anomalies often indicate failures, misconfigurations, or security breaches that can propagate across the system.

A central challenge in microservice anomaly detection is the severe class asymmetry, referring to both the extreme disproportion between normal and anomalous instances and the heterogeneity of anomaly patterns caused by the scarcity of labeled anomaly data [4]. Normal instances dominate the dataset, while anomalies are rare, diverse, and often subtle in both structure and attributes. For example, in financial fraud detection scenarios, anomalous events may account for only 0.1%

Graph data augmentation has been explored as a solution to the asymmetry problem [5], with strategies such as edge addition, node feature swapping, and edge perturbation aiming to improve model generalization. Yet most existing approaches are random or predefined, failing to consider dataset-specific asymmetry patterns in anomaly distributions. Inappropriate transformations may disrupt critical structural patterns and degrade detection performance. Empirical studies show that augmentation effectiveness varies drastically across datasets, emphasizing the need for adaptive selection strategies to tailor transformations according to anomaly distribution characteristics.

To address this challenge, we propose Heterogeneous Graph Adaptive Augmentation (HGAA), a framework that dynamically adjusts augmentation strategies based on feedback from anomaly distributions. HGAA guides augmentation towards transformations that are likely to produce meaningful variations while avoiding operations that could introduce noise or distort structural patterns. Experiments on two real-world datasets demonstrate that HGAA consistently outperforms competitive baselines in AUC and AP, showing the potential of adaptive augmentation to enhance microservice anomaly detection in heterogeneous environments.

Our main contributions are summarized as follows:

• HGAA, a dataset-adaptive graph augmentation framework designed to improve anomaly detection under severe and anomaly type asymmetry conditions, is proposed.
• A filter network that learns anomaly distributions and selectively retains effective augmentations—optimizing the training process—is designed.
• The effectiveness and efficiency of HGAA are validated through extensive comparative and ablation studies on two real-world microservice datasets: TraceLog and FlowGraph.

The structure of this paper is organized as follows. Section 1 introduces the research background, the related tasks, and the main contributions of this work. Section 2 provides a review of Graph Neural Networks (GNNs), the task of graph-level anomaly detection, and related studies, while also discussing existing graph data augmentation methods and their limitations. Section 3 presents the proposed approach, which consists of three components: the graph augmentation method, the filter network, and the adaptive augmentation training strategy. Section 4 reports the experimental results, where the effectiveness of the proposed method is validated across two datasets and multiple models. Finally, Section 5 concludes the paper by summarizing the main methodology and findings.

2. Related Work

2.1. From General GNNs to Graph Anomaly Detection

Graph Neural Networks (GNNs) have become powerful tools for modeling structured data. As the foundational architecture for processing non-Euclidean graph data [6], representative models such as GCN [7], GraphSAGE [8], and GAT [9] learn node and graph embeddings by aggregating neighbor information or applying attention to capture structural dependencies. However, these homogeneous GNNs have inherent limitations: GCN struggles with scalability due to its full-graph convolution mechanism; GraphSAGE improves efficiency via neighborhood sampling but ignores semantic differences between edge types; GAT employs attention to weigh neighbors yet cannot distinguish heterogeneous relations—all of which restrict their performance in task-specific scenarios like anomaly detection and under class imbalance [10,11]. For heterogeneous graph scenarios (e.g., microservice architectures with diverse node/edge types), heterogeneous GNNs like HetGNN [10], HAN [11], and HGT [12] are more naturally aligned with practical needs. HetGNN encodes node attributes and structures separately but incurs high computational overhead; HAN uses meta-path attention but relies on manually predefined paths, risking missing anomaly-critical relations; HGT learns meta-relations automatically with linear complexity yet still struggles with imbalanced type distributions [5].

Graph-level anomaly detection aims to identify abnormal entire graphs or substructures, playing a crucial role in cybersecurity, fraud detection, and biochemical analysis [13]. Building upon foundational GNN architectures, researchers have developed specialized methods for this task. Early adaptations include knowledge distillation approaches such as GLocalKD [14], which transfers knowledge from complex teacher GNNs to compact student models while preserving performance on both local and global graph properties, and sequence-based methods like DeepLog [15] and DeepTraLog [1]—DeepLog applies LSTM models to sequential data (and can be adapted to graph-derived sequences for temporal anomaly detection), while DeepTraLog integrates gated GNNs with DeepSVDD (a deep one-class classification method) to address class asymmetry and temporal dynamics in graph anomaly detection [1]. For heterogeneous graphs, HRGCN [5] constructs relational hierarchies and applies meta-path-specific convolutions to better model multi-relational systems. However, these methods often assume either sufficient anomalous data or homogeneous relational semantics, which weakens their effectiveness under severe class asymmetry or heterogeneous constraints. Recent surveys further emphasize that detecting rare anomalies in dynamic, multi-relational graphs remains an open challenge [13,16,17,18].

Gap

Most existing anomaly detection methods either (i) rely on abundant anomalous instances, (ii) overlook heterogeneity in graph relations (failing to leverage heterogeneous GNN advantages or address their limitations like HAN’s manual meta-paths), or (iii) neglect augmentation strategies that selectively amplify minority anomalous substructures. This motivates the need for augmentation-aware strategies tailored to imbalanced, heterogeneous anomaly detection.

2.2. Graph Data Augmentation

To improve robustness and generalization under limited or imbalanced training data (a core challenge in graph anomaly detection [19]), graph data augmentation (GDA) has become a central tool. Early GDA methods include GraphMix [20], which extends the Mixup technique from images to graphs by linearly interpolating existing node features to generate synthetic training examples with blended attributes; GraphSAINT [21], which adopts subgraph sampling to improve GNN scalability—this sampling process also serves as augmentation by exposing the model to diverse local graph views; and DropEdge [22], a simple yet effective regularization technique that randomly removes edges during training to prevent overfitting, though it risks deleting critical edges for anomaly distinction [23]. Contrastive learning frameworks (e.g., GraphCL [24]) further leverage augmentation by maximizing agreement between representations of two different augmented views of the same graph, aiming to learn rich, task-agnostic graph embeddings via positive/negative pair construction [24].

More sophisticated and recent advances in GDA emphasize adaptive and structure-aware strategies. Adversarial augmentation methods like FLAG [23] (Free Large-scale Adversarial Augmentation on Graphs) generate challenging training samples by adding small, structure-aware noise to node features (maximizing training loss to improve model robustness against adversarial attacks); structure-aware methods such as GraphCrop [25] and Graph Transplant [26]—GraphCrop performs instance-level cropping (masking or removing parts of graph instances) to enforce model robustness to incomplete information, while Graph Transplant generates diverse augmented graphs by transferring substructures between graphs to simulate unseen structural compositions [26]; consistency-based models like GRAND [27] (Graph Augmentation with Random propagation and Consistency regularization) create multiple augmented graph views via random propagation and use consistency regularization to ensure similar model outputs for perturbed views [27].

Furthermore, adaptive augmentation approaches (e.g., [28]) move beyond fixed random policies, learning optimal augmentation parameters or strategies from data or task feedback to generate task-specific variations. Adversarial and structure-aware methods like GAUG [29] and Graph Structure Learning [30] focus on generating augmentations that either enhance robustness against specific perturbations (GAUG) or explicitly manipulate graph structures to create meaningful training variations (Graph Structure Learning) [29,30]. For heterogeneous graphs, GAAD [31] combines augmentation with adaptive denoising, demonstrating that naive application of homogeneous augmentations may corrupt semantic constraints (e.g., invalid cross-type edges) and lose anomaly-relevant signals [31]. Despite these advancements, most adaptive methods still face limitations: they are designed under homogeneous graph assumptions [28,29], lack relation awareness (failing to model type-specific dependencies), and optimize for general classification rather than amplifying minority anomalous substructures—critical gaps for heterogeneous anomaly detection [19].

Current augmentation strategies face three limitations: (i) they assume homogeneous graphs, risking semantic violations when applied to heterogeneous domains, (ii) they are relation-unaware, ignoring type-specific interaction patterns crucial for anomaly detection, and (iii) they optimize for general representation quality rather than emphasizing rare anomalous substructures.

2.3. Positioning of HGAA

Bringing together the above threads, we observe that general GNN models (both homogeneous and heterogeneous) excel at representation learning but struggle under class asymmetry [6,11,12]; anomaly detection methods (e.g., GLocalKD, DeepTraLog, HRGCN) capture abnormality patterns but neglect adaptive augmentation [1,5,14]; and adaptive augmentation methods (e.g., FLAG, GRAND, GAAD) improve robustness but often ignore heterogeneity and anomaly-specific objectives [23,27,31]. This motivates our proposed Heterogeneous Graph Adaptive Augmentation (HGAA) framework.

Unlike prior methods, HGAA achieves the following: (i) introduces relation-aware augmentation operators that preserve heterogeneity (addressing limitations of [28,29]) while selectively amplifying minority anomalous substructures; (ii) employs a filter network to discard unrealistic or semantically invalid augmentations (solving the semantic corruption issue noted in [31]); (iii) integrates augmentation-aware training strategies that adapt to imbalanced settings (tackling class asymmetry challenges in [1,13]). In doing so, HGAA directly addresses the identified gaps in anomaly detection and adaptive augmentation, providing a principled solution for heterogeneous, imbalanced graph anomaly detection.

3. Methodology

In this section, the complete implementation process of the proposed method is systematically elaborated, which comprises three core components: the graph augmentation method, the filter network architecture, and the training algorithm. For the filter network design, knowledge distillation is innovatively incorporated into a heterogeneous Graph Neural Network (HGNN), enabling a graph augmentation framework tailored for heterogeneous graphs. Furthermore, to enhance the model’s adaptability and generalization across diverse application scenarios, two complementary training strategies are proposed.

A heterogeneous graph is denoted as $\mathcal{G}=(V,E,T_V,T_E)$, where $v_i\in V$ represents the i-th node and $e_{i,j}\in E$ denotes the directed edge from node $v_i$ to node $v_j$. The sets $T_V$ and $T_E$ contain the types of nodes and edges, respectively. Node indices start from 0, and $V_i$ refers to the $(i+1)$-th node. Each node $v_i$ is associated with a feature vector $x_i\in {\mathbb{R}}^n$, where n is the feature dimension. The notation $T_{v_i}$ indicates the type of node $v_i$, and $T_{e_{i,j}}$ indicates the type of edge $e_{i,j}$.

3.1. Graph Augmentation Methods

In this subsection, several graph augmentation techniques employed in this work are introduced, accompanied by their corresponding mathematical formulations.

The design of these graph augmentation techniques is motivated by the constraints of real-world edge systems.

3.1.1. Edge Addition

This method randomly adds new edges to the original graph to enhance connectivity and enable the model to access richer neighborhood information. Specifically, a fraction $\eta$ of the total edges is added by random sampling [5]:

$$E^{\prime }=E\cup \left\{e_{i,j}\right\}$$

(1)

The types of the newly added edges are sampled from the set of node types:

$$T_{e_{i,j}}\in T_E$$

(2)

To preserve dataset consistency, the types of sampled nodes and edges follow the original distributions:

$$v_i,v_j,e_{i,j}\sim P\left(T_{v_i}\right),P\left(T_{v_j}\right),P\left(T_{e_{i,j}}\right)$$

(3)

In microservice systems, anomalies often arise when certain services lack sufficient connectivity information (e.g., sparse call traces or incomplete logs). Edge addition simulates missing or latent dependencies by enriching neighborhoods, allowing the model to better generalize in the presence of incomplete or asymmetric graph structures.

3.1.2. Node and Edge Type Swap

This augmentation randomly swaps the types of nodes or edges while keeping the graph’s structure and node features unchanged. Given two distinct node types $T_{v_a}$ and $T_{v_b}$, their corresponding nodes are swapped accordingly. An analogous process applies for edge types:

$$Swap(T_{v_i},T_{v_j})$$

(4)

$$Swap(T_{e_{i,j}},T_{e_{m,n}})$$

(5)

In heterogeneous microservice graphs, anomaly detection is highly sensitive to type semantics (e.g., API calls vs. database queries). Type swap introduces controlled perturbations to simulate mislabeling or unexpected role changes of services and interactions. This challenges the model to distinguish between structural anomalies and benign type variations, improving robustness against asymmetric anomaly classes.

3.1.3. Heterogeneous Edge Perturbation

To simulate noise or uncertainty in heterogeneous graphs, this method perturbs edges by applying an XOR operation between the original adjacency matrix A and a perturbation matrix R generated from prior distributions [5]:

$$A^{\prime }=A\oplus R$$

(6)

$$R(T_{v_i},T_{v_j},T_e)\sim P(T_{v_i},T_{v_j}),P\left(T_e\right)$$

(7)

In distributed systems, anomalies can manifest as unexpected communication links (e.g., unauthorized service calls) or missing expected ones. Edge perturbation captures this by injecting or removing edges while respecting type distributions. It exposes the model to abnormal connectivity patterns that are especially relevant under severe class asymmetry, where rare anomalies may involve subtle topological changes.

3.1.4. Node Feature Swap

This method swaps the feature vectors between randomly selected pairs of nodes, thereby diversifying feature representation while preserving the graph topology:

$$N_{nodeswap}=\lfloor \eta ·\left|V\right|\rfloor$$

(8)

$${\mathbf{x}}_i\leftrightarrow {\mathbf{x}}_j$$

(9)

$$X^{\prime }=\{{\mathbf{x}}_i^{\prime },{\mathbf{x}}_j^{\prime }\}$$

(10)

In microservice traces, feature attributes often correspond to runtime statistics such as latency, throughput, or error codes. Swapping node features simulates unexpected context shifts (e.g., low-latency services suddenly behaving like high-latency ones). This helps the model generalize across diverse runtime conditions and avoid overfitting to majority anomaly types.

3.1.5. Edge Direction Swap

This augmentation reverses the direction of a fraction of randomly selected directed edges, helping the model better capture relational dynamics:

$$N_{edgeswap}=\lfloor \eta ·\left|E\right|\rfloor$$

(11)

$$e_{i,j}=(v_i\to v_j)⟶e_{j,i}=(v_j\to v_i)$$

(12)

$$E^{\prime }=\left\{e_{i,j}^{\prime }\right|e_{i,j}\in E,e_{j,i}^{\prime }=(v_j\to v_i)\}$$

(13)

Rationale: Microservice interactions are directional (e.g., client → service, service → database). Anomalies may occur when dependencies are reversed or misconfigured (e.g., a service calling its parent). Direction swap simulates these abnormal call patterns, making the model more sensitive to asymmetric anomalies that manifest as directional inconsistencies.

3.2. Filter Network

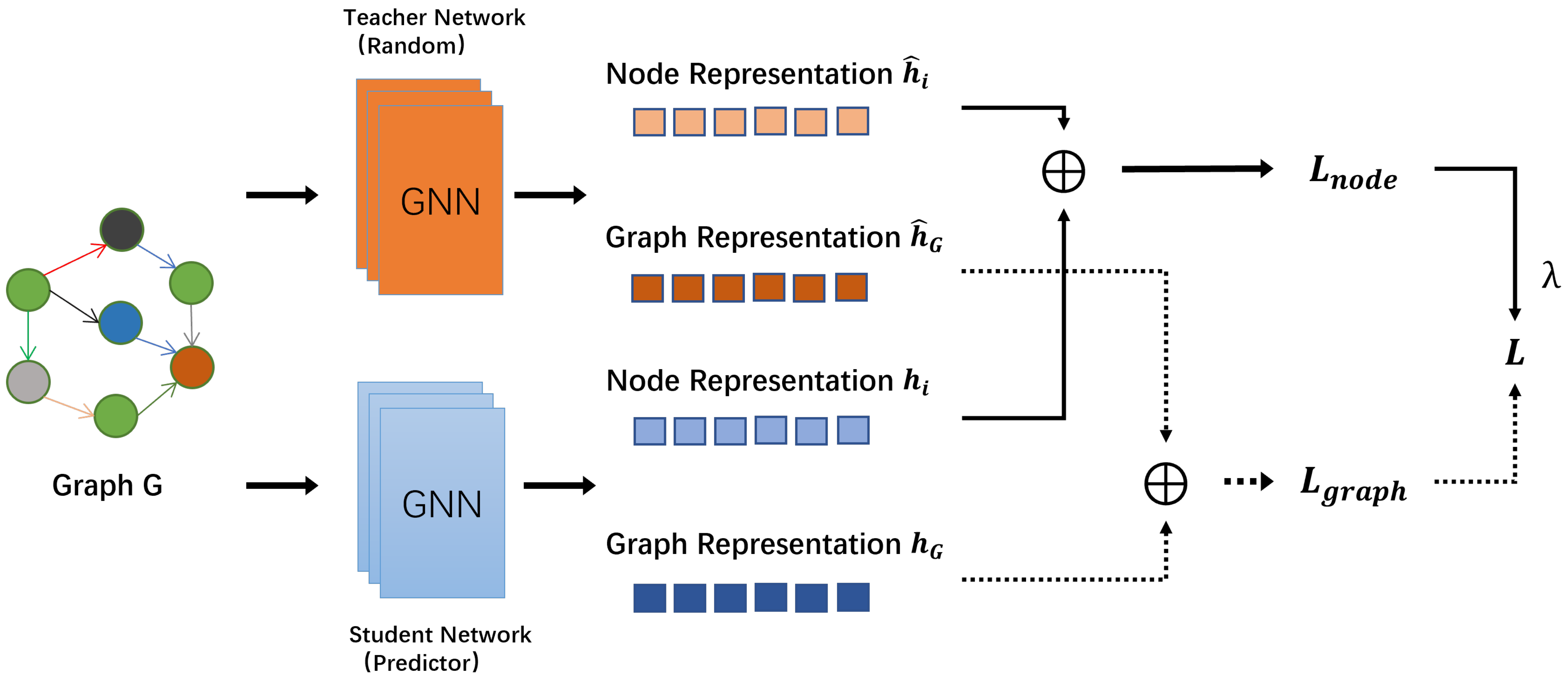
Graphs may exhibit two types of anomalies: local and global. Following [14], a graph $G=(V_G,E_G,T_{G_V},T_{G_E})$ is locally anomalous if it contains abnormal nodes, and globally anomalous if its overall properties deviate from the norm. To simultaneously capture both, a knowledge-distillation-based filter network using a heterogeneous Graph Neural Network is proposed.

The architecture consists of two networks (see Figure 1): a teacher network $N_{Teacher}$ with fixed parameters and a student network $N_{Student}$ initialized randomly. Both share identical structure. The teacher produces node and graph-level embeddings $(h_i,h_g)$, and the student produces $({\widehat{h}}_i,{\widehat{h}}_g)$. The node-level loss is computed as the maximum discrepancy across all nodes to emphasize extreme anomalies. This design differs from simpler anomaly scoring methods (e.g., one-class SVM, DeepSVDD, or autoencoders), which often focus only on either global consistency or local irregularities. By combining graph-level and node-level signals through knowledge distillation, the filter network ensures that both holistic distributional shifts and fine-grained deviations are simultaneously captured.

$$L=L_{graph}+\lambda L_{node}$$

(14)

$$L_{graph}={\displaystyle \frac{1}{\left|\mathcal{G}\right|}}\sum _{G\in \mathcal{G}}KD(h_g,{\widehat{h}}_g)$$

(15)

$$L_{node}={\displaystyle \frac{1}{\left|\mathcal{G}\right|}}\sum _{G\in \mathcal{G}}(max(KD(h_i,{\widehat{h}}_i))$$

(16)

where $\lambda$ is a hyperparameter that can be adjusted to balance the importance of node-level loss and graph-level loss. This dual-objective formulation allows the model to highlight rare or extreme local anomalies without losing sensitivity to global graph-level irregularities, which is crucial for asymmetric anomaly distributions.

The anomaly score for a graph is defined as:

$$f(G;\mathrm{\Theta },\widehat{\mathrm{\Theta }})=KD(h_G,{\widehat{h}}_G)+\lambda max(KD(h_i,{\widehat{h}}_i)$$

(17)

where $\mathrm{\Theta }$ and $\widehat{\mathrm{\Theta }}$ denote the trainable and fixed parameters of the filter model, respectively. Importantly, the teacher–student paradigm also reduces computational overhead compared to adversarial or ensemble-based anomaly scoring approaches, making the framework more suitable for resource-constrained edge environments.

3.3. Training Algorithm

3.3.1. Adaptive Augmentation and Training Strategy

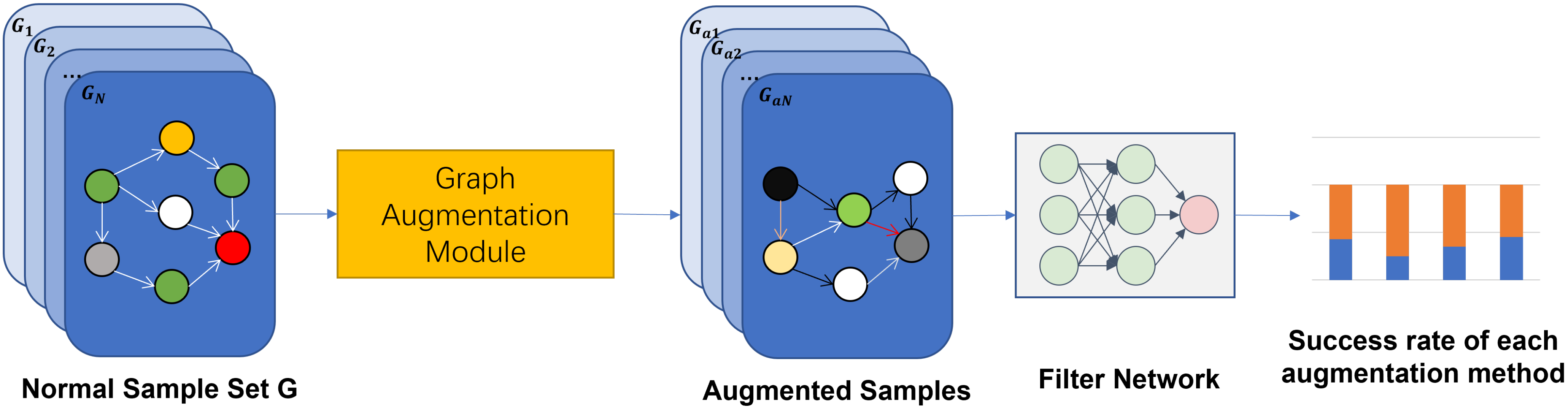
To ensure the quality and effectiveness of the augmented data used for anomaly detection, a filter-based adaptive augmentation strategy is designed. Each augmentation method is applied to a batch of normal graphs, resulting in augmented graphs denoted as $G_{\mathrm{aug}}$. These are input into a pre-trained filter network for inference:

$$\mathrm{score}=f_{\mathrm{filter}}(G_{\mathrm{aug}},\mathrm{\Theta },\widehat{\mathrm{\Theta }})$$

(18)

Here, score represents the filter network’s prediction output for $G_{\mathrm{aug}}$.

To assess the filtering quality of augmented samples, the precision metric is computed:

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

(19)

where $TP$ denotes true positives (correctly accepted augmented samples), and $FP$ denotes false positives (incorrectly accepted samples).

The number of successful augmentations $S_e$ for each augmentation method e is recorded, and the corresponding success rate is calculated as:

$$p_{\mathrm{success}}^e={\displaystyle \frac{S_e+1}{{\mathrm{TotalAug}}_e+1}}$$

(20)

where $S_e$ represents the count of successful augmentations using method e and ${\mathrm{TotalAug}}_e$ is the total number of augmentations performed using method e.

The success rates are then normalized to form a sampling distribution over augmentation methods:

$$p\left({\mathcal{A}}_e\right)={\displaystyle \frac{p_{\mathrm{success}}^e}{{\sum }_{e^{\prime }}{p}_{\mathrm{success}}^{e^{\prime }}}}$$

(21)

This ensures that augmentation methods with higher success rates are more likely to be selected in future training iterations, while still preserving exploration of other methods. The overall pipeline is depicted in Figure 2.

Training Workflow

Once $p\left({\mathcal{A}}_e\right)$ is obtained, training is initiated with dynamically sampled augmentations. For each normal sample, $D_1$, an augmentation method E is selected based on $p\left({\mathcal{A}}_e\right)$. The augmented sample $D_{\mathrm{aug}1}$ is then sent to the filter network with probability:

$$P_{\mathrm{check}}^E=min(1,\lambda (1-p_{\mathrm{success}}^E))$$

(22)

Here, $P_{\mathrm{check}}^E$ is the probability of checking $D_{\mathrm{aug}1}$ with the filter network. The hyperparameter $\lambda$ controls the aggressiveness of filtering: lower success rates result in higher checking probability. If $D_{\mathrm{aug}1}$ fails the filter test, a new sample $D_2$ is selected and re-augmented using method E, repeating the process until a qualified sample is produced.

This probabilistic filtering mechanism balances the trade-off between maintaining data diversity and ensuring sample quality by dynamically adjusting the filtering intensity based on augmentation method performance. Augmentation methods with lower reliability are more strictly filtered, while high-performing methods contribute more samples to the training set.

As illustrated in Figure 3, the augmentation pipeline proceeds in a probabilistic yet structured manner. First, a normal graph sample g is randomly selected from the dataset. An augmentation method E is then chosen according to its selection probability $p\left({\mathcal{A}}_E\right)$, producing an augmented graph $g^{\prime }$. For each augmented sample, there exists a probability $p_{\mathrm{check}}^E$ that it is further processed by the filter network. If $g^{\prime }$ is not selected for filtering, it is directly added to the training batch. If it is sent to the filter network, the network evaluates whether the augmentation preserves task-relevant semantics. Augmented samples that pass this check are admitted into the batch, while those that fail are discarded, and the pipeline re-samples a new normal graph g to undergo augmentation with method E again. This iterative process ensures that each training batch is enriched with both diverse and semantically valid augmentations, while filtering out low-quality or misleading samples.

Batch Composition

This process continues until the number of normal samples matches the number of augmented (pseudo-anomalous) samples in the batch:

$$N_{\mathrm{normal}}=N_{\mathrm{aug}}$$

(23)

where $N_{\mathrm{normal}}$ and $N_{\mathrm{aug}}$ are the counts of original and augmented samples, respectively.

Once this balance is reached, the batch is constructed as:

$$\begin{array}{cc}\hfill \mathrm{Batch}\_\mathrm{data}& =\{G_1,G_2,\dots ,G_n;G_1^{\mathrm{aug}},G_2^{\mathrm{aug}},\dots ,G_n^{\mathrm{aug}}\}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \mathrm{Label}& =\{\underset{n}{\underbrace{\mathrm{normal},\dots ,\mathrm{normal}}};\underset{n}{\underbrace{\mathrm{abnormal},\dots ,\mathrm{abnormal}}}\}\hfill \end{array}$$

(25)

This batch is then fed into the anomaly detection model for training. By continuously updating $p\left({\mathcal{A}}_e\right)$ and incorporating high-quality samples, the model gradually learns to detect subtle anomalies while maintaining generalization.

3.3.2. Bias-Aware Augmentation for Rare Anomaly Types

In real-world anomaly detection, the most critical anomalies, such as security breaches or rare system faults, are often the most underrepresented in training data. This leads to poor model performance on the cases where accuracy matters most. This issue is especially acute in resource-constrained edge computing systems, where the training process must be highly efficient and explicitly focused on detecting these high-priority anomalies.

Therefore, a bias-aware augmentation strategy is further introduced within the smart filtering framework to increase the representation of such anomalies during training without sacrificing diversity or balance. The process begins with an anomaly-type classifier that assigns each anomaly sample to a predefined class. Based on this categorization, anomalies are grouped into two categories: (1) critical/rare anomalies, which are subjected to a biased augmentation procedure and processed through the filter network; (2) common anomalies, which follow standard augmentation and bypass the filter. This ensures that the model pays special attention to critical cases while still learning from a broad range of patterns.

To implement this bias, a modified augmentation selection process is introduced. Let $p\left({\mathcal{A}}_E\right)$ represent the original probability of selecting augmentation method E. For prioritized anomaly types, a bias factor $T\in [0,1]$ that increases the likelihood of applying selected augmentation methods is defined. With probability T, a designated method E is force-selected, while with probability $1-T$, the method is sampled according to the original distribution. Formally, this becomes:

$${\mathcal{A}}_{\mathrm{selected}}=\left\{\begin{array}{cc}E,\hfill & \mathrm{with}\mathrm{probability}T\hfill \\ \mathrm{Sample}\mathrm{from}p\left({\mathcal{A}}_e\right),\hfill & \mathrm{with}\mathrm{probability}1-T\hfill \end{array}\right.$$

(26)

Example 1. 

Suppose a dataset contains two anomaly types: latency spike anomalies (accounting for 80% of all anomalies) and rare dependency–failure anomalies (only 5% of all anomalies). With a uniform augmentation strategy, the model would predominantly encounter latency spike anomalies during training, while the rare dependency–failure cases would remain severely underrepresented.

The bias-aware augmentation addresses this limitation by introducing a forced selection mechanism for augmentation methods critical to rare anomalies. For instance, assume edge perturbation (denoted as Method A) is particularly effective for enhancing the detection of dependency–failure anomalies, but it would only be selected with a 10% probability under the original probabilistic distribution. To prioritize Method A for this rare class, a 40% bias factor T is assigned to it. Specifically, when processing a dependency–failure anomaly:

First, generate a random value; if it is less than T (40% chance), Method A is directly selected.

Only if the first condition fails (60% chance), reversion to the original probabilistic selection process occurs—where Method A still retains its base 10% probability alongside other augmentation methods.

This two-step selection mechanism ensures Method A is prioritized for the rare dependency–failure class, resulting in a significantly higher effective selection rate than the original 10%, while preserving stochastic sampling for other anomaly types. Practically, this strategy increases the effective representation of dependency–failure anomalies in training batches, enabling the model to learn more balanced decision boundaries and remain sensitive to critical but infrequent anomaly patterns.

After an augmentation method is selected, samples from biased (rare/critical) categories proceed through the smart filtering pipeline, whereas non-prioritized anomalies follow the original unbiased augmentation and filtering workflow. This selective process continues until the number of augmented anomaly samples equals the number of original normal samples in the training batch.

By embedding this bias-aware augmentation into the training loop, the model is ensured to be better exposed to rare and significant anomaly types, improving detection robustness and enabling more effective learning from asymmetric datasets. The probabilistic bias mechanism also preserves augmentation diversity and provides fine-grained control over the training signal without introducing significant computational overhead Algorithm 1.

Algorithm 1 Adaptive graph augmentation with bias-aware sampling (retry version simplified)

Require: Normal graphs ${\mathcal{G}}_{\mathrm{normal}}$, augmentation set $\mathcal{A}$, filter network $f_{\mathrm{filter}}$, success counts $S_e$, totals ${\mathrm{TotalAug}}_e$, bias factor T for preferred augmentation method Ensure: Balanced training batches   1: Precompute success probabilities:   2: $p_{\mathrm{success}}^e\leftarrow (S_e+1)/({\mathrm{TotalAug}}_e+1),\forall e\in \mathcal{A}$   3: $p\left({\mathcal{A}}_e\right)\leftarrow p_{\mathrm{success}}^e/{\sum }_{e^{\prime }}{p}_{\mathrm{success}}^{e^{\prime }}$    (base probabilities)   4: for each training iteration do   5:    Initialize empty batches: $B_{\mathrm{normal}},B_{\mathrm{aug}}$   6:    while batch not full do   7:      Sample $g\in {\mathcal{G}}_{\mathrm{normal}}$   8:      Generate random number $r\in [0,1]$   9:      if $r<T$ then 10:         Select preferred augmentation method E (bias applied) 11:     else 12:         Sample $E\sim p\left(\mathcal{A}\right)$    (probabilistic fallback) 13:     end if 14:     repeat 15:         $g^{\prime }\leftarrow \mathrm{Augment}(g,E)$ 16:         $P_{\mathrm{check}}^E\leftarrow min(1,\lambda (1-p_{\mathrm{success}}^E))$ 17:     until rand() $\ge P_{\mathrm{check}}^E$ or $f_{\mathrm{filter}}\left(g^{\prime }\right)$ passes 18:     $B_{\mathrm{normal}}\leftarrow B_{\mathrm{normal}}\cup \left\{g\right\}$ 19:     $B_{\mathrm{aug}}\leftarrow B_{\mathrm{aug}}\cup \left\{g^{\prime }\right\}$ 20:   end while 21:   Train_model($B_{\mathrm{normal}}\cup B_{\mathrm{aug}}$, labels) 22: end for

4. Experiments

4.1. Datasets

Due to the lack of public asymmetric and heterogeneous graph datasets, two real-world datasets are employed for evaluation.

Train Ticket Graph Dataset (TraceLog): TraceLog [5] is a large-scale asymmetric and heterogeneous graph dataset from a train ticket booking microservice system [32]. This dataset is widely used for anomaly detection evaluation in system log sequences. TraceLog contains four main fault categories and fourteen specific subcategories, covering different types of system anomalies, such as asynchronous interactions, multi-instance issues, configuration-related failures, and single-point failures. In this dataset, all fourteen types of system failures are treated as anomalies in normal system traces.

4.2. Performance Analysis

Model performance is evaluated using four key metrics in anomaly detection (all range 0–1; higher values mean better performance):

AUC (Area Under ROC Curve): Reflects the model’s overall ability to distinguish between normal samples and anomalies (1 = perfect distinction, 0.5 = random guessing).

AP (Average Precision): Focuses on balancing “reducing false anomaly predictions” and “avoiding missing true anomalies,” especially critical for imbalanced anomaly detection scenarios.

Recall: Indicates how many true anomalies the model can successfully identify (higher values mean fewer true anomalies are missed).

F1-score: Synthesizes the balance between “reducing false anomaly predictions” and “avoiding missing true anomalies,” suitable for real-world deployment where a fixed classification threshold is needed.

4.2.1. Augmented Effect Analysis

The proposed augmentation method was evaluated using three networks [1,5,12] on two datasets [32,33]. The detailed results are presented in

Table 1. Ablation study results comparing different variants of our method on TraceLog and FlowGraph datasets.

Variant	Metric	HRGCN		DeepTraLog		HGT
		TraceLog	FlowGraph	TraceLog	FlowGraph	TraceLog	FlowGraph
Specific	AUC	0.804	1.000	0.842	0.883	0.829	0.955
	AP	0.730	1.000	0.754	0.719	0.826	0.905
	F1-score	0.792	1.000	0.796	0.806	0.803	0.862
	Recall	0.794	1.000	0.800	0.812	0.808	0.870
Ours	AUC	0.820	1.000	0.864	0.922	0.859	0.986
	AP	0.756	1.000	0.782	0.746	0.818	0.935
	F1-score	0.823	1.000	0.828	0.848	0.842	0.896
	Recall	0.826	1.000	0.832	0.854	0.848	0.902
Filter	AUC	0.768	0.988	0.825	0.879	0.806	0.952
	AP	0.729	0.953	0.722	0.689	0.772	0.898
	F1-score	0.785	0.872	0.790	0.798	0.792	0.856
	Recall	0.788	0.876	0.794	0.804	0.798	0.862
Percent	AUC	0.748	1.000	0.824	0.883	0.794	0.975
	AP	0.698	1.000	0.723	0.692	0.742	0.899
	F1-score	0.776	1.000	0.782	0.800	0.787	0.860
	Recall	0.780	1.000	0.786	0.806	0.792	0.866
Random	AUC	0.738	1.000	0.799	0.878	0.788	0.965
	AP	0.687	1.000	0.709	0.674	0.728	0.891
	F1-score	0.760	1.000	0.768	0.786	0.774	0.846
	Recall	0.762	1.000	0.770	0.790	0.778	0.852
Baseline	AUC	0.703	0.952	0.767	0.849	0.713	0.955
	AP	0.655	0.954	0.704	0.622	0.637	0.862
	F1-score	0.742	0.862	0.750	0.776	0.754	0.842
	Recall	0.744	0.864	0.752	0.780	0.758	0.848

, where the best performance for each metric is highlighted in bold.

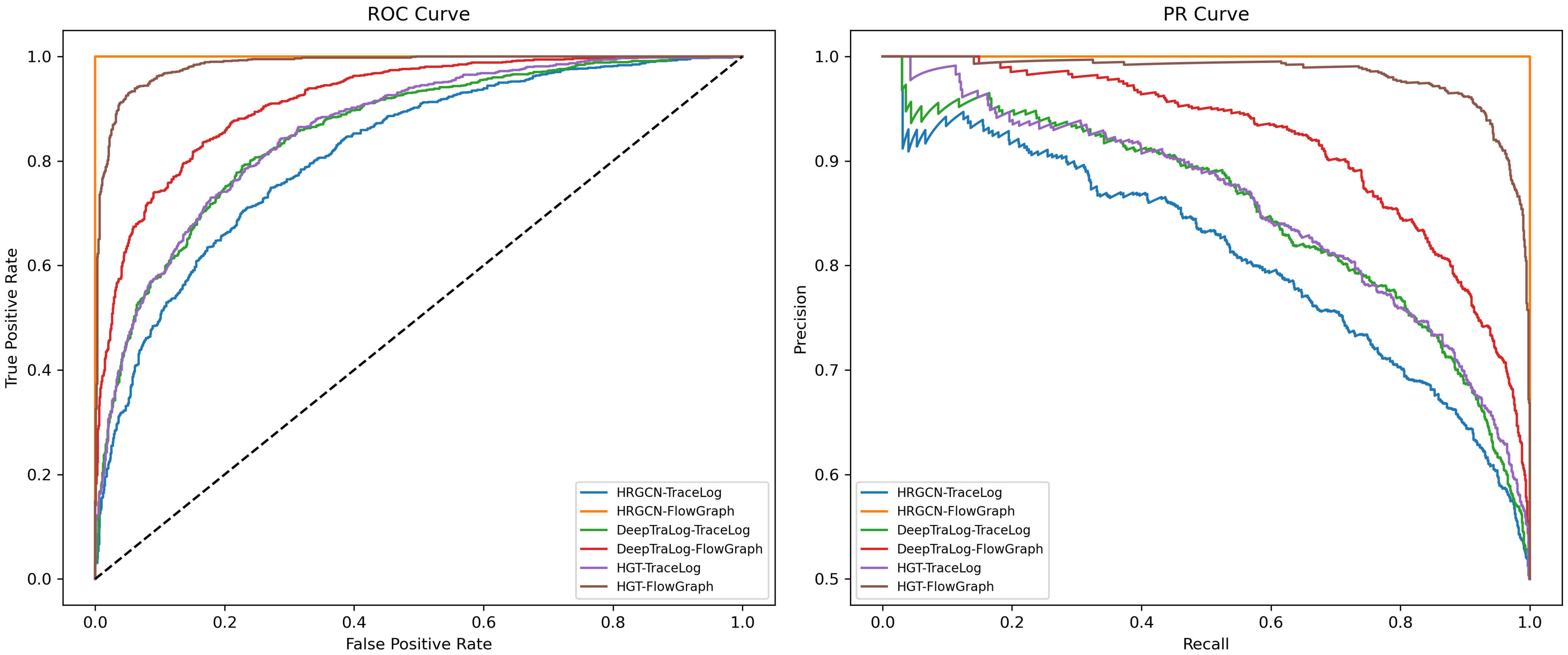
Across the TraceLog dataset, our full method (ours) achieves notable improvements over the baseline: AUC increases from 0.703 to 0.820, AP from 0.655 to 0.756, F1-score from 0.742 to 0.823, and recall from 0.744 to 0.826. On FlowGraph, improvements are also observed, though less pronounced due to near-saturated baseline performance, e.g., AUC rises from 0.952 to 1.000, AP from 0.954 to 1.000. These results confirm that the proposed method effectively enhances model performance under asymmetric anomaly distributions, with particularly strong gains on datasets where anomalies are underrepresented Figure 4.

4.2.2. Ablation Studies Furthermore, Efficiency Analysis

To further evaluate the contributions of each component in the proposed framework, we conducted a comprehensive ablation study across three models (HRGCN, DeepTraLog, and HGT) on the TraceLog and FlowGraph datasets. As shown in Table 1, the results are reported in terms of AUC, AP, F1-score, and recall, providing a detailed comparison of different variants. The ROC and PR curve as show in Figure 4.

• Filter network: compared to the baseline, integrating the filter network consistently improves model performance by emphasizing high-quality augmented samples. On TraceLog, AUC increases by 5.5%–6.5% across different models (e.g., HRGCN: 0.703 → 0.768, HGT: 0.713 → 0.806). On FlowGraph, improvements are smaller (e.g., HRGCN: 0.952 → 0.988), indicating that filtering alone has limited impact when baseline performance is already high. However, relying solely on filtering can discard useful augmented samples, as evidenced by DeepTraLog’s AP on FlowGraph, which only rises from 0.622 to 0.689—lower than the 0.746 achieved by our adaptive method.
• Percent-based selection: Using a fixed proportion of augmented samples without filtering results in moderate gains. On TraceLog with HGT, AUC improves from 0.788 (random) to 0.794 (percent), and on FlowGraph, AP reaches 0.899 compared to 0.891 (random). This demonstrates that controlling the selection ratio helps, but without filtering, low-quality or irrelevant augmentations limit effectiveness.
• Bias-aware augmentation: Random augmentation produces inconsistent or marginal improvements and may reduce robustness. On TraceLog with HGT, random augmentation yields an AUC of 0.788, while bias-aware augmentation in the proposed framework achieves 0.859, a 7.1% absolute increase. On FlowGraph, AP improves from 0.891 (random) to 0.935 (ours). This confirms that accounting for anomaly type asymmetry is critical for stabilizing and enhancing performance.
• Adaptive sampling: The proposed method (ours) leverages both the filter network and bias-aware probability adjustment. Compared to the filter variant, it improves AUC by an average of 4.5% and AP by 4.6% across all datasets and models. For instance, on TraceLog with DeepTraLog, AUC rises from 0.826 (filter) to 0.864 (ours), and AP from 0.743 to 0.782. On FlowGraph with HGT, AP increases from 0.905 (specific) to 0.935. These results indicate that adaptive sampling retains the benefits of filtering while avoiding excessive pruning, and effectively emphasizes rare or critical anomalies.
• Performance trends across datasets and models: Improvements are more pronounced on TraceLog, which exhibits a more asymmetric anomaly distribution and lower baseline scores, highlighting the framework’s capability in handling challenging imbalanced scenarios. On FlowGraph, gains are smaller but still meaningful, particularly for AP and F1-score, demonstrating robustness and consistency of the adaptive mechanism.

As shown in Table 1, each component contributes to performance improvement. The filter, percent, and random variants all improve over the baseline, but the combination of filtering, bias-aware augmentation, and adaptive sampling in the proposed HGAA framework achieves the highest and most consistent performance across both datasets and all models. These results confirm that the framework effectively addresses asymmetric anomaly distributions in microservice-based systems while maintaining model generalization and robustness.

Time Efficiency Analysis

While the method is not optimal in terms of computational time

Table 2. Training time comparison across different methods and datasets.

Model	TraceLog		FlowGraph
	Variant	Time (s)	Variant	Time (s)
HRGCN	Specific	213.42	Specific	81.32
	Ours	185.20	Ours	79.84
	Filter	530.31	Filter	86.54
	Percent	65.77	Percent	57.67
	Random	67.38	Random	62.80
	Baseline	64.63	Baseline	22.11
DeepTraLog	Specific	122.51	Specific	83.65
	Ours	83.85	Ours	78.53
	Filter	368.11	Filter	89.34
	Percent	24.41	Percent	65.96
	Random	23.35	Random	66.21
	Baseline	16.90	Baseline	2.10
HGT	Specific	189.32	Specific	101.32
	Ours	122.33	Ours	97.52
	Filter	444.49	Filter	103.86
	Percent	58.25	Percent	91.52
	Random	58.61	Random	91.39
	Baseline	31.43	Baseline	9.68

, it achieves a good balance between performance and efficiency. It outperforms the Filter method significantly in terms of time. In terms of time, an average improvement of 71% is achieved on TraceLog and 8.6% on FlowGraph. The difference in time improvement is substantial, which is due to the characteristics of the dataset itself. As shown in Figure 5, the TraceLog dataset has fewer successful augmentation samples. If all samples need to be tested by the filter before being sent to training, the time will be greatly extended. However, the ratio of successful augmentation samples in the FlowGraph dataset is very large, and most of them can pass the filter normally. Therefore, in terms of time efficiency reduction, the FlowGraph dataset is not as obvious as the TraceLog dataset, but there is still improvement.

Summary

The results show that our method outperforms other variants in terms of AUC, AP, F1-score, and recall, especially on the TraceLog dataset where the performance improvement is most significant. The strategy of dynamically adjusting the success rate of the augmentation method enables the model to better adapt to the dataset, improves the training effectiveness, and enhances the generalization capability on asymmetric and unseen data. As shown in

Table 3. Comparison of our method with the specific method in terms of AUC, AP, F1-score, recall and training time.

Method	Metric	HRGCN		DeepTraLog		HGT
		TraceLog	FlowGraph	TraceLog	FlowGraph	TraceLog	FlowGraph
Ours	AUC	0.820	1.000	0.864	0.922	0.859	0.986
	AP	0.756	1.000	0.782	0.746	0.818	0.935
	F1-score	0.823	1.000	0.828	0.848	0.842	0.896
	Recall	0.826	1.000	0.832	0.854	0.848	0.902
	Time (s)	185.20	79.84	83.85	78.53	122.33	97.52
Specific	AUC	0.804	1.000	0.842	0.883	0.829	0.955
	AP	0.730	1.000	0.754	0.719	0.826	0.905
	F1-score	0.792	1.000	0.796	0.806	0.803	0.862
	Recall	0.794	1.000	0.800	0.812	0.808	0.870
	Time (s)	213.42	81.32	122.51	83.65	189.32	101.32

, the comparison between our method and the Specific method further demonstrates the superiority of our approach. Moreover,

Table 4. Performance comparison of our method with baseline methods on TraceLog and FlowGraph datasets.

Model	TraceLog				FlowGraph
	AUC	AP	F1	Recall	AUC	AP	F1	Recall
HRGCN	0.820	0.756	0.823	0.826	1.000	1.000	1.000	1.000
	0.703	0.655	0.742	0.744	0.952	0.954	0.862	0.864
DeepTraLog	0.864	0.782	0.828	0.832	0.922	0.746	0.848	0.854
	0.767	0.704	0.750	0.752	0.849	0.622	0.776	0.780
HGT	0.859	0.818	0.842	0.848	0.986	0.935	0.896	0.902
	0.713	0.637	0.754	0.758	0.955	0.862	0.842	0.848

validates the consistent improvements of our method over the base model across AUC, AP, F1, and Recall. In addition,

Table 5. Distribution of the number of augmented samples selected by each method among the 100 generated for each dataset before and after applying augmentations for specific anomalies.

Aug Method	TraceLog		FlowGraph
	Ours	Specific	Ours	Specific
Eege addition	13	31	28	44
Node type swap	11	10	24	18
Node feature swap	6	6	22	22
Edge direct swap	3	3	26	16
Edge perturbation	59	45
Edge type swap	8	5

confirms the effectiveness of the Bias-Aware strategy in selecting appropriate augmentation methods. Furthermore, our method also balances the consideration of time with the limited resources in edge systems.

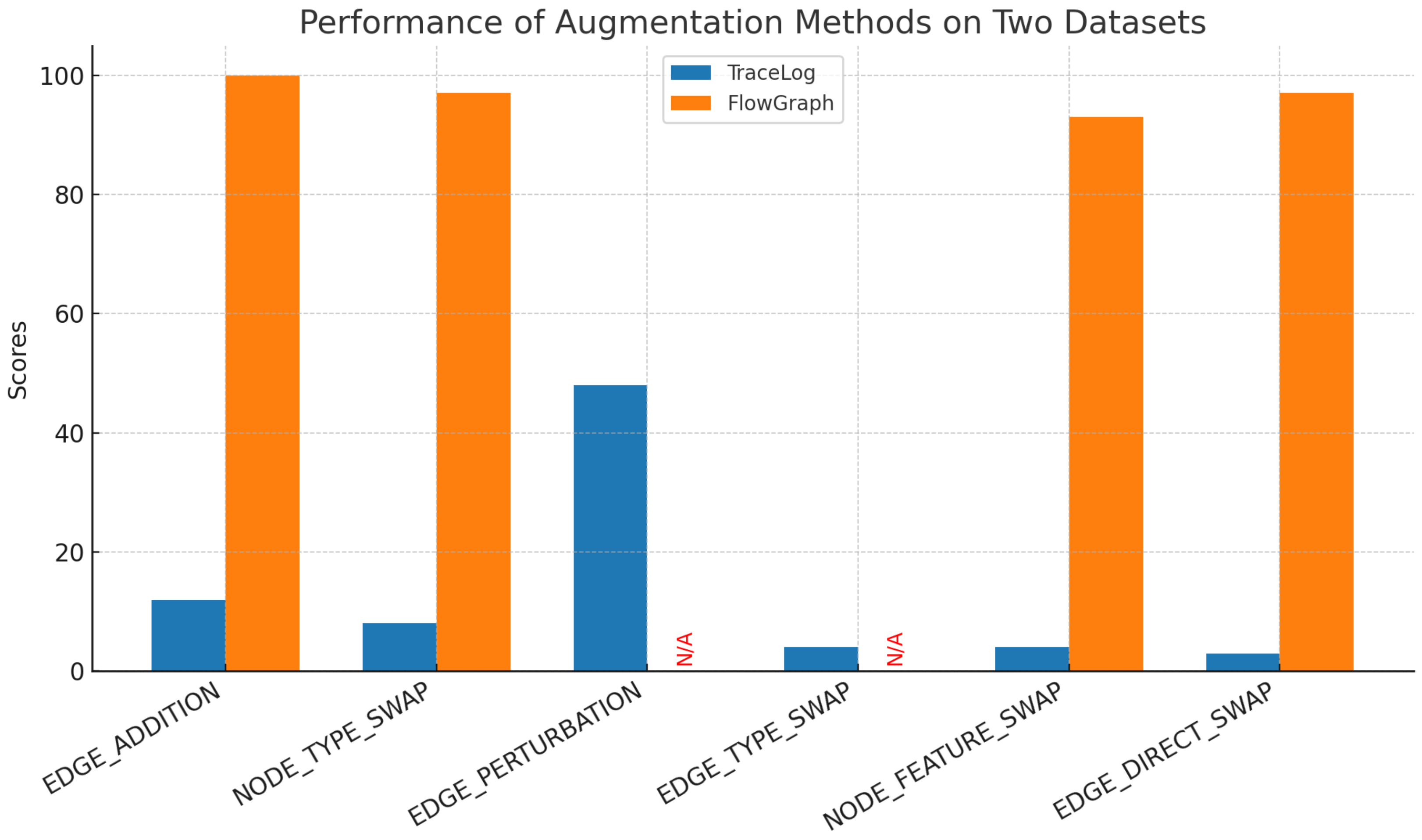
4.2.3. Performance Discrepancies of Augmentation Methods Across Datasets

The divergent effectiveness of augmentation methods between TraceLog and FlowGraph arises from their structural characteristics and method compatibility:

Edge Type Swap

This method is unsupported on FlowGraph due to its fixed edge type constraints— FlowGraph’s edges follow rigid service–data interaction rules, and swapping edge types would violate inherent semantic logic, resulting in invalid samples. On TraceLog, though technically supported, it performs poorly. TraceLog’s edges represent sequential API call relationships with weak type differentiation, and swapping edge types generates only meaningless perturbations that fail to form recognizable anomaly patterns.

Heterogeneous Edge Perturbation

This method is unsupported on FlowGraph. FlowGraph’s topology relies on fixed service–data dependencies, and any edge perturbation (addition/removal) would break its inherent structural integrity, producing samples that do not reflect real-world operations. On TraceLog, it is the only method with partial success. TraceLog’s sequential API call structure allows limited edge perturbations—about half of such operations retain temporal logic, simulating plausible anomalies like incomplete call chains, thus enabling partial detection effectiveness.

Edge Addition, Node Type Swap, Node Feature Swap, Edge Direction Swap

These four methods are all supported on FlowGraph and perform well. FlowGraph’s clear node/edge semantics and fixed topology allow these methods to generate meaningful perturbations that simulate real anomalies (e.g., adding necessary service links, swapping node types to mimic misconfigurations). On TraceLog, while technically supported, all four methods perform poorly. TraceLog’s sequential log structure and weak semantic boundaries mean these perturbations disrupt temporal logic or create meaningless noise, failing to provide effective training signals for anomaly detection

Table 6. Summary of notations used in this paper.

Symbol	Description
${\mathcal{G}}_{\mathrm{normal}}$	Set of normal graphs in training data
${\mathcal{G}}_{\mathrm{anomaly}}$	Set of anomalous graphs in training data
$\mathcal{A}$	Set of augmentation methods
E	Selected augmentation method
g	A graph sample
$g^{\prime }$	Augmented graph sample
$f_{\mathrm{filter}}$	Filtering network to check augmented samples
$S_e$	Number of successful augmentations for method e
${\mathrm{TotalAug}}_e$	Total number of augmentation attempts for method e
$p_{\mathrm{success}}^e$	Precomputed success probability of augmentation e
$p\left({\mathcal{A}}_e\right)$	Probability of selecting augmentation e
$P_{\mathrm{check}}^e$	Probability of performing filter check for augmentation e
$\lambda$	Scaling factor for filter probability adjustment
T	Bias factor for preferred augmentation methods
$B_{\mathrm{normal}}$	Batch of normal graphs
$B_{\mathrm{aug}}$	Batch of augmented graphs
$N_{\mathrm{normal}}$	Number of normal graphs in batch $B_{\mathrm{normal}}$
$N_{\mathrm{aug}}$	Number of augmented graphs in batch $B_{\mathrm{aug}}$

.

5. Conclusions

Anomaly detection in microservice-based systems under edge intelligence remains a formidable challenge due to the joint constraints of asymmetric anomaly types and limited computational resources. This work proposed Heterogeneous Graph Adaptive Augmentation (HGAA), which integrates heterogeneous GNNs, knowledge distillation, and bias-aware augmentation to dynamically tailor graph transformations according to dataset-specific anomaly distributions.

The framework demonstrated consistent advantages across two real-world datasets. In particular, HGAA achieved on average 4.5% higher AUC and 4.6% higher AP than the strongest baselines, with even larger improvements in challenging scenarios (e.g., AUC gain of 14.6% on TraceLog under HGT). Beyond quantitative performance, HGAA proved more robust to anomaly heterogeneity and better adapted to dataset-specific structural characteristics, validating its ability to alleviate anomaly type asymmetry while remaining efficient in resource-constrained environments.

Despite these encouraging results, several limitations remain. First, HGAA assumes the availability of a modest number of labeled anomalies to guide bias-aware augmentation, which may not always hold in extremely sparse or fully unsupervised settings. Second, although our efficiency analysis shows reduced overhead compared to filter-based methods (e.g., 71% faster on TraceLog), adaptive augmentation can still incur costs when scaling to ultra-large graphs or real-time applications. Finally, the empirical evaluation is limited to TraceLog and FlowGraph due to the scarcity of heterogeneous microservice anomaly benchmarks, which constrains the generality of conclusions.

Future research will address these limitations by exploring semi-supervised and unsupervised bias-aware augmentation, optimizing adaptive mechanisms for deployment on highly resource-constrained devices, and extending evaluations to larger, more diverse datasets across domains such as IoT security, financial fraud detection, and industrial monitoring. Furthermore, integrating HGAA with automated augmentation policy search and meta-learning will be investigated to further enhance scalability, adaptability, and trustworthiness in edge intelligence ecosystems.