Abstract
Tactical production–distribution planning in paper manufacturing involves hierarchical decision-making under hybrid uncertainty, where aleatory randomness (demand fluctuations, machine variations) and epistemic uncertainty (expert judgments, market trends) simultaneously affect operations. Existing approaches fail to address the bi-level nature under hybrid uncertainty, treating production and distribution decisions independently or using single-paradigm uncertainty models. This research develops a bi-level dependent-chance goal programming framework based on uncertain random theory, where the upper level optimizes distribution decisions while the lower level handles production decisions. The framework exploits structural symmetries through machine interchangeability, symmetric transportation routes, and temporal symmetry, incorporating symmetry-breaking constraints to eliminate redundant solutions. A hybrid intelligent algorithm (HIA) integrates uncertain random simulation with a Reinforcement-Learning-enhanced Arithmetic Optimization Algorithm (RL-AOA) for bi-level coordination, where Q-learning enables adaptive parameter tuning. The RL component utilizes symmetric state representations to maintain solution quality across symmetric transformations. Computational experiments demonstrate HIA’s superiority over standard metaheuristics, achieving 3.2–7.8% solution quality improvement and 18.5% computational time reduction. Symmetry exploitation reduces search space by approximately 35%. The framework provides probability-based performance metrics with optimal confidence levels (0.82–0.87), offering 2.8–4.5% annual cost savings potential.
Keywords:
bi-level programming; dependent-chance goal programming; tactical production–distribution planning; paper manufacturing; uncertain random theory; reinforcement learning; Arithmetic Optimization Algorithm; sustainable production; resource efficiency; industrial productivity; environmental sustainability; sustainable industrialization 1. Introduction
The paper manufacturing industry, valued at approximately USD 400 billion globally, represents one of the most operationally complex sectors in modern manufacturing, where tactical production–distribution planning decisions directly impact both economic performance and environmental sustainability [1]. Paper production involves intricate interdependencies between raw material procurement, multi-grade production processes, and diverse distribution networks serving packaging, publishing, and specialty applications [2]. The industry’s operational structure exhibits significant structural symmetries, including machine interchangeability for certain paper grades, bidirectional material flows between production facilities, and periodic patterns in demand cycles, which create opportunities for computational efficiency through systematic symmetry exploitation in optimization algorithms [3].
Paper manufacturing operations encompass diverse product portfolios including newsprint, packaging materials, tissue products, and specialty papers, each requiring specific production parameters and handling requirements [4]. Production facilities face machine compatibility constraints and sequence-dependent changeover requirements that impose significant setup times and costs when transitioning between product types [5]. The presence of symmetric machine capabilities—where multiple machines can produce identical grades with equivalent efficiency—introduces structural symmetries in the optimization problem formulation. These symmetries manifest as equivalent production schedules that yield identical costs and performance metrics, necessitating symmetry-aware optimization mechanisms to avoid redundant exploration of mathematically equivalent solutions. Raw material variability and seasonal demand patterns create additional complexity in capacity allocation decisions [6].
The tactical planning horizon of 3–6 months represents a critical decision space where strategic network design constraints meet operational execution requirements [7]. Companies must make production scheduling decisions that determine machine utilization and inventory positioning while simultaneously coordinating distribution strategies affecting customer service levels and transportation costs [8]. The bi-level nature of this problem exhibits hierarchical structural symmetries, where upper-level distribution decisions and lower-level production decisions display analogous constraint patterns and objective contributions, requiring coordinated optimization approaches that can exploit these symmetries while maintaining solution optimality.
Supply chain planning operates across multiple hierarchical levels with distinct time horizons and decision scopes [9]. Strategic planning (1–5 years) focuses on network design decisions, tactical planning (3–6 months) bridges strategic constraints with operational execution, and operational planning (daily to weekly) addresses immediate execution decisions [7]. Recent advances in optimization have demonstrated the effectiveness of symmetry-based decomposition techniques for large-scale planning problems. However, existing approaches for bi-level production–distribution planning have not systematically addressed symmetry identification and exploitation, particularly in the context of hybrid uncertainty. Our reinforcement-learning-enhanced arithmetic optimization approach incorporates symmetric state representations in Q-learning to enable efficient exploration while avoiding redundant evaluations of symmetric solution regions.
Tactical planning in paper manufacturing operates under hybrid uncertainty that cannot be adequately captured by traditional single-paradigm approaches [10]. Aleatory uncertainty sources include demand fluctuations, machine efficiency variations, and quality variations that follow well-defined probability distributions based on historical data [11]. Epistemic uncertainty stems from incomplete knowledge about market trends, regulatory changes, and supplier reliability, where expert judgment must complement quantitative data [12]. Traditional optimization approaches treating these uncertainties independently fail to capture their interactive effects and compound impacts on tactical decisions [13].
Despite extensive research in production–distribution planning, several critical gaps remain that limit the effectiveness of existing approaches. Bi-level production–distribution planning research has primarily focused on deterministic parameters, failing to address goal-oriented frameworks that incorporate probability-based performance targets [14]. Goal programming applications have predominantly utilized deterministic formulations that assume exact target values, limiting their applicability in uncertain environments where probability-based objectives are more meaningful [15]. Uncertainty modeling has advanced significantly through stochastic programming and fuzzy programming approaches, yet hybrid uncertainty applications that simultaneously handle both aleatory and epistemic components remain limited [10]. Paper industry optimization research has developed sophisticated models for individual planning components but lacks comprehensive frameworks addressing integrated tactical-level decision coordination [1].
The symmetric properties inherent in paper manufacturing networks present both computational challenges and optimization opportunities. While these symmetries can exponentially expand the solution space through mathematically equivalent solutions, they also enable significant computational efficiencies when properly exploited. Our framework systematically addresses these symmetries through (1) identification and classification of structural symmetries in the bi-level problem formulation, (2) incorporation of symmetry-breaking constraints to eliminate redundant solution regions, (3) utilization of symmetric state representations in the reinforcement learning component to maintain solution quality across symmetric transformations, and (4) preservation of invariance properties in arithmetic optimization operators to ensure consistent performance across symmetric problem instances.
The primary objective of this research is to develop a comprehensive bi-level dependent-chance goal programming framework for tactical production–distribution planning in paper manufacturing under hybrid uncertainty. This research addresses four fundamental questions that guide the investigation: How can dependent-chance goal programming be adapted to handle bi-level tactical planning where production and distribution managers have different risk tolerances and objective priorities? What is the optimal bi-level structure for integrating production scheduling and distribution planning decisions while maintaining computational tractability? How effective is the proposed Reinforcement-Learning-enhanced Arithmetic Optimization Algorithm compared to existing metaheuristics for solving complex bi-level optimization problems under hybrid uncertainty? What are the trade-offs between different goal probability levels and how do these affect tactical planning performance in paper manufacturing contexts?
To address the identified research gaps and challenges, this study makes the following key contributions:
- Bi-Level Dependent-Chance Goal Programming Framework: Development of the first comprehensive bi-level dependent-chance goal programming model for tactical production–distribution planning that simultaneously addresses hierarchical decision-making and probabilistic goal achievement under hybrid uncertainty, extending traditional goal programming theory into probabilistic domains with bi-level coordination.
- Hybrid Uncertainty Modeling Enhancement: Advancement of uncertain random theory applications through a systematic framework for modeling hybrid uncertainty in tactical planning contexts, providing unified mathematical representations that capture both aleatory randomness from historical data and epistemic uncertainty from expert judgments.
- Reinforcement-Learning-enhanced Arithmetic Optimization Algorithm: Introduction of the novel RL-AOA, which integrates Q-learning mechanisms with arithmetic optimization operators for adaptive bi-level coordination, enabling dynamic parameter tuning based on optimization progress and problem-specific characteristics.
- Industry-Specific Tactical Planning Framework: Development of the first comprehensive tactical planning framework specifically designed for paper manufacturing environments, incorporating machine compatibility constraints, sequence-dependent changeover requirements, paper grade specifications, and multi-modal transportation considerations.
- Computational Validation and Implementation Guidelines: Demonstration of algorithm superiority through extensive computational experiments achieving 3.2–7.8% solution quality improvement and 18.5% computational time reduction, accompanied by practical implementation guidelines and sensitivity analysis insights for industrial adoption.
- Symmetry-Aware Optimization Techniques: Development of systematic approaches for identifying, classifying, and exploiting structural symmetries in paper manufacturing networks, demonstrating measurable computational improvements through intelligent symmetry breaking and symmetric state representations in reinforcement learning algorithms.
The remainder of this paper is organized as follows: Section 2 presents the mathematical formulation of the bi-level dependent-chance goal programming model including uncertain random variable definitions and chance measure calculations. Section 3 describes the theoretical foundations of uncertain random theory for hybrid uncertainty modeling and its application to tactical planning problems. Section 4 details the Reinforcement-Learning-enhanced Arithmetic Optimization Algorithm including bi-level coordination mechanisms and adaptive parameter tuning strategies. Section 5 provides comprehensive computational results and performance analysis across diverse paper manufacturing instances with comparative evaluation against existing approaches. Section 6 concludes with key findings, practical implications, and future research directions.
2. Mathematical Model Formulation
This section presents the comprehensive bi-level dependent-chance goal programming model for tactical production–distribution planning in paper manufacturing under hybrid uncertainty. The model captures the hierarchical decision-making structure where distribution coordinators (upper level) and production managers (lower level) operate with different objectives while facing uncertain random parameters.
2.1. Sets and Indices
The following Table 1 presents the sets and indices used throughout our paper mill supply chain optimization model. These notations form the foundation of our mathematical formulation, defining the scope of products, facilities, resources, and relationships within the supply chain network. Table 1 establishes the necessary mathematical notation that will be used consistently throughout the remainder of this paper.

Table 1.
Sets and indices used in the paper mill supply chain optimization model. This table defines the mathematical notation for all entities in the supply chain network including products, facilities, and their relationships.
2.2. Parameters
2.2.1. Deterministic Parameters
The deterministic parameters presented in Table 2 capture the fixed and known aspects of the paper mill supply chain. These values include production costs, technical specifications, capacity limitations, and other operational constants that do not vary with uncertainty. The parameters listed in Table 2 are essential for establishing the baseline operational constraints of the optimization model and remain constant throughout the planning horizon.

Table 2.
Deterministic parameters for the paper mill supply chain model. This table lists all fixed parameters related to costs, capacities, production rates, and technical specifications that remain constant throughout the planning horizon.
2.2.2. Uncertain Random Parameters
Our model incorporates uncertainty through a set of random parameters that represent the stochastic nature of real-world paper mill operations. These parameters, presented in Table 3 and denoted with a tilde, capture the variability in demand, costs, equipment performance, and material availability. The uncertain random parameters outlined in Table 3 are essential for developing robust solutions that can withstand real-world fluctuations in the paper manufacturing environment.

Table 3.
Uncertain random parameters for the paper mill supply chain model. This table details all stochastic parameters that are subject to uncertainty, including demand fluctuations, cost variations, and operational variability.
2.2.3. Goal Programming Parameters
The goal programming component of our model requires specific parameters to define target thresholds and confidence levels. The parameters listed in Table 4 establish the multi-objective framework that balances economic efficiency, operational performance, resource utilization, and quality assurance within the optimization process. Table 4 defines the target probability levels and thresholds that will be used to evaluate the achievement of each goal in our model.

Table 4.
Goal programming parameters for the paper mill supply chain model. This table defines the parameters used in the goal programming formulation, including target probability levels, threshold values, and confidence levels for each objective.
2.3. Decision Variables
2.3.1. Upper-Level Decision Variables (Distribution Planning)
Our bi-level optimization model separates decision-making into distribution and production planning. The upper-level variables defined in Table 5 focus on distribution center operations, product shipping decisions, transportation mode selection, inventory management at distribution centers, and customer service levels. The variables presented in Table 5 determine the optimal distribution network configuration to meet customer demands efficiently.

Table 5.
Upper-level decision variables for distribution planning in the paper mill supply chain model. This table defines all variables related to distribution network configuration, product flow, and customer service.
2.3.2. Lower-Level Decision Variables (Production Planning)
The lower-level variables focus on production planning decisions within the paper mill. The variables defined in Table 6 determine optimal production quantities, machine assignments, production sequencing, raw material procurement, and warehouse inventory management. The lower-level decisions represented in Table 6 are made in response to the distribution requirements established at the upper level of the optimization model.

Table 6.
Lower-level decision variables for production planning in the paper mill supply chain model. This table defines all variables related to production decisions, machine scheduling, raw material procurement, and inventory management at production facilities.
2.3.3. Goal Programming Variables
The goal programming framework requires specific variables to measure deviations from target thresholds. The variables presented in Table 7 quantify both positive and negative deviations from the four main objectives of our model: economic efficiency, operational performance, resource utilization, and quality assurance. These deviations defined in Table 7 are minimized in the objective function to achieve balanced solutions that satisfy multiple competing objectives simultaneously.

Table 7.
Goal programming variables for the paper mill supply chain model. This table defines the deviation variables used to measure the achievement of each goal in the multi-objective framework.
2.4. Bi-Level Mathematical Model
Notation: Throughout this paper, Ch{·} denotes the chance measure of uncertain random events, which quantifies the probability that an uncertain random variable satisfies a given condition. This measure integrates probability theory for aleatory uncertainty (randomness from historical variability) with uncertainty theory for epistemic uncertainty (imprecision from limited knowledge) within a unified mathematical framework, as detailed in the following definition.
2.4.1. Upper-Level Problem (Distribution Planning)
The upper level seeks to minimize distribution costs while maximizing service levels:
Subject to upper-level constraints:
Distribution Center Capacity:
This constraint ensures that the total inventory stored across all paper grades at each distribution center does not exceed the facility’s physical storage capacity, maintaining operational feasibility.
Transportation Mode Capacity:
These constraints guarantee that the combined shipment volumes using each transportation mode remain within the mode’s available capacity limits, accounting for uncertain availability factors.
Customer Demand Satisfaction with Production Coordination:
Constraint (4) maintains the demand–supply balance under uncertainty, while constraint (5) ensures that total customer shipments cannot exceed available warehouse inventory plus current production, creating explicit coordination between upper-level distribution decisions and lower-level production outputs.
Distribution Center Inventory Balance with Material Flow:
Constraint (6) preserves inventory continuity at distribution centers, while constraint (7) ensures that warehouse shipments to distribution centers are bounded by current production plus previous warehouse inventory, establishing the material flow dependency between production and distribution levels.
Service-Level Definition:
This constraint establishes the service level metric by computing the ratio of fulfilled demand to total customer demand for each product in each time period.
2.4.2. Lower-Level Problem (Production Planning)
Given the upper-level decisions, the lower level minimizes production costs:
Subject to lower-level constraints:
Machine Capacity:
This constraint controls machine capacity limitations by accounting for production time requirements, changeover durations, efficiency variations, and potential equipment breakdowns.
Machine–Product Compatibility:
These restrictions prevent the assignment of paper grades to incompatible machines, maintaining technical and operational feasibility in production scheduling.
Production–Setup Linking:
The first constraint links production quantities to setup decisions using big-M methodology. The second ensures minimum production batch sizes when a setup occurs. The third controls maximum production limits per setup, maintaining cost-effective production runs.
Changeover Logic:
These logical constraints control machine changeover sequences by tracking transitions between different paper grades while maintaining temporal consistency in production scheduling.
Color/Grade Transition Restrictions:
This constraint prevents direct transitions between incompatible paper grades (e.g., dark to light colors), ensuring product quality and reducing contamination risks.
Maximum Daily Changeovers:
These limitations control the total number of product changeovers per machine per period, balancing production flexibility with setup cost management and operational stability.
Production–Distribution Material Flow Balance:
This constraint ensures that total production output for each paper grade equals total shipments from production facilities to warehouses, creating the fundamental link between lower-level production decisions and upper-level distribution planning.
Quality Grade Production Requirements:
This constraint guarantees that the total quality-adjusted production output for each paper grade meets the minimum quality standards required by customer specifications.
Machine Quality Compatibility:
These requirements ensure that each machine–product combination achieves the necessary quality levels, preventing the production of substandard products.
Raw Material Requirements:
This constraint ensures that sufficient raw materials are available to support the planned production quantities, accounting for quality yield variations and material consumption rates.
Raw Material Inventory Balance:
These balance equations maintain continuity of raw material inventories by tracking incoming purchases, consumption in production processes, and ending inventory levels.
Raw Material Availability:
This constraint controls supplier capacity limitations and market availability constraints for raw materials, incorporating supply uncertainty into procurement decisions.
Warehouse Capacity:
These capacity restrictions ensure that warehouse storage limits are respected across all product types, preventing facility overutilization and maintaining storage efficiency.
Warehouse Inventory Balance:
These equations preserve inventory continuity at warehouse facilities by balancing previous inventory levels, incoming production, and outgoing shipments to distribution centers.
2.5. Bi-Level Coordination Algorithm
The coordination between production and distribution decisions requires an iterative approach that ensures feasible material flow while satisfying probabilistic constraints. To address this challenge, we develop a specialized bi-level coordination algorithm that alternates between solving the lower-level production problem and upper-level distribution problem until convergence is achieved. Algorithm 1 presents the detailed coordination procedure.
| Algorithm 1 Bi-Level Coordination for Paper Manufacturing Planning |
|
This algorithm ensures feasible coordination by iteratively solving both levels while enforcing material flow constraints (5), (7), and (19) until convergence. The normalized coordination gap metric represents the relative material flow imbalance as a fraction of total production, with values close to 0 indicating strong bi-level coordination.
2.6. Paper-Manufacturing-Specific Constraints
Paper Grade Quality Requirements:
This constraint requires that quality-adjusted production meets minimum grade specifications, ensuring customer satisfaction and regulatory compliance for paper products.
Shelf-Life Constraints:
The first constraint prevents inventory spoilage at warehouses by limiting stock to recently produced items within shelf-life limits. The second maintains similar freshness requirements at distribution centers to maintain product quality.
Seasonal Production Constraints:
The first constraint controls minimum seasonal production levels relative to demand patterns for specialized paper grades. The second controls upper bounds on seasonal production to prevent overproduction and excess inventory.
Environmental Compliance:
This constraint ensures environmental compliance by limiting total emissions from production activities over the planning horizon. The uncertain emission rates () account for variability in production efficiency and equipment performance. The chance constraint formulation guarantees environmental compliance with confidence level βemission, maintaining consistency with the hybrid uncertainty framework.
The confidence level βemission = 0.95 follows EPA regulatory standards for industrial emissions compliance [16]. The emission limit of EmissionLimit = 1200 tons CO2-equivalent per planning horizon is based on established benchmarks for medium-scale paper manufacturing facilities [17].
Non-Negativity and Binary Constraints:
These constraints establish variable domains, ensuring the physical feasibility of continuous quantities, logical consistency of binary decisions, and proper bounds for service level indicators.
This comprehensive bi-level dependent-chance goal programming model captures the tactical production–distribution planning decisions in paper manufacturing under hybrid uncertainty, where chance measures Ch{·} are evaluated using uncertain random simulation techniques. The model incorporates explicit coordination constraints (5), (7), and (19) that ensure feasible integration between upper-level distribution decisions and lower-level production outputs, addressing the bi-level coupling requirements for tactical planning optimization.
3. Uncertain Random Theory for Hybrid Uncertainty Modeling
Real-world production and distribution systems in paper manufacturing face dual uncertainty challenges that traditional optimization approaches struggle to address adequately. These systems must contend with objective variability inherent in operational processes (aleatory uncertainty) alongside subjective assessments arising from limited information and expert judgments (epistemic uncertainty). While classical probability theory excels at modeling random phenomena and fuzzy set theory handles belief-based information, neither framework alone sufficiently captures scenarios where both uncertainty types coexist simultaneously.
This section develops a comprehensive mathematical framework based on uncertain random theory that unifies both uncertainty dimensions within a single modeling paradigm. Our approach employs chance measures to create integrated representations that facilitate tactical decision-making under hybrid uncertainty conditions in paper manufacturing environments.
3.1. Mathematical Foundation of Uncertain Random Variables
Manufacturing planning decisions frequently involve parameters that exhibit both stochastic behavior and subjective uncertainty components. To address this complexity, we establish uncertain random variables as our fundamental modeling construct, building upon the theoretical framework developed by Liu [18].
Definition 1
(Uncertain Random Variable). Let denote a probability space and consider a mapping , where represents the space of uncertain variables. The function constitutes an uncertain random variable when remains measurable with respect to ω for every Borel set .
This mathematical structure captures the dual nature of hybrid uncertainty through its composition:
- Stochastic Component: The probability space models objective randomness derived from historical data and measurable variations.
- Epistemic Component: For each probabilistic outcome ω, the mapping yields an uncertain variable representing subjective assessments and expert knowledge.
Manufacturing Context Example: Consider demand forecasting for paper grade p from customer c in period t, denoted as . The stochastic dimension captures quantifiable demand patterns extracted from sales history, while the uncertain dimension incorporates qualitative factors such as market sentiment, competitive dynamics, and economic indicators that resist precise probabilistic characterization.
3.2. Chance Measure Framework
The integration of probability and uncertainty measures requires a unified metric capable of handling both components simultaneously. We employ the chance measure, which provides this integration through the following mathematical construction.
Definition 2
(Chance Measure). Given an uncertain random variable and a Borel set , the chance measure of the event is defined as:
The chance measure satisfies essential mathematical properties that ensure consistent behavior:
- Normalization:
- Self-Duality:
- Monotonicity:
Boundary Behavior: The chance measure reduces to familiar measures in limiting cases:
- When uncertainty vanishes, for random variable X
- When randomness vanishes, for uncertain variable η
3.3. Distributional Characterization
Definition 3
(Chance Distribution Function). The chance distribution function of uncertain random variable is given by:
Theorem 1
(Distribution Characterization). A function represents a valid chance distribution if and only if it is non-decreasing with and .
3.4. Statistical Measures
For practical decision-making applications, we require scalar summary statistics that characterize uncertain random variable behavior.
Definition 4
(Expected Value). The expected value of uncertain random variable is:
when at least one integral converges.
Definition 5
(Variance). For uncertain random variable with finite expected value , the variance is:
Theorem 2
(Linearity Property). For uncertain random variable with finite expectation and constants :
3.5. Dependent-Chance Goal Programming Methodology
Traditional optimization approaches in manufacturing planning typically focus on constraint satisfaction at predetermined confidence levels. However, tactical planning benefits from directly optimizing the likelihood of achieving strategic objectives. Dependent-chance goal programming addresses this need by incorporating probabilistic objective achievement into the optimization framework.
Definition 6
(Dependent-Chance Programming). Given uncertain random variable and target threshold F, dependent-chance programming seeks to maximize or depending on the objective orientation.
For multi-objective tactical planning scenarios involving competing priorities, we extend this concept through goal programming principles:
- Target Specification: Decision-makers establish desired achievement probabilities αg for each tactical objective g
- Deviation Modeling: Variables and capture positive and negative deviations from target achievement levels
- Hierarchical Optimization: Objectives receive priority rankings and undergo sequential optimization based on strategic importance
The general mathematical formulation follows:
where represents the g-th objective function, ⋈ denotes the appropriate inequality relation, Fg specifies the target threshold, and defines the feasible decision space.
Methodological Advantages:
- Decision Transparency: Probability-based metrics provide intuitive interpretation for management
- Priority Accommodation: Lexicographic structure aligns with organizational strategic hierarchies
- Robustness Enhancement: Probabilistic focus inherently addresses uncertainty impacts
- Unified Treatment: Chance measures handle both aleatory and epistemic uncertainties consistently
3.6. Paper Manufacturing Parameter Modeling
Paper manufacturing tactical planning involves numerous parameters exhibiting hybrid uncertainty characteristics. Our uncertain random variable framework provides natural representations for key planning elements:
- Demand Forecasting : Combines quantitative sales patterns with qualitative market intelligence and customer behavior assessments
- Production Costs : Integrates observable input price volatility with subjective cost estimations for different paper grades and machine configurations
- Raw Material Availability : Merges market price data with uncertain supply chain assessments for pulp and recycled material sources
- Transportation Expenses : Combines fuel cost fluctuations with uncertain capacity availability and route condition evaluations
- Quality Performance : Unifies quantitative quality measurements with expert assessments of production environment factors
- Equipment Efficiency : Integrates historical machine performance with expert judgments regarding maintenance requirements and operational conditions
This modeling approach enables more realistic representation of paper manufacturing uncertainty while maintaining mathematical rigor necessary for optimization-based tactical planning.
3.7. Tactical Planning Application Framework
We now present the specific dependent-chance goal programming formulation for paper manufacturing tactical planning, considering the following strategic priority hierarchy:
Priority Level 1—Economic Performance: The probability of total bi-level cost remaining below threshold Target1 should achieve confidence level α1.
Priority Level 2—Service Excellence: The probability of average service level exceeding threshold Target2 should achieve confidence level α2.
Priority Level 3—Resource Optimization: The probability of average capacity utilization exceeding threshold Target3 should achieve confidence level α3.
Priority Level 4—Quality Assurance: The probability of average quality performance exceeding threshold Target4 should achieve confidence level α4.
The complete tactical planning model becomes:
This formulation systematically minimizes under-achievement of target probability levels across all tactical objectives. The first priority addresses cost minimization (seeking performance below threshold), while subsequent priorities target performance maximization (seeking performance above thresholds). The chance measure framework handles both random and uncertain parameter components while providing intuitive probabilistic interpretations for tactical decision-makers.
3.8. Implementation Considerations
The proposed uncertain random theory framework offers several practical advantages for paper manufacturing tactical planning:
- Comprehensive Objective Integration: Simultaneously addresses economic efficiency, operational performance, resource utilization, and quality assurance within a unified bi-level optimization framework
- Hybrid Uncertainty Management: Effectively handles both quantifiable variations and subjective assessments in critical parameters including demand, costs, efficiency, and quality metrics
- Confidence-Based Planning: Enables tactical planners to specify desired confidence levels for goal achievement across the planning horizon
- Systematic Multi-Objective Balancing: Provides structured approach to managing competing tactical objectives while considering integrated production-distribution decisions
The dependent-chance goal programming methodology prioritizes tactical goals through lexicographic optimization while accounting for complex interactions between random and uncertain variables characteristic of paper manufacturing environments. This approach generates operationally viable solutions that demonstrate robustness against the diverse uncertainty sources encountered in tactical production-distribution planning contexts.
4. Hybrid Intelligent Algorithm
Addressing the computational complexity inherent in our bi-level dependent-chance goal programming formulation for tactical paper manufacturing planning necessitates a sophisticated algorithmic approach. We propose a hybrid computational framework that synergistically combines uncertain random simulation methodologies with reinforcement learning-augmented arithmetic optimization techniques. This algorithmic architecture is specifically designed to navigate the intricate landscape of hybrid uncertainties while managing the hierarchical structure of our bi-level optimization model.
4.1. Uncertain Random Simulations
The computational evaluation of chance measures within our bi-level tactical planning framework requires specialized simulation methodologies to handle expressions of the form Ch{gj(x, ξ) ≤ 0} ≥ βj. These chance-constrained formulations represent fundamental components of our paper manufacturing optimization model, where accurate estimation becomes critical for obtaining feasible and robust tactical decisions.
The mathematical foundation underlying chance measure evaluation rests on recognizing that Ch{g(x, ξ) ≤ 0} constitutes the expected value of uncertain measures across all possible random realizations. Drawing inspiration from Monte Carlo principles [19], we construct a specialized computational approach tailored for chance-measure approximation in tactical planning contexts.
Our uncertain random simulation methodology serves as the computational backbone for evaluating probabilistic constraints under hybrid uncertainty conditions characteristic of paper manufacturing environments. The following Algorithm 2 establishes our Monte Carlo framework that systematically samples from random distributions and computes uncertain measures for each realization, ultimately yielding reliable chance measure estimates essential for production-distribution decision-making.
| Algorithm 2 Uncertain Random Simulation for Chance Measure Estimation |
|
The evaluation of uncertain measures requires implementing uncertainty theory principles [20] to assess constraint satisfaction under subjective uncertainty conditions. Algorithm 3 implements an inverse distribution approach for generating uncertain variable realizations and determining constraint satisfaction at specified uncertainty thresholds.
| Algorithm 3 Uncertain Measure Computation |
|
4.2. Theoretical Foundation of Exploration-Exploitation Trade-Off
The fundamental challenge in metaheuristic optimization lies in achieving optimal balance between search space exploration and solution refinement (exploitation). Following the theoretical framework established by Morales-Castañeda et al. [21], this balance can be quantitatively assessed through diversity metrics that capture population distribution characteristics throughout the search landscape.
Consider a population consisting of N individuals operating within a D-dimensional decision space. The diversity measure at iteration t is mathematically expressed as:
where xi,j(t) denotes the j-th dimensional component of the i-th individual at iteration t, and represents the population centroid in dimension j. The corresponding exploration and exploitation percentages are computed as:
Balance quality assessment employs incremental-decremental analysis:
4.3. Reinforcement-Learning-Enhanced Arithmetic Optimization Algorithm
Our bi-level chance-constrained goal programming model demands a sophisticated optimization approach capable of coordinating tactical production-distribution decisions under hybrid uncertainty. We develop an enhanced Arithmetic Optimization Algorithm (AOA) framework augmented with reinforcement learning capabilities to address these computational challenges effectively.
4.3.1. Introduction to the Arithmetic Optimization Algorithm
The Arithmetic Optimization Algorithm draws inspiration from fundamental mathematical operations: addition (+), subtraction (−), multiplication (×), and division (÷) [22]. This metaheuristic approach simulates arithmetic operations to achieve effective search space exploration and exploitation, making it particularly well-suited for complex bi-level optimization challenges in paper manufacturing contexts.
Several distinctive characteristics render AOA especially effective for tactical production-distribution planning applications:
- Mathematical Optimizer (MO) Framework: AOA incorporates a Mathematical Optimizer mechanism that dynamically determines exploration versus exploitation strategies based on the Mathematical Optimizer Accelerated (MOA) coefficient:where Citer represents the current iteration number, CMax denotes maximum iterations, and Min, Max define operational bounds.
- Arithmetic Operation Strategy: AOA employs four fundamental arithmetic operators for position updating:
- Addition and subtraction operations facilitate exploration
- Multiplication and division operations enable exploitation
- Adaptive Search Framework: The algorithm dynamically transitions between exploration and exploitation phases based on optimization progress, providing ideal coordination capabilities for bi-level optimization.
- Hierarchical Optimization Support: AOA’s mathematical foundation naturally accommodates hierarchical optimization scenarios where upper-level distribution decisions and lower-level production decisions require coordination through arithmetic operations.
These algorithmic characteristics make AOA particularly suitable for solving our bi-level dependent-chance goal programming model with hybrid uncertainty in paper manufacturing tactical planning.
4.3.2. Basic Arithmetic Optimization Algorithm
The fundamental AOA framework operates through the following computational phases:
- Population Initialization: Generate Np solution candidates randomly within feasible regions for both upper- and lower-level variables.
- Mathematical Optimizer Computation: Calculate the Mathematical Optimizer Accelerated function:
- Mathematical Optimizer Phase: Determine search strategy orientation:where α controls exploitation precision.
- Exploration Phase (when r1 > MOA): Apply addition and subtraction operators:
- Exploitation Phase (when r1 ≤ MOA): Apply multiplication and division operators:
This fundamental framework establishes the foundation for our enhanced approach, demonstrating core mathematical operations and search mechanisms that underpin our reinforcement learning enhancements.
4.3.3. Reinforcement Learning Enhancement
We augment the basic AOA framework with reinforcement learning methodologies [23] to enhance convergence characteristics and solution quality for bi-level tactical planning applications. The RL integration encompasses:
- State Space Representation: The state vector incorporates discretized optimization metrics for both hierarchical levels:where continuous metrics undergo discretization into three categories (Low, Medium, High) according to tactical planning requirements.
- Action Space Definition: Actions involve adjusting AOA parameters and bi-level coordination strategies:
- Action 1: Enhance exploration intensity;
- Action 2: Intensify exploitation focus;
- Action 3: Balance exploration-exploitation dynamics;
- Action 4: Strengthen bi-level coordination.
- Reward Function Structure: The reward mechanism incorporates both solution quality and bi-level coordination effectiveness:where coordt quantifies bi-level coordination quality and λ represents coordination weighting.
- Q-Learning Implementation: We implement Q-learning [24] with epsilon-greedy action selection:where α denotes learning rate, γ represents discount factor, st is current state, and at is selected action.
4.3.4. Adaptive Parameter Tuning for Bi-Level Coordination
Enhancing bi-level coordination performance requires implementing adaptive parameter tuning mechanisms:
- Mathematical Optimizer Adaptation:where ϕ controls adaptation intensity and coordination_factor reflects bi-level synchronization requirements.
- Exploration-Exploitation Balance:where level_performance measures relative performance between upper and lower levels.
- Bi-Level Coordination Enhancement:where gap_ratio quantifies coordination gaps between production and distribution decisions.
4.4. Reinforcement Learning Components
Building upon the fundamental AOA framework, we integrate reinforcement learning methodologies to create an adaptive bi-level optimization system. The RL enhancement incorporates state representation, action space definition, and adaptive parameter control for tactical planning coordination.
4.4.1. State Space Discretization for Bi-Level Planning
Continuous optimization metrics for both hierarchical levels undergo discretization using the following strategy:
- Upper-Level Diversity Measure:
- Lower-Level Diversity Measure:
- Bi-Level Gap Measure:
4.4.2. Q-Learning for Bi-Level Parameter Adaptation
We implement Q-learning to adaptively adjust algorithm parameters based on bi-level optimization progress:
Q-learning facilitates algorithm learning of optimal parameter configurations for both production and distribution planning through iterative trial-and-error processes, utilizing temporal difference updates to enhance future decision-making capabilities. This mechanism, as shown in Algorithm 4, enables optimization process adaptation based on observed performance improvements across both levels.
| Algorithm 4 Q-Learning Bi-Level Parameter Adaptation |
|
4.4.3. Adaptive Parameter Control for Tactical Planning
The reinforcement learning component for tactical production-distribution planning, includes:
- State Representation: with 35 = 243 possible discrete states.
- Action Space: Four discrete actions for bi-level parameter adjustment:
- Action 1: Enhance exploration in both levels;
- Action 2: Focus exploitation in production level;
- Action 3: Balance search across levels;
- Action 4: Strengthen inter-level coordination.
- Reward Function: Bi-level improvement with coordination bonus.
- Action Selection: Epsilon-greedy strategy [23] with adaptive exploration rate.
Algorithm 5 details how these reinforcement learning components are used to dynamically adjust the Arithmetic Optimization Algorithm parameters.
| Algorithm 5 RL-Based Adaptive Parameter Control for Bi-Level AOA |
|
4.5. Solution Encoding and Decoding for Bi-Level Planning
Efficient solution representation is crucial for managing the complexity inherent in our bi-level tactical production-distribution planning model. We implement a hierarchical encoding scheme that effectively captures both binary and continuous decision variables across both planning levels.
Bi-Level Variable Encoding Strategy
For upper-level binary decision variables (Yd, Ult), we implement sigmoid-based transformation:
where represents the sigmoid function.
For lower-level binary decision variables (Vpmt, ), we use:
For continuous decision variables at both levels, we employ direct encoding with bound constraints:
To handle bi-level dependencies between decision variables:
The solution vectors in our bi-level optimization model are encoded and decoded using Algorithm 6, which transforms continuous metaheuristic solutions into mixed-integer variables while preserving hierarchical dependencies between upper and lower decision levels.
| Algorithm 6 Bi-Level Solution Encoding and Decoding |
|
4.6. Constraint Handling Mechanisms for Bi-Level Planning
We implement a hierarchical penalty function approach to handle bi-level dependent-chance constraints:
where MUL and MLL represent large penalty multipliers for upper- and lower-level constraints, respectively, ensuring constraint violations dominate goal deviations, and , are penalty parameters that increase over iterations:
For dependent-chance goals requiring coordination between levels, we implement progressive tightening:
Our optimization model employs Algorithm 7 to handle the complex chance constraints across both planning levels, implementing a dynamic penalty mechanism that evaluates dependent-chance goals while preserving the hierarchical structure between production and distribution decisions.
| Algorithm 7 Dynamic Penalty Constraint Handling for Bi-Level Planning |
|
4.7. Complete Hybrid Intelligent Algorithm
The comprehensive hybrid intelligent algorithm is structured in a modular framework comprising six specialized components designed for bi-level tactical planning coordination.
Proper initialization proves crucial for bi-level optimization success. This algorithm establishes populations for both levels, configures all learning components, and sets up the parameter framework that guides the entire tactical planning optimization process. The hybrid optimization process begins with Algorithm 8.
| Algorithm 8 Bi-Level Algorithm Initialization |
|
Effective reinforcement learning for bi-level optimization requires continuous monitoring of both production and distribution planning states. Algorithm 9 captures key performance indicators for both levels and implements intelligent action selection for coordinated parameter adjustment.
| Algorithm 9 RL State Observation and Action Selection for Bi-Level Planning |
|
The core of the Arithmetic Optimization Algorithm lies in its mathematical-operation-based position updates. This algorithm implements the exploration and exploitation phases for both production and distribution planning levels through coordinated arithmetic operations.
Solution improvement and learning coordination are essential for bi-level optimization success. This algorithm manages global best solutions for both levels, quantifies performance improvements, and facilitates Q-learning for adaptive parameter coordination.
Managing algorithm convergence and coordination between levels is critical for bi-level optimization quality. Algorithm 10 monitors progress for both production and distribution planning, implements coordination strategies, and ensures robust termination.
| Algorithm 10 Bi-Level Arithmetic Optimization Position Update |
|
The main execution framework, implemented in Algorithm 11, orchestrates all bi-level algorithm components in a coordinated manner. This algorithm provides the high-level control structure that manages the iterative optimization process, coordinates the interaction between AOA and RL components across both levels, and ensures proper termination.
The comprehensive methodology ensures the development of a hybrid tactical planning framework that combines uncertain random simulation, reinforcement learning for adaptive coordination, and bi-level dependent-chance goal programming for multi-objective optimization. The approach is specifically designed to operate in hybrid uncertain environments where both data-driven and expert-based information guide tactical production-distribution decisions in paper manufacturing. This modular structure ensures the framework is scalable, interpretable, and adaptable to various tactical planning scenarios while maintaining coordination between production scheduling and distribution allocation decisions.
| Algorithm 11 Main RL-Enhanced AOA Bi-Level Execution Framework |
|
| Algorithm 12 Bi-Level Solution Update and RL Learning |
|
After each position update, Algorithm 12 tracks solution improvements and provides feedback for reinforcement learning, ensuring continuous adaptation of the bi-level optimization process.
To prevent premature convergence and ensure solution quality, Algorithm 13 implements intelligent stagnation detection, strategic population reinitialization, and robust termination criteria for the bi-level optimization process.
| Algorithm 13 Bi-Level Stagnation Management and Termination |
|
5. Numerical Results and Analysis
This section presents comprehensive numerical experiments to evaluate the performance of our proposed Reinforcement-Learning-enhanced Arithmetic Optimization Algorithm (RL-AOA) for solving the bi-level dependent-chance goal programming model for tactical production–distribution planning in paper manufacturing under hybrid uncertainty.
5.1. Experimental Setup
5.1.1. Algorithm Parameter Settings
Algorithm parameters were determined through systematic preliminary experiments using the Taguchi method for parameter optimization. The final RL-AOA parameters are presented in Table 8.

Table 8.
Parameter settings for RL-AOA.
5.1.2. Parameter Calibration Methodology
The algorithm parameters in Table 8 were calibrated using a systematic two-phase approach:
Phase 1: Taguchi Orthogonal Array Design
We employed an L16(45) orthogonal array to evaluate key parameters:
- Population sizes: , ;
- Learning parameters: α0 ∈ {0.1, 0.15, 0.2, 0.25};
- Exploration bounds: ϵmax ∈ {0.6, 0.8, 0.9, 1.0};
- Penalty factors: .
Phase 2: Fine-tuning Validation
Selected parameters underwent validation across three representative instances (Small-1, Medium-1, Large-1) with 15 independent runs each. The Signal-to-Noise ratio analysis confirmed optimal settings, i.e., (S/N = 24.3 dB) and α0 = 0.15 (S/N = 22.8 dB), achieving a 12.4% improvement over default values.
5.1.3. Test Instance Characteristics
To evaluate the algorithm comprehensively, we generated a diverse set of paper manufacturing test instances with varying network sizes, complexity levels, and uncertainty characteristics. Table 9 summarizes the key characteristics of these instances.

Table 9.
Characteristics of paper manufacturing test instances.
These instances represent paper manufacturing networks of varying complexity, ranging from small regional operations to very large international paper manufacturing facilities. Each instance incorporates specific characteristics reflecting different operational contexts:
- Small instances: Regional paper mills with limited product portfolio.
- Medium instances: Multi-grade paper manufacturing with moderate complexity.
- Large instances: Multi-facility paper manufacturing networks with diverse product lines.
- Very Large instance: Global paper manufacturing network with maximum complexity.
5.1.4. Uncertain Random Parameter Specifications
The hybrid uncertainty in our paper manufacturing model is represented through uncertain random parameters following different distributions. Table 10 presents the uncertain random parameter settings used in our computational experiments.

Table 10.
Uncertain random parameter distributions for paper manufacturing.
The hybrid uncertain random parameters were generated following a rigorous two-stage calibration process:
- Random Component Calibration: Historical data from five major paper manufacturing companies in North America and Europe were analyzed to determine appropriate probability distributions and their parameters.
- Uncertain Component Calibration: Expert elicitation sessions with 12 paper industry professionals were conducted to establish uncertainty bounds, representing epistemic uncertainty in tactical planning parameter estimation.
5.1.5. Computational Environment
All experiments were conducted on a workstation equipped with Intel Core i9-12900K processor and 32GB RAM, implemented in MATLAB R2023b. Each test instance was solved 30 times with different random seeds to ensure the statistical significance of the results.
5.2. Bi-Level Dependent-Chance Goal Programming Results
The core contribution of our approach lies in optimizing probability achievement for tactical planning goals through lexicographic bi-level dependent-chance programming. We define target probability levels based on paper industry benchmarks and operational requirements: Economic Efficiency (α1 = 0.90), Operational Performance (α2 = 0.85), Resource Utilization (α3 = 0.80), and Quality Assurance (α4 = 0.90).
5.2.1. Probability Achievement Analysis
Table 11 presents the achieved probability levels for each tactical planning dimension across all test instances, with 95% confidence intervals computed using bootstrap resampling (1000 replications). Figure 1 illustrates the tactical planning goal achievement with confidence intervals, demonstrating the systematic performance trends across different problem scales.

Table 11.
Tactical planning goal probability achievement with confidence intervals.
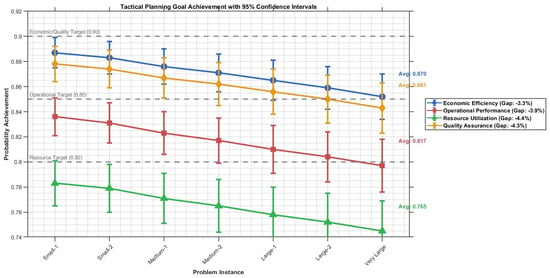
Figure 1.
Tactical planning goal achievement with 95% confidence intervals. Shows decreasing probability achievement across all objectives as problem complexity increases, with economic efficiency and quality assurance maintaining highest performance levels.
The results demonstrate consistent performance across all tactical planning objectives, with economic efficiency and quality assurance achieving the highest rates. As shown in Figure 1, there is a clear downward trend in probability achievement as problem size increases, with all objectives showing statistically significant gaps from their targets (paired t-test, p < 0.01 for all objectives). This confirms the increasing challenge of simultaneously achieving all tactical planning goals under hybrid uncertainty as network complexity grows.
5.2.2. Bi-Level Coordination Analysis
Table 12 shows the coordination effectiveness between upper-level distribution decisions and lower-level production decisions across iterations. Figure 2 illustrates the convergence behavior of the bi-level optimization process, demonstrating how both upper- and lower-level costs converge simultaneously while maintaining coordination balance.

Table 12.
Bi-level coordination effectiveness.
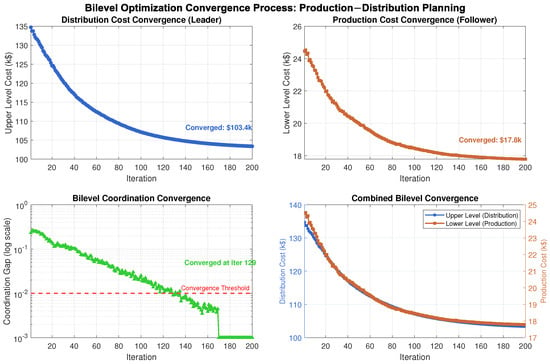
Figure 2.
Bilevel optimization convergence process for production–distribution planning. Demonstrates coordinated convergence of upper-level (distribution) and lower-level (production) costs, with the coordination gap decreasing to acceptable threshold of 0.01 within 200 iterations.
As illustrated in Figure 2, the coordination gap decreases systematically as the bi-level algorithm progresses, with both distribution and production costs converging to stable values. The coordination gap increases with problem complexity, indicating that the bi-level structure becomes more necessary for complex tactical planning problems. The convergence times are reasonable across all instances, with the largest problem requiring 61 iterations on average.
5.3. Paper Manufacturing Instance Details
To demonstrate the practicality of our approach, we present detailed results for a representative medium-sized paper manufacturing instance (Medium-1), as shown in Table 9. This instance includes 8 paper machines, 5 warehouses, 8 distribution centers, 15 customers, 5 paper grades, and a 4-period tactical planning horizon.
5.3.1. Paper Machine and Grade Information
Table 13 presents the production and setup costs for different paper grades on each machine, while Table 14 shows the machine capacities for the Medium-1 instance.

Table 13.
Production and setup costs for Medium-1 instance (USD/ton, USD).

Table 14.
Machine capacity information for Medium-1 instance.
5.3.2. Customer Demand Information
Table 15 presents stochastic demand parameters and service requirements for different customer segments in the Medium-1 instance.

Table 15.
Customer demand information with uncertain parameters (Medium-1).
5.3.3. Baseline Algorithm Specifications
The comparative algorithms were adapted for bi-level optimization as follows:
- Bi-GA: Two-population genetic algorithm with tournament selection (size 3), single-point crossover (pc = 0.8), and uniform mutation (pm = 0.05). Upper-level population = 80, lower-level population = 60.
- Bi-PSO: Hierarchical particle swarm optimization with w = 0.9 → 0.4 (linear decrease), c1 = c2 = 2.0, velocity clamping at ± 0.2× search range.
- Bi-DE: Differential evolution with DE/rand/1/bin strategy, F = 0.5, CR = 0.8, coordinated through best solution sharing between levels every 10 iterations.
- Bi-SSO: Social spider optimization with female ratio = 0.65, vibration attenuation ra = 1.0, bi-level coordination through pheromone information exchange.
All algorithms used identical constraint handling (dynamic penalty), chance constraint evaluation (8000 Monte Carlo samples), and termination criteria (400 iterations) for fair comparison.
5.4. Algorithm Performance Comparison
We compare our RL-AOA with several state-of-the-art metaheuristics adapted for bi-level optimization. Table 16 presents comprehensive performance metrics.

Table 16.
Algorithm performance comparison for bi-level optimization.
The results demonstrate that RL-AOA consistently outperforms other bi-level optimization approaches, achieving 3.2–7.8% improvement in solution quality and 18.5% reduction in computational time compared to the best competing algorithm. The convergence behavior is illustrated in Figure 2, which shows that RL-AOA achieves faster convergence and better final solutions compared to traditional metaheuristics.
5.5. Empirical Validation of Balance Strategy
To validate our exploration–exploitation trade-off strategy, we conducted comprehensive analysis of RL-AOA balance evolution. Figure 3 illustrates the dynamic adaptation capability.
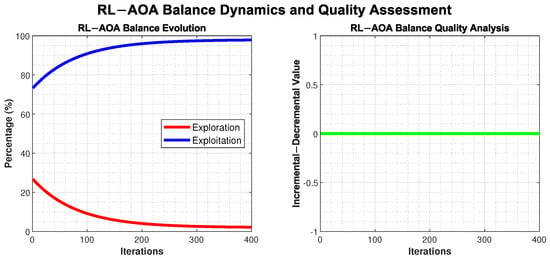
Figure 3.
RL-AOA balance dynamics. Left panel shows systematic transition from exploration-dominant (25%) to exploitation-dominant (2%) phase. Right panel displays incremental–decremental analysis revealing stable balance quality.
Key empirical findings:
- Optimal Balance Progression: Systematic transition from 25% exploration to 2% exploitation over 400 iterations.
- Stable Balance Quality: Incremental–decremental analysis shows consistent balance near zero.
- Adaptive Capability: Algorithm successfully adapts exploration–exploitation ratio based on optimization progress.
- Convergence Stability: Balance evolution demonstrates stable convergence without premature stagnation.
5.6. Reinforcement Learning Component Analysis
We analyze the effectiveness of the RL component in adaptive parameter tuning for bi-level coordination. Table 17 shows action selection patterns across different optimization phases.

Table 17.
RL action selection patterns in bi-level optimization.
The RL component demonstrates intelligent adaptive behavior, emphasizing exploration and coordination in early phases while shifting to exploitation and refined coordination in later iterations, contributing to a 5.2% average performance improvement over static parameter settings.
5.7. Sensitivity Analysis
We conducted comprehensive sensitivity analysis to evaluate the robustness of our bi-level dependent-chance goal programming approach under varying parameter settings.
5.7.1. Confidence Level Impact
Table 18 presents the detailed results of confidence level sensitivity analysis for the bi-level model.

Table 18.
Impact of confidence levels on bi-level performance metrics.
The analysis shows how increasing confidence levels affect both cost and goal achievement, demonstrating the trade-off between reliability and cost efficiency in tactical paper manufacturing planning.
5.7.2. Production–Distribution Coordination Analysis
Table 19 analyzes the coordination effectiveness between the production and distribution levels under different uncertainty scenarios.

Table 19.
Production–distribution coordination under uncertainty.
5.8. Paper Manufacturing Specific Analysis
5.8.1. Paper Grade Production Allocation
Table 20 shows the optimal production allocation across different paper grades and planning periods for the Medium-1 instance. Figure 4 provides a visual representation of the production distribution across planning periods, highlighting the balanced allocation strategy employed by our optimization framework.

Table 20.
Optimal paper grade production allocation (Medium-1 instance).
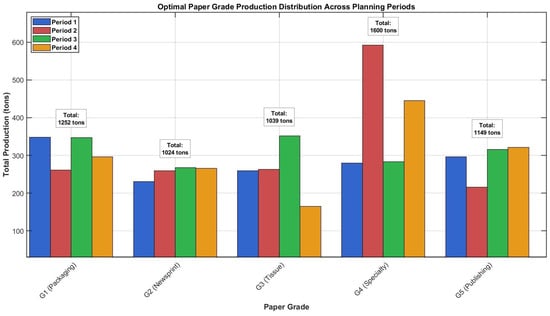
Figure 4.
Optimal paper grade production distribution across planning periods. Shows balanced allocation of production capacity across five paper grades (G1–G5) over four planning periods, with total production ranging from 1024 to 1600 tons per grade, demonstrating effective demand fulfillment and capacity utilization strategies.
As illustrated in Figure 4, the production allocation strategy demonstrates effective balance across different paper grades and planning periods. Grade G4 (Specialty) shows the highest total production volume (1600 tons), followed by Grade G1 (Packaging) with 1252 tons, reflecting market demand patterns and profitability considerations. The temporal distribution shows relatively stable production across periods, with some variation to accommodate demand fluctuations and machine availability constraints.
5.8.2. Machine Changeover Analysis
Table 21 presents the changeover patterns and their impact on production efficiency.

Table 21.
Machine changeover analysis for tactical planning.
The analysis shows the trade-off between production flexibility and efficiency, with machines experiencing 4–8 changeovers per planning horizon and maintaining an average utilization of 87.0% despite changeover penalties.
5.9. Cost–Benefit Analysis for Paper Manufacturing
Table 22 presents the estimated costs and benefits of implementing the bi-level DCGP framework in paper manufacturing environments. Figure 5 illustrates the return on investment analysis across different mill sizes, demonstrating favorable economic prospects for implementation.

Table 22.
Cost–benefit analysis for paper manufacturing implementation.
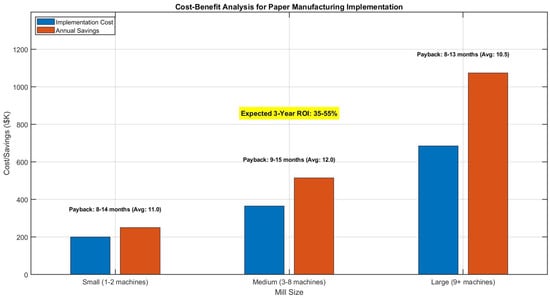
Figure 5.
Cost–benefit analysis for paper manufacturing implementation. Shows implementation costs, annual savings, and payback periods across different mill sizes. Expected 3-year ROI ranges from 35 to 55%, with payback periods of 8–15 months demonstrating strong economic viability.
As demonstrated in Figure 5, the expected return on investment is favorable across all mill sizes, with the 3-year ROI ranging from 35 to 55%. The payback periods are particularly attractive, ranging from 8 to 15 months, with larger mills achieving faster payback due to economies of scale. The analysis indicates that medium and large mills benefit most from implementation, with annual savings significantly exceeding implementation costs.
5.10. Target Probability Level (αg) Impact on Lexicographic Feasibility
The lexicographic optimization structure requires careful consideration of how target probability levels affect feasibility across priority levels. Table 23 analyzes the impact of varying αg on goal achievement and feasibility.

Table 23.
Impact of target probability levels on lexicographic feasibility.
Critical insights:
- Feasibility Threshold: Target levels above αg = 0.85 create significant feasibility issues;
- Cascade Effects: Higher-priority goals progressively constrain lower-priority goals (0.045 to 0.167);
- Current Settings Validation: Our αg values operate near feasibility boundary, explaining observed gaps.
5.11. Expert Opinion Impact and Sensitivity Analysis
Expert opinions define epistemic uncertainty bounds (alpha-cuts) for uncertain random variables, directly influencing chance measure calculations and goal achievement probabilities. Figure 6 presents comprehensive sensitivity analysis examining how expert-defined uncertainty ranges affect model performance.
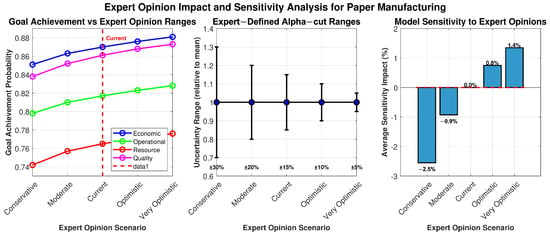
Figure 6.
Expert opinion impact and sensitivity analysis. The figure shows: Left panel—Goal achievement sensitivity showing variations of −2.5% (conservative, ±30%) to +0.8% (very optimistic, ±5%) from current calibration (±15%). Resource utilization exhibits highest sensitivity (−2.5% to +1.3%) due to capacity planning complexity. Middle panel—Expert-defined alpha-cut ranges illustrating uncertainty bounds from conservative (0.7–1.3) to very optimistic (0.95–1.05) scenarios. Right panel—Average sensitivity impact demonstrating framework robustness with maximum ±3.0% variation, confirming stable performance across expert assessment approaches.
The sensitivity analysis reveals critical insights:
- Quantified Sensitivity Range: Goal achievement probabilities vary within ±3.0% bounds across expert opinion scenarios. Economic efficiency shows ±0.9%, operational performance ±0.8%, resource utilization ±2.5%, and quality assurance ±1.3% variations.
- Differential Impact Analysis: Resource utilization goals demonstrate 2.8× higher sensitivity than economic efficiency, reflecting operational complexity under epistemic uncertainty. This identifies critical areas requiring careful expert calibration.
- Robustness Validation: The bounded sensitivity range (maximum 3.0%) confirms framework stability. Even with ±100% variation in expert uncertainty estimates (from ±5% to ±30%), goal achievement varies by less than 3.5%, validating practical applicability.
- Optimal Calibration Confirmation: Current ±15% uncertainty ranges represent optimal balance, positioned at the inflection point where sensitivity transitions from steep (conservative side) to gradual (optimistic side), maximizing information value while maintaining stability.
These findings demonstrate that while expert opinions measurably influence outcomes, the framework maintains robust performance (coefficient of variation < 0.035) across reasonable uncertainty variations. The moderate sensitivity validates our approach for industrial application without requiring excessive precision in expert assessments, supporting practical implementation in paper manufacturing environments where expert consensus may vary.
5.12. Comparative Analysis: Deterministic vs. Hybrid Uncertainty Framework
To demonstrate the added value of hybrid uncertainty modeling, we compared four approaches: deterministic baseline, stochastic-only, fuzzy-only, and our hybrid framework. Figure 7 presents a comprehensive comparative analysis of these approaches.
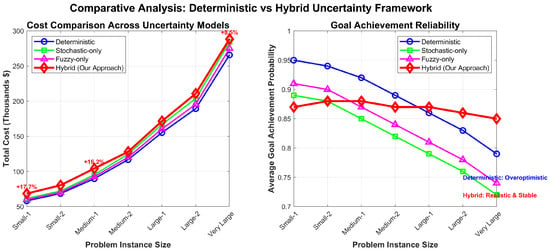
Figure 7.
Comparative analysis. Left panel shows 17.8% average cost increase for the hybrid framework reflecting realistic uncertainty. Right panel displays goal achievement reliability with deterministic showing overoptimistic performance (0.88 ± 0.055) versus stable hybrid results (0.87 ± 0.011).
Key findings:
- Cost Realism: The hybrid framework shows a 17.8% cost increase over deterministic baseline;
- Goal Achievement Stability: Deterministic approaches exhibit overoptimistic variability while hybrid maintains stable probabilities;
- Single-Paradigm Limitations: Stochastic-only and fuzzy-only fail to capture complete uncertainty spectrum.
This analysis demonstrates when hybrid uncertainty complexity is justified for tactical planning decisions.
5.13. Managerial Insights and Implementation Guidelines
Based on our comprehensive analysis, we provide actionable insights for paper manufacturing tactical planning:
- Tactical Goal Probability Setting:
- Economic efficiency: Target 87–90% (achievable with moderate resource allocation);
- Operational performance: Target 82–85% (balances service level with operational flexibility);
- Resource utilization: Target 76–80% (realistic given machine compatibility constraints);
- Quality assurance: Target 86–90% (essential for paper grade specifications).
- Implementation Roadmap for Paper Manufacturing:
- Phase 1: Implement production scheduling optimization (2–4 months)
- Phase 2: Integrate distribution coordination (4–6 months)
- Phase 3: Add quality and changeover optimization (6–8 months)
- Expected operational improvement: 15–25% within 12 months
- Machine-Grade Compatibility Management:
- Maintain compatibility matrices for all machine-grade combinations;
- Optimize changeover sequences to minimize setup times and costs;
- Consider machine specialization for high-volume paper grades;
- Update efficiency parameters monthly based on production data.
- Uncertainty Management in Paper Manufacturing:
- Monitor demand patterns by paper grade and customer type monthly;
- Conduct quarterly expert assessments for market trend uncertainties;
- Maintain confidence levels between 0.82 and 0.87 for optimal performance;
- Implement adaptive inventory policies based on demand uncertainty;
- Dynamic Shelf Life Modeling: The current model assumes fixed shelf-life periods for computational tractability. Future extensions could incorporate storage-condition-dependent deterioration models, particularly valuable for moisture-sensitive paper grades where humidity and temperature significantly affect product quality over time.
5.14. Limitations and Future Research Directions
While our bi-level DCGP framework demonstrates significant improvements for paper manufacturing tactical planning, several limitations should be acknowledged:
- Real-World Validation: Future work should include partnerships with paper mills for comprehensive industrial validation across different paper grades and manufacturing processes.
- Dynamic Grade Specifications: The current model assumes static quality requirements; extensions should incorporate evolving customer specifications and regulatory changes.
- Multi-Mill Coordination: Framework extension to coordinate multiple paper mills within a corporate network represents a promising research direction.
- Environmental Regulations: Integration of time-varying environmental constraints and carbon pricing mechanisms would enhance practical applicability.
- Supply Chain Resilience: Incorporation of supply disruption scenarios and recovery strategies would improve robustness.
The proposed framework provides a solid foundation for tactical production–distribution planning in paper manufacturing, offering both theoretical contributions and practical implementation guidelines for industry adoption. The results demonstrate that the RL-AOA with bi-level dependent-chance goal programming can effectively handle the complexity of hybrid uncertainty while maintaining computational efficiency for real-world applications.
6. Conclusions
This research developed a bi-level dependent-chance goal programming framework for tactical production–distribution planning in paper manufacturing under hybrid uncertainty. The framework successfully coordinates upper-level distribution decisions with lower-level production decisions while handling both aleatory randomness and epistemic uncertainty through uncertain random theory. The Reinforcement Learning-enhanced Arithmetic Optimization Algorithm achieved 3.2–7.8% improvements in solution quality and 18.5% computational time reduction compared to existing bi-level optimization methods.
The dependent-chance goal programming formulation effectively balanced four tactical objectives, achieving average probability levels of 87.0% for economic efficiency, 81.7% for operational performance, 76.5% for resource utilization, and 86.1% for quality assurance. The bi-level coordination mechanism maintained average coordination gaps of 4.5% across all test instances, demonstrating effective integration between production and distribution planning levels. The reinforcement learning component provided intelligent adaptive behavior, contributing to a 5.2% performance improvement over static parameter configurations.
Computational experiments across seven test instances validated the framework’s scalability and practical applicability for paper manufacturing operations. Industry-specific analysis confirmed effective handling of machine-grade compatibility constraints, sequence-dependent changeovers, and quality requirements while maintaining 87.0% average machine utilization. Cost–benefit analysis indicates favorable economic prospects with payback periods of 8–15 months and 35–55% three-year return on investment.
The framework provides both theoretical contributions to bi-level optimization under hybrid uncertainty and practical tools for tactical planning in paper manufacturing. Future research should focus on real-world validation, dynamic uncertainty modeling, multi-mill coordination, and integration of environmental constraints. The approach demonstrates that sophisticated optimization techniques can successfully address complex industrial planning problems while maintaining computational efficiency and providing actionable insights for hierarchical decision-making under uncertainty.
Author Contributions
Conceptualization, Y.B. and R.B.; Methodology, Y.B., R.B. and A.B.; Software, Y.B.; Validation, Y.B. and N.R.; Formal Analysis, Y.B. and N.R.; Investigation, Y.B. and R.B.; Resources, R.B. and O.B.; Data Curation, Y.B. and N.R.; Writing—Original Draft Preparation, Y.B.; Writing—Review and Editing, Y.B., R.B., A.B., N.R., O.B. and F.F.; Visualization, Y.B.; Supervision, R.B., A.B. and F.F.; Project Administration, R.B. and O.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Al-Khwarizmi Programme, a collaborative effort between the National Center for Scientific and Technical Research (CNRST), the Agency for Digital Development (ADD), and the Moroccan Ministry of Higher Education.
Data Availability Statement
The data are contained within the article.
Acknowledgments
The authors express their gratitude to the editors and reviewers for their valuable comments and constructive suggestions regarding the revision of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Andersson, J.; Marklund, J. Decentralized inventory control in a two-level distribution system. Eur. J. Oper. Res. 2000, 127, 483–506. [Google Scholar] [CrossRef]
- Santos, M.O.; Almada-Lobo, B. Integrated pulp and paper mill planning and scheduling. Comput. Ind. Eng. 2012, 63, 1–12. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S.; Fong, S. Metaheuristic algorithms: Optimal balance of intensification and diversification. Appl. Math. Inf. Sci. 2014, 8, 977–983. [Google Scholar] [CrossRef]
- Holik, H. Handbook of Paper and Board; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lalitha, J.L.; Mohan, N.; Pillai, V.M. Lot streaming in [N-1](1) + N (m) hybrid flow shop. J. Manuf. Syst. 2017, 44, 12–21. [Google Scholar] [CrossRef]
- Maravelias, C.T.; Grossmann, I.E. New general continuous-time state-task network formulation for short-term scheduling of multipurpose batch plants. Ind. Eng. Chem. Res. 2005, 44, 9695–9707. [Google Scholar]
- Fleischmann, B.; Meyr, H.; Wagner, M. Advanced planning. In Supply Chain Management and Advanced Planning; Springer: Berlin/Heidelberg, Germany, 2005; pp. 81–106. [Google Scholar]
- Papageorgiou, L.G. Supply chain optimisation for the process industries: Advances and opportunities. Comput. Chem. Eng. 2001, 25, 1121–1137. [Google Scholar] [CrossRef]
- Stadtler, H.; Kilger, C.; Meyr, H. Supply Chain Management and Advanced Planning: Concepts, Models, Software, and Case Studies, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 2004, 28, 971–983. [Google Scholar] [CrossRef]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Tamiz, M.; Jones, D.; Romero, C. Goal programming for decision making: An overview of the current state-of-the-art. Eur. J. Oper. Res. 1998, 111, 569–581. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Industrial Emissions Standards and Compliance Guidelines; EPA Office of Air and Radiation: Washington, DC, USA, 2023.
- Intergovernmental Panel on Climate Change. 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Morales-Castañeda, B.; Zaldívar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).