Abstract
With the rapid development of edge-intelligence systems, multi-UAV platforms have become vital for large-scale 3D reconstruction. However, efficient task scheduling remains a critical challenge due to constraints on UAV energy, communication range, and the need for balanced workload distribution. To address these issues, this paper presents a novel, centralized two-stage task scheduling framework. In the first stage, the framework partitions the target area into communication-feasible subregions by applying cell decomposition that accounts for no-fly zones and workload. It then models the subregion allocation as a Capacitated Vehicle Routing Problem (CVRP) with an added balancing constraint to optimize the traversal sequence for each operational sortie. In the second stage, a time-efficient, scan-based heuristic algorithm allocates viewpoints among UAVs to ensure workload balance, minimizing the mission completion time. Extensive simulations demonstrate that our proposed approach achieves superior performance in workload balance, path efficiency, and reconstruction quality. Overall, this work provides a scalable and energy-aware solution for centralized multi-UAV 3D reconstruction, highlighting an effective approach to ensure cooperation and efficiency in complex multi-agent systems.
1. Introduction
Multirotor UAV (Unmanned Aerial Vehicle)-based edge-intelligence systems have become indispensable for large-scale 3D reconstruction tasks [1], offering unparalleled operational flexibility and ease of deployment [2]. By flying at low altitudes, these systems can capture high-resolution imagery for various complex applications [3]. This capability has proven more effective than traditional methods for covering large and intricate environments [4], making them essential for applications ranging from urban planning to disaster response.
However, the effectiveness of such systems is fundamentally constrained by factors such as limited battery life, which directly impacts energy availability for missions [5], and restrictive communication ranges that limit the operational area [6]. These physical limitations make it impossible for a single drone, or even a small fleet, to survey a large area in one continuous operation. This necessitates a “divide and conquer” strategy, where the target area is partitioned into smaller, manageable subregions. Consequently, the problem shifts from simple coverage to a complex, multi-layered scheduling challenge. The critical goal becomes minimizing the total mission time, which is dictated not by the fastest UAV, but by the last one to complete its task. Therefore, achieving a balanced workload among all agents is not merely beneficial—it is essential for operational efficiency.
To tackle this, researchers have explored various strategies. For instance, to handle complex geometries with no-fly zones (NFZs), Bahnemann et al. [7] and Agarwal et al. [8] have successfully employed exact cell decomposition methods for area partitioning. Once an area is partitioned, it becomes necessary to plan traversal paths among the subregions [9]. While these methods are effective, a simple spatial division or a localized path optimization is insufficient. True operational efficiency requires a holistic, two-stage optimization approach that addresses the interdependencies between different levels of planning: (1) Inter-mission scheduling, which involves clustering subregions into energy-constrained sorties with balanced workloads, and (2) Intra-mission scheduling, which focuses on distributing viewpoint tasks evenly among UAVs within a single subregion for synchronized completion. Many existing methods address these stages in isolation or with simplistic heuristics, failing to produce a globally efficient solution and often leading to situations where some UAVs sit idle while others struggle with disproportionately large tasks.
To bridge this gap, we propose an efficient, centralized task scheduling framework for multi-UAV edge-intelligence systems. Our framework systematically optimizes both scheduling stages, ensuring that tasks are distributed fairly while considering a comprehensive set of constraints such as NFZs, communication range, and maximum flight distance.
The contributions of this paper are summarized as follows:
- Constraint-Aware Subregion Division: We propose an effective method to divide the large target area into smaller subregions using cell decomposition, simultaneously considering communication range, no-fly zones, and workload limitations. This ensures that each subregion is manageable within the operational constraints of the UAVs.
- Balanced Inter-Mission Path Planning via Constrained CVRP: By modeling the subregion allocation problem as a Capacitated Vehicle Routing Problem (CVRP) with a novel workload balancing constraint, we develop an efficient planning strategy that ensures equitable task distribution across missions and minimizes total travel distance.
- Time-Efficient Intra-Mission Task Allocation for Synchronized Operations: We propose a time-efficient, scan-based heuristic algorithm to solve the viewpoint allocation problem within each subregion. This method ensures that the workload is evenly distributed, which reduces individual UAV traversal time and facilitates synchronized mission completion.
- Comprehensive Validation: The framework’s effectiveness is rigorously validated through extensive simulations in a high-fidelity virtual urban environment and a large-scale (2 km2) real-world experiment. The results demonstrate statistically significant improvements in workload balance and path efficiency compared to state-of-the-art methods. The successful generation of a high-fidelity 3D campus model confirms the quality and completeness of the data acquired by our framework.
The remainder of this paper is organized as follows. Section 2 reviews the relevant literature. Section 3 formulates the task scheduling problem for large-scale 3D reconstruction and details the proposed multi-UAV task scheduling framework. Section 4 presents the experimental results and analysis of the proposed framework. Finally, Section 5 concludes the paper and highlights future work.
2. Related Work
In recent years, the application of UAV edge-intelligence systems for remote sensing has become increasingly widespread. However, when conducting 3D reconstruction tasks, UAVs face numerous challenges, including complex terrain, limited onboard resources, obstacles, and sensor performance limitations [10]. Additionally, UAVs must operate within strict constraints of battery life and communication range. To address these challenges, UAVs require efficient task scheduling strategies to complete high-quality 3D reconstruction tasks while satisfying various constraints. Based on the number of UAVs involved, these strategies can be broadly categorized into single-UAV and multi-UAV task scheduling.
2.1. Single-UAV Task Scheduling
Single-UAV task scheduling for 3D reconstruction must contend with various constraints such as no-fly zones (NFZs), energy consumption, and image resolution. For example, Ghaddar et al. [11] proposed a grid-based path planning method for environments containing NFZs. Their method generates a semi-directed graph representing all possible paths, which is then used to determine an optimal flight trajectory. However, such methods primarily focus on 2D coverage and have limited applicability to the complexities of 3D reconstruction.
Other studies have explored task allocation for single UAVs in 3D contexts, often dividing the planning process into global and local stages. Song et al. [12], for instance, proposed a method that leverages online-generated volume maps to guide path planning through exploration and inspection stages. While these approaches offer effective planning strategies, they often do not fully consider operational constraints like NFZs and energy consumption. Moreover, many rely heavily on the Next Best View (NBV) paradigm, which demands substantial computational resources at runtime and, thus, poses significant challenges for large-scale reconstruction tasks. The inherent limitations in battery life and flight time ultimately restrict a single UAV’s ability to cover large areas efficiently, motivating the shift towards multi-agent systems.
2.2. Multi-UAV Task Scheduling
With the increasing demand for efficient large-scale 3D reconstruction, the use of multiple UAVs, or UAV swarms, has garnered significant attention. Multi-UAV systems can enhance coverage efficiency and reconstruction quality through collaborative efforts. However, the key challenge lies in how to allocate tasks efficiently and coordinate UAV actions while considering constraints such as communication range and battery life.
Task scheduling in multi-UAV systems can be broadly classified into centralized and distributed approaches. Centralized approaches, which are the focus of this paper, typically rely on a ground station to compute a globally optimal or near-optimal plan for the entire swarm before or during the mission. This allows for sophisticated optimization but can be computationally intensive and creates a single point of failure. In contrast, distributed approaches empower individual UAVs to make decisions autonomously based on local information, which enhances scalability and robustness but may lead to sub-optimal global performance. For pre-mission planning in large-scale reconstruction, where achieving optimal efficiency and complete coverage is paramount, a centralized framework provides a robust and effective solution.
Several centralized strategies have been proposed. Some methods focus on area partitioning. Ghaddar et al. [11] extended their grid-based method to multi-UAV scenarios by using a boundary-parallel approach to divide the area into equal sub-regions. Similarly, Filatov et al. [13] proposed a method tailored for large rectangular buildings by pre-planning “lawnmower” trajectories. Other techniques utilize clustering to group viewpoints. For example, Nagasawa et al. [14] found that Fuzzy C-means clustering could achieve a more uniform viewpoint distribution than K-means. Chen et al. [15] formalized the allocation problem by considering UAV start points and endurance, then solving the Traveling Salesman Problem (TSP) for each UAV’s path. More advanced techniques like the NBV method have also been extended to multi-agent systems, as demonstrated by Hardouin et al. [16], who transformed the problem into solving the Maximum Asymmetric TSP.
More recently, deep learning-based approaches, particularly those using Pointer Networks [17] and Graph Neural Networks (GNNs) [18], have emerged as a new frontier for solving routing problems. These methods [19,20] learn effective heuristics directly from data, enabling them to generate high-quality solutions in milliseconds at inference time. While powerful, these approaches typically require extensive offline training on large, domain-specific datasets and may face challenges in generalizing to problem instances with different characteristics from the training distribution.
However, many of these existing methods exhibit notable limitations. The partitioning approach by Ghaddar et al. [11] struggles with arbitrarily shaped NFZs. The algorithm from Filatov et al. [13] is designed for simple geometries and lacks flexibility in complex environments. Clustering-based methods, such as that of Nagasawa et al. [14], often require satellite-derived prior models, and as shown by Chen et al. [15], their performance can be highly dependent on hyperparameter tuning. Crucially, these methods often fail to explicitly optimize for workload balance in terms of mission time, leading to inefficient operations where some UAVs finish long before others.
To enhance UAV operational efficiency in complex large-scale 3D reconstruction tasks, this study proposes an efficient multi-UAV task scheduling framework. This framework fairly distributes tasks among different UAVs by systematically addressing the two-stage nature of the problem, while explicitly considering constraints such as no-fly zones, communication range (approx. 1 km [21]), and maximum flight distance. It ensures that tasks are tailored to the performance capabilities and mission requirements of each UAV, thereby optimizing overall reconstruction efficiency and coverage quality.
3. Methodology
This section introduces the proposed multi-UAV task scheduling framework for large-scale 3D reconstruction edge-intelligence systems, which is divided into two main stages: sub-region scheduling and viewpoint scheduling. In the first stage, the target area is partitioned into sub-regions based on no-fly zones and communication range constraints. Given the power limitations of UAVs, sub-regions are then clustered into energy-constrained work paths using a novel, constrained CVRP model. In the second stage, after viewpoints are generated within each sub-region, they are allocated to each UAV using an efficient scan-based heuristic algorithm designed to balance workloads and synchronize mission completion times.
3.1. Target Area Segmentation Method
To meet the communication and battery limitations of UAVs in large-scale 3D reconstruction, it is a common and necessary practice to segment the target area into smaller, manageable sub-regions. A primary challenge in this process is handling complex environments that contain no-fly zones (NFZs), which are effectively “holes” within the operational area.
Our approach builds upon established methods in computational geometry to solve this. We first utilize the exact cell decomposition technique proposed by Bahnemann et al. [7] to partition a complex polygon with holes (PWH) into multiple, simpler sub-polygons. This method also calculates an optimal service direction for each sub-polygon, which is essential for planning efficient coverage paths. Subsequently, we incorporate the improvements developed by Agarwal et al. [8], who showed that merging adjacent sub-polygons that share the same service direction can reduce the total number of turns and minimize the creation of inefficiently small area fragments.
While these methods provide an effective initial partitioning, our framework introduces an additional segmentation step tailored to the specific operational constraints of multi-UAV systems. We further divide the generated sub-polygons into standardized, square-shaped units with a side length of a. We selected a square-based partitioning strategy over alternatives like Voronoi tessellation for two primary reasons. First, it provides a direct and verifiable guarantee that all points within a sub-region are within the UAV’s communication range from a central point, a critical constraint for maintaining stable control. Second, it produces regular units that simplify the subsequent CVRP formulation for inter-mission scheduling. This represents a deliberate trade-off favoring operational robustness and modeling tractability over the potentially more adaptive but complex partitioning offered by other shapes. The study assumes that the UAV’s communication range can fully cover a sub-region with side length a, as shown in Figure 1, and that this side length is smaller than the maximum communication distance.
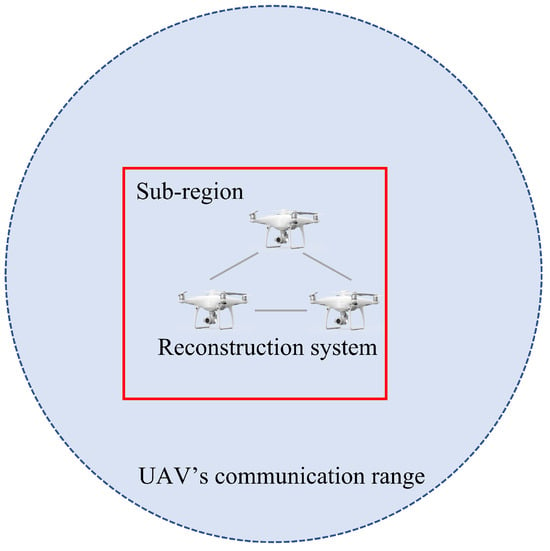
Figure 1.
Illustration of the communication range constraint for a square sub-region. The side length is chosen such that the maximum distance from the center to a corner (the diagonal radius) is less than the UAV’s reliable communication range, ensuring constant connectivity.
Therefore, the target area segmentation problem can be formally modeled as follows: Given a target area G represented by the polygon P with an outer contour and a set of no-fly zones , where each is a no-fly zone, how can we obtain a set of sub-regions ? Specifically, this set of sub-regions is a partition of the given polygon such that and , and each element is no larger than a square area with side length a.
The detailed process of the Target Area Segmentation Algorithm (TASA) is shown in Algorithm 1. The algorithm’s input includes the target area’s outer contour P and the no-fly zone set . As shown in Figure 2a, areas are represented by vertices arranged counterclockwise. The algorithm first processes no-fly zones, clipping any intersecting parts from the target area to produce the processed contour and no-fly zone set (Figure 2b). Next, the target area is initially segmented using the decomposition method from Bahnemann et al. [7], resulting in a set of sub-polygon-service direction pairs . To reduce the number of service paths, these directions are then improved using the merging method from Agarwal et al. [8], yielding an improved set (Figure 2c). Service paths are then generated parallel to these directions (Figure 2d), forming narrow rectangles that are subsequently cut into a set of square sub-regions (Figure 2e). Finally, to obtain the effective segmentation, the intersections of each square sub-region with the valid target area are calculated, resulting in the trimmed sub-region set (Figure 2f).

Figure 2.
Step-by-step visualization of the Target Area Segmentation Algorithm (TASA). (a) Original target area with No-Fly Zones (NFZs). (b) NFZs are clipped from the target area. (c) Initial partitioning via exact cell decomposition and service direction assignment. (d) Generation of parallel service paths based on merged service directions. (e) Creation of a standardized square grid along the service paths. (f) Valid sub-regions after intersecting the grid with the processed area.
Computational Complexity: The complexity of Algorithm 1 is dominated by the exact cell decomposition and polygon clipping operations. These are standard computational geometry procedures, and their complexity is polynomial in the total number of vertices of the input polygons (the target area and NFZs).
| Algorithm 1 Target Area Segmentation Algorithm (TASA) |
|
3.2. Sub-Region Allocation Method
After the target area is divided into sub-regions, the large-scale reconstruction sensing task is transformed into several sub-region sensing tasks. Given the limited battery capacity and the time required for UAVs to collect images, a single mission can only cover a limited area. Consequently, a multi-UAV system may not complete the reconstruction of all sub-regions in one go. To address this, sub-regions are clustered into groups before traversal, and each cluster is reconstructed within a single work path.
In our framework, the constraint on a work path is its total energy capacity. To establish a reasonable and tractable energy model, we conducted preliminary flight experiments using DJI Matrice 100 (Shenzhen, China) UAVs [22]. We observed that the energy consumption between two waypoints can be accurately modeled as a linear function of the flight distance, incorporating a fixed energy cost for operations at each waypoint such as hovering and image capture. As shown in Figure 3, our empirical data revealed a strong linear correlation between the predicted energy consumption from our model and the ground truth data from the UAV’s battery sensor. The close tracking in both flight distance and energy consumption validates our model.
Given this strong empirical evidence, and because the primary focus of this paper is on the scheduling logic rather than high-fidelity energy modeling, we simplify the energy cost to be directly proportional to the flight path distance for the purpose of our optimization model. This simplification is, therefore, empirically justified and allows for a tractable CVRP formulation, where the “capacity” of a vehicle (a single sortie) and the “demand” of a customer (a sub-region) are represented by flight distance.
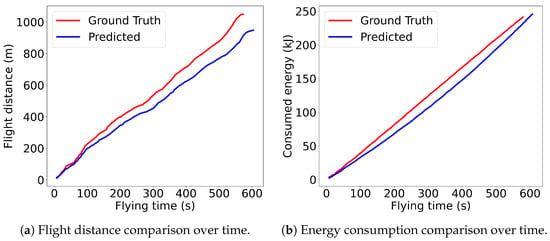

Figure 3.
Validation of the simplified energy model based on real-world flight data from a DJI Matrice 100. (a) compares the planned cumulative flight distance against the actual ground truth. (b) shows the strong linear correlation between the energy consumption predicted by our model and the actual energy consumed.
This section models the sub-region sensing problem as a Capacitated Vehicle Routing Problem (CVRP) [23]. While similar problems have been addressed through arc coverage path planning [24] and point coverage path planning [25], modeling it as a CVRP is particularly advantageous here. This approach not only clusters the sub-regions but also simultaneously determines the optimal traversal paths within each cluster by considering the positional relationships between them, achieving comprehensive coverage while ensuring relatively short traversal paths.
Our formulation, however, extends the standard CVRP to meet the specific demands of multi-UAV missions. The primary goal is not merely to satisfy capacity constraints, but to ensure that each work path is utilized efficiently to promote workload balance across different sorties. To achieve this, we introduce a novel route capacity balancing constraint (Equation (7)). This key modification mandates that the total workload of any path must be at least times the maximum capacity , which prevents the generation of inefficiently short paths and ensures a more uniform distribution of tasks. The problem is defined on a directed graph , where each element in represents a sub-region. The formal definition is as follows:
where denotes the transpose of the sub-region transition cost vector . The vector x is composed of elements , which are decision variables indicating whether the path from sub-region to sub-region is included in a work path. The notation represents the arcs originating from , while denotes the arcs terminating at . The set represents the arcs whose endpoints belong only to the node set , which consists of nodes representing sub-regions. The demand vector q is defined such that each element represents the area of the sub-region corresponding to node . The auxiliary variable represents the cumulative demand from the starting point to node .
The meanings of Equations (1)–(7) are as follows. Equation (1) is the objective function, aiming to minimize the total path length. Equations (2) and (3) ensure that each sub-region is visited exactly once. Equation (5) implements the Miller–Tucker–Zemlin (MTZ) constraints [26] to prevent subtours. Crucially, Equation (7) is our proposed route capacity balancing constraint, which distinguishes our model from standard CVRPs by enforcing a minimum workload for each path, thereby ensuring a balanced and efficient allocation.
The pseudo-code for solving this problem is shown in Algorithm 2. Before solving, two key inputs must be computed: the demand vector q and the sub-region transition cost vector . The area of each sub-region is calculated using the Shoelace formula [27]. The calculation of the cost vector , as detailed in Algorithm 3, is more involved. A simple Euclidean distance between the centers of sub-regions is insufficient, as it does not reflect feasible travel paths that must navigate through adjacent regions. Therefore, we construct a cost model that represents the shortest path distances through the adjacency graph of the sub-regions.
| Algorithm 2 MIP-based Sub-region Allocation Algorithm (MIP-SAA) |
|
This process begins by establishing an undirected graph , where is the set of center points of all sub-regions. To determine the connections between adjacent sub-regions (the edge set ), we employ the Delaunay triangulation algorithm [28]. As shown in Figure 4, this technique is ideal for connecting neighboring nodes with the shortest possible edges, creating a graph that accurately represents the topology of the sub-regions. With this graph constructed, we then apply the Floyd–Warshall algorithm to compute the shortest path distances between all pairs of nodes in , yielding a complete distance matrix D. This ensures that the cost between two distant sub-regions is the sum of the lengths of the intermediate adjacent connections, aligning well with the characteristics of a coverage path planning solution. Finally, the cost vector is derived from this matrix, retaining only the entries relevant for the CVRP model.
Computational Complexity: The sub-region allocation problem, modeled as a CVRP, is NP-hard. Therefore, Algorithm 2, which relies on a MIP solver, has a worst-case exponential time complexity. This approach is designed for offline pre-mission planning, where computational time is less critical than achieving a high-quality, balanced, and globally efficient solution. The complexity of the cost calculation in Algorithm 3 is dominated by the Floyd–Warshall algorithm, which is polynomial at , where is the number of sub-regions.


Figure 4.
Using Delaunay triangulation to establish an adjacency graph for sub-region cost calculation. (a) A set of 2D points representing sub-region centers. (b) The resulting triangulation connects adjacent centers, forming a graph used to compute the shortest feasible path distances between all sub-regions. The orange line represents the shortest path between sub-region A and sub-region B.
| Algorithm 3 Sub-region Transition Cost Vector Calculating Algorithm |
|
3.3. MIP-Based Viewpoint Allocation Method
After obtaining the sub-region traverse paths, the second stage of our framework is to solve the viewpoint allocation problem within each sub-region. The viewpoints themselves can be obtained using existing planning algorithms [29,30], which are not the focus of this paper. The problem can be described as follows: Given a set of viewpoints within a sub-region and a total of UAVs, find a path for each UAV such that the longest path among all UAVs is minimized, and the difference between the longest and shortest paths remains within a predefined threshold.
To solve this optimally, this section models the problem as a Vehicle Routing Problem (VRP) and solves it using a Mixed-Integer Programming (MIP) approach. This method provides a theoretical benchmark for path balance and efficiency. Our formulation makes two critical departures from a standard VRP. First, instead of minimizing the total distance traveled by all UAVs, our objective function is to minimize the longest individual path (), as shown in Equation (8). This directly targets the overall mission completion time, which is dictated by the last UAV to finish. Second, we introduce an explicit path balance constraint (Equation (16)) to ensure the workloads are evenly distributed.
The VRP is defined on a directed graph , where each element in represents a viewpoint. The formal problem definition is as follows:
where represents the longest path assigned to a UAV. The vector x consists of binary decision variables indicating if the path from viewpoint to is used. The meanings of Equations (8)–(16) are as follows. Equation (8) is our novel objective function, aiming to minimize the longest path to ensure timely mission completion. Equations (9) and (10) ensure each viewpoint is visited exactly once. Equation (11) sets the number of UAVs. Equations (13) and (14) are the Subtour Elimination Constraints (SECs). Finally, Equation (16) is our explicit path balance constraint, limiting the maximum difference between path lengths to a threshold g.
The specific steps are shown in Algorithm 4. A critical prerequisite for this algorithm is the calculation of the cost vector c, which represents the feasible travel distances between all pairs of viewpoints. Unlike the 2D case, calculating this in a 3D environment with obstacles is non-trivial. A direct Delaunay triangulation [28] in 3D space can result in edges that pass directly through the scene geometry, especially around corners of buildings where viewpoints are sparse (see Figure 5). Such paths are physically impossible for a UAV.
To resolve this, Algorithm 5 outlines our strategy for computing a valid, obstacle-aware cost vector. First, an initial 3D triangulation of the viewpoints is performed. The algorithm then identifies all edges that intersect with the scene’s mesh. For each invalid edge, the A* search algorithm is used to find a feasible flight path around the obstacles within a voxelized representation of the scene (Figure 6). The nodes along these A* paths are added to the point set as auxiliary vertices. A second, final triangulation is then performed on this augmented set of points. This ensures that all connections in the resulting graph are collision-free. The Floyd–Warshall algorithm is then applied to this graph to compute the all-pairs shortest path lengths, yielding a valid cost vector c.
Computational Complexity: The viewpoint allocation problem, modeled as a VRP with side constraints, is NP-hard. Consequently, Algorithm 4 has a worst-case exponential time complexity and is computationally intensive. Its primary role is not for real-time application, but to serve as a benchmark for obtaining optimal solutions in smaller-scale problems and to validate the quality of the heuristic algorithm proposed in the next section. The complexity of the cost calculation (Algorithm 5) is polynomial, dominated by the Floyd–Warshall step at , where is the total number of viewpoints and auxiliary nodes.
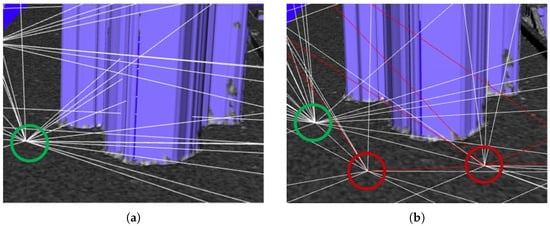


Figure 5.
Collision-free path generation using auxiliary vertices. (a) Initial 3D triangulation results in edges that incorrectly pass through obstacles. (b) By adding auxiliary vertices along obstacle-aware paths, the final triangulation produces a graph with only feasible, collision-free edges. The green circle indicates the vertices with collision edges and the red circles indicates the added auxiliary vertices.

Figure 6.
Workflow for computing the obstacle-aware viewpoint transition cost vector (Algorithm 5). (a) An initial triangulation with many infeasible edges is produced. (b) The scene is voxelized to create a grid for pathfinding. (c) The A* algorithm finds a collision-free path between the two viewpoints. (d) The final triangulation incorporates the A* path nodes, ensuring a valid connection.
| Algorithm 4 MIP-based Viewpoint Allocation Algorithm (MIVA) |
|
| Algorithm 5 Viewpoint Transition Cost Vector Calculating Algorithm |
|
3.4. Scan-Based Heuristic Viewpoint Allocation Method
The MIP-based method detailed in Section 3.3 offers an effective, optimal solution to the viewpoint allocation problem but is computationally demanding and time-consuming, making it impractical for large-scale scenarios. To address these limitations, this section introduces a time-efficient heuristic approach—the Scan-based Viewpoint Allocation (SVA) algorithm—that significantly reduces computation time while maintaining high-quality, balanced solutions.
The design of this heuristic is directly inspired by the structural properties of the optimal solutions generated by the MIP-based method. Analysis of these optimal solutions reveals that the allocated UAV paths predominantly fall within distinct, non-overlapping fan-shaped sectors originating from the UAV starting point. This observation provides a strong rationale for our approach: Instead of performing a complex global search, we can approximate the optimal solution structure by partitioning the viewpoints angularly around the starting point.
The SVA method implements this idea through a three-step process: viewpoint ordering, grouping, and path planning.
- Ordering: First, all viewpoints are projected onto the 2D horizontal plane. A virtual ray, originating from the UAV starting point, “scans” the viewpoints by rotating 360 degrees. The viewpoints are then sorted into an ordered sequence based on the angle at which the ray intersects their projections, as illustrated in Figure 7. If multiple viewpoints share the same angle, they are sub-sorted by their distance to the starting point.
 Figure 7. The angular sorting mechanism in the Scan-based Viewpoint Allocation (SVA) algorithm. (a) A virtual ray originates from the starting point. (b) As the ray rotates 360 degrees, viewpoints are ordered based on the angle of intersection, forming the basis for sector-based grouping. The index of the viewpoint is the order in which they appear in the scan sequence.
Figure 7. The angular sorting mechanism in the Scan-based Viewpoint Allocation (SVA) algorithm. (a) A virtual ray originates from the starting point. (b) As the ray rotates 360 degrees, viewpoints are ordered based on the angle of intersection, forming the basis for sector-based grouping. The index of the viewpoint is the order in which they appear in the scan sequence. - Grouping: Next, the sorted viewpoints are allocated into k groups, one for each UAV. The ”weight” of each viewpoint is defined as its path distance from the starting point (pre-calculated in the cost vector c). The algorithm iterates through the ordered sequence, accumulating these weights. When the accumulated weight for the current group reaches approximately of the total weight of all viewpoints, that group is considered complete, and the algorithm begins forming the next one. This ensures that each group of viewpoints represents a roughly equal workload in terms of distance from the base. The result is a set of spatially coherent, fan-shaped clusters, as shown in Figure 8a.
 Figure 8. The grouping and path planning stages of the SVA algorithm. (a) The angularly sorted viewpoints are partitioned into balanced, fan-shaped clusters. (b) An efficient TSP tour is then computed for each cluster to generate the final flight paths.
Figure 8. The grouping and path planning stages of the SVA algorithm. (a) The angularly sorted viewpoints are partitioned into balanced, fan-shaped clusters. (b) An efficient TSP tour is then computed for each cluster to generate the final flight paths. - Path Planning: Finally, with the viewpoints allocated, the task within each group becomes a standard Traveling Salesman Problem (TSP). To find an efficient path for each UAV, we first employ the Christofides algorithm [31] to generate a high-quality approximate solution. This algorithm is well suited as it guarantees an approximation ratio of no more than 1.5 when the triangle inequality holds. To further refine this solution, we apply the 2-opt local search algorithm [32], which iteratively improves the path by swapping pairs of edges to eliminate crossings and reduce the total length (Figure 8b).
The complete pseudo-code is presented in Algorithm 6.
| Algorithm 6 Scan-based Viewpoint Allocation Algorithm (SVA) |
|
Computational Complexity: The SVA method is designed for efficiency. The initial sorting of n viewpoints takes . The subsequent path planning for k UAVs is dominated by the Christofides algorithm, which has a complexity of for a group of size m. Since the viewpoints are distributed among k groups, the overall time complexity of Algorithm 6 is polynomial, approximately , which is far more time-efficient than the exponential complexity of the MIP-based Algorithm 4. This makes SVA suitable for practical, large-scale applications where planning time is a critical factor.
4. Experiment
To validate the effectiveness of our proposed multi-UAV task scheduling framework, we designed a comprehensive evaluation comprising extensive simulations and culminating in a large-scale, real-world deployment. The evaluation was structured to systematically assess each component and the integrated system’s performance through four key stages: (1) an analysis of the inter-mission sub-region allocation stage (MIP-SAA); (2) an analysis of the intra-mission viewpoint allocation stage (SVA); (3) an end-to-end performance evaluation of the complete framework (MIP-SVA) in simulation; and (4) a final validation through a large-scale 3D reconstruction experiment in a real-world campus environment.
4.1. Experimental Setup
4.1.1. Implementation Environment
All experiments were implemented on a desktop computer featuring an Intel(R) Core(TM) i7-9700F CPU @ 3.00 GHz, 32.0 GB of RAM, running Windows 10. The Mixed-Integer Programming (MIP) problems were solved using Gurobi Optimizer version 10.0 [33].
4.1.2. Simulation Environment
The virtual environment used for the end-to-end evaluation is “AirSimNH,” a high-fidelity environment provided by the AirSim library [34]. This environment features a large-scale, detailed urban landscape with complex building geometries, varying elevations, and occlusions, providing a challenging and realistic testbed for our reconstruction and scheduling algorithms.
4.1.3. Performance Metrics
To quantitatively evaluate the framework, we utilized the following metrics:
- Total Path Length (TPL): The sum of all planned path lengths. A shorter TPL indicates higher overall efficiency.
- Capacity Balance Ratio (CBR): The proportion of work paths whose total capacity falls within the desired range . A higher CBR signifies better inter-mission workload balance.
- Running Time (RT): The computational time required to generate a solution.
- Average Path Length (APL): The mean trajectory distance for each UAV within a sub-region. A shorter APL reflects lower energy consumption and faster mission execution.
- Proportion of Solutions within the Expected Difference Interval (PSEDI): The percentage of solutions where the maximum path length difference between any two UAVs is below a threshold g. A higher PSEDI indicates better intra-mission workload balance.
4.2. Evaluation of Sub-Region Allocation (MIP-SAA)
4.2.1. Objective and Comparative Algorithms
This experiment aimed to evaluate the performance of our MIP-based Sub-region Allocation Algorithm (MIP-SAA) from Section 3.2. We compared it against two state-of-the-art multi-robot task scheduling methods:
- MFC Method [35]: The Multi-robot Forest Coverage (MFC) method is a balanced workload allocation approach. It first constructs a minimum spanning forest from the graph of task locations. It then iteratively moves subtrees between the different trees in the forest (each representing a robot’s workload) to equalize the total weight (workload) of each tree.
- MSTC* Method [25]: The Minimum Spanning Tree Coverage (MSTC*) method is another spanning tree-based approach. It first builds a single minimum spanning tree covering all task locations, then converts this tree into a tour. The tour is then partitioned into segments of equal length, with each segment being assigned to a different robot.
- MFF Method [36]: This is an variant of the MFF-HVPP framework from Tan and Ni [36], a state-of-the-art deep reinforcement learning method for heterogeneous fleet capacitated VRP. It uses a multi-feature fusion encoder and a hierarchical decoder to sequentially choose a vehicle and then a node to visit. We apply this model to our sub-region allocation problem by treating sub-regions as customer nodes.
4.2.2. Settings
We first applied MIP-SAA to the complex area shown in Figure 2f, with hectares and . The result, shown in Figure 9, indicates that the proposed model can reasonably cluster sub-regions, with most path capacities concentrated within the desired interval. For a broader comparison, we created a test suite of 20 randomly generated pixel scenes with obstacles. For these tests, MIP-SAA used units and , while MFC, MSTC* and MFF were configured to allocate tasks to four platforms (i.e., 4 paths).

Figure 9.
Application of the MIP-SAA algorithm to the complex area from Figure 2f. (a) The resulting work paths, with each color representing a distinct sortie, show spatially coherent clustering. (b) The histogram of path capacities quantitatively confirms the workload balance, with the majority of paths falling within the target efficiency range of (i.e., the yellow shaded area), validating our model’s balancing constraint.
4.2.3. Results and Analysis
The comparative results, summarized in Table 1, highlight the distinct advantages of our optimization-based approach. The traditional heuristics, MFC and MSTC*, were outperformed on nearly all metrics, showing particular weakness in balancing workloads.
The learning-based method, MFF, demonstrated strong performance in path optimization, achieving a total path length (TPL) of 1237 m, which is significantly better than that of traditional methods. However, its capacity balancing capability was limited. As indicated by its capacity distribution (similar to the patterns shown in Figure 10), the MFF method’s lack of a strict balancing constraint resulted in a wide spread of path capacities, producing some paths that were too short and others that exceeded the optimal capacity range. This explains its modest Capacity Balance Ratio (CBR) of 59%, which is only marginally better than that of MSTC*.
In contrast, our MIP-SAA method delivered superior performance on both fronts. It not only achieved the shortest TPL of 1172m, but also obtained a significantly higher CBR of 81%. This superior balancing performance is a direct result of the explicit route capacity balancing constraint (Equation (7)) in our model, which forces solutions to adhere to the desired workload range. A paired t-test confirmed that MIP-SAA’s improvements in TPL are statistically significant (p < 0.01) compared to all baseline methods (The p-values for the paired t-test on total path length (TPL) were MIP-SAA vs. MFF (), vs. MFC (), and vs. MSTC* (). All are below the significance level of ). This demonstrates that while learning-based methods like MFF are powerful, our MIP-SAA approach is the superior choice for applications requiring not just efficient paths, but also strict, reliable, and balanced workload management.



Figure 10.
Qualitative comparison of workload balance among sub-region allocation methods. The proposed MIP-SAA method (d) generates visually balanced paths of comparable size, which corresponds to a quantitative success: No path’s capacity exceeds the maximum Q, and the vast majority fall within the ideal efficiency range of (i.e., the yellow shaded area). In contrast, the baseline methods (a–c) produce significant imbalances with both excessively short and long paths, visually confirming the superior performance reported in Table 1.

Table 1.
Comparative performance of sub-region allocation methods. The results demonstrate that the proposed MIP-SAA method significantly outperforms baseline approaches in both total path length (efficiency) and the Capacity Balance Ratio (workload balance), achieving the best scores on both key metrics.
Table 1.
Comparative performance of sub-region allocation methods. The results demonstrate that the proposed MIP-SAA method significantly outperforms baseline approaches in both total path length (efficiency) and the Capacity Balance Ratio (workload balance), achieving the best scores on both key metrics.
| Method | Total Path Length (m) | Capacity Balance Ratio- (%) |
|---|---|---|
| MFC [35] | 1348 | 10 |
| MSTC* [25] | 1404 | 57 |
| MFF [36] | 1237 | 59 |
| MIP-SAA (Ours) | 1172 | 81 |
4.3. Evaluation of Viewpoint Allocation (SVA)
4.3.1. Objective and Comparative Algorithms
This experiment was designed to validate the effectiveness of our heuristic Scan-based Viewpoint Allocation (SVA) method from Section 3.4. We compared it against our optimal MIP-based solver (MIVA) as a benchmark, and two other common methods:
- FCM Method [14]: The Fuzzy C-Means (FCM) method is a soft clustering algorithm that partitions viewpoints by assigning each point a degree of membership to all clusters, often resulting in balanced cluster sizes.
- KDF Method [37]: The K-D Fusion (KDF) method is a variant of the K-means algorithm that uses a K-D tree to efficiently partition the viewpoint space and assign viewpoints to the nearest cluster centroid.
- GAPN Method [19]: This is an variant of the Graph Attention-based Pointer Network (GAPN) from Fu et al. For multi-agent scenarios, it employs a two-stage “cluster-then-route” strategy. First, a heuristic algorithm clusters the nodes (viewpoints) for each agent. Then, the core GAPN model—a GNN-based Pointer Network trained with reinforcement learning—is used to plan the optimal tour for each cluster. We implement this methodology as a new baseline.
4.3.2. Settings
The evaluation used a dataset of 100 randomized test cases, each containing 50 viewpoints and 50 path points within a 50 m × 50 m area. The task was allocated to three UAVs, and the balance threshold was set to m.
4.3.3. Results and Analysis
The experimental results, detailed in Table 2, highlight the superior performance of our proposed SVA method in both solution quality and computational efficiency. As qualitatively illustrated in Figure 11, the simple clustering methods, FCM and KDF, produce fragmented and overlapping paths. In contrast, our SVA method generates spatially coherent, non-overlapping path clusters, providing a clear visual indication of its superior allocation strategy. Quantitatively, the simple clustering methods yielded poor workload balance, with PSEDI scores of only 37% and 57%, respectively. The deep learning-based method, GAPN, offered a significant improvement in balance, achieving a PSEDI of 69%. However, this came at the cost of a substantially longer running time of 29 s.

Figure 11.
Qualitative comparison of viewpoint allocation results. The proposed SVA method (c) generates more spatially coherent, non-overlapping, and balanced path assignments compared to the standard FCM (a) and KDF (b) clustering methods.
In contrast, our SVA method delivered the best performance among all practical approaches. It achieved a remarkably high PSEDI of 88%, demonstrating superior workload balance. Most importantly, it produced the shortest average path length (APL) of 268 m. A paired t-test confirmed that this improvement in APL is statistically significant (p < 0.05) (The p-values for the paired t-test on average path length (APL) were SVA vs. FCM (p = 0.0025), SVA vs. KDF (p = 0.0012), and SVA vs. GAPN (p = 0.0418). All are below the significance level of .) when compared to FCM, KDF, and GAPN. Critically, our SVA method achieved these high-quality results in just 18 s, making it not only more effective but also faster than the GAPN baseline.
This outcome underscores the primary advantage of our SVA algorithm: By leveraging problem-specific geometric insights (the fan-shaped structure of optimal solutions), it can directly construct a near-optimal solution that is both more balanced and path-efficient than those found by general-purpose learning frameworks. While our optimal MIP-based solver, MIVA, predictably achieved the best balance (94%), its impractical runtime confirms that SVA is the most effective and practical choice for this application.
The workload balance performance is further visualized in the histograms of Figure 12. The distributions for our SVA and MIVA methods are tightly concentrated near zero, confirming their excellent balancing capabilities, whereas the wide spreads for FCM and KDF visually demonstrate their inability to distribute tasks evenly.

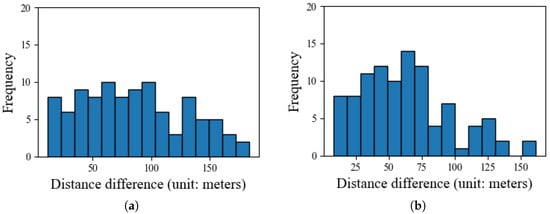
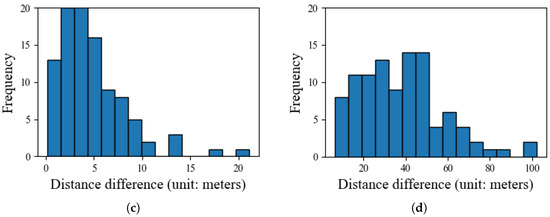

Table 2.
Performance comparison of viewpoint allocation methods. The proposed heuristic, SVA, achieves the best balance of solution quality and computational efficiency, yielding the shortest average path length (APL) and a high balance score (PSEDI) with a practical runtime. It closely approaches the optimal solution from the MIVA benchmark without its prohibitive computational cost.
Table 2.
Performance comparison of viewpoint allocation methods. The proposed heuristic, SVA, achieves the best balance of solution quality and computational efficiency, yielding the shortest average path length (APL) and a high balance score (PSEDI) with a practical runtime. It closely approaches the optimal solution from the MIVA benchmark without its prohibitive computational cost.
| Method | Running Time (s) | Average Path Length (m) | PSEDI < 50 (%) |
|---|---|---|---|
| FCM [14] | 3 | 295 | 37 |
| KDF [37] | 3 | 302 | 57 |
| GAPN [19] | 29 | 295 | 69 |
| MIVA (Ours) | 270 | 94 | |
| SVA (Ours) | 18 | 268 | 88 |


Figure 12.
Histograms of path length differences, illustrating workload balance. Our proposed SVA and optimal MIVA methods show distributions tightly concentrated around zero, indicating superior balance, whereas the FCM and KDF methods exhibit a wide spread, signifying imbalanced workloads. (a) FCM method result. (b) KDF method result. (c) MIVA method result. (d) SVA method result.
4.4. End-to-End Framework Evaluation
4.4.1. Objective and Comparative Algorithms
This final experiment evaluated the performance of our complete two-stage framework (MIP-SVA) on a large-scale 3D reconstruction task. We compared it against two composite baseline frameworks:
- MFC-FCM Method: Combines the MFC method for sub-region allocation and the FCM method for viewpoint allocation.
- MSTC*-KDF Method: Combines the MSTC* method and the KDF method for sub-region allocation and viewpoint allocation.
4.4.2. Settings
The experiment was conducted in the “AirSimNH” environment (Figure 13e). AirSimNH is a moderately complex urban scene provided by AirSim. It includes typical obstacles such as houses, trees, and utility poles, mainly distributed along both sides of the street, offering a certain level of 3D occlusion. This makes it well suited for low-altitude obstacle avoidance and path planning algorithm validation. Its default obstacle density is sufficient for training algorithms such as reinforcement learning, and users can further customize the environment through the UE4 editor. In terms of flight dynamics, AirSimNH does not impose restrictions on the flight model. It uses the SimpleFlight controller by default, supports customization of physical parameters, and allows integration with external flight controllers, offering strong extensibility and realism.

Figure 13.
End-to-end execution of the MIP-SVA framework in the AirSimNH environment. The process visualizes (a) the target urban area, (b) area segmentation by TASA, (c) inter-mission work paths from MIP-SAA, (d) a preliminary exploration model, (e) intra-mission viewpoint allocation by SVA for a detailed sub-region, and (f) the final high-fidelity 3D model.
The framework parameters were chosen based on a quantitative analysis of hardware constraints and operational safety margins. We set the sub-region side length to m, maximum work area to , capacity threshold to , and path balance threshold to m. The choice of a ensures a robust communication link, as the maximum required distance of 28.3 m remains safely within the conservative 30 m lower bound cited for technologies like Bluetooth 5 in non-line-of-sight environments [38]. The capacity threshold promotes high efficiency by mandating 90% energy utilization per sortie, while critically reserving the remaining 10% as a safety margin for a safe return under adverse conditions. Lastly, the path balance threshold g, scaled to the subregion size, provides a practical tolerance that ensures synchronized mission completion without being overly restrictive for the solver. All frameworks used the same underlying viewpoint planning strategy (“Nadir” for exploration and “MVPA” for exploitation [29]).
4.4.3. Results and Analysis
The qualitative results of our framework’s execution are shown in Figure 13. As detailed in Table 3, our MIP-SVA framework demonstrated superior performance in the critical first stage of sub-region allocation. It achieved a perfect CBR of 100% and a TPL of only 192 m, which is approximately half that of the baseline methods. This is because both MFC and MSTC* rely on spanning-tree heuristics that struggle with the complex geometry of the test scene, leading to unbalanced and inefficient work paths. While all methods achieved the same PSEDI in the second stage for this specific run, the dramatic improvement in the first-stage scheduling validates the effectiveness of our framework for large-scale tasks.

Table 3.
End-to-end performance evaluation of the integrated frameworks on the large-scale reconstruction task. The proposed MIP-SVA framework demonstrates decisive superiority, particularly in the inter-mission scheduling stage, achieving a perfect Capacity Balance Ratio (CBR) and reducing the total path length (TPL) by approximately 50% compared to the composite baseline methods.
4.5. Large-Scale Real-World Experiment
To validate the practical applicability and efficiency of our proposed framework, we conducted a large-scale 3D modeling experiment on the Jiulonghu Campus of Southeast University, an area exceeding 2 km2.
4.6. Experimental Setup and Procedure
As illustrated in Figure 14, the experiment utilized a fleet of three DJI Matrice 100 UAVs [22], each with an effective flight endurance of approximately 28 min, coordinated by a central Ground Control Station (GCS) where our two-stage scheduling framework was deployed. The procedure was executed as follows:
- Area Segmentation: First, using our Target Area Segmentation Algorithm (TASA), the 2 km2 campus was methodically partitioned into 56 uniform subregions, each measuring 200 m × 200 m and containing an average of approximately 185 viewpoints required for high-fidelity reconstruction.
- Task Allocation: Subsequently, the MIP-SAA algorithm was executed on the GCS to solve the sub-region allocation problem. This generated a set of balanced, conflict-free, and efficient work paths for the three-UAV fleet.
- Autonomous Execution: Finally, the generated missions were uploaded to the UAVs, which then autonomously performed the data collection flights at a constant speed of 10 m/s according to the optimized schedules.
4.7. Results and Analysis
The entire data collection task for the sprawling 2 km2 area was successfully completed in a total sampling time of just 168 min. To accomplish this, the framework generated an optimized mission plan that required the UAV cluster to perform a total of only eight collective sorties (i.e., eight-sub-region work path). This high level of coordination resulted in an average operational cycle time of just 21 min per sortie (including flight, landing, and battery swapping), underscoring the plan’s temporal efficiency.
For a direct performance comparison, a baseline test using the MFC-FCM method was conducted over the same area. The baseline method required over 4 h (more than 240 min) to complete the task. In contrast, our framework achieved a remarkable 35% reduction in total mission time, unequivocally validating the superiority of our optimized allocation strategy.


Figure 14.
The real-world experimental setup at Southeast University’s Jiulonghu Campus. Main image: the fleet of three DJI Matrice 100 UAVs deployed for the mission. Inset: operators at the Ground Control Station (GCS) overseeing the autonomous execution.
The mission yielded a comprehensive dataset that was processed to generate a high-fidelity 3D model of the campus, as shown in Figure 15. This outcome confirms the quality and completeness of the coverage achieved by the autonomous fleet. Ultimately, this large-scale field experiment provides compelling evidence for the practical feasibility and superior performance of our proposed framework in real-world environments.

Figure 15.
A section of the final high-fidelity 3D model of the Jiulonghu Campus. The detail and completeness of the model validate the quality of the data acquired through our framework’s automated flight plans.
5. Conclusions
This paper presents a novel framework that successfully addresses the challenge of asymmetry inherent in large-scale 3D reconstruction for multi-UAV edge-intelligence systems. Unlike traditional approaches that inadequately address real-world constraints, our framework comprehensively considers communication range limitations, no-fly zones, and workload balancing requirements through a two-stage approach. In the first stage, we employ cell decomposition to partition the target area into manageable sub-regions while respecting operational constraints. These sub-regions are then optimally allocated to UAVs through a Capacitated Vehicle Routing Problem (CVRP) formulation, ensuring balanced workloads and minimized travel distances across work paths. The second stage addresses viewpoint allocation within each sub-region through our novel scan-based heuristic algorithm. This polynomial-time complexity method effectively distributes viewpoints among multiple UAVs while maintaining path balance and minimizing total traversal time. Extensive experimental results demonstrate that our approach significantly outperforms existing methods in terms of workload distribution and overall system efficiency.
While this work effectively advances centralized multi-UAV coordination, a key direction for future research lies in adapting our framework for distributed control architectures. Developing decentralized scheduling models will require novel algorithms for autonomous coordination and decision-making among UAVs, promising to further enhance task execution flexibility and system resilience.
Author Contributions
Conceptualization, Y.X. (Yu Xia); methodology, Y.X. (Yu Xia) and X.X.; software, Y.X. (Yu Xia) and X.X.; validation, Y.X. (Yuhang Xu), A.L. and J.W.; data curation, X.X.; writing—original draft preparation, Y.X. (Yuhang Xu) and A.L.; writing—review and editing, C.F. and W.W.; supervision, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under grant Nos. 62232004, 62572120 and the Natural Science Foundation of Jiangsu Province under Grant No. BK20230024.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
We are thankful for the good advice and comments from anonymous reviews to help improve the quality of the paper.
Conflicts of Interest
Authors Yu Xia, Xueyong Xu, Yuhang Xu, and Jinchen Wang are employed by the company North Information Control Research Academy Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Zhang, X.; Cheng, S.; Wang, P.; Zheng, H.; Yang, X.; Guo, Y. 3D Reconstruction and Large-Scale Detection of Roads Based on UAV Imagery. Materials 2025, 18, 2133. [Google Scholar] [CrossRef]
- Ariante, G.; Del Core, G. Unmanned Aircraft Systems (UASs): Current State, Emerging Technologies, and Future Trends. Drones 2025, 9, 59. [Google Scholar] [CrossRef]
- Giordan, D.; Adams, M.S.; Aicardi, I.; Alicandro, M.; Allasia, P.; Baldo, M.; De Berardinis, P.; Dominici, D.; Godone, D.; Hobbs, P.; et al. The use of unmanned aerial vehicles (UAVs) for engineering geology applications. Bull. Eng. Geol. Environ. 2020, 79, 3437–3481. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Ghaddar, A.; Merei, A. Energy-aware grid based coverage path planning for uavs. In Proceedings of the Thirteenth International Conference on Sensor Technologies and Applications SENSORCOMM, Nice, France, 27–31 October 2019; pp. 27–31. [Google Scholar]
- Maboudi, M.; Homaei, M.; Song, S.; Malihi, S.; Saadatseresht, M.; Gerke, M. A review on viewpoints and path planning for UAV-based 3-D reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5026–5048. [Google Scholar] [CrossRef]
- Bähnemann, R.; Lawrance, N.; Chung, J.J.; Pantic, M.; Siegwart, R.; Nieto, J. Revisiting boustrophedon coverage path planning as a generalized traveling salesman problem. In Proceedings of the Field and Service Robotics: Results of the 12th International Conference; Springer: Singapore, 2021; pp. 277–290. [Google Scholar]
- Agarwal, S.; Akella, S. Area coverage with multiple capacity-constrained robots. IEEE Robot. Autom. Lett. 2022, 7, 3734–3741. [Google Scholar] [CrossRef]
- Xia, Y.; Li, A.; Xu, X.; Xu, Y.; Wang, J.; Chau, V.; Fu, C.; Wu, W. A Multi-Drone Task Allocation Algorithm for Large-Scale 3D Reconstruction. In Proceedings of the 2024 Twelfth International Conference on Advanced Cloud and Big Data (CBD), Brisbane, Australia, 28 November–2 December 2024; pp. 7–12. [Google Scholar]
- Di Franco, C.; Buttazzo, G. Energy-aware coverage path planning of UAVs. In Proceedings of the 2015 IEEE international conference on autonomous robot systems and competitions, Vila Real, Portugal, 8–10 April 2015; pp. 111–117. [Google Scholar]
- Ghaddar, A.; Merei, A.; Natalizio, E. PPS: Energy-Aware grid-based coverage path planning for UAVs using area partitioning in the presence of NFZs. Sensors 2020, 20, 3742. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Kim, D.; Choi, S. View path planning via online multiview stereo for 3-d modeling of large-scale structures. IEEE Trans. Robot. 2021, 38, 372–390. [Google Scholar] [CrossRef]
- Filatov, A.; Zaslavskiy, M.; Krinkin, K. Multi-drone 3D building reconstruction method. Mathematics 2021, 9, 3033. [Google Scholar] [CrossRef]
- Nagasawa, R.; Mas, E.; Moya, L.; Koshimura, S. Model-based analysis of multi-UAV path planning for surveying postdisaster building damage. Sci. Rep. 2021, 11, 18588. [Google Scholar] [CrossRef]
- Chen, F.; Lu, Y.; Cai, B.; Xie, X. Multi-drone collaborative trajectory optimization for large-scale aerial 3D scanning. In Proceedings of the 2021 IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), Bari, Italy, 4–8 October 2021; pp. 121–126. [Google Scholar]
- Hardouin, G.; Moras, J.; Morbidi, F.; Marzat, J.; Mouaddib, E.M. Next-Best-View planning for surface reconstruction of large-scale 3D environments with multiple UAVs. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 1567–1574. [Google Scholar]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. In Advances in Neural Information Processing Systems; NeurIPS: La Jolla, CA, USA, 2015; Volume 28. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Fu, C.; Gao, Z.; Wu, W.; Chau, V.; Wang, J.; Xu, X.; Luo, J. A learning approach for multi-agent travelling problem with dynamic service requirement in mobile IoT. Comput. Electr. Eng. 2022, 104, 108397. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, C.; Cao, Z.; Song, W.; Tan, P.S.; Zhang, J.; Wen, B.; Dauwels, J. Learning to solve multiple-TSP with time window and rejections via deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1325–1336. [Google Scholar] [CrossRef]
- Stanislav, K.; Vladimir, S.; Tomas, M.; Lubos, S.; Karel, H.; Lenka, H. Dynamic Flight Tracking: Designing System for Multirotor UAVs With Pixhawk Autopilot Data Verification. IEEE Access 2024, 12, 109806–109821. [Google Scholar] [CrossRef]
- DJI. Matrice 100—Product Information. 2015. Available online: https://www.dji.com/cn/support/product/matrice100 (accessed on 2 October 2025).
- Ibrahim, A.A.; Lo, N.; Abdulaziz, R.; Ishaya, J. Capacitated Vehicle Routing Problem; Éditions Universitaires Européennes: Chisinau, Moldova, 2019. [Google Scholar]
- Agarwal, S.; Akella, S. Line coverage with multiple robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Virtual, 31 May–31 August 2020; pp. 3248–3254. [Google Scholar]
- Tang, J.; Sun, C.; Zhang, X. MSTC: Multi-robot coverage path planning under physical constrain. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 2518–2524. [Google Scholar]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Lee, Y.; Lim, W. Shoelace formula: Connecting the area of a polygon and the vector cross product. Math. Teach. 2017, 110, 631–636. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphère vide. À la mémoire de Georges Voronoï. Izv. Ross. Akad. Nauk Ser. Mat. 1934, 6, 793–800. [Google Scholar]
- Hepp, B.; Nießner, M.; Hilliges, O. Plan3d: Viewpoint and trajectory optimization for aerial multi-view stereo reconstruction. ACM Trans. Graph. (TOG) 2018, 38, 1–17. [Google Scholar] [CrossRef]
- Pan, S.; Hu, H.; Wei, H. Scvp: Learning one-shot view planning via set covering for unknown object reconstruction. IEEE Robot. Autom. Lett. 2022, 7, 1463–1470. [Google Scholar] [CrossRef]
- Christofides, N. Worst-case analysis of a new heuristic for the travelling salesman problem. In Proceedings of the Operations Research Forum; Springer: Cham, Switzerland, 2022; Volume 3, p. 20. [Google Scholar]
- Lin, S. Computer solutions of the traveling salesman problem. Bell Syst. Tech. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Gurobi Optimization, L. Gurobi Optimizer Reference Manual, 10th ed.; Gurobi Optimization, LLC: Palo Alto, CA, USA, 2023. [Google Scholar]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. Airsim: High-fidelity visual and physical simulation for autonomous vehicles. In Proceedings of the Field and Service Robotics: Results of the 11th International Conference; Springer: Singaore, 2018; pp. 621–635. [Google Scholar]
- Zheng, X.; Koenig, S.; Kempe, D.; Jain, S. Multirobot forest coverage for weighted and unweighted terrain. IEEE Trans. Robot. 2010, 26, 1018–1031. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, J. Heterogeneous Vehicle Routing Problem Based on Multi-Feature Fusion. Model. Simul. 2025, 14, 694–715. [Google Scholar] [CrossRef]
- Kong, S.; Chen, S.; Zhong, Z.; Xu, B.; Shi, T.; Zhu, X.; Yue, Y.; Wang, W. Multi-objective path planning based on KD fusion algorithm. J. Physics Conf. Ser. 2021, 1828, 012037. [Google Scholar] [CrossRef]
- Böcker, S.; Arendt, C.; Wietfeld, C. On the Suitability of Bluetooth 5 for the Internet of Things: Performance and Scalability Analysis. In Proceedings of the 2017 IEEE Conference on Standards for Communications and Networking (CSCN), Helsinki, Finland, 18–20 September 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).