Geometric Properties and Applications in System Modeling for a Generalized q-Symmetric Operator

Abstract

This paper introduces a novel generalized q-symmetric differential operator for studying a certain subclass of univalent functions with negative coefficients. We establish several significant theoretical results for this class, including sharp coefficient bounds and characterization theorems based on the generalized Hadamard product. Two significant applications demonstrate the theoretical framework’s practical utility. First, in the context of geometric modeling, we demonstrate how the function class and operator can be utilized to create and control complex, non-overlapping transformations. Second, in digital signal processing, we show that these functions serve as stable digital filter prototypes and that our operator is an effective tool for fine-tuning the filter’s frequency response. These applications bridge the gap between abstract geometric function theory and practical system design by demonstrating the operator’s versatility as a tool for analysis and synthesis.

1. Introduction

The study of uniformly convex and starlike functions has progressed through several significant milestones in geometric function theory. Goodman [1,2] laid the foundations by officially defining these classes and establishing their essential geometric features. His work showed that sharper analytic bounds result from the stricter geometric constraints imposed by uniform convexity and starlikeness compared to their classical equivalents. Following this groundbreaking study, Bharati et al. [3] made significant contributions by creating coefficient inequalities that characterized these classes and offered vital tools for classifying functions.

Kanas and Srivastava [4] made a major contribution to the area by extending Goodman’s original concepts and introducing k-uniform generalizations through linear operators. Aqlan et al. [5] expanded on the theory by examining the nature of differential inequalities and generating new subclasses. Parallel to these advancements, Choi and Kim [6] introduced powerful new methods for function composition within these classes and made significant strides in the study of generalized Hadamard products.

The incorporation of q-calculus into geometric function theory represents a significant recent advancement. The introduction of q-symmetric functions and operators, such as those proposed by Brahim and Sidomou [7], has broadened the area by linking classical methodologies with quantum calculus viewpoints, laying the groundwork for the generalized operator investigated in this paper.

The practical application of geometric function theory is a well-established science with a long history, as documented in seminal treatises [8,9]. This tradition of bridging abstract theory and physical systems has been formalized, with direct connections established between the analytic aspects of functions and signal characteristics. This dynamic has intensified in the modern computer era, and concepts of univalent functions are now crucial in domains such as digital signal processing [10] and high-fidelity mesh generation [11]. This is still an active research area, with recent papers illustrating how modern tools such as q-operators can be applied to current problems of signal theory [12]. Our work builds on this tradition by demonstrating new, operator-driven approaches to challenges in geometric mapping and filter design.

In this study, we build upon these foundations by proposing a new generalized q-symmetric operator. Using this operator, we define and analyze a new subclass of uniformly univalent functions with negative coefficients, denoted by $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. We illustrate its fundamental features by establishing numerous key theoretical conclusions, such as sharp coefficient bounds and generalized Hadamard product theorems. Finally, we show how our findings can be applied in two detailed applications: designing and controlling geometric mappings and synthesizing and tuning reliable digital filters.

The paper is organized as follows. In Section 2, we provide the necessary definitions, notation, and mathematical preliminaries related to the generalized q-symmetric operator and uniform functions. Section 3 is devoted to developing the main theoretical results. In Section 4, we present several applications of the proposed operator and function class. Finally, Section 5 concludes the paper with a summary.

2. Mathematical Preliminaries

This section summarizes the key terminology and concepts that will serve as the basis for our subsequent investigation. We begin by recalling the standard class of analytic and univalent functions, which will be our primary focus of study. We then return to the fundamental q-symmetric difference operator, which is the foundation of our analysis. We present a novel generalized q-symmetric operator that extends and unifies numerous classical operators. In addition, we examine the definitions of $\rho$-uniformly starlike and convex functions, which culminate in the formal definition of our new function class. The section closes by creating the notation for the Hadamard product and its generalization, which are critical for obtaining the key results in this Section.

Consider $S\left(n\right)$ to be the class of

$$𝘍\left(z\right)=z+{\displaystyle \sum _{k=n}^{\infty }}{a}_k{z}^k\left(n\in \mathbb{N}\setminus \left\{1\right\}=\left\{2,3,\dots \right\}\right),$$

(1)

that are univalent and analytic in $\mathbb{U}=\left\{z:z\in \mathbb{C}\mathrm{and}\left|z\right|<1\right\}.$

The q-symmetric difference operator, a q-analogue of the conventional derivative, serves as the foundation for the q-symmetric analysis. The formal definition is provided as follows:

Definition 1.

Brahim and Sidomou [7] defined the q-symmetric difference ${\widetilde{▽}}_q𝘍\left(z\right)$ as

$${\widetilde{▽}}_q𝘍\left(z\right)=\left\{\begin{array}{c}{\displaystyle \frac{𝘍\left(qz\right)-𝘍\left(q^{-1}z\right)}{\left(q-q^{-1}\right)z}}\mathit{for}z\ne 0,\\ {𝘍}^{\prime }\left(0\right)\mathit{for}z=0,\end{array}\right.$$

that is,

$${\widetilde{▽}}_q𝘍\left(z\right)=1+{\displaystyle \sum _{k=n}^{\infty }}{\left[\tilde{k}\right]}_q{a}_k{z}^{k-1},$$

(2)

and

$${\left[\tilde{k}\right]}_q={\displaystyle \frac{q^k-q^{-k}}{q-q^{-1}}},{\left[\tilde{0}\right]}_q=0,$$

(3)

see also [4,13,14].

Building on the fundamental q-symmetric difference, numerous academics have proposed operators to examine various subclasses of univalent functions. An important example is the Sălăgean differential operator and its numerous generalizations, which have proven useful in this sector [14,15,16,17]. Motivated by the goal of creating a more flexible and comprehensive tool, we introduce a new generalized q-symmetric operator in the following definition.

Definition 2.

For $\gamma >0,$ $𝘍\in S\left(n\right),$ $0<q<1$ and $t\in {\mathbb{N}}_0=\mathbb{N}\cup \left\{0\right\},$ we define the operator ${\tilde{L}}_{q,\gamma }^t:S\left(n\right)⟶S\left(n\right)$ by

$${\tilde{L}}_{q,\gamma }^0𝘍\left(z\right)=𝘍\left(z\right),$$

$${\tilde{L}}_{q,\gamma }^1𝘍\left(z\right)=\left(1-\gamma \right)𝘍\left(z\right)+\gamma z{\widetilde{▽}}_q𝘍\left(z\right)$$

$$=z+{\displaystyle \sum _{k=n}^{\infty }}\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]a_k{z}^k,$$

(4)

and (in general)

$${\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)=\left(1-\gamma \right){\tilde{L}}_{q,\gamma }^{t-1}𝘍\left(z\right)+\gamma z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^{t-1}𝘍\left(z\right)\right)$$

$$=z+{\displaystyle \sum _{k=n}^{\infty }}{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t{a}_k{z}^k.$$

(5)

The newly established generalized q-symmetric operator serves as a significant unification and extension of several fundamental differential operators previously established in geometric function theory. We observe that for $q\to 1^{-}$, we obtain the differential operator $D_{\gamma }^n$ defined by Al-Oboudi [15] and Frasin [16] (with $m=1$). Also, for $q\to 1^{-}$ and $\gamma =1$, we obtain Sălăgean differential operator Dⁿ [14], and for $\gamma =1,$ we obtain the symmetric Sălăgean q-differential operator $D_q^n$ [17].

Goodman developed the foundational classes of uniformly convex and uniformly starlike functions [1,2]. Building on this work, several generalizations were investigated to include order and type. The researchers Bharati et al. [3] and Kanas and Srivastava [4] investigated the definitions of $\rho$-uniformly starlike and convex functions of order $\zeta$.

Definition 3.

For $0\le \zeta$$<1$ and $\rho \ge 0$, Bharati et al. [3] introduce the class of ρ-uniformly starlike functions of order ζ as follows:

$$ST\left(\zeta ,\rho \right)=\left\{𝘍\in S\left(n\right):\Re \left({\displaystyle \frac{z{𝘍}^{\prime }\left(z\right)}{𝘍\left(z\right)}}-\zeta \right)>\rho \left|{\displaystyle \frac{z{𝘍}^{\prime }\left(z\right)}{𝘍\left(z\right)}}-1\right|\right\},$$

and the corresponding class of ρ-uniformly convex functions of order ζ as follows:

$$CT\left(\zeta ,\rho \right)=\left\{𝘍\in S\left(n\right):\Re \left(1+{\displaystyle \frac{z{𝘍}^{″}\left(z\right)}{{𝘍}^{\prime }\left(z\right)}}-\zeta \right)>\rho \left|{\displaystyle \frac{z{𝘍}^{″}\left(z\right)}{{𝘍}^{\prime }\left(z\right)}}\right|\right\}.$$

To combine the previously described classes of starlike and convex functions into a single comprehensive framework, we now develop a new subclass of univalent functions. This class is defined by using a flexible analytic condition on our generalized operator ${\tilde{L}}_{q,\gamma }^t$.

Definition 4.

For $0\le \zeta$ $<1,$ $0\le \beta \le 1,$ $\rho \ge 0,$ $\gamma \ge 0$ and $t\in {\mathbb{N}}_0,$ let

$$U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)=:\left\{𝘍\in S\left(n\right)\mathit{such} \mathit{that}\right.$$

$$\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-\zeta \right\}$$

$$\left.\ge \rho \left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|\right\}.$$

(6)

The generality of the class $U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ is demonstrated by the following special cases, which connect our definition to various observed function classes:

(i)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,\rho ,\beta \right)=U{L}_q\left(\zeta ,\rho ,\beta \right)$ (see [5,18]);

(ii)

$U{L}_q\left(0,\gamma ,\zeta ,\rho ,0\right)={\check{S}}_q\left(\zeta ,\rho \right)=\left\{\mathit{F}:\Re \left\{{\displaystyle \frac{z{\widetilde{▽}}_q\left(\mathit{F}\left(z\right)\right)}{\mathit{F}\left(z\right)}}-\zeta \right\}\right.$$\left.\ge \rho \left|{\displaystyle \frac{z{\widetilde{▽}}_q\left(\mathit{F}\left(z\right)\right)}{\mathit{F}\left(z\right)}}-1\right|\right\}$ (see [19]);

(iii)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,0,0,0\right)=S^{\ast }$ (starlike), and $\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,0,0\right)=S^{\ast }\left(\zeta \right)$ (starlike of order $\zeta$) (see [20]);

(iv)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,0,0,1\right)=C$ (convex), and $\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,0,1\right)=C\left(\zeta \right)$ (convex of order $\zeta$), (see [20]);

(v)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,1,0\right)=S\left(\zeta \right)$ (uniformly starlike of order $\zeta$), and

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,\rho ,0\right)=S\left(\zeta ,\rho \right)$ ($\rho$-uniformly starlike of order $\zeta$) (see [21,22]);

(vi)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,1,1\right)=K\left(\zeta \right)$ (uniformly convex of order $\zeta$), and

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,\rho ,1\right)=K(\zeta ,\rho )$ ($\rho$-uniformly convex of order $\zeta$) (see [21,22]);

(vii)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,\rho ,0\right)=ST\left(\zeta ,\rho \right)$, and $\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,\rho ,1\right)=CT\left(\zeta ,\rho \right)$ (see [3]);

(viii)

$\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,0,0\right)=ST\left(\zeta \right)$, and $\underset{q\to 1^{-}}{lim}U{L}_q\left(0,\gamma ,\zeta ,0,1\right)=CT\left(\zeta \right)$ (see [13]);

(ix)

$U{L}_q\left(t,\gamma ,\zeta ,\rho ,0\right)=U{L}_q\left(t,\gamma ,\zeta ,\rho \right)$

$$=\left\{𝘍:\Re \left\{{\displaystyle \frac{z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)}}-\zeta \right\}\right.\left.\ge \rho \left|{\displaystyle \frac{z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)}}-1\right|\right\};$$

(x)

$U{L}_q\left(t,\gamma ,\zeta ,\rho ,1\right)=K_q\left(t,\gamma ,\zeta ,\rho \right)$

$$=\left\{𝘍:\Re \left\{{\displaystyle \frac{{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-\zeta \right\}\right.\left.\ge \rho \left|{\displaystyle \frac{{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|\right\};$$

(xi)

$U{L}_q\left(t,\gamma ,\zeta ,0,\beta \right)=U{L}_q\left(t,\gamma ,\zeta ,\beta \right)=\left\{𝘍:\right.$

$$\left.\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}\right\}\ge \zeta \right\};$$

(xii)

$U{L}_q\left(t,\gamma ,\zeta ,0,0\right)=U{L}_q\left(t,\gamma ,\zeta \right)=\left\{𝘍:\Re \left\{{\displaystyle \frac{z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)}}\right\}\ge \zeta \right\};$

(xiii)

$U{L}_q\left(t,\gamma ,\zeta ,0,1\right)=K_q\left(t,\gamma ,\zeta \right)=\left\{𝘍:\Re \left\{{\displaystyle \frac{{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}\right\}\ge \zeta \right\}.$

Let

$$T\left(n\right)=\left\{𝘍\in S\left(n\right):𝘍\left(z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}{a}_k{z}^k\left(a_k\ge 0\right)\right\},$$

(7)

and

$$T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)=U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)\cap T\left(n\right).$$

(8)

Our final theoretical results are based on the quality of the Hadamard product, which allows us to combine analytic functions. To prove our key theorems about the Hadamard product, we need the classical Hölder inequality, which regulates the behavior of sums of products. We will then formally define the standard Hadamard product for our class of functions, followed by the generalized Hadamard product.

Definition 5.

Beckenbach [23] defined the Hölder inequality as follows:

$${\displaystyle \sum _{i=2}^{\infty }}\left({\displaystyle \prod _{s=1}^m}{a}_{i,s}\right)\le {\displaystyle \prod _{s=1}^m}{\left({\displaystyle \sum _{i=2}^{\infty }}{\left(a_{i,s}\right)}^{p_i}\right)}^{{\displaystyle \frac{1}{p_i}}},p_i\ge 1\mathit{and}{\displaystyle \sum _{i=1}^m}{\displaystyle \frac{1}{p_i}}=1.$$

(9)

Definition 6.

Let ${𝘍}_s\in T\left(n\right)$$(s\in \mathbb{N})$ be in the following form:

$${𝘍}_s\left(z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}{a}_{k,s}{z}^k\left(n\ge 2\right).$$

(10)

Thus, for $s=1,2$, the Hadamard product (or convolution) is denoted by ${𝘍}_1\ast {𝘍}_2$, defined as follows:

$$\left({𝘍}_1\ast {𝘍}_2\right)\left(z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}{a}_{k,1}{a}_{k,2}{z}^k=\left({𝘍}_2\ast {𝘍}_1\right)\left(z\right).$$

(11)

Definition 7.

For ${𝘍}_s\left(z\right)(s=1,2)$ given by (10), Choi and Kim [6] defined the generalized Hadamard product $\left({𝘍}_1△{𝘍}_2\right)\left(p,r;z\right)$, where p and r are real numbers as follows:

$$\left({𝘍}_1△{𝘍}_2\right)\left(p,r;z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}{\left(a_{k,1}\right)}^p{\left(a_{k,2}\right)}^r{z}^k,$$

(12)

which reduces to the standard Hadamard product defined in Equation (11), for $p=r=1$.

3. Principal Findings

In this section, we derive the main theoretical properties of the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. We begin by defining a sharp coefficient inequality as a necessary and sufficient condition for class membership. Following that, we use the generalized Hadamard product to derive many characterization theorems, a line of inquiry explored in related contexts by [24,25,26].

Unless otherwise specified, we presume that $0\le \zeta$$<1,$ $0\le \beta \le 1,$ $\rho \ge 0,\gamma \ge 0$ and $0<q<1,$ $t\in {\mathbb{N}}_0,$ $𝘍\in S\left(n\right)$ and $z\in \mathbb{U}.$

We obtain coefficient estimates that provide the necessary condition for a function belonging to the class $U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ in the following theorem.

Theorem 1.

A function $𝘍\in U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ if

$${\displaystyle \sum _{k=n}^{\infty }}\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]\left|a_k\right|\le 1-\zeta .$$

(13)

Proof. 

It suffices to show that

$$\rho \left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|$$

$$-\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right\}\le 1-\zeta .$$

Since $-\Re \left\{z\right\}\le \left|z\right|$, then we have

$$-\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right\}$$

$$\le \left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|.$$

Thus, we can easily obtain

$$\rho \left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|$$

$$-\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right\}$$

$$\le \left(1+\rho \right)\left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|.$$

Thus, from (2) and (5), we obtain

$$\rho \left|{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right|$$

$$-\Re \left\{{\displaystyle \frac{\left(1-\beta \right)z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left(z{\widetilde{▽}}_q{\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}{\left(1-\beta \right)\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)+\beta z{\widetilde{▽}}_q\left({\tilde{L}}_{q,\gamma }^t𝘍\left(z\right)\right)}}-1\right\}$$

$$\le {\displaystyle \frac{\left(1+\rho \right){\displaystyle \sum _{k=n}^{\infty }}\left({\left[\tilde{k}\right]}_q-1\right)\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left|a_k\right|}{1-{\displaystyle \sum _{k=n}^{\infty }}\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left|a_k\right|}},$$

which is bounded above by $\left(1-\zeta \right)$ if

$${\displaystyle \sum _{k=n}^{\infty }}\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]\left|a_k\right|\le 1-\zeta .$$

□

We then obtain the coefficient estimates that provide the necessary and sufficient condition for a function belonging to the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ in the following theorem.

Theorem 2.

A function $𝘍\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ if and only if

$${\displaystyle \sum _{k=n}^{\infty }}\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]a_k\le 1-\zeta .$$

(14)

Proof. 

For the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ is defined by (8); therefore, membership in $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ implies membership in both $U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ and $T\left(n\right)$. The sufficiency (in part) is immediately derived from Theorem 1. If the coefficient inequality (13) applies, then $𝘍\in U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Since $𝘍\in T\left(n\right)$ from (7), then $𝘍\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Now, we need to prove that if $𝘍\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$, the coefficient (14) holds. Assuming $𝘍\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$, this implies $𝘍\in U{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Consequently, $𝘍$ satisfies the geometric condition given by (6). Thus, from (2), (5), and for z to be real, we have

$${\displaystyle \frac{1-{\displaystyle \sum _{k=n}^{\infty }}{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left\{{\left[\tilde{k}\right]}_q\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]\right\}{a}_k{z}^{k-1}}{1-{\displaystyle \sum _{k=n}^{\infty }}{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]a_k{z}^{k-1}}}-\zeta$$

$$\ge \rho \left|{\displaystyle \frac{{\displaystyle \sum _{k=n}^{\infty }}\left({\left[\tilde{k}\right]}_q-1\right)\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t{a}_k{z}^{k-1}}{1-{\displaystyle \sum _{k=n}^{\infty }}{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]a_k{z}^{k-1}}}\right|.$$

Letting $z⟶1^{-}$, we obtain (14). □

Theorem 2 provides an estimate of the coefficients $a_k$ for $k\ge n$ in the following corollary.

Corollary 1.

If the function ϝ is in the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$, then for each $k\ge n$, we have the coefficient bound:

$$a_k\le {\displaystyle \frac{1-\zeta }{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]}}.$$

(15)

Now, we examine the behavior of the generalized Hadamard product of two functions in the subclass $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right).$

Theorem 3.

For ${𝘍}_s\left(z\right)(s=1,2)$ given by (10), if ${𝘍}_s\left(z\right)\in T{L}_q\left(t,\gamma ,{\zeta }_s,\rho ,\beta \right)$, then

$$\left({𝘍}_1△{𝘍}_2\right)\left({\displaystyle \frac{1}{p}},{\displaystyle \frac{1}{r}};z\right)\in T{L}_q\left(t,\gamma ,\delta ,\rho ,\beta \right),$$

where $p,r>1$, and δ is given by

$$\delta =\underset{k\ge n}{min}\left[1-\frac{\left(1+\rho \right)\left({\left[\tilde{k}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\right\}}^{\frac{1}{p}+\frac{1}{r}-1}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_1+\rho \right)\right]}{1-{\zeta }_1}\right)}^{\frac{1}{p}}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_2+\rho \right)\right]}{1-{\zeta }_2}\right)}^{\frac{1}{r}}-1}\right].$$

Proof. 

Let ${𝘍}_s\left(z\right)\in T{L}_q\left(t,\gamma ,{\zeta }_s,\rho ,\beta \right);$ then, from (14), we have

$${\displaystyle \sum _{k=n}^{\infty }}{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}{a}_{k,s}\le 1\left(s=1,2\right).$$

Moreover

$${\left\{{\displaystyle \sum _{k=n}^{\infty }}\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_1+\rho \right)\right]}{1-{\zeta }_1}}\right]\left(a_{k,1}\right)\right\}}^{{\displaystyle \frac{1}{p}}}\le 1,$$

(16)

and

$${\left\{{\displaystyle \sum _{k=n}^{\infty }}\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_2+\rho \right)\right]}{1-{\zeta }_2}}\right]\left(a_{k,2}\right)\right\}}^{{\displaystyle \frac{1}{r}}}\le 1.$$

(17)

Applying (9) to (16), and (17), we obtain

$${\displaystyle \sum _{k=n}^{\infty }}{\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_1+\rho \right)\right]}{1-{\zeta }_1}}\right]}^{{\displaystyle \frac{1}{p}}}\times$$

$${\displaystyle \sum _{k=n}^{\infty }}{\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_2+\rho \right)\right]}{1-{\zeta }_2}}\right]}^{{\displaystyle \frac{1}{r}}}{\left(a_{k,1}\right)}^{{\displaystyle \frac{1}{p}}}{\left(a_{k,2}\right)}^{{\displaystyle \frac{1}{r}}}\le 1.$$

Since

$$\left({𝘍}_1△{𝘍}_2\right)\left({\displaystyle \frac{1}{p}},{\displaystyle \frac{1}{r}};z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}{\left(a_{k,1}\right)}^{{\displaystyle \frac{1}{p}}}{\left(a_{k,2}\right)}^{{\displaystyle \frac{1}{r}}}{z}^k\left(n\ge 2\right),$$

then,

$${\displaystyle \sum _{k=n}^{\infty }}\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\delta +\rho \right)\right]}{1-\delta }}\right]{\left(a_{k,1}\right)}^{{\displaystyle \frac{1}{p}}}{\left(a_{k,2}\right)}^{{\displaystyle \frac{1}{r}}}\le 1,$$

with

$$\delta =\underset{k\ge n}{min}\left[1-\frac{\left(1+\rho \right)\left({\left[\tilde{k}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\right\}}^{\frac{1}{p}+\frac{1}{r}-1}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_1+\rho \right)\right]}{1-{\zeta }_1}\right)}^{\frac{1}{p}}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_2+\rho \right)\right]}{1-{\zeta }_2}\right)}^{\frac{1}{r}}-1}\right].$$

Thus, the proof is completed using (14). □

From Theorem 3, we derive the subsequent corollary by setting ${\zeta }_s=\zeta (s=1,2)$.

Corollary 2.

If ${𝘍}_s\left(z\right)$$\left(s=1,2\right)$ given by (10), ${𝘍}_s\left(z\right)\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Then,

$$\left({𝘍}_1△{𝘍}_2\right)\left({\displaystyle \frac{1}{p}},{\displaystyle \frac{1}{r}};z\right)\in T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)\left(p,r>1\right).$$

Finally, we extend the previous results to a collection of functions $F_m$, which shows the broad applicability of earlier findings.

Theorem 4.

If ${𝘍}_s\left(z\right)$$\left(s=1,2,\dots ,m\right)$ given by (10), ${𝘍}_s\left(z\right)\in T{L}_q\left(t,\gamma ,{\zeta }_s,\rho ,\beta \right)$, and let

$$F_m\left(z\right)=z-{\displaystyle \sum _{k=n}^{\infty }}\left({\displaystyle \sum _{s=1}^m}{\left(a_{k,s}\right)}^p\right)z^k.$$

Then, $F_m\left(z\right)\in T{L}_q\left(t,\gamma ,\delta ,\rho ,\beta \right)$, where

$$\delta =1-{\displaystyle \frac{m\left(1+\rho \right)\left({\left[\tilde{n}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{n}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{n}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left({\displaystyle \frac{\left[\left(1+\rho \right){\left[\tilde{n}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }}\right)}^p-m}},$$

$\zeta =\underset{1\le s\le m}{min}\left\{{\zeta }_s\right\}$, and

$${\left\{\left[1+\beta \left({\left[\tilde{n}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{n}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left({\displaystyle \frac{\left[\left(1+\rho \right){\left[\tilde{n}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }}\right)}^p$$

$$\ge m\left[\left(1+\rho \right){\left[\tilde{n}\right]}_q-\rho \right].$$

Proof. 

Since ${𝘍}_s\left(z\right)\in T{L}_q\left(t,\gamma ,{\zeta }_s,\rho ,\beta \right),$ then, from (14), we have

$${\displaystyle \sum _{k=n}^{\infty }}{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}{a}_{k,s}\le 1,$$

$s=1,2,\dots m;n\ge 2$, and

$${\displaystyle \sum _{k=n}^{\infty }}{\left\{{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}\right\}}^p{\left(a_{k,s}\right)}^p\le$$

$${\left\{{\displaystyle \sum _{k=n}^{\infty }}{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}{a}_{k,s}\right\}}^{{\displaystyle \frac{1}{p}}}\le 1.$$

(18)

From (18), we obtain

$${\displaystyle \sum _{k=n}^{\infty }}\left\{{\displaystyle \frac{1}{m}}{\displaystyle \sum _{s=1}^m}{\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}\right]}^p\right.\left.{\left(a_{k,s}\right)}^p\right\}\le 1.$$

Taking $\zeta =\underset{1\le s\le m}{min}\left\{{\zeta }_s\right\}$; then, from (14), we have

$${\displaystyle \sum _{k=n}^{\infty }}{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\delta +\rho \right)\right]}{1-\delta }}{\displaystyle \sum _{s=1}^m}{\left(a_{k,s}\right)}^p\le$$

$${\displaystyle \sum _{k=n}^{\infty }}\left\{{\displaystyle \frac{1}{m}}{\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }}\right]}^p\right.{\displaystyle \sum _{s=1}^m}{\left(a_{k,s}\right)}^p$$

$$\le {\displaystyle \sum _{k=n}^{\infty }}\left\{{\displaystyle \frac{1}{m}}\right.{\displaystyle \sum _{s=1}^m}{\left[{\displaystyle \frac{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left({\zeta }_s+\rho \right)\right]}{1-{\zeta }_s}}\right]}^p{\left(a_{k,s}\right)}^p,$$

if

$$\delta \le 1-{\displaystyle \frac{m\left(1+\rho \right)\left({\left[\tilde{k}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }\right)}^p-m}}.$$

Let us now calculate the following:

$$g\left(k\right)=1-{\displaystyle \frac{m\left(1+\rho \right)\left({\left[\tilde{k}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{k}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }\right)}^p-m}}.$$

Then, $g^{\prime }\left(k\right)\ge 0$ if $p\ge 2$. Hence,

$$\delta =1-{\displaystyle \frac{m\left(1+\rho \right)\left({\left[\tilde{n}\right]}_q-1\right)}{{\left\{\left[1+\beta \left({\left[\tilde{n}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{n}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left(\frac{\left[\left(1+\rho \right){\left[\tilde{n}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }\right)}^p-m}}.$$

Using the following condition

$${\left\{\left[1+\beta \left({\left[\tilde{n}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{n}\right]}_q-1\right)\right]}^t\right\}}^{p-1}{\left({\displaystyle \frac{\left[\left(1+\rho \right){\left[\tilde{n}\right]}_q-\left(\zeta +\rho \right)\right]}{1-\zeta }}\right)}^p$$

$$\ge m\left[\left(\left(1+\rho \right){\left[\tilde{n}\right]}_q-\rho \right)\right],$$

we have $0\le \delta <1$. Thus, the proof is completed. □

Remark 1.

The generality of our main results is underscored by the fact that they contain, as special cases, a number of previously known theorems. We briefly explain some of these connections as follows:

(i)

The results obtained by Aouf et al. [18], Lemma 1, Theorem 1, and Theorem 2 can be recovered by setting $q\to 1^{-}$ and $t=0$ in our earlier results;

(ii)

The results obtained by Choi and Kim [6], Theorem 1, Corollary 1, and Theorem 3 can be recovered by setting $q\to 1^{-}$, $t=0$, and $\rho =\beta =0$ in our earlier results;

(iii)

The results obtained by Choi and Kim [6], Theorem 2, Corollary 2, and Theorem 4 can be recovered by setting $q\to 1^{-}$, $t=0$, $\rho =0$, and $\beta =1$ in our earlier results;

(iv)

The results obtained by Kanas et al. [19], Theorem 2.1 and Theorem 2.2 can be recovered by setting $t=0$ and $\rho =0$ in Theorem 1 and Theorem 2;

(v)

The results of the class $ST(\zeta ,\rho )$ follow from setting $q\to 1^{-}$, $t=0$, and $\beta =0$;

(vi)

The results of the class $CT(\zeta ,\rho )$ follow from setting $q\to 1^{-}$, $t=0$, and $\beta =1$.

4. Applications in System Modeling and Design

The theoretical framework presented in the preceding sections has significant applications. This section examines two such applications, illustrating the utility of the defined function class and the generalized q-symmetric operator in geometric modeling and digital signal processing.

4.1. Geometric Mapping Using the Generalized q-Symmetric Operator

Our first application is in the area of geometric modeling and image modification. Univalent functions form the mathematical underpinning of conformal mappings, which are essential tools in science and engineering because they can execute angle-preserving, non-overlapping transformations [27]. The subclass of functions investigated in this study, when paired with our adaptable q-symmetric differential operator, provides a powerful and versatile toolkit for building smooth, injective transformations. These are particularly useful in applications like advanced image warping and the creation of high-quality computational meshes [11]. In the following subsections, we visually demonstrate these abilities.

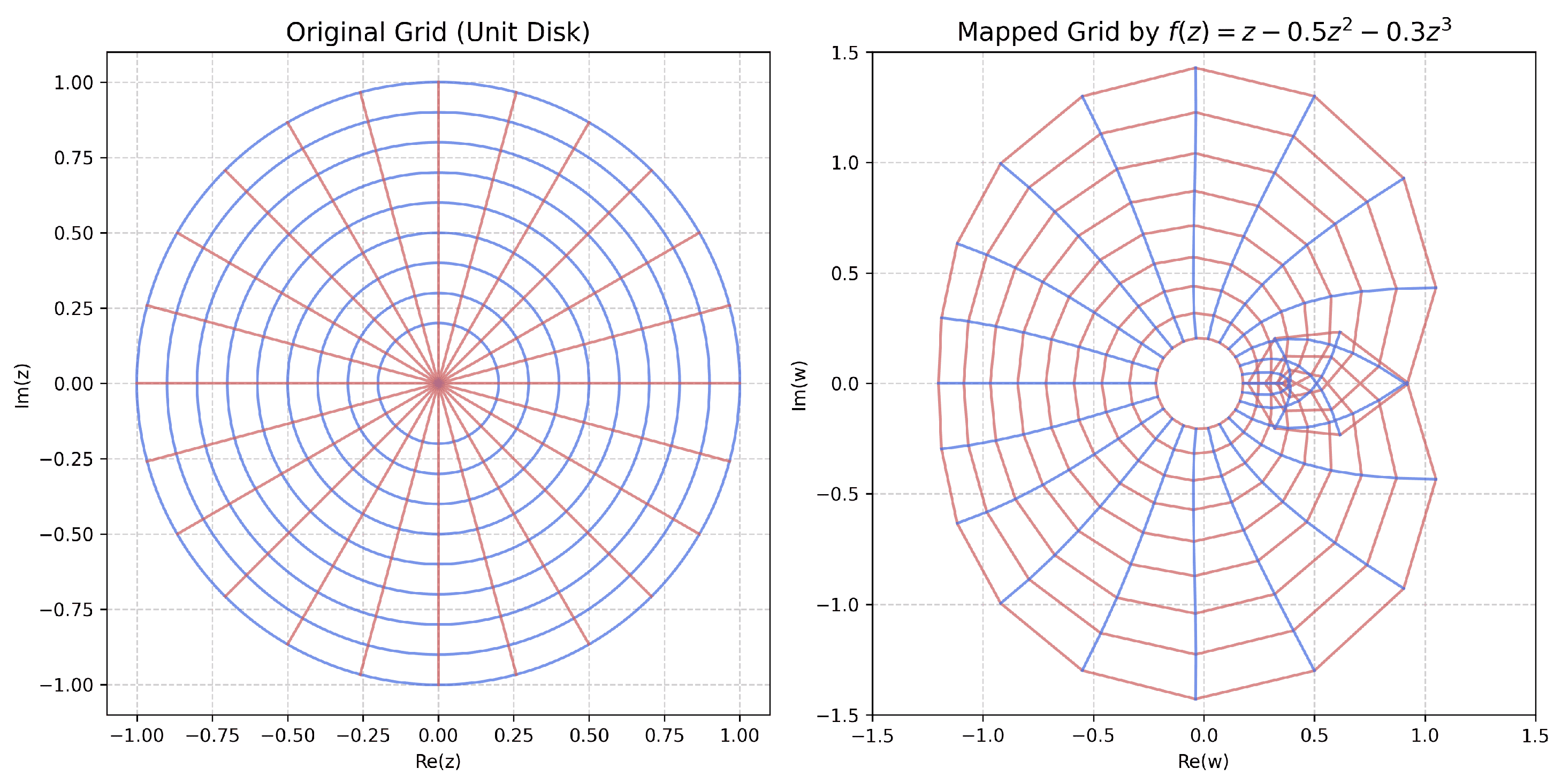
4.1.1. Analytic Transformation of the Unit Disk

To demonstrate a practical application in geometric modeling, we begin by considering a transformation on the open unit disk $\mathbb{U}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$. Such transformations are essential in fields such as computational mesh generation, where a non-overlapping mapping is a vital requirement [11]. We utilize the following univalent function with negative coefficients as a mapping tool for achieving this:

$$f\left(z\right)=z-0.5z^2-0.3z^3.$$

Its univalence ensures that the mapping from $\mathbb{U}$ to its image is injective, preventing the domain from folding or overlapping itself. To illustrate this, we use the following transformation:

$$w=f\left(z\right),$$

on a polar grid in $\mathbb{U}$. Figure 1 illustrates the resulting geometric deformation.

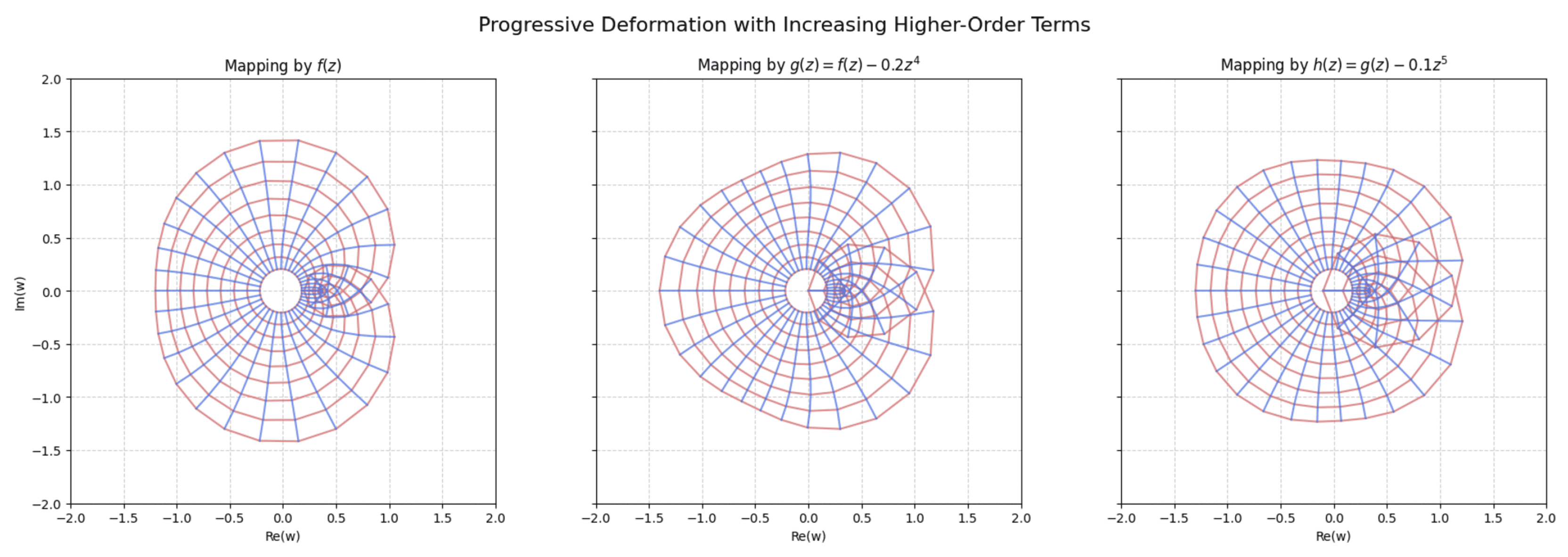
4.1.2. Progressive Deformation via Higher-Order Terms

To investigate the impact of successive higher-order terms, we introduce two new functions, $g\left(z\right)$ and $h\left(z\right)$, which are based on the example function of the previous section, $f\left(z\right)$. This sequence demonstrates a progressive increase in complexity:

$$f\left(z\right)=z-0.5z^2-0.3z^3,$$

$$g\left(z\right)=z-0.5z^2-0.3z^3-0.2z^4,$$

$$h\left(z\right)=z-0.5z^2-0.3z^3-0.2z^4-0.1z^5.$$

(19)

The sequence $f\left(z\right)\stackrel{\mathrm{add}{z}^4\mathrm{term}}{\to }g\left(z\right)\stackrel{\mathrm{add}{z}^5\mathrm{term}}{\to }h\left(z\right)$ provides a perfect, rigorous example of progressive deformation. As demonstrated by Figure 2, the sequential inclusion of higher-order terms serves as a powerful mechanism for managing the complexity of the transformation. This demonstrates how coefficients can be intelligently selected to mold the target domain with increasing detail and precision.

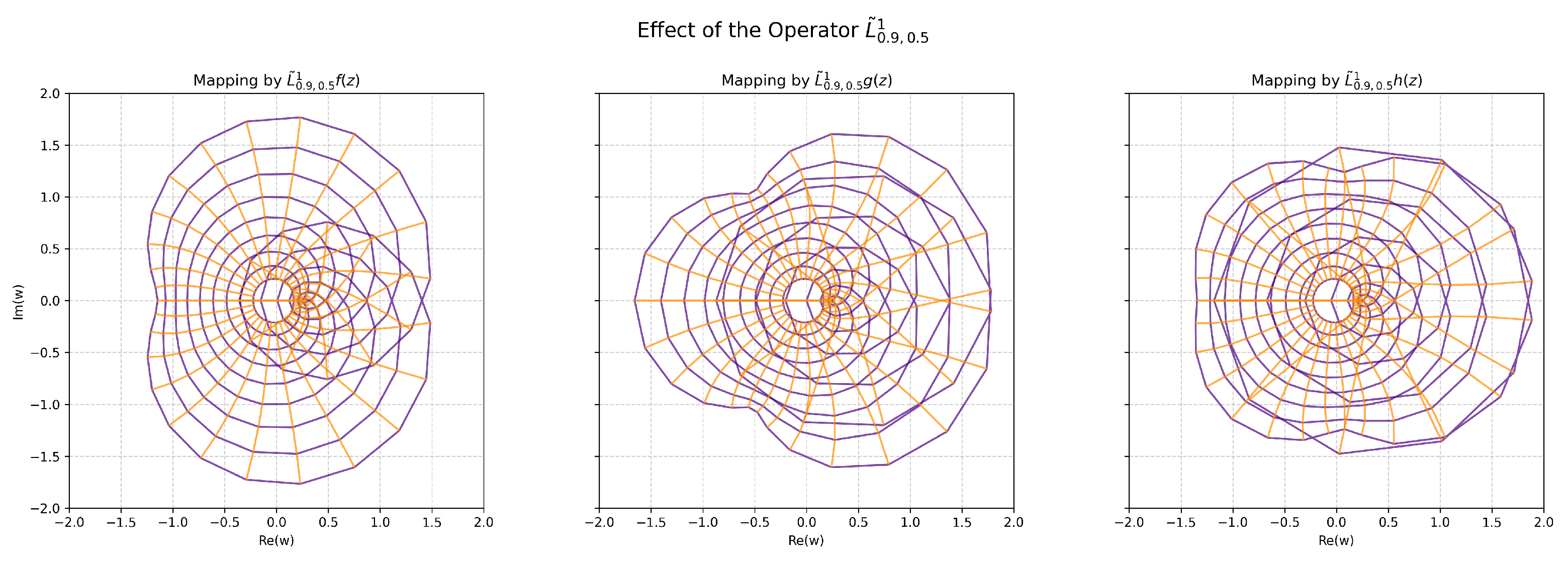
4.1.3. Operator-Driven Amplification of Mappings

A key contribution of this paper is the operator ${\tilde{L}}_{q,\gamma }^t$, which provides a flexible tool for modifying functions within the univalent class. To demonstrate its geometric impact, we now apply this operator to the functions $f\left(z\right)$, $g\left(z\right)$, and $h\left(z\right)$ from the previous section. For this visual demonstration, we fix the operator’s parameters to $q=0.9$ and $\gamma =0.5$ and apply it once by setting $t=1$. The ${\tilde{L}}_{0.9,0.5}^1$ operator, as defined in Equation (4), transforms the original functions into the following new forms with amplified coefficients:

$${\tilde{L}}_{0.9,0.5}^{1}f\left(z\right)=z-0.75275z^2-0.60525z^3,$$

$${\tilde{L}}_{0.9,0.5}^{1}g\left(z\right)=z-0.75275z^2-0.60525z^3-0.5112z^4,$$

$${\tilde{L}}_{0.9,0.5}^{1}h\left(z\right)=z-0.75275z^2-0.60525z^3-0.5112z^4-0.31115z^5.$$

Figure 3 shows a visualization of these transformed functions.

A simple comparison to Figure 2 shows that the operator functions as a deformation amplifier. The characteristic shapes of the original functions are retained, but the deformations are much more amplified. This visibly indicates that the operator provides an effective mechanism for regulating the intensity of the geometric transformation.

4.1.4. Numerical Verification Based on the Class Condition

Our theoretical work’s main contribution is Theorem 2, which establishes a strong coefficient inequality as a necessary and sufficient requirement for a function to belong to the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Aside from its theoretical significance, this theorem provides a practical, computable criterion for class membership. In this section, we run a numerical test to demonstrate how this process works.

We analyze whether the function $h\left(z\right)$, defined in Equation (19), which we utilized in our geometric mapping examples, is a member of our class for a given set of parameters. We test for membership in the subclass $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ by setting the following parameters:

$$t=1,\gamma =0.5,\zeta =0.3,\rho =0.2,\beta =0.5,andq=0.9.$$

According to Theorem 2, $h\left(z\right)$ belongs to this specific subclass if and only if its coefficients satisfy the inequality given by Equation (14). To simplify our calculations, let us define the coefficient multiplier from that inequality as $X_k$:

$$X_k=\left[1+\beta \left({\left[\tilde{k}\right]}_q-1\right)\right]{\left[1+\gamma \left({\left[\tilde{k}\right]}_q-1\right)\right]}^t\left[(1+\rho ){\left[\tilde{k}\right]}_q-(\zeta +\rho )\right],$$

where ${\left[\tilde{k}\right]}_q$ is the q-symmetric number given by (3). Theorem 2 can now be concisely written as follows:

$${\displaystyle \sum _{k=2}^5}{X}_k·a_k\le 1-\zeta .$$

Using the parameters stated and the coefficients $a_k$ of $h\left(z\right)$, we execute the numerical computation that yields

$${\displaystyle \sum _{k=2}^5}{X}_k·a_k\approx 2.1548.$$

We compare this result with the right-hand side of the inequality $1-\zeta =0.7$. Substituting the computed values into the condition yields $2.1548\cancel{\le }0.7$. The inequality is clearly not satisfied.

Conclusions of the Test

This result yields a conclusive answer: The function $h\left(z\right)$, despite being a legitimate univalent mapping, does not belong to the subclass $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ for this specific collection of parameters. This result is important because it indicates the selectivity of our defined class. This means that membership necessitates more stringent geometric criteria than univalence alone, and our theorem provides a precise numerical instrument for proving these properties. As a result, the condition is not trivial and serves as a useful criterion for classifying functions.

It is instructive to investigate what type of function would meet this stringent condition. Given the large multipliers generated by the operator and parameters, a function must have much smaller coefficients to be a member. For example, a function like $\tilde{h}\left(z\right)=z-0.05z^2-0.03z^3$ would have a summation value of roughly $0.41$, which is less than $0.7$, awarding it membership in this class. This emphasizes the selectivity of the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$.

To generate functions within the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$, controlled geometric and filter properties can be achieved by selecting coefficients to satisfy the inequality (15) in Corollary 1.

4.1.5. Synthesis of New Mappings via the Hadamard Product

A major difficulty in applied geometric modeling is the creation of new shapes by blending or merging existing ones [28]. Our theoretical findings on the Hadamard product provide a method for creating new geometric transformations. Theorem 3 outlines a formal framework for mixing the coefficients of two functions, $f_1\left(z\right)$ and $f_2\left(z\right)$, to create a new univalent mapping with a mixture of their properties. For a brief illustration, consider two univalent functions:

$$f_1\left(z\right)=z-0.5z^2-0.3z^4\mathrm{and}{f}_2\left(z\right)=z-0.2z^2-0.4z^3.$$

The standard Hadamard product (convolution), a specific example of the operation in Theorem 3, multiplies the coefficients. The final function, $f_3\left(z\right)$, is as follows:

$$f_3\left(z\right)=(f_1\ast f_2)\left(z\right)=z-(0.5·0.2)z^2=z-0.1z^2.$$

This result is significant because it can be applied to feature filtering and model simplification. The original function, $f_1\left(z\right)$, resulted in a complex mapping with two symmetric components ($z^2$ and $z^4$). Using the Hadamard product with a carefully chosen ‘filter’ function $f_2\left(z\right)$, we successfully isolated the two-fold component into the new function, $f_3\left(z\right)$.

The true significance of this process is guaranteed by Theorem 3. This ensures that the new mapping $f_3\left(z\right)$ is a legal and stable transformation that belongs to our defined class, rather than an arbitrary construct. This gives designers an accurate, analytical method for the following:

• Decomposing a complex transformation into fundamental geometric components.
• Creating simpler and computationally cheaper models ($f_3\left(z\right)$ is easier to compute than $f_1\left(z\right)$) while retaining the necessary fundamental properties and stability of the original.

This demonstrates a strong method for the analysis, simplification, and synthesis of geometric transformations, which could be explored in future research.

4.2. Stable Digital Filter Design Using Univalent Functions

The principles of geometric function theory find a wide range of applications in digital signal processing (DSP). The construction of reliable digital filters is a key component of DSP, as they are required to shape the frequency content of the signals without providing undesirable oscillations or divergence [10,29]. In this part, we demonstrate how our defined class of functions, along with the generalized q-symmetric operator, provides a sophisticated framework for developing and improving such filters.

4.2.1. Filter Design Using Analytic Functions

A linear time-invariant digital filter is defined by its transfer function, which is a complex function generally denoted as $H\left(z\right)$. A fundamental theorem in DSP states that a filter is stable if, and only if, all poles of $H\left(z\right)$ are contained within the unit disk $\mathbb{U}$ [10,29]. The functions examined in this study, which are subclasses of univalent functions, such as the ones we introduced $S\left(n\right)$, are analytic (and thus pole-free) in $\mathbb{U}$.

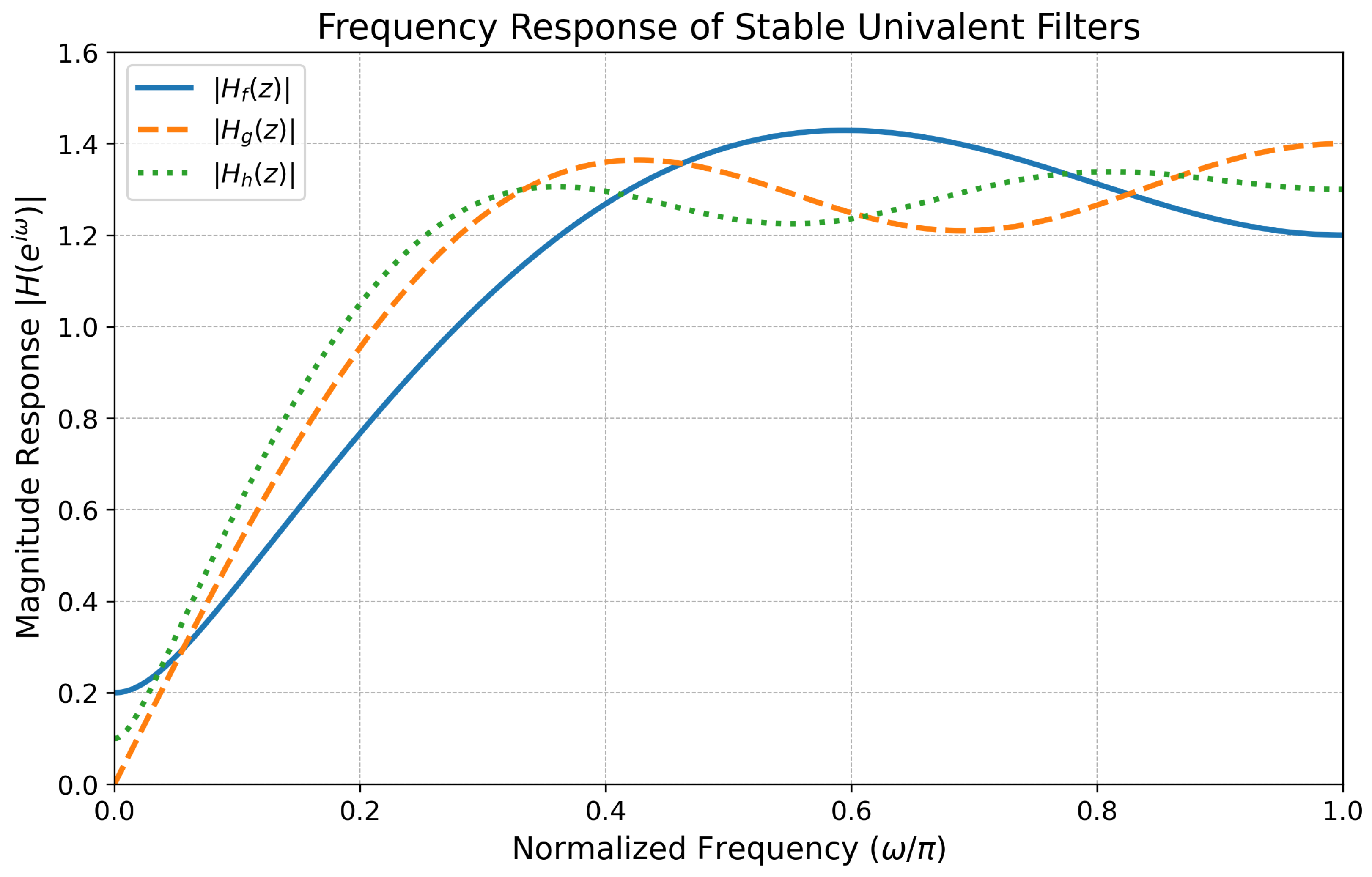
As a result, we can create a guaranteed stable filter using one of these univalent functions as its transfer function, such as setting $H\left(z\right)=f\left(z\right)$. To evaluate the performance of the filter, we examine its frequency response. This is obtained by evaluating the transfer function $H\left(z\right)$ on the unit circle, $z=e^{iw}$, where w is the normalized frequency.

To illustrate this principle, we will now utilize the univalent functions $f\left(z\right)$, $g\left(z\right)$, and $h\left(z\right)$ from our geometric mapping application in Section 4.1.2 as a set of example transfer functions. For this context, we denote them as $H_f\left(z\right)$, $H_g\left(z\right)$, and $H_h\left(z\right)$, respectively:

$$H_f\left(z\right)=z-0.5z^2-0.3z^3,$$

$$H_g\left(z\right)=z-0.5z^2-0.3z^3-0.2z^4,$$

$$H_h\left(z\right)=z-0.5z^2-0.3z^3-0.2z^4-0.1z^5.$$

To analyze their filter performance, we look at their frequency responses. This is achieved by determining the magnitude of each transfer function, $\left|H\right(z\left)\right|$, given values of z on the unit circle, where $z=e^{i\omega }$. The variable $\omega$ indicates the digital frequency, which ranges from 0 (DC) to $\pi$ (Nyquist frequency).

To provide a clear and universal illustration, we plot these magnitudes against the normalized frequency $\omega /\pi$, with the x-axis ranging from 0 to 1, representing the complete effective frequency range.

The plots in Figure 4 clearly indicate that these transfer functions are low-pass filters. They have a high magnitude in the pass-band (the region where $\omega /\pi$ is near 0), which means that low-frequency signal components can pass through with few amplitude changes. In contrast, they display a substantially reduced magnitude in the stop-band (where $\omega /\pi$ approaches 1), indicating that high-frequency signal components are strongly muted or blocked.

Furthermore, the figure demonstrates a crucial design principle in filter theory: adding higher-order terms to $H_g\left(z\right)$ and $H_h\left(z\right)$ results in a steeper transition from the pass-band to the stop-band (a sharper “roll-off”) and greater overall attenuation of high frequencies. This demonstrates how increasing the polynomial order of a univalent function can improve filtering performance.

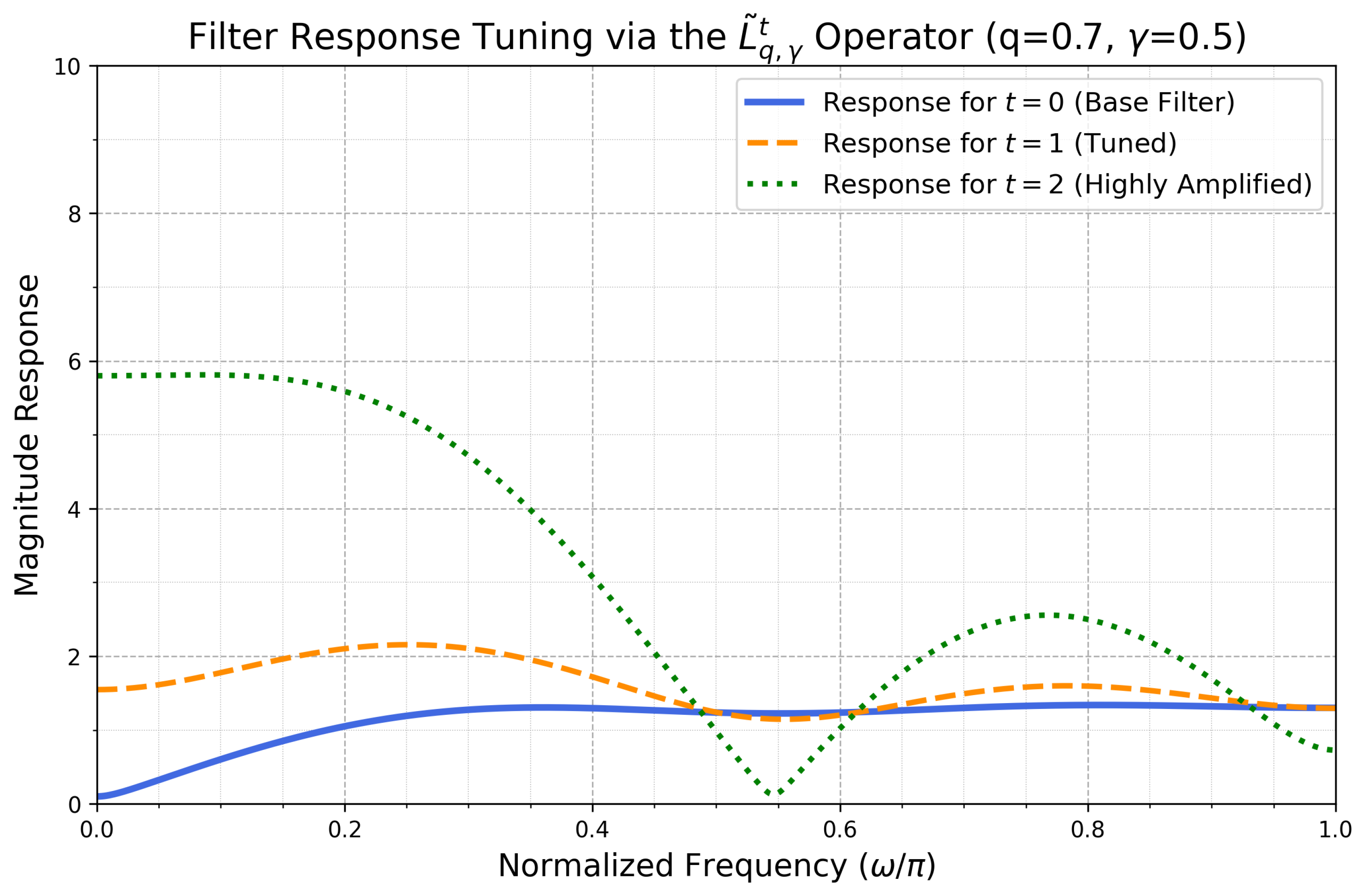
4.2.2. Fine-Tuning Filter Response with the Operator

Increasing the polynomial order of a transfer function can improve filter performance, but using the generalized q-symmetric operator, ${\tilde{L}}_{q,\gamma }^t$, is more flexible. This operator enables designers to start with a single base filter, $H_{base}\left(z\right)$, and produce a family of new filters, $H_t\left(z\right)$, defined as follows:

$$H_t\left(z\right)={\tilde{L}}_{q,\gamma }^t{H}_{\mathrm{base}}\left(z\right).$$

This process refines the filter’s characteristics while preserving the fundamental property of stability.

To illustrate this possibility, we use the transfer function $H_h\left(z\right)$ as our basis design. Equation (5) shows that applying the operator changes the coefficients $a_k$ of the original function. For $t\in \{0,1,2\}$, we generate the following filter family:

$$H_0\left(z\right)={\tilde{L}}_{q,\gamma }^0{H}_h\left(z\right)=H_h\left(z\right),$$

$$H_1\left(z\right)={\tilde{L}}_{q,\gamma }^1{H}_h\left(z\right)=z-{\displaystyle \sum _{k=2}^5}[1+\gamma ({\left[\tilde{k}\right]}_q-1)]a_k{z}^k,$$

$$H_2\left(z\right)={\tilde{L}}_{q,\gamma }^2{H}_h\left(z\right)=z-{\displaystyle \sum _{k=2}^5}{[1+\gamma ({\left[\tilde{k}\right]}_q-1)]}^2{a}_k{z}^k.$$

We hypothesize that as t increases, the operator’s amplification of the coefficients will translate into more aggressive rejection of high frequencies. In our numerical example, we selected $q=0.7$ and $\gamma =0.5$.

Employing the ${\tilde{L}}_{0.7,0.5}^t$$(t=0,1,2)$ operator on our base filter $H_h\left(z\right)$ gives the following transfer functions:

$$H_0\left(z\right)={\tilde{L}}_{0.7,0.5}^0{H}_h\left(z\right)=z-0.5z^2-0.3z^3-0.2z^4-0.1z^5,$$

$$H_1\left(z\right)={\tilde{L}}_{0.7,0.5}^1{H}_h\left(z\right)\approx z-0.804z^2-0.674z^3-0.588z^4-0.371z^5,$$

$$H_2\left(z\right)={\tilde{L}}_{0.7,0.5}^2{H}_h\left(z\right)\approx z-1.292z^2-1.514z^3-1.729z^4-1.375z^5.$$

The frequency responses of these three transfer functions $H_0\left(z\right)$, $H_1\left(z\right)$, and $H_2\left(z\right)$ are plotted in Figure 5.

The results in Figure 5 provide a fascinating insight into the operator’s power and sensitivity. A comparison of the $t=0$ (solid blue) and $t=1$ (dashed orange) curves demonstrates that a single application of the operator can increase the filter’s performance by introducing a deeper null in the stop-band. This proves its utility in focused filter enhancement.

However, the curve for $t=2$ (dotted green) demonstrates a strong, nonlinear effect from a second application. The operator now highly amplifies the coefficients to the point that the function’s behavior is substantially altered, resulting in a large peak in the pass-band and transforming the filter’s overall response. This demonstrates that the parameter t functions as a highly sensitive tuning parameter, capable of both mild refinements and of propelling the system into totally new behavioral regimes, all while maintaining the underlying stability provided by the function’s univalence.

4.2.3. Class Conditions as Advanced Filter Design Constraints

In modern signal processing, stability is frequently the minimum requirement for a filter. Advanced applications may require additional qualities to ensure peak performance, such as a maximally flat pass-band to avoid frequency distortion or a linear phase response to ensure that all frequencies are delayed by the same amount, thereby preserving the signal’s waveform. These engineering qualities are closely related to the geometric and analytic structure of the transfer function $H\left(z\right)$.

For example, it is well-established that the geometric properties of a function, such as membership in the class of functions with a positive real part (which is closely related to the class of starlike functions), are directly related to the stability and passivity of the corresponding physical system [30]. This is where the theoretical conditions of our work create a novel contribution. Theorem 2 establishes a membership requirement for the class $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$ that may be quantified as a constraint for a “well-behaved” filter. A filter whose transfer function $H\left(z\right)$ meets the inequality in Equation (14) is guaranteed to have the class’s special geometric regularities, which, as previously shown in Section 4.1.4, can be associated with desirable signal processing qualities. This introduces a new paradigm for filter design. Our theory can be used by engineers as a sophisticated design tool for selecting or validating transfer functions. To demonstrate, consider the results of our numerical test in Section 4.1.4:

• We found that the transfer function $H_h\left(z\right)$ failed to belong to the class
  $T{L}_{0.9}(1,0.5,0.3,0.2,0.5)$.
• In contrast, the function

  $$\tilde{H}\left(z\right)=z-0.05z^2-0.03z^3,$$

  successfully met the condition.

Engineers can utilize our theory to make educated decisions when choosing between two stable filters, $H_h\left(z\right)$ and $\tilde{H}\left(z\right)$. While $H_h\left(z\right)$ provides better attenuation (as shown in Figure 4), $\tilde{H}\left(z\right)$ belongs to our unique subclass, perhaps delivering superior performance in other measures, such as phase distortion. As a result, our theoretical findings from Section 3 immediately translate into a practical analytical criterion for a new subclass of high-performance digital filters. This enables designers to go beyond simple stability and apply stricter, mathematically specified quality restrictions to their designs.

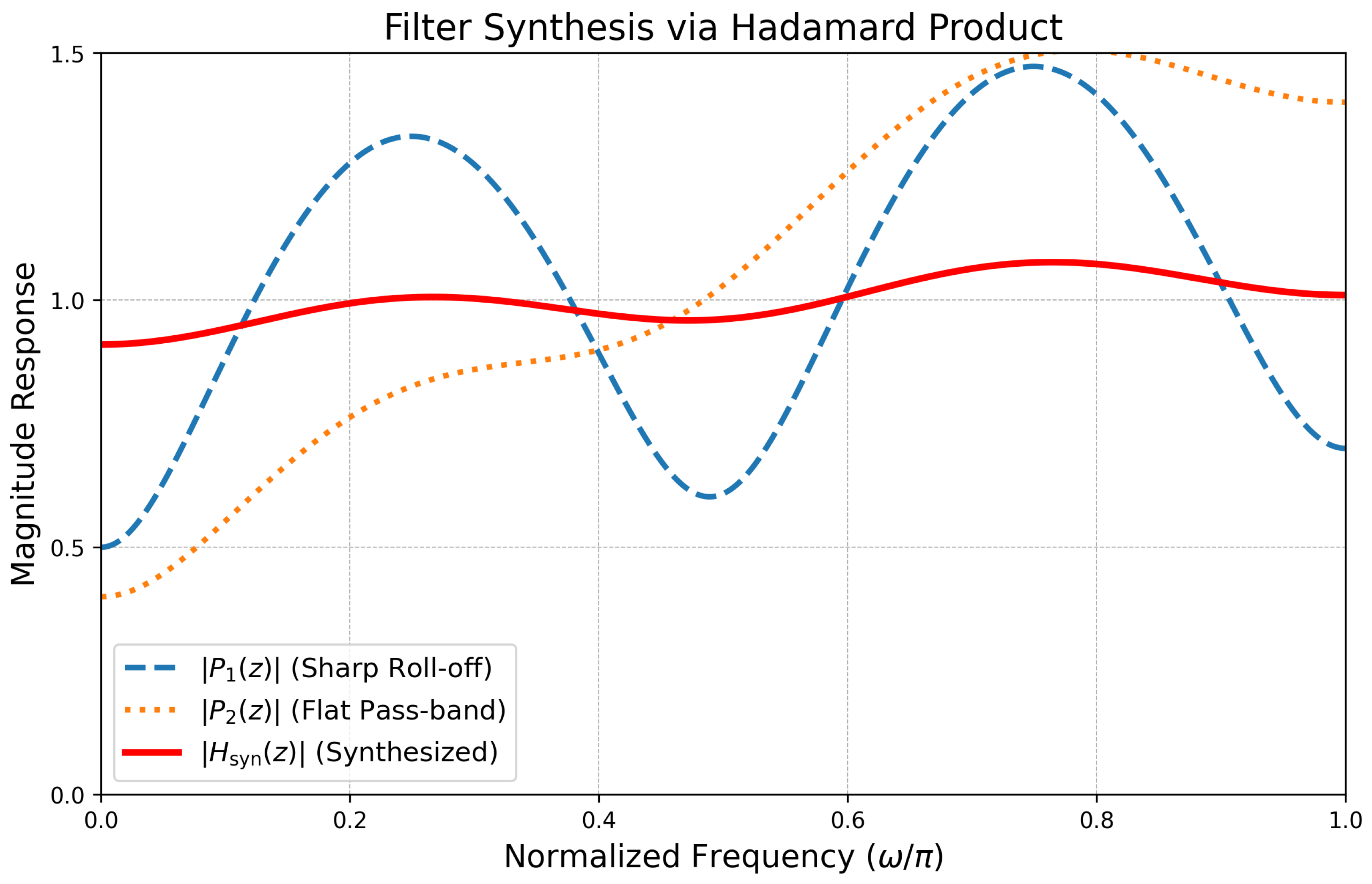
4.2.4. Filter Synthesis via the Hadamard Product

Our theoretical findings for the Hadamard product provide an effective framework for creating new filters from existing prototypes. Theorem 3 provides a formal approach for combining two stable filters to produce a new hybrid filter that is guaranteed to be stable and inherits a combination of their qualities. To illustrate, consider an engineering scenario where a designer has two prototype filters:

• $P_1\left(z\right)=z-0.1z^2-0.4z^5$, which has a desirable sharp roll-off.
• $P_2\left(z\right)=z-0.5z^2-0.1z^5$, which has a desirable flat pass-band.

Using the standard Hadamard product, a specific case of the operation in Theorem 3, we create a new filter, $H_{syn}\left(z\right)$:

$$H_{\mathrm{syn}}\left(z\right)=(P_1\ast P_2)\left(z\right)=z-(0.1·0.5)z^2-(0.4·0.1)z^5=z-0.05z^2-0.04z^5.$$

Theorem 3 guarantees that the newly synthesized filter $H_{syn}$ is stable and belongs to our class. Figure 6 shows the frequency responses of the two prototypes and the final synthesized filter.

Also, this demonstrates that the synthesized filter $H_{syn}$ effectively balances the two prototypes. It successfully inherits the desirable flat pass-band feature from $P_2$. Its stop-band attenuation is substantially better than that of $P_2$ and remains competitive with the more aggressive $P_1$. This clearly shows that the Hadamard product is a useful tool for navigating design trade-offs. Theorem 3 ensures stability and class membership for $H_{syn}$, transforming synthesis from a heuristic to a mathematically rigorous design technique.

5. Conclusions

In this study, we develop a generalized q-symmetric differential operator and use it to create and investigate a novel subclass of uniformly univalent functions with negative coefficients, $T{L}_q\left(t,\gamma ,\zeta ,\rho ,\beta \right)$. Our theoretical analysis yielded several key results for this class of functions, which exhibit uniformly convex and starlike properties. These results include sharp coefficient bounds (Theorem 2) and new Hadamard product characterization theorems (Theorems 3 and 4).

Beyond the theoretical contributions, we demonstrated the framework’s practical utility with two detailed applications. In geometric mapping, we demonstrated that the functions are versatile instruments for building complex, non-overlapping transformations, and that our operator operates as a “deformation amplifier,” adding another layer of control. In digital signal processing, we demonstrated that these functions can serve as stable filter prototypes. We also showed that our operator is an effective tool for fine-tuning a filter’s frequency response, and that our theoretical conditions for class membership and Hadamard products may be read as new, mathematically rigorous criteria for advanced filter design and synthesis.

These discoveries effectively bridge the gap between abstract geometric function theory and practical system modeling applications. The operator and function classes described here provide a viable and versatile toolkit for future study and practical design in pure and applied mathematics.