Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus
Abstract
1. Introduction
- This study combines classical and fractional differential equations to enhance compartmental models. This study enhances our comprehension of the dynamics of influenza virus transmission and the impact of vaccination and resistance to therapy.
- It uses fractional calculus and the Caputo operator to simulate the effects of influenza memory. This novel approach captures the disease’s nonlocal behaviour and genetic characteristics, providing insights that cannot be obtained with integer-order differential equations.
- The study utilises Saudi Arabian surveillance data and uses WHO epidemiological parameter estimation methodologies to develop its models. This enhances the relevance of the outcomes to the design and implementation of public health measures.
- The study examines the transmission patterns and evaluates the impact of vaccination and other control measures on the spread of influenza. Stability studies and computer simulations indicate that relying just on vaccination is inadequate for controlling the sickness, and other techniques are necessary.
- Fractional differential operators include memory traces and genetic characteristics, offering a novel technique for simulating illnesses. This methodology elucidates the impact of previous infections on epidemic patterns and facilitates the development of more effective long-term intervention strategies. This advancement enhances the understanding of fractional derivatives in the field of epidemiology. This study integrates traditional and fractional calculus methodologies to model influenza dynamics uniquely. It supports public health planning and research on infectious disease models.
2. Preliminaries
3. Model Construction
4. Analysis of the Model
4.1. Existence and Uniqueness
4.2. Boundedness and Non-Negativity
4.3. The Basic Reproduction Number
4.4. Stability Analysis
4.5. Global Stability
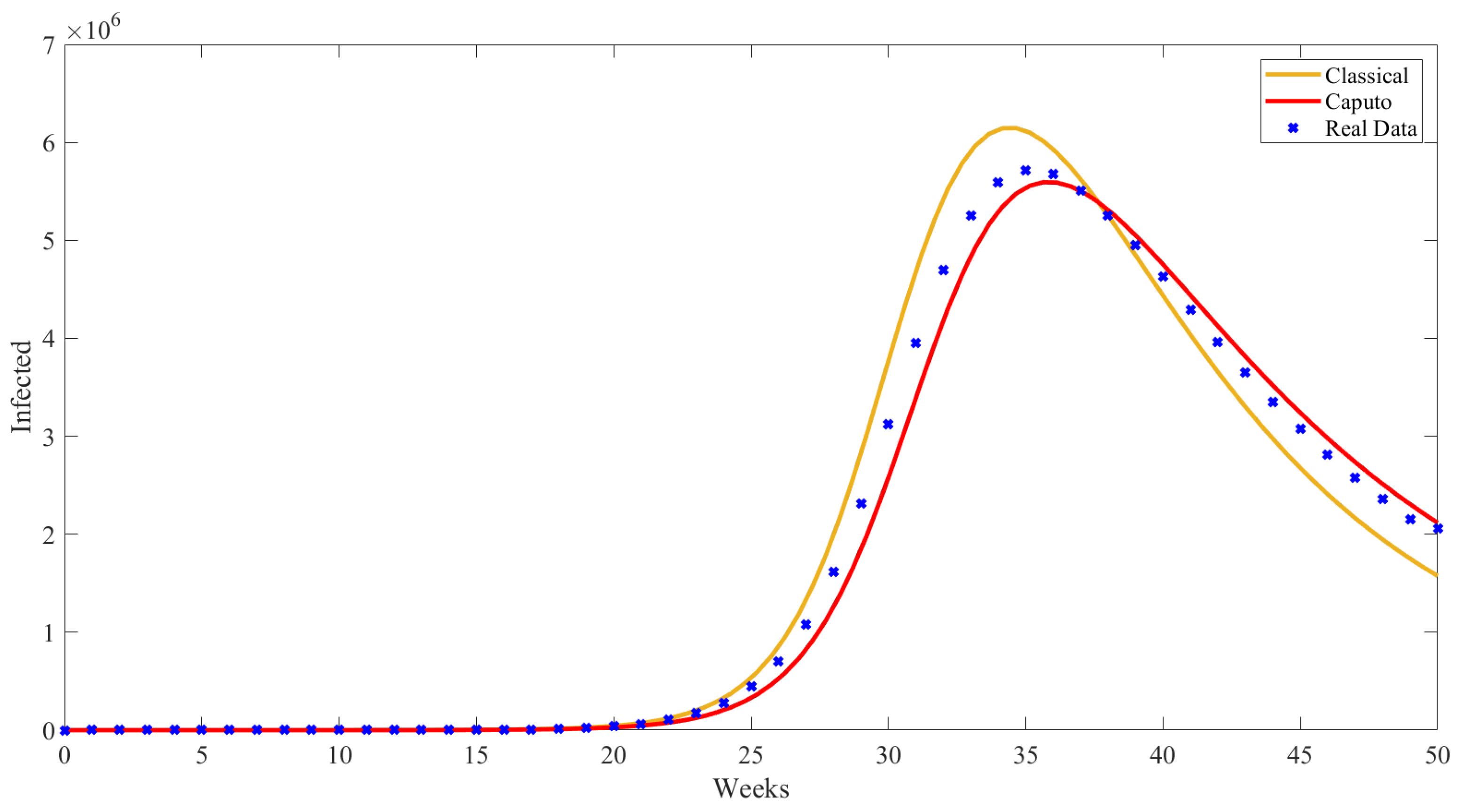
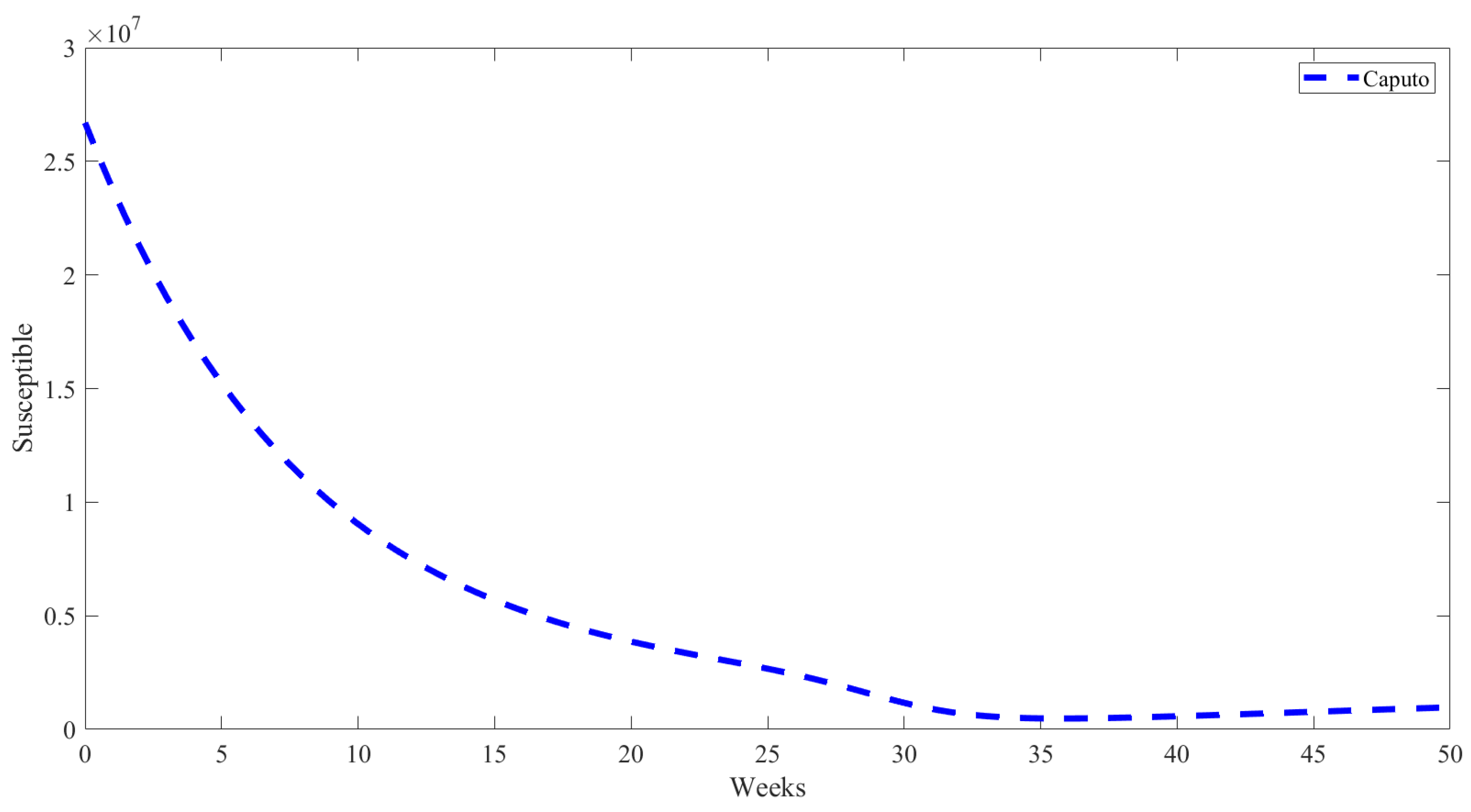
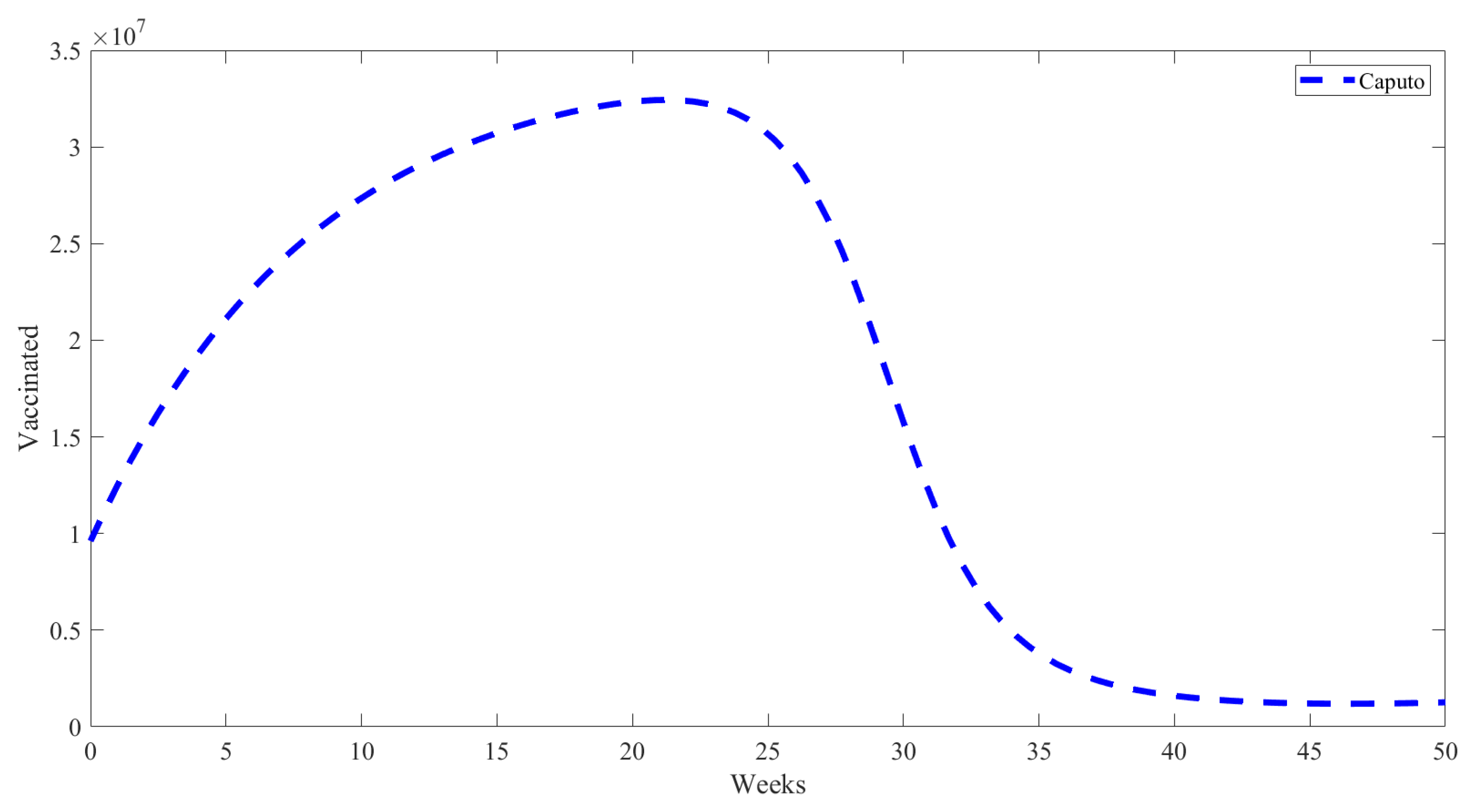
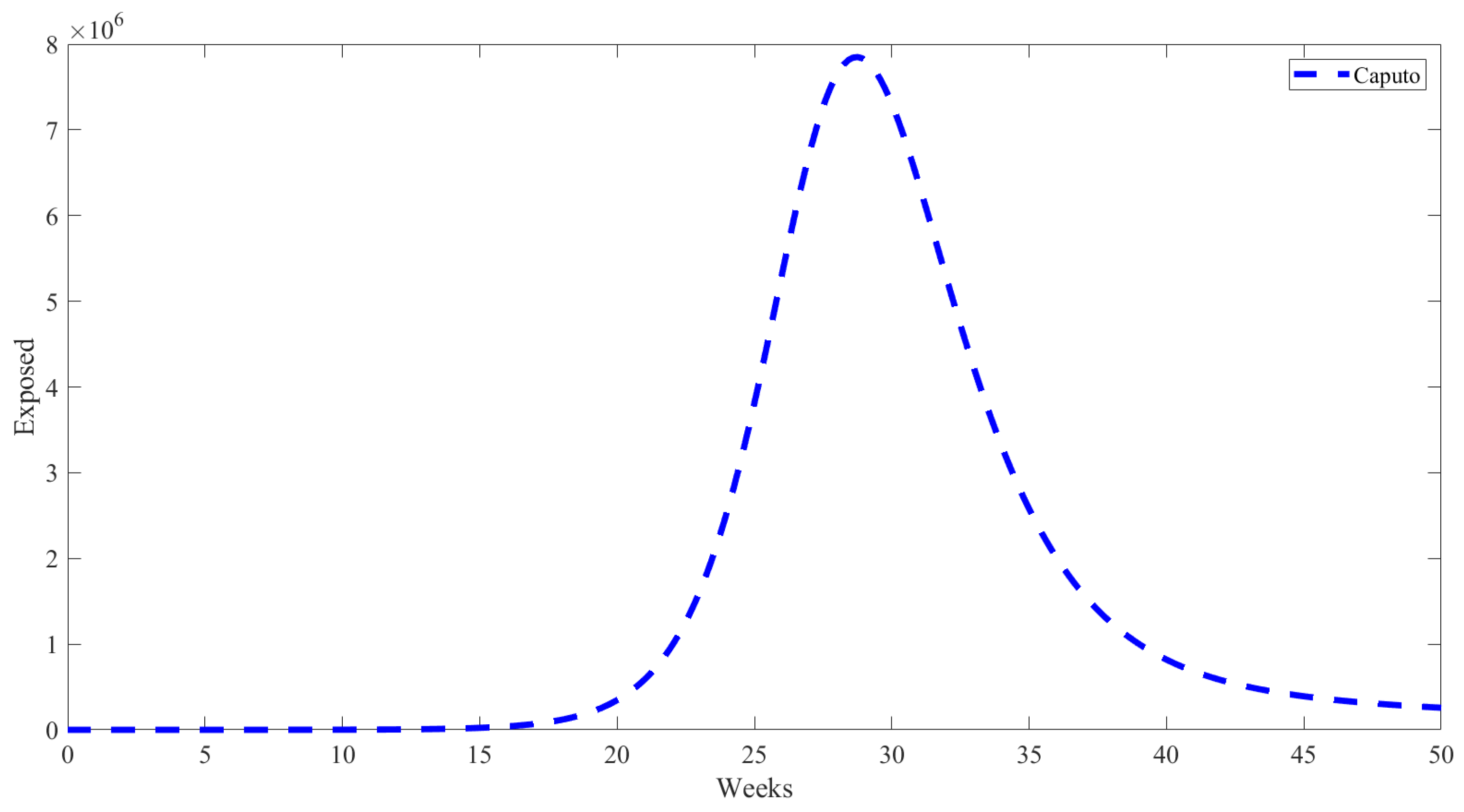
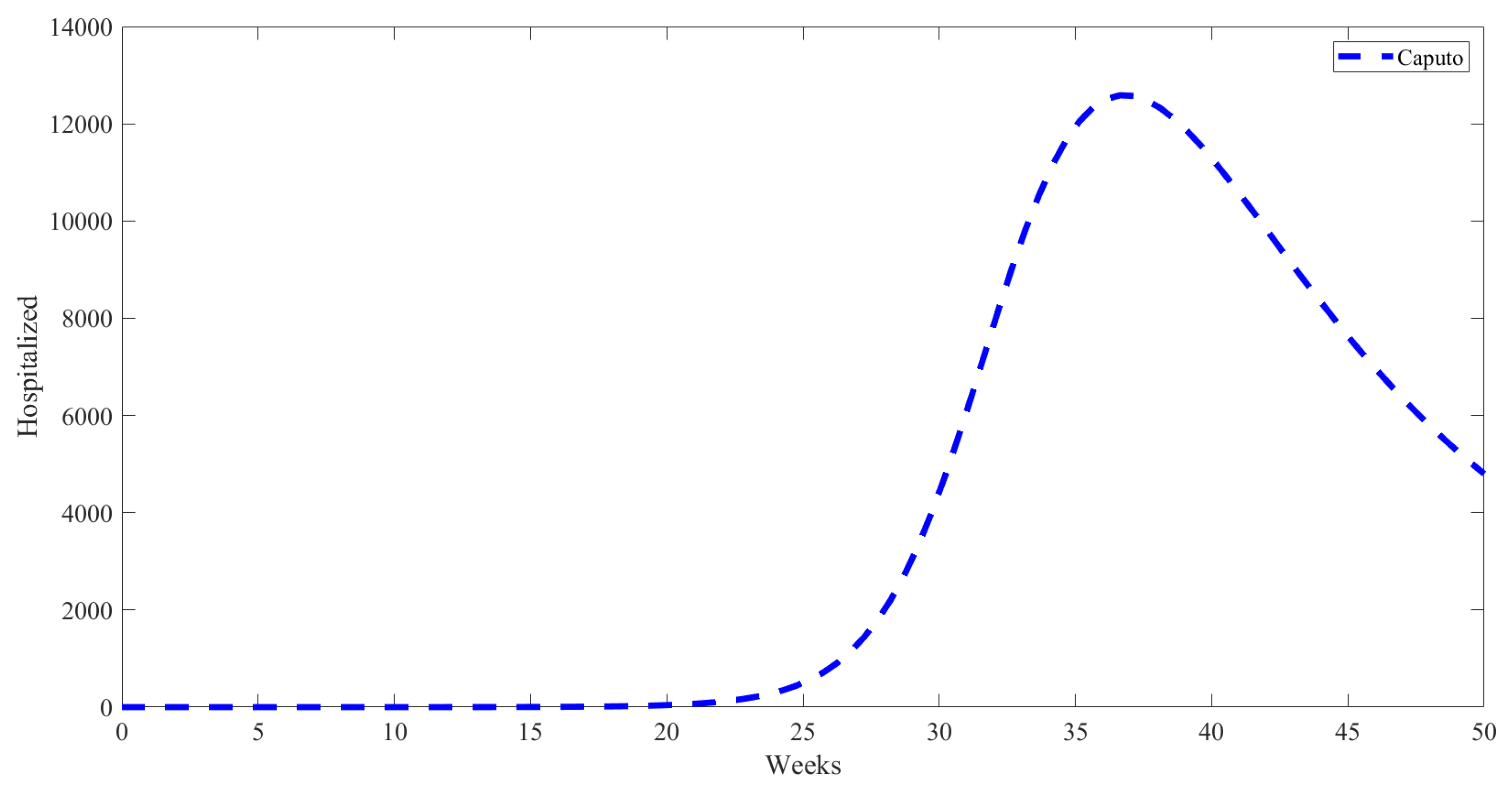
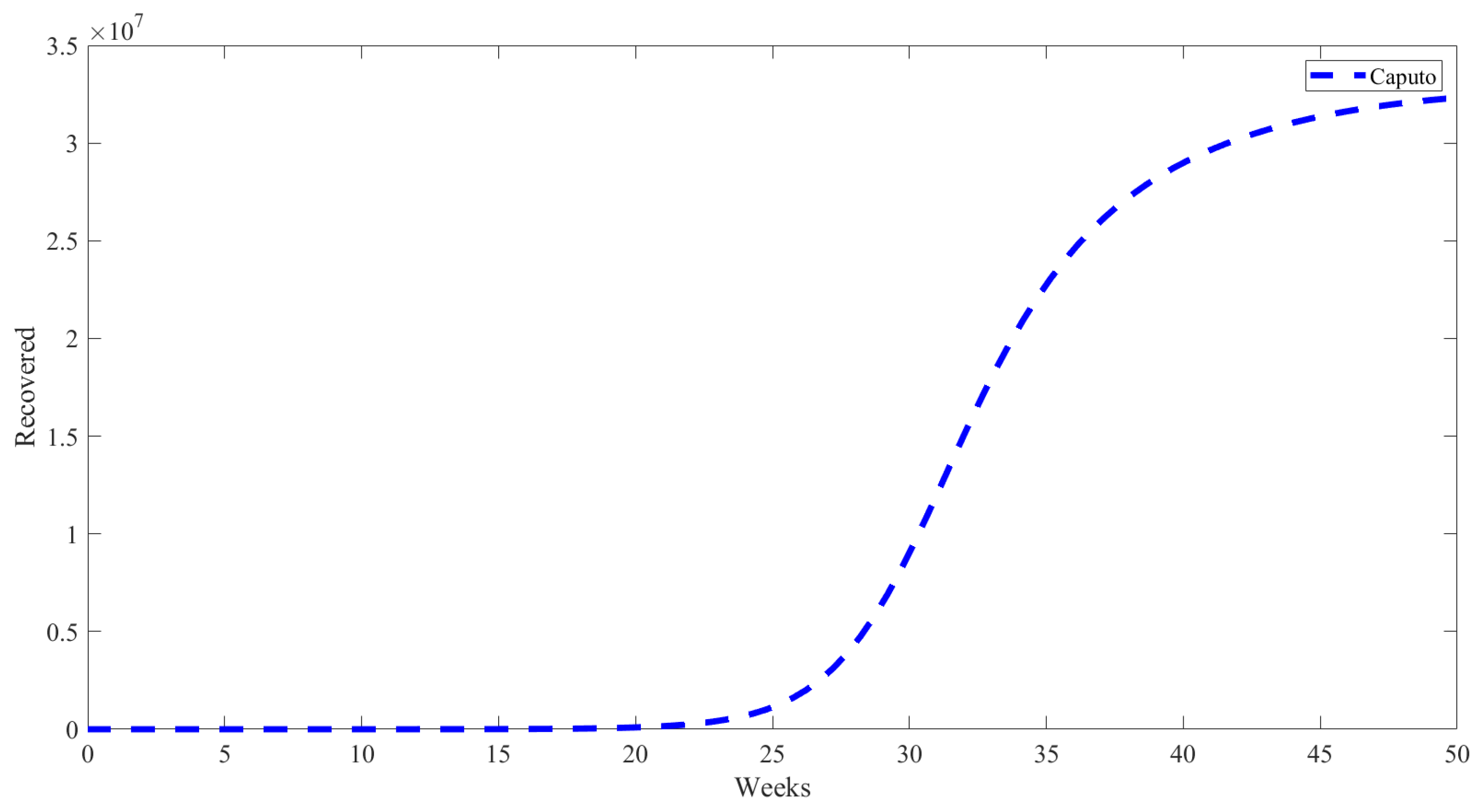
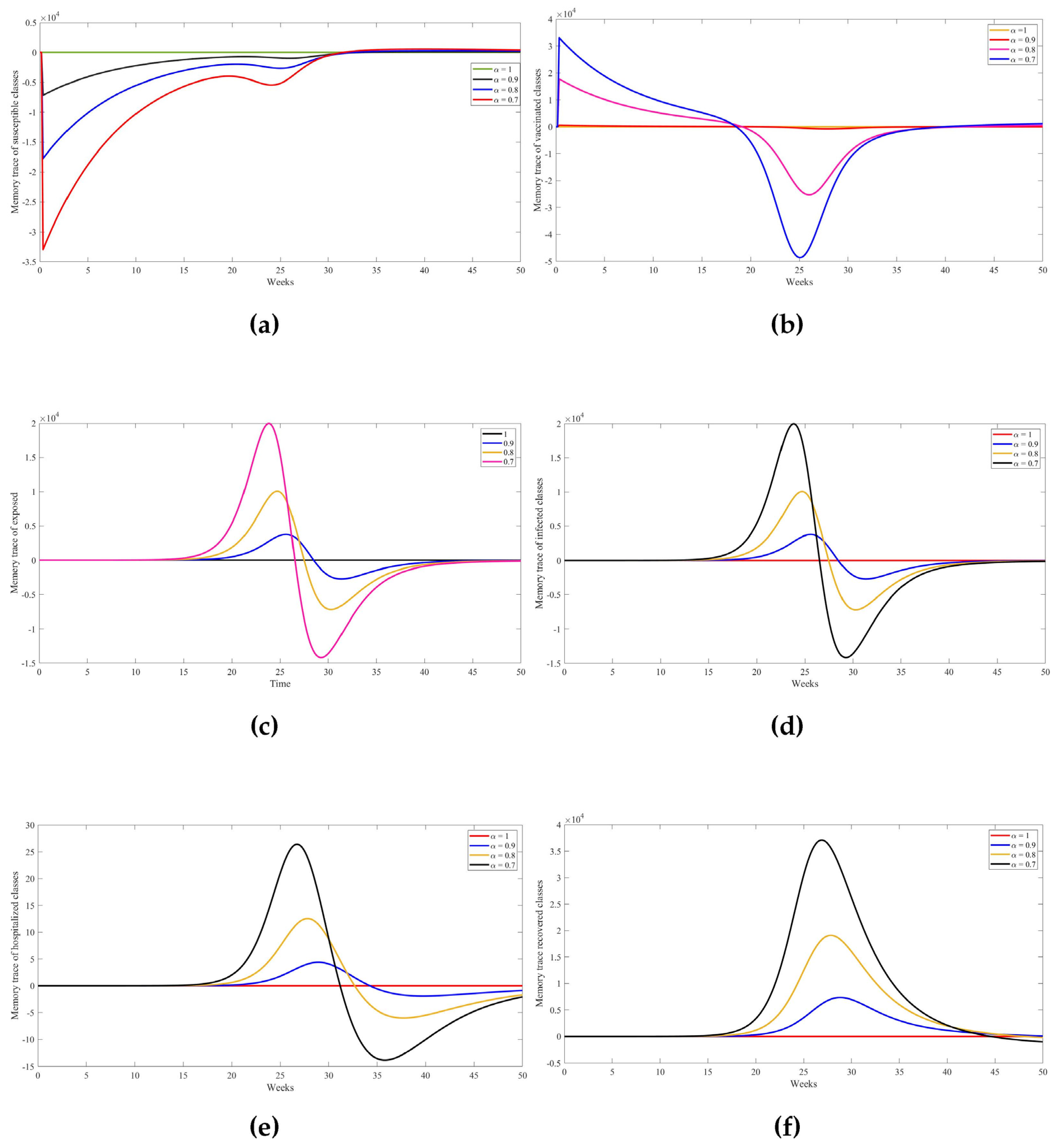
5. Numerical Results from Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saunders-Hastings, P.R.; Krewski, D. Reviewing the history of pandemic influenza: Understanding patterns of emergence and transmission. Pathogens 2016, 5, 66. [Google Scholar] [CrossRef] [PubMed]
- Barclay, W.; Openshaw, P. The 1918 Influenza Pandemic: One hundred years of progress, but where now? Lancet Respir. Med. 2018, 6, 588–589. [Google Scholar] [CrossRef] [PubMed]
- Moghadami, M. A Narrative Review of Influenza: A Seasonal and Pandemic Disease. Iran. J. Med. Sci. 2016, 42, 2–13. [Google Scholar]
- Dunning, J.; Thwaites, R.; Openshaw, P. Seasonal and pandemic influenza: 100 years of progress, still much to learn. Mucosal Immunol. 2020, 13, 566–573. [Google Scholar] [CrossRef] [PubMed]
- Monto, A.S.; Gravenstein, S.; Elliott, M.; Colopy, M.; Schweinle, J. Clinical Signs and Symptoms Predicting Influenza Infection. Arch. Intern. Med. 2000, 160, 3243–3247. [Google Scholar] [CrossRef] [PubMed]
- Paules, C.; Subbarao, K. Influenza. Lancet 2017, 390, 697–708. [Google Scholar] [CrossRef] [PubMed]
- Pleschka, S. Overview of influenza viruses. In Swine Influenza; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–20. [Google Scholar]
- Statista. Saudi Arabia: Life Expectancy at Birth from 2011 to 2022. Available online: https://www.statista.com/statistics/262477/life-expectancy-at-birth-in-saudi-arabia/ (accessed on 27 May 2024).
- Quirouette, C.; Younis, N.P.; Reddy, M.B.; Beauchemin, C.A.A. A mathematical model describing the localization and spread of influenza A virus infection within the human respiratory tract. PLoS Comput. Biol. 2020, 16, 1–29. [Google Scholar] [CrossRef]
- Dobrovolny, H.M.; Reddy, M.B.; Kamal, M.A.; Rayner, C.R.; Beauchemin, C.A.A. Assessing mathematical models of influenza infections using features of the immune response. PLoS ONE 2013, 8, e57088. [Google Scholar] [CrossRef] [PubMed]
- Boianelli, A.; Nguyen, V.K.; Ebensen, T.; Schulze, K.; Wilk, E.; Sharma, N.; Stegemann-Koniszewski, S.; Bruder, D.; Toapanta, F.R.; Guzmán, C.A.; et al. Modeling influenza virus infection: A roadmap for influenza research. Viruses 2015, 7, 5274–5304. [Google Scholar] [CrossRef]
- Handel, A.; Liao, L.E.; Beauchemin, C.A. Progress and trends in mathematical modelling of influenza A virus infections. Curr. Opin. Syst. Biol. 2018, 12, 30–36. [Google Scholar] [CrossRef]
- Rvachev, L.A.; Longini, I.M. A mathematical model for the global spread of influenza. Math. Biosci. 1985, 75, 3–22. [Google Scholar] [CrossRef]
- Kanyiri, C.W.; Mark, K.; Luboobi, L. Mathematical Analysis of Influenza A Dynamics in the Emergence of Drug Resistance. Comput. Math. Methods Med. 2018, 2018, 2434560. [Google Scholar] [CrossRef]
- Malek, A.; Hoque, A. Mathematical modeling of the infectious spread and outbreak dynamics of avian influenza with seasonality transmission for chicken farms. Comp. Immunol. Microbiol. Infect. Dis. 2024, 104, 102108. [Google Scholar] [CrossRef] [PubMed]
- Chlif, S.; Aissi, W.; Bettaieb, J.; Kharroubi, G.; Nouira, M.; Yazidi, R.; El Moussi, A.; Maazaoui, L.; Slim, A.; Ben Salah, A.; et al. Modelling of seasonal influenza and estimation of the burden in Tunisia. EMHJ-East. Mediterr. Health J. 2016, 22, 459–466. [Google Scholar] [CrossRef]
- Evirgen, F.; Uçar, S.; Evirgen, F.; Özdemir, N. Modelling Influenza A disease dynamics under Caputo-Fabrizio fractional derivative with distinct contact rates. Math. Model. Numer. Simul. Appl. 2023, 3, 58–73. [Google Scholar] [CrossRef]
- Yavuz, M.; Bonyah, E. New approaches to the fractional dynamics of schistosomiasis disease model. Phys. A Stat. Mech. Its Appl. 2019, 525, 373–393. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Nisar, K.S.; Ahmad, D.; Ahmad, A.; Kamangar, S.; Saleel, C.A. Epidemiological analysis of fractional order COVID-19 model with Mittag-Leffler kernel. AIMS Math. 2022, 7, 756–783. [Google Scholar] [CrossRef]
- Joshi, H.; Jha, B.K. Chaos of calcium diffusion in Parkinson’s infectious disease model and treatment mechanism via Hilfer fractional derivative. Math. Model. Numer. Simul. Appl. 2021, 1, 84–94. [Google Scholar] [CrossRef]
- Bonyah, E.; Yavuz, M.; Baleanu, D.; Kumar, S. A robust study on the listeriosis disease by adopting fractal-fractional operators. Alex. Eng. J. 2022, 61, 2016–2028. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Solitons Fractals 2022, 157, 111954. [Google Scholar] [CrossRef]
- Ahmed, I.; Akgül, A.; Jarad, F.; Kumam, P.; Nonlaopon, K. A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Math. Model. Numer. Simul. Appl. 2023, 3, 170–187. [Google Scholar] [CrossRef]
- Yavuz, M.; Özköse, F.; Susam, M.; Kalidass, M. A New Modeling of Fractional-Order and Sensitivity Analysis for Hepatitis-B Disease with Real Data. Fractal Fract. 2023, 7, 165. [Google Scholar] [CrossRef]
- Özköse, F. Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data. Fractal Fract. 2023, 7, 719. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Qureshi, S.; Soomro, A.; Abu Arqub, O.; Senol, M. Comparative analysis of classical and Caputo models for COVID-19 spread: Vaccination and stability assessment. Fixed Point Theory Algorithms Sci. Eng. 2024, 2024, 1–23. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophys. J. R. Astron. Soc. 2007, 13, 529–539. [Google Scholar] [CrossRef]
- Ma, W.; Ma, N.; Dai, C.; Chen, Y.; Wang, X. Fractional modeling and optimal control strategies for mutated COVID-19 pandemic. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Cori, A.; Valleron, A.-J.; Carrat, F.; Tomba, G.S.; Thomas, G.; Boëlle, P.-Y. Estimating influenza latency and infectious period durations using viral excretion data. Epidemics 2012, 4, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Abdoon, M.A.; Saadeh, R.; Berir, M.; EL Guma, F.; Ali, M. Analysis, modeling and simulation of a fractional-order influenza model. Alex. Eng. J. 2023, 74, 231–240. [Google Scholar] [CrossRef]
- den Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys. A Stat. Mech. Its Appl. 2019, 526, 121127. [Google Scholar] [CrossRef]
- Ali, M.; Alzahrani, S.M.; Saadeh, R.; Abdoon, M.A.; Qazza, A.; Al-Kuleab, N.; EL Guma, F.; Ali, M.; Alzahrani, S.M.; Saadeh, R.; et al. Modeling COVID-19 spread and non-pharmaceutical interventions in South Africa: A stochastic approach. Sci. Afr. 2024, 24, e02155. [Google Scholar] [CrossRef]
- Saadeh, R.; Abdoon, M.A.; Qazza, A.; Berir, M.; EL Guma, F.; Al-Kuleab, N.; Degoot, A.M. Mathematical modeling and stability analysis of the novel fractional model in the Caputo derivative operator: A case study. Heliyon 2024, 10, e26611. [Google Scholar] [CrossRef]
- Abdulkream Alharbi, S.; A. Abdoon, M.; Saadeh, R.; Alsemiry, R.D.; Allogmany, R.; Berir, M.; EL Guma, F. Modeling and analysis of visceral leishmaniasis dynamics using fractional-order operators: A comparative study. Math. Methods Appl. Sci. 2024, 47, 9918–9937. [Google Scholar] [CrossRef]
- EL Gumaa, F.; Abdoon, M.A.; Qazza, A.; Saadeh, R.; Arishi, M.A.; Degoot, A.M. Analyzing the Impact of Control Strategies on Visceral Leishmaniasis: A Mathematical Modeling Perspective. Eur. J. Pure Appl. Math. 2024, 17, 1213–1227. [Google Scholar] [CrossRef]
- Alzahrani, S.M.; Saadeh, R.; Abdoon, M.A.; Qazza, A.; Guma, F.E.; Berir, M. Numerical simulation of an influenza epidemic: Prediction with fractional SEIR and the ARIMA model. Appl. Math. 2024, 18, 1–12. [Google Scholar]
- Khan, M.S.; Ali, A.; Suhail, M.; Alotaibi, E.S.; Alsubaie, N.E. On the estimation of ridge penalty in linear regression: Simulation and application. Kuwait J. Sci. 2024, 51, 100273. [Google Scholar] [CrossRef]
- Albishri, S.B.; Albednah, F.A.; Alenazi, N.S.; Alsubaie, N.E.; Elserafy, O.S. National assessment of emergency staff level of practice in the management of forensic evidence. Forensic Sci. Res. 2023, 8, 265–273. [Google Scholar] [CrossRef]
- Alhuzaim, W.M.; Alojayri, A.M.; Albednah, F.A.; Alshehri, F.F.; Alomari, M.S.; Alyousef, M.A.; Alsubaie, N.E. Impact of work hours on the quality of life of adult employees with irritable bowel syndrome in Saudi Arabia. Cureus 2022, 14, e31983. [Google Scholar] [CrossRef]
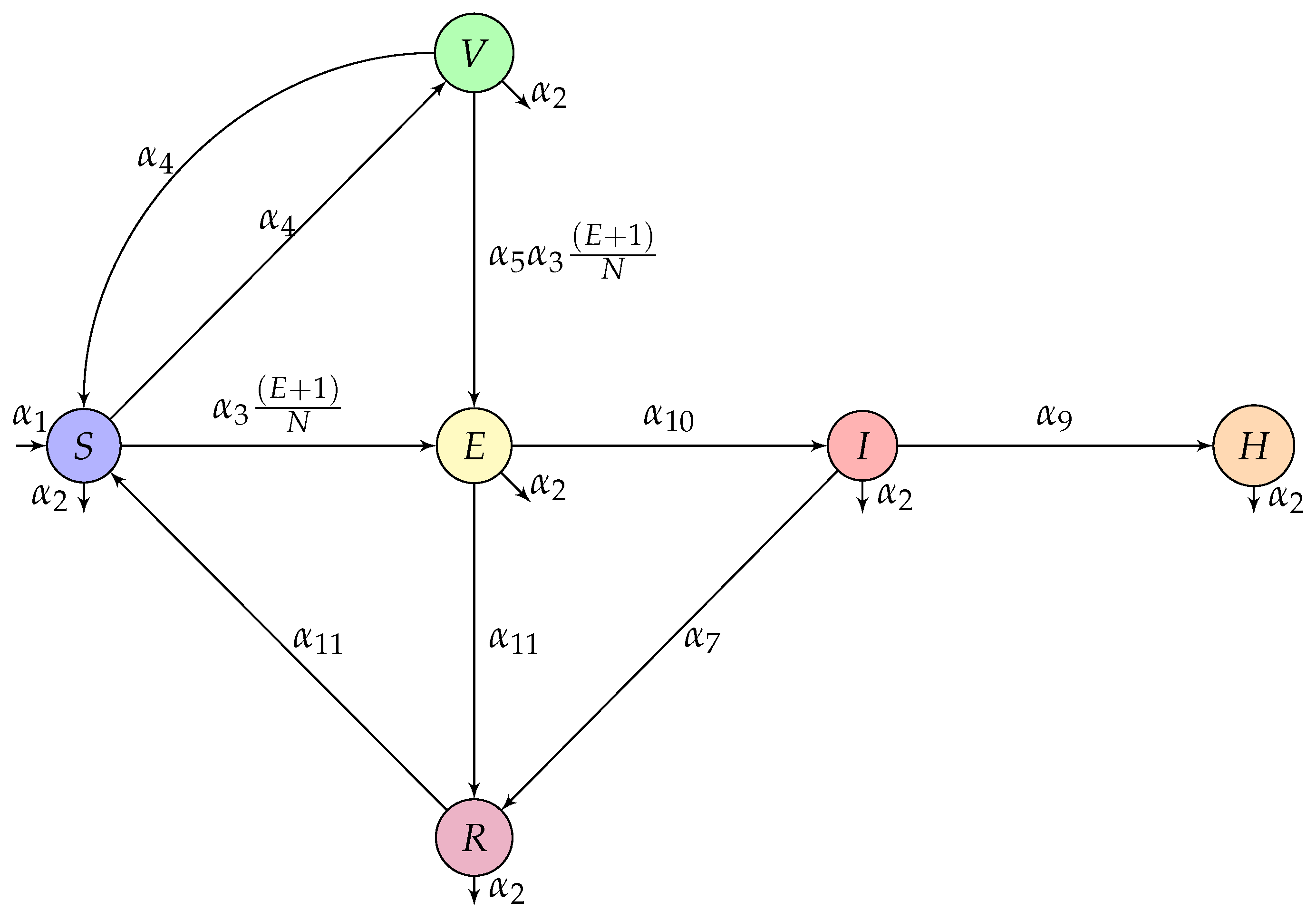
| Parameter | Description | Value | Source |
|---|---|---|---|
| Recruitment rate of individuals into the population | 0.114 | Fitted | |
| Natural death rate | 0.000256 | [8] | |
| Average effective contact rate | 0.858 | Fitted | |
| Vaccination rate | 0.114 | Fitted | |
| Vaccine inefficacy | 1.00 | Fitted | |
| Average hospitalization rate | 0.0015 | Fitted | |
| Recovery rate for infected individuals | 2.6 | Fitted | |
| Recovery rate for exposed individuals | 0.34 | Fitted | |
| Recovery rate for hospitalized individuals | 0.68 | Fitted | |
| Average latent or incubation period | 1.6 day | [30] | |
| Rate at which individuals lose immunity | 50 days | [8] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
E. Alsubaie, N.; EL Guma, F.; Boulehmi, K.; Al-kuleab, N.; A. Abdoon, M. Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus. Symmetry 2024, 16, 929. https://doi.org/10.3390/sym16070929
E. Alsubaie N, EL Guma F, Boulehmi K, Al-kuleab N, A. Abdoon M. Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus. Symmetry. 2024; 16(7):929. https://doi.org/10.3390/sym16070929
Chicago/Turabian StyleE. Alsubaie, Nahaa, Fathelrhman EL Guma, Kaouther Boulehmi, Naseam Al-kuleab, and Mohamed A. Abdoon. 2024. "Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus" Symmetry 16, no. 7: 929. https://doi.org/10.3390/sym16070929
APA StyleE. Alsubaie, N., EL Guma, F., Boulehmi, K., Al-kuleab, N., & A. Abdoon, M. (2024). Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus. Symmetry, 16(7), 929. https://doi.org/10.3390/sym16070929








