Spherical Superpixel Segmentation with Context Identity and Contour Intensity

Abstract

Superpixel segmentation is a popular preprocessing tool in the field of image processing. Nevertheless, conventional planar superpixel generation algorithms are inadequately suited for segmenting symmetrical spherical images due to the distinctive geometric differences. In this paper, we present a novel superpixel algorithm termed context identity and contour intensity (CICI) that is specifically tailored for spherical scene segmentation. By defining a neighborhood range and regional context identity, we propose a symmetrical spherical seed-sampling method to optimize both the quantity and distribution of seeds, achieving evenly distributed seeds across the panoramic surface. Additionally, we integrate the contour prior to superpixel correlation measurements, which could significantly enhance boundary adherence across different scales. By implementing the two-fold optimizations on the non-iterative clustering framework, we achieve synergistic CICI to generate higher-quality superpixels. Extensive experiments on the public dataset confirm that our work outperforms the baselines and achieves comparable results with state-of-the-art superpixel algorithms in terms of several quantitative metrics.

1. Introduction

The concept of a superpixel was introduced by Ren et al. [1] in 2003, with the aim of grouping similar pixels in a localized context of an image to extract coherent region-level features. From then on, superpixel segmentation gradually became a popular preprocessing tool for various advanced computer vision tasks so as to boost the running efficiency. The emerging superpixel algorithms have found applications in diverse fields, including semantic segmentation [2,3,4], object detection and tracking [5,6,7,8], robot vision [9], depth estimation [10], etc. Some interesting superpixel segmentation algorithms are equally worthy of attention, such as those based on metaheuristic techniques [11], agents [12], and cellular automata [13].

With the advancement of imaging technology, 360° panoramic cameras have unlocked novel visual representations of real-world scenarios. These cameras can capture virtual reality (VR) images, providing users with a comprehensive observation of surrounding information through a 360° horizontal and 180° vertical view. Nevertheless, most image processing algorithms have traditionally been designed for planar images, posing significant challenges in directly applying conventional approaches to spherical image analysis, especially for superpixel segmentation. In recent years, the increasing significance of spherical image processing in VR has prompted researchers to investigate superpixel applications. Zhao et al. introduce the spherical SLIC (SphSLIC) algorithm in their work [14]. They initialize superpixel seeds using Hammersley sampling [15] to narrow the search range for K-means clustering and employ cosine similarity as the distance metric between pixels and seeds. Both optimizations enhance the suitability of SphSLIC superpixels for spherical images. Similarly, spherical mean shift (SphMS) and spherical ETPS (SphETPS) [16] are proposed based on SphSLIC, with emphasis on distance metrics, neighborhood extent, and boundary issues. Another representative work is spherical shortest path-based superpixels (SphSPS) [17] proposed by Giraud et al., which trace the shortest path between a pixel and a seed on a spherical image. It utilizes color information and contour weights along the path to enhance segmentation accuracy and regularity. To meet the demand for real-time performance, Silveira et al. optimized two planar image superpixel algorithms: simple non-iterative clustering (SNIC) [18] and superpixel hierarchy (SH) [19]. They then propose two novel spherical image superpixel algorithms, spherical SNIC (SSNIC) and spherical SH (SSH) [20], which inherit the balanced performance of accuracy and efficiency.

Typically, spherical images are commonly subjected to equirectangular projection (ERP) [21] or cube map projection (CMP) [22], followed by relevant calculations, and the results are subsequently projected back onto the spherical image. Most of the current studies primarily focus on ERP images after equirectangular projection. However, it is worth noting that spherical images inherently represent a closed geometric sphere. When these images undergo ERP, they artificially introduce open regions and significant distortions, particularly at the top and bottom sides. Directly applying planar superpixel algorithms to ERP images cannot generate superpixels with continuous contour boundaries in their original closed regions when projecting the result back onto the spherical image, especially near its poles. As depicted in Figure 1a,c, simple linear clustering (SLIC) [23] performed on planar images, and the spherical superpixel algorithm (SphSLIC) [14] specialized for spherical images on ERP projections, respectively, demonstrate their respective segmentation results for comparison purposes on ERP images. In Figure 1b,d, the label maps of SLIC and SphSLIC projected back onto the spherical image show the disparities. Specifically, Figure 1b displays irregular superpixels in the black rectangular box, with open and discontinuous contours in the black elliptical box, whereas Figure 1d demonstrates superior performance.

Some researchers have applied superpixel algorithms to spherical image processing. Cabral et al. [24] introduced a superpixel algorithm for processing spherical images in 3D reconstruction. Hao et al. [25] developed a change detection algorithm that leverages superpixels to mitigate resolution degradation issues. However, these approaches usually overlook the inherent differences between spherical and planar images, resulting in superpixels that retain the aforementioned limitations and consequently impact performance. In addition, artificially processed spherical projection maps typically exhibit non-uniform content distribution, with a concentration of content in the equatorial region [18]. Existing superpixel algorithms tend to neglect this aspect and fail to adaptively adjust superpixel sizes based on content sparsity, leading to inadequate segmentation in smaller regions. Moreover, when different objects exhibit similar colors, clear contour boundaries may not always be present, posing challenges to segmentation accuracy.

Based on these considerations, a structurally optimized superpixel segmentation algorithm is proposed, termed context identity and contour intensity (CICI). In this work, we have adopted the fundamental framework of simple non-iterative clustering (SNIC). The key idea revolves around optimizing the conventional framework, with particular emphasis on enhancing the initialization phase and refining the similarity measurement stage. In the initialization phase, we consider the distinctive geometric attributes of spherical images and the context identity, thereby redefining the merging and emerging operations for seeds. By utilizing the proposed inter-pixel similarity measurement, we then employed a contour intensity constraint to efficiently discriminate between two pixels with different labels. The integration of the aforementioned strategies proves effectiveness not only in the context of spherical images but also extends to yielding accurate clustering results for planar images. This further exemplifies that our proposal encompasses a comprehensive optimization strategy for the framework rather than being solely an algorithmic refinement.

In the context of prior research, our contributions can be summarized as follows:

• An efficient seed-sampling method is proposed by defining a neighborhood range and regional context identity, which could optimize both the quantity and distribution of seeds, leading to evenly distributing seeds across the panoramic surface.
• A subtle inter-pixel correlation measurement is put forward to enhance boundary adherence across different scales, thereby integrating the contour intensity to pixel-superpixel correlation measurements.
• A context identity and contour intensity strategy is introduced to enhance the overall performance within a non-iterative clustering framework. Extensive experiments on two datasets were conducted, confirming its feasibility and comparable results.

The outline of this work is organized as follows: In Section 2, the preliminaries on SNIC superpixel algorithm are reviewed in brief. In Section 3, the implementation of CICI method is explained systematically. Experiments and analyses are explicated in Section 4. Finally, we give the conclusions in Section 5.

2. Preliminaries on SNIC

In this section, we will introduce the SNIC algorithm in detail. Since the proposed CICI can be regarded as a variant of SNIC, we briefly introduce the latter before entering into the subject. Given a visual image ${\rm I}={\left\{p_i\right\}}_{i=1}^N$ consisting of $N$ pixels and a pre-defined number of superpixel $K$, SNIC first divides $I$ into $K$ uniform grids, each approximately covering an area of $N/K$ and the initial seeds are placed at the center of each grid with an interval $s=\sqrt{N/K}$. Let us denote by $C_i=\left[l_i,a_i,b_i\right]$ and $P_i=\left[x_i,y_i\right]$ the CIELAB color and Euclidean position vector of each pixel $p_i\in I$, respectively. The color and spatial information of $k-\mathrm{th}$ seed $s_k$ are denoted as $C_k^{\mathrm{s}}$ and $P_k^{\mathrm{s}}$, respectively (note that the index $k$ in $C_k^{\mathrm{s}}$ and $P_k^{\mathrm{s}}$ is the index of the seed $s_k$ rather than the index of pixel $p_k$). SNIC measures the correlation of a pixel and a seed by calculating the feature distance $d_{i,k}$ between $p_i$ and $s_k$, and then assigning labels according to the global minimal distance as follows:

$$D\left(p_i,s_k\right)=\sqrt{{\displaystyle \frac{{\Vert C_i-C_k^{\mathrm{s}}\Vert }_2^2}{s}}+{\displaystyle \frac{{\Vert P_i-P_k^{\mathrm{s}}\Vert }_2^2}{m}}}$$

(1)

where $s=\sqrt{N/K}$ and the parameter $m$ are pre-set to control the compactness of superpixels. A greater $m$ enhances the significance of spatial distance, resulting in more compact superpixels. Conversely, when color differences play a more dominant role, superpixels become more sensitive to color changes, leading to diminished compactness. The aforementioned process is shared between SNIC and SLIC algorithms. On the other hand, a key distinction lies in the utilization of a priority queue in SNIC instead of multiple iterations in SLIC, which enables the former to effectively reduce the time complexity of the process. The non-iterative label assignment steps of the SNIC algorithm can be summarized as follows:

Step 1: Initialize a minimum priority queue $Q$ to store the vector nodes corresponding to all pixels and seeds, and a label map $L={\left\{L\left(p_i\right)\right\}}_{i=1}^N$ to store the label of each pixel within image $I$. For each vector node $e$, it records the color and spatial information, as well as the pixel-seed distance calculated by Equation (1), which acts as the key value for sorting in $Q$. For each seed $s_k$, a vector node $e_k^{\mathrm{s}}=\left\{P_k^{\mathrm{s}},C_k^{\mathrm{s}},k,d\right\}$ is defined and pushed onto $Q$. Since each seed is initially an image pixel, it acquires an initial label $k$ and establishes that $d=0$.

Step 2: Pop the element $e_i$ with the minimum $d$ from $Q$ if it exists. If the pixel $p_i$ corresponding to $e_i=\left\{P_i,C_i,k,D\left(p_i,s_k\right)\right\}$ is not labeled, then assign $L\left(s_k\right)=k$ to it and dynamically update the seed $s_k$ with $C_i$ and $P_i$ of $p_i$.

Step 3: Traverse the 8-neighboring pixel $p_j$ of $p_i$ successively. Determine if $p_j$ has been labeled. Then create a set $e_j=\left\{P_j,C_j,k,D\left(p_j,s_k\right)\right\}$ for pixel $p_j$ if it is not labeled. $e_j$ that corresponds to $p_j$ is then pushed onto $Q$.

Step 4: Repeat steps 2 and 3 until $Q$ is empty, and then output the label map $L$.

3. Method

The detailed introduction of the proposed CICI framework is presented in this section, and the overall processing flow is depicted in Figure 2.

Specifically, for an input ERP image in Figure 2a, CICI starts by extracting the corresponding contour map in Figure 2b. This process is implemented by the structured forest edge detection algorithm [26] to compute the regional context identity. A set of seeds is then generated through the Fibonacci sampling method [27], followed by the optimization of positions and existences, which is shown in Figure 2d,e. Finally, the refined seeds as well as the contour-perceptive distance metric are employed for superpixel segmentation within a non-iterative clustering framework.

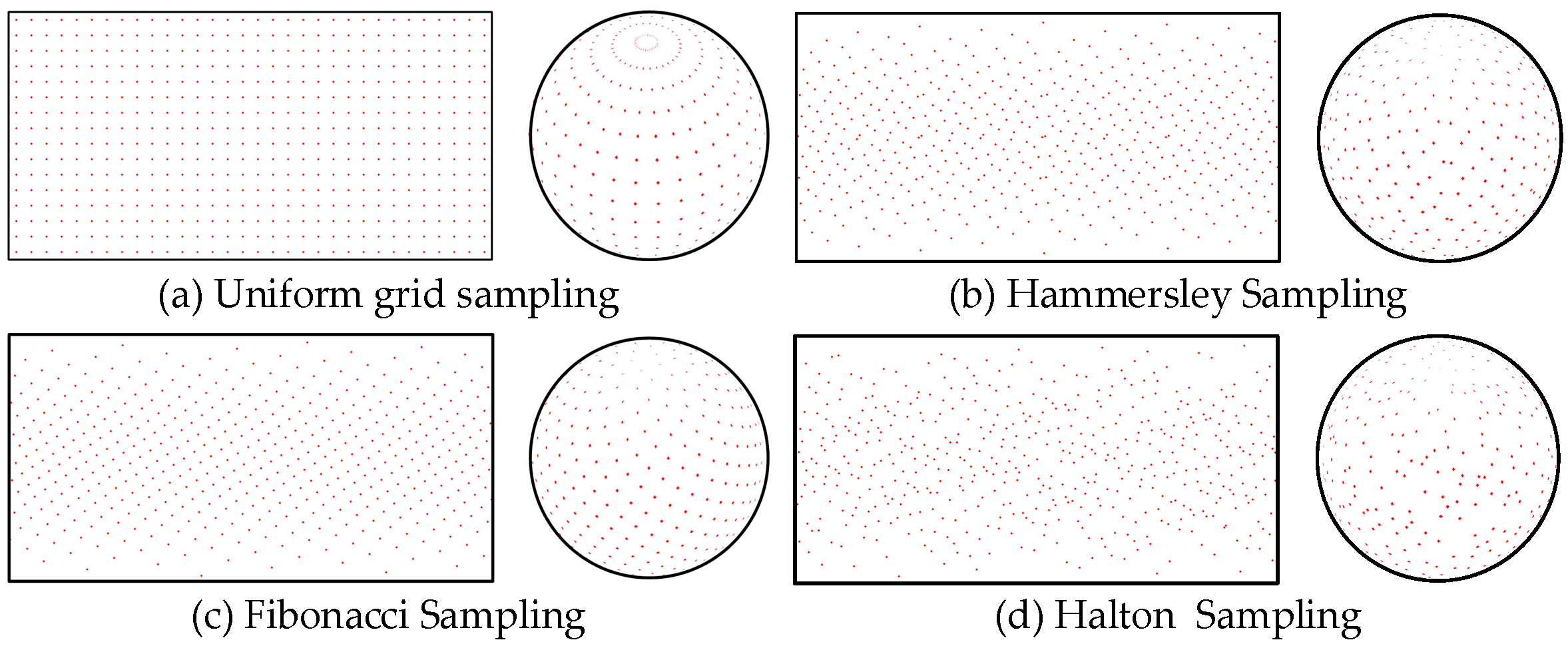
3.1. Sampling Strategies for Spherical Image

It is tough to directly initialize all seeds on the spherical image, according to previous research. Conventional approaches usually adopt a three-step strategy: converting the spherical image into an ERP image, sampling, and mapping back to the spherical image. It should be noted that there are an equal number of seeds on each latitude line of the spherical image. However, the radius of the latitude circle decreases when approaching the poles, resulting in a higher seed density near these regions. As shown in Figure 3a, if we initialize seeds on the ERP image in a SNIC-like manner, it would be unattainable to achieve a uniform distribution of seeds on the spherical image.

Currently, there are various sampling methods for spherical images, including geodesic sampling, Hammersley sampling, and Halton sampling [15]. The geodesic sampling method enables an approximately uniform distribution of seeds on spherical images. However, it is limited to generating only a specific number of subdivision-level-based sampling points rather than a specified number of seeds. On the other hand, despite Hammersley and Halton samplings supporting a fixed number of seeds, these seeds are randomly and uniformly distributed, as illustrated in Figure 3b,d.

To overcome the limitations of the aforementioned sampling methods, we introduce Fibonacci sampling that enables us to generate approximately uniform seeds on a spherical image with adjustable numbers. The procedure begins with the distribution of $K$ seeds on the ERP image, and the coordinates $\left(x_i,y_i\right)$ of these seeds are calculated as follows:

$$\left(x_i,y_i\right)=\left({\displaystyle \frac{i}{\phi }},{\displaystyle \frac{i}{K}}\right),i=0,1,2,\dots ,K-1$$

(2)

where $\phi =(1+\sqrt{5})/2$. Next, these seeds are mapped back to the spherical image by the following:

$$\{\begin{array}{l}X=\sin \left(\varphi \right)\cdot \cos \left(\theta \right)\hfill \\ Y=\sin \left(\theta \right)\cdot \sin \left(\varphi \right)\hfill \\ Z=\cos \left(\varphi \right)\hfill \end{array}$$

(3)

where $\theta =2\pi x$ and $\varphi =\arccos \left(1-2y\right)$. $\left(x,y\right)$ and $\left(X,Y,Z\right)$ are the coordinates of the seeds on the ERP and spherical image, respectively. Figure 3c demonstrates the distribution result.

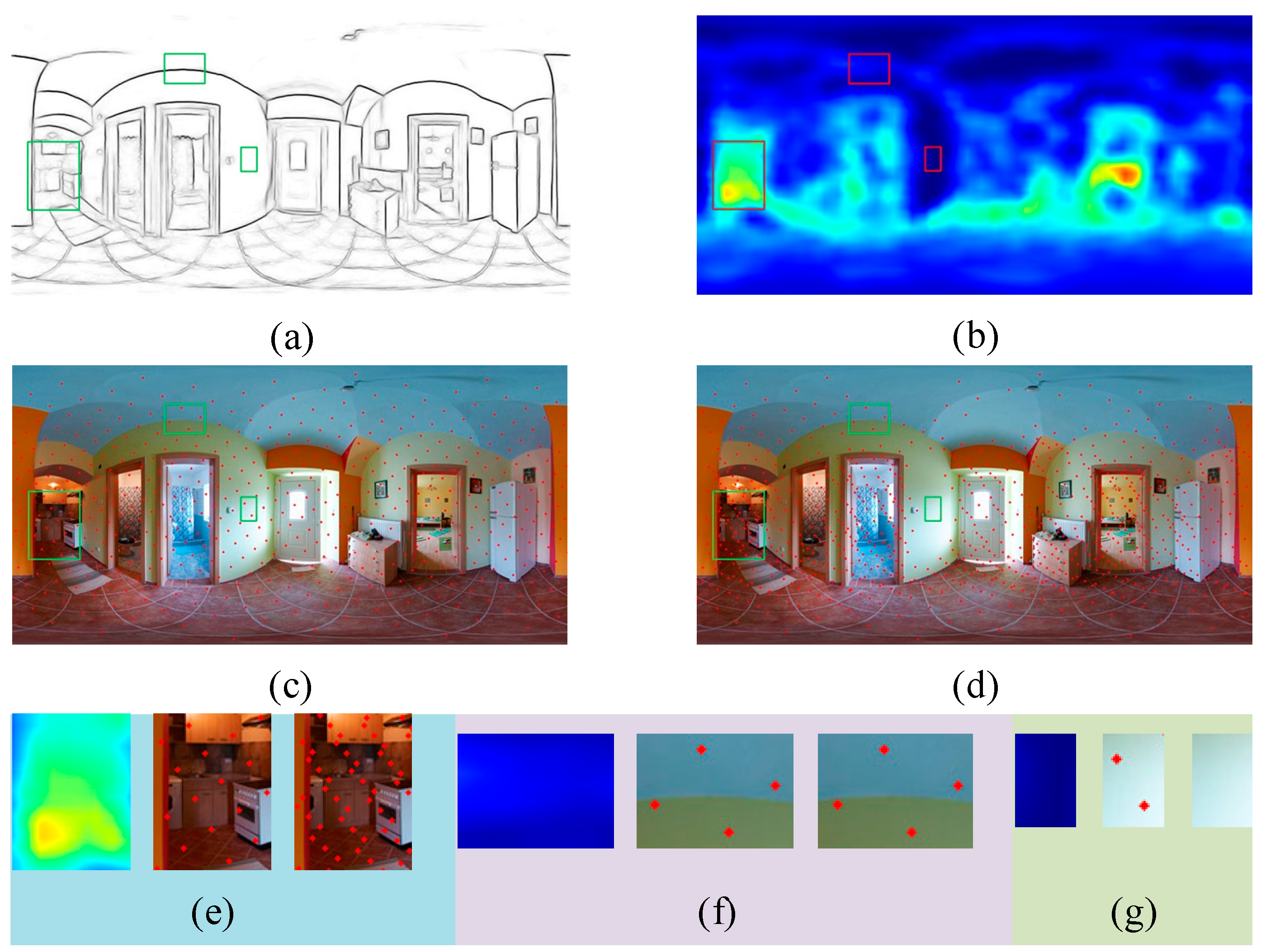
3.2. Optimized Initialization by Context Identity

This part presents a novel strategy for seed distribution based on Fibonacci sampling, which is shown in Figure 4. The local region context identity is computed based on the prior contour image, providing insight into the complexity of the region’s content. It is worth mentioning that context identity is reflected by content density, and there is no difference in its essence. To dynamically adjust the number of seeds in the local area according to content complexity, a five-step implementation is employed, which can be briefed as follows:

Step 1: Initialize seeds using Fibonacci sampling to achieve a uniform distribution on the spherical image (assuming the number of seeds is $K$).

Step 2: Determine the range of the region ${\left\{R_i\right\}}_{i=1}^K$ where the seeds ${\left\{s_k\right\}}_{k=1}^K$ are located.

$$R_i=\left\{\left[x,y\right]|x_i-{\displaystyle \frac{S}{\lambda sin\varphi }}\le x\le x_i+{\displaystyle \frac{S}{\lambda sin\varphi }},y_i-{\displaystyle \frac{S}{\lambda }}\le y\le y_i+{\displaystyle \frac{S}{\lambda }}\right\}$$

(4)

where $S=w/\sqrt{K\pi }$ is the initial size of each superpixel, $\varphi =y\pi /h$ is the pole angle on $y-\mathrm{th}$ row of the ERP image corresponding to the spherical image, $w$ and $h$ are the image width and height, respectively, $\lambda$ is a factor that regulates the overlap degree of adjacent areas, and $\lambda =1.5$ is taken in this paper.

Step 3: Calculate the context identity of region $R_i$ where seed $C_i$ is located. We utilize the structured forest edge detection algorithm to extract the contour of the original image, and the contour map is used as input in the form of a grayscale map. The context identity of region $R_i$ is calculated by the following:

$$D_i={\displaystyle \frac{P_{C_i}}{P_{N_i}}}$$

(5)

where $P_{C_i}$ represents the number of pixels in region $R_i$, with grayscale values less than $V_{th}$, with a default value of 150, and $P_{N_i}$ is the total number of pixels in $R_i$. The context density of the whole image is $D_{all}$, and the average context density of all regions ${\left\{R_i\right\}}_{i=1}^K$ is $\overline{D}$, which are calculated by the following:

$$D_{all}={\displaystyle \frac{P_{C_{all}}}{N}},\hspace{0.17em}\overline{D}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{i=1}^K{D}_i}$$

(6)

where $P_{C_{all}}$ is the number of pixels in the image with grayscale values less than $V_{th}$.

Step 4: The content complexity of all regions in the image can be divided into different levels according to the density information, which then guides the adjustment of seed number in the region. Define $D_{\max }=\max \left\{D_{all},\overline{D}\right\}$ and $D_{\min }=\min \left\{D_{all},\overline{D}\right\}$; if $D_i\ge D_{max}$, it indicates that the content complexity of the area is high; if $D_{min}<D_i<D_{max}$, the content complexity is moderate; if $D_i\le D_{min}$, the content complexity is low.

Step 5: Adjust the number of seeds in regions according to the determined complexity level in Step 4.

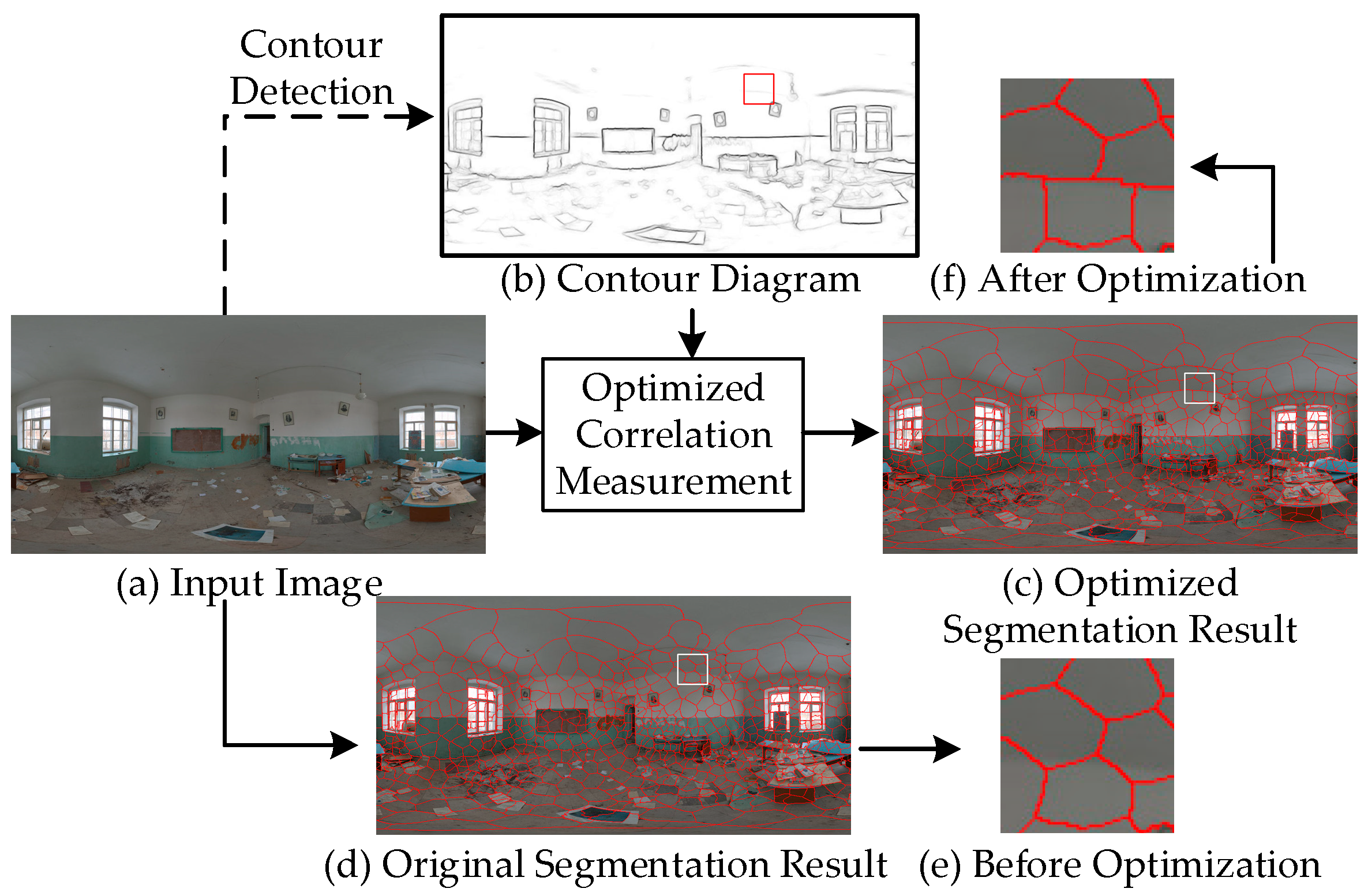
3.3. Optimized Correlation Measurement

This part presents an optimized correlation measurement. The correlation measurement between pixels plays an important role in the quality of the superpixel segmentation algorithm. In this paper, the distance measurement is improved by using the contour information in the contour map, so that the algorithm can accurately segment regions with less apparent boundaries.

The distance $D(p_i,s_i)$ between pixel $p_i$ and seed $s_i$ is shown as follows:

$$D\left(p_i,s_i\right)=\left(D_{lab}+\eta \cdot D_{xyz}\right)\cdot \left(1+\theta \cdot D_c\right)$$

(7)

where $D_{lab}$ is a measure of color difference between pixels, $D_{xyz}$ stands for measuring the spatial position between pixels, $\eta$ is the parameter that controls the distance weight, $D_c$ is a new metric component introduced by the contour diagram to indicate whether there is a contour between pixels, and $\theta$ is a weight parameter that controls the weight of the contour item. When $\theta =0$, $D(p_i,s_i)$ is similar to the distance metric of SNIC, each of the three metric components is described below:

• Distance measurement $D_{lab}$. The color component of pixel $p_i$ is $\left[l_{p_i},a_{p_i},b_{p_i}\right]$. The color component of seed $s_i$ is $\left[l_{s_i},a_{s_i},b_{s_i}\right]$, then $D_{lab}$ is defined as follows:

  $$D_{lab}=\sqrt{{\left(l_{s_i}-l_{p_i}\right)}^2+{\left(a_{s_i}-a_{p_i}\right)}^2+{\left(b_{s_i}-b_{p_i}\right)}^2}$$

  (8)
• Spatial distance metric $D_{xyz}$. The position mark of pixel $p_i$ on the spherical image is $[X_{p_i},Y_{p_i},Z_{p_i}]$. Similarly, the coordinate of seed $s_i$ on the spherical image is $[X_{s_i},Y_{s_i},Z_{s_i}]$. Therefore, $D_{xyz}$ is defined as follows:

  $$D_{xyz}=\sqrt{{\left(X_{s_i}-X_{p_i}\right)}^2+{\left(Y_{s_i}-Y_{p_i}\right)}^2+{\left(Z_{s_i}-Z_{p_i}\right)}^2}$$

  (9)
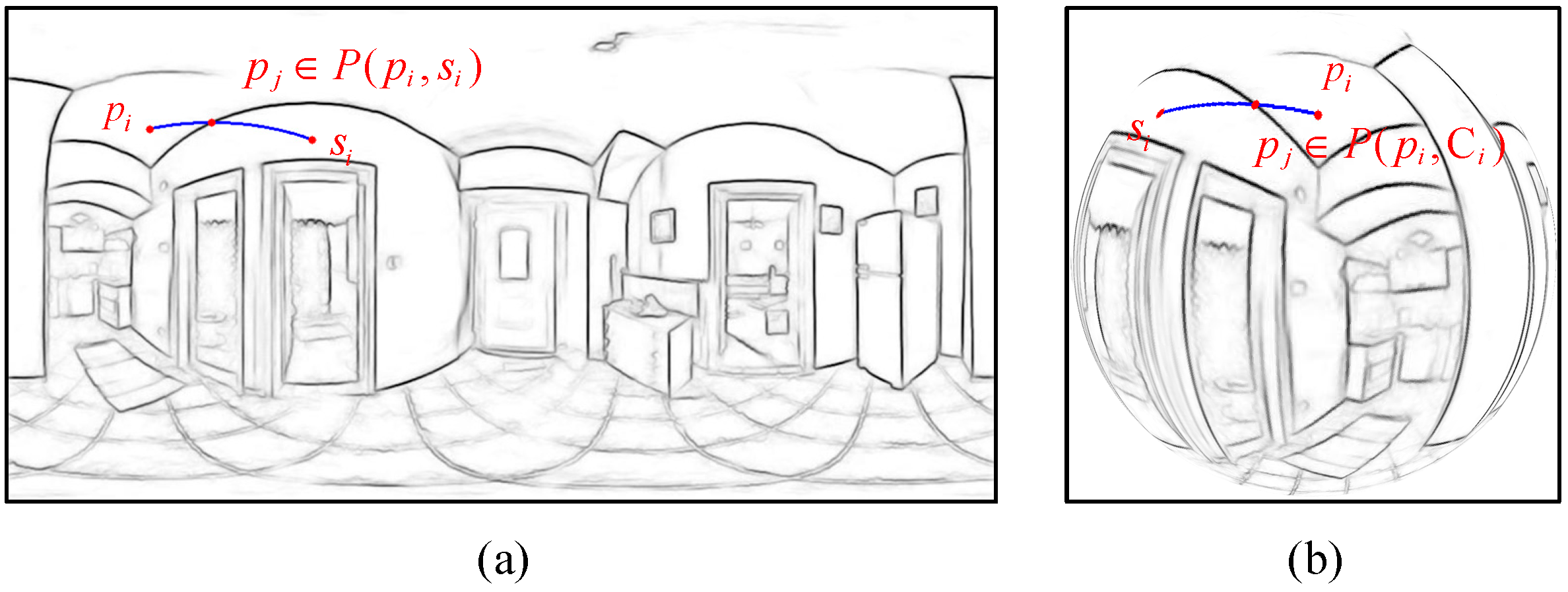
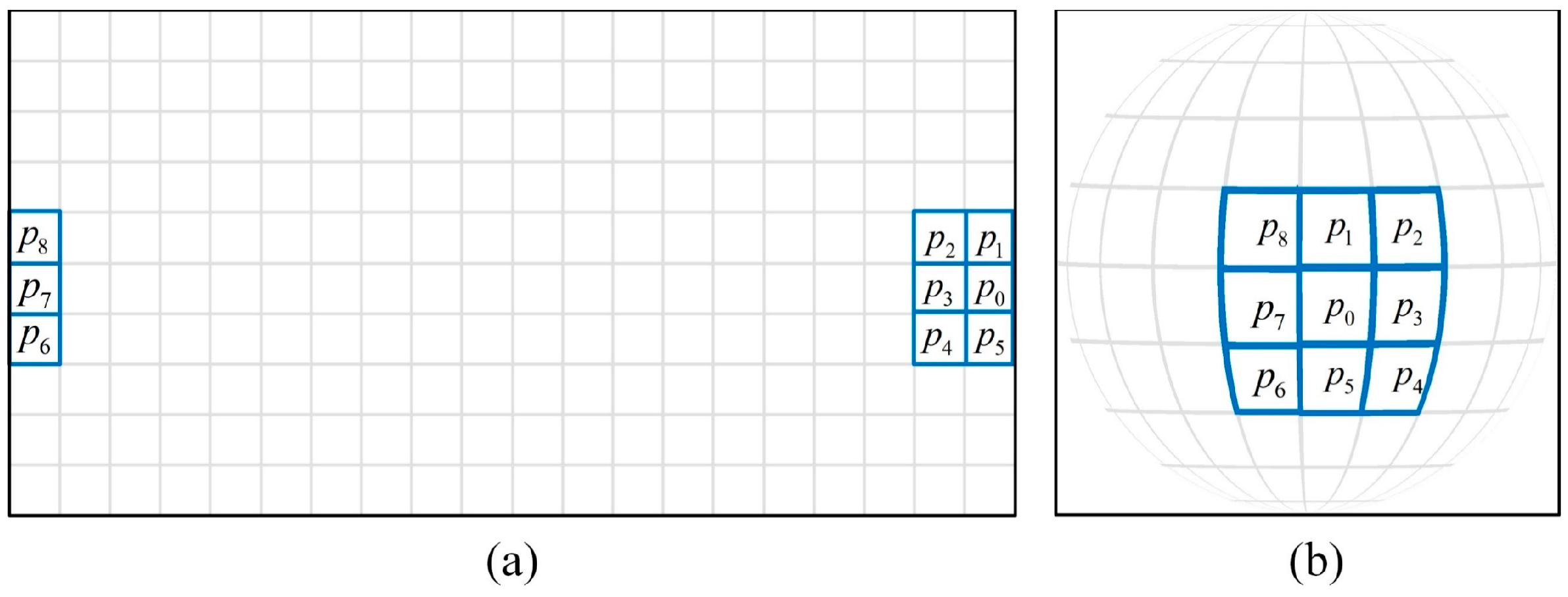
• Contour term component $D_c$. The contour term is solved on the contour diagram of the original image. On the ERP image, traverse the shortest path $P(p_i,s_i)$ between pixel $p_i$ in the contour map and seed $s_i$, as shown in Figure 5. If the gray value $\Phi (p_j)$ of pixel $p_j\in P(p_i,s_i)$ on the shortest path is less than $V_{th}$, $(V_{th}=150)$. Then it means that there is a contour line between $p_i$ and $s_i$. Therefore, $D_{xyz}$ is defined as follows:

  $$D_c=\{\begin{array}{ll}1,\hfill & \mathrm{if} \exists \hspace{0.17em}{p}_j\in P\left(p_i,s_i\right), \mathrm{s}.\mathrm{t}.{ \mathrm{V}}_{th}\ge \Phi \left(p_j\right)\hfill \\ 0,\hfill & \mathrm{if} \forall p_j\in P\left(p_i,s_i\right), \mathrm{s}.\mathrm{t}.{ \mathrm{V}}_{th}<\Phi \left(p_j\right)\hfill \end{array}$$

  (10)

The definition of distance measure and the calculation method of the contour term are described in detail. The visual effect of the algorithm after adding contour items is shown in Figure 6. It can be clearly seen that the algorithm has a qualitative improvement in the segmentation effect of the region with a small color difference after adding the contour term to the distance measurement.

3.4. Boundary Neighborhood

The presented algorithm is designed based on the non-iterative framework of SNIC, which is extensively described in Section 2. Once an element $e_i$ is popped from the priority queue in the non-iterative framework, a label is first assigned to its corresponding pixel $p_i$. The neighboring pixels of $p_i$ are then traversed within the 8 neighborhoods. If a label $p_j$ has not been assigned, further operations are executed. It is worth mentioning in Figure 7a that pixels $p_6$, $p_7$, and $p_8$ do not belong to the 8-neighborhood pixels of pixel $p_0$. In a planar image, the relative positions between pixels align with those in real-world scenarios. Nevertheless, since spherical image projection transformation is employed for ERP images, artificial boundaries are formed along their left and right sides. Consequently, while these boundary pixels appear distant from each other on ERP images, they are actually adjacent in both real-world and spherical representations.

Therefore, when applying non-iterative framework to ERP images, more care should be applied to the neighborhood range of the boundary pixels on both sides of the ERP image. As shown in Figure 7b, when traversing the pixels in the 8-neighborhood of pixel $p_0$, this work considers $p_6$, $p_7$, and $p_8$ as the 8-neighborhood pixels of $p_0$. Similarly, $p_0$, $p_1$, and $p_5$ are the 8-neighborhood pixels of $p_7$.

The optimization strategies of each part of the algorithm in this paper are introduced in detail. Each optimization strategy plays a different role in the CICI algorithm. A pseudocode summary of the framework is presented in Algorithm 1. Additionally, a CICI step flow diagram will increase the feasibility of algorithm implementation. See Figure 8.

Algorithm 1: CICI spherical superpixel segmentation framework

Input: the EPR image $I$, the contour map $G$, the expected superpixel number $K$

Output: Assigned label map $\mathbf{L}={\left\{L\left(p_i\right)\right\}}_{i=1}^N$

/*Initialization*/

Initialize cluster seeds ${\left\{s_i\right\}}_{i=1}^K$ by Fibonacci sampling. Initialize a priority queue $Q$ with a small root. Divided the area of each seed ${\left\{R_i\right\}}_{i=1}^K$ /*Seeds redistribution*/ for each region $R_i$ do  Calculate the context identity $D_i$ of the current region $R_i$. end for Calculate the context identity $D_{all}$ and the regional average context identity $\overline{D}$ of $I$ Adjust the number of initial seeds to $K^{\prime }$ according to the context identity. Determine $D_{\max }$ and $D_{\min }$.

for each region $R_i$ do  if $D_i\ge D_{\max }$ then   Add two new seeds to area $R_i$.  else if $D_{\min }<D_i<D_{\max }$ then   Keep the seeds in region $R_i$ unchanged.  else if $D_i\le D_{\min }$ then   Delete the seeds in area $R_i$.  end if

end for for$k\in \left[1,2,\dots ,K^{\prime }\right]$ do  Create element $e_k$ through seeds and push in priority queue $Q$. end for /*label map update*/

while $Q$ is not empty do

Pop the element $e_i$ from queue $Q$.  if $p_i$ is not labeled before then   Assign the label to $p_i$.   Update the corresponding cluster.   for traversing pixel $p_i$ new 8-neighborhood pixel $p_j$ do    if $p_j$ is not labeled before then     Update the distance $D\left(p_j,s_k\right)$ and create the corresponding node $e_j$.     Push $e_j$ onto $Q$.

end if

end for  end if end while

Return the label map $L$.

4. Experiments

In this section, the proposed CICI is evaluated to substantiate its superiority. Firstly, two datasets are introduced along with the benchmarks, including the Spherical Panorama Segmentation Dataset (SPSDataset75) [16] and the Berkeley Segmentation Data Set 500 (BSDS500) [28]. The qualitative and quantitative performance is then systematically tested and demonstrated from specific aspects to the overall evaluation. Subsequently, the computational efficiency is analyzed. The software and all algorithms are performed on an Intel Core i7 4.2 GHz with 16 GB RAM, without any parallelization or GPU processing.

4.1. SPSDataset75

The SPSDataset75 comprises 75 ERP images, accompanied by corresponding manual annotated ground truth, which usually serves as a comprehensive benchmark for evaluating spherical image segmentation quantitatively. A portion of the visual representations is illustrated in Figure 9, wherein each ERP image has a size of 1024 × 512.

4.1.1. Qualitative Result Analysis

The proposed algorithm CICI is qualitatively compared and analyzed with several up-to-date spherical superpixel algorithms, including SphSLIC [14], SphSPS [17], SSNIC [20], SLIC [23], and SNIC [18]. To ensure the optimal performance of the comparative algorithm, the experimental parameters are set to their default values as specified in the literature. The iterative algorithms were configured with a maximum iteration count of 10, and the initial number of superpixels was set to 500.

To demonstrate the regularity of the algorithm in generating superpixels at the polar regions of the spherical image, the viewpoints in the local are present. As can be seen in the details image of Figure 10, the contours of wall junctions lack clarity and there is minimal color contrast between adjacent regions. It is also difficult for observers to distinguish the boundary of the contour in the region. On the other hand, the proposed CICI can accurately capture the true contour boundary of wall junctions, resulting in a more regular segmentation result within the polar region of the spherical image.

Despite the regular distribution in polar regions, the segmentation results of SphSLIC, SphSPS, and SSNIC exhibit poor performance in accurately delineating the contour boundaries of wall junctions. If the conventional SNIC is directly applied to spherical images, there are irregular superpixels in polar regions. As shown in Figure 10, the contours at the wall junctions are inaccurately segmented where the color of the box and the wall is nearly identical. In this scenario, CICI outperforms other algorithms by accurately segmenting toilet boundaries even when boundary colors are not distinct. It achieves adaptability and regularity in superpixel shapes on spherical images by adjusting their sizes based on content density distribution. Conversely, SphSLIC, SphSPS, and SSNIC generate uniformly sized superpixels but fail to capture finer details in content-dense areas, resulting from a lack of adaptive adjustment.

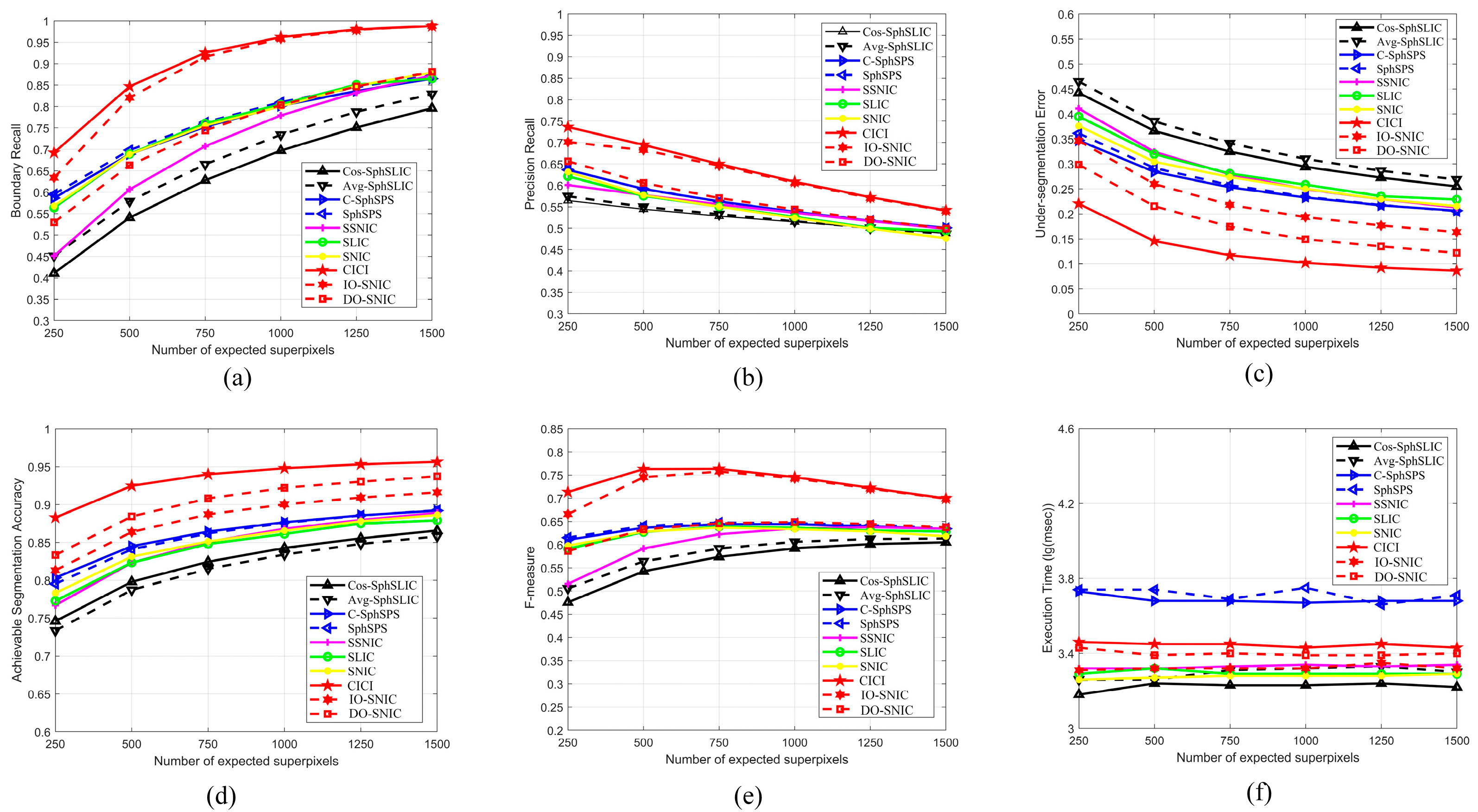
4.1.2. Quantitative Evaluation by Metrics

In qualitative analysis, it is obvious that the segmentation effect of CICI is better. In order to objectively evaluate the performance of the algorithm, five common evaluation metrics are used in the quantitative analysis [29]: boundary recall (BR), precision recall (PR), under-segmentation error (UE), achievable segmentation accuracy (ASA), F-measure, and the execution time of the algorithm. Quantitative evaluations are listed in Appendix A. In order to further illustrate the influence of CICI’s strategies, the initialization-optimized SNIC (IO-SNIC) based on seed distribution and the distance-optimized SNIC (DO-SNIC) based on an improved measurement are designed to be the baselines, respectively. Similarly, in the literature on the SphSLIC algorithm, two distance measures are proposed: the Avg-SphSLIC algorithm based on Euclidean distance and the Cos-SphSLIC algorithm based on cosine similarity. In the literature of the SphSPS algorithm, the path color term is added to the distance metric, so the method of adding the path color term is denoted as C-SphSPS.

Figure 11 quantitatively analyzes the ten SOTA methods. It is obvious that CICI performs the best in all four metrics. Both the boundary fitting degree and the segmentation accuracy are in the leading position. When the number of superpixels is the same, it can be seen from Figure 11a that CICI has the best boundary fit, followed by IO-SNIC, indicating that the seed optimization strategy plays an important role in the boundary fit of CICI. The reason is that this optimization strategy makes CICI generate smaller superpixels in the content-dense region and segment more contour boundaries. In Figure 11b, the curves of CICI and IO-SNIC gradually coincide with the increase in the number of superpixels, which indicates that the number of superpixels generated by CICI in the region with simple content is reduced by the seed optimization strategy. Figure 11c,d show that the contour intensity strategy has a large contribution so that the algorithm can accurately fit the real image boundary.

The F-measure value is the harmonic mean of BR and PR. Figure 11e shows the F-measure curves of all algorithms under different numbers of superpixels. When the number of superpixels is the same, the higher the F-measure value and the more effective the algorithm is. The F-measure value increases gradually when the number of superpixels increases from 250 to 500 and decreases gradually when the number of superpixels exceeds 500. The time consumption of the CICI mainly comes from the content perception strategy because there are trigonometric functions in the relevant calculation, which increases the computational cost. The algorithm in this paper has better application value than other algorithms. Although it is not at the top, CICI has more prominent advantages when considering other indicators, and its performance in terms of efficiency and accuracy is more balanced.

In summary, the proposed algorithm, CICI, has a significant performance improvement compared with the existing algorithms. The four indicators are increased by 17.78%, 13.4%, 8.85%, and 51.77% in turn (compared with the best existing algorithm under each indicator), and the F-measure is also increased by 15.19%. Through the above analysis, it is proven that the proposed algorithm has better performance.

4.2. BSDS500

In order to demonstrate that CICI is not only competitive on spherical panoramic images but also that the segmentation framework composed of the two optimization strategies can achieve excellent results on planar images, we deploy the optimization strategy on SNIC and conduct quantitative and qualitative experiments on the BSDS500 dataset. BSDS500 contains 500 images with a size of 481 × 321 or 321 × 481. The data set was provided by the computer vision group at the University of Berkeley. The 500 images consist of 200 training images, 100 validation images, and 200 test images. It is a common benchmark in image segmentation and detection. The sections are shown in Figure 12.

4.2.1. Qualitative Result Analysis

Figure 13 illustrates the visual performance of five methods evaluated on the BSDS500 with K = 100. SNIC is considered to be the ancestor of superpixel algorithms. IBIS [30], SCALE [31], and BACA [32] are all famous superpixel algorithms from the last two years. CICI inherits the compactness of SNIC while paying more attention to weak boundaries in images. Compared with CICI, the boundary perception of IBIS and BACA is slightly inadequate. The overall visual comfort of SCALE is slightly stronger, but compared with CICI, the segmentation accuracy is poor, mainly when the foreground and background colors are similar.

From the perspective of the overall segmentation effect, CICI and BACA can adaptively match the size and number of superpixel blocks according to the characteristics of the image itself, which is thanks to the strategy based on context identity. On this basis, the boundary degree fit of CICI is more competitive.

4.2.2. Quantitative Evaluation by Metrics

In order to objectively compare the performance of different superpixel algorithms, BR, UE, ASA, and CO are selected for quantitative evaluation. The number of superpixels ranges from 50 to 500. The four comparison algorithms selected in the experiment have been excellent in the past two years and have been compared with the commonly used superpixel algorithms like SLIC [23], SEEDS [33], ERS [34], LSC [35], FLIC [36], etc., so it is not necessary to go into details again. It is worth mentioning that because the four algorithms differ little from each other, we enumerate real values rather than plot curves. BR represents the boundary recall rate, which actually describes the degree of fit between the superpixel contour and the object boundary. A larger BR means that the superpixel boundary is closer to the true boundary of the image. It can be seen from

Table 1. Comparison of five algorithms in terms of boundary recall (↑) on BSDS500.

Algorithm	Expected Superpixel Number
	50	100	150	200	250	300	350	400	450	500
CICI	0.7843	0.8592	0.8878	0.9008	0.9138	0.9229	0.9343	0.9366	0.9380	0.9442
SNIC	0.7069	0.8112	0.8561	0.8779	0.9038	0.9134	0.9221	0.9335	0.9415	0.9505
IBIS	0.6545	0.7622	0.7954	0.8408	0.8633	0.8755	0.8919	0.9139	0.9176	0.9286
BACA	0.9340	0.8153	0.8498	0.8659	0.8758	0.8818	0.8964	0.9071	0.9102	0.9155
SCALE	0.7183	0.8074	0.8489	0.8791	0.9000	0.9155	0.9278	0.9380	0.9471	0.9532

that CICI is in the first tier of the dataset. When the number of superpixels does not exceed 400, it is always at the leading level. In

Table 2. Comparison of five algorithms in terms of under-segmentation error (↓) on BSDS500.

Algorithm	Expected Superpixel Number
	50	100	150	200	250	300	350	400	450	500
CICI	0.0720	0.0508	0.0420	0.0414	0.0391	0.0372	0.0355	0.0349	0.0344	0.0338
SNIC	0.1133	0.0707	0.0575	0.0517	0.0455	0.0432	0.0420	0.0401	0.0373	0.0360
IBIS	0.1377	0.0954	0.0819	0.0701	0.0640	0.0597	0.0553	0.0513	0.0499	0.0473
BACA	0.0853	0.0578	0.0475	0.0458	0.0430	0.0403	0.0394	0.0384	0.0382	0.0369
SCALE	0.1294	0.0897	0.0755	0.0667	0.0600	0.0579	0.0547	0.0537	0.0512	0.0500

, the UE values of the five algorithms continue to decrease as the number of superpixels increases. According to its definition, the performance of UE is negatively related to segmentation accuracy. The UE value of CICI reaches 0.0338 when k = 500, which is the best among the five algorithms. Combined with the comprehensive analysis in

Table 3. Comparison of five algorithms in terms of achievable segmentation accuracy (↑) on BSDS500.

Algorithm	Expected Superpixel Number
	50	100	150	200	250	300	350	400	450	500
CICI	0.9040	0.9317	0.9411	0.9442	0.9477	0.9499	0.9527	0.9539	0.9545	0.9558
SNIC	0.8677	0.9140	0.9293	0.9351	0.9425	0.9448	0.9476	0.9496	0.9525	0.9543
IBIS	0.8578	0.9004	0.9118	0.9234	0.9297	0.9337	0.9378	0.9424	0.9439	0.9462
BACA	0.8788	0.9113	0.9268	0.9313	0.9360	0.9380	0.9428	0.9456	0.9460	0.9477
SCALE	0.8730	0.9092	0.9227	0.9307	0.9350	0.9405	0.9434	0.9453	0.9476	0.9489

, CICI outperforms all other algorithms in UE and ASA, indicating that the generated superpixels are almost overlapping with a ground truth value object, which enables it to achieve good results in some practical segmentation applications. In the experiment of some algorithms, it pursues the considerable BR and loses its shape quality (poor visual regularity), that is, CO. However, in the actual segmentation task, the balance between precision and regularity is also the focus of research.

Table 4. Comparison of five algorithms in terms of compactness (↑) on BSDS500.

Algorithm	Expected Superpixel Number
	50	100	150	200	250	300	350	400	450	500
CICI	0.4002	0.4907	0.5569	0.5796	0.5849	0.5920	0.6496	0.7095	0.7196	0.7295
SNIC	0.3486	0.4321	0.4819	0.5046	0.5434	0.5536	0.5700	0.5920	0.6039	0.6233
IBIS	0.3315	0.3996	0.4365	0.4735	0.5008	0.5211	0.5332	0.5572	0.5691	0.5818
BACA	0.3917	0.4805	0.5429	0.5673	0.5753	0.5833	0.6357	0.6887	0.6983	0.7090
SCALE	0.3845	0.4313	0.4624	0.4859	0.5000	0.5228	0.5346	0.5486	0.5615	0.5717

shows the compactness performance of five algorithms on the data set. The larger the value of the indicator, the more uniform and regular its segmentation shape, and CICI’s indicator can correspond to its uniform segmentation visual display.

Table 5. Comparison of five algorithms in terms of generated superpixel number on BSDS500.

Algorithm	Expected Superpixel Number
	50	100	150	200	250	300	350	400	450	500
CICI	42	88	142	161	186	212	254	300	309	340
SNIC	40	96	150	187	260	294	330	400	442	504
IBIS	40	93	125	182	223	256	291	372	392	435
BACA	38	87	130	158	188	211	262	302	314	345
SCALE	50	100	150	200	250	300	350	400	450	500

shows the average number of superpixels actually segmented by five algorithms in 500 pictures on BSDS500. It is obvious that BACA has the smallest number of actual segmentations, which sacrifices a certain degree of segmentation accuracy. SCALE behaves exactly as the user-expected number and is controllable. CICI also performs well on the actual segmentation number of images; it achieves a balance of complexity and accuracy. It is worth noting that the best-performing algorithms are shown in red, followed by blue and green.

5. Conclusions

In this study, we propose a context identity and contour intensity (CICI) framework for superpixel segmentation in spherical images. Firstly, we optimize the number and placement of seeds using local context identity. Additionally, we incorporate a contour intensity prior strategy into the correlation measurement to effectively enhance segmentation accuracy. Furthermore, we compare CICI with several state-of-the-art superpixel algorithms on SPSDataset75. Qualitative analysis demonstrates that the proposed CICI achieves content-adaptive adjustment in superpixel size and delivers superior segmentation accuracy. To further demonstrate the effectiveness of our optimization strategy, we integrate CICI with SNIC, evaluate its performance on the BSDS500 dataset and yield satisfactory results.

Future research will primarily focus on applying CICI to advanced computational vision tasks. In virtual reality (VR) and augmented reality (AR), CICI can bring many potential advantages, including improved rendering efficiency, reduced data transfer and processing costs, and enhanced user interaction experiences, which are described in detail as follows:

(1) The CICI segmentation results are used to optimize the rendering process of virtual reality and augmented reality scenes. By reducing the number of primitives that need to be rendered, the storage and transmission costs are effectively reduced while maintaining visual quality.

(2) In AR applications, CICI can assist in extracting and identifying significant feature points or areas in the environment, enhancing user interaction experiences. For instance, identifying and tracking specific objects or landmarks can facilitate natural interaction between virtual information and the real world.