Study of Quantum Difference Coupled Impulsive System with Respect to Another Function

Abstract

In this paper, we study a quantum difference coupled impulsive system with respect to another function. Some quantum derivative and integral asymmetric graphs with respect to another function are shown to illustrate the behavior of parameters. Existence and uniqueness results are established via Banach contraction mapping principle and Leray–Schauder alternative. Examples illustrating the obtained results are also included. Our results are new and significantly contribute to the literature to this new subject on quantum calculus on finite intervals with respect to another function.

1. Introduction

The study of calculus without the notion of limits is known as quantum calculus or q-calculus. Historically, Euler (in the eighteenth century) obtained some basic formulae in q-calculus. However, what is now known as q-derivative and q-integral was defined by Jackson [1]. Quantum calculus has several applications in many areas, such as physics, quantum mechanics, analytic number theory, hypergeometric functions, theory of finite differences, gamma function theory, Bernoulli and Euler polynomials, combinatorics, multiple hypergeometric functions, Sobolev spaces, operator theory, geometric theory of analytic and harmonic univalent functions, Lie theory, particle physics, nonlinear electric circuit theory, mechanical engineering, theory of heat conduction, quantum mechanics, cosmology and statistics (see [2,3,4,5,6,7,8]). q-derivatives and q-integrals were generalized in non-integer orders by Al-Salam [9] and Agarwal [10]. For more details in quantum calculus, we refer to the monograph [11], and for some recent results, we refer to the papers [12,13,14,15,16,17,18,19] and references cited therein. The notion of quantum calculus on finite intervals was introduced by Tariboon and Ntouyas in [20]. For some recent results of quantum calculus on finite intervals we refer to [21].

Recently, in [22], the definitions of the quantum derivative and quantum integral on finite intervals were introduced with respect to another function and their basic properties were studied. The new theory of quantum calculus was applied and a new Hermite–Hadamard inequality for a convex function was obtained in addition to an existence and uniqueness result for an impulsive boundary value problem involving the quantum derivative with respect to another function.

In this research, we advance one step further in the study of quantum calculus on finite intervals with respect to another function of [22], by studying a quantum coupled impulsive system with respect to another function of the form

$$\left\{\begin{array}{c}{\displaystyle { }_{x_k}{D}_{q_k,{\psi }_k}s\left(x\right)=G_1(x,s\left(x\right),r\left(x\right)),x\in [x_k,x_{k+1}),k=0,1,\dots ,\mu ,}\hfill \\ {\displaystyle { }_{x_k}{D}_{q_k,{\psi }_k}r\left(x\right)=G_2(x,s\left(x\right),r\left(x\right)),x\in [x_k,x_{k+1}),k=0,1,\dots ,\mu ,}\hfill \\ {\displaystyle s\left(x_k^{+}\right)=a_{k}s\left(x_k^{-}\right)+b_k,r\left(x_k^{+}\right)=c_{k}r\left(x_k^{-}\right)+d_k,k=1,\dots ,\mu ,}\hfill \\ {\displaystyle us\left(0\right)+vr\left(T\right)={\lambda }_1,wr\left(0\right)+zs\left(T\right)={\lambda }_2,}\hfill \end{array}\right.$$

(1)

where

• $0<q_k<1,k=0,1,\dots ,\mu ;$
• ${\psi }_k\left(x\right),k=0,1,\dots ,\mu$ are strictly increasing functions on $[0,T];$
• $0=x_0<x_1<x_2<\cdots <x_{\mu }<x_{\mu +1}=T$ are fixed points in $[0,T];$
• $G_1,G_2:[0,T]\times {\mathbb{R}}^2\to \mathbb{R}$ are the nonlinear functions;
• $\left\{a_k\right\},\left\{b_k\right\},\left\{c_k\right\}$, and $\left\{d_k\right\},k=1,\dots ,\mu$ are the sequences of real numbers;
• $u,v,w,z$, and ${\lambda }_j,j=1,2$ are the real constants.

We establish existence and uniqueness results by applying Banach fixed-point theorem and Leray–Schauder alternative. Our results are new and they enrich the literature to this new subject on quantum calculus on finite intervals with respect to another function. The used method is standard, but its configuration on quantum coupled impulsive systems with respect to another function is new.

This paper is organized as follows: In Section 2, we recall the new results on quantum calculus on finite intervals with respect to another function. A basic lemma concerning a linear valiant of the problem (1) is also proved. In Section 3, we study a quantum coupled impulsive system with respect to another function. The obtained results are well illustrated by numerical examples.

2. Preliminaries

Let a strictly increasing function $\psi :[a,b]\to \mathbb{R},$$a\ge 0$ and q be a quantum number with $0<q<1$. Let us present the new definition of quantum derivative with respect to the function $\psi$.

Definition 1

([22]). Let $s:[a,b]\to \mathbb{R}$ be a continuous function. Then, the q-derivative of s with respect to ψ, on $[a,b]$, is defined by

$${ }_a{D}_{q,\psi }s\left(x\right)=\frac{s\left(x\right)-s(qx+(1-q\left)a\right)}{\psi \left(x\right)-\psi (qx+(1-q\left)a\right)},x\ne a,$$

(2)

and ${ }_a{D}_{q,\psi }s\left(a\right)={lim}_{x\to a}\left\{{ }_a{D}_{q,\psi }s\left(x\right)\right\}$.

Remark 1

([22]). $\left(i\right)$ If $\psi \left(x\right)=x$, then

$${ }_a{D}_{q,x}s\left(x\right)=\frac{s\left(x\right)-s(qx+(1-q\left)a\right)}{(1-q)(x-a)},$$

i.e., we obtain the Tariboon–Ntouyas quantum derivative defined in [20]. For $a=0$, we obtain the Jackson’s quantum derivative [1]:

$${ }_0{D}_{q,x}s\left(x\right)=\frac{s\left(x\right)-s\left(qx\right)}{(1-q)x}.$$

Example 1.

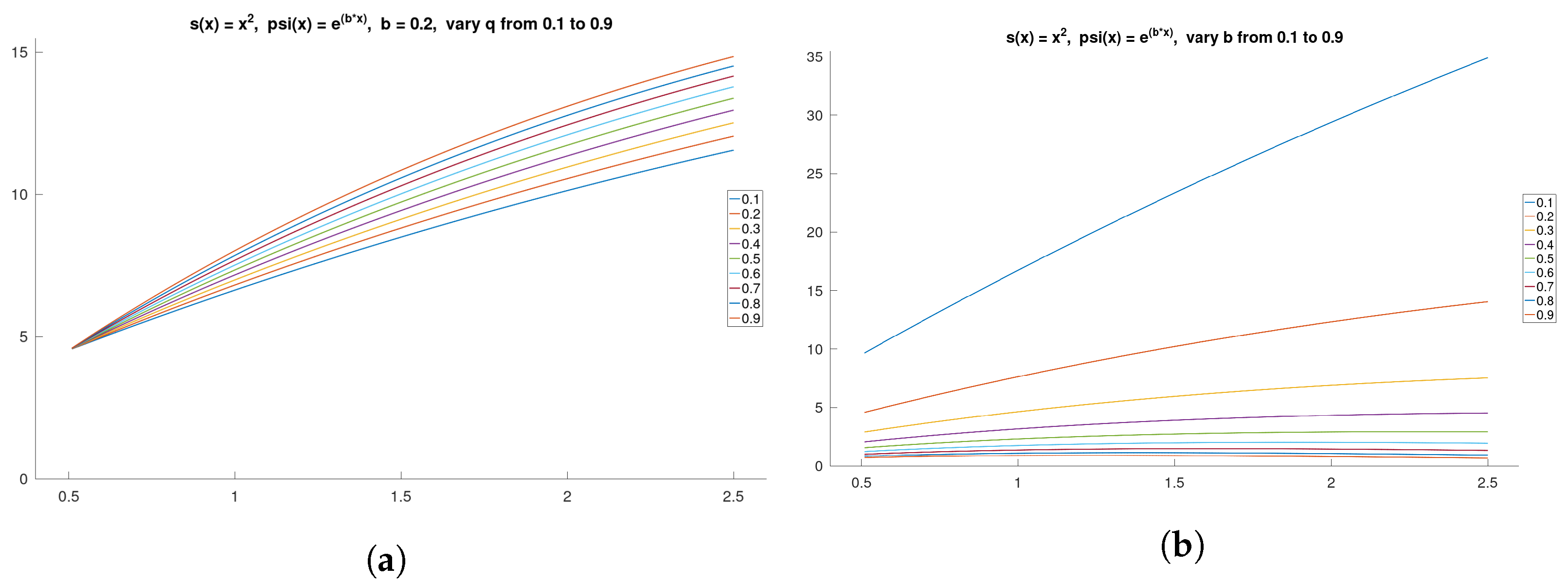
Let us consider an example for a computation of quantum derivative with respect to another function. Let $a=1/2$, $s\left(x\right)=x^2$ and $\psi \left(x\right)=e^{bx}$, then

$${ }_{\frac{1}{2}}{D}_{q,e^{bx}}\left(x^2\right)=\frac{x^2-{\left(qx+(1-q)(1/2)\right)}^2}{e^{bx}-e^{b\left(qx+(1-q)(1/2)\right)}}.$$

By varying the parameters q and b, we illustrate their influence on the quantum derivative to a given function $s\left(x\right)=x^2$. Figure 1a shows the impact of the quantum parameter q, varied from $0.1$ to $0.9$, while we fixed parameter b to $0.2$. Then, we fix the quantum number to $2/3$ and vary parameter b from $0.1$ to $0.9$, with the results displayed in Figure 1b. And the considered domain of this example is chosen to be $\left[1/2,5/2\right].$ The graphs demonstrate that increasing the quantum number q makes the curve slightly steeper, whereas increasing the parameter b results in more significant changes to the graph, but in an opposite manner.

In the next lemma, we collect the basic properties of the quantum derivative with respect to another function.

Lemma 1

([22]). We have the following:

(i)

${ }_a{D}_{q,\psi }(\alpha s\left(x\right)+\beta r\left(x\right))=\alpha { }_a{D}_{q,\psi }s\left(x\right)+\beta { }_a{D}_{q,\psi }r\left(x\right),\alpha ,\beta are real constants.$

(ii)

$\begin{array}{c}{ }_a{D}_{q,\psi }\left(sr\right)\left(x\right)=s\left(x\right){ }_a{D}_{q,\psi }r\left(x\right)+r(qx+(1-q)a){ }_a{D}_{q,\psi }s\left(x\right)\\ \hspace{1em}=r\left(x\right){ }_a{D}_{q,\psi }s\left(x\right)+s(qx+(1-q)a){ }_a{D}_{q,\psi }r\left(x\right).\end{array}$

(iii)

${\displaystyle { }_a{D}_{q,\psi }\left(\frac{s}{r}\right)\left(x\right)=\frac{r\left(x\right){ }_a{D}_{q,\psi }s\left(x\right)-s\left(x\right){ }_a{D}_{q,\psi }r\left(x\right)}{r\left(x\right)r(qx+(1-q\left)a\right)},}$ where $r\left(x\right)r(qx+(1-q\left)a\right)\ne 0$ for all $x\in [a,b]$.

Now, we define the quantum integral with respect to another function.

Definition 2

([22]). The definite quantum integral of $s:[a,b]\to \mathbb{R}$ with respect to function ψ and quantum number q, is defined by

$$\begin{array}{ccc}\hfill { }_a{I}_{q,\psi }s\left(x\right)& =& {\int }_a^{x}s\left(\tau \right){ }_a{d}_q^{\psi }\tau \hfill \\ & =& \sum _{k=0}^{\infty }\left[\psi (q^{k}x+(1-q^k)a)-\psi (q^{k+1}x+(1-q^{k+1})a)\right]s(q^{k}x+(1-q^k)a),\hfill \end{array}$$

(3)

which is well defined if the right-hand side exists. Moreover, for $c\in (a,b)$, the definite quantum integral can be written as

$$\begin{array}{ccc}\hfill {\int }_c^{x}s\left(\tau \right){ }_a{d}_q^{\psi }\tau & =& {\int }_a^{x}s\left(\tau \right){ }_a{d}_q^{\psi }\tau -{\int }_a^{c}s\left(\tau \right){ }_a{d}_q^{\psi }\tau \hfill \\ & =& \sum _{k=0}^{\infty }\left[\psi (q^{k}x+(1-q^k)a)-\psi (q^{k+1}x+(1-q^{k+1})a)\right]s(q^{k}x+(1-q^k)a)\hfill \\ & & -\sum _{k=0}^{\infty }\left[\psi (q^{k}c+(1-q^k)a)-\psi (q^{k+1}c+(1-q^{k+1})a)\right]s(q^{k}c+(1-q^k)a).\hfill \end{array}$$

Remark 2

([22]). $\left(i\right)$ If $\psi \left(x\right)=x$, then

$${ }_a{I}_{q,x}s\left(x\right)=(1-q)(x-a)\sum _{k=0}^{\infty }{q}^{k}s(q^{k}x+(1-q^k)a),$$

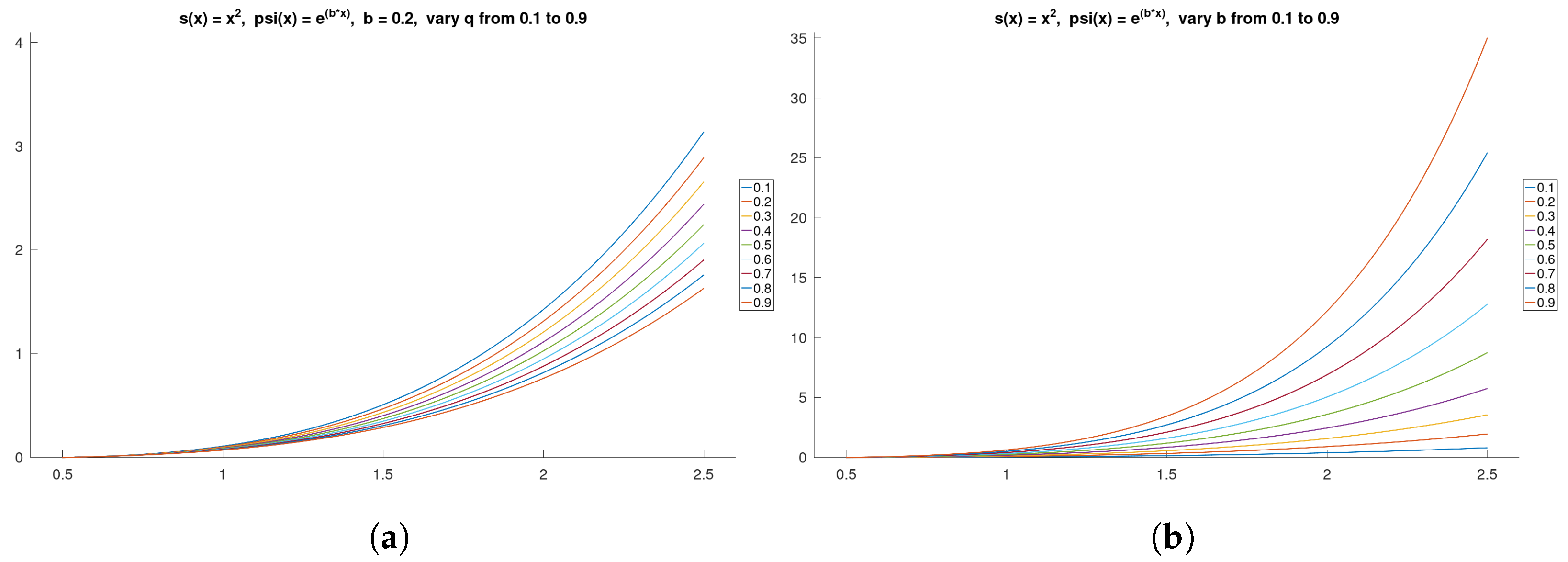
i.e., we have the Tariboon–Ntouyas [20] definite quantum integral; and if $a=0$, we have the Jackson [1] definite quantum integral:

$${ }_0{I}_{q,x}s\left(x\right)=(1-q)x\sum _{k=0}^{\infty }{q}^{k}s\left(q^{k}x\right).$$

Example 2.

Let us consider an example for the computation of the definite quantum integral with respect to another function. Let $a=1/2$, $s\left(x\right)=x^2$ and $\psi \left(x\right)=e^{bx}$, then

$${ }_{\frac{1}{2}}{I}_{q,e^{bx}}\left(x^2\right)=\sum _{k=0}^{\infty }\left[e^{b\left(q^{k}x+(1-q^k)\left(\frac{1}{2}\right)\right)}-e^{b\left(q^{k+1}x+(1-q^{k+1})\left(\frac{1}{2}\right)\right)}\right]{\left(q^{k}x+(1-q^k)\left(\frac{1}{2}\right)\right)}^2.$$

We investigate the impact of the quantum number q and parameter b on the definite quantum integral by varying these parameters. In Figure 2a, parameter b is set to $0.2$ while the quantum number q is adjusted from $0.1$ to $0.9$. Conversely, in Figure 2b, the quantum number q is fixed at $2/3$, and parameter b is varied from $0.1$ to $0.9$. The selected domain remains $[1/2,5/2]$. To visualize the result, we approximate the definite integral, which is expressed as an infinite sum, by setting $k=0,1,\dots ,1000$. The results indicate that increasing parameter b significantly sharpens the curve, whereas increasing the quantum number q slightly reduces its steepness. The observed pattern exhibits an opposite trend compared to the quantum derivative example.

The following lemma concerns a linear variant of the initial system (1) and is the basic tool to transform the nonlinear coupled impulsive quantum system (1) into a fixed-point problem.

Lemma 2.

Let $g_1,g_2\in C([0,T],\mathbb{R})$ and ${\Omega }_1\ne 0.$ Then, $\left(s\right(x),r(x\left)\right)$ satisfies the linear system

$$\left\{\begin{array}{c}{\displaystyle { }_{x_k}{D}_{q_k,{\psi }_k}s\left(x\right)=g_1\left(x\right),x\in [x_k,x_{k+1}),k=0,1,\dots ,\mu ,}\hfill \\ {\displaystyle { }_{x_k}{D}_{q_k,{\psi }_k}r\left(x\right)=g_2\left(x\right),x\in [x_k,x_{k+1}),k=0,1,\dots ,\mu ,}\hfill \\ {\displaystyle s\left(x_k^{+}\right)=a_{k}s\left(x_k^{-}\right)+b_k,r\left(x_k^{+}\right)=c_{k}r\left(x_k^{-}\right)+d_k,k=1,\dots ,\mu ,}\hfill \\ {\displaystyle us\left(0\right)+vr\left(T\right)={\lambda }_1,wr\left(0\right)+zs\left(T\right)={\lambda }_2,}\hfill \end{array}\right.$$

(4)

if and only if

$$\begin{array}{ccc}\hfill s\left(x\right)& =& \frac{w}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right]\prod _{k=1}^m{a}_k\hfill \\ & & -\frac{{\Omega }_2}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\prod _{k=1}^m{a}_k\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{a}_i{b}_k\right)\hfill \\ & & +{\int }_{x_m}^x{g}_1{\left(\tau \right)}_{x_m}{d}_{q_m}^{{\psi }_m}\tau ,m=0,1,\dots ,\mu ,\hfill \end{array}$$

(5)

and

$$\begin{array}{ccc}\hfill r\left(x\right)& =& \frac{u}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\prod _{k=1}^m{c}_k\hfill \\ & & -\frac{{\Omega }_3}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right]\prod _{k=1}^m{c}_k\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{c}_i{d}_k\right)\hfill \\ & & +{\int }_{x_m}^x{g}_2{\left(\tau \right)}_{x_m}{d}_{q_m}^{{\psi }_m}\tau ,m=0,1,\dots ,\mu ,\hfill \end{array}$$

(6)

where

$$\begin{array}{c}\hfill {\Omega }_1=uw-vz\prod _{k=1}^{\mu }{c}_k\prod _{k=1}^{\mu }{a}_k,{\Omega }_2=v\prod _{k=1}^{\mu }{c}_k,and{\Omega }_3=z\prod _{k=1}^{\mu }{a}_k.\end{array}$$

Proof. 

For $x\in [x_0,x_1)$, taking the operator ${ }_{x_0}{I}_{q_0,{\psi }_0}$ to both sides in the first equation in (4), we have

$$s\left(x\right)=s\left(0\right)+{\int }_{x_0}^x{g}_1\left(\tau \right){ }_{x_0}{d}_{q_0}^{{\psi }_0}\tau .$$

(7)

For $x\in [x_1,x_2)$, taking the operator ${ }_{x_1}{I}_{q_1,{\psi }_1}$ to both sides in the first equation in (4), we have

$$s\left(x\right)=s\left(x_1^{+}\right)+{\int }_{x_1}^x{g}_1\left(\tau \right){ }_{x_1}{d}_{q_1}^{{\psi }_1}\tau .$$

From conditions $s\left(x_1^{+}\right)=a_{1}s\left(x_1^{-}\right)+b_1$, we obtain

$$s\left(x\right)=a_1\left(s\left(0\right)+{\int }_{x_0}^{x_1}{g}_1\left(\tau \right){ }_{x_0}{d}_{q_0}^{{\psi }_0}\tau \right)+b_1+{\int }_{x_1}^x{g}_1\left(\tau \right){ }_{x_1}{d}_{q_1}^{{\psi }_1}\tau .$$

Once again, for $x\in [x_2,x_3)$, we obtain

$$\begin{array}{ccc}\hfill s\left(x\right)& =& s\left(x_2^{+}\right)+{\int }_{x_2}^x{g}_1\left(\tau \right){ }_{x_2}{d}_{q_2}^{{\psi }_2}\tau \hfill \\ & =& a_2\left(a_1\left(s\left(0\right)+{\int }_{x_0}^{x_1}{g}_1\left(\tau \right){ }_{x_0}{d}_{q_0}^{{\psi }_0}\tau \right)+b_1+{\int }_{x_1}^{x_2}{g}_1\left(\tau \right){ }_{x_1}{d}_{q_1}^{{\psi }_1}\tau \right)+b_2\hfill \\ & & +{\int }_{x_2}^x{g}_1\left(\tau \right){ }_{x_2}{d}_{q_2}^{{\psi }_2}\tau .\hfill \end{array}$$

Repeating the above process, for $x\in [x_m,x_{m+1})$, we have

$$\begin{array}{ccc}\hfill s\left(x\right)& =& s\left(0\right)\prod _{k=1}^m{a}_k+\sum _{k=1}^m\left(\prod _{i=k}^m{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{a}_i{b}_k\right)\hfill \\ & & +{\int }_{x_m}^x{g}_1{\left(\tau \right)}_{x_m}{d}_{q_m}^{{\psi }_m}\tau .\hfill \end{array}$$

(8)

Indeed, (8) is true for $m=0$ by (7) using ${\prod }_{\alpha }^{\beta }(·)=1$ and ${\sum }_{\alpha }^{\beta }(·)=0$, when $\alpha >\beta$. For $x\in [x_{m+1},x_{m+2})$, we have

$$\begin{array}{ccc}\hfill s\left(x\right)& =& s\left(x_{m+1}^{+}\right)+{\int }_{x_{m+1}}^x{g}_1\left(\tau \right){ }_{x_{m+1}}{d}_{q_{m+1}}^{{\psi }_{m+1}}\tau \hfill \\ & =& a_{m+1}s\left(x_{m+1}^{-}\right)+b_{m+1}+{\int }_{x_{m+1}}^x{g}_1\left(\tau \right){ }_{x_{m+1}}{d}_{q_{m+1}}^{{\psi }_{m+1}}\tau \hfill \\ & =& a_{m+1}[s\left(0\right)\prod _{k=1}^m{a}_k+\sum _{k=1}^m\left(\prod _{i=k}^m{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{a}_i{b}_k\right)\hfill \\ & & +{\int }_{x_m}^{x_{m+1}}{g}_1{\left(\tau \right)}_{x_m}{d}_{q_m}^{{\psi }_m}\tau ]+b_{m+1}+{\int }_{x_{m+1}}^x{g}_1\left(\tau \right){ }_{x_{m+1}}{d}_{q_{m+1}}^{{\psi }_{m+1}}\tau \hfill \\ & =& s\left(0\right)\prod _{k=1}^{m+1}{a}_k+\sum _{k=1}^{m+1}\left(\prod _{i=k}^{m+1}{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{m+1}\left(\prod _{i=k+1}^{m+1}{a}_i{b}_k\right)\hfill \\ & & +{\int }_{x_{m+1}}^x{g}_1{\left(\tau \right)}_{x_{m+1}}{d}_{q_{m+1}}^{{\psi }_{m+1}}\tau ,\hfill \end{array}$$

which shows that (8) is satisfied for $m+1.$ By mathematical induction, (8) holds for every $m\in \mathbb{N}$.

In a similar way, we can obtain

$$\begin{array}{ccc}\hfill r\left(x\right)& =& r\left(0\right)\prod _{k=1}^m{c}_k+\sum _{k=1}^m\left(\prod _{i=k}^m{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{c}_i{d}_k\right)\hfill \\ & & +{\int }_{x_m}^x{g}_2{\left(\tau \right)}_{x_m}{d}_{q_m}^{{\psi }_m}\tau .\hfill \end{array}$$

(9)

In particular, for $x=T$, we have

$$\begin{array}{ccc}\hfill s\left(T\right)& =& s\left(0\right)\prod _{k=1}^{\mu }{a}_k+\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right),\hfill \\ \hfill r\left(T\right)& =& r\left(0\right)\prod _{k=1}^{\mu }{c}_k+\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right).\hfill \end{array}$$

Substituting the values of $s\left(T\right)$ and $r\left(T\right)$ in the boundary conditions $us\left(0\right)+vr\left(T\right)={\lambda }_1$ and $wr\left(0\right)+zs\left(T\right)={\lambda }_2$ and solving the resulting system, we find

$$\begin{array}{ccc}\hfill s\left(0\right)& =& \frac{w}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right]\hfill \\ & & -\frac{{\Omega }_2}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill r\left(0\right)& =& \frac{u}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{g}_1{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\hfill \\ & & -\frac{{\Omega }_3}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{g}_2{\left(\tau \right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right].\hfill \end{array}$$

Substituting $s\left(0\right)$ and $r\left(0\right)$ in Equations (8) and (9), we obtain the solutions (5) and (6). We can prove the converse by direct computation. □

3. Main Results

The space of piecewise continuous functions $PC\left(\right[0,T],\mathbb{R})$ is defined as $PC\left(\right[0,T],\mathbb{R})=\{s:[0,T]\to \mathbb{R}:s(x)$ is continuous everywhere except for some $x_k$ such that $s\left(x_k^{+}\right)$ and $s\left(x_k^{-}\right)$ exist and $s\left(x_k^{+}\right)=s\left(x_k\right)$ for all $k=1,\dots ,\mu \}$. $PC\left(\right[0,T],\mathbb{R})$ is a Banach space with norm $\parallel s\parallel =sup\left\{s\right(x):x\in [0,T\left]\right\}.$ The product space $\left(PC\right([0,T],\mathbb{R})\times PC([0,T],\mathbb{R}),\parallel (s,r)\parallel )$ is a Banach space with norm $\parallel (s,r)\parallel =\parallel s\parallel +\parallel r\parallel .$

In view of Lemma 2, we define an operator $\mathcal{A}:PC\left(\right[0,T],\mathbb{R})\to PC\left(\right[0,T],\mathbb{R})$ by

$$\mathcal{A}(s,r)\left(x\right)=\left(\begin{array}{c}{\mathcal{A}}_1(s,r)\left(x\right)\\ {\mathcal{A}}_2(s,r)\left(x\right)\end{array}\right),$$

(10)

where

$$\begin{array}{ccc}& & {\mathcal{A}}_1(s,r)\left(x\right)\hfill \\ & =& \frac{w}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right]\prod _{k=1}^m{a}_k\hfill \\ & & -\frac{{\Omega }_2}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}s\right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\prod _{k=1}^m{a}_k\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m{a}_i{\int }_{x_{k-1}}^{x_k}{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{a}_i{b}_k\right)\hfill \\ & & +{\int }_{x_m}^x{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_m}{d}_{q_m}^{{\psi }_m}\tau ,\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\mathcal{A}}_2(s,r)\left(x\right)\hfill \\ & =& \frac{u}{{\Omega }_1}\left[{\lambda }_2-z\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{a}_i{\int }_{x_{k-1}}^{x_k}{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-z\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{a}_i{b}_k\right)\right]\prod _{k=1}^m{c}_k\hfill \\ & & -\frac{{\Omega }_3}{{\Omega }_1}\left[{\lambda }_1-v\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }{c}_i{\int }_{x_{k-1}}^{x_k}{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)-v\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }{c}_i{d}_k\right)\right]\prod _{k=1}^m{c}_k\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m{c}_i{\int }_{x_{k-1}}^{x_k}{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m{c}_i{d}_k\right)\hfill \\ & & +{\int }_{x_m}^x{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_m}{d}_{q_m}^{{\psi }_m}\tau ,m=0,1,\dots ,\mu .\hfill \end{array}$$

For convenience, the following notations are used:

$$\begin{array}{ccc}\hfill A_1& =& \left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\right]\left(\frac{|{\Omega }_2|}{|{\Omega }_1|}\left|z\right|\prod _{k=1}^{\mu }\left|a_k\right|+1\right),\hfill \\ \hfill A_2& =& \frac{\left|w\right|\left|v\right|}{|{\Omega }_1|}\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\right]\prod _{k=1}^{\mu }\left|a_k\right|,\hfill \\ \hfill A_3& =& \frac{|w|}{|{\Omega }_1|}\left(|{\lambda }_1|+|v|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)\right)\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left(|{\lambda }_2|+|z|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\right)\prod _{k=1}^{\mu }\left|a_k\right|+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right),\hfill \\ \hfill B_1& =& \left(\frac{\left|u\right|\left|z\right|}{|{\Omega }_1|}+1\right)\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\right]\prod _{k=1}^{\mu }\left|c_k\right|,\hfill \\ \hfill B_2& =& \left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\right]\left(\frac{|{\Omega }_3|}{|{\Omega }_1|}\left|v\right|\prod _{k=1}^{\mu }\left|c_k\right|+1\right),\hfill \\ \hfill B_3& =& \frac{\left|u\right|}{|{\Omega }_1|}\left(|{\lambda }_2|+|z|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\right)\prod _{k=1}^{\mu }\left|c_k\right|\hfill \\ & & +\frac{|{\Omega }_3|}{|{\Omega }_1|}\left(|{\lambda }_1|+|v|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)\right)\prod _{k=1}^{\mu }\left|c_k\right|+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right).\hfill \end{array}$$

(11)

Theorem 1.

Assume the following:

$\left(H_1\right)$

There exists positive constants ${\mathcal{L}}_1,{\mathcal{L}}_2$ such that for all $x\in [0,T]$ and ${\mu }_i,{\nu }_i\in \mathbb{R},i=1,2,$

$$\begin{array}{ccc}& & |G_1(x,{\mu }_1,{\mu }_2)-G_1(x,{\nu }_1,{\nu }_2)|\le {\mathcal{L}}_1\left(\right|{\mu }_1-{\nu }_1|+|{\mu }_2-{\nu }_2\left|\right),\hfill \\ & & |G_2(x,{\mu }_1,{\mu }_2)-G_2(x,{\nu }_1,{\nu }_2)|\le {\mathcal{L}}_2\left(\right|{\mu }_1-{\nu }_1|+|{\mu }_2-{\nu }_2\left|\right).\hfill \end{array}$$

If

$${\mathcal{L}}_1(A_1+B_1)+{\mathcal{L}}_2(A_2+B_2)<1,$$

(12)

then the impulsive quantum coupled system (1) has a unique solution.

Proof. 

Define $B_{\mathcal{R}}=\{(s,r)\in (PC([0,T],\mathbb{R})\times PC([0,T],\mathbb{R}):\parallel (s,r)\parallel \le \mathcal{R}\}$ with $\mathcal{R}$ satisfying

$$\mathcal{R}>\frac{\left(A_1+B_1\right)M_1+\left(A_2+B_2\right)M_2+\left(A_3+B_3\right)}{1-\left[{\mathcal{L}}_1\left(A_1+B_1\right)+{\mathcal{L}}_2\left(A_2+B_2\right)\right]}$$

where ${sup}_{x\in [0,T]}{G}_1(x,0,0)=M_1$ and ${sup}_{x\in [0,T]}{G}_2(x,0,0)=M_2$. Applying condition $\left(H_1\right)$, we obtain

$$\begin{array}{ccc}\hfill |G_1(x,s\left(x\right),r\left(x\right))|& \le & |G_1(x,s\left(x\right),r\left(x\right))-G_1(x,0,0)|+|G_1(x,0,0)|\hfill \\ & \le & {\mathcal{L}}_1(\parallel s\parallel +\parallel r\parallel )+M_1\hfill \\ & \le & {\mathcal{L}}_1\mathcal{R}+M_1.\hfill \end{array}$$

In the same way, we obtain

$$|G_2(x,s\left(x\right),r\left(x\right))|\le {\mathcal{L}}_2\mathcal{R}+M_2.$$

In the first step, we will show that $\mathcal{A}{B}_{\mathcal{R}}\subset B_{\mathcal{R}}.$ For any $(s,r)\in B_r$, we have

$$\begin{array}{ccc}& & |{\mathcal{A}}_1(s,r)\left(x\right)|\hfill \\ & \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|c_i|{\int }_{x_{k-1}}^{x_k}{\left|G_2(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m|a_i\left|\right|b_k|\right)\hfill \\ & & +{\int }_{x_m}^x{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_m}{d}_{q_m}^{{\psi }_m}\tau \hfill \\ & \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|\left({\mathcal{L}}_2\mathcal{R}+M_2\right)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|({\mathcal{L}}_1\mathcal{R}+M_1)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +({\mathcal{L}}_1\mathcal{R}+M_1)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|\left({\mathcal{L}}_2\mathcal{R}+M_2\right)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|({\mathcal{L}}_1\mathcal{R}+M_1)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +({\mathcal{L}}_1\mathcal{R}+M_1)\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& ({\mathcal{L}}_1\mathcal{R}+M_1)A_1+({\mathcal{L}}_2\mathcal{R}+M_2)A_2+A_3.\hfill \end{array}$$

Consequently, we have

$$\parallel {\mathcal{A}}_1(s,r)\parallel \le ({\mathcal{L}}_1\mathcal{R}+M_1)A_1+({\mathcal{L}}_2\mathcal{R}+M_2)A_2+A_3.$$

Similarly, we obtain

$$\parallel {\mathcal{A}}_2(s,r)\parallel \le ({\mathcal{L}}_1\mathcal{R}+M_1)B_1+({\mathcal{L}}_2\mathcal{R}+M_2)B_2+B_3.$$

Hence, we have

$$\begin{array}{ccc}\hfill \parallel \mathcal{A}(s,r)\parallel & \le & \left[{\mathcal{L}}_1\left(A_1+B_1\right)+{\mathcal{L}}_2\left(A_2+B_2\right)\right]\mathcal{R}\hfill \\ & & +\left(A_1+B_1\right)M_1+\left(A_2+B_2\right)M_2+\left(A_3+B_3\right)<\mathcal{R}.\hfill \end{array}$$

Therefore, $\mathcal{A}\left(B_{\mathcal{R}}\right)\subseteq B_{\mathcal{R}}$. In the next step, we will show that the operator $\mathcal{A}$ is a contraction. Let $(s_2,r_2),(s_1,s_1)\in B_{\mathcal{R}}$ and $t\in [0,T].$ Then, we have

$$\begin{array}{ccc}& & |{\mathcal{A}}_1(s_2,r_2)\left(x\right)-{\mathcal{A}}_1(s_1,r_1)\left(x\right)|\hfill \\ & \le & \frac{\left|w\right|\left|v\right|}{|{\Omega }_1|}\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|c_i|{\int }_{x_{k-1}}^{x_k}{|G_2(\tau ,s_2\left(\tau \right),r_2\left(\tau \right))-G_2(\tau ,s_1\left(\tau \right),r_1\left(\tau \right))|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\right]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left|z\right|\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|a_i|{\int }_{x_{k-1}}^{x_k}{|G_1(\tau ,s_2\left(\tau \right),r_2\left(\tau \right))-G_1(\tau ,s_1\left(\tau \right),r_1\left(\tau \right))|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\right]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m|a_i|{\int }_{x_{k-1}}^{x_k}{|G_1(\tau ,s_2\left(\tau \right),r_2\left(\tau \right))-G_1(\tau ,s_1\left(\tau \right),r_1\left(\tau \right))|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +{\int }_{x_m}^x{|G_1(\tau ,s_2\left(\tau \right),r_2\left(\tau \right))-G_1(\tau ,s_1\left(\tau \right),r_1\left(\tau \right))|}_{x_m}{d}_{q_m}^{{\psi }_m}\tau \hfill \\ & \le & {\mathcal{L}}_2\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right)\frac{\left|w\right|\left|v\right|}{|{\Omega }_1|}\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\right]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +{\mathcal{L}}_1\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right)\left[\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\right]\left(\frac{|{\Omega }_2|}{|{\Omega }_1|}\left|z\right|\prod _{k=1}^{\mu }\left|a_k\right|+1\right)\hfill \\ & =& {\mathcal{L}}_1{A}_1\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right)+{\mathcal{L}}_2{A}_2\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right)\hfill \\ & =& \left({\mathcal{L}}_1{A}_1+{\mathcal{L}}_2{A}_2\right)\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right).\hfill \end{array}$$

Thus

$$\parallel {\mathcal{A}}_1(s_2,r_2)-{\mathcal{A}}_1(s_1,r_1)\parallel \le \left({\mathcal{L}}_1{A}_1+{\mathcal{L}}_2{A}_2\right)\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right).$$

(13)

Similarly, we obtain

$$\parallel {\mathcal{A}}_2(s_2,r_2)-{\mathcal{A}}_2(s_1,r_1)\parallel \le \left({\mathcal{L}}_1{B}_1+{\mathcal{L}}_2{B}_2\right)\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right).$$

(14)

It follows from (13) and (14) that

$$\begin{array}{c}\hfill \parallel \mathcal{A}(s_2,r_2)-\mathcal{A}(s_1,r_1)\parallel \le \left[{\mathcal{L}}_1(A_1+B_1)+{\mathcal{L}}_2(A_2+B_2)\right]\left(\parallel s_2-s_1\parallel +\parallel r_2-r_1\parallel \right),\end{array}$$

Since ${\mathcal{L}}_1(A_1+B_1)+{\mathcal{L}}_2(A_2+B_2)<1$, $\mathcal{A}$ is a contraction operator. Consequently, applying Banach’s fixed-point theorem, a unique fixed point of operator $\mathcal{A}$ is obtained, which implies that the impulsive quantum coupled system (1) has a unique solution. The proof is completed. □

The next existence result is based on the Leray–Schauder alternative [23].

Theorem 2.

Let $G_1,G_2:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be continuous functions satisfying

$\left(H_2\right).$

There exists $s_i,r_i\ge 0$ for $i=1,2$ and $s_0,r_0>0$ such that for any $s,r\in \mathbb{R}$, we have

$$\begin{array}{ccc}\hfill |G_1(x,s,r)|& \le & s_0+s_1\parallel s\parallel +s_2\parallel r\parallel ,\hfill \\ \hfill |G_2(x,s,r)|& \le & r_0+r_1\parallel s\parallel +r_2\parallel r\parallel .\hfill \end{array}$$

If $(A_1+B_1)s_1+(A_2+B_2)r_1<1$ and $(A_1+B_1)s_2+(A_2+B_2)r_2<1$, where $A_i,B_i$ for $i=1,2$ are defined in (11), then the impulsive quantum coupled system (1) has at least one solution on $[0,T]$.

Proof. 

For the operator $\mathcal{A}:PC\left(\right[0,T],\mathbb{R})\to PC\left(\right[0,T],\mathbb{R})$, it can be seen that $\mathcal{A}$ is continuous from the fact that the functions $G_1,G_2:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous. Next, consider a bounded subset $B_{\rho }=\{(s,r)\in PC([0,T],\mathbb{R})\times PC([0,T],\mathbb{R}):\parallel (s,r)\parallel \le \rho \}$ of $PC\left(\right[0,T],\mathbb{R})\times PC\left(\right[0,T],\mathbb{R}).$ Note that for $(s,r)\in B_{\rho }$,

$$\begin{array}{ccc}\hfill |G_1(x,s\left(x\right),r\left(x\right))|& \le & s_0+s_1\left|s\right|+s_2\left|r\right|\le s_0+(s_1+s_2)\rho :=D_1,\hfill \\ \hfill |G_2(x,s\left(x\right),r\left(x\right))|& \le & r_0+r_1\left|s\right|+r_2\left|r\right|\le r_0+(r_1+r_2)\rho :=D_2.\hfill \end{array}$$

We will show that $\mathcal{A}{B}_{\rho }$ is uniformly bounded. For $(s,r)\in B_{\rho }$, we obtain

$$\begin{array}{ccc}& & |{\mathcal{A}}_1(s,r)\left(x\right)|\hfill \\ & \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|c_i|{\int }_{x_{k-1}}^{x_k}{\left|G_2(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m|a_i\left|\right|b_k|\right)\hfill \\ & & +{\int }_{x_m}^x{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_m}{d}_{q_m}^{{\psi }_m}\tau \hfill \\ & \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|D_2\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|D_1\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +D_1\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|D_2\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|D_1\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +D_1\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& A_1{D}_1+A_2{D}_2+A_3,\hfill \end{array}$$

which implies that

$$\parallel {\mathcal{A}}_1(s,r)\parallel \le A_1{D}_1+A_2{D}_2+A_3.$$

Similarly, we obtain

$$\parallel {\mathcal{A}}_2(s,r)\parallel \le B_1{D}_1+B_2{D}_2+B_3.$$

Consequently,

$$\parallel \mathcal{A}(s,r)\parallel = \parallel {\mathcal{A}}_1(s,r)\parallel +\parallel {\mathcal{A}}_2(s,r)\parallel \le (A_1+B_1)D_1+(A_2+B_2)D_2+A_3+B_3,$$

and thus, $\mathcal{A}$ is uniformly bounded.

Next, the equicontinuous property of operator $\mathcal{A}$ is proven. Let ${\vartheta }_1,{\vartheta }_2\in (x_l,x_{l+1})$ for some $l=0,1,\dots ,\mu$ with ${\vartheta }_1<{\vartheta }_2.$ Then, we have

$$\begin{array}{ccc}& & |{\mathcal{A}}_1(s,r)\left({\vartheta }_2\right)-{\mathcal{A}}_1(s,r)\left({\vartheta }_1\right)|\hfill \\ & =& \left|{\int }_{x_l}^{{\vartheta }_2}{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_l}{d}_{q_l}^{{\psi }_l}\tau -{\int }_{x_l}^{{\vartheta }_1}{G}_1{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_l}{d}_{q_l}^{{\psi }_l}\tau \right|\hfill \\ & \le & D_1|{\vartheta }_2-{\vartheta }_1|.\hfill \end{array}$$

Similarly, we have

$$\begin{array}{ccc}& & |{\mathcal{A}}_2(s,r)\left({\vartheta }_2\right)-{\mathcal{A}}_2(s,r)\left({\vartheta }_1\right)|\hfill \\ & =& \left|{\int }_{x_l}^{{\vartheta }_2}{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_l}{d}_{q_l}^{{\psi }_l}\tau -{\int }_{x_l}^{{\vartheta }_1}{G}_2{(\tau ,s\left(\tau \right),r\left(\tau \right))}_{x_l}{d}_{q_l}^{{\psi }_l}\tau \right|\hfill \\ & \le & D_2|{\vartheta }_2-{\vartheta }_1|.\hfill \end{array}$$

Therefore, the operator $\mathcal{A}(s,r)$ is equicontinuous, and thus, the operator $\mathcal{A}(s,r)$ is completely continuous.

Lastly, we will show that the set

$$\Theta =\left\{\right(s,r)\in PC([0,T])\times PC([0,T]\left)\right|(s,r)=\lambda \mathcal{A}(s,r),0\le \lambda \le 1\}$$

is bounded. Let $(s,r)\in \Theta$, then $(s,r)=\lambda \mathcal{A}(s,r)$. For any $x\in [0,T]$, we have

$$s\left(x\right)=\lambda {\mathcal{A}}_1(s,r)\left(x\right),r\left(x\right)=\lambda {\mathcal{A}}_2(s,r)\left(x\right).$$

Then,

$$\begin{array}{ccc}\hfill \left|s\right(x\left)\right|& \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|c_i|{\int }_{x_{k-1}}^{x_k}{\left|G_2(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z|\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^m\left|a_k\right|\hfill \\ & & +\sum _{k=1}^m\left(\prod _{i=k}^m|a_i|{\int }_{x_{k-1}}^{x_k}{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^m\left(\prod _{i=k+1}^m|a_i\left|\right|b_k|\right)\hfill \\ & & +{\int }_{x_m}^x{\left|G_1(\tau ,s\left(\tau \right),r\left(\tau \right))\right|}_{x_m}{d}_{q_m}^{{\psi }_m}\tau \hfill \\ & \le & \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v\left|\right(r_0+r_1\parallel s\parallel +r_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z\left|\right(s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +(s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|{\int }_{x_{k-1}}^{x_k}{\left(1\right)}_{x_{k-1}}{d}_{q_{k-1}}^{{\psi }_{k-1}}\tau \right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& \frac{\left|w\right|}{|{\Omega }_1|}\left[\right|{\lambda }_1|+|v\left|\right(r_0+r_1\parallel s\parallel +r_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|c_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|v\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|c_i\left|\right|d_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +\frac{|{\Omega }_2|}{|{\Omega }_1|}\left[\right|{\lambda }_2|+|z\left|\right(s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)\hfill \\ & & +\left|z\right|\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)]\prod _{k=1}^{\mu }\left|a_k\right|\hfill \\ & & +(s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )\sum _{k=1}^{\mu +1}\left(\prod _{i=k}^{\mu }\left|a_i\right|\left({\psi }_{k-1}\left(x_k\right)-{\psi }_{k-1}\left(x_{k-1}\right)\right)\right)+\sum _{k=1}^{\mu }\left(\prod _{i=k+1}^{\mu }|a_i\left|\right|b_k|\right)\hfill \\ & =& (s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )A_1+(r_0+r_1\parallel s\parallel +r_2\parallel r\parallel )A_2+A_3.\hfill \end{array}$$

Thus, we have

$$\parallel s\parallel \le (s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )A_1+(r_0+r_1\parallel s\parallel +r_2\parallel r\parallel )A_2+A_3.$$

Similarly, we have

$$\parallel r\parallel \le (s_0+s_1\parallel s\parallel +s_2\parallel r\parallel )B_1+(r_0+r_1\parallel s\parallel +r_2\parallel r\parallel )B_2+B_3.$$

Hence,

$$\begin{array}{ccc}\hfill \parallel s\parallel +\parallel r\parallel & \le & \left[(A_1+B_1)s_1+(A_2+B_2)r_1\right]\parallel s\parallel +\left[(A_1+B_1)s_2+(A_2+B_2)r_2\right]\parallel r\parallel \hfill \\ & & +(A_1+B_1)s_0+(A_2+B_2)r_0+A_3+B_3.\hfill \end{array}$$

Consequently,

$$\parallel (s,r)\parallel \le \frac{(A_1+B_1)s_0+(A_2+B_2)r_0+A_3+B_3}{M^{*}}$$

where $M^{*}=min\{1-(A_1+B_1)s_1+(A_2+B_2)r_1,1-(A_1+B_1)s_2+(A_2+B_2)r_2\},$ which proves that the set $\Theta$ is bounded. By the Leray–Schader alternative, the operator $\mathcal{A}$ has at least one fixed point. Hence, the impulsive quantum coupled system (1) has at least one solution on $[0,T],$ and this completes the proof. □

4. Examples

Example 3.

Consider the following given coupled system of impulsive quantum difference equations with coupled boundary conditions:

$$\left\{\begin{array}{c}{\displaystyle { }_{\frac{k}{3}}{D}_{\frac{k+1}{k+2},\frac{(k^2+1)\sqrt{x}}{k^2+3}}s\left(x\right)=G_1(x,s\left(x\right),r\left(x\right)),x\in \left[\frac{k}{3},\frac{k+1}{3}\right),k=0,1,2,3,4}\hfill \\ {\displaystyle { }_{\frac{k}{3}}{D}_{\frac{k+1}{k+2},\frac{(k^2+1)\sqrt{x}}{k^2+3}}r\left(x\right)=G_2(x,s\left(x\right),r\left(x\right)),x\in \left[\frac{k}{3},\frac{k+1}{3}\right),k=0,1,2,3,4,}\hfill \\ {\displaystyle s\left({\frac{k}{3}}^{+}\right)=\left(\frac{k+2}{k+4}\right)s\left({\frac{k}{3}}^{-}\right)+\left(\frac{k+6}{k+8}\right),k=1,2,3,4,}\hfill \\ {\displaystyle r\left({\frac{k}{3}}^{+}\right)=\left(\frac{k^2+1}{k^2+3}\right)r\left({\frac{k}{3}}^{-}\right)+\left(\frac{k^2+7}{k^2+9}\right),k=1,2,3,4,}\hfill \\ {\displaystyle 4s\left(0\right)+7r\left(\frac{5}{3}\right)=5,3r\left(0\right)-8s\left(\frac{5}{3}\right)=-2,}\hfill \end{array}\right.$$

(15)

where

$$\begin{array}{ccc}\hfill G_1(x,s,r)& =& \frac{13}{2(x+19)}\left(\frac{s^2+2\left|s\right|}{\left|s\right|+1}\right)+\frac{11|cosx|}{10{(x+2)}^2}\left(\frac{r^2+2\left|r\right|}{\left|r\right|+1}\right)+\frac{7}{2},\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill G_2(x,s,r)& =& \frac{9}{2(x+11)}sin\left(s\right)+\frac{14}{7\sqrt{x+9}}{tan}^{-1}\left(r\right)+\frac{2}{19}.\hfill \end{array}$$

(17)

From (15), we can set a function ${\psi }_k\left(x\right)=(k^2+1)\sqrt{x}/(k^2+3)$ and constants $q_k=(k+1)/(k+2)$, $x_k=k/3$, $k=0,1,2,3,4$, $\mu =4$, $x_{\mu +1}=T=5/3$, $a_k=(k+2)/(k+4)$, $b_k=(k+6)/(k+8)$, $c_k=(k^2+1)/(k^2+3)$, $d_k=(k^2+7)/(k^2+9)$, $k=1,2,3,4$, $u=4$, $v=7$, $w=3$, $z=-8$, ${\lambda }_1=5$, ${\lambda }_2=-2.$ With these parameters, we found ${\Omega }_1\approx 15.19548872$, ${\Omega }_2\approx 1.864035088$, ${\Omega }_3\approx 1.714285714$, $A_1\approx 0.4511934059$, $A_2\approx 0.1332498246$, $A_3\approx 3.691234138$, $B_1\approx 0.3083290623$, $B_2\approx 0.5445765601$, $B_3\approx 4.853219495$.

For all $s_1,r_1,s_2,r_2\in \mathbb{R}$ and $x\in [0,5/3]$, we can check the Lipschitz condition (condition $\left(H_1\right)$ in Theorem 1) of two given functions as

$$\begin{array}{ccc}\hfill |G_1(x,s_1,r_1)-G_1(x,s_2,r_2)|& \le & \frac{13}{19}|s_2-s_1|+\frac{11}{20}|r_2-r_1|\le \frac{13}{19}\left(\right|s_2-s_1|+|r_2-r_1\left|\right),\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill |G_2(x,s_1,r_1)-G_2(x,s_2,r_2)|& \le & \frac{9}{22}|s_2-s_1|+\frac{14}{21}|r_2-r_1|\le \frac{14}{21}\left(\right(|s_2-s_1|+|r_2-r_1\left|\right),\hfill \end{array}$$

(19)

Choosing ${\mathcal{L}}_1=13/19$ and ${\mathcal{L}}_2=14/21$ leads us to compute that

$${\mathcal{L}}_1(A_1+B_1)+{\mathcal{L}}_2(A_2+B_2)\approx 0.9715575242<1,$$

which is the satisfied inequality in Theorem 1. Since all assumptions of Theorem 1 are fulfilled, we deduce that the boundary value problem of a coupled impulsive quantum system with respect to another function in (15) with $G_1$, $G_2$ given by (18) and (19), respectively, has a unique solution on $[0,5/3]$.

Example 4.

Consider the following coupled impulsive system via quantum difference with respect to another function with coupled boundary conditions:

$$\left\{\begin{array}{c}{\displaystyle { }_{\frac{k}{4}}{D}_{\frac{2k+1}{3k+4},log\left(\frac{k^2+1}{k+3}+x\right)}s\left(x\right)=G_1(x,s\left(x\right),r\left(x\right)),x\in \left[\frac{k}{4},\frac{k+1}{4}\right),k=0,1,2,3,4,}\hfill \\ {\displaystyle { }_{\frac{k}{4}}{D}_{\frac{2k+1}{3k+4},log\left(\frac{k^2+1}{k+3}+x\right)}r\left(x\right)=G_2(x,s\left(x\right),r\left(x\right)),x\in \left[\frac{k}{4},\frac{k+1}{4}\right),k=0,1,2,3,4,}\hfill \\ {\displaystyle s\left({\frac{k}{4}}^{+}\right)=\left(\frac{\sqrt{k^2+1}}{k+1}\right)s\left({\frac{k}{4}}^{-}\right)+\left(\frac{k}{k+2}\right),k=1,2,3,4,}\hfill \\ {\displaystyle r\left({\frac{k}{4}}^{+}\right)=\left(\frac{\sqrt{k^2+1}}{k^2+3}\right)r\left({\frac{k}{4}}^{-}\right)+\left(\frac{k^2}{k^2+4}\right),k=1,2,3,4,}\hfill \\ {\displaystyle -\frac{3}{2}s\left(0\right)+\frac{5}{4}r\left(\frac{5}{4}\right)=\frac{1}{2},\frac{6}{5}r\left(0\right)-\frac{9}{4}s\left(\frac{5}{4}\right)=-\frac{4}{5},}\hfill \end{array}\right.$$

(20)

where

$$\begin{array}{ccc}\hfill G_1(x,s,r)& =& \frac{1}{2+x}+\frac{43e^{-r^2}}{13+\sqrt{x}}\left(\frac{s^{14}}{1+|s^{13}|}\right)+\frac{119r{sin}^{8}s}{39+\sqrt[3]{x}},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill G_2(x,s,r)& =& \frac{1}{7+x^2}+\frac{37s{cos}^{12}r}{17+\sqrt[5]{x}}+\frac{246{tan}^{-1}\left|s\right|}{\pi (43+\sqrt[7]{x})}\left(\frac{{\left|r\right|}^{2025}}{1+r^{2024}}\right).\hfill \end{array}$$

(22)

From the given system, we can choose a function ${\psi }_k\left(x\right)=log(x+(k^2+1)/(k+3))$ and constants $q_k=(2k+1)/(3k+4)$, $x_k=k/4$, $k=0,1,2,3,4$, $\mu =4$, $x_{\mu +1}=T=5/4$, $a_k=\left(\sqrt{k^2+1}\right)/(k+1)$, $b_k=k/(k+2)$, $c_k=\left(\sqrt{k^2+1}\right)/(k^2+3)$, $d_k=k^2/(k^2+4)$, $k=1,2,3,4$, $u=-3/2$, $v=5/4$, $w=6/5$, $z=-9/4$, ${\lambda }_1=1/2$, ${\lambda }_2=-4/5.$ Then, via Maple computing, we obtain ${\Omega }_1\approx -1.793758811$, ${\Omega }_2\approx 0.008073123480$, ${\Omega }_3\approx -0.7730823045$, $A_1\approx 0.2545620708$, $A_2\approx 0.01365467989$, $A_3\approx 3.503440378$, $B_1\approx 0.004721054780$, $B_2\approx 0.04768914706$, $B_3\approx 1.011654780$.

From the given functions (21) and (22), for each $x\in [0,5/4]$ and $s,r\in \mathbb{R}$, the bounds can be considered as

$$\begin{array}{ccc}\hfill |G_1(x,s,r)|& \le & \frac{1}{2}+\frac{43}{13}\left|s\right|+\frac{119}{39}\left|r\right|,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill |G_2(x,s,r)|& \le & \frac{1}{7}+\frac{37}{17}\left|s\right|+\frac{123}{43}\left|r\right|.\hfill \end{array}$$

(24)

By setting $s_0=1/2$, $s_1=43/13$, $s_2=119/39$, $r_0=1/7$, $r_1=37/17$, $r_2=123/43$, we obtain $(A_1+B_1)s_1+(A_2+B_2)r_1\approx 0.9911418352<1$ and $(A_1+B_1)s_2+(A_2+B_2)r_2\approx 0.9666178244<1$. Application Theorem 2 tells us that a coupled impulsive system via quantum difference with respect to another function with coupled boundary conditions (20) with $G_1$, $G_2$ given by (21) and (22), respectively, has at least one solution on an interval $[0,5/4]$.

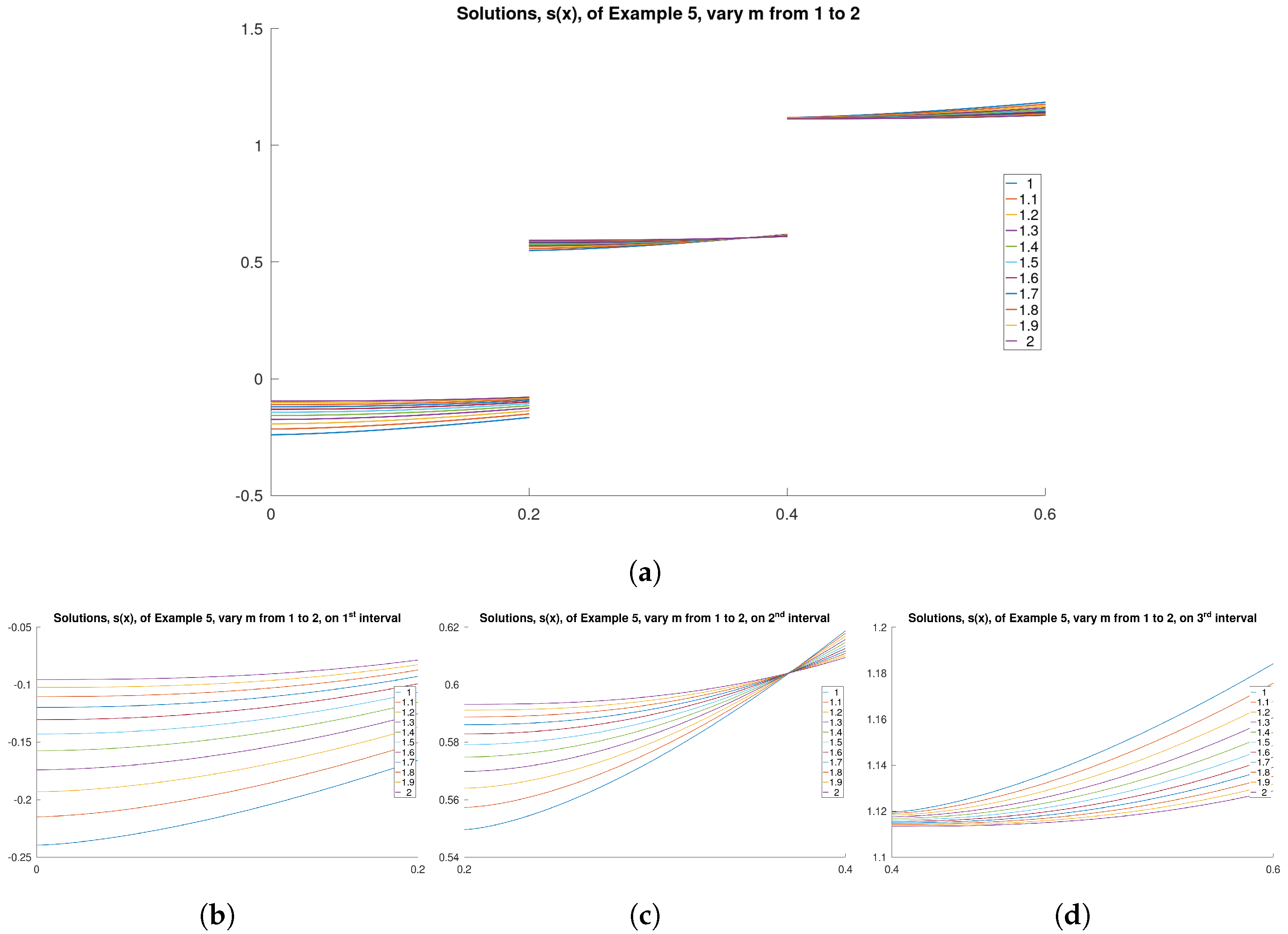
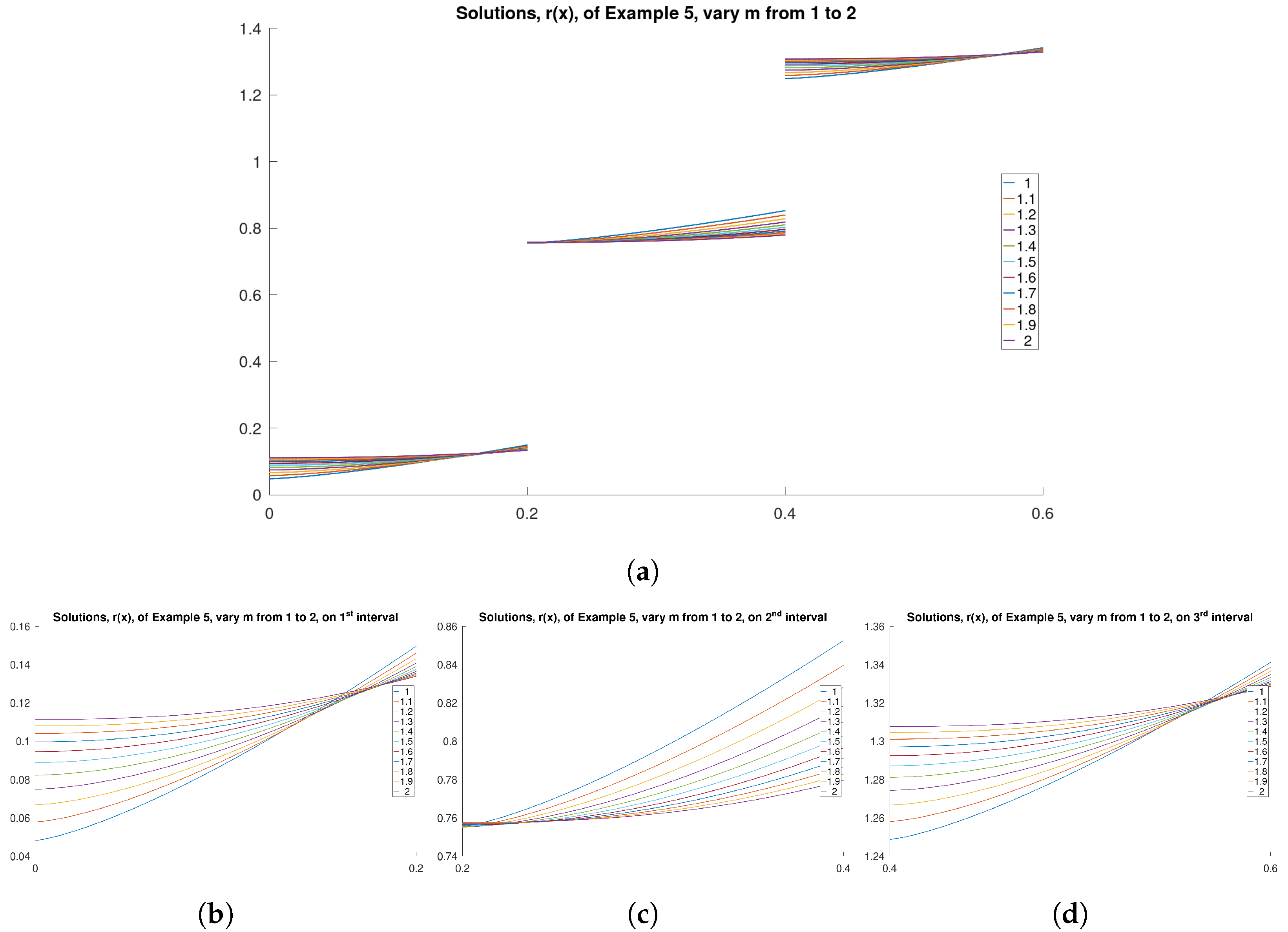
Example 5.

Consider the following linear coupled impulsive system via quantum difference with respect to another function with coupled boundary conditions:

$$\left\{\begin{array}{c}{\displaystyle { }_{\frac{k}{5}}{D}_{\frac{k^2+1}{k^2+3},{(x-\frac{k}{5})}^m}s\left(x\right)=\sqrt{x-\frac{k}{5}},x\in \left[\frac{k}{5},\frac{k+1}{5}\right),k=0,1,2,}\hfill \\ {\displaystyle { }_{\frac{k}{5}}{D}_{\frac{k^2+1}{k^2+3},{(x-\frac{k}{5})}^m}r\left(x\right)=\sqrt[3]{x-\frac{k}{5}},x\in \left[\frac{k}{5},\frac{k+1}{5}\right),k=0,1,2,}\hfill \\ {\displaystyle s\left({\frac{k}{5}}^{+}\right)=\left(\frac{k^2+2}{k^2+5}\right)s\left({\frac{k}{5}}^{-}\right)+\left(\sqrt{\frac{k+1}{k+4}}\right),k=1,2,}\hfill \\ {\displaystyle r\left({\frac{k}{5}}^{+}\right)=\left(\sqrt{\frac{k+3}{k+7}}\right)r\left({\frac{k}{5}}^{-}\right)+\left(\frac{k^2+5}{k^2+8}\right),k=1,2,}\hfill \\ {\displaystyle \frac{11}{53}s\left(0\right)+\frac{13}{59}r\left(\frac{3}{5}\right)=\frac{17}{61},\frac{19}{67}r\left(0\right)+\frac{23}{71}s\left(\frac{3}{5}\right)=\frac{29}{73}.}\hfill \end{array}\right.$$

(25)

Now, we set a function ${\psi }_k\left(x\right)={(x-k/5)}^m$, $m>0$, and constants $q_k=(k^2+1)/(k^2+3)$, $x_k=k/5$, $k=0,1,2$, $\mu =2$, $x_{\mu +1}=T=3/5$, $a_k=(k^2+2)/(k^2+5)$, $b_k=\left(\sqrt{k+1}\right)/\left(\sqrt{k+4}\right)$, $c_k=\left(\sqrt{k+3}\right)/\left(\sqrt{k+7}\right)$, $d_k=(k^2+5)/(k^2+8)$, $k=1,2$, $u=11/53$, $v=13/59$, $w=19/67$, $z=23/71$, ${\lambda }_1=17/61$, ${\lambda }_2=29/73.$ Then, via Maple computing, we obtain ${\Omega }_1\approx 0.04631692614$, ${\Omega }_2\approx 0.1161288406$, ${\Omega }_3\approx 0.1079812207$. From Lemma 2, we can obtain the unique solution $(s,r)\left(x\right)$ of system (25) as shown in the graphs.

We visualize the numerical example by plotting the solutions of Example 5 to provide the reader with a clearer understanding of this work. Figure 3 and Figure 4 depict the solution functions, s and r, respectively, of this example by varying parameter m from 1 to 2. The figures evidently demonstrate that functions s and r exhibit jump discontinuities as anticipated. Figure 3a and Figure 4a provide overviews of functions s and r across the entire considered domain, while Figure 3b–d and Figure 4b–d illustrate the values of functions s and r within each interval.

5. Conclusions

In this paper, we studied a quantum difference coupled impulsive system with respect to another function. First, we transformed the nonlinear coupled impulsive quantum system into a fixed-point problem by using a linear variant of the initial system. Then, we established the existence of a unique solution via Banach contraction mapping principle and the existence of a solution by using Leray–Schauder alternative. The main results are well illustrated by numerical examples.