Abstract
This study computationally investigates small-scale flickering buoyant diffusion flames in externally swirling flows and focuses on identifying and characterizing various distinct dynamical behaviors of the flames. To explore the impact of finite rate chemistry on flame flicker, especially in sufficiently strong swirling flows, a one-step reaction mechanism is utilized for investigation. By adjusting the external swirling flow conditions (the intensity and the inlet angle ), six flame modes in distinct dynamical behaviors were computationally identified in both physical and phase spaces. These modes, including the flickering flame, oscillating flame, steady flame, lifted flame, spiral flame, and flame with a vortex bubble, were analyzed from the perspective of vortex dynamics. The numerical investigation provides relatively comprehensive information on these flames. Under the weakly swirling condition, the flames retain flickering (the periodic pinch-off of the flame) and are axisymmetric, while the frequency nonlinearly increases with the swirling intensity. A relatively high swirling intensity can cause the disappearance of the flame pinch-off, as the toroidal vortex sheds around either the tip or the downstream of the flame. The flicker vanishes, but the flame retains axisymmetric in a small amplitude oscillation or a steady stay. A sufficiently high swirling intensity causes a small Damköhler number, leading to the lift-off of the flame (the local extinction occurs at the flame base). Under the same swirling intensity but large swirling angles, the asymmetric modes of the spiral and vortex bubble flames were likely to occur. With and increasing, these flames exhibit axisymmetric and asymmetric patterns, and their dynamical behaviors become more complex. To feature the vortical flows in flames, the phase portraits are established based on the velocity information of six positions along the axis of the flame, and the dynamical behaviors of various flames are presented and compared in the phase space. Observing the phase portraits and their differences in distinct modes could help identify the dynamical behaviors of flames and understand complex phenomena.
1. Introduction
The study of diffusion flames is closely related to the flame stability and fire safety of many industrial and environmental applications [1,2,3], for instance, combustor stability [4], wild firefighting [5], and energy generation [6,7]. The “flickering” or “puffing” of a buoyant diffusion flame has been of research interest for several decades. The vibratory motion of Bunsen diffusion flames was first discovered and referred to as “the flicker of luminous flames” by Chamberlin and Rose [8]. A similar phenomenon in a Burke–Schumann diffusion flame [9] was described as “the vibration is seen to consist of a progressive necking of the flame which can lead to the formation of a flame bubble, which burns itself out separated from the anchored flame”. It is now well known that the flicker of diffusion flames is a self-exciting flow oscillation and not caused by an externally forced vibration or by the alternate flame extinction and re-ignition.
Many works have attempted to study the underlying mechanism of flickering diffusion flames. Chen et al. [10] conducted flow visualization of a methane jet diffusion flame and provided a piece of confirmative experimental evidence to the vortex-dynamical physical picture that the luminous flame was elongated vertically and contracted horizontally by the outside large toroidal vortices (the buoyancy-induced instability), causing the formation of a “neck” or even the pinch-off of the flame top. For flame flickering, Sato et al. [11] experimentally observed two different modes of tip flickering (merely elongating periodically) and bulk flickering (being separated periodically). Many studies [12,13,14,15] have shown that the buoyancy-induced flickering of flames is a hydrodynamic global instability rather than a convective instability. Interestingly, similar flickering phenomena were observed in buoyant jet and plume flows [16,17,18] and the wake of droplets and porous spheres flame [19,20,21]. Such axisymmetric periodic oscillation can be observed in premixed and partially premixed flames [22,23].
Previous studies [24,25,26,27,28,29] found that the flickering of flame is a buoyancy-dominated flow phenomenon, which is relatively insensitive to other flame parameters. As a result, the flicker frequency is proportional to , where is the gravity and is the diameter of jet nozzle or pool, and the proportionality factor slightly varies among many fuels [25]. This correlation led to the dimensionless scaling law, , where is the Strouhal number and is the Froude number. By directly calculating the non-dimensional circulation of a toroidal vortex within a periodic process of flame flicker, Xia and Zhang [30] obtained
where is the Richardson number; is the flame density and is the ambient density; is the constant prefactor for the advective motion of the toroidal vortex and is a constant relating to the circulation addition of the inflow. By applying the criterion of constant for a vortex shedding process [31], they obtained a generalized scaling law of the flame flickering frequency and validated it with the previous scaling laws and data from existing literature for and . Recently, Yang and Zhang [32] studied the vortex dynamics in flickering buoyant diffusion flames in weakly swirling flows and extended a vortex-dynamical scaling theory for the flame flicker with an external swirl.
Dynamical behaviors of multiple flickering flames have recently attracted much research interest. Kitahata et al. [33] first reported the in-phase and anti-phase modes for two identical oscillating candle flames with different gap distances between flames. Dange et al. conducted flow visualization for dual flickering flames and found that the buoyancy-induced vortices have significant interactions in determining different dynamical modes [34]. This vortex-dynamical mechanism was substantiated by numerical simulations [35,36] and experiments [37,38] for various (laminar and turbulent) diffusion flames.
In recent years, Okamoto et al. [39] investigated three flickering candle flames in an equilateral triangle arrangement and observed four distinct dynamical modes such as the in-phase mode, the partial in-phase mode, the rotation mode, and the death mode. By computationally reproducing these four modes, Yang et al. [40] utilized the vortex interaction (vorticity reconnection and vortex-induced flow) to interpret the underlying mechanisms. For three flickering flames in the isosceles triangle arrangement, Chi et al. [41] carried out systematical experiments and developed a Wasserstein-space-based methodology to identify seven dynamical modes. Forrester [42] experimentally observed four candle flames in a square arrangement and reported an initial-arch-bow-initial “worship” oscillation mode. For larger systems of flickering flames, there are richer dynamical phenomena, while the flame–vortex interaction [43,44] and vortex–vortex interaction [18] present bases for causing dynamical flame modes.
The co-existence of swirling flows and flames is very common in nature and engineering applications. In nature, for example, fire whirls [1,3,45,46,47,48,49] formed by ambient swirls usually present a powerful but disastrous combustion. In many combustion engines, swirling flows are actively introduced to stabilize the diffusion flames [50], and the flame–vortex interaction mechanism is significant [44]. Particularly, there is a need to thoroughly understand the impact of swirling flows on flame flicker, leading to many impactful studies both through experimental approaches and numerical analysis. Chuah and Kushida [51] showed that the external vortical flows stabilized the flickering flame and increased the flame height. Gotoda and coworkers [52,53] studied the stabilization of flames with burner rotation and found that the flame axisymmetric flicker could turn into low-dimensional deterministic chaos at sufficiently large rotation speeds. Specifically, flames become non-axisymmetric and exhibit spiral oscillation, as shown in Figure 1a.
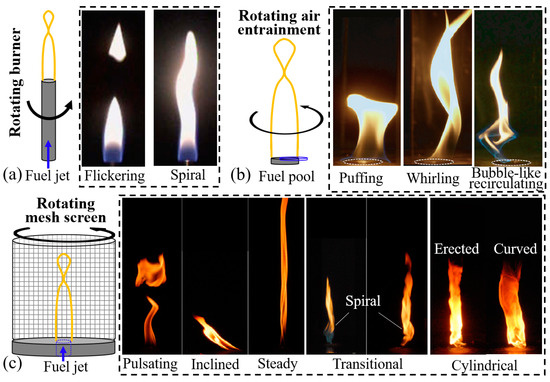
Figure 1.
Various patterns of flickering flames or puffing fires with swirl: (a) the rotating burner [53], (b) the rotating air entrainment due to arranged vanes [47], and (c) the rotating mesh screen [54].
By generating a spinning flow through spiral air entrainment, Coenen et al. [47] reported that sufficiently strong swirling flows could curb the puffing instability, and pool fires might transition into a helical instability or a vortex bubble, as shown in Figure 1b. These flames exhibit complex geometric fashions. Lei et al. [54] utilized the rotation of a mesh screen to generate a vortical flow around a buoyant diffusion flame and identified different flame patterns, such as pulsating, inclined, steady, transitional, and cylindrical flames, shown in Figure 1c. They found that the pressure variation in the azimuthal direction induces asymmetry in the flow field and the flame inclination. Particularly, buoyancy-driven flame oscillation still existed in the weak fire whirls and the pulsation frequencies were higher than that without any swirl [46]. Recently, Ju et al.’s experiments [49] reported a higher pulsating frequency of a fire whirl under increased circulation conditions.
Despite the above-mentioned noticeable progress toward understanding buoyant diffusion flames subject to externally swirling flow conditions, the dynamical behaviors of small-scale buoyant diffusion flames in a large range of swirling flow intensities are still unclear, and the corresponding interpretations based on vortex dynamics were inadequately attempted. Consequently, the present study aims to provide a relatively comprehensive investigation of the dynamical behaviors of flickering buoyant diffusion flames under variable external swirling flow conditions, as well as the vortex-dynamical analysis of the different dynamical behaviors. The rest of the paper is organized as follows. In Section 2, the computational methodology for the flickering buoyant diffusion flames and the external swirling flows is expatiated. Section 3 presents and discusses finite rate chemistry on the flame flicker and the six distinct flame dynamical behaviors. Some concluding remarks are given in Section 4.
2. Computational Methodology
In the present study, the unsteady, three-dimensional, low-Mach, and variable-density flow with chemical heat release was solved using the Fire Dynamics Simulator (FDS) [55], of which the governing equations are as follows:
where Equation (2) is the continuity equation including the density and the velocity vector ; in Equation (3) for mass fraction of specie , and are the diffusion coefficient and the mass production rate per unit volume by chemical reactions, respectively; Equation (4) is the momentum equation that includes the pressure perturbation of , the viscous stress of , the background air density of , and the gravity of ; Equation (5) denotes that the energy equation with the sensible enthalpy of under low Mach number approximation, the backpressure of , the heat release per unit volume of , and the heat flux vector of ; Equation (6) is the state for an ideal gas with the molecular weight of the gas mixture of , the universal gas constant of , and the temperature of . More details of the numerical algorithms for the governing equations can be referred to [55].
Figure 2a shows the square column of for the present computational domain. The characteristic length of the gaseous fuel jet is mm. The bottom wall (grey area) is set as an impermeable, non-slip, and adiabatic solid boundary, while the central fuel inlet of methane gas is ejected at the uniform velocity . The other sides are set as an open boundary condition. On these boundaries, the local pressure gradient determines whether gases flow inwards or outwards. A kinetic energy-conserving central difference scheme was used to carry out the spatial integration, and an explicit second-order predictor/corrector scheme was used to advance the time integration. In the present problem of small-scale buoyant diffusion flames, the one-step overall reaction of the methane/air combustion was adopted to avoid the complexity and high computation cost of a detailed reaction mechanism. The finite rate chemistry (OFC) of the one-step methane/air reaction was used and expatiated in Section 3.1. More details of the computational setups can refer to our recent work [32] on buoyant diffusion flames in weakly swirling flows. In addition, previous computational works [40,56] have proven the reliability of this computational platform in successfully reproducing various synchronization modes in dual and triple flickering flame systems.
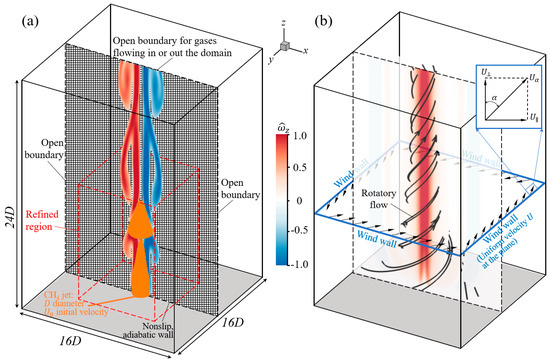
Figure 2.
(a) Schematic of the present simulations including the domain, mesh, and boundaries. (b) The swirling flow is adjusted by the four wind walls with inlet velocity , where is the included angle between velocity components and The contour of the Y−Z plane shows the vertical component of vorticity.
We carried out domain- and mesh-independence studies and adopted a uniform structure mesh of for the parametric studies to ensure high accuracy with reasonable computational cost. Our previous study [32,56] shows that the mesh refinement (each grid has ) is sufficient to capture the essential features of the buoyancy-induced flicker of a laminar diffusion flame. Particularly, the central region ( with ) is further refined in the present cases to analyze closely the flame lift-off behavior due to the emergence of local flame extinction [57]. Figure S1 shows that the flame frequency of the benchmark case (the flickering buoyant diffusion flame without local flame extinction) in the mesh can be accurately calculated.
To impose swirling flows into the computational domain, the four lateral sides loading the inlet air, namely the “wind wall”, are set up, as shown in Figure 2b. is the inlet velocity on the wind wall. and are the normal and azimuthal velocity components, respectively. is the angle between the two components. Consequently, the airflow circulation is formed in the central region. The magnitude and the angle of inlet airflow can be adjusted to control the central vortical flow. Similar approaches [58,59] have been reported to adjust the swirl of the incoming air. To facilitate the following presentation and discussion of results, all quantities are non-dimensionalized by , , and . The intensity of the swirling flow is measured by a dimensionless parameter , which has similarity with the swirl number in defining the ratio of the swirling quantity and the axial jet quantity [50]. The notations of all quantities are consistent with those in the previous study [32].
To validate the swirling flow generated by the present approach, we conducted a series of simulations of non-reacting flows up to . For example, the flow fields are at and in Figure 3a. The vortical flow is characterized by a circular area of significantly concentrated vorticity, forming a vortex core, according to the velocity fields and streamlines in the Y−Z plane and the X−Y planes at 3, 6, and 9. As shown in Figure 3b, the radial profiles of azimuthal velocity in several X−Y planes are plotted for quantifying the vortical flow fields. Importantly, along the radial direction linearly increases up to at and then gradually decays. The trend of is similar to the previous experimental measurement of transverse flow [48]. For the present vortical flows in a large range of , is proportional to and is around . In addition, the radial profiles of from eight azimuth positions are almost the same within the range of , indicating a good axis symmetry of the flow in the region that is of interest. It is noted that a slight non-symmetry of the flow may occur around the fuel inlet, but this has negligible influence on the flame downstream.
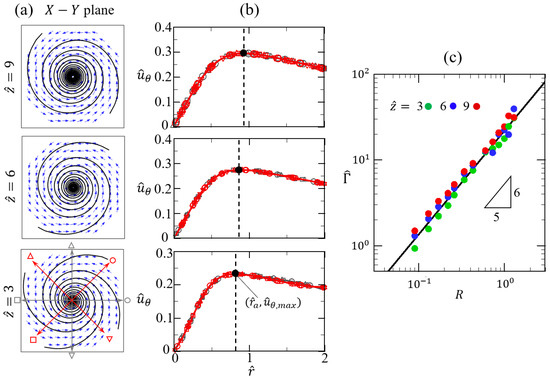
Figure 3.
(a) The flow field (velocity vector and streamline) of the X−Y planes at 3, 6, and 9 for the case at and . (b) The radial profiles of azimuthal velocity . A vortex core is formed within the radial location , where increases monotonously up to the maximum . Eight azimuth angles that are distributed with differences are denoted by different geometrical symbols. (c) The correlation between the circulation and the swirling intension with the fixed . The circulation is defined as along the closed circle with the radius at three cross-sections of , 6, and 9.
Figure 3c shows that the vortical strengths, defined by the dimensionless circulation , are enhanced with increasing when is fixed at . In addition, the scaling correlation of is valid for a quite wide vertical range up to . Figure S2 shows that the maximum azimuthal velocity is proportional to and the radial location of vortex cores generated at different is approximately a constant. Therefore, is proportional to the non-dimensional circulation imposed by the rotatory flow, which is evaluated as . It should be noted that the angular velocity of the swirling flow increases with and is estimated to .
3. Results and Discussion
In this section, we considered the finite rate chemistry on flame flicker and attempted to reproduce flame phenomena observed in the previous experiments [46,47,52,54]. The following questions will be answered.
- How finite rate chemistry affects a flickering buoyant diffusion flame;
- How a flickering buoyant diffusion flame exhibits when the surrounding airflow is swirling;
- Why the flame flicker vanishes once the swirling intensity increases to a certain degree;
- What the vortex-dynamical interpretations for the flame variation under different swirling conditions are.
3.1. Finite Rate Chemistry Effects on Flame Flicker
For pool flames and jet flames with relatively low flow velocities, the flow motion is dominated by buoyancy and remains laminar in most of the flow region (it could be turbulent far downstream of the flame). As a result, the flames are far from extinction when the flow characteristic time is much larger than the chemical reaction characteristic time , and the defined Damköhler number of a flickering buoyant diffusion flame [2,57] can be assumed to be sufficiently large:
where the flow characteristic time is defined as the smallest one among various flow time scales, such as the buoyancy time scale and the convection time scale .
and the chemical reaction characteristic time can be determined by the fastest reaction. Based on the large Damköhler number approximation, the previous computational works [32,40,56] were formulated and carried out on the computational platform of FDS. Consequently, the simplified chemistry model (e.g., the mixing-limited chemical reaction model [55]) is sufficient for modeling the flickering buoyant diffusion flames with relatively small sizes and reactive fuels, and more sophisticated combustion and turbulence models are usually unnecessary.
In the present problem, the externally swirling flow introduces an additional swirl time scale , where is the angular velocity of the swirling flow. Consequently, Equation (8) must be updated by
As a large range of the swirling flow intensity was considered in the present problem, can be too small to invalidate the large Damköhler number assumption, potentially causing local extinction of the flame [28,57]. To qualitatively capture the local extinction of diffusion flames and avoid the unnecessary complexity of a detailed reaction mechanism brought to the present problem, however, a prototypical one-step finite-rate reaction model was used:
where () and () are the concentrations (the reaction orders) of the fuel and the oxidizer, respectively. The reaction rate constant is a function of the pre-exponential factor , the activation energy , the flame temperature , and the universal gas constant . For the convenience of computation, we adopted methane/air combustion [60] as an example, where , J/mol, J/(K∙mol), , and . It should be noted that has a complex dimension in general but it is dimensionless in this example because of .
The biggest advantage of adopting Equation (10) is that only one chemical reaction time scale is introduced to the problem, which can be estimated by
As a result, the Damköhler number of a flickering buoyant diffusion flame under an externally swirling flow is defined by:
In the validation of the present computational methodology and models, we conducted many simulations for the flickering phenomenon of buoyant diffusion flames by adjusting m/s, mm, and m/s2 in the quiescent environment for the range of and . Figure 4 shows that the flickering frequencies of diffusion flames in the low Froude regime () agree well with previous experiments [22,26,61,62]. The scaling relations of and are available for flickering jet flames [27] and puffing pool fires [63], respectively, at a small Froude number regime. In addition, the comparisons between the reaction mechanisms show that the reaction has slight influences on the flickering frequency when the environment airflow is quiescent. The observation is consistent with the finding that the fuel types and the chemistry have an insensitive influence on the flame flicker [64,65,66]. Considering that the local extinction tends to occur with increasing intensities of the swirling flow, we used one-step finite-rate chemistry in all the simulations in the following analysis.
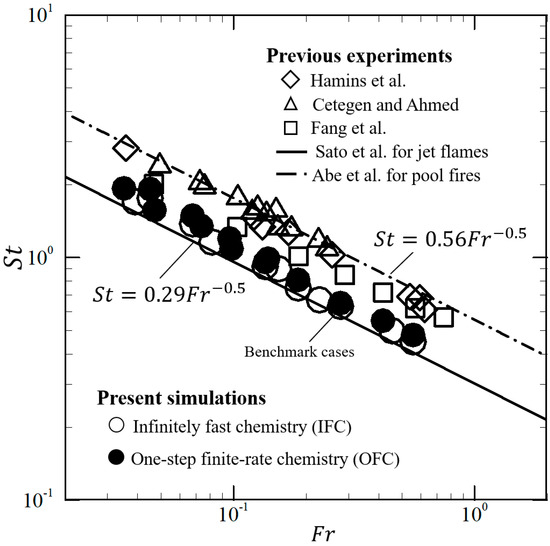
Figure 4.
Comparison of single flickering flames with the scaling laws [27,63] and previous experiments [26,61,62]. The numerical results are obtained by using infinitely fast chemistry (IFC) and one-step finite rate chemistry (OFC).
3.2. Flickering Flames: Benchmark Cases
Figure 5 shows two benchmark cases for a buoyant diffusion jet flame at ( 0.165 m/s, mm, and m/s2) in a quiescent environment (i.e., no externally swirling flow, R = 0), where the infinitely fast chemistry (IFC) assumption is used in Case I, whereas the one-step finite-rate chemistry (OFC) assumption is used in Case II. Due to the instability of flame-induced buoyancy [30,67], an axis-symmetric toroidal vortex is formed as the growth and roll-up of shearing between the flame sheet and the surrounding air, as shown in Figure 5a,b. It should be noted that the flickering flame is in varicose mode (outer buoyancy-induced shear layer is dominated) [67,68] and always keeps axial symmetry (the streamlines always stay in the plane crossing the central axis) during the up-and-down periodic motion.
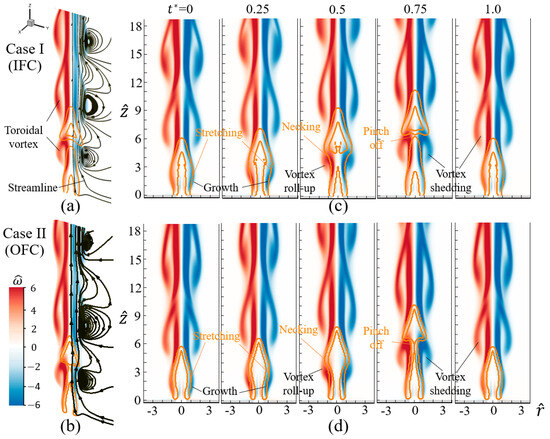
Figure 5.
The contour of vorticity of flickering buoyant diffusion flames for the benchmark cases ( 0.165 m/s, = 100, = 0.28, and no swirling flow) in Figure 2: (a) Case I (IFC) and (b) Case II (OFC). The flame is represented by the orange isoline of heat release. The streamlines are plotted around the flame. (c,d) The time-varying evolution of flames and vortices in the benchmark cases.
In addition, the calculated flickering frequencies are almost the same for the two cases, and the difference is less than 5%. Specifically, these two diffusion flames are nearly identical when comparing their flame behaviors and toroidal vortices during the entire cycle. The vortex formation stretches the flame, the vortex growth causes the flame necking, and the vortex shedding leads to the flame pinch-off. In Figure 5c,d, during the normalized time = = 0~0.25, the vorticity layer occurs at the bottom and stretches the flame; the layer grows curlily along the flame, and the flame is necked ( = 0.25~0.75); the vortex sheds off at = 0.75 to pinch off the flame. During = 0.75~1.0, the shedding vortex and the top bubble of the pinched flame come downstream. Meanwhile, the generation of a new vortex occurs at the flame base, which means the start of a new cycle. In this process, a periodic flickering of the flame forms, namely bulk flickering [11].
The phase portraits of flickering buoyant diffusion flames in Case I and Case II are shown in Figure 6. It is seen that each case has two phase trajectories, which are plotted by the axial components of velocities at three consecutive streamwise locations (i.e., three upstream locations and three downstream locations) in Figure 6a,b. During five periodic flickering processes, the upstream and downstream phase portraits for a flickering flame present the same closed ring shape, as shown in Figure 6c–f. Most remarkably, the nearly identical portraits in the phase space of Case I and Case II indicate that the chemistry has negligible effects on the flame flicker.
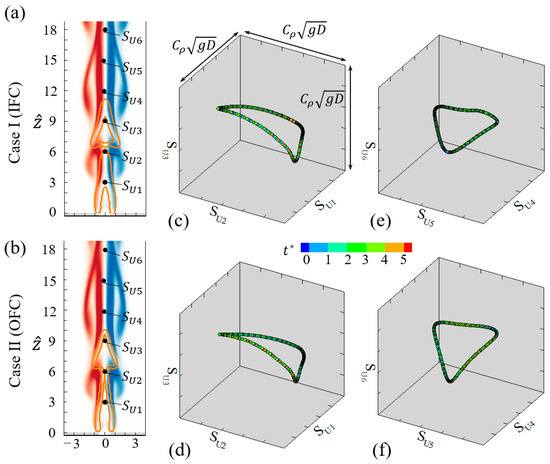
Figure 6.
(a,b) Six axial velocities 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis in the benchmark cases shown in Figure 5. (c–f) Their phase portraits in the cubic space with the same range of , where is the density ratio of ambient air and flame.
In the following sections, various distinct dynamical modes of the flickering buoyant diffusion flame in externally swirling flows with a wide range of swirling intensity 0 and the airflow angle will be illustrated in detail. First, the angle of inlet airflow is fixed at 45°, which sufficiently ensures that the generated region of swirling flow is much larger than flames. Then, are adjusted to obtain asymmetrical flame modes, including spiral and vortex bubble flames. It should be noted that is affected by the swirling intensity, the jet flow, and the computation geometry. A much smaller angle could cause no swirling flow, while a much larger angle would lead to constraints of the computational domain on swirling flow.
3.3. Faster Flickering Flames
Compared with the above benchmark cases of , a similar evolution of the toroidal vortex for the case of = 0.26 and is shown in Figure 7. The flame’s stretching, necking, and pinch-off processes still correspond to the vortex formation, vortex growth, and vortex shedding, respectively. Besides, Figure 7c,d shows that the phase portraits are still a closed ring shape, which means the external swirling flow does not break the topological structure of the dynamical system.
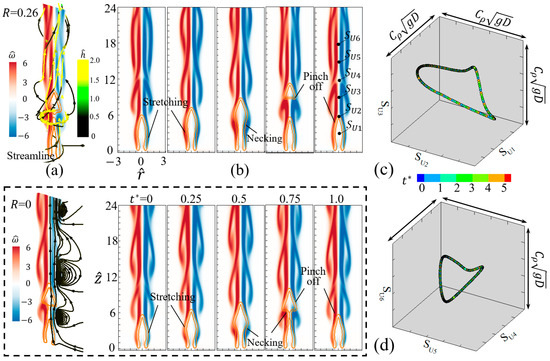
Figure 7.
Faster flicker of the buoyant diffusion flame ( = 100, = 0.28) at with the fixed : (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. All phase spaces have the same range of . The benchmark flame at is shown in the dotted rectangle.
Interesting observations can be made through a more detailed comparison. First, the pinch-off of the flame tends to occur further downstream when is increased and is fixed at . Specifically, the flame at R = 0 is pinched off at = 6.0, while the pinch-off position is = 6.6 in the case of = 0.26. Second, the increase causes the flame pinch-off earlier. It can be seen that the flame in the case of = 0 is just pinched off at = 0.75, while it has already been pinched off for the case R = 0.26. Our previous study [32] addressed this phenomenon in detail and interpreted that the external swirling flow induces an additional vertical flow that expedites the shedding of the toroidal vortex. Third, the streamlines around the flames at = 0 are plotted as the reference and 0.26 and colored by the local helicity density . In fluid mechanics, represents the local orthogonality of the streamline and the vorticity line and is usually used to quantify the local geometrical helix. Specifically, the reference case shows that the streamlines around the flame are in an axisymmetric plane as of streamlines is zero everywhere. In the swirling flow of = 0.26, streamlines are twisted along the circumferential direction to form a spiral ring in three-dimensional space, as shown in Figure 7a. appears in the region with high vorticity, and also the value of increases with . The flame morphology retains the approximate axis symmetry to a certain extent in the local helix flow [32].
We found that there are negligible changes in calculating the flickering frequency by using (the total heat release rate) or (the velocity component in the vertical direction at a fixed point), or (the local temperature) [32]. Here, for example, is used to carry out the fast Fourier transform caculation for the flickering frequency of flames. The results show that the periodic oscillation of for the case of has a frequency of Hz, which is smaller than Hz for the case of .26. The frequency comparison suggests that the flame flickers faster in the external swirling flow. To reveal the underlying mechanism of buoyancy-driven diffusion flames in weakly swirling flows, Yang and Zhang [32] theoretically modeled the frequency relation. First, the generation rate of total circulation inside a control mass was formulated by
where is the radius of the vortex layer around the flame; is the density ratio, which can be measured for a given flame ( in the present flames); and of the control mass represent the unit lengths of the vortex layer in the radial and vertical directions, respectively. Noteworthily, the contribution of the external swirling flow on is the first term of Equation (13) and is not considered in the theory of Xia and Zhang [30]. Second, Yang and Zhang [32] established the integration of Equation (13) to associate the periodic formation process of a toroidal vortex with the flickering process of the flame
where the buoyancy-induced flow is characterized by the constant ; the configuration and the jet inlet condition determine the constant ; the external swirling flow is featured by the prefactor . Third, the frequency relation was obtained by applying a circulation threshold for the toroidal vortex [31,69,70] (i.e., )
where of the initial jet flow and of the external swirling flow are combined into . When the flame has no swirling flow (), Equation (15) can degenerate into that of Xia and Zhang [30]. Therefore, we can obtain the frequency increase of flickering flames in weakly swirling flows as
In Figure 8, the frequency increase of flickering flames obeys the scaling relation of Equation (16). This finding agrees very well with the scaling theory for flickering buoyant diffusion flames in weakly swirling flows [32]. In physics, the swirl of external airflow enhances the gradient of the radial pressure around the flame, which results in an additional source from the baroclinic contribution of for the growth of toroidal vortices [32]. Therefore, the toroidal vortices can satisfy the circulation threshold and shed off from the flames early. Noteworthily, the faster flickering mode is limited to the situation of weakly swirling flows, where the vortex breakdown is absent.
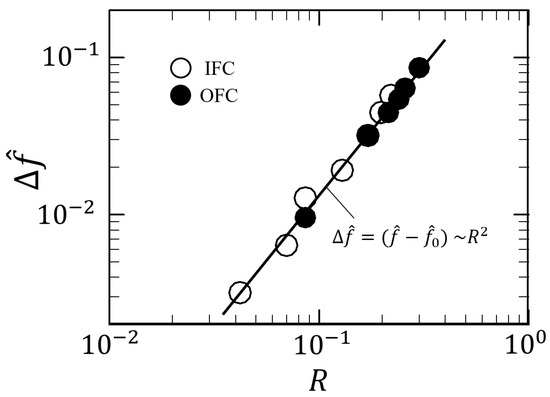
Figure 8.
Comparison between the correlation of with the numerical results of the infinitely fast chemistry (IFC) and the one-step finite rate chemistry (OFC) in the present study. The swirling flows are fixed at .
3.4. Oscillating Flames
As increases up to 0.31 and is fixed at , the diffusion flame is not pinched off anymore, and its top oscillates up and down at a frequency of 13.1 Hz, which is identical to the frequency of vortex shedding, as shown in Figure 9. Compared with the benchmark case of = 0, the circumferential motion of the ambient air is significant, as indicated by the very high helicity density in flame, and the shear layers are highly stretched so that the roll-up of the vortex vanishes. Remarkably, the vortex shedding occurs near the top of the flame. The flame oscillating mode is similar to the “tip flickering” phenomena without any swirl, in which no flame separation occurs and the top is merely oscillating or elongating periodically. Sato et al. [11,27] reported that the tip flickering of flame appears under high fuel jet velocity conditions (), but the bulk flickering (called the flickering int the study) corresponds to the low fuel jet velocity (). This indicates that the external swirling flow has an equivalent influence with the increase of the inlet velocity and can restrain the flame from being separated, namely the occurrence of the (bulk) flickering. In addition, Figure 9c,d shows that phase portraits of oscillating flame vary largely, as the downstream trajectory becomes a distinct disorder in a bigger range while the upstream is a smaller closed ring. The shear layer denoted by the vorticity contour presents that the upstream is compact, but the downstream is unstable and the vortex develops into fragments.
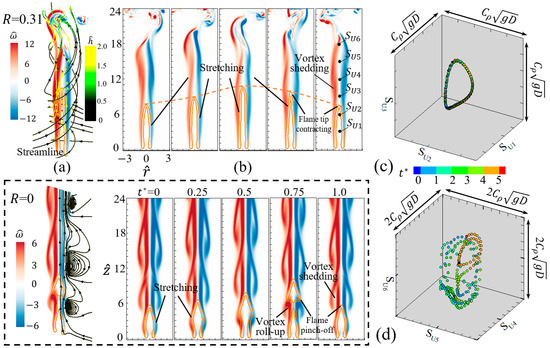
Figure 9.
Tip oscillation of the buoyant diffusion flame ( = 100, = 0.28) at with the fixed : (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. The upstream phase space is twice as large as the downstream is. The benchmark flame at is shown in the dotted rectangle.
3.5. Steady Flames
The steady flame at = 0.43 and is shown in Figure 10. Similar to the oscillating flame in the case of = 0.31, the buoyancy-driven flow around the flame is largely twisted compared with that in the benchmark case of = 0. In the highly swirling flow, the flame has no periodic motion, and its shape remains static all the time, as shown in Figure 10b. This observation was also reported in previous studies [51,54], where the flame flickering can be suppressed by a certain swirling flow. By adding vortical flows around Buk–Schumann diffusion flames, Chuah and Kushida [51] formulated an ideal fire whirl model in that the flame is more stretched and stabilized than the regular diffusion flame. Additionally, Lei et al. [54] experimentally reported that the weak fire whirl at a small heat release rate is steady with a smooth surface. Accordingly, the upstream phase portrait in Figure 10c degenerates into a point, while the downstream portrait in Figure 10d shows an oscillation along the direction. It is seen in Figure 10b that the shear layers are stable for and the instability happens downstream of = 15.
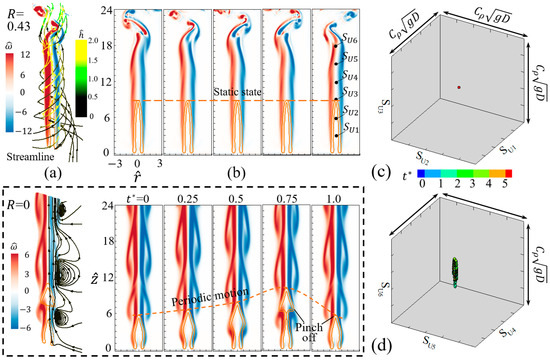
Figure 10.
Steady-state of the buoyant diffusion flame ( = 100, = 0.28) at with the fixed : (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. All phase spaces have the same range of . The benchmark flame at is shown in the dotted rectangle.
To facilitate the quantitative comparison between the vortex shedding and the change in flame height, we plot in Figure 11 the vertical position of the shedding vortex and the maximum flame height at the fixed but different . The change in the vortex shedding-off has three regimes: within (weak swirling flow regime), the buoyant diffusion flames retain the flicker (flickering mode) and gradually increases with ; for , increases rapidly and the pinch-off of flames is suppressed (oscillating mode); for , remains almost constant and the flames become steady (steady mode). Beyond the critical value of about 0.31, the flame flicker is suppressed by the strong swirl. Meanwhile, is nearly a constant between 9 and 10, with a slight decrease for . These three regions, corresponding to the small, intermediate, and large , correlate with the three flame modes illustrated above: the flickering flame, the oscillating flame, and the steady flame, respectively.
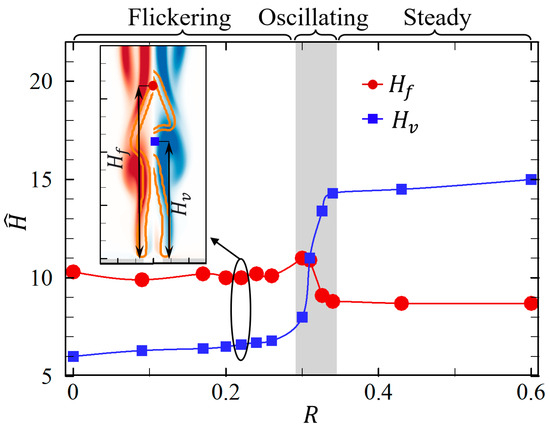
Figure 11.
The vertical position of vortex shedding-off vs. the maximum flame height at the fixed but different .
3.6. Lifted Flame
As increases up to 1.11, the diffusion flame does not attach to the bottom due to the local extinction, and the lifted flame is formed with the lifted height of about . In the present case, the swirl time scale s is much smaller than the buoyancy timescale s and the convection time scale s. Therefore, can be estimated to be at K. Under the strong swirling flow, the ratio of the residence time to the chemical time becomes very small. During the lift-off process of flame, it can be inferred that there is a balance between reaction and transport phenomena when the circulation reaches a certain value. To further decide the critical circulation of the formation, we need to explore more scenarios where detailed reaction mechanisms and complex flows are considered.
As shown in Figure 12a, the streamlines twine around the flame and have a higher at smaller . Additionally, the vorticity contour shows that the shear layers intrude into the central region and form a fishbone-like structure. Compared with the benchmark case of , Figure 12b shows that the flame in the case of and is stable but has no oscillation at all. The strongly swirling flow results in a corner-like flow near the fuel inlet instead of the vortex roll-up induced by the buoyancy in the benchmark flickering flame. The inflating flow with radially outward streamlines is caused by the turning of the incoming flow in the bottom boundary layer. Figure 12c,d shows the nearly motionless phase trajectories of the lifted flame, as the upstream portrait shows a slight change and the downstream one is almost unchanged.
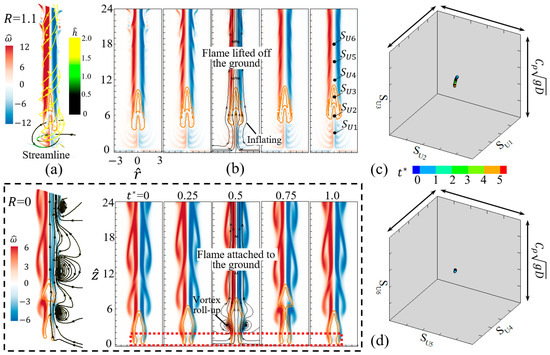
Figure 12.
Lift-off of the buoyant diffusion flame ( = 100, = 0.28) at with the fixed : (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. All phase spaces have the same range of . The benchmark flame at is shown in the dotted rectangle.
To further understand the formation mechanism of lifted flame, the flame formation process at the onset of lifted flame was investigated. The circulation evolution and the representative flame snapshots during the lift-off formation from the attached flame are shown in Figure 13, which shows that the circulation first grows and then plateaus around a constant value. From the beginning to = 6, no change in the circulation is observed, during which the swirling flow is still not imposed upon the central flame. The flame keeps flickering very well ( and ). From = 6 to = 11, the circulation continues to increase gradually, rendering a tall and slender flame ( and ). After = 11, the growth of circulation stops, which is accompanied by a steady flame mode (). During = 11~19, the flame lifts off, the boundary shear layer (a corner flow) intrudes into the central region, and a fishbone-like vortical structure is formed. In the initial stage of lift-off, the flame transitions into a small one (). Subsequently, the flame stabilizes gradually, and its size becomes big ().
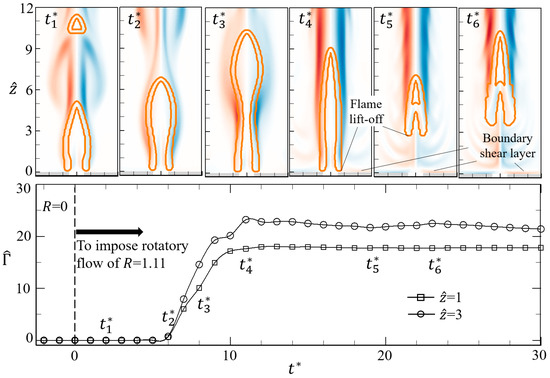
Figure 13.
The variation of circulation with time during the lift-off formation from the attached flame. The circulation is defined as along the closed circle with the radius . The two lines represent the cross-section at and 3, respectively. Six instantaneous snapshots of flame and vorticity are included.
3.7. Spiral Flame
An asymmetric flame was identified for the case of and , where the flame presents a spiral motion, especially the irregular spin of the top of the flame. The spiral flame is similar to the sinuous mode of non-swirling jet flames at large Froude number [67,68], in which the outer vortex helix grows and twines around the flame. In the downstream region, the flame tip inclines apparently, and the nearby streamlines are in the disturbance. As shown in Figure 14b, our simulations captured the dynamical feature of spiral flame. The top of the flame behaves like a swing instead of symmetrically up-and-down for the case of and the same . To clearly show the asymmetric swing, the streamlines crossing the flame are plotted within the vorticity contour. In the downstream region of , there is a symmetry break of shear layers around the flame, leading to the curved streamlines, while the symmetry of flame, vortical flow, and streamlines retain well for the case of .
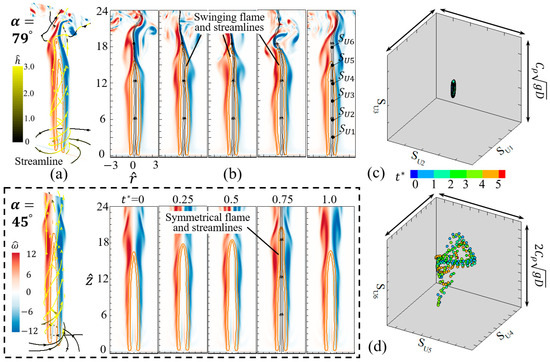
Figure 14.
Spiral structure of the buoyant diffusion flame (, = 0.40) in the swirling flow with and . (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. All phase spaces have the same range of . In the dotted rectangle, the oscillating flame (, = 0.40) at and is shown to facilitate comparison.
Detailed comparisons between the two flames in the three-dimensional view and their orthogonal projections are presented in Figure 15. By comparing the patterns of flames (the orange iso-surface of heat release) and vorticial structures (the grey iso-surface of vorticity) in the two cases, it should be noted that the external swirling flows with different have an impact on the vortical flow due to the formation of the twisted vortex around the flame surface. However, the vortical structure in the spiral flame presents a stronger spin than that in the case of . The outer vortex is dynamically coupled with the flame and shapes it into the sinuous. Particularly, the shedding vortex breaks into some small-scale structures (many small vortex tubes denoted by the iso-surface of vorticity in the downstream region) when the swirling flow has a big inlet angle. At the same , the bigger is, the smaller the radial component of the inlet velocity is. Therefore, the central flow in the case of is more likely to spread out than that in the case of . These observations provide more information about similar phenomena and could be useful to make comparisons in future experiments. In Figure 14c, the upstream phase portrait is a slender ellipse, while the downstream portrait shows a quasi-cycle in the bigger range, particularly at . Their two-dimensional projections are shown in Figure S3. The features of phase portraits are consistent with the dynamic behaviors of the spiral flame.
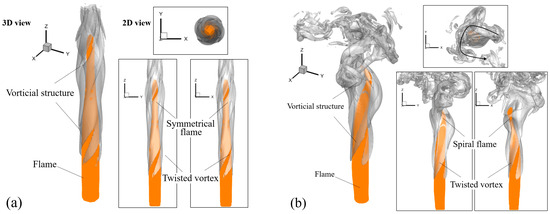
Figure 15.
The three-dimensional view and their three-view drawings of (a) the oscillating flame () and (b) the spiral flame () corresponding to Figure 14, respectively. The flame is represented by the orange iso-surface of heat release. The vorticial structure is denoted by the grey iso-surface of vorticity.
3.8. Vortex Bubble Flame
A hat-like flame is captured for the case of and , in which the lifted flame has a vortex bubble at the flame base. Different from the lifted height for the case of and , the vortex bubble is closer to the fuel inlet and stays close around the vertical position of , as shown in Figure 16a. Particularly, the higher helicity density in the vortex bubble flame can be observed along the streamlines at the bottom region, compared with that in the case of and . To clearly illustrate the dynamic features of the vortex bubble flame, the flame and vortex structures within the time interval of are shown in Figure 16b. Different from the lifted flame shown in Figure 12b, in which the inflating streamlines go through the flame and no circulation exists, the base of the vortex bubble flame kicks outward to form an apparent vortex bubble.
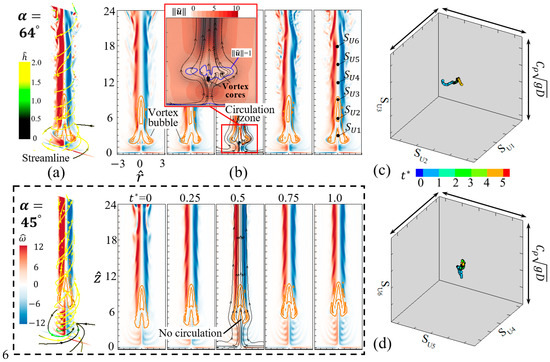
Figure 16.
Vortex bubble of the buoyant diffusion flame ( = 100, = 0.28) in the swirling flow with and . (a) the flow around the flame, (b) the time-varying evolution of the flame, (c,d) the phase portrait in the cubic space plotted by six velocity components 1, 2, 3, 4, 5, and 6 at 3, 6, 9, 12, 15, and 18, respectively, along the central axis. All phase spaces have the same range of . In the dotted rectangle, the lifted flame at and α = 45° is shown to facilitate comparison.
To understand the mechanism underlying the formation of vortex bubble flame, it should be noted that the basic definition of vortex breakdown is the abrupt change in vortex structure with retardation along the vortex core and the corresponding divergence of stream surfaces [71,72]. It is seen from Figure 16b that the streamlines contract in the central region, diverge outwardly, and finally form a convergence toward the downstream. The abrupt change causes a circulation zone where the flow velocities have relatively small magnitudes. In particular, the small vortex cores are generated within the range of . The bubble region for the vortex breakdown is unstable, and its barycenter and shape vary with time. As shown in Figure 16c,d, the phase portraits are a warping string within a relatively small range instead of a closed topological structure within a relatively big range.
As an interesting extension of the present study, Figure 17 shows a qualitative comparison of the vortex bubble flame with Chung et al.’s simulation of the blue whirl [73]. Similar features of the flame and the flow are captured in the present simulations. Previous studies [48,74,75,76] suggested that the formation of the blue whirl is accompanied by the occurrence of the vortex breakdown (the bubble, helical, or whirling structures), which is consistent with the present finding (the flame structure is shaped by the vortex bubble). Moreover, the present numerical investigation that the vortex bubble flame emerges at a relatively large (it corresponds to the swirling condition of ) agrees with the previous experimental observation that the blue whirl falls in a circulation-dominated flow regime. The implications of the vortex bubble flame for understanding blue whirl merits future studies.
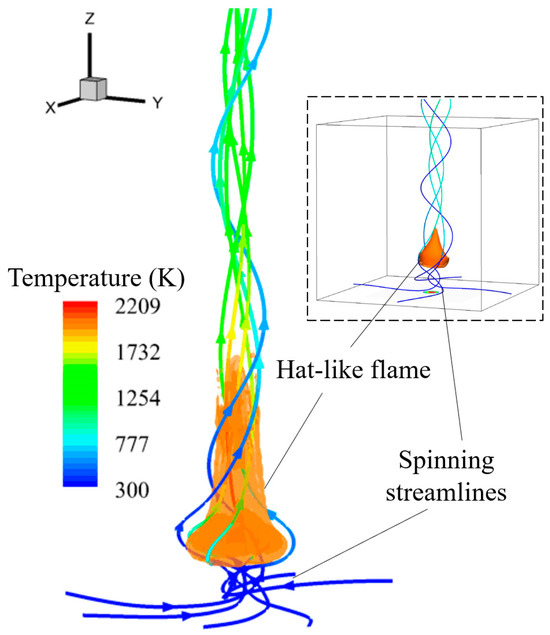
Figure 17.
Comparison of the flame with vortex bubble and the simulated blue whirl (insert figure) [73]. The streamlines are colored by the temperature and the flame is plotted by the iso-surface of the heat release rate at 1 MW/m3.
4. Concluding Remarks
Previous experimental works have made noticeable progress toward understanding buoyant diffusion flames in externally swirling flows. However, their dynamical behaviors in a large range of swirling flow intensity are still unclear, and the corresponding vortex interpretations were inadequately attempted due to the challenges of measuring the flow and temperature of flames. This study presents a comprehensive computational investigation of the small-scale flickering buoyant diffusion flames in externally swirling flows with a wide range of swirling intensity 0 and the angle of inlet airflow. Buoyant diffusion flames exhibit six distinct dynamical modes at different and , namely the flickering flame, the oscillating flame, the steady flame, the lifted flame, the spiral flame, and the flame with a vortex bubble, which were scattered and reported in a few previous experimental studies. These flames exhibit axisymmetric to asymmetric patterns. The dynamical behaviors of these flame modes are illustrated in the phase space and analyzed from the perspective of vortex dynamics.
In the weak swirl regime ( < 0.31), the buoyancy-induced flame flicker becomes faster nonlinearly with increasing , where the increase of obeys the scaling relation of . Since the vortex shedding occurs downstream of the flame, the flame flicker is suppressed, and instead, the flame has an oscillating tip or remains in a steady state. Higher can induce higher circulation at the flame base and a smaller Damköhler number to make the flame lift off the bottom. The local extinction phenomenon was qualitatively captured by using a one-step finite-rate chemistry model in the present simulation. In addition, the spiral flame mode and the vortex bubble flame mode were computationally reproduced by using larger swirl angles .
Based on the understanding that phase portraits are an invaluable tool in studying dynamical systems, different flame modes are illustrated and identified in the phase space. Specifically, the flame features and phase portraits for the six modes are summarized as follows:
- The flickering flames have the distinct feature that the periodic shedding of the toroidal vortex around the flame. The portraits of these flames are the closed ring shape. Additionally, the topological structure of the flames is broken when the externally swirling flow is weak, for instance, the weak swirling conditions of 0.31 and in this study.
- The oscillating mode exhibits that the toroidal vortex sheds off behind the flame and occurs at the intermediate region (for instance, and in this study). The upstream portrait of these oscillating flames is the closed ring, while a big disturbance occurs in the downstream portrait.
- The steady mode hardly has the formation of a toroidal vortex around the flame, as the vortex shedding occurs far behind the flame. In the steady flames, the upstream phase portrait degenerates into a point, while the downstream portrait exhibits small oscillation. The formation of steady flames corresponds to the relevantly large region, for instance, and in this study.
- The lifted flames detach from the bottom wall due to the relatively small number. The phase portraits of the flames are nearly motionless. The present study shows that the large (>1.10) with the fixed causes a very small ratio of the residence time to the chemical time at the flame base, thereby leading to the lift-off of the flame.
- The spiral flames have a distinct feature in that the symmetry of shear layers around the flame is broken, compared with the four modes of flickering, oscillating, steady, and lifted flames. In these flames, the upstream phase portrait is a small ellipse, while the downstream portrait shows a big quasi-cycle. The asymmetric flames occur at a large , while is the same. For instance, = 0.60 and = 79° in this study.
- The vortex bubble flames show a different pattern in the occurrence of the vortex bubble for the vortex breakdown in the flame base, compared with the lifted flame. The phase portraits present a warping string within a relatively small range as the unstable bubble has time-varying barycenter and shape. These flames occur at the relatively large and ; for instance, = 1.30 and = 64° in this study.
While the present work provides an understanding of various dynamical modes of diffusion flames, we fully recognize that it does not address the challenging problem of the origin and transition of these modes in a wider parameter space formed by the swirling intensity, the swirling angle, and the Reynolds number. In addition, the influences of turbulence/chemistry interaction in large-scale flames with radiative heat loss were not considered in the present study. The relevant studies merit future work.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/sym16030292/s1. See the supplementary material for more details about the validation of mesh refinement, the generated vortical flows, and the phase trajectories of the spiral flame.
Author Contributions
Conceptualization, T.Y. and P.Z.; resources, Y.M. and P.Z.; writing—original draft preparation, T.Y.; writing—review and editing, Y.M. and P.Z.; supervision, Y.M. and P.Z.; funding acquisition, P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 52176134) and partially by the APRC-CityU New Research Initiatives/Infrastructure Support from Central of City University of Hong Kong (No. 9610601).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge the National Supercomputer Center in Guangzhou (Tianhe-2) for high-performance computing services.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Emmons, H.W.; Ying, S.-J. The fire whirl. Proc. Combust. Inst. 1967, 11, 475–488. [Google Scholar] [CrossRef]
- Bilger, R.W. Turbulent diffusion flames. Annu. Rev. Fluid Mech. 1989, 21, 101–135. [Google Scholar] [CrossRef]
- Tohidi, A.; Gollner, M.J.; Xiao, H. Fire whirls. Annu. Rev. Fluid Mech. 2018, 50, 187–213. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, D.; Ni, S.; David, T.; Zhang, Y. Entropy and flame transfer function analysis of a hydrogen-fueled diffusion flame in a longitudinal combustor. Energy 2020, 194, 116870. [Google Scholar] [CrossRef]
- Liu, N.; Lei, J.; Gao, W.; Chen, H.; Xie, X. Combustion dynamics of large-scale wildfires. Proc. Combust. Inst. 2021, 38, 157–198. [Google Scholar] [CrossRef]
- Ruoso, A.C.; Corrêa Bitencourt, L.; Urach Sudati, L.; Klunk, M.A.; Caetano, N.R. New parameters for the forest biomass waste ecofirewood manufacturing process optimization. Periódico Tchê Química 2019, 16, 560–571. [Google Scholar] [CrossRef]
- Yang, F.; Wang, T.; Deng, X.; Dang, J.; Huang, Z.; Hu, S.; Li, Y.; Ouyang, M. Review on hydrogen safety issues: Incident statistics, hydrogen diffusion, and detonation process. Int. J. Hydrogen Energy 2021, 46, 31467–31488. [Google Scholar] [CrossRef]
- Chamberlin, D.S.; Rose, A. The flicker of luminous flames. Proc. Combust. Inst. 1948, 1–2, 27–32. [Google Scholar] [CrossRef]
- Barr, J. Diffusion flames. Proc. Combust. Inst. 1953, 4, 765–771. [Google Scholar] [CrossRef]
- Chen, L.-D.; Seaba, J.; Roquemore, W.; Goss, L. Buoyant diffusion flames. Proc. Combust. Inst. 1989, 22, 677–684. [Google Scholar] [CrossRef]
- Sato, H.; Amagai, K.; Arai, M. Flickering frequencies of diffusion flames observed under various gravity fields. Proc. Combust. Inst. 2000, 28, 1981–1987. [Google Scholar] [CrossRef]
- Maxworthy, T. The flickering candle: Transition to a global oscillation in a thermal plume. J. Fluid Mech. 1999, 390, 297–323. [Google Scholar] [CrossRef]
- Jiang, X.; Luo, K. Combustion-induced buoyancy effects of an axisymmetric reactive plume. Proc. Combust. Inst. 2000, 28, 1989–1995. [Google Scholar] [CrossRef]
- Moreno-Boza, D.; Coenen, W.; Sevilla, A.; Carpio, J.; Sánchez, A.; Liñán, A. Diffusion-flame flickering as a hydrodynamic global mode. J. Fluid Mech. 2016, 798, 997–1014. [Google Scholar] [CrossRef]
- Moreno-Boza, D.; Coenen, W.; Carpio, J.; Sánchez, A.L.; Williams, F.A. On the critical conditions for pool-fire puffing. Combust. Flame 2018, 192, 426–438. [Google Scholar] [CrossRef]
- Wimer, N.T.; Lapointe, C.; Christopher, J.D.; Nigam, S.P.; Hayden, T.R.; Upadhye, A.; Strobel, M.; Rieker, G.B.; Hamlington, P.E. Scaling of the puffing Strouhal number for buoyant jets and plumes. J. Fluid Mech. 2020, 895, A26. [Google Scholar] [CrossRef]
- Gergely, A.; Paizs, C.; Tötös, R.; Néda, Z. Oscillations and collective behavior in convective flows. Phys. Fluids 2021, 33, 124104. [Google Scholar] [CrossRef]
- Patil, O.T.; Meehan, M.A.; Hamlington, P.E. Puffing frequency of interacting buoyant plumes. Phys. Rev. Fluids 2022, 7, L111501. [Google Scholar] [CrossRef]
- Pandey, K.; Basu, S.; Krishan, B.; Gautham, V. Dynamic self-tuning, flickering and shedding in buoyant droplet diffusion flames under acoustic excitation. Proc. Combust. Inst. 2021, 38, 3141–3149. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Wei, Y.; Liu, S. Vortex shedding controlled combustion of the wake flame of an n-heptane wetted porous sphere. AIP Adv. 2022, 12, 105216. [Google Scholar] [CrossRef]
- Thirumalaikumaran, S.; Vadlamudi, G.; Basu, S. Insight into flickering/shedding in buoyant droplet-diffusion flame during interaction with vortex. Combust. Flame 2022, 240, 112002. [Google Scholar] [CrossRef]
- Durox, D.; Yuan, T.; Baillot, F.; Most, J. Premixed and diffusion flames in a centrifuge. Combust. Flame 1995, 102, 501–511. [Google Scholar] [CrossRef]
- Fujisawa, N.; Okuda, T. Effects of co-flow and equivalence ratio on flickering in partially premixed flame. Int. J. Heat Mass Transf. 2018, 121, 1089–1098. [Google Scholar] [CrossRef]
- Zukoski, E.; Cetegen, B.; Kubota, T. Visible structure of buoyant diffusion flames. Proc. Combust. Inst. 1985, 20, 361–366. [Google Scholar] [CrossRef]
- Buckmaster, J.; Peters, N. The infinite candle and its stability—A paradigm for flickering diffusion flames. Proc. Combust. Inst. 1988, 21, 1829–1836. [Google Scholar] [CrossRef]
- Cetegen, B.M.; Ahmed, T.A. Experiments on the periodic instability of buoyant plumes and pool fires. Combust. Flame 1993, 93, 157–184. [Google Scholar] [CrossRef]
- Sato, H.; Amagai, K.; Arai, M. Diffusion flames and their flickering motions related with Froude numbers under various gravity levels. Combust. Flame 2000, 123, 107–118. [Google Scholar] [CrossRef]
- Briones, A.M.; Aggarwal, S.K.; Katta, V.R. A numerical investigation of flame liftoff, stabilization, and blowout. Phys. Fluids 2006, 18, 043603. [Google Scholar] [CrossRef]
- Sitte, M.P.; Doan, N.A.K. Velocity reconstruction in puffing pool fires with physics-informed neural networks. Phys. Fluids 2022, 34, 087124. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, P. A vortex-dynamical scaling theory for flickering buoyant diffusion flames. J. Fluid Mech. 2018, 855, 1156–1169. [Google Scholar] [CrossRef]
- Gharib, M.; Rambod, E.; Shariff, K. A universal time scale for vortex ring formation. J. Fluid Mech. 1998, 360, 121–140. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, P. Faster flicker of buoyant diffusion flames by weakly rotatory flows. Theor. Comput. Fluid Dyn. 2023, 37, 781–798. [Google Scholar] [CrossRef]
- Kitahata, H.; Taguchi, J.; Nagayama, M.; Sakurai, T.; Ikura, Y.; Osa, A.; Sumino, Y.; Tanaka, M.; Yokoyama, E.; Miike, H. Oscillation and synchronization in the combustion of candles. J. Phys. Chem. A 2009, 113, 8164–8168. [Google Scholar] [CrossRef]
- Dange, S.; Pawar, S.A.; Manoj, K.; Sujith, R. Role of buoyancy-driven vortices in inducing different modes of coupled behaviour in candle-flame oscillators. AIP Adv. 2019, 9, 015119. [Google Scholar] [CrossRef]
- Bunkwang, A.; Matsuoka, T.; Nakamura, Y. Similarity of dynamic behavior of buoyant single and twin jet-flame (s). J. Therm. Sci. Technol. 2020, 15, JTST0028. [Google Scholar] [CrossRef]
- Tokami, T.; Toyoda, M.; Miyano, T.; Tokuda, I.T.; Gotoda, H. Effect of gravity on synchronization of two coupled buoyancy-induced turbulent flames. Phys. Rev. E 2021, 104, 024218. [Google Scholar] [CrossRef]
- Fujisawa, N.; Imaizumi, K.; Yamagata, T. Synchronization of dual diffusion flame in co-flow. Exp. Therm Fluid Sci. 2020, 110, 109924. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Ge, H.; Deng, J.; Zhou, S.; Wang, X.; Cheng, F. On the influence of distance between two jets on flickering diffusion flames. Combust. Flame 2019, 201, 23–30. [Google Scholar]
- Okamoto, K.; Kijima, A.; Umeno, Y.; Shima, H. Synchronization in flickering of three-coupled candle flames. Sci. Rep. 2016, 6, 36145. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Chi, Y.; Zhang, P. Vortex interaction in triple flickering buoyant diffusion flames. Proc. Combust. Inst. 2022, 39, 1893–1903. [Google Scholar] [CrossRef]
- Chi, Y.; Yang, T.; Zhang, P. Dynamical mode recognition of triple flickering buoyant diffusion flames in Wasserstein space. Combust. Flame 2023, 248, 112526. [Google Scholar] [CrossRef]
- Forrester, D.M. Arrays of coupled chemical oscillators. Sci. Rep. 2015, 5, 16994. [Google Scholar] [CrossRef]
- Xia, X.; Fu, C.; Yang, Y.; Yang, X.; Gao, Y.; Qi, F. Vortex formation and frequency tuning of periodically-excited jet diffusion flames. Proc. Combust. Inst. 2021, 38, 2067–2074. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, J.; Xu, L.; An, Q.; Han, X.; Zhang, C.; Li, L.; Xia, X.; Qi, F. Experimental investigation of the helical mode in a stratified swirling flame. Combust. Flame 2022, 244, 112268. [Google Scholar] [CrossRef]
- Battaglia, F.; Rehm, R.G.; Baum, H.R. The fluid mechanics of fire whirls: An inviscid model. Phys. Fluids 2000, 12, 2859–2867. [Google Scholar] [CrossRef]
- Lei, J.; Liu, N.; Satoh, K. Buoyant pool fires under imposed circulations before the formation of fire whirls. Proc. Combust. Inst. 2015, 35, 2503–2510. [Google Scholar] [CrossRef]
- Coenen, W.; Kolb, E.J.; Sánchez, A.L.; Williams, F.A. Observed dependence of characteristics of liquid-pool fires on swirl magnitude. Combust. Flame 2019, 205, 1–6. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.; Xia, X.; Zhang, P.; Qi, F. An experimental study of the blue whirl onset. Proc. Combust. Inst. 2022, 39, 3705–3714. [Google Scholar] [CrossRef]
- Ju, X.; Mizuno, M.; Matsuoka, T.; Yamazaki, T.; Kuwana, K.; Nakamura, Y. Effect of circulation on flame heights over liquid fuel pools. Combust. Flame 2022, 246, 112435. [Google Scholar] [CrossRef]
- Candel, S.; Durox, D.; Schuller, T.; Bourgouin, J.-F.; Moeck, J.P. Dynamics of swirling flames. Annu. Rev. Fluid Mech. 2014, 46, 147–173. [Google Scholar] [CrossRef]
- Chuah, K.H.; Kushida, G. The prediction of flame heights and flame shapes of small fire whirls. Proc. Combust. Inst. 2007, 31, 2599–2606. [Google Scholar] [CrossRef]
- Gotoda, H.; Ueda, T.; Shepherd, I.G.; Cheng, R.K. Flame flickering frequency on a rotating Bunsen burner. Chem. Eng. Sci. 2007, 62, 1753–1759. [Google Scholar] [CrossRef]
- Gotoda, H.; Asano, Y.; Chuah, K.H.; Kushida, G. Nonlinear analysis on dynamic behavior of buoyancy-induced flame oscillation under swirling flow. Int. J. Heat Mass Transf. 2009, 52, 5423–5432. [Google Scholar] [CrossRef]
- Lei, J.; Liu, N.; Jiao, Y.; Zhang, S. Experimental investigation on flame patterns of buoyant diffusion flame in a large range of imposed circulations. Proc. Combust. Inst. 2017, 36, 3149–3156. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire dynamics simulator user’s guide. NIST Spec. Publ. 2013, 1019, 1–339. [Google Scholar]
- Yang, T.; Xia, X.; Zhang, P. Vortex-dynamical interpretation of anti-phase and in-phase flickering of dual buoyant diffusion flames. Phys. Rev. Fluids 2019, 4, 053202. [Google Scholar] [CrossRef]
- Linán, A.; Vera, M.; Sánchez, A.L. Ignition, liftoff, and extinction of gaseous diffusion flames. Annu. Rev. Fluid Mech. 2015, 47, 293–314. [Google Scholar] [CrossRef]
- Mullen, J.B.; Maxworthy, T. A laboratory model of dust devil vortices. Dyn. Atmos. Ocean. 1977, 1, 181–214. [Google Scholar] [CrossRef]
- Kolb, E.J. An Experimental Approach to the Blue Whirl; University of California: San Diego, CA, USA, 2018. [Google Scholar]
- Westbrook, C.K.; Dryer, F.L. Chemical kinetic modeling of hydrocarbon combustion. Prog. Energy Combust. Sci. 1984, 10, 1–57. [Google Scholar] [CrossRef]
- Fang, J.; Wang, J.-W.; Guan, J.-F.; Zhang, Y.-M.; Wang, J.-J. Momentum-and buoyancy-driven laminar methane diffusion flame shapes and radiation characteristics at sub-atmospheric pressures. Fuel 2016, 163, 295–303. [Google Scholar] [CrossRef]
- Hamins, A.; Yang, J.; Kashiwagi, T. An experimental investigation of the pulsation frequency of flames. Proc. Combust. Inst. 1992, 24, 1695–1702. [Google Scholar] [CrossRef]
- Abe, H.; Ito, A.; Torikai, H. Effect of gravity on puffing phenomenon of liquid pool fires. Proc. Combust. Inst. 2015, 35, 2581–2587. [Google Scholar] [CrossRef]
- Sahu, K.; Kundu, A.; Ganguly, R.; Datta, A. Effects of fuel type and equivalence ratios on the flickering of triple flames. Combust. Flame 2009, 156, 484–493. [Google Scholar] [CrossRef]
- Darabkhani, H.G.; Bassi, J.; Huang, H.; Zhang, Y. Fuel effects on diffusion flames at elevated pressures. Fuel 2009, 88, 264–271. [Google Scholar] [CrossRef]
- Bahadori, M.; Zhou, L.; Stocker, D.; Hegde, U. Functional dependence of flame flicker on gravitational level. AIAA J. 2001, 39, 1404–1406. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, X.; Gao, Y. Instability transition of a jet diffusion flame in quiescent environment. Proc. Combust. Inst. 2021, 38, 4971–4978. [Google Scholar] [CrossRef]
- Cetegen, B.; Dong, Y. Experiments on the instability modes of buoyant diffusion flames and effects of ambient atmosphere on the instabilities. Exp. Fluids 2000, 28, 546–558. [Google Scholar] [CrossRef]
- Lawson, J.M.; Dawson, J.R. The formation of turbulent vortex rings by synthetic jets. Phys. Fluids 2013, 25, 105113. [Google Scholar] [CrossRef]
- Xia, X.; Mohseni, K. Far-field momentum flux of high-frequency axisymmetric synthetic jets. Phys. Fluids 2015, 27, 115101. [Google Scholar] [CrossRef]
- Hall, M. Vortex breakdown. Annu. Rev. Fluid Mech. 1972, 4, 195–218. [Google Scholar] [CrossRef]
- Lucca-Negro, O.; O’doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Chung, J.D.; Zhang, X.; Kaplan, C.R.; Oran, E.S. The structure of the blue whirl revealed. Sci. Adv. 2020, 6, eaba0827. [Google Scholar] [CrossRef]
- Xiao, H.; Gollner, M.J.; Oran, E.S. From fire whirls to blue whirls and combustion with reduced pollution. Proc. Natl. Acad. Sci. USA 2016, 113, 9457–9462. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Hariharan, S.B.; Qi, H.; Gollner, M.J.; Oran, E.S. Conditions for formation of the blue whirl. Combust. Flame 2019, 205, 147–153. [Google Scholar] [CrossRef]
- Carpio, J.; Coenen, W.; Sánchez, A.; Oran, E.; Williams, F. Numerical description of axisymmetric blue whirls over liquid-fuel pools. Proc. Combust. Inst. 2021, 38, 2041–2048. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).