Special Discrete Fuzzy Numbers on Countable Sets and Their Applications

Abstract

There are some drawbacks to arithmetic and logic operations of general discrete fuzzy numbers, which limit their application. For example, the result of the addition operation of general discrete fuzzy numbers defined by the Zadeh’s extension principle may not satisfy the condition of becoming a discrete fuzzy number. In order to solve these problems, special discrete fuzzy numbers on countable sets are investigated in this paper. Since the representation theorem of fuzzy numbers is the basic tool of fuzzy analysis, two kinds of representation theorems of special discrete fuzzy numbers on countable sets are studied first. Then, the metrics of special discrete fuzzy numbers on countable sets are defined, and the relationship between these metrics and the uniform Hausdorff metric (i.e., supremum metric) of general fuzzy numbers is discussed. In addition, the triangular norm and triangular conorm operations (t-norm and t-conorm for short) of special discrete fuzzy numbers on countable sets are presented, and the properties of these two operators are proven. We also prove that these two operators satisfy the basic conditions for closure of operation and present some examples. Finally, the applications of special discrete fuzzy numbers on countable sets in image fusion and aggregation of subjective evaluation are proposed.

1. Introduction

Parameter uncertainty is often involved in the process of information system representation and modeling and is usually described as a fuzzy number [1]. The general fuzzy numbers are triangular, trapezoidal, and Gaussian fuzzy numbers, etc. The most commonly used fuzzy number in engineering applications is the symmetrical triangular fuzzy number. The theoretical and mathematical modeling process of continuous fuzzy numbers and symmetric fuzzy numbers have been investigated extensively. As a powerful tool to characterize and process discrete uncertain information, discrete fuzzy numbers [2] have important theoretical value and a strong application background in fuzzy information processing [3], image interpretation [4], multiple-attribute group decision making [5,6], fuzzy transformation, and inversion.

In 2001, William Voxman [2] first put forward the discrete fuzzy numbers and constructed two kinds of canonical representations of general discrete fuzzy numbers. In 2005, the level set representation theorem of discrete fuzzy numbers was proven by Wang Guixiang et al. [7]. On this basis, the addition and multiplication operations of discrete fuzzy number space were defined. Using similar methods, Casasnovas and Riera [8,9] researched the problem of the maximum and minimum values of discrete fuzzy numbers and studied the triangular norms and triangular conorms to discrete fuzzy numbers in 2011. In the same year, Riera and Torrens [10] defined fuzzy implication functions on sets of discrete fuzzy numbers. Using the above operations, Riera and Torrens [11] defined an integration operator for discrete fuzzy numbers in 2012. Furthermore, Riera and Torrens investigated the coimplications [12] and residual implications [13] of discrete fuzzy number space. The two scholars further defined a pair of discrete aggregation functions on discrete fuzzy numbers sets and applied them to language decision models [14]. In 2015, Riera et al. [15,16] presented a fuzzy decision model and used discrete fuzzy numbers to model complete and incomplete qualitative information; then, they gave an aggregation method for this information.

In recent years, many achievements have been made in the theoretical and application research of discrete fuzzy numbers. In 2019, Zhao Meng et al. [17] proposed a sort method based on shape similarity, which used symbolic representation to construct the shape of discrete fuzzy membership function and describe the subjective language preference evaluation of experts. Ma Xiaoyu et al. [18] presented a semantic computing model based on discrete fuzzy numbers and measured the group decision results based on the model in order to reach a consensus. In 2021, Gong Zengtai et al. [4] defined the concept of the three-dimensional generalized discrete fuzzy number (3-GDFN) and the similarity of 3-GDFNs, which were applied to color image interpretation and color mathematical morphology. Riera et al. [19] discussed the application of an admissible order of discrete fuzzy number sets in decision problems in the same year. A new denoising method for color images based on three-dimensional discrete fuzzy number was proposed by Qin Na and Gong Zengtai [20] in 2023.

However, the general discrete fuzzy numbers have defects in arithmetic operations and logical operations, such as the addition and multiplication operations defined by the Zadeh’s extension principle [21] as the membership function of discrete fuzzy numbers may not satisfy the closure. The difference operation and the measurement of discrete fuzzy numbers especially cannot be reasonably defined, which limits the application of discrete fuzzy numbers in some aspects.

In order to solve these problems, scholars have proposed extended addition and multiplication operations that maintain the closure of discrete fuzzy numbers sets. The discrete fuzzy numbers whose support set was an arithmetic sequence on the set of natural numbers were defined in [22,23]. A closed-keeping addition operation for general discrete fuzzy numbers was presented in [7]. Then, the concepts of generalized discrete fuzzy numbers [24] and fuzzy integers [25] were proposed. In 2008, Wang Guixiang et al. [26] defined a discrete fuzzy number on a fixed set whose support set was a countable set. When the addition and subtraction operations on this countable set remained closed, the corresponding addition and subtraction operations on discrete fuzzy number spaces were also closed. Based on the definition of a special discrete fuzzy number proposed in [26], the related conceptions and application of special discrete fuzzy numbers on countable sets are researched in this article. The main contributions of this article are as follows:

• The endpoints function representation theorem of special discrete fuzzy numbers on countable sets is proven.
• Two metrics of special discrete fuzzy numbers on countable sets are defined and compared.
• The definitions and properties of t-norm operator and t-conorm operator of special discrete fuzzy numbers on countable sets are proposed and proven. In addition, these two operators are used in the practical application of image fusion and subjective evaluation.

The rest of the article is organized as follows: In Section 2, we review some basic concepts about discrete fuzzy numbers. In Section 3, the definition and representation theorem of the special discrete fuzzy numbers on countable sets are investigated and proven. In Section 4, we research the metrics of special discrete fuzzy numbers on countable sets and compare them with the uniform Hausdorff metric of general fuzzy numbers. The definitions of the t-norm operator and t-conorm operator of special discrete fuzzy numbers on countable sets are presented in Section 5. In Section 6, the pixel values of gray-scale images are represented by special discrete fuzzy numbers on countable sets. Furthermore, the application of the t-norm operator and t-conorm operator defined in Section 5 in gray image fusion is presented. The application of special discrete fuzzy numbers on countable sets in aggregation of subjective evaluation is proposed in Section 7. Finally, the conclusions are described in Section 8.

2. Preliminaries

The conception and theorem related to discrete fuzzy numbers are briefly introduced in this section. Firstly, the definition of fuzzy set [21] is given.

Let $\mathbb{R}$ be the Euclidean space; a fuzzy set of $\mathbb{R}$ is a mapping $u:\mathbb{R}\to [0,1].$ Let ${\left[u\right]}^r=\{x\in \mathbb{R}:u(x)\ge r\}$ for any $r\in (0,1]$ be its r-level set. With the notation supp u, we denote the support of u, i.e., supp u =$\{x\in \mathbb{R}:u(x)>0\}$. In addition, we denote the closure of supp u with ${\left[u\right]}^0$, i.e., ${\left[u\right]}^0=\overline{\{x\in \mathbb{R}:u(x)>0\}}$.

As a generalization of the concepts of real numbers and interval numbers, the discrete fuzzy numbers are special fuzzy sets that satisfy certain conditions.

Definition 1 ([2]). 

A fuzzy set $u:\mathbb{R}\to [0,1]$ is called a discrete fuzzy number if the support of u is finite, i.e., there exist $x_1,x_2,\dots ,x_n\in \mathbb{R}$ with $x_1<x_2<\dots <x_n$ such that ${\left[u\right]}^0=\{x_1,x_2,\dots ,x_n\}$, and there exist the natural numbers s, t with $1\le s\le t\le n$ such that

(1) 

$u(x_i)=1$ for any natural number i with $s\le i\le t$;

(2) 

$u(x_i)\le u(x_j)$ for any natural numbers i, j with $1\le i\le j\le s$;

(3) 

$u(x_i)\ge u(x_j)$ for any natural numbers i, j with $t\le i\le j\le n$.

We denote the collection of all discrete fuzzy numbers with ${\mathcal{F}}_{\mathcal{D}}$.

Remark 1. 

If the fuzzy set u is a discrete fuzzy number, then the support of u coincides with its closure, i.e., supp u = ${\left[u\right]}^0$.

The representation theorem of discrete fuzzy numbers is an important tool for the theoretical study of fuzzy analysis.

Theorem 1 ([7]). 

Let $u\in {\mathcal{F}}_{\mathcal{D}}$. Then, the following statements (1)–(4) hold:

(1) 

${\left[u\right]}^r$ is a nonempty finite subset of $\mathbb{R}$ for any $r\in [0,1]$;

(2) 

${\left[u\right]}^{r_2}\subset {\left[u\right]}^{r_1}$ for any $r_1$,$r_2\in [0,1]$ with $r_1\le r_2$;

(3) 

For any $r_1$,$r_2\in [0,1]$ with $0\le r_1\le r_2\le 1,$ if $x\in {\left[u\right]}^{r_1}\setminus {\left[u\right]}^{r_2},$ we have $x<y$ for all $y\in {\left[u\right]}^{r_2},$ or $x>y$ for all $y\in {\left[u\right]}^{r_2};$

(4) 

For any $r_0\in (0,1]$, there exists a real number $r_0^{\prime }$ with $0<r_0^{\prime }<r_0$ such that ${\left[u\right]}^{r_0^{\prime }}={\left[u\right]}^{r_0}$ (i.e., ${\left[u\right]}^r={\left[u\right]}^{r_0}$ for any $r\in [r_0^{\prime },r_0]$).

Conversely, if for any $r\in [0,1]$ there exists $A_r\subset \mathbb{R}$, satisfying the following conditions (i)−(iv):

(i) 

$A_r$ is nonempty and finite for any $r\in [0,1]$;

(ii) 

$A_{r_2}\subset A_{r_1}$ for any $r_1$,$r_2\in [0,1]$ with $r_1\le r_2$;

(iii) 

For any $r_1$,$r_2\in [0,1]$ with $0\le r_1\le r_2\le 1,$ if $x\in A_{r_1}\setminus A_{r_2},$ then $x<y$ for all $y\in A_{r_2},$ or $x>y$ for all $y\in A_{r_2};$

(iv) 

For any $r_0\in (0,1]$, there exists a real number $r_0^{\prime }$ with $0<r_0^{\prime }<r_0$ such that $A_{r_0^{\prime }}=A_{r_0}$ (i.e., $A_r=A_{r_0}$ for any $r\in [r_0^{\prime },r_0]$),

then, there exists a unique $u\in {\mathcal{F}}_{\mathcal{D}}$ such that ${\left[u\right]}^r=A_r$ for any $r\in [0,1]$.

Establishing proper measurement on discrete fuzzy number space ${\mathcal{F}}_{\mathcal{D}}$ is the basic starting point of using fuzzy mathematics theory to analyze and deal with practical problems. The definition of the supremum metric on ${\mathcal{F}}_{\mathcal{D}}$ space is proposed.

Definition 2. 

Let $u,v\in {\mathcal{F}}_{\mathcal{D}}$, for any $r\in [0,1]$, the mapping $D:{\mathcal{F}}_{\mathcal{D}}\times {\mathcal{F}}_{\mathcal{D}}\to [0,+\infty )$ is defined as follow:

$$\begin{array}{c}\hfill D(u,v)=\underset{r\in [0,1]}{sup}max\{\mid \underline{u}(r)-\underline{v}(r)\mid ,\mid \overline{u}(r)-\overline{v}(r)\mid \}.\end{array}$$

(1)

Obviously, $({\mathcal{F}}_{\mathcal{D}},D)$ is a metric space with respect to this supremum metric D.

3. Special Discrete Fuzzy Numbers on Countable Sets

In 2008, the conception of discrete fuzzy numbers with finite support sets on fixed sets was proposed by Wang Guixiang et al. [26]. The following definitions and discussion in this paper are carried out on the countable subset C of the real number field R.

Definition 3 ([26]). 

Let C be a countable subset of real number field R. If a fuzzy set $u:R\to [0,1]$ satisfies the following conditions:

(1) 

${\left[u\right]}^0\subset C$ and ${\left[u\right]}^0$ is finite;

(2) 

There exists $x_0\in C$ such that $u(x_0)=1$;

(3) 

For any $x_s,x_t\in C$ with $x_s\le x_t\le x_0$, $u(x_s)\le u(x_t)$ is tenable;

(4) 

For any $x_s,x_t\in C$ with $x_0\le x_s\le x_t$, $u(x_s)\ge u(x_t)$ is tenable.

Then, u is a discrete fuzzy number on C, and we denote the collection of all discrete fuzzy numbers with ${\mathcal{F}}_{\mathcal{DC}}$. Obviously, ${\mathcal{F}}_{\mathcal{DC}}\subset {\mathcal{F}}_{\mathcal{D}}$.

Let C be a countable subset of real number field R; for any $x^{\prime },y^{\prime }\in R$ with $x^{\prime }\le y^{\prime }$, we denote

$${[x^{\prime },y^{\prime }]}_C=\{z\in C:x^{\prime }\le z\le y^{\prime }\}.$$

The representation theorem of fuzzy numbers plays an important role in the basic theory of fuzzy analysis. In order to study the operation of discrete fuzzy numbers, the level sets representation theorem of discrete fuzzy numbers on a countable set C is presented in [26].

Theorem 2 ([26]). 

Let C be a countable subset of real number field R and $u\in {\mathcal{F}}_{\mathcal{DC}}$. Then,

(1) 

For any $r\in [0,1]$, there exist $x_r,y_r\in C$ with $x_r\le y_r$, such that ${\left[u\right]}^r={[x_r,y_r]}_C$, and ${[x_0,y_0]}_C$ is finite;

(2) 

For any $r_1,r_2\in [0,1]$ with $0\le r_1\le r_2\le 1$, ${\left[u\right]}^{r_2}\subset {\left[u\right]}^{r_1}$ is tenable;

(3) 

For any $r_0\in (0,1]$, there exists a real number $r_0^{\prime }$ with $0<r_0^{\prime }<r_0$, such that ${\left[u\right]}^{r_0^{\prime }}={\left[u\right]}^{r_0}$, i.e., for any $r\in [r_0^{\prime },r_0]$, ${\left[u\right]}^r={\left[u\right]}^{r_0}$ is tenable.

Conversely, if for any $r\in [0,1]$, there exists $A_r\subset R$ satisfying

(i) 

There exist $x_r,y_r\in C$ with $x_r\le y_r$, such that $A_r={[x_r,y_r]}_C$ and ${[x_0,y_0]}_C$ is finite;

(ii) 

For any $r_1$,$r_2\in [0,1]$ with $0\le r_1\le r_2\le 1$, $A_{r_2}\subset A_{r_1}$ is tenable;

(iii) 

For any $r_0\in (0,1]$, there exists a real number $r_0^{\prime }$ with $0<r_0^{\prime }<r_0$, such that $A_{r_0^{\prime }}=A_{r_0}$, i.e., for any $r\in [r_0^{\prime },r_0]$, $A_r=A_{r_0}$ is tenable.

Then, there exists a unique $u\in {\mathcal{F}}_{\mathcal{DC}}$ such that ${\left[u\right]}^r=A_r$ for any $r\in [0,1]$.

By means of Theorem 2, a discrete fuzzy number on countable sets can be regarded as a family of nonempty closed intervals satisfying some specific conditions. Next, let us prove the endpoints function representation theorem of special discrete fuzzy numbers on the countable set C. For any $u\in {\mathcal{F}}_{\mathcal{DC}},$u can be represented by two real-valued functions on the interval [0,1] that satisfy certain conditions. We denote $\underline{u}(r)=min{\left[u\right]}^r$ and $\overline{u}(r)=max{\left[u\right]}^r$; then, $\underline{u}(r)$ and $\overline{u}(r)$ have the following properties:

Theorem 3. 

If $u\in {\mathcal{F}}_{\mathcal{DC}},$ then $\underline{u}(r)$ and $\overline{u}(r)$ are two functions on $[0,1]$, and they satisfy the following conditions:

(1) 

$\underline{u}(r)$ is monotone nondecreasing left continuous;

(2) 

$\overline{u}(r)$ is monotone nonincreasing left continuous;

(3) 

$\underline{u}(r)\le \overline{u}(r)$ for all $r\in [0,1]$;

(4) 

$\underline{u}(r)$ and $\overline{u}(r)$ are right continuous at $r=0$.

Conversely, if for any $r\in [0,1]$, $X(r)$ and $Y(r)$ are two functions on $[0,1]$, and they satisfy the following conditions:

(i) 

$X(r)$ is monotone nondecreasing left continuous;

(ii) 

$Y(r)$ is monotone nonincreasing left continuous;

(iii) 

$X(r)\le Y(r)$ for all $r\in [0,1]$;

(iv) 

$X(r)$ and $Y(r)$ are right continuous at $r=0$.

Then, there exists a unique $u\in {\mathcal{F}}_{\mathcal{DC}}$ such that $\underline{u}(r)=X(r),\overline{u}(r)=Y(r)$ for any $r\in [0,1]$.

Proof. 

At first, we prove that $u\in {\mathcal{F}}_{\mathcal{DC}}$ implies conditions (1)–(4) of this theorem.

Because $u\in {\mathcal{F}}_{\mathcal{DC}}$, let ${\left[u\right]}^0=\{x_1,x_2,···,x_n\}\subset C,x_1<x_2<···<x_n,$ there exists $1\le k\le n$ such that $u(x_k)=1$. When $1\le i\le j\le k$, $u(x_i)\le u(x_j)$ is tenable, when $k\le i\le j\le n$, $u(x_i)\ge u(x_j)$ is tenable.

From the definitions of $\underline{u}(r)$ and $\overline{u}(r)$, the $\underline{u}(r)$ and $\overline{u}(r)$ can only be taken on ${\left[u\right]}^0$, and the set ${\left[u\right]}^0$ is finite, so $\underline{u}(r)$ and $\overline{u}(r)$ are the functions on $[0,1]$.

Let $r_1,r_2\in [0,1]$ and $r_1<r_2$. From Theorem 2 of the discrete fuzzy numbers on countable sets, ${\left[u\right]}^{r_1}\supset {\left[u\right]}^{r_2}$ is tenable, so we have $\underline{u}(r_1)=min{\left[u\right]}^{r_1}\le min{\left[u\right]}^{r_2}=\underline{u}(r_2)$ and $\overline{u}(r_1)=max{\left[u\right]}^{r_1}\ge max{\left[u\right]}^{r_2}=\overline{u}(r_2)$; then, $\underline{u}(r)$ is a monotone nondecreasing function and $\overline{u}(r)$ is a monotone nonincreasing function. Next, we prove that $\underline{u}(r)$ and $\overline{u}(r)$ are left continuous.

We denote $A_i=u(x_i),i=1,2,···,k$ for any $r_0\in (0,1],$ if $r_0\le A_1,$ and because $\underline{u}(r)=min{\left[u\right]}^r$, we know that when $r\in [0,r_0]$, $\underline{u}(r)=A_1$ holds. Therefore, $\underline{u}(r)$ is left continuous at $r_0$. If $r_0>A_1,$ then $\{A_i\ge r_0:i=1,2,···,k\}$, and $\{A_i<r_0:i=1,2,···,k\}$ are nonempty, so we set $a=min\{A_i\ge r_0:i=1,2,···,k\},b=max\{A_i<r_0:i=1,2,···,k\}$. Obviously, there exists $b<r_0\le a$. Then, from $\underline{u}(r)=min{\left[u\right]}^r$, when $r\in (b,r_0]$, $\underline{u}(r)=a$ holds; therefore, $\underline{u}(r)$ is left continuous at $r_0$.

We denote $B_i=u(x_i),i=k,k+1,···,n$ for any $r_0\in (0,1],$ if $r_0\le B_n,$ and because $\overline{u}(r)=max{\left[u\right]}^r$, we know that when $r\in [0,r_0]$, $\overline{u}(r)=B_n$ holds. Therefore, $\overline{u}(r)$ is left continuous at $r_0$. If $r_0>B_n,$ then $\{B_i\ge r_0:i=1,2,···,k\}$ and $\{B_i<r_0:i=1,2,···,k\}$ are nonempty. So, we set $c=min\{B_i\ge r_0:i=k,k+1,···,n\},d=max\{B_i<r_0:i=k,k+1,···,n\}$. Obviously, there exists $d<r_0\le c$. Then, from $\overline{u}(r)=max{\left[u\right]}^r$, when $r\in (d,r_0]$, $\overline{u}(r)=c$ holds; therefore, $\overline{u}(r)$ is left continuous at $r_0$.

For any $r\in [0,1]$, $\underline{u}(r)\le \underline{u}(1)=min{\left[u\right]}^1\le max{\left[u\right]}^1=\overline{u}(1)\le \overline{u}(r)$; then, $\underline{u}(r)\le \overline{u}(r)$ is tenable.

Then, because $\underline{u}(r)=A_1$ is tenable when $r\in [0,A_1]$, therefore $\underline{u}(r)$ is right continuous at $r=0$. Because $\overline{u}(r)=B_n$ is tenable when $r\in [0,B_n]$, therefore $\overline{u}(r)$ is right continuous at $r=0$.

The proof of the first part of this theorem is completed. Secondly, we prove the next part of the theorem.

Let $M_r=\{X(h):r\le h\le 1\}\bigcup \{Y(h):r\le h\le 1\}$ for any $r\in [0,1]$. Because $X(r)$ and $Y(r)$ are two functions on $[0,1]$, $M_r$ is nonempty and finite for any $r\in [0,1]$. So, $M_r$ satisfies condition (i) of Theorem 2. According to the definition of $M_r$, it also satisfies condition (ii) of Theorem 2.

Next, we prove that $M_r$ satisfies condition (iii) of Theorem 2.

Let $r_0\in (0,1]$. Because $X(r)$ is a function on $[0,1]$ and left continuous, there exists $r_0^{\prime }\in (0,r_0)$ such that when $r\in [r_0^{\prime },r_0]$, $X(r)=X(r_0)$ is tenable. Similarly, $Y(r)$ is a function on $[0,1]$ and left continuous, so there exists $r_0^{″}\in (0,r_0)$ such that when $r\in [r_0^{″},r_0]$, $Y(r)=Y(r_0)$ is tenable.

Let $h_0=min(r_0^{\prime },r_0^{″})$, when $r\in [h_0,r_0],$ we have $X(r)=X(r_0)$ and $Y(r)=Y(r_0)$. So, when $r\in [h_0,r_0],$

$$\begin{array}{ccc}\hfill M_r& =& \{X(h):r\le h\le 1\}\bigcup \{Y(h):r\le h\le 1\}\hfill \\ \hfill & =& \{X(h):r_0\le h\le 1\}\bigcup \{Y(h):r_0\le h\le 1\}\hfill \\ \hfill & =& M_{r_0},\hfill \end{array}$$

then, $M_r$ satisfies condition (iii) of the Theorem 2.

According to the Theorem 2, there is a unique $u\in {\mathcal{F}}_{\mathcal{DC}}$ such that ${\left[u\right]}^r=M_r$ is tenable for any $r\in [0,1]$, i.e.,

$$\begin{array}{ccc}\hfill \underline{u}(r)& =& min{\left[u\right]}^r=min{M}_r\hfill \\ \hfill & =& min(\{X(h):r\le h\le 1\}\bigcup \{Y(h):r\le h\le 1\})\hfill \\ \hfill & =& min(\{X(h):r\le h\le 1\})\hfill \\ \hfill & =& X(r),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \overline{u}(r)& =& max{\left[u\right]}^r=max{M}_r\hfill \\ \hfill & =& max(\{X(h):r\le h\le 1\}\bigcup \{Y(h):r\le h\le 1\})\hfill \\ \hfill & =& max(\{Y(h):r\le h\le 1\})\hfill \\ \hfill & =& Y(r).\hfill \end{array}$$

We completed the proof of this theorem. □

According to the level set representation theorem of the general discrete fuzzy numbers in [7] and the Theorem 2 of the discrete fuzzy numbers on countable sets, the following theorem can be obtained directly.

Theorem 4 ([26]). 

Let C be a countable subset of real number field R, and $u,v\in {\mathcal{F}}_{\mathcal{DC}}$, $k\in R$. Then, for any $r\in [0,1]$,

(1) 

${[u+v]}^r={\left[u\right]}^r+{\left[v\right]}^r$;

(2) 

${\left[ku\right]}^r=k{\left[u\right]}^r$;

(3) 

${\left[uv\right]}^r={\left[u\right]}^r{\left[v\right]}^r$.

The conditions of closure operations on ${\mathcal{F}}_{\mathcal{DC}}$ space are proven in Theorem 5; these conditions cannot be omitted, and the corresponding example can be found in Example 3.1 and Remark 3.2 of [26].

Theorem 5 ([26]). 

Let C be a countable subset of real number field R. If $u,v\in {\mathcal{F}}_{\mathcal{DC}},k\in R$, then

(1) 

$ku\in {\mathcal{F}}_{\mathcal{DC}}$ if C satisfies $kx\in C$ for any $x\in C$;

(2) 

$u+v\in {\mathcal{F}}_{\mathcal{DC}}$ if C preserves the closeness of the operations of addition and difference.

4. Metrics of Special Discrete Fuzzy Numbers on Countable Sets

Fuzzy numbers play an important role in applications in the fields of approximate reasoning, fuzzy control, and fuzzy decision [6]. In order to solve problems in practical application, it is necessary to research the properties of measurement in fuzzy number space and analyze the relationship between various measurements. Likewise, the measurement in fuzzy number space is also an important part of fuzzy analysis theory. In order to develop and perfect the theory of fuzzy analysis, the measurement of special discrete fuzzy numbers on countable sets is investigated in this section.

Because $({\mathcal{F}}_{\mathcal{D}},D)$ is a metric space and ${\mathcal{F}}_{\mathcal{DC}}\subset {\mathcal{F}}_{\mathcal{D}}$, D is also a metric on ${\mathcal{F}}_{\mathcal{DC}}$ space. Considering the particularity of ${\mathcal{F}}_{\mathcal{DC}}$ space and the investigation on this space-related theories and applications, two other definitions of metric on ${\mathcal{F}}_{\mathcal{DC}}$ space are proposed.

Definition 4. 

Let the mapping $\dot{D}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}\to [0,+\infty )$ be defined as follows:

if ${\left[u\right]}^0={\left[v\right]}^0$, then

$$\begin{array}{ccc}\hfill \dot{D}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}& \to & [0,+\infty )\hfill \\ \hfill (u,v)& \to & \dot{D}(u,v)=\underset{x\in C}{sup}\mid u(x)-v(x)\mid .\hfill \end{array}$$

(2)

Definition 5. 

Let the mapping $\widehat{D}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}\to [0,+\infty )$ be defined as follows:

$$\begin{array}{ccc}\hfill \widehat{D}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}& \to & [0,+\infty )\hfill \\ \hfill (u,v)& \to & \widehat{D}(u,v)=\underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid }{2}).\hfill \end{array}$$

(3)

Next, the basic properties of the two metrics defined in Definitions 4 and 5 are proven.

Theorem 6. 

For any $u,v,w\in {\mathcal{F}}_{\mathcal{DC}}$, $k\in R$, then $\dot{D}$ and $\widehat{D}$ satisfy:

(1) 

$\dot{D}(u,v)=\dot{D}(v,u),\widehat{D}(u,v)=\widehat{D}(v,u)$;

(2) 

$\dot{D}(u,v)\ge 0,\widehat{D}(u,v)\ge 0$;

(3) 

$\dot{D}(u,v)=0\iff u=v,\widehat{D}(u,v)=0\iff u=v$;

(4) 

$\dot{D}(u,v)\le \dot{D}(u,w)+\dot{D}(w,v)$, $\widehat{D}(u,v)\le \widehat{D}(u,w)+\widehat{D}(w,v)$;

(5) 

$\dot{D}(u+w,v+w)=\dot{D}(u,v),\widehat{D}(u+w,v+w)=\widehat{D}(u,v)$;

(6) 

$\dot{D}(ku,kv)=\left|k\right|\dot{D}(u,v),\widehat{D}(ku,kv)=\left|k\right|\widehat{D}(u,v)$.

Proof. 

Obviously, (1) and (2) of the theorem are true. Then, prove (3) of the theorem,

$\dot{D}(u,v)=0\iff u=v$ is tenable.

$$\begin{array}{ccc}\hfill & & \widehat{D}(u,v)=0\hfill \\ \hfill & \iff & \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid }{2})=0\hfill \\ \hfill & \iff & \mid \underline{u}(r)-\underline{v}(r)\mid =0and\mid \overline{u}(r)-\overline{v}(r)\mid =0\hfill \\ \hfill & \iff & \underline{u}(r)=\underline{v}(r)and\overline{u}(r)=\overline{v}(r)\hfill \\ \hfill & \iff & {[\underline{u}(r),\overline{u}(r)]}_C={[\underline{v}(r),\overline{v}(r)]}_C\hfill \\ \hfill & \iff & {\left[u\right]}^r={\left[v\right]}^r\hfill \\ \hfill & \iff & u=v.\hfill \end{array}$$

The proof of (4) of the theorem is as follows:

If ${\left[u\right]}^0={\left[v\right]}^0={\left[w\right]}^0$,

$$\begin{array}{ccc}\hfill \dot{D}(u,v)& =& \underset{x\in C}{sup}\mid u(x)-v(x)\mid \hfill \\ \hfill & =& \underset{x\in C}{sup}\mid u(x)-w(x)+w(x)-v(x)\mid \hfill \\ \hfill & \le & \underset{x\in C}{sup}\{\mid u(x)-w(x)\mid +\mid w(x)-v(x)\mid \}\hfill \\ \hfill & \le & \underset{x\in C}{sup}\mid u(x)-w(x)\mid +\underset{x\in C}{sup}\mid w(x)-v(x)\mid \hfill \\ \hfill & =& \dot{D}(u,w)+\dot{D}(w,v).\hfill \end{array}$$

For any $u,v,w\in {\mathcal{F}}_{\mathcal{DC}}$,

$$\begin{array}{ccc}\hfill \widehat{D}(u,v)& =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{w}(r)+\underline{w}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{w}(r)+\overline{w}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & \le & \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{w}(r)\mid +\mid \underline{w}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{w}(r)\mid +\mid \overline{w}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & \le & \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{w}(r)\mid +\mid \underline{w}(r)-\underline{v}(r)\mid }{2})+\underset{r\in [0,1]}{sup}(\frac{\mid \overline{u}(r)-\overline{w}(r)\mid +\mid \overline{w}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & =& \widehat{D}(u,w)+\widehat{D}(w,v).\hfill \end{array}$$

The proof of (5) of the theorem is as follows:

If ${\left[u\right]}^0={\left[v\right]}^0={\left[w\right]}^0$,

$$\begin{array}{ccc}\hfill \dot{D}(u+w,v+w)& =& \underset{x\in C}{sup}\mid (u+w)(x)-(v+w)(x)\mid \hfill \\ \hfill & =& \underset{x\in C}{sup}\mid (u(x)+w(x))-(v(x)+w(x))\mid \hfill \\ \hfill & =& \underset{x\in C}{sup}\mid (u)(x)-(v)(x)\mid \hfill \\ \hfill & =& \dot{D}(u,v).\hfill \end{array}$$

For any $u,v,w\in {\mathcal{F}}_{\mathcal{DC}}$,

$$\begin{array}{ccc}\hfill \widehat{D}(u+w,v+w)& =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{(u+w)}(r)-\underline{(v+w)}(r)\mid +\mid \overline{(u+w)}(r)-\overline{(v+w)}(r)\mid }{2})\hfill \\ \hfill & =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)+\underline{w}(r)-\underline{v}(r)-\underline{w}(r)\mid +\mid \overline{u}(r)+\overline{w}(r)-\overline{v}(r)-\overline{w}(r)\mid }{2})\hfill \\ \hfill & =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & =& \widehat{D}(u,v).\hfill \end{array}$$

Finally, the proof of (6) of the theorem is as follows:

$$\begin{array}{ccc}\hfill \dot{D}(ku,kv)& =& \underset{x\in C}{sup}\mid ku(x)-kv(x)\mid \hfill \\ \hfill & =& \underset{x\in C}{sup}\left|k\right|\mid u(x)-v(x)\mid \hfill \\ \hfill & =& \left|k\right|\underset{x\in C}{sup}\mid u(x)-v(x)\mid \hfill \\ \hfill & =& \left|k\right|\dot{D}(u,v).\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \widehat{D}(ku,kv)& =& \underset{r\in [0,1]}{sup}(\frac{\mid \underline{ku}(r)-\underline{kv}(r)\mid +\mid \overline{ku}(r)-\overline{kv}(r)\mid }{2})\hfill \\ \hfill & =& \underset{r\in [0,1]}{sup}(\frac{\left|k\right|\mid \underline{u}(r)-\underline{v}(r)\mid +\left|k\right|\mid \overline{u}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & =& \left|k\right|\underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid }{2})\hfill \\ \hfill & =& \left|k\right|\widehat{D}(u,v).\hfill \end{array}$$

The proof of the theorem is complete. □

Then, the relationship between the metric $\widehat{D}$ and D is proven. The metric D is introduced in Definition 2. D is also a metric on ${\mathcal{F}}_{\mathcal{DC}}$ space because of ${\mathcal{F}}_{\mathcal{DC}}\subset {\mathcal{F}}_{\mathcal{D}}$.

Theorem 7. 

For any $u,v\in {\mathcal{F}}_{\mathcal{DC}}$, the metric $\widehat{D}$ and D satisfy $\frac{1}{2}D\le \widehat{D}\le D$, i.e.,

$$\frac{1}{2}D(u,v)\le \widehat{D}(u,v)\le D(u,v).$$

Proof. 

For any $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ and $r\in [0,1]$, from the definitions of $\widehat{D}$ and D, we have the following equation:

$$\begin{array}{ccc}\hfill \frac{1}{2}D(u,v)& =& \frac{1}{2}\underset{r\in [0,1]}{sup}max\{\mid \underline{u}(r)-\underline{v}(r)\mid ,\mid \overline{u}(r)-\overline{v}(r)\mid \}\hfill \\ \hfill & =& \frac{1}{2}\underset{r\in [0,1]}{sup}(\frac{\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid +\mid (\mid \underline{u}(r)-\underline{v}(r)\mid -\mid \overline{u}(r)-\overline{v}(r)\mid )\mid }{2})\hfill \\ \hfill & \le & \underset{r\in [0,1]}{sup}\frac{1}{4}(\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid +\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid )\hfill \\ \hfill & =& \underset{r\in [0,1]}{sup}\frac{1}{2}(\mid \underline{u}(r)-\underline{v}(r)\mid +\mid \overline{u}(r)-\overline{v}(r)\mid )\hfill \\ \hfill & =& \widehat{D}(u,v)\hfill \\ \hfill & \le & \frac{1}{2}(2max\{\mid \underline{u}(r)-\underline{v}(r)\mid ,\mid \overline{u}(r)-\overline{v}(r)\mid \})\hfill \\ \hfill & =& D(u,v).\hfill \end{array}$$

From that, we can directly obtain the fact that for any $u,v\in {\mathcal{F}}_{\mathcal{DC}}$, $\frac{1}{2}D(u,v)\le \widehat{D}(u,v)\le D(u,v)$ is tenable.

The proof of the theorem is complete. □

5. The Triangular Norm and Triangular Conorm Operations of Special Discrete Fuzzy Numbers on Countable Sets

Propositional logic refers to a formula representing a “proposition” formed by a logical operator combined with an atomic proposition [27]. In fuzzy logic, a logical proposition is connected by fuzzy logic conjunctive words. In the process of a numerical operation, the logical connectives’ “conjunctions” are realized by a triangular norm operator, while the logical connectives’ “disjunction” are realized by a triangular conorm operator. In this section, we mainly investigate the triangular norm and triangular conorm operations of special discrete fuzzy numbers on countable sets and their properties. Firstly, some definitions and results of the triangular norm and triangular conorm operations on posets are reviewed; then, the discrete triangular norm operator $\mathbb{T}$ and triangular conorm operator $\mathbb{S}$ on ${\mathcal{F}}_{\mathcal{DC}}$ space are defined.

Let $(P,\le )$ be a nontrivial bounded partially ordered set with a maximum element “m” and a minimum element “e”.

If T (or S) is a triangular norm operator on the bounded countable set $C\subset R$, then we can define the binary operation $\mathbb{T}$ (or $\mathbb{S}$) on the ${\mathcal{F}}_{\mathcal{DC}}$ space. The following theorems illustrate the fundamental properties of the triangular norm operator and the triangular conorm operator.

Definition 6 ([28]). 

Let the triangular norm operator $T:P\times P\to P$ be a binary operation on the poset P; for any $x,y,z,x^{\prime },y^{\prime }\in P$, the following axioms are satisfied:

(1) 

Commutativity: $T(x,y)=T(y,x)$;

(2) 

Associativity: $T(T(x,y),z)=T(x,T(y,z))$;

(3) 

Monotonicity: $T(x,y)\le T(x^{\prime },y^{\prime })$ when $x\le x^{\prime },y\le y^{\prime }$;

(4) 

Boundary condition: $T(x,m)=x$.

Definition 7 ([28]). 

Let the triangular conorm operator $S:P\times P\to P$ be a binary operation on the poset P; for any $x,y,z,x^{\prime },y^{\prime }\in P$, the following axioms are satisfied:

(1) 

Commutativity: $S(x,y)=S(y,x)$;

(2) 

Associativity: $S(S(x,y),z)=S(x,S(y,z))$;

(3) 

Monotonicity: $S(x,y)\le S(x^{\prime },y^{\prime })$ when $x\le x^{\prime },y\le y^{\prime }$;

(4) 

Boundary condition: $T(x,e)=x$.

Generally speaking, when the algebraic operation or lattice operation is extended to the fuzzy number space, the membership function of the fuzzy number can be directly used for calculation based on the Zadeh expansion principle [21] or the equivalent level set representation can be used for calculation. However, the result of the calculation may not be a discrete fuzzy number in ${\mathcal{F}}_{\mathcal{D}}$ space [9].

Now, we consider the ${\mathcal{F}}_{\mathcal{DC}}$ space of special discrete fuzzy numbers on countable sets; for any $u,v\in {\mathcal{F}}_{\mathcal{DC}}$, there exist $x_u^r,y_u^r$, $x_v^r,y_v^r\in C$ and $x_u^r\le y_u^r$, $x_v^r\le y_v^r$ such that ${\left[u\right]}^r={[x_u^r,y_u^r]}_C$, ${\left[v\right]}^r={[x_v^r,y_v^r]}_C$.

Definition 8. 

For any $r\in [0,1]$, let us consider the set

$$\begin{array}{ccc}\hfill T({\left[u\right]}^r,{\left[v\right]}^r)& =& \left\{T(x,y)\right|x\in {\left[u\right]}^r,y\in {\left[v\right]}^r\}\hfill \\ \hfill & =& \left\{T(x,y)\right|x\in {[x_u^r,y_u^r]}_C,y\in {[x_v^r,y_v^r]}_C\},\hfill \end{array}$$

where ${\left[u\right]}^0=\mathrm{supp}u,{\left[v\right]}^0=\mathrm{supp}v$.

Proposition 1. 

For any $r\in [0,1]$, if any $x,y\in C$ satisfy $T(x,y)\in C$, then $T({\left[u\right]}^r,{\left[v\right]}^r)$ satisfies conditions (1), (2), and (3) in Theorem 2.

Proof. 

(1) For any $r\in [0,1]$, ${\left[u\right]}^r$ and ${\left[v\right]}^r$ are nonempty and finite, then $T({\left[u\right]}^r,{\left[v\right]}^r)$ is nonempty and finite, and $T({\left[u\right]}^0,{\left[v\right]}^0)$ is finite.

(2)

For any $r_1,r_2\in [0,1]$ and $0\le r_1\le r_2\le 1$, ${\left[u\right]}^{r_2}\subset {\left[u\right]}^{r_1}$ and ${\left[v\right]}^{r_2}\subset {\left[v\right]}^{r_1}$ are tenable; therefore, $x_u^{r_1}\le x_u^{r_2},y_u^{r_2}\le y_u^{r_1},x_v^{r_1}\le x_v^{r_2},y_v^{r_2}\le y_v^{r_1}$, because T satisfies monotonicity,

$$\begin{array}{ccc}\hfill T(x_u^{r_1},x_v^{r_1})& \le & T(x_u^{r_2},x_v^{r_2}),\hfill \\ \hfill T(y_u^{r_2},y_v^{r_2})& \le & T(y_u^{r_1},y_v^{r_1}),\hfill \\ \hfill T(x_u^{r_2},x_v^{r_2})& \le & T(y_u^{r_2},y_v^{r_2}).\hfill \end{array}$$

These three inequalities are combined:

$$T(x_u^{r_1},x_v^{r_1})\le T(x_u^{r_2},x_v^{r_2})\le T(y_u^{r_2},y_v^{r_2})\le T(y_u^{r_1},y_v^{r_1}).$$

Therefore,

$$T({\left[u\right]}^{r_2},{\left[v\right]}^{r_2})\subset T({\left[u\right]}^{r_1},{\left[v\right]}^{r_1}).$$

(3)

Because $u,v\in {\mathcal{F}}_{\mathcal{DC}}$, then for any $r_0\in [0,1]$, there exist $r_1^{\prime },r_2^{\prime }\in R$ that satisfy $0<r_1^{\prime }<r_0$ and $0<r_2^{\prime }<r_0$ such that ${\left[u\right]}^{r_1^{\prime }}={\left[u\right]}^{r_0}$ and ${\left[v\right]}^{r_2^{\prime }}={\left[v\right]}^{r_0}$ are tenable, i.e., ${\left[u\right]}^{{\alpha }_1}={\left[u\right]}^{r_0}$ is tenable for any ${\alpha }_1\in [r_1^{\prime },r_0]$, and ${\left[u\right]}^{{\alpha }_2}={\left[u\right]}^{r_0}$ is tenable for any ${\alpha }_2\in [r_2^{\prime },r_0]$. Therefore, if $\alpha ={\alpha }_1\vee {\alpha }_2$ then

$$T({\left[u\right]}^{\alpha },{\left[v\right]}^{\alpha })=T({\left[u\right]}^{r_0},{\left[v\right]}^{r_0}).$$

The proof of the theorem is complete. □

Theorem 8. 

There exists a unique discrete fuzzy number on countable set C denoted $\mathbb{T}(u,v)$ such that for any $r\in [0,1]$, the r-level set ${\left[\mathbb{T}(u,v)\right]}^r$ is defined by $T({\left[u\right]}^r,{\left[v\right]}^r)$, and

$$\mathbb{T}(u,v)(z)=sup\{r\in [0,1]|z\in T({\left[u\right]}^r,{\left[v\right]}^r)\}$$

is tenable.

Proof. 

Derived from Proposition 1 and Theorem 2. □

Similarly, the following propositions and theorems can be proven.

Definition 9. 

For any $r\in [0,1]$, let us consider the set

$$\begin{array}{ccc}\hfill S({\left[u\right]}^r,{\left[v\right]}^r)& =& \left\{S(x,y)\right|x\in {\left[u\right]}^r,y\in {\left[v\right]}^r\}\hfill \\ \hfill & =& \left\{S(x,y)\right|x\in {[x_u^r,y_u^r]}_C,y\in {[x_v^r,y_v^r]}_C\},\hfill \end{array}$$

where ${\left[u\right]}^0=\mathrm{supp}u,{\left[v\right]}^0=\mathrm{supp}v$.

Proposition 2. 

For any $r\in [0,1]$, if any $x,y\in C$ satisfy $S(x,y)\in C$, then $S({\left[u\right]}^r,{\left[v\right]}^r)$ satisfies conditions (1), (2), and (3) in Theorem 2.

Theorem 9. 

There exist unique discrete fuzzy numbers on countable sets denoted by $\mathbb{S}(u,v)$, whose r-level set ${\left[\mathbb{S}(u,v)\right]}^r$ is defined by $S({\left[u\right]}^r$, ${\left[v\right]}^r)$ for any $r\in [0,1]$, and

$$\mathbb{S}(u,v)(z)=sup\{r\in [0,1]|z\in S({\left[u\right]}^r,{\left[v\right]}^r)\}$$

is tenable.

Remark 2. 

According to the above results, if T is a triangular norm operator on the bounded countable set $C\subset R$, then we can define the binary operation $\mathbb{T}$ on the ${\mathcal{F}}_{\mathcal{DC}}$ space,

$$\begin{array}{ccc}\hfill \mathbb{T}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}& \to & {\mathcal{F}}_{\mathcal{DC}}\hfill \\ \hfill (u,v)& \to & \mathbb{T}(u,v).\hfill \end{array}$$

The $\mathbb{T}$ is called the triangular norm operator of discrete fuzzy numbers on ${\mathcal{F}}_{\mathcal{DC}}$.

Similarly, we define the triangular conorm operator of discrete fuzzy numbers, denoted as $\mathbb{S}$.

Remark 3. 

Generally speaking, the condition “for any $x,y\in C$ satisfy $T(x,y)\in C$” in Proposition 1 and the condition “for any $x,y\in C$ satisfy $S(x,y)\in C$” in Proposition 2 cannot be omitted. The following examples can be used to illustrate.

Example 1. 

Let $C=\{0,2,3,4,5\}$. $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ are defined by

$$u=\{0.2/0,0.5/2,1/3,0.8/5\},$$

$$v=\{0.8/3,1/4,0.6/5\}.$$

The $Lukasiewicz$ triangular norm operator is $T_L=max\{0,x+y-5\}$; according to the above definition and theorem, ${\mathbb{T}}_L(u,v)$ can be calculated as follows:

(1) 

When $r=0.2$, ${\left[u\right]}^{0.2}=\{0,2,3,5\}$, and ${\left[v\right]}^{0.2}=\{3,4,5\}$, then $T_L({\left[u\right]}^{0.2},{\left[v\right]}^{0.2})=\{0,1,2,3,4,5\}$,

(2) 

When $r=0.5$, ${\left[u\right]}^{0.5}=\{2,3,5\}$, and ${\left[v\right]}^{0.5}=\{3,4,5\}$, then $T_L({\left[u\right]}^{0.5},{\left[v\right]}^{0.5})=\{0,1,2,3,4,5\}$,

(3) 

When $r=0.6$, ${\left[u\right]}^{0.6}=\{3,5\}$, and ${\left[v\right]}^{0.6}=\{3,4,5\}$, then $T_L({\left[u\right]}^{0.6},{\left[v\right]}^{0.6})=\{1,2,3,4,5\}$,

(4) 

When $r=0.8$, ${\left[u\right]}^{0.8}=\{3,5\}$, and ${\left[v\right]}^{0.8}=\{3,4\}$, then $T_L({\left[u\right]}^{0.8},{\left[v\right]}^{0.8})=\{1,2,3,4\}$,

(5) 

When $r=1$, ${\left[u\right]}^1=\left\{3\right\}$, and ${\left[v\right]}^1=\left\{4\right\}$, then $T_L({\left[u\right]}^1,{\left[v\right]}^1)=\left\{2\right\}$.

Finally, we obtain

$${\mathbb{T}}_L(u,v)=\{0.5/0,0.8/1,1/2,0.8/3,0.8/4,0.6/5\},$$

then ${\left[{\mathbb{T}}_L(u,v)\right]}^0$ is not a subset of C. According to Theorem 2, ${\mathbb{T}}_L(u,v)\notin {\mathcal{F}}_{\mathcal{DC}}$, and it is not a discrete fuzzy number on the countable set C. So, the condition “for any $x,y\in C$ satisfy $T(x,y)\in C$” in Proposition 1 cannot be omitted.

Now, some examples of operations using discrete triangular norm and triangular conorm operator are presented.

Example 2. 

Let $C=\{0,1,2,3,4,5\}$. $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ are defined by:

$$u=\{0.2/0,0.5/2,1/3,0.8/5\},$$

$$v=\{0.1/1,0.8/3,1/4,0.6/5\}.$$

The $Lukasiewicz$ triangular norm operator $T_L=max\{0,x+y-5\}$, according to the above definition and theorem:

$${\mathbb{T}}_L(u,v)=\{0.5/0,0.8/1,1/2,0.8/3,0.8/4,0.6/5\},$$

then ${\mathbb{T}}_L(u,v)\in {\mathcal{F}}_{\mathcal{DC}}$.

Example 3. 

Let $C=\{0,1,2,3,4,5\}$. $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ are defined by:

$$u=\{0.2/0,0.5/2,1/3,0.8/5\},$$

$$v=\{0.1/1,0.8/3,1/4,0.6/5\}.$$

The $Lukasiewicz$ triangular conorm operator $S_L=min\{5,x+y\}$, according to the above definition and theorem:

$${\mathbb{S}}_L(u,v)=\{0.1/1,0.1/2,0.2/3,0.2/4,1/5\},$$

then ${\mathbb{S}}_L(u,v)\in {\mathcal{F}}_{\mathcal{DC}}$.

Example 4. 

Let $C=\{0,1,2,3,4,5\}$. $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ are defined by:

$$u=\{0.2/0,0.5/2,1/3,0.8/5\},$$

$$v=\{0.1/1,0.8/3,1/4,0.6/5\}.$$

The $Min$ triangular norm operator $T_{Min}=min\{x,y\}$, according to the above definition and theorem:

$${\mathbb{T}}_{Min}(u,v)=\{0.2/0,0.2/1,0.5/2,1/3,0.8/4,0.6/5\},$$

then ${\mathbb{T}}_{Min}(u,v)\in {\mathcal{F}}_{\mathcal{DC}}$.

Example 5. 

Let $C=\{0,1,2,3,4,5\}$. $u,v\in {\mathcal{F}}_{\mathcal{DC}}$ are defined by:

$$u=\{0.2/0,0.5/2,1/3,0.8/5\},$$

$$v=\{0.1/1,0.8/3,1/4,0.6/5\}.$$

The $Max$ triangular conorm operator $S_{Max}=max\{x,y\}$, according to the above definition and theorem:

$${\mathbb{S}}_{Max}(u,v)=\{0.1/1,0.1/2,0.8/3,1/4,0.6/5\},$$

then ${\mathbb{S}}_{Max}(u,v)\in {\mathcal{F}}_{\mathcal{DC}}$.

Some properties of the triangular norm and triangular conorm of special discrete fuzzy numbers on countable sets are investigated below.

Proposition 3. 

Let the triangular norm $T:P\times P\to P$ and the triangular conorm $S:P\times P\to P$ be binary operators on poset P; for any $x,y,z\in P$, the following properties hold:

(1) 

Commutativity:

$$T(x,y)=T(y,x),$$

$$S(x,y)=S(y,x).$$

(2) 

Associativity:

$$T(T(x,y),z)=T(x,T(y,z)),$$

$$S(S(x,y),z)=S(x,S(y,z)).$$

Proof. 

Straightforward. It can be obtained directly from the definitions of the triangular norm T and the triangular conorm S. □

Theorem 10. 

Let $\mathbb{T}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}\to {\mathcal{F}}_{\mathcal{DC}}$ be a triangular norm operator and $\mathbb{S}:{\mathcal{F}}_{\mathcal{DC}}\times {\mathcal{F}}_{\mathcal{DC}}\to {\mathcal{F}}_{\mathcal{DC}}$ be a triangular conorm operator; for any $u,v,w\in {\mathcal{F}}_{\mathcal{DC}}$, the following properties hold:

(1) 

Commutativity:

$$\mathbb{T}(u,v)=\mathbb{T}(v,u),$$

$$\mathbb{S}(u,v)=\mathbb{S}(v,u).$$

(2) 

Associativity:

$$\mathbb{T}(\mathbb{T}(u,v),w)=\mathbb{T}(u,\mathbb{T}(v,w)),$$

$$\mathbb{S}(\mathbb{S}(u,v),w)=\mathbb{S}(u,\mathbb{S}(v,w)).$$

Proof. 

We only prove the property of $\mathbb{T}$; the proof of $\mathbb{S}$ is similar.

Let the r-level sets of $u,v,w\in {\mathcal{F}}_{\mathcal{DC}}$ be ${\left[u\right]}^r={[x_u^r,y_u^r]}_C,{\left[v\right]}^r={[x_v^r,y_v^r]}_C,{\left[w\right]}^r={[x_w^r,y_w^r]}_C$ for any $r\in [0,1]$, respectively.

(1)

In order to prove $\mathbb{T}(u,v)=\mathbb{T}(v,u)$, we need to prove that for any $r\in [0,1]$, both sides of the equation have the same r-level set.

$$\begin{array}{ccc}\hfill {\left[\mathbb{T}(u,v)\right]}^r& =& T({\left[u\right]}^r,{\left[v\right]}^r)\hfill \\ \hfill & =& \left\{T(x,y)\right|x\in {\left[u\right]}^r,y\in {\left[v\right]}^r\}\hfill \\ \hfill & =& \left\{T(y,x)\right|y\in {\left[v\right]}^r,x\in {\left[u\right]}^r\}\hfill \\ \hfill & =& T({\left[v\right]}^r,{\left[u\right]}^r)\hfill \\ \hfill & =& {\left[\mathbb{T}(v,u)\right]}^r.\hfill \end{array}$$

(2)

In order to prove $\mathbb{T}(\mathbb{T}(u,v),w)=\mathbb{T}(u,\mathbb{T}(v,w))$, we need to prove that for any $r\in [0,1]$, both sides of the equation have the same r-level set.

$$\begin{array}{ccc}\hfill {\left[\mathbb{T}(\mathbb{T}(u,v),w)\right]}^r& =& T({\left[\mathbb{T}(u,v)\right]}^r,{\left[w\right]}^r)\hfill \\ \hfill & =& T(T({\left[u\right]}^r,{\left[v\right]}^r),{\left[w\right]}^r)\hfill \\ \hfill & =& \left\{T(T(x,y),z)\right|x\in {\left[u\right]}^r,y\in {\left[v\right]}^r,z\in {\left[w\right]}^r\}\hfill \\ \hfill & =& \left\{T(x,T(y,z))\right|x\in {\left[u\right]}^r,y\in {\left[v\right]}^r,z\in {\left[w\right]}^r\}\hfill \\ \hfill & =& T({\left[u\right]}^r,T({\left[v\right]}^r,{\left[w\right]}^r))\hfill \\ \hfill & =& {\left[\mathbb{T}(u,\mathbb{T}(v,w))\right]}^r.\hfill \end{array}$$

The proof of the theorem is complete. □

6. Application to Image Fusion

In this section, we apply the above-investigated special discrete fuzzy numbers on countable sets in the image fusion field [29,30,31]. Firstly, an interpretation of a gray image as a special discrete fuzzy numbers on countable sets is introduced.

The gray image is modeled as functions $f:D_f\subset R^2\to \tau \subset R$, where $D_f$ is the domain of the gray image, and $\tau$ is the corresponding gray-scale value space. We normalize the corresponding gray-scale value to the value in the interval [0,1].

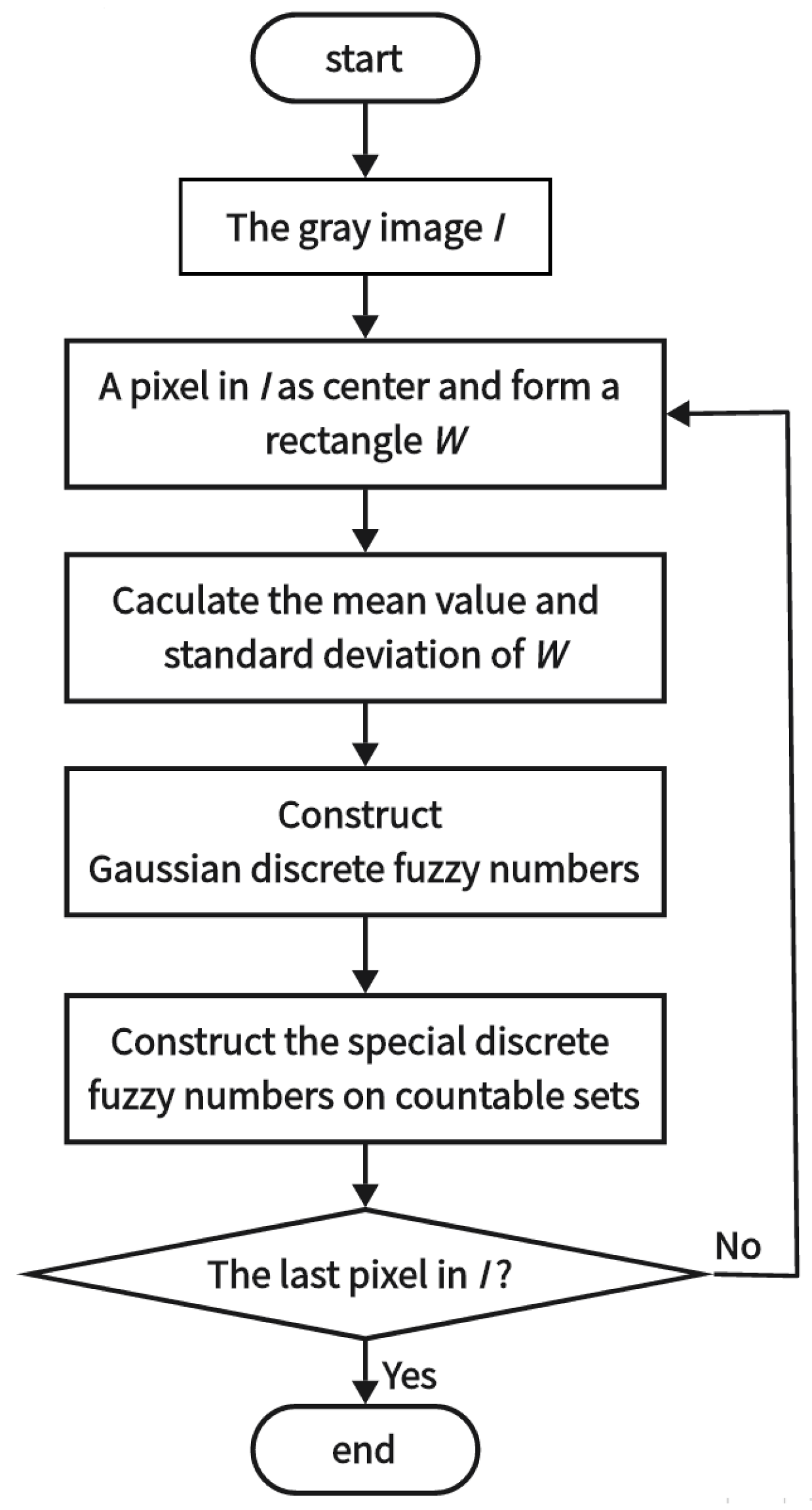
6.1. Interpretation of Gray Image as Special Discrete Fuzzy Numbers on Countable Sets

After the following steps, a gray image is represented by the special discrete fuzzy numbers on countable sets.

(1)

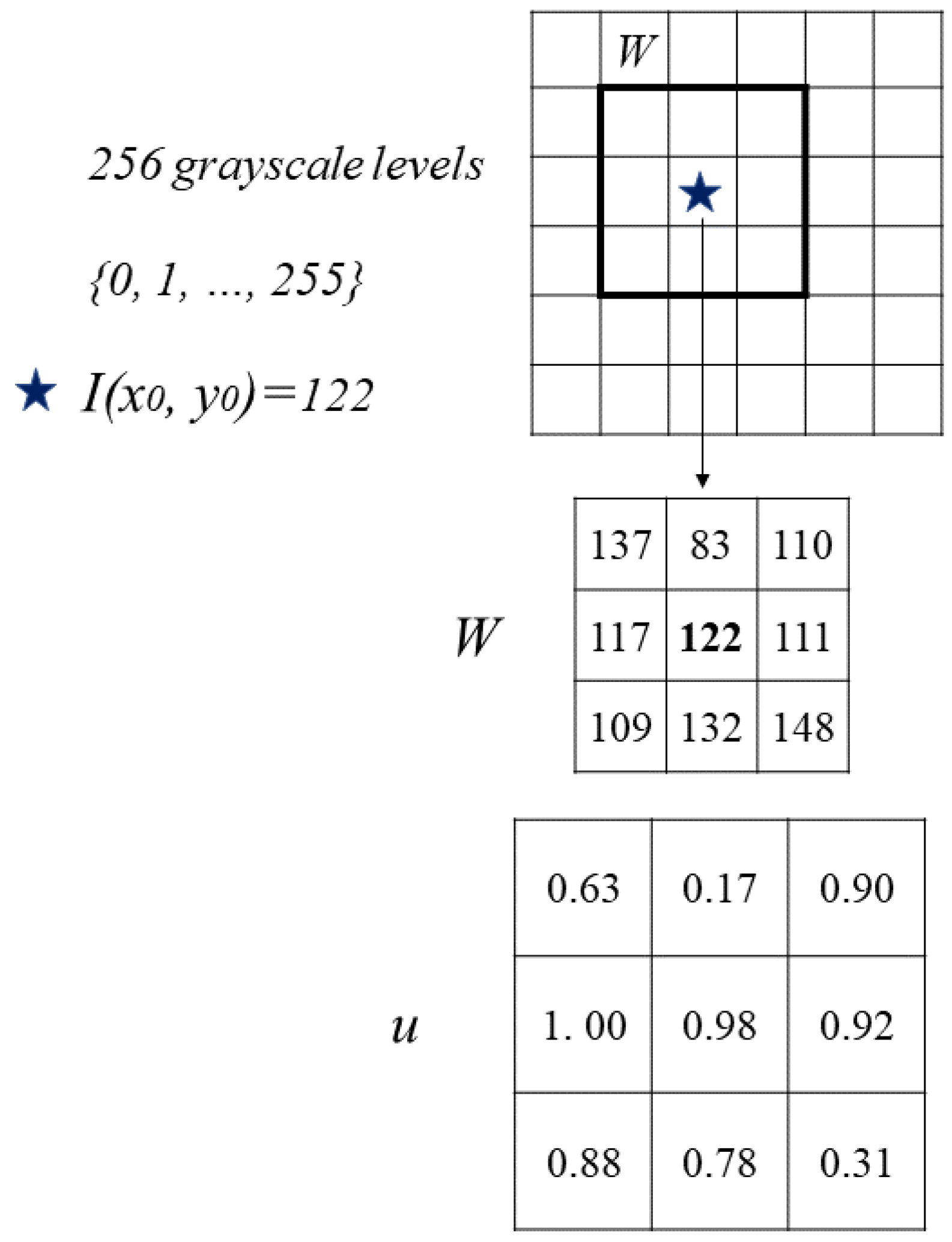
Let a gray image with 256 grayscale levels, i.e., $\{0,1,\dots ,255\}$, be I, and the size of I is $M\times N$. $I(x,y)$ represents a gray-scale value of $(x,y)$ in I, where $x\in \{1,2,\dots ,M\}$, $y\in \{1,2,\dots ,N\}$.

(2)

We take a point $(x_0,y_0),x_0\in \{2,3,\dots ,M-1\},y_0\in \{2,3,\dots ,N-1\}$ in I as the center and use the neighboring pixels around $(x_0,y_0)$ to form a rectangle, we call this rectangle W. The size of W is $n_W\times n_W$. When $n_W=3$, the points of W are represented as $(x_0+i,y_0+j),i,j=\{-1,0,1\}$ and the corresponding pixel value can be expressed as $I(x_0+i,y_0+j),i,j=\{-1,0,1\}$.

(3)

In order to represent the gray-scale pixel value, the mean value $\overline{W}$ and standard deviation $\overline{S}$ of W are calculated.

$$\overline{W}=\frac{{\sum }_{i=-1}^1{\sum }_{j=-1}^{1}I(x_0+i,y_0+j)}{3\times 3},$$

(4)

$$\overline{S}=\sqrt{\frac{{\sum }_{i=-1}^1{\sum }_{j=-1}^1{(I(x_0+i,y_0+j)-\overline{W})}^2}{3\times 3-1}}.$$

(5)

(4)

We construct Gaussian discrete fuzzy numbers for $I(x_0,y_0)$.

$u:R\to [0,1]$ is defined by:

$$u(I(x,y))=\left\{\begin{array}{cc}exp(-\frac{{(I(x,y)-\overline{W})}^2}{2{\overline{S}}^2}),\hfill & if(x,y)\in W\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

Then, u is the special discrete fuzzy numbers on countable sets with ${\left[u\right]}^0=\{I(x_0+i,y_0+j):i,j=\{-1,0,1\}\}$. In this case, the countable set is $C=\{0,1,\dots ,255\}$.

The above steps are shown in Figure 1.

Figure 1. The steps of using the special discrete fuzzy numbers on countable sets to represent pixel value of gray images.

In different gray image processing environments, the other sizes and shapes of W can be selected to construct special discrete fuzzy numbers on countable sets.

Example 6. 

Let image I be a gray image with 256 grayscale levels, i.e., $\{0,1,\dots ,255\}$. Let the point $(x_0,y_0)$ be a center and take its eight neighboring pixels to form a rectangle W. The size of W is $n_W\times n_W$ and $n_W=3$. The different objects I, $I(x_0,y_0)$ and the corresponding special discrete fuzzy numbers on countable sets are shown in Figure 2. When $I(x_0,y_0)=122$, its special discrete fuzzy numbers on countable set representation is shown in Figure 2.

Figure 2. Using the special discrete fuzzy numbers on countable sets to represent pixel value of gray images.

In this case, the countable set is $C=\{0,1,\dots ,255\}$ and u is the special discrete fuzzy numbers on countable sets with ${\left[u\right]}^0=\{83,109,110,111,117,122,132,137,148\}$. The corresponding membership degree is expressed as follows:

$$u=\{0.17/83,0.88/109,0.90/110,0.92/111,1.00/117,0.98/122,0.78/132,0.63/137,0.31/148\}.$$

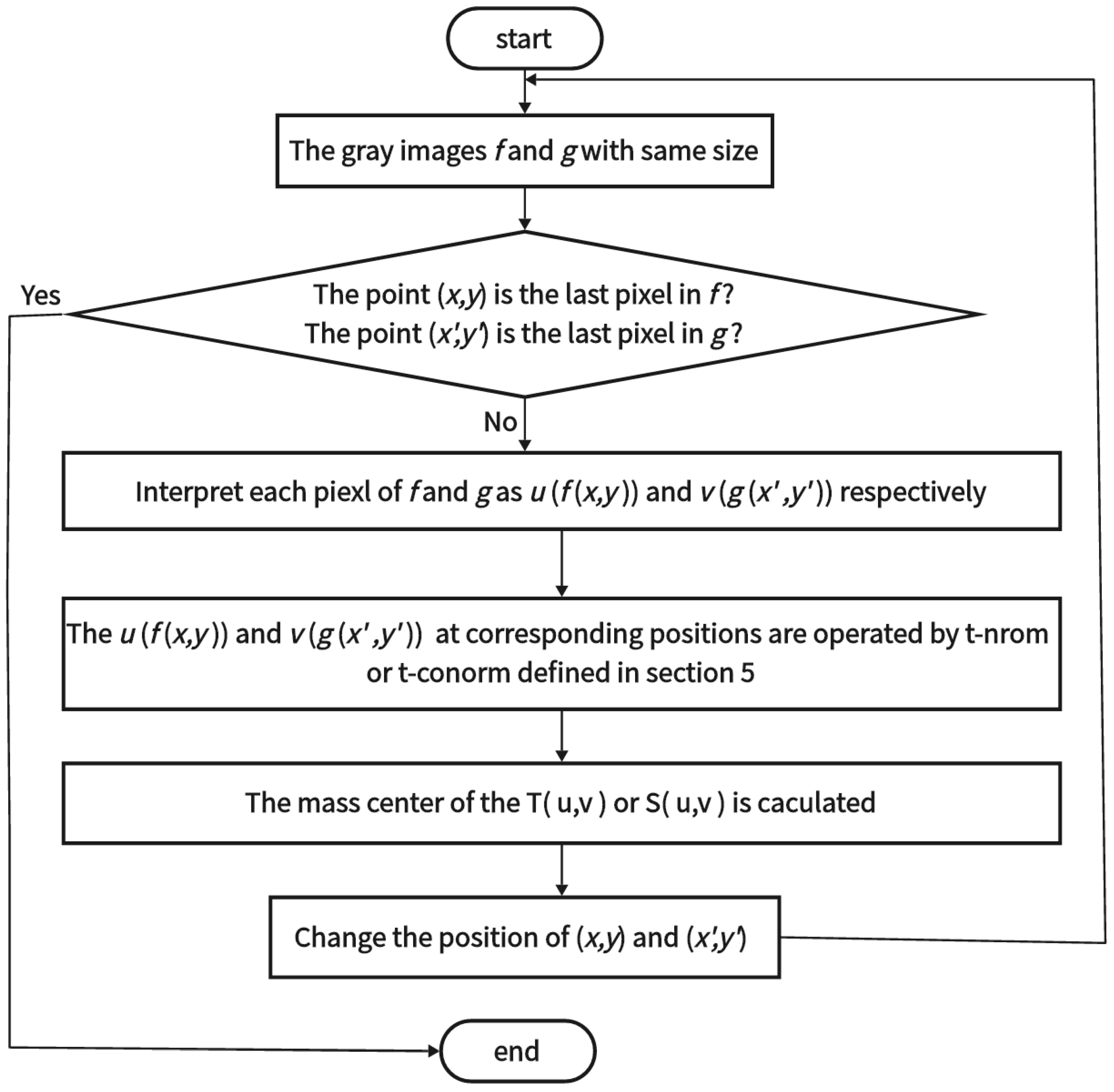
6.2. Gray Image Fusion by Means of the Triangular Norm and Triangular Conorm Operations of Special Discrete Fuzzy Numbers on Countable Sets

In order to construct the fusion algorithm of two gray-scale images, we first give a definition of the mass center of special discrete fuzzy numbers on countable sets.

Definition 10. 

Let w be a special discrete fuzzy number on countable sets, ${\left[w\right]}^0=\{x_1,x_2,\dots ,x_n\}.$ The mass center of w is defined as follows:

$$\overline{M}(w)=\frac{{\sum }_{i=1}^{n}w(x_i)x_i}{{\sum }_{i=1}^{n}w(x_i)}.$$

(7)

The mass center of special discrete fuzzy numbers on countable sets is a crisp number. When we use the special discrete fuzzy numbers on countable sets to represent the pixel value of gray images, the mass center is an approximation of the corresponding pixel value of gray images.

The image fusion algorithm of two gray-scale images will be given below. Let the two gray images be f and g with same size, and the size of them is $M\times N$. $f(x,y)$ is used to express the pixel gray value at the point $(x,y)$ in f, and $g(x^{\prime },y^{\prime })$ is used to express the pixel gray value at the point $(x^{\prime },y^{\prime })$ in f, where $x\in \{1,\dots ,M\},x^{\prime }\in \{1,\dots ,M\},y\in \{1,\dots ,N\},y^{\prime }\in \{1,\dots ,N\}$.

(1)

Let the point $(x,y)$ of f be the center and interpret it as special discrete fuzzy numbers on countable sets; this discrete fuzzy number is denoted as $u(f(x,y))$. Similarly, let the point $(x^{\prime },y^{\prime })$ of g be the center and interpret it as special discrete fuzzy numbers on countable sets; this discrete fuzzy number is denoted as $v(g(x^{\prime },y^{\prime }))$.

(2)

By using the triangular norm $\mathbb{T}$ or triangular conorm $\mathbb{S}$ defined in Section 5, two discrete fuzzy numbers $u(f(x,y))$ and $v(g(x^{\prime },y^{\prime }))$ at corresponding positions are operated, and a new discrete fuzzy number $\mathbb{T}(u,v)$ or $\mathbb{S}(u,v)$ is obtained.

(3)

The mass center of the new discrete fuzzy number is calculated according to Equation (7) as the pixel gray value of the fused image.

(4)

Change the points $(x,y)$ and $(x^{\prime },y^{\prime })$ to the same position and skip to step (1) until the points $(x,y)$ and $(x^{\prime },y^{\prime })$ traverse the image f and g, respectively.

After the above steps, images f and g are fused into a new image. The flowchart of the gray-scale image fusion algorithm is shown in Figure 3.

Figure 3. The flowchart of gray-scale image fusion algorithm.

To demonstrate the effectiveness of the above algorithm, an example of the fusion of the thermal image and the visible light image is presented. We conducted the experiments with the TNO Image Fusion Dataset the original thermal image and visible light image are shown in Figure 4.

Figure 4. The original images. (a) The thermal image. (b) The visible light image.

The fusion of the thermal image and the visible light image can not only reflect the military target but also have a certain ability of texture expression [32]. The corresponding experimental results are given in Figure 5. The software environment is Microsoft Windows 10 Home Edition and MATLAB R2018a. The hardware environment is a PC with an Intel(R) Core(TM)i5-8250U@1.60GHz CPU and 8.00 GB dual-channel DDR4 RAM.

Figure 5. The results of the fusion of thermal image and visible light image. (a) ${\mathbb{T}}_{Min}$. (b) ${\mathbb{S}}_{Max}$. (c) ${\mathbb{T}}_L$. (d) ${\mathbb{S}}_L$.

According to the experimental results in Figure 5, the different image fusion effects can be obtained by means of different aggregation operators defined in Section 5. For example, in Figure 5a, the texture and details of the road and leaves are clearer, while the outline of the pedestrian and roof is more pronounced in Figure 5b. In Figure 5c, the position of the person is more prominently displayed. The texture of the fence and grass in Figure 5d is more clearly distinguishable. Furthermore, the results of Figure 5a,b show that the aggregate result of the ${\mathbb{T}}_{Min}$ operator makes the overall image brightness low, while the aggregate result of ${\mathbb{S}}_{Max}$ operator has relatively high image brightness, which is consistent with the basic characteristics of these two operators. In practical applications, different aggregation operators can be selected according to different image fusion requirements.

7. Application to Aggregation of Subjective Evaluation

Scholars use discrete fuzzy numbers to describe human fuzzy language information, which can be applied to the realistic scenes such as group decision making, expert evaluation, or intelligent recommendation. The application of special discrete fuzzy numbers on countable sets to aggregation of subjective evaluation is proposed in this section. The specific steps of how to aggregate the subjective evaluations of multiple experts into a decision result are as follows:

The first step is to consider the semantic model $L=\{VB,B,MB,F,MG,G,VG\}$ where the letters refer to the linguistic terms “Very Bad”, “Bad”, “More or Less Bad”, “Fair”, “More or Less Good”, “Good”, and “Very Good”; they are arranged in ascending order:

$$VB\prec B\prec MB\prec F\prec MG\prec G\prec VG.$$

In order to facilitate the representation and operation of the special discrete fuzzy numbers on countable sets, the semantic pattern $L=\{VB,B,MB,F,MG,G,VG\}$ can be represented as the countable set $C=\{0,1,2,3,4,5,6\}$. In this case, the elements of set C correspond in a one-to-one manner with the elements of set L.

In the second step, the experts give subjective evaluation results based on the semantic pattern L. $E_i$ is used to represent the subjective evaluation results of each expert, where $i=1,2,3$. Each $E_i$ is a special discrete fuzzy number on countable sets with semantic pattern L as its support set. Moreover, let us consider the importance of each expert and use the weight ${\omega }_1,{\omega }_2,{\omega }_3\in {\mathcal{F}}_{\mathcal{DC}}$ to describe. $E_1,E_2,E_3,{\omega }_1,{\omega }_2,{\omega }_3\in {\mathcal{F}}_{\mathcal{DC}}$ are defined as follows:

$$E_1=\{0.3/1,0.4/2,0.7/3,1/4,0.8/5,0.6/6\},$$

$$E_2=\{0.2/0,0.4/1,1/2,0.4/3,0.2/4\},$$

$$E_3=\{0.5/2,0.6/3,0.7/4,1/5,0.7/6\},$$

$${\omega }_1=\{0.6/1,0.8/2,1/3,0.7/4\},$$

$${\omega }_2=\{0.4/2,0.6/3,1/4,0.8/5\},$$

$${\omega }_3=\{0.4/3,0.6/4,1/5,0.8/6\}.$$

In the third step, based on triangular norm and triangular conorm operations of special discrete fuzzy numbers on countable sets defined before, let us aggregate the subjective evaluations of multiple experts into a decision result. The final group consensus subjective evaluation results are still represented by special discrete fuzzy numbers on countable sets and can be interpreted directly.

Example 7. 

Let $C=\{0,1,2,3,4,5,6\}$, $E_1,E_2,E_3,{\omega }_1,{\omega }_2,{\omega }_3\in {\mathcal{F}}_{\mathcal{DC}}$, the $Lukasiewicz$ triangular norm operator $T_L=max\{0,x+y-6\}$, and $Lukasiewicz$ triangular conorm operator $S_L=min\{6,x+y\}$; according to the above definition and theorem in Section 5, we can calculate:

$$b_1={\mathbb{T}}_L(E_1,{\omega }_1)=\{0.8/0,1/1,0.8/2,0.7/3,0.6/4\},$$

$$b_2={\mathbb{T}}_L(E_2,{\omega }_2)=\{1/0,0.8/1,0.4/2,0.2/3\},$$

$$b_3={\mathbb{T}}_L(E_3,{\omega }_3)=\{0.5/0,0.6/1,0.6/2,0.7/3,1/4,0.8/5,0.7/6\},$$

then, $b_1,b_2,b_3\in {\mathcal{F}}_{\mathcal{DC}}$.

Next, we calculate the ${\mathbb{S}}_L$ for $b_1,b_2,b_3$,

$${\mathbb{S}}_L(b_1,{\mathbb{S}}_L(b_2,b_3))=\{0.5/0,0.6/1,0.6/2,0.7/3,0.8/4,1/5,0.8/6\}.$$

${\mathbb{S}}_L(b_1,{\mathbb{S}}_L(b_2,b_3))$ are discrete fuzzy numbers on countable set C. According to the semantic pattern $L=\{VB,B,MB,F,MG,G,VG\}$, the membership of "Very Bad” is 0.5, the membership of “Bad” is 0.6, the membership of "More or Less Bad” is 0.6, the membership of “Fair” is 0.7, the membership of “More or Less Good” is 0.8, the membership of “Good” is 1, and the membership of "Very Good" is 0.8. Therefore, the final group consensus subjective evaluation result is “Good”.

Example 8. 

Let $C=\{0,1,2,3,4,5,6\}$, $E_1,E_2,E_3,{\omega }_1,{\omega }_2,{\omega }_3\in {\mathcal{F}}_{\mathcal{DC}}$. The triangular norm operator $T_{Min}=min\{x,y\}$ and triangular conorm operator $S_{Max}=max\{x,y\}$,

$$d_1={\mathbb{T}}_{Min}(E_1,{\omega }_1)=\{0.6/1,0.8/2,1/3,0.7/4\},$$

$$d_2={\mathbb{T}}_{Min}(E_2,{\omega }_2)=\{0.2/0,0.4/1,1/2,0.4/3,0.2/4\},$$

$$d_3={\mathbb{T}}_{Min}(E_3,{\omega }_3)=\{0.5/2,0.6/3,0.7/4,1/5,0.7/6\},$$

then $d_1,d_2,d_3\in {\mathcal{F}}_{\mathcal{DC}}$.

Next, we calculate the ${\mathbb{S}}_{Max}$ for $d_1,d_2,d_3$,

$${\mathbb{S}}_{Max}(d_1,{\mathbb{S}}_{Max}(d_2,d_3))=\{0.5/2,0.6/3,0.7/4,1/5,0.7/6\}.$$

Similarly, the final group consensus subjective evaluation result is still “Good”.

8. Conclusions

In order to solve the problem in which the arithmetic operations and logic operations of general discrete fuzzy numbers do not satisfy the closure, a representation theorem in the form of endpoint functions of discrete fuzzy numbers defined on countable sets is proven in this paper. To overcome the defect that it is hard to define the measure of discrete fuzzy numbers reasonably in practical application, two different metrics are defined, and the relationship between them and the supremum metric (also called the uniform Hausdorff metric) of general fuzzy numbers is discussed. Further, the triangular norm and triangular conorm operations for discrete fuzzy numbers on countable sets are presented, and the properties of these two operators are investigated. We point out the conditions for maintaining the closure on ${\mathcal{F}}_{\mathcal{DC}}$ space of these two operators, which is a good property in specific applications. Finally, application examples of image fusion and group consensus opinion based on triangular norm and triangular conorm operations of special discrete fuzzy numbers on countable sets are given. In the near future, we want to extend to multi-dimensional discrete fuzzy numbers on countable sets and investigate their applications in the modeling and processing of multi-dimensional discrete uncertain data.