Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications
Abstract
:1. Introduction
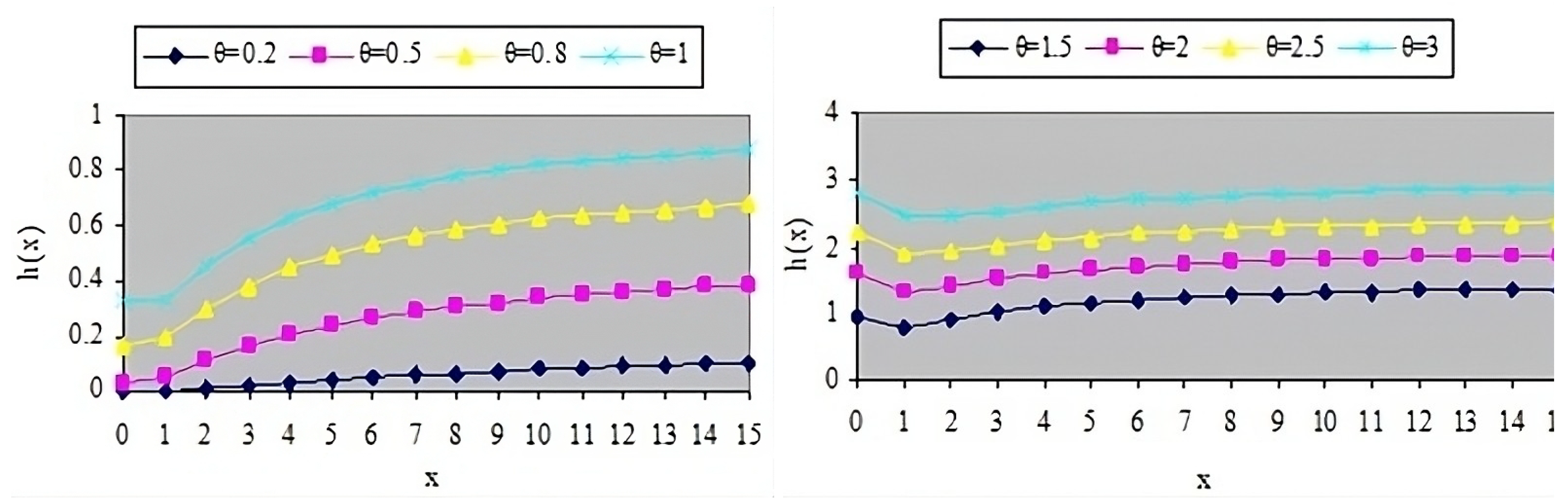
2. The Performance Index and Conforming Rate of the Ishita Distribution
3. Parameter Estimation and Testing Hypothesis
3.1. Maximum-Likelihood Estimation
3.2. Bayes Estimation
- Begin with the first suggestion .
- Specify .
- Generate from using the M-H method with the normal distribution
- (a)
- Produce a proposal from .
- (b)
- Determine the probability of acceptance
- (c)
- Produce a u from a uniform distribution.
- (d)
- Accept the proposal and set if ; otherwise set .
- Calculate the as
- Let .
- Steps (3)–(5) are repeated N times to obtain and
- Evaluate the credible intervals of and order and as and . Then, the credible intervals of be .
- Using the progressive type II censoring sample and the censoring scheme , find the MLE of the of the Ishita distribution.
- The L is predetermined; therefore, calculate the . The statistical test for lifetime performance is thus constructed as: against .
- Set the significance level.
- Determine the ’s lower bound as the lower confidence interval, .
- Lastly, the choice is made as if , and is rejected.
4. Real Data
- Step 1:
- Step 2:
- It is expected that the L is ; i.e., when the lifetime of the strength data for an aircraft window exceeds , the strength data are considered to be a conforming product. The of items must be greater than in order to address concerns raised by product buyers regarding lifetime performance. The value must exceed 1 according to Table 3. As a result, the is set at , and the following is tested: vs. .
- Step 3:
- Choose a level of significance of .
- Step 4:
- As a result, the one-sided CI for is .
- Step 5.
- As a result of the is refused.
| −11 | −0.25 | 0.333439 | 0.499 | 0.640043 | |
| −7 | 0.0000352065 | 0 | 0.423224 | 0.513 | 0.646582 |
| −6.5 | 0.000749944 | 0.1 | 0.463129 | 0.534 | 0.656405 |
| −6 | 0.000158733 | 0.2 | 0.505102 | 0.556 | 0.66671 |
| −5.75 | 0.000230328 | 0.25 | 0.526791 | 0.589 | 0.682179 |
| −5 | 0.000695385 | 0.3 | 0.548898 | 0.618 | 0.695765 |
| −4 | 0.00293547 | 0.32 | 0.557848 | 0.634 | 0.703252 |
| −3 | 0.0117921 | 0.34 | 0.566855 | 0.758 | 0.760654 |
| −2.5 | 0.0230645 | 0.35 | 0.571378 | 0.897 | 0.822204 |
| −2 | 0.0441834 | 0.353 | 0.572738 | 0.95 | 0.844379 |
| −1 | 0.014911 | 0.412 | 0.599694 | 1 | 0.864429 |
| −0.5 | 0.258413 | 0.478 | 0.630253 | 1.73215 | 1 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Computational procedure of performance assessment of lifetime index of Pareto lifetime businesses based on confidence interval. Appl. Soft Comput. 2008, 8, 698–705. [Google Scholar] [CrossRef]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Implementing lifetime performance index for the Pareto lifetime businesses of the service industries. Qual. Quant. 2009, 43, 291–304. [Google Scholar] [CrossRef]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Computational procedure of performance assessment of lifetime index of business for the Pareto lifetime model with right type II censored sample. Appl. Math. Comput. 2007, 184, 336–350. [Google Scholar]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Assessing the lifetime performance index of products from progressively type II right censored data using Burr-XII model. Math. Comput. Simul. 2009, 79, 2167–2179. [Google Scholar]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Assessing the lifetime performance index of products with the exponential distribution under progressively type II right censored samples. J. Comput. Appl. Math. 2009, 231, 648–656. [Google Scholar]
- Lee, W.C.; Wu, J.W.; Lei, C.L. Evaluating the lifetime performance index for the exponential lifetime products. Appl. Math. Model. 2010, 34, 1217–1224. [Google Scholar] [CrossRef]
- Wu, J.W.; Lee, W.C.; Hong, M.L.; Lin, L.S.; Chan, R.L. Assessing the lifetime performance index of Rayleigh products based on the Bayesian estimation under progressive type II right censored samples. J. Comput. Appl. Math. 2011, 235, 1676–1688. [Google Scholar]
- Ahmadi, M.V.; Doostparast, M.; Ahmadi, J. Estimating the lifetime performance index with Weibull distribution based on progressive first-failure censoring scheme. J. Comput. Appl. Math. 2013, 239, 93–102. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; El-Sagheer, R.M.; Soliman, A.A.; Abd Ellah, A.H. Inferences of the lifetime performance index with Lomax distribution based on progressive type II censored data. Econ. Qual. Control 2014, 29, 39–51. [Google Scholar] [CrossRef]
- Hassan, A.S.; Assar, S.M.; Selmy, A.S. Estimation of the lifetime performance index with Burr Type II distribution under type II censoring. In Proceedings of the 54th Annual Conference on Statistics, Computer Sciences and Operation Research, Cairo, Egypt, 9–11 December 2020. [Google Scholar]
- Majdah, M.B.; Ahmed, I.S.; Gamal, A.A. Hybrid censoring samples in assessment the lifetime performance index of Chen distributed products. Open Phys. 2019, 17, 607–616. [Google Scholar]
- Ramadan, D.A. Assessing the lifetime performance index of weighted Lomax distribution based on progressive type II censoring scheme for bladder cancer. Int. J. Biomath. 2021, 14, 2150018. [Google Scholar] [CrossRef]
- Howlader, H.A.; Hossain, A. Communications in statistics-theory and methods. In Quality and Quantity; Taylor & Francis: Abingdon, UK, 1995; Volume 24, pp. 2251–2259. [Google Scholar]
- Cohen, A.C. Life testing and early failure. Technometrics 1966, 8, 539–549. [Google Scholar] [CrossRef]
- Cohen, A.C. Truncated and Censored Samples Theory and Applications; Marcel Dekker: New York, NY, USA, 1991. [Google Scholar]
- Fernandez, A.J. On estimating exponential parameters with general type II progressive censoring. J. Stat. Plan. Inference 2004, 121, 135–147. [Google Scholar] [CrossRef]
- Sen, P.K. Progressive censoring schemes. In Encyclopedia of Statistical Sciences; John Wiley and Sons: New York, NY, USA, 1986; pp. 296–299. [Google Scholar]
- Al-Hussaini, E.K.; Abd El-Baset, A.A. On Bayesian predictive distributions of generalized order statistics. Metrika 2003, 57, 165–176. [Google Scholar] [CrossRef]
- Al-Hussaini, E.K.; Abd El-Baset, A.A. On Bayesian interval prediction of future records. Test 2003, 12, 79–99. [Google Scholar] [CrossRef]
- Asgharzadeh, A. Point and interval estimation for a generalized logistic distribution under progressive type II censoring. Commun. Stat.-Theory Methods 2006, 35, 1685–1702. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. Best linear unbiased and maximum likelihood estimation for exponential distributions under general progressive type II censored samples. Sankhya Indian J. Stat. Ser. B 1996, 58, 1–9. [Google Scholar]
- Balakrishnan, N.; Ng, H.K.T.; Kannan, N. A test of exponentiality based on spacings for progressively type II censored data. In Goodness-of-Fit Tests and Model Validity; Springer: Berlin/Heidelberg, Germany, 2002; pp. 89–111. [Google Scholar]
- Balakrishnan, N.; Lin, C. On the distribution of a test for exponentiality based on progressively type II right censored spacings. J. Stat. Comput. Simul. (Taylor Fr.) 2003, 73, 277–283. [Google Scholar] [CrossRef]
- Shukla, K.K.; Shanker, R. Ishita distribution and its applications. Biom. Biostat. Int. J. 2017, 5, 1–9. [Google Scholar]
- Elnagar, K.A.; Ramadan, D.A.; El-Desouky, B.S. Statistical inference to the parameter of the inverse power Ishita distribution under progressive type II censored data with application to COVID-19 data. J. Math. 2022, 2022, 7704167. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ahmed, E.A. Estimation of some lifetime parameters of generalized Gompertz distribution under progressively type II censored data. Appl. Math. Model. 2009, 39, 5567–5578. [Google Scholar] [CrossRef]
- Zehan, P.W. Invariance of maximum likelihood estimation. Ann. Math. Stat. 1966, 37, 744. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley and Sons: New York, NY, USA, 1982. [Google Scholar]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation; Springer: New York, NY, USA, 1988. [Google Scholar]
- Varian, H.R. Bayesian approach to real estate assessment. In Studies in Bayesian Econometrics and Statistics in Honor of L.J. Savage; Feinderg, S.E., Zellner, A., Eds.; North-Holland: Amsterdam, The Netherlands, 1975; pp. 195–208. [Google Scholar]
- Wu, J.W.; Lee, W.C.; Hong, C.W.; Yeh, S.Y. Implementing lifetime performance index of Burr XII products with progressively type II right censored sample. Int. J. Innov. Comput. Inf. Control 2014, 10, 671–693. [Google Scholar]
| −11 | −0.25 | 0.327713 | 0.499 | 0.611436 | |
| −7 | 0.0000382405 | 0 | 0.410495 | 0.513 | 0.617739 |
| −6.5 | 0.0000816901 | 0.1 | 0.447049 | 0.534 | 0.627266 |
| −6 | 0.000173278 | 0.2 | 0.485503 | 0.556 | 0.63734 |
| −5.75 | 0.000251629 | 0.25 | 0.505425 | 0.589 | 0.65264 |
| −5 | 0.000760398 | 0.3 | 0.525805 | 0.618 | 0.666279 |
| −4 | 0.0032004 | 0.32 | 0.534084 | 0.634 | 0.673885 |
| −3 | 0.0127309 | 0.34 | 0.542436 | 0.758 | 0.73503 |
| −2.5 | 0.0246903 | 0.35 | 0.546639 | 0.897 | 0.809544 |
| −2 | 0.0467506 | 0.353 | 0.547903 | 0.95 | 0.840259 |
| −1 | 0.152262 | 0.412 | 0.573104 | 1 | 0.870775 |
| −0.5 | 0.257434 | 0.478 | 0.602053 | 1.1818996 | 1 |
| 18.83 | 20.80 | 21.657 | 23.03 | 23.23 | 24.05 | 24.321 | 25.50 | |
| 10 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 25.52 | 25.80 | 26.69 | 26.77 | 26.78 | 27.05 | 27.67 | 29.90 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameter | MLE | SEL | LINEX | ||
|---|---|---|---|---|---|
| 0.089449 | 4.52857 | 10.0237 | 1.47632 | 4.52819 | |
| 0.99997 | 1.09643 | 2.20227 | 1.01326 | 1.09641 | |
| Parameter | MLE | MCMC |
|---|---|---|
| (−136.364, 136.543) | (0.291955, 10.1095) | |
| (0.99997, 1.22154) | (0.965014, 3.22197) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haj Ahmad, H.; Elnagar, K.; Ramadan, D. Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications. Symmetry 2023, 15, 1779. https://doi.org/10.3390/sym15091779
Haj Ahmad H, Elnagar K, Ramadan D. Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications. Symmetry. 2023; 15(9):1779. https://doi.org/10.3390/sym15091779
Chicago/Turabian StyleHaj Ahmad, Hanan, Kariema Elnagar, and Dina Ramadan. 2023. "Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications" Symmetry 15, no. 9: 1779. https://doi.org/10.3390/sym15091779
APA StyleHaj Ahmad, H., Elnagar, K., & Ramadan, D. (2023). Investigating the Lifetime Performance Index under Ishita Distribution Based on Progressive Type II Censored Data with Applications. Symmetry, 15(9), 1779. https://doi.org/10.3390/sym15091779






