Statistical Modeling of Financial Data with Skew-Symmetric Error Distributions

Abstract

Based on corporate financial data for almost all companies listed on the Prime Market of the Tokyo Stock Exchange in fiscal year 2021, we gradually refine a model to explain firms’ sales by the number of employees and total assets. Starting from a Cobb–Douglas-type functional form linearized by a log transformation, the assumption of a skew-symmetric distribution in the error structure and the introduction of industry dummies are shown to be useful not only in searching for a good-fitting model, but also in ensuring the accuracy of important parameters such as the labor share. The introduction of industry dummies helps to improve the accuracy of the model as well as to allow for interpretation as sector-wise total factor productivity.

1. Introduction

The purpose of this paper is to construct a model to predict firms’ sales by applying the Cobb–Douglas production function [1] to accounting data (financial statement data) for firms listed on the Prime Market of the Tokyo Stock Exchange. The Cobb–Douglas model has been in use in economics for so long, and has probably been the basis of so many different economic analyses, that it is rare for an analyst to change the model itself. We would like to improve the measure of fit by assuming a skew-symmetric distribution for the error term of Cobb–Douglas form, and further by splitting the constant term into industry dummies, to answer the following two econometric questions based on the best model at hand.

Note that the term ‘skew-symmetric distributions’ refers to the construction of a continuous probability distribution obtained by applying a certain form of perturbation to a symmetric density function (cf. [2]).

The first research question is the following: Are estimates of the labor share stable with respect to the statistical model specification? As shown in Section 5, the original Cobb–Douglas form, linearized by taking the logarithm of both sides and then estimated by the least squares method, overestimates the labor share by more than 20% compared to estimates based on a model that assumes a skew-t distribution for the error term and incorporates industry dummies. Given the overwhelming difference in the measures of fitness that take into account the number of parameters (namely the information criteria), it is clear which is the more reliable estimate of the labor share.

As will be explained later, our analysis is a cross-sectional analysis limited to fiscal year 2021 (ending 31 March 2022). From this choice of period, we naturally derive the following as our second research question. By observing the industrial sector-wise total factor productivity (TFP), can we highlight the economic situation in the COVID-19 period? There are many factors affecting TFP. Major factors are (1) the market and the economy, (2) technology and innovation, and (3) culture and society. As shown in Section 5, looking at TFP estimates by industry for FY2021, the impact of the COVID-19 pandemic can be seen in the lower end of the range, while the effect of the international political situation and Japan’s unique position in international finance can be seen in the upper end of the range.

A preliminary effort that underlies this paper is [3]. They analyzed a data set of the Nikkei NEEDS financial data (https://needs.nikkei.co.jp (accessed on 9 September 2023)), extracted from a database system [4]. There are over 1500 Japanese firms in the data set, and they are listed in the first section of the Tokyo Stock Market. They fit a log-log model (will be defined in Section 4.1) with the normal error fitted to the sales as the response variable and the number of employees and the total assets as the explanatory variables, based on the results of the data visualization.

Another related work [5] uses a financial data set that is extracted from the ‘Osiris’ database system (It is produced by the Bureau van Dijk KK), with information on over 80,000 listed and delisted firms. It reports that the log-log model with normal error is not suitable for the modeling of the sales caused by increasing the size of the data set, and the authors construct the log-log model with skew-symmetric error.

Both previous studies are based on exploratory data analysis (EDA) [6,7,8], and, in the same spirit, we analyze the Nikkei NEEDS financial data extracted from a database system (called SWKAD [9]) and re-examine the results of [3] based on EDA.

An interpretation of EDA is to obtain an appropriate model by repeating the cycle of statistical modeling based on the findings obtained by first summarizing and visualizing the data and then further summarizing and visualizing the results fitted to the data and refining the model by verifying the fitted results. This is a method to obtain an appropriate model by repeating this cycle. In this paper, as well, EDA is an important part of our research method. See also Figure 1 for EDA.

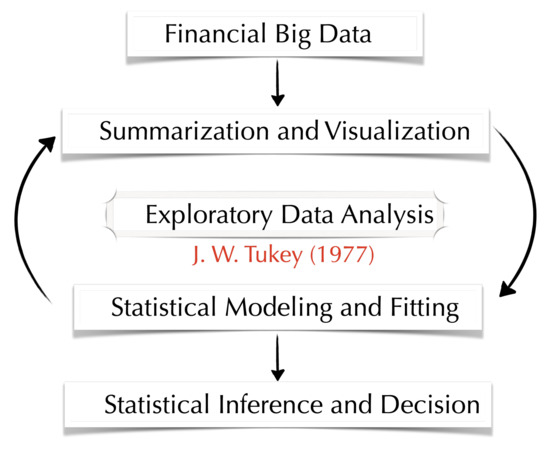
Figure 1. Concept diagram of EDA [6].

We use the data analysis environment R (e.g., [10]) and the {tidyverse} [8] and {plotly} [11] packages for data processing and visualization. For modeling, we consider solutions to problems that were difficult to handle in [3] by using the {sn} package to handle families of skew-symmetric distributions in R.

The structure of this paper is as follows. First, after explaining the financial data that we deal with in this paper (Section 2), we visualize the financial data in terms of a populational perspective (Section 3). Based on the findings obtained from data visualization, statistical modeling using a regression model for the cross-section data is performed, and the validity of the model is verified in an exploratory manner by applying it to the actual data (Section 4). Furthermore, after attempting to improve the model by fitting a log-log model that uses the industry information as a dummy variable to the cross-section data (Section 5), the model is modified to include the industry classification information as a dummy variable (Section 5). In the final section, we summarize the results of this paper and discuss future issues (Section 6). In the Supplementary Material, information on the Nikkei industrial classification codes and our computer environment, etc. is given.

2. Data Set

In this paper, we use the following data set (see Table 1). It contains financial data based on the consolidated financial results (for the fiscal year ending March 2022) of the population of (general business) firms listed on the Prime Market of the Tokyo Stock Exchange (hereinafter referred to as ‘TSE Prime’). The data in Table 1 are generally called cross-sectional data.

Table 1. Data set of TSE Prime listed firms extracted from Nikkei NEEDS financial database (the first ten data are extracted from all 1137 data).

	Name	YMD	Sector1	Sector2	Sector3	AC	Sales	Employees	Assets
1	KYOKUYO0000001	31 March 2022	2	35	341	1	253575	2208	130460
2	NIPPONSUISAN0000003	31 March 2022	2	35	341	1	693682	9662	505731
3	MARUHANICHIRO0000004	31 March 2022	2	35	341	1	866702	12352	548603
4	NITTETSUMINING0000022	31 March 2022	2	37	362	1	149082	2019	197732
5	MITSUIMATSUSHIMAHOLDINGS0000023	31 March 2022	2	37	361	1	46592	1305	67837
6	FURUKAWA0000043	31 March 2022	1	19	181	1	199097	2804	229727
7	MITSUIMINING&SMELTING0000045	31 March 2022	1	19	181	1	633346	11881	637878
8	TOHOZINC0000046	31 March 2022	1	19	181	1	124279	1051	145796
9	MITSUBISHIMATERIALS0000047	31 March 2022	1	19	181	1	1811759	23711	2125032
10	SUMITOMOMETALMINING0000049	31 March 2022	1	19	181	3	1259091	7202	2268756

Each column in Table 1 represents the following:

Name:

Firm name + Nikkei Firm Code (1137 firms)

YMD:

Closing date

Sector1:

Nikkei Industry Sector Code (Major) (1: manufacture, 2: non-manufacture)

Sector2:

Nikkei Industry Sector Code (Middle)

Sector3:

Nikkei Industry Sector Code (Minor)

AC: 

Accounting criterion (1: Japanese standard accounting, 2: United States standard accounting, 3: International Financial Reporting Standards (IFRS))

Sales:

Amount of sales (Unit: Million Yen)

Employee:

Number of employees (Unit: People)

Assets:

Total assets (Unit: Million Yen)

The data set is obtained by using the financial data extraction system SKWAD [9]. A summary of the data used is given by Figure 2.

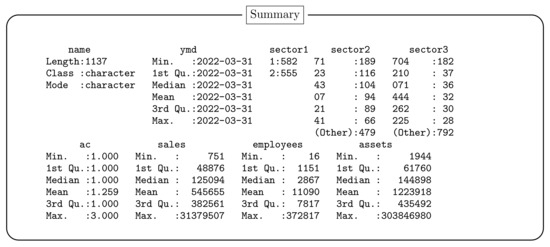
Figure 2. Summary of Data.

3. Data Visualization and Its Implications

In this paper, since we perform regression analysis using the cross-sectional data, we give some scatter plots. Note that the results of these visualizations give useful information for statistical modeling.

For more information on data visualization in general, see, for example, [12,13,14,15,16].

3.1. Data Visualization

Let us consider the visualization of the data set. We give some plots to visualize the distribution. In order to examine the simultaneous distribution between two variables, we draw a scatter plot for each 2 pair of variables in the form of a matrix (Figure 3). That is, a pairwise scatter plot or a scatter plot matrix provides useful information. From all the scatter plots in Figure 3, we can see that the data are ’dense’ near the origin and ’sparse’ away from the origin. This result can be regarded as a two-dimensional skewness.

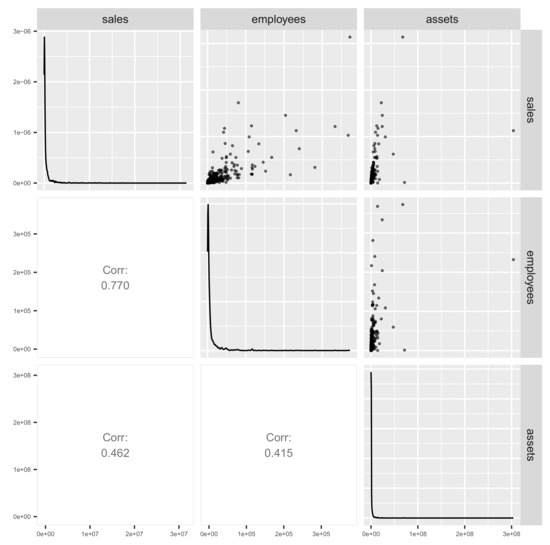
Figure 3. Pairwise scatter plot (or scatter plot matrix) of sales, number of employees, and total assets of firms in TSE Prime for the fiscal year ending March 2022.

Furthermore, in order to examine the simultaneous distribution among the three variables, we can do so by drawing a three-dimensional scatter plot. Figure 4 is a three-dimensional scatter plot of the sales, number of employees, and total assets of a company for the fiscal year ending 31 March 2022. As with the counter scatter plot, this plot shows that the data are ‘dense’ near the origin and ‘sparse’ away from the origin. This result can be regarded as a three-dimensional skewness.

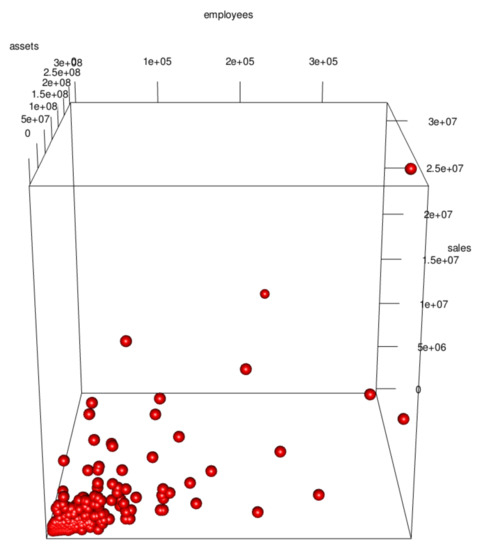
Figure 4. Three-dimensional scatter plot of sales, number of employees, and total assets of firms in TSE Prime for the fiscal year ending March 2022.

These results indicate that the cross-sectional data fixed at the period ending March 2022 follow a skewed distributionwith high density near the origin and low density away from the origin.

3.2. Implications of Visualization

The results of the data visualization so far suggest that the data are skewed, but it is difficult to obtain proper results by statistical inference or statistical modeling based on the normal distribution, ignoring this information. In order to solve this problem, as pointed out by [3], the logarithm of the data should be taken. This may lead to symmetrization by expanding small values near the origin and compressing large values (cf. [6,17,18,19]). From this point of view, the pairwise scatter plots (Figure 3) and the three-dimensional scatter plot (Figure 4) are redrawn on a logarithmic scale in Figure 5 and Figure 6, respectively.

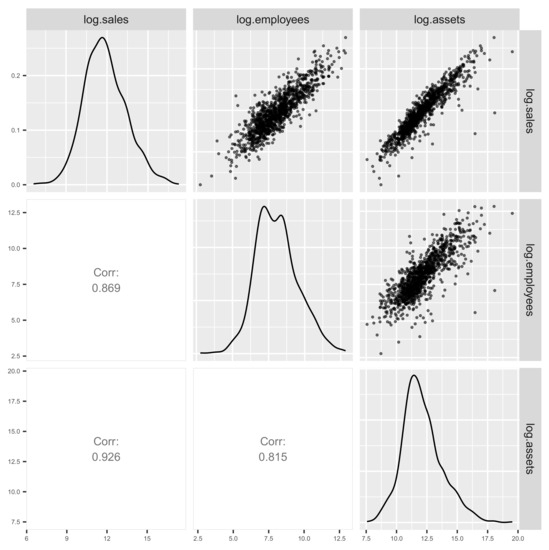
Figure 5. Logarithmic scale pairwise scatter plot.

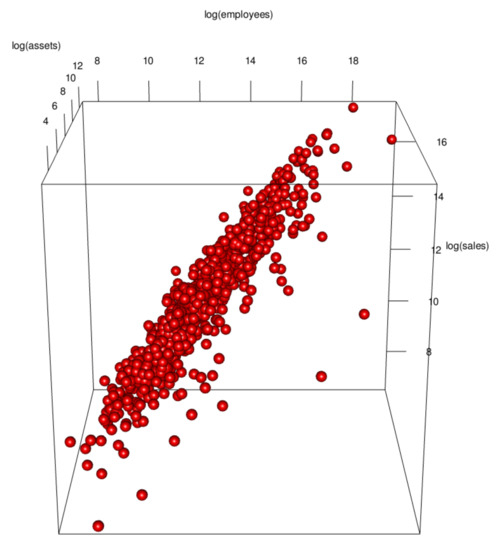
Figure 6. Logarithmic scale three-dimensional scatter plot.

From these visualizations, we can see that the distribution structure of the data on a logarithmic scale approaches symmetry, which suggests that statistical modeling based on the (multivariate) normal distribution is reasonable to some extent (cf. [3]). However, if we look carefully at the paired scatter plot (Figure 5), the distribution is slightly skewed to the right, and the logarithmic total assets (log.assets) and logarithmic sales (log.sales) can be seen to be ’slant’ from the lower right to the upper left, rather than being elliptical. In order to model distributions with such a structure, we can use distributions belonging to the family of skew-symmetric distributions proposed by [20,21].

In the next and subsequent sections, we will take the perspective of EDA [6] and perform statistical modeling based on the findings of these visualizations.

4. Regression Modeling of Cross-Sectional Data

In this section, we consider the financial data in terms of cross-sections and fit various regression models. The time period is fixed as the fiscal year ending March 2022.

4.1. Fitting Log-Log Model with Normal Error

We perform statistical modeling based on the visualization results given in the previous section. It is proposed to fit the following model:

$${\mathtt{sales}}_i=\gamma \times {\mathtt{employees}}_i^{{\alpha }_1}\times {\mathtt{assets}}_i^{{\alpha }_2}\times {ϵ}_i,{ϵ}_i\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathsf{LN}(0,{\sigma }^2)$$

(1)

This model is generally called the multiplicative model, where the error distribution is the lognormal distribution $\mathsf{LN}(0,{\sigma }^2)$. The model (1) is a Cobb–Douglas-type production function (cf. [1,22,23,24]). For the log-normal distribution, see, for example, [25].

The model (1) can be expressed as a normal linear model by taking the logarithm of both sides of the model:

$$log\left({\mathtt{sales}}_i\right)={\alpha }_0+{\alpha }_{1}log\left({\mathtt{employees}}_i\right)+{\alpha }_{2}log\left({\mathtt{assets}}_i\right)+log\left({ϵ}_i\right),log\left({ϵ}_i\right)\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathsf{N}(0,{\sigma }^2)$$

(2)

Now, the multiplicative model is linearized with respect to the parameters, with logarithmic variables on both sides of the equation. Here, we will call the model (2) the log-log model with normal error, following the classification of [26] (p. 59). Some log-log models have been applied for a long time to various fields, such as Economics and Biology. See, for example, [22] for its application to Econometrics and [27] for its application to Biology.

The regression coefficients ${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$ are estimated by the least squares method (say ${\widehat{\alpha }}_0$, ${\widehat{\alpha }}_1$, ${\widehat{\alpha }}_2$).

The coefficients of determination and the adjusted coefficients of determination are given as follows:

$$R^2=0.8964,{\overline{R}}^2=0.8962$$

However, the plot of regression diagnostics (Figure 7) indicate the existence of some influential data. In general, the analysis to detect influential data is called sensitivity analysis, and special indicators and plots have been proposed. Here, we give index plots of the most basic ones: the hat values, the Studentized residuals, and the Cook’s distances (Figure 8). For details, see [19,28].

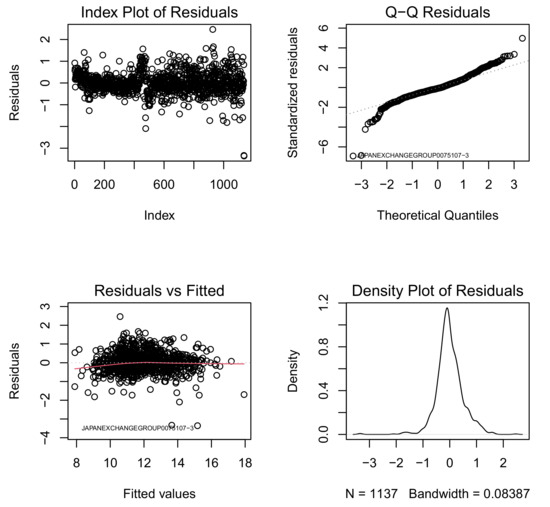
Figure 7. Plots of residuals based on the results of fitting log-log model with normal error to financial data for TSE Prime listed firms for the fiscal year ending March 2022. (upper-left) index plots of the residuals, (lower-left) plot of residuals against fitted values, (upper-right) normal Q-Q plot of residuals, and (lower-right) smoothed density function plot of the residuals.

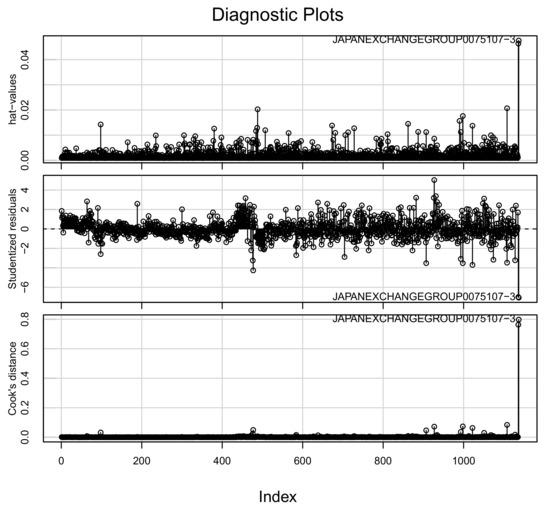
Figure 8. Plots for regression diagnostics (sensitivity analysis) when fitting the log-log model with normal error.

A numerical summary of these indices is given in Table 2. From these results, we can conclude that JAPANEXCHANGEGROUP0075107-3 (Japan Exchange Group, Inc., Credit & Leasing, Tokyo, Japan) is the most influential data set. The second most influential data set is JAPANSECURITIESFINANCE0070514-1 (Japan Securities Finance Co., Ltd. Credit & Leasing, Tokyo, Japan), followed by JAPANPOSTHOLDINGS0038793-1 (Japan Post Co., Ltd. Services, Tokyo, Japan) and TOMENDEVICES00306071-1 (Tomen Devices Co., Wholesale Trade, Tokyo, Japan), which can be confirmed to be highly influential. Note that these firms have very high or low sales relative to the number of employees and assets of the other firms.

Table 2. Studentized residuals, Hat values, and Cook’s distances of influential data.

	StudRes	Hat	CookD
TOMENDEVICES0030607-1	5.03	0.01	0.07
JAPANPOSTHOLDINGS0038793-1	−3.47	0.02	0.08
JAPANSECURITIESFINANCE0070514-1	−7.01	0.05	0.76
JAPANEXCHANGEGROUP0075107-3	−7.07	0.05	0.80

Of note, the banking industry has a unique profit structure in Japan, and for this reason it will not be included in the empirical analysis that follows. Even if the data set is processed with such a policy, in reality, some specific financial institutions may remain in the data set. The Japan Exchange Group and Japan Securities Finance are companies with particular roles. Japan Post was included in the primary screening because it is the holding company for a privatized post office and is classified as a service company.

Tomen Device (Wholesale Trade) has the same employee size and total assets as the previous year, yet somehow its sales grew 53% in FY2021. Given that this company is Samsung Electronics’ distributor in Japan, the reason for the rapid growth in sales may lie in the surge in demand for semiconductors as the digital transformation of the manufacturing industry progresses.

From the results of the above analysis, we remove these data as heterogeneous and re-fit a log-log model with normal errors. The coefficients of determination and the adjusted coefficients of determination are given as follows:

$$R^2=0.9081,{\overline{R}}^2=0.9079$$

We can see that the determination rate slightly increases to about 91%. In addition, the plot of regression diagnostics (Figure 9) shows no particularly influential data of note.

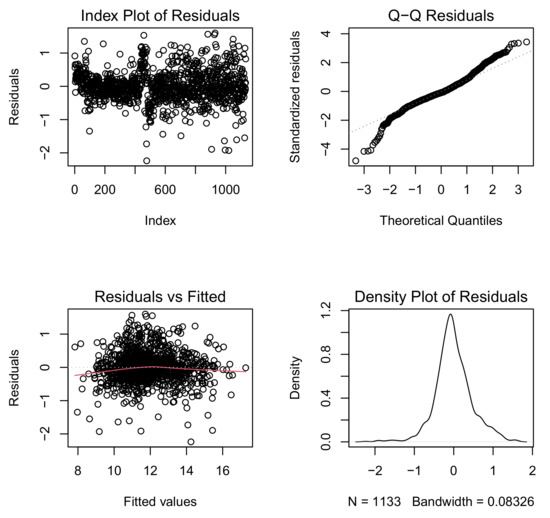
Figure 9. Plots of residuals based on the results of fitting a log-log model with normal errors after removing influential data.

However, looking at the normal Q-Q plot of the residuals in the regression diagnostic plots (Figure 9), it is questionable whether the residuals follow a normal distribution at the bottom, which makes the normality of the error doubtful. This phenomenon was also observed in [3], but the discussion was insufficient. In this paper, we consider an explanation of this problem by some models that assume errors following asymmetric families of distributions, such as the skew-normal (SN) and skew-t (ST) distributions treated in [5]. For details, see [20,21].

4.2. Fitting Log-Log Model with Skew-Normal Error

Consider the following model of a log-log model with skew-normal error:

$$log\left({\mathtt{sales}}_i\right)={\alpha }_0+{\alpha }_{1}log\left({\mathtt{employees}}_i\right)+{\alpha }_{2}log\left({\mathtt{assets}}_i\right)+log\left({ϵ}_i\right),log\left({ϵ}_i\right)\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathsf{SN}(0,{\omega }^2,\alpha )$$

(3)

where the notation ’$\mathsf{SN}(\xi ,{\omega }^2,\alpha )$’ denotes the skew-normal distribution with the direct parameter $(\xi ,{\omega }^2,\alpha )$.

Figure 10 gives some plots for regression diagnostics with the following residuals:

$$\begin{array}{cc}\hfill e_{\mathsf{SN}.\mathsf{CP}i}& :=log\left({\mathtt{sales}}_i\right)-\left\{({\widehat{\alpha }}_0+\widehat{\omega }b\widehat{\delta })+{\widehat{\alpha }}_{1}log\left({\mathtt{employees}}_i\right)+{\widehat{\alpha }}_{2}log\left({\mathtt{assets}}_i\right)\right\},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill z_{\mathsf{SN}.\mathsf{sDP}i}& :=\frac{log\left({\mathtt{sales}}_i\right)-\left\{{\widehat{\alpha }}_0+{\widehat{\alpha }}_{1}log\left({\mathtt{employees}}_i\right)+{\widehat{\alpha }}_{2}log\left({\mathtt{assets}}_i\right)\right\}}{\widehat{\omega }}\hfill \end{array}$$

(5)

where ${\widehat{\alpha }}_j$ ($j=0,1,2$), $\widehat{\omega }$, $\widehat{\alpha }$ are the maximum likelihood estimates (MLE) of ${\alpha }_j$, $\omega$, $\alpha$, respectively, and $b:=\sqrt{2/\pi }$, $\widehat{\delta }:=\widehat{\alpha }/\sqrt{1+{\widehat{\alpha }}^2}$. Note that (4) and () are called the centered parameter (CP) residuals and the scaled direct parameter (DP) residuals, respectively. For details, see [5,21].

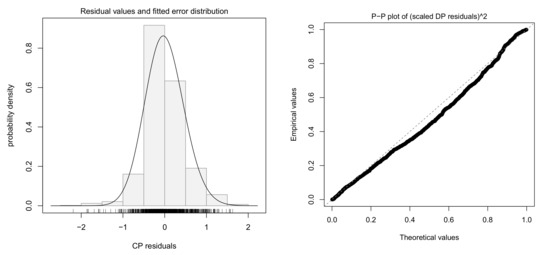
Figure 10. Histogram of CP residuals and statistical model (left panel); P-P plot of squared scaled DP residuals (right panel).

From the results, we can see that the P-P plot deviates slightly from the straight line. It is considered that the model does not capture the structure of the error distribution.

4.3. Fitting Log-Log Model with Skew-t Error

Consider the following model of the log-log model with skew-t error:

$$log\left({\mathtt{sales}}_i\right)={\alpha }_0+{\alpha }_{1}log\left({\mathtt{employees}}_i\right)+{\alpha }_{2}log\left({\mathtt{assets}}_i\right)+log\left({ϵ}_i\right),log\left({ϵ}_i\right)\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathsf{ST}(0,{\omega }^2,\alpha ,\nu )$$

(6)

where the notation ’$\mathsf{ST}(\xi ,{\omega }^2,\alpha ,\nu )$’ denotes the skew-t distribution with the direct parameter $(\xi ,{\omega }^2,\alpha ,\nu )$.

The results of fitting the model (6) to the data for the fiscal year ending March 2022 without the influential data are given in Table 3.

Table 3. Regression results: log-log model with skew-t error.

	Estimate	Std.Err	z-Ratio	Pr{>|z|}
(Intercept.DP)	1.0344	0.0980	10.56	0.0000
log(employees)	0.2985	0.0165	18.11	0.0000
log(assets)	0.6817	0.0150	45.40	0.0000
$\omega$	0.3623	0.0213	17.03	0.0000
$\alpha$	0.5435	0.1717	3.17	0.0016
$\nu$	3.7783	0.4997	7.56	0.0000

All parameters are significant from Table 3.

Here, the significance tests rely on the classical fact that the maximum likelihood estimates are approximately normal under certain conditions, and their asymptotic variance can be calculated in terms of the Fisher information. See [29] for example. The maximum likelihood estimate divided by its standard error can be used as a test statistic for the null hypothesis that the population value of the parameter equals zero; hence, the fourth column of Table 3 is labeled as ‘z-ratio’.

An adjusted sample regression plane is given by

$$\begin{array}{cc}\hfill log\left(\mathtt{sales}\right)& =({\widehat{\alpha }}_0+\widehat{\omega }{b}_{\widehat{\nu }+1}\widehat{\delta })+{\widehat{\alpha }}_{1}log\left(\mathtt{employees}\right)+{\widehat{\alpha }}_{2}log\left(\mathtt{assets}\right)\hfill \\ \hfill & =(1.034+0.362\times 1.016\times 0.478)+0.299log\left(\mathtt{employees}\right)+0.682log\left(\mathtt{assets}\right)\hfill \\ \hfill & =1.21+0.299log\left(\mathtt{employees}\right)+0.682log\left(\mathtt{assets}\right),\hfill \end{array}$$

(7)

where $b_{\widehat{\nu }+1}:=\sqrt{(\widehat{\nu }+1)/\pi }\Gamma \left(\left(\widehat{\nu }\right)/2\right)/\Gamma \left((\widehat{\nu }+1)/2\right)$, $\widehat{\delta }=\widehat{\alpha }/\sqrt{1+{\widehat{\alpha }}^2}$.

Figure 11 gives the logarithmic scale three-dimensional scatter plot and the adjusted sample regression plane when fitting the log-log model with skew-t errors.

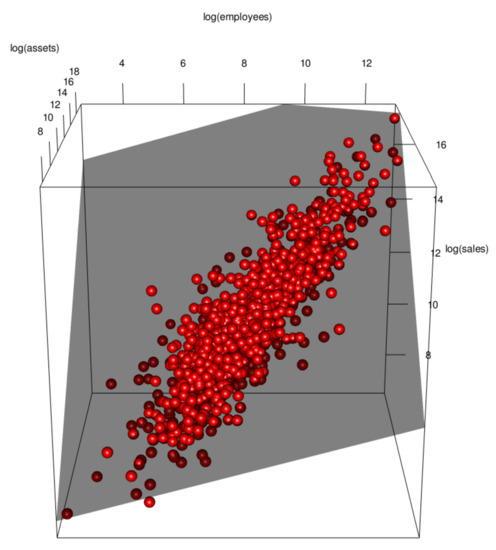
Figure 11. Logarithmic scale three-dimensional scatter plot and sample regression plane: log-log model with skew-t errors after removing the influential data.

Figure 12 gives some plots for regression diagnostics and the following residuals are used:

$$\begin{array}{cc}\hfill e_{\mathsf{ST}.\mathsf{pCP}i}& :=log\left({\mathtt{sales}}_i\right)-\left\{({\widehat{\alpha }}_0+\widehat{\omega }{b}_{\widehat{\nu }+1}\widehat{\delta })+{\widehat{\alpha }}_{1}log\left({\mathtt{employees}}_i\right)+{\widehat{\alpha }}_{2}log\left({\mathtt{assets}}_i\right)\right\},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill z_{\mathsf{ST}.\mathsf{sDP}i}& :=\frac{log\left({\mathtt{sales}}_i\right)-\left\{{\widehat{\alpha }}_0+{\widehat{\alpha }}_{1}log\left({\mathtt{employees}}_i\right)+{\widehat{\alpha }}_{2}log\left({\mathtt{assets}}_i\right)\right\}}{\widehat{\omega }}\hfill \end{array}$$

(9)

where (8) is called the pseudo-CP residuals. For details, see also [5,21].

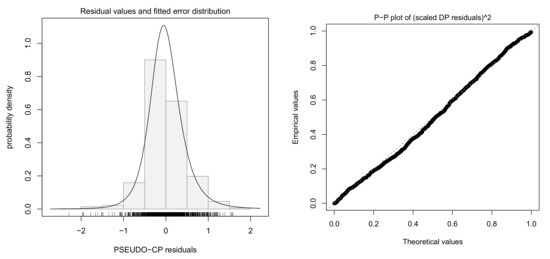
Figure 12. Histogram and P-P plot of residuals.

The results show that no particular problem is found.

4.4. Model Selection for Log-Log Models

Based on the previous results, it is expected that the log-log model with skew-t errors fits well. This is evaluated by the Akaike Information Criterion (AIC) [30] and Bayesian Information Criterion (BIC) [31,32,33,34].

The values of the dimension of parameters (‘dim’), $\mathrm{AIC}$, and $\mathrm{BIC}$ for the model are given in Table 4 when fitting a log-log model with the normal (‘Normal’), the skew-normal (‘Skew-Normal’), and the skew-t (‘Skew-t’) errors to the data, excluding the influential data, respectively.

Table 4. Table of AIC and BIC: log-log models.

	Dim	AIC	BIC
Normal	4	1496.43	1516.56
Skew-Normal	5	1494.69	1519.85
Skew-t	6	1397.36	1427.56

From this result, it is found that the best model is the log-log model with the skew-t errors.

5. Fitting Log-Log Model with Dummy Variables

Through the statistical modeling and fitting to the data so far, we were able to construct the log-log model with the normal errors to explain sales with a determination rate of nearly $90\%$ for the cross-sectional financial data for firms closing their fiscal year ending 31 March 2022. The regression diagnostics on the fits also show that those assuming a skew-symmetric distribution family in the error structure, especially the skew-t errors, are more appropriate.

On the other hand, the bubble chart (Figure 13) shows that every industry (adopting the Nikkei middle classification codes) seems to have a different regression line but with a more or less similar slope. Specifically, we can expect that the ‘intercept’ of the model is different for each industry. For details of these codes, please refer to Section S1 in the Supplementary Material.

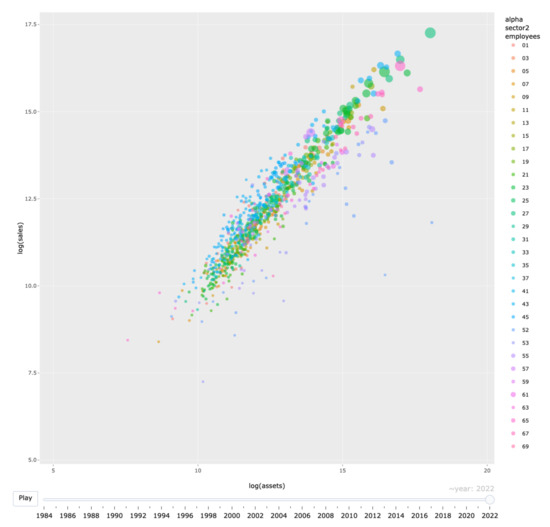
Figure 13. Bubble chart of financial data for firms closing in March 2022: color-coded according to Nikkei middle classification codes.

The simplest form of statistical modeling using information from this visualization is to extend the model using sector-specific dummy variables (cf. [3]). To generate dummy variables, we rely on the Nikkei industry middle classification, which consists of 33 industries. Whether or not dummies are used, constructing models by industrial sector is a common practice to improve the accuracy in the statistical modeling of entire industries. In [35], the industry sector is explained as a fundamental factor, as well as country and size (small cap, large cap, etc.). [36] (Chapter 32) also demonstrated how the industry sector works in terms of investment.

5.1. Fitting Log-Log Model with Skew-t Error and Dummy Variables

Consider the following log-log model with the skew-t error and some dummy variables:

$$log\left({\mathtt{sales}}_i\right)={\alpha }_0+{\alpha }_{1}log\left({\mathtt{employees}}_i\right)+{\alpha }_{2}log\left({\mathtt{assets}}_i\right)+\sum _{j=1}^m{\delta }_j{D}_{ij}+log\left({ϵ}_i\right),log\left({ϵ}_i\right)\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathsf{ST}(0,{\omega }^2,\alpha ,\nu )$$

(10)

where $j=1,\cdots ,m(=33)$, and

$$D_{ij}:=\left\{\begin{array}{cc}1,\hfill & \mathrm{if\; the\; firm} i \mathrm{belongs\; to\; the} j-\mathrm{th}\mathrm{industry},\hfill \\ 0,\hfill & \mathrm{if\; the\; enterprise} i \mathrm{does\; not\; belong\; to\; the} j\mathrm{th}\mathrm{industry}.\hfill \end{array}\right.$$

Note that we define ${\delta }_1:=0$ for uniqueness of estimation.

The estimated regression coefficients for this model are given in Table 5. Most regression coefficients are found to be significant. We can conclude that virtually all parameters are significant, but we will return to this point shortly. The group of the empirical regression planes is represented as follows (see also Figure 14).

$$\begin{array}{cc}\hfill log\left(\mathtt{sales}\right)& =({\widehat{\alpha }}_0+\widehat{\omega }{b}_{\widehat{\nu }+1}\widehat{\delta }+{\widehat{\delta }}_j)+{\widehat{\alpha }}_{1}log\left(\mathtt{employees}\right)+{\widehat{\alpha }}_{2}log\left(\mathtt{assets}\right)\hfill \\ \hfill & =(1.244+{\widehat{\delta }}_j)+0.294log\left(\mathtt{employees}\right)+0.702log\left(\mathtt{assets}\right),j=1,\cdots ,33\hfill \end{array}$$

(11)

Table 5. Regression results: log-log model with skew-t errors and dummy variables.

	Estimate	Std.Err	z-Ratio	Pr{>|z|}	TFP
log(employees)	0.2938	0.0157	18.73	0.0000	—
log(assets)	0.7024	0.0150	46.88	0.0000	—
$\omega$	0.2564	0.0158	16.18	0.0000	—
$\alpha$	−0.5675	0.1853	−3.06	0.0022	—
$\nu$	3.5863	0.4394	8.16	0.0000	—
Petroleum	0.6154	0.1416	4.35	0.0000	1.8594
Wholesale Trade	0.4497	0.0604	7.44	0.0000	1.6937
Retail Trade	0.3023	0.0718	4.21	0.0000	1.5463
Fish and Marine Products	0.2622	0.1422	1.84	0.0652	1.5062
Shipbuilding and Repairing	0.1085	0.2643	0.41	0.6813	1.3525
Foods (Intercept.DP)	1.3660	0.1057	12.92	0.0000	1.2440
Construction	−0.0029	0.0588	−0.05	0.9605	1.2411
Iron and Steel	−0.1624	0.0730	−2.22	0.0261	1.0816
Warehousing and Harbor Transportation	−0.2067	0.1117	−1.85	0.0644	1.0373
Sea Transportation	−0.2110	0.1273	−1.66	0.0973	1.0330
Non-Ferrous Metal and Metal Products	−0.2252	0.0674	−3.34	0.0008	1.0188
Utilities—Gas	−0.2267	0.1132	−2.00	0.0452	1.0173
Real Estate	−0.2507	0.0924	−2.71	0.0067	0.9933
Mining	−0.2623	0.1424	−1.84	0.0655	0.9817
Pulp and Paper	−0.2710	0.0912	−2.97	0.0030	0.9730
Trucking	−0.2751	0.0840	−3.28	0.0010	0.9689
Motor Vehicles and Auto Parts	−0.2935	0.0640	−4.59	0.0000	0.9505
Other Manufacturing	−0.3027	0.0770	−3.93	0.0001	0.9413
Services	−0.3048	0.0555	−5.49	0.0000	0.9392
Transportation Equipment	−0.3107	0.1125	−2.76	0.0058	0.9333
Chemicals	−0.3284	0.0562	−5.84	0.0000	0.9156
Communication Services	−0.4065	0.0943	−4.31	0.0000	0.8375
Stone, Clay, and Glass Products	−0.4198	0.0756	−5.55	0.0000	0.8242
Electric and Electronic Equipment	−0.4450	0.0561	−7.94	0.0000	0.7990
Machinery	−0.4734	0.0567	−8.36	0.0000	0.7706
Rubber Products	−0.4754	0.1016	−4.68	0.0000	0.7686
Drugs	−0.4848	0.0706	−6.86	0.0000	0.7592
Precision Equipment	−0.5204	0.0716	−7.27	0.0000	0.7236
Textile Products	−0.5943	0.0868	−6.85	0.0000	0.6497
Utilities—Electric	−0.6013	0.0900	−6.68	0.0000	0.6427
Credit and Leasing	−0.8536	0.1031	−8.28	0.0000	0.3904
Railroad Transportation	−1.0878	0.0749	−14.52	0.0000	0.1562
Air Transportation	−1.1681	0.1623	−7.20	0.0000	0.0759

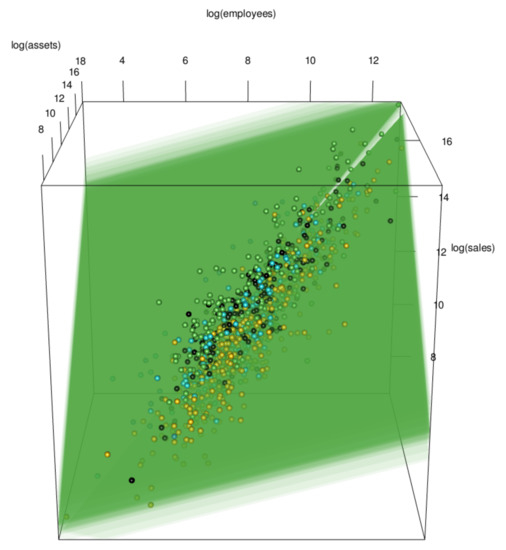
Figure 14. Logarithmic scale three-dimensional scatter plot and sample regression planes: log-log model with skew-t errors and dummy variables.

Note that $\widehat{\delta }$ is a function of $\widehat{\alpha }$, which is one of the direct parameters of the skew-t distribution.

The AIC of the estimated model is 701.23, with the number of estimated parameters being 38. Thus, the introduction of sector dummy variables has led to a large reduction in the AIC, from 1397.36 (see Table 4) to 701.23.

The constant term in the Cobb–Douglas production function (namely $\gamma$ in Equation (1)) is called total factor productivity (TFP). TFP is usually measured as the ratio of aggregate output to aggregate inputs. Thus, if we assume Cobb–Douglas production function $Y=\gamma L^{{\alpha }_1}{K}^{{\alpha }_2}$, where Y, L, K denote sales, employees, and assets, respectively, it is evident that TFP is calculated by $Y/L^{{\alpha }_1}{K}^{{\alpha }_2}$, which reduces to $\gamma$.

There are many factors affecting TFP. Major factors are (1) the market and the economy, (2) technology and innovation, and (3) culture and society. For a comprehensive review of TFP, see [37]. In Equation (11), ${\widehat{\alpha }}_0+\widehat{\omega }{b}_{\widehat{\nu }+1}\widehat{\delta }+{\widehat{\delta }}_j=1.244+{\widehat{\delta }}_j$ is the logarithm of TFP, but we refer to this term simply as TFP because there is probably no misunderstanding in this section.

The industry dummy estimates in Table 5 are sorted in descending order of TFP. The values for each industry in the ’estimate’ column are all ${\widehat{\delta }}_j$, except for the result for the food industry (‘Foods’), which is estimated as the direct parameter intercept of the model.

The ‘Foods’ sector is chosen as a reference because it includes a moderate number of firms, neither too few nor too many. We find that ${\widehat{\delta }}_j$s for ‘Construction’ and ‘Shipbuilding and Repairing’ is close to zero and apparently ‘insignificant’. This is correct as an interpretation of testing null of ${\widehat{\delta }}_j=0$, but it should be interpreted that the TFP of these industries is quite close to that of the reference industry, namely the ‘Foods’ industry. In fact, the TFP of these three industries is very similar. Therefore, virtually all the parameters are significant, but some of them might be grouped. We will return to this issue later in Section 5.3.

The plots for regression diagnostics (Figure 15) show that no particular problem is found.

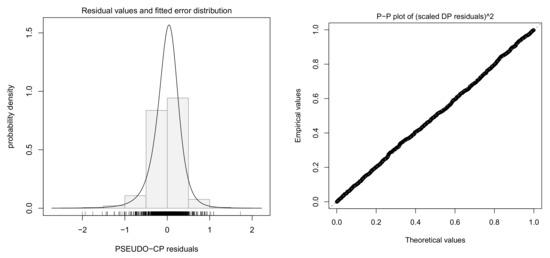
Figure 15. Histogram and P-P plot of residuals.

5.2. Economic Implications

In this subsection, we answer the two questions mentioned in the Introduction. As for the labor share estimates (${\widehat{\alpha }}_1$), they changed slightly with each refinement of the model. We observed ${\widehat{\alpha }}_1=0.3552$ with the log-log model with normal errors, while ${\widehat{\alpha }}_1=0.2938$ with the sector dummies introduced in the log-log model with skew-t errors (see Table 5). It is worth noting that the labor share estimated by least squares after simply linearizing the model with log transformation overestimates the labor share by more than 20% compared to the results of elaborate statistical modeling. It seems clear which estimate should be trusted in terms of predictability and explanatory power.

It should be noted, however, that the labor share here has a different meaning and level from the labor share in GDP statistics. Here, the number of employees corresponds to the labor input, while, in the GDP statistics, the compensation of employees is the input. Considering that the labor share in Japan has been declining in recent years, which has been problematic, but is still around 60% (see [38]), our problem setting should be regarded as a completely separate analysis from the national accounts.

The second issue presented in our Introduction concerned the econometric interpretation of industry dummies. It is called total factor productivity (TFP) and is discussed in Section 5.1. The industry dummy estimates reported in Table 5 are listed in descending order. In FY2021, we were still in the midst of the COVID-19 crisis, and the results of the analysis clearly show that the bottom two industries (railroad and air transportation) had almost no growth factors due to the shrinking travel demand.

On the other hand, the petroleum industry, which is at the top of the list, can be associated more with international conditions and the peculiarities of Japan’s monetary policy than to COVID-19-related factors. The petroleum industry showed record profits for the fiscal year ending 31 March 2022, as the weak yen and soaring crude oil prices boosted sales prices. This may have stemmed from the fact that our model is a model for sales, not a model that explains value added.

As for wholesale and retail trade, which are the top two and three TFP sectors, this could also be interpreted as an indication that the stay-home demand was still strong in the COVID-19 period. In general, for FY2021, the TFP reflected the social and economic conditions of the year, especially at the extremes of descending order.

5.3. Grouping ‘Insignificant’ Sectors and Final Model Comparison

Looking at Table 5, one might wonder whether distinct dummy parameters are necessary for all industries. In particular, it seems natural to group the industries with estimates that appear insignificant in Table 5 because their constant terms are close to the reference (Foods). Hence, we grouped the eight sectors (Foods, Shipbuilding and Repairing, Fish and Marine Products, Mining, Construction, Sea Transportation, Warehousing and Harbor Transportation, Utilities—Gas) and assumed that ${\delta }_j=0$ for all of them.

We avoid presenting a new version of Table 5 due to space limitations and note the main points of the estimation results for the constrained model. Now, the grouped eight industries, including Foods, are the reference, and their TFP estimate is ${\widehat{\alpha }}_0+\widehat{\omega }{b}_{\widehat{\nu }+1}\widehat{\delta }=1.363+0.2564\times 0.9641\times (-0.4475)=1.252$, a slight change from the unconstrained model estimate ($1.244$). It is observed that the ranking of industries in descending order of TFP is invariant. The grouped industries’ TFP is ranked between that of Retail Trade and Iron and Steel. The constrained model has seven fewer parameters, and its AIC is $704.14$ while its BIC is $860.15$.

Now, we present the table for final model comparison. In terms of the explanatory power regarding $log\left({\mathtt{sales}}_i\right)$, industry dummies have the largest effect, so we adopt a model with only sector dummies (‘Distinct Sector Dummies Only’) as the baseline for comparison. Then, by incorporating continuous explanatory variables $log\left({\mathtt{employees}}_i\right)$ and $log\left({\mathtt{assets}}_i\right)$, we consider the log-log normal model with distinct sector dummies (‘Log-Log Normal/w DSDs’), log-log skew-normal model with distinct sector dummies (‘Log-Log Skew-Normal/w DSDs’), log-log skew-t model with distinct sector dummies (‘Log-Log Skew-t/w DSDs’), and finally the log-log skew-t model with partially grouped sector dummies (‘Log-Log Skew-t/w PGSDs’). The results are summarized in Table 6, where ‘dim’ stands for the number of free parameters.

Table 6. Final model comparison by AIC and BIC.

	Dim	AIC	BIC
Distinct Sector Dummies Only	34	4013.01	4184.12
Log-Log Normal/w DSDs	36	840.75	1021.93
Log-Log Skew-Normal/w DSDs	37	820.13	1006.33
Log-Log Skew-t/w DSDs	38	701.23	892.47
Log-Log Skew-t/w PGSDs	31	704.14	860.15

The dummy variable has a large effect, but without the number of employees and total assets, the explanatory power of the model is very poor. Improvement by refining the error distribution is incremental. As to whether dummies should be grouped, the AIC and BIC lead to different conclusions. The AIC is a criterion based on the predictability of new data from the same probability structure, while the BIC is a selection criterion where one strongly believes that the currently assumed model family contains the true model. Users can choose according to the purpose of the analysis.

It is possible to proceed further with the annexation of industry dummies in this analysis, but it would be better to do so as a separate study based on a more systematic methodology. This point is also noted in Section 6.

6. Conclusions and Discussion

Based on the financial data for almost all companies listed on the TSE Prime market in FY2021, we gradually refined a model that explains sales by the number of employees and assets from the standpoint of exploratory data analysis. Starting from a Cobb–Douglas-type functional form linearized by a log transformation, the assumption of a skew-t distribution in the error structure and the introduction of industry dummies are useful not only in searching for a good-fitting model, but also in ensuring the accuracy of important parameters such as the labor share. The introduction of industry dummies, which is a frequently used method in practice, not only helps to improve the accuracy of the model, but also allows for interpretation in light of the socioeconomic situation at the time of the analysis.

There are a couple of possible directions to extend this analysis. One is to look at the results of the cross-section analysis over time to see how stable the estimated results are in each year. However, given the possible turnover in the group of firms analyzed, it is unclear how effective the introduction of a time-series model would be. Although frameworks and algorithms have been proposed for time series analysis based on skew-distributions, their implementation has been difficult, and no significant applicability has emerged. Rather, instead of relying a priori on industry classification, it may be interesting to search for a new clustering by TFP, in descending order of high sales potential. It could also be aided by some form of unsupervised learning, although it could be formulated as some sparse constraints on the firm-wise intercept terms.