Applications on Topological Indices of Zero-Divisor Graph Associated with Commutative Rings

Abstract

A topological index is a numeric quantity associated with a chemical structure that attempts to link the chemical structure to various physicochemical properties, chemical reactivity, or biological activity. Let $\mathcal{R}$ be a commutative ring with identity, and $Z^{*}(\mathcal{R})$ is the set of all non-zero zero divisors of $\mathcal{R}$. Then, $\Gamma (\mathcal{R})$ is said to be a zero-divisor graph if and only if $a·b=0$, where $a,b\in V(\Gamma (\mathcal{R}))=Z^{*}(\mathcal{R})$ and $(a,b)\in E(\Gamma (\mathcal{R}))$. We define $a\sim b$ if $a·b=0$ or $a=b$. Then, ∼ is always reflexive and symmetric, but ∼ is usually not transitive. Then, $\Gamma (\mathcal{R})$ is a symmetric structure measured by the ∼ in commutative rings. Here, we will draw the zero-divisor graph from commutative rings and discuss topological indices for a zero-divisor graph by vertex eccentricity. In this paper, we will compute the total eccentricity index, eccentric connectivity index, connective eccentric index, eccentricity based on the first and second Zagreb indices, Ediz eccentric connectivity index, and augmented eccentric connectivity index for the zero-divisor graph associated with commutative rings. These will help us understand the characteristics of various symmetric physical structures of finite commutative rings.

1. Introduction

Chemical graph theory is an area of mathematics that deals with the non-trivial applications of molecular problems. Chemical graph theory is an interdisciplinary science that studies molecular structures using graph theory and attempts to identify structural features involved in structure–property activity relationships using tools from graph theory, set theory, and statistics [1,2,3]. The topological characterization of chemical structures with the desired properties can be used to classify molecules and model unknown structures. In recent decades, much research has been conducted in this field. The topological index is a numerical value associated with chemical structures that purport to link chemical structures to various physicochemical properties, chemical reactivity, or biological activity. Topological indices are based on transforming a molecular graph into a number that describes the topology of the molecular graph [4,5,6,7]. Molecular modeling investigates the relationship between a chemical compound’s structure, properties, and activity. Molecular graphs are frequently used to represent molecules and molecular compounds. A chemical graph is a model for describing the properties of a chemical compound. A molecular graph is a simple graph with vertices representing atoms and edges representing bonds. It can be represented by a drawing, a polynomial, a series of numbers, a matrix, or a derived number known as a topological index, which was first introduced by Wiener [8] in 1947.

2. Definitions and Notations

A non-empty set $\mathcal{R}$ is said to be a ring $(\mathcal{R},+,·)$ if $(\mathcal{R},+)$ is an abelian group, and $(\mathcal{R},·)$ is a semi group and satisfies two distributive laws. A ring $\mathcal{R}$ is a commutative ring if $a·b=b·a;\forall a,b\in \mathcal{R}$. An element $a\ne 0$ of a commutative ring $\mathcal{R}$ is said to be zero-divisor if there exists an element $b\ne 0$ in $\mathcal{R}$ such that $a·b=0$. The zero-divisor graph $G(\mathcal{R})$ was first introduced in 1988 by Beck [9] where he considered the set of vertices as zero divisors including zero, with an edge set defined by $E=\{a·b=0;\forall a,b\in Z(\mathcal{R})\}$. Later, in 1999, Anderson and Livingston [10] continued their investigation of zero-divisor graphs, but this time they only examined non-zero zero divisors and constructed the zero-divisor graph as a simple graph with all non-zero zero divisors as vertices and an edge set defined by $E=\{a·b=0;\forall a,b\in Z^{*}(\mathcal{R})\}$, denoted by $\Gamma (\mathcal{R})$.

Let $\mathcal{R}$ be a commutative ring with identity, and $Z^{*}(\mathcal{R})$ is the set of all non-zero zero divisors of $\mathcal{R}$. Then, $\Gamma (\mathcal{R})$ is said to be a zero-divisor graph if and only if $a·b=0$ where $a,b\in V(\Gamma (\mathcal{R}))=Z^{*}(\mathcal{R})$ and $(a,b)\in E(\Gamma (\mathcal{R}))$.

In a graph $\Gamma (\mathcal{R})$, distance $d(a,b)$ is the number of edges in the shortest path between a vertex a and b. Eccentricity $e(a)$ is considered to be the maximum distance from a vertex to all other vertices, and degree $d(a)$ is the number of edges adjacent to a vertex a and the minimum vertex degree in a graph $\Gamma (\mathcal{R})$ is denoted by $\delta (\Gamma (\mathcal{R}))$, and the maximum vertex degree is denoted by $\Delta (\Gamma (\mathcal{R}))$. Furthermore, the degree sequence $D_V$ is a monotonic, non-increasing sequence of the vertex degrees of the graph vertices.

Farooq, and Malik [11] introduced the total eccentricity index, which is defined as

$$T\xi (\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}e(a).$$

The eccentric connectivity index was introduced by Sharma et al. [4] which is defined as

$$\xi C(\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}d(a)e(a).$$

The connective eccentric index was introduced by Gupta, Singh, and Madan [6] which is defined as

$$C\xi (\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}\frac{d(a)}{e(a)}.$$

The eccentricity-based Zagreb indices were introduced by Ghorbani, and Hosseinzadeh [12] which are defined as

$$\xi M_1(\Gamma (\mathcal{R}))=\sum _{ab\in E(\Gamma (\mathcal{R}))}[e(a)+e(b)],$$

$$\xi M_2(\Gamma (\mathcal{R}))=\sum _{ab\in V(\Gamma (\mathcal{R}))}[e(a)\times e(b)]$$

and

$$\xi M_1^{*}(\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}e{(a)}^2.$$

The Ediz eccentric connectivity index was introduced by Ediz [5] which is defined as

$$E\xi C(\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}\frac{S(a)}{e(a)}$$

where $S(a)={\sum }_{b\in N(a)}d(b).$

The augmented eccentric connectivity index was introduced by Gupta, Singh, and Madan [6] which is defined as

$$A\xi C(\Gamma (\mathcal{R}))=\sum _{a\in V(\Gamma (\mathcal{R}))}\frac{M(a)}{e(a)}$$

where $M(a)={\prod }_{b\in N(a)}d(b)$.

3. Results

Let $\mathcal{R}$ be a ring and $\mathcal{I}$ be the ideal of $\mathcal{R}$, then the set of all cosets $\mathcal{R}/\mathcal{I}=\{\mathcal{I}+a;a\in \mathcal{R}/\mathcal{I}\}$ forms a ring known as a factor ring. Let ${\mathbb{Z}}_n\left[x\right]=\{a_n{x}^n+\cdots +a_{1}x+a_0|a_i\in {\mathbb{Z}}_n\}$ be a polynomial of a commutative ring and ${\mathbb{Z}}_n\left[x\right]/\langle x^2\rangle$ be the factor ring. Here, we consider the finite commutative rings ${\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle$ and ${\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle$ to investigate some topological indices such as total eccentricity index, eccentric connectivity index, connective eccentric index, eccentricity based on first and second Zagreb indices, Ediz eccentric connectivity index and augmented eccentric connectivity index of zero-divisor graph for the commutative rings.

For $\mathcal{R}={\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle$ with any prime $q\ge 3$, then $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with $(q^3-1)$ zero divisors of $({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )-\{0\}$ considered to be vertices and $\frac{1}{2}(2q^5-2q^4-q^3-q^2+2)$ edges.

Then,

$$\begin{array}{c}V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\{q,2q,\dots ,(q-1)q,x,2x,3x,\dots ,(q^2-1)x,x+q,x+2q,\dots ,x+(q-1)q,\hfill \\ 2x+q,2x+2q,\dots ,2x+(q-1)q,\dots ,(q^2-1)x+q,(q^2-1)x+2q,\dots ,(q^2-1)x+(q-1)q\}\hfill \\ \Rightarrow V|\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/x^2)|=(q^3-1)\hfill \end{array}$$

Now, the vertex set has been divided by

$$\begin{array}{c}A=\{lqx|l=1,2,\dots (q-1)\&q\nmid l\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}\left|A\right|=(q-1)\hfill \\ B=\{lq,kx,lqx+lq|l=1,2,\dots (q-1),k=1,2,\dots (q^2-1)\&q\nmid k\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}\left|B\right|=2q(q-1)\hfill \\ C=\{kx+lq|l=1,2,\dots (q-1),k=1,2,\dots (q^2-1)\&q\nmid l,k\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}\left|C\right|=\frac{(q-1)}{2}[2q(q-1)]\hfill \end{array}$$

Additionally, $B(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))$ and $C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))$ are subdivided by

$$\begin{array}{c}{B}_1=\{kx|k=1,2,\dots (q^2-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|B_1|=q(q-1)\hfill \\ B_2=\{lq,lqx+lq|l=1,2,\dots (q-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|B_2|=q(q-1)\hfill \\ C_1=\{kx+q,kx+q(q-1)|k=1,2,\dots (q^2-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|C_1|=2q(q-1)\hfill \\ C_2=\{kx+2q,kx+q(q-2)|k=1,2,\dots (q^2-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|C_2|=2q(q-1)\hfill \\ ⋮\hfill \\ C_{(q-1)/2}=\{kx+((q-1)/2)q,kx+q(q+1)/2|k=1,2,\dots (q^2-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|C_{(q-1)/2}|=2q(q-1)\hfill \end{array}$$

It is clear to see that if $l_{i}qx,l_{j}qx\in A\Rightarrow (l_{i}qx)(l_{j}qx)=l_i{l}_j{q}^2{x}^2\equiv 0\mathrm{mod}{x}^2$, then every vertex is adjacent to each other in A, if $l_{i}qx,\in A,l_{j}q,k_{j}x,l_{j}qx+l_{j}q\in B\Rightarrow l_i{l}_j{q}^{2}x\equiv 0\mathrm{mod}{q}^2,l_i{k}_{j}q{x}^2\equiv 0\mathrm{mod}{x}^2,l_i{l}_j{q}^2{x}^2+l_i{l}_j{q}^{2}x\equiv 0\mathrm{mod}{q}^2$, then every vertex in A is adjacent to every vertex in B and if $l_{i}qx,\in A,k_{j}x+l_{j}q\in C\Rightarrow (l_{i}qx)(k_{j}x+l_{j}q)=l_i{k}_{j}q{x}^2+l_i{l}_j{q}^{2}x\equiv 0\mathrm{mod}{x}^2\mathrm{or}\mathrm{mod}{q}^2$, then every vertex in A is adjacent to every vertex in C.

In addition, if $k_{i}x,k_{j}x\in B_1\Rightarrow (k_{i}x)(k_{j}x)=k_i{k}_j{x}^2\equiv 0\mathrm{mod}{x}^2$, then every vertex is adjacent to each other in $B_1$. Similarly, it holds for $B_2$. However, $k_{i}x\in B_1,l_{j}q\in B_2\Rightarrow (k_{i}x)(l_{j}q)=k_i{l}_{j}qx\not\equiv 0\mathrm{mod}{x}^2$, then no vertex in $B_1$ is adjacent to vertex in $B_2$.

Additionally, if $k_{i}x+q,k_{j}x+q(q-1)\in C_1\Rightarrow (k_{i}x+q)(k_{j}x+q(q-1))=k_i{k}_j{x}^2+(k_1+k_j)q^{2}x+q^2(q-1)\equiv 0\mathrm{mod}{x}^2\mathrm{or}\mathrm{mod}{q}^2$ then $k_{i}x+q$ is adjacent to $k_{j}x+q(q1)$ in $C_1$ but no two $k_{i}x+q$ or $k_{j}x+q(q1)$ has zero product by modulo $x^2$ or $q^2$ in $C_1$. Similarly, it holds for $C_2,C_3,\dots ,C_{(q-1)/2}$.

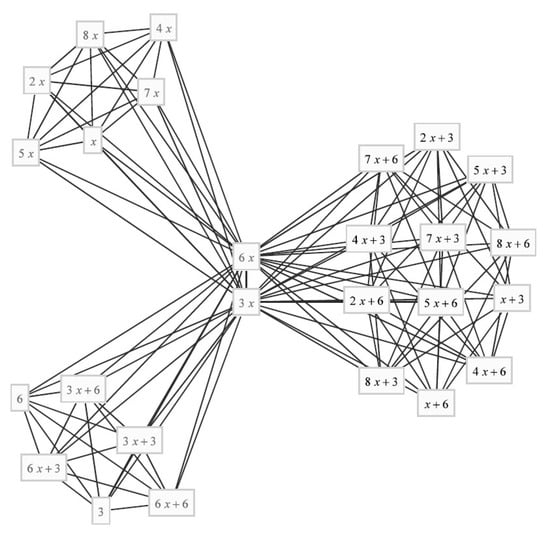
For example, $q=3$ then we have a graph $\Gamma ({\mathbb{Z}}_9\left[x\right]/\langle x^2\rangle )$ in Figure 1.

The vertex set $\Gamma ({\mathbb{Z}}_9\left[x\right]/\langle x^2\rangle )$ has been divided by

$$\begin{array}{c}A=\{3x,6x\}\hfill \\ B_1=\{x,2x,4x,5x,7x,8x\}\hfill \\ B_2=\{3,6,3x+3,3x+6,6x+3,6x+6\}\hfill \\ C_1=\{2x+3,5x+3,8x+3,x+6,4x+6,7x+6\}\hfill \\ C_2=\{x+3,4x+3,7x+3,2x+6,5x+6,8x+6\}\hfill \end{array}$$

Lemma 1.

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $q\ge 3$. Then,

$$\begin{array}{c}{D}_V=\{\underset{(q-1)times}{\underbrace{(q^3-2)}},\underset{2q(q-1)times}{\underbrace{(q^2-2)}},\underset{\frac{(q-1)}{2}\left[2q(q-1)\right]times}{\underbrace{(q^2-1)}}\}\hfill \\ {\xi }_V=\{\underset{(q-1)times}{\underbrace{1}},\underset{2q(q-1)times}{\underbrace{2}},\underset{\frac{(q-1)}{2}\left[2q(q-1)\right]times}{\underbrace{2}}\}\hfill \end{array}$$

where $D_V$ and ${\xi }_V$ are degree sequences and their eccentricity sequences of $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$.

Theorem 1.

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $q\ge 3$. Then,

$$\begin{array}{c}T\xi (\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=2q^3-q-1\\ \xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=2q^5+q^4-5q^3-4q^2+4q+2\\ C\xi (\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\frac{1}{2}(q^5+2q^4-4q^3-2q^2-q+4)\end{array}$$

Proof. 

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with $(q^3-1)$ vertices and $\frac{1}{2}(2q^5-2q^4-q^3-q^2+2)$ edges. Then,

$$\begin{array}{c}A=\{lqx|l=1,2,\dots (q-1)\&q\nmid l\}\hfill \\ \hspace{1em}\Rightarrow \left|A\right|=(q-1)\hfill \\ B=\{lq,kx,lqx+lq|l=1,2,\dots (q-1),k=1,2,\dots (q^2-1)\&q\nmid k\}\hfill \\ \hspace{1em}\Rightarrow \left|B\right|=2q(q-1)\hfill \\ C=\{kx+lq|l=1,2,\dots (q-1),k=1,2,\dots (q^2-1)\&q\nmid l,k\}\hfill \\ \hspace{1em}\Rightarrow \left|C\right|=\frac{(q-1)}{2}\left[2q(q-1)\right]\hfill \end{array}$$

By Lemma 1, we have

It is clear that $a\in A$ is adjacent to all divisors of ${\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle$, then $A=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^3-2)\&e(a)=1\}$ and $\left|A\right|=(q-1)$.

However, $a\in B$ is adjacent only to divisors in A & B, then $B=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-2)\&e(a)=2\}$ and $\left|B\right|=2[q(q-1)]$.

Additionally, $a\in C$ is adjacent to divisors in A and & C but no two $k_{i}x+q$ or $k_{j}x+q(q1)$ has zero product by modulo $x^2$ or $q^2$ in C. $C=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-1)\&e(a)=2\}$ and $\left|C\right|=\frac{(q-1)}{2}\left[2q(q-1)\right]$.

$$\begin{array}{c}T\xi (\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}e(a)\hfill \\ =(q-1)\left[1\right]+2q(q-1)\left[2\right]+\frac{(q-1)}{2}\left[2q(q-1)\right]\left[2\right]\hfill \\ =2q^3-q-1\hfill \end{array}$$

$$\begin{array}{c}\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}d(a)e(a)\hfill \\ =(q-1)[(q^3-2)\times 1]+2q(q-1)[(q^2-2)\times 2]+\frac{(q-1)}{2}[2q(q-1)][(q^2-1)\times 2]\hfill \\ =2q^5+q^4-5q^3-4q^2+4q+2\hfill \end{array}$$

$$\begin{array}{c}C\xi (\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}\frac{d(a)}{e(a)}\hfill \\ =(q-1)\left[\frac{(q^3-2)}{2}\right]+2q(q-1)\left[\frac{(q^2-2)}{2}\right]+\frac{(q-1)}{2}[2q(q-1)]\left[\frac{(q^2-1)}{2}\right]\hfill \\ =\frac{1}{2}(q^5+2q^4-4q^3-2q^2-q+4)\hfill \end{array}$$

□

Theorem 2.

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $q\ge 3$. Then,

$$\begin{array}{c}\xi M_1(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=2q^5+q^4-5q^3-4q^2+4q+2\\ \xi M_1^{*}(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=4q^3-3q-1\end{array}$$

and

$$\begin{array}{c}\xi M_2(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\frac{1}{2}(4q^5-8q^3-7q^2+9q+2)\end{array}$$

Proof. 

By Lemma 1, we have

$A=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^3-2)\&e(a)=1\}$

and $\left|A\right|=(q-1)$

$A=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-2)\&e(a)=2\}$

and $\left|B\right|=2[q(q-1)]$

$A=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-1)\&e(a)=2\}$

and $\left|C\right|=\frac{(q-1)}{2}[2q(q-1)]$

$E_1=\{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))|[d(a),d(b)]=[(q^3-2),(q^3-2)]\&[e(a),e(b)]=[1,1]\}$

and $|E_1|=\frac{1}{2}[q^2-3q+2]$

$E_2=\{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))|[d(a),d(b)]=[(q^3-2),(q^2-2)]\&[e(a),e(b)]=[1,2]\}$

and $|E_2{|=2q(q-1)}^2$

$E_3=\{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))|[d(a),d(b)]=[(q^3-2),(q^2-1)]\&[e(a),e(b)]=[1,2]\}$

and $|E_3{|=q(q-1)}^3$

$E_4=\{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))|[d(a),d(b)]=[(q^2-2),(q^2-2)]\&[e(a),e(b)]=[2,2]\}$

and $|E_4|=(q^4-2q^3+q)$

$E_5=\{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))|[d(a),d(b)]=[(q^2-1),(q^2-1)]\&[e(a),e(b)]=[2,2]\}$

and $|E_5|=\frac{q-1}{2}[{(q(q-1))}^2]$

$$\begin{array}{c}\xi M_1(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/x^2))}[e(a)+e(b)]\hfill \\ =\frac{1}{2}[q^2-3q+2][1+1]+2q{(q-1)}^2[1+2]+q{(q-1)}^3[1+2]\hfill \\ +(q^4-2q^3+q)[2+2]+\frac{(q-1)}{2}[{(q(q-1))}^3][2+2]\hfill \\ =2q^5+q^4-5q^3-4q^2+4q+2\hfill \end{array}$$

$$\begin{array}{c}\xi M_1^{*}(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/x^2))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )))}e{(a)}^2\hfill \\ =(q-1)[1^2]+2q(q-1)[2^2]+\frac{(q-1)}{2}[2q(q-1)][2^2]\hfill \\ =4q^3-3q-1\hfill \end{array}$$

$$\begin{array}{c}\xi M_2(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{ab\in E(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/x^2))}[e(a)(b)]\hfill \\ =\frac{1}{2}[q^2-3q+2][1\times 1]+2q{(q-1)}^2[1\times 2]+q{(q-1)}^3[1\times 2]\hfill \\ +(q^4-2q^3+q)[2\times 2]+\frac{(q-1)}{2}[{(q(q-1))}^3][2\times 2]\hfill \\ =\frac{1}{2}(4q^5-8q^3-7q^2+9q+2)\hfill \end{array}$$

□

Theorem 3.

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be zero-divisor graph with any prime $q\ge 3$. Then,

$$\begin{array}{c}\hfill \begin{array}{c}E\xi C({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )=\frac{1}{2}(2q^7-3q^5-13q^4+13q^3+9q^2-8)\\ A\xi C({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )=\begin{array}{cc}(q-1){(q^3-2)}^{(q-2)}[{(q^2-2)}^{2q(q-1)}{(q^2-1)}^{{(q(q-1))}^2}& \\ +\frac{q(q^3-2)}{2}\{2{(q^2-2)}^{q(q-1)-1}+q(q-1){(q^2-1)}^{q(q-1)}\}]\end{array}\end{array}\end{array}$$

Proof. 

By Lemma 1, we have

$A=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^3-2)\&e(a)=1\}$

and $\left|A\right|=(q-1)$

$B=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-2)\&e(a)=2\}$

and $\left|B\right|=2[q(q-1)]$

$C=\{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\ni d(a)=(q^2-1)\&e(a)=2\}$

and $\left|C\right|=\frac{(q-1)}{2}[2q(q-1)]$

$$E\xi C({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}\frac{S(a)}{e(a)}$$

where $S(a)={\sum }_{b\in N(a)}d(b)$

$$\begin{array}{c}E\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}\frac{S(a)}{e(a)}\hfill \\ =(q-1)\left[\frac{(q^5+q^4-4q^3-2q^2+q+4)}{1}\right]+2q(q-1)\left[\frac{(2q^4-2q^3-3q^2+4)}{2}\right]\hfill \\ +\frac{(q-1)}{2}\left[2q(q-1)\right]\left[\frac{(2q^4-2q^3-q^2-q+2)}{2}\right]\hfill \\ =\frac{1}{3}(2q^7-3q^5-13q^4+13q^3+9q^2-8)\hfill \end{array}$$

$$A\xi C({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}\frac{M(a)}{e(a)}$$

where $M(a)={\prod }_{b\in N(a)}d(b)$

$$\begin{array}{c}A\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))}\frac{M(a)}{e(a)}\hfill \\ =(q-1)\left[\frac{{(q^2-2)}^{2q(q-1)}{(q^2-1)}^{q{(q-2)}^2}{(q^3-2)}^{(q-2)}}{1}\right]\hfill \\ +2q(q-1)\left[\frac{{(q^2-2)}^{q(q-1)-1}{(q^3-2)}^{(q-1)}}{2}\right]\hfill \\ +\frac{(q-1)}{2}\left[2q(q-1)\right]\left[\frac{{(q^2-1)}^{q(q-1)}{(q^3-2)}^{(q-1)}}{2}\right]\hfill \\ =\begin{array}{cc}(q-1){(q^3-2)}^{(q-2)}[{(q^2-2)}^{2q(q-1)}{(q^2-1)}^{{(q(q-1))}^2}& \\ +\frac{q(q^3-2)}{2}\{2{(q^2-2)}^{q(q-1)-1}+q(q-1){(q^2-1)}^{q(q-1)}\}]\end{array}\hfill \end{array}$$

□

For $\mathcal{R}={\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle$ with any prime $2<p<q$, then $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with $(p{q}^2+p^{2}q-pq-1)$ zero divisors of $({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )-\{0\}$ considered as a vertices and $\frac{1}{2}[7p^2{q}^2-6p{q}^2-6p^{2}q+3pq+2]$ edges.

Then

$$\begin{array}{c}V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\hfill \\ \{p,2p,\dots ,(q-1)p,q,2q,\dots ,(p-1)q,x,2x,\dots ,(pq-1)x,\hfill \\ x+p,x+2p,\dots ,x+(q-1)p,x+q,x+2q,\dots ,x+(p-1)q,\hfill \\ 2x+p,2x+2p,\dots ,2x+(q-1)p,2x+q,2x+2q,\dots ,2x+(p-1)q,\dots ,\hfill \\ (q-1)px+p,(q-1)px+2p,\dots ,(q-1)px+(q-1)p,\hfill \\ (p-1)qx+q,(p-1)qx+2q,\dots ,(p-1)qx+(p-1)q\}\hfill \\ \Rightarrow V|\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )|=p{q}^2+p^{2}q-pq-1\hfill \end{array}$$

By using these vertices, there exists an edge defined between a and b by $E=\{ab=0;\forall a,b\in \mathcal{R}\}$ and $E|\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )|=\frac{1}{2}[7p^2{q}^2-6p{q}^2-6p^{2}q+3pq+2]$.

$$\begin{array}{c}{V}_1=\{jpx|j=1,2,\dots (p-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_1|=(p-1)\hfill \\ V_2=\{kx+mp|k=1,2,\dots (pq-1),m=1,2,\dots (q-1)\&p\nmid k\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_2|=(p-1)q(q-1)\hfill \\ V_3=\{lpx+mp|l=0,1,\dots (q-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_3|=q(q-1)\hfill \\ V_4=\{kx+nq|k=1,2,\dots (pq-1),n=1,2,\dots (p-1)\&q\nmid k\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_4|=p(p-1)(q-1)\hfill \\ V_5=\{lpx+nq|l=0,1,\dots (q-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_5|=p(p-1)\hfill \\ V_6=\{mpx|m=1,2,\dots (q-1)\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_6|=(p-1)q(q-1)\hfill \\ V_7=\{kx|k=1,2,\dots (pq-1)\&p,q\nmid k\}\hfill \\ \hspace{1em}\Rightarrow \hspace{0.33em}|V_7|=p(p-1)(q-1)\hfill \end{array}$$

It is clear to see that if $a,b\in V_1\Rightarrow ab\equiv 0\mathrm{mod}{x}^2$, then every vertex is adjacent to each other in $V_1$. Similarly, it holds $V_6$ and $V_7$. In addition, if $a\in V_1,b\in V_2\Rightarrow ab\equiv 0\mathrm{mod}{x}^2$ or $ab\equiv 0\mathrm{mod}pq$ then every vertex in $V_1$ is adjacent to every vertex in $V_2$. Similarly, every vertex in $V_1$ is adjacent to every vertex in $V_3\cup V_6\cup V_7$ and every vertex in $V_6$ is adjacent to every vertex in $V_4\cup V_5\cup V_7$. Additionally, every vertex in $V_2$ is adjacent to every vertex in $V_5$.

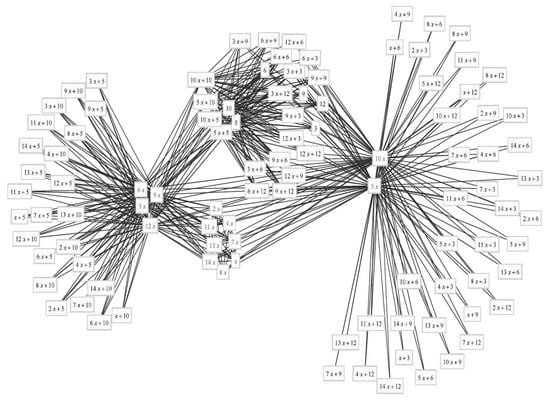
For example, if $p=3$ and $q=5$, then we have a graph $\Gamma ({\mathbb{Z}}_{15}\left[x\right]/\langle x^2\rangle )$ in Figure 2.

The vertex set $\Gamma ({\mathbb{Z}}_{15}\left[x\right]/\langle x^2\rangle )$ has been divided by

$$\begin{array}{c}{V}_1=\{5x,10x\}\hfill \\ V_2=\{x+3,x+6,x+9,x+12,\dots ,14x+3,14x+6,14x+9,14x+12\}\hfill \\ V_3=\{x+5,x+10,\dots ,14x+5,14x+10\}\hfill \\ V_4=\{3,6,9,12,3x+3,3x+6,3x+9,3x+12,\dots ,12x+3,12x+6,12x+9,12x+12\}\hfill \\ V_5=\{5,10,5x+5,5x+10,10x+5,10x+10\}\hfill \\ V_6=\{3x,6x,9x,12x\}\hfill \\ V_7=\{x,2x,4x,7x,8x,11x,13x,14x\}\hfill \end{array}$$

Lemma 2.

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $2<p<q$. Then,

$$\begin{array}{c}{D}_V=\{\underset{(p-1)times}{\underbrace{(p{q}^2-2)}};\underset{(p-1)q(q-1)times}{\underbrace{(p-1)}};\underset{q(q-1)times}{\underbrace{(p^2-1}};\underset{p(p-1)(q-1)times}{\underbrace{(q-1)}};\underset{p(p-1)times}{\underbrace{(q^2-1)}};\underset{(q-1)times}{\underbrace{(p^{2}q-2)}};\underset{(p-1)(q-1)times}{\underbrace{(pq-2)}}\}\hfill \\ {\xi }_V=\{\underset{(p-1)times}{\underbrace{2}};\underset{(p-1)q(q-1)times}{\underbrace{3}};\underset{q(q-1)times}{\underbrace{3}};\underset{p(p-1)(q-1)times}{\underbrace{3}};\underset{p(p-1)times}{\underbrace{3}};\underset{(q-1)times}{\underbrace{2}};\underset{(p-1)(q-1)times}{\underbrace{2}}\}\hfill \end{array}$$

where $D_V$ and ${\xi }_V$ are degree and eccentricity sequences of $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$.

Theorem 4.

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $2<p<q$. Then

$$\begin{array}{c}T\xi (\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=3p{q}^2+3p^{2}q-4pq-2\\ \xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=18p^2{q}^2-16p{q}^2-16p^{2}q+10pq+4\\ C\xi (\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\frac{1}{2}(2q^5-q^4-2q^3-q^2-2q+4)\end{array}$$

Proof. 

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be zero-divisor graph with $(p{q}^2+p^{2}q-pq-1)$ zero divisors of $({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )-\{0\}$ vertices and $\frac{1}{2}[7p^2{q}^2-6p{q}^2-6p^{2}q+3pq+2]$ edges.

By Lemma 2, we have

$$\begin{array}{c}T\xi (\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}e(a)\hfill \\ =(p-1)(2)+(p-1)q(q-1)(3)+q(q-1)(3)+p(p-1)(q-1)(3)+p(p-1)(3)\hfill \\ +(q-1)(2)+(p-1)(q-1)(2)\hfill \\ =3p{q}^2+3p^{2}q-4pq-2\hfill \end{array}$$

$$\begin{array}{c}\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}d(a)e(a)\hfill \\ =(p-1)[(p{q}^2-2)\times 2]+(p-1)q(q-1)[(p^{2}q-2)\times 3]+q(q-1)[(p-1)(q-1)\times 3]\hfill \\ +p(p-1)(q-1)[(p^2-1)\times 3]+p(p-1)[(q^2-1)\times 3]+(q-1)[(p-1)\times 2]\hfill \\ +(p-1)(q-1)[(q-1)\times 2]\hfill \\ =18p^2{q}^2-16p{q}^2-16p^{2}q+10pq+4\hfill \end{array}$$

$$\begin{array}{c}C\xi (\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\frac{d(a)}{e(a)}\hfill \\ =(p-1)\left[\frac{(p{q}^2-2)}{3}\right]+(p-1)q(q-1)\left[\frac{(p^{2}q-2)}{3}\right]+q(q-1)\left[\frac{(p-1)(q-1)}{3}\right]\hfill \\ +p(p-1)(q-1)\left[\frac{(p^2-1)}{3}\right]+p(p-1)\left[\frac{(q^2-1)}{3}\right]+(q-1)\left[\frac{(p-1)}{2}\right]\hfill \\ +(p-1)(q-1)\left[\frac{(q-1)}{2}\right]\hfill \\ =\frac{1}{2}(2q^5-q^4-2q^3-q^2-2q+4)\hfill \end{array}$$

□

Theorem 5.

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $2<p<q$. Then,

$$\begin{array}{c}\hfill \begin{array}{c}\xi M_1(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=18p^2{q}^2-16p{q}^2-16p^{2}q+10pq+4\\ \xi M_1^{*}(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=9p{q}^2+9p^{2}q-14pq-4\end{array}\end{array}$$

and

$$\begin{array}{c}\xi M_2(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=23p^2{q}^2-21p{q}^2-21p^{2}q+15pq+4\end{array}$$

Proof. 

By Lemma 2, we have

$$\begin{array}{c}\xi M_1(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{ab\in E(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}[e(a)+e(b)]\hfill \\ =\frac{1}{2}(p^2-3p+2)(2+2)+{(p-1)}^{2}q(q-1)(2+3)+(p-1)q(q-1)(2+3)\hfill \\ +(p-1)(q-1)(2+2)+{(p-1)}^2(q-1)(2+2)+p(p-1)q(q-1)(3+3)\hfill \\ +p(p-1)(q-1)(2+3)+(p-1){(q-1)}^2(2+2)+\frac{1}{2}(q^2-3q+2)(2+2)\hfill \\ +\frac{1}{2}(p^2{q}^2+{(p+q)}^2-2pq(p+q)-(p+q)+pq)(2+2)+{(q-1)}^{2}p(p-1)(3+2)\hfill \\ =18p^2{q}^2-16p{q}^2-16p^{2}q+10pq+4\hfill \end{array}$$

$$\begin{array}{c}\xi M_1^{*}(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(G\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )))}e{(a)}^2\hfill \\ =(p-1)(2^2)+(p-1)q(q-1)(3^2)+q(q-1)(3^2)+p(p-1)(q-1)(3^2)+p(p-1)(3^2)\hfill \\ +(q-1)(2^2)+(p-1)(q-1)(2^2)\hfill \\ =9p{q}^2+9p^{2}q-14pq-4\hfill \end{array}$$

$$\begin{array}{c}\xi M_2(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{ab\in E(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\left[e(a)(b)\right]\hfill \\ =\frac{1}{2}(p^2-3p+2)(2\times 2)+{(p-1)}^{2}q(q-1)(2\times 3)+(p-1)q(q-1)(2\times 3)\hfill \\ +(p-1)(q-1)(2\times 2)+{(p-1)}^2(q-1)(2\times 2)+p(p-1)q(q-1)(3\times 3)\hfill \\ +p(p-1)(q-1)(2\times 3)+(p-1){(q-1)}^2(2\times 2)+\frac{1}{2}(q^2-3q+2)(2\times 2)\hfill \\ +\frac{1}{2}(p^2{q}^2+{(p+q)}^2-2pq(p+q)-(p+q)+pq)(2\times 2)+{(q-1)}^{2}p(p-1)(3\times 2)\hfill \\ =23p^2{q}^2-21p{q}^2-21p^{2}q+15pq+4\hfill \end{array}$$

□

Theorem 6.

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with any prime $2<p<q$. Then,

$$\begin{array}{c}E\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))\hfill \\ =\frac{1}{6}(2p^3{q}^4-2p{q}^4+2p^4{q}^3+5p^3{q}^3-4p{q}^3-57p^2{q}^2\hfill \\ +42p{q}^2-2p^{4}q-4p^{3}q+42p^{2}q-12pq-12)\hfill \end{array}$$

and

$$\begin{array}{c}A\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))\hfill \\ =\frac{1}{3}\{q(q-1){(p{q}^2-2)}^{(p-1)}[(p-1)+{(q^2-1)}^{p(p-1)}]\hfill \\ +p(p-1){(p^{2}q-2)}^{(q-1)}[(q-1)+{(p^2-1)}^{q(q-1)}]\}\hfill \\ +\frac{1}{2}{(p{q}^2-2)}^{(p-2)}{(p^{2}q-2)}^{(q-2)}{(pq-2)}^{(pq-(p+q))}\hfill \\ \{[{(p-1)}^{(p-1)q(q-1)+1}{(p^2-1)}^{q(q-1)}(p^{2}q-2)(pq-2)]\hfill \\ +[{(q-1)}^{p(p-1)(q-1)+1}{(q^2-1)}^{p(p-1)}(pq-2)]+[(p-1)(q-1)(p^{2}q-2)]\}\hfill \end{array}$$

Proof. 

By Lemma 2, we have

$$E\xi C({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\frac{S(a)}{e(a)}$$

where $S(a)={\sum }_{b\in N(a)}d(b)$

$$\begin{array}{c}E\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\frac{S(a)}{e(a)}\hfill \\ =(p-1)\left[\frac{(5p^2{q}^2-5p{q}^2-4p^{2}q+pq+4)}{2}\right]+(p-1)q(q-1)\left[\frac{(p^2{q}^2-p{q}^2-2p+2)}{3}\right]\hfill \\ +q(q-1)\left[\frac{(2p^2{q}^2-2p{q}^2-p^2-p+2)}{3}\right]+p(p-1)(q-1)\left[\frac{(p^2{q}^2-p^{2}q-2q+2)}{3}\right]\hfill \\ +p(p-1)\left[\frac{(2p^2{q}^2-2p^{2}q-q^2-q+2)}{3}\right]+(q-1)\left[\frac{(5p^2{q}^2-4p{q}^2-5p^{2}q+pq+4)}{2}\right]\hfill \\ +(p-1)(q-1)\left[\frac{(3p^2{q}^2-2p{q}^2-2p^{2}q-2pq+4)}{2}\right]\hfill \end{array}$$

$$\begin{array}{c}=\frac{1}{6}(2p^3{q}^4-2p{q}^4+2p^4{q}^3+5p^3{q}^3-4p{q}^3-57p^2{q}^2\hfill \\ +42p{q}^2-2p^{4}q-4p^{3}q+42p^{2}q-12pq-12)\hfill \end{array}$$

$$A\xi C({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\frac{M(a)}{e(a)}$$

where $M(a)={\prod }_{b\in N(a)}d(b)$

$$\begin{array}{c}A\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\sum _{a\in V(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))}\frac{M(a)}{e(a)}\hfill \\ =(p-1)\left[\frac{{(p-1)}^{(p-1)q(q-1)}{(p^2-1)}^{q(q-1)}{(p^{2}q-2)}^{(p-1)(q-1)}{(p{q}^2-2)}^{(p-2)}}{2}\right]\hfill \\ +(p-1)q(q-1)\left[\frac{{(p{q}^2-2)}^{(p-1)}}{3}\right]+q(q-1)\left[\frac{{(p{q}^2-2)}^{(p-1)}{(q^2-1)}^{p(p-1)}}{3}\right]\hfill \\ +p(p-1)(q-1)\left[\frac{{(p^{2}q-2)}^{(q-1)}}{3}\right]+p(p-1)\left[\frac{{(p^{2}q-2)}^{(q-1)}{(p^2-1)}^{q(q-1)}}{3}\right]\hfill \\ +(q-1)\left[\frac{{(p{q}^2-2)}^{(p-1)}{(q-1)}^{p(p-1)(q-1)}{(q^2-1)}^{p(p-1)}{(pq-2)}^{(p-1)(q-1)}{(p^{2}q-2)}^{(q-2)}}{2}\right]\hfill \\ +(p-1)(q-1)\left[\frac{{(p{q}^2-2)}^{(p-1)}{(p^{2}q-2)}^{(q-1)}{(pq-2)}^{(pq-(p+q))}}{2}\right]\hfill \end{array}$$

$$\begin{array}{c}=\frac{1}{3}\{q(q-1){(p{q}^2-2)}^{(p-1)}[(p-1)+{(q^2-1)}^{p(p-1)}]\hfill \\ +p(p-1){(p^{2}q-2)}^{(q-1)}[(q-1)+{(p^2-1)}^{q(q-1)}]\}\hfill \\ +\frac{1}{2}{(p{q}^2-2)}^{(p-2)}{(p^{2}q-2)}^{(q-2)}{(pq-2)}^{(pq-(p+q))}\hfill \\ \{\left[{(p-1)}^{(p-1)q(q-1)+1}{(p^2-1)}^{q(q-1)}(p^{2}q-2)(pq-2)\right]\hfill \\ +\left[{(q-1)}^{p(p-1)(q-1)+1}{(q^2-1)}^{p(p-1)}(pq-2)\right]+\left[(p-1)(q-1)(p^{2}q-2)\right]\}\hfill \end{array}$$

□

4. Discussions and Applications

Algebraic structures were investigated separately because of their strong links to representation theory and number theory, as well as their widespread use in combinatorics [2,3]. As a result of extensive mathematical research in this area, finite rings and fields have received a significant amount of focus for their applications to cryptography and coding theory [13,14,15,16].

Here, we investigated the eccentricity-based indices associated with factor ring ${\mathbb{Z}}_n\left[x\right]/\langle x^2\rangle$ and obtained the zero-divisor graph of the factor rings ${\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle$ and ${\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle$.

Let $\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with prime $q\ge 3$, then $\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))=\xi M_1(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))$ and

$$\begin{array}{ccc}& T\xi (\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))<\xi M_1^{*}(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))<\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))& \\ <& \xi M_2(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))<E\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))<A\xi C(\Gamma ({\mathbb{Z}}_{q^2}\left[x\right]/\langle x^2\rangle ))\end{array}$$

Let $\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle )$ be a zero-divisor graph with prime $2<p<q$, then $\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))=\xi M_1(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))$ and

$$\begin{array}{cc}& T\xi (\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))<\xi M_1^{*}(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))<\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))\\ <& \xi M_2(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))<E\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))<A\xi C(\Gamma ({\mathbb{Z}}_{pq}\left[x\right]/\langle x^2\rangle ))\end{array}$$

These values help understand the characteristics of various symmetric physical structures of finite commutative rings and have received significant focus for their applications to cryptography and coding theory. They may also help design strong symmetric physical structures for robotics and identify computer network issues associated with speed, distance, and time. This research will aid in the understanding the properties of various physical structures such as carbohydrates, silicone structures, polymers, hexagonal chains, and cylindrical fullerenes [17,18,19]. They can also create a productive physical design in mechanics and solve various computer network problems.

5. Conclusions

In this paper, we explored various topological indices and discussed the total eccentricity index, eccentric connectivity index, connective eccentric index, eccentricity based on the first and second Zagreb indices, Ediz eccentric connectivity index, and augmented eccentric connectivity index for the zero-divisor graph associated with commutative rings. Additionally, we showed that the boundaries are related to topological indices for the zero-divisor graph.